A haplotype-aware de novo assembly of related individuals using pedigree sequence graph

Abstract

Motivation

Reconstructing high-quality haplotype-resolved assemblies for related individuals has important applications in Mendelian diseases and population genomics. Through major genomics sequencing efforts such as the Personal Genome Project, the Vertebrate Genome Project (VGP) and the Genome in a Bottle project (GIAB), a variety of sequencing datasets from trios of diploid genomes are becoming available. Current trio assembly approaches are not designed to incorporate long- and short-read data from mother–father–child trios, and therefore require relatively high coverages of costly long-read data to produce high-quality assemblies. Thus, building a trio-aware assembler capable of producing accurate and chromosomal-scale diploid genomes of all individuals in a pedigree, while being cost-effective in terms of sequencing costs, is a pressing need of the genomics community.

Results

We present a novel pedigree sequence graph based approach to diploid assembly using accurate Illumina data and long-read Pacific Biosciences (PacBio) data from all related individuals, thereby generalizing our previous work on single individuals. We demonstrate the effectiveness of our pedigree approach on a simulated trio of pseudo-diploid yeast genomes with different heterozygosity rates, and real data from human chromosome. We show that we require as little as 30× coverage Illumina data and 15× PacBio data from each individual in a trio to generate chromosomal-scale phased assemblies. Additionally, we show that we can detect and phase variants from generated phased assemblies.

Availability and implementation

https://github.com/shilpagarg/WHdenovo.

1 Introduction

The ability to faithfully reconstruct genomes is a crucial step in better understanding evolution and the nature of inherited disease (Tewhey et al., 2011). Advances in a variety of sequencing technologies have created enormous opportunities to yield full assemblies of every chromosome and its homologue (called as haplotypes). The reconstruction of both haplotype sequences of each chromosome from a combination of high-throughput sequencing datasets is known as diploid genome assembly. The main challenges are genome characteristics such as genomic repeats and varied heterozygosity rates; and datasets characteristics such as read length and sequencing errors. One promising approach to diploid genome assembly is incorporating sequencing information from a related set of individuals, particularly from mother–father–child trios, and using the Mendelian information offered by the corresponding pedigree to infer the layout of alleles along homologous sequences.

Some current short-read assemblers (Bankevich et al., 2012; Li, 2015; Simpson and Durbin, 2012) for single-individual assembly produce accurate, but fragmented assembly at repetitive and highly heterozygous regions. Other long-read assemblers (Berlin et al., 2015; Chin et al., 2013; Kolmogorov et al., 2019; Koren et al., 2017; Ruan and Li, 2019) resolve repeats to generate more contiguous sequences. Yet, these require high coverage due to the high error rate in long-read data, which is very costly. Hybrid assemblers utilize both short accurate reads and long reads to generate complete, high-quality haploid assemblies (Antipov et al., 2016; Bashir et al., 2012; Deshpande et al., 2013). However, these methods collapse differences between homologous pairs into a single consensus sequence, without regards for the rich information given by the layout of different alleles along two copies (Simpson and Pop, 2015). In contrast, other assemblers by Chin et al. (2016), Garg et al. (2018) and Weisenfeld et al. (2017) have been developed to generate haplotigs, haplotype-resolved assemblies for single individuals.

Certain assemblers have been developed to employ pedigree information into the process of assembly as well, specifically for the case of mother–father–child trios. For example, trio-sga utilizes NGS data to obtain haplotypes of the child based on parental Illumina data (Malinsky et al., 2016), while TrioCanu uses such Illumina data to partition child long-read data and subsequently assembles the partitioned reads separately (Koren et al., 2018). Yet, these two methods cannot phase variants which are heterozygous in all three individuals in a trio, and by relying solely on parental Illumina data, may not correctly haplotype long reads which cover repetitive genomic regions. Furthermore, TrioCanu is not designed for low coverages of long-read data and to obtain diploid assembly of three individuals in a trio.

Another reference-genome-based approaches for the diploid assembly involve aligning long-read data from all individuals in a pedigree to a reference-genome, then finding the most likely partitioning of reads as determined by the PedMEC problem (Garg et al., 2016). Essentially, the PedMEC (Weighted Minimum Error Correction on Pedigrees) problem finds the partitioning of reads from related individuals that incurs the least cost, which is calculated based on the likelihood of errors occurring at various locations along the reads as well as recombination costs between each site of heterozygosity. This method, however, only concerns bi-allelic variants, and contains reference bias, meaning that unique DNA sequences to every genome may not be detected or phased correctly.

Thus, developing a haplotype-resolved de novo assembly approach for related individuals which is cost-effective, flexible with regard to genomic complexity and heterozygosity rate, and which does not contain reference bias, is a pressing need for the genomics community.

Contributions

Our pedigree-based assembly method (WHdenovo) performs assembly in the space of a pedigree sequence graph, and is generalized to assemble pedigree of genomes (not humans) of varying heterozygosity rate and with multi-allelic variants, thus allowing for the creation of accurate, complete haplotigs.

Our approach builds a pedigree sequence graph using combined Illumina data from all individuals in a pedigree and the differences between haplotypes from these individuals are represented as alleles in bubbles, as shown in Figure 1. Given a pedigree sequence graph containing a series of bubbles, long-read (PacBio) data from each individual are threaded through this graph; in essence, the diploid assemblies are the most probable haplotype paths that the long reads trace through the bubbles in the pedigree sequence graph, and which obey the Mendelian constraints imposed by the pedigree. To solve this pedigree-aware diploid assembly problem over pedigree sequence graph, we propose a novel dynamic programming-based algorithm.

Fig. 1.

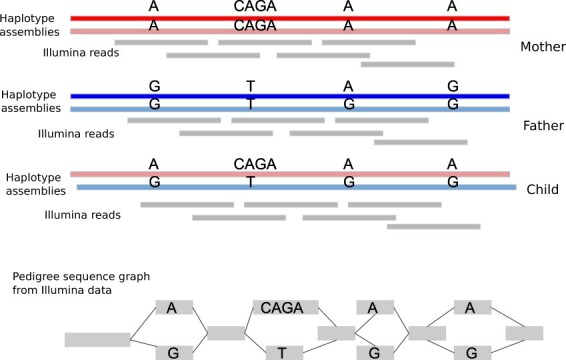
The Illumina data (middle) from the trio of genomes can be represented as a pedigree sequence graph (de Bruijn-based).The bubbles in the graph (bottom) show alleles from individuals, representing SNVs (SNPs) or SVs

Our pedigree-based assembly approach poses several advantages for accurate, continuous assemblies. We require relatively low coverage of costly long-read data and produce diploid assemblies of all individuals in cost-effective manner. We can detect and phase all types of small and large variants. We can also phase variants that are heterozygous in all individuals; for example, SNV1 from Figure 2. Moreover, by incorporating hybrid data from all related individuals, we can effectively phase reads in repetitive genomic regions, and as shown by SV2 in Figure 2, if parental reads span a variant but child reads do not, we can still correctly identify and phase the variant in all three individuals.

Fig. 2.

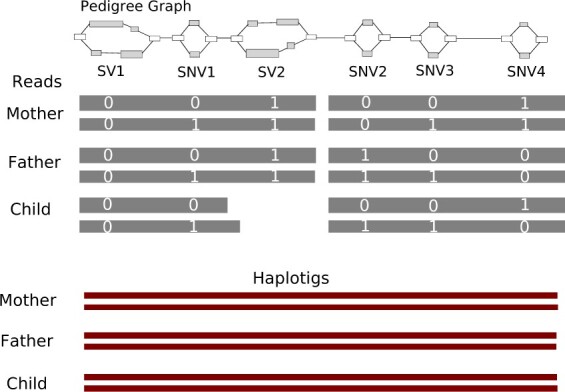
Input: This figure shows the pedigree sequence graph (top) (consisting of four SNVs and two SVs) and the PacBio reads (gray) with respective alleles (white digits). Output: the final haplotigs (crimson) for each individual in a trio. Our method can phase variants, including SNVs and SVs, that are heterozygous (SNV1) in all individuals and any variant covered by at least one read from any individual (SV2 in child), resulting in continuous and complete haplotigs. (Color version of this figure is available at Bioinformatics online.)

To demonstrate the practical effectiveness of our approach, we considered two sets of genomes. First, we haplotype the genomes of a simulated trio of pseudo-diploid yeast, which allows us to comprehensively study assembly at varying read coverage and heterozygosity rates. Then, we use real data to assemble the complete diploid genome of a trio of human chromosome. These results indicate that our pedigree-aware assembly method is adaptable to genomes of varying heterozygosity rates. We demonstrate that our method is cost-effective, requiring only 30× short-read coverage and 15× long-read coverage for every individual in a pedigree to generate near chromosomal-scale assemblies for all individuals. Moreover, at these coverages, we show that our assemblies for both real and simulated data are more accurate and contiguous when compared to those produced by TrioCanu at 45× child long-read coverage. In a final experiment, we also show that we can detect and phase variants.

2 Pedigree-aware phased assembly pipeline

In this section, we present the workflow of our pipeline, which takes as input the raw Illumina and PacBio sequencing data from all related individuals in a pedigree, and outputs final, polished haplotigs. We represent this raw data information in the form of a pedigree sequence graph. Our goal here is to find the walks through this graph that correspond to the true haplotypes of all related individuals. Due to errors of sequencing data and other genomic characteristics such as repeats, there are inevitably multiple paths through this graph that do not correspond to true haplotype paths. Thus, to construct the true haplotype paths, we seek the maximally likely paths based on confidence scores of how the nodes are connected to each other over long distances, which we determine using PacBio reads aligned to the graph.

This pipeline generalizes our previous single-individual approach (Garg et al., 2018) to related individuals to yield the chromosome-scale haplotigs. Figure 3 represents a conceptual workflow of our pedigree pipeline, detailed below.

Fig. 3.

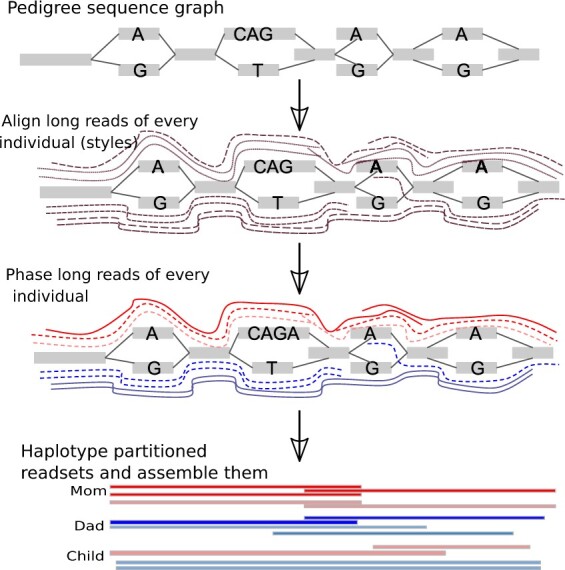
Overview of the pedigree-aware phased assembly pipeline. The steps include generating pedigree sequence graph from Illumina data, then aligning long reads from every individual through alleles of bubbles in the graph, and then finally partitioning these reads for every individual and assembling them separately

2.1 Pedigree sequence graph

We use short, accurate Illumina reads from all related individuals to construct a bi-directed graph known as pedigree sequence graph denoted as G_p, which contains a set of nodes N_p and a set of edges E_p. Conceptually, each node $n_i\in N_p$ represents a genomic sequence or errors from the Illumina data of individuals in a pedigree, and the node $n{\prime }_i$ represents its reverse complement. Every edge $e_{\mathit{ij}}\in E_p$ represents an adjacency between the sequences represented by node $n_i \text{and} n_j$.

Moreover, the pedigree sequence graph G_p contains a set of bubbles L that represents true alleles from individuals (or sequencing errors). The terminology bubble follows from the ultrabubble coined by Paten et al. (2018). Graphically speaking, bubbles are directed and acyclic, biconnected and minimal. We define each bubble l_k to be the set of allele paths with the common start and end nodes. Figure 1 demonstrates the bubbles representing alleles using Illumina data.

2.2 PacBio alignments

Next, we align PacBio long reads from all individuals to produce paths through the pedigree sequence graph G_p. For a given PacBio read, we define a read alignment r_i to be a path through G_p, defined by the oriented nodes $n_1\dots n_k$. Given a set of individuals $\mathcal{I}$, we align the PacBio reads from every individual $i\in \mathcal{I}$ to G_p, resulting in a set of read alignments $R_i=\{r_1,r_2,\dots ,r_j\}$ for every individual. As an intuitive checkpoint, note that as PacBio reads from different individuals trace different paths through nodes and bubbles in G_p, we gain information about not only the correct ordering of nodes to form the genome in question, but also the alleles and phasing present in each individuals.

2.3 Bubble chains

From PacBio alignments, we obtain the ordered bubble chains denoted as C, which represent the layout of heterozygous sites across the genome. On input $\mathcal{R}$, the set of all read alignments R_i for individuals $i\in \mathcal{I}$, we project all partial alignments to bubble space—that is, for every instance where a read traverses a bubble, we replace the corresponding set of nodes by the appropriate bubble ID. We now perform our filtration steps; for every node or bubble from every alignment path in $\mathcal{R}$, denoted as $x\in \mathcal{R}$, we compute the coverage $c_{(x)}$, and if $c_{(x)}<5$, we remove the node or bubble. Next, we calculate the degree of every remaining node x, and if $\text{deg}(x)\ge 3$, we remove all connections containing x. Using the resulting filtered graph, we then perform DFS to find U, an initial set of unambiguous bubble chains termed unitigs. Finally, if there is at least one read connecting two unitigs in U, we can gain information about the ordering between these initial unitigs. We record this ordering information to generate the final ordering of bubbles denoted as C.

2.4 Graph-based phasing on pedigrees

Next, we introduce the Graph version of Weighted Minimum Error Correction on Pedigrees Problem, or gPedMEC, as our central phasing algorithm. gPedMEC relates to the PedMEC formulation set forth by Garg et al. (2016), which performs reference-genome based phasing and applies only to bi-allelic variants. In gPedMEC, the main observation is that phasing bubble chains in the graph is similar to phasing multi-allelic variants, but with an additional insight that the child haplotype paths in bubbles can differ from parental ones under the condition that the variant encoded by the bubble is long, and a new allele were created as a result of recombination within the bubble itself.

Ultimately, the goal of solving gPedMEC is to recreate the haplotype paths of every individuals through the bubble chains C. The haplotype paths for a given individual are determined by deducing the two paths through the bubble chains which incur the least cost (i.e. are most likely), where cost is determined by confidence in alignment paths and recombination costs. Doing so will inherently also compute long-read partitionings.

In order to represent the paths taken through our bubble chains for each set of alignments R_i, we create bubble matrices ${\mathcal{F}}_i\in {\{0,1,\dots e,-\}}^{R_i\times M}$ for each individual i. Here, e is the maximum number of alleles contained in any bubble, and M is the number of bubbles in a chain. Below we consider an example having 3-bubble chain with PacBio reads from each individual aligned to it; the corresponding bubble matrices are shown below:

$$\begin{array}{cc}{\mathcal{F}}_1=\begin{array}{c}{r}_1\\ r_2\\ r_3\\ r_4\end{array}{\displaystyle \stackrel{\begin{array}{ccc}{l}_1& l_2& l_3\end{array}}{\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 1& 0& 1\\ 1& 0& \end{array}\right)}}& {\mathcal{F}}_2=\begin{array}{c}{r}_5\\ r_6\\ r_7\\ r_8\end{array}{\displaystyle \stackrel{\begin{array}{ccc}{l}_1& l_2& l_3\end{array}}{\left(\begin{array}{ccc}2& 1& 1\\ 2& 1& 1\\ 2& 0& 0\\ 2& 0& 0\end{array}\right)}}\\ {\mathcal{F}}_3=\begin{array}{c}{r}_9\\ r_{10}\\ r_{11}\\ r_{12}\end{array}{\displaystyle \stackrel{\begin{array}{ccc}{l}_1& l_2& l_3\end{array}}{\left(\begin{array}{ccc}0& 0& 0\\ 2& 1& 1\\ 0& 1& 0\\ & 1& 1\end{array}\right)}}& \end{array}$$ (1)

We define a bubble matrix to be conflict-free if the set of rows in that matrix ${\mathcal{F}}_i$ can be put to two partitions (bipartition) such that each of the two partitions is conflict free. Here, two rows are defined to be conflicting if they exhibit different non-dash values in the same column; that is, one entry is 0 and the other one is 1. If such a bipartition exists, the matrix is called feasible and the two haplotype-paths become self-evident. For example, ${\mathcal{F}}_2$ is conflict–free, and the corresponding haplotype paths are self-evident. However, due to long-read sequencing errors, conflicts within bubble matrices are inevitable. Thus, our goal is to find the optimal set of matrix entries which can be flipped in order to create conflict free matrices containing a bipartition of reads which follow the two haplotype paths of each individual (and which obey the Mendelian constraints of the pedigree). So, for every individual, we also need to introduce a weight matrix ${\mathcal{W}}_i\in {\mathbb{N}}^{R_i\times M\times e}$, where each entry ${\mathcal{W}}_i(j,k,x)$ represents the cost of flipping read j, at bubble l_k, to allele x, where $k\in \{0,1,\dots M\}$ and $x\in \{0,\mathrm{1\dots },|l_k\left|\right\}$. An example weight matrix, corresponding to ${\mathcal{F}}_1$, is shown below:

$${\mathcal{W}}_1=\begin{array}{c}{r}_1\\ r_2\\ r_3\\ r_4\end{array}\stackrel{\begin{array}{ccc}{l}_1& l_2& l_3\end{array}}{\left(\begin{array}{ccc}[2,0,10]& [0,1]& [0,10]\\ [0,10,10]& [0,2]& [0,5]\\ [12,0,5]& [0,1]& [4,10]\\ [7,0,8]& [0,10]& \end{array}\right)}$$ (2)

Other weight matrices can be written similarly.

We need to account for the Mendelian constraints imposed by the pedigree as well. Thus, we introduce the transmission vectors ${{\displaystyle \overrightarrow{t}}}_m,{{\displaystyle \overrightarrow{t}}}_f\in {\{0,1,\mathit{na}\}}^M$ for each triple $(m,f,c)\in \mathcal{T}$ to denote the alleles passed from each parent to child at every location in a bubble chain, where ${{\displaystyle \overrightarrow{t}}}_m=1$ if the mother passes on an allele from $h_m^1$, and so on. Under the circumstance that recombination occurs within a bubble, in which case the value of na is passed on, no haplotype of any parent is directly transmitted to the child. Thus, the recombined sequences will form allele-paths in the bubble.

Additionally, we introduce recombination costs $\mathcal{X}\in {\mathbb{N}}^M$, where $\mathcal{X}(k)$ denotes the cost between bubbles of indices k – 1 and k. For example, if a transmission vector ${{\displaystyle \overrightarrow{t}}}_f$ passes on an allele from $h_f^1$ at location k – 1 and an allele from $h_f^0$ at k, this would incur a recombination cost of $\mathcal{X}(k)$. Yet, when transmission vector ${{\displaystyle \overrightarrow{t}}}_m$ passes on na at location k – 1 and an allele from $h_f^0$ at bubble k, this would not incur any recombination cost.

Having defined all necessary terms, we are now ready to define the gPedMEC problem. Consider a pedigree sequence graph G_p containing bubble chains C and recombination costs $\mathcal{X}$, from a pedigree with individuals $\mathcal{I}$ and relationships $\mathcal{T}$; each individual has corresponding PacBio read alignments R_i, and matrices ${\mathcal{F}}_i$ and ${\mathcal{W}}_i$. The crux of gPedMEC is then to determine the set of all bubble matrix entries to be flipped which accrues the minimal cost, based on (i) the weight of flipping these entries coupled with (ii) the recombination cost incurred by the transmission vectors implied by the resulting child haplotype paths. Once these matrix entries are determined, the haplotypes $h_i^0$ and $h_i^1$ for all individuals become self-evident.

Dynamic programming to solve gPedMEC

In this section, we discuss our dynamic programming (DP) algorithm to solve gPedMEC.

DP cell initialization

We proceed by first computing the initial DP cell cost ${\Delta }_C(k,B,t)$ accrued by flipping entries in column k of each bubble matrix, where k is the index of bubble l_k, B is a bipartition of reads and $t\in {\{0,1,\mathit{na}\}}^2$ is a transmission tuple (at k column index) indicating which haplotype from mother and father is respectively inherited, if applicable.

Intuitively, there is a relationship between a bipartition B, a transmission tuple t and the resulting set of readsets induced at location k, termed $\mathcal{S}(k,B,t)$. For example, if the transmission tuple does not contain any na values, then the child’s haplotype path must be a combination of parental haplotypes—correspondingly, the reads in the child’s bubble matrix can be merged with bipartitions in the parental bubble matrices due to the identity by descent (IBD) condition. In the case of a trio, this would lead to two resulting bipartition readsets. In the presence of na values, the child’s reads would not be merged with parental reads, leading to three bipartition readsets in the case of a trio.

For a given bubble l_k, each bipartition can be assigned any pair of alleles (x, y), of which there are $(\left(\begin{array}{c}\left|l_k\right|\\ 2\end{array}\right)+|l_k|)$ (the added $\left|l_k\right|$ accounts for the possibility of assigning the same allele). To notate this, we let $W_{k,R}^d$ represent the cost of flipping reads for a specific bipartition readset $R\in \mathcal{S}(k,B,t)$ to an allele-pair $(d_1,d_2)\in A$, where A is the set of allele-pairs $\{(x,y)\in l_k\times l_k|x\le y\}$:

$$W_{k,R}^d=\min \{{\mathrm{w}}_{k,X}^x+{\mathrm{w}}_{k,Y}^y,{\mathrm{w}}_{k,Y}^x+{\mathrm{w}}_{k,X}^y\}$$

where X and Y are the readsets of a bipartition readset R. The cost of flipping to a given allele can be computed as:

$${\mathrm{w}}_{k,C}^d=\sum _{(i,j)\in C}\hspace{0.17em}[[{\mathcal{F}}_i(j,k)\ne d]]·{\mathcal{W}}_i(j,k,d),$$

Thus, to initialize the cost ${\Delta }_C(k,B,t)$, we need to find the assignment of allele pairs to all bipartition readsets which incurs the minimal flipping cost. This can be formalized in the following way:

$${\Delta }_C(k,B,t)=\underset{a\in A^{\mathcal{S}(k,B,t)}}{\min }\left\{\sum _{R\in \mathcal{S}(k,B,t)}{W}_{k,R}^{a(R)}\right\}$$ (3)

The inner sum computes the minimum allele-pair assignment cost from all bipartitions in $\mathcal{S}(k,B,t)$. The calculations in Figure 4 provide a more concrete example for calculating DP cell initialization cost. In this example, we assume a sample partition of reads and child partition as per transmission vector shown in Figure 4(c) where the mother passes on the green allele and the father passes on the blue. To calculate the DP cell initialization cost in (d), we find the assignment of allele-pairs to each of the bipartition readsets which incurs the lowest cost. For example, the cost associated with the allele-pair assignment (0, 2) and (0, 1) to bipartitions (green, purple) and (orange, blue), respectively, is (2) + (5 + 8) + (4 + 1) + (3 + 4 + 4) = 29 because the minimum cost of flipping all reads in the green partition to allele 0 is 2, that of flipping the purple partition to allele 2 is (5 + 8) = 13, and so on. In this way, we can compute costs for other allele-pair assignments and store the minimum in the DP cell.

Fig. 4.

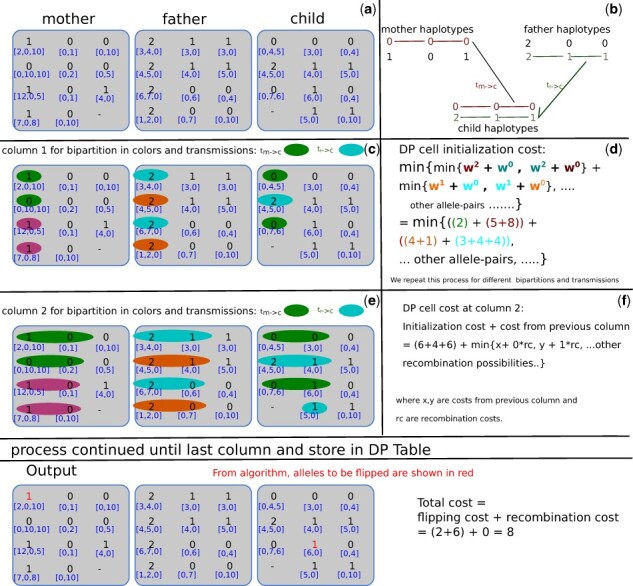
This figure shows the process of our DP algorithm. The top row shows the three input bubble matrices from mother, father and child, with their weights (a). In block (b), the expected output haplotypes are given. The following rows show sample processes for DP column initialization and recurrence. In block (c), sample bipartitions and transmission vectors (encoded in colors) are shown with the respective calculations in block (d). The cost calculation finds the best assignment of allele-pairs (encoded in colors and alleles as superscripts) to the example set of partitions which accrues the minimum cost. For example, for computing the allele assignment cost of allele 0 to the green partition, we pay a cost of 2. The other costs can be computed similarly. In block (e) and (f), the recurrence step for sample partition and transmission at second column is shown that minimizes the value of the sample partition at current column, conditioned on the previous column and allowing various possibilities of recombinations. This process will be repeated for all possible transmission vectors and compatible partitions until last column. Figure adapted from Garg (2018). (Color version of this figure is available at Bioinformatics online.)

DP column initialization

Every entry $C(1,B,t)$ in the first column of the DP table is filled with the corresponding cell initialization cost ${\Delta }_C(k,B,t)$ for all bipartitions B and transmissions t. Thus, on input the set of reads covering l₁, each $C(1,B,t)$ is calculated according to Equation 3.

As described in Patterson et al. (2014) and Garg et al. (2016), we enumerate over bipartitions in Gray code order, thus ensuring a runtime of $\mathcal{O}({(\left(\begin{array}{c}\left|l_k\right|\\ 2\end{array}\right)+|l_k|)}^{\left|\mathcal{I}\right|-\left|\mathcal{T}\right|}·2^{|\mathcal{F}(k)|+2·\left|\mathcal{T}\right|})$.

DP recurrence

In the recurrence step, we compute $C(k,B,t)$ at column k, which intuitively represents the optimal allele-pair assignment cost to bipartitions B until column k. In general, the cell $C(k,B,t)$ can be computed as the optimal accumulated cost of the bipartitions B until k – 1 columns plus ${\Delta }_C(k,B,t)$ under various possibilities of recombination. Thus we add ${\Delta }_C(k,B,t)$ to values from column k – 1, where possible recombination costs are incurred according to the various values of t. The additional constraint is that only entries in column k – 1 whose bipartitions are compatible with ${\Delta }_C(k,B,t)$ are considered, where two bipartitions are deemed compatible if they share the same readsets. By only considering compatible readsets, we are ensuring that we maintain the reality that a single PacBio read cannot come from more than one haplotype. For two bipartitions B and $B\prime$, compatibility is denoted as $B\simeq B\prime$.

In more formal terms, the value of $C(k,B,t)$ can be written as following:

$$\begin{array}{c}C(k,B,t)={\Delta }_C(k,B,t)\\ +\underset{\begin{array}{c}{B}^{\prime }\in \mathcal{B}(\mathcal{F}(k-1)):B^{\prime }\simeq B\\ t^{\prime }\in {\{0,1,\mathit{na}\}}^{2\left|\mathcal{T}\right|}\end{array}}{\min }\{C(k-1,B^{\prime },t^{\prime })+d_H(t,t^{\prime })·\mathcal{X}(k)\},\end{array}$$ (4)

In this equation, the term $d_H(t,t\prime )$ refers to the distance, or number of changes, between two transmission vectors and thereby represents the number of recombination costs which need to be considered. In the case where any entry is na we assume no recombination cost.

For a sample walkthrough calculation of DP recurrence, we again turn to Figure 4. The initialization cost of the sample cell ${\Delta }_C(2,B,t)$ is (6 + 4 + 6) = 16, as determined according to Equation (3). In order to find the minimal value for the DP cell cost in column 2, we need to consider the costs from column 1. In the calculations shown in part (f), we only consider partitions which agree on the readsets involved, but want to consider the possibilities of recombinations between the first and second bubbles. Minimizing over all possible previous transmission vectors and compatible bipartitions gives us our DP cell value $C(2,B,t)$.

We continue this process for all DP cells at column 2. In a similar manner, we repeat the DP algorithm until the last column.

Time complexity

The total running time of this algorithm is $\mathcal{O}\left(\left(\begin{array}{c}m\\ 2\end{array}\right)·2^{(c+2·t)}· \left|L\right|\right)$ for L bubbles, where m is the maximum number of alleles in any bubble from L, c is the maximum coverage from all individuals and t is the number of trio relationships. Running time is independent of read-length and, therefore, the algorithm is suitable for the increased read lengths available from upcoming sequencing technologies.

Backtracing

At the end of our DP algorithm, the minimal value stored in the final column represents the lowest possible cost incurred. We can backtrace through the DP table to find the transmission vectors, bipartitions of readsets and final haplotype paths that led to this value.

2.5 Generation of final assemblies

Once we obtain the partitions of long-read data for each individual, we can perform haplotype-aware error-correction on the reads. Subsequently, we can use an external assembler to assemble these partitions separately create final haplotype-resolved assemblies for all individuals in a pedigree.

Special cases

Solving for single individuals or parent–child can be seen as special cases of gPedMEC when ${\mathcal{F}}_i$ from any parent or both are empty.

3 Datasets and experimental setup

To demonstrate gPedMEC, we considered simulated trios which present different genomic heterozygosity rates, for the comprehensive study. Subsequently, we applied our method to real data of the human chromosome 22 in the Ashkenazim trio from the Genome in a Bottle Project (Zook et al., 2016).

To generate our simulated data, we created a series of diploid genomes by adding mutations at varying rates to the haploid yeast strain DBVPG6765 (Yue et al., 2017). The four parental haplotypes were generated in this way; subsequently, one haplotype from each parent was selected to form the child diploid genome.

We generated trios of pseudo-diploid yeast genomes with heterozygosity rates of 0.5, 1.0 and 1.5%. For each genome in each trio, we simulated Illumina data using Art with average read length of 150 bp at $30\times$ coverage and HiSeqX PCR free profile. Furthermore, we simulated PacBio data using pbsim for each individual in each trio at $5\times ,\hspace{0.17em}10\times$ and $15\times$ coverage and sample PacBio CLR profile. For the three trios of heterozygosity rates 0.5, 1.0 and 1.5%, the average PacBio read lengths, respectively, were: 6202, 6220 and 6212, at 5× coverage, 6202, 6157 and 6256 at 10× coverage and 6231, 6190 and 6220 at 15× coverage. Additionally, we simulated child PacBio data at $15,\times ,30\times ,45\times$ and $80\times$ coverage required for TrioCanu (Koren et al., 2018).

Additionally, we considered real pacbio data (ftp://ftp-trace.ncbi.nlm.nih.gov/giab/ftp/data/AshkenazimTrio/HG004_NA24143_mother—HG002_NA24385_son—HG003_NA24149_father/PacBio_MtSinai_NIST/PacBio_minimap2_bam/, ftp://ftp-trace.ncbi.nlm.nih.gov/giab/ftp/data/AshkenazimTrio/HG004_NA24143_mother—HG002_NA24385_son—HG003_NA24149_father/NIST_Illumina_2x250bps/novoalign_bams/) and nanopore data (ftp://ftp-trace.ncbi.nlm.nih.gov/giab/ftp/data/) of human chromosome 22 in Ashkenazim trio. For every individual, we extracted Illumina and PacBio/nanopore data aligned to this chromosome. We downsampled the long-read data for each individual to 15× coverage. For ground truth, we considered diploid assemblies that were previously produced by TrioCanu (Koren et al., 2018) and by DnaNexus (ftp://ftp-trace.ncbi.nlm.nih.gov/giab/ftp/data/AshkenazimTrio/analysis/JasonChin_Peregrine_TrioBinned_PacBioCCS_assembly_06042019/). The DnaNexus assemblies are generated using PacBio CCS (Wenger et al., 2019) and trio information and therefore, are the best available diploid assemblies.

3.1 Pipeline implementation

We used a modified version of SPAdes v3.10.1 (Bankevich et al., 2012) to construct our pedigree sequence graph based on Illumina data from all related individuals. In order to maintain heterozygosity information in our graph, we ignored the bubble removal step, running it with default parameters along with the—only-assembler flag, thereby producing our pedigree sequence graph, without any error correction and bubble popping. Then, with VG (Garrison et al., 2018), we converted the assembly graph to a bluntified sequence graph—that is, with redundant node sequences removed. Subsequently, we detected regions of heterozygosity, (i.e. snarls) with the snarl decomposition algorithm from VG (Paten et al., 2018). Using GraphAligner (Rautiainen et al., 2019), we aligned long reads from all individuals to the generated graph. Using our own implementation, we obtain bubble chains from the combined PacBio alignments according to the algorithm described in Section 2. Taking the resulting ordered bubble chains and long-read alignments, we solved the gPedMEC problem. In our calculations, we assumed constant recombination costs $\mathcal{X}$ and weights in the weight matrices ${\mathcal{W}}_i$ for all individuals. We determined the optimal partitions for each individual via backtracing, as detailed in our description of the algorithm. The final haplotigs were generated by assembling these computed partitions separately using Flye (Kolmogorov et al., 2019) or Shasta (https://github.com/chanzuckerberg/shasta). These steps have been implemented as a new feature in tool, WHdenovo.

3.2 Assembly performance assessment

We evaluate the child’s haplotype-resolved assemblies from our approach by aligning them to the true simulated genome in our yeast-based experiments, and to TrioCanu’s published assemblies. Below we describe our evaluation metrics:

Partitioning accuracy rate. We computed partitioning accuracy rate by comparing our predicted read partitions to the truth partitions, and divided by the total reads.

Average percent identity. We consider the best assignment of each haplotig to either of the two true references, obtained by aligning the haplotigs to references. For diploid assembly, we compute the average of the best-alignment percent identities over both haplotigs.

Assembly contiguity. We assess the contiguity of the assemblies by computing the N50 of haplotig size.

Assembly completeness. We assess the completeness using the total length of haplotigs assembled by each method.

4 Results

We now present the results of our analysis of the child diploid assemblies based on the datasets described above, as assembled by our method and by the only available trio-based assembler, TrioCanu, based on long reads.

Coverage and heterozygosity analysis

To explore a cost-effective method of assembling the child diploid genome when trio information is available, we consider PacBio datasets of varying coverage for each individual in a trio—specifically, 5×, 10× and 15× coverages. Table 1 reports the assembly performance statistics of our method applied to genomes of varying heterozygosity rates. We observe that as we increase the long read coverage from 5× to 15×, the average identity of the haplotigs from our approach increases from 99.3 to 99.9%. This behavior is consistent across genomes of different heterozygosity rates. In contrast, TrioCanu produced haplotigs with average identity of 88–90% at coverages of 15×, 30× and 45× for child data, indicating that TrioCanu require 80× to attain success comparable to our method. On real data from human chromosome 22 in GIAB trio, we produced haplotigs with >99.6% (or 0.2% discordance) average identity to high-coverage TrioCanu assemblies in both experiments. We believe that the Illumina-based graph used in our approach and optimally solving the gPedMEC formulation contributes to generating accurate haplotigs. Overall, our analysis suggests that our approach delivers accurate haplotype sequences even at a long read coverage as low as 15× for each individual in a trio.

Table 1.

Phased assembly performance of child averaged over both haplotypes from our approach (WHdenovo) and TrioCanu

Approach	Het	PacBio	#phased	%partition	Identity	N50	Total
	rate	cov.	bubbles	accuracy	[%]		length (m)
Child phased assemblies
Simulated data
WHdenovo	0.5	3*5×	55 561	94.2	99.3	21k	7.6
WHdenovo	0.5	3*10×	56 233	94.7	99.4	220k	11.5
WHdenovo	0.5	3*15×	56 563	94.9	99.9	720k	11.9
TrioCanu	0.5	1*45×	–	–	89.1	8.5k	51.1
TrioCanu	0.5	1*80×	–	–	99.9	730k	11.9
WHdenovo	1.0	3*5×	45 418	95.1	97.8	21k	7.6
WHdenovo	1.0	3*10×	46 228	96.3	99.4	210k	11.5
WHdenovo	1.0	3*15×	47 528	96.4	99.8	540k	11.9
TrioCanu	1.0	1*45×	–	–	88.8	8.6k	51.9
TrioCanu	1.0	1*80×	–	–	99.9	542k	11.9
WHdenovo	1.5	3*5×	35 027	97.4	97.5	20k	7.5
WHdenovo	1.5	3*10×	39 021	98.3	99.4	210k	11.5
WHdenovo	1.5	3*15×	41 126	98.6	99.8	520k	11.9
TrioCanu	1.5	1*45×	–	–	88.8	8.8k	51.5
TrioCanu	1.5	1*80×	–	–	99.9	540k	11.9
Real data (Human chromosome 22)
WHdenovo	0.1	3*15×	21 235	–	99.8	699k	34.5
WHdenovo	0.1	3*15× (n)	21 235	–	99.7	26m	38

Note: Please note that the PacBio coverage is for every individual in a trio for WHdenovo, whereas the coverage is for only child in TrioCanu. In real data, WHdenovo assemblies are compared to high-coverage TrioCanu assemblies. The last row experiment is performed using nanopore data.

To further investigate the 0.2% discordance of diploid assemblies between WHdenovo and TrioCanu in the real pacbio data, we additionally considered high-quality diploid assemblies from DnaNexus generated using PacBio CCS and trio information. Figure 5 shows three bars representing diploid assemblies from TrioCanu, WHdenovo and DnaNexus. The colors in the bars show the agreement status between these assemblies. The gray region represents the agreement of WHdenovo and TrioCanu assemblies with DnaNexus with an average identity of 99.36 and 99.29%, respectively. There are 0.2% cases where WHdenovo and TrioCanu disagree with each other. Out of these cases, the blue and red regions represent the agreement of WHdenovo and TrioCanu with DnaNexus by 83.20 and 61.29%, respectively. Thus, this three-way comparison analysis suggests that, WHdenovo is doing less mistakes compared to TrioCanu in missing SNPs. In other cases, either of the assemblies can be wrong.

Fig. 5.

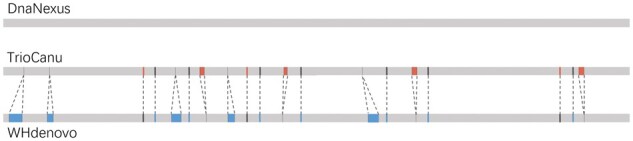
This figure shows the bars on the comparison between TrioCanu, WHdenovo and DnaNexus assemblies. The gray region represents the agreement of WHdenovo and TrioCanu assemblies with DnaNexus. Outside of gray is the region (0.2% cases) where TrioCanu and WHdenovo disagree. Out of these 0.2% cases, the blue and red regions represent the agreement of WHdenovo and TrioCanu assemblies with DnaNexus, respectively. (Color version of this figure is available at Bioinformatics online.)

In measuring partitioning accuracy of long reads, we considered reads to be classified only if covering a fixed threshold of bubbles. We observe that the partitioning accuracy improves with the heterozygosity rate. For example, for genomes with heterozygosity rate of 1.5%, our calculated partitioning accuracy rate is 98.6% for 15×-fold child data. In contrast, if the heterozygosity rate is low, at 0.5%, our partitioning accuracy is 94.9% at 15×-fold data of child.

With an increase in average PacBio coverage from 5× to 15×, the haplotype contiguity achievable using our approach dramatically improves from 21 to 720 kbp for trios with heterozygosity rate of 0.5%, approaching the contiguity of chromosomal-scale assemblies. When heterozygosity rate is high (≥1.0), our assemblies are somewhat fragmented (e.g. 540 kb) even at 15× coverage. This fragmentation is a result of repetitive and highly diverging regions, which cause assemblers to break contigs. For human chromosome 22, we produced haplotigs with 699 kb and 26 Mb N50 length by using 15× pacbio and nanopore coverage respectively of each individual. In comparison, TrioCanu produced N50 of length 621 kb at high-coverage PacBio data in child. This continuity analysis suggests that our approach can produce continuous diploid assemblies at 15× coverage of each individual in a trio.

Regarding haplotype completeness, our approach yields average child diploid assemblies of length ∼11.5 Mbp at 10× and 15× coverages. For real data from human chromosome 22, we can produce complete assemblies of 34.5 and 38 Mb at 15× pacbio and nanopore coverage, respectively, for each individual in a trio.

In summary, our approach delivered higher quality haplotypes from 15× long-read coverage of all individuals in a trio than TrioCanu at 45× coverage of the child. The results from these experiments indicate that our approach is generalized to produce phased assemblies for genomes with different heterozygosity rates. Further, our pedigree-based approach is also generalized to produce assemblies for both parents (in addition to that for the child), and can help find recombination maps.

4.2 Variant detection

As a second goal, we aimed to study haplotype-resolved variant detection. To pursue this, we aligned our predicted haplotype-resolved assemblies to each other and detected the variants, such as SNVs. From Figure 6, we observe that the number of predicted SNVs or short indels rises in response to increasing heterozygosity rate; for example, 58 541 and 178 743 for genomes with heterozygosity rates of 0.5 and 1.5%, respectively. This result is expected because the number of variations between two haplotypes directly depends on heterozygosity rate. Additionally, the plot indicates that the number of variants we can detect with our approach (red) is very close to the true number of variants (blue). In summary, this plot indicates that our haplotype-resolved assembly approach helps to detect variants.

Fig. 6.

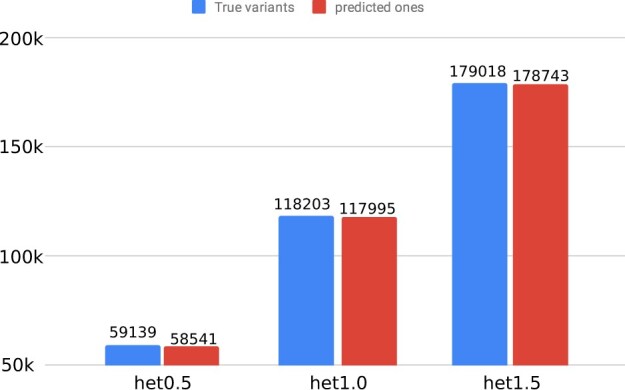
This figure shows the true and predicted variants from the phased assemblies generated using our method at various heterozygosity rates

4.3 Run time

Over human chromosome 22 experiment, running the whole pipeline took 2 h 38 min and up to 80 gb RAM. TrioCanu took 1 h 20 min on 96 cores, indicating comparable runtimes.

5 Discussion

Advances in sequencing technologies such as PacBio, ONT and others, which can span multiple heterozygous variants, have enabled the reconstruction of accurate phased assemblies for related individuals. The TrioCanu method (Koren et al., 2018) is a hybrid approach that takes advantage of parental Illumina data and long reads from the child in a trio; yet, it requires high coverage of long-read child data. We have developed a novel pedigree sequence graph based approach to the problem of diploid genome assembly for pedigrees that combines short- and long-read sequencing technologies. By combining the accuracy of short reads with the contiguity offered by long reads, along with pedigree information, our approach produces accurate, complete and contiguous haplotypes. By requiring relatively low long-read coverage, our method is also a cost-effective way of generating high quality diploid assemblies of all individuals. Furthermore, by performing phasing directly in the space of a pedigree sequence graph, we can detect and phase all variants (SVs or SNVs), including those that are heterozygous in all individuals.

One restriction in our model is the use of constant recombination rates; we aim to fine tune this parameter in the future according to genomic distances, and properly incorporate recombination hotspots. Other limitations are that the Illumina-based graphs are complex for human genomes and GraphAligner doesn’t scale well for long-read alignments through these graphs. To overcome these limitations, the next steps involve building an initial simplified graph from PacBio Hifi data and then applying the downstream principles from this work. Nevertheless, our framework, in principle, sets up a foundation to incorporate a variety of combination of datasets available from individuals in pedigree; in the future, we hope to provide relevant experiments on these combinations for various use cases. Finally, we will apply our approach to study the implication of haplotype-resolved variants to Mendelian diseases.