Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Nov 10;142(51):21420–21427. doi: 10.1021/jacs.0c09933

Exploring the Molecular Conformation Space by Soft Molecule–Surface Collision

Kelvin Anggara †, Yuntao Zhu ‡, Martina Delbianco ‡, Stephan Rauschenbach §,†,*, Sabine Abb †, Peter H Seeberger ‡,∥,*, Klaus Kern †,⊥,*
PMCID: PMC7760097  PMID: 33167615

Abstract

graphic file with name ja0c09933_0006.jpg

Biomolecules function by adopting multiple conformations. Such dynamics are governed by the conformation landscape whose study requires characterization of the ground and excited conformation states. Here, the conformational landscape of a molecule is sampled by exciting an initial gas-phase molecular conformer into diverse conformation states, using soft molecule–surface collision (0.5–5.0 eV). The resulting ground and excited molecular conformations, adsorbed on the surface, are imaged at the single-molecule level. This technique permits the exploration of oligosaccharide conformations, until now, limited by the high flexibility of oligosaccharides and ensemble-averaged analytical methods. As a model for cellulose, cellohexaose chains are observed in two conformational extremes, the typical “extended” chain and the atypical “coiled” chain—the latter identified as the gas-phase conformer preserved on the surface. Observing conformations between these two extremes reveals the physical properties of cellohexaose, behaving as a rigid ribbon that becomes flexible when twisted. The conformation space of any molecule that can be electrosprayed can now be explored.

1. Introduction

The three-dimensional structure of a biomolecule is of fundamental importance for its function and properties. Understanding the mechanism of action1,2 of a biomolecule requires identification of conformations beyond the most abundant ones since those are often not the bioactive species.3,4 Identifying these rare conformations is key to understanding the properties of materials made out of these biomolecules.5,6 Exploration of the conformation space beyond the most stable conformation is a prerequisite.

The conformational space of oligopeptides7−9 and oligonucleotides10 is well studied, while little is known about oligosaccharide (i.e., glycan or carbohydrate) conformations11,12—the most abundant biomolecules on earth that play a key role in cell recognition13 and structure.14 To date, oligosaccharide conformations in various environments have been probed by crystallography and spectroscopy techniques.5,6,11,15−22 However, these results remain limited to the few most abundant conformations and these measurements require deconvolution into contributions from individual conformers assumed to be rigid.11,16,23,24 This rigidity assumption complicates the study of oligosaccharide conformation since oligosaccharides are highly flexible.11,12,16 Mapping of the oligosaccharide conformation space requires single-molecule approaches that eliminate the ensemble averaging.

A combination of electrospray ion-beam deposition (ES-IBD)25,26 and scanning tunneling microscopy (STM) allows for single-molecule imaging of oligosaccharides deposited on a surface.27−29 Here, we show that soft collision (0.5–5.0 eV) of an oligosaccharide with a surface produces both ground and excited oligosaccharide conformations, whose imaging reveals the oligosaccharide conformation space. Our approach takes advantage of the mechanical excitation provided by molecule–surface collision that is known to excite low-frequency molecular vibrational modes30−32 that, for biomolecules, are associated with their backbone motions (i.e., their conformation dynamics).33−36 Adsorption on a cold surface (∼120 K) deactivates the thermal motion of the conformers generated from our collision experiment, allowing us to trap excited conformation states and image them as isolated single molecules. Imaging these conformation states reveals the intrinsic conformation space of the target oligosaccharide.

The conformation space of cellohexaose, an oligosaccharide composed of six glucose (Glc) units linked by β-1,4 glycosidic bonds (Figure 1a) serving as a model for cellulose,14 is explored by colliding a singly deprotonated cellohexaose anion, [M–H]−1, with a Cu(100) surface held at ∼120 K. STM imaging of the adsorbed molecules revealed that the collision-sampled diverse conformation states of cellohexaose (Figures 1 and 2). These states show the characteristic geometry and flexibility of the β-1,4 Glc-Glc glycosidic bond at varied pyranose ring orientations, thus providing insight into the intrinsic property of cellohexaose. Cellohexaose–surface collisions at either 0.5 or 5.0 eV collision energy (ECOL in Figure 1b) give the same types of conformers on the surface, but with substantially different populations (Figure 3). At low energies (∼0.5 eV), limited conformation states were sampled, thereby preserving the gas-phase conformation of cellohexaose as the major species on the surface; at higher energies (∼5.0 eV), more conformation states were sampled since the collision with ample energy was able to change the gas-phase conformation into many other conformation states. These results demonstrate that a fragile, gas-phase molecular conformer can be preserved on a surface for detailed structural characterization by single-molecule microscopy, and soft molecule–surface collision is a viable means to generate both the ground and excited conformation states of a complex molecule on the surface.

Figure 1.

Figure 1

Open in a new tab

Cellohexaose conformers imaged on a surface. (a) Chemical structure of cellohexaose—an oligosaccharide with six glucose (Glc) units linked via β-1,4 glycosidic bonds. The structure is drawn from the nonreducing end (the left end) to the reducing end (the right end). (b) Schematics of the experiment: a beam of cellohexaose anion, [M–H]−1, was aimed at the normal incident angle to a Cu(100) surface held at ∼120 K. The outcome of the collision at low energies (ECOL) of 0.5–5.0 eV was imaged by STM (see Materials and Methods for details). (c) STM image and STM simulation of cellohexaose on Cu(100) at 11 K, showing a spectrum of conformers between “extended”, which has six horizontal (H) pyranose rings, and “coiled”, which has six vertical (V) pyranose rings. The height of the V unit was measured as 2.5 ± 0.3 Å, while that for the H unit was 2.0 ± 0.3 Å. The STM simulation is superimposed with its corresponding computed structure, whose side view is given in GEOM, ascribing the middle of the imaged Glc protrusion to the center of the Glc pyranose ring.

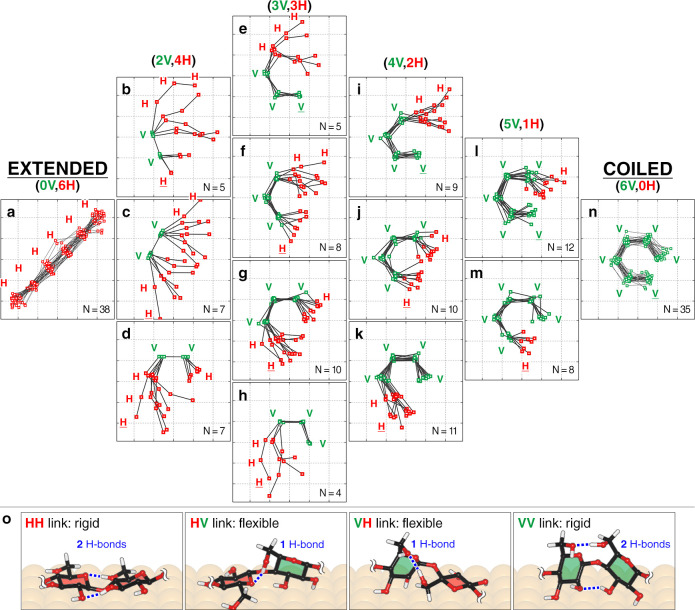
Figure 2.

Figure 2

Open in a new tab

Real-space conformations of cellohexaose. Least-square overlay of experimentally observed cellohexaose conformers, grouped on the basis of the number of vertical Glc units present: none in (a), two in (b–d), three in (e–h), four in (i–k), five in (l–m), and six in (n). The positions of the Glc units are shown as green squares for vertical Glc (V) and red squares for horizontal Glc (H). The nonreducing end of the chain has its V/H label underlined. The size of the square grid in each panel is 4.0 × 4.0 Å2. The number of molecules observed are given as an N value at the bottom-right of each panel. Detailed analysis of the spatial distribution is given in Figure S3. Panel (o) gives representative computed geometry of distinct linkages present in the cellohexaose chain, showing different interunit hydrogen bonding (blue dashed lines). The rings are colored in red for H units and green for V units. The axial H atoms on each of the pyranose rings are hidden for clarity.

Figure 3.

Figure 3

Open in a new tab

Dependence of the conformation ensemble on the molecule–surface collision energy. (a) The most stable conformation of the cellohexaose anion computed in the gas phase. This coiled structure features two types of interunit hydrogen bonds: (i) between OH6–OH6 (dotted blue line, “TOP” view), and (ii) between OH2–OH3 (dotted red line, “SIDE” view), with an average OO distance of 2.7 Å. The axial H atoms on each pyranose ring are hidden for clarity. (b) The observed conformer population at two collision energies (ECOL), showing coiled as the major species (green bar) at 0.5 eV collision energy and extended as the major species (red bar) at 5.0 eV. ECOL is defined as the translational energy of the molecule toward the surface along the surface normal. The error bar indicates the standard error.

2. Results and Discussion

Deposition of deprotonated cellohexaose anions ([M–H]−1) was found to give adsorbed cellohexaose that was imaged as a chain containing six protrusions, corresponding to the six Glc units in cellohexaose (Figure 1c). Representative conformer types observed include the fully linear (“extended”), the partially coiled, and the fully coiled (“coiled”) conformer. Molecular manipulation of the coiled species with the STM tip converted the coiled conformer into an extended conformer (Figure S1, Supporting Information), demonstrating that these two species are different conformations of the same molecule. The observation of partially and fully coiled cellohexaose conformers challenges the widely accepted paradigm that cellulose-like oligosaccharides can adopt only a linear conformation similar to the extended species, typically found in a solution18 and in a condensed phase.19

The Glc units in cellohexaose were observed in one of two orientations: the horizontal “H” or the vertical “V” state. Height measurements and STM simulations by density functional theory (DFT) show that, in the H state, the pyranose ring is oriented parallel to the surface, while in the V state, the ring is oriented perpendicular to the surface. Notably, the V state of the glucose unit in cellohexaose has the same height as the glucoses in α-cyclodextrin that also adsorbs with its ring perpendicular to the surface (Figure S2), confirming that the V unit in cellohexaose has the same geometry as the glucose in α-cyclodextrin.

The adsorbed cellohexaose was modeled by structures relaxed in DFT, guided by the results from molecular dynamics (MD) simulation of cellohexaose anion landing on the Cu surface. The final structures from the MD simulation show that the adsorbed cellohexaose chain containing V-unit coils in the clockwise direction, starting from the nonreducing to the reducing end. This information allows us to identify the nonreducing end for cellohexaose chains observed with any number of V units (Figure 1c and Figure 2). Calculations of the adsorbed cellohexaose show that the molecule exists as an alkoxide covalently bound to the Cu surface (RO–Cu) via one of the hydroxide groups (RO–) initially present in the gas phase (see the discussion of Figure 5 for more details). The computed binding strength of the molecule to the surface ranges from 9.7 eV for extended to 7.2 eV for coiled, of which 3.3 eV originates from the covalent RO–Cu bond.

Figure 5.

Figure 5

Open in a new tab

Computed dynamics of cellohexaose–Cu(100) collision. Time-dependent snapshots of cellohexaose colliding with (a) 0.5 eV and (b) 5.0 eV collision energy. The 0.5 eV collision preserves the gas-phase conformation of cellohexaose on the surface while the 5.0 eV collision induces a conformation change of cellohexaose. In both trajectories, the proton from OH3 of the Glc at the nonreducing end migrates to the O4 hydroxide, resulting in the formation of a O3–Cu bond. The rings in the final states are colored green for the vertical ring (V) or red for horizontal (H). The axial H atoms on each of the pyranose rings have been hidden for clarity.

To rationalize the conformation space of cellohexaose, we have grouped the conformers based on the number of V units in the chain (Figure 2a–n). The curvature of the cellohexaose chain depends on the orientation of one pyranose ring with respect to the neighboring ring, that is, VV, VH, HV, or HH linkages (nonreducing to reducing end) (Figure 2o and Figure S3). The HH linkage straightened the chain, while VV bent the chain by ∼60°, as shown for the extended conformer (Figure 2a) and the coiled conformer (Figure 2n). In contrast, HV and VH increased the geometric freedom of the chain, as evidenced by the diverse conformations observed (Figure 2b–m). The absence of conformers with only one V unit indicates that the V units are stabilized by the VV linkage, instead of HV or VH. The different geometric preferences observed in these four linkages provide an experimental measure of the potential energy landscape at these four interunit ring orientations.

The potential energy landscape computed by DFT reproduces the geometrical preferences of all four linkage types (Figure S3). The calculations attribute the increased geometric freedom in HV and VH, compared to that in HH and VV, to the reduced number of hydrogen bonds between glucoses at these orthogonal ring orientations. HV and VH allow for one interunit hydrogen bond, while VV and HH allow for two (Figure 2o). This is an intrinsic molecular property20 since the potential energy landscape of the Glc-Glc linkage for the adsorbed molecule was computed to be similar in the gas phase, free of environmental effects (Figure S4).

The results identify cellohexaose as a rigid ribbon that, when twisted, is highly flexible at the twisting point (i.e., at VH or HV link) because of reduced interunit hydrogen bonding. This increased flexibility due to twisting is consistent with studies that proposed the twisting of cellulose chains as a cause of disorder in dissolved cellulose37 and in amorphous cellulose.15,17 The twisting also increases the number of hydroxyl groups that can interact with their immediate environment. Increased environmental interactions and flexibility conferred by twisting may explain why cellulose-like oligosaccharides twist when bound by a carbohydrate binding module (CBM) in enzymes.38

The conformation space sampled by the cellohexaose–surface collision depends critically on the collision energy (ECOL)—that is, the translational energy of the molecule toward the surface along the surface normal (see Materials and Methods). Increasing ECOL from 0.5 to 5.0 eV increased the extended and decreased the coiled population (Figure 3). The dependence of the conformer population on ECOL shows that various conformation states resulting from the collision dynamics can be trapped on the cold surface. Collision at ECOL = 5.0 eV was thereby understood to convert the initial gas-phase conformer into many accessible conformation states; collision at ECOL = 0.5 eV was limited in energy to induce conformation change, causing the gas-phase conformer to be preserved on the surface as the major species. Thus, the gas-phase conformer of cellohexaose likely resembles the coiled species.

To obtain information concerning the gas-phase structure of cellohexaose anion, we performed DFT calculations of variously coiled cellohexaose gas-phase anions (Figure 4a). In agreement with the experiment, the computed gas-phase structure of cellohexaose anion (Figure 3a) is a fully coiled structure that closely resembles the observed coiled species on the surface. Both the coiled species at the surface and the coiled anion in the gas phase share identical glycosidic conformations (i.e., the (Φ, Ψ) torsion angles) that define the oligosaccharide conformation. The fully coiled anion structure was the most stable gas-phase conformation (Figure 4a), computed to be 2.1 eV more stable than its extended counterpart, largely because of new hydrogen bonds formed between the two terminal glucose units. The coiling direction was found to be specific since the anion in Figure 3a and Figure 4a is 1.5 eV more stable than the anion fully coiled in the opposite direction. The fully coiled anion was found to be the most stable when the negative charge is placed at the terminus of the chain (Figure 3a). In this specific instance, the stabilizing effect of the negative charge in the coiled anion was found to be secondary since, for the neutral cellohexaose in the gas phase, the coiled conformer is 1.9 eV more stable than its extended counterpart. This coiled anion possesses glycosidic conformations that are very similar to that in the gas-phase conformer of cellobiose (i.e., a Glc-(β-1,4)-Glc disaccharide), observed spectroscopically.21 Our observation of coiled cellohexaose in the hydrophobic gas-phase environment,8 as opposed to its linear conformation in the hydrophilic aqueous environment,18 thereby suggests a new path to form “cyclodextrin-like” molecules using noncovalent interactions.

Figure 4.

Figure 4

Open in a new tab

Potential energy profile for variously coiled cellohexaose in the gas phase and on a surface. Computed potential energy profile from DFT (black lines) is given for gaseous singly deprotonated cellohexaose anion (a) and adsorbed singly dehydrogenated cellohexaose (b). The hollow squares in (a) indicate the computed free energy at 298 K. The gas-phase conformation of cellohexaose anion is expected to be the most stable, fully coiled conformer because the ions in our apparatus undergo a thermalization process via collisions with gas molecules at room temperature before it collides with the Cu surface (see Materials and Methods). The collision dynamics, illustrated by the blue arrow, excites the coiled anion conformation into many conformation states on the surface. In all gas-phase conformers shown, the negatively charged hydroxide is located at the O4 of the Glc unit at the nonreducing end since it leads to the lowest energy structure. The potential energy for every partially coiled species on the surface is averaged between multiple conformer types illustrated by the cellohexaose chain images (also shown in Figure 2).

To gain insights into the conformational landscape sampled by cellohexaose–surface collision in the experiment, we computed the potential energies for all conformer types observed in the experiment (Figure 2a–n). The calculations (Figure 4b) show that coiled and partially coiled adsorbed cellohexaose are excited conformation states of cellohexaose on the surface, while extended is the ground conformation state. The observation of coiled and partially coiled cellohexaose chains on the surface thus provides clear evidence for the trapping of excited conformations states on the surface generated via the soft molecule–surface collision. By relating the computed energy profile (Figure 4b) to the observed conformer populations (Figure 3b), we show that the 0.5 eV collision traps the system in potential wells associated with structures that strongly resemble the initial gas-phase structure, while the 5.0 eV collision propels the system to access potential wells associated with structures that strongly differ from the initial gas-phase structure.

We performed MD calculations implemented in DFT to unveil the principal mechanism behind the cellohexaose–surface collision (Figure 5). The initial state in the MD simulation was the fully coiled, gas-phase conformer of cellohexaose anion with its center-of-mass velocity set to a known translational energy toward the surface. The collision was modeled as adiabatic dynamics on the ground potential energy surface by a net-neutral system of a coiled cellohexaose anion approaching a positively charged Cu slab understood to contain the image charge of the incoming cellohexaose anion (Figure S5). To gain qualitative insights into the collision dynamics, we limited our calculations to one of the many possible gas-phase orientations (i.e., the geometry where the C5–C6 points away from the surface).

In agreement with the experimental trend, MD calculations show that, at ECOL = 0.5 eV (Figure 5a and Video 1, Supporting Information), the collision preserved the coiled gas-phase conformer on the surface as coiled, and at ECOL = 5.0 eV (Figure 5b and Video 2 in the Supporting Information), the collision changed the gas-phase conformer into a final conformation similar to that in Figure 2j. Analysis of the computed dynamics (Figure S6) show the molecule to be accelerated toward the surface, followed by the conversion of its molecular translation into its low-frequency molecular vibrations. The molecular acceleration increasing the molecular translational energy by 2.7 eV in the 0.5 eV trajectory and by 1.8 eV in the 5.0 eV trajectory was understood to be mainly driven by the attraction between the hydroxide group (RO–) and the surface en route to form the covalent RO–Cu bond. The greater increase of translational energy in the 0.5 eV trajectory was due to the dynamical steering effect39 wherein a slow approaching molecule possesses more time to be reoriented by the attractive forces from the surface, allowing it to land on a more favorable adsorption site and give greater energy release.

The surface collision of the molecule initiates energy transfer from its translational degree-of-freedom to other degrees-of-freedom (Figure S6). This highly inelastic collision prevents the incident molecule from bouncing back to the vacuum by converting ∼80% of its incident translational energy into its rotations and vibrations, as well as the surface vibrations. The calculation shows that the substantial flow of the incident translational energy into the molecular vibrational energy (∼40%) is responsible for the molecular conformation dynamics. In the 0.5 eV trajectory, the ∼1 eV gain of vibrational energy is insufficient to significantly change the molecular conformation, while the ∼2 eV gain in the 5 eV trajectory is enough to initiate the conformation change. The motion that causes this conformation change is identified as the interunit rotation between glucose units (Figure 5b), which breaks the interunit hydrogen bonds. This interunit rotation changes the torsional angles of the glycosidic bond that dictate the oligosaccharide conformation (Figure S6). Our result shows that the collision directly converts the molecular translation into low-frequency torsional motions that are pertinent to conformation dynamics.

3. Conclusions

Soft molecule–surface collision was shown to sample the intrinsic conformation space of an oligosaccharide. Controlled exploration of the conformation space was achieved by tuning the collision energy that can be minimized to preserve the gas-phase conformer on the surface or can be increased to sample many conformation states. The preservation of a fragile molecular conformation from the gas phase to the surface was demonstrated. As an outlook, starting from a native electrospray,8 near native as well as excited conformation states can be isolated on the surface for structural investigations. Synthetic oligosaccharides40,41 can be examined to reveal the effect of chemical modification on their conformation with the goal to achieve chemical control of oligosaccharide conformation, and subsequently, function. These studies will shed light on the important role oligosaccharides play in biology13 as well as in material science.14

The collision-induced conformation change described here should be generally applicable for any complex molecule colliding with a surface. Altogether, this approach enables the study of both ground and excited conformation states at the single-molecule level of any complex molecule that can be electrosprayed. Preservation and imaging of gas-phase adducts on a surface will reveal molecular interactions that are central in biology9,22 and chemical reactions.42,43

4. Materials and Methods

4.1. Experiment

Cellohexaose was synthesized by previously reported methods44 and α-cyclodextrin (purity ≥98%) was purchased from Sigma-Aldrich. Both compounds were collided onto a surface using the home-built electrospray ion-beam deposition (ES-IBD) apparatus, described in detail elsewhere.26 In brief, the spray solution was prepared by adding 10 μL of 15% v/v aqueous NH3 into a 640 μL aliquot of 10–5 M cellohexaose or α-cyclodextrin in a 4:5 water/ethanol (v/v) mixture. The negative ions generated from the electrospray ionization of this solution at an emitter voltage of ∼3 kV were mass-selected by quadrupoles to give a chemically pure ion beam of cellohexaose monoanion ([M–H]−1, m/z = 988) or α-cyclodextrin monoanion ([M–H]−1, m/z = 971). We used the negative ion beam as opposed to the positive ion beam to avoid the sodium-molecule adducts that were present as an impurity in the positive beam. The ion beam was transmitted to an ultrahigh vacuum chamber (P ∼ 10–10 mbar) and steered to a Cu(100) substrate held at ∼120 K at a normal incident angle. The Cu(100) surface was chosen to prevent the molecular diffusion at ∼120 K. The ion–surface collision energy was controlled by applying a retarding potential on the Cu substrate, which decelerated the incident ion to a desired kinetic energy. Prior to the collision experiment, the Cu(100) was cleaned by repeated sputtering by Ar ions (1 keV beam energy) and annealing (∼600 K). After the collision experiment, the sample, while held at ∼90 K, was transferred to a commercial low-temperature scanning tunneling microscope (Omicron Fermi SPM) where the Cu surface was scanned at 11 K. All images shown were taken with constant-current mode using a current set point of 1 pA at a surface bias of +0.3 V. Tip manipulation of the adsorbed molecule was performed by increasing the set point from 1 to 10 pA, which caused mechanical contact between the STM tip and the molecule.

Real-space analysis of the molecules were done by WSxM software,45 yielding, for every cellohexaose molecule observed, a set of six coordinates from (X1,Y1) to (X6,Y6) that each corresponds to the center of the glucose pyranose ring (the index 1 refers to the unit at the nonreducing end and the index 6 refers to the unit at the reducing end). The least-squares overlay performed for every chain category in Figure 2 used two-dimensional translation and rotation of the measured chain coordinates to minimize the root-mean-square distance between the same-index V units for the coiled and partially coiled chains, or between the same-index H units for the extended chain. The curvature of the cellohexaose chain was computed as the difference between the estimated chain tangent at each Glc unit. For example, the curvature formed between the nth and (n+1)th Glc units is equal to the tangent difference at (Xn,Yn) and (Xn+1,Yn+1).

4.2. Theory

Density functional theory (DFT) using the plane-wave basis sets, as implemented in the Vienna Ab-initio Simulation Package (VASP, version 5.4.4),46,47 was used to model the experimental result. The calculation employed projection-augmented wave function (PAW)48,49 and Perdew–Burke–Ernzerhof (PBE) functional50 with a cutoff energy of 400 eV. van der Waals correction was added using Grimme’s DFT-D3 approach.51 The Cu(100) surface was modeled as a three-layer slab separated by 21 Å of vacuum space, with the bottom layer frozen. The molecular dynamics (MD) calculations used a (10 × 8) slab for 5.0 eV collision simulation and a (8 × 8) slab for 0.5 eV collision simulation, while the relaxation calculations used a (11 × 6) slab. All calculations sampled only the Γ point of the k mesh. For relaxation calculations, all atoms, except the bottom layer of the Cu slab, were relaxed until the forces were below 0.01 eV/Å. STM simulation was performed with the Tersoff-Hammann method52 and visualized by Hive software.53,54 Visualization of molecular structures were done using VESTA software.55

MD calculations, implemented in VASP, were performed as a microcanonical ensemble, preserving the total number of atoms (N), volume (V), and energy (E). The singly dehydrogenated cellohexaose molecule was placed ∼11 Å above the surface, giving the ground electronic state shown in Figure S5. The velocities in the cellohexaose molecule and the surface were initialized by a random velocities vector sampled from a Boltzmann distribution at room temperature (298 K) and at 120 K, respectively. On top of these velocities, the center-of-mass velocity corresponding to either 0.5 or 5.0 eV translational energy toward the surface was added to the cellohexaose molecule. The molecular dynamics calculations were performed with a time step of 0.5 fs, which gave a negligible energy drift as low as 25 meV/ps.

Gas-phase DFT calculations of isolated molecular anions were performed in ORCA (version 4.0.1.2)56 using the localized basis sets. The parameters used were similar to that used for VASP, that is, using PBE functional50 with Grimme’s DFT-D3 correction.51 The calculations were performed using the basis sets ma-def2-SVP57,58 and the auxiliary basis sets were chosen automatically.59

Acknowledgments

K.A. thanks the Alexander von Humboldt Foundation. M.D. thanks the Minerva Fast Track Program and the MPG-FhG Cooperation Project Glyco3Dysplay.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c09933.

  • Additional experimental results and additional ab initio calculation results (PDF)

  • Video 1: Computed dynamics of cellohexaose colliding with a Cu(100) surface at 0.5 eV incident translational energy; the simulation shows the gas-phase conformation to be preserved on the surface; the movie was rendered at 15 fps (MOV)

  • Video 2: Computed dynamics of cellohexaose colliding with a Cu(100) surface at 5.0 eV incident translational energy; the simulation shows the gas-phase conformer to undergo conformation change upon collision; the movie was rendered at 15 fps (MOV)

The authors declare no competing financial interest.

Supplementary Material

ja0c09933_si_001.pdf (794KB, pdf)
ja0c09933_si_002.mov (1.8MB, mov)
ja0c09933_si_003.mov (1.7MB, mov)

References

  1. Lindorff-Larsen K.; Best R. B.; DePristo M. A.; Dobson C. M.; Vendruscolo M. Simultaneous determination of protein structure and dynamics. Nature 2005, 433, 128–132. 10.1038/nature03199. [DOI] [PubMed] [Google Scholar]
  2. Lerner E.; Cordes T.; Ingargiola A.; Alhadid Y.; Chung S.; Michalet X.; Weiss S. Toward dynamic structural biology: Two decades of single-molecule Förster resonance energy transfer. Science 2018, 359, eaan1133 10.1126/science.aan1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Boehr D. D.; Nussinov R.; Wright P. E. The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol. 2009, 5, 789–796. 10.1038/nchembio.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Ma B.; Kumar S.; Tsai C.-J.; Nussinov R. Folding funnels and binding mechanisms. Protein Eng., Des. Sel. 1999, 12, 713–720. 10.1093/protein/12.9.713. [DOI] [PubMed] [Google Scholar]
  5. Jarvis M. Cellulose stacks up. Nature 2003, 426, 611–612. 10.1038/426611a. [DOI] [PubMed] [Google Scholar]
  6. Fernandes A. N.; Thomas L. H.; Altaner C. M.; Callow P.; Forsyth V. T.; Apperley D. C.; Kennedy C. J.; Jarvis M. C. Nanostructure of cellulose microfibrils in spruce wood. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, E1195–E1203. 10.1073/pnas.1108942108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Dill K. A.; MacCallum J. L. The Protein-Folding Problem, 50 Years On. Science 2012, 338, 1042–1046. 10.1126/science.1219021. [DOI] [PubMed] [Google Scholar]
  8. Marcoux J.; Robinson C. V. Twenty Years of Gas Phase Structural Biology. Structure 2013, 21, 1541–1550. 10.1016/j.str.2013.08.002. [DOI] [PubMed] [Google Scholar]
  9. Seo J.; Hoffmann W.; Warnke S.; Huang X.; Gewinner S.; Schöllkopf W.; Bowers M. T.; von Helden G.; Pagel K. An infrared spectroscopy approach to follow β-sheet formation in peptide amyloid assemblies. Nat. Chem. 2017, 9, 39–44. 10.1038/nchem.2615. [DOI] [PubMed] [Google Scholar]
  10. Rothemund P. W. K. Folding DNA to create nanoscale shapes and patterns. Nature 2006, 440, 297–302. 10.1038/nature04586. [DOI] [PubMed] [Google Scholar]
  11. Wormald M. R.; Petrescu A. J.; Pao Y.-L.; Glithero A.; Elliott T.; Dwek R. A. Conformational Studies of Oligosaccharides and Glycopeptides: Complementarity of NMR, X-ray Crystallography, and Molecular Modelling. Chem. Rev. 2002, 102, 371–386. 10.1021/cr990368i. [DOI] [PubMed] [Google Scholar]
  12. Woods R. J. Predicting the Structures of Glycans, Glycoproteins, and Their Complexes. Chem. Rev. 2018, 118, 8005–8024. 10.1021/acs.chemrev.8b00032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Varki A. Biological roles of glycans. Glycobiology 2017, 27, 3–49. 10.1093/glycob/cww086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Klemm D.; Heublein B.; Fink H.-P.; Bohn A. Cellulose: Fascinating Biopolymer and Sustainable Raw Material. Angew. Chem., Int. Ed. 2005, 44, 3358–3393. 10.1002/anie.200460587. [DOI] [PubMed] [Google Scholar]
  15. Mori T.; Chikayama E.; Tsuboi Y.; Ishida N.; Shisa N.; Noritake Y.; Moriya S.; Kikuchi J. Exploring the conformational space of amorphous cellulose using NMR chemical shifts. Carbohydr. Polym. 2012, 90, 1197–1203. 10.1016/j.carbpol.2012.06.027. [DOI] [PubMed] [Google Scholar]
  16. Cumming D. A.; Carver J. P. Virtual and solution conformations of oligosaccharides. Biochemistry 1987, 26, 6664–6676. 10.1021/bi00395a016. [DOI] [PubMed] [Google Scholar]
  17. Fink H.-P.; Philipp B.; Paul D.; Serimaa R.; Paakkari T. The structure of amorphous cellulose as revealed by wide-angle X-ray scattering. Polymer 1987, 28, 1265–1270. 10.1016/0032-3861(87)90435-6. [DOI] [Google Scholar]
  18. Sugiyama H.; Hisamichi K.; Usui T.; Sakai K.; Ishiyama J. A study of the conformation of β-1,4-linked glucose oligomers, cellobiose to cellohexaose, in solution. J. Mol. Struct. 2000, 556, 173–177. 10.1016/S0022-2860(00)00630-X. [DOI] [PubMed] [Google Scholar]
  19. Nishiyama Y.; Langan P.; Chanzy H. Crystal Structure and Hydrogen-Bonding System in Cellulose Iβ from Synchrotron X-ray and Neutron Fiber Diffraction. J. Am. Chem. Soc. 2002, 124, 9074–9082. 10.1021/ja0257319. [DOI] [PubMed] [Google Scholar]
  20. Simons J. P. Good vibrations: probing biomolecular structure and interactions through spectroscopy in the gas phase. Mol. Phys. 2009, 107, 2435–2458. 10.1080/00268970903409812. [DOI] [Google Scholar]
  21. Cocinero E. J.; Gamblin D. P.; Davis B. G.; Simons J. P. The Building Blocks of Cellulose: The Intrinsic Conformational Structures of Cellobiose, Its Epimer, Lactose, and Their Singly Hydrated Complexes. J. Am. Chem. Soc. 2009, 131, 11117–11123. 10.1021/ja903322w. [DOI] [PubMed] [Google Scholar]
  22. Cocinero E. J.; Carcabal P.; Vaden T. D.; Simons J. P.; Davis B. G. Sensing the anomeric effect in a solvent-free environment. Nature 2011, 469, 76–79. 10.1038/nature09693. [DOI] [PubMed] [Google Scholar]
  23. Rieping W.; Habeck M.; Nilges M. Inferential Structure Determination. Science 2005, 309, 303–306. 10.1126/science.1110428. [DOI] [PubMed] [Google Scholar]
  24. Kruschel D.; Zagrovic B. Conformational averaging in structural biology: issues, challenges and computational solutions. Mol. BioSyst. 2009, 5, 1606–1616. 10.1039/b917186j. [DOI] [PubMed] [Google Scholar]
  25. Grill V.; Shen J.; Evans C.; Cooks R. G. Collisions of ions with surfaces at chemically relevant energies: Instrumentation and phenomena. Rev. Sci. Instrum. 2001, 72, 3149–3179. 10.1063/1.1382641. [DOI] [Google Scholar]
  26. Rauschenbach S.; Ternes M.; Harnau L.; Kern K. Mass Spectrometry as a Preparative Tool for the Surface Science of Large Molecules. Annu. Rev. Anal. Chem. 2016, 9, 473–498. 10.1146/annurev-anchem-071015-041633. [DOI] [PubMed] [Google Scholar]
  27. Abb S.; Tarrat N.; Cortés J.; Andriyevsky B.; Harnau L.; Schön J. C.; Rauschenbach S.; Kern K. Carbohydrate Self-Assembly at Surfaces: STM Imaging of Sucrose Conformation and Ordering on Cu(100). Angew. Chem., Int. Ed. 2019, 58, 8336–8340. 10.1002/anie.201901340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Wu X.; Delbianco M.; Anggara K.; Michnowicz T.; Pardo-Vargas A.; Bharate P.; Sen S.; Pristl M.; Rauschenbach S.; Schlickum U.; Abb S.; Seeberger P. H.; Kern K. Imaging Single Glycans. Nature 2020, 582, 375–378. 10.1038/s41586-020-2362-1. [DOI] [PubMed] [Google Scholar]
  29. Singh A. Imaging single glycan molecules. Nat. Methods 2020, 17, 757. 10.1038/s41592-020-0919-4. [DOI] [PubMed] [Google Scholar]
  30. Kay B. D.; Raymond T. D.; Coltrin M. E. Observation of Direct Multiquantum Vibrational Excitation in Gas-Surface Scattering: NH3 on Au(111). Phys. Rev. Lett. 1987, 59, 2792–2794. 10.1103/PhysRevLett.59.2792. [DOI] [PubMed] [Google Scholar]
  31. Golibrzuch K.; Baraban J. H.; Shirhatti P. R.; Werdecker J.; Bartels C.; Wodtke A. M. Observation of Translation-to-Vibration Excitation in Acetylene Scattering from Au(111): A REMPI Based Approach. Z. Phys. Chem. 2015, 229, 1929. 10.1515/zpch-2015-0606. [DOI] [Google Scholar]
  32. Krumbein L.; Anggara K.; Stella M.; Michnowicz T.; Ochner H.; Abb S.; Rinke G.; Portz A.; Dürr M.; Schlickum U.; Baldwin A.; Floris A.; Kern K.; Rauschenbach S.. Fast Molecular Compression by a Hyperthermal Collision Gives Bond-Selective Mechanochemistry 2020. arXiv:2007.04497 [physics.chem-ph]. [DOI] [PubMed]
  33. Go N.; Noguti T.; Nishikawa T. Dynamics of a small globular protein in terms of low-frequency vibrational modes. Proc. Natl. Acad. Sci. U. S. A. 1983, 80, 3696–3700. 10.1073/pnas.80.12.3696. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Brooks B.; Karplus M. Harmonic dynamics of proteins: normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc. Natl. Acad. Sci. U. S. A. 1983, 80, 6571–6575. 10.1073/pnas.80.21.6571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Levitt M.; Sander C.; Stern P. S. Protein normal-mode dynamics: Trypsin inhibitor, crambin, ribonuclease and lysozyme. J. Mol. Biol. 1985, 181, 423–447. 10.1016/0022-2836(85)90230-X. [DOI] [PubMed] [Google Scholar]
  36. Dobbins S. E.; Lesk V. I.; Sternberg M. J. E. Insights into protein flexibility: The relationship between normal modes and conformational change upon protein–protein docking. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 10390–10395. 10.1073/pnas.0802496105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Almond A.; Sheehan J. K. Predicting the molecular shape of polysaccharides from dynamic interactions with water. Glycobiology 2003, 13, 255–264. 10.1093/glycob/cwg031. [DOI] [PubMed] [Google Scholar]
  38. Boraston A. B.; Bolam D. N.; Gilbert H. J.; Davies G. J. Carbohydrate-binding modules: fine-tuning polysaccharide recognition. Biochem. J. 2004, 382, 769–781. 10.1042/BJ20040892. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Gross A.; Wilke S.; Scheffler M. Six-Dimensional Quantum Dynamics of Adsorption and Desorption of H2 at Pd(100): Steering and Steric Effects. Phys. Rev. Lett. 1995, 75, 2718–2721. 10.1103/PhysRevLett.75.2718. [DOI] [PubMed] [Google Scholar]
  40. Delbianco M.; Kononov A.; Poveda A.; Yu Y.; Diercks T.; Jiménez-Barbero J.; Seeberger P. H. Well-Defined Oligo- and Polysaccharides as Ideal Probes for Structural Studies. J. Am. Chem. Soc. 2018, 140, 5421–5426. 10.1021/jacs.8b00254. [DOI] [PubMed] [Google Scholar]
  41. Guberman M.; Bräutigam M.; Seeberger P. H. Automated glycan assembly of Lewis type I and II oligosaccharide antigens. Chem. Sci. 2019, 10, 5634–5640. 10.1039/C9SC00768G. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Chang Y.-P.; Długołȩcki K.; Küpper J.; Rösch D.; Wild D.; Willitsch S. Specific Chemical Reactivities of Spatially Separated 3-Aminophenol Conformers with Cold Ca+ Ions. Science 2013, 342, 98–101. 10.1126/science.1242271. [DOI] [PubMed] [Google Scholar]
  43. Ingram A. J.; Boeser C. L.; Zare R. N. Going beyond electrospray: mass spectrometric studies of chemical reactions in and on liquids. Chem. Sci. 2016, 7, 39–55. 10.1039/C5SC02740C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Yu Y.; Tyrikos-Ergas T.; Zhu Y.; Fittolani G.; Bordoni V.; Singhal A.; Fair R. J.; Grafmüller A.; Seeberger P. H.; Delbianco M. Systematic Hydrogen-Bond Manipulations To Establish Polysaccharide Structure–Property Correlations. Angew. Chem., Int. Ed. 2019, 58, 13127–13132. 10.1002/anie.201906577. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Horcas I.; Fernández R.; Gómez-Rodríguez J. M.; Colchero J.; Gómez-Herrero J.; Baro A. M. WSXM: A software for scanning probe microscopy and a tool for nanotechnology. Rev. Sci. Instrum. 2007, 78, 013705. 10.1063/1.2432410. [DOI] [PubMed] [Google Scholar]
  46. Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  47. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  48. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  49. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  50. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  51. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  52. Tersoff J.; Hamann D. R. Theory of the scanning tunneling microscope. Phys. Rev. B: Condens. Matter Mater. Phys. 1985, 31, 805–813. 10.1103/PhysRevB.31.805. [DOI] [PubMed] [Google Scholar]
  53. Vanpoucke D.HIVE STM-program. The Delocalized Physicist. http://dannyvanpoucke.be/hive-stm-en/ (accessed Oct 25, 2020). [Google Scholar]
  54. Vanpoucke D. E. P.; Brocks G. Formation of Pt-induced Ge atomic nanowires on Pt/Ge(001): A density functional theory study. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 241308. 10.1103/PhysRevB.77.241308. [DOI] [Google Scholar]
  55. Momma K.; Izumi F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. 10.1107/S0021889811038970. [DOI] [Google Scholar]
  56. Neese F. The ORCA program system. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 73–78. 10.1002/wcms.81. [DOI] [Google Scholar]
  57. Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  58. Zheng J.; Xu X.; Truhlar D. G. Minimally augmented Karlsruhe basis sets. Theor. Chem. Acc. 2011, 128, 295–305. 10.1007/s00214-010-0846-z. [DOI] [Google Scholar]
  59. Stoychev G. L.; Auer A. A.; Neese F. Automatic Generation of Auxiliary Basis Sets. J. Chem. Theory Comput. 2017, 13, 554–562. 10.1021/acs.jctc.6b01041. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja0c09933_si_001.pdf (794KB, pdf)
ja0c09933_si_002.mov (1.8MB, mov)
ja0c09933_si_003.mov (1.7MB, mov)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES