Evaluation of a deep learning-based pelvic synthetic CT generation technique for MRI-based prostate proton treatment planning

Abstract

The purpose of this work is to validate the application of a deep learning-based method for pelvic synthetic CT (sCT) generation that can be used for prostate proton beam therapy treatment planning. We propose to integrate dense block minimization into 3D cycle-consistent generative adversarial networks (cycleGAN) framework to effectively learn the nonlinear mapping between MRI and CT pairs. A cohort of 17 patients with co-registered CT and MR pairs were used to test the deep learning-based sCT generation method by leave-one-out cross-validation. Image quality between the sCT and CT images, gamma analysis passing rate, dose-volume metrics, distal range displacement, and the individual pencil beam Bragg peak shift between sCT- and CT-based proton plans were evaluated. The average mean absolute error (MAE) was 51.32 ± 16.91 HU. The relative differences of the statistics of the PTV dose-volume histogram (DVH) metrics in between sCT and CT were generally less than 1%. Mean values of dose difference, absolute dose difference (in percent of the prescribed dose) were −0.07% ± 0.07% and 0.23% ± 0.08%. Mean gamma analysis pass rate of 1 mm/1%, 2 mm/2%, 3 mm/3% criteria with 10% dose threshold were 92.39% ± 5.97%, 97.95% ± 2.95% and 98.97% ± 1.62% respectively. The median, mean and standard deviation of absolute maximum range differences were 0.09 cm and 0.23 ± 0.25 cm. The median and mean Bragg peak shifts among the 17 patients were 0.09 cm and 0.18 ± 0.07 cm. The image similarity, dosimetric and distal range agreement between sCT and original CT suggests the feasibility of further development of an MRI-only workflow for prostate proton radiotherapy.

1. Introduction

Prostate cancer is the most commonly diagnosed cancer in men (Siegel et al 2019). Radiation therapy is a common treatment modality chosen by around 25% of prostate cancer patients in the United States (Cooperberg et al 2010). During the last a few decades, radiation planning and delivery techniques have improved treatment outcomes by escalating the dose to the prostate without exceeding the tolerance dose of healthy tissues (Thariat et al 2012). The recent adoption of proton beam therapy, more specifically, pencil beam scanning (PBS), allows proton beams to be delivered spot-by-spot, with flexible intensity, position and penetration depth. The steep dose gradient at the end of the proton beam path allows the delivery of a high dose to the target while sparing the structures on the distal side. While proton dose prediction is more accurately calculated by the stopping power ratio rather than the Hounsfield unit (HU), current proton treatment planning still depends on computed tomography (CT) as stopping power cannot be directly measured. At present, all treatment planning systems (TPSs) relate HU values to relative stopping power for dose calculation (Grant et al 2014). In addition, the CT HU values provide the electron density information necessary to generate digitally reconstructed radiograph (DRR) for planning design and daily patient setup. Poor soft tissue contrast is a major limitation of CT. Delineation of clinical target volumes (CTVs) remains a weak link in radiotherapy. This is especially important for modern radiation techniques such as PBS, as this error has a direct impact on treatment outcome. In the application of prostate contouring, the poor soft tissue contrast between the prostate, rectum and pelvic floor muscles on CT can attribute to on average a 30% overestimation of the prostate volume (Gao et al 2007). To precisely and robustly delineate target structures and organs at risk (OARs), magnetic resonance imaging (MRI) is often registered to the planning CT. T2-weighted MRI is currently the best modality to depict the anatomy of the prostate and periprostatic tissue, which leads to a significant reduction in both prostate volume and inter-observer variation over CT-based delineation (Salembier et al 2018). However, a new level of complexity and uncertainty is inherent in the MR-CT pair registration process. Because MR and CT images are acquired separately, registration errors are common, which can introduce a 2–5 mm uncertainty (Edmund and Nyholm 2017). At the site of the pelvis, an uncertainty of 2 mm was reported (Roberson et al 2005). Unlike small errors in treatment delivery and setup, which are occurred daily in a random fashion, uncertainties or errors introduced during the treatment planning process are more likely to be systematic and persist throughout the treatment course. Therefore, they harbor a huge potential for adversely affecting tumor control and/or normal tissue sparing. The need for stringent congruence between planning and treatment target to minimize the suboptimal treatment outcome is urgent. MRI-only treatment planning has become more popular because it does not have the aforementioned limitations as CT images and unavoidable registration uncertainty between MR and CT images. Moreover, MR-guided radiotherapy has been studied for advantages of motion correction (Lagendijk et al 2014, Kontaxis et al 2017, Oborn et al 2017), so the MRI images could be also used to synthesize CT images for potential on-line treatment planning. The benefit of MRI-only treatment workflow is obvious: besides more accurate target and normal tissue delineation, it can also spare the patient from CT radiation doses, which are particularly concerning for pediatric patients who are more sensitive to the effects of radiation exposure and for patients undergoing adaptive radiotherapy where multiple cone-beam CTs (CBCTs) are acquired (Pileggi et al 2018). Great attention must be paid to put the application of CT to rest, however, because the MR signals are not explicitly associated with HU values. Therefore, to replace CT, a major task in an MRI-only treatment workflow is the generation of synthetic CT (sCT) images that can be used as CT surrogates for dose calculation and DRR generation.

Currently available methods to produce sCT broadly fall into the following three categories: segmentation-based (Hsu et al 2013, Korhonen et al 2014, Juttukonda et al 2015, Ladefoged et al 2015, Bredfeldt et al 2017), atlas-based (Dowling et al 2012, 2015, Gudur et al 2014, Uh et al 2014, Sjölund et al 2015, Arabi et al 2016, Burgos et al 2017) and machine learning-based methods (Lei et al, Li et al 2014, Huynh et al 2016, Han, 2017, Nie et al 2017, Bayisa et al 2018, Emami et al 2018, Xiang et al 2018, Yang et al 2019). Although widely varied in approach and algorithm, the general idea is to use mathematical models based on pre-acquired MR-CT pairs to predict the new sCT from incoming MR images. (1) Segmentation-based methods usually assign single bulk densities to tissue classes delineated from either a CT or an MR image (Guerreiro et al 2017). Fuzzy C-means algorithms (Bredfeldt et al 2017) provide ways for automatic segmentation of MR images into predetermined classes. Subject-specific bone density can be obtained by using a second-order polynomial model (Korhonen et al 2014) or through the $R_2^{*}$ signal derived from the ultra-short echo time (UTE) images (Ladefoged et al 2015). (2) Atlas-based methods can use a single template or a database of co-registered MR and CT atlas pairs. First, the atlas MR images are deformably registered to the new MR images, and the same transformations are then applied to the corresponding atlas CT images. The HU information from the deformed atlas CT images can thereafter be transformed into the new incoming MR images (Dowling et al 2012). If multi-atlases are used, the atlas CT numbers can be fused to generate the final sCT (Dowling et al 2015, Burgos et al 2017). (3) Machine learning methods can directly learn MR-to-CT intensity mapping from the training MR-CT pairs. The detailed review of machine learning-based methods is given in the next paragraph. In general, there are two separate stages: training and prediction. Once the training is completed, a new sCT can be predicted in a short amount of time when a new MR is fed in. Compared to the learning-based method, segmentation-based methods are limited by the requirement of manually contouring or predetermine segmentation classes, and atlas-based methods are limited by computationally expensive and the strong dependence on the accuracy of the registration, limiting their application only to stationary anatomic regions (Andreasen et al 2016b). The drawbacks of current machine learning-based methods include discontinuous prediction results across slices due to the use of 2D model (Largent et al 2018), the often limited number of training samples available (Shen et al 2017), and the difficulty of obtaining MR and CT training pairs with the exactly same organ shape and location, which could degrade the prediction accuracy.

Learning-based methods can be mainly categorized into dictionary learning-based methods (Torrado-Carvajal et al 2016, Lei et al 2018b), random forests (Huynh et al 2016, Andreasen et al 2016a, Lei et al 2018a) and deep-learning-based methods (Nie et al 2016, 2017, 2018, Han 2017, Wolterink et al 2017, Emami et al 2018, Xiang et al 2018). The key difference between deep-learning and random forest/dictionary learning-based methods is that the former can automatically learn useful features of the data, eliminating the need for handcrafted features such as Haar-like, discrete cosine transform (DCT) and least absolute shrinkage and selection operator (LASSO) used in random forest methods (Huynh et al 2016) and dictionary learning (Xiang et al 2018). In the domain of deep-learning-based sCT generation, Liu et al used convolutional neural networks (CNNs) to generate a PET attenuation correction map from the corresponding MR image (Liu et al 2018). Nie et al proposed to train a patch-based relationship from an MR to a CT image by using 3D fully convolution neural network (FCN) (Nie et al 2016). In comparison to the patch-based method, Han et al applied the 2D FCN to learn an image-based mapping (Han 2017). One of the main limitations of the CNN-based methods is that even slight voxel-wise misalignment of MR-CT pairs may lead to blurred results (Wolterink et al 2017). Generative adversarial networks (GANs) have been introduced to improve the quality of the sCT. These models incorporate an adversarial loss term in addition to the conventional synthesis layers, aiming to produce more realistic CT data (Nie et al 2017, 2018, Emami et al 2018). While being a clear improvement over CNN-based method, GAN-based methods still suffer from misregistration, resulting in deteriorated sCT accuracy.

More recently, cycleGAN was proposed to deal with the unpaired training data (Zhu et al 2017). Wolterink et al (2017) showed that the use of cycleGAN can mitigate the sensitivity of training model to MR-CT misalignment. Their work was applied to 2D images without the use of the gradient consistency loss. Hiasa et al (2018) used 2D cycleGAN and gradient consistency loss. Wang et al (2018) applied deformation-invariant cycleGAN method by using deformable convolutional layers and new cycle-consistency losses. But the network is still based on 2D transverse plane that would lose some spatial and structural information. Recently, we have proposed 3D dense cycleGAN based networks to generate sCT from routine anatomical MR images (Lei et al 2019). Dense Blocks (Huang et al 2017) were used for better contextual and structural feature extraction. This work aimed to apply this method to generate pelvic sCT for patients with prostate cancer and evaluate the dosimetric accuracy of these sCTs in proton treatment planning. In prostate cancer PBS planning, the typical beam arrangement requires traversing the bony structures such as femoral head, pubic symphysis and ischial tuberosity. This requires high bone HU accuracy of the sCT, however, bones are ambiguous on MR images which make the MRto-CT prediction difficult. Therefore, the quality of the sCT in terms of HU accuracy can be rigorously evaluated by pelvic proton treatment planning. In this work, together with the commonly applied imaging endpoints, dosimetric endpoints, and the newly adopted distal range endpoint, we introduced the individual pencil beam Bragg peak shift analysis to fully evaluate the feasibility of MRI-only proton treatment planning using our 3D dense cycleGAN networks.

2. Materials and methods

2.1. Image acquisition and registration

17 prostate cancer patients who were treated with photon radiotherapy at a single academic center were randomly selected. Image data were extracted under an IRB-approved protocol. Routine treatment-planning pelvic CT and diagnostic MR scans were acquired. CT scans were acquired on a Siemens (Erlangen, Germany) SOMATOM Definition AS with a voxel size of 0.98 mm × 0.98 mm × 2 mm. T2-weighted MRIs were acquired on Siemens Avanto 1.5T scanner with a voxel size of 1 mm × 1 mm × 2 mm. The MR and CT were acquired at different time intervals, ranging from one day to two months. During the acquisition, the patients were in supine position and knee rest was used to minimize rotation of pelvis. The MR images were aligned to the corresponding CT images using the rigid registration method in Velocity AI 3.2.1 (Varian Medical Systems, Inc. Palo Alto, USA). The registered MR images were then resampled to obtain the same field-of-view and voxel size as the CT images. The resampled MR and CT pairs were used as the training dataset for our deep-learning-based algorithm.

2.2. sCT generation

We recently proposed a novel MR to sCT generation method (Lei et al 2019). The reader can find more specific information in Lei et al’s paper. The methodologies are briefly reviewed below. For the cohort of 17 prostate cancer patients, we used leave-one-out cross-validation. 3D cycleGAN that contains nine dense blocks (Huang et al 2017) was used in the generator to capture both structural and textural information and to cope with local mismatches between MR and CT images. A novel compound loss function was further employed to effectively differentiate the structure boundaries with HU variations and to retain the sharpness of the sCT image. Figure 1 shows the schematic flowchart of the proposed dense cycleGAN network for MRI-based sCT generation. The networks can be broken into two stages: training (shown on the upper) and synthesizing (shown on the bottom). In the generator architecture, the feature map first undergoes two down-sampling convolutional layers to be downsized, then it passes nine dense blocks, after which it goes through two deconvolutional layers and a tanh layer to enable an end-to-end mapping. In the dense-block structure, concatenated information of the input and the feature map from previous convolutional layer is brought forward to the next convolutional layer to produce a different feature map; in this way, both low- and high-frequency information can be learned. In the discriminator architecture, the feature map undergoes three down-sampling convolutional layers followed by a sigmoid layer to binarize the output. This output is regarded as the distribution of the input. During training, the patches from training MR and CT images are extracted and go through the generator networks to produce the corresponding synthetic images. The synthetic images patches then go through the opposite generators to produce the corresponding cycle images. The generator’s training objective is to produce synthetic/cycle images that are similar to the real images, while the discriminator’s training objective is to differentiate the synthetic/cycle images from the real images. After the training finished, an incoming MR image is fed into the well-trained MRI to CT model to produce the corresponding sCT image.

Figure 1.

Schematic flowchart of the proposed dense cycleGAN network for MRI-based sCT generation. The networks can be broken into two stages: training (shown on the upper) and synthesizing (shown on the bottom). During training, the patches from training MR and CT images are extracted and go through the generator networks to produce the corresponding synthetic images. The synthetic images patches then go through the opposite generator to produce the corresponding cycle images. The generator’s training objective is to produce synthetic/cycle images that are similar to the real images, while the discriminator’s training objective is to differentiate the synthetic/cycle images from the real images. Back-propagation is applied in both networks to enhance the performance of both the generators and discriminators, which ultimately result in optimal sCT prediction. The accuracies of both generator and discriminator network are directly dependent on the design of their corresponding loss functions. A novel compound loss function was employed in the generator network to better differentiate different structures, as well as to retain sCT sharpness. After the training finished, an incoming MR image is fed into the well-trained MRI to CT model to produce the corresponding sCT image.

The accuracies of both the generator and discriminator networks are directly dependent on the design of their corresponding loss functions. The generator loss function in this study consists of two losses: one is the adversarial loss to distinguish real images from synthetic images; the other is the distance loss to measure the distance between real and synthetic images or between real and cycle images. Distance loss consists of l_p-norm and the gradient difference (GD) between the two images. The l_p-norm (p = 1.5) distancewas used to overcome the limitations of the l₁-norm and l₂-norm distance loss such as misclassification by mean absolute distance (MAD) and blurry images by mean squared distance (MSD) (Michael et al 2015).

We used patch (64 × 64 × 64) with overlap (18 × 18 × 18) as input. The metrics were computed within the whole image field-of-view. Each patient’s MRI/CT data will have more than 6144 patches. The model was trained and tested on an NVIDIA Tesla V100 with 32 GB memory with a batch size of 5. The training was stopped after 150 000 iterations. Training the model took around 15 h, and sCT generation for one test patient took about 2 min.

2.3. Evaluation strategies

2.3.1. Image quality

To quantify the image quality of the sCT, three commonly used metrics were applied: mean absolute error (MAE), peak signal-to-noise ratio (PSNR), and normalized cross-correlation (NCC). MAE represents the overall HU discrepancies between sCT and the reference CT images. PSNR measures if the sCT is a evenly or sparsely distributed prediction. NCC is a measure of similarity between CT and sCT as a function of the displacement. The three metrics are defined as:

$$\text{MAE}=\left|I_{\text{CT}}-I_{\text{sCT}}\right|$$

$$\text{PSNR}=10{\log }_{10}\left(\frac{Q^2}{{\Vert I_{\text{CT}}-I_{\text{SCT}}\Vert }_2^2/C}\right)$$

$$\text{NCC}=\frac{1}{C}\sum _{x,y,z}\frac{\left(I_{\text{CT}}(x,y,z)-{\mu }_{\text{CT}}\right)\left(I_{\text{sCT}}(x,y,z)-{\mu }_{\text{sCT}}\right)}{{\sigma }_{\text{CT}}{\sigma }_{\text{sCT}}}$$

where I_CT is the HU value of the CT image, I_sCT is the HU value of the sCT image, Q is the maximal HU value between I_CT and I_sCT, and C is the number of voxels in the image. μ_CT and μ_sCT are the mean of CT and sCT image. σ_CT and σ_sCT are the standard deviation of CT and sCT image. In general, a better sCT image has lower MAE, and higher PSNR and NCC values.

To evaluate the geometric displacement of the bone contour between CT and sCT images, we calculated Dice similarity coefficient (DSC), Hausdorff distance 95% (HD95), mean surface distance (MSD), and the residual mean square distance (RMSD). A displacement is associated with low DSC, HD, MSD and RMSD scores. For the bone area, HU > 300 was set as the threshold. Dilation was performed, followed by erosion to get a smooth boundary. Bone MAE was also calculated.

Compared to CT, MR images have more structural information and contrast in soft tissue regions and less at the bone and air interfaces. The traditional MR-to-CT synthesizing model is thus at risk of generating erroneous predictions and blurred images due to this un-constrained issue of many-to-one and one-to-many mapping. CycleGAN can deal with these issues by incorporating an additional CT-to-MR projection to approach one-to-one MR to CT mapping. This method is therefore able to produce sCT images with clearer tissue boundaries with varying HU intensities. For quantitative analysis of how our method was not sensible for local mismatch, we compared the proposed method, and the method without using cycle strategy. Spatial nonuniformity (SNU) was calculated in the selected regions of interest (ROIs). SNU is defined as follows:

$$\text{SNU}=\frac{{\overline{HU}}_{\max }-{\overline{HU}}_{\min }}{1000}\times 100\%.$$

${\overline{HU}}_{\max }$ and ${\overline{HU}}_{\min }$ are the averaged maximum and the minimum intensity of several ROIs. These ROIs were selected in the sCT image at the bony structure. The higher the SNU, the higher contrast and clearer bony structure of the sCT.

To compare to the state-of-art algorithms, we performed the sCT generation using Han’s deep convolution neural network (DCNN) (Han 2017, Arabi et al 2018) using the same patient cohort. Similar to Han’s study, the sagittal plane was set as the input patch. GAN based method was also evaluated. Two-tailed paired t-test was performed to calculate the p-value between our proposed and DCNN/GAN methods in terms of MAE, PSNR and NCC for body outline and MAE, DSC, HD95, and SNU for bone mask.

2.3.2. Dosimetric analysis

The cohort of prostate patients was treated with photon radiotherapy. The original planning CT images and associated structures were transferred to RayStation (RaySearch Laboratories, Stockholm, Sweden) TPS (version 8A). sCT images were then uploaded for dose comparison. Pencil beam scanning proton therapy was used as the treatment technique. An experienced dosimetrist performed the planning using Monte Carlo (v4.2) dose calculation engine. The prescribed dose and beam arrangement were carefully chosen to be representative of real clinical scenarios. Depending on the PTV geometry, two-beam and three-beam arrangements were selected with a total dose of either 4500 or 7920 cGy.

After the original CT images planning doses were generated, the evaluation dose calculations were performed on the sCT images with the same beam settings. Given the purpose of acquiring MR images in this patient cohort was to help target volume delineation, the derived sCT images only included the area directly adjacent to the prostate. The sCT thus have fewer axial slices than the longer CTs that are necessary for conventional treatment planning. The limited bore size of the MRI scanner also had a limited field of view (FOV), which results in lateral tissue truncation in the pelvis. To make the OAR comparison feasible, the surrounding tissues which fell outside the MRI FOV were adopted from the original CT to construct the complete volume of the patient to match the dimensions of the original CT.

The differences between the sCT and CT dose statistics were retrieved from RayStation. The following metrics were extracted: PTV dose-volume histogram (DVH) metrics including D_98%, D_mean and D_max; OAR rectum DVH metrics including V_{40 Gy}, V_{60 Gy}, V_{65 Gy}, V_{70 Gy}, and V_{75 Gy}; penile bulb and seminal vesicle DVH metrics including D_mean, D_max and D_50%; bladder DVH metrics including V_{40 Gy}, V_{65 Gy}, D_25%, D_50%; together with femoral head DVH metric D_10%. To evaluate the plane dose consistency of the CT and sCT, the dose DICOM files were exported from RayStation to MyQA (IBA Dosimetry, Germany). Mean dose difference, mean absolute dose difference and gamma analysis with 1%/1 mm, 2%/2 mm and 3%/3 mm criteria with 10% dose threshold were performed in coronal, transversal and sagittal planes that intersect with the treatment isocenter.

2.3.3. Distal range analysis

The depth-doses of both CT- and sCT-based plans were retrieved from RayStation TPS. This was chosen using the beam-line direction that crosses the isocenter, which is most likely to have the broadest spread out Bragg peak (SOBP) crossing the PTV. In this study, the proton beam range was defined at the distal depth where 80% (R₈₀) of the SOBP plateau dose was located. The plateau dose was determined by averaging the values of the central 80% of the SOBP plateau. If single field optimization (SFO) was used in treatment planning, the individual beam SOBP was usually flat so R₈₀ can be determined directly. For two patients, however, multiple field optimization (MFO) was applied such that there was no plateau dose region of the individual beams that can be used to calculate R₈₀. The summed plan SOBP plateau doses were retrieved to determine the R₈₀. The range difference and relative range difference between planning CT and sCT were calculated by:

$$\text{Range}\text{difference}=R_{80\text{sCT}}-R_{80\text{CT}}$$

$$\text{Relative}\text{range}\text{difference}=\left(R_{80}\_\text{sCT}-R_{80}\_\text{CT}\right)/R_{80}\_\text{CT}\times 100\%$$

and compared with the Harvard Massachusetts General Hospital (MGH) uncertainty criterion (Paganetti, 2012):

$$\text{Uncertainty}<3.5\%R_{80}\_CT+1\text{mm}.$$

2.3.4. Individual pencil beam Bragg peak shift

For the 17 prostate patients, the number of pencil beam spots used for their treatment plans ranged from 1317 to 13 525, depending on the number of beams, the size of the patient as well as the volume of the PTV. In RayStation, we retrieved the location of each spot’s Bragg peak, where the proton pencil beam deposited most of its energy. The Bragg peak shift between CT and sCT was calculated by the following equation:

$$\text{Spot}\text{shift}=\sqrt[2]{{\left(X-X^{\prime }\right)}^2+{\left(Y-Y^{\prime }\right)}^2+{\left(Z-Z^{\prime }\right)}^2}.$$

Where X, Y, Z and X′, Y′, Z′ represent each individual pencil beam Bragg peak DICOM coordinates obtained from the plans generated on the original CT and the sCT respectively.

2.3.5. Correlation evaluation between the imaging and proton treatment plan endpoints

To evaluate the correlations between the imaging endpoints (MAE, PSNR and NCC) and the treatment plan endpoints (gamma analysis pass rate in coronal plane with 1 mm/1% criteria, distal range difference and Bragg peak spot shift), correlation coefficient analysis was carried out. A good quality sCT image is associated with small MAE, large PSNR, NCC, high gamma analysis passing rate, small distal range difference, and small Bragg peak spot shift. If an endpoint is correlated with another, it is supposed to have a correlation coefficient value close to 1 or −1.

3. Results

3.1. Image quality

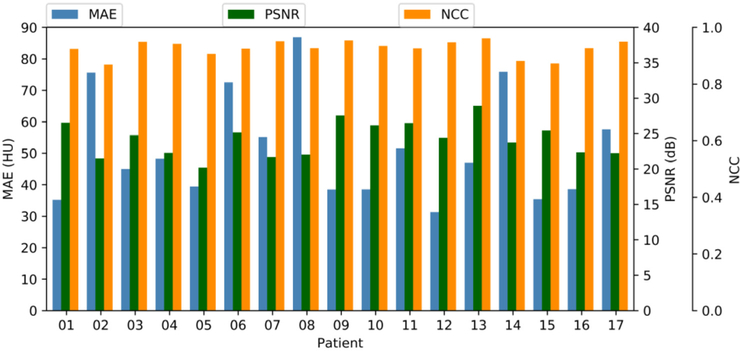
Figure 2 shows the MAE, PSNR and NCC for each patient of this cohort. The mean (±standard deviation, abbreviation: SD) MAE, PSNR and NCC are 51.32 ± 16.91 HU, 24.2 ± 2.46 dB, and 0.94 ± 0.03 respectively.

Figure 2.

MAE, PSNR and NCC for each patient.

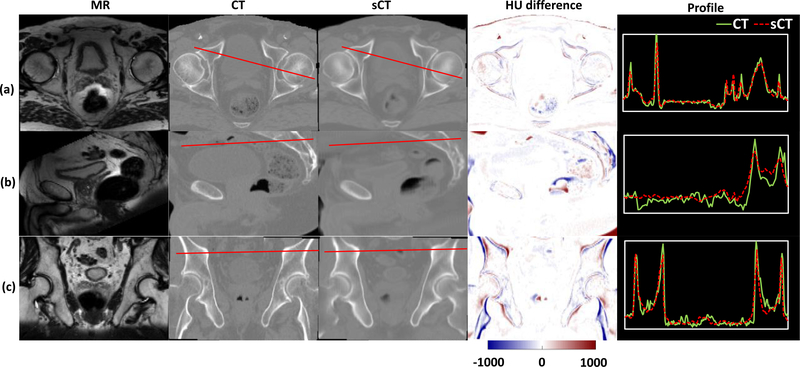
The original MR and CT images as well as the sCT images generated by our proposed algorithm were compared side-by-side (figure 3). Relative large HU differences can be seen at the tissue-air, bone-tissue, and air-tissue interfaces due to the non-ideal MR-CT pair registration. Overall, the images show small HU differences and similar HU profiles across regions with sharp HU changes.

Figure 3.

From left to right: MR image, CT image, sCT image, HU difference image between CT and sCT images, plot profile of red line in CT and sCT images of a representative patient. (a)–(c) Represent the transverse, sagittal and coronal views of a representative patient (P09) ‘s pelvic images.

Some discrepancies can be seen at the bony structures. The MAE of bone was 104.89 ± 21.39 HU. The mean DSC, HD, MSC and RMSD for the cohort were 0.85 ± 0.05, 4.22 ± 1.02, 0.61 ± 0.19, 1.77 ± 0.38, respectively.

3.2. Comparison with state-of-art method

Our proposed method outperforms Han’s DCNN and GAN-based method in terms of MAE, PSNR and NCC for body outline and MAE, DSC, HD95, and SNU for bone mask (table 1). Significant differences (P < 0.05) were founded between ours and the other two methods.

Table 1.

Numerical comparison between DCNN, GAN and the proposed cycleGAN method.

	Metrics within body outline			Metrics within bone mask
Method	MAE (HU)	PSNR (dB)	NCC	MAE (HU)	DSC	HD95 (mm)	SNU (%)
DCNN	58.98 ± 18.64	23.74 ± 2.96	0.928 ± 0.045	117.53 ± 19.08	0.81 ± 0.06	4.85 ± 1.47	58.71 ± 20.99
GAN	74.66 ± 19.96	22.07 ± 2.72	0.877 ± 0.053	125.33 ± 23.24	0.81 ± 0.06	4.71 ± 1.40	50.74 ± 22.92
Proposed	51.32 ± 16.91	24.20 ± 2.46	0.936 ± 0.031	104.89 ± 21.39	0.85 ± 0.05	4.22 ± 1.02	70.64 ± 14.15
P-value DCNN versus proposed	0.009	0.011	0.013	<0.001	<0.001	0.005	<0.001
P-value GAN versus proposed	<0.001	0.002	0.002	<0.001	<0.001	0.017	<0.001

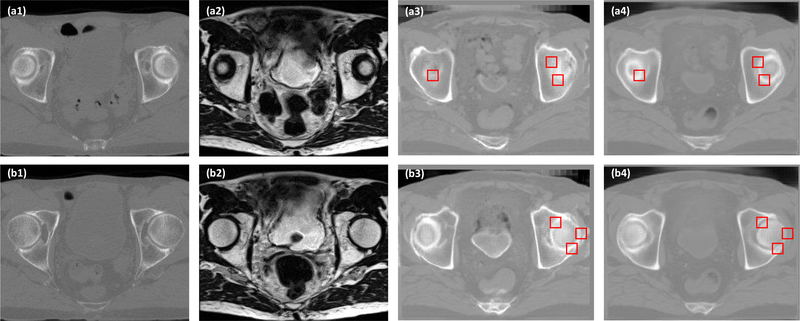
Figure 4 demonstrates examples of how the ROIs were selected in the sCT images at the bony structure. Due to the local mismatch, the sCT images generated by GAN have blurred estimations at the boundaries of bony structures, whereas our proposed method can maintain similar and sharp bony boundaries comparable to the original CT images. Similar SNU were found between the sCT generated by cycleGAN (70.64% ± 14.15%) and the original CT (75.88% ± 9.43%), while SNU is much smaller for the sCTs generated by GAN (50.74% ± 22.92%) and DCNN (58.71% ± 20.99%).

Figure 4.

A comparison of the proposed method and GAN. (a1) is CT image shown in axial plane. (a2) Shows the MR image. (a3) Shows the sCT generated by GAN. (a4) Shows the sCT generated by the proposed cycleGAN method. (b1-b4) show the same sequence images as (a1)–(a4). The selected ROIs are the red rectangles.

3.3. Dosimetric comparison

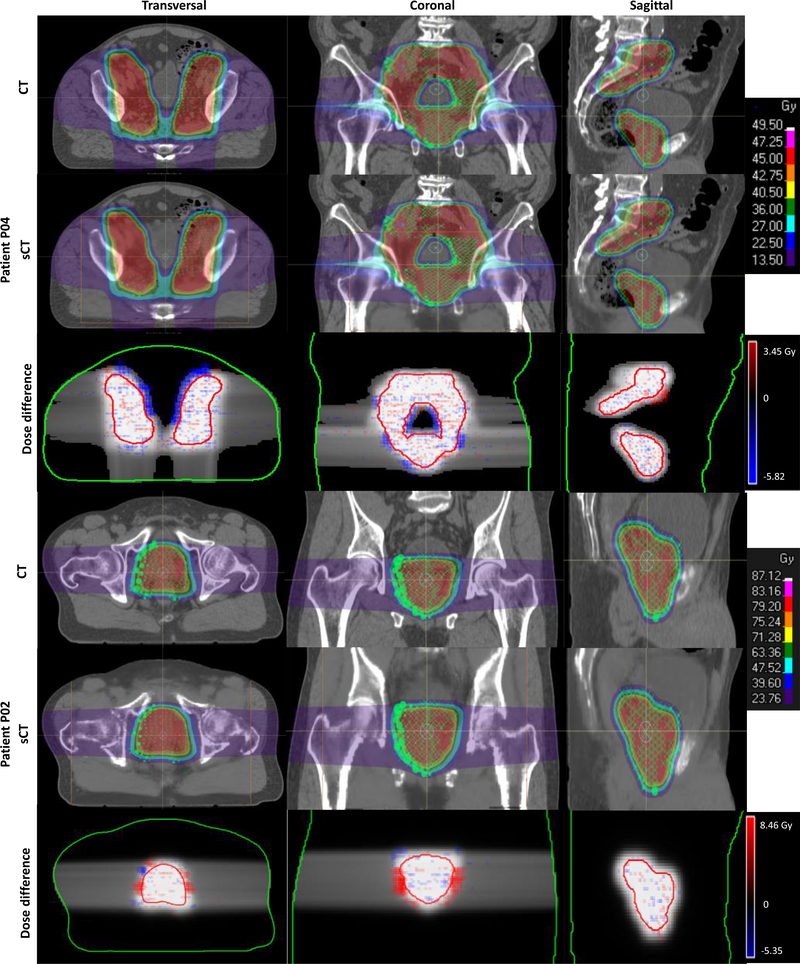
Figure 5 exhibits the dose difference (expressed as percent of the prescribed dose) of two representative patients. The voxel dose differences were generally much less than 10% except at the distal edge of the beams. Due to the relative difficulty of accurately predicting bone regions from MR images, and the sensitivity of proton dose calculations to HU variation, the large bony structures in the beam direction appear to be the largest source of dose inconsistency. The spot Bragg peaks falling into these representative planes were included in the CT and sCT-based dose map in figure 5. Though slight Bragg peak shifts of some individual spots can be observed with careful examination, in general, the spot locations in sCT-based dose maps agree with those in the CT-based dose maps.

Figure 5.

From left to right: transverse, coronal and sagittal views. Two representative patients were used to demonstrate the dose differences between plans calculated on original CT and sCT. The dose profiles were retrieved from the three different views that intersect with the isocenter. The individual spot Bragg peak location (green ‘O’ or ‘×’ markers, different marks were used in TPS to present different spot weighting) were included in the dose map. The MRI FOV was marked with orange lines. In the dose difference map, the body (in green line) and PTV contours (in red line) together with the reference dose (grey scaled CT-based dose map) as background were added to represent the location of dose discrepancy.

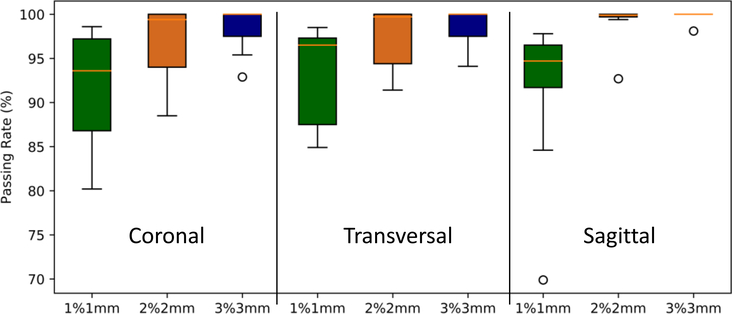
Table 2 tabulates the mean (±SD) and range of voxel-wise dose differences, absolute dose differences (in percent of the prescribed dose) and gamma analysis with 10% dose threshold in each of the 3 planes that intersect with the isocenter. Mean dose difference, and absolute dose difference (in percent of the prescribed dose) among the 17 patients were −0.07% ± 0.07% and 0.23% ± 0.08%. Total mean gamma analysis pass rates at 1 mm/1%, 2 mm/2%, 3 mm/3% criteria with 10% dose threshold were 92.39% ± 5.97%, 97.95% ± 2.95% and 98.97% ± 1.62%, respectively. Figure 6 shows the boxplot of the gamma analysis in the three planes.

Table 2.

Mean (±SD) and range of voxel-wise absolute dose difference and mean (±SD) and range of Gamma pass rates for 1 mm/1%, 2 mm/2% and 3 mm/3% criteria.

	Coronal	Transversal	Sagittal	Total%
Mean dose difference (%)
Mean(±SD)	−0.13 (0.23)	−0.04 (0.16)	−0.02 (0.09)	−0.07 (0.07)
Range	−0.68–0.07	−0.34–0.25	−0.36–0.09	−0.68–0.25
Mean absolute dose difference (%)
Mean(±SD)	0.32 (0.26)	0.24 (0.12)	0.12 (0.12)	0.23 (0.08)
Range	0.08–0.94	0.11–0.50	0.04–0.55	0.04–0.94
Gamma 1 mm/1% (%)
Mean(±SD)	91.88 (5.81)	92.73 (5.40)	92.54 (6.71)	92.39 (5.97)
Range	80.2–98.6	84.9–98.5	69.9–97.8	69.9–98.6
Gamma 2 mm/2% (%)
Mean(±SD)	97.18 (3.63)	97.24 (3.46)	99.42 (1.74)	97.95 (2.95)
Range	88.5–100	91.4–100	92.7–100	88.5–100
Gamma 3 mm/3% (%)
Mean(±SD)	98.47 (2.19)	98.55 (2.21)	99.89(0.46)	98.97 (1.62)
Range	92.9–100	94.1–100	98.1–100	92.9–100

Figure 6.

Gamma pass rates for 3 criteria: 1 mm/1%, 2 mm/2%, and 3 mm/3% with 10% dose threshold in coronal, sagittal and transverse planes. The central orange line indicates the median value, and the borders of the box represent the 25th and 75th percentiles. The outliers are plotted by the black ‘O’ marker.

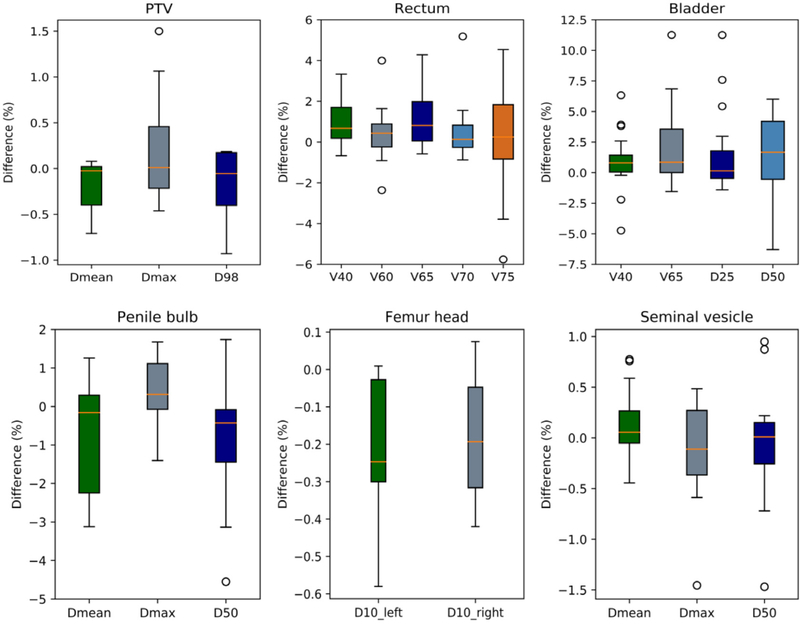
Figure 7 shows the box plot of relative DVH differences (in percent of the CT-based DVH value) for PTV and OARs. The PTV dose-volume metrics were generally less than 1%, except for one patient (p08) whose Dmax difference was 1.5%. Penile bulb, femoral head and seminal vesicle DVHs were relatively consistent between CT- and sCT-based plans, with differences much less than 5%. Discrepancies greater than 5% were observed for the rectal (from p10 and p12) and bladder (from p10, p15 and p16) DVHs in select patients. Small rectal volumes received 70 and 75 Gy on the original CT, therefore a minimal absolute difference can result in large relative differences. Large discrepancies in bladder DVH metrics can be caused by differences in organ filling between MR and CT images and variations in femoral head HU that lead to beam overshooting.

Figure 7.

Box plot of the relative DVH difference between sCT and CT for the PTV and OARs (in percent of the DVH value from the CT-based plan). The central orange line indicates the median value, and the borders of the box represent the 25th and 75th percentiles. The outliers are plotted by the black ‘O’ marker.

3.4. Range evaluation

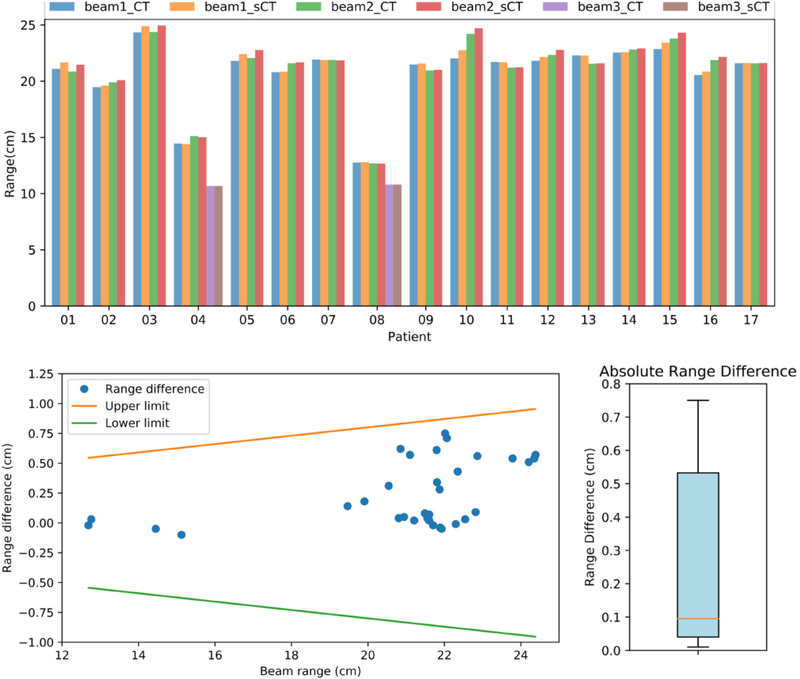
We compared the proton beam range between the CT- and sCT-based plans (figure 8). The largest absolute range difference (0.75 cm) was found in patient P10 with maximum proton energy of 209.6 MeV. The median and mean absolute range differences were 0.085 cm and 0.234 ± 0.252 cm. Based on the MGH range uncertainty criteria, all beam ranges were within the tolerance level (figure 8, bottom left).

Figure 8.

Range comparison between CT- and sCT-based plans. Top: CT and sCT beam ranges of each patient. Bottom left: the distribution of the range differences as a function of the actual range value from the plan calculated on the original CT. The upper and lower limits were obtained from the MGH range uncertainty criteria. Bottom right: box plot of absolute range difference.

3.5. Individual pencil beam Bragg peak shift

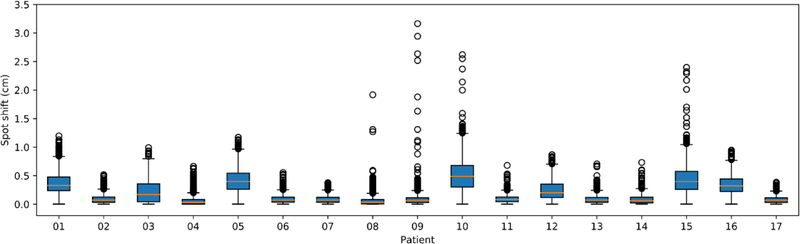
We evaluated the pencil beam Bragg peak shift of two representative cases and the statistics for each patient (figure 9). The largest shift, 3.16 cm, was found in patient P09. The shift occurred at the rectum, due to the MRI-CT mismatch of the tissue-air interface. The median and mean Bragg peak shifts among the 17 patients were 0.09 cm and 0.18 ± 0.07 cm.

Figure 9.

Box plot of the spot Bragg peak shift statistics of each patient. The central orange line indicates the median value, and the borders of the box represent the 25th and 75th percentiles. The outliers are plotted by the black ‘O’ marker.

3.6. Correlation among imaging and proton treatment plan endpoints

Table 3 lists the correlation coefficients for each two of the endpoints in imaging and treatment plan evaluations. The imaging endpoints are not well correlated to each other and to the treatment plan endpoints. For example, MAE is supposed to be positively related to spot shift, range difference and negatively related gamma analysis pass rate (i.e. the lower the MAE, the smaller the spot shift and range difference, and the higher the gamma pass rate), but we found contrary results in this study. On the other hand, better associations can be found between the spot shift and range difference (0.81), as well as between spot shift and gamma analysis pass rate (−0.79).

Table 3.

Correlation between imaging and treatment plan endpoints.

	PSNR	NCC	Spot shift	Range difference	Gamma pass rate
MAE	−0.35	−0.30	−0.65	−0.58	0.54
PSNR		0.30	0.06	0.37	0.03
NCC			−0.24	0.00	0.03
spot shift				0.81	−0.79
range difference					−0.62

4. Discussion

This work sought to evaluate the feasibility of MRI-only prostate proton treatment planning by applying a dense cycleGAN model to generate sCTs (Lei et al 2019). Side-by-side imaging comparisons revealed good agreement. The overall average MAE, PSNR and NCC of the sCT were 51.32 ± 16.91 HU, 24.2 ± 2.46 dB, and 0.93 ± 0.03, respectively. A comparative study of six synthetic CT generation algorithms done by Arabi et al presents the mean MAEs ranging from 32.7 ± 7.9 HU to 52.1 ± 11.1 HU, with the lowest MAE obtained using DCNN (Han 2017). In this study, we also performed sCT generation using DCNN with our patient cohort, and the mean MAE was 58.98 ± 18.64 HU. The different patient cohorts could contribute to the mean MAE differences between the sCTs generated by DCNN method with our patient cohort (58.98 ± 18.64 HU) and the patient cohort used in the comparative study (32.7 ± 7.9 HU). The specific parameters that we used to duplicate Han’s algorithm might be different. Overall, the mean MAE achieved in this study comparable to the state-of-art methods. As shown in table 3, there are little correlations between MAE/PSNR/NCC to range difference/Bragg peak spot shift/gamma pass rate. Proton treatment planning has the capability of tightly conforming the dose distribution to the target with better normal tissue sparing over photon-based plans. Therefore it is sensitive to the local HU accuracy in the beam-line direction rather than full-scale imaging endpoints. This suggests that a comprehensive evaluation of the CT- and sCT-based treatment plans need to be performed to validate the sCT generation method for further clinical development.

In the application of prostate proton beam therapy, since most of the beams must cross large bony structures before reaching the target, accurate bone HU value predictions are of paramount importance. However, the bone prediction is particularly challenging in sCT generation due to the nature of its appearance on MR images. In this study, we calculated the mean bone MAE and compared it with the other methods. Ours was 104.89 ± 21.39 HU, compared to 141.05 ± 26.85 HU from DCNN and 129.86 ± 27.63 HU from GAN. Ours is better but large discrepancies still exit that may due to the misalignment between CT and sCT and the limitation of the network. One advantage of the machine learning-based algorithm over the segmentation- and the atlas-based algorithm is that the former has the potential to learn patient specific HU differences across the bone rather than assigning a bulk identical density or HU values from the atlas CT images. However, the effectiveness of learning depends how well the networks are designed. In figure 3 we presented the HU profiles to demonstrate that our method can successfully predict the HU variations across bones and other organs. The side-by-side plane dose comparison shown in figure 5 showed an overall good dosimetric agreement. However, discrepancies can still be seen at the distal range due to the range shift caused by non-ideal bone HU prediction and local mismatch. The underestimation of bone HU could be caused by the truncated normal distribution, which is a common issue of the deep-learning algorithms. Normalization is required for the deep-learning algorithm to maintain the stability of the architecture. In our network, we used 99.9% maximum HU value as the largest HU and 5% minimum HU value as the smallest HU value. This procedure will slightly shorten the range of sCT HU values, which causes HU underestimation of the bone region.

Gamma analyses in coronal, sagittal and transverse dose planes were performed. The mean values of 2D 1 mm/1%, 2 mm/2%, 3 mm/3% criteria in the three planes were 92.39% ± 5.97%, 97.95% ± 2.95% and 98.97% ± 1.62%, respectively. The results were comparable to the pelvis proton study done by Maspero et al (2017) and Koivula et al (2016). In Maspero et al’s study, a bulk-assigned commercially available vendor solution was used. Adapted bone HU values were used to minimize the proton range differences initially found in the default software solution. A retrospective study on ten prostate patients showed an average 3D 2 mm/2% gamma pass rate of 98.4%. In Koivula et al’s study, a segmentation based (dual model HU conversion technique) was used. A retrospective study on ten prostate patients showed an average 3D 1 mm/1%, 2 mm/2%, 3 mm/3% gamma pass rate of 95%, 98.6% and 99.6%. Our results were a bit worse may due to different methods, different datasets, beam arrangements, and 2D versus 3D gamma analysis.

Clinically important PTV and OAR DVHs were also evaluated. Large discrepancies were observed for the rectum and bladder DVH metrics. A major reason for the disagreement was because the MR and CT images were not acquired simultaneously, therefore natural differences in organ filling status led to geometry inconsistencies. In addition, the rectal volumes receiving 70 and 75 Gy were small, such that a small difference can result in a relatively large relative difference. The bone HU inaccuracy also contributed to the difference in bladder dose.

Range evaluation was performed by retrieving the line dose along the beam-line direction that crossed the isocenter. The median absolute range difference was 0.085 cm. The Pileggi et al brain study (Pileggi et al 2018) reported a median value of 0.05 cm and the Maspero et al pelvis study (Maspero et al 2017) reported a mean median of 0.01 cm. Since the median absolute range difference is generally much higher than the median range difference, we were unable to perform inter-comparison among the different studies. Nonetheless, as shown in figure 8, all beam range displacements from this study were acceptable by the MGH range uncertainty criteria (Paganetti 2012).

Individual pencil beam Bragg peak shifts were evaluated. The advantage of this method is its sensitivity to the displacement of individual beams. We can use the X, Y, Z coordinate information to locate where the shift occurred and evaluate its dosimetric impact based on spot weighting. In contrast to the 2D gamma analysis and range shift analyses, which are highly user-dependent on the plane, dose threshold and dose-line selection, the box plot of Bragg peak shift synthesizes a more complete picture of the performance of the sCT.

One limitation of this study is the constrained field-of-view (FOV) that the MRI scanner can provide homogeneous magnetic field. Tissue truncation happens that cannot cover the whole pelvic region. To make the OAR comparison feasible, tissues which fell outside the MRI FOV were adopted from the original CT in order to construct the complete volume. As can be seen in the transverse view in figure 5, this issue affected less than 10% of the volume of the sCT and the majority of the bony structures in the sCT images were generated based on MR images. Therefore, the agreement between dose distributions mainly demonstrated the HU agreement between different image information sources. Indeed, the implementation of an MRI-only treatment planning workflow depends on a large FOV fully encompasses the body. As large-bore MR scanners have already been used in many clinics and will be more prevalent in the future, the concern of body truncation will be eliminated.

Another limitation is that only 17 patients were used in this study. Relatively small training dataset and large imaging volume are regarded as limitations of the application of machine learning in medical imaging. 17MR-CT training pairs with leave-one-out cross-validation can predict good result but results are supposed to be better by increasing training pairs. However, we think a standardized procedure to take care the issue of MR distortion, a better and faster way to perform the MR scanning to minimize the patient motion induced artifact, and a combined ‘in-one-day’ CT and MR scan are more important in terms of the prediction accuracy enhancement.

A common issue inherent to MRI-only treatment planning is image distortion. Its effect on highly conformal treatment such as prostate proton therapy can be significant (Seibert et al 2016, Wang et al 2013). Although not currently included as part of a standard package, many manufacturers have supplied solutions to correct these distortions (Jovicich et al 2006, Doran et al 2005, Baldwin et al 2007) and a standard guideline is under development (American Association of Physicists in Medicine Task Group No. 117). Together with the increased prevalence of commercially-available MRI simulators (Devic 2012) and development of novel MRI image guidance (Oborn et al 2017), high precision in target definition is the future for proton therapy. Precise target delineation is ineffective without accurate alignment of the target at the treatment site. To avoid potentially large source of uncertainty from CT-MR registration, the unprecedented proton dose conformity supports the need for MRI-only treatment process.

5. Conclusion and future directions

We applied a novel learning-based approach to integrating dense-block into cycleGAN to synthesize pelvic sCT images from routine MR images (Lei et al 2019) for potential MRI-only prostate proton therapy. The proposed method demonstrated a comparable level of precision in reliably generating sCT images for dose calculation, which supports further development of MRI-only treatment planning. Unlike photon therapy, the accuracy of proton dose calculation is highly dependent on stopping power rather than HU values. Therefore, the future directions of MRI-only proton treatment planning include prediction of the stopping power map based on the MR images and generating elemental concentration maps that can be used for Monte Carlo simulations.