Abstract
The suitability of Ti as a band gap modifier for -Ga2O3 was investigated, taking advantage of the isostructural phases and high band gap difference between Ti2O3 and Ga2O3. Films of (Ti,Ga)2O3 were synthesized by atomic layer deposition on sapphire substrates, and characterized to determine how crystallinity and band gap vary with composition for this alloy. We report the deposition of high quality -(TixGa1−x)2O3 films with x = 3.7%. For greater compositions the crystalline quality of the films degrades rapidly, where the corundum phase is maintained in films up to x = 5.3%, and films containing greater Ti fractions being amorphous. Over the range of achieved corundum phase films, that is 0% ≤ x ≤ 5.3%, the band gap energy varies by ∼270 meV. The ability to maintain a crystalline phase at low fractions of Ti, accompanied by a modification in band gap, shows promising prospects for band gap engineering and the development of wavelength specific solar-blind photodetectors based on -Ga2O3.
Keywords: gallium oxide, wide band gap semiconductors, solar-blind detection, atomic layer deposition, thin films, alloying, bandgap
1. Introduction
Alpha phase gallium oxide (-Ga2O3) is an ultra-wide band gap semiconductor, with most measurements of its band gap lying between 5.1 eV and 5.3 eV [1,2,3,4,5]. It is of particular interest for applications in solar-blind ultraviolet (UV) photodetectors [2,4,6,7]. Uses for photodetectors that can absorb efficiently in this regime, of wavelengths <285 nm, include water and air purification systems [8], flame detection, UV astronomy, missile defence systems and engine monitoring [4,9].
-Ga2O3 is a metastable phase of Ga2O3, a polymorphic group-III sesquioxide, with commonly reported phases , , , and [10] as well as the more recent [11]. Previous research on this material has been mostly focused on the stable, monoclinic phase [10,12,13], however, due to recent advances in thin film growth techniques, such as mist chemical vapour deposition (mist-CVD) [1,14,15] and atomic layer deposition (ALD) [4,5,16,17], it has become possible to synthesise high quality films of -Ga2O3. These films are grown epitaxially on sapphire (-Al2O3), which shares its rhombohedral corundum crystal structure [1] (inset Figure 1) with -Ga2O3. This has been achieved at temperatures as low as 250 C by ALD [4,5,16] and the material has been successfully integrated into solar-blind UV photodetectors, already showing an advantage over photodetectors based on -Ga2O3, by having shorter response times [4].
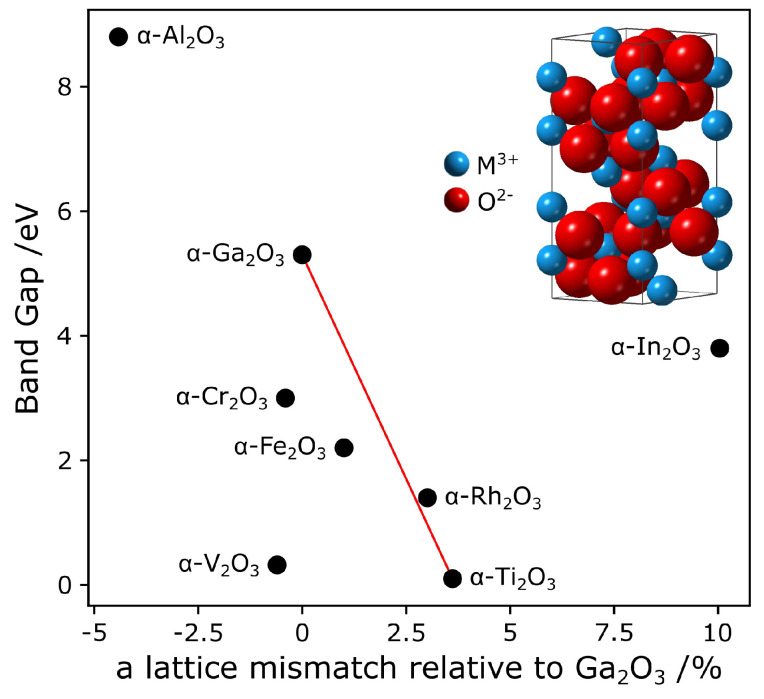
Figure 1.
Diagram of the corundum phase semiconducting sesquioxide design space, centered on -Ga2O3. The band gaps of the materials [1,27,28,29,30,31,32,33,34,35] are plotted against their ‘a’ lattice parameters relative to -Ga2O3 [36,37,38,39,40,41,42]. The red line indicates the alloys of -Ti2O3 and -Ga2O3, assuming that the band gap varies linearly with the lattice constants. Inset: Rhombohedral, corundum crystal structure of M2O3 (M: metal).
Apart from sapphire, the corundum crystal structure is also shared by many other semiconducting sesquioxides [18,19,20], as shown in Figure 1, providing great potential for band gap engineering [15,21]. Band gap engineering in the solar-blind region would be pivotal for producing layered device structures and for tuning the application of devices, for example, by producing wavelength-specific biochemical or flame sensors where the material would be tuned to match the peak absorption wavelength of a given micro-organism or molecule [22,23]. Previously, alloying of corundum phase Ga2O3 with Al2O3 [24], In2O3 [25], Cr2O3 [19], Fe2O3 [19,20] and Rh2O3 [26] has been attempted.
The aim of this work is to study the feasibility of using Ti as a band gap modifier for -Ga2O3, by characterizing a number of oxide films grown by ALD with different Ti to Ga ratios. -Ti2O3 adopts the corundum crystal structure [39,43] with lattice parameters: a = 5.157 Å and c = 13.613 Å [39], giving a relatively small lattice mismatch of about 3.5% with -Ga2O3 (a = 4.983 Å and c = 13.433 Å [36]). Its direct band gap of 0.1 eV [29,30] is very small relative to that of -Ga2O3, such that a band gap engineering over a few 100 meV (required for wavelength specific solar-blind photodetectors) would be achievable by alloying -GaO with only very small amounts of -TiO. An even wider range of band gaps may be achievable, provided that an alloy of the two sesquioxides exhibits miscibility and crystallinity across a range of Ti:Ga ratios. This may be inhibited if Ti adopts a +4 oxidation state and preferentially forms TiO2, which would not have a corundum structure. In -Ga2O3, Ti was found to incorporate in the Ga2O3 host material for low compositions, but led to a phase separated Ga2O3-TiO2 composite at greater compositions [44,45,46]. In the present study it is hoped that the shared corundum structure and low lattice mismatch between -Ga2O3 and -Ti2O3 would allow to alleviate these issues. Another property of -Ti2O3 that is of interest is that it is a p-type semiconductor [30]. Alloying with Ti2O3 could thus provide a route to achieve p-type conductivity in -Ga2O3, as was also demonstrated in an phase Rh:Ga2O3 alloy by Kaneko et al. [26].
2. Experimental Methods
Ga2O3 and (Ti,Ga)2O3 thin films were grown using an Oxford Instruments OpAL plasma enhanced atomic layer deposition (PEALD) reactor. All films were grown on 0.25 miscut c-plane sapphire substrates with a temperature of 250 C and chamber wall temperatures set to 150 C. Triethylgallium (TEGa) from Epichem and Titanium(IV) Isopropoxide (TTIP) from Sigma-Aldrich were used as Ga and Ti precursors, respectively. The TEGa and TTIP precursors were held at 30 C and 80 C, respectively, with line temperatures for both precursors set at 90 C and 100 C, increasing in temperature closer to the reaction chamber. One cycle of Ga2O3 consisted of 0.1 s TEGa with 100 sccm Ar bubbling, 5 s 100 sccm Ar purge, 3 s O2 flow stabilisation, 5 s 20 sccm 300 W O2 plasma, 5 s 100 sccm Ar purge. One cycle of TiOx consisted of 2 s TTIP with 100 sccm Ar bubbling, 10 s 100 sccm Ar purge, 0.04 s H2O, 10 s 100 sccm Ar purge. The chosen growth parameters were adapted from Ref. [47]. Supercycles of Ga2O3 and TiOx were used to produce Ti alloyed Ga2O3 films, with cycle ratios (TiOx:Ga2O3) of 0:1, 1:32, 1:19, 1:9, 1:4 and 1:1, which are hereafter referred to as samples 0%Ti, 3%Ti, 5%Ti, 10%Ti, 20%Ti and 50%Ti, respectively. 500 total cycles were used for the 0%Ti film, 429 cycles for the 3%Ti film and 400 cycles for the remaining films. Film thicknesses after growth were measured using a HORIBA Jobin Yvon spectroscopic ellipsometer fitted to a mixed Cauchy -Ga2O3/TiO2 model and are shown in Table 1. We estimate the film thicknesses obtained using this approach to be within ∼10% accuracy, due to the model itself.
Table 1.
Summary of film characteristics. Samples are named after the percentage of Ti ALD cycles used for growth. Film thicknesses, obtained by ellipsometry, are estimates, since an appropriate fitting model for -Ga2O3, amorphous Ga2O3 or -Ti2O3 was unavailable. Composition, measured by RBS, represents the amount of Ti relative to Ga in the films. RMS roughness and band gaps were determined by AFM and UV-vis transmittance spectroscopy, respectively.
| Sample | Thickness/nm | Composition x/% | RMS Roughness/nm | Band Gap/eV |
|---|---|---|---|---|
| 0%Ti | 33 ± 3 | 0 | 0.71 ± 0.01 | ∼5.04 |
| 3%Ti | 22 ± 2 | 3.7 ± 0.4 | 0.49 ± 0.02 | ∼4.88 |
| 5%Ti | 21 ± 2 | 5.3 ± 0.4 | 0.30 ± 0.01 | ∼4.77 |
| 10%Ti | 21 ± 2 | 12.8 ± 0.8 | 0.22 ± 0.01 | ∼4.78 |
| 20%Ti | 21 ± 2 | 23.1 ± 1.0 | 0.19 ± 0.01 | ∼4.63 |
| 50%Ti | 16 ± 2 | 61 ± 3 | 0.16 ± 0.01 | ∼3.91 |
The Ti:Ga ratio of the samples was determined using Rutherford backscattering spectrometry (RBS) with 1.615 MeV He incident beam from a 1.7 MV Pelletron accelerator. The samples were tilted to 5 and the scattering angle was 165. The measured spectra were analysed in the SimNRA program [48] which was used to calculate the Ti:Ga ratios from the respective peak areas in the raw data and weighting them against the corresponding Rutherford scattering cross-sections. Given that the peaks are clearly separated, no fitting was required to analyse these data.
The crystallinity of the samples was assessed by X-ray diffraction (XRD). A PANalytical Empyrean diffractometer was used with a Cu source and a hybrid two-bounce primary monochromator giving Cu K1 radiation, and either a two-bounce Ge crystal analyser, for 2- scans, or a PIXcel detector, for reciprocal space maps (RSMs).
High-angle annular dark field scanning transmission electron microscopy (HAADF-STEM) using an aberration-corrected FEI Titan [49] operated at 200 kV was used to observe the sub-surface structure of the samples observed in cross-section. The annular dark field detector semi-angle used was 69.1 mrad. Compositional mapping was obtained using energy dispersive X-ray spectroscopy (EDX) in the same microscope and strain mapping was obtained using geometrical phase analysis [50]. The samples were prepared for imaging using standard mechanical grinding followed by Ar+ ion milling at 5 kV and cleaning at 0.1–1 kV.
The surface morphology of the samples was investigated by atomic force microscopy (AFM) in a Bruker Dimension Icon operated in peak force tapping mode. Bruker SCANASYST-AIR tips with a nominal radius of 2 nm were used.
The band gaps of the films were determined from transmittance spectra of the films, measured using a Cary 7000 UV-VIS-NIR spectrometer in the range 200–800 nm. The system was calibrated for 100% and 0% transmittance.
3. Results and Discussion
RBS was used for compositional analysis of the films. The main quantity of interest was the ratio of Ti to Ga in the films. RBS spectra were obtained for each film, showing peaks for Ga and Ti (except in the pure Ga2O3 sample) clearly separated due to the difference in atomic mass, as well as steps associated with Al and O from the sapphire substrate. The compositions x, here defined as x = at.%Ti /(at.%Ti + at.%Ga), attained from the integrated counts of the Ti and Ga peaks in the RBS spectra and corrected for by the respective Rutherford scattering cross sections, are tabulated in Table 1. The film compositions determined by RBS, are in relatively good agreement with those predicted from the ALD cycle ratios, deviating by about 10–30%. Deviations resulting from unequal growth rates of the different species are expected in ALD, with the growth being strongly affected by several factors, including temperature, chemistry of the precursors used, and the growth surface [51,52].
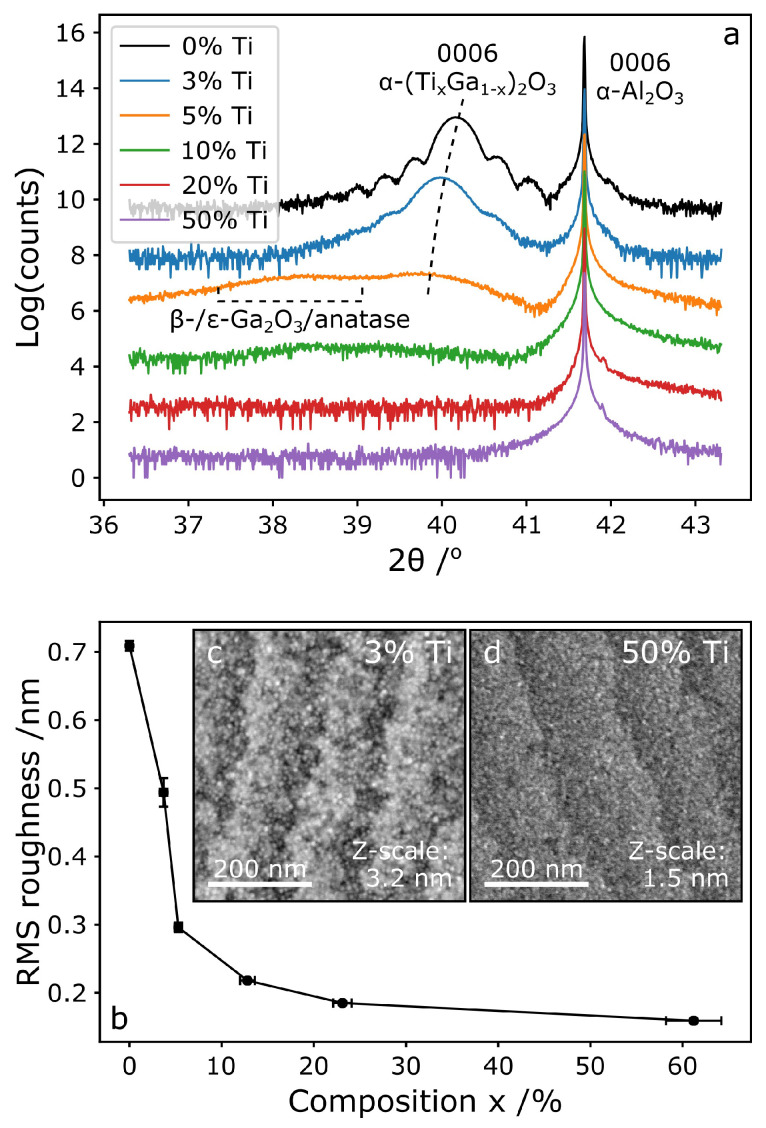
XRD was used to study the crystallinity of the films. The measured 2- XRD scans (Figure 2a) show the 0 0 0 6 reflection from the sapphire substrate and, for the 3 samples of lowest Ti fraction, also a peak from the film.
Figure 2.
(a) 2- XRD scans of the symmetric 0 0 0 6 reflection of the phase. (b) Variation of RMS surface roughness with Ti concentration. (c,d) 500 nm size AFM images of the 3%Ti (c) and 50%Ti (d) samples.
The pure -Ga2O3 sample (sample 0%Ti) gives the peak of greatest intensity at 2 = 40.16, which is within the range of reported values in epitaxial films (40.05–40.25 [1,16,36]). Differences in lattice parameter may be due to residual strain from the epitaxial relationship with the substrate. (Annealing the samples at approximately 400 C has been shown to release that residual strain [7]). Interference fringes can be distinguished on the base of the diffraction peak, with a spacing that is representative of the film thickness—here 28 nm, in reasonable agreement with the thickness estimated by ellipsometry (Table 1).
As the concentration of Ti increases, the (Ti,Ga)2O3 peak becomes broader and weaker, vanishing completely for samples 20%Ti and 50%Ti, which is typical for amorphous materials with very short range order only. For those diffractograms where peaks are observed, that is, for compositions up to 5.3%, the (Ti,Ga)2O3 peak shifts to smaller angles as the Ti content increases, indicating that the lattice parameter of the crystal increases. This is expected, as the lattice parameters of -Ti2O3 are larger and suggests that Ti has been incorporated into the films to form an -(TixGa1−x)2O3 alloy. However, the measured c lattice parameters exceed those expected from the compositions calculated from RBS data, using literature values for lattice parameters and assuming the applicability of Vegard’s Law [53,54]. A likely cause of this is that the -(TixGa1−x)2O3 layers are compressively strained onto the sapphire substrate. However, due to insufficiently strong signals, it was not possible to verify and quantify the strain in the films by conducting a strain analysis from RSMs of symmetric and asymmetric reflections.
Lastly, for sample 5%Ti we note the presence of a second, broad and weak, peak located at a lower angle (∼38) than the -(TixGa1−x)2O3 peak (indicated in Figure 2a). Although it is too broad and weak to be uniquely identified, this peak could indicate the presence of one or more additional phases such as -Ga2O3, -Ga2O3 or anatase TiO2 in this film.
The surface topography of each sample was obtained by AFM and the root mean square (RMS) roughness determined at a 500 nm scan size. The AFM images (Figure 2c,d) are representative of the topographies observed for all samples. The surface was smooth on a nanometer scale, as shown by the RMS roughness given in Table 1 and Figure 2b.
The surface of all samples also bears ledges with a constant spacing, mostly independent of Ti content. These ledges likely arise from the morphology of the sapphire substrates, which, due to having a miscut angle of 0.25, also have steps on the surface. These provide two distinct regions: a flat (0 0 0 1) oriented surface and the step. Given preferential growth at one of these sites in ALD, a step pattern with the same spacing would be expected. A topographical scan of a pristine sapphire wafer (not shown here) shows similar step widths as Figure 2c,d.
The surfaces of the low Ti fraction samples (Figure 2c) exhibit small grains of the order of 1–10 nm, presumably due to the termination of phase columns as was observed in Refs. [5,16]. As the Ti fraction increases (Figure 2d) these features cannot be identified anymore, which may indicate that the films are amorphous, in line with our XRD results. The plot of the RMS roughness vs. Ti fraction (Figure 2b) shows that the roughness decreases quickly with Ti fraction. This decrease in RMS roughness coincides with the disappearance of the small grain features as the Ti fraction increases. This trend (together with the images Figure 2c,d as well as XRD results Figure 2a) implies that the low Ti fraction (x ≤ 5.3%) films are crystalline, whilst the films with high Ti fraction (x ≥ 12.8%) are amorphous.
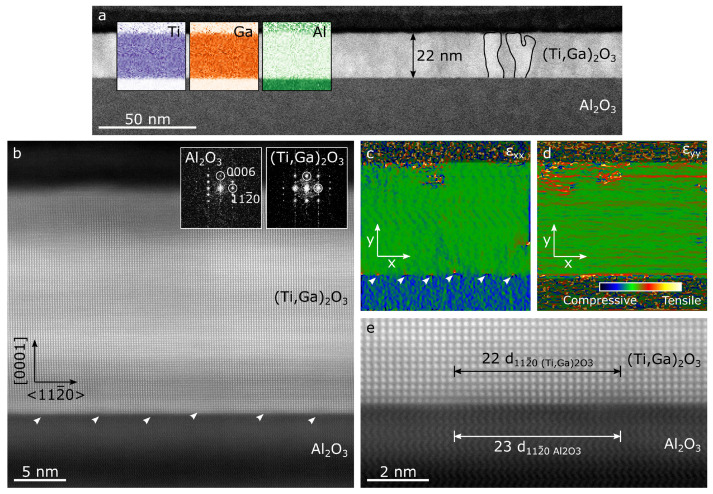
STEM was used to analyse a cross section of sample 3%Ti, allowing the interface between substrate and film to be studied as well as giving a local insight to crystallinity, strain and composition across the film. The results are compiled in Figure 3, showing large, vaguely columnar regions of crystallinity in the film (two such columns are outlined in Figure 3a) with, in places, regions of amorphous material. This is in agreement with prior work on ALD grown, pure -Ga2O3 [16]. The film thickness measured by HAADF-STEM images (Figure 3a) is consistent with that measured by ellipsometry. We also note that the film is continuous with a fairly uniform thickness, exhibiting only sub-nanometre variation in surface height that is consistent with the low surface roughness obtain from AFM (Figure 2c). The high resolution data and Fast-Fourier transforms (FFT) of the film and substrate regions (Figure 3b) confirm that the film has the corundum structure with the epitaxial relationship with the sapphire substrate being 〈110〉Al2O3 ‖ 〈110〉(TixGa1−x)2O3 and [0002]Al2O3 ‖ [0002](TixGa1−x)2O3, in agreement with previous studies [16].
Figure 3.
(a,b) HAADF-STEM images of a cross-section of sample 3%Ti, showing the (Ti,Ga)2O3 film and its interface with the sapphire substrate. EDS maps are overlaid in (a), showing a uniform distribution of Ti and Ga throughout the film. Two columnar regions of crystallinity in the (Ti,Ga)2O3 film are also outlined in (a). In inset of (b), the FFTs of the film and substrate confirm the corundum structure. Strain in the film, perpendicular () (c) and parallel () (d) to the growth direction, was obtained from geometrical phase analysis. Regularly spaced misfit dislocations are indicated by arrows in (b,c). (e) High resolution HAADF-STEM image of film-substrate interface, clearly showing 2 misfit dislocations and their separation. All images are taken along the zone axis.
Observation of the interface region reveals the presence of a high density of periodically spaced misfit dislocations, with an average spacing of 4.9 ± 0.4 nm. Apart from these, there are also some dislocations located within the film, approximately 1–3 nm from the interface (not shown here) although these are more rare. The misfit dislocations at the interface can be easily seen in Figure 3b,c (indicated by arrows), the latter showing them as dipoles of tensile and compressive strain. Figure 3e shows two misfit dislocations at greater magnification such that it is possible to count the number of lattice planes between them. They are separated by 23 × d110 Al2O3 or 22 × d110 (TixGa1−x)2O3. This indicates that the film is almost fully relaxed (nominally 22 × d110 Al2O3 = 5.232 nm, 21 × d110 Ga2O3 = 5.232 nm and 21 × d110 (TixGa1−x)2O3 = 5.238 nm assuming x = 3.7%). The strain maps in Figure 3c,d confirm that all the strain relaxation occurs at the interface, and that the strain is otherwise uniform throughout the film. The strain relaxation of the film observed in STEM is in contradiction with the XRD data, which instead suggests that the film is strained. A possible explanation may be that these probe the material at different scales: TEM focuses on a small nanometre-scale region of the sample—typically looking at the scale of an individual column—whereas XRD looks at average/global properties of the film. Another possibility is that the observed imperfect spacing of the misfit dislocations for (TixGa1−x)2O3 is unable to fully accommodate the strain.
EDS analysis of the film shows that the distribution of Ti across the film was uniform, with no visible segregation (Figure 3a). Compositional analysis using Cliff-Lorimer method yielded a composition of x ∼ 5%, which is in fair agreement with the RBS data (we note however that EDS quantification is here less reliable than the RBS data, because the sample was imaged on the zone-axis for the phase and was therefore susceptible to interference from electron channeling).
UV-vis transmittance spectroscopy was conducted to attain the optical band gap of the films. Only transmittance spectra were taken. Ignoring reflected intensity is justified by the fact that the films were transparent and only weakly reflecting to the eye, at normal incidence. Using the assumption of negligible reflectance, Beer-Lambert law could be applied to calculate absorptivity from the transmittance [2,55]. Film transmittances were isolated from the transmittances of the samples by measuring that of a reference pristine sapphire substrate. Absorptivity could then be used to produce Tauc plots using the relation in Equation (1), from which the band gap was determined. A Tauc exponent of n = for a direct energy band gap and allowed transition was used, as was also applied in other works [1,2,3,4,5]:
| (1) |
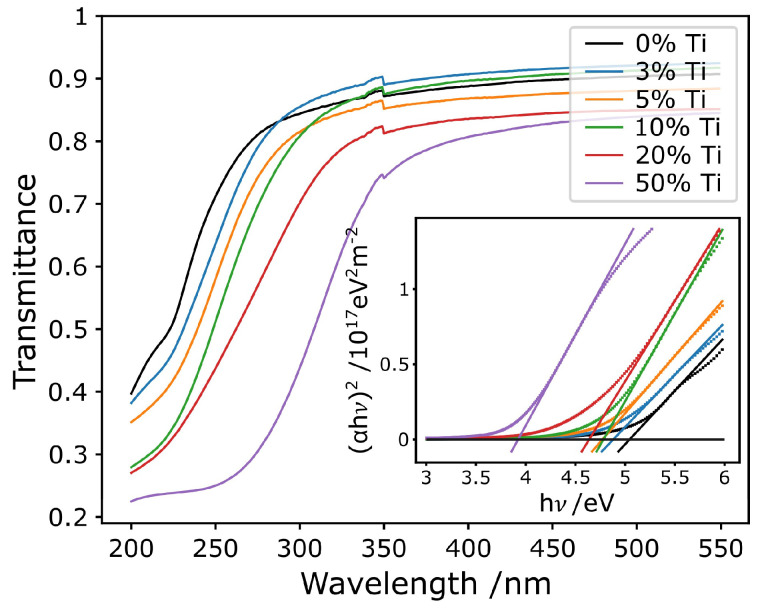
The collected transmittance spectra for the films are depicted in Figure 4 with an inset of the Tauc plots used to attain the band gap energy. The transmittance spectra clearly show that the absorption edge shifts to longer wavelengths as the Ti concentration of the films increases—as is represented by the band gap energies values listed in Table 1. Above the absorption edge, the transmittance is very high, suggesting that the assumption of little reflection or scattering, when calculating absorptivity is justified (the small discontinuity in the spectrum at ∼350 nm is a systematic instrumental error, due to the source change that occurs in the system at that wavelength). The transmittance at wavelengths longer than the absorption edge seems to decrease with increasing Ti concentration, which could be due to increased scattering or reflection from the films which are not crystalline.
Figure 4.
UV-vis transmittance spectra for the (Ti,Ga)2O3 samples. The inset shows Tauc plots evaluated using the transmittance data for each film. The straight, solid lines are the fits to the linear region of the Tauc plots and their intercepts with the dotted black line ( = 0) gives the band gaps of the respective films.
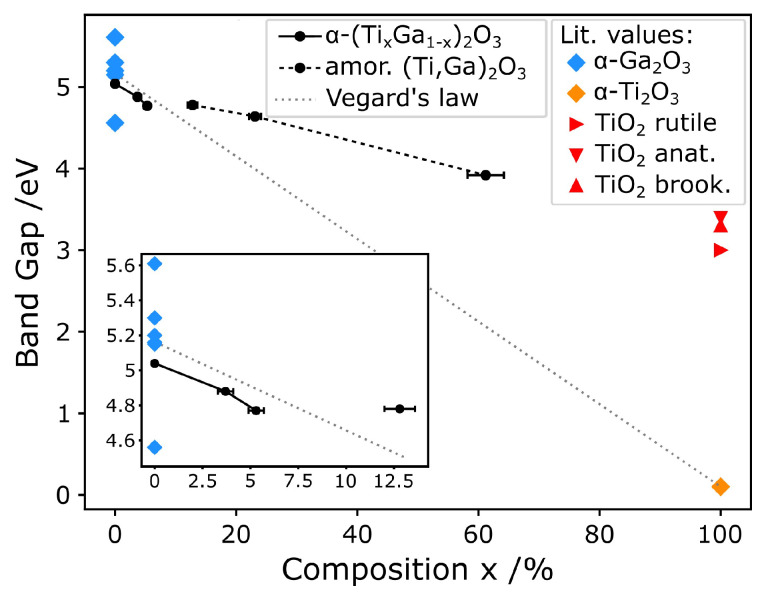
Figure 5 collates the main findings of the study in terms of film composition, crystallinity and optical band gap. The decrease in band gap energy with increasing Ti concentration can be clearly seen. The figure also displays literature values of band gaps for -Ga2O3, -Ti2O3 and 3 common phases of TiO2: rutile [56,57], anatase [58] and brookite [59]. The band gap measured for pure -Ga2O3 is well within the range of literature values [1,2,3,4,5,60,61]. The linear trend in band gap with composition predicted by Vegard’s law for -(TixGa1−x)2O3 has been plotted to guide the eye. For the samples with Ti concentration up to 5.3%, that are, the crystalline -(TixGa1−x)2O3 films, the optical band gap seems to follow that trend although this observation should be nuanced as it is based on just 3 data points. Over this range of compositions the band gap varies by ∼270 meV. For the samples with greater Ti concentration, that are, the amorphous films, the band gap follows a different linear trend, with a shallower slope—over this range of composition the band gap varies by ∼1.12 eV.
Figure 5.
Plot showing the measured variation of band gap energy with the RBS composition alongside literature values of band gaps for pure oxides [1,2,3,4,5,30,56,57,58,59,60,61,62] and a Vegard’s law trend between -Ga2O3 and -Ti2O3. The inset is an enlargement of the low Ti fraction region. The plot also differentiates between compositions based on whether crystallinity was observed by XRD.
Given that the solar-blind region covers the range of band gap energies wider than 4.4 eV approximately, our results indicate that -(TixGa1−x)2O3 alloys could be an attractive material for solar-blind photodetector applications. Further improvement in crystal growth could lead to a broader composition range of crystalline films, potentially allowing the production of wavelength-specific photodetectors beyond the solar-blind region.
4. Conclusions
Owing to a common crystal structure, low lattice mismatch and wide band gap difference, we investigated the use of Ti as a band gap modifier in -Ga2O3. Films of (Ti,Ga)2O3 with a range of Ti concentrations were synthesized by ALD and the resulting film crystallinity and band gap characterized. The deposition of high quality -(TixGa1−x)2O3 films was achieved for x = 3.7%. The corundum phase was maintained in films of compositions up to x = 5.3%, although the crystalline quality degraded rapidly with increasing Ti fraction. Films with greater Ti content were amorphous. Over the range where corundum phase films were obtained, that is for 0% ≤ x ≤ 5.3%, we report a variation of band gap energy of ∼270 meV. Despite further effort required to increase the crystalline quality of films with greater Ti fraction, this study is a promising proof-of-principle that Ti could be used for band gap engineering of -Ga2O3, and opens the path for the fabrication of wavelength-specific optoelectronic devices operating in the UV.
Acknowledgments
The data that support the findings of this study are openly available in PurePortal at https://doi.org/10.15129/3708a522-189e-4a41-8419-89e5f626237b.
Author Contributions
Conceptualization, F.M. and J.R.; methodology, F.M.; validation, A.B., J.R., M.N., M.F., T.H., and A.K.; formal analysis, A.B., M.N., and F.M.; investigation, A.B., J.R., M.N., M.F., T.H., and A.K.; resources, J.R.; data curation, A.B., J.R., M.N., M.F., T.H., and A.K.; writing—original draft preparation, A.B. and F.M.; writing—review and editing, all authors; visualization, A.B., M.N. and F.M.; supervision, F.M.; project administration, P.C., T.S., R.O. and F.M.; funding acquisition, P.C., T.S. and R.O. All authors have read and agreed to the published version of the manuscript.
Funding
This project is funded by the Engineering and Physical Sciences Research Council (EPSRC Grants No. EP/P00945X/1 and No. EP/M010589/1). T.N.H. acknowledges funding from the EPSRC Centre for Doctoral Training in Graphene Technology (Grant No. EP/L016087/1). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 823717 – ESTEEM3.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Shinohara D., Fujita S. Heteroepitaxy of corundum-structured α-Ga2O3 thin films on α-Al2O3 substrates by ultrasonic mist chemical vapor deposition. Jpn. J. Appl. Phys. 2008;47:7311–7313. doi: 10.1143/JJAP.47.7311. [DOI] [Google Scholar]
- 2.Guo D., Zhao X., Zhi Y., Cui W., Huang Y., An Y., Li P., Wu Z., Tang W. Epitaxial growth and solar-blind photoelectric properties of corundum-structured α-Ga2O3 thin films. Mater. Lett. 2016;164:364–367. doi: 10.1016/j.matlet.2015.11.001. [DOI] [Google Scholar]
- 3.Oshima Y., Villora E.G., Shimamura K. Halide vapor phase epitaxy of twin-free α-Ga2O3 on sapphire (0001) substrates. Appl. Phys. Express. 2015;8:055501. doi: 10.7567/APEX.8.055501. [DOI] [Google Scholar]
- 4.Lee S.H., Lee K.M., Kim Y.B., Moon Y.J., Kim S.B., Bae D., Kim T.J., Kim Y.D., Kim S.K., Lee S.W. Sub-microsecond response time deep-ultraviolet photodetectors using α-Ga2O3 thin films grown via low-temperature atomic layer deposition. J. Alloys Compd. 2019;780:400–407. doi: 10.1016/j.jallcom.2018.11.333. [DOI] [Google Scholar]
- 5.Roberts J.W., Chalker P.R., Ding B., Oliver R.A., Gibbon J.T., Jones L.A.H., Dhanak V.R., Phillips L.J., Major J.D., Massabuau F.C.P. Low temperature growth and optical properties of α-Ga2O3 deposited on sapphire by plasma enhanced atomic layer deposition. J. Cryst. Growth. 2019;528:125254. doi: 10.1016/j.jcrysgro.2019.125254. [DOI] [Google Scholar]
- 6.Zhao X., Wu Z., Guo D., Cui W., Li P., An Y., Li L., Tang W. Growth and characterization of α-phase Ga2-xSnxO3 thin films for solar-blind ultraviolet applications. Semicond. Sci. Technol. 2016;31:065010. doi: 10.1088/0268-1242/31/6/065010. [DOI] [Google Scholar]
- 7.Moloney J., Tesh O., Singh M., Roberts J., Jarman J., Lee L., Huq T., Brister J., Karboyan S., Kuball M., et al. Atomic layer deposited α-Ga2O3 solar-blind photodetectors. J. Phys. D Appl. Phys. 2019;52:475101. doi: 10.1088/1361-6463/ab3b76. [DOI] [Google Scholar]
- 8.Gross A., Stangl F., Hoenes K., Sift M., Hessling M. Improved Drinking Water Disinfection with UVC-LEDs for Escherichia Coli and Bacillus Subtilis Utilizing Quartz Tubes as Light Guide. Water. 2015;7:4605–4621. doi: 10.3390/w7094605. [DOI] [Google Scholar]
- 9.Razeghi M. Short-wavelength solar-blind detectors-status, prospects, and markets. Proc. IEEE. 2002;90:1006–1014. doi: 10.1109/JPROC.2002.1021565. [DOI] [Google Scholar]
- 10.Roy R., Hill V.G., Osborn E.F. Polymorphism of Ga2O3 and the System Ga2O3—H2O. J. Am. Chem. Soc. 1952;74:719–722. doi: 10.1021/ja01123a039. [DOI] [Google Scholar]
- 11.Playford H.Y., Hannon A.C., Barney E.R., Walton R.I. Structures of Uncharacterised Polymorphs of Gallium Oxide from Total Neutron Diffraction. Chem. A Eur. J. 2013;19:2803–2813. doi: 10.1002/chem.201203359. [DOI] [PubMed] [Google Scholar]
- 12.Stepanov S.I., Nikolaev V.I., Bougrov V.E., Romanov A.E. Gallium Oxide: Properties and Applications—A Review. Rev. Adv. Mater. Sci. 2016;44:63–86. [Google Scholar]
- 13.Pearton S.J., Yang J., Cary P.H., Ren F., Kim J., Tadjer M.J., Mastro M.A. A review of Ga2O3 materials, processing, and devices. Appl. Phys. Rev. 2018;5:011301. doi: 10.1063/1.5006941. [DOI] [Google Scholar]
- 14.Kaneko K., Kawanowa H., Ito H., Fujita S. Evaluation of Misfit Relaxation in α-Ga2O3 Epitaxial Growth on α-Al2O3 Substrate. Jpn. J. Appl. Phys. 2012;51:020201. doi: 10.1143/JJAP.51.020201. [DOI] [Google Scholar]
- 15.Fujita S., Oda M., Kaneko K., Hitora T. Evolution of corundum-structured III-oxide semiconductors: Growth, properties, and devices. Jpn. J. Appl. Phys. 2016;55:1202A3. doi: 10.7567/JJAP.55.1202A3. [DOI] [Google Scholar]
- 16.Roberts J.W., Jarman J., Johnstone D., Midgley P., Chalker P., Oliver R., Massabuau F.C.P. α-Ga2O3 grown by low temperature atomic layer deposition on sapphire. J. Cryst. Growth. 2018;487:23–27. doi: 10.1016/j.jcrysgro.2018.02.014. [DOI] [Google Scholar]
- 17.Wheeler V., Nepal N., Boris D., Qadri S., Nyakiti L., Lang A., Koehler A., Foster G., Walton S., Eddy C., Jr., et al. Phase Control of Crystalline Ga2O3 Films by Plasma-Enhanced Atomic Layer Deposition. Chem. Mater. 2020;32:1140. doi: 10.1021/acs.chemmater.9b03926. [DOI] [Google Scholar]
- 18.Lee S.D., Ito Y., Kaneko K., Fujita S. Enhanced thermal stability of alpha gallium oxide films supported by aluminum doping. Jpn. J. Appl. Phys. 2015;54:030301. doi: 10.7567/JJAP.54.030301. [DOI] [Google Scholar]
- 19.Kaneko K., Nomura T., Fujita S. Corundum-structured α-phase Ga2O3-Cr2O3-Fe2O3 alloy system for novel functions. Phys. Status Solidi C. 2010;7:2467–2470. doi: 10.1002/pssc.200983896. [DOI] [Google Scholar]
- 20.Kaneko K., Kakeya I., Komori S., Fujita S. Band gap and function engineering for novel functional alloy semiconductors: Bloomed as magnetic properties at room temperature with α-phase (Ga,Fe)2O3. J. Appl. Phys. 2013;113:233901. doi: 10.1063/1.4807651. [DOI] [Google Scholar]
- 21.Wang T., Li W., Ni C., Janotti A. Band Gap and Band Offset of Ga2O3 and (AlxGa1-x)2O3 alloys. Phys. Rev. Appl. 2018;10:011003. doi: 10.1103/PhysRevApplied.10.011003. [DOI] [Google Scholar]
- 22.Song K., Mohseni M., Taghipour F. Application of ultraviolet light-emitting diodes (UV-LEDs) for water disinfection: A review. Water Res. 2016;94:341. doi: 10.1016/j.watres.2016.03.003. [DOI] [PubMed] [Google Scholar]
- 23.Smith E. The emission spectrum of hydrocarbon flames. Proc. R. Soc. Lond. A. 1940;174:110. doi: 10.1098/rspa.1940.0009. [DOI] [Google Scholar]
- 24.Ito H., Kaneko K., Fujita S. Growth and Band Gap Control of Corundum-Structured α-(Al,Ga)2O3 Thin Films on Sapphire by Spray-Assisted Mist Chemical Vapor Deposition. Jpn. J. Appl. Phys. 2012;51:100207. doi: 10.1143/JJAP.51.100207. [DOI] [Google Scholar]
- 25.Fujita S., Kaneko K. Epitaxial growth of corundum-structured wide bandgap III-oxide semiconductor thin films. J. Cryst. Growth. 2014;401:588–592. doi: 10.1016/j.jcrysgro.2014.02.032. [DOI] [Google Scholar]
- 26.Kaneko K., Fujita S., Hitora T. A power device material of corundum-structured α-Ga2O3 fabricated by MIST EPITAXY technique. Jpn. J. Appl. Phys. 2018;57:02CB18. doi: 10.7567/JJAP.57.02CB18. [DOI] [Google Scholar]
- 27.Innocenzi M.E., Swimm R.T., Bass M., French R.H., Villaverde A.B., Kokta M.R. Room-temperature optical absorption in undoped α-Al2O3. J. Appl. Phys. 1990;67:7542–7546. doi: 10.1063/1.345817. [DOI] [Google Scholar]
- 28.Weiher R.L., Ley R.P. Optical Properties of Indium Oxide. J. Appl. Phys. 1966;37:299–302. doi: 10.1063/1.1707830. [DOI] [Google Scholar]
- 29.Chi T.C., Sladek R.J. Elastic Constants and the Electrical Transition in Ti2O3. Phys. Rev. B. 1973;7:5080–5085. doi: 10.1103/PhysRevB.7.5080. [DOI] [Google Scholar]
- 30.Li Y., Weng Y., Yin X., Yu X., Kumar S.R.S., Wehbe N., Wu H., Alshareef H.N., Pennycook S.J., Breese M.B.H., et al. Orthorhombic Ti2O3: A Polymorph-Dependent Narrow-Bandgap Ferromagnetic Oxide. Adv. Funct. Mater. 2018;28:1705657. doi: 10.1002/adfm.201705657. [DOI] [Google Scholar]
- 31.Guo Y., Clark S., Robertson J. Calculation of metallic and insulating phases of V2O3 by hybrid density functionals. J. Chem. Phys. 2014;140:054702. doi: 10.1063/1.4863325. [DOI] [PubMed] [Google Scholar]
- 32.Al-Kuhaili M., Saleem M., Durrani S. Optical properties of iron oxide (α-Fe2O3) thin films deposited by the reactive evaporation of iron. J. Alloys Compd. 2012;521:178–182. doi: 10.1016/j.jallcom.2012.01.115. [DOI] [Google Scholar]
- 33.Cheng R., Xu B., Borca C.N., Sokolov A., Yang C.S., Yuan L., Liou S.H., Doudin B., Dowben P.A. Characterization of the native Cr2O3 oxide surface of CrO2. Appl. Phys. Lett. 2001;79:3122–3124. doi: 10.1063/1.1416474. [DOI] [Google Scholar]
- 34.Koffyberg F.P. Optical bandgaps and electron affinities of semiconducting Rh2O3(I) and Rh2O3(III) J. Phys. Chem. Solids. 1992;53:1285–1288. doi: 10.1016/0022-3697(92)90247-B. [DOI] [Google Scholar]
- 35.Thomas G.A., Rapkine D.H., Carter S.A., Millis A.J., Rosenbaum T.F., Metcalf P., Honig J.M. Observation of the Gap and Kinetic Energy in a Correlated Insulator. Phys. Rev. Lett. 1994;73:1529–1532. doi: 10.1103/PhysRevLett.73.1529. [DOI] [PubMed] [Google Scholar]
- 36.Yao Y., Okur S., Lyle L.A.M., Tompa G.S., Salagaj T., Sbrockey N., Davis R.F., Porter L.M. Growth and characterization of α-, β-, and ϵ-phases of Ga2O3 using MOCVD and HVPE techniques. Mater. Res. Lett. 2018;6:268–275. doi: 10.1080/21663831.2018.1443978. [DOI] [Google Scholar]
- 37.Lee W.E., Lagerlof K.P.D. Structural and electron diffraction data for sapphire (α-Al2O3) J. Electron Microsc. Tech. 1985;2:247–258. doi: 10.1002/jemt.1060020309. [DOI] [Google Scholar]
- 38.Zhang K.H.L., Lazarov V.K., Galindo P.L., Oropeza F.E., Payne D.J., Lai H.H.C., Egdell R.G. Domain Matching Epitaxial Growth of In2O3 Thin Films on α-Al2O3 (0001) Cryst. Growth Des. 2012;12:1000–1007. doi: 10.1021/cg201474h. [DOI] [Google Scholar]
- 39.Rice C.E., Robinson W.R. Structural changes in the solid solution (Ti1-xVx)2O3 as x varies from zero to one. J. Solid State Chem. 1977;21:155–160. doi: 10.1016/0022-4596(77)90155-4. [DOI] [Google Scholar]
- 40.Di Cerbo R.K., Seybolt A.U. Lattice Parameters of the α-Fe2O3-Cr2O3 Solid Solution. J. Am. Ceram. Soc. 1959;42:430–431. doi: 10.1111/j.1151-2916.1959.tb12968.x. [DOI] [Google Scholar]
- 41.Coey J.M.D. The crystal structure of Rh2O3. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1970;26:1876–1877. doi: 10.1107/S0567740870005022. [DOI] [Google Scholar]
- 42.McWhan D.B., Remeika J.P. Metal-Insulator Transition in (V1-xCrx)2O3) Phys. Rev. B. 1970;2:3734–3750. doi: 10.1103/PhysRevB.2.3734. [DOI] [Google Scholar]
- 43.Mott N. Metal-insulator transition in Ti2O3. J. Phys. 1981;42:277–281. doi: 10.1051/jphys:01981004202027700. [DOI] [Google Scholar]
- 44.Manandhar S., Ramana C. Direct, functional relationship between structural and optical properties in titanium-incorporated gallium oxide nanocrystalline thin films. Appl. Phys. Lett. 2017;110:061902. doi: 10.1063/1.4974042. [DOI] [Google Scholar]
- 45.Manandhar S., Battu A., Tan S., Panat R., Shutthanandan V., Ramana C. Effect of Ti doping on the crystallography, phase, surface/interface structure and optical band gap of Ga2O3 thin films. J. Mater. Sci. 2019;54:11526. doi: 10.1007/s10853-019-03663-w. [DOI] [Google Scholar]
- 46.Bandi M., Zade V., Roy S., Nair A., Seacat S., Sreenivasan S., Shutthanandan S., Van de Walle C., Peelaers H., Ramana C. Effect of Titanium Induced Chemical Inhomogeneity on Crystal Structure, Electronic Structure, and Optical Properties of Wide Band Gap Ga2O3. Cryst. Growth Des. 2020;20:1422. doi: 10.1021/acs.cgd.9b00747. [DOI] [Google Scholar]
- 47.Ritala M., Leskela M., Niinisto L., Haussalo P. Titanium isopropoxide as a precursor in atomic layer epitaxy of titanium dioxide thin films. Chem. Mater. 1993;5:1174–1181. doi: 10.1021/cm00032a023. [DOI] [Google Scholar]
- 48.Mayer M. SIMNRA User’s Guide for Version 7.0. Max-Planck-Institut für Plasmaphysik; Garching, Germany: 2017. [Google Scholar]
- 49.Ernst Ruska-Centre for Microscopy and Spectroscopy with Electrons. J. Large-Scale Res. Facil. 2016;2:A43. doi: 10.17815/jlsrf-2-68. [DOI] [Google Scholar]
- 50.Hÿtch M.J., Snoeck E., Kilaas R. Quantitative measurement of displacement and strain fields from HREM micrographs. Ultramicroscopy. 1998;74:131–146. doi: 10.1016/S0304-3991(98)00035-7. [DOI] [Google Scholar]
- 51.Mackus A.J.M., Schneider J.R., MacIsaac C., Baker J.G., Bent S.F. Synthesis of Doped, Ternary, and Quaternary Materials by Atomic Layer Deposition: A Review. Chem. Mater. 2019;31:1142–1183. doi: 10.1021/acs.chemmater.8b02878. [DOI] [Google Scholar]
- 52.Coll M., Napari M. Atomic layer deposition of functional multicomponent oxides. APL Mater. 2019;7:110901. doi: 10.1063/1.5113656. [DOI] [Google Scholar]
- 53.Vegard L. Die Konstitution der Mischkristalle und die Raumfüllung der Atome. Die Konstitution Der Mischkristal. Z. Phys. 1921;5:17. doi: 10.1007/BF01349680. [DOI] [Google Scholar]
- 54.Denton A.R., Ashcroft N.W. Vegard’s law. Phys. Rev. A. 1991;43:3161–3164. doi: 10.1103/PhysRevA.43.3161. [DOI] [PubMed] [Google Scholar]
- 55.Chen Z., Jaramillo T. The Use of UV-Visible Spectroscopy to Measure the Band Gap of a Semiconductor. Department of Chemical Engineering, Stanford University; Stanford, CA, USA: 2017. [Google Scholar]
- 56.Pascual J., Camassel J., Mathieu H. Fine structure in the intrinsic absorption edge of TiO2. Phys. Rev. B. 1978;18:5606–5614. doi: 10.1103/PhysRevB.18.5606. [DOI] [Google Scholar]
- 57.Amtout A., Leonelli R. Optical properties of rutile near its fundamental band gap. Phys. Rev. B. 1995;51:6842–6851. doi: 10.1103/PhysRevB.51.6842. [DOI] [PubMed] [Google Scholar]
- 58.Tang H., Levy F., Berger H., Schmid P.E. Urbach tail of anatase TiO2. Phys. Rev. B. 1995;52:7771–7774. doi: 10.1103/PhysRevB.52.7771. [DOI] [PubMed] [Google Scholar]
- 59.Mattsson A., Osterlund L. Adsorption and Photoinduced Decomposition of Acetone and Acetic Acid on Anatase, Brookite, and Rutile TiO2 Nanoparticles. J. Phys. Chem. C. 2010;114:14121–14132. doi: 10.1021/jp103263n. [DOI] [Google Scholar]
- 60.Hou Y., Wu L., Wang X., Ding Z., Li Z., Fu X. Photocatalytic performance of α-, β-, and γ-Ga2O3 for the destruction of volatile aromatic pollutants in air. J. Catal. 2007;250:12–18. doi: 10.1016/j.jcat.2007.05.012. [DOI] [Google Scholar]
- 61.Segura A., Artus L., Cusco R., Goldhahn R., Feneberg M. Band gap of corundumlike α-Ga2O3 determined by absorption and ellipsometry. Phys. Rev. Mater. 2017;1:024604. doi: 10.1103/PhysRevMaterials.1.024604. [DOI] [Google Scholar]
- 62.Shin S.H., Chandrashekhar G.V., Loehman R.E., Honig J.M. Thermoelectric Effects in Pure and V-Doped Ti2O3 Single Crystals. Phys. Rev. B. 1973;8:1364–1372. doi: 10.1103/PhysRevB.8.1364. [DOI] [Google Scholar]