Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Nov 9;60(12):6135–6146. doi: 10.1021/acs.jcim.0c01041

tmQM Dataset—Quantum Geometries and Properties of 86k Transition Metal Complexes

David Balcells †,*, Bastian Bjerkem Skjelstad ‡
PMCID: PMC7768608  PMID: 33166143

Abstract

graphic file with name ci0c01041_0010.jpg

We report the transition metal quantum mechanics (tmQM) data set, which contains the geometries and properties of a large transition metal–organic compound space. tmQM comprises 86,665 mononuclear complexes extracted from the Cambridge Structural Database, including Werner, bioinorganic, and organometallic complexes based on a large variety of organic ligands and 30 transition metals (the 3d, 4d, and 5d from groups 3 to 12). All complexes are closed-shell, with a formal charge in the range {+1, 0, −1}e. The tmQM data set provides the Cartesian coordinates of all metal complexes optimized at the GFN2-xTB level, and their molecular size, stoichiometry, and metal node degree. The quantum properties were computed at the DFT(TPSSh-D3BJ/def2-SVP) level and include the electronic and dispersion energies, highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energies, HOMO/LUMO gap, dipole moment, and natural charge of the metal center; GFN2-xTB polarizabilities are also provided. Pairwise representations showed the low correlation between these properties, providing nearly continuous maps with unusual regions of the chemical space, for example, complexes combining large polarizabilities with wide HOMO/LUMO gaps and complexes combining low-energy HOMO orbitals with electron-rich metal centers. The tmQM data set can be exploited in the data-driven discovery of new metal complexes, including predictive models based on machine learning. These models may have a strong impact on the fields in which transition metal chemistry plays a key role, for example, catalysis, organic synthesis, and materials science. tmQM is an open data set that can be downloaded free of charge from https://github.com/bbskjelstad/tmqm.

Introduction

Machine learning (ML) is revolutionizing several research fields in which chemistry plays a central role.1−4 By minimizing the error relative to reference data (i.e., training data set), ML algorithms deliver predictive models mapping a set of descriptors (i.e., features) into one or more properties of interest (i.e., targets). These models can robustly handle data sets that can be both very large and complex and, once compiled, can compute accurate predictions in a simple laptop within a fraction of a second. The fast execution of ML predictions enables the exploration of the vast chemical compound space (CCS)5−7 with different approaches, including multi-objective optimization8 and inverse design.9−11 Neural networks12−16 and other ML models have been used successfully in a wide range of applications, with numerous examples in materials science17−21 and drug discovery.22−26 ML and data-driven approaches are also making rapid progress in catalytic,27−41 organic,42−47 inorganic,48,49 and theoretical50−56 chemistry.

Despite the high potential of ML, a major challenge in its application is the need for big data sets for the training and validation of the models. There are fields of high interest, for example, catalysis, in which the size and scope of experimental data is small. An efficient solution is to use computational results as training data.57−60 This is one of the fundamental concepts underlying quantum-based ML (QML),61 in which the ML models are trained with data from quantum mechanical (QM) calculations. QML models are used to predict highest occupied molecular orbital (HOMO)/lowest unoccupied molecular orbital (LUMO) energies and gaps, dipole moments, polarizabilities, and other quantum properties governing the macroscopic behavior of chemical systems. State-of-the-art QML models, including atomistic62 and message-passing neural networks,63 yield predictions approaching chemical accuracy.64 However, the training of these models requires quantum data sets that must be large and comprehensive to avoid overfitting and to ensure the unbiased exploration of the CCS. These data sets are scarce, and their generation remains hampered by the high computational cost of quantum mechanics calculations, thus limiting the scope of QML. Quantum data set examples include the Materials Project,65 PubChemQC,66 and the GDB1367-based QM series for organic chemistry (QM7,54 QM7b,68 QM8,69,70 and QM971). Ab initio molecular dynamics trajectories and off-equilibrium conformations are also available from the MD1772 and ANI-173 data sets, respectively. Quantum data sets for transition metal (TM) complexes cover either small27 or large but specific8 regions of the chemical space. Other data-driven approaches to organometallic chemistry have focused on the isolated ligands.74

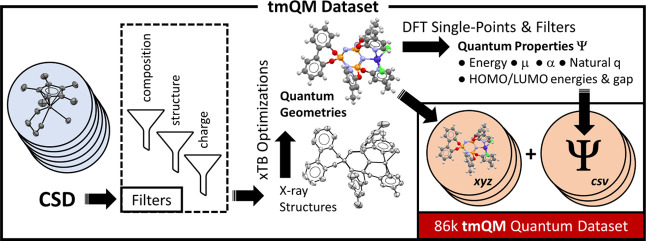
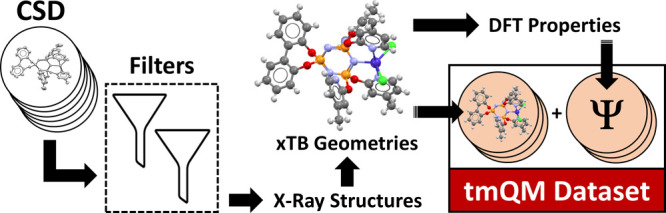
We herein report the transition metal quantum mechanics data set (tmQM), which contains a curated collection of TM compounds, including Werner, bioinorganic and organometallic complexes. The computational protocol used in the generation of the tmQM data set consists of filtering structures from the Cambridge Structural Database (CSD), followed by xTB geometry optimizations and density functional theory (DFT) single points (Figure 1). In total, tmQM contains 86,665 complexes extracted from the CSD, representing the diversity of the TM–organic chemical space with a large variety of organic ligands bound to all the 3d, 4d, and 5d TMs from groups 3 to 12. tmQM provides the Cartesian coordinates optimized at the GFN2-xTB level and a set of quantum properties computed at the DFT(TPSSh-D3BJ/def2-SVP) level, including the electronic and dispersion energies, metal center natural charge, HOMO/LUMO energies and gap, and dipole moment. Polarizabilities are also provided at the GFN2-xTB level. The pairwise representations of the properties revealed unusual regions within the CCS, for example, TM complexes with large polarizabilities and wide HOMO/LUMO gaps.

Figure 1.

Figure 1

Open in a new tab

Computational protocol used to generate the tmQM data set. CSD = Cambridge Structural Database; xTB = extended tight-binding; DFT = density functional theory; μ = dipole moment; α = polarizability; q = charge.

The tmQM data set will enable the training of ML models, which can be exploited in the data-driven discovery of new catalysts and functional materials. Traditional predictive models, including multivariate linear regression,75−77 and quantitative structure–activity relationships,78,79 will also benefit from the availability of the tmQM data set, which can be downloaded free of charge from https://github.com/bbskjelstad/tmqm and http://quantum-machine.org/datasets/.

Chemical Subspace Extracted from the CSD

The tmQM data set fully comprises structures extracted from the 2020 release of the CSD by using the seven filters listed below. The filters were implemented by means of the CSD Python API.

  • 1.

    Composition filter (metal elements): Excluded all structures except those containing a single TM.80

  • 2.

    Composition filter (nonmetal elements): Excluded all structures except those containing a minimum of one C and one H atoms. The other elements allowed in the structures were as follows: B, Si, N, P, As, O, S, Se, F, Cl, Br, and I.

  • 3.

    Component filter: Excluded the structure of all molecular components, except that of the metal complex.

  • 4.

    Polymer filter: Excluded all polymeric structures.

  • 5.

    Spatial coordinates filter: Excluded all structures without three-dimensional coordinates.

  • 6.

    Disorder filter: Excluded all structures with disordered atoms.

  • 7.

    Charge filter: Excluded all structures with charge higher than 1 and lower than −1.

Filters 1–2 extract mononuclear TM–organic compounds from the CSD, including Werner, organometallic, and bioinorganic complexes. Filter 3 removes the solvent molecules and counterions that are found in many crystal structures. Filters 4–6 ensure the correctness of the structures passed to the software used in the QM calculations. Filter 7 removes highly charged species, which may cause charge-separation artifacts in the gas-phase QM calculations.

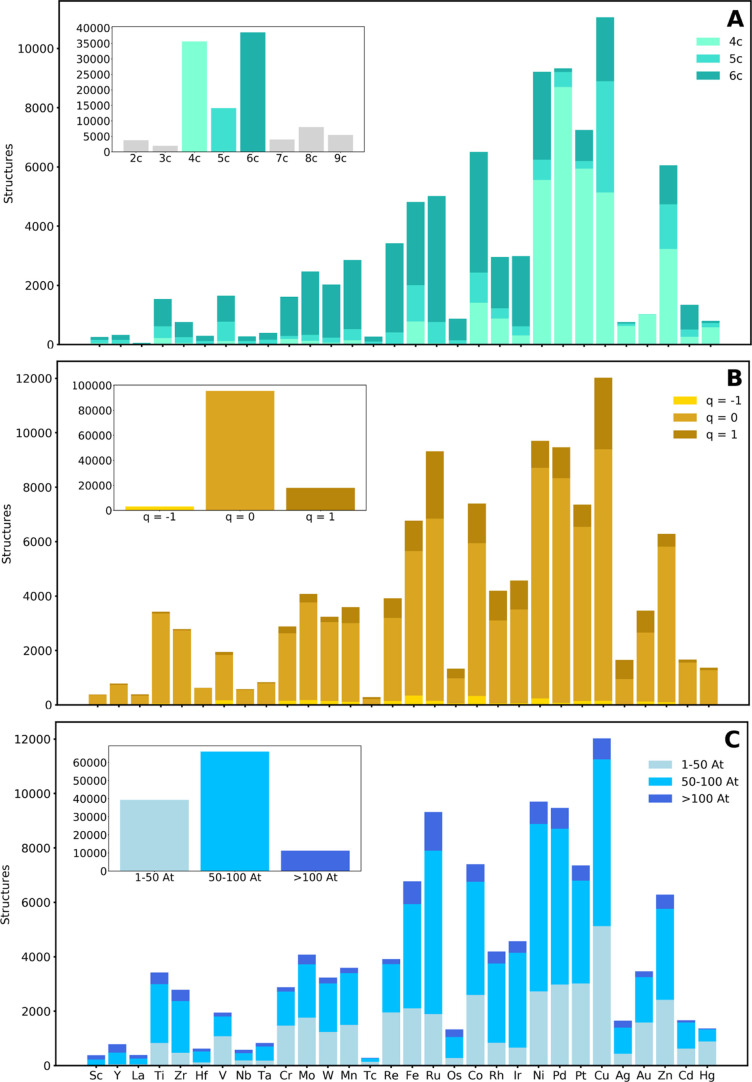
In total, 116,332 structures were extracted from the CSD with filters 1–7. Figure 2 shows the distribution of different molecular properties over the TM series. The number of bonds involving the metal center (Figure 2A) peaks at 4, 5, and 6 (31, 12, and 33% of the total, respectively). The latter is the most abundant instance and dominates with most TMs. Notable exceptions to this trend are Ni, Pd, Pt, and Cu, which show a preference for making four bonds. These observations can be associated to the prevalence of the tetrahedral (4 bonds), square planar (4 bonds), trigonal bipyramidal (5 bonds), square pyramidal (5 bonds), and octahedral (6 bonds) coordination geometries. However, it should be noted that the number of metal bonds was extracted from the connectivity table of the CSD mol2 files. Thus, this number is equal to the degree of the metal center node in the molecular graph of the complex, which is not necessarily equal to the coordination number.81 For example, the η5-Cp ligand counts five bonds but, in an octahedral complex, and from a molecular orbital perspective, it only occupies three coordination sites. With Ti and other early TMs forming stable arene complexes, 8 is one of the most abundant metal bond counts (i.e., octahedral complexes with three monodentate ligands and one Cp ligand). In contrast, at the extreme of the late TM groups, the number of metal bonds peaks at the lowest possible values. For example, 2 is the most common metal bond count with Au.

Figure 2.

Figure 2

Open in a new tab

Distributions over the 3–5d TM series by (A) metal node degree; i.e. number of bonds to the metal, (B) molecular charge q, and (C) size in number of atoms. The insets show the totals. The data are for the 116,332 structures extracted from the CSD with filters 1–7.

The figure also shows the distribution of the TM complex charges (Figure 2B) and sizes (Figure 2C). The former distribution clearly shows the dominance of q = 0 for all TMs, without any exception, and with the neutral complexes comprising 82% of the total. The molecular size distribution, measured in number of atoms, is balanced between the small (1–50 atoms) and medium-size (50–100 atoms) classes, which include 34 and 57% of the total, respectively. The large class (>100 atoms) includes a smaller portion of structures (9%), being the smallest fraction with all TMs.

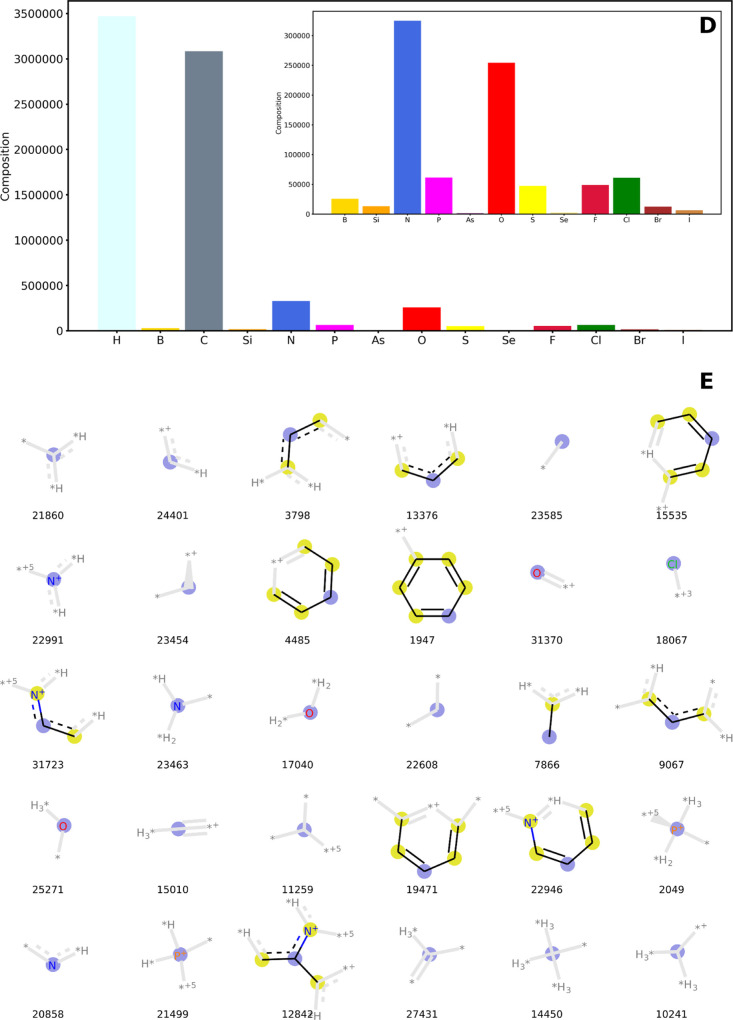
Figure 3 reflects the strong organic component of the TM complexes extracted from the CSD. C and H account for 87% of the chemical composition of the entire space (Figure 3D). After these two elements, N, O, P, Cl, and F are, in this order, the most abundant. These elements are found in the most common ligands, including amines, carboxylates, heterocycles, phosphines, and halides. The nature of the chemical space was also explored by computing Morgan fingerprints, using radius = 3, and a large number of bits (i.e., 32,768) to avoid hash collisions. The connectivity needed to generate the fingerprints is available from the CSD database and can be retrieved by using the CSD code provided for all entries of the tmQM data set. Figure 3E shows the 30 most abundant fingerprints, which account for conjugated C–C bonds (e.g., bits 21,860 and 24,401), aromatic rings based on C (e.g., 15,535 and 1947) and N (e.g., 22,946), amines (e.g., 23,463), and other fragments that are commonly found in organic ligands. Other groups and ligands, including chloride, alkoxy, oxo, and phosphines, can also be easily recognized in fingerprints 18,067, 25,271, 31,370, and 2049, respectively.

Figure 3.

Figure 3

Open in a new tab

Composition by the number of non-TM atoms in the chemical formula (D), with the inset excluding C and H, and the 30 most abundant Morgan fingerprints (E). The data are for the structures extracted from the CSD with filters 1–7.82 Fingerprint legend: All nonlabeled atoms are C, and the gray fragments show the fingerprint connectivity but are not part of it; fingerprint label = bit number, blue circle = central atom in the fingerprint, yellow circle = aromatic atom, star = arbitrary atom.

Figures 4 and 5, which show one random example for each of the 30 TM elements, give a glimpse of the vast diversity of the chemical space extracted from the CSD. The 30 complexes in the two figures (i.e., a mere 0.03% of the full space) include 48 ligands, which are bound to the metal center in five different coordination modes (κ1, κ2, κ3, η2, and η5), four different coordination numbers (2, 4, 5, and 6) and six different coordination geometries (linear, tetrahedral, square planar, trigonal bipyramidal, square pyramidal, and octahedral). Interestingly, the further extension of these variables by considering all the 116,332 structures extracted with filters 1–7 would allow for a combinatorial explosion yielding a massive number of TM complexes. Thus, despite the large size of the CSD, this database represents a minuscule fraction of the full TM–organic compound space, which also underlines the need for predictive models enabling the efficient exploration of this vast space.

Figure 4.

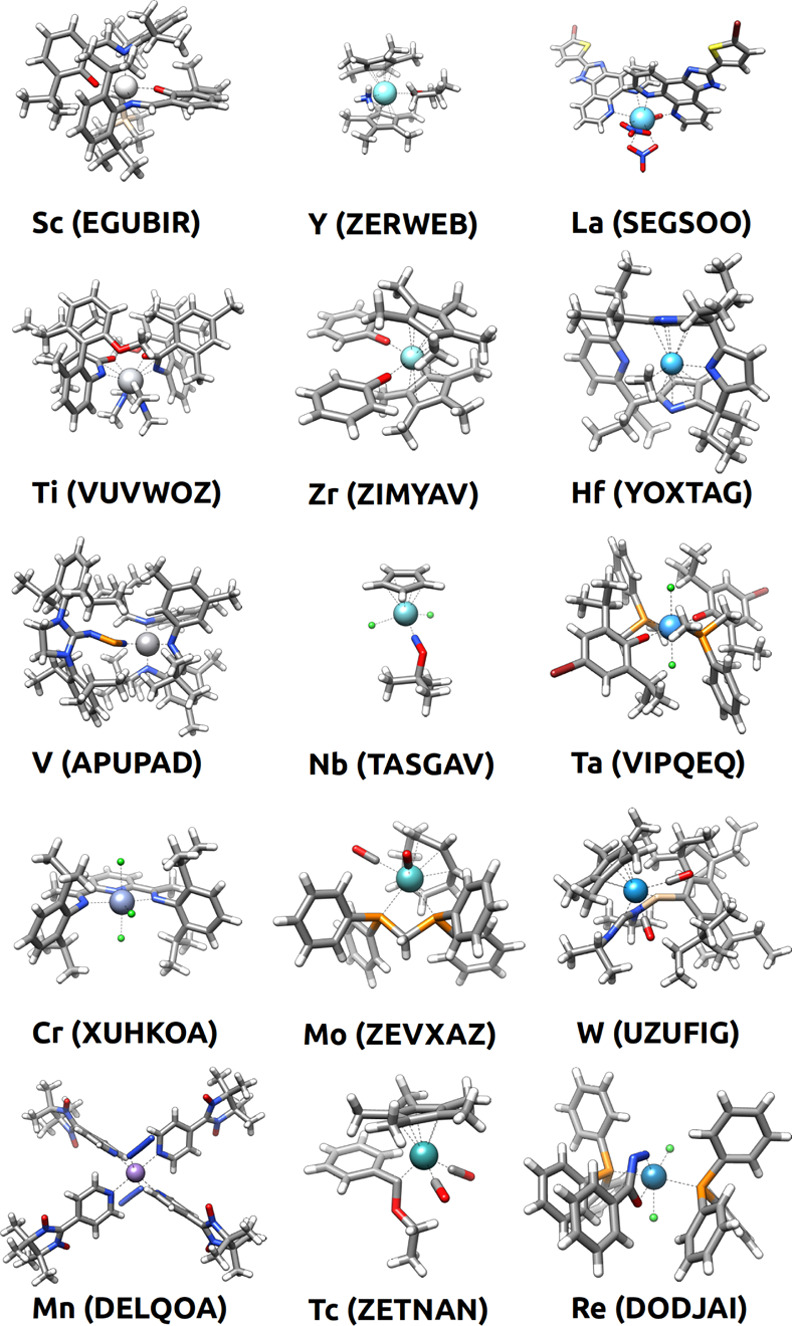
Figure 4

Open in a new tab

Randomly selected structures, and their CSD codes, for each TM in groups 3–7. The selection was made among the 116,332 structures extracted from the CSD with filters 1–7.

Figure 5.

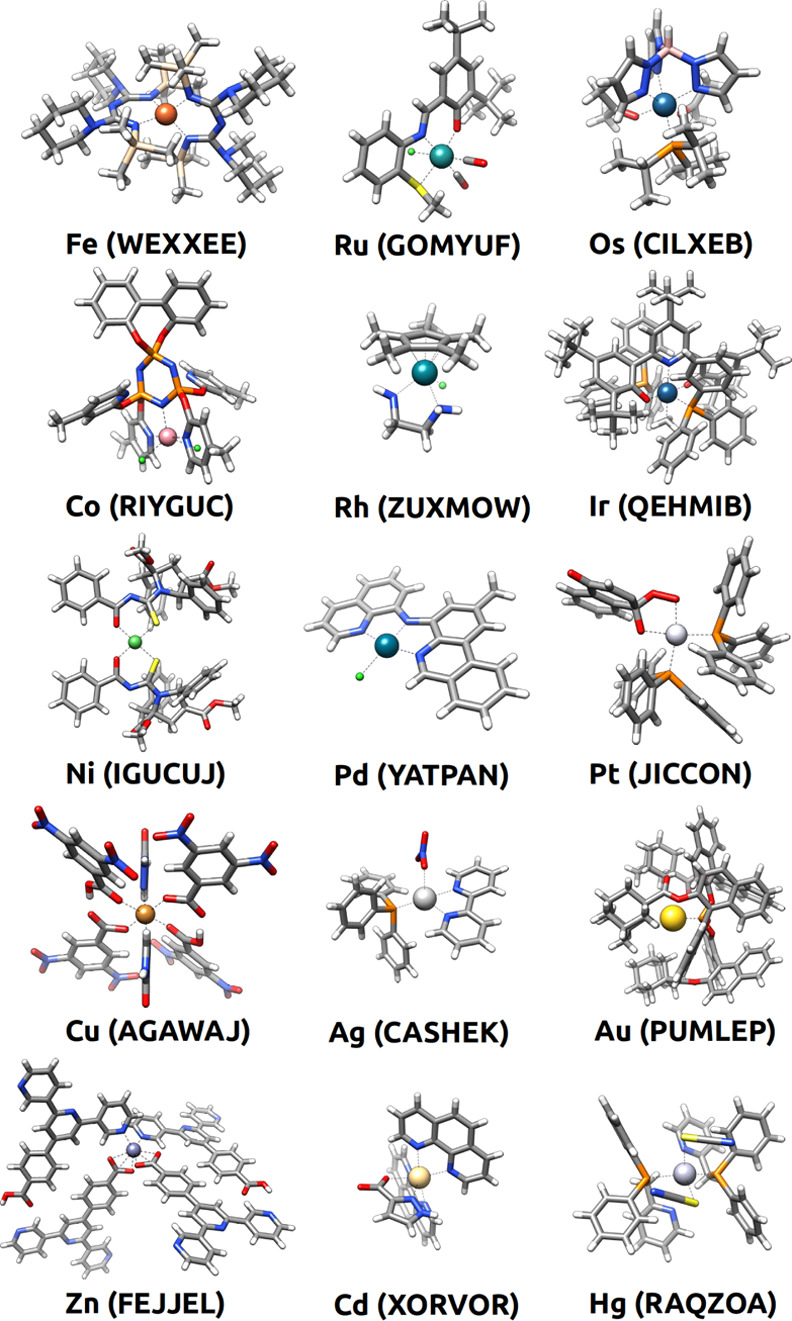
Figure 5

Open in a new tab

Randomly selected structures and their CSD codes for each TM in groups 8–12. The selection was made among the 116,332 structures extracted from the CSD with filters 1–7.

Quantum Geometries and Properties

The structures of the TM complexes extracted from the CSD with filters 1–7 were used as the basis to construct the tmQM data set. The advantage of using the CSD as the source of structures is that the TM complexes in the resulting data set can be accessed experimentally through documented synthesis procedures. Thus, ML models trained with the tmQM data set will embed synthetic accessibility in their internal representations used for prediction and generation tasks.

The CSD structures were fully optimized in gas phase with the extended tight-binding xTB method.83 The second-generation parametrization for geometries, frequencies, and noncovalent interactions (GFN2-xTB84) was used. The GFN2-xTB parametrization is less empirical than the GFN1, and it was proven to be more robust in geometry optimization.85 The tight optimization level was used in the GFN2-xTB calculations to set the convergence thresholds to 1 × 10–6Eh (energy) and 8 × 10–4Ehα–1 (gradient). The calculations were carried out with the xtb program. Before passing the geometries to the software used for the DFT calculations, the following three filters were applied

  • 1.

    Convergence filter: Excluded all geometries that did not reach the convergence thresholds.

  • 2.

    Geometry quality: The GFN2-xTB-optimized geometries were ranked based on their deviation from the initial CSD crystal structure. The deviation was measured for each geometry by computing a structure quality index Sq with eq 1

graphic file with name ci0c01041_m001.jpg 1

in which the norm of the displacement (dn) is summed over all optimization cycles (ocyc) and divided by the size of the system in atoms (NAt) and the CSD R factor. The 7% geometries yielding the largest Sq values were excluded.85

  • 3.

    Electron-count filter: Excluded all structures with an odd number of electrons.

The first two filters excluded geometries with major flaws (e.g. erroneous coordination number and geometry). The third filter excluded all TM complexes that are forced to have an open-shell ground state, due to an odd number of electrons (i.e. 22,325 of the 116,332 structures extracted from the CSD). This filter excludes the errors and high computational cost associated to QM calculations on open-shell systems. In total, 86,699 geometries passed filters 1–3.

The GFN2-xTB optimized Cartesian coordinates of all TM complexes are included in the tmQM data set. By using chemoinformatics software like RDKit, molSimplify, and Open Babel, these coordinates can be easily transformed into features for ML models, including Morgan fingerprints,86 SMILES,87−89 and autocorrelation functions.90 All geometries are provided together with their CSD code, molecular size, charge, spin multiplicity, stoichiometry, and metal node degree (i.e., number of bonds involving the metal center).

The quantum properties of the tmQM data set were obtained from single-point calculations at the DFT level on the GFN2-xTB optimized geometries. All properties were computed for the closed-shell singlet state. The calculations were performed in gas phase with the hybrid meta-GGA TPSSh functional91 and the double-ζ polarized def2-SVP basis set,92 including effective core potentials for Z > 36. Dispersion was introduced by means of the D3BJ model.93 The calculations were carried out with the Gaussian16 program, using the ultrafine pruned (99,590) grid for high numerical accuracy. This level of theory was used to compute the following properties: electronic and dispersion energies, HOMO and LUMO energies, HOMO/LUMO gap, dipole moment, and metal center charge, which was derived from natural population analysis.94 In total, the computation of the quantum properties converged for 86,665 TM complexes. In addition to the GFN2-xTB geometries, the tmQM data set provides these DFT properties for all TM complexes. Polarizabilities are also provided at the GFN2-xTB level based on the self-consistent D4 model using a Gaussian-weighting scheme.84

Pairwise Property Representations

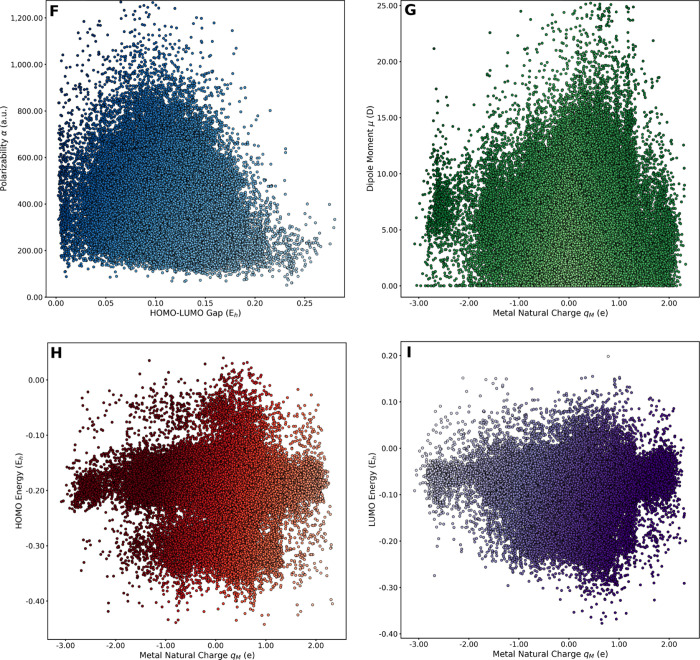
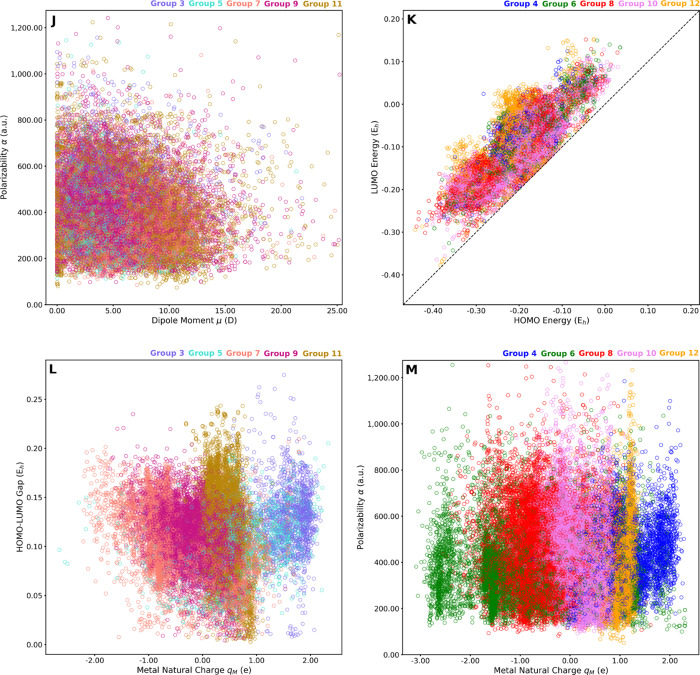
The nature of the tmQM data set was explored by representing quantum property pairs in scatter plots. Figure 6 includes a selection of four plots showing the poor correlation between the HOMO/LUMO gap and the polarizability (Figure 6F) and between the metal natural charge and the dipole moment (Figure 6G), the HOMO energy (Figure 6H), and the LUMO energy (Figure 6I). The plots have blob shapes with an almost continuous variation of the two properties represented in each case. This lack of correlation was also observed in the pairwise representations of the HOMO/LUMO gap versus the dipole moment (Figure S1), polarizability versus dipole moment (Figure S2), HOMO/LUMO gap versus metal center natural charge (Figure S3), and polarizability versus metal center natural charge (Figure S4). Interestingly, these representations also show that unusual regions of the chemical space have small, yet significant, populations, for example, complexes with large polarizabilities and wide HOMO/LUMO gaps, complexes with small dipole moments and highly charged metal centers, complexes with low HOMO energies and electron-rich metal centers, and complexes with high LUMO energies and electron-poor metal centers.

Figure 6.

Figure 6

Open in a new tab

Pairwise correlations, with color gradients based on property values; α vs HOMO/LUMO gap (F), μ vs qM (G), HOMO energy vs qM (H), and LUMO energy vs qM (I). Level of theory: TPSSh-D3BJ/def2-SVP, except GFN2-xTB for α.

The pairwise scatters were also plotted by using the color of the data points to encode the periodic table group of the metal center (Figure 7). For the sake of clarity, the plots were divided in two sets, one accounting for groups 3, 5, 7, 9, and 11, and one accounting for groups 4, 6, 8, 10, and 12. The data points were added to the scatter plots in a random order; that is regions with a dominant color are mostly associated to a given TM group. Most of the plots have no color structure, that is, any metal can give any combination of properties with the appropriate choice of ligands. This is the case, for instance, of polarizability versus dipole moment (Figure 7J). However, there are property pairs with some structure, for example, the HOMO versus LUMO energies (Figure 7K), in which group 12 yields the largest gaps. The most structured property pairs are those involving the metal natural charge, with the scatter plots yielding color bands (Figure 7L,M). Following the periodic trends, the groups closest to the d0 configuration, or exceeding the d10 configuration, yielded the highest positive charges, whereas the groups closest to the d10 configuration yielded the lowest negative charges. More pairwise representations of the quantum properties are available in the Supporting Information (Figures S5–S8).

Figure 7.

Figure 7

Open in a new tab

Pairwise correlations colored by the periodic table group; α vs μ (J), LUMO vs HOMO energies (K), HOMO/LUMO gap vs qM (L), and α vs qM (M). Level of theory: TPSSh-D3BJ/def2-SVP, except GFN2-xTB for α.

Data Benchmarks

The tmQM data set was assessed by performing three different benchmarks for a set of quantum properties including the metal center natural charge (qM), dipole moment (μ), HOMO/LUMO gap, and polarizability (α).

  • Benchmark 1: The qM, μ, and HOMO/LUMO gaps of the GFN2-xTB-optimized geometries, computed at the TPSSh-D3BJ/def2-SVP level, were compared to their values recomputed at the B2PLYP-D3/def2-SVP level.95

  • Benchmark 2: The qM, μ, and HOMO/LUMO gaps of the GFN2-xTB-optimized geometries, computed at the TPSSh-D3BJ/def2-SVP level, were compared to their values recomputed after reoptimizing the geometries at the same TPSSh-D3BJ/def2-SVP level.

  • Benchmark 3: The α of the GFN2-xTB-optimized geometries, computed at the same GFN2-xTB level, were compared to their values recomputed at the TPSSh-D3BJ/def2-SVP level.

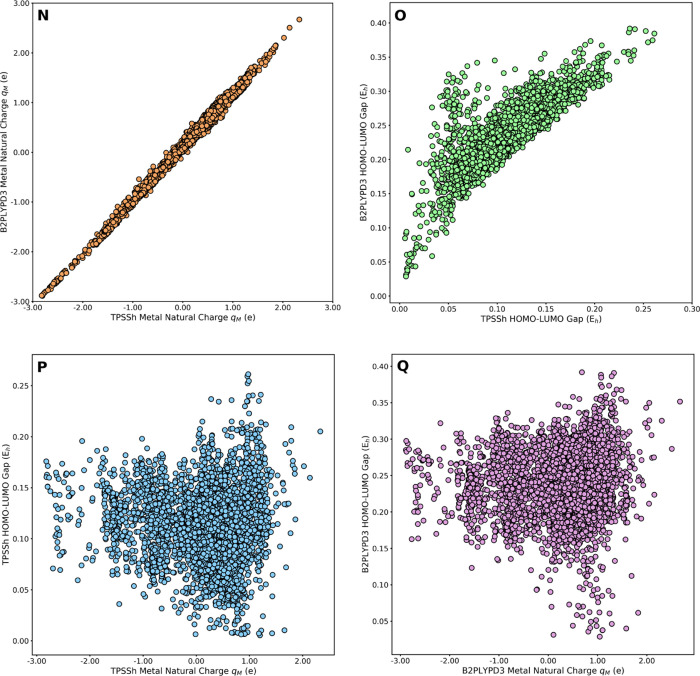
Benchmark 1 showed how the quantum properties vary upon lifting the DFT level from the meta-GGA TPPSh hybrid functional to the B2PLYP-D3 double-hybrid functional. Benchmark 2 showed how much sensible are the quantum properties to the level of theory used in the geometry optimization of the CSD structures, by comparing GFN2-xTB to DFT(TPSSh-D3BJ). Benchmark 3 showed the deviation of the GFN2-xTB polarizabilities relative to the DFT(TPPSh). Table 1 gives the mean absolute error (MAE) and r2 score for each benchmark.96

Table 1. Data Benchmarks and Their Associated MAE (in Atomic Units, Except for μ, in D) and r2 Scores.

property qM
 μ
 gap
 α
benchmark MAE r2 MAE r2 MAE r2 MAE r2
1 (B2PLYP-D3) 0.12 0.99 0.53 0.98 0.124 0.69    
2 (DFT-Opt) 0.05 0.99 0.56 0.94 0.007 0.92    
3 (DFT-α)             19.8 0.81
Open in a new tab

Table 1 shows that in both benchmarks 1 and 2, q and μ yielded the smallest MAEs, with r2 → 1. The largest deviations were found for the HOMO/LUMO gaps, in line with the strong dependence of this property on the theory levels used in the single-point and geometry optimization calculations. This scenario is illustrated for benchmark 1 with qM (Figure 8N) and the HOMO/LUMO gap (Figure 8O). However, despite the larger uncertainty of the HOMO/LUMO gap relative to qM, the pairwise correlations of these two properties at the TPSSh-D3BJ (Figure 8P) and B2PLYP-D3 (Figure 8Q) levels have essentially the same shapes, with three adjacent clusters at qM ≈ −1.50e, −0.75e, and 0.50e, that increase in size from qM ≈ −2 to qM ≈ +2. In benchmark 3, the deviation of the GFN2-xTB α values relative to the DFT(TPSSh-D3BJ) is larger than those of qM and μ in benchmarks 1 and 2, though significantly smaller than that of the HOMO/LUMO gap in benchmark 1. More pairwise representations of the quantum property benchmarks are provided in the Supporting Information (Figures S9–S12).

Figure 8.

Figure 8

Open in a new tab

Pairwise property correlations from the B2PLYP-D3 benchmark 1; qM (N), HOMO/LUMO gap (O), TPSSh-D3BJ HOMO/LUMO gap vs qM (P), and B2PLYP-D3 HOMO/LUMO gap vs qM (Q).

Data Availability

tmQM is an open data set freely available at GitHub (https://github.com/bbskjelstad/tmqm) and from Quantum-Machine (http://quantum-machine.org/datasets/). Quantum features, geometries and properties computed at the GFN2-xTB and TPSSh-D3BJ/def2-SVP levels of theory are provided in the xyz and csv file formats.

Conclusions

This article reported the tmQM data set, which provides the quantum geometries and properties of a large amount of TM complexes. The complexes were extracted from the CSD database with a series of filters imposing constraints on chemical composition, structure, and charge. After optimization at the GFN2-xTB level, additional filters were applied to control geometry quality and electronic structure. A total of 86k TM complexes passed these filters and were included in the tmQM data set after computing their quantum properties at the TPSSh-D3BJ/def2-SVP level, including the electronic and dispersion energies, HOMO/LUMO energies and gap, dipole moment and metal center natural charge. Polarizabilities are also provided at the GFN2-xTB level. The pairwise representations of these properties allowed for mapping regions of the chemical space with unusual properties; for example, TM complexes combining electron-rich metal centers with low HOMO energies. The tmQM data set, which is open and freely available at https://github.com/bbskjelstad/tmqm, will enable the training of ML models for the discovery of new molecular materials based on TMs.

Acknowledgments

D.B. acknowledges the support from the Research Council of Norway through its Centers of Excellence Scheme (project number 262695) and the Norwegian Supercomputing Program (NOTUR; project number NN4654K).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.0c01041.

  • Pairwise representations of the quantum properties by their values and periodic table group, including data benchmarks (PDF)

The authors declare no competing financial interest.

Supplementary Material

ci0c01041_si_001.pdf (13.8MB, pdf)

References

  1. Gromski P. S.; Henson A. B.; Granda J. M.; Cronin L. How to Explore Chemical Space Using Algorithms and Automation. Nat. Rev. Chem. 2019, 3, 119–128. 10.1038/s41570-018-0066-y. [DOI] [Google Scholar]
  2. Butler K. T.; Davies D. W.; Cartwright H.; Isayev O.; Walsh A. Machine Learning for Molecular and Materials Science. Nature 2018, 559, 547–555. 10.1038/s41586-018-0337-2. [DOI] [PubMed] [Google Scholar]
  3. Bartók A. P.; De S.; Poelking C.; Bernstein N.; Kermode J. R.; Csányi G.; Ceriotti M. Machine Learning Unifies the Modeling of Materials and Molecules. Sci. Adv. 2017, 3, e1701816 10.1126/sciadv.1701816. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Tkatchenko A. Machine Learning for Chemical Discovery. Nat. Commun. 2020, 11, 4125. 10.1038/s41467-020-17844-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Reymond J.-L. The Chemical Space Project. Acc. Chem. Res. 2015, 48, 722–730. 10.1021/ar500432k. [DOI] [PubMed] [Google Scholar]
  6. von Lilienfeld O. A. Quantum Machine Learning in Chemical Compound Space. Angew. Chem., Int. Ed. 2018, 57, 4164–4169. 10.1002/anie.201709686. [DOI] [PubMed] [Google Scholar]
  7. Fey N. Lost in Chemical Space? Maps to Support Organometallic Catalysis. Chem. Cent. J. 2015, 9, 38. 10.1186/s13065-015-0104-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Janet J. P.; Ramesh S.; Duan C.; Kulik H. J. Accurate Multiobjective Design in a Space of Millions of Transition Metal Complexes with Neural-Network-Driven Efficient Global Optimization. ACS Cent. Sci. 2020, 6, 513–524. 10.1021/acscentsci.0c00026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Freeze J. G.; Kelly H. R.; Batista V. S. Search for Catalysts by Inverse Design: Artificial Intelligence, Mountain Climbers, and Alchemists. Chem. Rev. 2019, 119, 6595–6612. 10.1021/acs.chemrev.8b00759. [DOI] [PubMed] [Google Scholar]
  10. Gómez-Bombarelli R.; Wei J. N.; Duvenaud D.; Hernández-Lobato J. M.; Sánchez-Lengeling B.; Sheberla D.; Aguilera-Iparraguirre J.; Hirzel T. D.; Adams R. P.; Aspuru-Guzik A. Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules. ACS Cent. Sci. 2018, 4, 268–276. 10.1021/acscentsci.7b00572. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Sanchez-Lengeling B.; Aspuru-Guzik A. Inverse Molecular Design Using Machine Learning: Generative Models for Matter Engineering. Science 2018, 361, 360–365. 10.1126/science.aat2663. [DOI] [PubMed] [Google Scholar]
  12. Schütt K. T.; Arbabzadah F.; Chmiela S.; Müller K. R.; Tkatchenko A. Quantum-Chemical Insights from Deep Tensor Neural Networks. Nat. Commun. 2017, 8, 13890. 10.1038/ncomms13890. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Janet J. P.; Chan L.; Kulik H. J. Accelerating Chemical Discovery with Machine Learning: Simulated Evolution of Spin Crossover Complexes with an Artificial Neural Network. J. Phys. Chem. Lett. 2018, 9, 1064–1071. 10.1021/acs.jpclett.8b00170. [DOI] [PubMed] [Google Scholar]
  14. Wei J. N.; Duvenaud D.; Aspuru-Guzik A. Neural Networks for the Prediction of Organic Chemistry Reactions. ACS Cent. Sci. 2016, 2, 725–732. 10.1021/acscentsci.6b00219. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Ma J.; Sheridan R. P.; Liaw A.; Dahl G. E.; Svetnik V. Deep Neural Nets as a Method for Quantitative Structure–Activity Relationships. J. Chem. Inf. Model. 2015, 55, 263–274. 10.1021/ci500747n. [DOI] [PubMed] [Google Scholar]
  16. Janet J. P.; Duan C.; Yang T.; Nandy A.; Kulik H. J. A Quantitative Uncertainty Metric Controls Error in Neural Network-Driven Chemical Discovery. Chem. Sci. 2019, 10, 7913–7922. 10.1039/c9sc02298h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Raccuglia P.; Elbert K. C.; Adler P. D. F.; Falk C.; Wenny M. B.; Mollo A.; Zeller M.; Friedler S. A.; Schrier J.; Norquist A. J. Machine-Learning-Assisted Materials Discovery Using Failed Experiments. Nature 2016, 533, 73–76. 10.1038/nature17439. [DOI] [PubMed] [Google Scholar]
  18. Gómez-Bombarelli R.; et al. Design of Efficient Molecular Organic Light-Emitting Diodes by a High-Throughput Virtual Screening and Experimental Approach. Nat. Mater. 2016, 15, 1120–1127. 10.1038/nmat4717. [DOI] [PubMed] [Google Scholar]
  19. Le T. C.; Winkler D. A. Discovery and Optimization of Materials Using Evolutionary Approaches. Chem. Rev. 2016, 116, 6107–6132. 10.1021/acs.chemrev.5b00691. [DOI] [PubMed] [Google Scholar]
  20. Jensen Z.; Kim E.; Kwon S.; Gani T. Z. H.; Román-Leshkov Y.; Moliner M.; Corma A.; Olivetti E. A Machine Learning Approach to Zeolite Synthesis Enabled by Automatic Literature Data Extraction. ACS Cent. Sci. 2019, 5, 892–899. 10.1021/acscentsci.9b00193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Fernandez M.; Boyd P. G.; Daff T. D.; Aghaji M. Z.; Woo T. K. Rapid and Accurate Machine Learning Recognition of High Performing Metal Organic Frameworks for CO2 Capture. J. Phys. Chem. Lett. 2014, 5, 3056–3060. 10.1021/jz501331m. [DOI] [PubMed] [Google Scholar]
  22. Zhavoronkov A.; et al. Deep Learning Enables Rapid Identification of Potent DDR1 Kinase Inhibitors. Nat. Biotechnol. 2019, 37, 1038–1040. 10.1038/s41587-019-0224-x. [DOI] [PubMed] [Google Scholar]
  23. Mamoshina P.; Vieira A.; Putin E.; Zhavoronkov A. Applications of Deep Learning in Biomedicine. Mol. Pharmaceutics 2016, 13, 1445–1454. 10.1021/acs.molpharmaceut.5b00982. [DOI] [PubMed] [Google Scholar]
  24. Altae-Tran H.; Ramsundar B.; Pappu A. S.; Pande V. Low Data Drug Discovery with One-Shot Learning. ACS Cent. Sci. 2017, 3, 283–293. 10.1021/acscentsci.6b00367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Mayr A.; Klambauer G.; Unterthiner T.; Steijaert M.; Wegner J. K.; Ceulemans H.; Clevert D.-A.; Hochreiter S. Large-Scale Comparison of Machine Learning Methods for Drug Target Prediction on ChEMBL. Chem. Sci. 2018, 9, 5441–5451. 10.1039/c8sc00148k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Chen H.; Engkvist O.; Wang Y.; Olivecrona M.; Blaschke T. The Rise of Deep Learning in Drug Discovery. Drug Discovery Today 2018, 23, 1241–1250. 10.1016/j.drudis.2018.01.039. [DOI] [PubMed] [Google Scholar]
  27. Friederich P.; dos Passos Gomes G.; De Bin R.; Aspuru-Guzik A.; Balcells D. Machine Learning Dihydrogen Activation in the Chemical Space Surrounding Vaska’s complex. Chem. Sci. 2020, 11, 4584–4601. 10.1039/d0sc00445f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Rosales A. R.; Wahlers J.; Limé E.; Meadows R. E.; Leslie K. W.; Savin R.; Bell F.; Hansen E.; Helquist P.; Munday R. H.; Wiest O.; Norrby P.-O. Rapid Virtual Screening of Enantioselective Catalysts Using CatVS. Nat. Catal. 2019, 2, 41–45. 10.1038/s41929-018-0193-3. [DOI] [Google Scholar]
  29. Foscato M.; Jensen V. R. Automated in Silico Design of Homogeneous Catalysts. ACS Catal. 2020, 10, 2354–2377. 10.1021/acscatal.9b04952. [DOI] [Google Scholar]
  30. Kitchin J. R. Machine Learning in Catalysis. Nat. Catal. 2018, 1, 230–232. 10.1038/s41929-018-0056-y. [DOI] [Google Scholar]
  31. Tran K.; Ulissi Z. W. Active Learning Across Intermetallics to Guide Discovery of Electrocatalysts for CO2 Reduction and H2 Evolution. Nat. Catal. 2018, 1, 696–703. 10.1038/s41929-018-0142-1. [DOI] [Google Scholar]
  32. Cordova M.; Wodrich M. D.; Meyer B.; Sawatlon B.; Corminboeuf C. Data-Driven Advancement of Homogeneous Nickel Catalyst Activity for Aryl Ether Cleavage. ACS Catal. 2020, 10, 7021–7031. 10.1021/acscatal.0c00774. [DOI] [Google Scholar]
  33. Ulissi Z. W.; Tang M. T.; Xiao J.; Liu X.; Torelli D. A.; Karamad M.; Cummins K.; Hahn C.; Lewis N. S.; Jaramillo T. F.; Chan K.; Nørskov J. K. Machine-Learning Methods Enable Exhaustive Searches for Active Bimetallic Facets and Reveal Active Site Motifs for CO2 Reduction. ACS Catal. 2017, 7, 6600–6608. 10.1021/acscatal.7b01648. [DOI] [Google Scholar]
  34. Artrith N.; Lin Z.; Chen J. G. Predicting the Activity and Selectivity of Bimetallic Metal Catalysts for Ethanol Reforming using Machine Learning. ACS Catal. 2020, 10, 9438–9444. 10.1021/acscatal.0c02089. [DOI] [Google Scholar]
  35. Takahashi K.; Takahashi L.; Nguyen T. N.; Thakur A.; Taniike T. Multidimensional Classification of Catalysts in Oxidative Coupling of Methane through Machine Learning and High-Throughput Data. J. Phys. Chem. Lett. 2020, 11, 6819–6826. 10.1021/acs.jpclett.0c01926. [DOI] [PubMed] [Google Scholar]
  36. Baumes L. A.; Serra J. M.; Serna P.; Corma A. Support Vector Machines for Predictive Modeling in Heterogeneous Catalysis: A Comprehensive Introduction and Overfitting Investigation Based on Two Real Applications. J. Comb. Chem. 2006, 8, 583–596. 10.1021/cc050093m. [DOI] [PubMed] [Google Scholar]
  37. Ohyama J.; Nishimura S.; Takahashi K. Data Driven Determination of Reaction Conditions in Oxidative Coupling of Methane via Machine Learning. ChemCatChem 2019, 11, 4307–4313. 10.1002/cctc.201900843. [DOI] [Google Scholar]
  38. Ahneman D. T.; Estrada J. G.; Lin S.; Dreher S. D.; Doyle A. G. Predicting Reaction Performance in C–N Cross-Coupling Using Machine Learning. Science 2018, 360, 186–190. 10.1126/science.aar5169. [DOI] [PubMed] [Google Scholar]
  39. Zahrt A. F.; Henle J. J.; Rose B. T.; Wang Y.; Darrow W. T.; Denmark S. E. Prediction of Higher-Selectivity Catalysts by Computer-Driven Workflow and Machine Learning. Science 2019, 363, eaau5631 10.1126/science.aau5631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Lakuntza O.; Besora M.; Maseras F. Searching for Hidden Descriptors in the Metal–Ligand Bond through Statistical Analysis of Density Functional Theory (DFT) Results. Inorg. Chem. 2018, 57, 14660–14670. 10.1021/acs.inorgchem.8b02372. [DOI] [PubMed] [Google Scholar]
  41. Besora M.; Olmos A.; Gava R.; Noverges B.; Asensio G.; Caballero A.; Maseras F.; Pérez P. J. A Quantitative Model for Alkane Nucleophilicity Based on CH Bond Structural/Topological Descriptors. Angew. Chem., Int. Ed. 2020, 59, 3112–3116. 10.1002/anie.201914386. [DOI] [PubMed] [Google Scholar]
  42. Segler M. H. S.; Preuss M.; Waller M. P. Planning Chemical Syntheses with Deep Neural Networks and Symbolic AI. Nature 2018, 555, 604–610. 10.1038/nature25978. [DOI] [PubMed] [Google Scholar]
  43. Granda J. M.; Donina L.; Dragone V.; Long D.-L.; Cronin L. Controlling an Organic Synthesis Robot with Machine Learning to Search for New Reactivity. Nature 2018, 559, 377–381. 10.1038/s41586-018-0307-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Coley C. W.; Green W. H.; Jensen K. F. Machine Learning in Computer-Aided Synthesis Planning. Acc. Chem. Res. 2018, 51, 1281–1289. 10.1021/acs.accounts.8b00087. [DOI] [PubMed] [Google Scholar]
  45. Liu B.; Ramsundar B.; Kawthekar P.; Shi J.; Gomes J.; Luu Nguyen Q.; Ho S.; Sloane J.; Wender P.; Pande V. Retrosynthetic Reaction Prediction Using Neural Sequence-to-Sequence Models. ACS Cent. Sci. 2017, 3, 1103–1113. 10.1021/acscentsci.7b00303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Maryasin B.; Marquetand P.; Maulide N. Machine Learning for Organic Synthesis: Are Robots Replacing Chemists?. Angew. Chem., Int. Ed. 2018, 57, 6978–6980. 10.1002/anie.201803562. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. St. John P. C.; Guan Y.; Kim Y.; Kim S.; Paton R. S. Prediction of Organic Homolytic Bond Dissociation Enthalpies at Near Chemical Accuracy with Sub-Second Computational Cost. Nat. Commun. 2020, 11, 2328. 10.1038/s41467-020-16201-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Nandy A.; Duan C.; Janet J. P.; Gugler S.; Kulik H. J. Strategies and Software for Machine Learning Accelerated Discovery in Transition Metal Chemistry. Ind. Eng. Chem. Res. 2018, 57, 13973–13986. 10.1021/acs.iecr.8b04015. [DOI] [Google Scholar]
  49. Janet J. P.; Liu F.; Nandy A.; Duan C.; Yang T.; Lin S.; Kulik H. J. Designing in the Face of Uncertainty: Exploiting Electronic Structure and Machine Learning Models for Discovery in Inorganic Chemistry. Inorg. Chem. 2019, 58, 10592–10606. 10.1021/acs.inorgchem.9b00109. [DOI] [PubMed] [Google Scholar]
  50. Duan C.; Janet J. P.; Liu F.; Nandy A.; Kulik H. J. Learning from Failure: Predicting Electronic Structure Calculation Outcomes with Machine Learning Models. J. Chem. Theory Comput. 2019, 15, 2331–2345. 10.1021/acs.jctc.9b00057. [DOI] [PubMed] [Google Scholar]
  51. Wang J.; Olsson S.; Wehmeyer C.; Pérez A.; Charron N. E.; de Fabritiis G.; Noé F.; Clementi C. Machine Learning of Coarse-Grained Molecular Dynamics Force Fields. ACS Cent. Sci. 2019, 5, 755–767. 10.1021/acscentsci.8b00913. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Behler J. Perspective: Machine Learning Potentials for Atomistic Simulations. J. Chem. Phys. 2016, 145, 170901. 10.1063/1.4966192. [DOI] [PubMed] [Google Scholar]
  53. Wellendorff J.; Lundgaard K. T.; Møgelhøj A.; Petzold V.; Landis D. D.; Nørskov J. K.; Bligaard T.; Jacobsen K. W. Density functionals for Surface Science: Exchange-Correlation Model Development with Bayesian Error Estimation. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 235149. 10.1103/physrevb.85.235149. [DOI] [Google Scholar]
  54. Rupp M.; Tkatchenko A.; Müller K.-R.; von Lilienfeld O. A. Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning. Phys. Rev. Lett. 2012, 108, 058301. 10.1103/physrevlett.108.058301. [DOI] [PubMed] [Google Scholar]
  55. Gastegger M.; Behler J.; Marquetand P. Machine Learning Molecular Dynamics for the Simulation of Infrared spectra. Chem. Sci. 2017, 8, 6924–6935. 10.1039/c7sc02267k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Duan C.; Liu F.; Nandy A.; Kulik H. J. Semi-Supervised Machine Learning Enables the Robust Detection of Multireference Character at Low Cost. J. Phys. Chem. Lett. 2020, 11, 6640–6648. 10.1021/acs.jpclett.0c02018. [DOI] [PubMed] [Google Scholar]
  57. Bo C.; Maseras F.; López N. The Role of Computational Results Databases in Accelerating the Discovery of Catalysts. Nat. Catal. 2018, 1, 809–810. 10.1038/s41929-018-0176-4. [DOI] [Google Scholar]
  58. Sadowski P.; Fooshee D.; Subrahmanya N.; Baldi P. Synergies Between Quantum Mechanics and Machine Learning in Reaction Prediction. J. Chem. Inf. Model. 2016, 56, 2125–2128. 10.1021/acs.jcim.6b00351. [DOI] [PubMed] [Google Scholar]
  59. Back S.; Tran K.; Ulissi Z. W. Toward a Design of Active Oxygen Evolution Catalysts: Insights from Automated Density Functional Theory Calculations and Machine Learning. ACS Catal. 2019, 9, 7651–7659. 10.1021/acscatal.9b02416. [DOI] [Google Scholar]
  60. Jinich A.; Sanchez-Lengeling B.; Ren H.; Harman R.; Aspuru-Guzik A. A Mixed Quantum Chemistry/Machine Learning Approach for the Fast and Accurate Prediction of Biochemical Redox Potentials and Its Large-Scale Application to 315 000 Redox Reactions. ACS Cent. Sci. 2019, 5, 1199–1210. 10.1021/acscentsci.9b00297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. von Lilienfeld O. A.; Müller K.-R.; Tkatchenko A. Exploring Chemical Compound Space with Quantum-Based Machine Learning. Nat. Rev. Chem. 2020, 4, 347–358. 10.1038/s41570-020-0189-9. [DOI] [PubMed] [Google Scholar]
  62. Schütt K. T.; Sauceda H. E.; Kindermans P.-J.; Tkatchenko A.; Müller K.-R. SchNet – A Deep Learning Architecture for Molecules and Materials. J. Chem. Phys. 2018, 148, 241722. 10.1063/1.5019779. [DOI] [PubMed] [Google Scholar]
  63. Gilmer J.; Schoenholz S. S.; Riley P. F.; Vinyals O.; Dahl G. E. In Machine Learning Meets Quantum Physics; Schütt K. T., Chmiela S., von Lilienfeld O. A., Tkatchenko A., Tsuda K., Müller K.-R., Eds.; Springer, 2020; Chapter Message Passing Neural Networks, pp 199–214. [Google Scholar]
  64. Faber F. A.; Hutchison L.; Huang B.; Gilmer J.; Schoenholz S. S.; Dahl G. E.; Vinyals O.; Kearnes S.; Riley P. F.; von Lilienfeld O. A. Prediction Errors of Molecular Machine Learning Models Lower than Hybrid DFT Error. J. Chem. Theory Comput. 2017, 13, 5255–5264. 10.1021/acs.jctc.7b00577. [DOI] [PubMed] [Google Scholar]
  65. Jain A.; Ong S. P.; Hautier G.; Chen W.; Richards W. D.; Dacek S.; Cholia S.; Gunter D.; Skinner D.; Ceder G.; Persson K. a. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. 10.1063/1.4812323. [DOI] [Google Scholar]
  66. Nakata M.; Shimazaki T. PubChemQC Project: A Large-Scale First-Principles Electronic Structure Database for Data-Driven Chemistry. J. Chem. Inf. Model. 2017, 57, 1300–1308. 10.1021/acs.jcim.7b00083. [DOI] [PubMed] [Google Scholar]
  67. Blum L. C.; Reymond J.-L. 970 Million Druglike Small Molecules for Virtual Screening in the Chemical Universe Database GDB-13. J. Am. Chem. Soc. 2009, 131, 8732–8733. 10.1021/ja902302h. [DOI] [PubMed] [Google Scholar]
  68. Montavon G.; Rupp M.; Gobre V.; Vazquez-Mayagoitia A.; Hansen K.; Tkatchenko A.; Müller K.-R.; von Lilienfeld O. A. Machine Learning of Molecular Electronic Properties in Chemical Compound Space. New J. Phys. 2013, 15, 095003. 10.1088/1367-2630/15/9/095003. [DOI] [Google Scholar]
  69. Ruddigkeit L.; van Deursen R.; Blum L. C.; Reymond J.-L. Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17. J. Chem. Inf. Model. 2012, 52, 2864–2875. 10.1021/ci300415d. [DOI] [PubMed] [Google Scholar]
  70. Ramakrishnan R.; Hartmann M.; Tapavicza E.; von Lilienfeld O. A. Electronic Spectra from TDDFT and Machine Learning in Chemical Space. J. Chem. Phys. 2015, 143, 084111. 10.1063/1.4928757. [DOI] [PubMed] [Google Scholar]
  71. Ramakrishnan R.; Dral P. O.; Rupp M.; von Lilienfeld O. A. Quantum Chemistry Structures and Properties of 134 Kilo Molecules. Sci. Data 2014, 1, 140022. 10.1038/sdata.2014.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Chmiela S.; Tkatchenko A.; Sauceda H. E.; Poltavsky I.; Schütt K. T.; Müller K.-R. Machine Learning of Accurate Energy-Conserving Molecular Force Fields. Sci. Adv. 2017, 3, e1603015 10.1126/sciadv.1603015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Smith J. S.; Isayev O.; Roitberg A. E. ANI-1, A Data Set of 20 Million Calculated Off-Equilibrium Conformations for Organic Molecules. Sci. Data 2017, 4, 170193. 10.1038/sdata.2017.193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Durand D. J.; Fey N. Computational Ligand Descriptors for Catalyst Design. Chem. Rev. 2019, 119, 6561–6594. 10.1021/acs.chemrev.8b00588. [DOI] [PubMed] [Google Scholar]
  75. Wu K.; Doyle A. G. Parameterization of phosphine ligands demonstrates enhancement of nickel catalysis via remote steric effects. Nat. Chem. 2017, 9, 779–784. 10.1038/nchem.2741. [DOI] [PMC free article] [PubMed] [Google Scholar]
  76. Santiago C. B.; Guo J.-Y.; Sigman M. S. Predictive and Mechanistic Multivariate Linear Regression Models for Reaction Development. Chem. Sci. 2018, 9, 2398–2412. 10.1039/c7sc04679k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Harper K. C.; Sigman M. S. Three-Dimensional Correlation of Steric and Electronic Free Energy Relationships Guides Asymmetric Propargylation. Science 2011, 333, 1875–1878. 10.1126/science.1206997. [DOI] [PubMed] [Google Scholar]
  78. Maldonado A. G.; Rothenberg G. Predictive Modeling in Homogeneous Catalysis: A Tutorial. Chem. Soc. Rev. 2010, 39, 1891–1902. 10.1039/b921393g. [DOI] [PubMed] [Google Scholar]
  79. Cruz V. L.; Martinez S.; Ramos J.; Martinez-Salazar J. 3D-QSAR as a Tool for Understanding and Improving Single-Site Polymerization Catalysts. A Review. Organometallics 2014, 33, 2944–2959. 10.1021/om400721v. [DOI] [Google Scholar]
  80. Ligands containing metals, including ferrocene, were excluded.
  81. From a graph theory perspective, the number of metal bonds is equal to the degree of the metal node.
  82. Due to the transition metal organic nature of the systems, 26,384 structures could not be fingerprinted with the RDKit software.
  83. Grimme S.; Bannwarth C.; Shushkov P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. 10.1021/acs.jctc.7b00118. [DOI] [PubMed] [Google Scholar]
  84. Bannwarth C.; Ehlert S.; Grimme S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. 10.1021/acs.jctc.8b01176. [DOI] [PubMed] [Google Scholar]
  85. Bursch M.; Neugebauer H.; Grimme S. Structure Optimisation of Large Transition-Metal Complexes with Extended Tight-Binding Methods. Angew. Chem., Int. Ed. 2019, 58, 11078–11087. 10.1002/anie.201904021. [DOI] [PubMed] [Google Scholar]
  86. Rogers D.; Hahn M. Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. 10.1021/ci100050t. [DOI] [PubMed] [Google Scholar]
  87. Weininger D. SMILES, a Chemical Language and Information System. 1. Introduction to Methodology and Encoding Rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. 10.1021/ci00057a005. [DOI] [Google Scholar]
  88. Weininger D.; Weininger A.; Weininger J. L. SMILES. 2. Algorithm for Generation of Unique SMILES Notation. J. Chem. Inf. Comput. Sci. 1989, 29, 97–101. 10.1021/ci00062a008. [DOI] [Google Scholar]
  89. Weininger D. SMILES. 3. DEPICT. Graphical Depiction of Chemical Structures. J. Chem. Inf. Comput. Sci. 1990, 30, 237–243. 10.1021/ci00067a005. [DOI] [Google Scholar]
  90. Janet J. P.; Kulik H. J. Resolving Transition Metal Chemical Space: Feature Selection for Machine Learning and Structure–Property Relationships. J. Phys. Chem. A 2017, 121, 8939–8954. 10.1021/acs.jpca.7b08750. [DOI] [PubMed] [Google Scholar]
  91. Tao J.; Perdew J. P.; Staroverov V. N.; Scuseria G. E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. 10.1103/physrevlett.91.146401. [DOI] [PubMed] [Google Scholar]
  92. Schäfer A.; Horn H.; Ahlrichs R. Fully Optimized Contracted Gaussian Basis Sets for Atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. 10.1063/1.463096. [DOI] [Google Scholar]
  93. Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
  94. Reed A. E.; Weinstock R. B.; Weinhold F. Natural Population Analysis. J. Chem. Phys. 1985, 83, 735–746. 10.1063/1.449486. [DOI] [Google Scholar]
  95. Grimme S.; Neese F. Double-Hybrid Density Functional Theory for Excited Electronic States of Molecules. J. Chem. Phys. 2007, 127, 154116. 10.1063/1.2772854. [DOI] [PubMed] [Google Scholar]
  96. With the aim of reducing the computational cost of the data benchmarks, 4000 systems with a maximum size of 50 atoms were selected.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ci0c01041_si_001.pdf (13.8MB, pdf)

Data Availability Statement

tmQM is an open data set freely available at GitHub (https://github.com/bbskjelstad/tmqm) and from Quantum-Machine (http://quantum-machine.org/datasets/). Quantum features, geometries and properties computed at the GFN2-xTB and TPSSh-D3BJ/def2-SVP levels of theory are provided in the xyz and csv file formats.

Articles from Journal of Chemical Information and Modeling are provided here courtesy of American Chemical Society

RESOURCES