Background Removal and Vessel Filtering of Non-Contrast Ultrasound Images of Microvasculature

Abstract

Objective:

recent advances in ultrasound Doppler imaging have made it possible to visualize small vessels with diameters near the imaging resolution limits using spatiotemporal singular value thresholding of long ensembles of ultrasound data. However, vessel images derived based on this method present severe intensity variations and additional background noise that limits visibility and subsequent processing such as centerline extraction and morphological analysis. The goal of this paper is to devise a method to enhance vessel-background separation directly on the power Doppler images by exploiting blood echo-noise independence.

Method:

we present a two-step algorithm to mitigate these adverse effects when using singular value thresholding for obtaining gross vasculature images. Our method comprises a morphological-based filtering for removing global and local background signals and a multi-scale Hessian-based vessel enhancement filtering to further improve the vascular structures. We applied our method for in vivo imaging of the microvasculature of kidney in one healthy subject, liver in five healthy subjects, thyroid nodules in five patients, and breast tumors in five patients.

Results:

singular value thresholding, top-hat filtering and Hessian-based vessel enhancement filtering each provided an average peak-to-side level gain of 1.11dB, 18.55dB and 2.26dB respectively, resulting in an overall gain of 21.92dB when compared to the conventional power Doppler imaging using infinite impulse response filtering.

Conclusion:

singular value thresholding combined with morphological and Hessian-based vessel enhancement filtering provides a powerful tool for visualization of the deep-seated small vessels using long ultrasound echo ensembles without requiring any type of contrast enhancing agents.

Significance:

this method provides a fast and cost-effective modality for in vivo assessment of the microvasculature suitable for both clinical and preclinical applications.

I. Introduction

Imaging of the deep-seated sub-millimeter vessels still remains a challenging task in medical imaging. Different conditions and diseases can alter vasculature at different size scales, affecting overall functionality of the cardiovascular system. In diabetes, for examples, macrovasculature deterioration are linked to the progression of microvasculature damages in kidney leading to diabetic nephropathy and promoting chances for larger scale cardiovascular diseases [1]. Additionally, angiogenesis is known to be a driving factor in prognosis of cancerous tumors [2]. Several studies have shown that malignant tumor growth coincides with changes in vascularity of the nonnal tissue [3–5]. Furthermore, malignant tumors are known to present different mechanobiological features leading to the growth of more penneable and tortuous vessels [6, 7].

Contrast-enhanced magnetic resonance angiography [8, 9] and microscopic computed tomography (micro-CT) [10] have been conventionally used for vessel analysis for in vivo and ex vivo studies respectively. More recently, contrast enhanced ultrasound imaging has also emerged as a promising modality for visualization and segmentation of the vasculature trees at the expense of administrating exogenous labels [11–13]. In addition to requiring injection of contrast enhancement agents, issues such as high cost, long imaging times and lack of portability of these modalities remain as the limiting factors for their utility in research and clinical applications.

Doppler ultrasound has been traditionally used for real-time imaging of the tissue blood vessels and large-scale hemodynamics. However, it suffers from low resolution and weak performance in highly cluttered tissue areas such as abdominal organs. Additionally, due to short ensemble length and weak clutter removal capability, the blood vessel maps from these methods are highly fragmented that makes interpretation of the vessel network morphological features impossible.

Recently, ultrasensitive Doppler has been introduced as a novel ultrasound-based modality for visualization of the vessels in sub-millimeter range [14]. This method is based on the plane wave imaging with multiple-angle compounding which enables high quality imaging of a wide field of view at high frame rates. Hence, large ensembles of the data with high spatial and temporal coherence can be acquired. Based on this imaging method and using singular value thresholding, superb visualization of the vasculatures at micron levels has been recently reported [14]. The main assmnption in this approach is that tissue and blood flow leave different signatures on the ultrasound backscattered echoes which occupy two different sub-spaces. While tissue clutter signal mostly lies in a highly correlated low rank sub-space that constitutes most of the backscattered energy, blood flow backscatter is present in a weakly correlated sub-space. Hence, a singular value thresholding (SVT) of a spatiotemporal matrix can effectively separate the two sub-spaces via a thresholding operation [14–16]. However, in addition to blood signal, additive noise is also present in the weakly correlated sub-space. The noise signal mostly originates from the electronic front-end such as amplifiers and time-gain compensation (TGC) circuitry. When forming power Doppler images, due to statistical independence of noise and blood signals, local image intensity is the direct summation of the blood power and background noise power. Hence, any increase or decrease in the local background noise power is directly reflected as an additive background and consequently alters the intensity levels at which vessels have their best visibility. When depth dependent amplifications such as TGC are employed, due to progressively increasing noise power, deeper vessels appear at higher intensities (due to elevated background) compared to the more superficial ones. Additionally, high intensity signals resulting from blood flow in large arteries can overwhelm the image dynamic range and limit the visibility of small vessels. These effects are highlighted in Fig. 1(d) where the power Doppler image obtained from SVT is presented for an in vivo example of microvasculature in kidney.

Fig. 1:

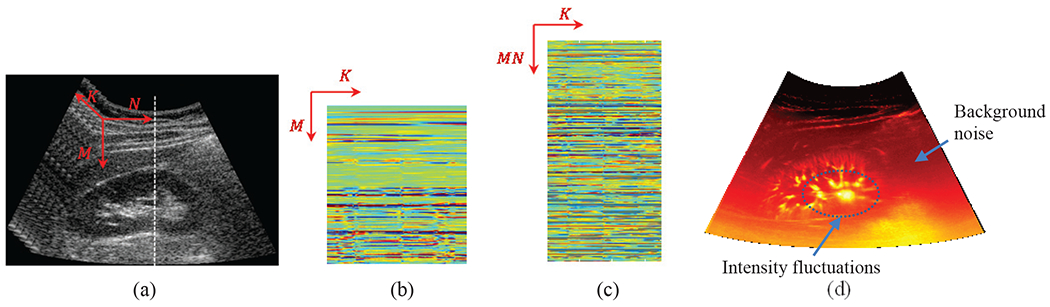
(a) sequence of B-mode images from a healthy kidney in vivo, (b) spatiotemporal raw data matrix R_j from the scan-line j shown by a white dashed line in (a) and (c) spatiotemporal raw data matrix R formed by submatrices from all scan-lines. M, N and K are the number of samples in the axial, lateral and temporal directions respectively (d) power Doppler image after SVT. Additional background noise and severe intensity fluctuations (highlighted by arrows) limit the visibility of the vessels at different size scales and depths.

While TGC is rarely used in the Doppler sequences in conventional imaging systems, the advent of plane wave imaging has made it possible to acquire both Doppler and B-mode images using the same imaging sequence. Hence methods that can provide equal vessel visibility under different noise amplification conditions are desired. A SVT-based noise suppression method was proposed in [17] based on local singular value truncation. However, the study in [16] highlights the fact that noise and blood signals present similar energy decay rates in the singular value domain; hence singular value truncation for de-noising purposes may also remove part of the useful blood energy which in turn may lead to degradation of the vessel mage contrast.

The aim of this study is to devise a vessel enhancement method to improve vessel visibility directly on the power Doppler images. Toward this goal, we present a method that while benefits from strong clutter removal capability of SVT clutter filtering, it addresses the background noise issue in the power Doppler mode via a two-step approach. In the first step, we propose to use shape-aware structure filtering based on morphological operations for background removal and intensity equalization. Specifically, we propose top-hat filtering to remove slowly varying background noise and severe intensity fluctuations without affecting small vessel morphologies which appear as tubular structures in the power Doppler images. Such method has been used in enhancement of optical angiography of retinal vasculature [18] and in the context of digital image analysis for text enhancement of the scanned documents under different illuminations [19]. While top-hat filtering significantly reduces background signals, residual noise may still be present. In the second step, to further suppress residual spurious background noise and improve intensity equalization and vessel connectivity, we propose a multi-scale Hessian-based vessel enhancement filtering based on Frangi’s vessel function [20]. The addition of these processing steps will be shown to provide significant vessel visibility improvement and quantitative peak-to-side level gain over conventional power Doppler imaging and SVT alone.

In section II we provide a brief overview of the SVT-based ultrasound clutter removal algorithm and introduce a tissue rank selection criterion which is based on detecting changes in the singular value decay rate. We also discuss different factors affecting the behavior of the additional background noise and present a background removal strategy based on the morphological top-hat filtering. A multi-scale Hessian-based vessel enhancement formulation is also introduced as a final step in processing the images of small vessels. The experimental setup used for in vivo studies and related parameters are discussed in section III. In section IV we present various results highlighting different aspects of our method including quantitative evaluation via peak-to-side level values. The results are discussed in section V. The paper concludes in section VI with a discussion of the main outcomes and a brief summary of the potential future applications.

II. THEORY AND METHODS

A. Singular Value Thresholding for Ultrasound Clutter Removal

Assuming multiple consecutive frames of beamfonned ultrasound data, for a data point at depth z_i along a single scanline, the beamfonned signal observed over multiple frames can be represented as

$$r(z_i,t_k)=G_{atgc}(z_i)G_{dtgc}(z_i)A(z_i)[s_c(z_i,t_k)+s_b(z_i,t_k)]+G_{atgc}(z_i)G_{dtgc}(z_i)n(z_i,t_k)$$ (1)

where s_c(z_i, t_k) and s_b(z_i, t_k) are the tissue clutter and blood components respectively sampled at depth z_i and (slow) time t_k, n(z_i, t_k) is the additive white Gaussian noise due to electrical components, A(z_i) is a depth dependent attenuation function, and G_atgc(z_i) and G_dtgc(z_i) represent the analog and digital time-gain compensation (referred to as ATGC and DTGC) respectively. The attenuation function usually combines the effect of geometrical wave decay and tissue absorption. G_atgc is a fixed depth-dependent analog amplification and G_dtgc is a variable digital attenuation for manual compensation of the depth-dependent intensity variations.

For scanline j, let’s arrange the echo data from K consequtive frames in a matrix in the form of

$$R_j=\left[\begin{array}{ccc}{r}_{1j1}& \cdots & r_{1jK}\\ ⋮& \ddots & ⋮\\ r_{Mj1}& \dots & r_{MjK}\end{array}\right]$$ (2)

where r_ijk represents the ultrasound raw data from j^th scanline sampled at depth z_i and time t_k. Fig. 1 (b) shows an example of forming this matrix by observing raw beamfonned data along a scanline from in vivo imaging of a healthy kidney.

The corresponding matrices from multiple scanlines (or all scanlines) can be vertically stacked to form a giant spatial-temporal matrix (also known as Casorati matrix) (Fig. 1(c)).

$$R=\left[\begin{array}{c}{R}_1\\ R_2\\ ⋮\\ R_N\end{array}\right]=\left[\begin{array}{ccc}{r}_{111}& \cdots & r_{11K}\\ ⋮& \ddots & ⋮\\ r_{MN1}& \cdots & r_{MNK}\end{array}\right]$$ (3)

Due to larger nmnber of spatial samples compared to temporal samples (number of frames), matrix R is usually a skinny matrix. Additionally, most of its energy is embedded in a low rank sub-space comprised of strong but slowly varying coherent signals from the clutter tissue. The singular value thresholding clutter removal seeks a low rank approximation of R which can best represent and remove the tissue contribution. The best rank K approximation of the matrix R can be found via SVT as

$$R_{clutter}={\mathrm{argmin}}_{rank(z)<K}\Vert R-Z{\Vert }_F={\sum }_{i=1}^K{\sigma }_i{u}_i{v}_i^H$$ (4)

where R = UΣV^H is the singular value decomposition (SVD) of R, U = [u₁, u₂, …, u_S] and V = [v₁, v₂, …, v_S] are unitary matrices, Σ = diag(σ₁, σ₂, ⋯, σ_r) is a diagonal matrix of singular values, S is the rank of R and ‖.‖_F indicates the Ferobinous norm. Hence the combined blood and noise sub-space can be represented as

$$R_{blood+noise}={\sum }_{i=K+1}^S{\sigma }_i{u}_i{v}_i^H$$ (5)

In ideal situations where all attenuations are compensated by TGC and tissue clutter signal is perfectly removed by SVT, using Eq. (1), the blood and noise signal at depth z_i of a scanline can be approximated as

$$r_{blood+noise}(z_i,t_k)\approx s_b(z_i,t_k)+G_{atgc}(z_i)G_{dtgc}(z_i)n(z_i,t_k)$$ (6)

Eq. (6) represents the estimated blood signal which is also contaminated by depth dependent (due to TGC) additive noise. Using this data, the corresponding power Doppler intensity can be formed as

$$p{w}_{blood+noise}(z_i)=\frac{1}{K}{\sum }_k^K{\left(|s_b(z_i,t_k)+G_{atgc}(z_i)G_{dtgc}(z_i)n(z_i,t_k)|\right)}^2\approx \frac{1}{K}{\sum }_k^K|s_b(z_i,t_k){|}^2+|G_{atgc}(z_i)G_{dtgc}(z_i){|}^{2}p{w}_{noise}$$ (7)

where the last equation follows from the assumption that blood and noise signals are independent ergodic random processes such that

$$p{w}_{noise}=\frac{1}{K}{\sum }_{k=1}^K|n(t_k){|}^2$$ (8)

and noise is modelled as independent identically distributed (i.i.d) for all points through the depth. As it can be seen in Eq. (7), the SVT-filtered power Doppler images of the vessels are expected to be superimposed on a background signal formed by noise. If TGC is employed, the background signals present spatial variability which stems for the depth dependent amplifications of the noise as predicted by Eq. (7).

B. Clutter Rank Selection

Sorting singular values in the descending order can provide a tool for selection of the appropriate rank which can properly represent the high energy clutter contribution. In an ideal situation where there is no motion, tissue signal can be represented using a rank 1 approximation. However, some degree of motion is unavoidable during in vivo studies either due to physiological activities (e.g. blood pulsation, breathing, etc) or sonographer’s hand motion. Hence, the rank of tissue contribution can increase based on the strength of these motions and the degree of signal decorrelation occurring throughout an ensemble [21].

Previous studies [14, 17] have shown that the optimal clutter rank coincides with a point at which significant singular value decay rate change (i.e. decay acceleration) occurs. However, direct calculation of the decay rate and decay acceleration result in severe fluctuations which may limit the suitability of using a constant threshold. Assume the singular values of matrix R in (3) are such that σ₁ ≥ σ₂ ≥ ⋯ ≥ σ_S and f(σ) is a monotonically decreasing function representing the singular value decay. A log-compressed normalized decay function is defined as

$$\stackrel{\_}{f}=20{\mathit{log}}_{10}\frac{f(\sigma )}{{\sigma }_1}$$ (9)

To detect changes in the singular value energy decay rate (decay acceleration) we obtain the band-limited first and second derivatives of the log compressed nonnalized singular

$${\partial }_{bl}\stackrel{\_}{f}=\frac{\partial \stackrel{\_}{f}}{\partial \sigma }*\Pi (\sigma ),{\partial }_{{}_{bl}}^2\stackrel{\_}{f}=\frac{{\partial }^2\stackrel{\_}{f}}{\partial {\sigma }^2}*\Pi (\sigma )$$ (10)

respectively, where * is the convolution operation and Π(σ) is the zero-phase (forward-backward) impulse response of a filtering kernel. The tissue clutter rank, K, is defined as the largest singular value index for which ${\partial }_{{}_{bl}}^2\stackrel{\_}{f}$ falls below a predefined threshold. Here, a Hamming window was chosen as the filtering kernel. Due to presence of the noise, the observation matrix R always has full rank which is equal to min{MN,K}. The kernel length can be selected dynamically based on this value to create a balance between suppressing the second derivative fluctuations and the bias introduced in the fast decay region (first few singular values). In this study, a kernel length of 33 was chosen. The singular value decay acceleration threshold was empirically optimized and was set to 10⁻⁴ for best tissue clutter removal. The same value was used in all in vivo examples presented in this paper.

C. Background Removal Using Morphological Filtering

Removing background signal from the power Doppler images while preserving details of small vascular structures is not a trivial task. In this section, we introduce a morphological-based filtering (i.e. top-hat filtering) to estimate and remove the background signal from the SVT-derived power Doppler images using nonlinear operations.

Morphological filtering is often employed for feature extraction from digital images where a structuring element is used in combination of a series of morphological operations. A top-hat filtering (THF) is comprised of a background estimation followed by a subtraction operation [22]. For an image, I, the white top-hat filtering is defined as

$$I_w=I-I\circ \mathrm{SE}$$ (11)

where SE is a morphological structuring element and ∘ is an opening operation. The opening of image I by a structuring element b is defined as

$$I\circ b=(I\ominus b)\oplus b$$ (12)

where ⊖ and ⊕ are the erosion and dilation operations respectively. The gray-scale dilation and erosion are the two basic mathematical morphological operations which at pixel (x, y) are defined as

$$\{\begin{array}{cc}[I\ominus b](x,y)={\min }_{(s,t)\in b}\{I(x+s,y+t)\}& \mathrm{Erosion}\\ [I\oplus b](x,y)={\max }_{(s,t)\in b}\{I(x-s,y-t)\}& \mathrm{Dialtion}\end{array}$$ (13)

I(x + s, y + t) and I(x − s, y − t) are simple translational shifts of the image I performed for all pairs (s, t) selected from the structuring element b [23]. Hence, the white top-hat filtering of image x by structuring element SE is

$$I_w=I-(I\ominus \mathrm{SE})\oplus \mathrm{SE}$$ (14)

D. Hessian-Based Vessel Enhancement Filtering (VEF)

Morphological filtering can enhance the visibility of the vascular structures in presence of the strong background signals. However, the randomness of the background noise might create image features with morphological structures smaller than the size of the structuring elements. Hence, in addition to vessel-like structures these random patterns will be also present at the output of the top-hat filtering. To further promote vascular structures and penalize the residual random background a vessel enhancement filtering is required.

In power Doppler images, the second derivative of intensity near the vessels is expected to be large in the direction perpendicular to the vessel orientation and very small along the vessels. Hence, this characteristic can be employed to devise filters which can significantly promote the vessel-like structures and penalize unstructured random shapes. The Hessian matrix of an image can provide information about the second derivative. However, in order to capture curvature features independent of the vessel direction, the eigenvalues along the two eigenvectors of the Hessian matrix can be used instead. Additionally, in order to make the analysis of the curvature less sensitive to scaling, intensity variations and limit noise amplification, direct derivatives can be replaced by the scale space Gaussian derivatives. Using this approach, the intensity signal, I, within δr distance from a pixel located at r can be written as

$$I(r+\delta r,s)\approx I(r)+\delta r^T{\nabla }_s+\delta r^T{\mathcal{H}}_s\delta r$$ (15)

where ∇_s and ${\mathcal{H}}_s$ are the Gaussian gradient vector and the Hessian matrix at size scale s respectively. In the scale space theory, true derivatives are replaced by the scaled bandlimited differentiation using a Gaussian kernel as

$$\frac{\partial }{\partial r}I\left(r,s\right)=\frac{\partial }{\partial r}\left(I\left(r\right)\ast \Gamma \left(r,s\right)\right)=I\left(r\right)\ast \frac{\partial }{\partial r}\Gamma \left(r,s\right)$$ (16)

where Γ(r, s) is a Gaussian kernel defined as

$$\Gamma (r,s)=\frac{1}{2\pi s^2}{e}^{-\frac{\Vert r{\Vert }^2}{2s^2}}$$ (17)

Based on this definition of the differentiation, the Hessian matrix at scale s in the Cartesian coordinate can be calculated as

$${\mathcal{H}}_s=\left[\begin{array}{cc}\frac{{\partial }^2}{\partial x^2}(I(x,y)*\Gamma (x,y,s))& \frac{{\partial }^2}{\partial x\partial y}(I(x,y)*\Gamma (x,y,s))\\ \frac{{\partial }^2}{\partial y\partial x}(I(x,y)*\Gamma (x,y,s))& \frac{{\partial }^2}{\partial y^2}(I(x,y)*\Gamma (x,y,s))\end{array}\right]=I(x,y)*\left[\begin{array}{cc}\frac{1}{2\pi s^4}\left(\frac{x^2}{s^2}-1\right)e^{-\frac{x^2+y^2}{2s^2}}& \frac{1}{2\pi s^6}(xy)e^{-\frac{x^2+y^2}{2s^2}}\\ \frac{1}{2\pi s^6}(xy)e^{-\frac{x^2+y^2}{2s^2}}& \frac{1}{2\pi s^4}\left(\frac{y^2}{s^2}-1\right)e^{-\frac{x^2+y^2}{2s^2}}\end{array}\right]$$ (18)

Eigenvalue decomposition of ${\mathcal{H}}_s$ provides curvature information along two principle directions represented by their corresponding eigenvectors and eigenvalues. Since vessel orientation is not of any interest, the eigenvalues, λ₁ and λ₂ (assuming |λ₂| > |λ₁|) are only considered for further vessel analysis. In the vicinity of any intensity increase both eigenvalues become negative numbers. Noise-like variations, however, do not result in significant eigenvalues. Therefore, the energy of the eigenvalues can be used as a measure for assessment of the structured shapes (e.g. tubes and blubs) as opposed to random patterns. The Hessian eigenvalues can be computed for a number of size scales which are defined based on different vessels sizes present in the imaged region. Based on the eigenvalues at each size scale, Frangi et al. [20] proposed a vessel enhancement and thresholding function as the following

$${\Delta }_s=\{\begin{array}{ll}0& ,{\lambda }_2>0\\ e^{-\frac{{\mathcal{M}}^2}{2{\beta }^2}}\left(1-e^{-\frac{{\wedge }^2}{2{\alpha }^2}}\right)& ,elsewhere\end{array}$$ (19)

The output of (19) is an intensity image which is maximum at vessels with size s. In (17), $\mathcal{M}=\frac{{\lambda }_1}{{\lambda }_2}$ defines the eccentricity of the second order ellipse defined by the eigenvectors and $\wedge =\sqrt{{{\lambda }_1}^2+{{\lambda }_2}^2}$ is used to penalize any unstructured patterns such as background noise. Parameter α defines the roll-off rate for soft-thresholding of the unstructured patterns; a large α penalizes the noise-like areas more aggressively but may result in damages to the vascular structures. A small α may allow more noise in the final image limiting the utility of the vessel filter. Parameter β controls the dynamic range of the output intensity such that large values of β decrease the final image intensity at a vessel area and vice versa. An important aspect of using the scale space analysis is the fact that the structures can be analyzed at different size scales simultaneously. In other word, the output of the vessel function, Δ_s, is only sensitive to the shape similarities instead of image intensities. Hence the final power Doppler vessel image, Δ, can be formed by taking the maximum value of δ_s over all estimated size scale values s

$$\Delta ={\max }_s{\Delta }_s$$ (20)

E. Quantitative Assessment

In order to quantify the incremental gain of using SVT, THF and VEF compared to the conventional power Doppler imaging using IIR filtering, for each detected vessel, we calculated the peak-to-side level (PSL) intensity as

$$PSL=20{\mathit{log}}_{10}\left(\frac{{\Delta }_{peak}}{{\Delta }_{side}}\right)(dB)$$ (21)

where Δ_peak is the image intensity of the brightest part of the visible vessel (peak intensity level) and Δ_side is the intensity at the darkest part of the image in the vicinity of the peak (side intensity level). PSL calculation was discarded for cases where THF or VEF completely removed the background (side levels equal to zero) to avoid infinity values. To minimize measurement bias, in each case, three different regions presenting high number of small vessels were analyzed.

III. Experiments

All imaging were performed using an Alpinion Ecube12-R ultrasound machine (ALPINION Medical Systems, Seoul, Korea). The system provided a sequence of frames in the form of raw in-phase and quadrature (IQ) beamfonned data for a total duration of 3 seconds. Each frame of the data was formed using 5-angle coherent plane wave compounding similar to [24]. The study of kidney and liver were performed using a curved array, SC1-4H (ALPINION Medical Systems, Seoul, Korea) at 3MHz. A linear array operating at 11.5MHz, L3-12H (ALPINION Medical Systems, Seoul, Korea) was used for studying subjects with thyroid nodules and breast lesions. Prior to our study, all subjects signed an informed institutional review board (IRB) consent form. To emphasis the effect of TGC on background noise distribution, in addition to presenting the results for the original acquired data (with TGC), an attenuation profile (equal to the inverse of the overall TGC gain) was employed in the kidney example and the results are presented. The remaining examples are presented without altering TGC to highlight the ability of the proposed method in removing these effects while maintaining the enhanced B-mode dynamic range provided by the TGC. The 3s acquisition time, when used with different imaging depths, resulted in variable frame rates (and consequently variable nmnber of frames) for each dataset. We present one representative case from each organ to describe different aspects of our method. To further highlight the utility of this new technique in vivo, extended patient studies were performed on 5 liver cases, 5 patients with thyroid nodules and 5 patients with breast lesions. All liver subjects were healthy volunteers with no history of liver disease. The thyroid cases comprised one malignant, two benign and two indeterminate nodules based on the fine needle aspiration (FNA) cytology results. The breast cases comprised two benign and three malignant masses based on the core needle or surgical biopsy. Table 1 summarizes the imaging parameters imposed by the system for all cases.

Table 1:

Imaging system parameters

	Frame rate (compounded frames per sec)	Imaging frequency (MHz)
Kidney	592	3.2
Liver	648	3.2
Thyroid nodule	575	11.5
Breast lesion	771	11.5

Due to different vessel sizes expected in each in vivo study and different imaging resolution provided by each transducer, vessel enhancement parameters were specified accordingly. The curved array was used at 3.2MHz transmission frequency with an axial resolution of ~240μm. Considering the theoretical imaging diffraction limit (λ/2) as a hard limit, the minimum detectable vessel size was set to 300μm. The linear transducer operating at 11.5MHz provided an axial resolution of ~67μm. Hence, we chose a minimum vessel size of 100μm. The maximum vessel size was chosen based on inspection of the gross SVT images. For the case of kidney and liver, due to presence of large arteries and veins, a maximum vessel diameter of 5mm was selected. For the case of thyroid nodule and breast lesion the maximum vessel size was set to 2mm. The maximum vessel size was used to define the size of the top-hat filtering structuring element in each case. Parameters α (which penalizes random structures) and β (which promotes tubular structures) were set to 0.6 and 50 respectively for all cases. A constant singular value decay acceleration threshold of 10⁻⁴ was used for all cases. We also performed conventional power Doppler imaging using an infinite impulse response (IIR) 5^th-order Butterworth high pass filtering for each case. In order to provide fair comparison with SVT, a cut-off frequency of the IIR filter was chosen to create the best small vessel visibility and maximum clutter suppression. Filter transient response was removed before calculating the power Doppler images. The parameters used in different parts of each method are summarized in Table 2.

Table 2:

Top-hat and vessel enhancement filtering parameters

	THF disk	VEF	VEF	α	β	Singular value decay acceleration threshold
Kidney	5000μm	300μm	5000μm	0.6	50	10−4
Liver	5000μm	300μm	5000μm	0.6	50	10−4
Thyroid nodule	2000μm	100μm	2000μm	0.6	50	10−4
Breast lesion	2000μm	100μm	2000μm	0.6	50	10−4

IV. Results

A. Tissue Clutter Rank Selection

The blue curve in Fig. 2(a) shows the normalized singular values in logarithmic scale as a function of rank, acquired from the SVD of the measurement matrix of the in vivo data from kidney of a healthy volunteer. As it can be seen, there is a distinct change in the singular value energy decay rate as rank increases (a fast decay followed by a slowly decaying tail). The fast part represents mostly the high energy clutter motion while the slow decay region is mostly comprised of the blood signal and noise. The overlaid red curve is a smoothed approximation obtained by forward-backward filtering of the log compressed normalized singular values (10). Fig. 2(b) and (c) show the first and second derivatives of the raw (blue) and band-limited (red) decay curves. As it can be seen the raw data present severe fluctuations in both curves which limit the determination of a reliable threshold. The band-limited curves, however, provide a better estimate of the decay rate and decay acceleration from which reliable rank thresholds can be obtained. A decay acceleration threshold value of 10⁻⁴ (green line in Fig. 2(c)) resulted in a tissue clutter rank of 354 in this case which is shown in Fig. 2(a) as a black dot.

Fig. 2:

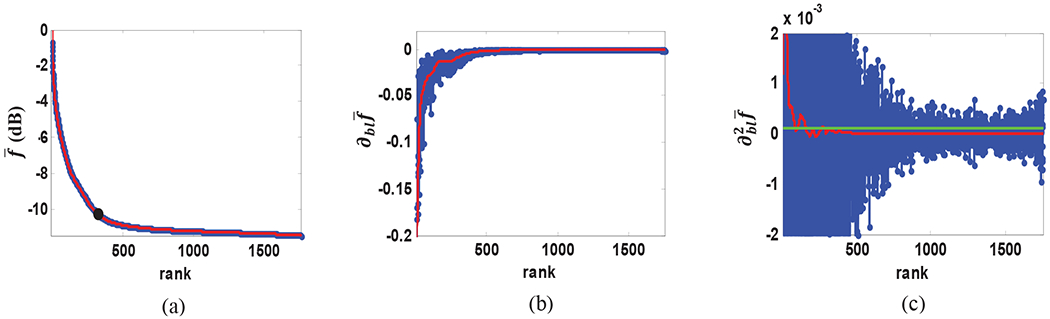
(a) normalized singular values in logarithmic scale (blue) and a smooth approximation using zero-phase FIR filtering (red) with automated tissue rank shown as a black dot (b) decay rate function using raw data (blue) and band-limited decay rate (red) (d) decay acceleration using raw data (blue) and band-limited acceleration data (red) and a threshold line at 10⁻⁴ (green).

Fig. 3 shows the singular value decay profile for one representative case from each organ studied in this paper. All curves were obtained while TGC was on. The optimal tissue clutter rank for each case was obtained automatically using the same singular value decay acceleration threshold of 10⁻⁴. From these curves, one can observe a considerable difference between the decay profiles of the breast case compared to other organs. This can be directly attributed to the larger tissue motions induced by heart or pulsation in the large arteries (in the case of thyroid, kidney and liver) compared to breast.

Fig. 3:

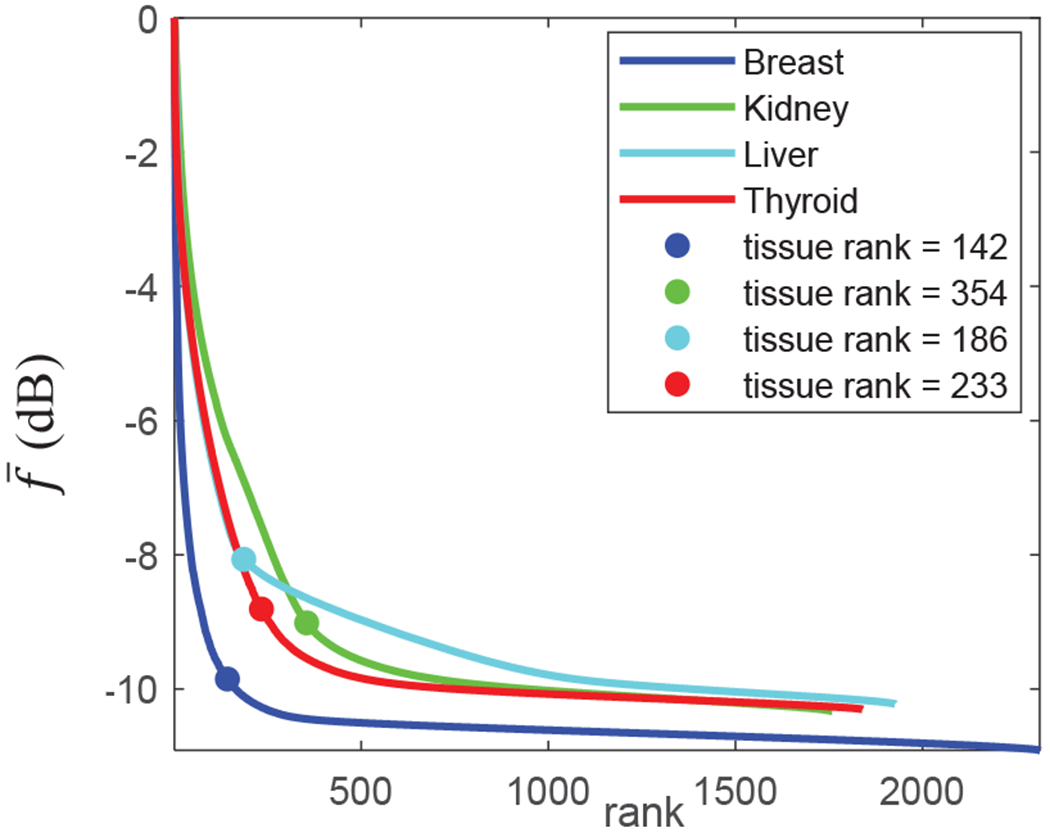
singular value decay profiles from representative in vivo cases. A constant decay acceleration rate automatically determined the optimal tissue clutter rank for all cases.

B. Effect of TGC

Fig. 4. depicts the TGC profile employed by the imaging system while scanning the kidney of a healthy volunteer. In most systems, ATGC provides a depth dependent amplification and DGTC is used to provide intensity equalization via attenuation. Hence, the combined gain (in dB values) is the final effective gain as depicted as the black curve in Fig. 4.

Fig. 4:

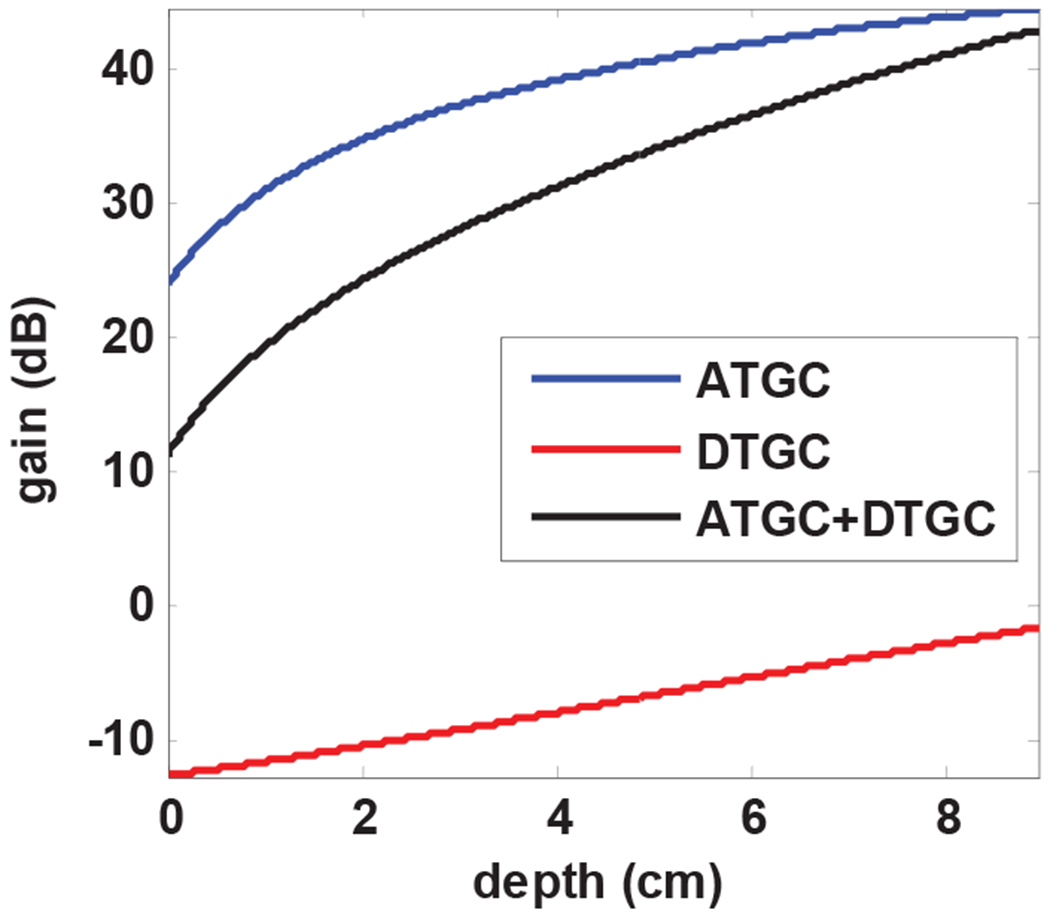
The blue curve shows a depth-dependent gain referred to as analog TGC (ATGC) and red curve presents a customized digital attenuation referred to as digital TGC (DTGC). The overall gain profile after adding the two TGC profiles is shown in black. The overall gain was used to analyze the effect of TGC on the performance of SVT clutter removal.

Fig. 5 represents the effect of TGC on B-mode images obtained from the plane wave imaging sequence and the corresponding power Doppler images of kidney microvasculature using SVT clutter removal. As it can be seen from Fig. 5(a) and (b), TGC provides significant improvement in equalization of the B-mode images such that all parts of the image provide equal visibility. However, the amplified residual noise creates a background signal which progressively increases with depth as a result of TGC. This can be clearly seen in Fig. 5(c), while this effect is mostly removed in Fig. 5(d) after TGC compensation.

Fig. 5:

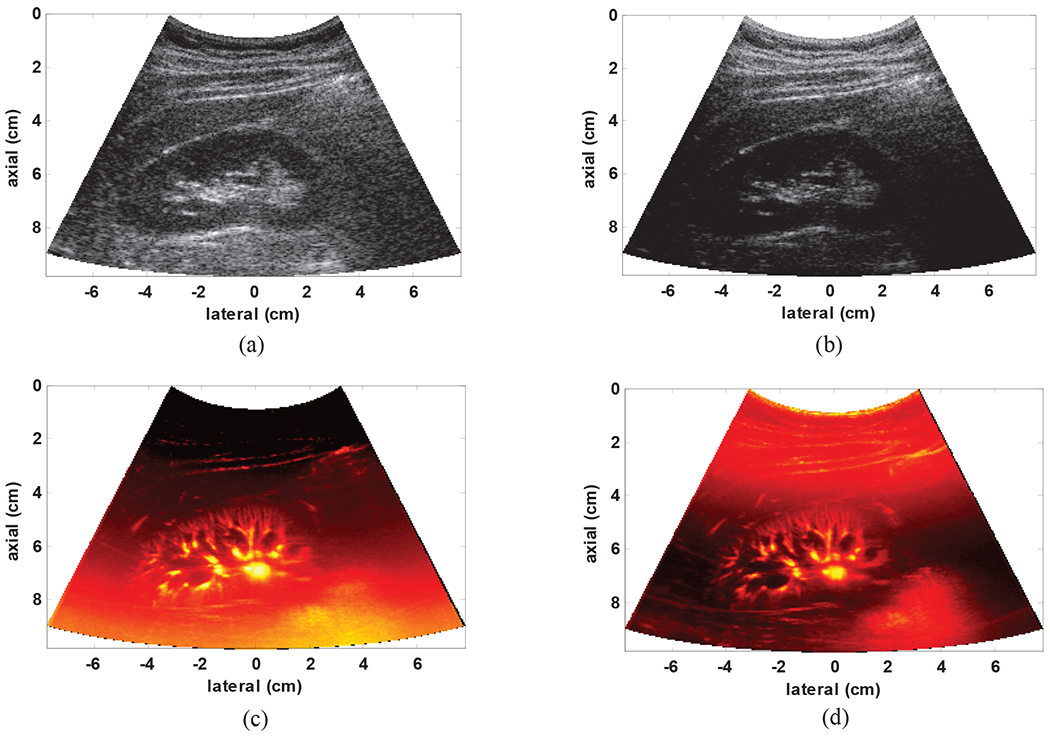
(a) B-mode image based on clutter power with TGC (b) B-mode image based on clutter energy without TGC (c) gross SVT image with TGC and (d) gross SVD image without TGC.

C. In Vivo Examples and Evaluation of Processing Gains

To demonstrate the qualitative and quantitative gains achieved by our method, one representative case from each organ is discussed. The overall quantitative assessment will be made using the results obtained from all patients.

1). Microvasculature in healthy human kidney

Fig. 6(a) shows the B-mode image and an outlined boundary delineating the kidney in a healthy volunteer. As it is seen, the speckle pattern stemming for the strong tissue clutter has completely covered the underlying vasculature. The power Doppler image using conventional IIR filtering and SVT, SVT+THF and SVT+THF+VEF are shown in Fig. 6(b), Fig. 6(c), Fig. 6(d) and Fig. 6(e) respectively. The conventional power Doppler using Butterworth IIR filtering, though has provided an acceptable visualization of the microvasculature, was unable to completely remove the clutter signal (note the area shown by the green arrow in Fig. 6(b)). The SVT based on automated tissue rank selection, on the other hand, has effectively removed the tissue clutter (Fig. 6(c)). However, the amplified background noise and intensity fluctuations have significantly limited the visibility of deeper vessels. Fig. 6(c) shows the microvasculature image after adding the top-hat filtering to SVT. As it can be seen, THF has resulted in significant reduction in the background signal with minor effect on the vascular structures at different size scales. Fig. 6(d) presents the final microvasculature image after adding the vessel enhancement filtering. As it can be seen, some intensity variations and discontinuities observed in the top-hat filtered image are eliminated by the vessel enhancement filtering while vessel shapes and dimensions are mostly preserved. In order to quantify the processing gain at each step, cross-sectional segments were selected from three different regions that presented high number of small vessels (overlaid green line in Fig. 6(b), Fig. 6(c), Fig. 6(d) and Fig. 6(e)). The average PSL values were calculated from all vessels (31 PSL values) in these three regions. The SVT, THF and VEF each provided an additional gain of 0.76dB, 15.85dB and 1.72dB respectively with an overall gain of 18.33dB compared to IIR filtering method.

Fig. 6:

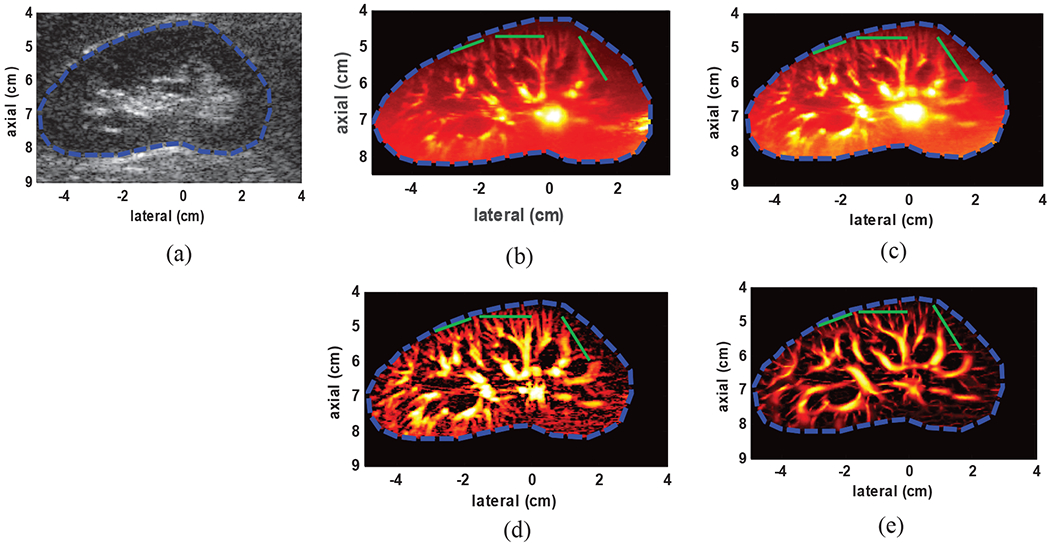
(a) B-mode image of kidney (b) power Doppler image using conventional IIR filtering (green arrows shows an area with residual clutter signal) with 100Hz cutoff frequency (c) SVT clutter removal (d) after adding top-hat filtering to SVT (SVT+THF) (e) after adding the top-hat and vessel enhancement filtering to SVT (SVT+THF+VEF). The overlaid green lines indicate cross-sections from which PSL values were calculated.

2). Microvasculature in healthy human liver

Fig. 7(a) presents the B-mode image of the right lobe liver in a representative healthy volunteer. The vasculature image using conventional power Doppler imaging is shown in Fig. 7(b). As it can be seen, while residual clutter signal is present (green arrow), only few small vessels are visible in the lower depths. The SVT, on the other hand, has provided larger number of small vessels, while effectively removing the clutter signal (Fig. 7(c)). The results of applying THF and TH+VEF are shown in Figs. 7(d) and 7(e) respectively with noticeable vessel improvement after adding each stage. The PSL values from three regions (highlighted by overlaid green lines; 20 PSL values) resulted in an overall gain of 25.12dB compared to conventional Doppler imaging.

Fig. 7:

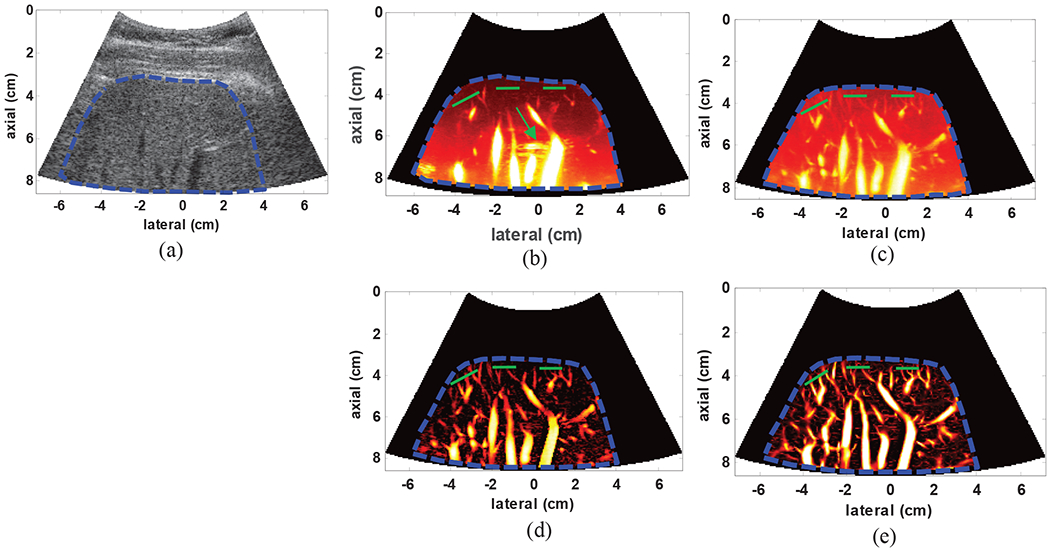
(a) B-mode image of the liver in a healthy subject (b) power Doppler using conventional IIR filtering (green arrow shows residual clutter signal) with 70Hz cutoff frequency (c) gross image of the vessels using SVT, (d) vasculature image after SVT+THF and (e) final image of the hepatic vasculature network after SVT+THF+VEF. The overlaid green lines indicate cross-sections from which PSL values were calculated.

3). Microvasculature in malignant human thyroid nodule

The next example presents vasculature network in thyroid nodule from a representative subject. Fig. 8(a) shows the B-mode image of the nodule revealed by histology as a malignant papillary carcinoma. The nodule can be identified as a uniform scattering area with two shadowing columns on the sides. The conventional power Doppler imaging has provided acceptable small vessel visibility as seen in Fig. 8 (b). However, this has been possible at the cost of admitting some residual clutter signals which prohibits further vessel analysis in some regions. The SVT, on the other hand, has provided uniform clutter removal throughout the entire nodule area as seen in Fig. 8(c).

Fig. 8:

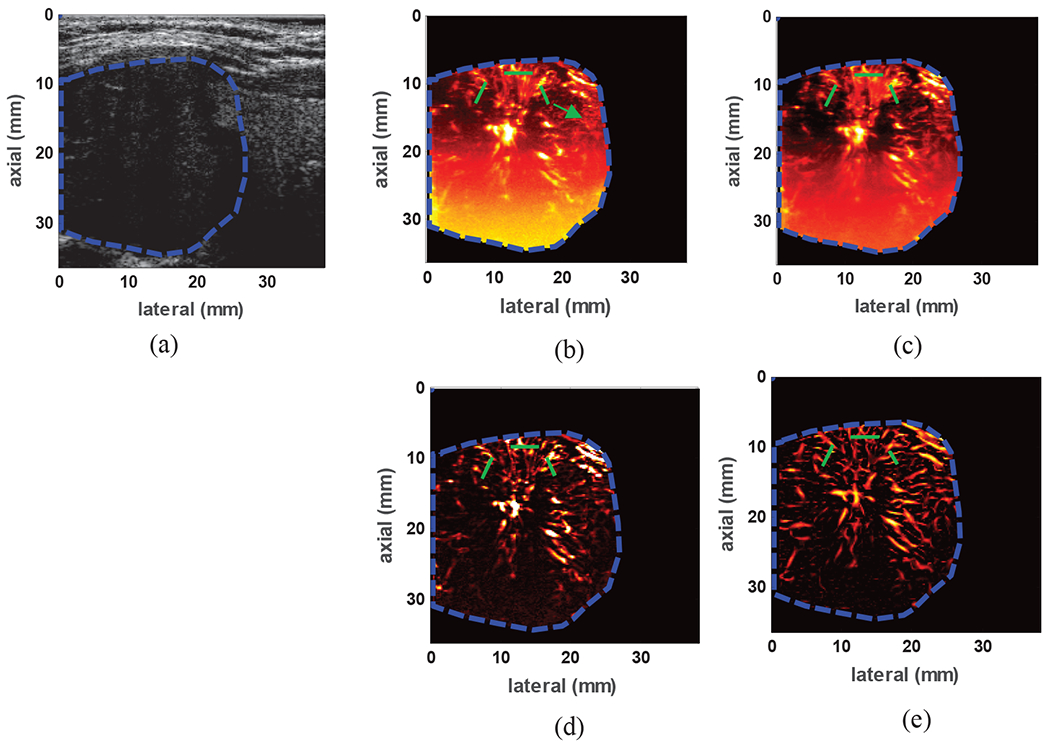
(a) B-mode image of a malignant papillary carcinoma identified between two vertical black columns (b) power Doppler image using conventional IIR filtering (green arrow indicates residual clutter signal) with 75Hz cutoff frequency (c) gross vasculature image in the nodule using SVT, (d) vasculature image after SVT+THF (e) final image of the vasculature network inside the nodule after SVT+THF+VEF. The overlaid green lines indicate cross-sections from which PSL values were calculated.

Fig. 8(d) shows that the depth-dependent background signal is mostly removed by the THF with minimal impact on the vessel structures and morphology and VEF processing has provided additional regularization to and noise suppression (especially at deeper areas) as seen in Fig. 8(e). The overall PSL gain obtained by SVT+THF+VEF (calculated from three regions highlighted by green lines; 13 PSL values) compared to conventional Doppler imaging was 25.32dB.

4). Microvasculature in human breast lesion

To demonstrate the suitability of the proposed method for imaging small vessels in breast lesions, the results from one representative patient with a benign fibroadenoma are presented. The lesion can be identified in Fig. 9(a) as a well-circumscribed hypoechoic region. Fig. 9(b) shows the power Doppler image obtained via conventional high pass filtering method. Compared to the SVT image in Fig. 9(c), conventional power Doppler has failed to visualize some of the small vessels. The SVT+THF and SVT+THF+VEF images are shown in Fig. 9(c) and (d) respectively. The incremental enhancement after THF and VEF processes can be well appreciated in terms of suppression of background signal and enhanced vessel visibility. The PSL values from the areas highlighted by green lines (14 PSL values) are summarized in Table 3 where SVT+THF+VEF provided and overall PSL gain of 36.49dB compared to conventional Doppler imaging using IIR filtering.

Fig. 9:

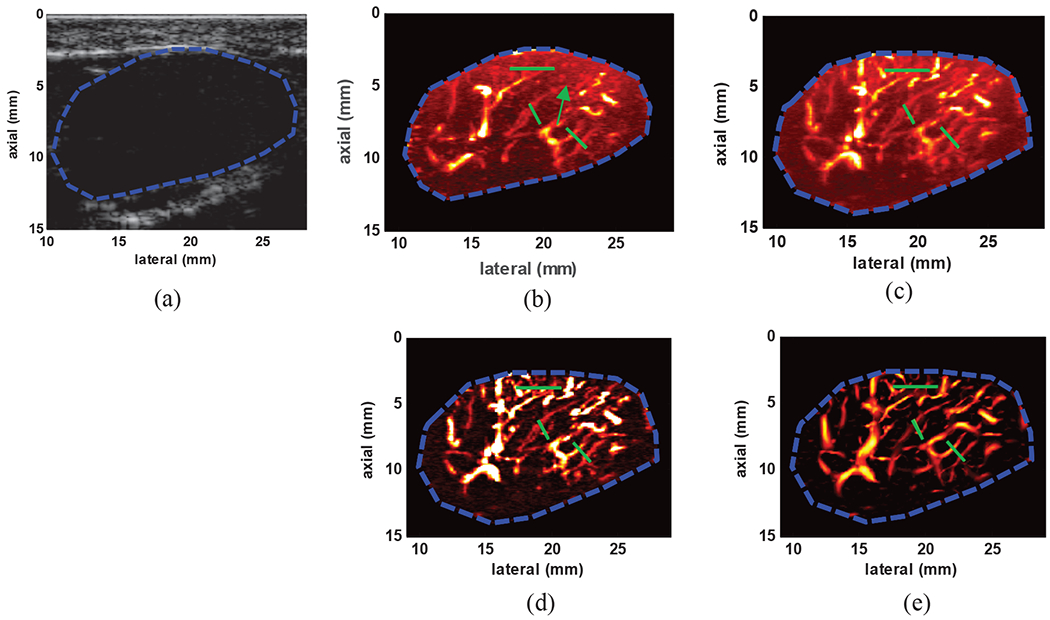
(a) B-mode image of a benign breast fibroadenoma identified as hypoechoic region with well-defined boundaries (b) power Doppler image using conventional IIR filtering with 50Hz cutoff frequency (c) image of the gross vasculature imaging inside the lesion using SVT, (d) vasculature image after SVT+THF (e) final image of the vasculature network inside the lesion after SVT+THF+VEF. The overlaid green lines indicate cross-sections from which PSL values were calculated.

Table 3:

PSL values obtain from in vivo studies

	Liver	Thyroid	Breast	All cases
Number of subjects	5	5	5	15
IIR	1.35±1.06dB	2.35±1.08dB	0.99±0.52dB	1.56±1.04dB
SVT	2.58±0.42dB	3.58±1.96dB	1.84±0.71dB	2.67±1.36dB
SVT+THF	22.62±1.94dB	19.65±5.96dB	21.38±5.89dB	21.22±4.76dB
SVT+THF+VEF	24.90±2.28dB	22.50±5.04dB	23.03±8.05dB	23.48±5.33dB

5). Extended patient studies

To further evaluate the utility of the proposed method for imaging small vessels in each organ, PSL values were obtained from 5 subjects. For each subject, multiple ROIs were selected to provide statistically meaningful assessment of the PSL values. These results are summarized in Table 3.

The conventional power Doppler imaging using IIR filtering provided a PSL value of only 1.56dB which translates into a very limited dynamic range for visualization of the small vessels. Using SVT instead of temporal filtering, this value was increased to 2.67dB. THF and VEF each provided an incremental gain of 18.55dB and 2.26dB respectively with a cumulative gain of 21.92dB compared to the conventional Doppler. These quantitative gains corroborate well with the enhanced vessel visibility in the vasculature images seen in the representative cases from each organ after adding each processing step.

V. DISCUSSION

SVT combined with the high frame rate plane wave imaging has been shown to be a powerful tool in separating highly correlated tissue clutter backscatter signals from the blood signal. As shown in [14], the blood signals can be well below the clutter signal levels (down to −30dB and less). Hence, conventional Doppler imaging based on classic frequency domain filtering provides unreliable vessel mapping in case of strong bandwidth overlap such that a large cut-off frequency would significantly suppress small vessel. A too small cut-off frequency, on the other hand, would fail to completely suppress clutter signals as shown in several examples in this study and by other groups [14]. The high degree of spatial and temporal coherence provided by plane wave imaging, creates an ideal framework for low rank approximation of the clutter signal such that even in the presence of strong frequency bandwidth overlap, blood signals can be separated from the strong clutter signals. Despite superior performance of SVT in removing clutter, additive noise can hinder the useful dynamic range of the resulting power Doppler images. While one may be tempted to address noise suppression in singular value domain via singular value truncation (e.g. as suggested in [17]), shared eigen-spectrum might adversely damage energy accumulation (via power Doppler integration) from blood activity in the smallest vessels which might present noise like features in tenns of singular value behavior. Additionally, plane wave imaging has made it possible to acquire both B-mode images and full field of view Doppler ensembles from the same imaging sequence. While TGC is beneficial for B-mode image equalization, when used in plane wave imaging for combined Doppler+Bmode sequences, it can cause depth-dependent noise amplification which can in turn hinder the visibility of small vessels at different depths for a given image dynamic range. This latter effect, can render noise suppression problematic if a global singular value thresholding is employed, hence localized approaches should be employed at a significant computational cost [17].

In this paper, a novel approach was introduced to enhance small vessel visibility directly on power Doppler images. Our method comprises two shape-aware processing steps, both tuned to promote tubular structures and penalize randomness. The first step, morphological-based filtering, is capable of removing background signals appearing at size scales larger than a specified range. We proposed gray-scale top-hat filtering with a disk structuring element for this purpose. The diameter of the structuring element was chosen based on the largest desired vessel diameter. Through multiple in vivo examples we showed that THF can effectively remove most of the background signals as well as alleviate rapid local intensity variations which are reminiscent of the ultrasound echo fluctuations. The algorithm is then accompanied by a Hessian-based vessel enhancement filtering to further improve the background suppression and vessel visibility. In addition to visible enhancement provided by the VEF, significant quantitative gains were achieved after each processing stage. In our method, the highest processing gain was achieved by top-hat filtering background removal (18.55dB) which is indicative of strong noise suppression enhancement provided by this method without affecting small vascular structures. The vessel enhancement filtering, in addition to suppressing spurious background residues via enforcing tubular structures, provided a processing gain of 2.67dB which further improved small vessel visualization and image equalization. The elevated vessel-background separation presented in this paper through multiple in vivo studies enables direct segmentation and additional analysis of the morphological alterations which can be used for assessment of microvasculature alterations. In studying cancer, increased perfusion is considered as a hallmark of malignancy as large blood supply is provided by fonnation of new blood vessels through a process called angiogenesis. Using contrast-enhanced acoustic angiography method [25], the study in [26] has shown that the morphological features can serve as potential biomarkers for identification of cancerous tumors. The significant processing gain of our method was shown to provide continuous vessel maps without requiring injection of contrast agents. Additionally, the proposed method can provide deeper penetration compared to acoustic angiography as the vessel image are derived from the fundamental frequency instead of higher harmonics. These features facilitate adaptation of this imaging method into routine clinical work ups as the methods benefits from all safety and versatility feature of conventional Doppler imaging. From the implementation point of view, the proposed method does not add a significant amount of processing burden to the methods based on SVT as both THF and VEF are simple operations which can be implemented using highly parallelized algorithms.

Despite significant improvements in the vessel visibility, applying VEF on 2-D images poses a number of challenges and limitations. A fundamental limitation of imaging vascular structures using 2-D imaging is overlapping and crossing of the vessels in highly perfused areas. Such crossings cannot be resolved using our VEF algorithm and may lead to erroneous bifurcation or brandling. Additionally, single-plane imaging of the 3-D vessel structures always leads to partial cross-sectional imaging of some vessels. These areas may appear as bright blobs in the gross vascular images. Although the VEF fonnulation in (18) penalizes non-tubular structures including disks, high amplitude intensities may affect the appearance of the small vessels in vicinity of such areas, leading to misinterpretation of the vasculature network. Hence, extension of the current method to 3-D imaging may prevent such artifacts and result in more consistent vessel connectivity. Nevertheless, the vessel-background separation offered by our method enables further segmentation and analysis of the vessel morphology which might provide clinically relevant information regarding different disease and conditions that cause alterations in the tissue vascularity. Finally, though no attempt was made to optimize the computational cost of our method, the most expensive operation is SVD with complexity of O(min((MNK², K(MN)²)). Both THF and VEF are directly applied on the power Doppler images using pixel-based operations; hence imposing a constant time complexity (i.e. O(1)). In order to overcome the computational cost of SVD, random sub-space sampling can be utilized. Using this approach, the complexity of a rank S approximation of matrix R in (3) can be reduced to O(MNS²) such that S ≪K.

VI. CONCLUSION

In this paper, we introduced a two-step background removal and vessel enhancement filtering for improved visualization of the microvasculature power Doppler images obtained by non-contrast ultrasound imaging. We first discussed the limitations of SVT in mitigating residual noise, especially in the case of TGC amplified echo data which causes sever depth dependent noise amplification. Our key assumption was independence of the blood and noise signals which allowed us to treat the residual noise as a background signal in the SVT filtered power Doppler images. We proposed shape-aware morphological top-hat filtering to remove spatially variable background while preserving vascular structures. To further improve visibility and vessel-background separation we proposed a multi-scale Hessian filtering to mitigate residual unstructured noise and promote tubular structures as vessels. The incremental improvements achieved by adding these steps over SVT gross images were examined through multiple in vivo examples and the results were quantitatively analyzed. The overall results of this study highlight the significant visual and quantitative gains of our method in clutter and background-free visualization of the microvasculature which enables further analysis for assessment of the morphological features.