Abstract
DEAD-box proteins (DBPs) couple ATP utilization to conformational rearrangement of RNA. In this chapter, we outline a combination of equilibrium and kinetic methods that have been developed and applied to the analysis of ATP utilization and linked RNA remodeling by DBPs, specifically Escherichia coli DbpA and Saccharomyces cerevisiae Mss116. Several important considerations are covered, including solution conditions, DBP assembly/aggregation, and RNA substrate properties. We discuss practical experimental methods for determination of DBP-RNA-nucleotide binding affinities and stoichiometries, steady-state ATPase activity, ATP binding, hydrolysis and product release rate constants, and RNA unwinding. We present general methods to integrate and analyze this combination of experimental data to identify the preferred kinetic pathway of ATP utilization and linked dsRNA unwinding.
1. Introduction
DEAD-box proteins (DBPs) utilize ATP to perform work on RNA (Henn et al., 2012). Such molecular-scale work includes double-stranded RNA (dsRNA) unwinding and rearrangement, alteration of single-stranded RNA (ssRNA) conformation, and displacement of RNA-bound proteins (RNPs) (Linder and Jankowsky, 2011; Pan and Russell, 2010). Multiple and distinct low-energy RNA conformations increase the likelihood of kinetically trapping cellular RNAs in misfolded conformations. In the cell, resolution of misfolded conformations requires RNA helicases and chaperones (Herschlag, 1995; Woodson, 2010). Disruption of DBP function or loss of regulation has been linked to a variety of human pathologies, including the development and progression of several forms of cancer and heart disease (Abdelhaleem, 2004; Akao, 2009; Chao et al., 2006; Godbout et al., 2007; Ramasawmy et al., 2006; Sahni et al., 2010). These diseases likely originate from incorrect RNA folding and RNP assembly or disassembly, all of which can severely alter RNA transcription, splicing, maturation, export, translation, and degradation (Doma and Parker, 2007; Herschlag, 1995; Schroeder et al., 2004).
RNA binding stimulates the ATPase activity of many DBPs (Cordin et al., 2006). Therefore, rate-limiting step(s) in the intrinsic DBP ATPase cycle are accelerated or bypassed by RNA (Scheme 2.1). Progression through the ATPase cycle is coupled to transduction of the chemical energy in ATP binding, hydrolysis, and/or product release to mechanical work production on RNAs and RNPs (Henn et al., 2012; Hilbert et al., 2009; Jarmoskaite and Russell, 2011). Understanding the thermodynamic coupling between RNA affinity and the chemical state (ATP, ADP-Pi, ADP) of the bound adenine nucleotide (Scheme 2.1), identifying the preferred kinetic pathway of ATP utilization and the distribution of populated biochemical and structural intermediates, and determining rate-limiting step(s) of the RNA-stimulated DBP ATPase cycle are all essential for developing mechanistic models of DBP-dependent RNA rearrangement.
Scheme 2.1.
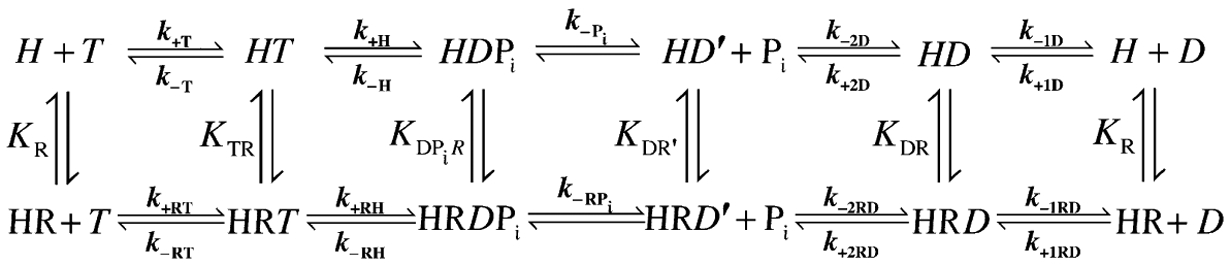
Minimal ATPase cycle reaction scheme for a DBP with two ADP-bound states. H is the DBP, R is an RNA substrate, T and D are ATP and ADP, respectively, and Pi is inorganic phosphate. The ki are rate constants and Ki are equilibrium constants of ATPase cycle transitions.
In this chapter, we outline a combination of equilibrium and kinetic methods that have been developed for analysis of ATP utilization and linked RNA remodeling by DBPs (Henn et al., 2012). We discuss practical experimental methods for determination of DBP-RNA-nucleotide binding affinities and stoichiometries, steady-state ATPase activity, ATP binding, hydrolysis and product release rate constants, and RNA unwinding. These methods have been applied to Escherichia coli DbpA (Henn et al., 2008, 2010; Talavera and De La Cruz, 2005; Talavera et al., 2006) and Saccharomyces cerevisiae Mss116 (Cao et al., 2011). We refer to these examples throughout the text.
2. Reagents and Equipment
2.1. Solution conditions and temperature
Quantitative kinetic and thermodynamic analyses of E. coli DbpA (Henn et al., 2008, 2010; Talavera and De La Cruz, 2005; Talavera et al., 2006) and S. cerevisiae Mss116 (Cao et al., 2011) were carried out in KMg75 buffer (20 mM Hepes, pH 7.5, 75 mM KCl, 5 mM MgCl2, 1 mM DTT) or a very similar buffer (e.g., 100 mM instead of 75 mM KCl; Talavera and De La Cruz, 2005). If different solution conditions are required or desired, the ionic strength should be maintained between 50 and 200 mM with 1–5 mM Mg2+ in excess of [ATP] or [RNA nucleotides]. We consistently employ a temperature of 25 °C to allow direct comparison of observed reactions between experiments and different DBPs. It is critical to maintain identical solution conditions and temperature in experiments integrated for analysis. RNAase-free working conditions must be maintained in all experiments.
2.2. RNA substrate(s)
Synthesized and gel or HPLC-purified RNA substrates are commercially available (Dharmacon/Thermo-Fisher). The 2′-hydroxyl is deprotected following the manufacturer’s protocol, samples desiccated in a SpeedVac concentrator, resuspended in deionized water at 200+ μM (polymer), and stored at −20 °C in 100–200 μL aliquots. RNA substrates with significant secondary structure are refolded in KMg75 by heating to 95 °C and slowly cooling to 15 °C in a thermocycler before freezing. RNA hairpins are refolded at lower concentrations, typically <40 μM polymer, to minimize oligomerization.
2.3. DEAD-box proteins
DBPs have been expressed in E. coli and purified to >95% purity (estimated by overloaded SDS-PAGE) (Cao et al., 2011; Henn et al., 2001, 2008). [DBP] is determined spectrophotometrically (Grimsley and Pace, 2003). DBP aliquots (100–200 μL at 20–200 μM) are flash frozen in liquid N2 and stored at −80 °C in 20 mM K-Hepes, pH 7.5, 200 mM KCl, 1 mM DTT. Glycerol or other stabilizing agent(s) may be added for protein stability.
2.4. ATP, ADP, and mant-labeled nucleotides
ATP and ADP are prepared from >99% pure free-acid powder (Roche or Sigma). Concentrated stocks (20–100 mM) are prepared on ice in deionized water and pH adjusted to 7.0 with KOH. Aliquots (200–500 μL) are stored at −20 or −80 °C. mant-labeled nucleotides can be synthesized (Hiratsuka, 1983) or purchased (Molecular Probes/Life Technologies) and stored at −20 or −80 °C. Equimolar MgCl2 is added to nucleotide stocks immediately prior to use and stored on ice while in use. mant-nucleotide stocks should be stored in opaque tubes on ice or covered with aluminum foil. Nucleotide concentrations are determined spectroscopically using absorptivities of 15,400 M−1 cm−1 at 259 nm for unlabeled (ATP and ADP), and 23,300 M−1 cm−1 at 255 nm for mant-labeled nucleotide (mantATP and mantADP, both mixed and single 3′(2′-deoxy) isomers) measured in deionized water and/or KMg75 buffer.
2.5. UV–visible spectrophotometer
A computer-controlled UV-visible spectrophotometer capable of both absorbance spectrum and kinetics measurements at multiple wave lengths and allows digital storage of data. The instrument should have high wavelength accuracy (≤1.0 nm), low noise (<0.001 Abs) and stray light (<0.05%) in the UV-visible range, and it must be equipped with a temperature control device. We use a Perkin Elmer Lambda 20 and have used instruments made by Shimadzu, Agilent, and Jasco for satisfactory and reproducible results.
2.6. Fluorimeter
Equilibrium binding measurements utilizing changes in fluorescence, fluorescence anisotropy, or light scattering require an instrument with these capabilities. Fluorimeters equipped with relatively high-power light sources (75–200 W) in the T-format (two detectors) and monochromators on the excitation and detection channels are preferred. Instruments using optical filters on the emission channels are adequate provided changes in the emission profile upon binding and/or isomerization are significant. The instrument must be equipped with a temperature control device. We use a Photon Technology International (PTI) QuantaMaster 40.
2.7. Stopped-flow apparatus
Transient kinetics measurements of DBP ATPase cycle transitions require an instrument with millisecond time resolution to measure rate constants of several hundred per second or faster. A variety of rapid mixers with absorbance and fluorescence detection are commercially available. Those driven by compressed air or stepper motors offer the most efficient perturbation and rapid-mixing time, though manual-mixing attachments can suffice in some cases (De La Cruz and Pollard, 1994, 1995, 1996). The instrument must include a temperature control device. We have used instruments from KinTek, Applied Photophysics, Hi-Tech as well as in-house assembled instruments with satisfactory and reproducible results.
2.8. Quench-flow apparatus
Several rapid-mixing chemical-quench-flow instruments are commercially available. As with stopped-flow, millisecond time resolution is needed to measure rapid rates and rate constants. The instrument must include a temperature control device. We use the KinTek Model RQF-3 instrument.
3. Important Considerations for Initial DBP Characterization
3.1. DBP oligomeric state and stability/aggregation
The assembly state of a DBP (i.e., oligomerization) could potentially influence the affinities, rates, and internal equilibria of reaction steps that determine the overall reaction pathway and mechanism (Wyman and Gill, 1990). Protein oligomerization is strongly linked to concentration, and often to temperature, pH, solvent composition, bound ions, and ligands (e.g., nucleotide and RNA binding to DBPs). The oligomeric state of DBPs under experimental conditions must be defined if one wishes to develop mechanistic models. Ideally, self-association should be assessed at [DBP]> 10× higher than that used in other assays. If self-association occurs, it is advantageous to determine the oligomerization equilibrium constant(s), since it permits estimation of oligomeric species concentration at any [DBP], thereby identifying conditions favoring monomer or oligomer(s).
E. coli DbpA (Talavera et al., 2006) and S. cerevisiae Mss116 (Cao et al., 2011; Mallam et al., 2011) behave as nonassociating monomers in solution at concentrations up to tens of micromolar. This behavior is unlikely to hold for all DBPs, given the variability in N- and C-terminal domains, which may contain oligomerization motifs (Klostermeier and Rudolph, 2009). Nonspecific aggregates, as opposed to defined oligomers (e.g., dimers, tetramers, hexamers, etc.), can also form at high [DBP], and potentially affect observed DBP activities (Cao et al., 2011). As such, efforts to identify the predominant oligomeric and/or aggregation state of a DBP should not be dismissed or overlooked.
3.2. RNA substrate selection/design
3.2.1. DBP-RNA binding specificity
DBPs characterized to date display little, if any, RNA sequence specificity (Linder and Jankowsky, 2011), presumably because of a lack of direct DBP contacts with RNA nucleotide bases (Collins et al., 2009; Del Campo and Lambowitz, 2009; Sengoku et al., 2006). RNA recognition is achieved through sugar-phosphate backbone contacts with DBPs (Hilbert et al., 2009). Accordingly, RNA-DBP binding interactions are affected by RNA length and conformation based on complementarity with the RNA binding cleft of DBPs (Del Campo and Lambowitz, 2009). In cases where DBPs display RNA sequence-specific ATPase activity, and/or dsRNA unwinding, either the DBP contains additional RNA binding domains (Kossen et al., 2002; Tsu et al., 2001; Wang et al., 2006) or interacts with other RNA binding proteins that play a role in targeting specific cellular RNAs (Le Hir and Andersen, 2008). For DBPs that display RNA sequence specificity, observation of RNA-stimulated ATPase activity may depend on using an RNA substrate that contains a targeting sequence/structure. For example, hairpin 92 from E. coli rRNA is required to observe RNA stimulation of the ATPase activity of DbpA (Diges and Uhlenbeck, 2001).
3.2.2. RNA-stimulated ATPase activity
RNA-stimulated ATPase activity is a convenient diagnostic for selecting an RNA substrate for a DBP without a known target RNA. Based on current knowledge of commonalities among DBPs, it is unexpected but not impossible for a DBP to display ATP-dependent RNA remodeling of an RNA substrate without RNA-stimulated ATPase activity (Henn et al., 2012; Hilbert et al., 2009). Therefore, characterization of an RNA substrate that activates DBP ATPase can reveal valuable mechanistic information, even if it is not a physiological substrate.
3.2.3. DBP-RNA binding affinity
A key issue in RNA substrate selection is DBP-RNA affinity, particularly in the absence of bound nucleotide. DBPs possessing additional RNA binding domains bind target RNA substrates with high-affinity (Kd<50 nM) (Henn et al., 2008; Polach and Uhlenbeck, 2002). Short (<20 nt) ssRNA or (<20 bp) dsRNA nonspecific DBP substrates typically bind to the nucleotide-free DBP core helicase with <100 to ~500 nM affinity (Cao et al., 2011; Lorsch and Herschlag, 1998). Considering that a Kd of ~500 nM requires 5 μM titrant for ~90% saturation and 50 μM titrant for ~99% saturation, achieving saturating DBP concentrations may not be feasible for weak DBP-RNA affinities.
3.2.4. ATP-dependent RNA unwinding
A major impetus of DBP ATPase characterization is to link ATP utilization to dsRNA unwinding. Unwinding using a strand displacement assay is readily observed for short duplexes (6–10 bp) but is slow and/or inefficient (i.e., characterized by low amplitude) for duplexes ≥12–16 bp (Bizebard et al., 2004; Diges and Uhlenbeck, 2001; Rogers et al., 1999; Yang and Jankowsky, 2006). It is therefore beneficial to choose RNA substrates with a short duplex region (<10 bp) (Chen et al., 2008; Henn et al., 2010) or dsRNA section interrupted by a break in the sugar-phosphate backbone (Fig. 2.1) to favor strand displacement in unwinding assays.
Figure 2.1.

Model RNA substrates for use with DEAD-box proteins. Sequences illustrate important RNA substrate design principles. “unwinding substrate” has a 5′-fluorescent tag (“F”), such as fluorescein. The triangle indicates a break in the sugar-phosphate backbone, such that the labeled strand is displaced with 8 bp unwinding. 5′-fluorescent tagged dsRNA substrate(s) can be used for binding without strand displacement.
3.2.5. RNA substrate characteristics
DBP-RNA binding interactions depend on the RNA structure (Fig. 2.1), including the presence and length of dsRNA, hairpin loops, blunt-end dsRNA versus 5′, 3′, or both types of ssRNA overhang, and overhang length. A primary consideration is the overall length of both ss- and dsRNA regions, with the key issue being the formation of a single DBP binding site.
Although RNA sequence does not appear to contribute to DBP binding specificity for the helicase core, sequence significantly affects RNA structure and assembly, which could dramatically influence DBP binding. RNA substrates predicted to have a single predominant secondary topology in solution (e.g., model substrates in Fig. 2.1), predicted using Sfold (Ding et al., 2004) and RNA structure software packages (Reuter and Mathews, 2010) are desirable. Because certain RNA hairpins can potentially self-associate in solution, it is important to avoid sequence repeats within the dsRNA region, which increase the number of potential oligomerization species. Refolding of the RNA should be evaluated over a broad concentration range (e.g., 10–100 μM) to identify conditions minimizing oligomerization. Analytical ultracentrifugation should be performed to affirm the RNA substrate is predominantly monomeric following refolding (Lebowitz et al., 2002). Light scattering may provide evidence of large RNA multimers in solution (Attri and Minton, 2005; Murphy, 1997). When designing a hairpin-containing dsRNA, the loop sequence (e.g., UUCG tetraloop, Fig. 2.1) can play an important role in stabilizing the overall structure (Antao et al., 1991). An additional consideration is the potential for poly-purine base-stacking to favor a helical structure (Seol et al., 2007) versus polypyrimidine sequences that adopt a more random coil in solution (Seol et al., 2004).
3.3. Measuring RNA binding affinity and stoichiometry
Structural, biochemical, and biophysical data acquired with several DBPs and short RNA substrates (≤20 nt or bp) reveal a 1:1 RNA:DBP binding stoichiometry (Cao et al., 2011; Polach and Uhlenbeck, 2002; Talavera et al., 2006). The combination of equilibrium and kinetic analyses presented here apply to 1:1 RNA:DBP interactions. Different expressions may be needed for other binding stoichiometries. If a DBP possesses two distinct RNA binding sites (or RNA can accommodate two DBPs), analysis of the binding data with a 1:1 binding model will, at best, give an estimate of the average affinity of the two sites and could lead to erroneous conclusions (Wyman and Gill, 1990). Therefore, quantitative determination of the binding stoichiometry is critical.
3.3.1. Measuring the equilibrium RNA binding affinity in the absence of bound nucleotide and with saturating ADP
Numerous methods for measuring RNA binding have been developed. We favor fluorescence measurements for DBP-RNA binding experiments because of their high sensitivity and the ability to measure binding under true equilibrium conditions. Changes in fluorescence intensity (quenching or enhancement) (Lakowicz, 2006) or anisotropy (Henn et al., 2010) are useful signals that can be used for real-time kinetic assays, as discussed below. Fluorescently labeled RNA and protein are amenable to fluorescence correlation spectroscopy (FCS), which assays binding from changes in diffusion (Cao et al., 2011). Fluorescent probes conjugated to RNA and/or protein can affect binding, so evaluating various labels and utilizing competition techniques to measure the “true” binding affinity of the unlabeled molecules is essential (Bujalowski and Jezewska, 2011; Thomä and Goody, 2003).
Equilibrium binding titrations are commonly performed with one reactant (DBP or RNA) at a constant concentration and varying the other “titrant” over a broad concentration range while monitoring an experimental signal that scales with bound complex. The equilibrium binding affinity is determined from least-squares fitting of the data. In an experiment where ~10–100 nM fluorescently labeled RNA (the smallest amount providing a reliable fluorescence signal) is titrated with a range of [protein], the following quadratic expression for the equilibrium binding density ([protein]bound: [RNA]total) accounts for protein depletion when [RNA]total is not ≪ Kd, as is often the case (Cao et al., 2011; Henn et al., 2010):
| (2.1) |
Rtot is the total [RNA], HR is the [helicase-RNA], Htot is the total [helicase], and Kd is the dissociation equilibrium constant (KR), assuming 1:1 binding. If RNA binding is associated with a change in DBP fluorescence (intrinsic or of a conjugated probe), unlabeled RNA should be titrated with a fixed [DBP]. In this case, the Rtot and Htot terms in Eq. (2.1) should be switched.
Binding density values will range from 0.0 (no DBP) to 1.0 for stoichiometric helicase-RNA complexes. In practice, a range of helicase or RNA concentrations that span 100-fold above and below the Kd (a 104 range in the [titrated molecule]) will generate binding density values ranging from 0.01 to 0.99 and provide an excellent estimate of the Kd value. An iterative process is recommended, where an initial titration with ~12 points spanning ~1000-fold range in [helicase] (e.g., 5 nM to 5 μM) is used for a rough Kd estimate, followed by a full titration with ~20 points spanning the suggested 104 range in [helicase] (or [RNA]).
The DBP-bound nucleotide affects the RNA binding affinity (Henn et al., 2012;Hilbert et al., 2009; Jarmoskaite and Russell, 2011; Linder and Jankowsky, 2011), such that weak and strong RNA binding states are transiently populated as a DBP progresses through its ATPase cycle (Henn et al., 2012). These nucleotide-linked changes in RNA binding are associated with work production (e.g., unwinding and rearrangement) (Howard, 2001). Quantitating the RNA binding affinity in the various nucleotide states (ATP,ADP-Pi, and ADP) is therefore of central importance.
The ADP-bound state(s) of DBPs are the only native nucleotide state(s) that can be studied under true equilibrium conditions. ATP is hydrolyzed and Pi binds too weakly to saturate without introducing secondary effects from changes in solution ionic strength. RNA binding with DBP-bound ATP analogs such as AMPpNp, ADP-BeF3, ADP-AlF4, etc., can also be measured as described.
The RNA binding affinity of DBP-ADP (KDR,overall) is measured as above, except with saturating ADP. Knowledge of the DBP-ADP binding affinity (when bound to RNA, KRD,overall) is therefore needed to ensure saturating [ADP] during the titration. The overall ADP affinity (KRD,overall) can be estimated from the concentration-dependence of the mantADP binding amplitudes (Cao et al., 2011) and/or the rate constants and “overall binding” Eq. (2.5). However, this presents a “chicken and egg” problem in cases where the ADP and RNA affinities are strongly linked. Such a situation requires an iterative approach measuring approximate affinities of RNA and ADP binding to the DBP in the presence of each other, ultimately leading to determination of precise affinities under conditions where the other molecule is present at saturating concentration. As a first approximation, it is useful to keep in mind that the measured KRD,overall for both DbpA (Henn et al., 2008) and Mss116 (Cao et al., 2011) have been <100 μM, meaning that 10 mM MgADP is saturating when bound to RNA.
The two DBP-RNA equilibrium binding experiments described provide the overall affinity of RNA binding to DBP (KR) and DBP-ADP (KDR,overall). Although these two states do not appear to be active unwinding intermediates of characterized DBPs (Henn et al., 2010, 2012), these two binding parameters are needed for analysis of ATP utilization by DBPs (Scheme 2.1). Knowledge of KR combined with the suite of transient kinetic, nucleotide binding experiments described below, permits calculation of linked DBP-RNA equilibrium binding constants and provides a means to assess thermodynamic consistency in experimentally determined parameters. Adhering to the principle of detailed balance associated with the thermodynamic boxes comprising Scheme 2.1, KTR and can be calculated as follows (Cao et al., 2011; Henn et al., 2008)
| (2.2) |
where KT = k−T/k+T, KRT = k−RT/k+RT, KH = k−H/k+H, and KRH = k−RH/k+RH. Accordingly, KDR and KDR′ (Scheme 2.1) can be calculated from Cao et al. (2011) and Henn et al. (2008)
| (2.3) |
where K1D = k−1D/k+1D, K1RD = k−1RD/k+1RD, K2D = k−2D/k+2D, and K2RD = k−2RD/k+2RD.
The DBP-RNA equilibrium dissociation constant in the presence of saturating ADP, KDR,overall, measured as described above, provides an internal consistency check for the combination of KR and the fundamental ADP binding/dissociation rate constants measured by transient kinetics as follows (Cao et al., 2011; Henn et al., 2008)
| (2.4) |
where
| (2.5) |
4. Steady-State ATPase Measurements
4.1. Motivation for measuring DBP ATPase activity at steady state
Thorough characterization of the DBP steady-state ATPase activity (Fig. 2.2) is an essential starting point of quantitative biochemical and biophysical analysis of ATP utilization. A primary objective of steady-state ATPase analysis is to determine the maximal per-enzyme cycling rate, or kcat (in units of s−1 DBP−1), at saturating [ATP] and in the presence and absence of saturating [RNA]. Some DBPs display little or undetectable ATPase in the absence of a suitable RNA substrate (Henn et al., 2008), while others have modest intrinsic ATPase activity (Cao et al., 2011). In all cases studied to date, suitable RNA substrates accelerate ATPase kcat>5 to 2000+ fold.
Figure 2.2.
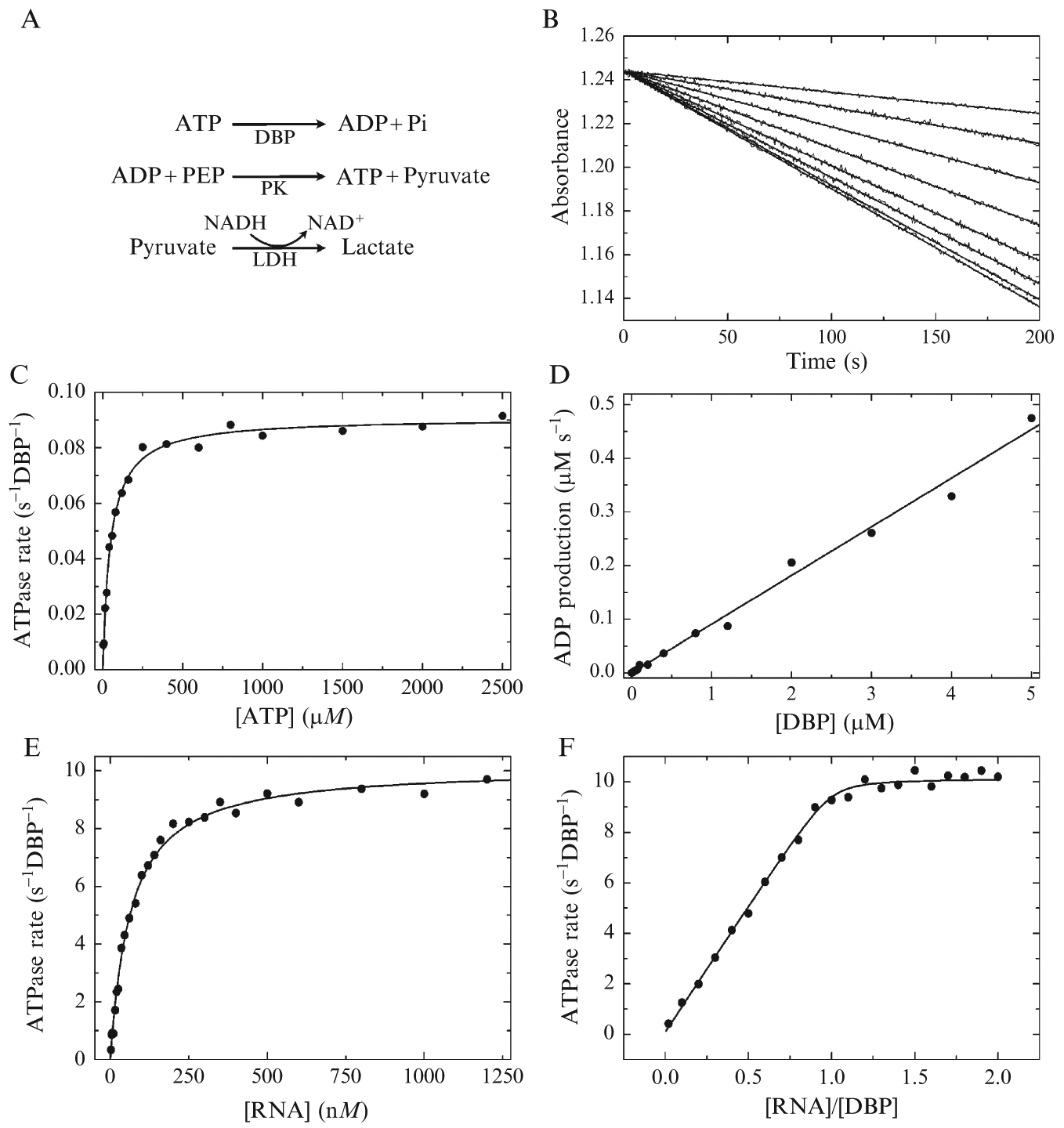
Steady-state DBP ATPase activity. (A) Schematic of the coupled enzyme reactions. DBP is DEAD-box protein, PEP is phosphoenolpyruvate, PK is pyruvate kinase, LDH is lactate dehydrogenase, NADH and NAD+ are the reduced and oxidized forms, respectively, of nicotinamide adenine dinucleotide. (B) NADH oxidation is monitored by absorbance at 340 nm. Time courses of absorbance change for 1 μM DBP (kcat = 0.09 s−1 DBP−1 and Km,ATP = 48 μM) cycling in the presence of 10–1000 μM ATP (upper to lower). (C) [ATP]-dependence of the DBP steady-state ATPase rate with model fit (solid line) to Eq. (2.7) with [DBP] ≤ 400 nM. (D) [DBP]-dependence of the observed ATPase rate in the presence of 10 mM (saturating) ATP. The slope of the linear fit yields kcat. (E) [RNA]-dependence of DBP (10 nM) steady-state ATPase in the presence of 10 mM (saturating) ATP. Continuous model curve is generated by Eq. (2.9) with kcat = 10.1 s−1 DBP−1 and KM,RNA = 60 nM. (F) Estimating the RNA stoichiometry of DBP ATPase activation. The [DBP] is constant (10 μM≫ KM,RNA) with varying [RNA] in the presence of 10 mM ATP. The continuous model curve is generated by the implicit bimolecular binding equations (Cao et al., 2011) with a stoichiometry parameter of 1.0. All data are simulated with introduced Gaussian noise.
The RNA-stimulated DBP ATPase cycle kcat provides the minimum rate at which ATP is utilized to perform mechanical work on RNA, in the absence of “futile,” nonproductive ATPase cycles. This rate can be compared with direct measurements of RNA rearrangement kinetics (Cao et al., 2011; Henn et al., 2010). If RNA rearrangement is ≪ kcat, multiple ATPase cycles are required to yield the observed rearrangement and/or nonproductive ATPase cycles occur with regularity. As part of a complete DBP ATPase kinetic analysis, kcat can be directly compared with the rate constants of individual cycle steps (Scheme 2.1) to determine which biochemical transition(s) limit(s) ATP utilization, providing candidate force-producing and load-bearing state(s) during ATPase cycling.
The “Michaelis constant,” or Km, is defined as the concentration required to half-saturate the observed ATPase rate (Fig. 2.2) (Cornish-Bowden, 2004). The Km,ATP in the presence and absence of RNA is a true Km, while the Km, RNA is an apparent Km because RNA rearrangement is not monitored in the ATPase assay. The Km reflects the mole-fraction weighted affinities (Kd) of DBP states populated during steady-state ATPase cycling (Henn et al., 2008). In experiments where saturating RNA or other regulatory components of the DBP ATPase activity are included, effects on the Km of any other species (such as ATP or RNA) reveal altered binding affinities, that is, cooperativity, during one or more ATPase cycle steps. Given an ATPase cycle scheme (e.g., Scheme 2.1), relationships between Km values for each molecular species and the rate and equilibrium constants of individual steps in the ATPase cycle can be derived (Cao et al., 2011; Henn et al., 2008, 2010). As such, the measured steady-state Km values provide a consistency check on the combination of rate constants measured by transient kinetics. In addition, the Km values provide constraints on difficult to measure rate constants that can instead be estimated using multiple lines of equilibrium, steady-state, and transient kinetics experimental evidence (see Section 9).
Regulatory proteins can affect kcat and Km,ATP (with or without RNA), and Km,RNA of some DBPs. Examples include eIF4A (Marintchev et al., 2009; Rogers et al., 2001), eIF4AIII (Le Hir and Andersen, 2008), and Dbp5/Ddx19 (Montpetit et al., 2011; Weirich et al., 2006). For DBPs that display this additional level of ATPase regulation, it is important to determine the steady-state parameters in the presence of a saturating concentration of the regulatory molecule(s).
4.2. Steady-state ATPase method: Real-time enzyme-coupled assay
While several methods have been used to measure ATPase activity from liberation of Pi (De La Cruz and Ostap, 2009) or ADP (Charter et al., 2006), we prefer the NADH-linked enzyme-coupled assay (De La Cruz et al., 2000; Tsu and Uhlenbeck, 1998) based on our results with DBPs (Cao et al., 2011; Henn et al., 2008, 2010) and myosins (De La Cruz et al., 2000; Henn and De La Cruz, 2005). The NADH-linked assay has several advantages over other assays, including real-time measurement, ATP regeneration, and minimal interference from Pi contamination (De La Cruz et al., 2000; Furch et al., 1998). The assay relies on absorbance detection of NADH oxidation resulting from ADP production (Fig. 2.2A). One NADH molecule is oxidized per liberated ADP, allowing for direct conversion of the change in absorbance versus time to the [ADP] produced per second using the absorptivity of NADH (6220 M−1 cm−1 at 340 nm).
It is helpful to confirm that the assay responds rapidly to ADP (under experimental conditions) prior to beginning an experiment. The NADH absorbance at 340 nm should decrease and reach a minimum within a few seconds, remaining flat thereafter. If the change in signal is slower, use more coupling enzymes, make fresh stocks, or both. The change in absorbance, ΔA340, should be used to calculate the change in [NADH]. This value should correspond closely (within a few percentage) to the [ADP] added, up to the total final concentration of NADH. If this is not the case, use more PEP and/or a fresh PEP stock. The same is true for NADH, although the characteristic absorbance peak at 340 nm is a good indicator of the NADH integrity, and with a 1 cm path length, the starting absorbance value with 200 μM NADH should be close to 1.244 (Fig. 2.2B). Using more NADH is not recommended unless the path length is decreased, since the signal to noise is reduced at higher absorbance.
Stock solutions
10× KMg75 buffer (add DTT to 5 mM upon dilution to 5 × or 1 mM upon dilution to 1 × prior to use) or other suitable buffer tested as above with known ADP aliquots. Store at 4 °C in a large volume (50 mL or more).
100 mM PEP, prepared by dissolving pure powder (Sigma) in water and adjusting the pH to 7.0 with KOH. Aliquots (100–200 μL) can be stored at −20 or −80 °C for over 1 year as long as repeated freeze-thaw cycles are avoided. Keep on ice while in use.
100 mM ATP (see Section 2) thawed on ice and vortexed to thoroughly mix upon adding MgCl2 (1 M stock in deionized water, equimolar to ATP upon addition), prior to further dilution.
Stock aliquot of RNA substrate, thawed on ice (previously refolded if containing secondary/tertiary structure).
Pyruvate kinase (PK) from rabbit muscle, prepared from lyophilized powder (Sigma) in 10 mM Tris or Hepes, pH 7.0–7.5, 50% glycerol at a stock concentration of 10,000 U/mL, and stored in aliquots (200–500 μL) at −20 °C.
Lactate dehydrogenase (LDH) from porcine heart (recombinant), prepared from lyophilized powder (BBI enzymes) in 10 mM Tris or Hepes, pH 7.0–7.5, 50% glycerol at a stock concentration of 4000 U/mL and stored in aliquots (200–500 μL) at −20 °C.
DBP of interest, aliquot thawed on ice.
Working solutions (freshly made)
15 mM NADH, prepared in 1 mL deionized water from desiccated powder (Sigma) stored at 4 °C. Store the solution in an opaque tube on ice for up to 12 h. Aliquots may be frozen at −20 °C for several days, but the [NADH] should be checked spectrophotometrically.
1 M DTT, prepared in deionized water from desiccated powder (Sigma or American Bioanalytical) stored at 4 °C. Store stock solution on ice.
5× coupling assay “cocktail” made in 1× KMg75 buffer containing: 1 mM NADH, 100 U/mL LDH, 500 U/mL PK, 2.5 mM PEP. Make a large enough volume to mix at 1× final in the reaction volume for all replicate measurements. Note that in titrations where [ATP] will be held constant (and saturating), ATP may be included in the “cocktail” at 5× final concentration. Store on ice for up to 12 h in an opaque tube or 15 mL tube covered by aluminum foil. Check for activity at 1× with MgADP standards.
Diluted stocks of DBP, RNA, MgATP, and MgADP in 1× KMg75 buffer. Use the smallest stock concentration (requiring the largest volume addition to the final reaction mixture) possible to achieve the desired reaction concentration after adding all the other components. This greatly improves reproducibility and reduces experimental errors due to pipetting small volumes of highly concentrated reaction components.
Method
Prepare a clean (RNAase free) quartz cuvette with a 1 cm path-length that requires ≤ 100 μL to fill the observation window.
Prepare the thermostated UV-visible spectrophotometer according to the manufacturer’s protocol and set for collection of an absorbance time course at 340 nm. Recording data points every 0.5 s for 200+ s total is usually sufficient for steady-state measurements.
Prepare at the reaction temperature a series of tubes (“tube A series”) containing the variable component (2× final concentration in 1× buffer) in ½ the reaction volume. These tubes may also contain one or more reaction components kept at constant concentration (2× final).
Prepare a single tube (“tube B”) containing all other components not in tube A (2× final concentration) in a large enough volume to aliquot ½ the reaction volume for each tube in the “A series.” DBP and ATP must be in separate tubes prior to mixing.
For each measurement, mix an equal volume from tube B into tube A and gently pipette up and down to mix while avoiding introduction of bubbles. The ATPase reaction should now be “running.” Quickly transfer the full reaction volume (120–150 μL) to the cuvette and check that no bubbles are visible in the cuvette window. Place the cuvette in the spectrophotometer and collect the time course absorbance data (Fig. 2.2B).
Analysis
Time courses of absorbance change should be linear (Fig. 2.2B) and fitted to obtain the slope, m (ΔA340 s−1). Deviations from linearity at early times (<3 s) are likely due to incomplete mixing, differences in temperature between incubation tube and cuvette, contaminating ADP in the ATP, or the approach to steady state, and should not be used for analysis. Time courses must be corrected for the background oxidation of NADH by subtracting the slopes of time courses acquired in the absence of DBP from those of experimental samples.
Background-corrected time course slopes, m (in A340 s−1), can be converted to observed ATPase rates, vobs, (ADP molecules produced s−1 DBP−1) according to
| (2.6) |
where l is the path length of the cuvette (in cm), Htot is the total (active) [DBP] (in M), and εNADH,340 is the NADH absorptivity at 340 nm (6220 M−1 cm−1).
To obtain kcat and Km,ATP, vobs is plotted as a function of [ATP] and fitted by nonlinear regression. If the [DBP] ≪ [ATP] for all data points (Fig. 2.2C), the hyperbolic form of the Briggs-Haldane equation is appropriate (Cornish-Bowden, 2004)
| (2.7) |
where kcat is the maximal ATP turnover rate (s−1 DBP−1) at saturating MgATP in the absence of RNA and T is the [MgATP]total ≈ [MgATP]free. Analysis of the raw data is identical for experiments in which the [DBP] is varied. In this case, Htot is not included in Eq. (2.6) (Fig. 2.2D) since the slope of the DBP concentration dependence in the absence of RNA provides an estimate of kcat (in ADP production s−1 DBP−1), when ATP is saturating.
Since DBP ATPase is usually slow in the absence of RNA (<0.1 s−1 DBP−1), [DBP] > [ATP]/10 may be needed to observe a measureable absorbance change above background, particularly at low [ATP]. Such conditions require the quadratic form of the Briggs-Haldane equation when fitting (Fig. 2.2C),
| (2.8) |
where Ttot is the [MgATP]total ≠ [MgATP]free.
RNA-stimulated ATPase activity is measured in the presence of saturating [ATP] over a broad [RNA] range (Fig. 2.2E). Km,ATP could vary with RNA, so an iterative process is required to estimate saturating concentrations of both RNA and MgATP, followed by precise measurements of Km,RNA with saturating MgATP and Km,ATP in the presence of saturating RNA. “Saturating” means >20× (ideally >100 ×) the Km value for either species, based on reaching >95% (ideally >99%) of the maximum value with either the hyperbolic or quadratic forms of the Briggs-Haldane equation (see above). The [RNA] dependence of the steady-state ATPase rate in the presence of saturating [ATP] (Fig. 2.2E) should be fitted to the following modified version of the quadratic Briggs-Haldane steady-state equation (Cao et al., 2011)
| (2.9) |
where kcat,R is the maximal DBP ATPase rate (s−1 DBP−1) at saturating [RNA], Rtot is the [RNA]total, Km,RNA is the apparent Michaelis constant for RNA stimulation of the DBP ATPase activity, k0 = kcat in the absence of RNA, and Htot is the [DBP]total.
The RNA:DBP stoichiometry during steady-state cycling can be estimated from the [RNA] dependence of the DBP ATPase rate saturation, fit with a system of implicit equations, when [DBP]total ≫ Km,RNA (Fig. 2.2F; Cao et al., 2011). An accurate Km,RNA value is best measured with [DBP] ≪ Km,RNA, whereas an accurate stoichiometry parameter, n, is best measured at [DBP] ≫ Km,RNA, while Km,RNA is held constant during the fitting of n.
5. Transient Kinetic Analysis of the DBP ATPase Cycle
Many important questions about DBP function require additional methods besides equilibrium binding and steady-state kinetic analysis. How does RNA stimulate DBP ATPase activity? What is the degree of thermodynamic coupling between RNA binding and transiently populated DBP intermediates (e.g., ATP and ADP-Pi bound)? When during the ATPase cycle does a DBP unwind dsRNA? What is the mechanism and preferred kinetic pathway for DBP utilization of ATP “fuel” used to rearrange RNA and RNP substrates? Addressing these questions requires quantitative analysis of the transient (pre-steady-state) kinetics of DBP binding to ATP and RNA, catalysis of ATP hydrolysis, rearrangement of the DBP-RNA complex, release of the hydrolysis products Pi and ADP, and release of RNA strand(s).
Transient kinetic measurements of biomolecules in solution usually require mixing techniques such as stopped-flow and quench-flow (Johnson, 1992). Measurement of pre-steady-state relaxations with observed rate constants >1 s−1 requires the ability to mix the reaction components and acquire data in a fraction of a second. Faster relaxations with observed rate constants ~100–500 s−1 require (sub)millisecond time resolution, and demand short (<2 ms) dead times. Observed rate constants in this range or faster may occur with DBPs, especially with nucleotide and RNA association reactions (Fig. 2.3; Cao et al., 2011; Henn et al., 2008).
Figure 2.3.
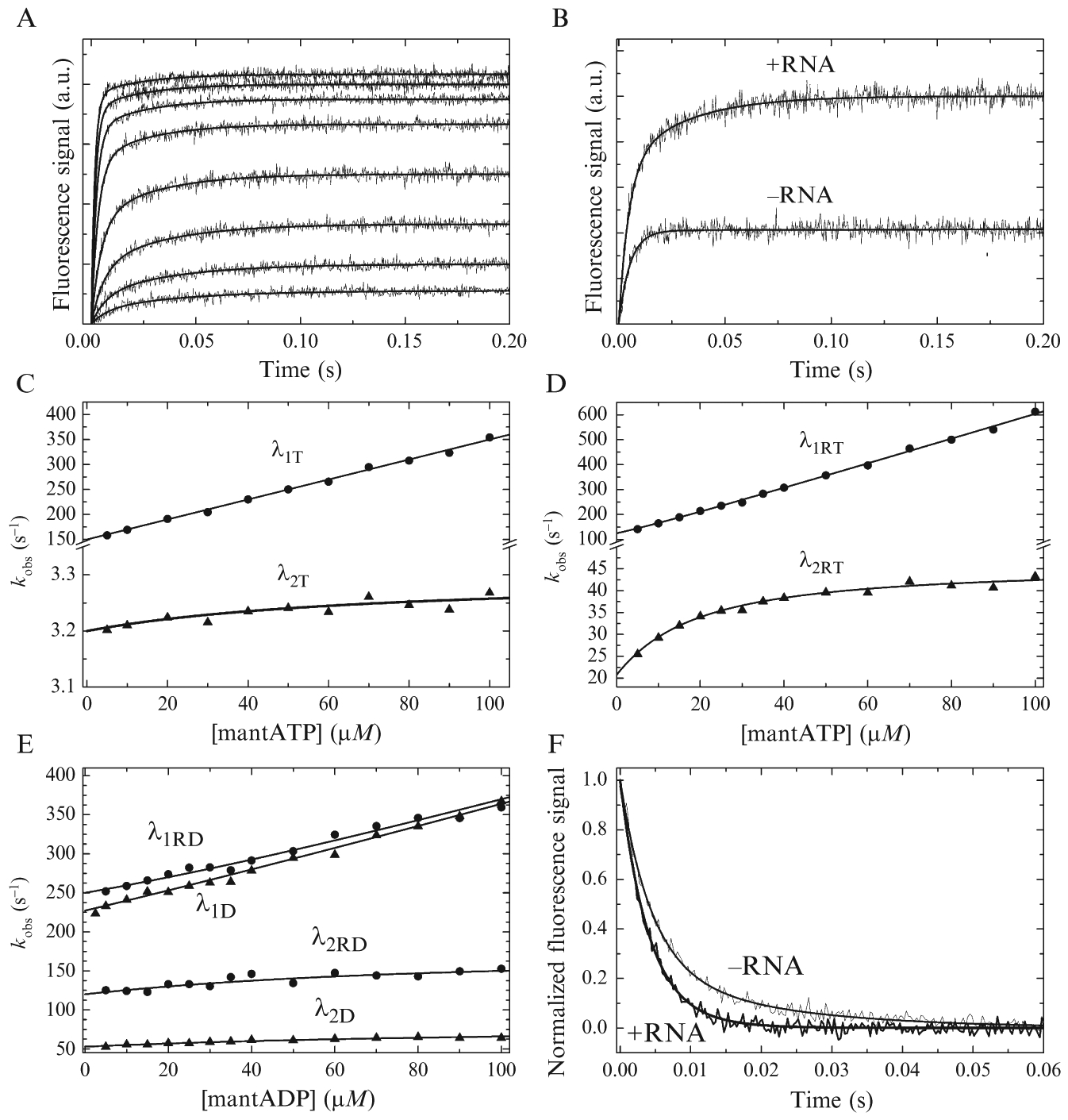
Transient kinetics of mant-nucleotide binding interactions. (A) Time courses of fluorescence change after mixing mantATP (5–100 μM, lower to upper) with DBP (500 nM) and saturating RNA (10 μM). Smooth lines are model curves with observed rate constants plotted in (D). (B) Comparison of fluorescence time courses after mixing DBP ± saturating RNA with 50 μM mantATP. (C, D) Concentrationdependence of the fast and slow relaxations from (A) and (B) of mantATP binding to DBP in the absence (C) and presence (D) of saturating RNA. Solid lines are model curves generated with Eq. (2.11). (E) Representative mantADP data. The solid lines are model curves generated with Eq. (2.14) (F) Normalized fluorescence transients of mantADP (60 μM) release from pre-equilibrated DBP (1 μM) or DBP with saturating RNA (40 μM) upon mixing with excess ADP (10 mM). The solid lines are model curves showing the sum of two exponentials with rate constants according to Eq. (2.15). All data are simulated with introduced Gaussian noise.
5.1. RNA saturation in transient kinetics experiments
The suite of transient kinetics experiments described in this review should be performed with and without saturating RNA substrate. For experiments conducted with ATP (labeled and unlabeled), a good estimate for RNA saturation is >20 × Km,RNA measured using the steady-state ATPase method or >20 × KR measured using equilibrium DBP-RNA binding, whichever is greater. For experiments conducted with added ADP (labeled or unlabeled), a good estimate for RNA saturation is >20 × KDR,overall measured with equilibrium binding in the presence of saturating [ADP], or >20 × KR, whichever is greater. These conditions ensure that nucleotide binding/dissociation and other ATPase cycle transitions measured in the presence of RNA arise only from the DBP-RNA complex.
5.2. Fluorescent-labeled ATP and ADP: Reporting on nucleotide binding/dissociation, hydrolysis, isomerization, and product release
Fluorescent-labeled nucleotide analogs allow measurement of nucleotide binding, dissociation, and often other ATPase cycle transitions. ATP and ADP labeled with methylanthraniloyl (mant) labels covalently attached to either the 2′ or 3′ hydroxyl of the nucleotide ribose ring have proven to be useful analogs that behave similarly to unlabeled parent nucleotides, displaying small (less than twofold) differences in some kinetic transitions (Cao et al., 2011; Henn and De La Cruz, 2005; Henn et al., 2008; Talavera and De La Cruz, 2005). The photophysical characteristics of the mant moiety allow for relatively strong FRET between mant and nearby tryptophan and/or tyrosine residues within the protein. Using tyrosine/tryptophan excitation (~278 to ~295 nm), FRET signal is observed through a 400 nm long-pass filter to selectively detect mant-nucleotide. Other labeled nucleotides can provide useful fluorescent probes for helicase/motor protein investigations (Jezewska et al., 2005; Lucius et al., 2006).
Method
Excellent FRET signals have been observed using final [DBP] of 500 nM–2 μM. Reactions must achieve pseudo-first-order conditions for the expressions presented to be valid (Gutfreund, 1995; Johnson, 1992). As a general rule, maintain [nucleotide] ≥10 × [DBP].
mantATP/ADP association experiments
Prepare the stopped-flow for fluorescence measurements, including the desired excitation wavelength, emission filter, PMT voltage, etc.
Wash both sets of drive syringes and flow lines and the observation cell with several milliliters of RNAse-free ddH2O followed by 1× buffer. Empty the drive syringes to prepare for sample loading.
Starting with the lowest [mantATP], load one drive syringe at 2× final concentration. Load the other drive syringe with DBP alone at 2× final concentration. Both syringes should be loaded with enough volume, typically 500–1000 μL total, to “prime” the flow lines when applicable, and acquire several transients (“shots”).
Acquire multiple (3+) replicate shots at each [mantATP]. Time courses can be averaged for subsequent fitting and analysis.
Wash the drive syringe and flow line containing mantATP as above. Load with the lowest [mantADP] and proceed with steps 3 and 4 above using mantADP.
Wash both drive syringes and flow lines as above.
Repeat steps 3–5 except using DBP with saturating RNA substrate and/ or other regulatory molecules.
mantADP dissociation
Prepare DBP and DBP-RNA complex samples at the concentrations used in the association experiments above, with 10–50 μM mantADP, or the smallest [mantADP] that gave a strong FRET signal change in the association experiment.
Prepare a stock of 10–50 mM unlabeled MgADP (1000× the [mantADP] above) in 1× buffer in enough volume for several repeated measurements with DBP alone and DBP-RNA.
Using the stopped-flow prepared as above, load the equilibrated mantADP-DBP sample in one drive syringe and the excess unlabeled ADP sample in the other.
Record several replicate shots. The FRET signal is expected to decrease (Fig. 2.3F) due to irreversible mantADP release in the presence of excess unlabeled ADP competitor.
Analysis
FRET data from mantATP-DBP interactions (±RNA) have provided information about ATP binding/dissociation (k+T, k−T, k+RT, k−RT), as well as fundamental rate constants associated with ATP hydrolysis (k+H, k−H, k+RH, k−RH) and phosphate (Pi) release (, ; Scheme 2.1; Cao et al., 2011; Henn et al., 2008). Time courses of changes in FRET should be fit to a sum of exponentials according to
| (2.10) |
where t is time (in s), F is the fluorescence signal as a function of time, C is an arbitrary signal offset at t = 0, Ai is the amplitude of the ith exponential component, ki,obs is the observed rate constant (in s−1) of the ith exponential component, and n is the number of exponential components required to remove systematic trends in the best-fit residuals (typically n = 1–4). Small amplitude exponential phases are often observed using mant nucleotides; however, their ki,obs do not show concentration dependence and/or are too slow (<kcat) to be part of the ATPase cycle (Cao et al., 2011; Henn et al., 2008). Such phases could reflect isomerization of the mant moiety.
In cases where mantATP FRET time courses follow a double exponential (or two exponentials >kcat), the fast phase ki,obs is λ1T (or λ1RT on RNA), the slow phase ki,obs is λ2T (or λ2RT), and the [mantATP]-dependence of the time courses (Fig. 2.3C and D) should be fitted to the following expression (Cao et al., 2011)
| (2.11) |
with
| (2.12) |
and
| (2.13) |
where λ2RT,∞ is the maximum value of λ2RT at (infinite) saturating [mantATP], λ2RT,0 is approximately equal to the value of λ2RT at zero [mantATP], [T] is the total [mantATP], and the individual rate constants are defined in Scheme 2.1 (Henn et al., 2008). The same expressions apply in the absence of RNA.
The global fit for the [mantATP] dependence has four free parameters, k+RT, k−RT, λ2RT,∞, and λ2RT,0 (k+T, k−T, λ2T,∞, and λ2T,0 are fit independently for DBP alone) and Eq. (2.11) should be solved globally and simultaneously, using the two expressions (add the square root term for λ1RT, subtract it for λ2RT) and the [mantATP] dependence of both relaxations (Fig. 2.3C and D; Cao et al., 2011). The best-fit values for λ2RT,∞ and λ2RT,0 (or λ2T,∞ and λ2T,0) are used in conjunction with the Pc-value from 18O-exchange measurements to solve for k+RH, k−RH, and (or k+H, k−H, and ) (Section 9).
As noted in Henn et al. (2008), Eqs. (2.11)–(2.13) are only valid under the following conditions:
substrate binding and dissociation are more rapid than hydrolysis (k+RT[T]+kRT k+RH),
substrate binding is more rapid than substrate resynthesis (k+RT[T]>k−RH), and
substrate dissociation is more rapid than product release .
Biphasic time courses of mantADP association contain information about ADP binding/dissociation (k+D1, k−D1, k+RD1, k−RD1) and ADP-bound state isomerization (k+D2, k−D2, k+RD2, k−RD2; Scheme 2.1). The time courses are fitted to a sum of exponentials as above, but the concentration-dependence of the fast and slow relaxations, λ1D (or λ1RD on RNA) and λ2D (or λ2RD on RNA) are globally/simultaneously fitted with a different function
| (2.14) |
where [D] is the total [mantADP] and the fundamental rate constants are defined in Scheme 2.1. The same expressions (with different subscripts) apply for DBP-RNA. The global fitting in each case (DBP alone and DBP-RNA) involves four free parameters, k+1D, k−1D, k+2D, k−2D or k+1RD, k−1RD, k+2RD, k−2RD.
In cases where time courses follow single exponentials, kobs could vary linearly or hyperbolically with [mant nucleotide]. If linear, the association rate constant is obtained from the slope and dissociation rate constant from the intercept. If hyperbolic, binding occurs following (minimally) a two-step binding mechanism (Robblee et al., 2005).
The irreversible mantADP dissociation experiment (Fig. 2.3F) provides additional data to support or refute the occurrence of a DBP-ADP (or DBP-ADP-RNA) isomerization. Time courses of mantADP dissociation should be fitted to a sum of exponentials. The expectation is that DBP-ADP (or DBP-ADP-RNA) isomerization will yield biphasic dissociation time courses. The relaxation rate constants for these two observed exponential processes (λdiss1, λdiss2) should be predicted by the fundamental rate constants of the underlying ADP dissociation and isomerization steps (Scheme 2.1) from
| (2.15) |
The same expressions are used (with different subscripts) for DBP-RNA. Note that Eq. (2.15) is a special case of Eq. (2.14) when [mantADP] = 0 for the association step, because no rebinding occurs. If dissociation time courses follow single exponentials, kobs directly yields the ADP dissociation rate constant, because λdiss1 = k−1D.
5.3. Measuring the ATP hydrolysis and Pi release rates
5.3.1. ATP hydrolysis measured using quench-flow
It is possible to measure the ATP hydrolysis/resynthesis rate constants (k+H, k−H, or k+RH, k−RH) of some ATPase enzymes using radiolabeled ATP and quench-flow methods (Johnson, 1995). This approach quantifies the total amount of ATP hydrolyzed as a function of time, including DBP-bound ADP-Pi, with millisecond resolution (Johnson, 1995). When hydrolysis (or conformational isomerization that precedes rapid hydrolysis) is either too fast to measure (completed within the mixing/measurement dead time) or (partially) rate limiting, time courses will be linear, reflecting steady-state turnover (Henn et al., 2008). However, if a step following hydrolysis such as Pi release, ADP release, or a conformational isomerization limits ATP turnover, then it may be possible to observe a pre-steady-state hydrolysis “burst” with amplitude that is proportional to [DBP]. In the presence of saturating [ATP], both amplitude and observed exponential rate constant contain information about k+H, k−H, and possibly (or the DBP-RNA rate constants) (Johnson, 1986, 1992). DBPs characterized to date at this level of detail do not display a detectable “burst” because hydrolysis is partially rate limiting (Henn et al., 2008). The values of k+H, k−H, k+RH, k−RH, , and were determined by 18O-exchange and mantATP/Pi-release (Section 9; Cao et al., 2011).
5.3.2. Pi release measured using stopped-flow
The Pi release experiment utilizing the A197C mutant of E. coli phosphate binding protein (PBP) labeled with the fluorescent dye N-[2-(1-maleimidyl)ethyl]-7-(diethylamino)coumarin-3-carboxamide (MDCC) has been extensively described (Brune et al., 1994; Webb, 2003). We typically use 5–10 μM MDCC-PBP and 500 nM–1 μM DBP when measuring the [MgATP] dependence of the Pi release time courses. Note that the [MDCC-PBP] should be >4 μM to saturate the Kd for Pi binding (~200 nM in KMg75) (Henn et al., 2008) and 5–10× the [DBP] in order to observe both pre-steady-state behavior and several turnovers of the steady-state ATPase prior to Pi saturation of MDCC-PBP (Cao et al., 2011; Henn et al., 2008). It is crucial to remove contaminating Pi from the instrument, flow-lines, and drive syringes by overnight incubation with the “Pi mop” (purine nucleoside phosphorylase with excess 7-methylguanosine) (Webb, 2003). We also include the “Pi mop” in the reaction components, which is kept at a low enough concentration that it does not interfere with Pi binding to MDCC-PBP on the 10+ s timescale (Webb, 2003). The “Pi mop” is incubated with the reaction components for at least 30 min on ice prior to mixing in the stopped-flow to reduce background Pi.
5.3.3. Pi release data fitting and analysis
Time courses of Pi release from E. coli DbpA-RNA (Henn et al., 2008) and S. cerevisiae Mss116-RNA (Cao et al., 2011) display pre-steady-state lag phases (see Fig. 2.4). The lag phases are indicative of at least two consecutive ATPase cycle transitions (Scheme 2.1) with comparable rate constants (Johnson, 2003; Robblee et al., 2005). These lag phases persist in the presence of saturating ATP for DbpA and Mss116, where the calculated ATP binding rates with bound RNA are >2000 s−1 (Cao et al., 2011; Henn et al., 2008). Given that ADP isomerization and release do not limit the observed 2–4 s−1 DBP−1 kcat values in the presence of RNA (Cao et al., 2011; Henn et al., 2008), the two or more steps with similar rate constants producing the observed lags must include both ATP hydrolysis (or an isomerization that precedes rapid hydrolysis) and Pi release (Scheme 2.1). This is apparent in the simulated data in Fig. 2.4, where and k+RH are 20 and 25 s−1, respectively.
Figure 2.4.
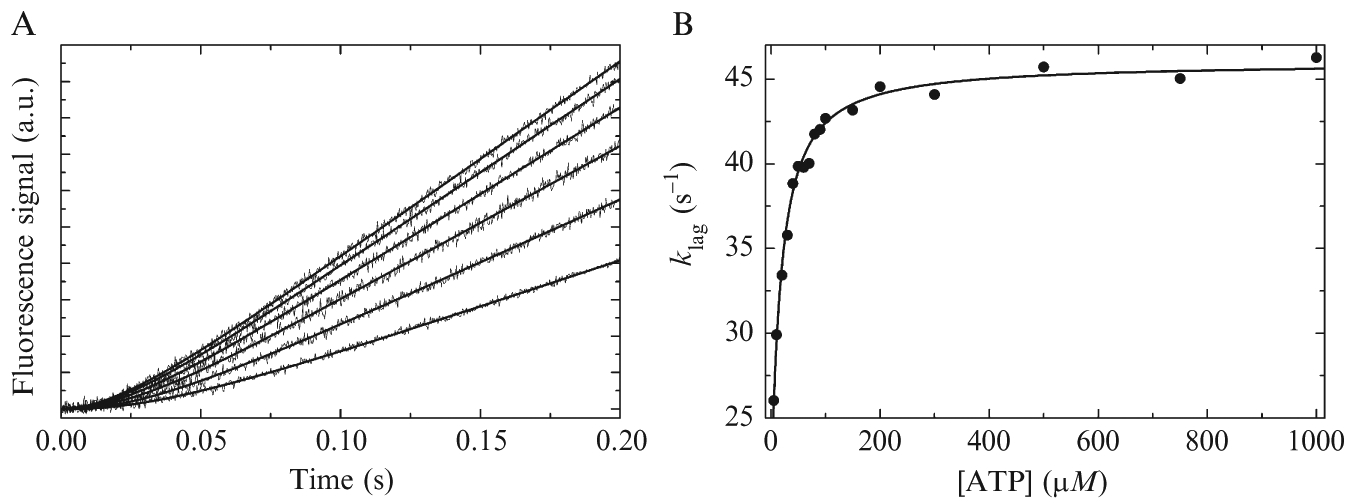
Transient phosphate (Pi) release from DBP-RNA assayed with MDCClabeled phosphate binding protein (PBP). (A) Time courses of fluorescence change after mixing RNA-saturated DBP (500 nM) with a range of ATP (10 μM–1 mM, lower to upper). Smooth lines are model curves generated with Eq. (2.16). (B) [ATP]-dependence of the observed lag phase rate constant from (A). The smooth line is the model curve generated with Eq. (2.11) where λ2RT = λlag. All data are simulated with introduced Gaussian noise.
Pi release time courses that exhibit pre-steady-state lag phases (Fig. 2.4A) can be fit with a function that combines a negative amplitude exponential with a straight line arising from the steady-state ATPase (Cao et al., 2011; Henn et al., 2008):
| (2.16) |
where [Pi] is the phosphate concentration (as a function of time), [E]tot is the total [DBP], β is the steady-state ATPase rate (ATP hydrolyzed s−1 DBP−1 at a given [ATP], ±saturating RNA), and λlag is the observed rate constant of the pre-steady-state lag phase fit with a single exponential. In practice, the product b[E]tot can substituted with a constant (C) that includes the MDCC-PBP molar incremental fluorescence increase upon binding Pi to fit the raw fluorescence time courses. This relationship holds as long as [Pi] <[MDCC-PBP]active, where “active” refers to labeled PBP with a strong fluorescence increase upon binding Pi (Brune et al., 1998). Additional caveats concerning conditions where more than one exponential may be required to fit the lag, where a lag might not occur, or where a “burst” could be observed with this assay are discussed in Henn et al. (2008).
Based on the derivation from Henn et al. (2008), the [ATP] dependence of λlag is expected to match λ2RT from the mantATP experiments (Eq. 2.11). Therefore, the best-fit values of λlag,0 and λlag,∞ (Fig. 2.4B) should be comparable to λ2RT,0 and λ2RT,1. Note that much higher [ATP] can be used in fitting λlag,1 versus the highest [mantATP] used with λ2RT,1, which provides more confidence in the value from the Pi release assay (compare Fig. 2.3D with Fig. 2.4B). However in the absence of RNA, or any case with a very slow steady-state ATPase activity, it may be very difficult to reliably fit the lag with an exponential due to the lack of observed signal change on the 0.01–1 s timescale. In contrast, the fluorescence signal in the mantATP assay does not suffer from this limitation, and therefore λ2T,0 and λ2T,∞ may provide more reliable data in the absence of RNA. The [ATP] dependence of C (steadystate fluorescence increase) can be fit with either Eq. (2.7) or (2.8) to estimate Km,ATP in the presence and absence of saturating RNA and corroborate the values measured using the enzyme-coupled assay (Cao et al., 2011).
6. ATP Hydrolysis Reversibility Measured by Isotope Exchange
We refer the reader to the oxygen isotope exchange methodology chapter in this volume (Hackney, 2012). Briefly, we measure 18O isotope incorporation into phosphate ions free in solution that originated in ATP molecules mixed with the DBP (± saturating RNA) under steady-state cycling conditions in the presence of ~5 mM PEP and the PK enzyme (see Section 4) to regenerate ATP. The reaction proceeds until a large fraction (~80%) of the PEP is consumed, generating ~4 mM free phosphate in 100–200 μL reaction volume. When ATP is hydrolyzed, an oxygen atom from a water molecule is incorporated into the phosphate product. The distribution of 18O incorporated into Pi from 18O—H2O (Fig. 2.5) depends on the percentage of 18O—H2O and the probability of ATP resynthesis from bound ADP and Pi (k−H, or k−RH) relative to Pi release ( or ), indicated by the partition coefficient, Pc, calculated as (Henn et al., 2008),
| (2.17) |
Figure 2.5.

Distributions of 18O incorporation into phosphate (Pi) during steady-state DBP ATPase cycling in 18O-water. Up to four 18O/Pi can be incorporated with multiple hydrolysis and resynthesis events per ATP turnover. The observed distribution depends on both the percentage of 18O-water enrichment and the partition coefficient (Pc value) associated with the hydrolysis reversal (k−H or k−RH) and Pi release ( or ) rate constants, see Eq. (2.17).
where the fundamental rate constants are defined above and the same expression is used (with different subscripts) for DBP-RNA. The Pc value is calculated from the observed distribution of 18O incorporation into free phosphate, detected by mass spectrometry given the percentage of 18O water (Hackney, 2012). The best-fit Pc value and Eq. (2.17) are used in conjunction with either the mantATP data (λ2T,0 and λ2T,∞) or the Pi release data (λlag,0 and λlag,∞) to calculate k+H, k−H, and (see Section 9).
7. RNA Unwinding Assays and ATPase Coupling
A variety of RNA unwinding assays have been reported using DBPs (Chen et al., 2008; Diges and Uhlenbeck, 2001; Henn et al., 2010; Iost et al., 1999; Liu et al., 2008; Yang and Jankowsky, 2006). Most have relied on a discontinuous assay that requires separation and detection of unwinding products using gel electrophoresis and autoradiography, and often required a large excess of [DBP] to observe strand displacement. However, stopped-flow fluorescence methods using dye-labeled RNA substrates (Fig. 2.1) have shown great utility in measuring real-time dsRNA unwinding (Cao et al., 2011; Henn et al., 2010) and have the potential for even greater insights as has been demonstrated with DNA helicases (Lohman et al., 2008). The approach is discussed in detail in Chapter 1.
In general, the observed RNA unwinding amplitude depends on the [DBP]. However, an effort must be made to distinguish between mechanisms where one DBP per RNA molecule is required to observe unwinding versus multiple DBP molecules. Furthermore, an estimate of the number of ATP molecules required per unwinding event is desired, and requires comparison between the observed unwinding rate constant and the DBP ATPase kcat in the presence of saturating RNA and MgATP (Cao et al., 2011; Henn et al., 2010). One good approach is to observe unwinding using fast-mixing techniques (stopped-flow or quench-flow) under conditions where the DBP-RNA complex is both (1) formed at a concentration >20× Km,RNA and/or KR, whichever is greater (to ensure >95% DBP-RNA binding during ATPase cycling) and (2) formed at ~1:1 stoichiometry. With these starting conditions, the observed unwinding rate and amplitude should be compared between no nucleotide cofactor and in the presence of MgATP, MgADP, or ATP analogs, and as a function of [nucleotide]. It may be necessary to increase the DBP:RNA stoichiometry for unwinding, indicating multiple-bound DBP molecules per RNA unwinding event. Because DBPs are thought to be nonprocessive (Linder and Jankowsky, 2011; Pyle, 2008), observed dsRNA unwinding that requires a stoichiometry >1DBP:1RNA may be a consequence of RNA substrate length, including both dsRNA base pairs and any ssRNA overhang. Conclusions drawn from RNA unwinding assays must consider all of the above factors.
Determining if dsRNA and ssRNA substrates differentially affect the ATP utilization mechanism, and the degree to which substrate affects the DBP-RNA affinity at each DBP-bound nucleotide intermediate, are important aspects of quantitative DBP studies. The inclusion of RNA strand displacement adds another level of complexity to the complete reaction scheme (Henn et al., 2010). As a consequence, the equilibrium binding, steady-state ATPase, and transient kinetic analyses should be repeated with both dsRNA (with hairpins, eliminating strand dissociation) and ssRNA (unwinding product) substrates. The unwinding substrate should resemble the dsRNA prior to strand displacement.
8. Kinetic Simulations
Numerical integration of the differential equations describing the changes in [reactants], [intermediates], and [products] given a kinetic scheme (e.g., Scheme 2.1) have been employed to study complex enzyme reaction mechanisms for ~30 years (Barshop et al., 1983). In cases with many free parameters (e.g., Scheme 2.1), multiple different experiments are required to obtain one or a few of the reaction constants, thereby allowing for their constraint during optimization of the remaining parameters. Kinetic simulations provide an excellent tool for estimation of some of the hard-to-measure parameters, including feasible upper/lower bounds (Henn et al., 2010).
Given a kinetic scheme (e.g., Scheme 2.1), some simulation programs have the capability to fit the full time courses of one or more experiments and extract best-fit parameter estimates for one or more parameters while holding others constant (Johnson et al., 2009b; Zimmerle and Frieden, 1989). We regularly use two program packages, KinTek Global Kinetic Explorer (Johnson, 2009; Johnson et al., 2009a,b) and Tenua, which is freely downloadable (provided by Dr. D. Wachsstock, available at http://bililite.com/tenua/).
9. Putting It All Together: Quantitative Analysis of the DBP ATPase Cycle
The combination of equilibrium, steady-state, and transient kinetics experiments described above require additional analysis to assign values or ranges to the parameters in Scheme 2.1. As noted above, the Pc values (saturating RNA) determined by 18O-isotope exchange can be combined with either λ2T,0 and λ2T,∞ from mantATP experiments or λlag,0 and λlag,∞ from Pi release experiments (saturating RNA) using Eqs. (2.12), (2.13), and (2.17). In both cases, the best-fit value of k−T (and k−RT) from mantATP experiments must be known. The values of the three fundamental rate constants, k+H, k−H, and (or k+RH, k−RH, and ) can be obtained by solving these three equations with three unknowns using Mathematica (Wolfram Research).
With the entire set of fundamental rate constants assigned, calculated values for the steady-state kinetic constants can be compared with those measured experimentally. Using the derivation of Km,RNA (Cao et al., 2011), an additional approximation is required. For the example DBP used in this review, two ADP-bound DBP (and DBP-RNA) states are observed (Scheme 2.1; Fig. 2.3E and F). While the overall DBP-RNA binding affinity in the presence of saturating ADP, KDR,overall, can be measured using equilibrium binding, the overall ADP release rate, k−D,overall (or k−RD,overall) is estimated as follows: During vectorial cycling through the ATPase kinetic pathways on and off of the RNA (Scheme 2.1), the overall rate of ADP release is limited by isomerization of the ADP-bound DBP state, k−2D (or k−2RD). Therefore, k−D,overall ≈ k−2D.
The following expressions account for the steady-state kinetic constants in terms of fundamental ATPase cycle rate constants (Henn et al., 2008):
| (2.18) |
and
| (2.19) |
where the same expressions with different subscripts are used for the RNA-stimulated values of kcat and Km,ATP. Equation (2.19) for Km,ATP holds in the absence of significant [ADP], which is the case using the enzyme-coupled assay or very early in the steady-state part of the Pi release time courses. An additional expression for Km,ATP that varies with [ADP] and discussion of caveats are presented in (Henn et al., 2008). Similarly, the following expression yields the Km,RNA (Cao et al., 2011):
| (2.20) |
These expressions for the steady-state ATPase kinetic parameters in the presence and absence of RNA bring together the full combination of equilibrium and kinetic experiments presented in this review. Their derivations are based on the minimal ATPase cycle schemes, given the available DBP data, such as the existence of two ADP-bound DBP states (Cao et al., 2011; Henn et al., 2008). Qualitative agreement between the calculated and measured steady-state parameters provides additional confidence in measurements of the underlying fundamental rate and equilibrium constants and the veracity of the minimal ATPase cycle scheme. There are several potential explanations if qualitative agreement is not observed. Chief among these are changes in the DBP oligomeric state during ATPase cycling, ATPase cycles that include additional states, additional cofactors or regulatory molecules whose concentrations are not accounted for, and ATPase cycle steps that do not conform to the conditions and caveats stated in the derivations presented in Henn et al. (2008) and Cao et al. (2011).
ACKNOWLEDGMENTS
We thank Dr. Wenxiang Cao for helpful discussions on combining experiments and help with the simulated data used in this review, and Dr. Arnon Henn for valuable discussions regarding experimental design and execution. The authors thank the National Science Foundation for supporting DEAD-box protein related research activities under NSFCAREER Award MCB-0546353 (awarded to E. M. D. L. C.) and the National Institutes of Health for supporting research activities investigating molecular motor proteins of the cytoskeleton under award GM097348. E. M. D. L. C. is an American Heart Association Established Investigator (0940075N) and Hellman Family Fellow.
REFERENCES
- Abdelhaleem M (2004). Do human RNA helicases have a role in cancer? Biochim. Biophys. Acta 1704, 37–46. [DOI] [PubMed] [Google Scholar]
- Akao Y (2009). A role of DEAD-Box RNA helicase rck/p54 in cancer cells. Curr. Drug Ther 4, 29–37. [Google Scholar]
- Antao VP, Lai SY, and Tinoco I (1991). A thermodynamic study of unusually stable RNA and DNA hairpins. Nucleic Acids Res 19, 5901–5905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attri AK, and Minton AP (2005). Composition gradient static light scattering: A new technique for rapid detection and quantitative characterization of reversible macromo- lecular hetero-associations in solution. Anal. Biochem 346, 132–138. [DOI] [PubMed] [Google Scholar]
- Barshop BA, Wrenn RF, and Frieden C (1983). Analysis of numerical methods for computer simulation of kinetic processes: Development of KINSIM—A flexible, portable system. Anal. Biochem 130, 134–145. [DOI] [PubMed] [Google Scholar]
- Bizebard T, Ferlenghi I, Iost I, and Dreyfus M (2004). Studies on three E. coli DEAD- box helicases point to an unwinding mechanism different from that of model DNA helicases. Biochemistry 43, 7857–7866. [DOI] [PubMed] [Google Scholar]
- Brune M, Hunter JL, Corrie JET, and Webb MR (1994). Direct, real-time measurement of rapid inorganic phosphate release using a novel fluorescent probe and its application to actomyosin subfragment 1 ATPase. Biochemistry 33, 8262–8271. [DOI] [PubMed] [Google Scholar]
- Brune M, Hunter JL, Howell SA, Martin SR, Hazlett TL, Corrie JET, and Webb MR (1998). Mechanism of inorganic phosphate interaction with phosphate binding protein from Escherichia coli. Biochemistry 37, 10370–10380. [DOI] [PubMed] [Google Scholar]
- Bujalowski W, andJezewska MJ (2011). Macromolecular competition titration method: Accessing thermodynamics of the unmodified macromolecule-ligand interactions through spectroscopic titrations of fluorescent analogs. Methods Enzymol 488, 17–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao W, Coman MM, Ding S, Henn A, Middleton ER, Bradley MJ, Rhoades E, Hackney DD, Pyle AM, and De La Cruz EM (2011). Mechanism of Mss116 ATPase reveals functional diversity of DEAD-box proteins. J. Mol. Biol 409, 399–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao CH, Chen CM, Cheng PL, Shih JW, Tsou AP, and Lee YH (2006). DDX3, a DEAD box RNA helicase with tumor growth-suppressive property and transcriptional regulation activity of the p21waf1/cip1 promoter, is a candidate tumor suppressor. Cancer Res 66, 6579–6588. [DOI] [PubMed] [Google Scholar]
- Charter NW, Kauffman L, Singh R, andEglen RM (2006). A generic, homogenous method for measuring kinase and inhibitor activity via adenosine 5′-diphosphate accumulation. J. Biomol. Screen 11, 390–399. [DOI] [PubMed] [Google Scholar]
- Chen Y, Potratz JP, Tijerina P, Del Campo M, Lambowitz AM, and Russell R (2008). DEAD-box proteins can completely separate an RNA duplex using a single ATP. Proc. Natl. Acad. Sci. U. S. A 105, 20203–20208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins R, Karlberg T, Lehtiö L, Schütz P, van den Berg S, Dahlgren LG, Hammarstrom M, Weigelt J, and Schüler H (2009). The DEXD/H-box RNA helicase DDX19 is regulated by an alpha-helical switch. J. Biol. Chem 284, 10296–10300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordin O, Banroques J, Tanner NK, and Linder P (2006). The DEAD-box protein family of RNA helicases. Gene 367, 17–37. [DOI] [PubMed] [Google Scholar]
- Cornish-Bowden A (2004). Fundamentals of Enzyme Kinetics 3rd edn Portland Press, London. [Google Scholar]
- De La Cruz EM, and Ostap ME (2009). Kinetic and equilibrium analysis of the myosin ATPase. Methods Enzymol 455, 157–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De La Cruz EM, and Pollard TD (1994). Transient kinetic analysis of rhodamine phalloidin binding to actin filaments. Biochemistry 33, 14387–14392. [DOI] [PubMed] [Google Scholar]
- De La Cruz EM, and Pollard TD (1995). Nucleotide-free actin: Stabilization by sucrose and nucleotide binding kinetics. Biochemistry 34, 5452–5461. [DOI] [PubMed] [Google Scholar]
- De La Cruz E, and Pollard TD (1996). Kinetics and thermodynamics of phalloidin binding to actin filaments from three divergent species. Biochemistry 35, 14054. [DOI] [PubMed] [Google Scholar]
- De La Cruz EM, Sweeney HL, and Ostap EM (2000). ADP inhibition of myosin V ATPase activity. Biophys.J 79, 1524–1529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Campo M, and Lambowitz AM (2009). Structure of the Yeast DEAD box protein Mss116p reveals two wedges that crimp RNA. Mol. Cell 35, 598–609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diges CM, and Uhlenbeck OC (2001). Escherichia coli DbpA is an RNA helicase that requires hairpin 92 of23S rRNA. EMBO J 20, 5503–5512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Y, Chan CY, and Lawrence CE (2004). Sfold web server for statistical folding and rational design of nucleic acids. Nucleic Acids Res 32, W135–W141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doma MK, and Parker R (2007). RNA quality control in eukaryotes. Cell 131, 660–668. [DOI] [PubMed] [Google Scholar]
- Furch M, Geeves MA, and Manstein DJ (1998). Modulation of actin affinity and actomyosin adenosine triphosphatase by charge changes in the myosin motor domain. Biochemistry 37, 6317–6326. [DOI] [PubMed] [Google Scholar]
- Godbout R, Li L, Liu RZ, and Roy K (2007). Role of DEAD box 1 in retinoblastoma and neuroblastoma. Future Oncol 3, 575–587. [DOI] [PubMed] [Google Scholar]
- Grimsley GR, and Pace CN (2003). Spectrophotometric determination of protein concentration. Curr. Protoc. Protein Sci 33, 3.1.1–3.1.9. [DOI] [PubMed] [Google Scholar]
- Gutfreund H (1995). Kinetics for the Life Sciences: Receptors, Transmitters and Catalysts 1st edn Cambridge University Press, Cambridge. [Google Scholar]
- Hackney DD (2012). Oxygen isotopic exchange probes of ATP hydrolysis by RNA helicases. Methods Enzymol 511, 65–73. [DOI] [PubMed] [Google Scholar]
- Henn A, and De La Cruz EM (2005). Vertebrate myosin Vllb is a high duty ratio motor adapted for generating and maintaining tension. J. Biol. Chem 280, 39665–39676. [DOI] [PubMed] [Google Scholar]
- Henn A, Medalia O, Shi SP, Steinberg M, Franceschi F, and Sagi I (2001). Visualization of unwinding activity of duplex RNA by DbpA, a DEAD box helicase, at single-molecule resolution by atomic force microscopy. Proc. Natl. Acad. Sci. U. S. A 98, 5007–5012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henn A, Cao W, Hackney DD, and De La Cruz EM (2008). The ATPase cycle mechanism of the DEAD-box rRNA helicase, DbpA. J. Mol. Biol 377, 193–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henn A, Cao W, Licciardello N, Heitkamp SE, Hackney DD, and De La Cruz EM (2010). Pathway of ATP utilization and duplex rRNA unwinding by the DEAD-box helicase, DbpA. Proc. Natl. Acad. Sci. U. S. A 107, 4046–4050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henn A, Bradley MJ, and De La Cruz EM (2012). ATP utilization and RNA conformational rearrangement by DEAD-box proteins. Annu. Rev. Biophys 41, 11.1–11.21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herschlag D (1995). RNA chaperones and the RNA folding problem. J. Biol. Chem 270, 20871–20874. [DOI] [PubMed] [Google Scholar]
- Hilbert M, Karow AR, and Klostermeier D (2009). The mechanism of ATP-dependent RNA unwinding by DEAD box proteins. Biol. Chem 390, 1237–1250. [DOI] [PubMed] [Google Scholar]
- Hiratsuka T (1983). New ribose-modified fluorescent analogs of adenine and guanine nucleotides available as subtrates for various enzymes. Biochim. Biophys. Acta 742, 496–508. [DOI] [PubMed] [Google Scholar]
- Howard J (2001). Mechanics of Motor Proteins and the Cytoskeleton Sinauer Associates, Sunderland, MA. [Google Scholar]
- lost I, Dreyfus M, and Linder P (1999). Ded1p, a DEAD-box protein required for translation initiation in Saccharomyces cerevisiae, is an RNA helicase. J. Biol. Chem 274, 17677–17683. [DOI] [PubMed] [Google Scholar]
- Jarmoskaite I, and Russell R (2011). DEAD box proteins as RNA helicases and chaperones. WIREs: RNA 2, 135–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jezewska MJ, Lucius AL, and Bujalowski W (2005). Binding of six nucleotide cofactors to the hexameric helicase RepA protein of plasmid RSF1010. 1. Direct evidence ofcooperative interactions between the nucleotide-binding sites of a hexameric helicase. Biochemistry 44, 3865–3876. [DOI] [PubMed] [Google Scholar]
- Johnson KA (1986). Rapid kinetic analysis of mechanochemical adenosinetriphosphatases. Methods Enzymol 134, 677–705. [DOI] [PubMed] [Google Scholar]
- Johnson KA (1992). Transient-state kinetic analysis of enzyme reaction pathways In “The Enzymes,” (Sigman DS, ed.), pp. 1–61. Academic Press, New York. [Google Scholar]
- Johnson KA (1995). Rapid quench kinetic analysis of polymerases, adenosinetriphosphatases, and enzyme intermediates. Methods Enzymol 249, 38–61. [DOI] [PubMed] [Google Scholar]
- Johnson KA (2003). Introduction to kinetic analysis of enzyme systems In “Kinetic Analysis of Macromolecules. A Practical Approach,” (Johnson KA, ed.), pp. 1–18. Oxford University Press, New York. [Google Scholar]
- Johnson KA (2009). Fitting enzyme kinetic data with KinTek Global Kinetic Explorer. Methods Enzymol 467, 601–626. [DOI] [PubMed] [Google Scholar]
- Johnson KA, Simpson ZB, andBlom T (2009a). FitSpace Explorer: An algorithm to evaluate multidimensional parameter space in fitting kinetic data. Anal. Biochem 387, 30–41. [DOI] [PubMed] [Google Scholar]
- Johnson KA, Simpson ZB, and Blom T (2009b). Global Kinetic Explorer: A new computer program for dynamic simulation and fitting of kinetic data. Anal. Biochem 387, 20–29. [DOI] [PubMed] [Google Scholar]
- Klostermeier D, and Rudolph MG (2009). A novel dimerization motif in the C-terminal domain ofthe Thermus thermophilus DEAD box helicase Hera confers substantial flexibility. Nucleic Acids Res 37, 421–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kossen K, Karginov FV, and Uhlenbeck OC (2002). The carboxy-terminal domain of the DExDH protein YxiN is sufficient to confer specificity for 23S rRNA. J. Mol. Biol 324, 625–636. [DOI] [PubMed] [Google Scholar]
- Lakowicz JR (2006). Principles of Fluorescence Spectroscopy 3rd edn Springer, New York. [Google Scholar]
- Le Hir H, and Andersen GR (2008). Structural insights into the exon junction complex. Curr. Opin. Struct. Biol 18, 112–119. [DOI] [PubMed] [Google Scholar]
- Lebowitz J, Lewis MS, and Schuck P (2002). Modern analytical ultracentrifugation in protein science: A tutorial review. Protein Sci 11, 2067–2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linder P, and Jankowsky E (2011). From unwinding to clamping—The DEAD box RNA helicase family. Nat. Rev. Mol. Cell Biol 12, 505–516. [DOI] [PubMed] [Google Scholar]
- Liu F, Putnam A, and Jankowsky E (2008). ATP hydrolysis is required for DEAD-box protein recycling but not for duplex unwinding. Proc. Natl. Acad. Sci. U. S. A 105, 20209–20214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohman TM, Tomko EJ, and Wu CG (2008). Non-hexameric DNA helicases and translocases: Mechanisms and regulation. Nat. Rev. Mol. Cell Biol 9, 391–401. [DOI] [PubMed] [Google Scholar]
- Lorsch JR, and Herschlag D (1998). The DEAD box protein eIF4A. 1. A minimal kinetic and thermodynamic framework reveals coupled binding of RNA and nucleotide. Biochemistry 37, 2180–2193. [DOI] [PubMed] [Google Scholar]
- Lucius AL, Jezewska MJ, and Bujalowski W (2006). The Escherichia coli PriA helicase has two nucleotide-binding sites differing dramatically in their affinities for nucleotide cofactors. 1. Intrinsic affinities, cooperativities, and base specificity of nucleotide cofactor binding. Biochemistry 45, 7202–7216. [DOI] [PubMed] [Google Scholar]
- Mallam AL, Jarmoskaite I, Tijerina P, Del Campo M, Seifert S, Guo L, Russell R, and Lambowitz AM (2011). Solution structures of DEAD-box RNA chaperones reveal conformational changes and nucleic acid tethering by a basic tail. Proc. Natl. Acad. Sci. U. S. A 108, 12254–12259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marintchev A, Edmonds KA, Marintcheva B, Hendrickson E, Oberer M, Suzuki C, Herdy B, Sonenberg N, and Wagner G (2009). Topology and regulation of the human eIF4A/4G/4H helicase complex in translation initiation. Cell 136, 447–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montpetit B, Thomsen ND, Helmke KJ, Seeliger MA, Berger JM, and Weis K (2011). A conserved mechanism of DEAD-box ATPase activation by nucleoporins and InsP6 in mRNA export. Nature 472, 238–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy RM (1997). Static and dynamic light scattering of biological macromolecules: What can we learn? Curr. Opin. Biotechnol 8, 25–30. [DOI] [PubMed] [Google Scholar]
- Pan C, and Russell R (2010). Roles of DEAD-box proteins in RNA and RNP Folding. RNA Biol 7, 667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polach KJ, and Uhlenbeck OC (2002). Cooperative binding of ATP and RNA substrates to the DEAD/H protein DbpA. Biochemistry 41, 3693–3702. [DOI] [PubMed] [Google Scholar]
- Pyle AM (2008). Translocation and unwinding mechanisms of RNA and DNA helicases. Annu. Rev. Biophys 37, 317–336. [DOI] [PubMed] [Google Scholar]
- Ramasawmy R, Cunha-Neto E, Faé KC, Müller NG, Cavalcanti VL, Drigo SA, Ianni B, Mady C, Kalil J, and Goldberg AC (2006). BAT1, aputative anti-inflammatory gene, is associated with chronic Chagas cardiomyopathy. J. Infect. Dis 193, 1394–1399. [DOI] [PubMed] [Google Scholar]
- Reuter J, and Mathews D (2010). RNAstructure: Software for RNA secondary structure prediction and analysis. BMC Bioinformatics 11, 129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robblee JP, Cao W, Henn A, Hannemann DE, and De La Cruz EM (2005). Thermodynamics ofnucleotide binding to actomyosin V and VI: A positive heat capacity change accompanies strong ADP binding. Biochemistry 44, 10238–10249. [DOI] [PubMed] [Google Scholar]
- Rogers GW Jr., Richter NJ, and Merrick WC (1999). Biochemical and kinetic characterization of the RNA helicase activity of eukaryotic initiation factor 4A. J. Biol. Chem 274, 12236–12244. [DOI] [PubMed] [Google Scholar]
- Rogers GW Jr., Richter NJ, Lima WF, and Merrick WC (2001). Modulation of the helicase activity of eIF4A by eIF4B, eIF4H, and eIF4F. J. Biol. Chem 19, 30914–30922. [DOI] [PubMed] [Google Scholar]
- Sahni A, Wang N, and Alexis JD (2010). UAP56 is an important regulator of protein synthesis and growth in cardiomyocytes. Biochem. Biophys. Res. Commun 393, 106–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroeder R, Barta A, and Semrad K (2004). Strategies for RNA folding and assembly. Nat. Rev. Mol. Cell Biol 5, 908–919. [DOI] [PubMed] [Google Scholar]
- Sengoku T, Nureki O, Nakamura A, Kobayashi S, and Yokoyama S (2006). Structural basis for RNA unwinding by the DEAD-box protein Drosophila Vasa. Cell 125, 287–300. [DOI] [PubMed] [Google Scholar]
- Seol Y, Skinner GM, and Visscher K (2004). Elastic properties of a single-stranded charged homopolymeric ribonucleotide. Phys. Rev. Lett 93, 118102. [DOI] [PubMed] [Google Scholar]
- Seol Y, Skinner GM, Visscher K, Buhot A, and Halperin A (2007). Stretching of homopolymeric RNA reveals single-stranded helices and base-stacking. Phys. Rev. Lett 98, 158103. [DOI] [PubMed] [Google Scholar]
- Talavera MA, and De La Cruz EM (2005). Equilibrium and kinetic analysis of nucleotide binding to the DEAD-box RNA helicase DbpA. Biochemistry 44, 959–970. [DOI] [PubMed] [Google Scholar]
- Talavera MA, Matthews EE, Eliason WK, Sagi I, Wang J, Henn A, and De La Cruz EM (2006). Hydrodynamic characterization of the DEAD-box RNA helicase DbpA. J. Mol. Biol 355, 697–707. [DOI] [PubMed] [Google Scholar]
- Thoma N, and Goody RS (2003). What to do if there is no signal: Using competition experiments to determine binding parameters In “Kinetic Analysis of Macromolecules. A Practical Approach,” (Johnson KA, ed.), pp. 153–170. Oxford University Press, New York. [Google Scholar]
- Tsu CA, and Uhlenbeck OC (1998). Kinetic analysis of the RNA-dependent adenosinetriphosphatase activity of DbpA, an Escherichia coli DEAD protein specific for 23S ribosomal RNA. Biochemistry 37, 16989–16996. [DOI] [PubMed] [Google Scholar]
- Tsu CA, Kossen K, and Uhlenbeck OC (2001). The Escherichia coli DEAD protein DbpA recognizes a small RNA hairpin in 23S rRNA. RNA 7, 702–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Hu Y, Overgaard MT, Karginov FV, Uhlenbeck OC, andMcKay DB (2006). The domain of the Bacillus subtilis DEAD-box helicase YxiN that is responsible for specific binding of 23S rRNA has an RNA recognition motif fold. RNA 12, 959–967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webb MR (2003). A fluorescent sensor to assay inorganic phosphate In “Kinetic Analysis ofMacromolecules. A Practical Approach,” (Johnson KA, ed.), pp. 131–152. Oxford University Press, New York. [Google Scholar]
- Weirich CS, Erzberger JP, Flick JS, Berger JM, Thorner J, and Weis K (2006). Activation of the DExD/H-box protein Dbp5 by the nuclear-pore protein Gle1 and its coactivator InsP6 is required for mRNA export. Nat. Cell Biol 8, 668–676. [DOI] [PubMed] [Google Scholar]
- Woodson SA (2010). Taming free energy landscapes with RNA chaperones. RNA Biol 7, 677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wyman J, and Gill SJ (1990). Binding and Linkage: Functional Chemistry of Biological Macromolecules University Science Books, Mill Valley. [Google Scholar]
- Yang Q, and Jankowsky E (2006). The DEAD-box protein Ded1 unwinds RNA duplexes by a mode distinct from translocating helicases. Nat. Struct. Mol. Biol 13, 981–986. [DOI] [PubMed] [Google Scholar]
- Zimmerle CT, and Frieden C (1989). Analysis of progress curves by simulations generated by numerical integration. Biochem. J 258, 381–387. [DOI] [PMC free article] [PubMed] [Google Scholar]


