Resurgence as choice in context: Treatment duration and on/off alternative reinforcement

Abstract

Resurgence as Choice (RaC) is a quantitative theory suggesting that an increase in an extinguished target behavior with subsequent extinction of an alternative behavior (i.e., resurgence) is governed by the same processes as choice more generally. We present data from an experiment with rats examining a range of treatment durations with alternative reinforcement plus extinction and demonstrate that increases in treatment duration produce small but reliable decreases in resurgence. Although RaC predicted the relation between target responding and treatment duration, the model failed in other respects. First, contrary to predictions, the present experiment also replicated previous findings that exposure to cycling on/off alternative reinforcement reduces resurgence. Second, RaC did a poor job simultaneously accounting for target and alternative behaviors across conditions. We present a revised model incorporating a role for more local signaling effects of reinforcer deliveries or their absence on response allocation. Such signaling effects are suggested to impact response allocation above and beyond the values of the target and alternative behaviors as longer-term repositories of experience. The new model provides an excellent account of the data and can be viewed as an integration of RaC and a quantitative approximation of some aspects of Context Theory.

Resurgence is an increase in a previously suppressed behavior resulting from a relative worsening in conditions for a more recently reinforced behavior (Epstein, 1985; Lattal & Wacker, 2015; Shahan & Craig, 2017). Theoretically, resurgence is important because it provides a means to explicitly study the processes governing how historically and more recently effective behaviors are allocated in an environment characterized by shifting contingencies over time. As such, a better understanding of the phenomenon might also provide important insights into problem solving and creativity (e.g., Epstein, 1985; Shahan & Chase, 2002). Clinically, resurgence is important because such recurrence with changing consequences appears to be a source of relapse to previously treated undesirable behavior. For example, in applications of differential-reinforcement-of-alternative-behavior (i.e., DRA), an undesirable target behavior is typically placed on extinction while an appropriate alternative behavior is reinforced (see Petscher, Rey, & Bailey, 2009; Tiger, Hanley, & Bruzek, 2008). Although such treatments are highly effective, elimination or reduction of reinforcement for the alternative behavior can produce increases in the previously suppressed problem behavior (see Briggs, Fisher, Greer, & Kimball, 2018; Volkert, Lerman, Call, & Trosclair-Lasserre, 2009; Wacker et al., 2011). Similarly, alternative-reinforcement-based interventions for substance abuse are highly effective (see Higgins, Heil, & Lussier, 2004; Prendergast, Podus, Finney, Greenwell, & Roll, 2006), but relapse to drug seeking is common when treatment ends and alternative reinforcers are suspended (e.g., Silverman et al., 1998, Silverman, Chutuape, Bigelow, & Stitzer, 1999; see Podlesnik, Jiminez-Gomez, & Shahan, 2006; Quick, Pyszczynski, Colston, & Shahan, 2011).

In laboratory examinations of resurgence, a three-phase procedure is typically used. In Phase 1, a target behavior (e.g., left lever press) is reinforced on some schedule of reinforcement. In Phase 2, the target behavior is typically placed on extinction and alternative behavior (e.g., right lever press) is reinforced. In Phase 3, the alternative behavior is also placed on extinction, and as a result, the rate of the target behavior increases (i.e., resurgence occurs).

Resurgence as Choice (RaC) theory suggests that resurgence results from the same basic processes governing choice more generally (Shahan & Craig, 2017). RaC is an extension of the concatenated matching law (Baum & Rachlin, 1969) and suggests that the rate of target behavior is a function of the relative values of the histories of consequences produced by the target and alternative behaviors over time. Specifically, RaC suggests that the absolute response rate of target behavior is given by,

$$B_T=\frac{k{V}_T}{V_T+\frac{V_{Alt}}{b}+\frac{1}{A}}A=a(V_T+V_{Alt})$$ (1)

where B_T is the rate of the target behavior, V_T and V_Alt are the current values of the histories of consequences provided by the target and alternative behaviors, k is a parameter reflecting the asymptotic rate of B_T, the parameter b reflects any unaccounted for bias related to other factors (e.g., topographically different responses, differences in effort) for one option or the other (b > 1 = bias for the target; b < 1 = bias for the alternative), and A represents the invigorating (i.e., arousing) effects of the current values of the two options (the parameter a represents how much of an impact the current values of the options have on invigoration and is likely reflective of current motivational state). Simply re-expressing Equation 1 in terms of the relative value of the alternative behavior provides a similar equation for absolute response rate of the alternative behavior (i.e., B_Alt),

$$B_{Alt}=\frac{k\frac{V_{Alt}}{b}}{V_T+\frac{V_{Alt}}{b}+\frac{1}{A}}$$ (2)

where all terms are as in Equation 1.

RaC supplements the concatenated matching law by providing a formal means to calculate the values of the histories of changing consequences produced by the target and alternative behaviors over time (i.e., V_T and, V_Alt), even when those histories include extinction of one or both options. Specifically, RaC uses a modified temporal weighting rule (e.g., Devenport & Devenport, 1994) to calculate V_T and, V_Alt. This weighting rule provides a series of weightings to be applied to experiences (e.g., reinforcement rates) in the past,

$$w_x=\frac{1/t_x^c}{\sum _{i=1}^{n}1/t_i^c}$$ (3)

where w_x is the weighting for a particular session in the past. The numerator reflects the recency of an experience, where t_x is the time (number of sessions plus 1) between that experience and the session of interest. The denominator is the sum of the recencies for all sessions prior to and including the session of interest. The exponent c reflects how quickly the impact of experiences in past sessions decreases, with lower values of c resulting in less relative weight for more recent sessions. RaC assumes that organisms should be influenced more by recent experiences when the reinforcement rate is high and to be influenced by experiences over a longer period of time when reinforcement rate is low (Killeen, 1981), formalized as,

$$c=\lambda r+1$$ (4)

where r is the running average rate of reinforcement provided by a particular response across all sessions under consideration, and λ is a free parameter representing sensitivity to running reinforcement rate. Equation 3 generates weighting functions that are hyperbolic as a function of session, with more recent sessions receiving higher weights than more temporally distant sessions (see Shahan & Craig, 2017 for discussion).

In order to calculate values of the target (i.e., V_T ) and alternative (i.e., V_Alt) options across sessions to be used in Equations 1 and 2, the reinforcement rates (i.e., R_x) experienced across all sessions for each option are multiplied by the weightings for those sessions provided by Equation 3, and those weighted reinforcement rates are summed across the sequence of sessions under consideration. Formally, that is:

$$V_T=\sum _x{w}_x{R}_{xT}{V}_{Alt}=\sum _x{w}_x{R}_{xAlt}$$ (5)

where R_xT and R_xAlt are the reinforcement rates (in reinforcers/hr) for the target and alternative behaviors experienced across the sequence of sessions. When reinforcement rates are constant and nonzero across time, Equations 3–5 generate value functions for the target and alternative options that correspond to the veridical reinforcement rates. However, when an option is placed on extinction and its true reinforcement rate is zero, the hyperbolic weighting function results in a value function that decreases from the previously arranged reinforcement rate quickly at first, and more slowly as time in extinction progresses. As a result, in the typical three-phase resurgence procedure a target behavior that has been on extinction for some time reaches a low, but relatively constant value. When the alternative behavior is also placed on extinction, the initial precipitous drop in its value results in a relative (although not absolute) increase in the value of the target behavior in Equation 1 (i.e., the denominator decreases with the large drop in V_Alt), and as a result B_T increases (see Shahan & Craig, 2017 for examples). This increase in the target behavior is what has been called resurgence, and according to RaC it is the result of the shifting relative values of the target and alternative options over time. That is, resurgence is simply a natural outcome of the Matching Law.

RaC as formalized in Equations 1–5 has provided a reasonably good quantitative account of a wide range of findings in the resurgence literature, including a number of findings where the only other quantitative theory of resurgence (i.e., Behavioral Momentum Theory; Shahan & Sweeney, 2011) has failed (see Craig & Shahan, 2016; Shahan & Craig, 2017; Nevin et al., 2017, for reviews). Further, RaC makes novel predictions relevant for both basic theoretical and clinical domains (see Greer & Shahan, 2019), and it provides a way to integrate the phenomenon of resurgence into the wider conceptual and quantitative framework of matching theory.

The purpose of this paper is threefold. First, RaC makes specific quantitative predictions about the effects of the duration of exposure to extinction+alternative reinforcement (i.e., treatment duration) in Phase 2 on subsequent resurgence. The data available on this issue are either complicated by interpretive difficulties or examine a small number of treatment durations. Thus, novel data from an experiment with rats examining a wide range of treatment durations on subsequent resurgence will be presented. Second, RaC appears to struggle to account for the effects of alternating exposures to sessions of alternative reinforcement and extinction (hereafter “on/off” alternative reinforcement) during Phase 2. Although exposure to such on/off alternative reinforcement seems to reduce resurgence, there are some inconsistencies in the literature, as detailed below. Thus, the experiment also included such a condition allowing comparison with conditions testing for resurgence after a wide range of constantly “on” alternative reinforcement. Third, formal fitting of RaC to the obtained data reveals the nature of some of the limitations of the model with respect to treatment duration, but especially its failure with respect to on/off alternative reinforcement. Thus, in order to remedy these inadequacies, we present an augmented version of the model that might be considered a hybrid of RaC and a quantitative approximation to Bouton’s Context Theory (e.g., Bouton, Winterbauer, & Todd, 2012; Trask, Schepers, & Bouton, 2015; Winterbauer & Bouton, 2010). In what follows, we will address these points in order.

Treatment Duration and RaC

The effects of treatment duration on resurgence could be of particular clinical importance if longer exposure to treatment might reduce subsequent resurgence of problem behavior. Theoretically, the effects of treatment duration are a fundamental aspect of resurgence, and any viable theory must be able account for this variable. The two studies examining the widest range of treatment durations (both with rats) have generated somewhat mixed results. Leitenberg, Rawson, and Mulick (1975) found that 27 sessions of treatment in Phase 2 reduced resurgence compared to 3 and 9 sessions. However, Winterbauer, Lucke, and Bouton (2013) found that 4, 12, and 36 sessions led to statistically equivalent magnitudes of resurgence, although the four-session group showed somewhat numerically higher resurgence. Unfortunately, it appears that both studies confounded rates of alternative reinforcement with duration of Phase 2 by using ratio schedules of reinforcement for the alternative behavior (i.e., alternative response rates, and thus reinforcement rates increased with training duration). Nevertheless, two additional experiments from our laboratory without this confound examined target responding previously maintained by alcohol or cocaine reinforcement and have similarly obtained no statistical difference in resurgence with 5 and 20 sessions of Phase 2 (Nall, Craig, Browning, & Shahan, 2018). As in Winterbauer et al. (2013), rats in the alcohol experiment (but not in the cocaine experiment) showed numerically, but not statistically, greater resurgence in the 5-session compared to the 20-session group. Thus, as a whole, the existing data with rats suggest that longer treatment duration has relatively little impact on resurgence, although there may be some small effect that is difficult to detect statistically.

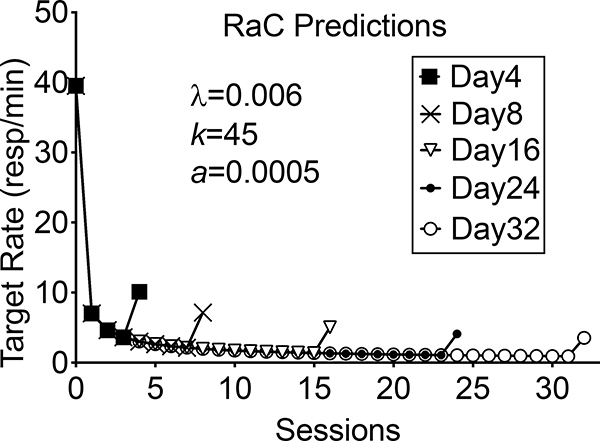
Consistent with the data described above, RaC predicts that longer treatment durations have only relatively small effects on resurgence. Figure 1 shows the quantitative predictions of RaC across treatment durations of 3, 7, 15, 23, and 31 sessions (i.e., testing for resurgence on days 4, 8, 16, 24, and 32). The simulation assumes that the target behavior was reinforced on a variable-interval (VI) 30-s schedule in Phase 1 for 30 sessions. In Phase 2, target behavior was placed on extinction and the alternative behavior was reinforced on VI 10-s schedule for the appropriate number of sessions. In Phase 3, both target and alternative behaviors were extinguished. The simulation suggests that RaC predicts that response rates in the Phase-3 test decrease somewhat with increases in treatment duration. However, this predicted decrease might be too small to detect statistically, or to be of clinical significance.

Fig. 1.

Predicted target response rates across a range of Phase 2 treatment durations during which the target behavior (previously reinforced on a VI 30-s schedule for 30 days in Phase 1) is extinguished and the alternative behavior is reinforced on a VI 10-s schedule. The alternative behavior is also then placed on extinction on the 4th, 8th, 16th, 24th, or 32^nd session. The data points at zero on the x-axis represent Phase 1 target response rates.

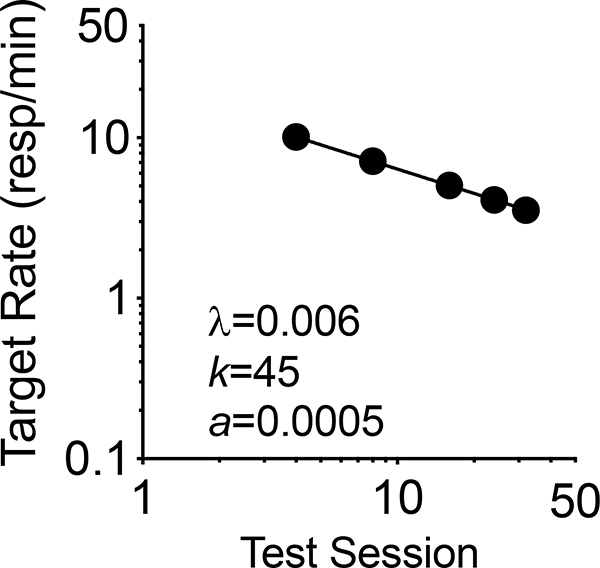
Although longer treatment durations are predicted to have relatively little effect on resurgence, RaC predicts the specific form of the function relating response rates in Phase 3 to treatment duration. This predicted function is shown in Figure 2. Note that both axes are logarithmic. The simulation depicts predicted target response rates during the first session of resurgence testing occurring in sessions 4, 8, 16, 24, and 32. Target response rates do indeed decrease, but the decreases across the range are quite small. The fact that the function is linear in these log–log coordinates means that RaC predicts that resurgence in the first session of Phase 3 decreases as a negative power function of treatment duration (i.e., y = ax^-b). Given both the potential clinical and theoretical importance of the effects of treatment duration on resurgence, the experiment described below was designed in part to test the prediction in Figure 2.

Fig. 2.

Predicted first-session Phase 3 target response rates in the as a function of the session in which alternative reinforcement is removed for the alternative behavior (4th, 8th, 16th, 24th, or 32nd session). Note that both axes are logarithmic.

On/Off Alternative Reinforcement

Two additional experiments have often been cited to suggest that increases in treatment duration produce more meaningful reductions in resurgence (Sweeney & Shahan, 2013; Wacker et al., 2011). The Wacker et al. (2011) experiment examined the effects of increasing durations of exposure to DRA on the problem behavior of children with intellectual and developmental disabilities (IDD). However, the study included cycles of DRA and extinction across months of treatment. Removal of DRA for a session generated an increase in the rate of the problem behavior (i.e., resurgence), and across time with these on/off cycles of DRA, these increases in problem behavior became smaller—leading to the interpretation that longer treatment reduces resurgence. However, it is possible that the decreases in resurgence resulted from the alternating cycles of DRA and extinction, rather than the increases in treatment duration per se. Similarly, Sweeney and Shahan (2013) found with pigeons that alternating sessions of alternative reinforcement and extinction resulted in decreases in resurgence in those sessions in which alternative reinforcement was removed (i.e., the off sessions). But again, it is not clear if the robust decreases in resurgence during “off” days were a result of increasing time in treatment, or if they were due to the history of exposure to alternating sessions of on/off alternative reinforcement. Data from a control group in Sweeney and Shahan was consistent with the possibility that time in treatment alone might be responsible for the decreases across the repeated “off” resurgence tests in the on/off group. The control group experienced the same number of sessions in Phase 2, but with alternative reinforcement constantly available in every session. In the final resurgence test, this “constant on” alternative reinforcement group did not differ from the “on/off” group in terms of the degree of resurgence.¹ This result suggests that the decreases in resurgence in the repeated “off” sessions were not due to exposure to the alternating sequence of on/off alternative reinforcement, and that time in treatment was itself responsible for the decreases.

However, two additional experiments with rats (Schepers & Bouton, 2015; Trask, Keim, & Bouton, 2018) have produced a different outcome. Like Wacker et al. (2011) and Sweeney and Shahan (2013), both Schepers and Bouton (2015) and Trask et al. (2018) have shown that exposure to alternating sessions of on/off alternative reinforcement gradually reduces the amount of resurgence observed across successive “off” sessions. However, in both Schepers and Bouton and in Trask et al., control groups exposed to the same number of Phase 2 sessions except with alternative reinforcement available constantly in each session showed significantly more resurgence than groups exposed to on/off alternative reinforcement. Importantly, Trask et al. examined the effects of on/off alternative reinforcement across two different overall treatment durations (i.e., 5 vs. 25 sessions). As with the treatment duration experiments discussed above, the 5- and 25-session constant alternative reinforcement groups both showed resurgence, and the groups did not differ from one another statistically. However, for the alternating on/off alternative reinforcement groups, neither the 5-session nor the 25-session group showed significant resurgence (although mean target response rates for both groups were higher during the test). In addition, for the 25-session alternating on/off group, resurgence was significantly reduced as compared to the 25-session constant alternative reinforcement group. A similar, although only marginally significant, effect was observed for the 5-session on/off and constant groups. These findings suggest that in contrast to Sweeney and Shahan, it does appear that experience with on/off reinforcement across sessions reduces resurgence, and thus, the effect of treatment duration in Wacker et al. with children with IDD could be due to this aspect of their study.

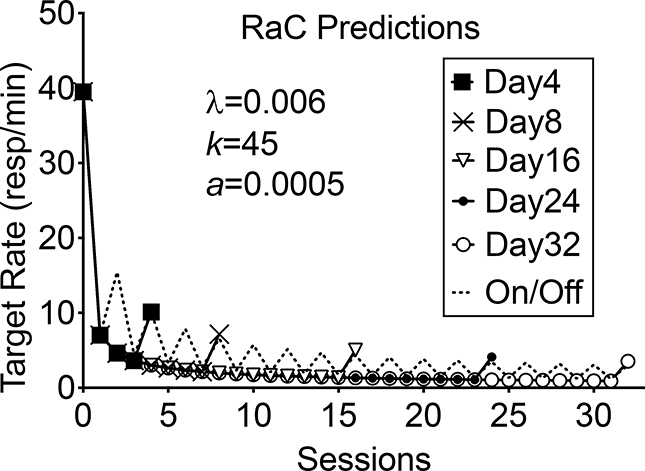
As noted by Shahan and Craig (2017), RaC predicts that exposure to on/off alternative reinforcement produces essentially the same amount of resurgence as similar durations of exposure to constant alternative reinforcement. Figure 3 shows the same simulation as in Figure 1 with the inclusion of a condition in which on/off alternative reinforcement is presented. Note that there is no meaningful difference between the on/off and constant alternative reinforcement conditions. Obviously, the data of Schepers and Bouton (2015) and Trask et al. (2018) with rats appear to suggest that this prediction is incorrect. Thus, in addition to examining a range of constant alternative reinforcement durations, the experiment described below also included a group of rats exposed to on/off alternative reinforcement and tested all the conditions depicted in Figure 3. RaC was fitted to the resulting data using Equations 1–5 and its adequacy was assessed.

Fig. 3.

Predicted target response rates presented as in Figure 1, but with the inclusion of the predictions for a condition in which on/off alternative reinforcement is presented across sessions.

Method

Subjects

Sixty male Long-Evans rats (Charles River, Portage, MI), approximately 71–90 days old upon arrival, served as subjects. Rats were individually housed in a humidity- and temperature-controlled colony room with a 12:12 hr light/dark cycle. Rats had ab libitum access to water in the home cages and were maintained at 80% of their free feeding weights. Animal housing and care and all procedures reported below were conducted in accordance with Utah State University’s Institutional Animal Care and Use Committee.

Apparatus

Ten identical Med Associates (St. Albans, VT) operant chambers were used. Chambers measured 30 cm × 24 cm × 21 cm and were housed in sound- and light-attenuating cubicles.

Each chamber was constructed of work panels on the front and back walls, and a clear Plexiglas ceiling, door, and wall opposite the door. Two retractable levers on the front wall, with stimulus lights above them, were positioned on either side of a food receptacle that was illuminated with the delivery of 45-mg grain-based food pellets (Bio Serv, Flemington, NJ). A house light positioned above the food receptacle on the front panel was used for general chamber illumination. All experimental events and data collection were controlled by Med-PC software run on a computer in an adjacent control room.

Procedure

Sessions were conducted 7 days per week at approximately the same time each day. All sessions were 30 min excluding time for reinforcement delivery during which all experimental timers were paused for 3 s. During reinforcement delivery, the pellet dispenser dropped a single food pellet into the illuminated food receptacle and the stimulus and house lights were darkened.

Training.

Rats were first trained to consume food pellets from the food aperture. Food pellets were delivered response-independently according to a variable-time (VT) 60-s schedule of reinforcement for four sessions. The VT schedule and all variable-interval (VI) schedules described below were constructed of 10 intervals derived from the Flesher and Hoffman (1962) constant-probability distribution. Levers remained retracted and lever lights and house lights were darkened throughout magazine training. The day following magazine training, a single acquisition session was conducted to train rats to press the target lever (left–right, counterbalanced across subjects). This acquisition session began with illumination of the house and target-lever lights and insertion of the target lever. To facilitate target lever pressing, the first response on the target lever produced a food pellet and thereafter food pellets were delivered for lever pressing according to a VI 10-s schedule of reinforcement.

Phase 1: Baseline.

Sessions during baseline began as described for the lever-response acquisition session. Responses to the target lever produced food pellets according to a VI 30-s schedule of reinforcement. This phase lasted 30 sessions. Following baseline, rats were divided into a total of six groups. Rats were assigned to groups such that average responses per minute across the last three sessions of baseline were comparable between groups (overall M = 42.20, range: 41.19–43.36) and did not differ statistically F(5, 52) = .001, p = .999.

Phase 2: Treatment.

For five constant alternative reinforcement groups, alternative reinforcement was available in every session of this phase. The five groups differed in terms of the length of this treatment phase, and group names reflect the day on which Phase 3 started and alternative reinforcement was removed (i.e., Day4, Day8, Day16, Day24, and Day32 groups). For example, the Day8 group was exposed to constant alternative reinforcement for seven sessions and alternative reinforcement was suspended on session 8. A sixth group received alternating sessions of alternative reinforcement availability and extinction of alternative-lever pressing (i.e., On/Off group). That is, alternative responding produced alternative reinforcement only on odd-numbered days and extinction was in effect on even-numbered days. This alternating treatment continued for a total of 31 daily sessions. This arrangement allowed comparison of an “off” day for the On/Off group with the first “off” day of Phase 3 for each of the constant alternative reinforcement groups after a comparable number of Phase 2 sessions. There were 10 rats in each group, with the exception of the Day16 and Day24 groups which had only nine rats each due to an experimental scheduling error.

Sessions during this phase began as in baseline with the addition of insertion of the alternative lever (right–left, counterbalanced across subjects) and illumination of the alternative-lever stimulus light. During the first session of this phase, the first response on the alternative lever produced a food pellet, after which food was delivered according to a VI 10-s schedule for the remainder of the first session and in all sessions in which alternative reinforcement was available for each group as described above.

Phase 3: Resurgence test.

Beginning on the session following the completion of Phase 2 treatment and corresponding to the session designated by group names for the constant alternative reinforcement groups (and “on” session 32 for the On/Off group), alternative responding was also placed on extinction for all groups. Stimulus conditions remained as in Phase 2, but neither the target nor the alternative lever produced reinforcer deliveries. This phase lasted for 10 sessions for all groups.

Results and Discussion

Treatment Duration after Constant Alternative Reinforcement

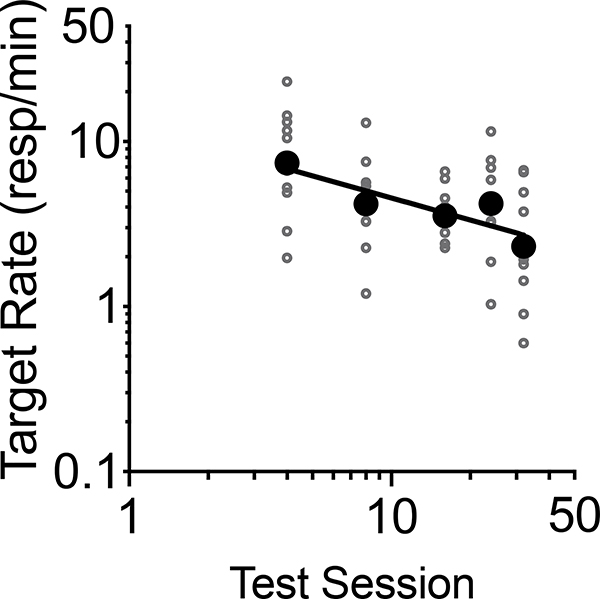
We begin with a focus on the effects of treatment duration on resurgence. Figure 4 shows target response rates in the first session of the Phase 3 resurgence test as a function of the session in which resurgence testing began for all groups exposed to constant alternative reinforcement in Phase 2. The small data points reflect target response rates of individual rats in each treatment duration group. In general, target response rates decreased with increases in treatment duration prior to the resurgence test. Linear regression of all subject data conducted on logarithmic transformed data on both dimensions (corresponding to the double log axes depicted in the figure) revealed that target response rates decreased significantly (i.e., a significant nonzero slope) with longer Phase 2 durations F(1,46) = 11.53, p = .0014. The larger data points depict geometric means (appropriate for the regression in log space) for each group and are provided only as a visual aid. The significant linear relation in double logarithmic space in the figure is consistent with prediction of RaC that target responding should decrease as a power function of treatment duration. Although this is a positive outcome for RaC, the story becomes increasingly less positive with further inspection of the full data set.

Fig. 4.

Obtained target response rates in the first session of the Phase 3 resurgence test as a function of the session in which resurgence testing began (4th, 8th, 16th, 24th, or 32nd session) for all groups exposed to constant alternative reinforcement in Phase 2. The small data points represent individual rats in each treatment duration group. The line is a linear regression using all individual-subject data. The large data points represent group geometric means. Note the log–log axes.

Constant Versus On/Off Alternative Reinforcement

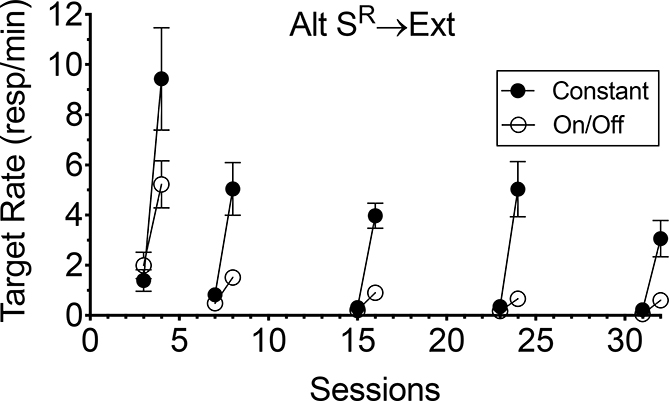
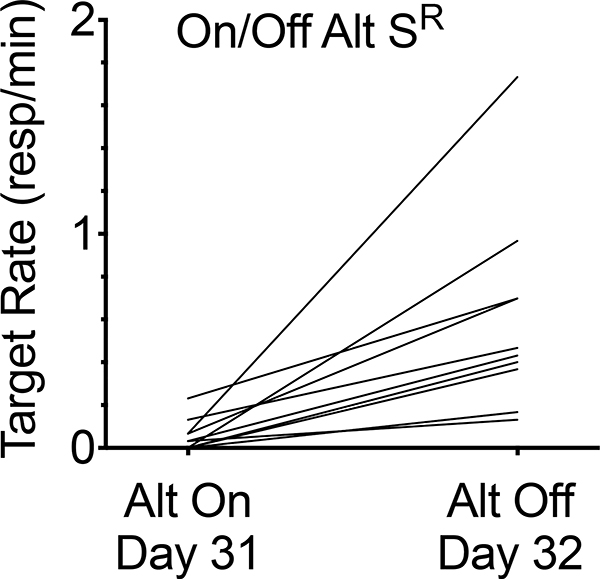
Next, consider the effects of constant versus on/off alternative reinforcement. Figure 5 shows mean target response rates during the last session with alternative reinforcement in Phase 2 versus the first resurgence test session in Phase 3 for the constant alternative reinforcement groups and similar data for the corresponding sessions for the On/Off alternative reinforcement group. Planned comparisons employing 2 (phase; Alt SR present versus absent) × 2 (condition; constant versus on/off) mixed ANOVAs (see Table 1 for details) reveal significant main effects of phase for all treatment durations, significant main effects of condition for all test days (i.e., treatment durations) except the Day 4 comparison, and significant phase × condition interactions for all test days except for the Day 4 comparison (although the interaction for Day 4 was marginal p = .052). Follow up t-tests (see Table 2 for details) comparing the last session of alternative reinforcement present and the first resurgence test session for the constant and on/off conditions individually at each test day reveal that responding significantly increased for all comparisons. Thus, in summary, removal of alternative reinforcement generated significant resurgence of target behavior for both constant and On/Off alternative reinforcement groups across a range of treatment durations. As compared to when reinforcement was constantly available during Phase 2, alternating sessions of on/off alternative reinforcement significantly reduced, but did not eliminate, resurgence across the entire range of treatment durations, including at the longest treatment duration. The fact that on/off alternative reinforcement reduced resurgence is consistent with both Schepers and Bouton (2015) and Trask et al. (2018) and inconsistent with Sweeney and Shahan (2013). However, unlike in the current experiments, both Schepers and Bouton and Trask et al. reported that although all of their on/off alternative reinforcement groups showed numerical increases in target rates in the final extinction test session (i.e., session 8 for Schepers & Bouton and sessions 6 and 26 for Trask et al.), none of those increases were statistically significant. In contrast, although the significant increases in target behavior observed across all treatment durations in the on/off condition in the present experiment were small, they were extremely reliable. Indeed, 10 of 10 rats in the on/off condition showed increases in responding at every timepoint depicted in Figure 5 except for Day 4 and Day 16, in which 8 of 10 and 9 of 10 rats, respectively, showed increases in target response rate. As an illustrative example, Figure 6 shows that even with 16 cycles of on/off alternation (i.e., at the Day 32 timepoint), responding increased for every rat when alternative reinforcement was removed in session 32.

Fig. 5.

Mean target response rates during the last session with alternative reinforcement in Phase 2 versus the first resurgence test session in Phase 3 for the all constant alternative reinforcement groups and similar data for the corresponding sessions for the On/Off alternative reinforcement group. Error bars represent ±1 SEM.

Table 1:

Results from planned 2 × 2 (Phase: Alt SR present vs absent × Condition: Constant vs On/Off) mixed-model ANOVA conducted on target response rates during the last session with alternative reinforcement in Phase 2 versus the first resurgence test session in Phase 3 for the all constant alternative reinforcement groups and similar data for the corresponding sessions for the On/Off alternative reinforcement group

				Degrees of Freedom
Comparison	Effect	F	Effect	Error	p	ηp2
Day 4	Phase	23.77	1	18	< .001	.57
	Condition	2.31	1	18	.146	.11
	Phase × Condition	4.34	1	18	.052	.19
Day 8	Phase	25.40	1	18	< .001	.59
	Condition	11.81	1	18	.003	.40
	Phase × Condition	9.41	1	18	.007	.34
Day 16	Phase	70.77	1	17	< .001	.81
	Condition	32.91	1	17	< .001	.66
	Phase × Condition	32.97	1	17	< .001	.66
Day 24	Phase	25.98	1	17	< .001	.60
	Condition	16.88	1	17	< .001	.50
	Phase × Condition	41.62	1	17	.001	.50
Day 32	Phase	23.52	1	18	< .001	.57
	Condition	11.46	1	18	.003	.39
	Phase × Condition	10.74	1	18	.004	.37

Table 2:

Results from paired-samples t-tests conducted on target response rates from the last session of alternative reinforcement present and the first resurgence test session for the constant groups and the corresponding sessions for the On/Off group individually at each test day

Condition	Duration	t	Degrees of Freedom	pa	d
Constant	Day 4	3.98	9	.003	1.26
	Day 8	4.10	9	.003	1.29
	Day 16	7.18	8	< .001	2.39
	Day 24	4.38	8	.002	1.46
	Day 32	4.15	9	.002	1.31
On/Off	Day 4	2.87	9	.018	0.90
	Day 8	6.27	9	< .001	1.98
	Day 16	3.88	9	.004	1.22
	Day 24	4.99	9	< .001	1.58
	Day 32	3.78	9	.004	1.19

^aBonferroni correction: α = .005

Fig. 6.

Target response rates for individual rats in the On/Off alternative reinforcement group for the final transition between alternative reinforcement on (i.e., day 31) versus off (day 32).

Quantitative Assessment of RaC

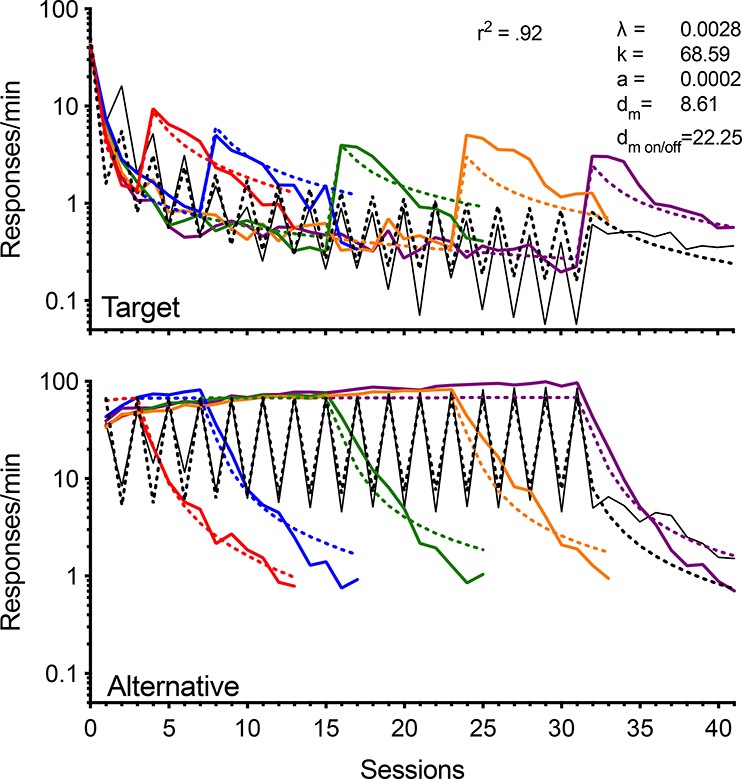
In order to better evaluate the nature of RaC’s shortcomings with the present data, the model was fitted to data across conditions for both the target and alternative behaviors. Figure 7 shows response rates for the target (top panel) and alternative (bottom panel) behaviors across all Phase 2 and 3 sessions for all groups (solid lines). In addition, the figure shows the best fitting functions generated by RaC using least-squares regression (Microsoft Excel Solver). Response rates for the target and alternative behaviors were fitted simultaneously using Equations 1 and 2, respectively, with the relevant values of V_T and V_Alt across sessions provided by Equations 3–5. The fit was conducted on logarithmic transformed data in order to provide more proportional weighting of the many-fold lower response rates associated with the target as compared to alternative behavior across sessions². The fit involves 346 data points and three free parameters (λ, k, and a) and is quite poor with r² = .56. The bias parameter (i.e., b) is omitted because identical levers served as the target and alternative behaviors, and there is no reason to expect any meaningful bias.

Fig. 7.

Response rates for target (top panel) and alternative (bottom panel) behavior across sessions for all groups. Data for the different groups are represented by differently colored solid lines. Mean target behavior response rates in the final three sessions of Phase 1 are presented above zero on the x axis. The predictions of RaC for each group are shown as dotted lines of the same color as for the data. All data were fitted simultaneously. Note the logarithmic y axes.

A couple of issues with the fit of the model are apparent in Figure 7. First, as expected based on the simulations above, the model predicts no differences in target response rates when comparing resurgence for the constant and on/off alternative reinforcement conditions. Although the model predicts the sawtooth patterns of responding for both target and alternative behaviors across cycles of on/off alternative reinforcement, the location and size of the functions are inaccurate. Second, the model generally overpredicts response rates for the target behavior (except for the later resurgence tests after constant alternative reinforcement where there is a tendency to underpredict) and generally underpredicts response rates for the alternative behavior. If the bias parameter (i.e., b) is included and allowed to vary freely (an unprincipled and unreasonable assumption, and the fit is not depicted), target response rates decrease somewhat (all fitted functions in Fig. 7 shift down), alternative response rates increase somewhat (the functions shift up), and r² increases to .73 (fit not shown). But, overall the pattern of mispredictions described above remains largely unchanged. Thus, we conclude that RaC as formalized solely in Equations 1–5 is inadequate to account for the effects of on/off alternative reinforcement, and the model also does a poor job accounting for target and alternative response rates simultaneously.

Context Theory

Schepers and Bouton (2015) and Trask et al. (2018) have suggested that the effects of on/off alternative reinforcement are consistent with the qualitative account of resurgence provided by Context Theory. According to Context Theory (e.g., Bouton et al., 2012; Trask et al., 2015; Winterbauer & Bouton, 2010), resurgence is an example of the ABC renewal of extinguished behavior. In ABC renewal, behavior that is trained in the presence of one set of stimuli (i.e., Context A) and then extinguished in the presence of a different set of stimuli (i.e., Context B), increases with a switch to a set of stimuli that is different from both the training and extinction contexts (i.e., Context C). Context Theory suggests ABC renewal occurs because of a failure of new learning during extinction in Context B (i.e., learning not to respond or to inhibit the response) to generalize to Context C, and thus responding increases. As applied to resurgence, Context Theory suggests that the presence and absence of reinforcer deliveries provide the relevant stimulus contexts. Specifically, reinforcement of target behavior in Phase 1 serves as the stimulus for Context A. In Phase 2, reinforcement of alternative behavior serves as the stimulus for Context B. Finally, in Phase 3, the absence of reinforcement serves as the stimulus for Context C, and target responding increases as a result of the failure of the extinction learning during Phase 2 to generalize.

When specifically applied to the effects of on/off alternative reinforcement, Context Theory suggests that “off” days provide experience with what will be the Phase 3 testing conditions (i.e., extinction of both target and alternative behavior), thus facilitating generalization of extinction learning to the resurgence test. Thus, the account essentially asserts that on/off alternative reinforcement gives the organism the opportunity to learn that reinforcement is not coming for the target behavior, even when the alternative reinforcer is absent.

Resurgence as Choice in Context (RaC²)

RaC in its most general sense conceptualizes resurgence as resulting from a choice between the target and alternative behaviors, and it focuses on how shifting relative values of the options over time produce shifts in the allocation of behavior. Context Theory as applied to resurgence focuses on the role of stimulus control by more local aspects of reinforcer deliveries or their absence. Clearly, these two options are not mutually exclusive. RaC can be thought of as providing a longer-term accounting of what is traditionally conceptualized as a reinforcement history for the two options. But in order for exposure to reinforcement histories (including extinction) to impact an organism, it must discriminate reinforcer deliveries (or their absence). Indeed, from our perspective, choice, relative value, and the matching law involve nothing more than an organism discriminating the signaling effects of rates and patterns of reinforcer deliveries across time and response options, and then behaving accordingly based on an innate strategy known as “matching” (Davison & Baum, 2006; Gallistel et al., 2007; Gallistel, Mark, King, & Latham, 2001; see Shahan, 2017 for discussion). In RaC, such discriminations are assimilated over time and carried forward by the shorthand concept of “value” which updates with experience according to the temporal weighting rule. The long tails of the hyperbolic weighting functions generated by the temporal weighting rule mean that although value does update with recent experience, it also nevertheless serves as a relatively stable repository of longer-term histories. It is this longer-term repository of more distant experience that allows RaC to account for why a behavior that has not been reinforced for quite some time might nevertheless suddenly increase in relative frequency when conditions worsen for a more recently reinforced behavior. Although Context Theory provides an informal qualitative account of how more local stimulus effects of reinforcer deliveries might contribute to resurgence, it provides no account of how a longer-term history is constructed, or why the organism is choosing to engage in these behaviors at all. Our goal in what follows is to provide a first attempt at quantitatively integrating the roles of more global histories of experiences and shorter-term discriminating in an account of resurgence. The account that emerges might be thought of as a mashup of RaC and a quantitative approximation to aspects of Context Theory. We call this mashup Resurgence as Choice in Context (RaC²).

As noted above, Context Theory suggests that on/off alternative reinforcement reduces resurgence because it gives the organism an opportunity to learn two discriminations: 1) that during “alternative reinforcement on” sessions, reinforcer deliveries for the alternative behavior (i.e., Context B) come to signal that the target will not be reinforced, and 2) that during “alternative reinforcement off” sessions, the absence of reinforcement for alternative behavior (i.e., Context C) comes to signal that reinforcement is not coming for either option. In order to integrate these more local discriminations into RaC, one must somehow quantify their effects and incorporate them into RaC’s equations. It is critical to note that the discriminations suggested by Context Theory are not occurring only during conditions involving on/off alternative reinforcement, but also under the usual circumstances arranged by Phases 2 and 3 in the typical resurgence preparation—in which constant alternative reinforcement is available in Phase 2 and then removed in Phase 3. In short, the discriminations described above must be applied uniformly to all sessions in which alternative reinforcement is present versus absent.

Thus, in order to incorporate these discriminations into RaC we take inspiration from the Matching-Law based model of stimulus control/detection (e.g., Davison & Nevin, 1999; Davison & Tustin, 1978) where the modulating effects of stimuli are characterized as a source of bias. Thus, we propose the following for target response rates in sessions where alternative reinforcement is present and target behavior is being extinguished (i.e., normal Phase 2 sessions in the typical procedure or “on” sessions for on/off alternative reinforcement):

$$B_T\mathit{(}\mathit{on}\mathit{)}=\frac{k{V}_T}{V_T\mathit{+}{d}_1(V_{\mathit{Alt}})\mathit{+}\frac{\text{1}}{A}}A=a(V_T+V_{\mathit{Alt}})$$ (6)

where all terms are as in Equation 1 above and the added term d₁ reflects the biasing effects of discriminating that the presence of alternative reinforcement signals the local absence of reinforcement for the target behavior.³ Calculations of V_T and V_Alt remain unchanged and are as described in Equations 3–5 above. Similarly, the equation for the alternative behavior under these same conditions is:

$$B_{\mathit{Alt}}\mathit{(}\mathit{on}\mathit{)}\text{=}\frac{{kd}_1(V_{\mathit{Alt}})}{{V_T\mathit{+}d}_1(V_{\mathit{Alt}})\mathit{+}\frac{\text{1}}{A}}$$ (7)

where all terms are as above. The d₁ term is the same in both equations and reflects the biasing effect of the discrimination, because as it grows more behavior is allocated toward the alternative option (and away from the target) above and beyond what would be expected based on V_T and V_Alt alone as repositories of longer-term histories. When d₁ = 1, there is no additional bias and rates of both responses are governed by their relative values. But, as d₁ grows to >1, discrimination produces a bias toward the alternative behavior and away from the target. Thus, B_T decreases and B_Alt increases. In the terms of Context Theory, one could think of such a bias away from the target behavior as the organism learning not to engage in the target behavior as much.

In sessions where alternative reinforcement is absent and target behavior is being extinguished (i.e., Phase 3 sessions in the typical procedure or “off” sessions for on/off alternative reinforcement):

$$B_T\mathit{(}\mathit{off}\mathit{)}\text{=}\frac{k{V}_T/d_0}{V_T/d_0\mathit{+}{V}_{Alt}/d_0\mathit{+}\frac{\text{1}}{A}}$$ (8)

for the target behavior and,

$$B_{\mathit{Alt}}\mathit{(}\mathit{off}\mathit{)}\text{=}\frac{k{V}_{\mathit{Alt}}/d_0}{V_T/d_0\mathit{+}{V}_{Alt}/d_0\mathit{+}\frac{\text{1}}{A}}$$ (9)

for the alternative behavior, where all terms for both equations are as above, and d₀ reflects the biasing effects of learning to discriminate that reinforcement is not available for either option (i.e., the absence of alternative reinforcement signals that target reinforcement is also unavailable). Both V_T and V_Alt are divided by d₀ in Equations 8 and 9, thus representing a bias away from both options (i.e., a bias toward not responding). When d₀ =1 there is no additional bias and rates of both responses are governed by their relative values. As d₀ grows to >1, discrimination produces more bias away from both options and both B_T and B_Alt decrease.⁴

Equations 6–8 describe how the biasing terms related to discriminating based on the presence or absence of alternative reinforcement might impact target and alternative response rates above and beyond the longer-term values of the options. But, those equations are not particularly useful until numbers are actually provided for the d₁ and d₀ biasing terms across sessions. Context Theory suggests that the organism is learning the discriminations with exposure to the relevant stimuli across sessions. Thus, we assume that both d terms increase across sessions according to a simplified version of the learning curve suggested by Gallistel, Fairhurst, and Balsam (2004)⁵. Thus,

$$d_1=d_m(1-e^{-x_{on}})$$ (10)

and

$$d_0=d_m(1-e^{-x_{off}})$$ (11)

where d_m is a free parameter representing a shared asymptotic value of d₁ and d₀, and x_on and x_off correspond to sessions of exposure to “on” and “off” alternative reinforcement, respectively. It is important to note that both d₁ and d₀ are bias terms that are unitless ratios, just like other bias terms in the Matching Law. Such bias terms represent the ratio of responding to the two options that would result from the source of bias if the values of the two options were equal. Thus, for example d₁ = 3 represents a 3/1 bias toward the Alt, if all else were equal. Accordingly, the right-hand sides of all the response rate equations (i.e., Eqs. 6–9) are dimensionally consistent and deliver responses/min, as they should. But, to be more specific, these unitless bias terms represent the biasing effects of the proposed learned discriminations, and Equations 10 and 11 describe how such bias grows with experience with the things being discriminated. d_m (also a unitless ratio) is the asymptotic value of these biasing terms. Although it is certainly not impossible that the asymptotic values for the two functions could be different, we have yoked them at the same value in the interest of simplicity. According to Equations 10 and 11, the biasing effects of discriminating the relevant conditions during on and off sessions increase relatively quickly toward an asymptote with increasing sessions of exposure those conditions (i.e., alternative reinforcement either on or off).

Figure 8 shows a simultaneous fit of RaC² to target and alternative response rates from the present experiment. Again, the fit was conducted on logarithmic transformed data. Equations 6 and 7 were used to generate response rates for all sessions in which alternative reinforcement was present (i.e., all sessions of Phase 2 for the constant alternative reinforcement groups and all “on” sessions for the on/off group). Equations 8 and 9 were used to generate response rates for all sessions when alternative reinforcement was absent (i.e., all sessions of Phase 3 for the constant alternative reinforcement groups and all “off” sessions for the on/off group). The discrimination-based biasing terms d₁ and d₀ were applied to each session with their current-session values determined by Equations 10 and 11, in which x_on and x_off incremented by sessions of exposure to on and off conditions, respectively. The fit includes 346 data points and a total of five parameters: λ, k, a, and one d_m parameter for the constant alternative reinforcement groups (i.e., d_m) and one for the On/Off group (i.e., d_{m on/off}). Separate d_m parameters were permitted for the constant and On/Off alternative reinforcement groups based on the assumption that the on/off conditions might provide training that results in better discrimination of the relevant dimensions (i.e., essentially an assumption of Context Theory).⁶ The model simultaneously provides a good description of both target and alternative behaviors across all conditions with r² = .92. The model does a much better job than the original version of RaC, and remedies its problems with respect to the levels of target and alternative response rates, and the difference between the constant and on/off conditions of alternative reinforcement. Thus, we conclude that RaC² as formalized in Equations 6–11 provides a promising approach for combining aspects of RaC and Context Theory.

Fig. 8.

Response rates for target (top panel) and alternative (bottom panel) behavior across sessions for all groups. Data for the different groups are represented by differently colored solid lines. Mean target behavior response rates in the final three sessions of Phase 1 are presented above zero on the x axis. The predictions of RaC² for each group are shown as dotted lines of the same color as for the data. All data were fitted simultaneously. Note the logarithmic y axes.

One potential criticism of the fit in Figure 8 is that it involves five free parameters. Although five free parameters might seem like a lot, one must keep in mind that this is not a fit typical of that which occurs in much of the quantitative analysis of behavior, where a quantitative model is fitted to relatively few data points. For example, while the generalized matching law has only two free parameters, it is usually fitted to 10 or fewer data points representing only averages across sessions of steady-state performance. Thus, the fits of more well-accepted models often involve data-to-parameter ratios that are more than tenfold worse than the fit in Figure 8. The fit in Figure 8 involves 346 data points representing absolute response rates for behavior in transition in six different conditions and for two separate responses simultaneously.

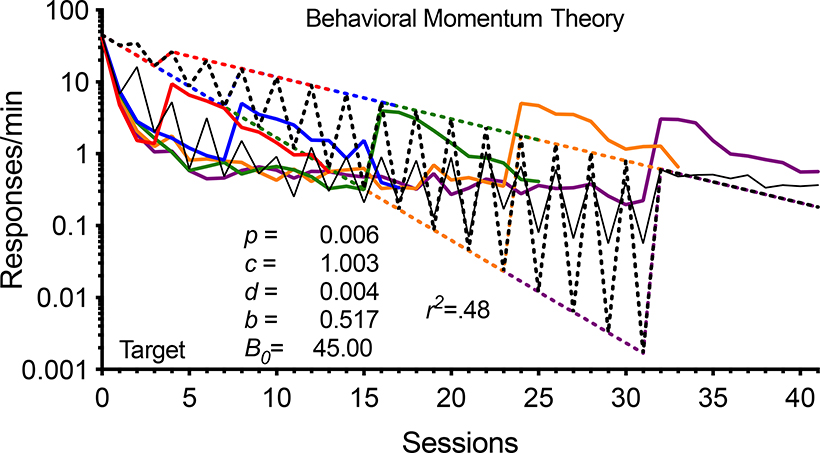
By way of comparison to the fit of RaC² in Figure 8, consider the only other existing quantitative model of resurgence. The Behavioral Momentum Theory of resurgence (Shahan & Sweeney, 2011) suggests

$$B_t=B_0\cdot 10^\left(\frac{-t(p{R}_a+c+dr)}{{(r+R_a)}^b}\right)$$ (12)

where Bt is the absolute rate of the target behavior at time t in extinction and B₀ is the baseline rate of the target response before extinction, c is a parameter reflecting disruption associated with breaking the target-response reinforcer contingency, d is a parameter scaling disruption associated with elimination of reinforcers from the situation (i.e., generalization decrement), r is a variable reflecting the rate of reinforcement for the target during baseline, and b is a parameter reflecting sensitivity to reinforcement rate. The variable R_a is the rate of reinforcement for alternative behavior during extinction, and the parameter p scales the additional disruptive impact of alternative reinforcement on the target behavior during extinction. Thus, like RaC² this model has five free parameters (c, d, b, p, and B₀). Unlike RaC², this model has no means to account for alternative behavior. In fact, it is not even clear how to apply the general conceptual approach of disruption by extinction and alternative reinforcement to the alternative behavior in Phase 2 at all. Thus, before beginning, Behavioral Momentum Theory has failed to provide any account for half of the data. Nevertheless, Equation 12 was fitted to the data for the target response in the present experiment, and the result is shown in Figure 9. Despite having exactly the same number of free parameters and only attempting to account for half of the data (i.e., 173 rather than 346 data points), Equation 12 fails marvelously, as is apparent visually and based on the poor quality of the fit (i.e., r² = .48). Thus, with the same number of parameters and twice the data, RaC² does a considerably better job than its only quantitative competitor.

Fig. 9.

Response rates for target behavior across sessions for all groups. Data for the different groups are represented by differently colored solid lines. Mean target behavior response rates in the final three sessions of Phase 1 are presented above zero on the x axis. The predictions of Behavioral Momentum Theory for each group are shown as dotted lines of the same color as for the data. Note the logarithmic y axes.

General Discussion

The data from the present experiment suggest that increases in the duration of treatment with extinction plus alternative reinforcement significantly reduce resurgence. The present study is the first to examine a range of treatment durations in the absence of other confounds, and it is the first to clearly demonstrate that decreases in target behavior with longer treatment durations are rather small, but reliable. Although RaC did a reasonably good job predicting the relation between target response rates in the first session of the resurgence test and treatment duration, the model failed in other respects. First, the present experiment replicated the previous findings of Schepers and Bouton (2015) and Trask et al. (2018) that exposure to alternating on/off alternative reinforcement reduces resurgence. RaC predicted that there should be no meaningful difference between constant and on/off alternative reinforcement. Second, fits of RaC’s equations to both target and alternative behavior across sessions and conditions revealed that the model did a poor job simultaneously accounting for both behaviors.

As a result of RaC’s failures with these data, we have proposed an expanded version of the model. Inspired by Context Theory, the new version (i.e., RaC²) quantitatively incorporates a role for more local discriminations of the relevant conditions of reinforcement for target and alternative behaviors—presumably based on the signaling effects of reinforcer deliveries or their absence. The model suggests that the biasing effects of such discriminations on response allocation are above and beyond the values of target and alternative options as longer-term repositories of experience (as provided by the temporal weighting rule). Thus, the new model represents an integration of RaC and a quantitative approximation of at least some aspects of Context Theory. This new model provides an excellent fit for the large dataset generated in the present experiment and does a good job simultaneously accounting for target and alternative behavior across different treatment durations and for both constant and on/off alternative reinforcement in Phase 2.

Although on/off alternative reinforcement reduced resurgence as compared to constant alternative reinforcement, it did not eliminate it completely. Even after 16 cycles of on/off alternative reinforcement across sessions, target behavior still increased when alternative reinforcement was removed in session 32. The increase was small, but it was reliable both statistically and at the individual subject level. We suggest that these increases reflect the relatively stable influence of the value of the target option over extended exposures to extinction. Although the improved discrimination of local reinforcement availabilities encouraged by on/off alternative reinforcement reduces resurgence as compared constant alternative reinforcement, the effects of the more extended history as represented in value seem to contribute to resurgence for a rather long time.

Clinically the effects of on/off alternative reinforcement could be important because they might provide a means to reduce resurgence as compared to standard implementations of DRA with constant alternative reinforcement. However, the small increases in target behavior with the omission of alternative reinforcement after even extended exposure to on/off alternative reinforcement suggest that the intervention could result in some tendency for problem behavior to return. Even a small increase in the tendency for problem behavior to return could result in reinforcement of that behavior via errors of commission and likely further increase problem behavior (see Greer & Shahan, 2019, for discussion). Thus, although on/off alternative reinforcement appears to hold promise as a means to reduce resurgence, additional research should consider means to improve the efficacy of the procedure by identifying ways to further reduce the impact of the longer-term history of reinforcement for the target behavior.

The need for additional research on the effects of on/off alternative reinforcement is also apparent in the continued discrepancy between the findings of Sweeney and Shahan (2013) and those of the present study, Schepers and Bouton (2015), and Trask et al. (2018). As noted above, (see Footnote 1) Sweeney and Shahan found that both on/off and constant alternative reinforcement generated resurgence, and that the magnitude of resurgence did not differ between the conditions. There are many differences between the studies, including the use of pigeons and a within-subjects design in which all pigeons experienced multiple exposures to extinction and resurgence tests. However, it is not apparent why such differences would be expected to eliminate the difference in resurgence between the on/off and constant reinforcement conditions. Perhaps more promising is the fact that Sweeney and Shahan used leaner schedules of reinforcement in Phase 1 (i.e., VI 60 s) and in Phase 2 (VI 30 s) than did the present study, Schepers and Bouton, and Trask et al.—all of which used a VI 30 s in Phase 1 and a VI 10 s in Phase 2. Given the robust effects of Phase 2 rate of alternative reinforcement and the relatively smaller effects of Phase 1 target reinforcement rate on resurgence (see Craig & Shahan, 2016), we suspect that the difference in results could be due to the difference in Phase 2 alternative reinforcement rate. Indeed, if the effects of on/off alternative reinforcement are due to the learning of discriminations related to the presence versus absence of alternative reinforcement, then it stands to reason that the lower rate of Phase 2 alternative reinforcement might be less effective at training such discriminations. Future research should systematically examine this possibility.

Ghosts of Models Past and Future

The original version of RaC was developed as a result of the accumulation of serious failings (see Craig & Shahan, 2016; Nevin et al., 2017, for reviews) of its predecessor, the Behavioral Momentum Theory of resurgence (Shahan & Sweeney, 2011). Fits of Behavioral Momentum Theory to the data from the present experiment reveal yet more serious problems for the model. At this point, it appears to us that the current version of the Behavioral Momentum Theory of resurgence need not be seriously considered further. Nevertheless, we note that a more recent formulation of the general framework of behavioral momentum (Killeen & Nevin, 2018) based on Killeen’s (1994) Mathematical Principles of Reinforcement is couched in terms of response competition, and as those authors note, shares some conceptual similarities to the choice-based approach of RaC. As of yet, this new approach has not been extended to resurgence or other relapse phenomena. Perhaps such an extension could revive a momentum-based approach to resurgence and provide a reasonable quantitative competitor to the amended version of RaC developed here.

We also note that the model developed here shares many conceptual similarities with a discrimination-based approach to choice in which behavioral allocation is said to be governed by discrimination of reinforcers distributed in time and space (see Cowie & Davison, 2016; Cowie, Davison, & Elliffe, 2016, for reviews). The quantitative formulation of this model is based on the Matching Law, and more specifically, a refined version of the more general Davison and Nevin (1999) model of stimulus control. A version of this model (Bai, Cowie, & Podlesnik, 2017) has been extended to account for a resurgence-like effect in the free-operant psychophysical procedure typically used to study timing, but it is not clear how that version of the model could be applied to resurgence data from more typical arrangements. Nevertheless, should such an approach be extended to resurgence more generally, it might also provide a reasonable quantitative competitor to the model developed here.

Finally, the present model quantifies some aspects of the purely descriptive, narrative account of resurgence provided by Context Theory. Our previous concerns about Context Theory (e.g., Greer & Shahan, 2019; Shahan & Craig, 2017) have never been rooted in a denial that reinforcer deliveries might serve as signaling stimuli (in fact we would assert that is all they ever do; Shahan, 2017), but rather that the narrative nature of Context Theory is not sufficiently precise to allow rigorous empirical assessment. There is no doubt that the unparalleled scope of Context Theory in accounting for relapse phenomena in general has been admirable, but this scope has come at the extreme expense of precision. It is our hope that the quantitative integration of some aspects of Context Theory into the choice-based framework of RaC will lead to a formal quantitative account of relapse in general with the scope of Context Theory. For example, the biasing effects of discriminations of reinforcer presence or absence might be extended to reinstatement, or replaced with the biasing effects of explicit contextual stimuli signaling differential reinforcement conditions in an extension to renewal. We postpone until a subsequent paper further exposition and evaluation of such a more general quantitative approach to relapse as choice in context.