Summary
Meta-analyses of a treatment’s effect compared to a control frequently calculate the meta-effect from standardized mean differences (SMDs). SMDs are usually estimated by Cohen’s d or Hedges’ g. Cohen’s d divides the difference between sample means of a continuous response by the pooled standard deviation, but is subject to non-negligible bias for small sample sizes. Hedges’ g removes this bias with a correction factor. The current literature (including meta-analysis books and software packages) is confusingly inconsistent about methods for synthesizing SMDs, potentially making reproducibility a problem. Using conventional methods, the variance estimate of SMD is associated with the point estimate of SMD, so Hedges’ g is not guaranteed to be unbiased in meta-analyses. This article comprehensively reviews and evaluates available methods for synthesizing SMDs. Their performance is compared using extensive simulation studies and analyses of actual datasets. We find that because of the intrinsic association between point estimates and standard errors, the usual version of Hedges’ g can result in more biased meta-estimation than Cohen’s d. We recommend using average-adjusted variance estimators to obtain an unbiased meta-estimate, and the Hartung–Knapp–Sidik–Jonkman method for accurate estimation of its confidence interval.
Keywords: bias, Cohen’s d, confidence interval, Hedges’ g, meta-analysis, standardized mean difference
1 |. INTRODUCTION
Meta-analysis is a statistical tool for combining sources of evidence from multiple related but independent studies. It was introduced decades ago and is now increasingly used across a wide range of disciplines, especially in medical sciences.1,2,3 Despite the rapid development of meta-analysis methods and their increasing use to address real-world questions, the practices of meta-analyses often overlook fundamental problems, including conventional assumptions about within-study variances and normality,4,5 as well as discrepancies in statistical methods used to perform the analyses.6 These practices may lead to biased and conflicting results from different meta-analyses on the same topic.7 Specifically, most meta-analyses treat the sample within-study variance as the true variance; this assumption leads to misunderstanding about properties of the commonly-used Q test for heterogeneity8 and, more importantly, considerable biases in meta-estimates when sample sizes are small.9 This article focuses on problems in the meta-analysis of standardized mean differences (SMDs), including inconsistent notation and estimators for the SMD and biases caused by conventional methods for synthesizing SMDs. We use simulation studies and analyses of empirical data to compare the performance of various SMD estimators in meta-analysis.
When the outcome of a study is a continuous measure, it is common to compare the treatment and control groups using the difference between their sample means, i.e., the mean difference. Because a meta-analysis synthesizes results from all available studies, different studies commonly use different scales for the continuous measure.10 For example, in a meta-analysis of the body-mass response to an intervention, body mass may be measured in some studies as body weight and in other studies as body mass index (calculated as body weight divided by the square of body height).11 In such cases, the mean difference can be transformed to a common scale by dividing by the measure’s standard deviation (SD); the resulting effect size is referred to as the SMD, which is considered to be more comparable across studies.12,13 An SMD can be obtained readily from most published studies with continuous outcomes; for example, the SMD is proportional to the t-statistic, and p-values from t-tests are commonly reported.14 Compared to an SMD, the raw mean differences (or the SDs) may be less often present in published data, limiting their availability in systematic reviews.
Despite the flexibility offered by the SMD, several problems attend their use in practice. First, various estimators are available to calculate the SMD, including Glass’ Δ, Cohen’s d, and Hedges’ g. This article focuses on the last two estimators because they are more widely used than other estimators. Second, notation used to denote the estimator of the SMD may be inconsistent in publications in different disciplines. For example, in the landmark book of Hedges and Olkin15 (pp. 78 and 81) on statistical methods for meta-analysis, the estimator that is commonly called Hedges’ g in current medical meta-analyses was originally denoted by d, while Cohen’s d was denoted by g. This inconsistent notation may lead to misuse of statistical formulas to calculate the estimators and their variances.7 Third, from a practical perspective, many clinicians may find the SMD difficult to interpret,16 and understanding estimation of the SMD and its variance requires non-trivial statistical knowledge. Fourth, various methods are available to estimate the variance of the SMD, leading to different choices of weights for the studies in a meta-analysis. Consequently, practitioners may be confused about choosing a proper variance estimator or weight. Inconsistent use of these methods may impact the reproducibility of meta-analyses of SMDs,17 and may lead to substantial disagreement when a meta-analysis is validated by other researchers.18
In addition, commonly-used estimators of the SMD’s variance depend on the point estimate of the SMD, and this intrinsic association within each study may introduce considerable bias in meta-estimates.9,19,20 This bias was noted in early work by Hedges,21,22,23 but it is frequently neglected in recent meta-analysis practice. Approaches to combining SMDs therefore need to be clearly reviewed and examined by meta-analysts.
This article is organized as follows. Section 2 comprehensively reviews estimators of the SMD and its variance. Section 3 explains the bias in the synthesized SMD in conventional meta-analysis methods and summarizes alternative methods designed to reduce this bias. It also gives approaches to constructing a confidence interval (CI) for the synthesized SMD. Section 4 presents extensive simulation studies to compare various estimators of the SMD and its variance. Section 5 gives two examples of empirical datasets. Section 6 provides a summary of popular software packages for meta-analyses of SMDs, and Section 7 closes with a brief discussion.
2 |. STANDARDIZED MEAN DIFFERENCE
2.1 |. Notation
Consider a meta-analysis of N independent studies with continuous outcomes; each study compares the same two groups (say, control and treatment). Let ni0 and ni1 be the numbers of subjects in the control and treatment groups in study i, respectively. Define
Assume the outcome measures of the subjects in each group independently follow a normal distribution; the distributions in the control and treatment groups within each study have population means μi0 and μi1, respectively, and share a common SD σi. Let and be the sample mean and sample variance in the control group, respectively, and define and analogously for the treatment group. These estimates are commonly reported in published articles and can be used to calculate the SMD.
The true value of the SMD in study i is defined as
A straightforward estimator for this estimand plugs in the point estimates of the three parameters μi0, μi1, and σi. The common SD σi of the two groups is estimated as the pooled sample SD, i.e.,
Thus, one estimator of the SMD is
| (1) |
which is called Cohen’s d, referring to Cohen24 (p. 66). This estimator can be shown to be biased; a bias-corrected estimator, called Hedges’ g, is widely used as an alternative and is described below.21 Sections 2.2 and 2.3 introduce properties of the two estimators in detail.
2.2 |. Cohen’s d
To examine the bias of Cohen’s d as an estimate of SMD for a single study, we first focus on its distribution. Although conventional meta-analysis methods model the SMDs as normal random variables, Cohen’s d actually follows a t-distribution (after multiplying by a constant ), which may or may not be a central t, depending on the true SMD. Specifically, consider , where the numerator follows and thus can be written as , for Zi a standard normal random variable with mean 0 and variance 1. Note that and follow χ2 distributions with ni0 − 1 and ni1 − 1 degrees of freedom, respectively. They are mutually independent because they are based on different subjects in the control and treatment groups; they are also independent of the sample means and (see, e.g., Theorem 5.3.1 in Casella and Berger25). The denominator of , siP/σi, can be written as , where Vi follows a χ2 distribution with mi degrees of freedom, and it is independent of the numerator. Consequently, , so it follows a t-distribution with mi degrees of freedom and noncentrality parameter .
Using properties of the noncentral t-distribution, the expectation and variance of Cohen’s d are (Hedges and Olkin,15 p. 104):
| (2) |
| (3) |
where and Γ(·) is the gamma function. The expectation in Equation (2) is valid for mi > 1 and the variance in Equation (3) is valid for mi > 2; otherwise, they do not exist. Equation (2) indicates that the bias of Cohen’s d is [1/J(mi) − 1]θi. Section A1 in the Supplemental Material shows that J(mi) increases in mi, so the bias converges to 0 as the total sample size increases. Cohen’s d is unbiased if the true SMD θi is 0, but the bias increases (in absolute magnitude) as the true value θi departs from 0.
In practice, J(mi) is frequently approximated as . Figure 1A compares these two forms. Their values are nearly identical for mi > 5, and their difference at mi = 3 is less than 0.004, so the approximation is considered excellent. Using the approximation became a convention because of limited computational capacity, but the exact form J(mi) can now be calculated accurately and quickly using various software; Section 6 gives more details. To avoid any inaccuracy caused by the approximation, throughout this article we use the exact form J(mi) in analyses regarding properties of the SMDs.
FIGURE 1.
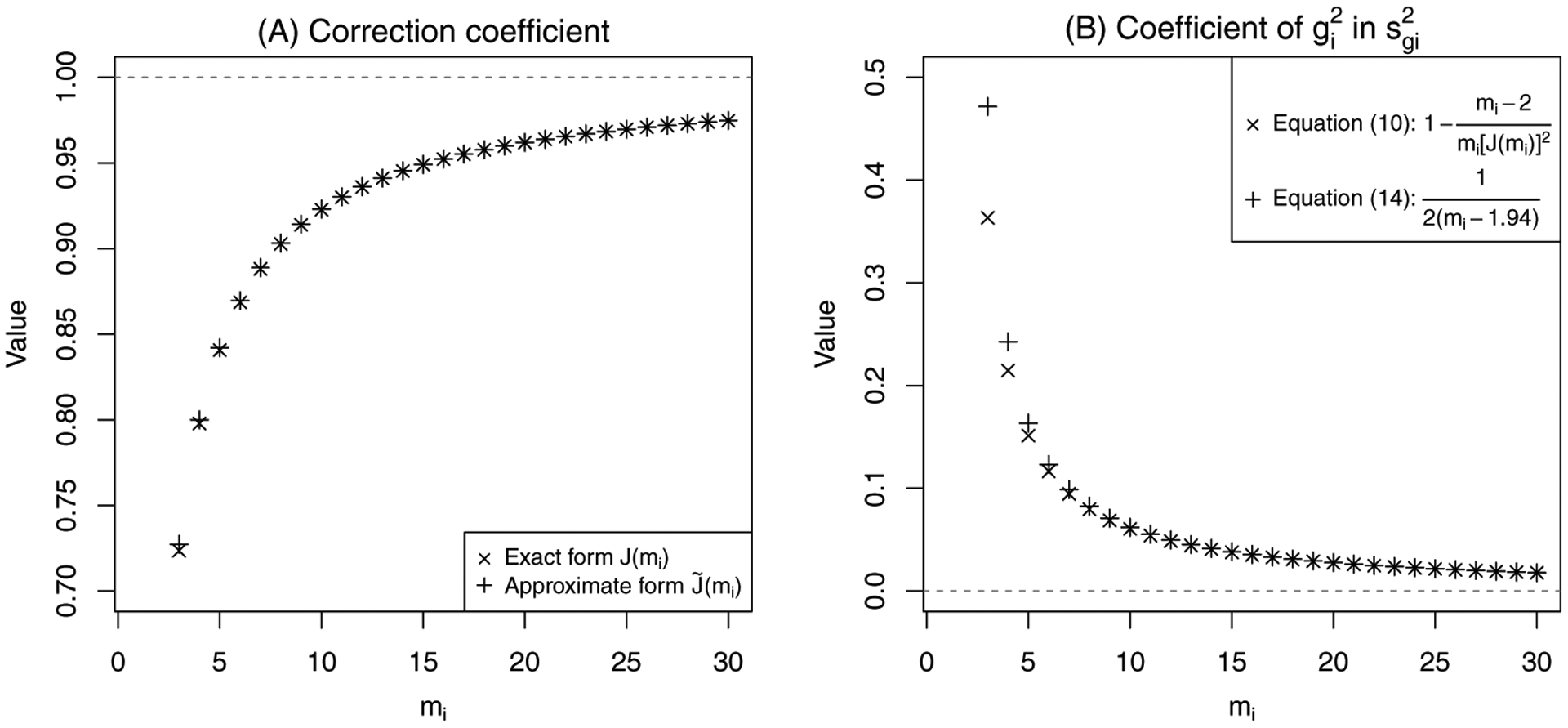
(A) The exact form of the correction coefficient J(mi) and its approximate form ; and (B) the coefficients of in the variance estimators of Hedges’ g in Equations (10) and (14) for mi = 3, 4, …, 30.
A meta-analysis synthesizes the SMDs by using their within-study variances to determine the studies’ weights. The exact variance in Equation (3) cannot be used directly, because it contains the unknown true SMD θi. Various estimators are available for the variance of Cohen’s d. For example, an unbiased estimator is26
| (4) |
This unbiased estimator is seldom used in meta-analysis applications. Instead, the variance is commonly approximated using large-sample properties, while various meta-analysis guidebooks suggest different approximations. For example, Egger et al.27 (p. 290) and Hartung et al.28 (p. 15) suggested
| (5) |
while Cooper et al.29 (p. 226), Borenstein et al.30 (p. 27), and Stangl and Berry31 (p. 37) suggested
| (6) |
Essentially, the first two terms of Equations (5) and (6), , reflect the variance of the numerator of Cohen’s d, and the third term, a function of , reflects the variance of the denominator of Cohen’s d. The two estimators have slightly different denominators due to different assumptions used for their large-sample approximation (see p. 28 of Borenstein et al.30).
Sections A2–A4 in the Supplemental Material give derivations of Equations (2)–(6).
2.3 |. Hedges’ g
Because Cohen’s d is biased when the true SMD θi ≠ 0, Hedges21 proposed a bias-corrected estimator
| (7) |
multiplying Cohen’s d by J(mi). This estimator is called Hedges’ g. Equations (2) and (3) give the expectation and variance of Hedges’ g as
| (8) |
| (9) |
Equation (8) shows Hedges’ g is unbiased.
Based on the unbiased estimator of the variance of Cohen’s d in Equation (4), note that implies , so is an unbiased estimator of the variance of Hedges’ g. Specifically, this estimator is26
| (10) |
As for Cohen’s d, meta-analysts seldom use this unbiased estimator in practice; instead, they usually use the large-sample approximation of the variance of Cohen’s d in Equation (5) or (6) to estimate the variance of Hedges’ g:
| (11) |
or
| (12) |
Besides the above estimators, because J(mi) converges to 1 when the sample sizes are large, Hedges and Olkin15 (p. 86) suggested estimating the variance using
| (13) |
Koricheva et al.32 (p. 63), Pigott33 (p. 10), and Lipsey and Wilson34 (p. 49) also used this variance estimator.
Some books (e.g., p. 25 in Schwarzer et al.35 and p. 212 in Schlattmann36) used another variance estimator:
| (14) |
This likely originated from Equation (8) in the seminal work of Hedges and Olkin15 (p. 80); however, readers should be aware that the original equation contained the true SMD, and Hedges and Olkin15 did not directly suggest replacing the true value with the estimated SMD to obtain the above Equation (14). More importantly, the symbol g used by Hedges and Olkin15 actually refers to Cohen’s d, while the symbol d in that book refers to Hedges’ g; see Section 2.5 for more discussion. Therefore, the rationale of the variance estimator of Hedges’ g in Equation (14) has never been well justified.
Figure 1B compares the coefficient of in Equation (14), , with that in the unbiased estimator in Equation (10), . It shows that the two coefficients are very similar when mi ≥ 5, so the estimator in Equation (14) may perform similarly to the unbiased estimator in Equation (10).
2.4 |. Alternative estimators of standardized mean difference
Besides Cohen’s d and Hedges’ g, alternative estimators for SMD are available. For example, Glass37 and Glass et al.38 (p. 29) suggested using the sample variance in the control group to standardize the mean difference. This estimator is called Glass’ Δ. Specifically,
| (15) |
where si0 is the sample SD in study i’s control group. The rationale for Glass’ Δ is that the control group represents a general population, and it may be preferred if the true standard deviations in the two groups differ greatly (e.g., based on Levene’s test).39
Cohen’s d in Equation (1) uses the unbiased pooled variance . The maximum-likelihood variance estimator may alternatively be used to estimate the SMD (Hedges and Olkin,15 pp. 81 and 82). We denote this estimator by
| (16) |
Hedges and Olkin15 (p. 82) also introduced a shrunken estimator with smaller mean squared error (MSE) than Cohen’s d and Hedges’ g. Cohen40 (p. 44) gave an SMD estimator that uses the average of the variances from the treatment and control groups, without assuming homoscedasticity. Because Cohen’s d and Hedges’ g are applied much more commonly than other estimators in practice, the analyses in this article focus on these two estimators.
2.5 |. Inconsistent notation in different publications
Most meta-analysis books introduce only some of the above SMD estimators, and their notation is frequently inconsistent. Table 1 summarizes notation for four SMD estimators in 13 books. Rigorous meta-analysis methods were developed in educational, psychological, and ecological sciences in the 1980s; the estimator in Equation (7), which we call Hedges’ g, is often called d in these disciplines (e.g., Hedges and Olkin15 and Koricheva et al.32). In the medical and epidemiological literature, meta-analysis was extensively debated and began to thrive in 1990s,41,42,43,44,45,46 and researchers prefer the name Hedges’ g for the estimator in Equation (7) (e.g., Egger et al.27). Consequently, when referring to books from different disciplines, meta-analysts should be aware of the definitions of the estimators and apply the corresponding formulas with great caution.
TABLE 1.
Notation for estimators of the standardized mean difference in 13 meta-analysis books (sorted by publication years).
| Book | Notation | |||
|---|---|---|---|---|
| Glass’ Δ in Equation (15) | Cohen’s d in Equation (1) | Cohen’s d′ in Equation (16) | Hedges’ g in Equation (7) | |
| Hedges and Olkin15 (1985) | g′ | g | d | |
| Hunter and Schmidt81 (1990) | dG | d | NA | d⋆ |
| Stangl and Berry31 (2000) | NA | z | NA | NA |
| Egger et al.27 (2001) | Δ | d | NA | g |
| Lipsey and Wilson34 (2001) | NA | ESsm | NA | |
| Hartung et al.28 (2008) | Δ | g | d | g⋆ |
| Borenstein et al.30 (2009) | NA | d | NA | g |
| Cooper et al.29 (2009) | NA | d | NA | g |
| Schlattmann36 (2009) | NA | d | NA | g |
| Card82 (2012) | gGlass | g | d | gadjusted |
| Pigott33 (2012) | NA | NA | NA | d |
| Koricheva et al.32 (2013) | NA | NA | NA | d |
| Schwarzer et al.35 (2015) | NA | NA | NA | g |
Note: NA, not available.
3 |. META-ANALYSIS OF STANDARDIZED MEAN DIFFERENCES
3.1 |. Conventional methods
A meta-analysis synthesizes SMDs from the N studies based on their summary data, i.e., , where yi = di and for Cohen’s d or yi = gi and for Hedges’ g. The estimated within-study variances are treated as if they are the true values, but this assumption is valid only for sufficiently large sample sizes. The synthesized SMD is , where the study-specific weights are in the common-effect model and in the random-effects model.47 Here, is the estimate of the between-study variance τ2 under the random-effects model. The most widely-used estimator of τ2 was a method-of-moments estimator proposed by DerSimonian and Laird.48 Several alternatives have since been shown to outperform it, such as the restricted maximum-likelihood (REML) estimator and the Paule–Mandel estimator.49,50,51,52,53,54,55
Note that the conventional variance estimators reviewed in Section 2 can be expressed as for either Cohen’s d or Hedges’ g, where ai and bi are constants (i.e., functions of the sample sizes ni0 and ni1) in each study. For example, and in Equation (10). Because the conventional variance estimators always include the term , the SMD estimates yi and their weights wi are associated within studies for both Cohen’s d and Hedges’ g. Without treating as fixed values as in conventional meta-analysis methods, it is invalid to simply decompose the expectation of the synthesized SMD as . For example, consider the common-effect setting where the true SMDs θi in all studies equal a common value θ. The expectation of the synthesized SMD is
where is the probability density function (pdf) of yi (Cohen’s d or Hedges’ g) in study i. Recall that (equivalently, ) follows a (noncentral) t-distribution with mi degrees of freedom and noncentrality parameter, with pdf denoted by . The pdf of the SMD estimate yi is then
The exact expectation of cannot be derived. Even if each study-specific random variable follows central t-distributions with θ = 0, it is still very challenging to derive the distribution of their linear combination.56
3.2 |. Illustration of asymptotic bias produced by conventional methods
Because yi is associated with (equivalently, with the weights wi), an estimator (e.g., Hedges’ g) that is unbiased at the individual-study level may not give a synthesized estimator that is unbiased. To briefly illustrate this problem, we focus on the common-effect setting with θi = θ as in Section 3.1, and assume that each study has the same sample sizes ni0 = n0 and ni1 = n1 in the control and treatment groups. Then the study-specific SMD estimates yi are independent and identically distributed (iid). The constants ai and bi in the variance estimators depend only on ni0 and ni1, so they are the same in all studies and can be denoted by ai = a and bi = b. Similarly, mi = m = n0 + n1 −1 and qi = q = n0n1/(n0 + n1). We consider the asymptotic case in which the number of studies N → ∞. Although these settings are not useful in practice, they simplify expressions and suffice for our illustrative purpose.
Under the above assumptions,
where the numerator and denominator converge to and in probability, respectively, by the law of large numbers. Consequently, by the continuous mapping theorem,57
| (17) |
where denotes the convergence in probability.
If the true SMD θ = 0, then yi multiplied by a constant c follows a central t-distribution with m degrees of freedom. Here, for Cohen’s d and for Hedges’ g. Let ti = cyi be N such t-distributed random variables. Because a > 0 and b > 0,
Applying properties of the central t-distribution, E[|ti|] < ∞ if the degrees of freedom m > 1, which is generally true in practice; thus, exists. Because the pdf of the central t-distribution is symmetric around 0, i.e., t(x; m, 0) = t(−x; m, 0), we have
Consequently, , so the synthesized SMD is asymptotically unbiased when the true SMD θ = 0.
The argument above does not generalize to the situation of θ ≠ 0, where the random variables ti have noncentral t-distributions. It is difficult to theoretically calculate the asymptotic bias by solving the integrals in Equation (17)’s expectations. Instead, Monte Carlo methods can be used to numerically approximate those expectations and thus derive the asymptotic bias. Figure 2 presents the (approximated) asymptotic biases of the synthesized SMD produced by the conventional common-effect meta-analysis using Cohen’s d and Hedges’ g with different variance estimators, including those in Equations (4)–(6) and (10)–(14). These biases are approximated by sampling 107 iid random variables to approximate the expectations in Equation (17). In the panels of Figure 2, the sample size ratio r = n0/n1 is 1 or 2, and the true SMD θ is ±0.2, ±0.5, or ±0.8, representing different treatment effects (Cohen,40 pp. 25–27).
FIGURE 2.
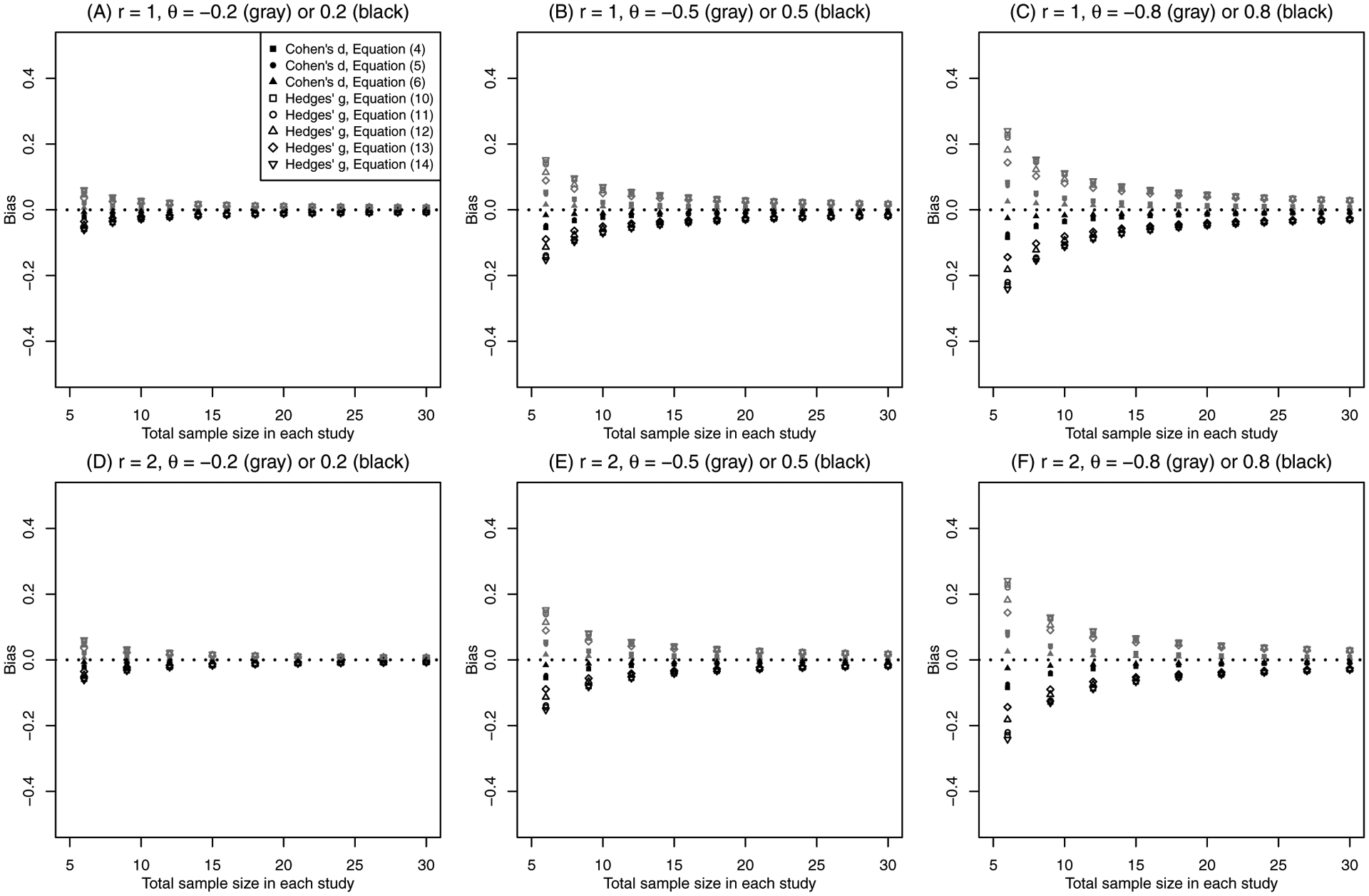
Asymptotic bias of the synthesized standardized mean difference using conventional variance estimators under the common-effect setting. The sample size ratio r is 1 (upper panels) or 2 (lower panels), and the true standardized mean difference θ changes from ±0.2 (left panels), to ±0.5 (middle panels), and to ±0.8 (right panels). The filled points represent the results of Cohen’s d, and the unfilled points represent those of Hedges’ g.
Figure 2 implies that both Cohen’s d and Hedges’ g are biased asymptotically for all variance estimators introduced in Sections 2.2 and 2.3, but the magnitude of bias differs for different estimators. Although Hedges’ g is an unbiased estimator of the SMD within each individual study, the synthesized Hedges’ g is noticeably more biased than the synthesized Cohen’s d. Generally, in meta-analyses Hedges’ g with the variance estimator in Equation (14) produces the largest bias in absolute magnitude, while Cohen’s d with the variance estimator in Equation (6) produces the smallest bias. A larger true SMD leads to a larger bias in absolute magnitude. As the total sample size in each study increases, the bias converges to 0. For θ = ±0.8, the asymptotic bias can be influential (around 0.2) when the total sample size is very small (e.g., 6), and it still reaches as high as 0.03 for a moderate total sample size of 30. The sample size ratio r (varying from 1 to 2) has little impact on trends in the asymptotic bias.
In the conventional random-effects meta-analysis, the estimated between-study variance depends on the data from all studies and is incorporated in the studies’ weights . As in the common-effect meta-analysis, these weights are associated with the study-specific SMD estimates yi, so the synthesized SMD is also subject to bias.
These illustrative examples show that the rationale for using Hedges’ g with conventional variance estimators needs to be carefully examined. Although Hedges’ g is designed to reduce bias in individual studies, in meta-analysis it may not perform as researchers expect. Section 4 shows extensive simulation studies under more realistic settings to evaluate the performance of different meta-analysis methods for synthesizing SMDs. Before that, Sections 3.3 introduces several attempts to reduce bias of the synthesized SMD in meta-analyses.
3.3 |. Alternative methods for reducing bias in meta-analysis
The bias in the synthesized SMD was noted by Hedges,22,23 but this problem is neglected in many current meta-analyses. Doncaster and Spake9 showed that even without bias, the variability in the variance estimate may lead to underestimation of the meta-variance and thus low coverage of the CI. To eliminate the bias in the common-effect setting, Hedges22 proposed to remove from the variance of Hedges’ g in Equation (9) the part associated with θi, and thus use
| (18) |
to determine the studies’ weights. Because weights based on the above variances depend only on sample sizes and are not associated with the study-specific Hedges’ g, the synthesized Hedges’ g is guaranteed to be unbiased. However, these weights are not optimal because they ignore the reality that the within-study variances increase with effect sizes. The synthesized SMD may have a larger MSE than an estimator weighted by the more accurate variance estimators in Equations (10)–(13), especially when the true SMD departs from 0.20
In the random-effects meta-analysis, Hedges23 used the unbiased estimator of the variance of Hedges’ g in Equation (10) to derive the weights , but he acknowledged the bias produced by this weighting. He suggested alternative weights based on study-specific total sample sizes, i.e., wi = ni0 + ni1. The resulting sample-size-weighted SMD estimate is23
| (19) |
This weighting helps remove the bias in the meta-estimator but it may still be inefficient.58
Rather than using weights computed by completely removing the terms associated with θi in the variance estimators, we may instead consider replacing these study-specific terms with a cross-study averaged term. This approach reduces the association between the SMD estimates gi and their estimated variances within studies, and thus reduces the bias in the synthesized estimator of SMD. Of note, this approach is not limited to the SMD but can also apply to other effect measures including the mean difference, response ratio, and odds ratio.9,59
Specifically, we may use the sample-size-weighted SMD estimate in Equation (19) to calculate adjusted within-study variances as
| (20) |
Alternatively, Hedges22 suggested first calculating based on the variance estimator in Equation (13) and then plugging it into Equation (20) to better adjust the within-study variances. Hedges and Olkin15 (p. 129) suggested replacing the arithmetic mean with the study-specific true SMD θi in Equation (9), leading to this variance estimator:
| (21) |
Doncaster and Spake9 proposed a variance adjustment based on Equation (12). They replaced the study-specific squared Cohen’s d, , in Equation (12) with its average across studies, , that is,
| (22) |
The foregoing approaches were originally considered for Hedges’ g and they can also be applied to synthesize Cohen’s d. However, because Cohen’s d is biased within studies, it may be of less interest to apply such bias-reduction procedures to Cohen’s d. Due to the bias at the individual-study level, the synthesized Cohen’s d is still biased even if the association between the study-specific Cohen’s d and its corresponding weight can be reduced.
3.4 |. Confidence interval for the synthesized standardized mean difference
Besides the point estimates of the synthesized SMD, several methods are available to construct a CI. Recall that the synthesized SMD is , where yi is Cohen’s d or Hedges’ g and wi is the inverse of the marginal variance of yi; under the common-effect setting, and under the random-effects setting. A conventional (1 − α) × 100% CI is:
| (23) |
where z1−α/2 is the 1 − α/2 quantile of the standard normal distribution. This CI is applicable under both the common- and random-effects settings. Hartung and Knapp62,61 and Sidik and Jonkman60,63 proposed an alternative CI for the random-effects setting:
| (24) |
where tN−1,1−α/2 is the 1 − α/2 quantile of the t-distribution with N − 1 degrees of freedom.
The CI in Equation (23) corresponds to conventional meta-analysis methods, in which the variance of the synthesized SMD is calculated as . The used in the weights wi can be any study-specific variance estimator from Sections 2.2 and 2.3 or an alternative variance estimator in Equation (18), (20), or (22) in Section 3.3.
Two key assumptions are required for this CI to be valid: (i) follows a normal distribution; and (ii) the weights wi are fixed, known values. Asymptotically, both assumptions are approximately true if the sample sizes in each study, ni0 and ni1, are sufficiently large. Strictly speaking, assumption (i), normality, can never be true because the synthesized SMD is a linear combination t-distributed random variables. Assumption (ii) may not be exactly true because the study-specific variance estimators in Sections 2.2 and 2.3 involve the point estimate of the SMD and the estimated between-study variance under the random-effects setting may be highly variable. If either assumption is seriously violated, the CI in Equation (23) may have poor coverage probability.
The CI in Equation (24) partly relaxes assumption (ii). Specifically, in the random-effects setting the weights wi depend on , while the variation in is ignored in the conventional CI in Equation (23). The Hartung–Knapp–Sidik–Jonkman CI in Equation (24) is designed to account for variation in . This alternative CI has been shown to have better coverage probability in meta-analyses generally (i.e., not just meta-analyses of SMDs), especially when the number of studies is small.51,64
Variation in the study-specific sample variances impacts the validity of assumption (ii). When combining Hedges’ g using the variance estimator in Equation (18) or using the sample-size-weighted estimator in Equation (19), the depend only on sample sizes and thus can be treated validly as fixed values. The variance estimators in Equations (20)–(22) use the averaged SMD to adjust the study-specific variance; a single study’s estimate of variance may considerably exceed the averaged estimate. Assumption (ii) may be better satisfied by the techniques in Section 3.3 than when using the variance estimators in Sections 2.2 and 2.3.
Although the average-adjusted variance estimators in Section 3.3 are more suitable for assumption (ii), they may be inaccurate for calculating the variance of the synthesized SMD and thus constructing the CI in Equation (23), especially if the effect sizes substantially differ across studies. We may borrow the idea of Henmi and Copas,65 in the context of publication bias, to refine the CI of in Equation (23). Specifically, they propose to calculate the point estimate of the overall effect size under the common-effect setting but derive its CI under the random-effects setting. Given that studies with larger sample sizes may be of higher quality and less subject to risk of bias, the common-effect point estimate may be preferable because it assigns larger weights to larger studies compared with the random-effects point estimate. On the other hand, by allowing potential heterogeneity when deriving the variance in the random-effects setting, the CI may have a better coverage probability.
When synthesizing SMDs we may use a similar idea, applying two types of variance estimators, to construct the CI. That is, use a variance estimator from Section 3.3—which is less associated with study-specific estimates and better satisfies assumption (ii)—to derive study-specific weights, and use a different variance estimator from Section 2.3—which is more accurate for a single study—to calculate the variance of the synthesized SMD. Specifically, let be the within-study variance estimator used to derive the weights, and be the estimator used to calculate the variance of the synthesized SMD. In the random-effects setting, is used to estimate the between-study variance and the weights are ; in the common-effect setting the weights are simply . Under assumption (ii), the variance of is
Note that Var(yi) is no longer 1/wi as in the CI construction in Equation (23). Instead, in the common-effect setting, the study-specific variance is , so the (1 − α) × 100% CI of the synthesized SMD can be constructed as
| (25) |
In the random-effects setting, the study-specific marginal variance is estimated as , so the (1 − α)×100% CI is
| (26) |
4 |. SIMULATION STUDIES
4.1 |. Simulation designs
We devised simulation studies to evaluate the performance of the various methods for synthesizing SMDs. The simulation settings were in a factorial design. Specifically, the number of studies in a simulated meta-analysis was set to N = 5 or 20, the true between-study SD τ was 0.1 or 0.5, and the true overall SMD θ was 0, 0.3, or 0.8, representing no, moderate, or large treatment effects, respectively. The study-specific true SMDs were sampled as θi ~ N(θ, τ2). For simulated meta-analyses with N = 5 studies, the sample size within each study was ni = {6, 8, 10, 12, 14} (small sample sizes) or ni = {30, 40, 50, 60, 70} (moderately large samples sizes). The treatment allocation ratio was 1:1; thus, each study’s control and treatment groups had ni0 = ni1 = ni/2 individuals. For simulated meta-analyses with N = 20 studies, each of these 5 sample sizes was repeated four times. The study-specific true SDs of the continuous outcome measures were σi = {1, 2, 3, 4, 5} in both treatment groups for meta-analyses with N = 5 studies; for meta-analyses with N = 20 studies, each of these 5 study-specific SDs was repeated 4 times. Without loss of generality, the true population mean of the outcome measures in each study’s control group was μi0 = 0, and in study i’s treatment group was μi1 = μi0 + θiσi. In study i, the outcome measures for individuals in the control group were generated as for j = 1, …, ni0, and those in the treatment group were generated as for k = 1, …, ni1. From these outcome measures, we obtained the sample means, and , and sample variances, and , in the control and treatment groups, respectively. Cohen’s d, Hedges’ g, and their estimated variances based on the various methods were then computed in each study. The above factorial design led to a total of 24 settings (resulting from 2 values of the number of studies, 2 values of the between-study variance, 3 values of the true overall SMD, and 2 sets of study-specific sample sizes). We simulated 10,000 meta-analysis datasets for each setting. We used the REML method to estimate the between-study variance; for some datasets, optimization of the restricted likelihood did not converge, leading to computational errors. The error rate depended on the simulation settings. We omitted such datasets and simulated new meta-analysis datasets until we obtained 10,000 replicates for which the REML maximization converged.
For each simulated meta-analysis, we considered Cohen’s d with variance estimators in Equations (4)–(6) and Hedges’ g with variance estimators in Equations (10)–(14) and (20)–(22), i.e., a total of 11 methods. Recall that the variance estimators in Equations (20)–(22) use an averaged SMD to reduce the association between Hedges’ g and its variance. We used the method suggested by Hedges22 to obtain the estimator in Equation (20), as detailed in Section 3.3. All meta-analyses were performed using the R package “metafor” under the random-effects setting, because heterogeneity is generally expected.66
We calculated the point estimate specified by each method. As described in Section 3.4, we derived the 95% CI for each method using the conventional interval in Equation (23) and the Hartung–Knapp–Sidik–Jonkman interval in Equation (24).62,60,64 For the three methods based on the average-adjusted variance estimators in Equations (20)–(22), we also computed 95% CIs using Equation (26). The performance of each method was evaluated by the point estimate’s bias and root mean squared error (RMSE), and by the CI’s coverage probability, which were estimated as , , and , respectively. Here, M = 10,000 is the number of replicates under each simulation setting, denotes the synthesized SMD in the mth simulated meta-analysis, and and denote the lower and upper bounds of its 95% CI.
4.2 |. Simulation results
Different methods for synthesizing SMDs led to noticeably different biases, RMSEs, and coverage probabilities; as study-specific sample sizes decreased, biases tended to depart from 0 (Tables 2 and 3). The Monte Carlo standard errors of all biases were less than 0.005, those of all RMSEs were less than 0.003, and those of all coverage probabilities were less than 0.4%. Specifically, as N increased from 5 to 20, biases became generally larger in magnitude (with some exceptions) while RMSEs became smaller by about half. When N = 5, the coverage probabilities of the conventional CIs derived from Equation (23) were less than 90% for some methods, while those using the Hartung–Knapp–Sidik–Jonkman method in Equation (24) were generally close to 95% with some exceptions for small samples and large θ. As τ increased from 0.1 to 0.5, both biases (in magnitude) and RMSEs became slightly larger, and most CIs had slightly lower coverage probabilities. As study-specific sample sizes ni decreased, both biases (in magnitude) and RMSEs became smaller, but the coverage probabilities seemed to interact with other factors. For example, when τ = 0.5, larger ni generally had lower coverage probabilities when N = 5 but had higher coverage probabilities when N = 20 and θ = 0.8.
TABLE 2.
Performance of different methods for synthesizing standardized mean differences based on 10,000 replicates of simulated meta-analyses with N = 5 studies under various settings.
| Method | τ = 0.1 | τ = 0.5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ni = 6–14 | ni = 30–70 | ni = 6–14 | ni = 30–70 | |||||||||
| Bias | RMSE | CP, % | Bias | RMSE | CP, % | Bias | RMSE | CP, % | Bias | RMSE | CP, % | |
| θ = 0: | ||||||||||||
| Cohen’s d, Eq. (4) | 0.000 | 0.299 | 97.6 (95.4) | −0.001 | 0.137 | 95.2 (94.6) | 0.001 | 0.367 | 95.4 (95.8) | 0.002 | 0.260 | 89.6 (95.4) |
| Cohen’s d, Eq. (5) | 0.000 | 0.303 | 96.3 (96.0) | −0.001 | 0.137 | 95.2 (94.6) | 0.001 | 0.371 | 94.0 (96.1) | 0.002 | 0.260 | 89.6 (95.4) |
| Cohen’s d, Eq. (6) | 0.000 | 0.312 | 96.0 (95.9) | −0.001 | 0.138 | 95.2 (94.6) | 0.000 | 0.383 | 93.6 (96.0) | 0.002 | 0.260 | 89.6 (95.4) |
| Hedges’ g, Eq. (10) | 0.000 | 0.267 | 97.6 (95.6) | −0.001 | 0.135 | 95.3 (94.6) | 0.001 | 0.327 | 95.5 (96.0) | 0.002 | 0.255 | 89.6 (95.4) |
| Hedges’ g, Eq. (11) | 0.000 | 0.271 | 96.3 (95.9) | −0.001 | 0.135 | 95.2 (94.7) | 0.001 | 0.330 | 94.1 (96.2) | 0.002 | 0.255 | 89.6 (95.4) |
| Hedges’ g, Eq. (12) | 0.000 | 0.279 | 96.0 (95.8) | −0.001 | 0.135 | 95.2 (94.7) | 0.000 | 0.341 | 93.7 (96.0) | 0.002 | 0.256 | 89.6 (95.4) |
| Hedges’ g, Eq. (13) | 0.000 | 0.281 | 97.1 (95.5) | −0.001 | 0.135 | 95.3 (94.6) | 0.000 | 0.345 | 94.7 (95.8) | 0.002 | 0.256 | 89.6 (95.4) |
| Hedges’ g, Eq. (14) | 0.000 | 0.266 | 97.6 (95.6) | −0.001 | 0.135 | 95.3 (94.6) | 0.001 | 0.326 | 95.5 (96.0) | 0.002 | 0.255 | 89.7 (95.4) |
| Hedges’ g, Eq. (20) | −0.001 | 0.313 | 96.2 (95.2) [96.9] | −0.001 | 0.137 | 95.2 (94.5) [95.3] | −0.001 | 0.382 | 93.7 (95.4) [94.8] | 0.002 | 0.260 | 89.3 (95.2) [89.5] |
| Hedges’ g, Eq. (21) | 0.000 | 0.309 | 96.9 (94.9) [96.6] | −0.001 | 0.137 | 95.2 (94.5) [95.2] | 0.000 | 0.381 | 94.4 (95.1) [94.0] | 0.002 | 0.260 | 89.4 (95.2) [89.4] |
| Hedges’ g, Eq. (22) | −0.001 | 0.315 | 95.1 (95.5) [97.4] | −0.001 | 0.137 | 95.0 (94.6) [95.3] | −0.001 | 0.382 | 92.6 (95.6) [95.5] | 0.002 | 0.260 | 89.3 (95.2) [89.6] |
| θ = 0.3: | ||||||||||||
| Cohen’s d, Eq. (4) | −0.001 | 0.300 | 97.7 (95.6) | 0.000 | 0.138 | 95.6 (95.0) | −0.007 | 0.372 | 95.2 (95.3) | 0.000 | 0.263 | 88.5 (94.8) |
| Cohen’s d, Eq. (5) | 0.002 | 0.303 | 96.4 (95.9) | 0.000 | 0.138 | 95.4 (95.0) | −0.001 | 0.378 | 93.8 (95.8) | 0.000 | 0.263 | 88.4 (94.8) |
| Cohen’s d, Eq. (6) | 0.010 | 0.312 | 96.1 (95.8) | 0.000 | 0.138 | 95.3 (95.0) | 0.007 | 0.391 | 93.5 (95.8) | 0.000 | 0.264 | 88.4 (94.8) |
| Hedges’ g, Eq. (10) | −0.032 | 0.270 | 97.5 (95.7) | −0.005 | 0.135 | 95.6 (95.0) | −0.037 | 0.334 | 95.1 (95.5) | −0.006 | 0.259 | 88.5 (94.8) |
| Hedges’ g, Eq. (11) | −0.030 | 0.272 | 96.4 (96.0) | −0.005 | 0.136 | 95.4 (95.0) | −0.033 | 0.338 | 93.9 (95.7) | −0.005 | 0.259 | 88.5 (94.8) |
| Hedges’ g, Eq. (12) | −0.023 | 0.280 | 96.0 (95.9) | −0.005 | 0.136 | 95.4 (95.0) | −0.026 | 0.349 | 93.5 (95.7) | −0.005 | 0.259 | 88.5 (94.8) |
| Hedges’ g, Eq. (13) | −0.020 | 0.281 | 97.0 (95.6) | −0.005 | 0.136 | 95.6 (95.0) | −0.023 | 0.352 | 94.6 (95.4) | −0.005 | 0.259 | 88.6 (94.8) |
| Hedges’ g, Eq. (14) | −0.033 | 0.269 | 97.6 (95.6) | −0.005 | 0.135 | 95.6 (95.0) | −0.039 | 0.333 | 95.2 (95.5) | −0.006 | 0.259 | 88.5 (94.8) |
| Hedges’ g, Eq. (20) | 0.003 | 0.311 | 96.3 (95.4) [97.1] | −0.001 | 0.137 | 95.3 (94.9) [95.4] | 0.002 | 0.393 | 93.6 (95.0) [94.6] | 0.000 | 0.264 | 88.3 (94.6) [88.4] |
| Hedges’ g, Eq. (21) | 0.002 | 0.307 | 97.0 (95.2) [96.6] | −0.001 | 0.137 | 95.4 (94.9) [95.4] | 0.001 | 0.391 | 94.2 (94.8) [93.9] | 0.000 | 0.264 | 88.3 (94.6) [88.3] |
| Hedges’ g, Eq. (22) | 0.002 | 0.313 | 95.3 (95.6) [97.5] | −0.001 | 0.138 | 95.1 (94.9) [95.5] | 0.001 | 0.393 | 92.7 (95.3) [95.4] | 0.000 | 0.264 | 88.2 (94.6) [88.5] |
| θ = 0.8: | ||||||||||||
| Cohen’s d, Eq. (4) | −0.006 | 0.308 | 98.0 (95.8) | 0.000 | 0.141 | 95.8 (95.0) | −0.023 | 0.386 | 94.6 (95.0) | 0.000 | 0.261 | 89.2 (95.2) |
| Cohen’s d, Eq. (5) | 0.004 | 0.313 | 96.4 (95.9) | 0.000 | 0.141 | 95.6 (95.0) | −0.009 | 0.390 | 93.5 (95.4) | 0.001 | 0.261 | 89.2 (95.2) |
| Cohen’s d, Eq. (6) | 0.023 | 0.324 | 96.1 (95.9) | 0.000 | 0.141 | 95.6 (95.0) | 0.013 | 0.402 | 93.4 (95.4) | 0.002 | 0.261 | 89.2 (95.2) |
| Hedges’ g, Eq. (10) | −0.087 | 0.289 | 96.7 (94.9) | −0.013 | 0.139 | 95.6 (94.9) | −0.103 | 0.359 | 93.5 (94.3) | −0.013 | 0.257 | 89.2 (95.1) |
| Hedges’ g, Eq. (11) | −0.082 | 0.292 | 95.1 (95.2) | −0.013 | 0.139 | 95.3 (94.9) | −0.093 | 0.360 | 92.0 (94.7) | −0.012 | 0.257 | 89.1 (95.1) |
| Hedges’ g, Eq. (12) | −0.065 | 0.296 | 95.0 (95.2) | −0.013 | 0.139 | 95.3 (94.9) | −0.075 | 0.365 | 92.2 (94.8) | −0.012 | 0.257 | 89.1 (95.1) |
| Hedges’ g, Eq. (13) | −0.056 | 0.294 | 96.5 (95.1) | −0.012 | 0.139 | 95.5 (94.9) | −0.068 | 0.366 | 93.5 (94.6) | −0.012 | 0.257 | 89.1 (95.0) |
| Hedges’ g, Eq. (14) | −0.090 | 0.289 | 96.7 (94.8) | −0.013 | 0.139 | 95.6 (94.9) | −0.107 | 0.359 | 93.4 (94.2) | −0.013 | 0.257 | 89.2 (95.1) |
| Hedges’ g, Eq. (20) | 0.005 | 0.334 | 96.3 (95.0) [97.0] | −0.002 | 0.141 | 95.5 (94.9) [95.7] | −0.001 | 0.405 | 93.3 (94.4) [94.3] | 0.002 | 0.261 | 89.0 (94.9) [89.2] |
| Hedges’ g, Eq. (21) | 0.002 | 0.327 | 97.1 (94.8) [96.8] | −0.002 | 0.141 | 95.7 (94.9) [95.6] | −0.004 | 0.403 | 93.9 (94.1) [93.7] | 0.002 | 0.261 | 89.1 (94.9) [89.1] |
| Hedges’ g, Eq. (22) | 0.003 | 0.337 | 95.0 (95.3) [97.4] | −0.002 | 0.141 | 95.3 (94.9) [95.7] | −0.004 | 0.405 | 92.1 (94.7) [95.0] | 0.002 | 0.261 | 89.1 (95.0) [89.3] |
Abbreviation: CP, coverage probability of 95% confidence interval; RMSE, root mean squared error.
Notation: N, no. of studies; τ, between-study standard deviation; ni, study-specific sample size; θ, true overall standardized mean difference.
Note: coverage probabilities include those based on conventional meta-analysis method in Equation (23) (outside parentheses and square brackets), based on the Hartung–Knapp–Sidik–Jonkman method in Equation (24) (inside parentheses), and based on the method in Equation (26) (inside square brackets).
TABLE 3.
Performance of different methods for synthesizing standardized mean differences based on 10,000 replicates of simulated meta-analyses with N = 20 studies under various settings.
| Method | τ = 0.1 | τ = 0.5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ni = 6–14 | ni = 30–70 | ni = 6–14 | ni = 30–70 | |||||||||
| Bias | RMSE | CP, % | Bias | RMSE | CP, % | Bias | RMSE | CP, % | Bias | RMSE | CP, % | |
| θ = 0: | ||||||||||||
| Cohen’s d, Eq. (4) | 0.001 | 0.144 | 97.7 (95.6) | 0.000 | 0.068 | 95.2 (95.0) | 0.000 | 0.177 | 95.4 (95.9) | 0.002 | 0.129 | 93.4 (95.3) |
| Cohen’s d, Eq. (5) | 0.001 | 0.144 | 96.3 (96.1) | 0.000 | 0.068 | 95.2 (95.0) | 0.000 | 0.178 | 94.6 (96.4) | 0.002 | 0.129 | 93.4 (95.3) |
| Cohen’s d, Eq. (6) | 0.001 | 0.148 | 95.9 (96.1) | 0.000 | 0.068 | 95.1 (95.0) | −0.001 | 0.184 | 94.4 (96.3) | 0.002 | 0.129 | 93.4 (95.2) |
| Hedges’ g, Eq. (10) | 0.001 | 0.129 | 97.7 (95.8) | 0.000 | 0.067 | 95.2 (95.0) | 0.000 | 0.157 | 95.6 (96.1) | 0.002 | 0.127 | 93.4 (95.3) |
| Hedges’ g, Eq. (11) | 0.001 | 0.129 | 96.4 (96.2) | 0.000 | 0.067 | 95.2 (95.0) | 0.000 | 0.159 | 94.7 (96.5) | 0.002 | 0.127 | 93.4 (95.2) |
| Hedges’ g, Eq. (12) | 0.001 | 0.133 | 95.9 (96.1) | 0.000 | 0.067 | 95.2 (95.0) | −0.001 | 0.164 | 94.4 (96.3) | 0.002 | 0.127 | 93.4 (95.2) |
| Hedges’ g, Eq. (13) | 0.001 | 0.135 | 97.0 (95.8) | 0.000 | 0.067 | 95.3 (95.0) | 0.000 | 0.167 | 95.1 (95.9) | 0.002 | 0.127 | 93.4 (95.2) |
| Hedges’ g, Eq. (14) | 0.001 | 0.128 | 97.8 (95.8) | 0.000 | 0.067 | 95.2 (95.0) | 0.000 | 0.157 | 95.7 (96.1) | 0.002 | 0.127 | 93.4 (95.3) |
| Hedges’ g, Eq. (20) | 0.001 | 0.154 | 95.8 (95.1) [96.5] | 0.000 | 0.069 | 95.1 (94.7) [95.2] | −0.001 | 0.192 | 94.1 (95.1) [95.2] | 0.002 | 0.130 | 93.4 (95.0) [93.5] |
| Hedges’ g, Eq. (21) | 0.001 | 0.153 | 96.3 (94.9) [96.2] | 0.000 | 0.069 | 95.1 (94.7) [95.1] | −0.001 | 0.192 | 94.3 (94.8) [94.4] | 0.002 | 0.130 | 93.4 (95.0) [93.5] |
| Hedges’ g, Eq. (22) | 0.001 | 0.156 | 94.9 (95.3) [97.2] | 0.000 | 0.069 | 94.9 (94.8) [95.2] | −0.001 | 0.193 | 93.9 (95.3) [96.0] | 0.002 | 0.130 | 93.4 (95.0) [93.6] |
| θ = 0.3: | ||||||||||||
| Cohen’s d, Eq. (4) | −0.012 | 0.145 | 97.6 (95.8) | −0.001 | 0.068 | 95.2 (94.9) | −0.023 | 0.179 | 95.5 (95.8) | −0.003 | 0.130 | 93.3 (95.1) |
| Cohen’s d, Eq. (5) | −0.010 | 0.145 | 96.3 (96.2) | −0.001 | 0.068 | 94.9 (94.9) | −0.016 | 0.179 | 94.7 (96.3) | −0.003 | 0.130 | 93.3 (95.1) |
| Cohen’s d, Eq. (6) | −0.002 | 0.148 | 96.0 (96.1) | 0.000 | 0.069 | 95.0 (94.9) | −0.006 | 0.184 | 94.7 (96.2) | −0.003 | 0.131 | 93.3 (95.1) |
| Hedges’ g, Eq. (10) | −0.042 | 0.136 | 96.9 (94.9) | −0.006 | 0.068 | 95.1 (94.9) | −0.051 | 0.166 | 94.6 (95.4) | −0.008 | 0.128 | 93.3 (95.0) |
| Hedges’ g, Eq. (11) | −0.041 | 0.136 | 95.2 (95.2) | −0.006 | 0.068 | 94.9 (94.9) | −0.046 | 0.166 | 93.9 (95.8) | −0.008 | 0.128 | 93.3 (95.0) |
| Hedges’ g, Eq. (12) | −0.034 | 0.137 | 95.0 (95.5) | −0.005 | 0.068 | 94.9 (94.9) | −0.038 | 0.169 | 94.0 (96.0) | −0.008 | 0.129 | 93.3 (95.0) |
| Hedges’ g, Eq. (13) | −0.029 | 0.138 | 96.5 (95.4) | −0.005 | 0.068 | 95.0 (94.9) | −0.035 | 0.170 | 94.7 (95.7) | −0.008 | 0.129 | 93.3 (95.0) |
| Hedges’ g, Eq. (14) | −0.043 | 0.136 | 96.9 (94.8) | −0.006 | 0.068 | 95.1 (94.9) | −0.053 | 0.166 | 94.6 (95.3) | −0.008 | 0.128 | 93.3 (95.0) |
| Hedges’ g, Eq. (20) | 0.000 | 0.155 | 95.7 (95.2) [96.5] | 0.000 | 0.069 | 95.0 (94.7) [95.1] | −0.001 | 0.193 | 94.6 (95.4) [95.6] | −0.001 | 0.131 | 93.3 (94.9) [93.5] |
| Hedges’ g, Eq. (21) | 0.000 | 0.154 | 96.3 (95.2) [96.2] | 0.000 | 0.069 | 95.0 (94.7) [95.0] | −0.002 | 0.192 | 94.8 (95.2) [94.9] | −0.001 | 0.131 | 93.3 (94.9) [93.4] |
| Hedges’ g, Eq. (22) | 0.000 | 0.157 | 95.1 (95.3) [97.1] | 0.000 | 0.069 | 94.8 (94.7) [95.2] | −0.002 | 0.194 | 94.4 (95.7) [96.3] | −0.001 | 0.131 | 93.3 (94.9) [93.4] |
| θ = 0.8: | ||||||||||||
| Cohen’s d, Eq. (4) | −0.030 | 0.152 | 97.2 (95.3) | −0.002 | 0.070 | 95.4 (95.0) | −0.054 | 0.191 | 94.5 (95.1) | −0.006 | 0.131 | 93.6 (95.3) |
| Cohen’s d, Eq. (5) | −0.023 | 0.151 | 95.9 (96.0) | −0.002 | 0.070 | 95.3 (95.1) | −0.037 | 0.188 | 94.0 (95.8) | −0.005 | 0.131 | 93.6 (95.3) |
| Cohen’s d, Eq. (6) | −0.004 | 0.153 | 96.0 (96.1) | −0.001 | 0.070 | 95.2 (95.1) | −0.013 | 0.190 | 94.3 (96.3) | −0.004 | 0.131 | 93.6 (95.4) |
| Hedges’ g, Eq. (10) | −0.108 | 0.171 | 92.3 (89.2) | −0.015 | 0.071 | 94.7 (94.4) | −0.131 | 0.209 | 87.8 (89.5) | −0.019 | 0.130 | 93.4 (95.2) |
| Hedges’ g, Eq. (11) | −0.105 | 0.170 | 89.7 (90.1) | −0.015 | 0.071 | 94.5 (94.4) | −0.118 | 0.203 | 87.6 (91.0) | −0.019 | 0.130 | 93.3 (95.2) |
| Hedges’ g, Eq. (12) | −0.088 | 0.163 | 91.1 (91.8) | −0.014 | 0.071 | 94.6 (94.5) | −0.097 | 0.195 | 89.8 (92.6) | −0.018 | 0.130 | 93.4 (95.2) |
| Hedges’ g, Eq. (13) | −0.076 | 0.158 | 94.0 (92.6) | −0.014 | 0.071 | 94.6 (94.5) | −0.089 | 0.193 | 91.4 (93.0) | −0.018 | 0.130 | 93.4 (95.2) |
| Hedges’ g, Eq. (14) | −0.111 | 0.173 | 92.1 (88.6) | −0.015 | 0.071 | 94.7 (94.4) | −0.135 | 0.211 | 87.3 (89.0) | −0.019 | 0.130 | 93.3 (95.2) |
| Hedges’ g, Eq. (20) | 0.001 | 0.162 | 95.7 (95.1) [96.8] | 0.001 | 0.071 | 95.2 (94.9) [95.4] | 0.001 | 0.200 | 94.4 (95.3) [95.6] | −0.001 | 0.131 | 93.5 (95.1) [93.6] |
| Hedges’ g, Eq. (21) | 0.000 | 0.160 | 96.4 (94.7) [96.3] | 0.001 | 0.071 | 95.3 (94.9) [95.3] | 0.000 | 0.199 | 94.5 (95.0) [94.5] | −0.001 | 0.131 | 93.4 (95.1) [93.5] |
| Hedges’ g, Eq. (22) | 0.001 | 0.164 | 95.0 (95.2) [97.1] | 0.001 | 0.071 | 95.2 (95.0) [95.5] | 0.000 | 0.201 | 94.2 (95.4) [96.3] | −0.001 | 0.131 | 93.5 (95.1) [93.6] |
Abbreviation: CP, coverage probability of 95% confidence interval; RMSE, root mean squared error.
Notation: N, no. of studies; τ, between-study standard deviation; ni, study-specific sample size; θ, true overall standardized mean difference.
Note: coverage probabilities include those based on conventional meta-analysis method in Equation (23) (outside parentheses and square brackets), based on the Hartung–Knapp–Sidik–Jonkman method in Equation (24) (inside parentheses), and based on the method in Equation (26) (inside square brackets).
When the true overall SMD θ = 0, the point estimates produced by all methods were nearly unbiased. This was expected because the true variances of Cohen’s d and Hedges’ g depend only on sample sizes as shown in Equations (3) and (9). Although the estimated variances might be still correlated with Cohen’s d or Hedges’ g, the correlation is likely negligible. Cohen’s d was also nearly unbiased when θ = 0 because by Equation (2) its marginal expectation is E[θi/J(mi)] = θ/J(mi) = 0 = θ.
Biases departed slightly from 0 as θ increased to 0.3. When θ = 0.8, many conventional methods led to noticeable or even substantial biases. Bias reached as high as 0.135 when N = 20, τ = 0.5, and ni = 6–14. Note that Cohen’s d with variance estimators in Equations (4)–(6) generally led to smaller biases than Hedges’ g with variance estimators in Equations (10)–(14), although with larger RMSE in most but not all cases. Under the aforementioned setting (N = 20, τ = 0.5, and ni = 6–14), Cohen’s d based on Equations (4)–(6) outperformed Hedges’ g based on Equations (10)–(14) for all three performance measures (smaller biases, smaller RMSEs, and higher coverage probabilities). On the other hand, Hedges’g with average-adjusted variance estimators in Equations (20)–(22) led to nearly unbiased point estimates because these methods were specifically designed to reduce the association between Hedges’ g and its variance. This generally led to better coverage probabilities than methods using the variance estimators in Equations (10)–(14) under several settings, especially when N = 20 and ni = 6–14. The CIs derived from Equation (26) may have better coverage probabilities than the conventional CIs derived from Equation (23) but they were generally outperformed by the Hartung–Knapp–Sidik–Jonkman method in Equation (24). Nevertheless, RMSEs based on the average-adjusted variance estimators were sometimes larger than those produced by other methods, likely because weights based on them were not optimal for individual studies.
5 |. EMPIRICAL DATA ANALYSES
We applied the various methods for synthesizing SMDs to two published datasets, each having two subgroups of studies. The first dataset was reported by Gracie et al.67 It consisted of 14 studies investigating the effect of psychological therapy on disease activity indices in quiescent inflammatory bowel disease. These studies were classified into a subgroup studying patients with Crohn’s disease and another studying patients with ulcerative colitis; each subgroup had 7 studies. The second dataset was from Köhler et al.,68 who investigated the effect of anti-inflammatory intervention on depression and depressive symptoms. A total of 13 studies were collected, which were classified into a subgroup studying depression and another studying depressive symptoms.
Figure 3 shows forest plots of these two datasets, where the individual studies’ SMDs were estimated using Hedges’ g and their 95% CIs were based on the variance estimator in Equation (13). The studies in the first dataset had relatively small sample sizes; the study-specific sample size had a median of 37 (minimum, 11; maximum, 73; interquartile range [IQR], 18–51). In the second dataset, the depression subgroup also had relatively small sample sizes (minimum, 18; maximum, 60); the depressive-symptoms subgroup had large sample sizes, with a median of 353 (minimum, 96; maximum, 2233; IQR, 291–377). The last two studies in this dataset had much larger sample sizes (over 1200) than the other studies. This scenario is common in practice, where a few studies are large while most are much smaller. The first dataset also tended to have smaller SMDs (in magnitude) with more homogeneous effects compared to the second dataset. Specifically, based on a preliminary analysis using the estimated SMDs presented in Figure 3, in the first dataset the synthesized overall SMD (across both subgroups) was −0.032, the estimated between-study SD , and the heterogeneity measure I2 statistic was 0%. For the Crohn’s disease subgroup, the synthesized SMD was −0.120 with and I2 = 0%; for the ulcerative colitis subgroup, the synthesized SMD was 0.061 with and I2 = 0%. In the second dataset, the synthesized overall SMD (across both subgroups) was −0.324 with and I2 = 84.3%, implying substantial heterogeneity. For the depression subgroup, the synthesized SMD was −0.539 with and I2 = 64.7%; for the depressive symptoms subgroup, the synthesized SMD was −0.265 with and I2 = 86.4%. Each dataset contributed three meta-analyses (within each subgroup and combining the two subgroups) and represented different settings of meta-analyses of SMDs.
FIGURE 3.
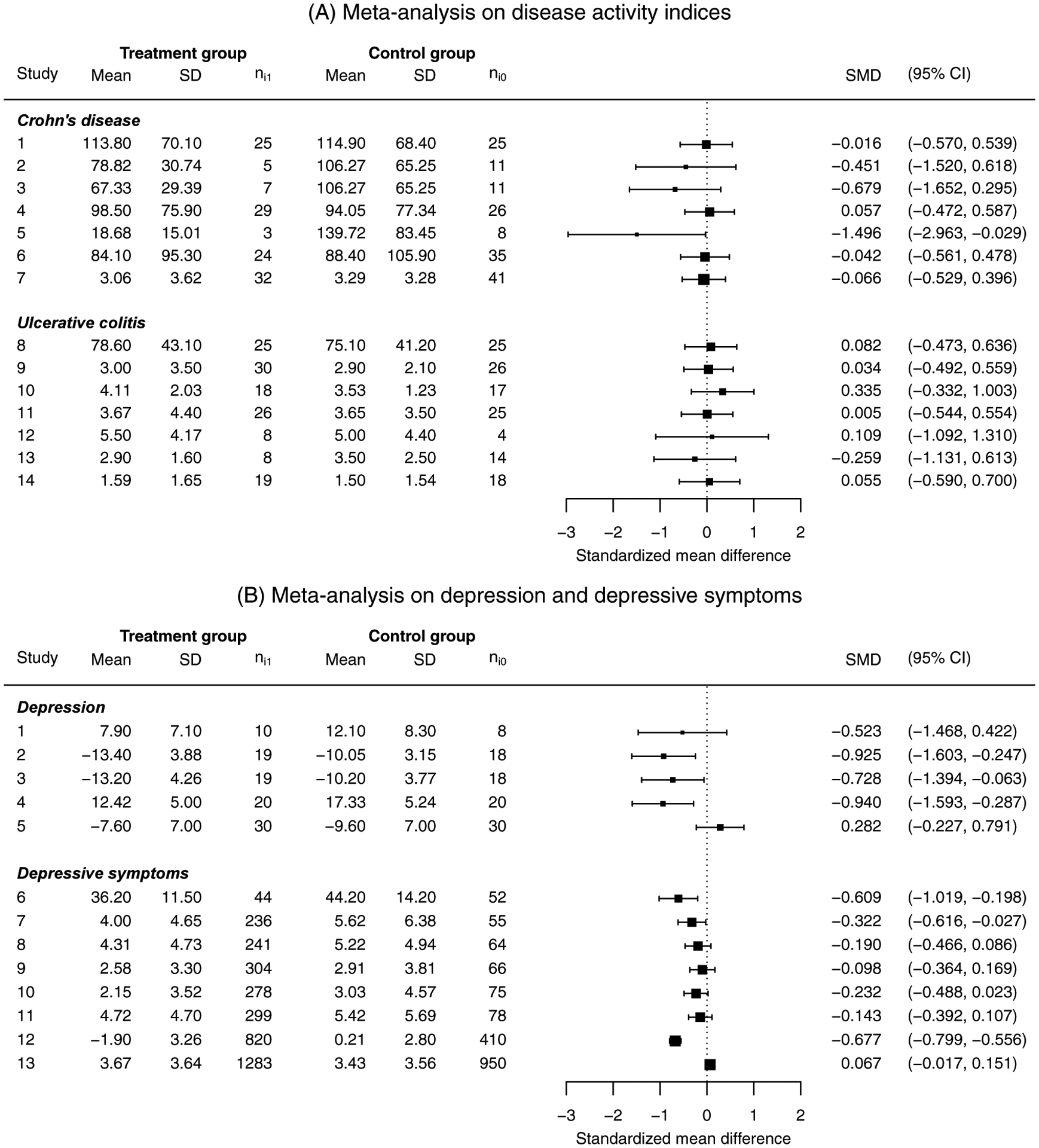
Forest plots of meta-analyses on disease activity indices (A) and on depression and depressive symptoms (B). The columns “Mean” and “SD” represent the continuous outcome measures’ sample means and sample standard deviations in the control or treatment group, respectively. The column “SMD” gives the standardized mean difference with its 95% confidence interval for individual studies, calculated using Hedges’ g with the variance estimator in Equation (13).
We applied the 11 methods considered in the simulation studies to both datasets. Again, all meta-analyses were performed under the random-effects setting using the R package “metafor”; the between-study variance was estimated using the REML method. Both the conventional and the Hartung–Knapp–Sidik–Jonkman methods in Equations (23) and (24) respectively were used to compute a 95% CI. The CI in Equation (26) was also used for the synthesized Hedges’ g based on the variance estimators in Equations (20)–(22).
Table 4 presents the synthesized SMDs and their 95% CIs using the 11 methods. For the first dataset, the meta-analysis of the Crohn’s disease subgroup had noticeable differences in both point and interval estimates when the SMDs were estimated by the various methods. For example, Hedges’ g with Equation (10) gave estimated overall SMD −0.117 with 95% CI (−0.355, 0.122) using the conventional CI, while using Equation (22) gave −0.142 with 95% CI (−0.381, 0.097). As the study-specific sample sizes in this subgroup were moderately small, our simulation studies in Section 4 indicate that the variance estimator in Equation (10) generally produced larger biases than the variance estimator in Equation (22); that is, the point estimate of −0.142 was likely subject to less bias. For the meta-analysis of the ulcerative colitis subgroup, the SMD estimators differed only slightly because the SMDs of these individual studies were close to 0. This is consistent with our simulation studies with θ = 0, in which the point estimates were generally similar. Moreover, the overall meta-analyses (combining the two subgroups) had noticeable differences between methods.
TABLE 4.
Synthesized standardized mean differences and 95% confidence intervals produced by various methods in the two datasets.
| Method | Meta-analysis on disease activity indices | Meta-analysis on depression and depressive symptoms | ||||
|---|---|---|---|---|---|---|
| Crohn’s disease | Ulcerative colitis | Overall | Depression | Depressive symptoms | Overall | |
| Cohen’s d, Eq. (4) | −0.115 | 0.062 | −0.028 | −0.552 | −0.265 | −0.326 |
| (−0.358, 0.129) | (−0.187, 0.311) | (−0.202, 0.146) | (−1.071, −0.034) | (−0.456, −0.075) | (−0.516, −0.136) | |
| [−0.405, 0.176] | [−0.078, 0.203] | [−0.176, 0.119] | [−1.236, 0.131] | [−0.484, −0.046] | [−0.542, −0.111] | |
| Cohen’s d, Eq. (5) | −0.124 | 0.062 | −0.033 | −0.554 | −0.266 | −0.329 |
| (−0.363, 0.115) | (−0.182, 0.306) | (−0.203, 0.138) | (−1.068, −0.040) | (−0.456, −0.075) | (−0.519, −0.138) | |
| [−0.430, 0.182] | [−0.080, 0.204] | [−0.187, 0.121] | [−1.234, 0.126] | [−0.484, −0.047] | [−0.545, −0.112] | |
| Cohen’s d, Eq. (6) | −0.126 | 0.062 | −0.034 | −0.554 | −0.266 | −0.329 |
| (−0.365, 0.113) | (−0.182, 0.306) | (−0.204, 0.136) | (−1.068, −0.041) | (−0.456, −0.075) | (−0.520, −0.139) | |
| [−0.436, 0.184] | [−0.080, 0.204] | [−0.190, 0.122] | [−1.234, 0.125] | [−0.485, −0.047] | [−0.546, −0.113] | |
| Hedges’ g, Eq. (10) | −0.117 | 0.061 | −0.030 | −0.539 | −0.265 | −0.324 |
| (−0.355, 0.122) | (−0.183, 0.304) | (−0.200, 0.141) | (−1.044, −0.033) | (−0.455, −0.075) | (−0.512, −0.136) | |
| [−0.400, 0.166] | [−0.077, 0.198] | [−0.174, 0.115] | [−1.207, 0.130] | [−0.483, −0.046] | [−0.536, −0.111] | |
| Hedges’ g, Eq. (11) | −0.126 | 0.060 | −0.035 | −0.540 | −0.265 | −0.326 |
| (−0.360, 0.108) | (−0.178, 0.299) | (−0.202, 0.132) | (−1.041, −0.039) | (−0.455, −0.075) | (−0.515, −0.138) | |
| [−0.425, 0.172] | [−0.078, 0.199] | [−0.186, 0.116] | [−1.205, 0.125] | [−0.483, −0.047] | [−0.540, −0.113] | |
| Hedges’ g, Eq. (12) | −0.128 | 0.060 | −0.036 | −0.541 | −0.265 | −0.327 |
| (−0.362, 0.105) | (−0.178, 0.299) | (−0.203, 0.131) | (−1.041, −0.040) | (−0.455, −0.075) | (−0.515, −0.138) | |
| [−0.431, 0.174] | [−0.078, 0.199] | [−0.189, 0.117] | [−1.206, 0.124] | [−0.483, −0.047] | [−0.540, −0.113] | |
| Hedges’ g, Eq. (13) | −0.120 | 0.061 | −0.032 | −0.539 | −0.265 | −0.324 |
| (−0.359, 0.118) | (−0.183, 0.304) | (−0.202, 0.139) | (−1.044, −0.034) | (−0.455, −0.075) | (−0.512, −0.136) | |
| [−0.411, 0.170] | [−0.077, 0.198] | [−0.179, 0.116] | [−1.207, 0.129] | [−0.483, −0.046] | [−0.537, −0.112] | |
| Hedges’ g, Eq. (14) | −0.116 | 0.061 | −0.030 | −0.539 | −0.265 | −0.324 |
| (−0.355, 0.122) | (−0.183, 0.304) | (−0.200, 0.141) | (−1.044, −0.033) | (−0.455, −0.075) | (−0.512, −0.136) | |
| [−0.399, 0.166] | [−0.077, 0.198] | [−0.174, 0.115] | [−1.207, 0.130] | [−0.483, −0.046] | [−0.536, −0.111] | |
| Hedges’ g, Eq. (20) | −0.130 | 0.061 | −0.037 | −0.545 | −0.266 | −0.330 |
| (−0.368, 0.107) | (−0.182, 0.304) | (−0.207, 0.133) | (−1.046, −0.044) | (−0.456, −0.075) | (−0.519, −0.140) | |
| [−0.440, 0.179] | [−0.077, 0.199] | [−0.193, 0.119] | [−1.210, 0.120] | [−0.484, −0.047] | [−0.544, −0.115] | |
| {−0.370, 0.109} | {−0.183, 0.305} | {−0.208, 0.134} | {−1.050, −0.040} | {−0.456, −0.075} | {−0.520, −0.139} | |
| Hedges’ g, Eq. (21) | −0.126 | 0.061 | −0.035 | −0.544 | −0.265 | −0.328 |
| (−0.367, 0.115) | (−0.184, 0.306) | (−0.206, 0.136) | (−1.048, −0.040) | (−0.456, −0.075) | (−0.517, −0.139) | |
| [−0.429, 0.176] | [−0.077, 0.199] | [−0.188, 0.118] | [−1.211, 0.123] | [−0.484, −0.047] | [−0.542, −0.114] | |
| {−0.365, 0.113} | {−0.182, 0.305} | {−0.206, 0.136} | {−1.048, −0.039} | {−0.456, −0.075} | {−0.518, −0.139} | |
| Hedges’ g, Eq. (22) | −0.142 | 0.061 | −0.043 | −0.545 | −0.266 | −0.331 |
| (−0.381, 0.097) | (−0.178, 0.299) | (−0.212, 0.126) | (−1.043, −0.047) | (−0.456, −0.075) | (−0.520, −0.141) | |
| [−0.468, 0.184] | [−0.079, 0.200] | [−0.206, 0.120] | [−1.209, 0.118] | [−0.484, −0.047] | [−0.545, −0.116] | |
| {−0.382, 0.098} | {−0.183, 0.304} | {−0.214, 0.128} | {−1.048, −0.042} | {−0.456, −0.075} | {−0.521, −0.140} | |
Note: the confidence intervals inside parentheses are derived using the conventional method in Equation (23); those inside square brackets are derived using the Hartung–Knapp–Sidik–Jonkman method in Equation (24); and those inside braces are derived using the method in Equation (26).
The confidence intervals not encompassing 0 are in boldface.
For the depression subgroup in the second dataset, the point and interval estimates of Cohen’s d and Hedges’ g produced by the various methods were noticeably different. The differences between the results of several estimators were larger than 0.01; as the upper bound of the CI for the synthesized SMD was close to 0, such differences could affect interpretation of the treatment effect. Because this subgroup had relatively small sample sizes, these differences were likely due to biases in the meta-estimates produced by conventional estimators. The subgroup of depressive symptoms had large sample sizes, so the various methods produced nearly the same estimates. The overall meta-analysis combined both small studies on depression and large studies on depressive symptoms; the results by the various methods had slight differences.
The CIs produced by the Hartung–Knapp–Sidik–Jonkman method dramatically differed from those by other methods, because the number of studies was not large in both datasets. Our simulation studies indicated that the CIs by the Hartung–Knapp–Sidik–Jonkman method likely had higher coverage probabilities. For example, in the second dataset’s depression subgroup, all Hartung–Knapp–Sidik–Jonkman CIs contained 0, indicating no significant effects of anti-inflammatory intervention. The CIs produced by other methods, however, were slightly below 0, leading to significant effects.
6 |. SOFTWARE PACKAGES
Practitioners with little statistical background may use software packages to perform meta-analyses of SMDs. Just like different meta-analysis books have inconsistent notation of SMD estimators, as discussed in Section 2.5, software packages may differ in the way they calculate the SMD and its within-study variance.
We investigated how popular meta-analysis software packages handle the SMD, including the two R core packages for meta-analysis, “metafor” (version 2.4–0)69 and “meta” (version 4.14–0),70 the commands “metan” and “meta” in Stata 16, Review Manager 5 (RevMan 5, version 5.4.1),71 and the Comprehensive Meta-Analysis (CMA, version 3).30 The R packages “metafor” and “meta” are freely available on the Comprehensive R Archive Network (CRAN, https://cran.r-project.org/). Stata is a paid general-purpose statistical software package available on https://www.stata.com/, which has various commands, including the main commands “metan” and “meta,” for performing meta-analysis. Instructions for meta-analysis of SMDs using the command “metan” can be found in Palmer and Sterne72 (pp. 35, 36, and 53). The Stata command “meta” is a new feature in Stata 16; instructions about SMDs can be found in the manual at https://www.stata.com/manuals/meta.pdf (pp. 83 and 84). RevMan is software specially designed for preparing and maintaining systematic reviews in the Cochrane Library. It is available at https://community.cochrane.org/ and can be freely used to prepare Cochrane reviews or for purely academic purposes. The CMA is a commercial program for meta-analysis which can be ordered on https://www.meta-analysis.com/. Both RevMan and CMA do not require statistical coding, so they can be used easily by practitioners with no statistical training.
Table 5 describes how the aforementioned packages compute the SMD. Most packages use the approximate form of the correction coefficient, while the R package “metafor” uses the exact form J(·) by default and the “meta” package offers the exact form as an option. To use the exact form in the “meta” package, one specifies the argument exact.smd = TRUE in the function metacont(). The “metafor” package and RevMan do not have options to calculate Cohen’s d.
TABLE 5.
Calculations of the standardized mean difference in popular software packages for meta-analysis.
| Software package | Default estimate of standardized mean difference | Within-study variance of Cohen’s d, | Within-study variance of Hedges’ g, | Bias correction coefficient | |||
|---|---|---|---|---|---|---|---|
| Default | Other options | Default | Other options | J (⋅) (Exact) | |||
| R package “metafor” (version 2.4–0) | Hedges’ g | NA | NA | Eq. (13) | Eq. (10); Eq. (20) with in Eq. (19) | Default | NA |
| R package “meta” (version 4.14–0) | Hedges’ g | Eq. (4) ×[J (⋅)]2 for J (⋅); Eq. (6) for | NA | Eq. (10) for J (⋅); Eq. (14) for | NA | Available | Default |
| Command “metan” in Stata 16 | Cohen’s d | Eq. (5) | NA | Eq. (14) | NA | NA | Default |
| Command “meta” in Stata 16 | Hedges’ g | Eq. (6) | Eq. (5) | Eq. (12) | Eq. (14) | NA | Default |
| RevMan 5 (version 5.4.1) | Hedges’ g | NA | NA | Eq. (14) | NA | NA | Default |
| Comprehensive Meta-Analysis (version 3) | Both Cohen’s d and Hedges’ g | Eq. (6) | NA | Eq. (12) | NA | NA | Default |
Note: NA, not available.
Different packages use different estimators of the variance of the SMD. The “meta” package, the commands “metan” and “meta” in Stata 16, and RevMan 5 use the estimator in Equation (14) by default or provide this as an option, which may be due to the confusion of the notation d and g used in Hedges and Olkin.15 In the “metafor” package, the default variance estimator of Hedges’ g is Equation (13), which is specified by the argument vtype = “LS” (for “large-sample”) with measure = “SMD” in the function escalc(). The unbiased estimator in Equation (10) can be specified by vtype = “UB” (for “unbiased”), and the sample-size-averaged estimator in Equation (20) with in Equation (19) can be specified by vtype = “AV” (for “average”).
Because the various software packages have different default options, when practitioners apply these packages, they should be fully aware of the specific formulas used in the analysis and report sufficient information about the package. In this way, they can avoid reproducibility problems when other researchers want to validate the results with different software.
7 |. DISCUSSION
This article reviewed methods to estimate the SMD and evaluated their performance in meta-analysis. Cohen’s d and Hedges’ g are widely used as SMD estimators; their variances can be estimated in many different ways. We found that meta-analysis books and software packages differ substantially in their notation and use of these estimators. As a result, practitioners must be unusually careful when they perform meta-analyses of SMDs. We recommend that they report sufficient details about the analyses, including software packages and estimator types, so their results can be reproduced readily.
Hedges’ g has been used frequently to reduce bias in studies with small sample sizes. However, both the asymptotic illustrations in Section 3.2 and the finite-sample simulation studies in Section 4 show that Hedges’ g actually has larger bias (in magnitude) than Cohen’s d using the conventional methods reviewed in Sections 2.2 and 2.3. In other words, the bias reduction of Hedges’ g in individual studies is not inherited by the meta-analysis. This phenomenon is caused mainly by the association between the study-specific point estimates and their variance estimates. To maintain the bias reduction of Hedges’ g in meta-analysis, the variance estimators reviewed in Section 3.3 should be used, including those in Equations (20)–(22).These estimators use an averaged SMD to adjust the sample variance of Hedges’ g within individual studies, thus reducing the association between Hedges’ g and their variances and reducing bias. The simulation studies in Section 4 indicated that these average-adjusted variance estimators had similar performance. Although they reduce the bias of the synthesized SMD, the average-adjusted variance estimators may not be optimal for individual studies, so the synthesized SMD might have a larger MSE in certain situations.
Our findings suggest that researchers should be careful when making statements like “because the sample sizes are small, we use the unbiased Hedges’ g as the effect measure in meta-analysis.” Such statements are true for individual studies or for meta-analyses using the average-adjusted estimators of the variance of Hedges’ g, but not for conventional methods that are currently used in most applications. Our simulation studies also showed that the Hartung–Knapp–Sidik–Jonkman method gives CIs with satisfactory coverage probabilities. This method is highly recommended in general meta-analysis practice.
We chose estimators of the SMD considered in this article by focusing on bias reduction; other estimators are available for other purposes. For example, Hedges and Olkin15 (p. 82) introduced shrunken estimators and Van Den Noortgate and Onghena73 introduced the empirical Bayes estimator for reducing the MSE. We have considered only a general framework of meta-analysis; other issues, such as subgrouping or nesting of patients, may need specific methods to better synthesize SMDs.74 Also, the between-study variance was estimated using the REML method in all analyses in this article, because it has been shown to perform better than other methods (such as the DerSimonian–Laird estimator48) in general.55 For meta-analyses of SMDs, measure-specific variance estimators are available.75 In future studies, it is worthwhile to investigate their performance for the different point and variance estimators of the SMD reviewed in this article.
Cohen’s d or Hedges’ g and the corresponding sample variance use aggregated data (AD) from each study. If available, individual patient data (IPD) might help standardize the statistical analyses (choice of SMD and variance estimator) across different studies.76 More appropriate or advanced methods, such one-step approaches via Bayesian hierarchical models or mixed-effects models that make fewer or weaker assumptions, may be used for synthesizing IPD with continuous outcomes.77,78 Meta-analyses of IPD may offer considerable benefits compared with AD when sample sizes are small, while their performance is known to be similar for large sample sizes.79,80
Supplementary Material
ACKNOWLEDGMENTS
We thank Professor James S. Hodges of the Division of Biostatistics, University of Minnesota, for helping us with writing. We also thank an Associate Editor and two anonymous referees for constructive comments that have substantially improved this article. This research was supported in part by the U.S. National Institutes of Health/National Library of Medicine grant R01 LM012982 and National Institutes of Health/National Center for Advancing Translational Sciences grant UL1 TR001427. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
SUPPORTING INFORMATION
Additional supplemental material that contains theoretical results and R code for all analyses can be found online in the supporting information tab for this article.
References
- 1.Gurevitch J, Koricheva J, Nakagawa S, Stewart G Meta-analysis and the science of research synthesis. Nature. 2018;555(7695):175–182. [DOI] [PubMed] [Google Scholar]
- 2.Berlin JA, Golub RM Meta-analysis as evidence: building a better pyramid. JAMA. 2014;312(6):603–606. [DOI] [PubMed] [Google Scholar]
- 3.Murad MH, Montori VM, Ioannidis JPA, et al. How to read a systematic review and meta-analysis and apply the results to patient care: users’ guides to the medical literature. JAMA. 2014;312(2):171–179. [DOI] [PubMed] [Google Scholar]
- 4.Hoaglin DC We know less than we should about methods of meta-analysis. Res Synth Methods. 2015;6(3):287–289. [DOI] [PubMed] [Google Scholar]
- 5.Jackson D, White IR When should meta-analysis avoid making hidden normality assumptions?. Biom J. 2018;60(6):1040–1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hacke C, Nunan D Discrepancies in meta-analyses answering the same clinical question were hard to explain: a meta-epidemiological study. J Clin Epidemiol. 2020;119:47–56. [DOI] [PubMed] [Google Scholar]
- 7.Ioannidis JPA Massive citations to misleading methods and research tools: Matthew effect, quotation error and citation copying. Eur J Epidemiol. 2018;33(11):1021–1023. [DOI] [PubMed] [Google Scholar]
- 8.Hoaglin DC Misunderstandings about Q and ‘Cochran’s Q test’ in meta-analysis. Stat Med. 2016;35(4):485–495. [DOI] [PubMed] [Google Scholar]
- 9.Doncaster CP, Spake R Correction for bias in meta-analysis of little-replicated studies. Methods Ecol Evol. 2018;9(3):634–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Murad MH, Wang Z, Chu H, Lin L When continuous outcomes are measured using different scales: guide for meta-analysis and interpretation. BMJ. 2019;364:k4817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Boulé NG, Haddad E, Kenny GP, Wells GA, Sigal RJ Effects of exercise on glycemic control and body mass in type 2 diabetes mellitus: a meta-analysis of controlled clinical trials. JAMA. 2001;286(10):1218–1227. [DOI] [PubMed] [Google Scholar]
- 12.Kirsch I, Deacon BJ, Huedo-Medina TB, Scoboria A, Moore TJ, Johnson BT Initial severity and antidepressant benefits: a meta-analysis of data submitted to the Food and Drug Administration. PLoS Med. 2008;5(2):e45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Takeshima N, Sozu T, Tajika A, Ogawa Y, Hayasaka Y, Furukawa TA Which is more generalizable, powerful and interpretable in meta-analyses, mean difference or standardized mean difference?. BMC Med Res Methodol. 2014;14(1):30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Turner EH, Matthews AM, Linardatos E, Tell RA, Rosenthal R Selective publication of antidepressant trials and its influence on apparent efficacy. N Engl J Med. 2008;358(3):252–260. [DOI] [PubMed] [Google Scholar]
- 15.Hedges LV, Olkin I Statistical Methods for Meta-Analysis. Orlando, FL: Academic Press; 1985. [Google Scholar]
- 16.da Costa BR, Rutjes AW, Johnston BC, et al. Methods to convert continuous outcomes into odds ratios of treatment response and numbers needed to treat: meta-epidemiological study. Int J Epidemiol. 2012;41(5):1445–1459. [DOI] [PubMed] [Google Scholar]
- 17.Gøtzsche PC, Hróbjartsson A, Marić K, Tendal B Data extraction errors in meta-analyses that use standardized mean differences. JAMA. 2007;298(4):430–437. [DOI] [PubMed] [Google Scholar]
- 18.Tendal B, Higgins JP, Jüni P, et al. Disagreements in meta-analyses using outcomes measured on continuous or rating scales: observer agreement study. BMJ. 2009;339:b3128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lin L Bias caused by sampling error in meta-analysis with small sample sizes. PLoS One. 2018;13(9):e0204056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hamman EA, Pappalardo P, Bence JR, Peacor SD, Osenberg CW Bias in meta-analyses using Hedges’ d. Ecosphere. 2018;9(9):e02419. [Google Scholar]
- 21.Hedges LV Distribution theory for Glass’s estimator of effect size and related estimators. J Educ Stat. 1981;6(2):107–128. [Google Scholar]
- 22.Hedges LV Estimation of effect size from a series of independent experiments. Psychol Bull. 1982;92(2):490–499. [Google Scholar]
- 23.Hedges LV A random effects model for effect sizes. Psychol Bull. 1983;93(2):388–395. [Google Scholar]
- 24.Cohen J Statistical Power Analysis for the Behavioral Sciencies. New York, NY: Academic Press; 1977. [Google Scholar]
- 25.Casella G, Berger RL Statistical Inference. Belmont, CA: Duxbury Press; 2nd ed2001. [Google Scholar]
- 26.White IR, Thomas J Standardized mean differences in individually-randomized and cluster-randomized trials, with applications to meta-analysis. Clin Trials. 2005;2(2):141–151. [DOI] [PubMed] [Google Scholar]
- 27.Egger M, Davey Smith G, Altman D Systematic Reviews in Health Care: Meta-Analysis in Context. London, UK: BMJ Publishing Group; 2nd ed2001. [Google Scholar]
- 28.Hartung J, Knapp G, Sinha BK Statistical Meta-Analysis with Applications. Hoboken, NJ: John Wiley & Sons; 2008. [Google Scholar]
- 29.Cooper H, Hedges LV, Valentine JC The Handbook of Research Synthesis and Meta-Analysis. New York, NY: Russell Sage Foundation; 2nd ed2009. [Google Scholar]
- 30.Borenstein M, Hedges LV, Higgins JPT, Rothstein HR Introduction to Meta-Analysis. Chichester, UK: John Wiley & Sons; 2009. [Google Scholar]
- 31.Stangl DK, Berry DA Meta-Analysis in Medicine and Health Policy. New York, NY: Marcel Dekker; 2000. [Google Scholar]
- 32.Koricheva J, Gurevitch J, Mengersen K Handbook of Meta-Analysis in Ecology and Evolution. Princeton, NJ: Princeton University Press; 2013. [Google Scholar]
- 33.Pigott TD Advances in Meta-Analysis. New York, NY: Springer; 2012. [Google Scholar]
- 34.Lipsey MW, Wilson DB Practical Meta-Analysis. Thousand Oaks, CA: Sage Publications; 2001. [Google Scholar]
- 35.Schwarzer G, Carpenter JR, Rücker G Meta-Analysis with R. Cham, Switzerland: Springer; 2015. [Google Scholar]
- 36.Schlattmann P Medical Applications of Finite Mixture Models. Berlin, Germany: Springer; 2009. [Google Scholar]
- 37.Glass GV Primary, secondary, and meta-analysis of research. Educ Res. 1976;5(10):3–8. [Google Scholar]
- 38.Glass GV, McGaw B, Smith ML Meta-Analysis in Social Research. Newbury Park, CA: Sage Publications; 1981. [Google Scholar]
- 39.Cruz N, Desai SC, Dewitt S, et al. Widening access to Bayesian problem solving. Front Psychol. 2020;11:660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cohen J Statistical Power Analysis for the Behavioral Sciences. Hillsdale, NJ: Lawrence Erlbaum Associates; 1988. [Google Scholar]
- 41.Thompson SG, Pocock SJ Can meta-analyses be trusted?. Lancet. 1991;338(8775):1127–1130. [DOI] [PubMed] [Google Scholar]
- 42.Eysenck HJ Meta-analysis and its problems. BMJ. 1994;309(6957):789–792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Thompson SG Why sources of heterogeneity in meta-analysis should be investigated. BMJ. 1994;309(6965):1351–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cappelleri JC, loannidis JPA, Schmid CH, et al. Large trials vs meta-analysis of smaller trials: how do their results compare?. JAMA. 1996;276(16):1332–1338. [PubMed] [Google Scholar]
- 45.LeLorier J, Gregoire G, Benhaddad A, Lapierre J, Derderian F Discrepancies between meta-analyses and subsequent large randomized, controlled trials. N Engl J Med. 1997;337(8):536–542. [DOI] [PubMed] [Google Scholar]
- 46.Moher D, Cook DJ, Eastwood S, Olkin I, Rennie D, Stroup DF Improving the quality of reports of meta-analyses of randomised controlled trials: the QUOROM statement. Lancet. 1999;354(9193):1896–1900. [DOI] [PubMed] [Google Scholar]
- 47.Borenstein M, Hedges LV, Higgins JPT, Rothstein HR A basic introduction to fixed-effect and random-effects models for meta-analysis. Res Synth Methods. 2010;1(2):97–111. [DOI] [PubMed] [Google Scholar]
- 48.DerSimonian R, Laird N Meta-analysis in clinical trials. Control Clin Trials. 1986;7(3):177–188. [DOI] [PubMed] [Google Scholar]
- 49.Paule RC, Mandel J Consensus values and weighting factors. J Res Natl Bur Stand. 1982;87(5):377–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Normand SLT Meta-analysis: formulating, evaluating, combining, and reporting. Stat Med. 1999;18(3):321–359. [DOI] [PubMed] [Google Scholar]
- 51.Cornell JE, Mulrow CD, Localio R, et al. Random-effects meta-analysis of inconsistent effects: a time for change. Ann Intern Med. 2014;160(4):267–270. [DOI] [PubMed] [Google Scholar]
- 52.Langan D, Higgins JPT, Simmonds M An empirical comparison of heterogeneity variance estimators in 12894 meta-analyses. Res Synth Methods. 2015;6(2):195–205. [DOI] [PubMed] [Google Scholar]
- 53.Veroniki AA, Jackson D, Viechtbauer W, et al. Methods to estimate the between-study variance and its uncertainty in meta-analysis. Res Synth Methods. 2016;7(1):55–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.van Aert RCM, Jackson D Multistep estimators of the between-study variance: the relationship with the Paule-Mandel estimator. Stat Med. 2018;37(17):2616–2629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Langan D, Higgins JPT, Jackson D, et al. A comparison of heterogeneity variance estimators in simulated random-effects meta-analyses. Res Synth Methods. 2019;10(1):83–98. [DOI] [PubMed] [Google Scholar]
- 56.Walker GA, Saw JG The distribution of linear combinations of t-variables. J Am Stat Assoc. 1978;73(364):876–878. [Google Scholar]
- 57.Boos DD, Stefanski LA Essential Statistical Inference: Theory and Methods. New York, NY: Springer; 2013. [Google Scholar]
- 58.Sánchez-Meca J, Marín-Martínez F Weighting by inverse variance or by sample size in meta-analysis: a simulation study. Educ Psychol Meas. 1998;58(2):211–220. [Google Scholar]
- 59.Berkey CS, Hoaglin DC, Mosteller F, Colditz GA A random-effects regression model for meta-analysis. Stat Med. 1995;14(4):395–411. [DOI] [PubMed] [Google Scholar]
- 60.Sidik K, Jonkman JN A simple confidence interval for meta-analysis. Stat Med. 2002;21(21):3153–3159. [DOI] [PubMed] [Google Scholar]
- 61.Knapp G, Hartung J Improved tests for a random effects meta-regression with a single covariate. Stat Med. 2003;22(17):2693–2710. [DOI] [PubMed] [Google Scholar]
- 62.Hartung J, Knapp G A refined method for the meta-analysis of controlled clinical trials with binary outcome. Stat Med. 2001;20(24):3875–3889. [DOI] [PubMed] [Google Scholar]
- 63.Sidik K, Jonkman JN On constructing confidence intervals for a standardized mean difference in meta-analysis. Commun Stat Simul Comput. 2003;32(4):1191–1203. [Google Scholar]
- 64.IntHout J, Ioannidis JPA, Borm GF The Hartung-Knapp-Sidik-Jonkman method for random effects meta-analysis is straightforward and considerably outperforms the standard DerSimonian-Laird method. BMC Med Res Methodol. 2014;14(1):25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Henmi M, Copas JB Confidence intervals for random effects meta-analysis and robustness to publication bias. Stat Med. 2010;29(29):2969–2983. [DOI] [PubMed] [Google Scholar]
- 66.Higgins JPT Commentary: Heterogeneity in meta-analysis should be expected and appropriately quantified. Int J Epidemiol. 2008;37(5):1158–1160. [DOI] [PubMed] [Google Scholar]
- 67.Gracie DJ, Irvine AJ, Sood R, Mikocka-Walus A, Hamlin PJ, Ford AC Effect of psychological therapy on disease activity, psychological comorbidity, and quality of life in inflammatory bowel disease: a systematic review and meta-analysis. Lancet Gastroenterol Hepatol. 2017;2(3):189–199. [DOI] [PubMed] [Google Scholar]
- 68.Köhler O, Benros ME, Nordentoft M, et al. Effect of anti-inflammatory treatment on depression, depressive symptoms, and adverse effects: a systematic review and meta-analysis of randomized clinical trials. JAMA Psychiatry. 2014;71(12):1381–1391. [DOI] [PubMed] [Google Scholar]
- 69.Viechtbauer W Conducting meta-analyses in R with the metafor package. J Stat Softw. 2010;36(3):1–48. [Google Scholar]
- 70.Schwarzer G meta: An R package for meta-analysis. R News. 2007;7(3):40–45. [Google Scholar]
- 71.Higgins JPT, Thomas J, Chandler J, et al. Cochrane Handbook for Systematic Reviews of Interventions. Chichester, UK: John Wiley & Sons; 2nd ed2019. [Google Scholar]
- 72.Palmer TM, Sterne JAC Meta-Analysis in Stata: An Updated Collection from the Stata Journal. College Station, TX: Stata Press; 2nd ed2016. [Google Scholar]
- 73.Van Den Noortgate W, Onghena P Estimating the mean effect size in meta-analysis: bias, precision, and mean squared error of different weighting methods. Behav Res Methods Instrum Comput. 2003;35(4):504–511. [DOI] [PubMed] [Google Scholar]
- 74.Walwyn R, Roberts C Meta-analysis of standardised mean differences from randomised trials with treatment-related clustering associated with care providers. Stat Med. 2017;36(7):1043–1067. [DOI] [PubMed] [Google Scholar]
- 75.Bakbergenuly I, Hoaglin DC, Kulinskaya E Estimation in meta-analyses of mean difference and standardized mean difference. Stat Med. 2020;39(2):171–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Riley RD, Lambert PC, Abo-Zaid G Meta-analysis of individual participant data: rationale, conduct, and reporting. BMJ. 2010;340:c221. [DOI] [PubMed] [Google Scholar]
- 77.Higgins JPT, Whitehead A, Turner RM, Omar RZ, Thompson SG Meta-analysis of continuous outcome data from individual patients. Stat Med. 2001;20(15):2219–2241. [DOI] [PubMed] [Google Scholar]
- 78.Riley RD, Lambert PC, Staessen JA, et al. Meta-analysis of continuous outcomes combining individual patient data and aggregate data. Stat Med. 2008;27(11):1870–1893. [DOI] [PubMed] [Google Scholar]
- 79.Zeng D, Lin DY On random-effects meta-analysis. Biometrika. 2015;102(2):281–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Tierney JF, Fisher DJ, Burdett S, Stewart LA, Parmar MKB Comparison of aggregate and individual participant data approaches to meta-analysis of randomised trials: an observational study. PLoS Med. 2020;17(1):e1003019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Hunter JE, Schmidt FL Methods of Meta-Analysis: Correcting Error and Bias in Research Findings. Newbury Park, CA: SAGE Publications; 1990. [Google Scholar]
- 82.Card NA Applied Meta-Analysis for Social Science Research. New York, NY: Guilford Press; 2012. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


