Brain Connectomes Come of Age

Abstract

Databases of consistent, directed- and weighted inter-areal connectivity for mouse, macaque and marmoset monkeys, have recently become available and begun to be used to build structural and dynamical models. A structural hierarchy can be defined based by laminar patterns of cortical connections. A large-scale dynamical model of the macaque cortex endowed with a laminar structure accounts for empirically observed frequency-modulated interplay between bottom-up and top-down processes. Signal propagation in the model with spiking neurons displays a threshold of stimulus amplitude for the activity to gain access to the prefrontal cortex, reminiscent of the ignition phenomenon associated with conscious perception. These two examples illustrate how connectomics informs structurally-based dynamic models of multi-regional brain systems. Theory raises novel questions for future anatomical and physiological empirical research, in a back-and-forth collaboration between experimentalists and theorists.

Introduction

In 1991 Felleman and van Essen published a landmark paper where they collated data from existing literature to propose a hierarchy model of the macaque monkey cortex (1). This paper provided an impetus for efforts that, 10 years later, led to an inter-areal cortical connectivity matrix, the Collation of Connectivity data on the Macaque brain (CoCoMac) (2). The CoCoMac matrix was fairly rough, with connections between area pairs assigned as absent, weak or strong. The diversity of experimental approaches means that collated data bases are not consistent. Nevertheless, it represented a pioneering event in the field now referred to as brain connectomics.

The past two decades have seen significant advances (3–9). Novel approaches and technologies have made it possible to determine wiring of neural circuits in the brain at micro-, meso- and macroscopic spatial scales (10–13). Importantly, while it may be true that a picture is worth a thousand words, systematic measurements translated into precise numbers are essential for discovering general principles of large-scale cortical organization. This short review covers recent advances in our description of the cortico-cortical connections, and computational modeling based on the new quantitative databases. We shall summarize recent approaches and findings, as well as challenges that need to be addressed in order for the field to move forward. The word “connectome” as currently used sometimes refers to collations of data obtained with different methods, with disparate resolutions. The present review focuses on the connectome defined with consistent approaches exploiting cellular-resolution tracers (14), which at present can only be used in nonhuman animals.

From spatially constrained large scale anatomical models to multi-regional cortical dynamics

A major advance in recent years has been provided by quantitative and consistent databases of inter-areal connectivity macaque (14–17), mice (18–21), and marmoset (22–23). Quantification of connection weight has played a major role and this has been greatly facilitated by a systematic analysis of retrograde tracing. Specifically, the weight of cortico-cortical connection is indexed by fraction of labeled neurons (FLNs) between 0 and 1, which measures the relative weight of projection from a given source area with respect to all source areas to a particular target area (15,16,20,22). In this manner connections are weighted parametrically, which is considerably more informative than a binary matrix. It is also directed, unlike diffusion tractography which, although non-invasive, cannot differentiate fibers from area A to area B and those in the reversed direction. Whereas stream line weights can be inferred from tractography, measurements from tract tracing are direct and thus constitute a “ground truth”. Data from tractography have relatively low signal-to-noise ratio (with numerous false positives and false negatives), and the correlation is modest between log-transformed tractography and tracer connection weights in the macaque (r ≃ 0.59). Further, this correlation drops dramatically when the confounding influence of distance is removed via partial correlations (24).

Three results are noteworthy. First, the Felleman-van Essen structural model is significantly modified by quantification (16,25) (Figure 1). Retrograde tracers show that source neurons for a feedforward projection (e.g., from V1 to V2) reside principally in the superficial layers (above layer 4), and are reciprocated by a feedback projection (V2 to V1) originating principally from neurons in the deep layers (below layer 4) (16). Quantitative formulation of these laminar-depedent projections is based on the measured fraction of supragranular layered neurons (SLNs) for a given projection (Figure 1). This allows a description of a determined model of hierarchy (Figure 1). Fururthermore, SLN has been used to extracting a functional hierarchy in macaque (26) and, via comparison of homologous pathways, in the human brain (27). Second, the weight of connections between two areas decays exponentially with their distance as measured by their estimated white matter tract (the exponential distance rule EDR). The EDR has been shown to be a powerful organizing principal that predicts numerous empirical features of the inter-areal network including motif distributions, global and local efficiency, core-periphery organization and wire minimization in both non-human primates and rodents (17,20,23,28). Third, the weights of inter-areal connections are highly heterogeneous, spanning five orders of magnitude and following a lognormal distribution (15). Therefore, a graph-theoretical view of cortical networks is inadequate unless spatial relationships between areas are taken into consideration (29). This finding has inspired a new class of generative models for the cortical networks that are explicitly spatially embedded (30).

Figure 1. Quantitatively defined hierarchical model of the macaque visual cortex.

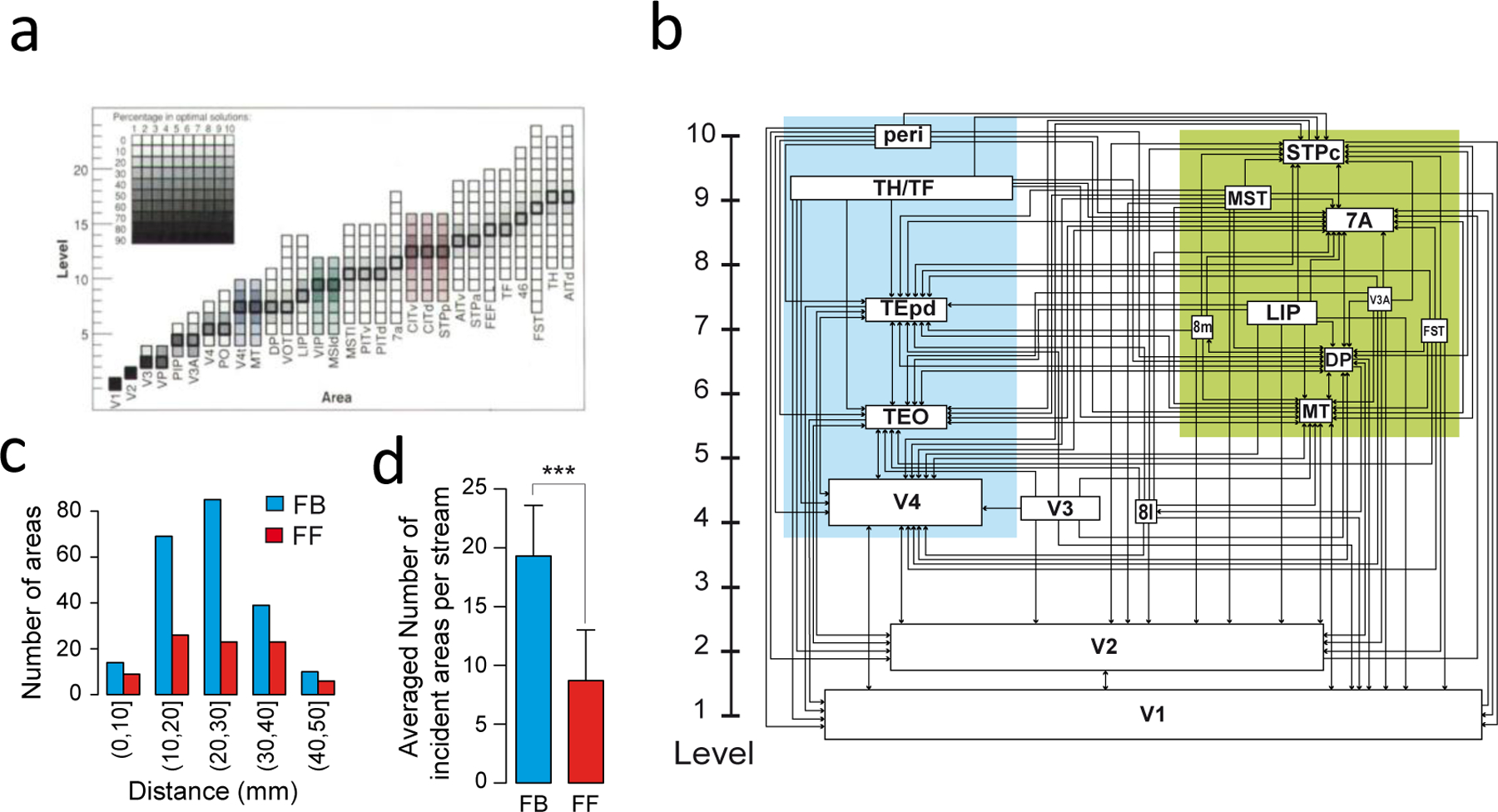
(a) Area frequency distributions of the 150,000 solutions to the Felleman and Van Essen (1991) model (77). (b) The indeterminacy shown in (a) is resolved by statistically modeling the SLN index. In this scheme the hierarchical distance between levels is determined by the laminar distributions of the set of areas (66). This captures many of the features of the Felleman and Van Essen model but there are significant differences namely the relatively low level of the small-saccade component of the FEF which is at a considerably lower lever. In this version of the hierarchy, the box sizes indicating individual areas are proportional to there dimensions in the brain. (c) Influence of distance from target area, shows that feedback (FB) connections have considerably longer reach than do feedforward (FF). (d) Proportions of the two pathways show that FB pathways are twice as numerous as FF pathways. (a) is reproduced from(77); (b), (c) and (d) are modified from (16).

The directed and weighted macaque connectivity matrix provides a structural scaffolding for the development of large-scale functional dynamical models of macaque cortex. Chaudhuri et al. (31) constructed a multi-regional model of macaque monkey cortex with the inter-areal connectivity matrix from (15). In the model, each area was mathematically modeled by a generic excitatory-inhibitory network, in accordance with the commonly accepted notion of the canonical cortical circuit (32). The quantitative connection strengths, however, vary from one area to another. These variations are not random, but systematically change along low-dimensional axes across the cortical mantle. Chaudhuri et al. (31) considered the number of spines (loci of excitatory synapses) in the basal dendritic tree of pyramidal neurons, as a proxy of the strength of synaptic excitation per neuron, which displays an increasing gradient along the cortical hierarchy (33). Interestingly, in this model, temporal dynamics of each area is dominated by a time constant that ranges from tens of milliseconds for early sensory areas to more than a second for prefrontal areas at the top of the cortical hierarchy, precisely what is required for functional differentiation. Importantly, the prevalent time constant of an area is not a monotonic function of its hierarchical position. For instance, the frontal eye field in the quantitatively defined hierarchy is located at a relatively low position in the hierarchy as shown in figure 1 (16), but it displays a slow time constant by virtue of being part of the frontal lobe in close interactions with other frontal areas that display slow dynamics. The timescale spectrum in the cortex is constrained by both the macroscopic gradient of synaptic connection strength and the weighted inter-areal cortical network. Experiments lend empirical evidence in support of such hierarchy of temporal response windows in macaque monkey (34), mouse (35) and human (36).

The concept of macroscopic gradients (37) applies to both synaptic excitation and inhibition processes. For instance, counts of diverse inhibitory cell-types across the mouse cortex shows that the density of GABAergic cells expressing calcium-binding protein parvalbumin (PV), which control spiking outputs of excitatory pyramidal neurons, is highest in the primary visual cortex and much lower in association areas (38–39). Assessment of such macroscopic gradients can be carried out using a variety of data, including levels of gene expression that encode receptors for synaptic excitation and inhibition (40–41). This approach allows identification of the biological fingerprint of different cortical areas; these data can then be incorporated into dynamical computational modeling. They also are valuable for comparison across species. In particular, we will discuss below the definition of cortical hierarchy in primates versus rodents.

Cortical hierarchy in mouse and marmoset

Cortico-cortical connectivity in mouse also displays a wide range of connection weights and the exponential distance rule (20,28). However, whether the mouse cortex displays a well-defined hierarchy remains unsettled. Previous studies note various biological markers are high in V1 and low in association areas, such as PV neuron density (38) and the T1w:T2w ratio from structural magnetic resonance imaging, which is thought to correlate with the level of myelin content in the grey matter (42). Such measures gradually change across the cortex in a way reminiscent of a hierarchy. However, many biomarkers exhibit statistical macroscopic gradients (37). Ideally, one would like to identify an objective and robust definition of hierarchy, then assess the variations of properties as dependent variables along the hierarchy defined as an independent variable.

A recent study examined the issue of hierarchy in the mouse cortex based on anterograde fluorescent labeling of axons (21). Using multiple Cre driver lines, Harris et al selectively traced layer- and cell type-specific projection patterns. An unsupervised method was used to consistently assign these laminar projections at the target area to be either feedforward or feedback in a hierarchy framework. For instance, different types of thalamocortical connections targeting L4 versus L1 in the cortex were separately quantified. Interestingly, it was found that the inclusion of the thalamocortical projections enhanced the consistency of the hierarchy defined in this manner (21). In a neurophysiological experiment using a mouse performing a detection task, the latency of spiking response to a visual stimulus was extracted from neurons in 6 visual areas (35), Person correlation of response latency with the anatomically defined Harris hierarchy was found to be high ( 0.9).

Another approach was inspired by a recent study of the organization of transmodal default-mode networks in human and macaque (43). The work was based on a nonlinear dimensionality reduction method called diffusion maps (44). Briefly, the connectivity matrix is used to define an abstract diffusion between pairs of areas in a hypothetical diffusion process. This distance produces a diffusion space where closer areas in this space share a larger number of paths connecting them, while areas far apart are less connected. In general, the diffusion distance depends on a low number of ‘principal directions’ or ‘principal gradients’ in diffusion space, leading to a low dimensional embedding of the connectivity. Applying this approach to the whole mouse brain data in (45) and by choosing V1 as the origin in the diffusion space, a hierarchy among areas can be built by sorting areas by their diffusion distance to the origin.

Figure 2 shows the pairwise correlations between the anatomically defined hierarchy from (21), the hierarchy deduced from the diffusion map, PV density (38) and T1w:T2w ratio in the mouse brain (41). Intriguingly, Spearman correlation coefficient values are in the range of 0.35 to 0.5. The explanation of substantial but far from perfect correlations is presently unclear, indicating that future research is warranted to achieve a consensus on the definition of cortical hierarchy in the mouse.

Figure 2: Cortical hierarchy in the mouse can be defined by four different measures:

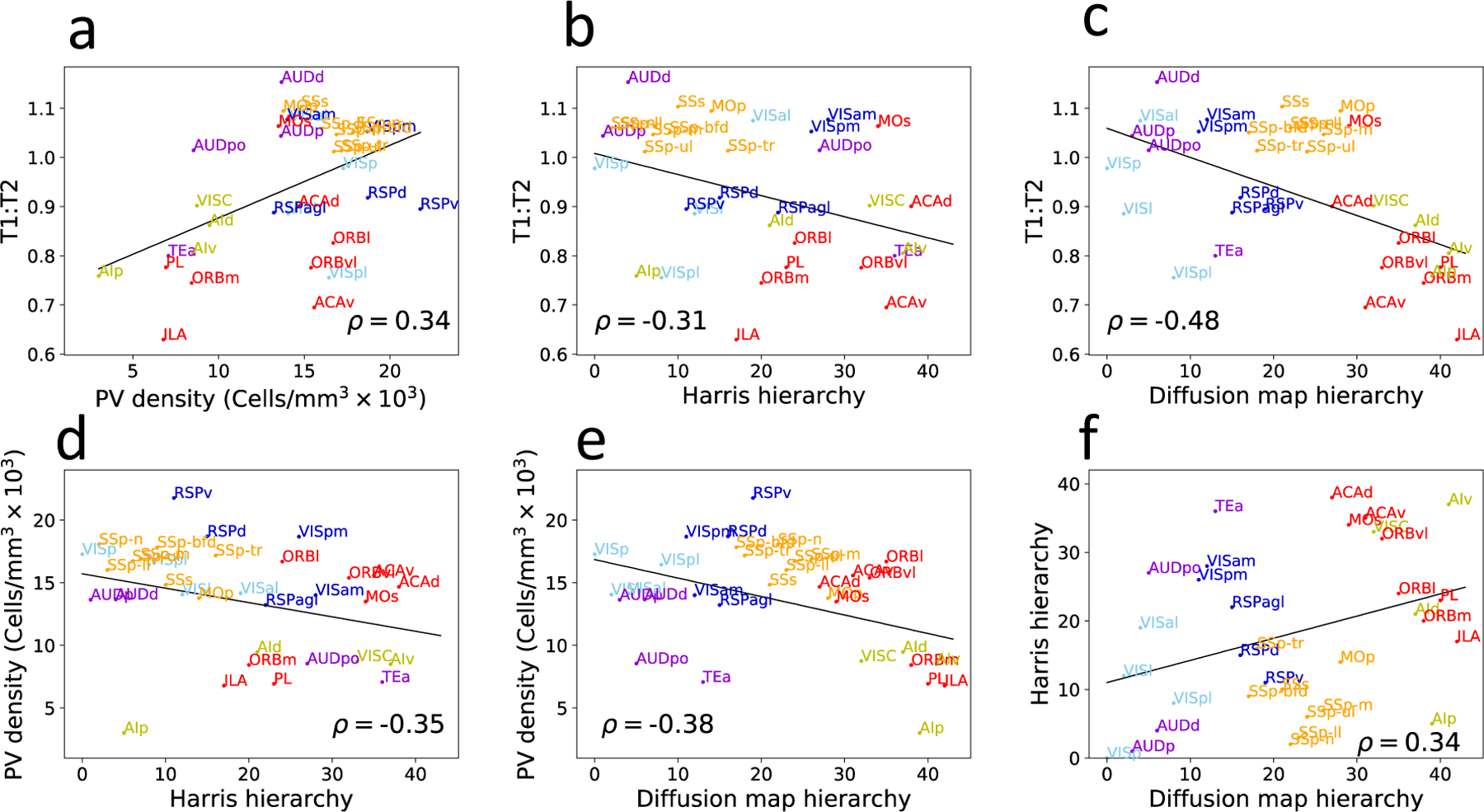
T1w:T2w ratio (41) and PV neuron density (38) decrease, whereas the diffusion map measure and the Harris measure based on layer-dependent connectivity (21) generally increase with the hierarchy. The pairwise correlation between these four measures, however, typically have a correlation of about 0.3–0.5.

It is possible that a cortical hierarchy is flatter or less developed in rodents than primates (20). This difference in organization could emerge from simple scaling laws (46–47), which predict that brain size is inversely correlated with “percent connectedness” (the fraction of brain cells with which any cell communicates directly). This, in turn, could have the effect of increasing the variety of inputs to any given cortical area, hence reducing the dominance of any single source, and “blurring” the definition of hierarchical levels. Thus, the current evidence point to specific differences between primates and rodents, which are likely to have emerged due to specific evolutionary pressures.

Recent analyses based on a dataset of directed and weighted connections in the marmoset cortex shed light on this issue (22,23). Marmosets, like macaques, are simian primates, but are much smaller (on average, the mass of the marmoset brain is 12 times smaller than that of M. fascicularis). In line with the scaling hypothesis, previous studies have indicated that the sources of afferents to both sensory and association areas are more widely distributed spatially across the cortex in marmosets than in macaques. However, a recent comprehensive study of the cortical connectome using statistical techniques applied to retrograde tracer data also revealed that this is accomplished without loss of specificity: the cortical connectivity matrix is very similar to that in the macaque in terms of overall density (approximately 2/3 of the possible connections that could exist are observed experimentally in both species), but they both differ from the mouse (where 97% of the possible connections exist). The similarity between macaque and marmoset extends to more detailed properties of the connectome, such as occurrence of reciprocal versus unidirectional connections. Other properties of the marmoset connectome, such as the presence of a well-defined core-periphery arrangement and the log-normal distribution of connection weights, also bring the two primates in close alignment. Importantly for the present argument, the marmoset cortex is also characterized by a well-defined hierarchy (23), where areas belonging to the different sensory domains occupy defined levels, from primary visual, auditory and somatosensory areas, though several higher-order association areas, to sensory association and polysensory areas. These multiple hierarchies converge to a core of frontal, posterior parietal, rostral temporal areas, which occupy the highest hierarchical levels, and include those regions of the cortex that expanded most during primate evolution (48). Furthermore, the hierarchical levels defined by connectivity are highly correlated with structural measures such as neuronal density (49) and number of spines in the basal dendritic trees of pyramidal cells (50). Further studies in marmosets, including the integration of cellular connectivity data with high-resolution tractography and functional connectivity measures using neuroinformatic platforms (51–52) offer the promise of greater insight onto the correlation with non-invasive measurements in the human brain, which promise to increase our ability to investigate the bases of neuropsychiatric conditions (53–56).

Dynamic models of hierarchical information processing in the macaque cortex

In order to develop a dynamic model showing how bottom-up and top-down processes interact, a computational model of inter-areal processing in the cortex is improved by the incorporation of a laminar cortical structure (57). In the model, a local area has a superficial and a deep layer; each with an excitatory-inhibitory microcircuit (Fig. 3a). The superficial layer exhibits noisy synchronous oscillations in the gamma (≃ 40 Hz) frequency range (58–59); whereas the deep layer shows coherent oscillations at low beta (≃ 15–20 Hz) or alpha (≃ 10 Hz) frequency range (58,60–61). The inter-laminar connections were calibrated based on the exiting literature. Consequently, gamma activities in the superficial layer were shown to be modulated by alpha (Fig. 3b), agreeing with empirical findings (62).

Figure 3: A multi-regional model of the macaque monkey cortex endowed with a laminar structure.

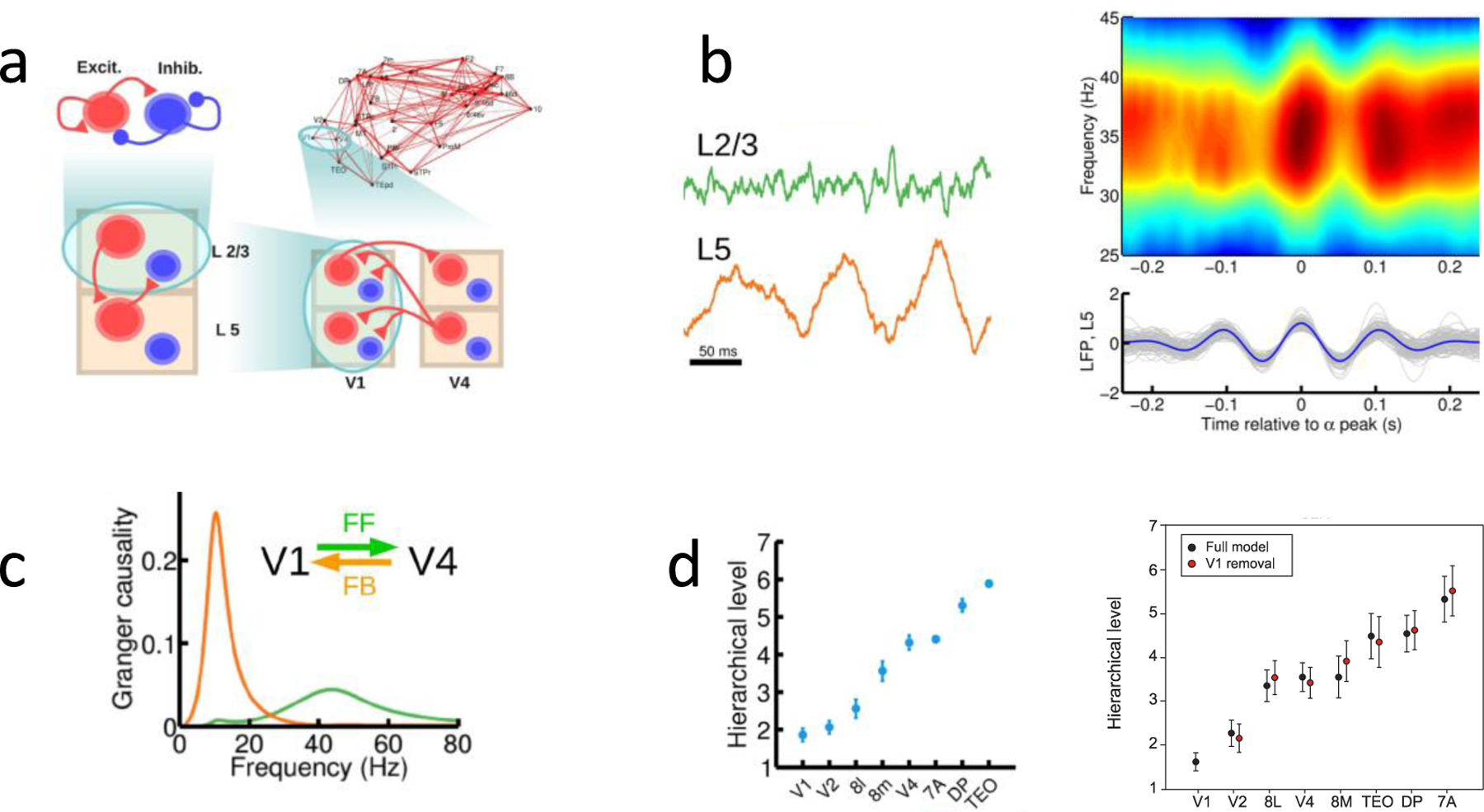
(a) The scheme shows the four levels considered: a within-layer local microcircuit consisting of an excitatory(red) and an inhibitory (blue) population (upper left), a laminar circuit with two laminar modules (corresponding to supra- and infra-granular layers, lower left), an inter-areal circuit with laminar-specific projections (lower right), and a large-scale network of 30 cortical areas based on macaque anatomical connectivity (upper right). Each level is anatomically constrained. Only the connections at each level not shown at a lower level are plotted, for clarity. (b) Left panel: the superficial layer and deep layer display gamma (upper panel) and alpha (lower panel) oscillations. Right panel: the periodogram of the superficial layer shows gamma modulated by alpha wave (top), whereas the deep layer is dominated by alpha rhythmicity (bottom). (c) Granger causality as a function of frequency for feedforward signaling from V1 to V4 (green) and feedback (orange). (d) Cortical hierarchy deduced from the frequency-dependent Granger causality measure in the model (left panel) and in a monkey experiment (right panel). Reproduced with permission from (57) with experimental data from (26).

To assess the plausibility of this model, Mejias et al. (57) evaluated frequency-dependent Granger causality, which is a measure of directionality of information flow. Monkey physiological studies showed that Granger causality is enhanced in the gamma frequency band for a feedforward projection (for example, from V1 to V4) but in the alpha frequency band for a feedback projection (V4 to V1) (26,63). This observation was captured by the model (Fig. 3c). Bastos et al. (26) had shown that the difference in the Granger causality peak values at the gamma and alpha frequencies could be used to establish a functional cortical hierarchy. Subsequently, frequency-dependent Granger causality analysis applied to magnetoencephalography revealed a functional hierarchy in human species (27). The hierarchy, thus deduced purely by physiological measurements, is strongly correlated with that from the anatomical analysis in the macaque monkey. The large-scale laminar network (57) reproduces this hierarchy (Fig. 3d), thus substantially validating the computational model.

This model highlights several questions that deserve attention in future experiments. Firstly, inter-areal connectivity weights anatomically do not directly map onto physiological strengths of synaptic connections, although both show lognormal distributions (15,64–65). In the local microcircuit, synaptic strengths typically vary over 2–3 orders of magnitude (65) rather than five found in the inter-areal network (15). Hence an interesting open question is to quantify synaptic strengths for long-distance cortical projections. Secondly, the laminar targets of diverse top-down projections are poorly understood (66). These issues need to be investigated with viral tracers which in principal can overcome the technical limitations of classical tracers such as fibers of passage. Thirdly, major distinct inhibitory neuron types have relative proportions that vary from area to area and layer to layer. They are differentially targeted by long-range connections, but this information is crucially lacking at the present time.

Modeling has also been used to re-visit a classical problem in computational neuroscience, namely, signal propagation across multiple neural population. Most previous models formulated the problem in a purely feedforward network, where neural group 1 receives an input and fires a burst of spikes, activating neural group 2, which in turn projects to neural group 3, etc (67). A signal either successfully propagates throughout the system, or dies out in the middle of the network. As already mentioned the macaque cortical connectivity is endowed with numerous, highly heterogenous, feedback projections. As a consequence, it is nontrivial to ensure reliable yet stable propagation of activity, say triggered by brief visual input to area V1. In a spiking neuron version of the multi-regional large-scale macaque cortex model, it was found that whereas activity increases with stimulus intensity in areas of the occipital lobe, those in the prefrontal cortex (PFC) exhibit near zero response when the stimulus intensity is below a threshold (Fig. 4a, upper panel, black versus red) (68). In other words, the sensory stimulus needs to be sufficiently strong in order to be propagated along the cortical hierarchy and gain access to the PFC. This phenomenon emerged unexpectedly in the model. Moreover, it is abolished when in the model feedback projections are disconnected (Fig. 4a, lower panel), demonstrating the importance of top-down signaling. Threshold crossing for access to the PFC has been hypothesized as a signature of awareness of a sensory input (Fig. 4b). When a stimulus appears in the environment with a small amplitude, we sometimes detect it, sometimes not. With the same physical stimulation of our sense organs, evoked activity remains largely confined to the posterior part of the cortex, and the input is reported as absent. When we are conscious of its presence, the Global Workspace Theory posits that the cortical core, largely centered in the PFC “lights up” as in an “ignition” and activates the whole brain via feedback projections (69). Further work is warranted to see if our model can indeed account for salient observations from monkey physiology about the ignition phenomenon (70).

Figure 4: Signal propagation and the ignition phenomenon in the cortex.

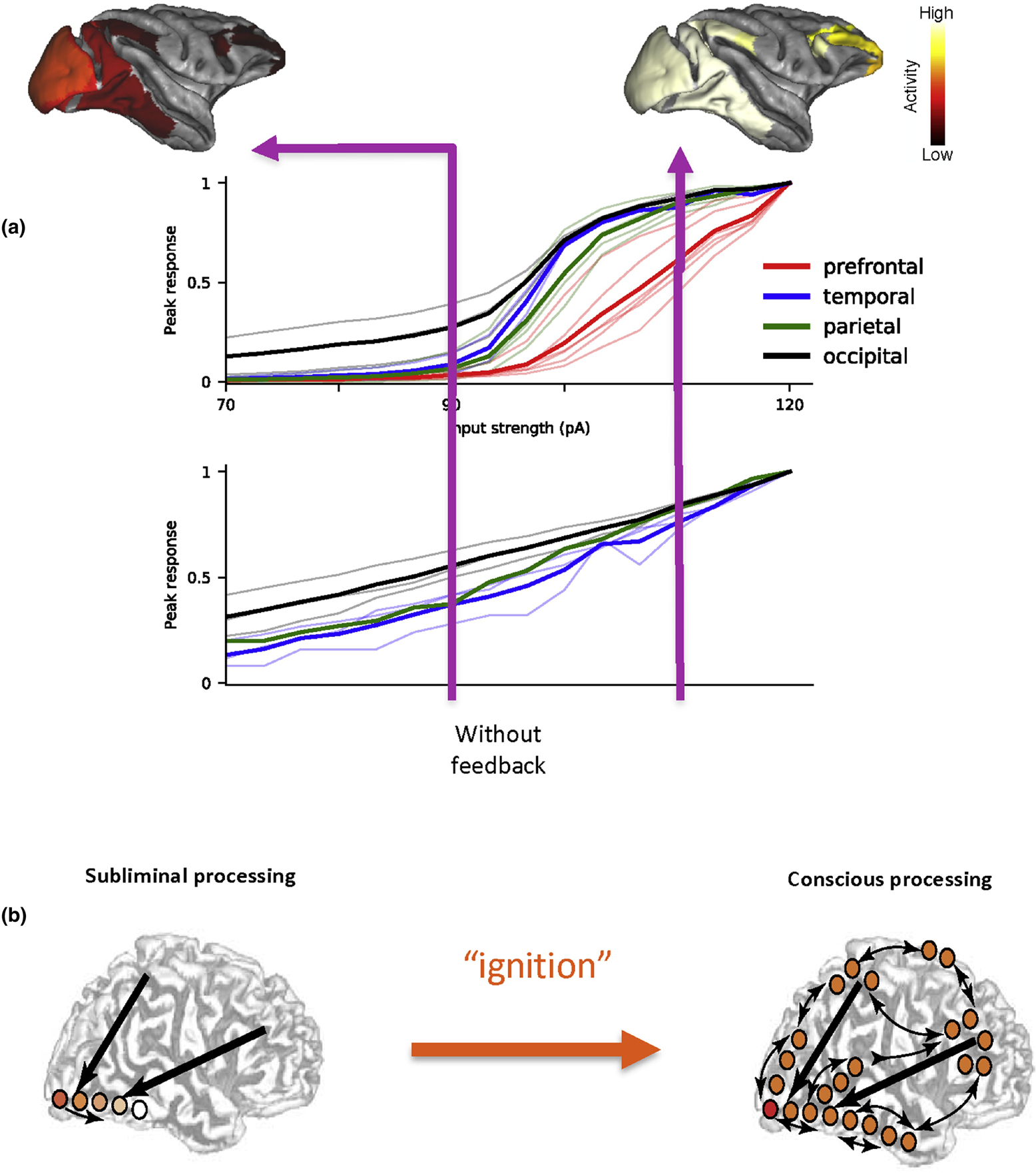
(a) Top and middle: In a macaque cortex model of spiking neurons, as the amplitude of an input to V1 is gradually increased, the peak response in areas of the occipital lobe (black) grows gradually. By contrast, activity is absent in the prefrontal cortex unless the stimulus intensity exceeds a threshold level (red). The activity map is confined to the posterior part of the cortex when the input is weak; if the input is above the threshold, access to the PFC leads to enhanced activity throughout the cortex. Note that this model included only a subset of cortical areas for which connectivity data are available, therefore the activity map is restricted only to those areas in the model. Bottom: The thresholding effect disappears when top-down connections in the model are deleted, demonstrating an important role of long-range feedback loops. (b) The model behavior is akin to the all-or-none ignition phenomenon associated with consciousness, that was observed experimentally with humans. Panel (a) is reproduced from (68).

Looking into Future

In summary, quantitative connectomic databases are now available (Table 1), including directed- and weighted-inter-areal cortical connection matrices for macaque, marmoset and mouse. These data are of a different kind from connectomics on μm spatial scale, achieved using electron microscopy for much smaller animals such as Drosophila fly (71) but possibly for mammals in the future (72). Combined with genetic tools, research in this direction blurs the boundary between macroscopic and mesoscopic connectomes towards cell-type specific connectivity.

Table 1.

Brain connectomes resources

Species	Method	Spatial scale	References	Open access database
Fly	Electron microscopy	Synaptic/sub-cellular	(71)	https://temca2data.org/
Mouse	Viral anterograde tract tracing	Cellular (cell-type specific)	(18,21)	http://connectivity.brain-map.org/
Monkey	Retrograde tract tracing	Cellular	(15)	https://core-nets.org/
Marmoset	Retrograde tract tracing	Cellular	(22,23)	http://marmosetbrain.org
Human	fMRI	1–2mm	(79)	www.humanconnectome.org

For monkeys, existent datasets are incomplete as they only include a subset of cortical areas. This limitation makes it difficult for dynamical models to simulate functional connectivity, defined by the covariance of activities between cortical areas. A subnetwork does not encompass all areas and their feedback loops, and this could impact on global brain dynamics. Therefore, ongoing efforts to complete the full graph of monkey cortico-cortical connectivity should be a priority for the field.

The cortico-cortical connectivity discussed above is not cell-type specific. In the short term, by parallel laminar specific viral tracing of connections in nonhuman primates coupled with laminar resolution fMRI could lead to major progress. This is particularly relevant for top down pathways which are thought to play a major role in higher cognitive processes. Empowered by genetic tools, future work will yield cell-type specific connection patterns, such as how different populations of pyramidal neurons in deep layers 5 and 6 project to distinct cortical and subcortical structures in primates. Again, quantification into numbers would be required for such data to be utilized in computational modeling, which plays an increasing role in our investigations of complex cortical circuitry with its abundance of feedback loops.

A long list of open questions can be made for future research; here is a short one. First, how can a multi-regional network model shed new insights into distributed cognitive processes such as working memory (78)? Second, why do different circuits operate in different dynamical regimes, such as brief response, sequential activity and persistent activity? Third, can we harness genomic data to quantify biological properties in different cell types across cortical areas, that will inform future development of dynamical modeling? Fourth, what are the concise rules for the interactions between the cortex, the hippocampus, thalamus, amygdala, claustrum, basal ganglia and cerebellum?

In summary, technological advances, experiments and computational modeling have identified several general principles of large-scale cortical organization: (1) weights of inter-areal connections obey the exponential distance rule, (2) distributions of cortico-cortical connection weights are lognormal, (3) a cortical hierarchy can be parametrically quantified, (4) synaptic excitation and inhibition vary across the cortex in the form of macroscopic gradients. In the next phase of the brain connectome, genetically powered and cell-type specific connectome, single-cell RNA-seq mapping, large-scale neurophysiology using Neuropixels probes (73–76) will produce a deluge of data. Novel analysis tools, new ideas and theory will be critical for us to transform data into knowledge, ushering in an era of computational neuroscience of the whole brain.

• Directed- and weighted inter-areal cortical connectivity matrices of macaque, marmoset and mouse exhibit similarities as well as marked differences.

• The new connectomic data provide quantitative information for structural and dynamical modeling of multi-regional cortical circuit providing insight to the global cortical function.

• Quantification of cortical hierarchy guides investigations of interplay between bottom-up and top-down information processes.