Real-time passive acoustic mapping using sparse matrix multiplication

Abstract

Passive acoustic mapping enables the spatiotemporal monitoring of cavitation with circulating microbubbles during focused ultrasound (FUS)-mediated blood-brain barrier opening. However, the computational load for processing large data sets of cavitation maps or more complex algorithms limit the visualization in real-time for treatment monitoring and adjustment. In this study, we implemented a graphical processing unit (GPU)-accelerated sparse matrix-based beamforming and time exposure acoustics in a neuronavigation-guided ultrasound system for real-time spatiotemporal monitoring of cavitation. The system performance was tested in silico through benchmarking, in vitro using non-human primate (NHP) and human skull specimens, and demonstrated in vivo in NHPs. We demonstrated the stability of the cavitation map for integration times longer than 62.5 μs. A compromise between real-time displaying and cavitation map quality obtained from beamformed RF data sets with the size of 2000×128×30 (axial pixels × lateral pixels × samples) was achieved for an integration time of 1.44 μs, which required a computational time of 0.27 s (frame rate of 3.7 Hz) and could be displayed in real-time between pulses at PRF=2 Hz. Our benchmarking tests show that the GPU sparse-matrix algorithm process the RF data set at a computational time rate of 0.03±0.01 μs/pixel/sample, which enables adjusting the frame rate and the integration time as needed. The neuronavigation system with real-time implementation of cavitation mapping facilitated the localization of the cavitation activity and helped to identify distortions due to FUS phase aberration. The in vivo test of the method demonstrated the feasibility of GPU-accelerated sparse matrix computing in a close to a clinical condition, where focus distortions exemplify problems during treatment. These experimental conditions show the need for spatiotemporal monitoring of cavitation with real-time capability that enables the operator to correct or halt the sonication in case substantial aberrations are observed.

I. INTRODUCTION

Focused ultrasound (FUS) can drive microbubble-seeded cavitation that enhances drug delivery through the blood-brain barrier (BBB) – a semipermeable structure of the brain vasculature that prevents drug uptake into the central nervous system [1]. FUS-induced cavitation can transiently and locally disrupt the BBB [2] via transcytosis, tight junction opening, and inhibition of active transport proteins in the brain endothelial cells [3]–[5]. Preclinical studies have demonstrated the potential of FUS-mediated BBB opening to deliver variable-sized molecules such as antibody-based anticancer agents [6]–[8], antiamyloid antibodies [6], [9], [10], brain-derived neurotrophic factor [11]–[13], adeno-associated viruses [14], [15], and stem cells [16]. Currently, clinical studies are assessing the safety and feasibility of the technique for the treatment of Alzheimer’s disease [17] and glioblastoma [18].

Passive cavitation detection (PCD) using single-element transducers has been used to monitor potential harmful cavitation regime in real-time in open-loop and closed-loop systems [19]–[22] inside and outside the magnetic resonance imaging (MRI) scanner [23], [24]. However, single-element PCD limits the monitoring to a temporal analysis, where cavitation activity cannot be resolved spatially. Neuronavigation-guided ultrasound with real-time passive acoustic mapping (PAM) [25] can provide a high precision therapy at lower cost in comparison to magnetic resonance-guided focused ultrasound (MRgFUS) systems. The FUS neuronavigation system allows for planning trajectories towards specific brain targets that avoid pre-existent lesions, large vessels, ventricles, and other brain structures to be circumvented while PAM enables spatiotemporal monitoring of cavitation associated with BBB-opening. The spatial mapping of acoustic cavitation recorded by a multielement transducer is reconstructed using delay-and-sum (DAS) beamforming either in the time or in the frequency domain [26]–[36]. Altogether, this system can help detect beam aberration due to the skull [32], [37], which could be compensated by repositioning the transducer for an efficient and safe sonication at the prescribed location, especially when multiple sonications are required for covering a larger brain volume.

Modern graphics processing units (GPUs) offer parallel processing designed for high-peak computational throughput in a short period. Previous studies have demonstrated implementations of GPU acceleration, which generated real-time visualization of microbubble activity in the brain at variable frame rates, sample integration times, number of channels, and field-of-view (FOV) (respectively, Collin et al. [38]: 5 Hz, 4000 samples, 32 channels, 40 × 10 mm²; Jones et al. [37]: 3.3 Hz, 200 samples, 128 channels, 20 × 20 × 20 mm³; Lyka et al. [34]: 3 Hz, N/A samples, 128 channels, 20 ×10 mm²; Lyka et al. [39]: 0.25 Hz and 0. 625 mHz, 2000 samples, 128 channels, 660 voxels; Jones et al. [40]: 1 Hz, 30,000 samples (3 ms integration time at 10 MS/s), 256 channels, 10 × 10 × 10 mm³).

Programmable multiprocessing-unit architectures provide library routines optimized for sparse matrices computations, which improves real-time performance of numerical operations [41], [42]. Data processing with a sparse matrix provides higher performance than a fully sampled matrix because it eliminates operations with zero-valued elements of the matrix. In addition, sparse representation reduces data storage as it stores only the nonzero elements and their row indices. Sparse matrix operations can be accelerated even more when performed in parallel using GPU computing. Sparsity methods have been employed widely in medical imaging [43] to speed up and improve image processing and machine-learning techniques in a variety of imaging methods, such as MRI [44]–[46], digital pathology images [47], [48], computed tomography (CT) [49], [50], and ultrasound [25], [51]–[54].

In this study, we present an implementation of PAM using GPU-accelerated sparse matrix-based beamforming and time exposure acoustics (TEAs) [55], [27], which can be performed in real-time with large maps and short-duration data sets or vice versa. This study builds on prior reports by our group as indicated in Wu et al. [25], which employed real-time PAM focusing on the neuronavigation system implementation, where the GPU sparse-matrix implementation was not detailed or compared with other standard methods, and Hou et al. [51], where active mapping (harmonic motion imaging using tissue displacement tracking) was employed, but not in passive detection or for microbubble-based therapy monitoring. The novel contributions of this article are the detailed description of the implementation of the sparse matrix-based algorithm for PAM and a benchmarking comparison of the non-sparse and sparse implementations in both CPU and GPU. Tests were performed in silico through benchmarking, in vitro using skull specimens of human and non-human primate (NHP), as well as in vivo BBB opening experiments in NHP.

II. Material and Methods

A. Passive beamforming algorithm

The passive beamforming algorithm based on TEA [27] was implemented with a conventional 128-channel linear array imaging probe (L7–4, Philips, Bothell, WA, USA; center frequency: 5.208 MHz). A programmable ultrasound scanner (Vantage 256, Verasonics, Kirkland, WA, USA) recorded the acoustic emissions, with time t, from cavitating bubbles during sonications. The radio frequency (RF) channel data was used to reconstruct the passive cavitation maps using dynamic receive beamforming (${\sum }_{n=1}^N{S}_n\left(r_n,r,t\right)$) and then time-integrated (${\int }_0^{T_i}{|\cdot |}^{2}dt$) over a period T_i defined as the integration time:

$$C(r)={{\int }_0^{T_i}\left|{\sum }_{n=1}^N{S}_n\left(r_n,r,t\right)\right|}^{2}dt,$$ (1)

$$S_n\left(r_n,r,t\right)=c_n\left(t+d\left(r_n,r\right)/c\right),$$ (2)

where N is the number of elements in the array, S_n is the channel data for the n-th element, r_n is the location of the n-th transducer element, r is the location of the pixel to be reconstructed, c_n(t + d(r_n,r)/c) the received cavitation signal for the n-th channel after adjusting for the time delay based on the distance between r_n and r, and c the speed of sound. Skull-specific aberration corrections were not performed.

B. Sparse-matrix construction

Although GPU-based sparse matrix beamforming has been described elsewhere [25], [51], its specific implementation and application for TEA-PAM is detailed here. In our previous study, the sparse matrix algorithm was implemented using sequences with short imaging pulses. In contrast, therapeutic pulses used in BBB opening are typically composed of thousands of acoustic cycles. Therefore, the duration of received RF signals during PAM or the total amount of beamformed data is significantly larger than the active imaging described before. The DAS beamforming was accelerated using the fast sparse matrix operation performed on a GPU [Tesla K40 (real-time) or Quadro P6000 (offline processing), NVIDIA, USA]. All sparse matrix operations were performed in Matlab (2017b, MathWorks, Natick, MA, USA), which has built-in GPU support for sparse matrices since version 2015a. The computing acceleration was accomplished by implementing the term ${\sum }_{n=1}^N{S}_n\left(r_n,r,t\right)$ from (1) using a sparse matrix multiplication followed by temporal summation of the squared beamformed RF data. The sparse matrix multiplication can be written as y=Ax, where the reconstructed RF data y is the result from the multiplication of A, a sparse matrix associated with the DAS operation, and x, a matrix containing the channel data reshaped into column vectors for each sample of the integration time. The number of rows in A is equal to the total number of pixels in the reconstructed image, which is the product of the lateral map size N_x and the axial map size N_z. The number of columns in A is equal to the product of the number of samples acquired per channel Z, and the number of array elements N. Table I presents all values for the parameters used in this study.

Table I.

Parameters used for GPU-based sparse matrix multiplication in passive acoustic mapping.

Symbol	Parameter	Value / Units
Nx	Lateral map size	128 pixels
Nz	Axial map size	2,000 pixels
NT	Integrated samples	10 – 2,000 samples
Ti	Integration time	1.44 – 96.1 μs
Z	Acquired RF data samples per channel	2,000 samples
N	Number of array elements	128
fs	Sampling frequency	20.8 MHz
n	Assigned number of transducer element or channel	1–128
l	Iteration number of the standard basis vector	1–256,000

The sparse matrix was built offline prior to the experiments, as it requires minutes-to-hours of calculation. The computational time depends on the number of samples in the acquired channel data, the number of array elements N, as well as the number of pixels in the reconstructed image (N_x × N_z). The sparse matrix was designed here to compute images of approximately 74 mm (depth, N_z=2,000 axial pixels) by 38 mm (width, N_x=128 lateral pixels), with Z equal to 2000 samples acquired by N=128 transducer elements (or channels) at sampling frequency 20.8 MHz (4 times the receiving center frequency of the L7–4 array, which is 5.208 MHz) that can be displayed in real-time once the sparse matrix is built. The sparse matrix needs to be built offline only once and then can just be loaded into memory for real-time beamforming.

The following describes how to build the reconstruction sparse matrix numerically. First, a conventional 3D matrix representation (Figure 1a) containing the distance D in sample units between each image pixel and transducer element is calculated by

$$D=\left|\overrightarrow{r_n}-\overrightarrow{r}\right|N_w$$ (3)

where $\overrightarrow{r}$ is the pixel location in the reconstructed image in wavelength units, $\overrightarrow{r_n}$ is the location of the n-th element in wavelength units, and N_w is the number of samples per wavelength (N_w=4, yielding a sampling frequency 4 times the center frequency of the receiving array). The speed of sound associated with the wavelength was 1540 m/s, which is equal to the speed of sound in tissue.

Fig. 1.

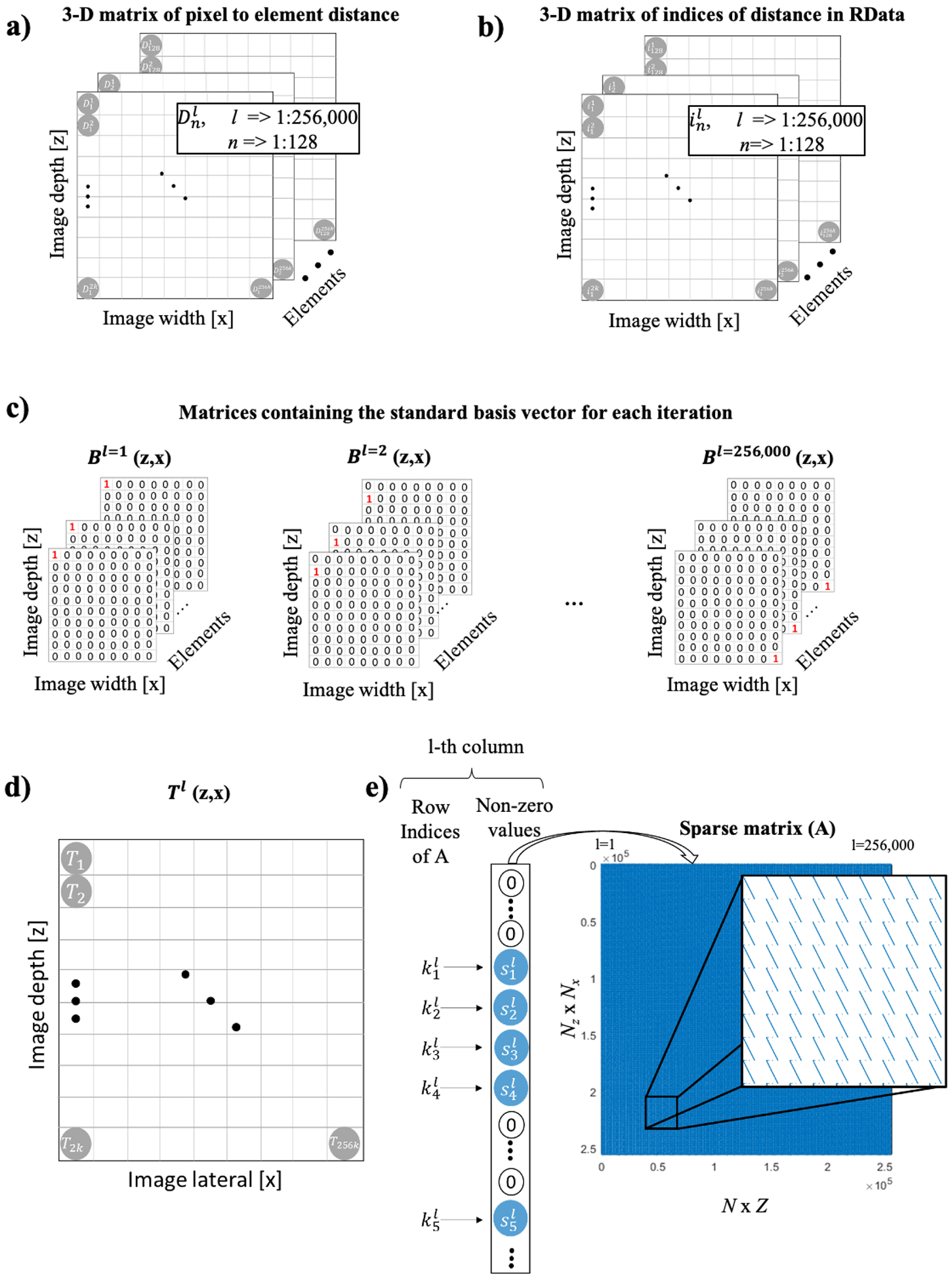
Sparse matrix construction. (a) 3D matrix of distance from the pixel to transducer element in sample units calculated for an imaging array with 128 elements, and a reconstructed image of 2000×128=256000 pixels. (b) 3D matrix of re-indexed distance to follow data output by Verasonics Vantage. (c) Standard basis vectors used for the DAS iterative calculation. (d) Matrix resulting from DAS operation on a given standard basis vector. (e) Sparse matrix values allocation following 2D representation.

Then, the values in the distance matrix are converted into indices associated with the size of a given data point of channel data provided by Verasonics Vantage (sample segments acquired by each transducer element per frame). The indexed distance (Figure 1b) is given by

$$i\left(z,x,n\right)=D\left(z,x,n\right)+\left(n-1\right)Z$$ (4)

where i is the indexed pixel to element distance in the channel data, and Z is the total depth in sample units, with Z=2000 samples and n = 1 to 128. After that, the DAS operation is performed to compute the matrix T^l(z,x)

$$T^l\left(z,x\right)=\sum _{n=1}^N\left(\left(1-d\left(z,x,n\right)\right).B^l\left(i\left(z,x,n\right)\right)+d\left(z,x,n\right).B^l\left(i(z,x,n\right)+1\right)$$ (5)

where l is iterated from 1 to 256,000 (Z x N) and

$$d\left(z,x,n\right)=mod\left[D\left(z,x,n\right), 1\right]$$ (6)

where mod is the module operator, and B^l is the l-th standard basis vector of the 256,000-dimensional Euclidian space, containing zeros everywhere except at the l-th position (B^l(i) = δ_il, where δ_il is the Kronecker delta, Figure 1c and d). Finally, the sparse matrix A is allocated with nonzero values obtained from the matrix T^l, which can be obtained in Matlab using [k^l,~,s^l] = find(T^l(:)), where k^l is the vector of indices of nonzero values in T^l and s^l is the corresponding vector of nonzero values in T^l. The sparse matrix (Figure 1e) is given by

$$A\left(k^l,l\right)=s^l$$ (7)

C. Time exposure acoustics real-time processing

Once the sparse matrix is loaded in the computer or GPU memory, the RF data can be beamformed in real-time by simply multiplying the sparse matrix by the channel data. This is the only step in the processing where the sparse matrix is used. The acquired data sets comprise 2,000 samples per receiving element, that is, a signal duration of 96.1 μs and a sampling frequency of 20.8 MHz. To acquire data sets with reduced integration times that would accelerate computation, the beamformed time-domain signal was truncated at the relevant sample after t = 0. For example, only the first 30 samples were used for an integration time of 1.44 μs, the first 300 samples for an integration time of 14.4 μs. An important property of the multiplication using the sparse matrix is that it can be applied regardless of the number of samples, as it refers to a multiplication involving two 2D matrices (Figure 2a). Then, the cavitation map is obtained from the TEAs processing (Eq. 1) using the beamformed data (Figure 2b). Finally, the image is reshaped in 2D (N_z x N_x) and displayed in real-time (Figure 2c).

Fig. 2.

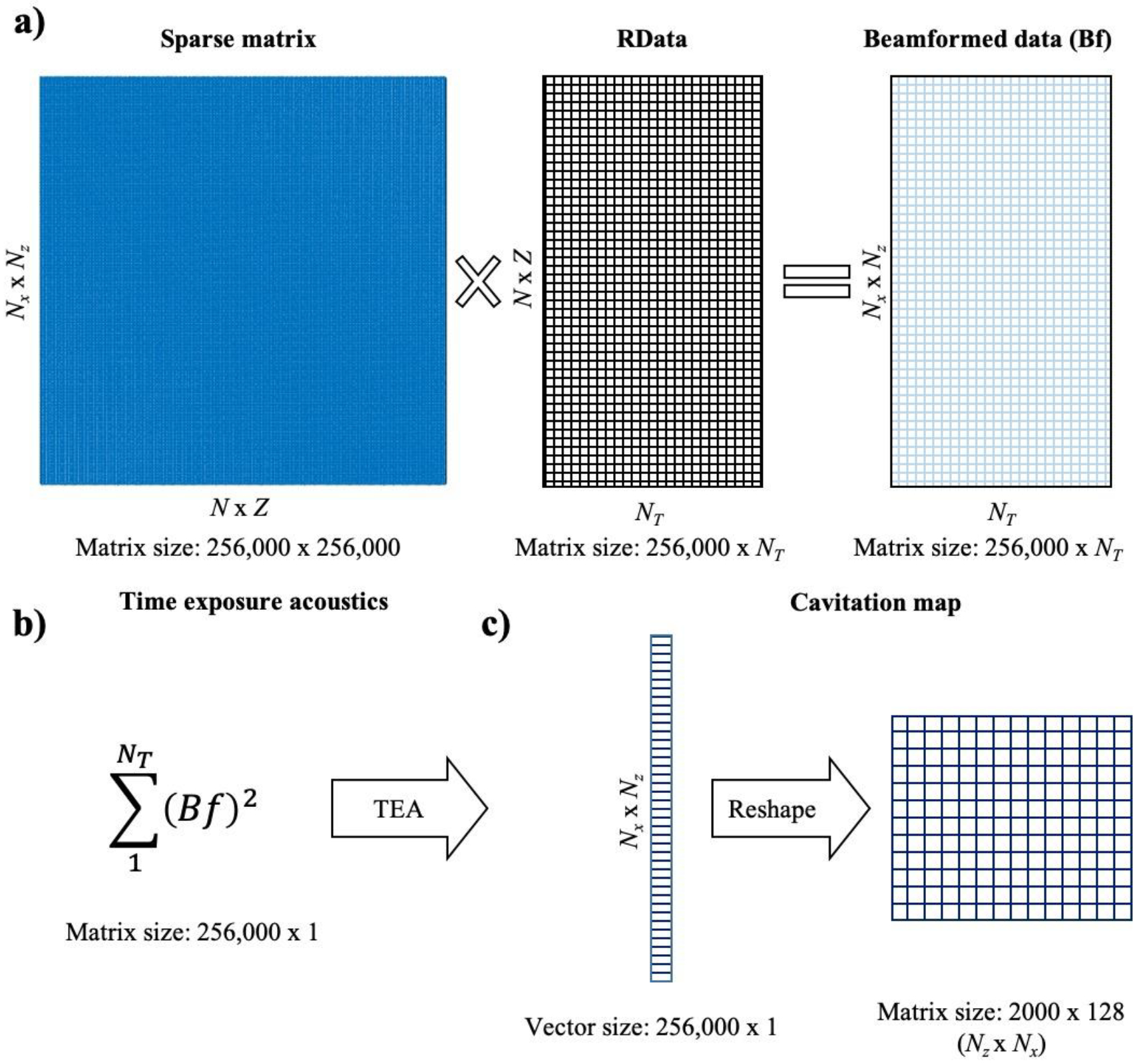
TEA-PAM real-time algorithm using sparse matrix operation. (a) DAS beamforming algorithm using GPU-accelerated sparse matrix operation. (b) TEA operation. (c) Cavitation maps.

D. In vitro experiments

The in vitro test of the system with and without the skull specimens (NHP and human, parietal bone) was performed in a silicon phantom with a 4-mm diameter tube where in-house, lipid-shell, monodisperse microbubbles (median diameter: 4–5 μm, diluted to 2×10⁵ bubbles/mL [56], [57]) circulated at a flow rate of 0.25 mL/s using a syringe pump (Figure 3A). The skull specimens were degassed 24h before the experiment. A customized Matlab code controlled a single-element, 0.5-MHz FUS transducer (diameter: 64 mm, focal depth: 62.6 mm; H-107, Sonic Concepts, Bothell, WA, USA) driven by a function generator (model 33220A, Agilent Technologies, Santa Clara, CA, USA) with 50-dB amplification (A075, ENI, NY, USA). A PCD array (L7–4, Philips, Bothell, WA, USA; center frequency: 5.208 MHz, sampling frequency: 20.8 MHz, channel data length: 2,000 samples) and a single PCD transducer (Y-107, Sonic Concepts, USA; sensitivity: 10 kHz to 15 MHz, sampling frequency: 50 MHz) were simultaneously used to monitor the cavitation generated using derated peak negative pressure (PNP): 100–600 kPa, pulse length: 5000 cycles (10 ms), pulse repetition frequency (PRF): 10 Hz, duration: 2 s. The skull specimen was placed between the phantom and the PCD array immediately after acquisitions without the skull to assess the skull effects on the PCD data in similar experimental conditions.

Fig. 3.

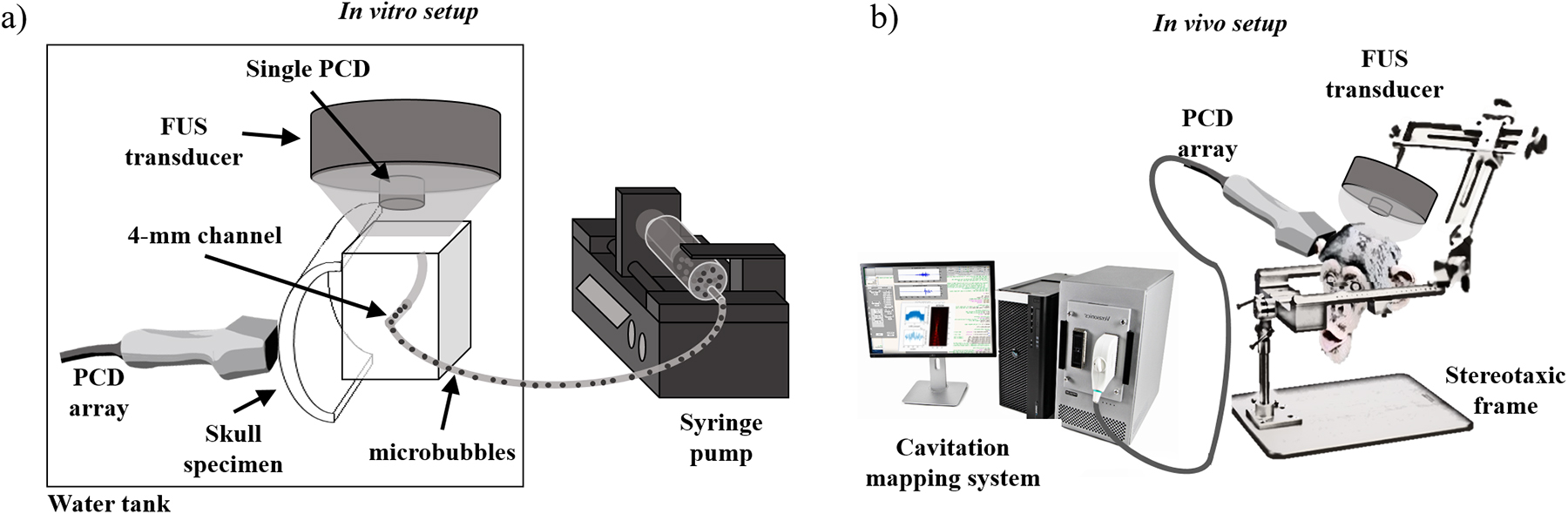
Experimental setups for (a) the in vitro skull and phantom and (b) the in vivo BBB opening in NHP. In the in vitro experiment, the FUS transducer was placed on top of the phantom and orthogonal to the PCD array. The skull was placed between the phantom and the PCD array for assessing the skull effects on the cavitation mapping. In the in vivo experiment, the FUS transducer was targeted to the region-of-interest based on the neuronavigation coordinates while the PCD array was placed against the temporal bone window toward the FUS focus.

E. In vivo NHP experiments

All procedures and experiments with animals were reviewed and approved by the Institutional Animal Care and Use Committee at Columbia University and the New York State Psychiatric Institute following the National Institutes of Health Guidelines for animal research. The in vivo experiments were performed in two male adult macaques (Macaca mulatta, weight: 9–11 kg, age: 18–20 years old). The FUS transducer was placed on the top of the animal’s head using a stereotaxic frame for head fixation (Figure 3b), with targets set at the caudate-putamen and hippocampus using a neuronavigation system (Brainsight Vet System, Rogue Research Inc., Montreal, QC, Canada). The neuronavigation guidance was performed using anatomical T1-weighted magnetic resonance (MR) brain images (3D turbo field echo sequence, TR/TE = 11.1/5.1 ms, FA = 8°, resolution = 0.7 × 0.7 × 0.7 mm³; Philips 3 Tesla scanner). The animals received in-house manufactured monodisperse microbubbles injected intravenously (2.5×10⁸ bubbles/kg) and were sonicated for 2 min (derated peak-negative pressure = 450 kPa, excitation frequency = 0.5 MHz, pulse length = 10 ms, PRF = 2 Hz). The reported pressures correspond to in situ values, following transmission through an NHP or human skull, and were estimated prior to the experiment using a capsule hydrophone (HGL-0200, ± 3-dB frequency range: 0.25 – 40 MHz, electrode aperture: 200 mm; Onda Corp., Sunnyvale, CA, USA). The cavitation activity was monitored in real-time using the same PCD array and single PCD transducer described in the in vitro test. The PCD array was aligned with the focal region of the FUS transducer using neuronavigation-guidance through the skull temporal window (a thinner part of the skull serving as an acoustic window). The BBB opening and safety were assessed by MR images acquired 1h after sonication. The BBB opening was confirmed by comparing T1-weighted contrast-enhanced images (Gd-DTPA-BMA, Omniscan®, GE Healthcare, Princeton, NJ, USA; 0.2 mL/kg) acquired before and following the sonication (3D spoiled gradient echo sequence, TR/TE = 8.5/4.8 ms, FA = 8°, resolution = 1 × 1 × 1 mm³). Safety was evaluated with T2-weighted MR images for assessing potential edemas (TR/TE = 3000/80 ms, flip angle or FA = 90°, resolution = 0.4 × 0.4 × 2 mm³).

F. Quantification of acoustic cavitation emission using the single-element PCD

Stable cavitation dose (SCD_h), stable cavitation dose with ultra-harmonics (SCD_u), and the inertial cavitation dose (ICD) were calculated following the same methodology of previous studies [58], [59]. Harmonic components with frequency bandwidths of 20 kHz (n × f, where f = 0.5 MHz and n = 3, 4, 5…, 10) were extracted from the frequency spectrum obtained from the PCD signal in Volts. Similarly, ultra-harmonic components (m/2 × f, where f = 0.5 MHz and m = 5, 7, 9…, 19) were extracted using the same frequency bandwidth size. SCD_h was calculated by the root-mean-square (RMS) of the harmonic components, SCD_u, by the RMS of the ultra-harmonic components and ICD by the RMS of all other components not included in SCD_h and SCD_u, between 1.25–5.00 MHz.

G. Benchmarking

The first benchmarking test compared the computational time and sample processing rate of CPU and GPU implementations of the sparse and standard DAS matrix multiplication using the NHP in vivo data set (Z = 2000 samples, N = 128 elements, N_z = 2000 axial pixels, N_x = 128 lateral pixels). All GPU computations were performed using GPU-enabled Matlab functions. Both GPU and CPU tests were performed using a number of samples N_T from 10 to 1500, except for the CPU standard DAS implementation that was limited to 500 samples as it reached unpractical computational times (several hours). The second benchmarking test compared the computational time with Z = 2000 samples, N = 128 elements, and N_T = 30 for different sizes of FOV, where the lateral map size N_x remained constant equal to 128 pixels, and the axial map size varied: N_z = 50, 100, 200, 500, 1000, and 2000 pixels. The testing routines included only the beamforming processing (figure 2) and did not include the sparse matrix construction (figure 1). Similarly, the memory allocation for the standard processing was disregarded to allow an adequate comparison of processing time only with both methods. The benchmarking was performed offline in a Dell Precision T7910 workstation (dual-processor Intel Xeon CPU E5–2650 v4 @ 2.20GHz, 128 GB of RAM) equipped with a GPU (NVIDIA Quadro P6000, 24 GB memory, 3840 cores, driver: 392.56) running MS Windows 10 Pro 64-bits and Matlab 2017b.

III. Results

The effect of the integration time T_i on the GPU sparse-matrix algorithm computational time T_c (including both beamforming time and integration time) and cavitation mapping quality was assessed off-line in phantoms with and without skull specimens. The computational time increased linearly with the integration time as the number of beamformed samples for each cavitation map increased with T_i (figure 4a). To achieve real-time monitoring the maximum computational time was limited by the time between pulses (T_c < 1/PRF), which in the case of NHP BBB opening sessions was defined as 0.5 s (for PRF= 2 Hz). A maximum T_i of 1.44 μs was found in order to achieve a real-time cavitation mapping with N_T equaling 30 samples. In addition to that, the maximal intensity in the mapping plateaued at approximately 62.5 μs (1300 samples). The maximum intensity for each integration time was defined as the pixel intensity with the highest value in each reconstructed passive map. The −6-dB cavitation region size defined in the map was quantified and found to increase with T_i with a transient formation of discrete spots of cavitation activity during the first 20 μs (figure 4b). Then, the cavitation region size decreased, possibly due to the destruction of resonant microbubbles at the periphery of the focus, reaching a steady-state spatial distribution at around 62.5 μs.

Fig. 4.

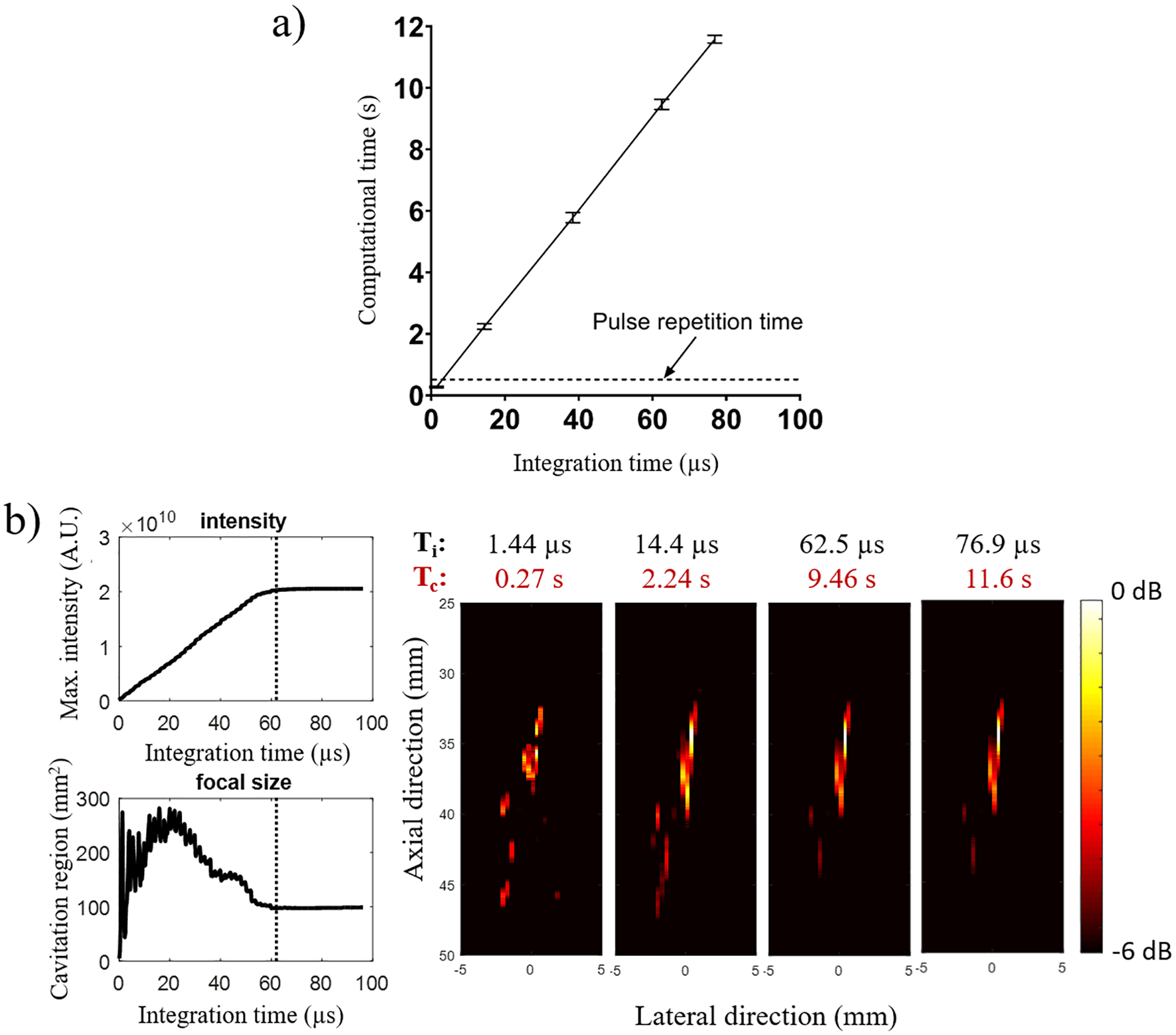
Effect of integration time on computational time and cavitation mapping characteristics. (a) The computational time T_c increased linearly with the integration time T_i, which limited the integration time to a maximum of 1.44 μs for PRF= 2 Hz (0.5 s of pulse repetition period). (b) Ti also affected the mapping quality with lower values providing maps with discrete cavitation spots out of focus and values higher than 62.5 μs reaching a steady state of cavitation map. This representative case was performed at 450 kPa. Computational times T_c refers to the reconstruction of large acoustic maps (2,000 axial pixels × 128 lateral pixels).

The cavitation detectability determined by system sensitivity was then tested in phantoms using 62.5-μs integration time for pressure levels ranging from 150 to 600 kPa (figure 5). Cavitation maps without the skull showed localized cavitation distributions at all pressure levels (figure 5a). Acquisitions with skull samples presented a threshold for cavitation detection at 300 kPa and 450 kPa for NHP skull (figure 5b) and human skull (figure 5c), respectively. The cavitation activity was spatially distorted in the presence of both skulls, forming an elongated pattern as a result of the beamforming degradation caused by the skull scattering. The pressure thresholds identified here are in the range used for BBB opening in NHP.

Fig. 5.

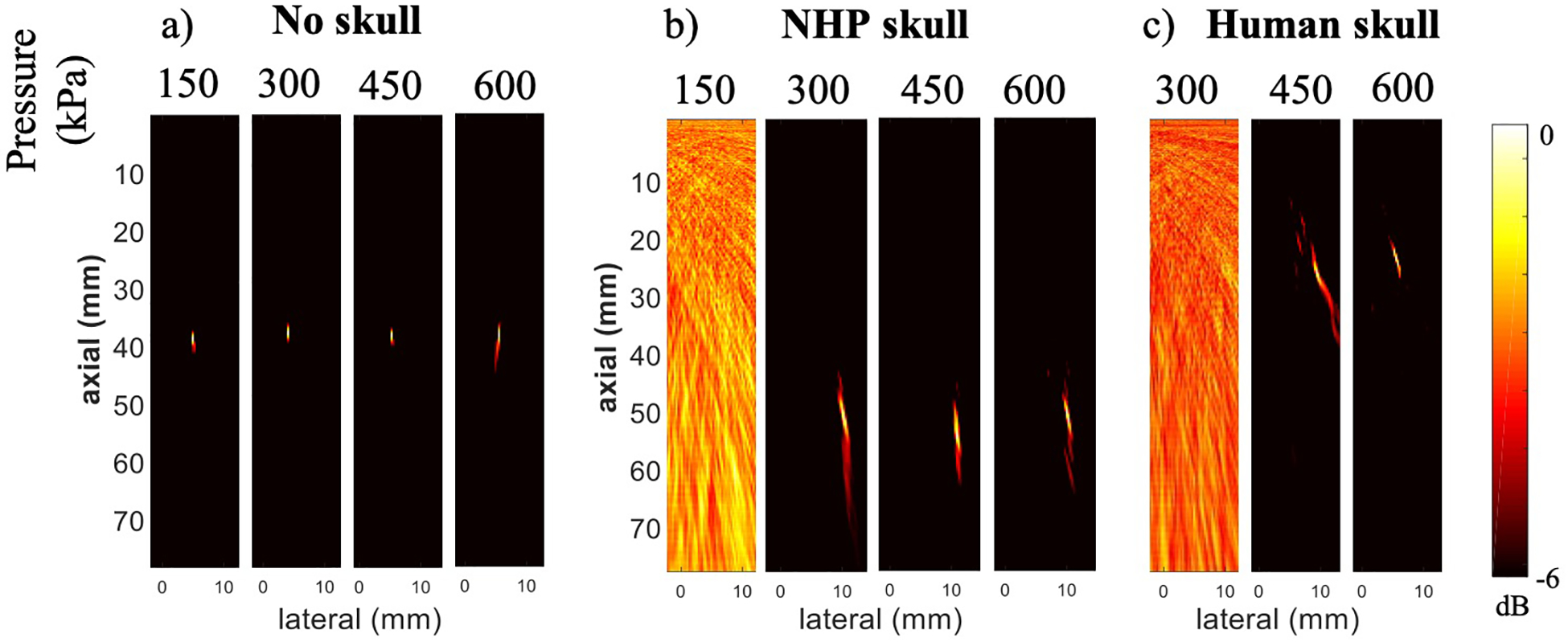
Cavitation mapping sensitivity through primate skull. Cavitation maps using 62.5-μs integration time at variable pressure levels were acquired (a) without a skull, (b) with NHP skull, and (c) with human skull between the PCD array and the phantom.

Following the in vitro experiments, the in vivo experiments were performed in NHP during the BBB opening sessions. The PCD array was placed on the temporal window aiming at the FUS targeted area, with the PAM plane covering a lateral cross-section of the FUS focus (figure 6a). The BBB opening and monitoring result at 450 kPa obtained from NHP 1 is shown in figure 6a. The frequency spectra from the beamformed signals at the location of maximum image intensity acquired during control and acquisitions with microbubbles are shown in figure 6b. The cavitation levels obtained from the single-element PCD acquisition following spectral filtering showed a substantial increase of both stable and inertial cavitation once microbubbles perfused the brain (figure 6c). The cavitation intensity (figure 6d) obtained from consecutive cavitation maps (figure 6e) was qualitatively consistent with the cavitation activity observed with the single-element PCD. The single-element PCD traces are presented with independent components cavitation (harmonic, ultra-harmonic, and inertial), whereas the cavitation activity detected by the PCD array shows the total activity without spectral filtering.

Fig. 6.

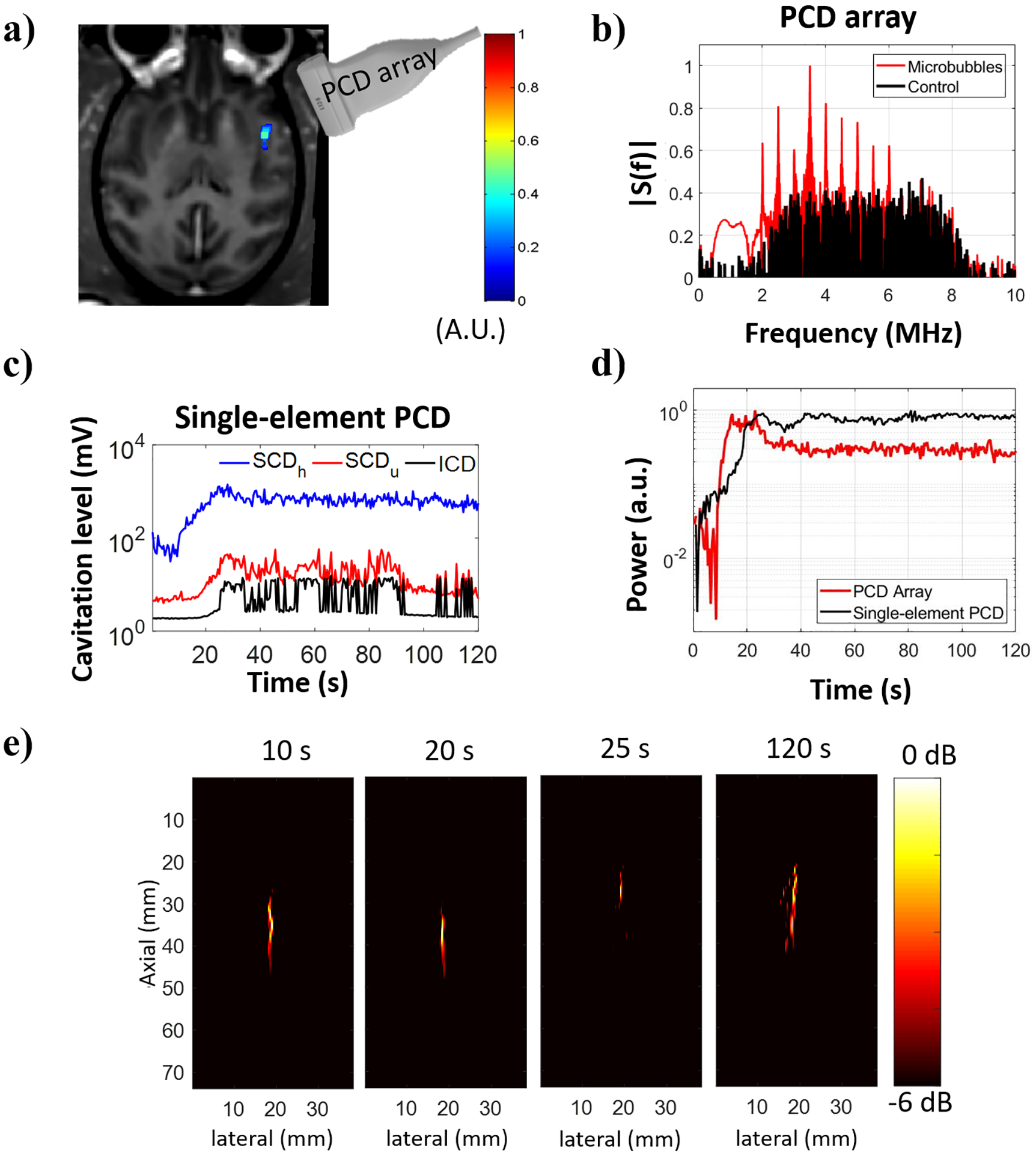
Cavitation activity recorded during BBB opening in NHP 1. (a) BBB opening (in color) induced by sonication at 450 kPa revealed in contrast-enhanced T1-weighted MR image. (b) Frequency spectra obtained from the beamformed signal at the location of maximum image intensity. (c) Cavitation activity evaluated with a single-element PCD transducer (cavitation dose). (d) Normalized power detected with a PCD array positioned at the temporal window and a single-element PCD transducer co-aligned with the FUS transducer. Power was defined as the sum of squared beamformed data using 1.44-μs integration time for the PCD array and the entire signal duration for the single-element PCD transducer. (e) Spatial distribution of the cavitation activity shown in cavitation maps (−6 dB) for different samples.

The results from the second test performed at 450 kPa in the NHP 2 are shown in figure 7. In this case, only stable cavitation was observed from data acquired with the single-element PCD (figure 7c). The majority of the observed stable cavitation was harmonic-based, with only a few pulses having ultra-harmonic dose higher than the baseline. The frequency spectra obtained with the PCD array at the location of maximum image intensity are shown in figure 7b. As shown in previous studies, the skull attenuation is highly variable across different skull locations and across animals due to bone thickness variation and different ratios of cortical to trabecular bone [22], [60]. The variation of the skull attenuation contributed to the differences in the signal components using the single-element (figure 7c) and PCD array (figure 7d). In addition, the single-element PCD presents a higher sensitivity and much broader frequency bandwidth. The single-element PCD had a higher sampling frequency (50 MHz versus 20.8 MHz) than the PCD array, thereby providing spectra at higher frequencies without aliasing. These differences highlight the importance of multiple cavitation detectors for safety redundancy. The cavitation maps in the logarithmic intensity scale (in decibel) were used for monitoring both the spatial location and intensity of cavitation over time (figure 7e). Interestingly, cavitation events were detected in two locations, possibly caused by cavitation in the neighboring larger vessels or caused by the side lobes of the FUS beam.

Fig. 7.

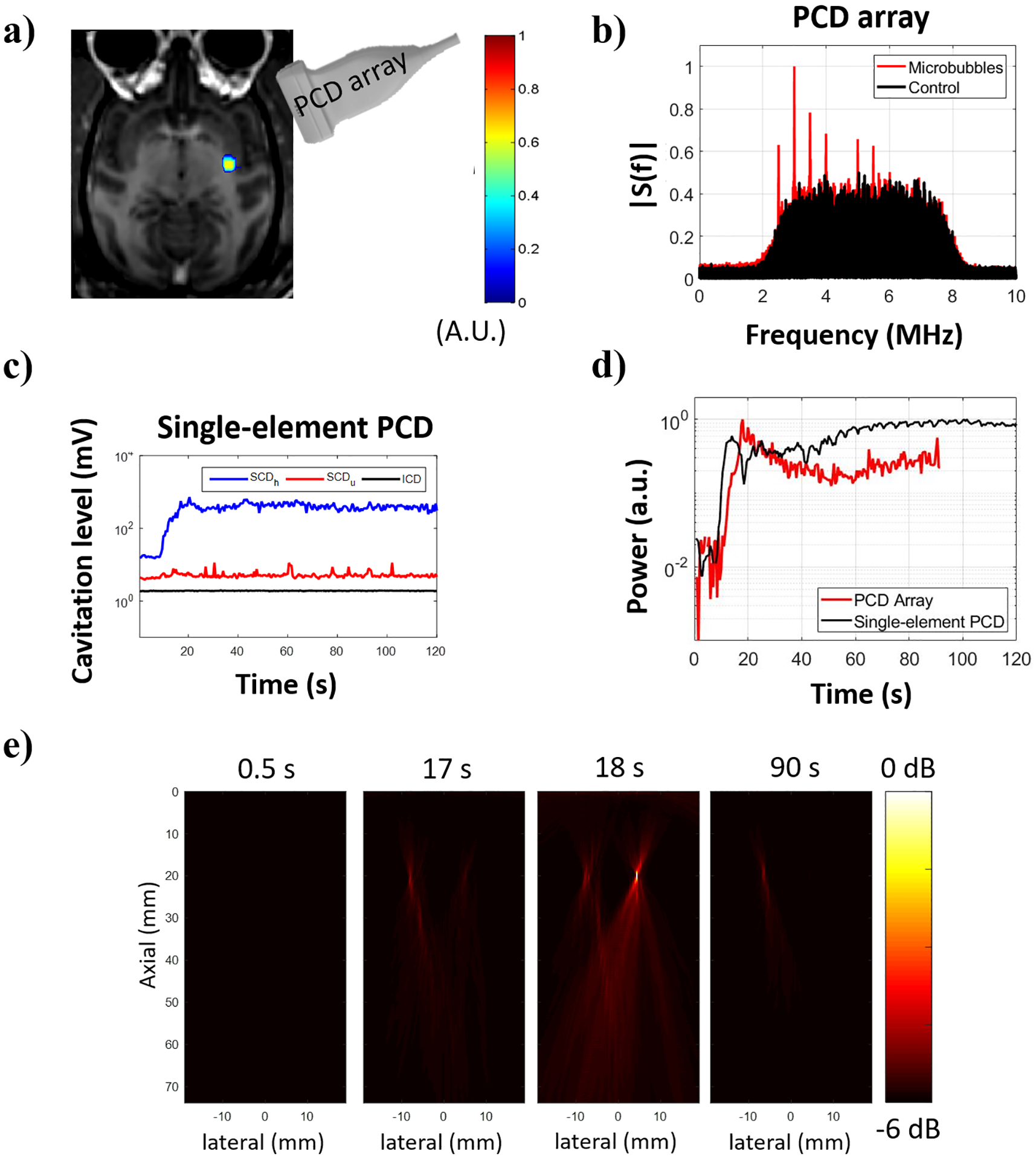
Cavitation activity recorded during BBB opening in NHP 2. (a) BBB opening (in color) induced by sonication at 450 kPa revealed in contrast-enhanced T1-weighted MR image. (b) Frequency spectra obtained from the beamformed signal at the location of maximum image intensity. (c) Cavitation dose detected using a single-element PCD transducer indicating only stable cavitation throughout the sonication duration. (d) Normalized power detected with a PCD array positioned at the temporal window and a single-element PCD transducer co-aligned with the FUS transducer using 1.44-μs integration time. (e) Reconstructed cavitation maps (−6 dB) for different samples.

The benchmarking revealed that sparse matrix operation improved both GPU and CPU performance. The computational time had a linear relation with the number of samples, and it is presented in log scale as the CPU standard DAS implementation resulted in computational times four orders of magnitude higher than the GPU sparse implementation (figure 8a). In GPU, the sparse matrix performed approximately 50 times faster than the standard DAS matrix, whereas, in CPU, the same comparison resulted in approximately 600 times difference. Interestingly, the CPU sparse and GPU standard DAS implementations presented similar results with sample processing rates of 7.3 s⁻¹ and 7.5 s⁻¹, respectively (Figure 8b). On the other side, the GPU standard DAS implementation presented a much higher average sample processing rate of 360.8 s⁻¹. Similarly, for a fixed number of samples N_T = 30, the sparse matrix implementation reduced the computational time for variable FOV sizes (figure 8c). The GPU sparse matrix implementation decreased the computational time by a minimum of 21.9 times (FOV: 50 × 128 pixels) in comparison with GPU standard matrix implementation and a maximum of 55.3 times (FOV: 2000 × 128 pixels) with an average of 28.5 times across different FOV. The sparse matrix performed on CPU was an average of 617 times faster than the CPU standard implementation and 1.33 times faster than the GPU standard implementation. The processing times required per PAM pixel for FOV varying from 50 to 2000 pixels axially x 128 pixels laterally using 30 samples were on average 0.03±0.01, 0.51±0.01, 0.67±0.09, and 311.71±3.94 μs/pixel/sample for GPU sparse, CPU sparse, GPU standard, and CPU standard implementations, respectively. For both CPU and GPU implementations, the sparse matrix was loaded in the memory prior to the time testing routines. Similarly, for the standard DAS method, the time for memory allocation was disregarded. The loading time was 6.86±0.13 s and the CPU to GPU transfer time was 0.79±0.06 s.

Fig. 8.

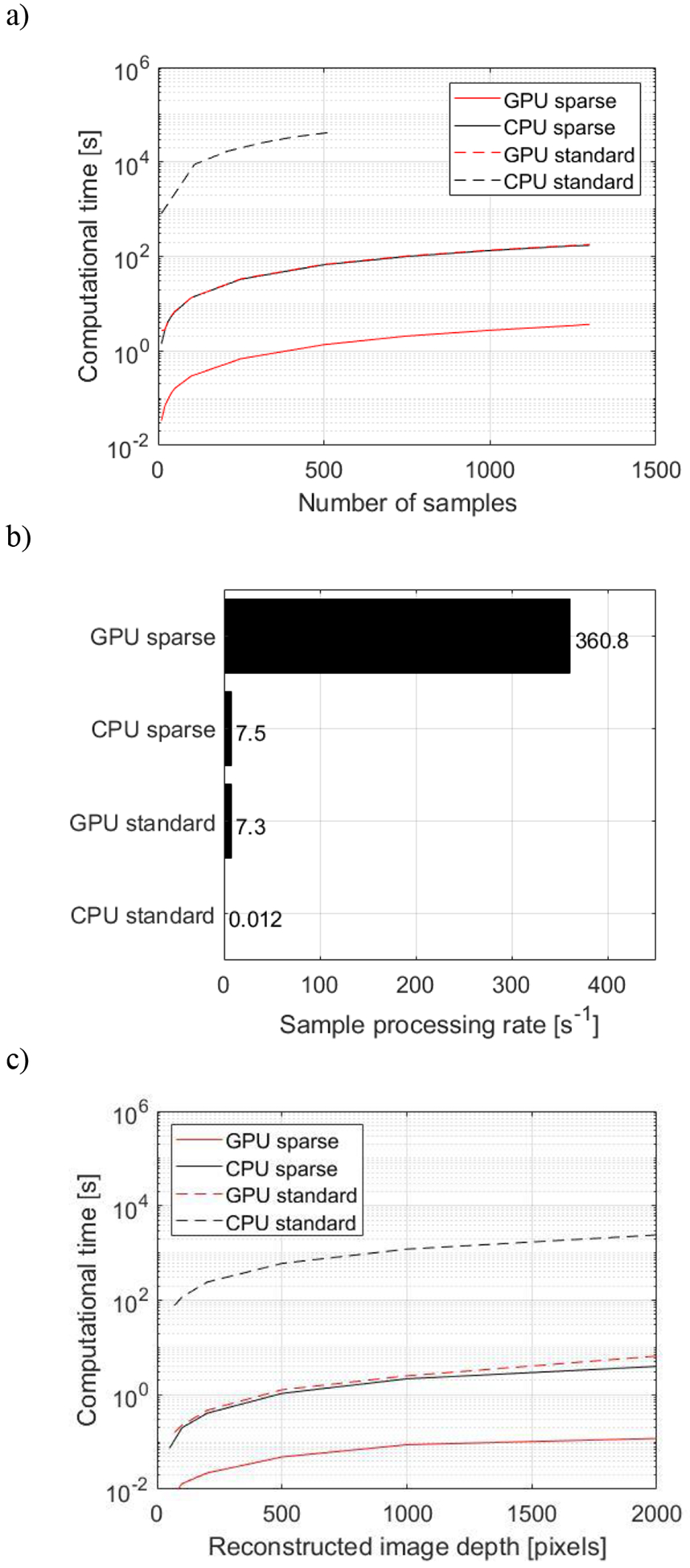
Benchmarking for sparse matrix operation. (a) Computational time of CPU and GPU implementations for the sparse matrix multiplication and standard DAS using the NHP in vivo data set for integrated sample N_T varying from 10 to 1500 (Z: 2000 samples, N: 128 elements, N_x: 128 lateral pixels, N_z: 2000 axial pixels). (b) Sample processing rate at the same conditions. (c) Computational time with N_T = 30 for different sizes of FOV, where the lateral map size N_x remained constant equal to 128 pixels and the axial map size varied: N_z = 50, 100, 200, 500, 1000, and 2000 pixels. The benchmarking was performed offline in a Dell Precision T7910 workstation (dual processor Intel Xeon CPU E5–2650 v4 @ 2.20GHz, 128 GB of RAM) equipped with a GPU (NVIDIA Quadro P6000, 24 GB memory, 3840 cores, driver: 392.56) running MS Windows 10 Pro 64-bits and Matlab 2017b.

IV. Discussion

In this study, we demonstrated the implementation of sparse matrix beamforming and TEAs on a GPU for real-time transcranial cavitation mapping. The system was tested in vitro using human and NHP skull specimens, which allowed to investigate the computational time for real-time cavitation mapping, and in vivo during ultrasound-mediated BBB opening sessions in NHP, which allowed to test the setup and algorithm in a close to clinical setup condition.

The summation over the integration time used in TEA algorithm enhanced the continuously scattered signal from microbubbles by suppressing the background noise, which affected the mapping quality and homogeneity of cavitation distribution [61], [62]. Noisier maps (discrete cavitation spots outside the transducer focus potentially associated with very transient bubble activity) were found in vitro for short integration times, while a steady cavitation distribution could be achieved with long integration time duration (>62.5 μs). Despite the higher SNR achieved with a high number of beamformed samples, the computational load and the number of frames were limited by the total integration time to lie within the pulse repetition period. For the PRF used in the test in vivo (2 Hz), 30 samples could be reconstructed for an integration time of 1.44 μs. The increased number of pixels in the axial direction (i.e., 2,000) was chosen based on active imaging parameters, however the pixel size of 37 μm is significantly smaller than the nominal passive acoustic mapping resolution at these imaging depths. The nominal axial resolution of PAM would be equal to 2.1 mm, assuming an imaging depth of 40 mm, an aperture size of 38.4 mm, and a mean receive wavelength of 0.28 mm [63]. As demonstrated by the benchmarking, the sparse matrix density (N_x x N_z by N x Z) and the RF data set density (N x Z by N_T) (Fig. 2a) can be modified, which ultimately changes the computational time at a rate of 0.03±0.01 μs/pixel/sample. Therefore, a reduced number of pixels can accelerate the processing, which allows a longer integration time. Future work will involve cavitation maps with a larger axial pixel size, to accelerate computation times and enable real-time mapping with integration of longer data sets, while preserving spatial information. As previously reported by Acconcia et al., 2017 [64], the microseconds time scale can potentially provide insights into bubble dynamics such as the rapid bubble cloud evolution and its stochastic nature as opposed to long integration times. Furthermore, the majority of cavitation activity is constrained within the first hundreds of microseconds of a ms-long therapeutic pulse. Previous in vitro work has shown that 80% of the total cavitation energy is emitted within 200 μs (or 0.2% of the total pulse length) during therapeutic ultrasound exposure [65], [66]. This is likely due to destruction of resonant microbubbles at the beginning of the therapeutic pulses, with smaller non-resonant microbubbles emitting lower cavitation energy for the remainder of the pulse. Future studies will correlate time exposure with bubble dynamics observed with high speed videography [67]. The pressure thresholds for the cavitation detection through human and NHP parietal bone specimens using the PCD array were in the range of pressure employed in previous studies [25], [58], [59], [68]. These results demonstrate the capability of the system to map spatial and temporal microbubble activity in real-time.

The benchmarking results revealed that the sparse matrix operation can decrease considerably the computational time in both CPU and GPU. For the computer configuration tested here, the CPU sparse implementation performed very similar to the GPU standard DAS implementation. Despite differences that other computer configurations may present (i.e. less powerful CPU processors with more powerful GPU), the sparse matrix operation is demonstrated to be a feasible solution for decreasing the computational time of operations with dense data sets, which enables either larger FOV or larger data sets relevant to therapeutic applications. An interesting characteristic of the sparse matrix operation is that it can be applied regardless of the number of processed samples, thus the integration time can be adapted easily to result in high image quality based on the trade-off of integration time and real time visualization. It is important to note that similar operation is not practical with a fully sampled reconstruction matrix as for the data set used here matrix (256,000 × 256,000), the fully sampled matrix would require 488.3 GB of computer memory as opposed to sparse representation that requires only 1.05 GB. On the other hand, the sparse matrix-based beamforming presents limitations such as the need to construct the sparse matrix (equations 3 to 5) offline and several hours prior to its use. This method requires time-consuming iterative calculations and memory allocation to allow the element indentation. This is partially resolved as only a single matrix construction at the highest sampling is needed. Then, the matrix can be down-sampled to adjust to any reduced FOV or channel data size. Once the sparse matrix size is adjusted, the multiplication of the sparse matrix and channel data can be performed, which will result in the beamformed data. The allocation of the pre-constructed sparse matrix in the computer or GPU memory is performed only once and it takes a few seconds, which will depend on the computer performance and sparse matrix size.

Next, we demonstrated an in vivo test of our system during FUS-mediated BBB opening session in NHP. The skull presents high variability in the thickness, variable proportion of cortical and trabecular bone distribution across skull regions, and, subsequently, high variability of the ultrasound attenuation [60]. Therefore, it is important to monitor cavitation activity with as low attenuation as possible, especially since high frequency emissions from microbubbles are more heavily attenuated through the skull. Cavitation mapping was therefore performed through the thin temporal bone, which presents lower attenuation than other skull bones. This experimental configuration was shown to be viable at mapping cavitation activity and demonstrated the feasibility of GPU-accelerated sparse matrix computing in a close to clinical setup. The system was qualitatively compared against single-element PCD acquisitions, which presented the same trend for the cavitation activity. Passive cavitation detection with both single-element and multi-element transducers was performed to illustrate the qualitative similarities in the temporal evolution of the signals [Figs. 6(d) and 7(d)]. However, we have used the normalized values, because a direct quantitative comparison is not possible, due to different receiving center frequencies, sensitivity patterns, and sampling frequencies. In the foreseen clinical use, device limitations can be ameliorated by using multiple safety monitoring redundancy, which in this case both single-element and array transducers can detect independently potentially high-risk cavitation activity. Future implementations will include simulations based on CT-scans [35], [37], [69] with the co-registration of MR images from the neuronavigator and simulated acoustic beam profiles.

Beamforming degradation caused by the diffraction pattern of the receiving array and interference caused by multiple bubbles emitting acoustic signals at the same time generated spatial distortions of cavitation activity, which resulted in an elongated pattern of cavitation activity. Differences in the beam shift can be explained due to differences in the skull curvatures of human and NHP specimens. As previously reported [32], [61], [69], potential focal shifts may be present, but were not studied here. Differences in the human and NHP specimen size forced different positioning of the imaging array in relation to the therapeutic transducer. Thus, the location of focus was not consistent across acquisitions. Nevertheless, the focal distortion is an example of problems encountered during treatment that shows the need of real time spatial monitoring of cavitation.

Frequency-domain approaches can significantly accelerate processing even without a GPU, due to the spectral filtering of narrowband harmonics or ultra-harmonics [35], [36]. However, the quality and speed of such approaches depends on the pulse length. Shortening the pulse length leads to progressively wider harmonic and ultra-harmonic peaks, thereby increasing the integration bandwidth and computational load. Furthermore, discrimination of different cavitation modes, e.g., inertial vs. non-inertial cavitation, becomes increasingly more difficult with shorter pulse lengths. Therefore, frequency-domain algorithms need to be modified for different excitation sequences, especially for the examined frequency windows. Finally, to calculate the total acoustic energy emitted by the exposed microbubbles, one needs to integrate throughout the frequency domain, which negates the need for frequency-based analysis.

On the other hand, time-domain approaches can be very slow when examining long RF signals with a traditional CPU approach (Figure 8a). Time-domain DAS is a simple process inducing a relatively low computational load and provides direct information about the total cavitation energy produced within the focus, regardless of the pulse length or cavitation mode. Cavitation energy has been previously correlated with the induced bioeffect, such as the drug delivery efficiency [70]. The same algorithm can be applied without modification using any excitation sequences, ranging from μs-long pulse sequences for BBB opening [71] to s-long sequences for HIFU ablation [30]. Our study describes a method for accelerating time-domain PAM for both CPU- and GPU-based systems (Figure 8) across the broad spectrum of ultrasound therapies. Sparse-matrix multiplication provides a general method to accelerate PAM processing at any pulse length (Figure 8a) or map size (Figure 8c).

The sparse matrix implementation demonstrated here employed a simple DAS algorithm that allowed for accelerated image acquisitions. However, as previously described by Haworth et al. [36], the axial resolution using this algorithm can be 10 times worse than lateral resolution when using small-aperture 1D receiver arrays. When large-aperture 2D receiver arrays are employed the axial dimension of the point-spread function obtained via DAS beamforming is approximately twice that of its lateral counterpart [61], [72], [73]. As we demonstrated in NHP, this can be partially overcome by changing the orientation of the passive array at an acute angle using the temporal window so the mapping can be provided with a compromise of resolution between the axial and lateral orientations (worst case in coaxial orientation with the therapy transducer). In addition, introduction of the skull may have caused shifts in the position of cavitation activity in reconstructed images. Yet, the algorithm tested in this study demonstrates the capability of the GPU-accelerated sparse matrix operation using large RF data sets. Despite the higher spatial resolution achieved with more sophisticated algorithms such as the robust Capon beamforming [74], [75], its computational load is still challenging for GPU-processing. We recognize that including a comparison against other cavitation mapping algorithms would have been desirable; however, limited key information and expertise in alternative methods would yield misrepresentative conclusions. Coded excitation can also be implemented to improve the confinement of microbubble activity [76] and the decoding on receive could enable higher SNR [77]. Additionally, implementation of a closed-loop feedback control for cavitation mapping may be beneficial for online treatment optimization [78]. This would provide a more reliable control of the microbubble activity from regions inside the brain while avoiding artifact from other sources such as acoustic coupling media or regions outside the brain [22]. In our future work, L7–4 will be replaced with a lower frequency array, to facilitate cavitation mapping through the human skull and reduce aberrations occurring at higher frequencies.

Finally, the sparse matrix implementation in GPU is a feasible method for accelerating image formation. This method can enable enlarging the FOV that could potentially help identify in real time off-target cavitation activity. In the context of the current study, real-time imaging was enabled only for extremely short integration times (i.e., 1.44 μs duration or 30 samples). Future work will involve generation of maps with a reduced number of pixels but larger pixel sizes in the axial direction, in order to accelerate beamforming of longer data sets. Such reduction of the axial pixel number by -for example- 50-fold would lead to an equivalent increase of the permissible integration time by 50-fold. Together with the neuronavigation system [25], the therapeutic transducer could be realigned at normal incidence angles [79] during sonication or the sonication could be halted if substantial beam aberrations are observed.

V. Conclusion

Passive acoustic mapping has a great potential in clinical cavitation-based FUS applications especially for monitoring and guiding the treatments. A detailed implementation of sparse matrix beamforming on a GPU for cavitation mapping is demonstrated here as a method to accelerate processing. We demonstrate with in vitro and in vivo tests that the GPU-based sparse matrix method can accelerate passive acoustic mapping compared to standard GPU or CPU processing, and allow real-time processing of large maps (e.g., 2,000 axial pixels × 128 lateral pixels) with limited integration times (e.g., 30 samples). This methodology was proven efficient for both CPU and GPU implementations. Moreover, cavitation mapping through the human skull bone showed the feasibility to use this technique in clinical applications. Finally, the real time capability together with the neuronavigation system enable the operator to correct or halt sonications in case substantial aberrations are observed.