The relative biological effectiveness of carbon ion radiation therapy for early stage lung cancer

Abstract

Background and purpose:

Carbon ion radiation therapy (CIRT) is recognized as an effective alternative treatment modality for early stage lung cancer, but a quantitative understanding of relative biological effectiveness (RBE) compared to photon therapy is lacking. In this work, a mechanistic tumor response model previously validated for lung photon radiotherapy was used to estimate the RBE of CIRT compared to photon radiotherapy, as a function of dose and the fractionation schedule.

Materials and Methods:

Clinical outcome data of 9 patient cohorts (394 patients) treated with CIRT for early stage lung cancer, representing all published data, were included. Fractional dose, number of fractions, treatment schedule, and local control rates were used for model simulations relative to standard photon outcomes. Four parameters were fitted: α, α/β, and the oxygen enhancement ratios of cells either accessing only glucose, not oxygen (OER_I), or cells dying from starvation (OER_H). The resulting dose–response relationship of CIRT was compared with the previously determined dose–response relationship of photon radiotherapy for lung cancer, and an RBE of CIRT was derived.

Results:

Best-fit CIRT parameters were: α = 1.12 Gy⁻¹ [95%-CI: 0.97–1.26], α/β = 23.9 Gy [95%-CI: 8.9–38.9], and the oxygen induced radioresistance of hypoxic cell populations were characterized by OER_I = 1.08 [95%-CI: 1.00–1.41] (cells lacking oxygen but not glucose), and OER_H = 1.01 [95%-CI: 1.00–1.44] (cells lacking oxygen and glucose). Depending on dose and fractionation, the derived RBE ranges from 2.1 to 1.5, with decreasing values for larger fractional dose and fewer number of fractions.

Conclusion:

Fitted radiobiological parameters were consistent with known carbon in vitro radiobiology, and the resulting dose–response curve well-fitted the reported data over a wide range of dosefractionation schemes. The same model, with only a few fitted parameters of clear mechanistic meaning, thus synthesizes both photon radiotherapy and CIRT clinical experience with early stage lung tumors.

Carbon ion radiation therapy (CIRT) is recognized as having distinctive physical and radiobiological traits that may provide advantages over traditional photon beam radiotherapy [1–4]. The unique depth-dose distribution with a finite range, along with a sharp lateral penumbra, allows increased dose to the target volume, compared to photon therapy, while minimizing the dose to surrounding normal tissues [3,5].

With its higher linear energy transfer (LET), CIRT produces a much denser energy deposition per unit length, resulting in a much higher probability of cell killing, compared to the low-LET photon radiation [6,7]. This can be expressed in terms of the relative biological effectiveness (RBE), which is defined as the ratio of radiation dose from standard photon radiation to the dose from test radiation for the same biological effect. Note that this implies that the RBE is dose and fraction dependent. The RBE is unity for photons, by definition, but can be higher for particle radiation as the LET increases. It is generally known that CIRT has an RBE in the range of 2–3 or higher [8,9]. CIRT is also known to have other radiobiological advantages, including less cell cycle dependency and lower oxygen effect, which are two unfavorable effects for low-LET photon RT [10–14]. An extensive topical review on the different aspects of the RBE for carbon ions is given by Karger and Peschke [15].

According to the PTCOG, there are thirteen operating CIRT centers worldwide as of June 2019¹. The majority of the centers are in Japan, where most clinical trials to date have been performed. Encouraging outcomes stimulated world-wide interest, and currently five new centers are under construction and two are in planning stage¹.

Recently, Paz et al. [16] surveyed outcome data from early stage lung cancer patients treated with various CIRT fractionations at the National Institute of Radiological Sciences (NIRS) in Japan. In that work, four different clinical trials were included, in which the treatment schedules were successively reduced from 18 fractions in 6 weeks to a single fraction [17–20]. Seeking to understand the differences in outcome between CIRT and conventional photon RT in a more mechanistic and quantitative manner, we fit our previously validated tumor control probability (TCP) model for early stage lung tumors [21,22] to this unique dataset. Our previous fit of this model to data from photon treatments for early stage lung cancer provided a good description of the TCP for various fractionation schedules, from single fraction delivery to standard (2 Gy/weekday) regimes [22]. Here we adapted the model to CIRT to account for the distinct radiobiological mechanisms of carbon ions which differ from photon therapy. These factors include cell cycle independence, increased cell kill per unit Gy, reduced fractionation sensitivity, and a reduced impact of hypoxia. We then use the resulting best-fit TCP response as a function of fractionation regime, compared to the photon predicted response, to define an RBE.

Materials and methods

Clinical outcome datasets

Individual clinical data included in the study of Paz et al. [16] were reviewed, including four different fractionation protocols: 18 fractions in 6 weeks, 9 fractions in 3 weeks, 4 fractions in 1 week, and single fraction treatment. In total, nine patient cohorts were identified with distinct outcome data, comprising 394 early stage lung cancer patients (396 lesions).

For each cohort, the fractionation schedule, including the fractional dose, the number of fractions per week, the overall treatment duration (in days), and the local control (LC) rate were extracted. To be consistent with the photon outcome data that was previously used to derive dose–response relationship, 2-year LC rates were used. When LC rate was reported in different follow-up time, the 2-year LC rate was read from survival curve at that time point. Detailed information regarding the included patient cohorts is shown in Supplementary Table 1.

In the original publications, the dose was reported in terms of the so-called clinical dose, which included the biological effectiveness, rather than the physical dose. This required us to estimate the original physical dose, which was derived from the reported clinical dose in GyE (Gy equivalent) by dividing by the reported RBE value at the center of spread-out Bragg peak (SOBP). As the RBE at the center of SOBP is dependent on the width of SOBP in the dose specification system used at NIRS [23,24], the most typical size of SOBP was determined from the mean tumor size and margin recipe for each cohort to estimate the physical dose for the cohort, as given in Supplementary Table 1.

Mechanistic tumor response model

We previously showed that our mechanistic tumor response model can predict the treatment outcomes of early stage lung cancer treated with photon radiotherapy in various fractionation schedules [22]. The model-derived dose metric, the equivalent dose in 2 Gy/fx (EQD2_model), fits all the outcome data, from conventional fractionation (2 Gy/fx, 5fx/wk) to a single fraction treatment, onto a single dose response curve.

Briefly, the TCP model simulates the time course of cellular sub-populations in a tumor based on a local energy budget limiting oxygen and glucose. In particular, the model incorporates basic tumor biological mechanisms including the linear-quadratic model (LQ-model), hypoxia, repopulation, reoxygenation, and the cell cycle variability of radiosensitivity, which are known to be important factors determining tumor response. In addition, the model assumes there is an energy budget, such that the total amount of oxygen and glucose delivered to a ‘tumorlet’ (i.e., tumor subvolume) is assumed to be constant over the course of radiotherapy. Although other factors may be hypothesized to impact response, the model fitting and validation previously reported shows that only these basic radiobiological effects are required to accurately predict TCP.

In the model, tumor cell populations are divided into three different states (proliferating (P), intermediate (I), and hypoxic (H)) with respect to the blood supply, as shown in Fig. 1a. Cells with adequate oxygen and glucose supply near blood vessel (P-compartment) are actively proliferating, whereas cells distant from vessels (H-compartment) are starving and dying. Cells in different state have different cell growth/death dynamics and radiosensitivity based on the energy budget. After radiotherapy begins, a fraction of cells in each compartment becomes doomed depending on compartment-specific radiosensitivity and die in an attempt of mitosis in the proliferative P-compartment (Fig. 1b). After the post-mitotic cell death in the P-compartment, oxygen and nutrient become available to other cells and reoxygenation of hypoxic cells takes place. More details of the model can be found in previously published papers [21,22,25].

Fig. 1.

Schematic diagrams of the mechanistic tumor response model and estimation of EQD2_model, based on two separate simulations in which the different radiobiological factors between CIRT and photon RT are considered: (a) Three compartments in the model based on the tumor microenvironment with respect to blood supply; (b) Cell death process in each compartment after RT begins; (c) The cell survival fraction is estimated for the given CIRT schedule (8 GyE × 9 fractions in 3 weeks) from Miyamoto et al. [18]; and (d) A conventional photon 2 Gy/weekday regime was simulated until the same level of survival fraction was achieved, resulting in an EQD2_model value of 115.0 Gy. The arrows indicate the days of irradiation. (Fig. 1(a) and (b) are reprinted from ref [22]).

Model simulation for CIRT and estimation of EQD2_model

The derived dose response curve for photon therapy in various fractionation was used for the comparison with CIRT outcome in deriving the RBE of CIRT. Although the model was focused on photon radiotherapy in the previous studies, the model is flexible enough to add/remove effects to adapt it for CIRT. The major difference is caused by the large difference in linear energy transfer (LET) along the particle tracks between photons and relatively slow carbon ions. Carbon ions create a massive amount of ionization per unit length, resulting in much denser and more complex DNA damage, which is much more difficult to repair.

In addition to a higher radiosensitivity value, α, compared to low-LET photons, the fractionation sensitivity of CIRT is also lower, i.e., the α/β ratio is larger. The oxygen enhancement ratio (OER) is known to be lower for CIRT compared to photon RT [12–14]. Therefore, to adapt the model to CIRT, these three parameters were refitted. Moreover, carbon ions are known to exhibit a much lower cell-cycle dependency [10,11], and so this dependency was turned off in the model.

To enable the comparison between CIRT and photon RT in various fractionation schedules, the cell-kill effects of CIRT for various fractionations were normalized using a model-derived dose metric: the model-equivalent photon dose in conventional fractionation of 2 Gy/weekday (denoted EQD2_model). As in our previous studies, a two-step simulation method was used: a CIRT model simulation was run given a set of (alpha, alpha/beta, OERs) parameter values (plus unchanged parameters given in Table 1) to find the overall cell survival fraction for a given CIRT treatment scheme. A second simulation is then performed for conventional photon treatment (2 Gy/weekday). The total number of fractions is increased until the final cell survival fraction is equivalent to the value obtained in the first simulation for CIRT. An example process of estimating EQD2_model for the 9-fraction CIRT cohort [18] is shown schematically in Fig. 1c and d.

Table 1.

Parameters used for the model simulation for early stage lung cancer. The numbers in the bracket after the values are the references. All parameters except for the radiosensitivity parameters are the same as those used in Jeong et al. [22].

Parameters		Values
Tumor parameters
Tumor cell density (⍴t)		106 mm−3 [26]
Tumor volume (Vt)		30 cc
Stem cell fraction (fs)		0.01 [27]
Cell cycle time (Tc)		2 days [28]
Compartment parameters
Growth fraction (GF)		0.25 [29]
Tumor doubling time (TD)		100 days [30]
Cell loss half-time in H (T1/2,loss)		2 days [31]
Survival rate of progeny after mitosis (km)		0.2 [22]
Lysis half-time (T1/2,lysis)		3 days [22]
Cell cycle parameters
Fraction of cells in P-compartment (fP)		50%a
G1-phase in P (fPG1)		28% [32]
S-phase in P (fPs)		12% [32]
G2/M-phase in P (fPG2/M)		10% [32]
Fraction of cell in I-compartment (fI)		27%a
Fraction of cell in H-compartment (fH)		23%a
Radiosensitivity parameters	Photon RT	CIRT
Ratio of alpha of G1- to S-phase (αG1/αS)	2b	1c
Ratio of alpha of G2/M- to S-phase (αG2/M/αS)	3b	1c
Reference radiosensitivity at 2 Gy/fx (α)	0.305 Gy−1 [22]	1.12d Gy−1
Alpha-beta ratio (α/β)	2.8 Gy [22]	23.9d Gy
OER of I-compartment at 2 Gy/fx (OERI)	1.7 [22]	1.08d
OER of H-compartment at 2 Gy/fx (OERH)	1.37 [33]	1.01d

^aEstimated from GF and T_D in the model.

^bAssumed parameters based on radiosensitivity analysis of synchronized cell population[34,35].

^cThe cell cycle effect is ignored for CIRT as the cell-cycle radiosensitivity variations are negligible for the high LET heavy ion[10,11].

^dThe best-fit parameter values found from the model parameter fitting.

The initially assumed parameter values used for the CIRT simulations and the previously established parameter values for photon RT are summarized in Table 1.

Model parameter fitting

In the previous work, we found a representative dose response relationship for early stage lung cancer in terms of EQD2_model: The tumor dose at which a TCP of 50% is expected (TD₅₀) was found to be 62.1 Gy, with the slope of the dose–response curve (γ₅₀) of 1.5 [22]. Note that the upper bound of the dose response curve was set to be 95%, as clinically observed local control typically saturates at around 95% [22]. The same dose response relationship was used in current study, as shown in the equation below.

$$TCP(D)=\frac{0.95}{1+{\left(\frac{T{D}_{50}}{D}\right)}^{4{\gamma }_{50}}}$$ (1)

where TD₅₀ is the tumor dose at which 50% of TCP is expected, γ₅₀ is the slope of the curve at TD₅₀, and D is the total dose of the treatment, which is EQD2_model in this analysis.

In this study, the most relevant parameter values for CIRT (α, α/β ratio, OER_I, and OER_H) were found, with which CIRT outcomes fit well on the derived dose response curve for photons (TD₅₀ = 62.1-Gy and γ₅₀ = 1.5). All four parameter values were simultaneously optimized. Starting with a broader range of the parameter values, the range of each parameter value was narrowed until the best-fit parameter values were found based on the maximum log likelihood method. The fit was evaluated using χ² tests and the 95% confidence interval (95% CI) of each parameter was found through the profile likelihood method [37,38].

Estimation of relative biological effectiveness (RBE)

As the cell-kill effect of each CIRT cohort was normalized in terms of photon equivalent dose (EQD2_model) based on the outcome data, a direct comparison with the photon RT was possible. To compare the treatment efficacy among the CIRT fractionation schedules, the ratio of EQD2_model over physical carbon dose (EQD2_model/D_phy) was derived, which quantifies the relative cell-kill efficacy of a given CIRT fractionation schedule, relative to the conventional 2 Gy/weekday photon fractionation.

As the RBE should be derived under identical condition, except for the radiation type, equivalent photon dose (resulting in the same EQD2_model as CIRT) with matching fractionation schedule was found for each CIRT cohort. An RBE was defined as the ratio of the equivalent photon dose over the total physical dose of carbon ion.

$$RBE=\frac{D_{photon}}{D_{CIRT}}$$ (2)

where D_CIRT is the total physical does of CIRT and D_photon is the equivalent photon dose that results in the same EQD2_model as CIRT for the same fractionation schedule. Note that the physical dose is not uniform throughout the target volume for CIRT (see Fig. 5 in reference [23]) and the central dose at the center of the SOBP was chosen as a representative physical dose, we therefore estimated the physical dose as described in Section 2.1 above. For example, the fractional dose for the 9-fx CIRT cohort (the case shown in Fig. 1) was 3.33 Gy at the center of the SOBP with the total physical dose of 30 Gy (Supplemental Table S1). To test the variability of the RBE values, the parameter values were varied within the 95% confidence intervals and the range of the RBE was evaluated for each fractionation schedule.

Results

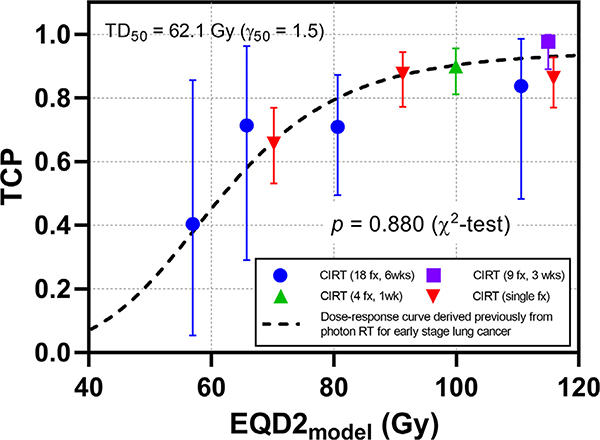
The optimal fit values and uncertainty ranges are: α = 1.12 Gy⁻¹ [95% CI: 0.97–1.26], α/β ratio = 23.9 Gy [95% CI: 8.9–38.9], OER_I = 1.08 [95% CI: 1.00–1.41], and OER_H = 1.01 [95% CI: 1.00–1.44]. The 2D log-likelihood distributions around the best-fit parameter values are shown in Supplementary Fig. 1. The total CIRT outcome data could be fit to the previously derived dose response curve with a high χ² p-value (p = 0.880), as shown in Fig. 2.

Fig. 2.

All CIRT cohorts with best-fit parameter values (α = 1.12 Gy⁻¹, α/β = 23.9 Gy, OER_I = 1.08 and OER_H = 1.01), overlaid with the previously derived photon 2 Gy/weekday dose–response curve (TD₅₀ = 62.1 Gy and γ₅₀ = 1.5, dashed curve). The resulting χ² test p-value was 0.880, indicating a good fit.

The relative treatment efficacy of each CIRT cohort was quantified by the ratio of EQD2_model/D_phy, as shown in Table 2 and Fig. 3a. The treatment efficacy tends to increase as the fraction size increases: 2.4–3.1 for the 18-fx cohorts; 3.8 for the 9-fx cohort; 4.3 for the 4-fx cohort; and 5.2–6.1 for the single fraction cohorts, which increases quickly at low fractional dose but seems to reach a plateau with high fractional dose. The error bars indicate the range of the ratio when the parameters varied within 95% confidence intervals.

Table 2.

The relative biological effectiveness (RBE) of CIRT, derived from the comparison with the equivalent photon dose of matching fractionation schedule.

Fraction Schedule	Fractional physical carbon dose (Gy)	Total physical carbon dose (Gy)	Model-derived EQD2 (Gy)	EQD2model/Dphy	Equivalent photon dose of matching fractionation (Gy)	RBE [range]
18 fx, 6 wks	1.32	23.8	57.0	2.40	50.8	2.14 [1.862.47]
	1.44	25.9	65.8	2.54	54.6	2.10 [1.832.45]
	1.64	29.5	80.7	2.73	60.6	2.06 [1.792.43]
	2.00	35.9	110.6	3.08	71.8	2.00 [1.712.37]
9 fx, 3 wks	3.33	30.0	115.0	3.83	60.1	2.00 [1.642.47]
4 fx, 1 wk	5.85	23.4	99.9	4.27	47.7	2.04 [1.532.55]
Single fx	13.61	13.6	70.2	5.16	22.2	1.63 [1.142.20]
	16.23	16.2	91.3	5.62	25.2	1.55 [1.072.14]
	19.03	19.0	115.9	6.09	28.5	1.50 [1.042.10]

Fig. 3.

The ratio of EQD2_model over physical dose (EQD2_model/D_phy) and the relative biological effectiveness (RBE) as a function of fractional dose of CIRT: (a) The EQD2_model/D_phy, comparing the treatment efficacy of CIRT relative to the conventional photon RT, increases with the increase of fractional dose; (b) The RBE tend to decreases as the fractional dose increases. The error bars in both figures indicate the range of the ratio of EQD2_model/D_phy or RBE values, when the parameters varied within 95% confidence intervals.

To find the RBE of each CIRT fractionation schedule, the photon dose of the matching fractionation schedule (D_photon) was found, which results in the same cell-kill as the CIRT. As the fractionation schedule was reduced with a higher fractional dose, the relative treatment efficacy of the photon fractionation (EQD2_model/D_phy) was increased, as shown in Fig. 3a. The RBE was finally calculated by dividing the equivalent photon dose of the same fractionation by the total carbon dose, as given in Table 2. The RBE tends to decrease as the fraction size increases: 2.0–2.1 for the 18-fx cohorts; 2.0 for the 9-fx cohort; 2.0 for the 4-fx cohort; and 1.5–1.6 for the single fraction cohorts, as shown in Fig. 3b. The error bars indicate the range of RBE when the parameters varied within 95% confidence intervals.

Discussion

In this work, we applied a previously developed and validated mechanistic tumor response model to the CIRT outcome data of early stage lung cancer. Known radiobiological differences between CIRT and photon RT were implemented and best-fit radiobiological parameter values were found, resulting in good fits across all fractionation regimes. Treatment efficacy in tumor control was normalized in terms of EQD2_model and the CIRT outcomes were fitted to a previously established dose response curve in EQD2_model for photon RT. The derived best-fit radiosensitivity values, α = 1.12 Gy⁻¹ and α/β = 23.9 Gy, are radiobiologically reasonable, given that CIRT has much higher LET (high α) and lower fractionation sensitivity (high α/β ratio) [6]. Moreover, these values are comparable to estimated radiosensitivity values for pre-clinical lung tumor models irradiated with carbon ions of similar LET (~77 keV/μm): α = 1.46 Gy⁻¹ and α/β = 23 Gy for squamous carcinoma and α = 0.72 Gy⁻¹ and α/β = 14 Gy for adenocarcinoma [36].

The OER values found in this study were close to unity, although the uncertainty level is quite large up to 1.44 (OER_I = 1.08 [95% CI: 1.00–1.41] and OER_H = 1.01 [95% CI: 1.00–1.44]). In vitro measurements showed that carbon has reduced OER values compared to photon [12–14]. The measured carbon OER decreased with the increase of LET and, for the LET of about 100 keV/μm, the value was found to be around two. Considering that the in vivo measurements of OER often show lower values than the in vitro measurements and the best-fit OER_I values for photon was 1.7 [22], the lower OER values found in this work seem to be reasonable.

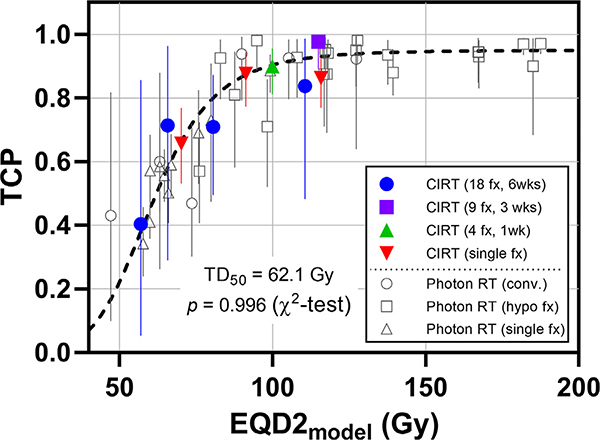
In this work, the dose metric, EQD2_model, was derived from the two-step simulation method. For a given treatment regimen, the treatment efficacy can be calibrated in terms of EQD2_model, a standardized dose index that enables direct comparison among different treatment regimens, and which can be used as a powerful tool in comparing the treatment outcome from different modalities or different fractionation schedules. As shown in Fig. 4, the photon RT and CIRT outcomes of various fractionation schedules can be fit well into a single dose response curve, in terms of EQD2_model.

Fig. 4.

The combined photon and CIRT outcome data, overlaid with the previously derived dose–response curve (TD₅₀ = 62.1 Gy and γ₅₀ = 1.5). All data fit well in a single dose response curve with the resulting χ² test p-value of 0.996. Photon RT results are from Jeong et al. [22], including conventional 1.8–2 Gy/weekday fractionation, hypofractionation (3–8 fxs), and single fraction schedules.

Also, the ratio of EQD2_model over physical dose can provide an index showing relative treatment efficacy, compared to the conventional 2 Gy-weekday photon. As shown in Fig. 3a, the ratio increases as fractional dose increases for CIRT, from 2.4 to 6.1, which means CIRT is 2.4 to 6.1 times more efficient than the conventional photon treatment, for a given amount of physical dose (per Gy). It should be noted that the ratio results from two factors: different modality and different fractionation schedule. The treatment efficacy of photon is also increasing with larger fractional dose (asterisk symbol in Fig. 3a), from 1.1 for 18-fx to 4.1 for single fraction photon. The effect only from different modality (carbon vs. photon) can be separated out by dividing the ratio of CIRT by ratio of photon, and the RBE can be acquired. The RBE tends to decreases as the fraction size increases with shorter treatment schedule, ranging from 2.1 for 18-fx to 1.5 for single fraction CIRT. Although the overall treatment efficacy of CIRT, shown by the ratio of EQD2_model/D_phy, increases with larger fraction size, the increase of the treatment efficacy of photon (EQD2_model/D_phy) is greater with higher fractionation sensitivity of photon (lower α/β), resulting in decreasing RBE.

As discussed in detail by Karger and Peschke [15], previous studies on carbon RBE were mainly focused on establishing dose specification system and deriving a RBE-weighted dose distribution that is used in treatment planning. Due to the difference in beam delivery systems, Japan and Germany have developed and used different RBE systems [8,39]. Briefly, NIRS in Japan had used a passive beam delivery system and adopted a phenomenological model (so called ‘clinical RBE model’) to find a physical depth dose distribution that provides a uniform biological effect within the SOBP [40] for the clinical trials included in this study, although the beam system was later updated to active scanning beam with microdosimetric kinetic model. At Gesellschaft für Schwerionenforschung (GSI) in Germany, an active scanning beam is used and a more complex model, the Local Effect Model (LEM), was developed based on the microscopic energy deposition pattern of the beam. Although there were attempts to validate and update the models through in vivo and clinical outcome data analysis [16,41–45], those models are fundamentally based on in vitro cell survival experiments, without any consideration on other radiobiological factors, such as hypoxia, reoxygenation, repopulation, and cell cycle dependency, known to be important in clinical tumor response.

The assumed RBE values used in the dose specification system at NIRS for the included clinical data (2.4–2.5 at the center of SOBP) were larger than the RBE values derived from the outcome data in this work (1.5–2.1). This implies the dose system might overestimate the treatment efficacy of CIRT without consideration of the radiobiological factors. As the evaluated RBE decreases with larger fractional dose and shorter treatment duration (from 2.1 to 1.5), the overestimation might be more significant for the single fraction schedule. Although current work is not intended to be directly used for dose specification or clinical treatment planning, the results demonstrate that those radiobiological factors need to be included in evaluating a realistic RBE in a clinical setting.

Current approach is similar to the study by Cometto et al. [46], in that the radiobiological parameters are directly derived from the clinical outcome data and then the relevant RBE is estimated. In deriving the RBE in this work, not only the difference in radiation quality, but also other radiobiological differences between CIRT and photon RT are considered, including radiosensitivity, fractionation sensitivity and oxygen and cell cycle effects. As all the possible effects/differences should be considered in the comparison of treatment efficacy, the RBE, established in this study, can be a good representation of the radiobiological effectiveness of CIRT.

In CIRT, a non-uniform physical dose is typically used along the SOBP to maintain an iso-effectiveness throughout SOBP. In this work, we estimated the physical dose at the center of the SOBP based on the mean tumor size and margin configuration and the physical dose was assumed to be constant over the tumor area. This simplification can be justified by the facts that the dose variation is not large over the tumor as the tumors included in this study are all fairly small. Moreover, the treatment involves multiple beams from various directions, in which the dose gradients from each beam overlap and the overall dose variation would be reduced.

Although the mechanisms are not clear, CIRT is known to involve other radiobiological effects, which can include inhibition of angiogenesis [47], suppressed migration and metastatic potential [48,49], less lymphocyte damage [50] and greater immune stimulation [51,52]. Our results indicate that these effects may not be needed to fit and understand the quantitative response rate for early stage lung tumors.

Using a mechanistic tumor response model previously validated for photon treatments, we derived best-fit relevant radiobiological parameter values for carbon beam radiotherapy which are radiobiologically reasonable. The results synthesize the clinical experience with early stage lung tumors via RBE values that vary, for 18 fractions to single fraction therapy, from 2.1 decreasing to 1.5.