Abstract
Purpose
The incorporation of cone‐beam computed tomography (CBCT) has allowed for enhanced image‐guided radiation therapy. While CBCT allows for daily 3D imaging, images suffer from severe artifacts, limiting the clinical potential of CBCT. In this work, a deep learning‐based method for generating high quality corrected CBCT (CCBCT) images is proposed.
Methods
The proposed method integrates a residual block concept into a cycle‐consistent adversarial network (cycle‐GAN) framework, called res‐cycle GAN, to learn a mapping between CBCT images and paired planning CT images. Compared with a GAN, a cycle‐GAN includes an inverse transformation from CBCT to CT images, which constrains the model by forcing calculation of both a CCBCT and a synthetic CBCT. A fully convolution neural network with residual blocks is used in the generator to enable end‐to‐end CBCT‐to‐CT transformations. The proposed algorithm was evaluated using 24 sets of patient data in the brain and 20 sets of patient data in the pelvis. The mean absolute error (MAE), peak signal‐to‐noise ratio (PSNR), normalized cross‐correlation (NCC) indices, and spatial non‐uniformity (SNU) were used to quantify the correction accuracy of the proposed algorithm. The proposed method is compared to both a conventional scatter correction and another machine learning‐based CBCT correction method.
Results
Overall, the MAE, PSNR, NCC, and SNU were 13.0 HU, 37.5 dB, 0.99, and 0.05 in the brain, 16.1 HU, 30.7 dB, 0.98, and 0.09 in the pelvis for the proposed method, improvements of 45%, 16%, 1%, and 93% in the brain, and 71%, 38%, 2%, and 65% in the pelvis, over the CBCT image. The proposed method showed superior image quality as compared to the scatter correction method, reducing noise and artifact severity. The proposed method produced images with less noise and artifacts than the comparison machine learning‐based method.
Conclusions
The authors have developed a novel deep learning‐based method to generate high‐quality corrected CBCT images. The proposed method increases onboard CBCT image quality, making it comparable to that of the planning CT. With further evaluation and clinical implementation, this method could lead to quantitative adaptive radiation therapy.
Keywords: adaptive radiation therapy, cycle‐GAN, deep learning, image quality improvement, quantitative imaging
1. Introduction
The incorporation of cone‐beam computed tomography (CBCT) onto medical linear accelerators has allowed for three‐dimensional (3D) daily image guidance for radiation therapy, enhancing the reproducibility of patient setup. CBCT is typically used either daily or weekly to verify patient setup and to monitor patient changes over the course of treatment. While CBCT is an invaluable tool for image guidance, the physical imaging characteristics, namely a large scatter‐to‐primary ratio, lead to image artifacts such as streaking, shading, cupping, and reduced image contrast. All of these factors prevent quantitative CBCT, hindering full utilization of the information provided by frequent imaging.1, 2, 3, 4, 5 The incorporation of CBCT into the clinic has led to increased interest in adaptive radiation therapy (ART), where dose would be calculated daily based on the patient's true setup on the treatment table. ART could mitigate patient setup errors and account for day‐to‐day patient changes such as weight loss or inflammation. Removal of these uncertainties could allow for decreased margins on target volumes and increased sparing of organs at risk, potentially leading to higher target doses.6
Many investigators have proposed correction methods to produce quantitative CBCT. These methods can broadly be classified as hardware corrections, such as anti‐scatter grids, and model‐based methods, which typically use Monte Carlo techniques to model the scatter contribution to CBCT projection data. Hardware modifications include, in addition to anti‐scatter grids, partial beam blockers which allow simultaneous measurement of scatter data and transmission data.7 The measured scatter contribution can be extrapolated from the partially blocked portions of the image and applied over the whole field. The scattered signal can then be subtracted from projection data, leading to improved image contrast. Stankovic et al. developed an iterative model relying on a partial‐beam blocking method while simultaneously characterizing the scatter reduction for a variety of anti‐scatter grids.8 While hardware approaches to scatter correction have proven promising, they inherently reduce the system's quantum efficiency and can degrade image quality. Installation and setup of devices on the onboard imager further inhibit clinical implementation. Many software‐based approaches attempt to model the scatter distribution via some combination of analytical methods or Monte Carlo algorithms.9, 10, 11 While many Monte Carlo‐based techniques suffer from long computational times, Xu et al. developed a GPU‐accelerated correction method which carried out the correction in under 30 s, potentially allowing for online image correction in an ART setting.4 The primary limitation to model‐based methods comes from the physics models.
Another approach to correcting CBCT artifacts is the use of machine learning‐based algorithms. Rather than truly correcting for scatter or other physical effects, a machine learning‐based method will learn to map voxels from a source distribution (CBCT) to a target distribution (planning CT).12 A variety of machine learning‐based methods have been used in other applications of radiation therapy13, including conversion of MR images to CT images,14, 15 prediction of radiation toxicities,16, 17 dose calculation,18, 19 and automatic segmentation.20 Although machine learning‐based methods can be computationally expensive to train, once a well‐trained model is developed, the image correction can be applied in seconds, making this approach ideal for online ART. Machine learning and deep learning methods have also been applied to the CBCT intensity correction problem. Hansen et al implemented a convolutional neural network in a Unet architecture in the projection domain to correct CBCT images, achieving mean absolute error (MAE) between 20 and 50 HU for multiple prostate patients as compared to a scatter‐corrected CBCT.21 Similarly, Maier et al. implemented a Unet to learn the scatter distribution from CBCT projections, and then subtract this scatter away and reconstruct “scatter‐free” CBCT images.22 Their algorithm achieved MAE ranging from 33 to 250 HU depending on the tube voltage used for the CBCT image acquisition. Kida et al. implemented a Unet in the image domain to improve the signal nonuniformity in CBCT images.23 Finally, Landry et al. evaluated the performance of a Unet on projection domain and image domain CBCT data and found that CBCT corrections in the image domain achieved lower mean error (ME) and MAE.24
In this work, we propose a deep learning method, a cycle‐consistent adversarial network (cycle‐GAN), based on paired CT and CBCT images to correct CBCT images.25 The cycle‐GAN framework is appealing for CBCT correction because it can efficiently convert images between the source domain and the target domain when the underlying structures are similar, even if the mapping between domains is nonlinear. Additionally, cycle‐GAN enforces an inverse transformation, that is, the model can convert a corrected CBCT back to an original CBCT. This cycle consistency allows for higher accuracy levels than other machine learning‐based methods because the model is doubly constrained. GANs and cycle‐GANs applied to this problem have gained interest recently. Kida et al implemented a GAN to generate planning CT‐like images from CBCTs in pelvis patients. Their method achieved tissue‐specific MAE less than 10 in muscle, fat, prostate, and bladder. However, for computational efficiency, they limited CT HU values from −500 to 200 HU, making evaluations on the whole range of human tissues not possible.26 Liang et al implemented a cycle‐GAN which achieved an MAE of around 40 HU in head‐and‐neck patient test cases.27 In this work, we seek to enhance both the accuracy and efficiency of the proposed method by introducing a residual block concept.28 Residual blocks enforce the learner to minimize a residual, or error, image between the CBCT (source) and the desired planning CT (target). This incorporation, along with a novel loss function based on the mean p‐norm error and gradient magnitude distance, allows the proposed method to robustly generate more accurate corrected CBCT images. The proposed method is evaluated in patient datasets and is compared to conventional scatter‐based method as well as another machine learning‐based correction method.
2. Materials and methods
2.A. Method overview
The proposed CBCT correction algorithm consists of a training stage and a correction stage. The images are first registered and the planning CT image is used as the deep learning‐based target of the CBCT image. Since the CBCT image is often contaminated with artifacts and small mismatches between CT and CBCT images still exist after rigid registration, training a CBCT‐to‐CT transformation model is highly underconstrained, meaning small data errors will be amplified during the transformation. To cope with this issue, a cycle‐GAN is introduced to capture the relationship from CBCT to CT images while simultaneously supervising an inverse CBCT‐to‐CT transformation model.25 While the original cycle‐GAN implementation used unpaired training data, we use paired data in this work. This helps enforce both anatomical and quantitative accuracy as well as enhancing image contrast. Since the source image (CBCT) and target image (CT) are largely similar, the network can be made to learn based on the residual image, that is, the difference between the source and target, rather than the entire images. This mode of learning is termed a residual network, and has previously been shown to enhance convergence.28 The network can be thought of as two‐pronged, simultaneously making itself better at both creating synthetic CT (called as corrected CBCT) images and learning how to identify corrected CBCT images. The overall algorithm is outlined in Fig. 1, and individual components of the algorithm are outlined in further detail in the following sections.
Figure 1.
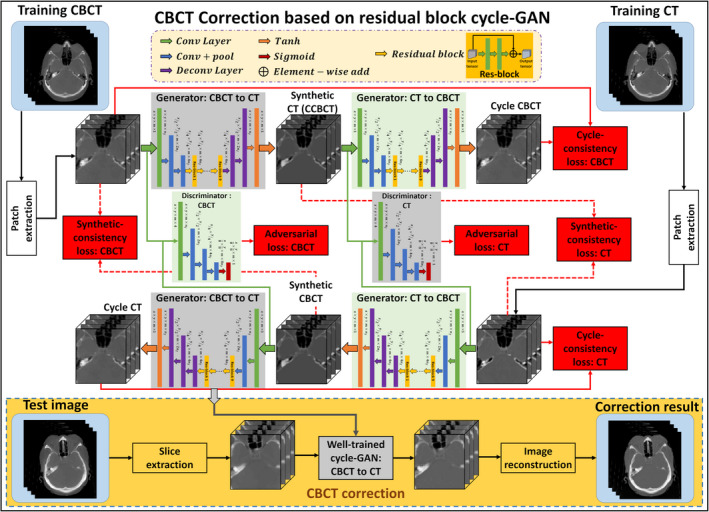
Schematic flow chart of the proposed method. The top region of the figure represents the training stage, and the yellow‐outlined region represents the test stage. During training, patches are extracted from paired cone‐beam computed tomography (CBCT) and CT images. A convolutional neural network is used to downsample the CBCT, and the residual difference between the CBCT and the CT is minimized at this coarsest layer. The synthetic CT (corrected CBCT) image is then upsampled to its original resolution, and a discriminator is trained to learn the difference between this synthetic CT (corrected CBCT) and the planning CT. The inverse of this process is then carried out to generate the cycle CBCT. Simultaneously to training the network to go from CBCT to cycle CBCT, a complementary network is trained to go from planning CT to cycle CT. After training, a CBCT image can be fed into the network which quickly generates a corrected CBCT image. [Color figure can be viewed at wileyonlinelibrary.com]
2.B. Cycle‐GAN
Traditional adversarial network methods, GANs, rely on two subnetworks, a generator and a discriminator, which work in opposition. Given two training datasets, for example, a planning CT and a CBCT, an initial mapping is learned to be able to generate a CT‐like image from a CBCT image, called a corrected CBCT (CCBCT) image in this work. The generator's training objective is to fool the discriminator. Thus, the generator produces a CCBCT image which is very similar to the planning CT image. Conversely, the discriminators' training objective is to decrease the judgment error of the discriminator network, enhance the ability to differentiate CBCTs from CCBCTs. As these networks are pitted against each other, the capabilities of each improve, leading to more accurate CCBCT generation in this example.29 The whole network is optimized sequentially in a zero‐sum framework. A cycle‐GAN doubles the process of a typical GAN by enforcing an inverse transformation, that is, translating a CBCT image to a CCBCT image and translating a CT image to a CBCT‐like image. This doubly constrains the model and can increase accuracy in output images.
2.C. Residual block
Convolution neural networks with residual blocks have achieved promising results in tasks where source and target images are largely similar, much like the relationship between CBCT and CT images.30 Each residual block includes a residual connection and multiple hidden layers. Through the residual connection, an identity (input) bypasses the hidden layers of a residual block; thus, these hidden layers are enforced to learn specific differences between CBCT and CT. As shown in generator architecture of Fig. 1, after two downsampled convolution layers to reduce the feature map sizes, the feature map goes through nine short‐term residual blocks, and then through two deconvolution layers and a tanh layer to perform end‐to‐end mapping. A residual block is implemented by two convolution layers within residual connection and an element‐wise sum operator.
2.D. Compound loss function
As described above, the network relies on continuous improvement of a generator network and a discriminator network. The accuracy of both networks is directly dependent on the design of their corresponding loss functions. The original cycle‐GAN study optimized the networks in tandem according to a two‐part loss function, consisting of an adversarial loss and a cycle consistency loss.25 The adversarial loss function, which relies on the output of the discriminators, applies to both the CBCT‐to‐CT generator and the CT‐to‐CBCT generator , but here we present only formulation for for clarity. The adversarial loss function in this work is defined by
| (1) |
where is the CBCT image and is the output of the CBCT‐to‐CT generator, that is, the CCBCT. is the CT discriminator which is designed to return a binary value indicating whether a pixel region is real (from a CT) or fake (from a CCBCT), so this measures the number of incorrectly generated pixels in the CCBCT image. The function is the mean absolute difference between the discriminator map of the generated CCBCT and a unit mask.
The cycle consistency loss function in this work consists of a compound loss function. In the original cycle‐GAN paper, this loss function constrained the inverse transformation, which in this work would be CBCT to cycle CBCT, for both generators. In addition to these constraints, we minimize the distance between the synthetic image (CCBCT) and the real image (CT), which we call the synthetic consistency, to directly enforce them to have same intensity distribution. The first component of the loss function is the mean lp ‐norm loss (MPL)
| (2) |
where is the total number of pixels in the image, and are parameters which control the cycle consistency and synthetic consistency, respectively. The symbol signifies the lp ‐norm for a vector
| (3) |
In this work, p was set to 1.5. Previous cycle‐GAN methods have used the l1 ‐norm or the l2 ‐norm to measure error, but we empirically found that l2 ‐norm regularization smooths the boundary between bone and soft tissue, leading to misclassification. Furthermore, we found that l1 ‐norm regularization leads to tissue misclassification, which may be because l1 ‐norm regularization is a linear programming problem. lp ‐norm regularization, however, can be designed to provide a quadratic cone constraint, which may give the Adam gradient descent method a more stable optimization space.31 The second component of the loss function is the gradient magnitude distance (GMD). Between any two images, the GMD is defined as:
| (4) |
where Z and Y are any two images, and i, j, and k represent pixels in x, y, and z. To provide additional clarity in this work, we define a gradient magnitude loss (GML), which is a function of the generator networks
| (5) |
The total cycle and synthetic consistency loss function is then optimized according to
| (6) |
where and are tuning parameters that balance the MPL and GML functions. The global generator loss function can then be written
| (7) |
where is a regularization parameter that controls the weights of the adversarial loss. The discriminators are optimized in tandem with the generators according to
| (8) |
As mentioned above, the cycle‐GAN framework relies on learning the forward and inverse relationships between the source image and target image. In addition to training itself to generate images, it trains itself to differentiate between synthetic and real images. This framework produces a model that is robust to noisy data or data that are ridden with artifacts. Given two images with similar underlying structures, the cycle‐GAN is designed to learn both an intensity and textural mapping from a source distribution to a target distribution.
2.E. Image acquisition and preprocessing
We retrospectively analyze the CBCT and CT data acquired during radiation treatment planning of 24 brain and 20 pelvic patients. All CT datasets were acquired using a Siemens SOMATOM Definition AS CT scanner with voxel size 1.0 mm3 × 1.0 mm3 × 1.0 mm3, and CBCT datasets were acquired using the onboard imager of a Varian TrueBeam with voxel size 1.2 mm3 × 1.2 mm3 × 2.0 mm3. Before images were fed into the model, the CBCT data were first resampled to match the resolution of CT data. The CBCT images were then rigidly registered to their corresponding planning CT images using Velocity AI 3.2.1 (Varian Medical Systems, Palo Alto, CA, USA). The body contour was also rigidly brought from CBCT to planning CT. While we registered CBCT to CT in this work, algorithm performance should be independent of whether CBCT was registered to CT or vice versa. Following intra‐patient registration, the images from patient‐to‐patient were registered, that is, interpatient registration. This was carried out by rigid registration to a single target patient. Inter‐patient registration is implemented, so that the images could be closely truncated outside the body to improve computational efficiency. We note that the cycle‐GAN algorithm was originally developed for unpaired image‐to‐image translation. However, in medical imaging, it is important to preserve the quantitative image values. For that reason, we still pair and register the images before feeding them into the network. We note that there are still mismatches after registration between the images, but the network is relatively robust to these small perturbations.
2.F. Implementation and evaluation
The CBCT and CT images are fed into the network in 96 × 96 × 5 patches, with an overlap between any two patches of 78 × 78 × 2. This overlap ensures that a continuous whole‐image output can be obtained and allows for increased training data for the network. No image thresholding was implemented. The hyperparameter values from Eqs. (6) and (7) are listed as follows: , , , , . Since it will be more difficult to generate an accurate cycle image from a real image due to the two transformations introduced, the value of should be larger than . Additionally, preserving the body contour in the cycle transformation is desired over forcing the CCBCT geometry to match that of the CT. The learning rate for Adam optimizer was set to 2e‐4, and the model is trained and tested on an NVIDIA TITAN XP GPU with 12 GB of memory with a batch size of 8. During training, 3.4 GB CPU memory and 10.2 GB GPU memory were used for each batch optimization. It takes about 12 min per 2000 iterations during training. In testing, it takes about 2 min to generate a CCBCT for one patient. The training was stopped after 150000 iterations. Training the model takes about 15 h, and CCBCT generation for one test patient takes about 2 min. After CCBCT image patches are output by the network, they are simply combined to produce a 3D image. In patches which overlap upon output, pixel values in the same position are averaged. Tensorflow is used to implement the network architecture.
Leave‐one‐out cross validation is used for evaluation of the proposed algorithm. In this evaluation method, we exclude one patient from each dataset when training the model. After training, this excluded patient's images are used as test images. This procedure is repeated for each patient in each dataset. Since each image set is registered for training, the test set is also inherently registered; however for application of the method, no registration is necessary. It should be noted, however, that in clinical implementation of the proposed method, it is likely that images will already be rigidly registered as their registration is used to calculate shifts for daily radiotherapy treatment. In addition to characterizing the proposed method, we compare to both a conventional scatter correction method for CBCT and a machine learning‐based method for CBCT correction. The conventional method relies on measuring the nonuniformity by segmenting out soft tissue types and assuming that these should have similar mean HU values.32 The method then generates a compensation map to readjust HU values in the corrected CBCT image, reducing shading and cupping artifacts. For comparison to the scatter‐correction‐based method, we evaluate algorithm performance on the pelvis patient dataset. The machine learning‐based method we compare the proposed method to is a random forest‐based learning method that relies on feature extraction from image patches. The algorithm trains a set of binary decision trees to predict a CT image similar to the planning CT from a paired CBCT image.33 This feature extraction means that the size of the image patch will fundamentally change the mapping from CBCT to CT. This is an important difference between this previous method and the proposed method. Cycle‐GAN is implemented on image patches in this work to enhance computational efficiency, but algorithm performance is independent of patch size. Image patches for the random forest method are 32 × 32 × 32.
For quantitative comparisons, CCBCTs are compared with planning CTs, which are taken as the ground truth, for calculation of MAE, peak signal‐to‐noise ratio (PSNR), and normalized cross correlation (NCC). MAE is the magnitude of the difference between the planning CT and the evaluated image
| (9) |
where is the value of pixel in the planning CT image, is the value of pixel in the target image, and is the total number of pixels. PSNR is calculated
| (10) |
where is the maximum signal intensity possible, and is the mean‐squared error (or difference) of the image. The NCC is a measure of the similarity of image structures and is used commonly in pattern matching and image analysis5, 34
| (11) |
where is the standard deviation of planning CT image, and is the standard deviation of the target image. Standard deviations for both images are calculated in a uniform region of interest. Finally, spatial nonuniformity (SNU) is calculated for both brain and pelvis patients. SNU is a measure of the difference in HU values within the same material. First, the mean value in each ROI outlined in Fig. 2 is calculated for all images. SNU is the difference between the maximum calculated HU value and the minimum HU value, scaled by 1000. This is calculated for each patient image, and the mean value is reported in this work. All comparison metrics are calculated for each patient during evaluation. Quantitative analyses are conducted over the entire image set. In order to illustrate the statistical significance of quantitative improvement by the proposed method, paired two‐tailed t‐tests were used for comparison of the outcomes between numerical results groups calculated from all patient data.
Figure 2.
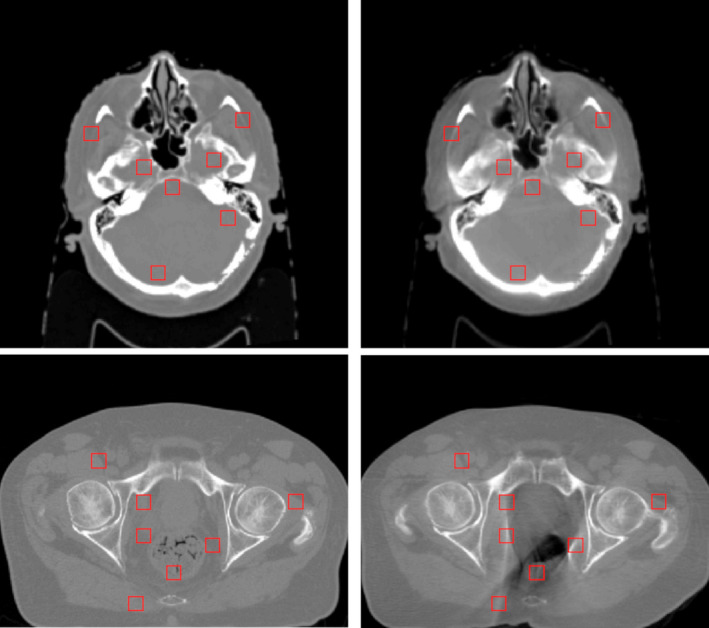
Selected ROIs for measuring spatial nonuniformity. [Color figure can be viewed at wileyonlinelibrary.com]
3. Results
3.A. Correction performance
Figure 3 summarizes the results of a correction algorithm on a brain patient test case. The inserts shown the second and fourth rows show that the correction algorithm can nearly restore finely detailed image structures seen on the planning CT whereas the CBCT tends to blur these structures. The CT HU distribution is nearly restored using the proposed correction algorithm, and the line profile more closely reflects the planning CT as seen by Fig. 4. Additionally, many of the errors around tissue boundaries that are seen in the CBCT are reduced in the CCBCT. In the CBCT‐CCBCT difference images, major differences are seen in the nasopharynx.
Figure 3.
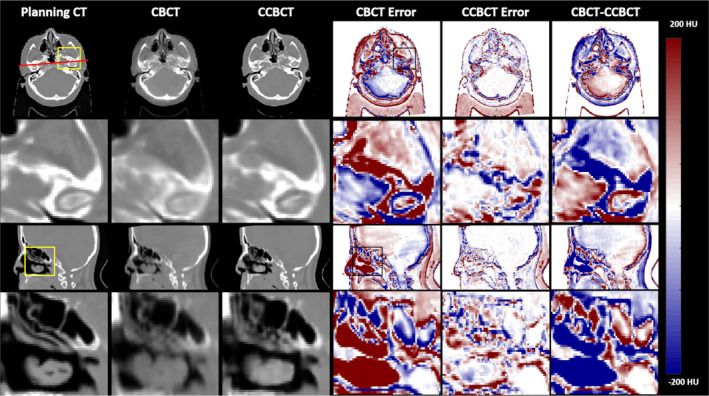
Summary of cone‐beam computed tomography (CBCT) correction results in one brain patient. The first column shows various views of the planning CT images, the second column shows corresponding views of the original CBCT image, the third column shows the corrected CBCT image, and fourth and fifth columns show the CBCT error and CCBCT error, respectively. For error images, the planning CT was taken as the ground truth. The planning CT is taken as the ground truth for error calculations. The top row shows an axial slice of the patient, with the highlighted insert shown directly below. The final column shows the difference image between the CBCT and CCBCT. A sagittal slice is shown with an ROI in pharynx shown below. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 4.
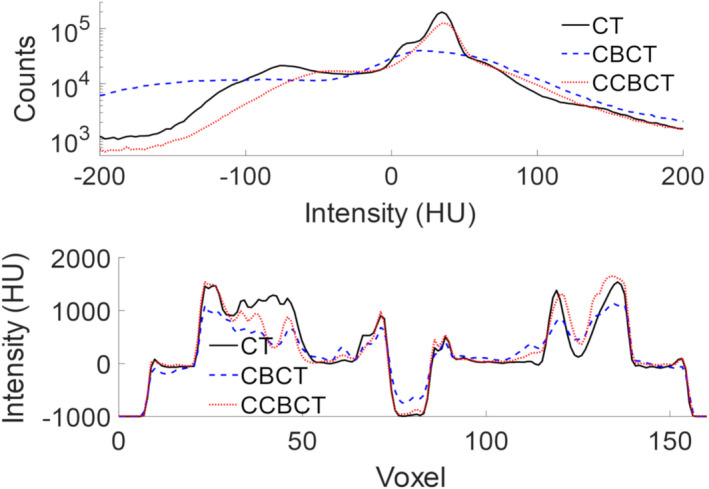
Histogram of HU values for the images shown in for the full 3D image seen Fig. 3 (top) and line profile through the axial images shown in Fig. 3 corresponding to the red line drawn on the planning CT (bottom). [Color figure can be viewed at wileyonlinelibrary.com]
Figure 5 shows results from two pelvis patients. The first row shows an inferior slice of the pelvis region where the patient's anatomy changed between the planning CT and the CBCT. In the first patient case, air in the small intestine caused artifacts throughout the anterior portion of the patient. After correction, these artifacts are greatly reduced, as shown in the inserts in the second row of Fig. 5. In the second case shown in the lower row, the CCBCT again suppresses artifacts in the CBCT, and considerably reduces the error present in the initial image. The two error columns are taken relative to the planning CT image. In all cases, the soft tissue error is reduced with the proposed method. The CBCT‐CCBCT difference images in the first patient case show that the body contour in the CCBCT image closely resembles the body in the CBCT image and not the planning CT. This is especially important in an ART workflow because the body contour shows the patient's true position on the treatment table. The final row of Fig. 5 displays the CCBCT image quality in a soft tissue window. The artifacts in the CBCT are severe enough to eliminate any soft tissue contrast. The CCBCT does not fully restore the HU values, for example, in the bladder, but structures can be delineated using the proposed algorithm. In this patient, the artifacts effectively changed the body contour of the patient, as seen on the CBCT error and CBCT‐CCBCT images. This resulted in a deviation of the CCBCT body contour. Overall, this effect was not seen widely across other images, but it does happen in a few slices. As the body contour is important to the dose distribution, this is something that will warrant further investigation before clinical implementation of the proposed algorithm.
Figure 5.
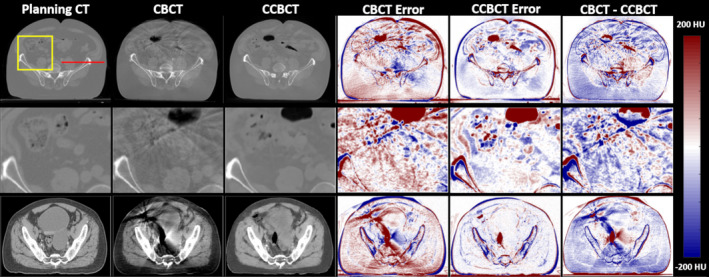
Cone‐beam computed tomography (CBCT) correction results on two sets of pelvis patient data. The first column shows various views of the planning CT images, the second column shows corresponding views of the original CBCT image, the third column shows the corrected CBCT image, the fourth and fifth columns show the CBCT error and CCBCT error, and the final column shows the difference between the CBCT and CCBCT images, respectively. The CT images and inserts in the first two rows are shown on a window of [−1000 1000] HU, the final row of CT images and the error images are both shown on a window of [−200 200] HU. [Color figure can be viewed at wileyonlinelibrary.com]
For both cases shown here, the CCBCT does not exactly recreate the planning CT. This is to be expected as the patient's anatomy and setup will change on a day‐to‐day basis. The pelvis proves a more challenging region than the brain because the region is larger and there is more possibility for day‐to‐day movement. However, the CCBCT greatly improves upon the CBCT, effectively removing the streak artifacts, and reducing error across the whole patient.
3.B. Comparison to conventional scatter correction method
The proposed method is compared to the conventional scatter correction method, testing cases in a pelvis patient, as shown in Fig. 6. Both methods reduce the shading and streaking artifacts created by scatter in the CBCT, In addition to removing the scatter and streaking artifacts, the proposed method reduces the noise on the image. The efficacy of the scatter correction method is limited in regions surrounding air on the CBCT. While the proposed method does not completely mitigate artifacts in this region, it largely reduces them and the image quality of the CCBCT by the proposed method is closer to the planning CT.
Figure 6.
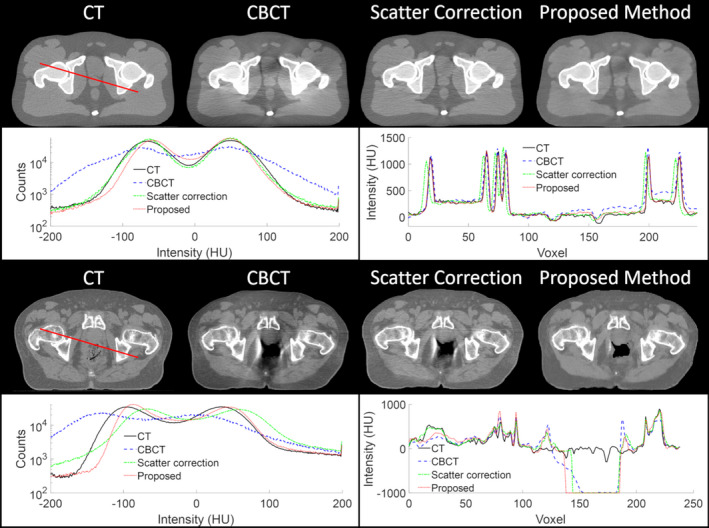
Comparison of the proposed method to a conventional scatter correction on a pelvis patient. The top row shows an axial slice of the computed tomography (CT), cone‐beam CT (CBCT), and corrected CBCT by the scatter correction and the proposed method. The second row shows the histogram of the full 3D image on the left and the line profile outlined on the CT image on the right. [Color figure can be viewed at wileyonlinelibrary.com]
3.C. Comparison with random forest‐based method
Figure 7 shows the comparison between the proposed method and the random forest‐based method for two pelvis patients. The proposed method produces sharper images with less blurring and lower noise levels as compared to the random forest‐based method. The case shown in Fig. 7 demonstrates an area where critical evaluation of the method is necessary. In the planning CT image, there rectum was filled; however, in the CBCT on the day of treatment, there is gas in the patient's rectum. It can be seen that CBCT exaggerates the effects of air cavities, and they result in streaking artifacts. In this case, the proposed algorithm reduces the amount of air seen in the image. Since there is no ground truth CT from the day of treatment, it is not clear whether the amount of air shown in the CBCT or the CCBCT is correct.
Figure 7.
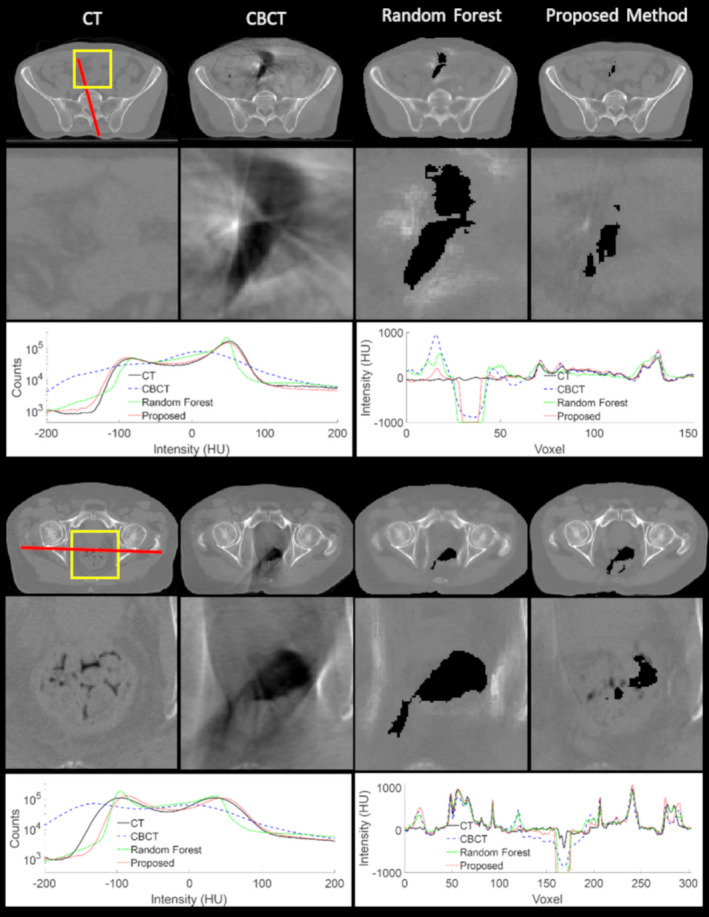
Cone‐beam computed tomography correction visual results on two sets of pelvis patient data. The first and fourth columns show the computed tomography images for the patients, the second and fifth rows show zoomed‐in inserts of the respective regions outlined in yellow, and the third and sixth rows show the image histograms and line profiles. [Color figure can be viewed at wileyonlinelibrary.com]
The quantitative results for all test cases are summarized in Table 1. As is shown in Table 1, our proposed method significantly outperformed random forest‐based method by PSNR, NCC, SNU in both brain and pelvic sites. While all methods improved upon the CBCT image, the machine learning‐based methods were found to be superior to the scatter correction method. The proposed method only statistically outperforms the random forest method in PSNR. It should be noted that this does not mean the proposed method has an advantage. In quantities such as ME, MAE, and NCC, the effects of subtle errors, such as those pointed out in Figs. 6 and 7, may be lost by averaging over the large number of pixels in a 3D image. While these subtle differences may not be seen in a quantitative comparison, they can be seen on the images, and they are important both for image evaluation and for radiation dose calculation.
Table 1.
Quantitative results and p‐value obtained by comparison between proposed method and RF‐based method. For all tests, the planning CT image was taken as the ground truth image
| ME (HU) | MAE (HU) | PSNR (dB) | NCC | SNU | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pelvis | Brain | Pelvis | Brain | Pelvis | Brain | Pelvis | Brain | Pelvis | Brain | |
| CBCT | 3 ± 29 | −2 ± 4 | 56.3 ± 19.7 | 23.8 ± 5.1 | 22.2 ± 3.4 | 32.3 ± 5.9 | 0.96 ± 0.02 | 0.98 ± 0.02 | 0.26 ± 0.16 | 0.15 ± 0.07 |
| RF | −5 ± 5 | 0 ± 1 | 17.7 ± 6.5 | 13.1 ± 2.0 | 28.0 ± 4.1 | 34.6 ± 1.7 | 0.95 ± 0.01 | 0.98 ± 0.02 | 0.16 ± 0.08 | 0.06 ± 0.05 |
| Proposed | −3 ± 4 | 0 ± 1 | 16.1 ± 4.5 | 13.0 ± 2.2 | 30.7 ± 3.7 | 37.5 ± 2.3 | 0.98 ± 0.01 | 0.99 ± 0.00 | 0.09 ± 0.05 | 0.05 ± 0.04 |
| P‐value (proposed vs. RF) | 0.19 | 0.17 | 0.24 | 0.78 | <0.001 | <0.001 | <0.001 | 0.12 | <0.001 | 0.04 |
RF, random forest; MAE, mean absolute error; PSNR, peak signal‐to‐noise ratio; NCC, normalized cross‐correlation; SNU, spatial nonuniformity; CBCT, cone‐beam computed tomography.
4. Discussion
The proposed algorithm is well suited to the task of CBCT image correction because CBCT and CT images have similar structures. A limitation of the algorithm is that it operates entirely in the image domain, and does not use any physical information, unlike conventional scatter‐based methods. This means that the attainable image quality in CCBCT images is fundamentally limited by the planning CT image. For adaptive dose calculation, this is not a true limitation since dose is already calculated on the planning CT, but it does limit the image quality of CCBCT images. It also means that, unlike with conventional scatter correction techniques, any artifacts present in the planning CT will inherently be propagated to the CCBCT image. This could pose a problem for patients with hip prostheses, for example, when the metal artifact is not effectively reduced in the planning stage.
In the context of ART, reduction of the streaking and shading artifacts, specifically at material boundaries, is an important step to being able to accurately calculate patient dose on CBCT images. Accurate dose calculation relies on accurate HU measurement and conversion to electron density. The proposed method results in CCBCT images that have HU distributions which reflect the HU distributions of the planning CT, while conventional scatter or artifact corrections typically enhance the image quality without changing HU levels. Although impacts of the algorithm on dose calculation were not evaluated in this work, recent work by our group studied the dosimetric impact of the random forest‐based method that is compared to the proposed method.35 As the proposed method is more accurate than the random forest method, the accuracy of CCBCT dose calculation is expected to be slightly better than what is presented in that work.
The proposed algorithm uses paired training data while the original implementation of cycle‐GAN relied on unpaired data. When using paired data, the geometric mismatch at body boundaries is relatively less than it would be if using unpaired data. This allows the algorithm to focus on reducing image artifacts and enhancing soft tissue contrast, rather than focusing on the large geometric mismatches. Additionally, this speeds up the training model because relative differences are reduced from the beginning.
While the proposed algorithm works well on streaking artifacts, the corrections it applies on air cavities, like gas within the bowel, are not perfect. It approximates the boundaries of the cavities, but typically outputs CT values at −1000 HU. While this may be an accurate representation of gas within the body, it is hard to determine given the strength of the artifacts around air cavities in the original CBCT image. This sharp drop is because the algorithm does not inherently know whether a dark region in the image corresponds to an internal air gap, like gas, or an external air gap, like the surface of the body. This effect may not be significant within the brain and pelvis patients displayed in this work, but the algorithm will need to be better trained to account for this when application is extended to other disease sites such as the lung and liver.
CBCT image quality is not the only hindrance to clinical ART. In addition to having images from which to generate electron density maps, ART requires rapid dose calculation and contouring of structures based on the CCBCT. An appealing application of the proposed algorithm could be application to both steps in the treatment planning process. Much like training the model to learn CT images from CBCT images, the model could be trained to learn deformed dose distributions or organ contours based on CBCT image corrections. The accuracy of dose calculation could be further enhanced by learning from Monte Carlo calculated data rather than from analytical dose calculation algorithms. This approach to dose calculation, although computationally expensive initially, could allow for adaptive doses to be calculated within a few seconds, reducing the time the patient spends on the treatment table.
Before clinical implementation of the proposed algorithm, full validation of the method needs to be carried out. The algorithm needs to be trained for each disease site such as the lungs and head‐and‐neck regions. In addition to training more models, dosimetric studies need to be carried out to validate the proposed method. Additionally, it is anticipated that certain disease sites where patient anatomy changes widely over the course of treatment, such as head‐and‐neck, will benefit more greatly from ART, so these areas will need to undergo more training and validation relative to anatomically static sites. Furthermore, the inherent limitations of the proposed algorithm must be understood. For example, in the brain sites, there is an inherent 2 mm uncertainty in the image registration process. The results presented in this work were based on patient cohorts of 24 brain and 20 pelvic patients. If the proposed algorithm were to be implemented in the clinic, more patients are needed for each site.
5. Conclusions
This work has shown a deep learning‐based algorithm which can correct for many image artifacts present in CBCT images. The proposed algorithm relies on learning a mapping from CBCT images to paired planning CT images, which have similar structures but higher image quality. The proposed algorithm can reduce the MAE from planning CT images to CBCT images from 24 HU to 13 HU. It should be noted that, in this work, the planning CT was taken as the ground truth for evaluations. While the planning CT is of higher image quality than the CBCT, it is not the real ground truth. The CT and CBCT images are taken on different days and it is expected that the images do not reflect the exact same patient anatomy, even if it is similar. Additionally, the proposed algorithm effectively removes streaking and shading artifacts typical of CBCT images. This preliminary work shows that with deep learning‐algorithms, it is possible to correct CBCT images to equivalent quality with planning CT images. Furthermore, HU distributions of CCBCT images approach that of CT images, trending toward quantitative imaging, increasing the utility of CBCT for both for monitoring patient changes throughout treatment and for dose calculations.
Conflict of interest
The authors declare no conflicts of interest.
Acknowledgments
This research is supported in part by the National Cancer Institute of the National Institutes of Health under Award Number R01CA215718 (XY), the Department of Defense (DoD) Prostate Cancer Research Program (PCRP) Award DoD W81XWH‐17‐1‐0438 (TL), and Dunwoody Golf Club Prostate Cancer Research Award, a philanthropic award provided by the Winship Cancer Institute of Emory University.
References
- 1. Endo M, Tsunoo T, Nakamori N, Yoshida K. Effect of scattered radiation on image noise in cone beam CT. Med Phys. 2001;28:469–474. [DOI] [PubMed] [Google Scholar]
- 2. Siewerdsen JH, Jaffray DA. Cone‐beam computed tomography with a flat‐panel imager: magnitude and effects of x‐ray scatter. Med Phys. 2001;28:220–231. [DOI] [PubMed] [Google Scholar]
- 3. Shi L, Tsui T, Wei J, Zhu L. Fast shading correction for cone beam CT in radiation therapy via sparse sampling on planning CT. Med Phys. 2017;44:1796–1808. [DOI] [PubMed] [Google Scholar]
- 4. Xu Y, Bai T, Yan H, et al. A practical cone‐beam CT scatter correction method with optimized Monte Carlo simulations for image‐guided radiation therapy. Phys Med Biol. 2015;60:3567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Yoo J‐C, Han TH. Fast normalized cross‐correlation. J Circ Sys Signal Proc. 2009;28:819. [Google Scholar]
- 6. Acharya S, Fischer‐Valuck BW, Kashani R, et al. Online magnetic resonance image guided adaptive radiation therapy: first clinical applications. Intl J Radiat Oncol Biol Phys. 2016;94:394–403. [DOI] [PubMed] [Google Scholar]
- 7. Zhu L, Xie Y, Wang J, Xing L. Scatter correction for cone‐beam CT in radiation therapy. Med Phys. 2009;36:2258–2268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Stankovic U, Ploeger LS, van Herk M, Sonke JJ. Optimal combination of anti‐scatter grids and software correction for CBCT imaging. Med Phys. 2017;44:4437–4451. [DOI] [PubMed] [Google Scholar]
- 9. Wei Z, Stephen B, Kai N, Sebastian S, Kevin R, Guang‐Hong C. Patient‐specific scatter correction for flat‐panel detector‐based cone‐beam CT imaging. Phys Med Biol. 2015;60:1339. [DOI] [PubMed] [Google Scholar]
- 10. Shi L, Vedantham S, Karellas A, Zhu L. Library based x‐ray scatter correction for dedicated cone beam breast CT. Med Phys. 2016;43:4529–4544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Bootsma G, Verhaegen F, Jaffray D. Efficient scatter distribution estimation and correction in CBCT using concurrent Monte Carlo fitting. Med Phys. 2015;42:54–68. [DOI] [PubMed] [Google Scholar]
- 12. Lei Y, Tang X, Higgins K, et al. Learning‐based CBCT correction using alternating random forest based on auto‐context model. Med Phys. 2018;46:601–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. El Naqa I, Brock K, Yu Y, Langen K, Klein EE. On the fuzziness of machine learning, neural networks, and artificial intelligence in radiation oncology. Intl J Radiat Oncol Biol Phys. 2018;100:1–4. [DOI] [PubMed] [Google Scholar]
- 14. Huynh T, Gao Y, Kang J, et al. Estimating CT image from MRI data using structured random forest and auto‐context model. IEEE Trans Med Imag. 2016;35:174–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Xiang L, Wang Q, Nie D, et al. Deep embedding convolutional neural network for synthesizing CT image from T1‐Weighted MR image. Med Imag Anal. 2018;47:31–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Pota M, Scalco E, Sanguineti G, et al. Early prediction of radiotherapy‐induced parotid shrinkage and toxicity based on CT radiomics and fuzzy classification. Artif Intel Med. 2017;81:41–53. [DOI] [PubMed] [Google Scholar]
- 17. Gilmer V, Timothy DS, Marina H, Lyle U, Charles BS II. Using machine learning to predict radiation pneumonitis in patients with stage I non‐small cell lung cancer treated with stereotactic body radiation therapy. Phys Med Biol. 2016;61:6105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Nguyen D, Jia X, Sher D, et al. Three‐dimensional radiotherapy dose prediction on head and neck cancer patients with a hierarchically densely connected U‐net deep learning architecture. arXiv preprint arXiv:10397. 2018. [DOI] [PubMed]
- 19. Fan J, Wang J, Chen Z, Hu C, Zhang Z, Hu W. Automatic treatment planning based on three‐dimensional dose distribution predicted from deep learning technique. Med Phys. 2019;46:370–381. [DOI] [PubMed] [Google Scholar]
- 20. Kamnitsas K, Bai W, Ferrante E, et al. Ensembles of multiple models and architectures for robust brain tumour segmentation. Computer Vision and Pattern Recognition. 2018:450–462.
- 21. Hansen DC, Landry G, Kamp F, et al. ScatterNet: a convolutional neural network for cone‐beam CT intensity correction. Med Phys. 2018;45:4916–4926. [DOI] [PubMed] [Google Scholar]
- 22. Maier J, Eulig E, Vöth T, et al. Real‐time scatter estimation for medical CT using the deep scatter estimation: Method and robustness analysis with respect to different anatomies, dose levels, tube voltages, and data truncation. Med Phys. 2019;46:238–249. [DOI] [PubMed] [Google Scholar]
- 23. Kida S, Nakamoto T, Nakano M, et al. Computed tomography image quality improvement using a deep convolutional neural network. Cureus. 2018;10:e2548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Landry G, Hansen D, Kamp F, et al. Comparing Unet training with three different datasets to correct CBCT images for prostate radiotherapy dose calculations. Phys Med Biol. 2019;64:035011. [DOI] [PubMed] [Google Scholar]
- 25. Zhu J‐Y, Park T, Isola P, Efros AA. Unpaired image‐to‐image translation using cycle‐consistent adversarial networks. Paper presented at: Int. Conf. Comput. Vis. 2017.
- 26. Kida S, Kaji S, Nawa K, et al. Cone‐beam CT to Planning CT synthesis using generative adversarial networks. arXiv preprint arXiv:05773. 2019.
- 27. Liang X, Chen L, Nguyen D, et al. Generating synthesized computed tomography (CT) from cone‐beam computed tomography (CBCT) using CycleGAN for adaptive radiation therapy. Phys Med Biol. 2019;64:125002. [DOI] [PubMed] [Google Scholar]
- 28. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. Paper presented at: Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.
- 29. Goodfellow I, Pouget‐Abadie J, Mirza M, et al. Generative adversarial nets. Paper presented at: Adv. Neural Info. Proc. Sys; 2014.
- 30. He K, Zhang X, Ren S, Sun J. Identity mappings in deep residual networks. Paper presented at: Eur. Conf. Comput. Vis. 2016; Cham.
- 31. Rahimi A, Xu J, Wang L. Lp‐Norm regularization in volumetric imaging of cardiac current sources. J Comput Mathemat Methods Med. 2013;2013:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Wang T, Zhu L. Image‐domain non‐uniformity correction for cone‐beam CT. Paper presented at: IEEE 14th Intl. Sym. Biomed. Imag. (ISBI 2017) 2017.
- 33. Lei Y, Tang X, Higgins K, et al. Improving image quality of cone‐beam CT using alternating regression forest. SPIE Med Imag. 2018;10573:1057345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Briechle K, Hanebeck UD. Template matching using fast normalized cross correlation. Paper presented at: Optic. Pattern Recognit. XII2001.
- 35. Wang T, Lei Y, Manohar N, et al. Dosimetric study on learning‐based cone‐beam CT correction in adaptive radiation therapy. Med Dosim. 2019. S0958‐3947(19)30034‐2. 10.1016/j.meddos.2019.03.001 [DOI] [PMC free article] [PubMed] [Google Scholar]


