Statistical genomics in rare cancer

Abstract

Rare cancers make of more than 20% of cancer cases. Due to the rare nature, less research has been conducted on rare cancers resulting in worse outcomes for patients with rare cancers compared to common cancers. The ability to study rare cancers is impaired by the ability to collect a large enough set of patients to complete an adequately powered genomic study. In this manuscript we outline analytical approaches and public genomic datasets that have been used in genomic studies of rare cancers. These statistical analysis approaches and study designs include: gene set / pathway analyses, pedigree and consortium studies, meta-analysis or horizontal integration, and integration of multiple types of genomic information or vertical integration. We also discuss some of the publicly available resources that can be leveraged in rare cancer genomic studies.

1. Introduction

Rare cancers are roughly defined as cancers with fewer than 15 new diagnoses in 100,000 people a year; however there is no universally adopted definition. Collectively rare cancer account for more than 20% of all cancer diagnoses in a year [1]. In the United States, pediatric and adolescence young adults are disproportionally impacted by rare cancers, with more than 2/3 of cancers in pediatric, adolescent or young adult individuals (age < 20 years) being rare [2]. Due to the rare nature, less research has been conducted on rare cancers resulting in worse outcomes for patients with rare cancers compared to common cancers. In a study conducted by the Surveillance of Rare Cancers in Europe (RARECARE) Project, they found the five-year survival rate to be 47% for rare cancers compared to 65% for common cancers [3]. Additionally, not much is known regarding ways to prevent and adequately diagnoses many rare cancers.

Rare cancers are often defined in terms of their uncommon site of origin (heart), uncommon cell type of origin (small cell cancer of the cervix), unique molecular feature (RYB6-NTRK3 fusion in breast cancer), or uncommon host (male breast cancer). Recently, with the advent of high-throughput genomics, researchers have been able to further stratify common cancers into unique subtypes based on a set of molecular features, where often the number of patients that fall into these specific subtypes becomes small and meets the general definition of a rare cancer. The ability to study these rare cancers and subtypes is impaired by the ability to collect a large enough set of patients to complete an adequately powered genomic study. As illustrated in Fig. 1, the power to detect a moderate effect size (Cohen’s d = 0.50) for differentially expressed genes with a type I error rate of 0.00001 (Bonferroni adjustment for testing 5000 genes) improves greatly as the sample size increase, where 226 subjects are needed in each group to be able to detect the moderately differentially expressed genes with 80% power. In the following sections, we outline some analytical approaches and public genomic datasets that have been used in genomic studies of rare cancers.

Fig. 1.

Power to detect a moderate effect size (0.50) as a function of power and sample size, with a significance level set to 0.00001 to account for the testing of multiple genes.

2. Public data resources

Large genomic repositories have been created for use by cancer researchers. These repositories can be used to: (1) combine with other studies of a given rare cancer to increase sample size (e.g. meta-analysis or horizontal integration); (2) determine novel hypothesis to be tested in future prospective studies; (3) replication or validation of findings; or (4) compare / contrast between cancers (pan-cancer). Below we outline three large public data resources that can be leveraged in the study of rare cancers.

2.1. Gene expression omnibus (GEO)

GEO is a public repository for high-throughput transcriptomic datasets generated by array- and sequence-based technologies [4,5]. Such datasets hold great value for knowledge discovery, particularly when integrated. The GEO repository is publicly accessible at (https://www.ncbi.nlm.nih.gov/geo) and includes hundreds of studies on a variety of rare cancers. For example, GEO contains 5420 studies on Osteosarcoma, 550 on Ewing’s sarcoma, 160 on male breast cancer, 1480 on Gastrointestinal stromal tumors (GISTs), 426 on chondrosarcoma, 1331 on mesothelioma, and 1547 on ependymoma.

2.2. The Cancer genome atlas (TCGA)

The TCGA was a multi-institutional collaborative project aimed to comprehensively catalogue genomic alterations of a variety of cancers through high-throughput genomic and bioinformatic analyses [6]. TCGA has characterized 33 cancer types, including 10 rare cancers: adrenocortical carcinoma (ACC) [7], cholangiocarcinoma (CHOL) [8], kidney chromophobe carcinoma (KICH) [9], mesothelioma (MESO) [10], pheochromocytoma and paraganglioma (PCPG) [11], sarcoma (SARC) [12], testicular germ cell tumor (TGCT) [13], thymoma (THYM) [9], uterine carcinosarcoma (UCS) [14], and uveal melanoma (UVM) [15] (https://portal.gdc.cancer.gov). TCGA has generated integrative multi-omics data including large-scale genomic, epigenomic, transcriptomic and proteomic datasets along with slide images for histopathology and details on patient’s information which have become a great resource for cancer research.

2.3. Therapeutically applicable research to generate effective treatment (TARGET)

The TARGET initiative is employing genomic data to accelerate molecular discoveries and drug development for difficult to treat childhood cancers, such as, acute lymphoblastic leukemia (ALL) [16], acute myeloid leukemia (AML) [17], neuroblastoma (NBL) [18], osteosarcoma (OS), and Wilms’ tumor (WT) [19]. Pediatric ALL was the first disease to be piloted for the TARGET initiative, which is jointly managed by the NCI Office of Cancer Genomics (OCG) and Cancer Therapy Evaluation Program (CTEP). TARGET datasets include large-scale genomic data including gene-expression, copy number variation, epigenetics, along with annotated clinical information for a selected set of pediatric cancers (https://ocg.cancer.gov/programs/target/data-matrix).

3. Consortium and collaborative networks

One major limitation in the study of rare cancers is the lack of sufficiently size cohort of cancer patients by any one given research group. Hence, consortium and networks have been created to pool resources in the study of rare cancers [20]. This approach has also been employed in studies of common cancers as a means to increase power to detect relative small effects, particular in the context of genome-wide genetic association studies (GWAS) [21–23]. One of the largest initiative of this kind for studying rare cancers is the International Rare Cancer Initiative (IRCI)1 and the International Cancer Genome Consortium (ICGC) [24,25]. Common cancers are the primary cancers being studied in the ICGC. However, some studies are underway involving rare cancers, such as Ewing’s sarcoma, osteosarcoma, chondrosarcoma and medulloblastoma, which all primary effect children or adolescent young adults. The pooling of familial data for rare genetic based rare cancer has often been done to localize disease loci for rare cancers. This approach has been successfully in the setting of Li-Fraumeni syndrome (LFS) [26,27]. LFS rare inherited syndrome that can lead to the development of a number of cancers, including sarcoma (such as osteosarcoma and soft-tissue sarcomas), leukemia, brain (central nervous system) cancers, cancer of the adrenal cortex and breast cancer.

In completing statistical analyses in the context of consortium or networks, additional care is needed to insure adequacy of results. In particular, assessment of batch effects in the genomic data between studies is a major concern and needs to be considered when completing statistical analyses. Batch effects in large datasets can often been visualized using data reduction method, such as plotting the first two principal components from a principal component analysis (PCA), as illustrated in Fig. 2. If study or batch effects are observed, adjusting for study/batch in the model or normalization of the data using more sophisticated methods (e.g., COMBAT [28]) are warrented [29]. In the setting of GWAS adjustment for population stratification is also required when completing the statistical analysis [30].

Fig. 2.

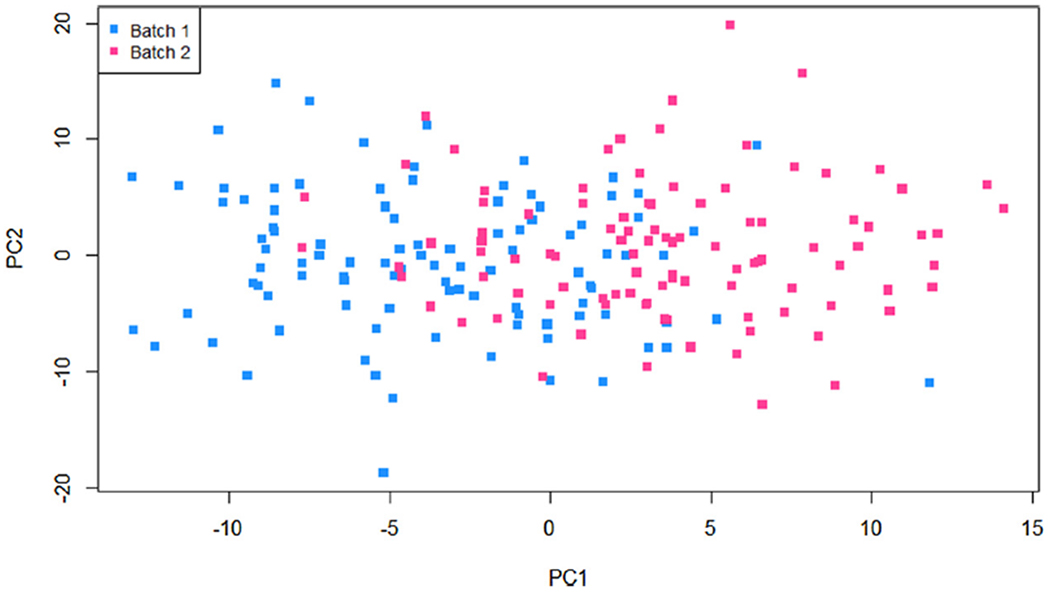
Plot of first and second principal components (PCs) from principal component analysis (PCA) for visualization of batch effects.

4. Analysis of cancer “families” and meta-analysis

Since the etiology, diagnosis, and treatment of some rare cancers are similar to more common cancers, often researchers look at biologically similarly common cancers to the rare cancer of interest to extrapolated or compare findings. As an example, male breast cancer is a rare disease accounting for approximately <1% of all breast cancer diagnoses worldwide [31–34] and shares many similarities with female breast cancer [31,35]. Another way to overcome some of the challenges in studying rare cancers is to group rare cancers into “families”. In addition, genetic information is increasingly used to group cancers according to a tumor’s molecular subtype. However, a limitation in grouping rare cancers together in “families” is that this can add heterogeneity. In the following section we discuss various statistical approaches for meta-analysis for the analysis of cancer families. Many of these methods allow researcher to assess the degree of heterogeneity between the cancers being pooled together.

4.1. Meta-analysis methods

Due to the large number of features and limited sample size in rare cancer study, multi-study genomic data integration called “horizontal integration” has been considered to improve the discovery of new biological insights and reach more general and reliable conclusions along with increasing statistical power [36–39]. Meta-analysis methods are based on summary statistics from the analysis of each individual study (e.g., effect sizes, p-values), whereby these study specific summary statistics are aggregated together to get a combined level of association for the entire set of studies or cancer “family” [40–43]. Several meta-analysis methods have been suggested to genomic applications such as combining p-values, effect sizes, and rankings. The strengths and limitations of meta-analysis methods are evaluated particularly with respect to their ability to assess variation across independent genomic studies (e.g., platform variability, inconsistent annotation, various methods for data processing, and patient heterogeneity) beyond within-study variation.

4.1.1. Methods combining p-values

Combining the p-values from multiple independent studies has a benefit of its simplicity and extensibility to different kinds of outcome variables [36,42,44]. When the outcome variable is not binary (e.g. multi-class or censored survival), association p-values can be computed, while effect sizes may not be well defined. Fisher’s method [45] and Stouffer’s method [46] are widely used to combine results from different studies [47]. Other p-values based meta-analysis methods have been applied such as taking the minimum and maximum p-values [48,49], or a weighted modification to Fisher’s method [50]. Major limitation of such traditional methods of combining p-values is that they can be performed parametrically under the assumption that p-values are uniformly distributed under the null hypothesis [51,52]. In addition, the existing traditional combining p-values typically do not account the data heterogeneity and do not take into account direction of effect.

4.1.2. Methods combining effect sizes

Most popular statistical methods to combine effect sizes (e.g., standardized mean differences, correlation coefficients, odds ratios, etc.) are based on fixed- and random-effects model [53]. Under the fixed-effects model, estimated effect sizes are assumed to be homogeneous across studies and all differences in observed effects are due to sampling error or within-study variability, while in practice such assumption is questionable. In contrast, the random-effects model incorporates the variability of the effect size across studies in addition to the within-study variability using two-stage hierarchical process [44,54–56]. One of the most troublesome aspects of a meta-analysis is the determination of whether there is true heterogeneity (i.e., across study variability), as it can influence the choice of the statistical method to combine effect sizes. Cochran (1954) [57] proposed a Q test to determine the heterogeneity across studies; however its statistical power depends on the number of studies [58,59]. Another approach is to assume a random-effects model that consists of estimating the across study variance (τ²). To address the limitations of Q test and the between-study variance methods, Higgins et al. (2002, 2003) proposed the I² statistic that is the percentage of the total variability in a set of effect sizes due to true heterogeneity [60,61].

To illustrate these methods for assessing heterogeneity, we used the data from the TCGA sarcoma (SARC) study, were multiple types of sarcomas were represented. Using RNA-seq data collected on 58 dedifferentiated liposarcoma (DDLPS), 104 leiomyosarcoma (LMS), 25 myxofibrosarcoma (MFS), and 50 undifferentiated pleomorphic sarcoma (UPS) we applied fixed- and random-effects meta-analysis for to determine the association of gene expression with overall survival using hazard ratios (HZ) from Cox PH models. Fig. 3 presents forest plots for TRPV6 (I² = 85%, p-value < 0.01) and KIF21A (I² = 62%, p-value = 0.05), both showing substantial heterogeneity across 4 studies.

Fig. 3.

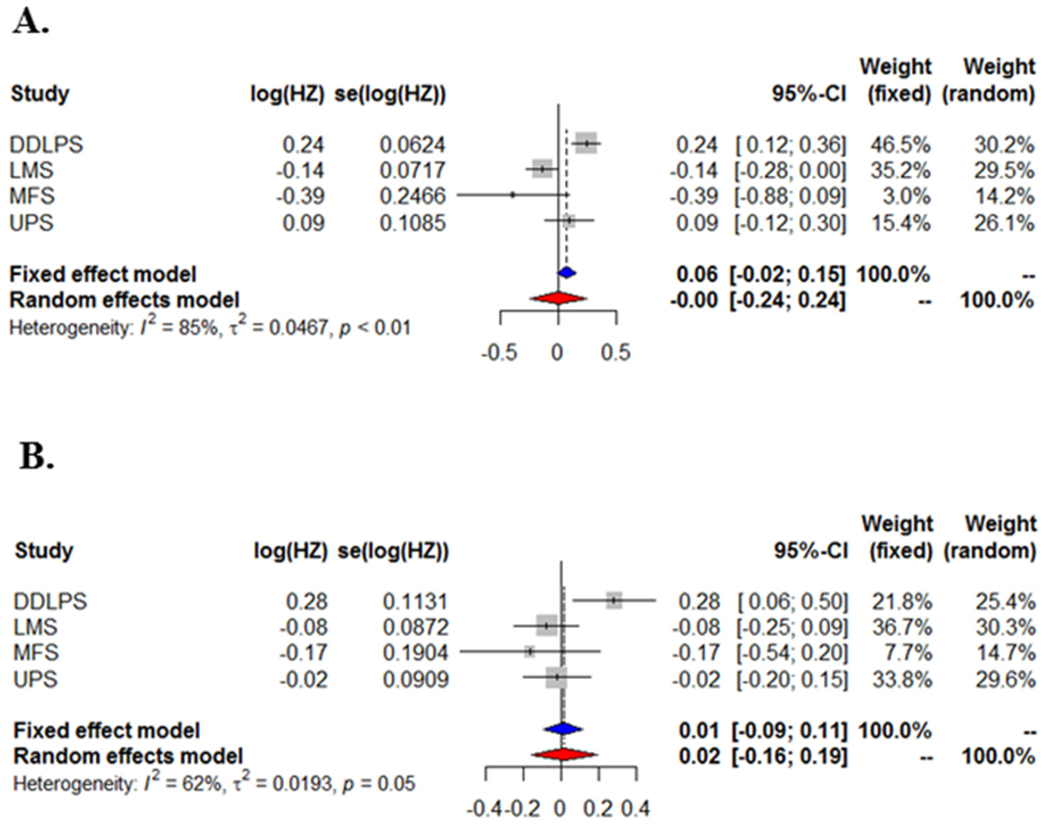
Forest plots for TCGA SARC study to assess true heterogeneity across 4 types of sarcoma (DDLPS, LMS, MFS, and UPS) using fixed- and random-effects models for overall survival with gene expression for (A) TRPV6 and (B) KIF21A.

4.1.3. Methods combining ranks

Proposed ranking-based meta-analysis methods combine robust rank statistics instead of p-values or effect sizes to address issues regarding outliers and heterogeneity in genomic studies [62,63]. The product, mean or sum of ranks [64–66] from genomic studies is calculated as the test statistics along with assessing the statistical significance using permutation testing [67–69].

5. Pedigree and population based genetic studies

Pedigree or family studies have been the backbone for studying rare Mendelian or inherited cancers and cancer syndromes. Mendelian traits are traits that are controlled by a single locus in which one inherits the disease predisposing allele from either their mother or father. An example is BRCA1 related breast cancer, ovarian cancer, and Lynch Syndrome, as illustrated in two example pedigrees from the National Cancer Institute (Fig. 4). Often in the study of these cancers, pedigrees are recruited based on the proband, the person serving as the starting point for the genetic study of a family and usually the first person enrolled in the family. These study design are often used in genetic epidemiology studies [70] involving familial aggregation [71], segregation [72,73], and linkage [74–76] studies of both rare and common cancers. Pedigrees studies have been successfully applied to the study of Li-Fraumeni Syndrome (LFS). LFS is a rare inherited syndrome that leads to the development of many cancers, often at a younger age of onset. LFS families are predisposed to both rare cancers (e.g., osteosarcoma, Wilms tumors) and common cancers (e.g., colon and breast cancer) at a higher rate than the general population [77,78]. Using 39 pedigrees, researchers were able to determine that the most common cause of LFS is inherited mutations in the tumor suppressor gene TP53 [26].

Fig. 4.

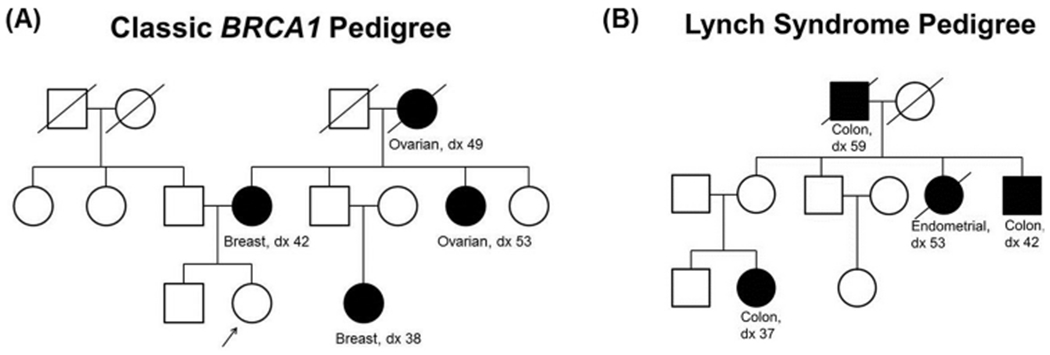
Example pedigrees of for two inherited cancers. (A) BRCA1 related breast and ovarian cancer and (B) Lynch Syndrome.

With the advent of microarray technology and the ability to genotype thousands of single-nucleotide polymorphism, as opposed to genotyping hundreds of micro-satellites or restriction fragment-length polymorphisms (RFLPs), population based genetic association studies involving families or unrelated individuals became common place as a means to study the genetic basis of cancer risk [79]. However, these approaches often failed in the study of rare cancers due to the limited sample size to detect the small effect size, as the majority of cancer susceptibility loci discovered in genome-wide association studies (GWAS) have low effect sizes (OR < 1.3) [80]. However, GWAS have been successfully applied in the setting of some rare cancers, such as neuroblastoma, where GWAS have been able to determine 8 neuroblastoma risk loci including BARD1 [81] (OR = 1.4) and a loci within 6p22 [82] (OR = 1.4) (see GWAS catalog at https://www.ebi.ac.uk/gwas/home for entire list of known risk loci).

6. Analysis of pathways and gene sets

Due to the limited power in the study of rare cancers due to relatively small sample size, researchers often focus on particular pathways of interest, thus reduced the multiple testing burden. As defined by the NHGRI, “a biological pathway is a series of actions among molecules in a cell that leads to a certain product or a change in the cell. It can trigger the assembly of new molecules, such as a fat or protein, turn genes on and off, or spur a cell to move”. However, it should be noted that assigning genes to a pathway is somewhat artificial, as pathways are not entities in of themselves, but rather inter-related dynamic groups of genes. Often researchers use pathways as defined in KEGG: Kyoto encyclopedia of gene and genomes [83,84]. Other possible pathway or gene sets often use are those defined in Gene Ontology (GO) [85] (sets of genes that are biological related) and those genes related to a particular transcription factor defined by ChIP-Seq studies [86].

There are two approaches for using pathway information, a “hypothesis-driven” approach or an “agnostic” approach. The “hypothesis-driven” approach is one in which a researcher a priori looks only at the biological factors within a particular pathway of interest, as illustrated in the paper by Mezzapelle et al [87]. In this research, mesothelioma researchers focused on EGRF and downstream signaling pathways in a set of 77 malignant pleural mesothelioma tumors. In the “agnostic” approach, a researcher is looking at aggregation of signal or enrichment of signal in a large set of pathways, such as investigation of all KEGG pathways. Aggregation of the association signals for a set of genes within a pathway may be beneficial as it incorporates biological knowledge, reduces the multiple-testing burden, and may increase the association signal, thus increasing the power to detect biologically meaningful results. In agnostic pathway analysis, there are two types of statistical methods for assessing pathways: competitive/enrichment methods or self-contained methods [88,89]. These two approaches are based on two different null hypotheses. In the competitive or enrichment methods one is testing the null hypothesis that genes within the pathway are more associated with the phenotype of interest (i.e., survival) then genes outside the pathway. That is, one is looking to determining if there is more “signal” within the pathway than expected or if the pathway is “enriched for signal”. Commonly used pathway analysis approaches that are competitive in nature are GSEA: gene set enrichment analysis [90] or methods in the flavor of Fisher Exact Test, such as those implemented in commonly used online tool EnrichR [91,92]], and DAVID [93,94], where users upload a list of genes found to be associated with the phenotype of interest (i.e., genes differentially expressed between two treatment conditions). Additionally, commercially available software tools, such as Ingenuity Pathway Analysis (IPA) and MetaCore software analysis tool (GeneGo), have implementations of enrichment or competitive pathway analysis methods. In using the competitive or enrichment methods, experiments and analyses need to be genome-wide (i.e., transcriptomic studies conducted using high-throughput sequencing or microarray technologies). These agnostic enrichment approaches have been successfully used in Ewing’s sarcoma genomic studies [95,96].

In contrast, the self-contained pathway or gene set approaches are assessing if the genes in the pathway are associated with the phenotype of interest. These methods can be used in both candidate pathway studies (i.e., targeted or custom panels) and genome-wide studies. Examples of methods in this framework are modeling based methods like the global test Bioconductor package which uses a random effects model [97] or summarization methods which aggregate the results for the genes in the pathway to the pathway level, such as Fisher’s Method for meta-analysis [45] and variations on Fisher’s Method, such as the Gamma Method [98,99]. A study of acute megakaryoblastic leukemia (AMKL), a rare subtype of acute myeloid leukemia (AML), researchers combined two studies of pediatric cases (N = 14 and N = 79) and completed high-throughput sequencing. The self-contained global testing method was used successfully to assess the genomic features in a gene set with determine subtypes of AMKL [100].

7. Network analysis and module construction

In contrast to gene set or pathway analysis, where the analysis is focused on a prior defined set of genes, network analysis is focused on determining sets of molecular features that are co-expressed or related and form a tight network or modules which aid researchers in understanding of gene regulation (i.e., co-regulated genes) or signaling networks. Additionally, many network analysis methods are used as the basis for determining modules of related features (i.e., co-expressed genes) [101]. In the study of rare cancers, reducing the dimensionally from individual features to a module of related features can reduce the multiple testing burden and therefore increase the power to detect biological relevant associations. Methods for determining networks primarily falling into three different paradigms: relevance networks, Gaussian graphical models (GMMs) and Bayesian belief networks [102,103]. Relevance networks [104] are based on a pairwise distance measures, often the correlation coefficient, where genes are connected if the absolute value of the measure is greater than some threshold. Since originally proposed in 2000, this approach has been modified extensive, with correlation based networks the basis of many module detection algorithms, including weighted gene co-expression network analysis (WGCNA) [105–107] which has been successfully applied to studies of Wilms tumors [108], Adrenocortical carcinoma [109] and Osteosarcoma [110]. However, a drawback of using correlation as the pairwise measure of relatedness captures both the direct and indirect relationship between features. To overcome this limitation, GMMs based on the partial correlation coefficient (i.e., inverse covariance matrix) only incorporate the direct relationship between features are often used to construct networks [111]. This approach has been used extensive in analysis of genomic data, with a recent publication applying GMMs to molecular data collected on 15 cancers in the TCGA [112]. Finally, Bayesian belief networks (BBNs) [113,114], or probabilistic directed acyclic graphical models are based on probability statements and infer direction of causation. BBNs have been applied extensively in the study of protein signaling networks [115,116], and gene expression networks [113].

One challenge in determining networks from high-dimensional molecular data is the enormous number of possible networks due to the large number of possible nodes (genes) and edges (connections). To overcome this challenge, many methods impose a sparsity or penalty term to estimate a robust correlation or partial correlation matrix for which the network is derived [117–121]. For example, Schafer and Strimmer (2005) proposed a shrinkage approach for estimating the covariance matrix needed for determining the partial correlation coefficients involving thousands of genes [122].

8. Integrative analyses

Due to advances in our ability to assess genomic, transcriptomic, epigenomic and proteomic features in cancer, many studies are assessing multiple layers of information on the same set of samples/subjects. In the context of rare cancers, the accumulation of multiple types of data on the same set of subjects can aid in the detection of biologically relevant findings, even when the sample size is relative small. In these multiple-omic studies, the data can be arranged vertically, where each of the data sets is represented by a data matrix with columns corresponding to samples and rows corresponding to genomic features (Fig. 5A). How to integrate these high-dimensional multi-omics data has become a great challenge for biostatisticians and bioinformaticians. In general, multi-omics data analysis can be classified as supervised or unsupervised integrative analysis. We will use examples to illustrate typical supervised and unsupervised analyses in the following sections. For comprehensive review of integrative analysis, we refer the readers to Kristensen et al. [123], Richardson et al. [41], and Wu et al. [124].

Fig. 5.

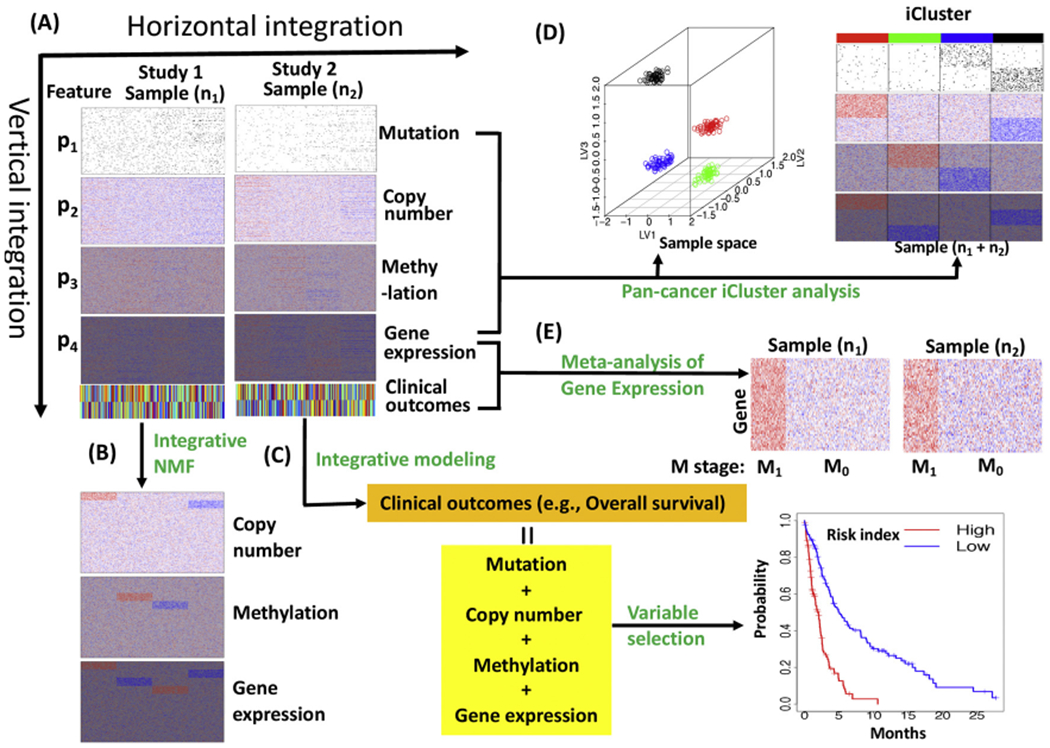
A scheme of integrative analyses of multi-omics data. (A) multi-omics data including mutation, DNA copy number, methylation and gene expression for two TCGA-like studies. (B) Unsupervised vertical integration analysis of copy number, methylation and gene expression using integrative NMF. (C) Supervised vertical integration analysis of mutation, copy number, methylation and gene expression. (D) Unsupervised pan-cancer iCluster analysis (vertical and horizontal integration). (E) Supervised horizontal integration analysis (Meta-analysis) of gene expression for pathological metastasis (M) stages. M1: metastasis, M0: no metastasis.

In supervised integrative analyses (e.g., classification or signature development), a clinical phenotype of the samples (e.g., overall survival, progression free survival) is usually include the dependent variable (Y) and the multi-omics features are included as exploratory variables (X’s) for statistical modeling (Fig. 5C & E). The supervised analyses could reveal genomic predictors of diseases and lead to identification of drug-targetable molecular alterations. In genomic application, supervised analysis is to identify omics features that are associated with clinical outcomes such as patient survival in a vertical integrative analysis (Fig. 5C) and tumor pathological stages (or treatment responses) in a horizontal integrative analysis or meta-analysis (Fig. 5E).

For example, in a vertical supervised integrative analysis, Jiang et al. developed prognostic Cox models for cutaneous melanoma that included clinical variables, mutation, mRNA gene expression, methylation and copy number data into the model [125]. To reduce the high dimensional omics variables into low dimensional variables that can be modeled, they used variable selection and dimension reduction approaches. For the variable selection approach, first, they fit a penalized Cox model with the clinical variables to identify 5 most important variables. Next, they fitted a penalized Cox model with single-omics data to identify the 10 most informative variables for each molecular data type. Lastly, they fit Cox models with the selected clinical and omics variables. For the dimension reduction approach, they used sparse principal component (SPCA) and sparse partial least squares (SPLS) to reduce the single-omics data to 10 SPCA and 10 SPLS components, respectively; then they fitted Cox models with various combination of the selected clinical variables and SPCA (or SPLS) components. As a result, they found that inclusion of multi-omics variables led to prognostic models with improved prediction performances. Zhao et al. used a similar approach to integrate multi-omics data to develop prognostic models for breast invasive carcinoma, glioblastoma multiforme (GBM), acute myeloid leukemia (AML) and lung squamous cell carcinoma (LUSC) [126].

For horizontal integrative analysis, if omics data from different cancer types are combined for analysis, it often refers to as a “pancancer” analysis (Fig. 5D). The major goal of pan-cancer analysis is to define commonalities and differences of genomic alterations across cancer types [6]. For example, Kandoth et al. [127] analyzed the mutation landscape of 12 major cancer types and found that TP53 and PIK3CA were the most commonly mutated genes, ARID1A were frequently mutated in bladder urothelial carcinoma (BLCA), uterine corpus endometrial carcinoma (UCEC), lung adenocarcinoma (LUAD) and lung squamous cell carcinoma (LUSC), and EGFR were frequently mutated in GBM and LUAD. In contrast, VHL and PBRM1 mutations were exclusive to kidney renal clear cell carcinoma (KIRC), and NPM1 and FLT3 mutations were exclusive to AML. Numerous pan-cancer analyses have been performed, including pan-cancer analyses of copy number alteration, enhancer expression, oncogenic signaling pathways, and transcriptional metabolic dysregulation [128–131]. If omics data from different cohorts of the same study are combined for analysis, horizontal integrative analysis often refers to meta-analysis (Fig. 5E). Meta-analysis is often used to increase statistical power and achieve a consensus conclusion (see section above on meta-analysis).

In unsupervised analysis, clinical variables are not directly used in the analysis and the major goal is to understand the underlying structure of omics data. Integrative clustering is an important unsupervised method that has been widely used to characterize cancers by grouping cancer samples and genomic features into meaningful subgroups (Fig. 5B & D). To characterize a specific cancer, it is often involved in vertical integrative analysis of multi-omics data sets. Traditionally, multi-omics data sets were clustered separately and with the resulting clusters manually integrated for characterization of the cancer. This single-omics clustering approach was used to cluster TCGA rare cancer studies involving Pheochromocytoma and Paraganglioma (PCPG) [11], uterine carcinosarcoma (USC) [14], uveal melanoma (UVM) [15] and testicular germ cell tumors (TGCT) [13].

An obvious disadvantage of the single-omics clustering analysis was that the inherent correlations among the multi-omics data sets were not taken into account during the analysis. As a result, it was not easy to identify molecular patterns across multiple platforms. Realizing the weakness of the single-omics clustering approach, researchers used cluster-of-clusters-analysis (COCA) in order to achieve integrative clustering assignments for breast cancer [132]. This approach is a step-wise integration approach. At the first step, single-omics clustering analysis was performed and a sample cluster assignment matrix was generated. At the second step, clustering analysis was performed on the sample cluster assignment matrix to generate joint cluster assignments for the samples. The COCA approach has been used to perform clustering analysis of rare cancers of adrenocortical carcinoma (ACC) [7], cholangiocarcinoma (CHOL) [8] and thymic epithelial tumors (THYM) [133]. It should be noted that the resulting integrative clusters were not directly driven by the genomic patterns embedded in the multi-omic data sets because the COCA approach does not directly use the multi-omics data.

Unlike the step-wise clustering approach or COCA, the integrative clustering method iCluster developed by Shen et al. [134] directly models multi-omic data sets to obtain clusters. The iCluster model is a Gaussian latent variable model in which a latent variable is used to capture the correlative structure of multi-omics data. A penalized expectation-maximization algorithm using a lasso-like penalty is used to obtain optimized solutions. Integrative sample cluster assignments are obtained by performing k-means clustering on the latent variable matrix. In an effort to accommodate different natures of multi-omics data, Shen et al. further extended the iCluster method by making use of lasso, elastic net and fused lasso penalty functions to make feature selection more flexible [135]. A limitation of the iCluster method is that it can only model continuous multi-omics data. Besides continuous data, omics data can be in the forms of binary (e.g., gene mutation status: yes, or no), multi-category (e.g., copy number states: gain, normal, loss) and counts (e.g., gene expression measurement by RNA-seq). The iClusterPlus method developed by Mo et al. [136] is a significant enhancement of the iCluster method, which uses linear regression to model continuous data, Poisson regression to model count data, logistic regression to model binary data, and multi-logit regression to model multi-categorical data. Recently, Mo et al. [137] developed the iClusterBayes method, a fully Bayesian latent variable model under the iClusterPlus framework. This method uses Bayesian variable selection techniques to identify informative features that contribute to sample clustering. An advantage of the iClusterBayes method is that it provides posterior probability estimation for each omics feature, which can be used as a criterion for feature selection. The iCluster methods have been used by TCGA and other research groups to characterize common and rare cancers, including mesothelioma (MESO) [10] and adult soft tissue sarcoma (SARC) [12].

Integrative non-negative matrix factorization (intNMF) is another powerful method for integrative clustering analysis of multi-omics data. NMF was initially applied to microarray gene expression data to identify cancer subtypes [138–140]. Usually, analysis is completed for a range of number of clusters (e.g., 2–10) with the selection of number of clustered determined by a number of diagnostic measures (e.g., consensus matrix [141], cophenetic correlation coefficient [138], dispersion coefficient [140]). Zhang et al. [142] extended NMF to multi-omics data to identify multi-dimensional modules (patterns). The joint NMF framework of Zhang et al. was effective in detection coordinated patterns across multiple data sets, but it was sensitive to random noise and confounding effects [142]. To remedy that, Yang and Michailidis (2016) extended the joint NMF framework by using a new factorization algorithm that was more robust to heterogeneous effects in the multi-omics data [143]. Chalise and Fridley (2017) further extended the joint NMF framework with a focus on integrative clustering analysis [144]. By analyzing the TCGA breast cancer (BRCA) and glioblastoma (GBM) multi-omics data sets, Chalise and Fridley found that the clusters identified by intNMF and iCluster largely overlapped, demonstrating its capability in identification of cancer subtypes inherent in the data.

To illustrate the integrative clustering analysis, we analyzed 241 sarcoma tumor samples from the TCGA SARC study that had somatic mutation, copy number, methylation and mRNA expression data using the recently developed iClusterBayes software [137]. Fig. 6A shows the three iClusters of SARC along with the driver omics features that made major contribution to the sample clustering. These three iClusters highly overlapped with the five iClusters reported by TCGA that were based on the iCluster analysis of copy number, methylation, mRNA, and miRNA expression data [12]. Specifically, iCluster 1 contained only leiomyosarcoma (LMS) tumors; iCluster 2 is dominated by dedifferentiated liposarcoma (DDLPS), leiomyosarcoma (LMS) and synovial sarcoma (SS); iCluster 3 is dominated by undifferentiated pleomorphic sarcoma (UPS), DDLPS, myxofibrosarcoma (MFS) and LMS (Fig. 6B). Fig. 6C shows the samples clustering on the two-dimensional latent variable spaces. The iCluster 1 was characterized by relatively low mutation rates of the driver genes except for RB1 and TP53, normality of chr12:58018979-70771592, trend to loss of chr13:49062990-50471179, and cluster-specific methylation and mRNA expression patterns (Fig. 6A). In contrast, the iCluster 2 and 3 were characterized by relatively high mutation rates of the driver genes, trend to amplification of chr12:58018979-70771592, normality of chr13:49062990-50471179, and cluster-specific methylation and mRNA expression patterns (Fig. 6A). In terms of overall survival, the iCluster 1 was the best, followed by the iCluster 2 the second, and the iCluster 3 the worst (p = 0.009, Fig. 6D).

Fig. 6.

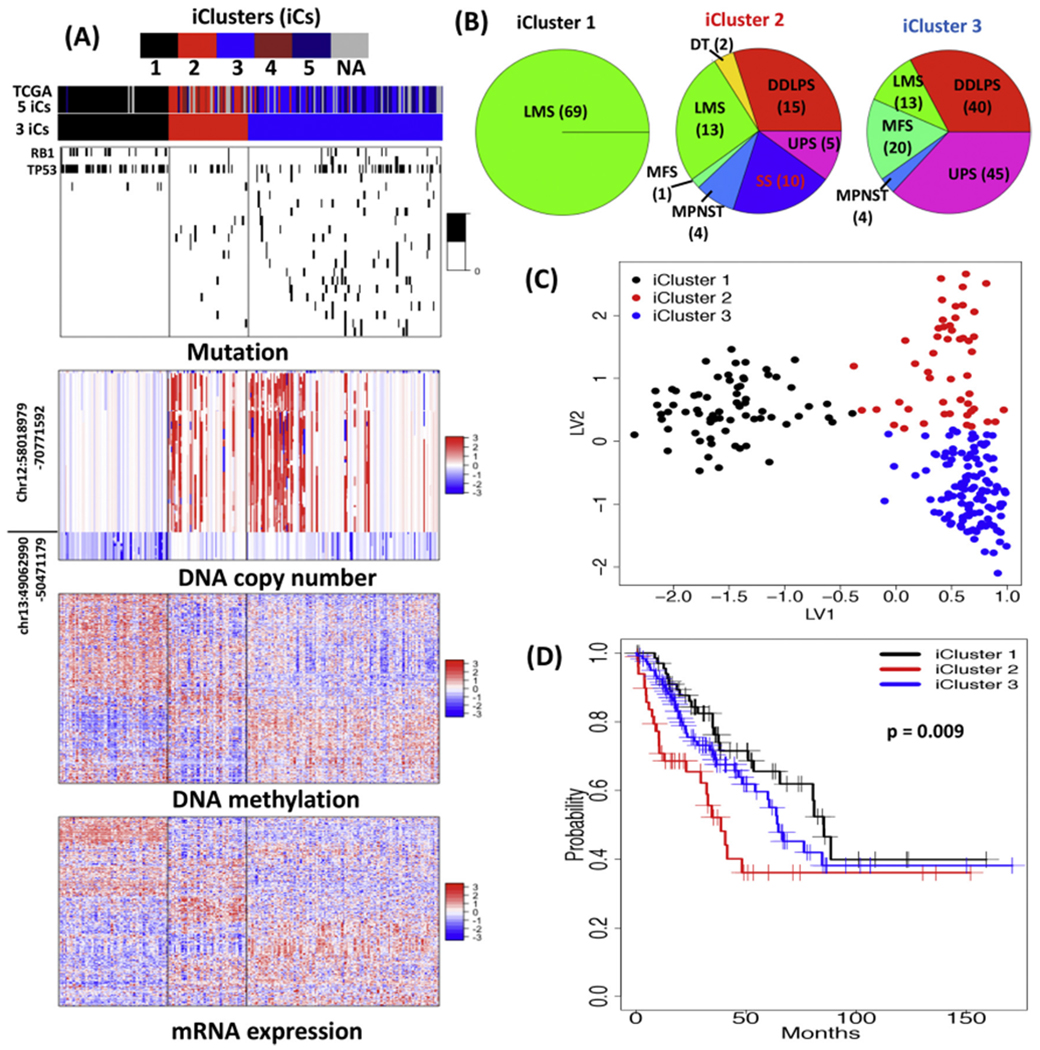
SARC iClusters. (A) Heatmaps of the driver omics features. The color bars on the heatmaps indicate the 3 iClusters and TCGA 5 iClusters12. Heatmaps from the top to bottom are for the mutation (black: mutated; white: normal), copy number (red: trend to amplification; white: normal; blue: trend to deletion), methylation (red: hyper-methylated; blue: hypo-methylated) and gene expression (red: high expression; blue: low expression), respectively. The driver genes from top to bottom on the mutation heatmap are RB1, RYR2, TP53, CAC1F, PTEN, MKI67, MYH7, MGAM, TRDN, KRTAP5-5, FAT3, CFTR, ZNF831, MYOCD, WNK2, DCC, PEG3, DSCAM, ASTN2, PAPPA, DH6, MYHB. (B) Numbers of sarcoma distributed in the 3 iClusters. DT: desmoid tumor; MPNST: malignant peripheral nerve sheath tumor. (C) Sample clusters on the two-dimensional latent spaces. LV: latent variable. (D) Kaplan-Meir survival curves of the 3 iClusters and Log-rank test p-value.

9. Conclusions

There are numerous challenges in completing genomic studies of rare cancers. In terms of statistical analysis of genomic studies, the primary challenge is the limited sample size for an adequately powered study. This review paper outlines and illustrates various approaches that can be leveraged to increase the power to detect biologically relevant genomic factors related to rare cancers. Many of these approaches involve some level of integration or aggregation, whether it involves combination of association signal across a set of studies (i.e. meta-analysis or horizontal integration), integration of information across multiple types of omic data (i.e., vertical integration), or aggregations of association signal in a pathway (i.e., pathway or gene set analysis). In completing horizontal integration or meta-analysis, consortiums are often developed to bring together multiple research groups to increase the sample size; however, care is needed in the analysis of consortium data to assess degree of heterogeneity and potential batch effects which can impact the interpretability of the statistical results. Most genomic studies involve unrelated individuals, but family-based studies that leverage the pedigree structure have been successfully applied to rare cancer genetic epidemiology studies. Lastly, leveraging all possible publicly available resources and information is an important consideration when planning and completing genomic studies of rare cancers.