THREE-WAY CLUSTERING OF MULTI-TISSUE MULTI-INDIVIDUAL GENE EXPRESSION DATA USING SEMI-NONNEGATIVE TENSOR DECOMPOSITION

Abstract

The advent of high-throughput sequencing technologies has led to an increasing availability of large multi-tissue data sets which contain gene expression measurements across different tissues and individuals. In this setting, variation in expression levels arises due to contributions specific to genes, tissues, individuals, and interactions thereof. Classical clustering methods are ill-suited to explore these three-way interactions and struggle to fully extract the insights into transcriptome complexity contained in the data. We propose a new statistical method, called MultiCluster, based on semi-nonnegative tensor decomposition which permits the investigation of transcriptome variation across individuals and tissues simultaneously. We further develop a tensor projection procedure which detects covariate-related genes with high power, demonstrating the advantage of tensor-based methods in incorporating information across similar tissues. Through simulation and application to the GTEx RNA-seq data from 53 human tissues, we show that MultiCluster identifies three-way interactions with high accuracy and robustness.

1. Introduction.

Owing to advances in high-throughput sequencing technology, multi-tissue expression studies have provided unprecedented opportunities to investigate transcriptome variation across tissues and individuals (Lonsdale et al. 2013; Melé et al. 2015; Hawrylycz et al. 2012). A typical multi-tissue experiment collects gene expression profiles (e.g. via RNA-seq or microarrays) from different individuals in a number of different tissues, and variation in expression levels often results from complex interactions among genes, individuals, and tissues (Melé et al. 2015). For example, a group of genes may perform coordinated biological functions in certain contexts (e.g. specific tissues or individuals), but behave differently in other settings through tissue- and/or individual-dependent gene regulation mechanisms.

Clustering has proven useful to reveal latent structure in high-dimensional expression data (Tibshirani et al. 1999; Lazzeroni and Owen 2002; Liu et al. 2008). Traditional clustering methods (such as K-means, PCA, and t-SNE (Maaten and Hinton 2008)) assume that gene expression patterns persist across one of the different contexts (either tissues or individuals), or assume that samples are i.i.d. or homogeneous. Direct application of these algorithms to multi-tissue expression data requires concatenating all available samples from different tissues into a single matrix, precluding potential insights into tissue × individual specificity (Bahcall 2015). Alternatively, inferring gene modules separately for each tissue ignores commonalities among tissues and may hinder the discovery of differentially-expressed (DE) genes that characterize tissues or tissue groups. Likewise, individuals vary by their biological attributes (such as race, gender, and age), and ignoring such heterogeneity impedes the accurate estimation of gene- and/or tissue-wise correlations. The development of a statistical method that integrates multiple modes (defined in Section 3) simultaneously is therefore essential for elucidating the complex biological interactions present in multi-tissue multi-individual gene expression data.

Several methods have been proposed in multi-tissue multi-individual expression studies, but they are often unable to fully exploit the three-mode structure of the data. Pierson et al. (2015) propose a hierarchical transfer learning algorithm to learn gene networks in which they first construct a global tissue hierarchy based on mean expression values and subsequently infer gene networks for each tissue conditioned on the tissue hierarchy. Dey, Hsiao and Stephens (2017) instead use topic models to cluster samples (i.e. tissues or individuals) and identify genes that are distinctively expressed in each cluster. Both algorithms take a two-step procedure to uncover expression patterns in tissues and genes. Other methods offer one-shot approaches by identifying subsets of correlated genes that are exclusive to, for example, female individuals. Gao et al. (2016) adopt the biclustering framework and propose decomposing the expression matrix into biclusters of subsets of samples and features with latent structure unique to the overlap of particular subsets. However, in the case of multi-tissue measurements across individuals, concatenating the data sample-wise to create a single expression matrix will not explore the three-way interactions among genes, tissues, and individuals. A more recent work (Hore et al. 2016) develops sparse decomposition of arrays (SDA) for multi-tissue expression experiments. Because their focus is not on clustering tissues or individuals, the proposed i.i.d. prior on individual/tissue loadings may not be suitable to detect tissue- and individual-wise correlation.

We address the aforementioned challenges by developing a tensor-based method, called MultiCluster, to simultaneously cluster genes, tissues, and individuals. As illustrated in Figure 1a, multi-tissue multi-individual gene expression measurements can be organized into a three-way array, or order-3 tensor, with gene, tissue, and individual modes. Our goal is to identify subsets of genes that are similarly expressed in subsets of tissues and individuals; mathematically, this reduces to detecting three-way blocks in the expression tensor (Figure 1b). We utilize the flexible tensor decomposition framework to directly identify gene modules in a tissue × individual specific fashion, which traditional clustering methods would struggle to capture.

Fig 1.

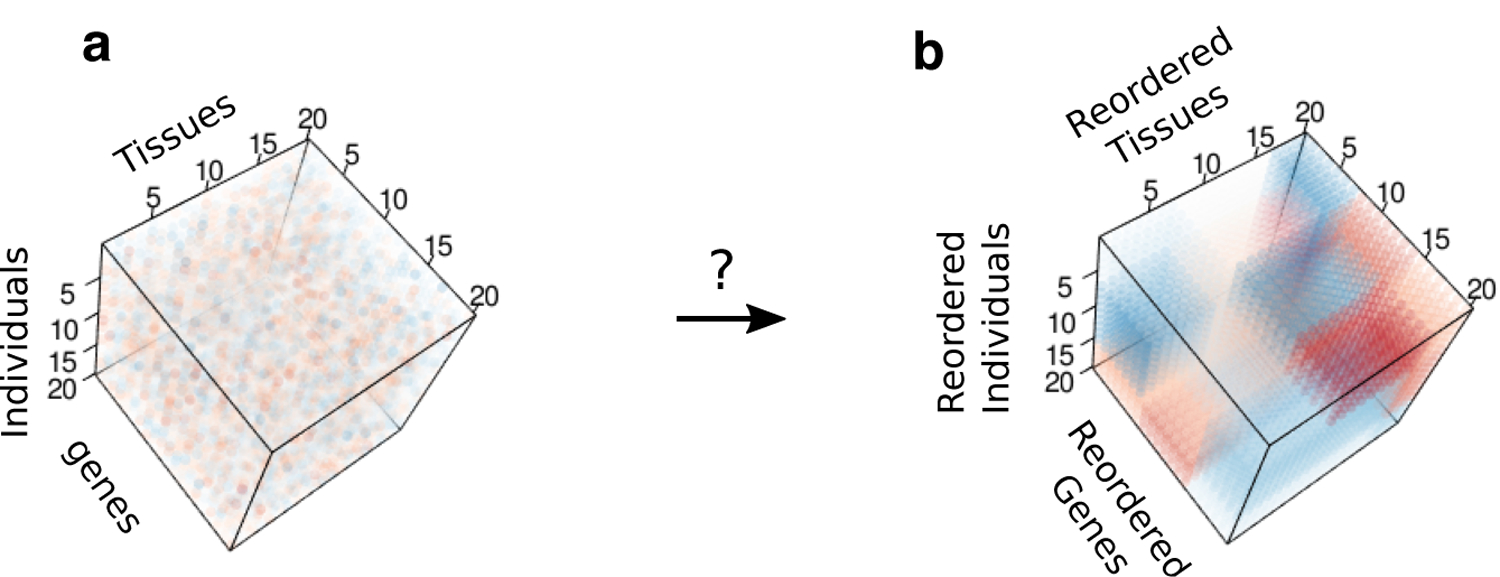
Three-way clustering problem. (a) Input tensor of gene expression. (b) Shuffled, de-noised output tensor containing local blocks. Both (a) and (b) are color images of a data tensor $\mathcal{Y}=〚Y_{ijk}]]$, with each entry colored according to the value of Y_ijk.

Our tensor decomposition method can be viewed as a generalization of matrix PCA. Compared to matrices, tensors provide greater flexibility to describe data but entail a higher computational cost. Indeed, extending familiar matrix concepts such as SVD to tensors is not straightforward (De Silva and Lim 2008; Kolda and Bader 2009; Wang et al. 2017), and the associated computational complexity has proven to be NP-hard (Hillar and Lim 2013). Motivated by recent advances in tensor decomposition (Anandkumar et al. 2014; Wang and Song 2017), we develop a robust clustering method to simultaneously infer common and distinctive gene expression patterns among tissues and individuals which utilizes triplets of sorted loading vectors in a constrained tensor decomposition. This approach handles heterogeneity in each mode and learns the clustering patterns across different modes of the data in an unsupervised manner analogous to PCA and SVD. In addition, we develop a tensor projection procedure which detects covariate-related genes with high power, demonstrating the advantage of tensor-based methods in incorporating information across similar tissues. When applied to the Genotype-Tissue Expression (GTEx) RNA-seq data, our method uncovers different types of gene expression modules, including (i) global, shared expression modules; (ii) expression modules specific to certain subsets of tissues; (iii) modules with differentially expressed genes across individual-level covariates (e.g., age, sex or race); and (iv) expression modules that are specific to both tissues and individuals.

Section 2 discusses the GTEx data set which serves as the motivating example for our method. Section 3 covers tensor preliminaries and presents our three-way clustering method via the use of semi-nonnegative tensor decomposition. We then describe the fitting procedure and develop a tensor projection method for detecting covariate-related genes. Section 4 presents simulation studies that compare our method with a number of alternatives. In Section 5 we describe the application of our method to the GTEx multi-tissue multi-individual gene expression data set. We conclude in Section 6 with a discussion of our findings and avenues for future work.

2. Motivating data set.

We demonstrate the usefulness of MultiCluster using the GTEx v6 gene expression data, which consist of RNA-seq samples collected from 544 individuals across 53 human tissues, including 13 brain subregions, adipose, heart, artery, skin, and more. These data are available from https://www.gtexportal.org/home/datasets. The experiment is described in detail in Lonsdale et al. (2013) and further in Melé et al. (2015). After cleaning and preprocessing the data as detailed in the Supplement (Wang, Fischer and Song 2018), gene expression measurements were organized into a gene × individual × tissue multi-way array $\mathcal{Y}\in {ℝ}^{n_G\times n_I\times n_T}$, where n_G = 18,481 (genes), n_I = 544 (individuals) and n_T = 53 (tissues).

The GTEx data set contains categorical clinical variables such as sex (n = 357 females vs. n = 187 males), race (n = 77 African Americans vs. n = 467 European Americans), and age (1st and 3rd age quantiles of 47 and 62, respectively). Given its inherent structure and levels of individual heterogeneity, this data set naturally lends itself to a tensor framework and allows us to systematically investigate multifactorial patterns of transcriptome variation.

3. Models and methods.

We begin by reviewing a few basic facts about tensors (Kolda and Bader 2009). We use $\mathcal{Y}=〚Y_{i_1{i}_2\dots i_k}〛\in {ℝ}^{d_1\times d_2\times \cdots \times d_k}$ to denote a (d₁, d₂, … , d_k)-dimensional real-valued tensor, where k corresponds to the number of modes of $\mathcal{Y}$ and is called the order. Given our intended application to multi-way gene expression data, we describe the method in the context of order-3 tensors, though it is also applicable to higher-order tensors. A tensor $\mathcal{Y}$ is called a rank one tensor if it can be written as an outer product of vectors such that $\mathcal{Y}=x\otimes y\otimes z$, where $x\in {ℝ}^{d_1}$, $y\in {ℝ}^{d_2}$, $z\in {ℝ}^{d_3}$, and ⊗ denotes the Kronecker product.

The inner product between two tensors $\mathcal{Y}=〚Y_{ijk}〛$ and ${\mathcal{Y}}^{\prime }=〚Y_{ijk}^{\prime }〛$ in ${ℝ}^{d_1\times d_2\times d_3}$ is the sum of the product of their entries given by

$$\langle \mathcal{Y},{\mathcal{Y}}^{\prime }\rangle =\sum _{i=1}^{d_1}\sum _{j=1}^{d_2}\sum _{k=1}^{d_3}{Y}_{ijk}{Y}_{ijk}^{\prime }.$$

The Frobenius norm of $\mathcal{Y}$ is defined as

$$\parallel \mathcal{Y}{\parallel }_F=\sqrt{\langle \mathcal{Y},\mathcal{Y}\rangle }={\left(\sum _{i=1}^{d_1}\sum _{j=1}^{d_2}\sum _{k=1}^{d_3}{Y}_{ijk}^2\right)}^{1/2}.$$

Following Lim (2005), we define the covariant multilinear matrix multiplication of a tensor $\mathcal{T}\in {ℝ}^{d_1\times d_2\times d_3}$ by matrix ${\mathit{M}}_1=〚m_{i{\mathcal{l}}_1}^{(1)}〛\in {ℝ}^{d_1\times s_1}$, ${\mathit{M}}_2=〚m_{j{\mathcal{l}}_2}^{(1)}〛\in {ℝ}^{d_2\times s_2}$, and ${\mathit{M}}_3=〚n_{k{\mathcal{l}}_3}^{(3)}〛\in {ℝ}^{d_3\times s_3}$ as

$$\mathcal{Y}\left({\mathit{M}}_1,{\mathit{M}}_2,{\mathit{M}}_3\right)=〚\sum _{i=1}^{d_1}\sum _{j=1}^{d_2}\sum _{k=1}^{d_3}{Y}_{ijk}{m}_{i{\mathcal{l}}_1}^{(1)}{m}_{j{\mathcal{l}}_2}^{(2)}{m}_{k{\mathcal{l}}_3}^{(3)}〛,$$

which results in a tensor in ${ℝ}^{s_1\times s_2\times s_3}$. When M₁ is an identity matrix, we often write $\mathcal{Y}\left(\cdot ,{\mathit{M}}_2,{\mathit{M}}_3\right)$ for brevity; similar shorthand rules apply to other modes. Note than when s₁ = 1, $\mathcal{Y}\left({\mathit{M}}_1,{\mathit{M}}_2,{\mathit{M}}_3\right)$ degenerates to an s₂-by-s₃ matrix, and when both s₁ = s₂ = 1, $\mathcal{Y}\left({\mathit{M}}_1,{\mathit{M}}_2,{\mathit{M}}_3\right)$ degenerates to a length-s₃ vector. Mildly abusing notation, we use symbols such as $\mathcal{Y}(\cdot ,\cdot ,k)$ to denote the k-th matrix slice of the tensor in which the first two indices may vary and the last index is held fixed for some 1 ≤ k ≤ d₃.

For ease of notation, we allow the basic arithmetic operators (+, −, ≥, etc) to be applied to pairs of vectors in an element-wise manner. We use the shorthand [n] to denote the n-set {1, … , n} for $n\in {\mathbb{N}}_{+}$.

3.1. Tensor decomposition model.

Figure 2 provides a schematic illustration of the MultiCluster method. In a multi-tissue multi-individual gene expression experiment, the data take the form of an order-3 tensor, $\mathcal{Y}=〚Y_{ijk}〛\in {ℝ}^{n_G\times n_I\times n_T}$, where Y_ijk denotes the expression value (possibly after a suitable transformation) of gene i measured in individual j and tissue k, n_G is the total number of genes, n_I is the total number of individuals, and n_T is the total number of tissues. We propose to model the expression tensor $\mathcal{Y}$ as a perturbed rank-R tensor,

$$\mathcal{Y}=\sum _{r=1}^R{\lambda }_r{G}_r\otimes I_r\otimes T_r+\mathcal{E},$$ (3.1)

where ${\lambda }_r\in {ℝ}_{+}$ are singular values; G_r, I_r, and T_r are norm-1 singular vectors in ${ℝ}^{n_G}$, ${ℝ}^{n_I}$, and ${ℝ}^{n_T}$, respectively; and $\mathcal{E}=〚E_{ijk}〛$ is a noise tensor with each entry E_ijk i.i.d. $N\left(0,{\sigma }_e^2\right)$. We refer to the loading vectors G_r, I_r, T_r as “eigen-genes”, “eigen-individuals”, and “eigen-tissues”, respectively.

Fig 2.

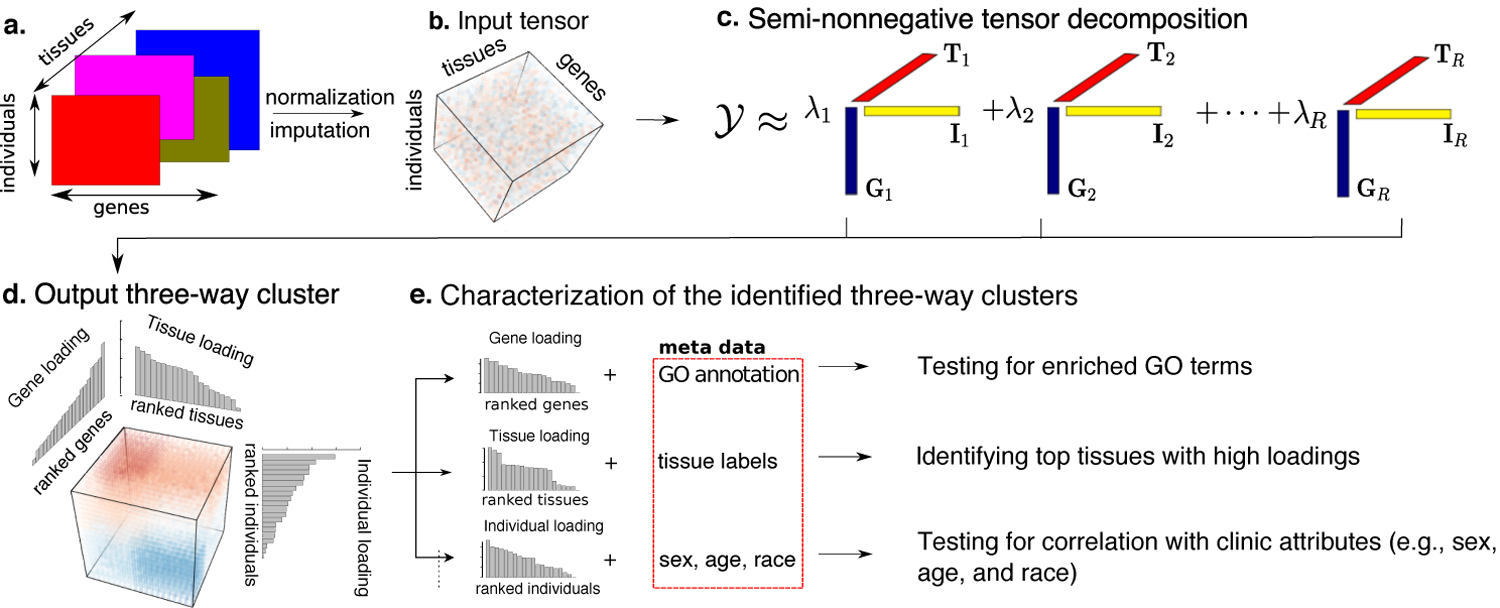
Schematic diagram of MultiCluster method. (a) Multi-tissue multi-individual gene expression data. (b) Input expression tensor after normalization and imputation. (c) Our method decomposes the expression tensor into a set of rank-1 tensors, G_r ⊗I_r ⊗T_r, where G_r, I_r, and T_r are, respectively, gene, individual, and tissue singular vectors. (d) Each three-way cluster is represented by the three sorted singular vectors. (e) We utilize metadata, such as gene ontology (GO) annotation, tissue labels, and individual-level covariates, to identify the sources of variation in each loading vector.

The rank-1 component G_r ⊗I_r ⊗ T_r in (3.1) can be interpreted as the basic unit of an expression pattern (called an expression module), in which the (i, j, k)-th entry of G_r ⊗I_r ⊗T_r is the multiplicative product of the corresponding entries in the three modes, i.e., (G_r ⊗I_r ⊗T_r)_(i,j,k) = G_r,iI_r,jT_r,k. The tissue loadings indicate the “activity” of the expression module r for each tissue. To facilitate the biological interpretation, we impose entry-wise nonnegativity conditions, T_r ≥ 0, on the tissue loading vectors T_r; the manner of execution and motivation for this constraint are discussed in Section 3.2. Note that no sign constraint is imposed on individual and gene loadings, so our method is flexible enough to handle mixed-sign data tensors. We refer to such constraints as “semi-nonnegative” tensor decomposition.

3.2. Estimation via optimization.

We wish to recover the tensor components of interest,

$$\left\{\left({\lambda }_r,{\mathit{G}}_r,{\mathit{I}}_r,{\mathit{T}}_r\right):{\Vert {\mathit{G}}_r\Vert }_2={\Vert {\mathit{I}}_r\Vert }_2={\Vert {\mathit{T}}_r\Vert }_2=1,{\lambda }_r>0,{\mathit{T}}_r\ge 0,r\in [R]\right\},$$

from the observation $\mathcal{Y}$. The negative log-likelihood under the Gaussian model (3.1) is equal (ignoring constants) to

$${\Vert \mathcal{Y}-\sum _{r=1}^R{\lambda }_r{G}_r\otimes I_r\otimes T_r\Vert }_F^2,$$ (3.2)

which will be the cost function in our estimation procedure. Before presenting the algorithm, we first state some conditions for the model identifiability. The first complication is the indeterminacy due to sign flips and permutation:

• Sign flips: changing the factors from (G_r, I_r, T_r) to (−G_r, −I_r, T_r) does not affect the likelihood.

• Permutation: applying permutation to the index set [R] does not affect the likelihood.

To deal with the above indeterminacy, we adopt the following convention. The sign of I_r is chosen such that ${\text{max}}_{j\in \left[n_I\right]}{I}_{r,j}={\text{max}}_{j\in \left[n_I\right]}\left|I_{r,j}\right|$ for all r ∈ [R]. Because of the nonnegativity constraints on T_r, this convention fixes the sign of I_r (and thus G_r). Furthermore, component indices are arranged such that λ₁ ≥ λ₂ ≥ ⋯ ≥ λ_R. In the degenerate case where not all eigenvalues are unique, we break ties by first choosing the module r with larger ${\text{max}}_{j\in \left[n_I\right]}{I}_{r,j}$.

The second complication comes from the possible non-uniqueness of tensor decomposition even after accounting for sign and permutation indeterminacy. Fortunately, we are able to utilize sufficient conditions for the uniqueness of tensor decomposition. These conditions were initially developed for unconstrained tensor decomposition, but they also apply to our semi-nonnegative tensor decomposition.

• (Kruskal 1977) A rank-R semi-nonnegative tensor decomposition is unique if k_G +k_T +k_I ≥ 2R+2, where k_G is the Kruskal-rank of the gene factor matrix G = [G₁, … , G_R], i.e., the maximum value k such that any k columns are linearly independent. The definitions for k_T and k_I are similar, except that the tissue factor matrix T = [T₁, … ,T_R] is nonnegative in our case.

• (De Lathauwer 2006) Suppose n_G > n_I > n_T (as in the GTEx data). If R ≤ n_T and R(R − 1) ≤ n_G(n_G − 1)n_I(n_I − 1)/2, then the rank-R semi-nonnegative tensor decomposition is unique for almost all such tensors except on a set of Lebesgue measure zero.

In parameter estimation, we decompose the tensor $\mathcal{Y}$ via successive rank-1 approximations coupled with deflation. Although successive rank-1 approximations of a tensor do not necessarily yield its best rank-R approximation, recent work shows that they provide a flexible estimation procedure with well-controlled error in many cases (Allen 2012; Mu, Hsu and Goldfarb 2015).

We modify our earlier algorithm (Wang and Song 2017) to solve for ${\widehat{\lambda }}_r$, ${\widehat{G}}_r$, ${\widehat{I}}_r$, ${\widehat{T}}_r$ via the following optimization:

$$\begin{gathered} \underset{{\lambda }_r,G_r,I_r,T_r}{\text{minimize}}{\Vert \mathcal{Y}-{\lambda }_r{G}_r\otimes I_r\otimes T_r\Vert }_F, \\ \text{ subject to }{\Vert G_r\Vert }_2={\Vert I_r\Vert }_2={\Vert T_r\Vert }_2=1,\text{ and }{T}_r\ge 0, \end{gathered}$$ (3.3)

where $\mathcal{Y}$ denotes either the original or residual tensor after deflation. As the optimization (3.3) is separable into each of its factors, we can optimize this in an iterative block-wise manner:

Property 1. Let (${\widehat{\lambda }}_r$, ${\widehat{G}}_r$, ${\widehat{I}}_r$, ${\widehat{T}}_r$) be the optimizer of (3.3). Then the following properties hold (assuming the denominators are non-zero):

$$\begin{gathered} {\widehat{\mathit{G}}}_r=\mathcal{Y}\left(\cdot ,{\widehat{\mathit{I}}}_r,{\widehat{\mathit{T}}}_r\right)/{\Vert \mathcal{Y}\left(\cdot ,{\widehat{\mathit{I}}}_r,{\widehat{\mathit{T}}}_r\right)\Vert }_2, \\ {\widehat{\mathit{I}}}_r=\mathcal{Y}\left({\widehat{\mathit{G}}}_r,\cdot ,{\widehat{\mathit{T}}}_r\right)/{\Vert \mathcal{Y}\left({\widehat{\mathit{G}}}_r,\cdot ,{\widehat{\mathit{T}}}_r\right)\Vert }_2, \\ {\widehat{\mathit{T}}}_r=\mathcal{Y}{\left({\widehat{\mathit{G}}}_r,{\widehat{\mathit{I}}}_r,\cdot \right)}_{+}/{\Vert \mathcal{Y}{\left({\widehat{\mathit{G}}}_r,{\widehat{\mathit{I}}}_r,\cdot \right)}_{+}\Vert }_2, \\ {\widehat{\lambda }}_r=\mathcal{Y}\left({\widehat{\mathit{G}}}_r,{\widehat{\mathit{I}}}_r,{\widehat{\mathit{T}}}_r\right), \end{gathered}$$ (3.4)

where a₊ := max(a, 0) and we allow this operator to be applied to vectors in an element-wise manner.

A proof is provided in Supplement (Wang, Fischer and Song 2018). The above result suggests an alternating optimization scheme. The tensor factors ${\widehat{G}}_r$, ${\widehat{I}}_r$ and ${\widehat{T}}_r$ are initialized using outputs from unconstrained tensor decomposition (Wang and Song 2017). Each factor is then updated alternatively while keeping the other two factors fixed. The update step requires solving a (either constrained or unconstrained) least-square problem and the optimal solution is given explicitly by the right-hand side of equality (3.4). In particular, the entry-wise nonnegativity of the tissue loading vectors ${\widehat{T}}_r$ is imposed by setting negative values of ${\widehat{T}}_r$ to 0. As each coordinate update reduces the objective function, which is bounded below by 0, convergence of this scheme is assured. After obtaining the r-th component (${\widehat{\lambda }}_r$, ${\widehat{G}}_r$, ${\widehat{I}}_r$, ${\widehat{T}}_r$), we take the residual tensor as the new input and repeat the algorithm to find the next component via the update $\mathcal{Y}\leftarrow \mathcal{Y}-{\widehat{\lambda }}_r{\widehat{G}}_r\otimes {\widehat{I}}_r\otimes {\widehat{T}}_r$. The full algorithm is provided in the Supplement (Wang, Fischer and Song 2018).

The requirement of nonnegative tissue loadings effectively introduces zeros in the vector ${\widehat{T}}_r$; a sparse ${\widehat{T}}_r$ implies that the module r is active in only a few tissues, whereas a dense ${\widehat{T}}_r$ implies that the module r is common to several tissues. Without the nonnegativity constraint, it is possible, and in our experience likely, that each ${\widehat{T}}_r$ contains two tissue groups: one corresponding to positively-loaded tissues and one to negatively-loaded tissues. Consequently, gene and individual loading patterns become less interpretable due to ambiguities in the identity of the tissue group with which they are associated.

Before concluding this section, we briefly comment on two implementation details. First, the algorithm assumes that R is given. In practice, the rank R is often unknown and must be determined from the data $\mathcal{Y}$. There are many heuristics developed for choosing R in the matrix case, and similar ideas can be adopted here. For example, one can plot the sum of squared residuals (3.1) as a function of R and identify the elbow point in the curve. Second, when some entries Y_ijk are missing, tensor decomposition is not well-defined. In such a case, one could instead use the cost function ${{\sum }_{[i,j,k]\in \Omega }\left(Y_{ijk}-{\sum }_r{\lambda }_r{G}_{r,i}{I}_{r,j}{T}_{r,k}\right)}^2$, where Ω ⊂ [n_G] × [n_I] × [n_T] is the index set for non-missing entries. To implement this, we iteratively approximate missing data with fitted values based on current parameter estimates and proceed with the algorithm until convergence. This procedure has been commonly used in matrix factorization (Lee, Huang and Hu 2010; Lee and Huang 2014), and we adopt it for tensor factorization.

3.3. Characterizing expression modules.

For each expression module 1 ≤ r ≤ R, we propose a straightforward procedure to characterize the biological significance of the loading vectors ${\widehat{G}}_r$, ${\widehat{I}}_r$, and ${\widehat{T}}_r$. For ease of presentation, in what follows we drop the subscript r and simply write $\widehat{G}$, $\widehat{I}$, and $\widehat{T}$.

3.3.1. GO enrichment based on gene loadings.

Let $\widehat{G}={\left({\widehat{G}}_1,\dots ,{\widehat{G}}_{n_G}\right)}^T$ be the estimated eigen-gene. Genes with extreme loadings contribute more to this module, and we are particularly interested in the overexpressed and underexpressed gene clusters ${\mathcal{G}}_{\text{top }}=\left\{i\in \left[n_G\right]:{\widehat{G}}_i\ge c_{\text{top }}\right\}$ and ${\mathcal{G}}_{\text{bottom }}=\left\{i\in \left[n_G\right]:{\widehat{G}}_i\le c_{\text{bottom }}\right\}$, respectively, where c_top and c_bottom are thresholds which control the cluster sizes.

We use a permutation-based procedure (see Supplement (Wang, Fischer and Song 2018)) to determine the cut-off values at significance level α = 0.05. To characterize the biological significance of the declared gene clusters, we perform gene ontology (GO) enrichment analyses among both the overexpressed and underexpressed genes. A standard test for enrichment is to conduct a hypergeometric test for each GO, and we employ such a procedure to identify GO terms that are overrepresented in the gene clusters ${\mathcal{G}}_{\text{top }}$ and ${\mathcal{G}}_{\text{bottom }}$. The Benjamini-Hochberg correction (Benjamini and Hochberg 1995) is applied to the set of enrichment p-values to account for multiple hypothesis testing.

3.3.2. Covariate effects on individual loadings.

To identify the sources of variation in the individual loadings, we consider the following linear model for the estimated eigen-individual $\widehat{I}={\left({\widehat{I}}_1,\dots ,{\widehat{I}}_{n_I}\right)}^T$:

$$\widehat{I}=X\beta +\epsilon ,$$ (3.5)

where X represents the n_I-by-p covariate matrix including the intercept, β = (β₁, … ,β_p)^T represents the column vector of unknown coefficients, and the error vector satisfies $\mathbb{E}(\epsilon )=0$ and $\text{Var}(\epsilon )={\sigma }^2{I}_{n_I\times n_I}$.

If one wishes to test whether covariate ℓ (1 ≤ ℓ ≤ p) affects the expression of the candidate gene, the following hypothesis test can be carried out:

$${\mathcal{H}}_0:{\beta }_{\mathcal{l}}=0\text{ vs. }{\mathcal{H}}_{\alpha }:{\beta }_{\mathcal{l}}\ne 0.$$

To perform this test we use the standard Wald statistic, which under weak assumptions (i.e., the first two moments concerning the means and variance-covariance matrix of ε) asymptotically follows a standard normal distribution, permitting approximate inference in large samples. We declare expression modules as “age-, sex-, or race-related” if the eigen-individual loadings are significantly correlated with age, sex, or race, respectively. Upon fitting the model (3.5), we calculate the proportion of variance explained by each covariate using ANOVA.

3.3.3. Tensor projection for detecting tissue-specific differentially expressed (DE) genes.

Let $\widehat{T}={\left({\widehat{T}}_1,\dots ,{\widehat{T}}_{n_T}\right)}^T$ be the estimated eigen-tissue. Recall that the nonnegative tissue loading ${\widehat{T}}_i$ indicates the strength of tissue i in this expression module. We define $\mathcal{Y}(\cdot ,\cdot ,\widehat{T})$ to be the tensor projection of $\mathcal{Y}$ through the eigen-tissue $\widehat{T}$,

$$\mathcal{Y}(\cdot ,\cdot ,\widehat{T})=\sum _{k=1}^{n_T}{\widehat{T}}_k\mathcal{Y}(\cdot ,\cdot ,k).$$

Note that $\mathcal{Y}(\cdot ,\cdot ,\widehat{T})$ is an n_g-by-n_I matrix, with each entry encoding the weighted average of gene expression across tissues.

Given a candidate gene to be tested for covariate-association, we propose the following linear model:

$$\mathcal{Y}(\text{test gene},\cdot ,\widehat{T})=X\beta +\epsilon ,$$

where $\mathcal{Y}(\text{test gene},\cdot ,\widehat{T})\in {ℝ}^{n_I}$ denotes the row in $\mathcal{Y}(\cdot ,\cdot ,\widehat{T})$ corresponding to the test gene, Xβ represents the intercept and covariate (such as age, sex, and race) effects of interest, and the error vector ε satisfies $\mathbb{E}(\epsilon )=0$ and $\text{Var}(\epsilon )={\sigma }^2{I}_{n_I\times n_I}$. Here we take the tensor projection $\mathcal{Y}(\text{test gene},\cdot ,\widehat{T})$ as the response variable and test for the covariate effects. Such an analysis differs from (3.5) in that the detected covariate effect corresponds to a single gene rather than the overall gene module. By examining the entries of the tissue vector $\widehat{T}$, we can infer which tissues drive the signal of differential expression.

4. Numerical comparison.

We now compare our method with several competing approaches.

4.1. A simple example.

As a basic illustration, we generated an expression tensor consisting of 60 genes, 20 individuals and 10 tissues. The 20 individuals were partitioned into two groups (“young” vs. “elderly”), each of size 10. The genes and tissues were each partitioned into three groups (denoted by A, B, C). The mean expression value for each block is described in Table 1. Such pattern represents the tissue-specific DE structure across individuals. In particular, the Gene Group A are age-downregulated in Tissue Group A but are age-upregulated in Tissue Group B. The Gene Group B are age-downregulated in both Tissue Groups B and C but with different effect sizes. The Gene Group C are age-downregulated in only Tissue Group C. All other gene-by-tissue combinations have no age effects. Finally, independent N(0, 1) noise was added to every entry of the tensor.

Table 1.

Mean expression value of the illustrative tensor.

	Tissue Group A		Tissue Group B		Tissue Group C
Gene╲Individual	Young	Elderly	Young	Elderly	Young	Elderly
Gene Group A	1	−1	−1	1	0	0
Gene Group B	0	0	0.5	−0.5	0.1	−0.1
Gene Group C	0	0	0	0	0.5	−0.5

This example represents a challenging scenario in which traditional methods may fail. For example, if we average the expression over individuals and apply matrix PCA to the resulting data, then neither the mode-specific grouping nor the three-way interaction can be recovered. In fact, matrix PCA (Figure 3a) reveals little information on the gene/tissue clustering. This is because the matricization destroys the three-way structure encoded in the higher-order tensor data.

Fig 3.

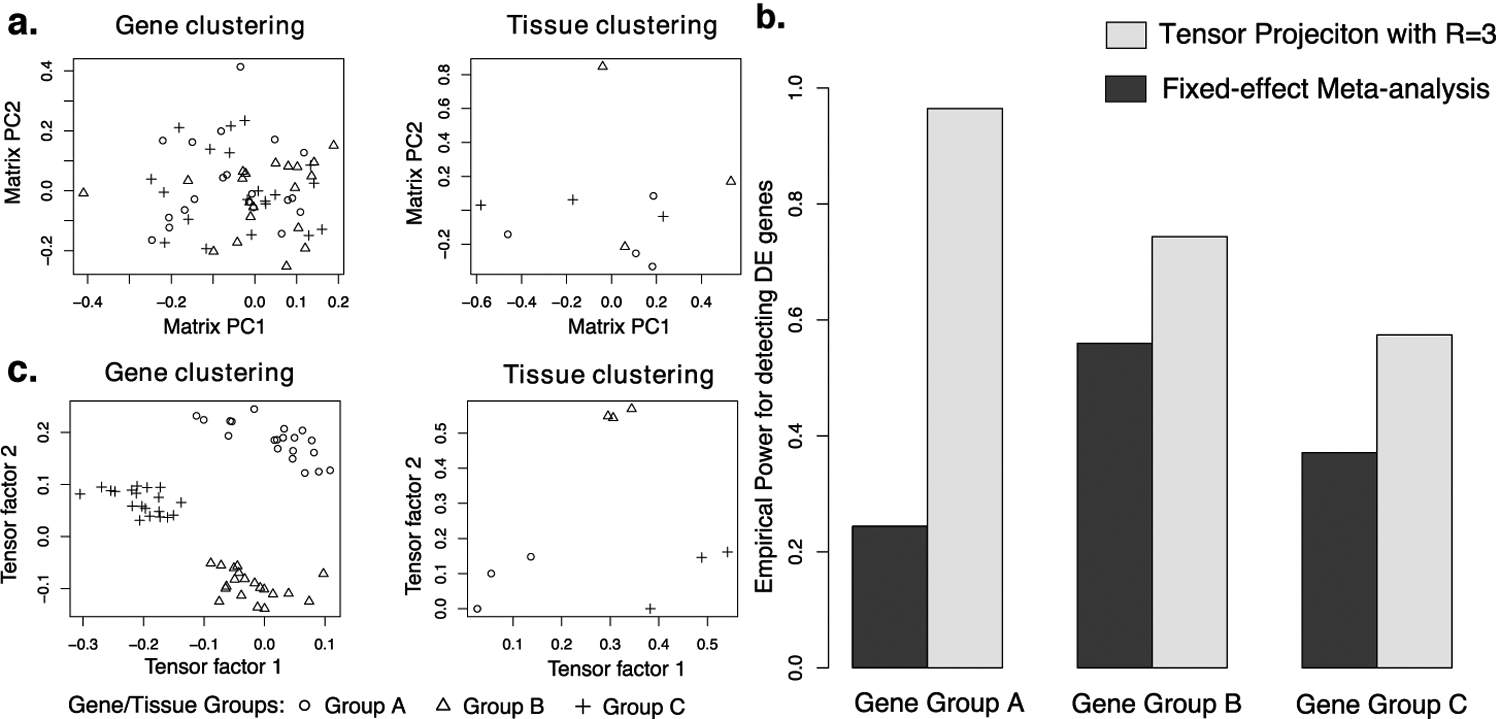
Performance comparison for the illustrative example. (a) First two gene/tissue factors in the matrix PCA. (b) Power comparison for detecting age effects in three gene groups. (c) First two gene/tissue factors in the tensor decomposition.

The standard (fixed-effect) meta-analysis also suffers from low power for detecting DE genes in this example. To see this, we tested the age effects in each tissue separately and combined the test statistics into a pooled estimate using z-score method (Kelley and Kelley 2012). This approach detected few DE genes in group A and also exhibited limited power in groups B and C (Figure 3b). The meta-analysis’ poor performance is due to the tissue-specificity of DE genes: genes in Gene Group A have opposite age effects in two of the tissue groups, so the signals partially cancel out; moreover, genes in Gene Groups B and C have age effects in only subsets of tissues, potentially diluting observed DE patterns.

In contrast to matrix PCA, the factors from our tensor decomposition ably capture the true clustering patterns (Figure 3c). Furthermore, tensor projection significantly improves detection power across all three gene groups (Figure 3b). As the tissue loadings are used as the weights in the tensor projection (Section 3.3.3), testing based on eigen-tissues allows us to test for age effects in a group-specific fashion. Consider Gene Group A as an example. Genes in this group have opposite age effects in Tissue Groups A and Group B. Since the first eigen-tissue has nearly-zero loadings in Tissue Group A, it only contains information about differential expression in Tissue Group B without including unwanted noise from Tissue Group A. This toy example demonstrates the ability of MultiCluster to improve detection power by automatically identifying similar tissues and borrowing information among them.

4.2. Accuracy of three-way clustering.

We also performed more extensive simulations to evaluate the ability of MultiCluster to perform multi-way clustering. Since matrix methods may perform poorly in such cases (see Section 4.1), we focus our attention on tensor-based methods. Specifically, we compare MultiCluster with: (i) sparse decomposition of arrays (SDA) (Hore et al. 2016) and (ii) tensor higher-order singular value decomposition (HOSVD) (Omberg, Golub and Alter 2007).

Both MultiCluster and SDA are built upon the Canonical Polyadic decomposition (Hitchcock 1927), which decomposes a tensor into a sum of rank-1 tensors. Conversely, HOSVD is based on the Tucker decomposition (Tucker 1966), which factorizes a tensor into a core tensor multiplied by orthogonal matrices in each mode.

We simulated noisy expression tensors $\mathcal{Y}=〚Y_{ijk}〛\in {ℝ}^{500\times 50\times 10}$ with three-way blocks from models which are detailed in the next paragraph. In each tensor, we created five gene clusters, four individual clusters, and three tissue clusters. Block means {μ_lmn} were generated according to the following two block models (as well as sparse versions):

1. Additive-mean model: ${\mu }_{lmn}={\mu }_l^g+{\mu }_m^i+{\mu }_n^t$, where ${\mu }_l^g,{\mu }_m^i$, and ${\mu }_n^t$ represent the marginal means for gene cluster l, tissue cluster m, and individual cluster n, respectively.

2. Multiplicative-mean model: ${\mu }_{lmn}={\mu }_l^g{\mu }_m^i{\mu }_n^t$, where the notation remains the same.

The marginal means (${\mu }_l^g$, ${\mu }_m^i$ and ${\mu }_n^t$) were drawn independently from a N(1, 1) distribution. Let ${\mathcal{Y}}_{\text{true }}$ denote the noiseless tensor with three-way block means generated from each of the above schemes, i.e., ${\mathcal{Y}}_{\text{true }}(i,j,k)={\mu }_{lmn}$ when i is in block l, j in block m, and k in block n. For both the additive- and multiplicative-mean models, we also considered a sparse setting in which expression matrices ${\mathcal{Y}}_{\text{true }}(i,\cdot ,\cdot )$ were zeroed out for 90% of genes i = 1, … ,500. The observed expression data were then simulated as $\mathcal{Y}={\mathcal{Y}}_{\text{true }}+\mathcal{E}$, where $\mathcal{E}\in {ℝ}^{500\times 50\times 10}$ is a random Gaussian tensor with i.i.d. N(0, σ²) entries. We assessed the recovery accuracy of each algorithm using the relative error, defined as

$$\text{RelErr}=\underset{R\le 10}{\text{min}}\frac{{\Vert {\widehat{\mathcal{Y}}}_{\text{est},R}-{\mathcal{Y}}_{\text{true}}\Vert }_F^2}{{\Vert {\mathcal{Y}}_{\text{true}}\Vert }_F^2},$$

where ${\widehat{\mathcal{Y}}}_{\text{est},R}$ denotes the rank-R approximation obtained from tensor decomposition.

The simulation models we consider here span a range of scenarios. The additive-mean model can be viewed as an extension of the plaid model for biclustering (Lazzeroni and Owen 2002) to three-way clustering while the multiplicative-mean model is a special case of the tensor decomposition model (3.1). The sparse setting represents a realistic scenario in RNA-seq studies in which a high number of genes are lowly expressed across individuals and tissues. As we designed these simulations to potentially violate the modeling assumptions in (3.1), they are well suited to evaluate the robustness of each method.

As seen in Figure 4, MultiCluster is able to recover the block structure well in all scenarios, demonstrating its robustness to model misspecification. In particular, the recovery error of MultiCluster grows noticeably more slowly than that of SDA in the non-sparsity settings (Figure 4a and Figure 4b). One possible explanation is that SDA is designed to cluster genes rather than tissues and individuals, so the i.i.d. prior imposed on tissues/individuals may not be optimized to detect local blocks, especially when the blocks are small. Another possibility is the algorithmic stability of MultiCluster relative to SDA; the latter usually requires multiple restarts in order to reduce spurious components (Hore et al. 2016). We also found that, even in the sparse settings, MultiCluster compares favorably with the other two methods (Figure 4c and Figure 4d). Note that these three methods adopt different regularization schemes: tissue nonnegativity for MultiCluster, gene sparsity for SDA, and orthogonality for HOSVD. Our results suggest the flexibility of MultiCluster to handle a range of models.

Fig 4.

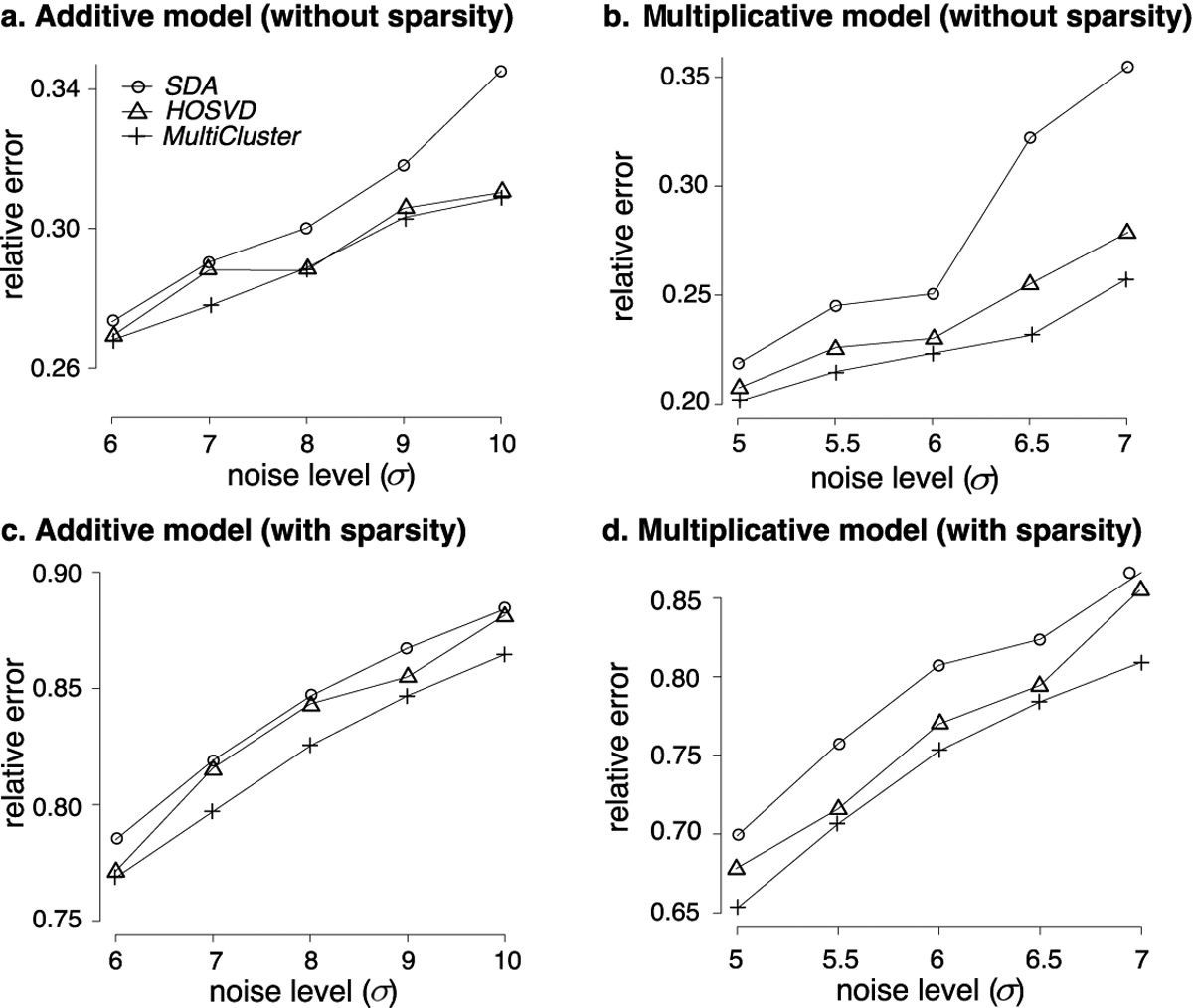
Recovery accuracy of different tensor-based methods. MultiCluster achieves the lowest error rates.

4.3. Power to detect differentially-expressed genes.

To study how our tensor projection procedure affects the detection of covariate-associated gene expression, we simulated age-related genes. This required modifying the earlier additive model to

$$Y_{ijk}={\mu }_l^g+{\mu }_{[i:n]}\text{Age}(j)+{\mu }_n^t+{\epsilon }_{ijk},\text{ where }{\epsilon }_{ijk}\stackrel{\text{ i.i.d}}{~}N(0,1),$$ (4.1)

where Y_ijk denotes the expression level of gene i, individual j, and tissue k; ${\mu }_l^g$ and ${\mu }_n^t$ denote the same parameters as before (the marginal means for gene cluster l = l(i) and tissue cluster n = n(k)); and

$${\mu }_{[i:n]}\stackrel{\text{i.i.d.}}{~}\{\begin{array}{ll}\text{Unif}[\alpha ,\beta ],\hfill & \text{ if gene }i\text{ is age-related in the tissue cluster }n\text{ , }\hfill \\ 0,\hfill & \text{otherwise.}\hfill \end{array}$$

We again simulated 50 tensors $\mathcal{Y}\in {ℝ}^{500\times 50\times 1}$. In each tensor, we planted five gene clusters plus three tissue clusters and further assigned 100 genes to be age-related. We considered two parameter settings: 1) α = 0, β = 0.06, i.e., age effects are in the same direction, and 2) α = −0.06, β = 0.06, i.e., age effects are in the opposite direction. Individual ages were drawn i.i.d. from Unif[40, 70]. The final expression data were generated based on model (4.1).

We decomposed each simulated tensor into R = 3 and 10 components and applied our tensor-projection procedure to test for age-relatedness. We declared a gene age-related if its p-value was less than the nominal significance level in at least one of the R eigen-tissues. To compare to single-tissue tests, we performed standard linear regressions in each tissue separately and declared a gene age-related if its p-value was less than the nominal level in at least one of the 10 tissues. We also performed a fixed-effect meta-analyses by aggregating the age effects across single-tissue tests using z-score method. Neither SDA (Hore et al. 2016) nor HOSVD (Omberg, Golub and Alter 2007) allow association tests on single-gene bases, so we did not consider them here.

Figure 5 shows the receiver operating characteristic (ROC) curves for each method. We found that the testing procedure based on tensor projection had higher detection power than single-tissue analyses, demonstrating the advantage gained when tensor-based methods incorporate information from similar tissues. Notably, the power appears stable when the decomposition rank R increases from 3 (the number of latent tissue groups) to 10 (the number of total tissues). We note that the power of a meta-analysis relies on genes being age-related in several tissues with effects primarily in the same direction (Figure 5a). Violations of these assumptions may well arise in practical applications and result in substantial losses in power (Figure 5b). In contrast, our tensor approach teases apart tissue-specific expression patterns by using eigen-tissues to synthesize information from sufficiently similar tissues. Subsequent examination of the entries of eigen-tissues allows one to determine in which tissues DE patterns are present, something that requires additional steps in meta-analyses.

Fig 5.

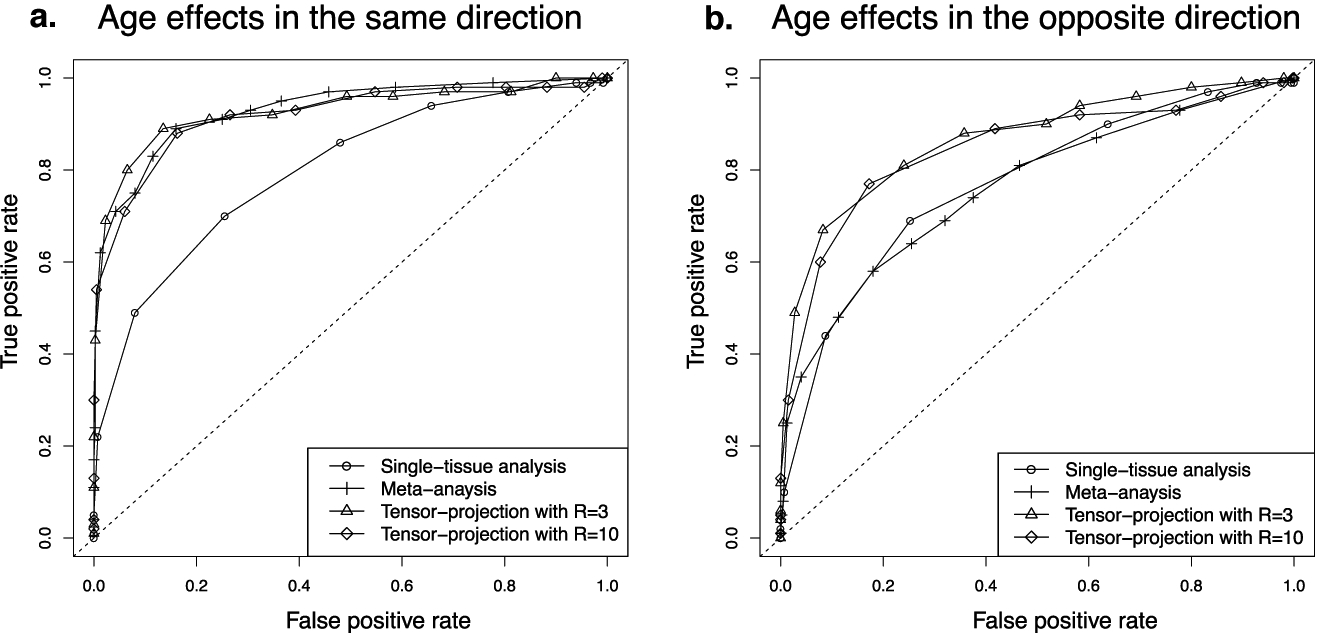
ROC curves for detecting age-related genes. The ROC curves were obtained under various nominal significance levels using 50 simulations.

4.4. Run time.

To compare the computational performance of each algorithm, we simulated a large order-3 tensor of 18,000 genes × 500 individuals × 40 tissues as these dimensions mimic those of the processed GTEx RNA-seq data set. We then recorded the run times for each method when decomposing the tensor into 10 components. We found that MultiCluster is computationally competitive with HOSVD while being more computationally efficient than SDA. In particular, it took ≈ 1.6 hours for HOSVD, ≈ 1.7 hours for MultiCluster, and ≈ 20.1 hours for SDA to complete the task.

5. Analysis of GTEx RNA-seq data.

The GTEx V6 gene expression data consist of RNA-seq samples collected from 544 human individuals spanning 53 tissues. Prior to analysis, we performed a standard data processing procedure described in depth in the Supplement (Wang, Fischer and Song 2018). Briefly, these steps included correction for sequencing depth, removal of lowly expressed genes, log transformation of the data, correction for nuisance variation arising due to technical effects, removal of sex-specific tissues, and imputation of missing data. We focus here on two tissue collections, one consisting of 44 somatic tissues and the other consisting of 13 brain tissues. Results for other tissue groups can be found in the Supplement (Wang, Fischer and Song 2018).

5.1. Analysis of 44 somatic tissues.

To interrogate the dominant features in the human transcriptome, we performed a global clustering analysis to identify gene × tissue × individual expression modules in 44 somatic tissues by applying MultiCluster to the GTEx tensor after excluding Y chromosome genes and sex-specific tissues. Supplemental Table S1 summarizes the top expression modules.

5.1.1. Component I: shared, global expression.

Tissues with positive loadings in a given eigen-tissue are said to be active in the associated module. As expected, the first eigen-tissue and eigen-individual are essentially flat (Supplemental Table S1), so this expression module captures baseline global expression common to all samples. The top genes in the corresponding eigen-gene (Supplemental Table S1) are mainly mitochondrial genes (15/20 top genes), comporting with their high transcription rates and the large number of mitochondria within most cells (Melé et al. 2015). In addition, we detected several non-mitochondrial genes, most of which are related to essential protein synthesis functions and eukaryotic cell activities (Supplemental Table S1). For example, ACTB encodes highly conserved proteins and is known to be involved in various types of cell motility (Fishilevich et al. 2016). Two other nuclear genes, EEF1A1 and EEF2, encode eukaryotic translation elongation factors, and their isoforms are widely expressed in the brain, placenta, liver, kidney, pancreas, heart, and skeletal muscle (Fishilevich et al. 2016).

5.1.2. Component II: brain tissues.

The second eigen-tissue clearly separates brain tissues from non-brain tissues, with the pituitary gland being the only non-brain tissue in the cluster (Figure 6a). We note that while not explicitly labeled as a brain tissue, the pituitary gland protrudes from the base of the brain. The sharp decline in tissue loadings (Figure 6a) highlights the distinctive expression pattern in the brain. We found that, in the eigen-individual (Figure 6c and Figure 6e), age explains more variation (24.4%, p < 2 × 10⁻¹⁶) than sex (0.3%, p = 0.12) or race (4.3%, p = 2.3 × 10⁻⁸). The eigen-gene (Figure 6b) produces a gene clustering that is biologically coherent with aging signals in the brain (Yang et al. 2015), and we observed an enrichment of genes associated with the glutamate receptor signaling pathway (p = 1.2 × 10⁻²⁰), chemical synaptic transmission (p = 1.8×10⁻¹⁶), excitatory postsynaptic potential (p = 2.4×10⁻¹⁶), and memory (p = 1.2 × 10⁻¹¹) (Figure 6d). Among the 899 genes in this cluster, we identified 675 age-related genes using tensor-projection (with significance threshold α = 10⁻³/899 ≈ 10⁻⁷ via Bonferroni correction), 556 of which exhibit decreased expression with age. The association of brain disease and neurological disorders with age is well-documented, and our findings support that aging affects brain tissues in a manner not shared by other tissues. We present further evidence of multi-way clustering in the brain in Section 5.2.

Fig 6.

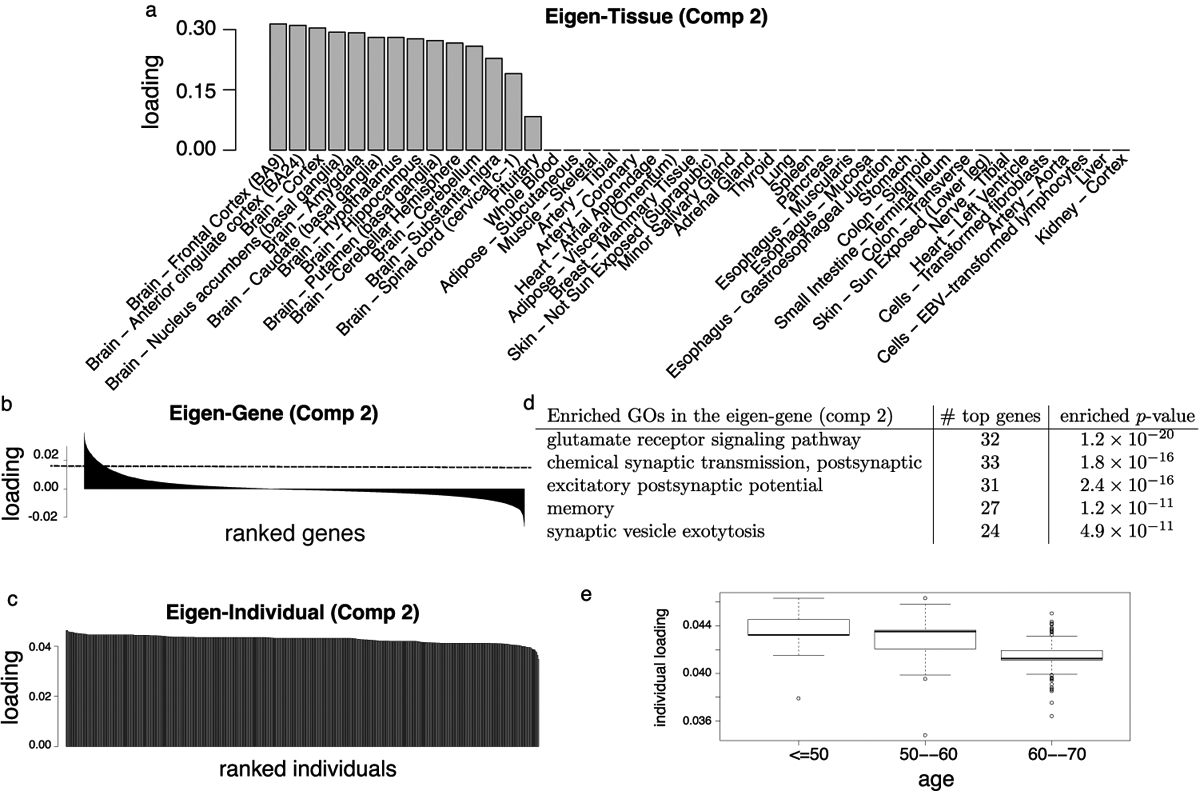
Expression module II: brain tissues. (a) Barplot of the sorted tissue loading vector. (b) Barplot of the sorted gene loading vector, where the dotted line represents the threshold for the top genes. (c) Barplot of the sorted individual loading vector. (d) Enriched GO annotations among the top 899 genes identified from the gene loading vector. Enrichment p-values are obtained from hypergeometric tests with BH correction. (e) Boxplot of individual loadings against age.

5.1.3. Component III: tissues involved in immune response.

The third component captures an expression module heavily loaded on tissues with roles in the immune system. The eigen-tissue is led by two blood tissues (whole blood and EBV-transformed lymphocytes), the spleen, and the liver (Supplemental Table S1). These tissues mediate the direct immune response (whole blood and lymphocytes), production and storage of antibodies (spleen), and filtering of antigens (spleen and liver). Correspondingly, the eigen-gene loads heavily on immunity-related genes (e.g. IGHM, FCRL5, IGJ, MS4A1) (Supplemental Table S1). The eigen-individual does not correlate with any covariate as strikingly as the brain does with age, but we do find a significant correlation with race (explaining 4.5% variation among individuals, p = 5.8 × 10⁻⁷; Supplemental Table S1). The top genes in the eigen-gene are functionally related to the B cell receptor signaling pathway (p = 3.0×10⁻¹⁵), humoral immune response mediated by circulating immunoglobulin (p = 7.5×10⁻¹³), phagocytosis recognition (p = 5.3×10⁻¹⁰), and plasma membrane invagination (p = 2.1 × 10⁻⁹) (Supplemental Table S1).

5.1.4. Other expression modules identified in the global analysis.

Like modules II and III, each of the remaining expression modules is active in only a subset of tissues, indicating the presence of tissue specificity (Supplemental Table S1). These detected modules are specific to artery (tibial, aorta, coronary), skin (exposed and non-exposed), cell lines (EBV-transformed lymphocytes and transformed fibroblasts), liver, muscle (skeletal and cardiac), and cerebellar regions (Supplemental Table S1). Of note is the strong signal of gender-related differential expression in the cerebellum. As seen in Supplemental Table S1, the enriched gene ontologies are consistent with the functions of the associated tissues. For example, the artery-specific module is enriched with collagen catabolic/metabolic genes, the skin-specific module is enriched with keratin-related genes, the two cell lines are enriched with genes responsible for cell division (e.g. chromosome segregation, meiosis, sister chromatid segregation). Conversely, most eigen-individuals have limited descriptive power compared to eigen-genes and eigen-tissues (Supplemental Table S1). This was expected because variation in gene expression is usually lower among individuals than among tissues (Melé et al. 2015). Consequently, we turned our attention to smaller tensors of similar tissues to fully showcase MultiCluster’s three-way clustering capabilities.

5.2. Brain transcriptome data.

Although our global analysis successfully uncovers distinctive expression patterns in the GTEx data, it may miss finer-scale structure within similar tissues or within similar individuals because of the high degree of inter-tissue heterogeneity. In order to reveal the crucial individual × tissue specificity, we considered 13 brain tissues and applied MultiCluster to the resulting tensor, revealing substantial individual-level variation most notably associated with age.

5.2.1. Comparison with other tensor methods.

Figure 7 shows the top six expression components for the brain tensor identified by MultiCluster. To assess the goodness-of-fit, we plotted the sum of squared residuals (see equation (3.2)) as a function of rank R (Supplemental Figure S1). Visual inspection suggested R = 6 in our case. We also applied HOSVD and SDA to the brain tensor; the results are summarized in Supplemental Figures S2 and S3. Both MultiCluster and HOSVD successfully clustered the 13 tissues into functionally similar groups, while SDA failed in tissue clustering. Furthermore, MultiCluster enjoyed better interpretability as it yielded sparse tissue factors. In particular, we found that most expression modules are spatially restricted to specific brain regions, such as the two cerebellum tissues (component 2), three cortex tissues (component 4), and three basal ganglia tissues (component 5).

Fig 7.

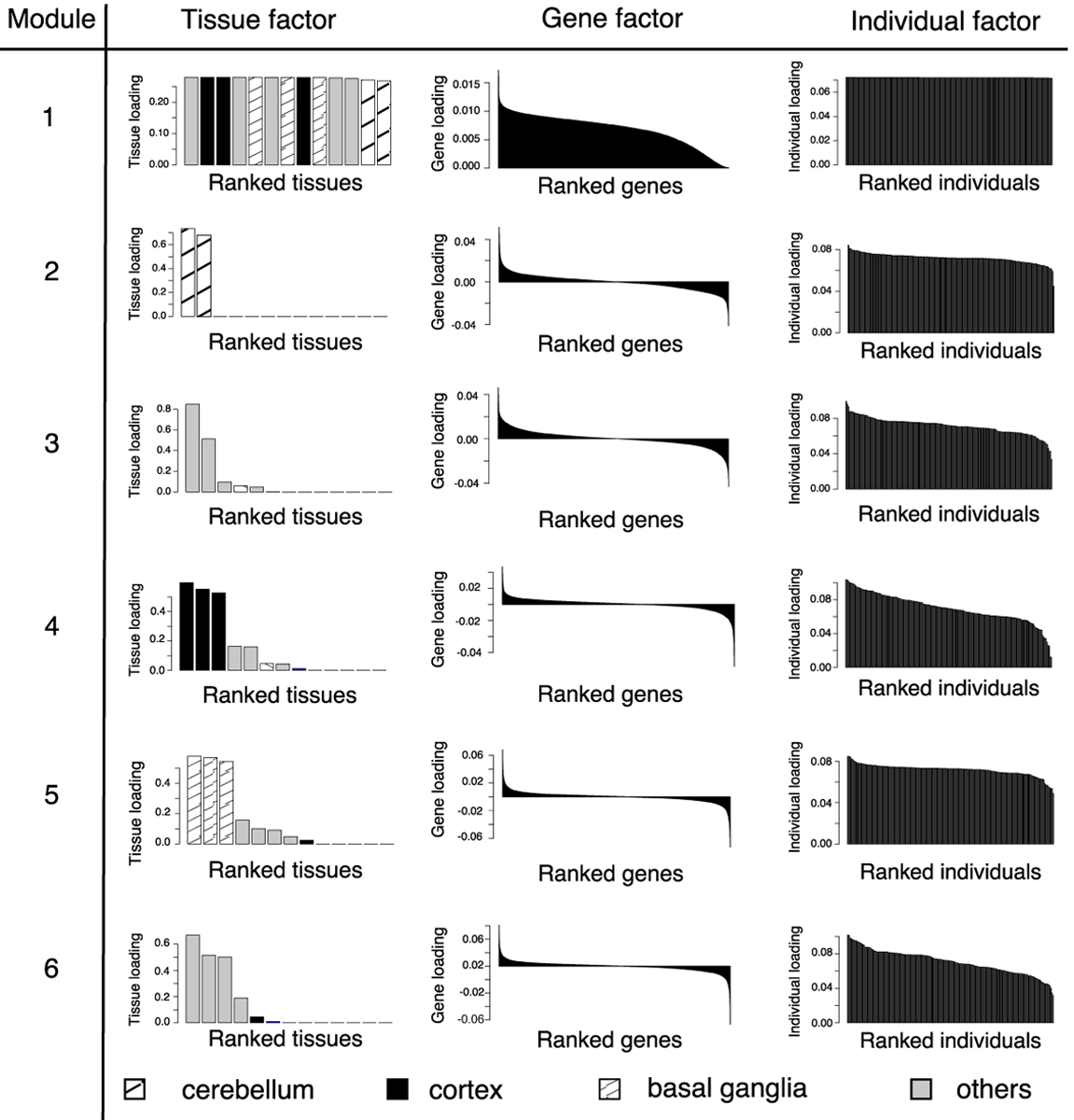
Top expression modules in the brain tensor. The top expression modules are ranked by their singular values. For each module, we plot the barplots for the sorted tissue loadings, gene loadings, and individual loadings, respectively.

5.2.2. Spatially-restricted expression in the brain.

Table 2 summarizes the biological interpretation for the expression modules detected in the brain tensor. Consistent with the tissue clustering, the gene clusters capture distinctly-expressed genes that are over- or underexpressed in each brain region. Genes overexpressed in the cerebellum region are strongly enriched for dorsal spinal cord regulation (p = 9.8 × 10⁻⁷) whereas the underexpressed genes are most strongly enriched for forebrain development (p = 3.4×10⁻⁸); the opposite enrichment pattern is observed for basal ganglia region. The enriched GOs are consistent with the spatial locations of the cerebellum (located in the hindbrain) and basal ganglia (situated at the base of the forebrain). In addition, we noticed an abundance of overexpressed HOX genes in the spinal cord (cervical C-1) compared to other brain regions (Supplemental Figure S4a). The HOX gene family (HOXA–HOXD) is a group of related genes that control the body plan and orientation of an embryo. The non-uniform expression of HOX genes across brain regions may suggest the particularly important role of the spinal cord during early embryogenesis.

Table 2.

Top expression modules in the brain tensor. Number in bold indicates p < 10⁻³.

Module	Eigen-tissue	Eigen-gene	Eigen-individual
	enriched region	enriched GO	% variance explained
			age	sex	race
1	all	neuronal synaptic plasticity	1.5	7.8	2.2
2	cerebellum	dorsal spinal cord development	0.0	8.0	0.2
3	spinal cord	embryonic skeletal system morphogenesis	9.3	0.9	5.2
4	cortex	fear response, behavior defense response	17	0.6	1.4
5	basal ganglia	forebrain generation of neurons	3.4	0.8	2.2
6	hypothalamus and hippocampus	neuropeptide signaling pathway	32	2.2	2.2

5.2.3. Sex/age-related expression in the brain.

Many expression modules in the brain also exhibited considerable individual-specificity. We identified two sex-related and three age-related expression modules among the top tensor components (bold in Table 2). The second gene module was found to be both cerebellum-specific and sex-related. By ranking genes based on their p-values for sex effect in the direction of eigen-tissue, we found that the top sex-related signal in this module is the X-Y gene pair PCDH11X/Y. In fact, the combined expression of PCDH11X/Y was significantly lower in the cerebellum (paired t-test p-value < 2×10⁻¹⁶) and in females (p = 8.0×10⁻¹¹), with expression levels also decreasing with age (p = 3 × 10⁻³). Notably, PCDH11X was the first reported gender-linked susceptibility gene for late-onset Alzheimer’s disease (Carrasquillo et al. 2009), and it may also be implicated in developmental dyslexia (Veerappa et al. 2013). However, its Y-chromosome paralog, PCDH11Y, is believed to be regulated differently. Previous studies (Priddle and Crow 2013) have shown that this difference is due at least in part to retinoic acid, which stimulates the activity of PCDH11Y but suppresses PCDH11X and perhaps explains the sex-specificity we observed for this gene pair in most brain tissues.

Significant age effects are widely present in the identified expression modules (Table 2). In particular, age explains over 15% of individual-level variation in module 4 (cortex) and module 6 (hypothalamus and hippocampus). Notably, the hippocampus is associated with memory, in particular longterm memory, and is vulnerable to Alzheimer’s disease (Lam et al. 2017). In module 4, GPR26 is found to be the top age-related gene. For comparison with our results we used linear regression, confirming the significant decrease of GPR26 expression with age in all three cortex tissues (cortex, p = 1.9 × 10⁻¹⁸; frontal cortex, p = 8.8 × 10⁻¹², anterior cingulate cortex, p = 1.9 × 10⁻⁷) but not in the substantia nigra (p = 0.17) or cerebellum (p = 0.64). It is worth noting that both the substantia nigra and cerebellum have zero loadings in the 4th eigen-tissue, so our tensor-based approach automatically detects the tissue-specificity of this aging pattern. In line with our findings, a recent study shows that GPR26 plays an important role in the degradation of intranuclear inclusions in several age-related neurodegenerative diseases (Mori et al. 2016).

6. Discussion.

We presented a new multi-way clustering method, MultiCluster, and demonstrated its utility in identifying three-way gene expression patterns in multi-tissue multi-individual experiments. We were able to uncover three-way specificities with clear statistical and biological significance in both simulations and the GTEx data set, and we showed that our method effectively identifies tissues which drive expression modules. In particular, it is able to do so even when gene × covariate interactions are not common across tissues, and clustering into modules provides information about joint expression patterns that may not be identified by meta-analyses without additional steps. Moreover, we provided evidence that the distinctions among human tissue gene expression profiles are usually driven by small sets of functionally coherent genes and that many age-, race- or gender-related genes exhibit tissue-specificity even within functionally similar tissues.

We also implemented a tensor projection procedure to test for differential expression of genes that are correlated with biological attributes (age, sex, or race) and found that we generically achieve improved power relative to single-tissue tests. Additionally, higher power is attained relative to meta-analyses when genes are differentially expressed in opposing directions in different tissues, allowing for finer resolution when seeking relevant genes. The tensor projection approach can be naturally extended to (trans)eQTL analyses by testing the projected expression of each gene against genetic variants across the genome. Alternatively, one can test each individual loading vector against genetic variants to identify eQTLs (Hore et al. 2016). Existing multi-tissue eQTL analyses usually proceed by identifying eQTLs in each tissue separately before combining single-tissue results via meta analysis (Battle et al. 2017). However, the large numbers of genes, tissues, and genetic variants potentially incur a substantial penalty for multiple testing and there is also the risk of under-powered tests due to limited sample sizes. Hence applying MultiCluster to perform eQTL discovery in large multi-tissue expression studies is an avenue worth pursuing.

One benefit of MultiCluster and tensor projection, as well as tensor-based methods in general, over existing tissue comparison methods (GTEx Consortium 2015) is the substantially reduced number of comparisons which must be considered (Hore et al. 2016). For instance, if one wanted to analyze every possible tissue pairing in a set of n tissues, roughly n² analyses would have to be performed and the results would need to be synthesized via a metaanalysis. Such an analysis could be even more prohibitive if one wanted to examine the 2ⁿ possible tissue-specific configurations (GTEx Consortium 2015). In contrast, MultiCluster constructs clusters across each mode of the data and associates the resulting variation with biological contexts via eigen-genes, -tissues, and -individuals. Each of these resulting components can then serve as the basis for testing, removing the need for many marginal tests. Though prior knowledge of tissue function can greatly reduce the number of pairwise comparisons, doing so constrains potential insights to the set of hypothesized tissue modules. For instance, components III and IV of our global tensor decomposition consist of diverse tissues which may not have been grouped together a priori.

One assumption made by our algorithm is that expression matrices for different tissues are of the same dimension. In the present work, we do not directly model the missing data mechanisms but instead iteratively impute them based on the fitted value. This allows the implementation to exploit standard fast array operation routines. Another possible approach which avoids the need for imputation is to make use of the connection between tensor decomposition and joint matrix factorization (Lock et al. 2013; Hore et al. 2016). For example, one could model the $n_G-\text{by}-n_{I_t}$ expression matrix M_t, where t indexes the tissue, as M_t ≈ AΛ_tB_t with some identifiability conditions. This model is a relaxation of tensor decomposition because it allows different tissues to have different column (individual) spaces B_t while sharing the same row (gene) space A. The diagonal matrix Λ_t captures the tissue-sharing and specificity as before. Another potential approach is to implement tensor imputation and decomposition simultaneously via a low-rank approximation, an idea which has roots in the matrix literature (Candès and Recht 2009).

Statistical inference based on tensor decomposition can be further extended. Measures of uncertainty, such as confidence intervals for tissue-, gene-, or individual-loadings, would be useful. Standard resampling techniques such as bootstrapping may help in this regard, and we have employed this approach to select gene cluster sizes. Further details on our bootstrap analysis can be found in Section 1.6 of the Supplement (Wang, Fischer and Song 2018).

Although we have presented MultiCluster in the context of multi-tissue multi-individual gene expression data, the general framework applies to more general multi-way data sets. One possible extension is the integrative analysis of omics data, in which multiple types of omics measurements (such as gene expression, DNA methylation, microRNA) are collected in the same set of individuals (Lock et al. 2013). In such cases, tensor decomposition may be applied to a stack of data or correlation matrices, depending on the specific goals of the project. Other applications include multi-tissue gene expression studies under different experimental conditions in which one may be interested in identifying 4-way expression modules arising from the interactions among individuals, genes, tissues, and conditions. The tensor framework can also be applied to time-course multi-tissue gene expression. In this instance one may treat time as the 4th mode and extend the tensor projection approach to identify the time trajectories of three-way expression modules. Finally, in certain experimental designs, our method could be used to model batch effects while preserving biological information.