Label-driven magnetic resonance imaging (MRI)-transrectal ultrasound (TRUS) registration using weakly supervised learning for MRI-guided prostate radiotherapy

Abstract

Registration and fusion of magnetic resonance imaging (MRI) and transrectal ultrasound (TRUS) of the prostate can provide guidance for prostate brachytherapy. However, accurate registration remains a challenging task due to the lack of ground truth regarding voxel-level spatial correspondence, limited field of view, low contrast-to-noise ratio, and signal-to-noise ratio in TRUS. In this study, we proposed a fully automated deep learning approach based on a weakly supervised method to address these issues. We employed deep learning techniques to combine image segmentation and registration, including affine and nonrigid registration, to perform an automated deformable MRI-TRUS registration. To start with, we trained two separate fully convolutional neural networks (CNNs) to perform a pixel-wise prediction for MRI and TRUS prostate segmentation. Then, to provide the initialization of the registration, a 2D CNN was used to register MRI-TRUS prostate images using an affine registration. After that, a 3D UNET-like network was applied for nonrigid registration. For both the affine and nonrigid registration, pairs of MRI-TRUS labels were concatenated and fed into the neural networks for training. Due to the unavailability of ground -truth voxel-level correspondences and the lack of accurate intensity-based image similarity measures, we propose to use prostate label-derived volume overlaps and surface agreements as an optimization objective function for weakly supervised network training. Specifically, we proposed a hybrid loss function that integrated a Dice loss, a surface-based loss, and a bending energy regularization loss for the nonrigid registration. The Dice and surface-based losses were used to encourage the alignment of the prostate label between the MRI and the TRUS. The bending energy regularization loss was used to achieve a smooth deformation field. Thirty-six sets of patient data were used to test our registration method. The image registration results showed that the deformed MR image aligned well with the TRUS image, as judged by corresponding cysts and calcifications in the prostate. The quantitative results showed that our method produced a mean target registration error (TRE) of 2.53 ± 1.39 mm and a mean Dice loss of 0.91 ± 0.02. The mean surface distance (MSD) and Hausdorff distance (HD) between the registered MR prostate shape and TRUS prostate shape were 0.88 and 4.41 mm, respectively. This work presents a deep learning-based, weakly supervised network for accurate MRI-TRUS image registration. Our proposed method has achieved promising registration performance in terms of Dice loss, TRE, MSD, and HD.

1. Introduction

High-dose-rate (HDR) brachytherapy has become a popular treatment modality for prostate cancer. Conventional transrectal ultrasound (TRUS)-guided prostate HDR brachytherapy could benefit significantly if the dominant intraprostatic lesions defined by multiparametric magnetic resonance imaging (MRI) can be incorporated into TRUS to guide HDR catheter placement.

The biggest challenge of MRI-TRUS registration is that it lacks robust image similarity measurement. In other words, a reliable image-intensity-based statistical correlation between MRI and TRUS images is not available. Thus, intensity-based models, which are based on optimizing image similarity (Brock et al 2017), show inferior performance for MRI-TRUS registration (Hu et al 2018b). Due to the lack of an image similarity measurement, it is also difficult to derive the driving force solely based on image intensity similarities for a physics-based model (Broit 1981, Sotiras et al 2013). In addition, supervised deep learning techniques are not feasible for MRI-TRUS registration due to the unavailability of ground truth deformation. To tackle this issue, research nowadays focuses on three popular approaches: knowledge-based models (Ferrant et al 2001, Mohamed et al 2002, van de Ven et al 2015, Fleute and Lavallee 1999, Rueckert et al 2003, Ashraf et al 2006), weakly supervised or unsupervised deep learning models (de Vos et al 2017, Yang et al 2017, Hu et al 2018a, 2018b, Lei et al 2019a), and the combination of those two approaches (Hu et al 2018).

Regarding the knowledge-based models, Mohamed et al (2002) firstly incorporated biomechanical model into SDMs to simulate prostate deformation. The main idea is to firstly use finite element analysis (FEA) to generate a series of deformations, which later are used to construct a statistical model, bypassing the similarity measure problem. However, one major issue in the biomechanical model is the uncertainty of biomechanical parameter setting. Hu et al (2011, 2012) attempted to address this issue by randomly sampling the biomechanical parameters from physically plausible parametric ranges. Further, Wang et al (2016) utilized patient-specific tissue parameters obtained with ultrasound elastography. Nonetheless, due to its unavailability in many hospitals and large variability in tissue stiffness measurements, the use of ultrasound elastography seems inconvenient and impractical for image registrations with respect to clinical practice.

Meanwhile, some researchers have been attempting to apply deep learning techniques for MRI-TRUS registration. Hu et al proposed a weakly supervised dense correspondence learning method with a fully convolutional neural network (FCN) (Hu et al 2018a, 2018b). The idea of this method is to use labels to represent anatomical structures (Zhou 2018), and then train a registration neural network to register those labels; in the inference stage, the MR and TRUS images are input into the trained registration neural network to predict the deformation occurring during prostate cancer interventions.

This weakly supervised method avoids the intensity-based similarity measure. In addition, their method is fully automated without registration initialization. However, the registration accuracy of their results was rather limited. In their work, they used whole image pairs as the input. The size of the training samples, which are high dimensional, is small and may be insufficient. This relatively small training data size could cause the network to be susceptible to overfitting. To alleviate this problem, for training the neural network, they labeled more than 4000 pairs of diverse anatomical landmarks from 111 pairs of T2-weighted MR and 3D TRUS images (Hu et al 2018a). However, the manual labeling process is time-consuming and laborious. Even with so many anatomical landmarks, the registration results (a median target registration error of 4.2 mm on a landmark) are far from meeting the clinical requirement of 1.9 mm, which is required to correctly grade 95% of the aggressive tumor components (van de Ven et al 2013). Another reason for the limited registration accuracy may be the labeling uncertainty. Though a large number of manual labels have been obtained for training, many of them such as cysts and calcification deposits, were not readily identifiable or even unreliably labeled. The inaccurate labels may result in the degradation of the performance of the neural network prediction. Furthermore, the training labels overlapped with each other, which may lead to the degradation of the performance of the registration.

Apart from the above-mentioned methods, recently, Hu et al (2018) combined the knowledge-based models with deep learning techniques to perform the MRI-TRUS image registration. In this study, FEA was used to produce a series of deformations, and then an adversarial convolutional neural network (CNN) was designed to train for image registration. The results do not seem very accurate, partly due to the above-mentioned limitation in the biomechanical model, the network architecture they employed, and the limited dataset.

In addition to the difficulties of designing accurate and efficient methods, the great challenges of implementing robust and reliable evaluation metrics exist for MRI-TRUS image registration (Brock et al 2017, Paganelli et al 2018). Generally, qualitative and quantitative validation can be integrated to evaluate the overall registration process (Paganelli et al 2018). For qualitative validation, we can use split screen and checkerboard displays, image overlay displays, difference image displays, and contour/structure mapping displays (Paganelli et al 2018). For quantitative validation, the following metrics are available: target registration error (TRE), mean distance to agreement, the Dice similarity coefficient, the Jacobian determinant, consistency, etc. For the details of each definition of the metrics, please refer to (Paganelli et al 2018).

We make the following contributions: (1) We proposed a novel fully automated MRI-TRUS image registration method. Specifically, we combined three major networks: one for prostate contour segmentation, one for affine registration, and the third one for nonrigid registration, into a workflow of MRI-TRUS registration. In the inference stage of segmentation, a pair of MRI-TRUS images was required; in the inference stage of affine and nonrigid registration, the pair of MRI-TRUS labels obtained from the segmentation step were treated as inputs into the registration network to generate a dense displacement field (DDF). The workflow is as follows: we firstly utilized two separate FCNs to extract the hierarchical feature maps to segment the MRI-TRUS prostate labels. To provide a better global registration initialization, we employed a 2D CNN to perform affine registration. A 3D UNET-like network was applied afterward to achieve fine local nonrigid registration. (2) We conducted a comparison qualitatively and quantitively among our method, Hu’s fullyautomated registration method with a composite neural (CN) network (Hu et al 2018a, 2018b), and a point matching (PM) method. Additionally, we also compared two variants of our method, one using only pairs of MRI-TRUS prostate labels as inputs of registration networks and the other one using only pairs of MRI-TRUS images as inputs.

The remaining content is organized into four sections as follows: section 2 introduces our proposed method; section 3 presents the experimental results; section 4 provides a discussion, followed by a conclusion in section 5.

2. Methods

Our method combines three major networks into the workflow of MRI-TRUS registration. These networks are described as follows: first, we utilized two separate whole-volume-based 3D FCNs to perform prostate segmentation on MRI and TRUS images; second, we applied a 2D CNN to train an affine registration network using the segmented MRI and US prostate labels; third, we employed a 3D UNET-like network to train a nonrigid registration network using the same MRI-TRUS labels. All the above-mentioned networks are trained separately.

2.1. FCN for segmentation

FCNshave demonstrated promising performances in medical image automated segmentation. Dense pixel-wise prediction enables the FCN to have end-to-end predictions from the whole image in a single forward pass. We separately trained two FCNs for MRI and TRUS segmentation. Manual prostate labels of MRI and TRUS images were used as the learning targets for the two FCNs. A 3D supervision mechanism was integrated into the FCN’s hidden layers to facilitate informative features extraction. We combined a binary cross-entropy loss and a batch-based Dice loss into a hybrid loss function for deeply supervised training. The implementation details of the FCN have been presented in our previous studies (Wang et al 2019, Lei et al 2019b). Once trained, the FCNs were able to rapidly segment the prostate from whole volume MRI and TRUS images of a new patient.

2.2. Affine registration

Magnetic resonance (MR) and TRUS labels were designated as moving and fixed labels, respectively, since we aim to use the warped preoperative MRI, which matches the intra-operative TRUS, as image guidance during the procedure. According to research (van de Ven et al 2015, Wang et al 2016), it is very helpful to set a good rigid or affine registration as an accurate initialization prior to subsequent nonrigid registration. Therefore, we designed a 2D CNN which takes 3D image as inputs to predict 12 affine transformation parameters to warp the original MR images and labels, as an initialization step of nonrigid registration. The automatic affine registration aimed to optimize the Dice similarity coefficient. The Dice similarity coefficientrepresents the overlap between the binary fixed and warped labels. Its definition is given as follows:

$$C_{\mathit{Dice}}(A,B)=\frac{2\sum _{i=1}^I{a}_i\cdot b_i}{\sum _{i=1}^I{a}_i+\sum _{i=1}^I{b}_i},$$ (1)

where the a and b denote the binary value (0 or 1) for a voxel in a moving label and fixed label, respectively, and I is the total number of voxels over the label.

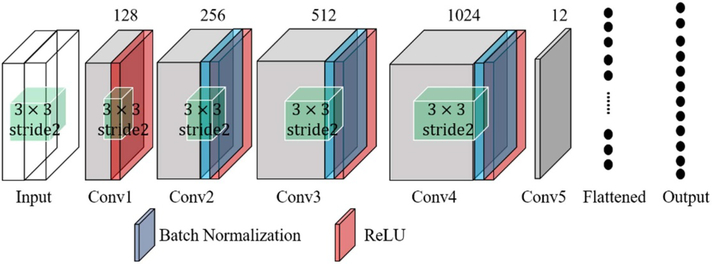
The architecture is shown in figure 1. The MRI and TRUS images are concatenated as ‘two-channel’ images as inputs. The tensor shape of the input is [4, 120, 108, 100], where 4 is the batch size, 120 and 108 are the number of voxels in the x- and y-directions, respectively, and 100 is the number of voxels in the z-direction, representing the number of channels. The number of filters used for the five convolutional layers was 128, 256, 512, 1024, and 12 respectively. These convolutional layers are followed by a flatten layer and a fully connected layer. The first four convolutional layers are followed by a batch normalization and a rectified linear unit as the activation. All the convolutional filters with a size of 3 × 3 and a stride of 2. The number of units for the fully connected layer is 12, which equals that of the 3D affine transformation parameters.

Figure 1.

CNN for affine registration.

2.3. 3D UNET-like network for nonrigid registration

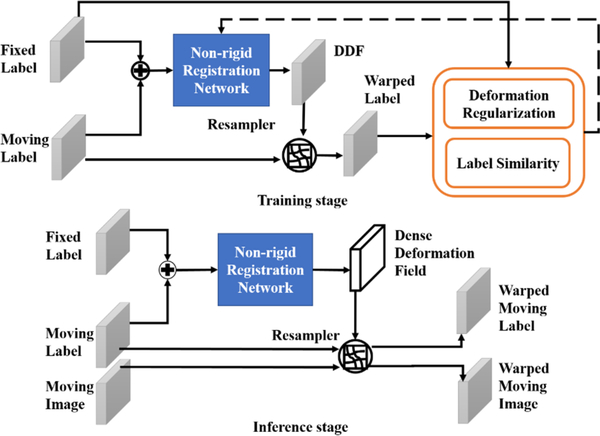
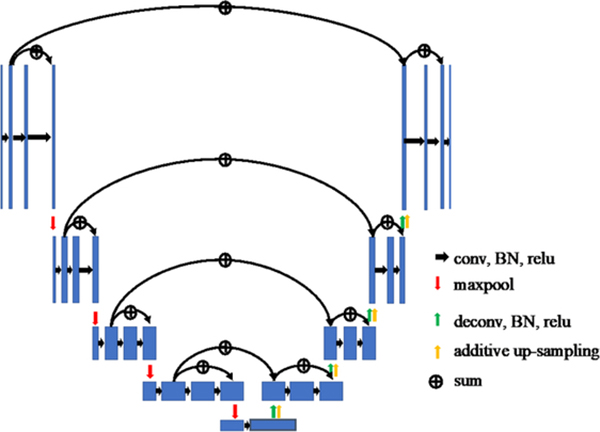
We compared two frameworks for nonrigid registration. One framework is to use only MRI-TRUS images as network inputs, similar to that of (Hu et al 2018b), and the other framework is to use pairs of MRI-TRUS labels as the input, as shown in figure 2. The nonrigid registration network architecture (Hu et al 2018b) is illustrated in figure 3. The MRI-TRUS labels are concatenated and input into a network similar to a U-NET, which has four down-sampling blocks followed by four up-sampling blocks. Compared to U-NET, this nonrigid neural network is more densely connected. In addition, it has two more types of summation-based residual shortcuts: one type is the standard residual network shortcutting two sequential convolution layers in each block; the other is the trilinear additive up-sampling layers, which shortcut the deconvolution layers in adjacent up-sampling blocks and are added onto the deconvolution layers (Wojna et al 2019).

Figure 2.

Nonrigid registration using labels as inputs into the networks.

Figure 3.

Illustration of the nonrigid neural network.

The Dice loss was employed as part of label similarity cost function. The Dice loss could encourage the network to have a high volume overlap between the warped MR prostate label and the fixed TRUS prostate label. However, a high volume overlap does not necessarily translate into good surface matching. Therefore, we have proposed including surface PM as an additional loss function to encourage prostate shape matching. The surface-based loss function is defined as the distance between the specific prostate surface points on the registered MRI and the corresponding surface points on the TRUS in certain directions. This cost function can be given as follows:

$$C_{surface}(A,B)=\frac{1}{L}\sum _{i=1}^L\left(d\left(P_i^A,P_i^B\right)\right),$$ (2)

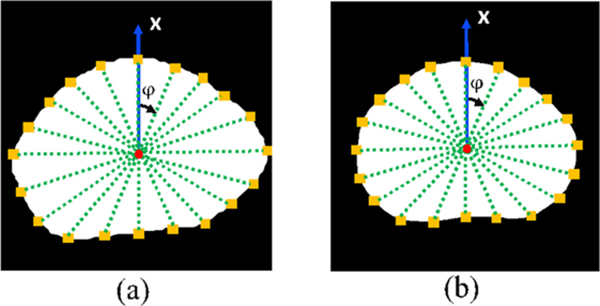
where $P_i^A$ and $P_i^B$ indicate the surface point in the i-direction in image A or B, and L is the total number of directions, d(·) is the L₂ norm Euclidean distance. In our work, we consider 40 different directions (the projection on the x-y plane is shown in figure 4). Using (θ, φ) to denote the inclination and azimuth, respectively, the θ and φ of these lines can be given as follows:

$$\{\begin{array}{c}\theta \in \left\{{45}^{°},-{45}^{°}\right\}\\ \phi =n\ast {18}^{°},n\in \{1,\dots ,20\}\end{array}.$$ (3)

Figure 4.

Prostate surface point (yellow square) projection at the X-Y plane at multiple directions on the (a) MRI and (b) TRUS images. Red dots indicate centroids of the prostate; green dashed lines denote line directions.

Radial projection was used to find the corresponding prostate surface points in these directions. We have observed that 40 surface control points are adequate given the smooth prostate deformation. More surface points can provide very marginal benefits (see supplementary material at stacks.iop.org/PMB/65/135002/mmedia). Therefore, we empirically chose 40 surface points.

Since image registration is an ill-posed problem, regularization is necessary (Sotiras et al 2013). In our work, we added bending energy as a regularization term in the loss function, to smooth the deformation field and penalize non-regular Jacobian values for the transformations (Christensen and Johnson 2001). The formula of the bending energy is given as follows:

$$C_{smooth}=\frac{1}{V}{\int }_0^X{\int }_0^Y{\int }_0^Z\left[\begin{array}{l}{\left(\frac{{\partial }^{2}T}{\partial x^2}\right)}^2+{\left(\frac{{\partial }^{2}T}{\partial y^2}\right)}^2+{\left(\frac{{\partial }^{2}T}{\partial z^2}\right)}^2\hfill \\ +2{\left(\frac{{\partial }^{2}T}{\partial x\partial y}\right)}^2+2{\left(\frac{{\partial }^{2}T}{\partial x\partial z}\right)}^2+2{\left(\frac{{\partial }^{2}T}{\partial y\partial z}\right)}^2\hfill \end{array}\right]dxdydz,$$ (4)

where T is the transformation, V is penalty of non-regular Jacobian values, and C represents the cost. We used finite central difference to approximate the second order partial derivatives terms in equation (4).

Given the Dice loss, surface-based loss, and the bending energy loss, we can write the total cost function as

$$C_{total}=-C_{Dice}+C_{surface}+\lambda C_{smooth},$$ (5)

where λ is the smooth regularization weight.

2.4. Dataset

Experiments were conducted on a dataset of 36 pairs of T2-weighted MR and TRUS images collected from 36 prostate cancer patients who have been treated with HDR brachytherapy. TRUS data were acquired with a Hitachi HI VISION with a voxel size of 0.12 × 0.12 × 2.0 mm³. The T2-weighted MR images were obtained using a Siemens Avanto 1.5 T scanner (Spin-echo sequence with a repetition time/echo time of: 1200 ms/123 ms, flip angle 150°, voxel size 1 × 1 × 1 cm³ with each slice of 256 × 256 pixels, and pixel bandwidth 651 Hz), and then resampled to the same sizes and resolutions as those of the TRUS images. Both the original MR and TRUS images were reconstructed into a 3D volume and resampled to 0.5 × 0.5 × 0.5 mm³ isotropic voxels by a third order spline interpolation. The manual prostate labels of the TRUS and MRI, represented by binary masks, were contoured by one and three radiologists, respectively, using VelocityAI 3.2.1 (Varian Medical Systems, Palo Alto, CA). In addition, the TRUS and MR labels were resampled to 0.5 × 0.5 × 0.5 mm³.

Our proposed methods were implemented in TensorFlow with a 3D image augmentation layer from an open-source code in NiftyNet (Gibson et al 2018). The augmentation generated 300 times more training datasets. Each network was trained with a 12 GB NVIDIA Quadro TITAN Linux general-purpose graphic process unit.

2.5. Experiments

We used leave-one-out cross-validation for the registration network. Regarding the training of the network, we utilized the Adam optimizer with a learning rate of 10⁻⁵. In addition, a trilinear resampled module was implemented, and a slip boundary condition was applied on the boundary of the grid. The initial values for all network parameters, except those in the final displacement prediction layers, were assigned using an Xavier initializer (Glorot and Bengio 2010). All the applicable hyper-parameters were kept same between our proposed method and the to-be-compared ones, unless otherwise stated.

We performed quantitative and qualitative evaluation of image registration accuracy. For quantitative evaluation, we employed the following metrics: target registration error (TRE), Dice loss, mean surface distance (MSD), and Hausdorff distance (HD) (Huttenlocher et al 1993, Litjens et al 2014). The target registration error (TRE) is defined as root-mean-square distance over all paris of landmarks in the MRI-TRUS images for each patient. Such landmarks include anatomical structures such as urethra, calcifications and cysts, etc In this study, an experienced radiologist carefully selected reliable landmarks on MR and TRUS images for TRE calculation. The MSD measures the average surface distance between two surfaces, and HD is defined as the greatest of all the distances from a point on one surface to the closest point on another surface. In contrast, the qualitative evaluation was mainly based on the visualization of contour overlays and image fusion. For example, in fusion images, a set of landmarks were denoted on registered MRI and US images, and a well alignment of the landmarks counterparts indicates good inner prostate registration.

3. Results

3.1. Registration performance

In this subsection, we will compare the quantitative results and qualitative results with our datasets from our method using MRI-TRUS labels as inputs for affine and nonrigid registration (SR-L), our method using MRI-TRUS images as inputs for affine and nonrigid registration (SR-I), Hu’s fully automated method with a CN network (Hu et al 2018a, 2018b), and the point matching (PM) method.

3.1.1. Quantitative results

Our segmentation neural networks generated Dice losses of 0.88 ± 0.05 and 0.92 ± 0.03 for the MRI and for TRUS segmentation, respectively (Wang et al 2019, Lei et al 2019b). On the training dataset, using SR, the total loss, Dice similarity loss, surface loss, and regularization loss converged at around 100 epochs with approximate values of 0.165, 0.08, 0.08, and 0.005, respectively. On the validation dataset, these loss functions converged at around 100 epochs with values of 0.196, 0.09, 0.100, and 0.006, respectively. Table 1 compares the registration results in terms of MSD and HD (Huttenlocher et al 1993, Litjens et al 2014), obtained with the CN, PM, SR-I, and SR-L methods. The MSD and HD from our proposed SR-L method are 0.88 and 4.41 mm, respectively, and these values obtained with SR-I method are 1.05 and 4.86 mm, respectively. On the other hand, the MSD and HD generated by the CN network are 2.31 and 8.38 mm; whereas these values obtained with PM are 0.37 and 3.41 mm. We also present the results after only affine registration: the MRD and HD are 1.14 and 5.49 mm, respectively. In addition, we applied paired Wilcoxon signed-rank tests to compare the leave-one-out cross-validation results between affine/CN/PM/SR-I and SR-L, as given by the fourth sub-column for each metric in table 1. The results show that both the resulting p-values of the pairs of SR-CN, and SR-PM are smaller than the significant level. Consequently, our proposed SR-L method is significantly better than the affine/CN/SR-I method, but not as good as PM in terms of a surface-based metric.

Table 1.

The MSD and HD values for the CN network, PM, and our segmentation-registration methods (SR-I and SR-L).

	MSD (mm)					HD (mm)
	Mean	Std	Median	IQR	p-values	Mean	Std	Median	IQR	p-values
Affine	1.14	0.38	1.05	0.40	<0.001	5.49	1.70	5.42	1.81	<0.001
CN	2.31	0.64	2.28	0.93	<0.001	8.38	1.94	7.97	2.74	<0.001
PM	0.37	0.12	0.33	0.16	<0.001	3.41	1.54	3.20	2.31	<0.001
SR-I	1.05	0.29	1.03	0.33	<0.001	4.86	1.49	4.66	1.30	0.050
SR-L	0.88	0.20	0.84	0.27	—	4.41	1.05	4.21	1.48	—

Table 2 presents the results in terms of Dice and TRE. SR-L achieves a mean Dice of 0.91 ± 0.02, compared to that of 0.89 ± 0.03 from SR-I, 0.76 ± 0.06 from the CN network, and 0.96 ± 0.02 from PM. In addition, SR-L obtained a mean TRE of 2.53 ± 1.39 mm, compared to that of 2.85 ± 1.72 mm from SR-I, 6.04 ± 3.14 mm from the CN network, and 4.46 ± 2.09 mm obtained with PM. Also, the median values and the first- and third quartiles are also listed. For example, SR-L generates a median Dice of 0.90 with the interquartile range (IQR) being 0.03, and a median TRE of 2.38 mm with the IQR being 1.41 mm. More detailed results are given in table 2 and figure 5. Again, paired Wilcoxon signed-rank tests have been done and show that both the p-values in terms of and the TRE of the pairs SR-L and CN network, and SR-L and PM are smaller than the significant level. As a result, we can conclude that in terms of both surface-based and volume-based metrics, our proposed method is significantly better than the CN network method, but not comparable to PM; whereas regarding TRE, our proposed method is significantly better than both the CN network and PM methods. The minimal possible TRE is dependent on the image voxel sizes.

Table 2.

The measured Dice and TRE values for affine registrationthe CN) network, PM, and our segmentation-registration methods (SR-I and SR-L).

	DICE					TRE (mm)
	Mean	Std	Median	IQR	p-values	Mean	Std	Median	IQR	p-values
Affine	0.88	0.04	0.89	0.05	<0.001	2.93	1.20	2.61	1.34	0.05
CN network	0.76	0.06	0.76	0.04	<0.001	6.04	3.14	6.02	5.14	<0.01
PM	0.96	0.02	0.96	0.03	<0.001	4.46	2.09	3.86	3.07	<0.01
SR-I	0.89	0.03	0.90	0.05	<0.001	2.85	1.72	2.43	1.81	0.330
SR-L	0.91	0.02	0.90	0.03	—	2.53	1.39	2.38	1.41	—

Figure 5.

Boxplots of the leave-one-out registration results obtained with affine registration, the SR-I, SR-L, CN network, and PM methods. (a) Dice similarity coefficient in [0, 1], (b) TRE in mm.

We performed additional experiments to test the effectiveness of our surface loss terms. Without the surface loss term, the mean MSD, HD, Dice, and TRE were 1.10, 4.90, 0.89, and 2.86 mm, respectively. The slightly worse metrics results without surface loss show the efficacy of the surface loss.

3.1.2. Qualitative results

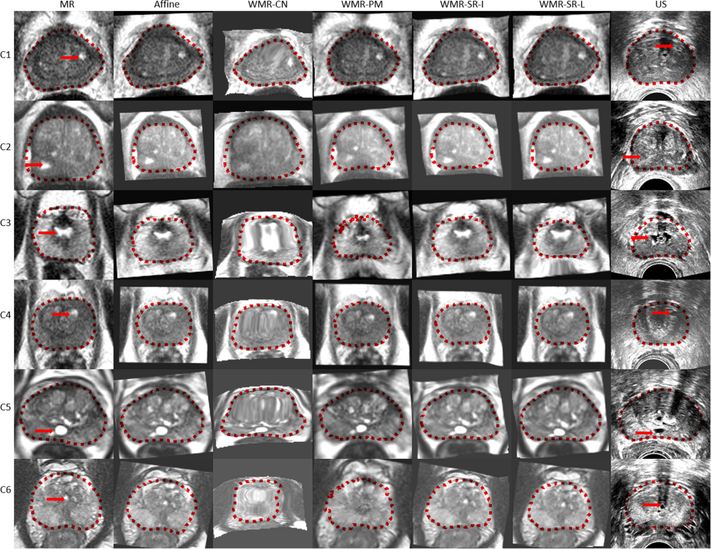
Figures 6 and 7 present a qualitative visual assessment of the results on the test dataset. Each row represents a patient case. In figure 6, from the left to the right column, we show the transverse slice in the original MR image, registered MR images from the CN network, PM, SR-I, SR-L methods, and the TRUS image. The dotted lines indicate the corresponding prostate gland contour. In addition, figure 7 demonstrates their corresponding fusion registered MRI-TRUS images from the affine, CN network, PM, SR-I, and SR-L methods. The yellow arrow points to some identified landmarks in the test dataset. 108 landmarks were manually selected for validation. The warped MR prostate labels obtained by PM are most similar to the labels on the TRUS images, whereas the warped labels obtained with the CN networkhave the least resemblance with the TRUS labels. In addition, figures 6 and 7 show that not only does the CN network generate warped labels that highly disagree with the fixed labels, but the CN network also produces blurred warped MR images. This registration performance implies a physically implausible deformation caused by the CN network. Apart from the unsatisfied registered results from the CN network presented in this work, results reported by Hu et al (2018a, 2018b) seem also non-realistic. In contrast to PM and the CN network, our proposed SR methods can generate realistic warped MR images with relatively good alignment between MRI-TRUS labels. In addition, the well-aligned landmark indicates the efficacy of our proposed method.

Figure 6.

Example of the registered results from six cases (each row represents the results from one case). From the left to the right column in the figure, we show the transverse slice in original MR image, warped MR images from the affine, CN network (WMR-CN), PM (WMR-PM), SR-I (WMR-SR-I), and SR-L (WMR-SR-L) methods, and the TRUS image. The dotted lines indicate the corresponding prostate gland contour, and the red arrows point out the pairs of landmarks on the MRI-TRUS images.

Figure 7.

Fusion of registered MRI-TRUS images from the affine, CN network, PM, SR-I, and SR-L methods. The arrows denote the landmarks which are well aligned post registration.

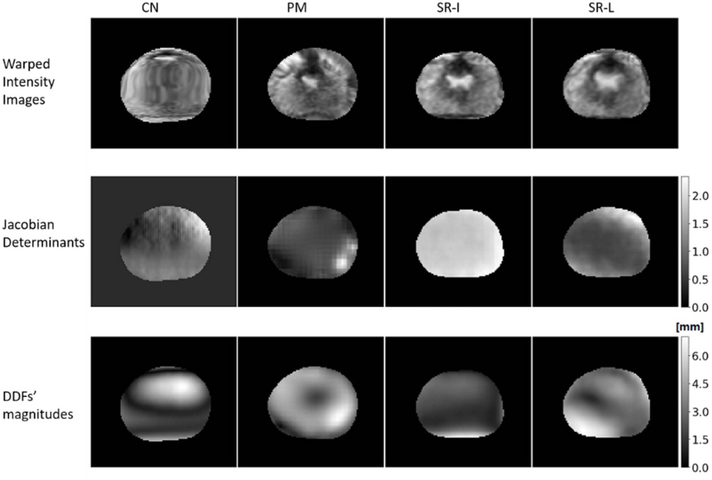
Furthermore, figure 8 demonstrates the results of other validation metrics that are based on DDF. From the top to bottom rows, we plotted the warped intensity MRI, Jacobian determinants, and the magnitudes of DDF, obtained with the CN network (first column), PM (second column), SR-I (third column), and SR-L (fourth column), respectively. No negative Jacobian determinants were found in SR (the minimum is 0.04 across all patient cases), supporting that the DDF by SR is physically plausible. On the contrary, zero Jacobian determinants appeared in the CN network, implying that physically implausible deformation may exist.

Figure 8.

Inspection of the warped MRI (first row), Jacobian determinants (second row), and DDF’s magnitudes (third row) from the CN network (first column), PM (second column), SR-I (third column), and SR-L (fourth column).

4. Discussion

In this paper, we proposed a new MRI-TRUS image registration framework, following a step-by-step procedure including segmentation, affine registration, and nonrigid registration. Specifically, the framework consists of three major networks: one for prostate contour segmentation, one for affine registration, and the third one for nonrigid registration, and these networks were built into a pipeline to automate the workflow of MRI-TRUS registration. In the inference stage, pairs of MRI-TRUS images are required without the need for manual contour segmentation or manual initialization. Experiments on 36 patients indicate that our proposed method has promising registration performance in terms of registration accuracy.

For comparison purposes, in table 3, we summarized and compared our results in terms of and the TRE with the published results obtained with some other previously proposed methods (Hu et al 2012, 2018, 2018b, Khallaghi et al 2015, Sun et al 2015, van de Ven et al 2015, De Silva et al 2017) which avoided using intensity-based registration. We skip the results obtained with intensity-based methods due to their poor performance in registering MR and TRUS images. For example, Hu et al (2018b) reported that all nine intensity-based methods that they tested produced median TREs larger than 24 mm and median Dice lower than 0.77. Thus, table 3 only presents previously proposed methods based on biomechanical models, statistical deformation models, and deep learning models without intensity-based loss functions.

Table 3.

Summary of MRI-TRUS registration results.

Registration method	DICE	TRE (mm)	No. of cases	Initialization method
Hu et al (2012)	n/a	2.4 (median)	8	Manual landmarks
Khallaghi et al (2015)	n/a	2.4 (mean)	19	Gland centroid
van de Ven et al (2015)	n/a	2.8 (median)	10	Rigid surface registration
Sun et al (2015)	0.86 (median)	1.8 (median)	20	Manual landmarks
Wang et al (2016)	n/a	1.4 (mean)	18	Rigid surface registration
De Silva et al (2017)	n/a	2.3 (mean)	29	Learned motion model
Hu et al (2018a)	0.88 (median)	4.2 (median)	76	n/a
Hu et al (2018b)	0.82 (median)	6.3 (median)	76	n/a
Composite network	0.76 (median)	6.0 (median)	36a	n/a
PM method	0.96 (median)	3.9 (median)	36a	Affine surface registration
Our method—image inputs	0.89 (mean)	2.9 (mean)	36a	n/a
Our method—labels inputs	0.91 (mean)	2.5 (mean)	36a	n/a

^aTesting with our dataset.

For methods based on biomechanical models or statistical deformation models (Hu et al 2012, Khallaghi et al 2015, Sun et al 2015, van de Ven et al 2015, De Silva et al 2017), which are not fully automated, an expected-TRE range of 1.4–2.8 mm was reported, and the experiments were conducted on 8–29 cases. The expected TRE from these methods seem small and satisfactory. Nonetheless, these methods usually rely on manual or customized optimization initialization. For instance, to the best of the authors’ knowledge, based on the biomechanical model, Wang et al (2016) reported the lowest expected TRE. However, their method relies on the rigid surface registration and requires prostate surface segmentation. In addition to the dependence on the initialization, biomechanical models have their clinical limitations due to the requirement of patient-specific biomechanical simulation data, which are not readily available for practical clinical application. As a result, these methods may suffer from inconvenience or infeasibility for practical clinic application.

As for the PM method, although it generates better results in terms of surface-based metrics such as Dice, MSD, and HD than those by our method, it does not mean that PM enables a good match inside the prostate, which can be indicated by the TRE. The PM method has the following drawbacks: (1) it takes only the surface points into account without considering inner prostate matching; as a result, it is likely to have non-smooth deformations inside the prostate gland for moving images, as shown in figure 6. (2) Since the PM method applies strong local shape alignment, it may be oversensitive to erroneous prostate segmentation. On the contrary, our method can yield much better results than PM regarding the TRE, implying superior registration to PM. This indicates that the bending energy in our network is better than the interpolation used in PM.

In contrast to the above-mentioned non-fully automated methods, recently, Hu et al proposed a fully automated deep learning-based method with a CN network. This method does not require any initialization or pre- or intra-procedural segmentation. With our dataset, the CN network generated a relatively large expected TRE of 6.0 mm. This is probably due to the incompetence of their network architecture for the extraction of hierarchical feature from the 3D contexts. This method does not have any segmentation prior to the registration. However, during the registration, their network tries to minimize a cost function based on the constructed segmentation that is determined by the generated DDF and the ‘ground-truth’ segmentation. In this way, in the inference stage, without the ground-truth segmentation, the relation between the inputs and cost function is too weak to allow backpropagation. In other words, this network may suffer from the ill-posedness issue, which impedes its ability to extract hierarchical features for generating accurate DDF.

Compared to methods in other works, our novel method is fully automated, accurate, and has sound feasibility for practical clinical applications. The benefits of our method are as follows. Firstly, by integrating the deep learning image segmentation technique with the FCN into our registration workflow, we were able to extract hierarchical features to explicitly obtain the prostate labels in the MRI-TRUS, which is one of the key steps for successful registration. Secondly, to provide better registration initialization for nonrigid registration, we trained a separate CNN for affine registration. We argue that these two benefits enable our method higher registration accuracy than that of another fully automated method (Hu et al 2018a, 2018b). The improved registration accuracy indicates a step forward toward the clinical requirement. Thirdly, similar to that work (Hu et al 2018a, 2018b), to overcome the lack-of-similarity ground-truth issue, we used the weakly supervised method that leverages labels to represent the anatomical structures, along with bending energy regularization. Our method yielded smoother deformation within the contour than that by PM. Fourth, our work does not rely on FEA for model training, thereby avoiding the measurement of patient-specific tissue elastic parameters.

Nevertheless, there are several limitations to our proposed methods. Firstly, although the intensity-based similarity measure is bypassed, the TRE was relatively large since the network was not fully knowledgeable about the inner prostate deformation pattern. Obtaining reliable multimodal image mapping relations on the voxel level will help improve the multimodal image registration accuracy. This may be done by the biomechanical model or the feature-based image registration method. Secondly, we used Dice loss and a surface-based loss to maximize the similarity between the MRI and TRUS labels. On addition to that, the registration model may benefit a lot by including the physically correspondence loss into the loss function. Thirdly, we used bending energy as the regularization to achieve a topologically smooth deformation field. Again, it may help for the prediction of physically plausible deformation by incorporating biomechanical regularization terms into the cost function, apart from bending energy regularization. Finally, we have a limited dataset. A limited dataset may cause neural networks to suffer from overfitting. To reduce overfitting, we implemented data augmentation. With data augmentation, the mean Dice after nonrigid registration we obtained for the testing dataset is 0.91, compared to that of 0.87 without data augmentation. However, data augmentation based on the existing dataset could only mitigate the problem. To reduce overfitting and increase the network’s generalizability, we plan to collect more datasets in our future work to help improve the performance for application in clinic practice.

5. Conclusion

This work presents a novel fully automated and accurate network with a weakly supervised method for MRI-TRUS image registration. The MRI-TRUS registration problem is difficult due to the considerably distinctive modalities of the two matching images, which in turn lead to little useful image features of prostates for the registration process. Our approaches are capable of solving this difficult problem by using a weakly supervised method to bypass the intensity similarity measurements, and by using deep learning to learn the complex image features for consistent prostate segmentation. What is more, we make the first attempt at integrating the automatic deep learning-based segmentation method into the registration procedure. By doing this, we not only enable a fully automated registration procedure, but also obtain accurate registration results. In addition, our proposed registration method can potentially be extended to other intervention procedures of soft tissue organs such as liver and breast. Future research aims to study the combination of our deep learning-based model with the biomechanical model or the feature-based image registration method to improve the registration accuracy and to make it available for a wider range of applications.