Differential Relation between Neuronal and Behavioral Discrimination during Hippocampal Memory Encoding

Summary

How are distinct memories formed and used for behavior? To relate neuronal and behavioral discrimination during memory formation, we use in vivo 2-photon Ca²⁺ imaging and whole-cell recordings from hippocampal subregions in head-fixed mice performing a spatial virtual reality task. We find that subthreshold activity as well as population codes of dentate gyrus neurons robustly discriminate across different spatial environments, whereas neuronal remapping in CA1 depends on the degree of difference between visual cues. Moreover, neuronal discrimination in CA1, but not in the dentate gyrus, reflects behavioral performance. Our results suggest that CA1 weights the decorrelated information from the dentate gyrus according to its relevance, producing a map of memory representations that can be used by downstream circuits to guide learning and behavior.

Highlights

• •Dentate gyrus activity robustly remaps in response to small or large contextual changes
• •Membrane potential of silent granule cells is selective for environmental context
• •Neural discrimination in CA1, but not in dentate gyrus, reflects behavioral performance

How does the brain tell apart similar information during memory storage and recall? Allegra et al. show that the input and output regions of the hippocampus play distinct roles in forming non-overlapping memory representations that are differentially related to an animal’s memory-guided behavioral performance.

Introduction

To distinctly represent similar objects and events that have different behavioral significance, the hippocampus is charged with the fundamental task of transforming similar inputs into well-separated neuronal memory representations. The input region of the hippocampus, the dentate gyrus, has been suggested to implement this function by orthogonalizing cortical inputs through sparse firing activity and cellular expansion (Gilbert et al., 2001; GoodSmith et al., 2017; Leutgeb et al., 2007; McNaughton and Nadel, 1990; Neunuebel and Knierim, 2014; O’Reilly and McClelland, 1994; Rolls and Treves, 1998; Treves and Rolls, 1992). In contrast, the downstream circuits CA3 and CA1 are thought to retrieve memorized patterns from incomplete or degraded input via attractor dynamics and to transfer these memory representations to the neocortex, where they are processed to drive behavior (Frankland and Bontempi, 2005; Guzman et al., 2016; Hasselmo et al., 1995; Marr, 1971; McNaughton and Morris, 1987). However, it is unclear how and where the hippocampus encodes distinct memories of similar objects and events (Danielson et al., 2016a, 2017; van Dijk and Fenton, 2018; Gilbert et al., 2001; GoodSmith et al., 2017; Hainmueller and Bartos, 2018; Leutgeb et al., 2007; Neunuebel and Knierim, 2014; Senzai and Buzsáki, 2017). In particular, little is known about how these distinct representations are used for behavioral decisions (Leal and Yassa, 2018).

Results

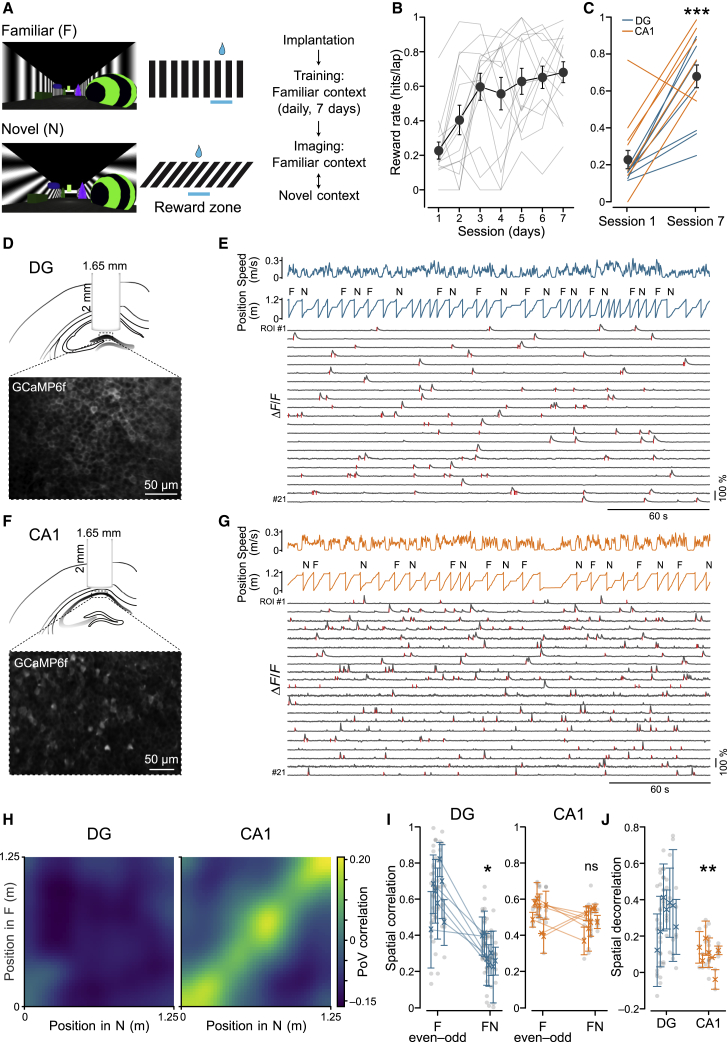
To precisely control the degrees of difference between spatial environments while accurately monitoring neuronal activity and behavior, we performed in vivo 2-photon Ca²⁺ imaging from hippocampal subregions of head-fixed mice executing a spatial memory discrimination task in virtual reality (Schmidt-Hieber and Häusser, 2013; Figures 1 and S1). Mice were initially trained to stop in a reward zone at the end of a linear virtual corridor that contained several distinct objects and that was enclosed by lateral walls covered with vertical grating patterns (Figure 1A). After successful training (~7 sessions; Figures 1B and 1C; reward rate, session 1 versus session 7, p < 0.001), mice were introduced to a novel environment with oblique grating patterns on the lateral walls but otherwise identical visual cues. To quantify the mouse’s behavioral discrimination between the memorized familiar (F) environment and the novel (N) one, we moved the reward zone to the middle of the N corridor.

Figure 1.

Small Differences in Virtual Environments Lead to Larger Spatial Remapping in the DG Than in CA1

(A) Left: views of the familiar (F; vertical grating) and novel (N; oblique grating) virtual reality environments. Center: schematic indicating the reward locations along the track. Right: experimental timeline.

(B) Quantification of behavioral performance, measured as reward rate (hits per lap), during the training sessions in the F virtual environment. Grey lines represent performance of individual animals, whereas large circles indicate mean ± SEM across all animals (n = 14; one-way repeated-measures (RM) ANOVA, F = 7.78, p = 1 × 10⁻⁶; DG: n = 7 mice; one-way RM ANOVA, F = 3.08, p = 0.015; CA1: n = 7 mice; one-way RM ANOVA, F = 5.27, p = 0.0005).

(C) Comparison of behavioral performance during session 1 and session 7 for mice implanted in the dentate gyrus (DG, blue; reward rate [hits/lap]: day 1, 0.15 ± 0.01; day 7, 0.60 ± 0.09; n = 7; Wilcoxon test, t = 28, p = 0.015) or CA1 (orange; day 1, 0.30 ± 0.09; day 7, 0.77 ± 0.06; n = 7; Wilcoxon test, t = 26, p = 0.03; all animals: day 1, 0.23 ± 0.05; day 7, 0.68 ± 0.06; Wilcoxon test, t = 99, p = 0.0006).

(D) Top: schematic of the imaging implant in the DG. Bottom: representative fluorescence image of GCaMP6f-expressing DG neurons in vivo.

(E) Representative imaging session showing animal speed, position along the track, and context type for each lap (F or N). Traces at the bottom show fluorescence extracted from example regions of interest (ROIs) in the DG. Significant transients during running periods are indicated by red tick marks.

(F and G) Same as in (D) and (E) but for CA1.

(H) Spatial population vector (PoV) correlation matrices. PoV correlations were computed for each spatial bin in the N environment (x axis) with each bin in the F environment (y axis). Note the absence of distinct high correlations in the DG (left) throughout the matrix. In contrast, correlations are high along the diagonal in CA1, indicating that neuronal activities are correlated at corresponding positions in F and N along the linear track.

(I) Correlations between mean spatial activity maps across recording sessions within the F environment (even-odd laps) and between different environments (FN) in the DG (left; spatial correlation: F even-odd, 0.62 ± 0.05; FN, 0.30 ± 0.03, n = 7 mice; Wilcoxon test, t = 0, p = 0.018) and CA1 (right; spatial correlation: F even-odd, 0.51 ± 0.03; FN, 0.48 ± 0.02, n = 7 mice; Wilcoxon test, t = 11, p = 0.61). Symbols with error bars represent mean ± SEM of individual animals. Gray circles represent recording sessions.

(J) Spatial decorrelation, quantified as the difference between spatial correlations within the F environment (even-odd) and between different environments (FN) in the DG and CA1. Circles indicate single recorded sessions from different animals (spatial decorrelation: DG, 0.32 ± 0.06, n = 7; CA1, 0.03 ± 0.05, n = 7; linear mixed model [LMM], p = 0.002). Same symbols as in (I).

^∗p < 0.05. ^∗∗p < 0.01. ^∗∗∗p < 0.001. See also Figures S1A–S1F.

We focused our recordings on the input and output regions of the hippocampus, the dentate gyrus and CA1 (Figures 1D–1J and S1). We compared the firing properties of spatially modulated cells in the two similar but distinct virtual environments. Spatially modulated neurons in the dentate gyrus (20.5% [F] and 20.9% [N] of all active cells in the respective environment) differed significantly in their spatial firing patterns in the two environments, as quantified by low correlations between the corresponding spatial activity maps (Figures 1H and 1I; spatial correlations in FF versus FN, p < 0.05; see Table S1 for statistics details of the linear mixed model; Figures S1A and S1B). In the downstream region CA1, spatial population firing patterns were similar across the two environments (Figures 1H and 1I; spatial correlations in FF versus FN, p > 0.05; Figures S1C and S1D). We then directly compared spatial decorrelation (i.e., the reduction in correlation; STAR Methods) between the two regions. This analysis revealed that decorrelation between F and N environments was significantly more pronounced in the dentate gyrus than in CA1 (Figure 1J; decorrelation in the dentate gyrus [DG] versus CA1, p < 0.01; Figure S1E). Thus, our data suggest that small visual differences between environments are sufficient to result in pronounced pattern separation in the DG, whereas pattern completion in the downstream circuit CA1 leads to similar spatial representations of familiar and novel environments.

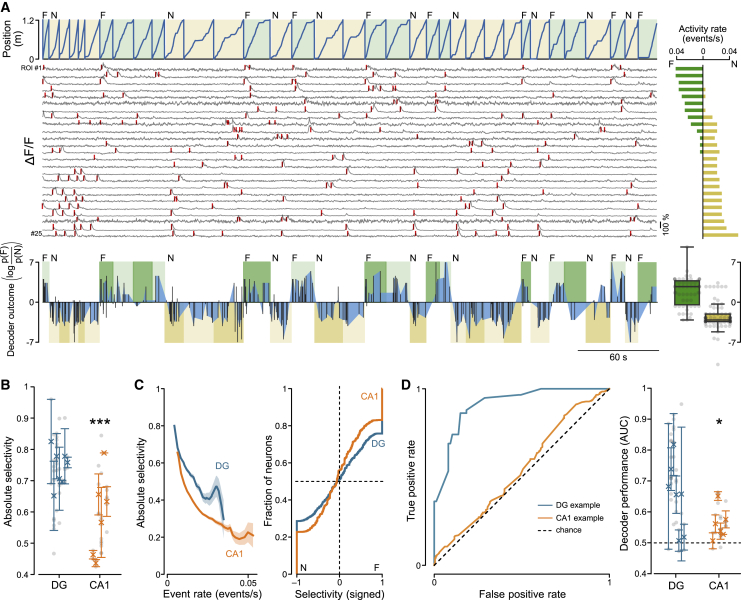
In addition to physical space, the hippocampus also encodes non-spatial dimensions and experiences (Aronov et al., 2017; Hampson et al., 1999; Lenck-Santini et al., 2005; Stefanini et al., 2020; Tanaka et al., 2018; Wiener et al., 1989; Wood et al., 1999). To assess neuronal coding beyond spatial decorrelation, we sought to analyze neuronal discrimination of the different contexts (vertical versus oblique gratings) independent of the spatial position of the animal (Figure 2). We first quantified how selectively neurons, including all spatially modulated and unmodulated cells, fired in the F or N environment (Figure 2A). We defined “selectivity” as the normalized absolute difference in event rates between the two environments (STAR Methods). Our analysis revealed that population activity in the DG was significantly more selective for the environment than in CA1 (Figure 2B; selectivity in the DG versus CA1, p < 0.001). The higher selectivity in the DG was not only a consequence of its overall lower activity levels because selectivity in the DG was higher than in CA1 throughout the whole range of observed activity rates (Figure 2C). This observation was confirmed when cells with near-perfect selectivity (absolute selectivity > 0.99) were excluded from the analysis (Figure S1I), suggesting that the higher selectivity in the DG is not only driven by cells that exclusively fire in one or the other environment.

Figure 2.

The DG Discriminates between Small Changes in Contextual Information

(A) Top: example session recorded from the DG, showing the position of the animal against time, the context type for each lap (F, vertical gratings in green; N, oblique gratings in yellow), and fluorescence traces extracted from the 25 most active neurons (gray), with significant transients during running periods indicated by red tick marks. For each fluorescence trace on the left, the corresponding event rate in the F (green) and N (yellow) environments is reported on the right. Bottom: decoder outcome for the session shown above. Light and dark color shades refer to training and test data, respectively (same color code as above). Black bars connected by blue areas represent the decoder outcome (difference in log likelihood of the two environments; F, positive; N, negative). Bottom right: summary of decoder outcome for the test data of the example session. Data points represent time bins.

(B) Absolute selectivity (STAR Methods) for the two environments F and N in DG (blue) and CA1 (orange) (DG, 0.74 ± 0.02; n = 7 mice; CA1, 0.59 ± 0.05; n = 6 mice; LMM, p = 0.0007). Symbols with error bars represent mean ± SEM of individual animals. Gray circles represent recording sessions.

(C) Left: absolute selectivity for DG and CA1 neurons plotted against their firing rate. Right: cumulative histogram; each neuron was scored depending on its selectivity for the F (positive) or N (negative) environment (DG, n = 4,667 active cells; CA1, n = 10,587 active cells).

(D) Left: example quantification of decoder performance (receiver operating characteristic [ROC]). Blue trace, DG session; orange trace, CA1 session. Right: comparison of decoder performance, quantified as area under the ROC curve (AUC), between the DG and CA1 (DG, 0.65 ± 0.04, n = 7 mice; CA1, 0.56 ± 0.02, n = 6 mice; LMM, p = 0.04; chance level, 0.5). Same symbols as in (B).

^∗p < 0.05, ^∗∗∗p < 0.001. See also Figures S1G–S1L.

To quantify more rigorously how informative the population activity is about the environment, we established a binary decoder that uses activity rates to classify population activity vectors into one of the two environments (Posani et al., 2017). We found that the decoder was significantly more successful at classifying DG than CA1 activity (Figure 2D; F-N decoder performance [area under the receiver operating characteristic (ROC) curve (AUC)] in the DG versus CA1, p < 0.05). To control for possible contributions of the different reward locations, we ran the same analysis only on data collected in the first part of the track, before any reward is presented. This analysis yielded comparable performance values (Figure S1L; F-N decoder performance [AUC] in the DG versus CA1, p < 0.05), indicating that the reward location had little effect on the observed differential neuronal discrimination. Thus, our results indicate that, independent of positional information and reward location, activity in two similar environments is more orthogonalized in the DG than in CA1.

To further explore the role of spatial representations in neuronal discrimination, we ran the analysis on the population activity of spatially unmodulated cells only (STAR Methods). Consistent with our results above, we found that selectivity and decoding performance were significantly higher in the DG than in CA1 when only spatially unmodulated cells were included in the analysis, with CA1 performance comparable with chance levels (Figures S1G and S1J; AUC in the DG versus CA1, p < 0.01). When only spatially modulated cells were included in the analysis, differences in selectivity and decoding performance were less pronounced between the DG and CA1 (Figures S1H and S1K). In conjunction with our previous results, this finding is consistent with the notion that CA1 performs “rate remapping” (Leutgeb et al., 2005) in the subpopulation of spatially modulated cells, which only change their firing rates but not their firing locations. Consequently, spatial correlations in CA1 are relatively high, but the environments can still be decoded from spatially modulated cells because of the change in their firing rates. In contrast, the DG performs “global remapping;” i.e., independent populations of spatially modulated and unmodulated neurons are active in the two environments, consistent with the definition of neuronal pattern separation (GoodSmith et al., 2017; Lee et al., 2020).

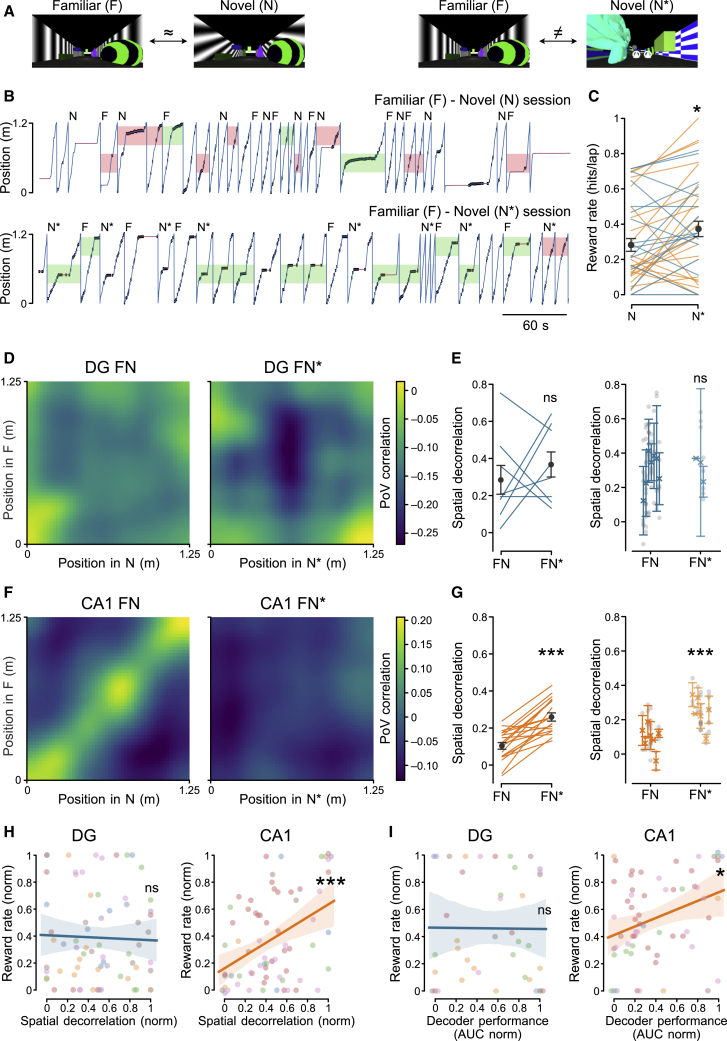
Because previous work has shown that spatial coding in CA1 is affected by goals, task relevance, and engagement (Danielson et al., 2016b; Dupret et al., 2010; Markus et al., 1995; Sarel et al., 2017), we next examined how decorrelation in the DG and CA1 relates to behavioral discrimination of small and large environmental differences (Figure 3). Addressing this question required us to explore a large range of degrees of neuronal discrimination in the DG and CA1. However, because the similar environments F and N we had used so far had failed to elicit substantial decorrelation in CA1 (Figures 1 and 2), we designed another N environment (N^∗) that differed substantially from the F one with the aim of increasing neuronal discrimination in CA1 (Figures 3A and 3B). To assess behavioral discrimination, the reward zone was placed at the center of N^∗. Animals showed higher performance in discriminating between F and N^∗ than between F and N (Figure 3C; reward rate, N versus N^∗, p < 0.05; Figures S2E–S2G). This increase in behavioral performance was accompanied by larger neuronal discrimination in CA1 but not in the DG (Figures 3D–3G; spatial decorrelation in DG: FN versus FN^∗, p > 0.05; in CA1: FN versus FN^∗, p < 0.001; Figures S2A–S2D). These data indicate that neuronal discrimination in CA1, but not in the DG, reflects behavioral discrimination between the two environments. Further supporting this notion, we found that in CA1, but not in the DG, behavioral and neuronal discrimination were positively correlated (Figure 3H; reward rate versus spatial decorrelation in DG, p > 0.05; in CA1, p < 0.05; Figure 3I; reward rate versus decoding AUC in DG, p > 0.05; in CA1, p < 0.05; Figures S2H–S2K). Our data suggest that neuronal discrimination in the DG can occur below the animal’s threshold for behaviorally relevant changes in the environment, whereas representations in CA1 reflect the behavioral decision of the animal.

Figure 3.

Neuronal Discrimination in CA1, but Not in the DG, Reflects Behavioral Discrimination

(A) Views of the virtual environment pairs (similar pair, F versus N; distinct pair, F versus N^∗).

(B) Representative recording sessions in the F-N (top) and F-N^∗ (bottom) environments. Blue traces represent the position of the animal along the track, and black tick marks indicate animal licks. Green rectangles indicate the correct licking choice in the F and N (N or N^∗) laps, whereas red ones indicate the incorrect choice (i.e., the animal licking in the wrong reward zone) for the F and N (N or N^∗) laps.

(C) Quantification of behavioral performance in the N (N and N^∗) environments, measured as reward rate (STAR Methods). Blue lines refer to single sessions of DG-implanted animals, orange lines refer to single sessions of CA1-implanted animals, and circles with error bars represent mean ± SEM (N, 0.28 ± 0.03; N^∗, 0.37 ± 0.04; n = 42 sessions; Wilcoxon test, t = 204, p = 0.02).

(D) PoV correlations between all pairs of positions in the two tracks FN (left) or FN^∗ (right) across all imaging recording sessions in DG-implanted animals. The left panel shows the same data as Figure 1H, left panel, but with a different color map scale.

(E) Left: paired spatial decorrelation between different environments (FN and FN^∗) in the DG (FN, 0.33 ± 0.07; FN^∗, 0.37 ± 0.06; n = 8 sessions; Wilcoxon test, t = 13, p = 0.49). Right: spatial decorrelation, quantified as the difference between spatial correlations within the same and different environments (FN and FN^∗), in the DG (FN, 0.32 ± 0.06, n = 7; FN^∗, 0.29 ± 0.04, n = 3 mice; LMM, p = 0.99). FN decorrelation in the right panel represents the same data as Figure 1J, left. Symbols with error bars represent mean ± SEM of individual animals. Gray circles represent recording sessions.

(F) Same as (D) but for CA1-implanted animals. The left panel shows the same data as Figure 1H, right panel, but with a different color map scale.

(G) Same analysis and same symbols as in (E) but for CA1-implanted animals (left: FN, 0.12 ± 0.02; FN^∗, 0.26 ± 0.02; n = 19 sessions, Wilcoxon test, t = 1, p = 2 × 10⁻⁵); right: FN, 0.03 ± 0.05, n = 7 mice; FN^∗, 0.18 ± 0.05, n = 6 mice; LMM, p = 0.0004). FN decorrelation in the right panel represents the same data as Figure 1J, right.

(H) Correlation between behavioral performance (reward rate) and spatial decorrelation in the DG (left: n = 7 mice and 70 sessions; Pearson’s r = –0.03; LMM, p = 0.75) and CA1 (right: n = 7 mice and 69 sessions; Pearson’s r = 0.43; LMM, p = 0.0002).

(I) Correlation between behavioral performance (reward rate) and decoder performance in the DG (AUC; left: n = 7 mice and 41 sessions, Pearson’s r = –0.01; LMM, p = 0.95) and in CA1 (right: n = 7 mice and 61 sessions, Pearson’s r = 0.25; LMM, p = 0.04).

ns, not statistically significant. ^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001. See also Figure S2.

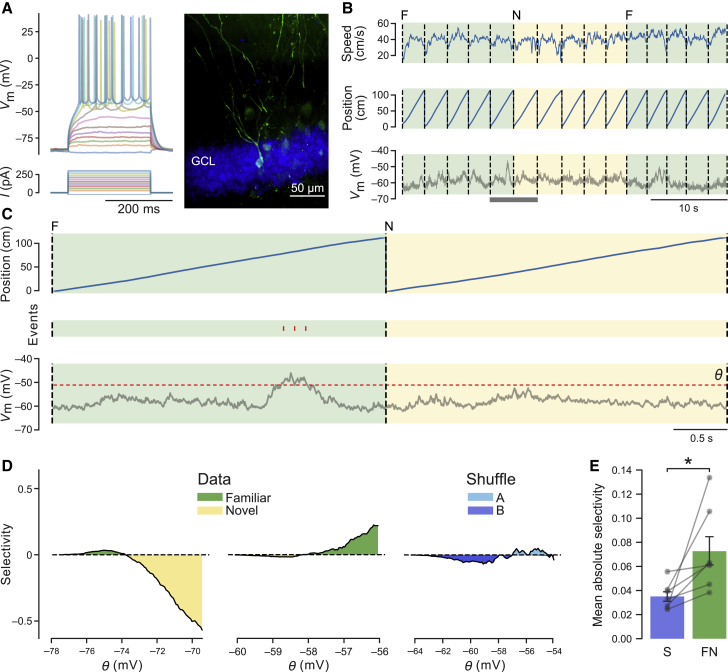
How is the sparse and selective fraction of DG neurons synaptically recruited from the total population? Inputs that are specific to an environment could be selectively routed to the active population, sparing the silent neurons. In such a scenario, selectivity would be largely governed by the connectivity between the entorhinal cortex and the DG. Alternatively, all neurons may receive similarly specific inputs, but only some of them are sufficiently depolarized to fire action potentials. These firing neurons would then silence the others in a “winner takes all” fashion; for example, by lateral inhibition. To distinguish between these possibilities, we obtained whole-cell patch-clamp recordings from DG granule cells during a virtual discrimination task between an F and an N environment (Figures 4A, 4B, and S4). To compare the selectivity of whole-cell-recorded silent neurons with the selectivity of active neurons we had recorded by imaging, we inferred the expected firing profile of silent neurons by applying a range of thresholds to the membrane potential (V_m) trace and imposing a minimal interspike interval (Figure 4C; STAR Methods). We then computed the selectivity for one or the other environment using these putative spikes in the same way as for the imaging data. We observed that cells showed substantial selectivity for the F or N environment (Figure 4D). This selectivity was significantly larger than the one expected from shuffled (S) data from the same recordings (Figure 4E; mean absolute selectivity, FN versus S, p < 0.05). Thus, our results are consistent with recent work indicating that silent granule cells receive spatially tuned input (Zhang et al., 2020) and support a scenario where active and silent neurons similarly receive specific information about the environment, but the small fraction of firing neurons then silences the others.

Figure 4.

Subthreshold Contextual Selectivity in DG Granule Cells

(A) Example recording. Left: sub- and suprathreshold membrane potential responses to current injections in a DG granule cell. Right: fluorescence image of a biocytin-filled granule cell. GCL, granule cell layer.

(B) Example recording from a “silent” neuron in F and N virtual environments. Traces show animal speed (top), position along the virtual corridor (center), and V_m (bottom).

(C) The same recording at higher magnification, as indicated by the gray bar at the bottom in (B). Membrane potential was thresholded (see bottom trace, threshold θ). The resulting predicted spikes are shown as a raster plot (red tick marks) in the middle.

(D) Selectivity for an environment was computed from the predicted spikes (STAR Methods) and plotted against the threshold θ. Selectivity was computed for 100 values of θ spanning a range of 2 standard deviations around the mean V_m of the recording. Examples show a recording with higher selectivity for the N than for the F environment (left), a recording with higher selectivity for the F environment (center), and a bootstrapped recording showing lack of clear selectivity for any two groups of S laps (A versus B, right).

(E) Bar graph summarizing mean absolute selectivity ± SEM across cells recorded with environment alternation (FN) versus bootstrap (S) (FN, 0.073 ± 0.012; S, 0.035 ± 0.004; n = 7 cells, Wilcoxon test, t = 0, p = 0.018).

^∗p < 0.05. See also Figure S4.

Discussion

In summary, our data reveal that the DG produces highly orthogonalized output by activating sparse non-overlapping subpopulations of neurons in response to small or large changes between environments. This high selectivity is observed in the population firing patterns of active cells as well as in the subthreshold membrane potential dynamics of silent neurons, consistent with a scenario where pattern separation is implemented by expansion coding in concert with inhibition (Cayco-Gajic and Silver, 2019; Espinoza et al., 2018; Guzman et al., 2019; Marr, 1969; McNaughton and Nadel, 1990; Rolls and Treves, 1998). Such a model does not require any specifically targeted connectivity from the entorhinal cortex because sub- and suprathreshold selectivity can emerge from random feedforward connectivity between an input population to an expanded layer (Marr, 1969), with feedforward or lateral inhibition ensuring that only a sparse population is firing. In addition, excitatory interneurons in the DG, the mossy cells, may contribute to pattern separation by controlling the level of activity in granule cells (Danielson et al., 2017; Myers and Scharfman, 2009), and their dense firing activity has been shown recently to display robust remapping across environments (Danielson et al., 2017; GoodSmith et al., 2017; Senzai and Buzsáki, 2017), which may provide an additional pattern separation signal (Lee et al., 2020). In contrast to the feedforward circuitry of the DG, recurrent connectivity between CA3 principal neurons enables them to perform a “pattern completion” operation, where representations fall into one of several “attractor” states that are robust to degraded or incomplete input information (Guzman et al., 2016; Marr, 1971; McNaughton and Morris, 1987). Thus, representations in CA3 abruptly switch from pattern completion to separation when differences exceed a threshold (Alme et al., 2014; Leutgeb et al., 2004; Neunuebel and Knierim, 2014). Although this switch between pattern completion and separation may be less pronounced in CA1 (Leutgeb et al., 2004), attractor properties can still explain why population activity in CA1 sharply remaps from one representation to the other when the differences between environments are sufficiently large (Wills et al., 2005), whereas the DG feedforward circuit produces a more constant decorrelation throughout a range of differences between environments, as observed in our experiments.

How can we reconcile the notions that the DG performs constant decorrelation, whereas the downstream circuits appear to remap independently? During exploration of the novel environment, the robustly decorrelated inputs from the DG are pushing downstream circuits toward forming a new representation, whereas their attractor dynamics counteract this process by stabilizing the familiar map (Knierim and Neunuebel, 2016). Additional inputs, such as information about the saliency and unexpectedness of the novel environment, are required to switch from recalling a familiar memory to formation of a new representation in CA3 and CA1. Several candidate input streams may contribute to this switch, such as cholinergic inputs from the medial septum, which are thought to provide a signal indicating novelty and attention to several hippocampal subregions (Hasselmo, 2006). Direct inputs from the entorhinal cortex to CA3 may act as a cue for recall, with recent modeling work suggesting that nonlinear interactions between entorhinal, dentate, and neuromodulatory inputs are essential for recalling large numbers of memories with low interference (Kaifosh and Losonczy, 2016).

Our data suggest that the levels of saliency and behavioral relevance decide whether the decorrelated information from the DG can shift CA3 and CA1 cell assemblies toward a new attractor state. We observe that the DG population activity distinguishes between familiar and novel environments even when the animal performs poorly in the discrimination task. This apparent lack of relation between behavioral and neuronal discrimination in the DG can be explained by our observation that the DG produces highly decorrelated representations throughout a range of small and large changes in the environment. In contrast, we find a close relationship between behavioral and neural discrimination in CA1, suggesting that the degree of separation in downstream hippocampal populations is related to the ability of the animal to behave differently in the two settings. Although further experiments are needed to establish a definite causality between hippocampal remapping and task performance, our data are compatible with a scenario where behavioral relevance and saliency trigger formation of new representations in CA3/1, instructed by the highly decorrelated information from the DG, that are then critical for ensuing behavioral decisions (Figure S4C). How neuronal and behavioral discrimination in the DG and downstream circuits evolve as the animal familiarizes itself with the novel stimuli remains to be explored. Recent work suggests that experience shapes remapping in CA1 (Plitt and Giocomo, 2019), whereas classification of learned olfactory stimuli by the DG correlates with behavioral discrimination after training in a contextual fear conditioning task (Woods et al., 2020).

Previous work on neuronal discrimination in different hippocampal subregions has provided inconsistent results, reporting stronger (Leutgeb et al., 2007; Neunuebel and Knierim, 2014) or weaker (Hainmueller and Bartos, 2018; Senzai and Buzsáki, 2017) neuronal pattern separation in DG granule cell populations compared with principal neurons in downstream hippocampal circuits. Our finding that the behavioral relevance of the navigational task is differentially related to the amount of neuronal discrimination can partly explain these discrepancies because it follows that differences in spatial cues alone are not the sole determinants of neuronal discrimination. Furthermore, neuronal “pattern separation” can be quantified in multiple ways, such as spatial correlations between place fields or population firing vectors across different environments (Hainmueller and Bartos, 2018). However, when pattern separation is defined in more general terms, independent of any assumptions of the spatial firing patterns, as implemented by our selectivity and decoder analyses, most studies to date report strong orthogonalization in DG representations (Lee et al., 2020), consistent with the present study.

Our data reveal how orthogonalized neuronal memory representations in the input and output regions of the hippocampus are related to behavioral discrimination. We propose that the DG robustly reports changes in external and internal variables even when they are not sufficiently relevant to reach the animal’s perception. In contrast, representations in the output region CA1, instructed by decorrelated inputs from the DG, remap in response to behaviorally relevant changes in sensory inputs that exceed a saliency threshold. Downstream neocortical circuits then use this map to drive behavioral decisions.

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
pAAV.Syn.GCaMP6f.WPRE.SV40	Addgene	100837-AAV1
Chemicals, Peptides, and Recombinant Proteins
Biocytin	Sigma-Aldrich	B4261; CAS: 576-19-2
Deposited Data
Analyzed data	This paper	N/A
Experimental Models: Organisms/Strains
Mouse: C57BL/6J	Janvier Labs	SC-C57J-M4S
Software and Algorithms
Suite2p	Pachitariu et al., 2017	https://github.com/MouseLand/suite2p
Python	https://www.python.org	N/A
Blender	https://www.blender.org	N/A

Resource Availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Christoph Schmidt-Hieber (christoph.schmidt-hieber@pasteur.fr).

Materials availability

This study did not generate new unique reagents.

Data and code availability

The datasets and analysis code supporting the current study are available from the lead contact on request.

Experimental Model and Subject Details

Mice

All procedures were carried out in accordance with European and French guidelines on the ethical use of animals for experimentation (EU Directive 2010/63/EU) and were approved by the Ethics Committee CETEA of the Institut Pasteur (protocol number 160066). 6-16 week-old male C57BL/6J wild-type mice (Janvier Labs) were used for all experiments. After their arrival at 4-5 weeks old, mice were housed in a room kept at 21°C in groups of two to four in polycarbonate individually ventilated cages enriched with running wheels, with a 12 h inverted light/dark cycle and ad libitum access to food and water until the start of the experiments. All animals were treated identically. When experiments started, mice were placed under controlled water supply (0.5 mg of HydroGel per day, ClearH₂O) and maintained at 80%–85% of their initial body weight over the course of imaging and electrophysiology experiments. In total, imaging data from 14 mice (DG, n = 7; CA1, n = 7) and electrophysiology data from 7 mice were used in this study.

Method Details

Surgical procedures

All surgical procedures were performed in a stereotaxic apparatus (Kopf instruments). Combined analgesia, buprenorphine (0.05 mg/kg, Vetergesic) and meloxicam (10 mg/kg, Metacam), was administered through intraperitoneal injection at least 30 min before any surgical intervention and the incision sites were infiltrated with lidocaine. Mice were anesthetized with isoflurane (3%–5% for induction and 1%–2% for maintenance, vol/vol). During the surgery, mice were kept at a body temperature of ~36°C using a heating blanket, and their eyes were protected with artificial tear ointment. Postoperative analgesia (meloxicam 5 mg/kg) was administered orally in combination with surgical recovery DietGel (ClearH₂O) for 2 days after surgery.

Stereotaxic injections

After application of povidone-iodine (Betadine), the skin was incised and the exposed skull was cleared of overlying connective tissue. A small craniotomy was performed above the right dorsal hippocampus (2 mm posterior and 1.5 mm lateral to bregma), and 500 nL of AAV1.Syn.GCaMP6f.WPRE.SV4 (titer 3.4x10¹² TU/mL; Addgene) were injected via a glass micropipette (Wiretrol, 5-000-1010 Drummond) at a depth of 1.7 mm from the dural surface for targeting the DG, and 1.2 mm for CA1. Mice were allowed to recover for at least 2 days after injection before undergoing any subsequent procedure.

Chronic imaging window and headpost implantation

To record Ca²⁺-dependent fluorescence changes of the GCaMP6f sensor, we used two different imaging implant strategies, either a custom-made imaging cannula, or a graded index lens (GRIN; 1 mm diameter, 3.4 mm height, NA = 0.5, G2P10 Thorlabs). The imaging cannula was assembled by UV curing (Norland optical adhesive) a circular coverglass (1.6 mm diameter, 0.16 mm thickness, produced by Laser Micromachining) to a cylindrical stainless-steel tube (2 mm height, 1.65 mm outer and 1.39 mm inner diameter; Coopers Needleworks). Imaging window implantations were performed several days after the initial viral injection. Mice were anesthetized as described above and, after the skull was exposed, a craniotomy (~1 or ~1.6 mm diameter) was centered on the previous injection site. For cannula implants, the overlying cortex (including parts of the somatosensory and posterior parietal association cortices) was gently aspirated with a 27 gauge needle while constantly being rinsed with aCSF solution (Danielson et al., 2016a; Dombeck et al., 2010), and bleeding was controlled with a gel dental sponge (Gelfoam, Pfizer). We terminated the aspiration when the external capsule became visible. The outer part of the external capsule was then gently peeled away using fine forceps, leaving the inner capsule and the hippocampal formation itself undamaged for CA1 imaging recordings. To provide optical access to the dorsal blade of the dentate gyrus, we continued to gently aspirate CA1 directly dorsal to the dentate gyrus until the loose fibers and vasculature of stratum moleculare were visible. GRIN lens implants were used as an alternative strategy to the optical cannula that reduces the lesion to the tissue. For GRIN lens implants, a beveled stainless-steel cylinder (1 mm diameter) was slowly lowered to the target region (1.2 mm depth for CA1, 1.85 mm for the dentate gyrus) without any cortical aspiration, and removed before proceeding with the implant. For cannula implants, the window was gradually lowered into the craniotomy until the tip was in contact with the internal capsule for CA1 imaging, or 100-200 μm above the hippocampal fissure for dentate gyrus imaging. GRIN lenses were implanted at a final depth of 1.2 mm for CA1 or 1.85 mm for the dentate gyrus. Protruding parts of the GRIN lens or cannula were secured to the skull with opaque dental cement (Super-bond C&B, Sun Medical). Mice were then implanted with a stainless-steel headpost for head fixation (Luigs & Neumann) during imaging and electrophysiology experiments. Finally, the conical portion of a nitrile rubber seal (749-575, RS Components) was glued to the headpost with dental cement and filled with a silicone elastomer (900-2822, Henry Schein) to protect the window preparation during recovery and between recording sessions.

A comparison of neuronal activity in GRIN- and cannula-implanted animals revealed that in both DG and CA1, there was no significant difference in spatial decorrelation between the two implant strategies (Figures S3A and S3B). When a decoder was used to assess neuronal discrimination, FN decoding performance was higher in GRIN implants than in cannula implants in both regions, suggesting that the lesion size similarly affects DG and CA1, without introducing any region-specific bias (Figures S3C and S3D). When we examined whether the implant strategy affected the animals’ behavioral performance (measured as both reward rate and d-prime), we did not observe any systematic differences between GRIN- and cannula-implanted animals (Figures S3E–S3H). Furthermore, all DG-implanted animals showed similar reward rates and d-prime scores as CA1 animals (Figures S2E–S2G), suggesting that our conclusions are independent of the depth of the implant (CA1 versus dentate gyrus) and the surgical implant strategy (GRIN versus cannula).

Virtual-reality environments

A virtual reality setup was implemented as previously described (Schmidt-Hieber and Häusser, 2013). Briefly, head-fixed mice navigated on a cylindrical polystyrene treadmill (20 cm in diameter), rotating forward or backward. Cylinder rotation associated with animal locomotion was read out with a computer mouse (G203, Logitech) at a poll rate of 1KHz and linearly converted to one-dimensional movement along the virtual reality corridor. The virtual environments were projected onto a spherical dome screen (120 cm in diameter, 240°), covering nearly the entire field of view of the animal, using a quarter-sphere mirror (45 cm diameter) and a projector (Casio XJ-A256) located below the mouse. The virtual linear corridor was 1.2 m long, with objects placed along the linear track and vertical or oblique grating textures on the lateral walls. A reward zone was located within each linear virtual track, at the end (0.81-1.15 m) or at the center (0.34-0.68 m) of the vertical and oblique corridors, respectively. An enriched environment, used to increase behavioral discrimination and neuronal discrimination in CA1, consisted in a substantially different virtual scene, with different visual cues and textures on the walls, but maintaining the same reward location as for the oblique corridor. For the electrophysiology experiments, two different variations of the virtual environment were used as familiar and novel environments (Figure S4). The Blender Game Engine (https://www.blender.org/) was used in conjunction with the Blender Python API to drive the virtual reality system.

Behavioral training and analysis

Two weeks after the imaging window implantation, water-restricted mice were handled 10 min per day for 3 days and placed on the treadmill for 10-20 min for 2 consecutive days to get habituated to both the experimenter manipulation and the experimental setup. After habituation, mice underwent 7 training sessions, 30 min each, over the course of 1-2 weeks before recordings (Figures 1B and 1C). Mice were trained to run along the linear virtual corridor. A drop of sugar water (10 μl, 8 mg/mL sucrose) was dispensed by a spout placed in front of their mouth as a reward if they spent 2 s or more within the reward zone. When the animals reached the end of the linear track, they were “teleported” back to the start of the virtual corridor after crossing a black frontal wall, indicating the end of a lap and the onset of the subsequent one. No punishments were provided in our experimental design. During the training, only the familiar (vertical gratings) environment was displayed, while from the first day of imaging sessions, mice were presented with a random alternation of familiar and novel environments. Each imaging session was organized into about 10 min of recording, where similar environments (familiar: vertical gratings (F) versus novel: oblique gratings (N)) or substantially different environments (familiar: vertical gratings (F) versus novel: enriched environment (N^∗)) were randomly displayed. Training and imaging recordings were performed during the dark cycle of the mice.

In vivo two-photon calcium imaging

In vivo imaging was performed using a resonant-galvanometer high speed laser-scanning two-photon microscope (Ultima V, Bruker), with a 16x, 0.8 NA water immersion objective (Nikon). Time-series images were acquired at 30 Hz frame rate (512 × 512 pixels, 0.8–1.2 μm/pixel), with a femtosecond-pulsed excitation laser beam (Chameleon Ultra II, Coherent) tuned to 920 nm for imaging GCaMP6f expressing cells. To block diffused light from the projection system, a black foam rubber ring was positioned between the animal’s implant and the objective, and a green light blocking filter (FES0450, Thorlabs) was placed in front of the projector light output.

In vivo whole-cell patch-clamp recordings

Two craniotomies (0.5 mm diameter) were drilled 3–24 h before the recording session for the recording electrode (right hemisphere, 2.0 mm posterior and 1.5 mm lateral from Bregma) and the reference electrode (left hemisphere, 2.0 mm posterior and –1.5 mm lateral from Bregma). The dura mater was removed and the cortical surface was kept covered with artificial cerebrospinal fluid of the following composition: 150 mM NaCl, 2.5 mM KCl, 10 mM HEPES, 2 mM CaCl₂, 1 mM MgCl₂. Recording electrodes were pulled from filamented borosilicate glass and filled with internal solution of the following composition: 135 mM potassium methanesulfonate, 7 mM KCl, 0.3 mM MgCl₂, 10 mM HEPES, 0.1 mM EGTA, 3.0 mM Na₂ATP, 0.3 mM NaGTP, 1 mM sodium phosphocreatine and 5 mg/ml biocytin, with pH adjusted to 7.2 with KOH. Pipette resistance was 4–8 MΩ. Electrodes were positioned to penetrate perpendicularly to the cortical surface at the center of the craniotomy and the depth of the recorded cell was measured from the distance advanced with the micromanipulator (Luigs & Neumann), taking as a reference the point where the recording electrode made contact with the cortical surface. Whole-cell patch-clamp recordings were obtained using a standard blind-patch approach, as previously described (Margrie et al., 2002). Only recordings with a seal resistance >1 GΩ were used. Recordings were made in current-clamp mode with no holding current. No correction was applied for the liquid junction potential. Typical recording durations were ~5 min, although longer recordings (~30 min) were occasionally obtained. Membrane potential signals were low-pass filtered at 10 kHz and acquired at 50 kHz. To synchronize behavioral and electrophysiological recordings, TTL pulses were triggered by the virtual reality system whenever a new frame was displayed (frame rate: 100 Hz) and recorded with both the behavioral and the electrophysiological acquisition systems.

Histology for imaging area detection and cell identification

At the end of the experiments, mice were deeply anesthetized with an overdose of ketamine/xylazine administered intraperitoneally and transcardially perfused with phosphate-buffered saline (PBS, 1x) followed by 4% paraformaldehyde solution. Brains were removed and post-fixed overnight in 4% paraformaldehyde/PBS. Brains were then cut into 60-70 μm coronal slices. Sections containing the area underneath the imaging window were collected, and the correct positioning of the imaging cannula or GRIN lens was confirmed by fluorescence microscopy. Brain slices from electrophysiology experiments were stained with Alexa Fluor 488-streptavidin to reveal biocytin-filled neurons and patch electrode tracts. DAPI was applied as a nuclear stain to reveal the general anatomy of the preparation. Fluorescence images were acquired with a spinning disc confocal microscope (Opterra, Bruker). The accuracy of the recording coordinates was confirmed in all cases by either identification of the recorded neuron or the recording electrode tract.

Quantification and Statistical Analysis

Imaging data processing

Motion correction of the imaging data was performed using a phase-correlation algorithm built into the suite2p software (Pachitariu et al., 2017; https://github.com/cortex-lab/Suite2P). Segmentation into regions of interest (ROIs) was performed with suite2p using a singular value decomposition algorithm. To select dentate gyrus granule cells, we only used ROIs corresponding to small, densely packed cell bodies. ROIs corresponding to large isolated cell bodies were discarded in order to exclude putative interneurons and mossy cells. The neuropil signal was subtracted from the extracted fluorescence using suite2p. Neuronal activity was quantified by adapting previously published methods (Dombeck et al., 2010): “events” were identified as contiguous regions in the normalized relative change in fluorescence (ΔF/F) signal exceeding a threshold of mean + 2.5 standard deviations of the overall ΔF/F signal, a minimal duration above threshold of 300 ms (approximately the half decay time of the GCaMP6f signal (Dana et al., 2019)), and exceeding an integral of 50 ΔF/F × 1 s. These parameters were confirmed by visual inspection of the event detection result.

Identification of spatially modulated cells and place fields

To compute spatial activity maps, we used data from continuous running periods with a duration >1 s at a speed >0.5 cm/s. For each lap crossing, spatial maps were computed by dividing the track into 50 spatial bins. We then divided the sum of events in each spatial bin by the occupancy (dwell time) of the animal in this bin. Spatial maps were smoothed with a Gaussian filter (sigma = 5 cm).

We defined spatially modulated cells as those neurons that fire consistently at the same location across different lap crossings, independently of the exact shape of their place fields. Therefore, we identified spatially modulated cells by computing the mean pairwise circular cross-correlation between spatial maps across all different lap crossings within a session. We used circular (periodic) cross-correlation to account for the circular nature of our data, as the animals are teleported back to the beginning of the track when they reach the end of the previous track. We then searched for maximum cross correlation within 4 bins surrounding lag 0 (out of a total of 50 bins). Using Pearson’s R instead of circular cross correlation yielded consistent results (Figure S1E). To obtain a null model for the mean cross correlation, for each neuron, we dissociated firing activity and spatial position by shuffling the recorded position in chunks of 300 ms, and repeated this bootstrap procedure 100 times. Those neurons whose mean cross-correlation exceeded the bootstrap with a Z-score higher than 2.0 were identified as spatially modulated cells. This approach accounts for both coherence and stability of spatially modulated cells, as a cell will not be identified as spatially modulated if it only fires in one lap (low stability), or if it fires in different locations across laps (low coherence), or if it fires sparsely yielding a high mean pairwise correlation by chance (low stability, giving low Z score from the bootstrap procedure).

To determine the width of place fields (Figure S1F), we identified place cells according to published methods (Dombeck et al., 2010; Hainmueller and Bartos, 2018). We define place cells as a subset of spatially modulated cells with one or more significant peaks in their spatial firing maps. We divided the linear track into 50 spatial bins and computed the mean ΔF/F in each bin. Spatial ΔF/F maps were then smoothed using a moving average filter across 3 adjacent bins. Potential place fields were initially identified as contiguous regions in these ΔF/F maps in which all of the points were greater than 50% of the difference between the bin with the highest ΔF/F value and a baseline value (mean of the lowest 25 out of 50 bins’ ΔF/F values). In addition, the candidate place fields had to satisfy the following criteria: (i) The corresponding place cell had to fulfill our criteria for spatial modulation (see above); (ii) the potential field had to have a width of at least 3 bins (7.2  cm); (iii) significant calcium transients had to be present at least 30% of the time in which the mouse was moving in the field; and (iv) the mean ΔF/F value inside the field had to be at least three times the mean of the ΔF/F value outside the field. Place cells (as a subset of spatially modulated neurons) were only used for determining place field width (Figure S1F) in this study. Place fields in the familiar and novel environments showed similar widths in the dentate gyrus and CA1 (Familiar F: DG versus CA1, p < 0.05; Novel N: DG versus CA1, p > 0.05).

Spatial correlation and decorrelation

To quantify session-wise correlations between spatial activity maps of the F and N environments (“FN correlation”), we first computed the circular cross-correlation between spatial activity maps for the F and for the N environments for each neuron that was spatially modulated in the F environment (see above), and then computed the mean of these correlation values for a session. As a reference, we computed correlations within the F environment (“F even-odd correlation”) by splitting the exploration of the familiar environment into odd and even lap crossings, and then computing spatial correlations between even and odd spatial activity maps as described above for the FN correlations. Decorrelation was computed by subtracting the FN correlation from the F even-odd correlation.

Population vector (PoV) correlations

Population vectors (PoV) were defined as the collection of event rates of the population of all spatially modulated neurons measured in a spatial bin of a given environment. PoV correlations were obtained by computing Pearson’s R between corresponding PoVs of different environments (F versus N or N^∗) or of the same environment split into even and odd lap crossings (F even-odd or N(^∗) even-odd). PoV correlation matrices depict color-coded PoV correlations between all spatial bins in F versus all spatial bins in N (or N^∗). For PoV correlations comparing F versus N or N^∗, spatial modulation was assessed in environment F.

Rate vector and selectivity

To compute selectivity, the event rate for the i-th cell r_i was defined as the number of identified neural events of a cell divided by the total running time in a lap or in a session. For each session, selectivity of the i-th neuron was defined as the normalized difference of event rates of that neuron computed during familiar and novel lap crossings (referred to as F and N, respectively): |r_i^F – r_i^N| / (r_i^F + r_i^N). “Signed” selectivity was defined accordingly, with no absolute value at the numerator. The rate vector was defined as the collection of event rates of a population of neurons during a lap crossing or a session.

Inference-based decoder for environmental representation

To decode the environmental representation from neural activity alone (i.e., with no information on the precise location of the animal on the track), we employed published methods based on probabilistic modeling of population activity and Bayesian hypothesis testing (Posani et al., 2017). In brief, two statistical models, one for each environmental condition, were inferred from two collections of binarized activity vectors (discretized and binarized events in a time window of 120 ms) recorded during exploration of the two corresponding environments, denoted here as A and B.

By defining the binarized activity of the i-th cell in a time bin as s_i ∈ {0, 1}, each model describes a probability distribution for the activity vector s = (s₁, s₂, ⋯, s_N) given the environmental variable M ∈ {A, B}. The model reads

$$P\left(\mathbf{s}|M\right)=\prod _{i=1}^N\frac{e^{h_i^M{s}_i}}{1+e^{h_i^M}},$$

where parameters h_i^M control the mean event rate of the i-th neuron and are inferred such that the probabilistic model reproduces, on average, the mean event rate observed in the training set. For this particular class of models (statistically independent neurons), this procedure can be carried out analytically and yields

$$h_i^M=\log \frac{{⟨s_i⟩}_M}{1-{⟨s_i⟩}_M},$$

where the notation ⟨.⟩_M indicates the average over the activity vectors in the training set for environment M.

We then decoded the environmental variable M from the test activity vectors by comparing the two probabilistic models in a Bayesian hypothesis test. For each test vector s, we computed the log-likelihood difference between the two environments as

$$\Delta \mathcal{L}\left(\mathbf{s}\right)=\log \frac{P\left(\mathbf{s}|A\right)}{P\left(\mathbf{s}|B\right)}.$$

A positive value of Δ$\mathcal{L}$(s) indicates that the test activity vector s is more likely to have been sampled from environmental conditions A than B and vice-versa for negative values.

Cross-validated performance of the environment decoder

Events were discretized into binary population activity vectors corresponding to time windows of 120 ms. Lap crossings in a recording session were then divided according to the two environmental conditions, and then further into training and test lap crossings (half and half, randomly). Activity vectors corresponding to training lap crossings were used to train the binary decoder, which was used to predict the environmental conditions of activity vectors sampled during test lap crossings. For each test vector s, we computed the decoder outcome Δ$\mathcal{L}$(s) and assessed the performance of the decoder on the population of Δ$\mathcal{L}$(s) values. Performance was assessed by contextualizing the Δ$\mathcal{L}$(s) signal within the binary decoder theory and receiving-operator characteristic curves (Bradley, 1997), as established in previous publications (Posani et al., 2017, 2018). In brief, a threshold Δ$\mathcal{L}$₀ is chosen, and activity vectors whose delta log-likelihood difference Δ$\mathcal{L}$(s) exceeded the threshold were classified as “positive” (corresponding to environment A), while the ones below were classified as “negative” (corresponding to environment B). The threshold value is varied in a large interval, and for every value we compute the fraction of correctly classified A patterns (true positive rate, TPR) and the fraction of falsely classified A patterns (false positive rate, FPR). Each pair of TPR-FPR draws a point on the so-called ROC curve. The area under the ROC curve (AUC) is taken as a measure of performance. This procedure was repeated for n = 100 random assignments of training and test labels to individual lap crossings; the mean AUC value over these 100 repetitions was then taken as a measure of decoding performance for the session.

Inclusion criteria for environment decoding analysis

The decoding analysis aims to establish whether two environmental representations are dissimilar/decorrelated (high decoding performance) or similar/correlated (low decoding performance). However, a negative result (low decoding performance) could also be caused by the lack of a stable and coherent firing activity within individual environments resulting from external factors such as noise, mis-positioning of the field of view, or low engagement of the animal. We therefore chose to include only sessions that satisfy a minimal criterion of stability of firing activity within the familiar environment, as would be expected from hippocampal representations after repeated exposure to a context. To assess a position-agnostic measure of stability, we computed the mean firing rate vector (RV) in each individual lap crossing in the session; we then defined stability as the mean Pearson correlation between RVs of all pairs of lap crossings in the familiar environment. We included those sessions where stability was higher than a minimal threshold (set to 0.01).

Selectivity analysis for subthreshold membrane potential

To analyze subthreshold membrane potential, traces were digitally low-pass filtered at 5 kHz and resampled at 10 kHz. Membrane potential traces were then high-pass filtered at >10⁻⁵ Hz to remove slow trends such as reference drifts. To infer the expected firing profile of silent neurons, we applied a range of thresholds ϴ to the recorded membrane potential trace. Action potentials were inferred whenever membrane potential exceeded ϴ, and a minimal interspike interval of 100 ms was imposed on the inferred action potentials. Environment selectivity was then computed as S_AB = (f_A – f_B) / (f_A + f_B), where f_A and f_B are the predicted action potential frequencies in environment A and B, respectively, for a given value of ϴ. A positive value of S_AB indicates selectivity for environment A while a negative value indicates selectivity for environment B. Mean absolute selectivity was calculated by computing the average of the mean absolute value of S_AB for 100 values of ϴ spanning a range of 2 standard deviations around the mean membrane potential of the recording.

Behavioral discrimination between contexts

For each session, we used the lick behavior of the animal in the novel environment to quantify behavioral discrimination. If the animal confuses the novel environment with the familiar one, we expect it to lick in anticipation of a reward in the reward zone corresponding to the wrong (familiar) environment, i.e., at the end of the track. Likewise, we expect the animal to lick only in the correct reward zone (novel, center of the track) when it recognizes the novel environment and learns the task. To quantify behavioral discrimination, for each lap crossing we detected a hit if the ratio between number of licks in the correct (novel) reward zone and the region of the track outside any reward zone was higher than a threshold (set to 1.2). Likewise, an error was detected if the ratio between the number of licks in the wrong (familiar) reward zone and the region of the track outside the reward zone was higher than the same threshold. By contrast, in order to exclude noisy data, the ratios below the threshold (1.2) were considered neither correct nor errors, and were not included in the analysis. d-prime was computed for each session by using all errors and hits of the corresponding lap crossings, excluding those laps where both an error and a hit were recognized.

In order to minimize the variability between animals and compute a multilevel statistical analysis, the quantifications for the correlations between neuronal and behavioral discrimination were normalized within the range value of each animal. Therefore, both the behavioral scores (reward rate or d-prime) and the spatial decorrelation (or decoder performance) values have a range score spanning from 0 to 1, i.e., from the worst to the best behavioral performance and neuronal discrimination.

To rule out that neuronal discrimination between different environments could be performed when the presentation of the visual virtual-reality environment is uncoupled from the behavior of the animal, we passively presented previously recorded virtual reality sessions to the animals in an open-loop paradigm (Figure S3I). These experiments confirmed that neuronal discrimination in both the dentate gyrus and CA1 required active engagement of the animal in a navigational task, as we found that neuronal discrimination between highly different virtual environments (F and N^∗) was reduced in both regions when a movie was passively presented (Figure S3J).

Statistics and visualization

Data are presented as mean ± SEM across animals, unless stated otherwise. Statistical significance was assessed using Wilcoxon signed-rank tests (“Wilcoxon tests”), one-way repeated-measures (RM) ANOVA, or a linear mixed model (LMM; see Table S1), as appropriate. In some figures, a small amount of jitter was applied to coinciding data points to improve visual clarity.

Published: October 16, 2020