Optimal strategies for social distancing and testing to control COVID-19

Abstract

The coronavirus disease (COVID-19) has infected more than 79 million individuals, with 1.7 million deaths worldwide. Several countries have implemented social distancing and testing policies with contact tracing as a measure to flatten the curve of the ongoing pandemic. Optimizing these control measures is urgent given the substantial societal and economic impacts associated with infection and interventions. To determine the optimal social distancing and testing strategies, we developed a mathematical model of COVID-19 transmission and applied optimal control theory, identifying the best approach to reduce the epidemiological burden of COVID-19 at a minimal cost. The results demonstrate that testing as a standalone optimal strategy does not have a significant effect on the final size of an epidemic, but it would delay the peak of the pandemic. If social distancing is the sole control strategy, it would be optimal to gradually increase the level of social distancing as the incidence curve of COVID-19 grows, and relax the measures after the curve has reached its peak. Compared with a single strategy, combined social distancing and testing strategies are demonstrated to be more efficient at reducing the disease burden, and they can delay the peak of the disease. To optimize these strategies, testing should be maintained at a maximum level in the early phases and after the peak of the epidemic, whereas social distancing should be intensified when the prevalence of the disease is greater than 15%. Accordingly, public health agencies should implement early testing and switch to social distancing when the incidence level begins to increase. After the peak of the pandemic, it would be optimal to gradually relax social distancing and switch back to testing.

1. Introduction

The ongoing outbreak of the novel coronavirus disease (COVID-19) has considerably affected public health and the economy worldwide. As of December 27, 2020, more than 79 million COVID-19 cases and 1.7 million deaths have been reported (WHO, 2020a). The severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), which causes the COVID-19 pandemic, is highly contagious, with an estimated basic reproduction number ranging from 1.5 to 6.5 (Shim et al., 2020b, You et al., 2020, Kucharski et al., 2020, Liu et al., 2020, Mizumoto and Chowell, 2020a, Mizumoto and Chowell, 2020b, Mizumoto et al., 2020a, Park et al., 2020a, Rocklöv et al., 2020). Additionally, it has been suggested that 40% to 80% of COVID-19 infections are caused by pre-symptomatic or asymptomatic individuals, indicating that a large number of unknown infectious individuals may continue to be exposed others without being aware of their status (Arav et al., 2020, Ferretti et al., 2020, Li et al., 2020, Mizumoto et al., 2020b, Nishiura et al., 2020, Prakash, 2020, Tindale et al., 2020).

As COVID-19 infections have increased exponentially, urgent efforts to contain and mitigate transmission around the world have been made, although the COVID-19 vaccine supply is still limited in many countries. Nevertheless, non-pharmaceutical interventions have been implemented to mitigate the epidemic wave of COVID-19, or suppress it over a period of time that is sufficient to develop and implement vaccines and treatments. Such non-pharmaceutical public health interventions include social distancing (Anderson et al., 2020, Lewnard and Lo, 2020, Shim et al., 2020b, Park et al., 2020b, Wilder-Smith and Freedman, 2020), testing (Cohen and Kupferschmidt, 2020, Omori et al., 2020, Piguillem and Shi, 2020, Ferretti et al., 2020, Sousa-Pinto et al., 2020, Tuite et al., 2020), wearing face masks (Eikenberry et al., 2020, Feng et al., 2020, Ngonghala et al., 2020, Organization, 2020), and delaying school openings (Kim et al., 2020).

Numerous countries have selected social distancing as the main mitigation strategy for COVID-19 transmission because this measure can be easily implemented and does not rely on microbiological data (Greenstone and Nigam, 2020, Kim et al., 2020, Lewnard and Lo, 2020, Park et al., 2020b, Viner et al., 2020, Wilder-Smith and Freedman, 2020). As the number of confirmed COVID-19 patients and the spread of the disease have entered a global exponential growth phase, a wide range of unprecedented social distancing measures have been implemented, including school, workplace, and public transport closures, as well as lockdowns and restrictions on mass gathering (Islam et al., 2020). Recent studies have reported that the implementation of social distancing interventions was associated with an overall reduction in the risk of infection (Cowling et al., 2020, Islam et al., 2020, Pan et al., 2020, Shim et al., 2020b).

Another major non-pharmaceutical strategy for mitigating the spread of COVID-19 is contact tracing followed by testing; thereby, community infections can be prevented by screening individuals and isolating them before they transmit the disease. For example, South Korea has instituted large-scale testing efforts using drive-through testing stations, a survey of clusters related to infections, nursing hospitals, and social welfare facilities (Cohen and Kupferschmidt, 2020, Kwon et al., 2020). South Korea was testing approximately 15,000 individuals per day from the time when the number of daily confirmed cases was approximately 1,000 per day at the end of February until the end of March. This strategy was effective, reducing the number of daily new cases to under 30 from April 13 to May 9, 2020, although the subsequent relaxation of social distancing resulted in a resurgence in the number of new cases (KCDC, 2020, Shim et al., 2020a). Additionally, some studies have demonstrated that aggressive and extensive testing can reduce the number of infections by detecting and isolating infected individuals before they come into contact with others (Omori et al., 2020, Piguillem and Shi, 2020, Shim et al., 2020b, Ferretti et al., 2020, Jenny et al., 2020, Li et al., 2020, Sousa-Pinto et al., 2020, Tuite et al., 2020).

Although these aggressive measures are expected to effectively reduce the transmission of COVID-19, they can result in substantial economic loss and societal disruption (Ugarov, 2020). Additionally, non-pharmaceutical interventions may slow disease transmission and appear to be successful in reducing the number of confirmed cases; however, rebound of infection may occur rapidly once such interventions are halted (Ferguson et al., 2006, Ferguson et al., 2020). Therefore, it is important to determine the optimal mitigation and containment strategies so that an acceptable balance between economic and public health goals may be achieved, and the potential transmission risk of the COVID-19 pandemic may be minimized.

In this study, we developed a mathematical model of COVID-19 transmission considering time-dependent social distancing and testing strategies. Optimal control theory was then applied to the model to identify the optimal strategies under various epidemiological conditions. Specifically, we identified the optimal strategies that minimize the costs associated with infection and intervention under scenarios in which single or combined controls are available.

2. Method

2.1. Model description and reproduction number

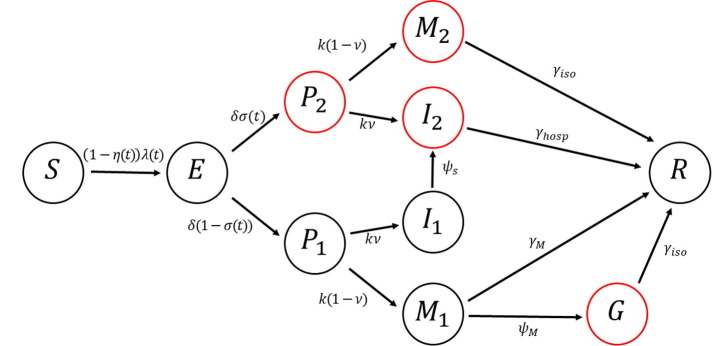
We constructed a mathematical model of COVID-19 transmission considering social distancing and testing as intervention strategies (Fig. 1 ). We assumed that all individuals who tested positive were isolated or hospitalized. The model classifies individuals based on their epidemiological status, namely, susceptible ($S$), exposed ($E$), infectious ($P_1,P_2,M_1,M_2,G,I_1,I_2$), and recovered ($R$) (Table 1 ). Infectious individuals are further subdivided into seven groups depending on their isolation and symptom status. Specifically, pre-symptomatic and tested individuals who are isolated ($P_2$) progress into the class $M_2$ or $I_2$ if they develop none-to-mild or severe symptoms, respectively. Similarly, pre-symptomatic individuals who are not (yet) isolated ($P_1$) are included in the non-isolated class $M_1$ or $I_1$ if they develop none-to-mild or severe symptoms, respectively. For simplicity, it is also assumed that individuals with severe symptoms who have not been tested will be eventually hospitalized. That is, individuals in $I_1$ will later be hospitalized and enter the class $I_2$. Similarly, non-tested and pre-symptomatic individuals in $P_1$ will move to $M_1$ if they develop none-to-mild symptoms. Some individuals in $M_1$ will be isolated and move to the class $G$. Upon recovery, all infected individuals will enter the recovered class $R.$

Fig. 1.

Diagram of the model of COVID-19 transmission with social distancing and testing as control strategies. Classes that are isolated/hospitalized are indicated by red circles. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 1.

Description of the model variables.

Variable	Description
$S$	Susceptible individuals
$E$	Exposed individuals
$P_1$	Pre-symptomatic individuals who are not (yet) tested
$P_2$	Pre-symptomatic and tested individuals who are isolated
$M_1$	Mildly infectious individuals who are not tested
$M_2$	Mildly infectious and tested individuals who are isolated
$G$	Mildly infectious individuals who are isolated
$I_1$	Severely infectious individuals who are not yet hospitalized
$I_2$	Infectious individuals who are hospitalized due to severe symptoms
$R$	Recovered individuals

It was recently reported that approximately 80% of confirmed COVID-19 patients have none-to-mild symptoms (WHO, 2020b, Wu and McGoogan, 2020). In the proposed model, it is noted that the classes $M_1,M_2,$ and $G$ include those who are infectious with none-to-mild symptoms. Furthermore, we assume equal infectiousness among pre-symptomatic individuals, infected individuals with no, mild or severe symptoms (He et al., 2020, Slifka and Gao, 2020, Yin and Jin, 2020). Thus, it is assumed that susceptible individuals become infected at a rate

$$\frac{{\beta }_0(1-\eta )\left(P_1+M_1+I_1+(1-\theta )\left(P_2+M_2+G+I_2\right)\right)}{N-\theta (P_2+M_2+G+I_2)},$$

where the total population size is given by $N\left(t\right)=S\left(t\right)+E\left(t\right)+P_1\left(t\right)+P_2\left(t\right)+M_1\left(t\right)+M_2\left(t\right)+G\left(\mathrm{t}\right)+I_1\left(t\right)+I_2\left(t\right)+R\left(\mathrm{t}\right)$. As the time scale in this study is relatively short, we ignore births and deaths, allowing the population to be asymptotically constant (i.e., $\underset{t\to \infty }{\lim }N(t)=K$). In the model, $\theta$ indicates the effectiveness of hospitalization and isolation in terms of preventing further transmission ($0\le \theta \le 1$). That is, θ = 0 means that hospitalized and isolated infected people are free to mix with the rest of the population. On the other hand, θ = 1 indicates that the isolation and hospitalization is fully effective. Accordingly, (1- θ) measures the contribution of hospitalized and isolated infected people to the force of infection (Ngonghala et al., 2020). Here, ${\beta }_0$ denotes the transmission rate, and we incorporate social distancing into the model by assuming that susceptible individuals reduce their rate of contact by a fraction $\eta \left(t\right)(0\le \eta (t)\le {\eta }_{\mathit{max}}<1)$.

We define $1/{\psi }_m$ and $1/{\psi }_s$ as the average delay from symptom onset to diagnosis for infected individuals with none-to-mild and severe symptoms, respectively. Furthermore, $1/\delta$ is defined as the latent period, and $1/k$ denotes the infectious period prior to symptom onset. The proportion of severely infectious individuals who will be hospitalized is denoted by $\nu$. Additionally, the recovery rate of mildly infectious individuals is assumed to be ${\gamma }_M$. The average duration of isolation and hospitalization are denoted by $1/{\gamma }_{\mathit{iso}}$ and $1/{\gamma }_{\mathit{hosp}}$, respectively.

We incorporate testing with contact tracing into the model by assuming that exposed individuals are isolated with a probability $\sigma \left(t\right)$, where $0\le \sigma (t)\le {\sigma }_{\mathit{max}}<1$, based on their test results. The probability of identifying exposed individuals is determined by the intensity of testing. Recovered individuals are assumed to remain immune from re-infection for the duration of the epidemic. The baseline values for the epidemiological parameters are listed in Table 2 .

Table 2.

Definitions of parameters and their baseline values used in numerical simulations.

Parameter	Description	Value	References
${\mathcal{R}}_0$	Basic reproduction number	2.8	(Deng et al., 2020, Linka et al., 2020, Wu et al., 2020, You et al., 2020)
${\beta }_0$	Transmission rate	0.50	Estimated from ${\mathcal{R}}_0$
$\eta$	Social distancing level	control	Derived from optimization
$\sigma$	Probability that pre-symptomatic individuals will be tested and isolated	control	Derived from optimization
$1/\delta$	Length of latent period (days)	3.1	(Lauer et al., 2020)
$1/k$	Length of pre-symptomatic infectious period (days)	2	(Wei et al., 2020)
$\nu$	Proportion of severely infectious individuals who are hospitalized	0.2	(WHO, 2020b)
$1/{\gamma }_M$	Infectious period of mild infections (days)	7	(Zhou et al., 2020)
$1/{\gamma }_{\mathit{iso}}$	Average time in isolation of mildly infectious individuals (days)	10	(CDC, 2020a)
$1/{\gamma }_{\mathit{hosp}}$	Average duration of hospitalization of severely infectious individuals (days)	14.5	(Fonfría et al., 2020)
${1/\psi }_m$	Average duration from the onset of symptoms to diagnosis among infectious individuals with none-to-mild symptoms (days)	4	(Burrer et al., 2020)
$1/{\psi }_s$	Average duration from the onset of symptoms to diagnosis among infectious individuals with severe symptoms (days)	4	(Burrer et al., 2020)
$\theta$	Effectiveness of hospitalization and isolation in terms of preventing further transmission	0.9	Assumed
${\chi }_T$	Average number of tests required to identify one infectious individual	10	(CDC)
$C_S$	Cost of social distancing (USD)	178	(WorldBank, 2020)
$C_T$	Cost of diagnostic test for COVID-19 (USD)	142	(Nisha Kurani et al., 2020)
$C_I$	Cost to treat a hospitalized patient with COVID-19 (USD)	25,617	(Chen et al., 2020)
$C_M$	Cost of treatment for individuals with mild COVID-19 infection (USD)	3,045	(Bartsch et al., 2020)
${\eta }_{\mathit{max}}$	Upper bound of social distancing level	0.5	Assumed
${\sigma }_{\mathit{max}}$	Upper bound of testing intensity	0.2	Assumed

Given the definitions and assumptions discussed above, a transmission dynamic model that incorporates the time-dependent control parameters $\eta \left(t\right)$ and $\sigma \left(t\right)$ can be described by the following ordinary differential equations:

$$\frac{\mathit{dS}}{\mathit{dt}}=-\left(1-\eta (t)\right)\lambda \left(t\right)S\left(t\right),$$

$$\frac{\mathit{dE}}{\mathit{dt}}=\left(1-\eta (t)\right)\lambda \left(t\right)S\left(t\right)-\delta E\left(t\right),$$

$$\frac{{\mathit{dP}}_1}{\mathit{dt}}=\delta \left(1-\sigma (t)\right)E\left(t\right)-k{P}_1\left(t\right),$$

$$\frac{{\mathit{dP}}_2}{\mathit{dt}}=\delta \sigma (t)E\left(t\right)-k{P}_2\left(t\right),$$

$$\frac{{\mathit{dM}}_1}{\mathit{dt}}=k\left(1-\nu \right)P_1\left(t\right)-({\psi }_m+{\gamma }_M)M_1\left(t\right),$$

$$\frac{{\mathit{dM}}_2}{\mathit{dt}}=k\left(1-\nu \right)P_2(t)-{\gamma }_{\mathit{iso}}{M}_2\left(t\right),$$

$$\frac{\mathit{dG}}{\mathit{dt}}={\psi }_m{M}_1\left(t\right)-{\gamma }_{\mathit{iso}}G(t),$$

$$\frac{d{I}_1}{\mathit{dt}}=k\nu P_1\left(t\right)-{\psi }_s{I}_1\left(t\right),$$

$$\frac{d{I}_2}{\mathit{dt}}=k\nu P_2\left(t\right)+{\psi }_s{I}_1\left(t\right)-{\gamma }_{\mathit{hosp}}{I}_2\left(t\right),$$

$$\frac{\mathit{dR}}{\mathit{dt}}={\gamma }_M{M}_1\left(t\right)+{\gamma }_{\mathit{iso}}{M}_2\left(t\right)+{\gamma }_{\mathit{iso}}G(t)+{\gamma }_{\mathit{hosp}}{I}_2\left(t\right),$$

where the force of infection $\lambda \left(t\right)$ is defined as

$$\lambda \left(t\right)=\frac{{\beta }_0\left(P_1+M_1+I_1+(1-\theta )\left(P_2+M_2+G+I_2\right)\right)}{N-\theta (P_2+M_2+G+I_2)}.$$

In the model, we note that the variable $R(t)$ appears only in $\mathit{dR}/dt$, and thus we determine it after solving for the other classes. In addition, we use dimensionless variables $(s=\frac{S}{K},e=\frac{E}{K},p_1=\frac{P_1}{K},p_2=\frac{P_2}{K},m_1=\frac{M_1}{K},m_2=\frac{M_2}{K},g=\frac{G}{K},i_1=\frac{I_1}{K},i_2=\frac{I_2}{K})$ and present the following simplified model:

$$\frac{\mathit{ds}}{\mathit{dt}}=-\left(1-\eta (t)\right)\lambda \left(t\right)s\left(t\right),$$

$$\frac{\mathit{de}}{\mathit{dt}}=\left(1-\eta (t)\right)\lambda \left(t\right)s\left(t\right)-\delta e\left(t\right),$$

$$\frac{{\mathit{dp}}_1}{\mathit{dt}}=\delta \left(1-\sigma (t)\right)e\left(t\right)-k{p}_1\left(t\right),$$

$$\frac{{\mathit{dp}}_2}{\mathit{dt}}=\delta \sigma (t)e\left(t\right)-k{p}_2\left(t\right),$$

$$\frac{{\mathit{dm}}_1}{\mathit{dt}}=k\left(1-\nu \right)p_1\left(t\right)-({\psi }_m+{\gamma }_M)m_1\left(t\right),$$

$$\frac{{\mathit{dm}}_2}{\mathit{dt}}=k\left(1-\nu \right)p_2(t)-{\gamma }_{\mathit{iso}}{m}_2\left(t\right),$$

$$\frac{\mathit{dg}}{\mathit{dt}}={\psi }_m{m}_1\left(t\right)-{\gamma }_{\mathit{iso}}g(t),$$

$$\frac{d{i}_1}{\mathit{dt}}=k\nu p_1\left(t\right)-{\psi }_s{i}_1\left(t\right),$$

$$\frac{d{i}_2}{\mathit{dt}}=k\nu p_2\left(t\right)+{\psi }_s{i}_1\left(t\right)-{\gamma }_{\mathit{hosp}}{i}_2\left(t\right),$$

where $\lambda \left(t\right)=\frac{{\beta }_0\left(p_1+m_1+i_1+(1-\theta )\left(p_2+m_2+g+i_2\right)\right)}{1-\theta (p_2+m_2+g+i_2)}.$

The disease-free equilibrium (DFE) of the model is

$$\mathit{DFE}=\left(s^{\ast },e^{\ast },p_1^{\ast },p_2^{\ast },m_1^{\ast },m_2^{\ast },g,i_1^{\ast },i_2^{\ast }\right)=\left(1,0,0,0,0,0,0,0\right)$$

The control reproduction number ${\mathcal{R}}_{\mathrm{c}}(\eta ,\sigma )$ measures the average number of secondary infections generated by an infected individual when control measures are in effect and constant over time ($\eta \left(t\right)=\eta$ and $\sigma \left(t\right)=\sigma$). We use the next-generation operator method to determine ${\mathcal{R}}_{\mathrm{c}}(\eta ,\sigma )$ (van den Driessche and Watmough, 2002). Specifically, we define the matrices $\mathcal{F}$ and $\mathcal{V}$ using the new infection and transition terms, respectively:

$\mathcal{F}=\left[\begin{array}{c}\begin{array}{c}(1-\eta )\lambda \left(t\right)s\left(t\right)\\ 0\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right]$ and $\mathcal{V}=\left[\begin{array}{c}\begin{array}{c}\delta e\left(t\right)\\ -\delta \left(1-\sigma \right)e\left(t\right)+k{p}_1\left(t\right)\\ -\delta \sigma e\left(t\right)+k{p}_2\left(t\right)\end{array}\\ -k\left(1-\nu \right)p_1\left(t\right)+({\psi }_m+{\gamma }_M)m_1\left(t\right)\\ -k\left(1-\nu \right)p_2\left(t\right)+{\gamma }_{\mathit{iso}}{m}_2\left(t\right)\\ -{\psi }_m{m}_1\left(t\right)+{\gamma }_{\mathit{iso}}g\left(t\right)\\ -k\nu p_1\left(t\right)+{\psi }_s{i}_1\left(t\right)\\ -k\nu p_2\left(t\right)-{\psi }_s{i}_1\left(t\right)+{\gamma }_{\mathit{hosp}}{i}_2\left(t\right)\end{array}\right].$

We linearize the matrices $\mathcal{F}$ and $\mathcal{V}$ at the DFE as follows:

$$F={\beta }_0\left(1-\eta \right)\left[\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}1\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}(1-\theta )\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}1\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}(1-\theta )\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}(1-\theta )\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}1\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}(1-\theta )\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right]$$

and $V=\left[\begin{array}{c}\begin{array}{c}\delta \\ -\delta \left(1-\sigma \right)\end{array}\\ -\delta \sigma \\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}0\\ k\end{array}\\ 0\\ -k\left(1-\nu \right)\\ 0\\ 0\\ -k\nu \\ 0\end{array}\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ k\\ 0\\ -k\left(1-\nu \right)\\ 0\\ 0\\ -k\nu \end{array}\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ 0\\ {\psi }_m+{\gamma }_M\\ 0\\ -{\psi }_m\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ 0\\ 0\\ {\gamma }_{\mathit{iso}}\\ 0\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ 0\\ 0\\ 0\\ {\gamma }_{\mathit{iso}}\\ 0\\ 0\end{array}\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\\ {\psi }_s\\ -{\psi }_s\end{array}\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\\ 0\\ {\gamma }_{\mathit{hosp}}\end{array}\right].$

Then, the control reproduction number ${\mathcal{R}}_c\left(\eta ,\sigma \right)$ is defined by the spectral radius of the next generation matrix $F{V}^{-1}$ as

$${\mathcal{R}}_c\left(\eta ,\sigma \right)={\mathcal{R}}_{\mathit{Pc}}+{\mathcal{R}}_{\mathit{Mc}}+{\mathcal{R}}_{\mathit{Ic}},$$

where

$${\mathcal{R}}_{\mathit{Pc}}={\beta }_0\left(1-\eta \right)\left[\frac{1-\sigma }{k}+\frac{(1-\theta )\sigma }{k}\right],$$

${\mathcal{R}}_{\mathit{Mc}}={\beta }_0\left(1-\eta \right)\left[\frac{\left(1-\sigma \right)\left(1-\nu \right)}{{\psi }_m+{\gamma }_M}+\frac{(1-\theta )\sigma \left(1-\nu \right)}{{\gamma }_{\mathit{iso}}}+\frac{(1-\theta )\left(1-\sigma \right)\left(1-\nu \right){\psi }_m}{{\gamma }_{\mathit{iso}}\left({\psi }_m+{\gamma }_M\right)}\right],$ and

$${\mathcal{R}}_{\mathit{Ic}}={\beta }_0\left(1-\eta \right)\left[\frac{\left(1-\sigma \right)\nu }{{\psi }_s}+\frac{(1-\theta )\nu }{{\gamma }_{\mathit{hosp}}}\right].$$

The quantity ${\mathcal{R}}_c$ is the sum of the reproduction numbers associated with the number of new COVID-19 cases generated by pre-symptomatic individuals (${\mathcal{R}}_{\mathit{Pc}}$), mildly infectious individuals (${\mathcal{R}}_{\mathit{Mc}}$), and severely infectious individuals (${\mathcal{R}}_{\mathit{Ic}}$). The level curve of the control reproduction number (${\mathcal{R}}_c$) is shown in Fig. 2 .

Fig. 2.

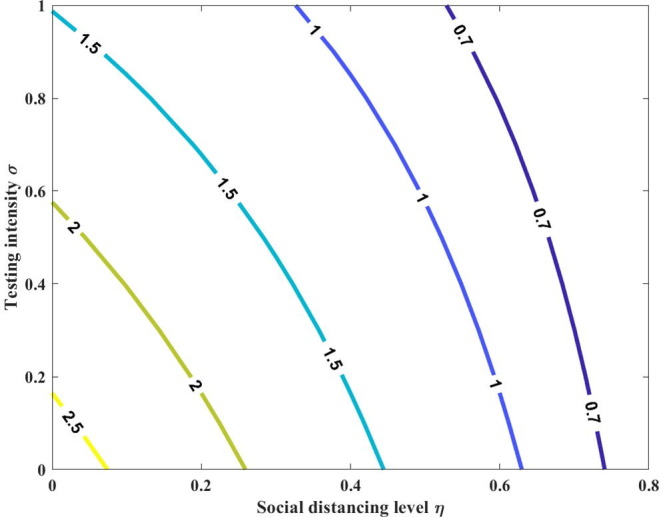
Contour plot of ${\mathcal{R}}_c$ as a function of both the social distancing level $\eta$ and testing intensity $\sigma$. Here, we assume the constant values for the social distancing level and testing intensity, i.e., $\eta \left(t\right)=\eta$ and $\sigma \left(t\right)=\sigma$.

The basic reproduction number ${\mathcal{R}}_0$ represents the average number of secondary infections resulting from introducing one infected individual into the entire susceptible population in the absence of control measures, and it is defined as

$${\mathcal{R}}_0={\mathcal{R}}_c\left(0,0\right)={\beta }_0\left[\frac{1}{k}+\frac{1-\nu }{{\psi }_m+{\gamma }_M}+\frac{(1-\theta )\left(1-\nu \right){\psi }_m}{{\gamma }_{\mathit{iso}}\left({\psi }_m+{\gamma }_M\right)}+\frac{\nu }{{\psi }_s}+\frac{(1-\theta )\nu }{{\gamma }_{\mathit{hosp}}}\right].$$

2.2. Sensitivity analysis

We now investigate the sensitivity of the model outcomes to parameter variations, focusing specifically on parameters that can affect ${\mathcal{R}}_0$: transmission rate (${\beta }_0$), rate of progression to symptomatic stage ($k$), proportion of severely infectious individuals who are hospitalized ($\nu$), rate of recovery for mild cases (${\gamma }_M$), and rate of diagnosis (${\psi }_m$ and ${\psi }_s$). For sensitivity analysis, we varied transmission rate ${\beta }_0$ and investigated the changes in the epidemic curve of infectious individuals (Figs. S1 and S2). It was shown that an increase in the transmissibility increases the attack rate. We also varied each parameter individually (except ${\beta }_0$) across the 95% confidence interval of its uncertainty distribution and determined the minimum and maximum values of ${\mathcal{R}}_0$ (Table S1). The tornado plot shows the one-way sensitivities of ${\mathcal{R}}_0$ to the values of five parameters in the model (Fig. 3 ). The simulation shows that the most influential parameter is the rate of progression to symptomatic stage ($k$), and the least influential parameter was found to be the proportion of severely infectious individuals who are hospitalized ($\nu$).

Fig. 3.

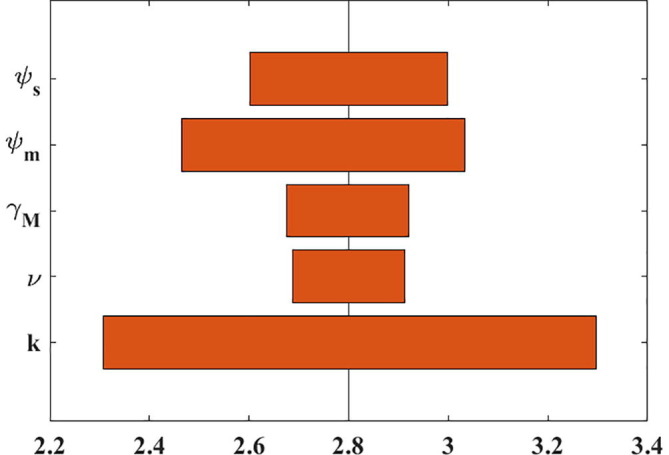
One-way, local sensitivity analysis of parameter contributions to the uncertainty of basic reproduction number. The vertical line represents the basic reproduction number under baseline conditions.

2.3. Application of optimal control theory

We apply optimal control theory to minimize the cost associated with COVID-19 infection and control strategies. Specifically, we define an optimal control problem with the following objective function to be minimized:

$$\mathcal{F}\left(\eta \left(t\right),\sigma \left(t\right)\right)={\int }_{t=0}^T\{C_M(k\left(1-\nu \right)p_2\left(t\right)+{\psi }_m{m}_1\left(t\right))+C_I(k\nu p_2\left(t\right)+{\psi }_s{i}_1\left(t\right))+C_S{\eta }^2\left(t\right)s\left(t\right)+C_T{\chi }_T\delta e\left(t\right){\sigma }^2\left(t\right)\}dt$$

Here, the control effect is modeled by the quadratic terms in $\eta \left(t\right)$ and $\sigma (t)$, where $C_S$ and $C_T$ are the costs of social distancing and testing, respectively. We define $C_M$ and $C_I$ as the costs associated with the isolation of mildly symptomatic individuals, and the hospitalization of infected individuals with severe symptoms, respectively. We let ${\chi }_T$ denote the average number of tests required to identify one infectious individual. It is assumed that the medical cost associated with fatal cases are included in the cost of hospitalizations ($C_I$).

The optimal social distancing and testing strategies can be obtained by determining the functions ${\eta }^{\ast }\left(t\right)$ and ${\sigma }^{\ast }(t)$ satisfying

$$\mathcal{F}\left({\eta }^{\ast }\left(t\right),{\sigma }^{\ast }\left(t\right)\right)=\underset{\mathrm{\Theta }}{\mathit{min}}\mathcal{F}\left(\eta \left(t\right),\sigma \left(t\right)\right)$$

where $\mathrm{\Theta }=\{\left(\eta ,\sigma \right)\in L^1(0,T)|0\le \eta \le {\eta }_{\mathit{max}},0\le \sigma \le {\sigma }_{\mathit{max}}\}$. We apply Pontryagin’s maximum principle to solve this optimal control problem. The corresponding Hamiltonian function is defined as

$$H=C_M(k\left(1-\nu \right)p_2\left(t\right)+∊{\psi }_m{m}_1\left(t\right))+C_I(k\nu p_2\left(t\right)+{\psi }_s{i}_1\left(t\right))+C_S{\eta }^2\left(t\right)s\left(t\right)+C_T{\chi }_T\delta e\left(t\right){\sigma }^2\left(t\right)+{\xi }_s\left\{-\left(1-\eta \right)\lambda \left(t\right)s\left(t\right)\right\}+{\xi }_e\left\{\left(1-\eta \right)\lambda \left(t\right)s\left(t\right)-\delta e\left(t\right)\right\}+{\xi }_{p_1}\left\{\delta \left(1-\sigma \right)e\left(t\right)-k{p}_1\left(t\right)\right\}+{\xi }_{p_2}\left\{\delta \sigma e\left(t\right)-k{p}_2\left(t\right)\right\}+{\xi }_{m_1}\left\{k\left(1-\nu \right)p_1\left(t\right)-(∊{\psi }_m+\left(1-∊\right){\gamma }_M)m_1\left(t\right)\right\}+{\xi }_{m_2}\left\{k\left(1-\nu \right)p_2\left(t\right)-{\gamma }_{iso}{m}_2\left(t\right)\right\}+{\xi }_g\left\{∊{\psi }_m{m}_1\left(t\right)-{\gamma }_{iso}g\left(t\right)\right\}+{\xi }_{i_1}\left\{k\nu p_1\left(t\right)-{\psi }_s{i}_1\left(t\right)\right\}+{\xi }_{i_2}\left\{k\nu p_2\left(t\right)+{\psi }_s{i}_1\left(t\right)-{\gamma }_{hosp}{i}_2\left(t\right)\right\}.$$

By applying Pontryagin’s maximum principle, we obtain the following adjoint system:

$$\frac{d{\xi }_s}{\mathit{dt}}=-\frac{\partial H}{\partial s},\frac{d{\xi }_e}{\mathit{dt}}=-\frac{\partial H}{\partial e},\frac{d{\xi }_{p_1}}{\mathit{dt}}=-\frac{\partial H}{\partial p_1},\frac{d{\xi }_{p_2}}{\mathit{dt}}=-\frac{\partial H}{\partial p_2},$$

$$\frac{d{\xi }_{m_1}}{\mathit{dt}}=-\frac{\partial H}{\partial m_1},\frac{d{\xi }_{m_2}}{\mathit{dt}}=-\frac{\partial H}{\partial m_2},\frac{d{\xi }_g}{\mathit{dt}}=-\frac{\partial H}{\partial g},\frac{d{\xi }_{i_1}}{\mathit{dt}}=-\frac{\partial H}{\partial i_1},\frac{d{\xi }_{i_2}}{\mathit{dt}}=-\frac{\partial H}{\partial i_2}.$$

This system is evaluated for the optimal controls and the corresponding states. The above equations can be reduced to

$$\frac{d{\xi }_s}{\mathit{dt}}=-\frac{\partial H}{\partial s}=-C_S{\eta }^2\left(t\right)+\left(1-\eta \right)\lambda \left(t\right)\left({\xi }_s-{\xi }_e\right),$$

$$\frac{d{\xi }_e}{\mathit{dt}}=-\frac{\partial H}{\partial e}=\delta \left({\xi }_e-C_T{\chi }_T{\sigma }^2\left(t\right)-{\xi }_{p_1}\left(1-\sigma \right)-{\xi }_{p_2}\sigma \right),$$

$$\frac{d{\xi }_{p_1}}{\mathit{dt}}=-\frac{\partial H}{\partial p_1}=\frac{\left(1-\eta \right){\beta }_0}{1-\theta \left(p_2+m_2+g+i_2\right)}\left({\xi }_s-{\xi }_e\right)s\left(t\right)+k\left({\xi }_{p_1}-\left(1-\nu \right){\xi }_{m_1}-\nu {\xi }_{i_1}\right),$$

$$\frac{d{\xi }_{p_2}}{\mathit{dt}}=-\frac{\partial H}{\partial p_2}=\frac{\left(1-\eta \right){\beta }_0\left\{(1-\theta )+\theta \left(p_1+m_1+i_1\right)\right\}}{{\left(1-\theta \left(p_2+m_2+g+i_2\right)\right)}^2}\left({\xi }_s-{\xi }_e\right)s\left(t\right)+k\{{\xi }_{p_2}-\left(1-\nu \right)({\xi }_{m_2}+C_M)-\nu ({\xi }_{i_2}+C_I)\},$$

$$\frac{d{\xi }_{m_1}}{\mathit{dt}}=-\frac{\partial H}{\partial m_1}=\frac{{\beta }_0\left(1-\eta \right)\left({\xi }_s-{\xi }_e\right)s\left(t\right)}{1-\theta (p_2+m_2+g+i_2)}-∊{\psi }_m{C}_M+{\left(∊{\psi }_m+\left(1-∊\right){\gamma }_M\right)\xi }_{m_1}-∊{\psi }_m{\xi }_g,$$

$$\frac{d{\xi }_{m_2}}{\mathit{dt}}=-\frac{\partial H}{\partial m_2}=\frac{\left(1-\eta \right){\beta }_0\left\{(1-\theta )+\theta \left(p_1+m_1+i_1\right)\right\}}{{\left(1-\theta \left(p_2+m_2+g+i_2\right)\right)}^2}\left({\xi }_s-{\xi }_e\right)s\left(t\right)+{\gamma }_{\mathit{iso}}{\xi }_{m_2,}$$

$$\frac{d{\xi }_g}{\mathit{dt}}=-\frac{\partial H}{\partial g}=\frac{{\beta }_0(1-\eta )\left\{(1-\theta )+\theta \left(p_1+m_1+i_1\right)\right\}}{{\left(1-\theta \left(p_2+m_2+g+i_2\right)\right)}^2}\left({\xi }_s-{\xi }_e\right)s\left(t\right)+{\gamma }_{\mathit{iso}}{\xi }_g,$$

$$\frac{d{\xi }_{i_1}}{\mathit{dt}}=-\frac{\partial H}{\partial i_1}=\frac{{\beta }_0\left(1-\eta \right)\left({\xi }_s-{\xi }_e\right)s\left(t\right)}{1-\theta \left(p_2+m_2+g+i_2\right)}+{\psi }_s{\xi }_{i_1}-{\xi }_{i_2}-C_I{\psi }_s,$$

$$\frac{d{\xi }_{i_2}}{\mathit{dt}}=-\frac{\partial H}{\partial i_2}=\frac{{\beta }_0\left(1-\eta \right)\left\{(1-\theta )+\theta \left(p_1+m_1+i_1\right)\right\}}{{\left(1-\theta \left(p_2+m_2+g+i_2\right)\right)}^2}\left({\xi }_s-{\xi }_e\right)s\left(t\right)+{\gamma }_{\mathit{hosp}}{\xi }_{i_2}.$$

The transversality conditions are

$${\xi }_s\left(T\right)={\xi }_e\left(T\right)={\xi }_{p_1}\left(T\right)={\xi }_{p_2}\left(T\right)={\xi }_{m_1}\left(T\right)={\xi }_{m_2}\left(T\right)={\xi }_g\left(T\right)={\xi }_{i_1}\left(T\right)={\xi }_{i_2}\left(T\right)=0.$$

The Hamiltonian $H$ is minimized with respect to the controls at the optimal levels, yielding the following optimality conditions:

${\left(\frac{\partial H}{\partial \eta }\right|}_{\eta \left(t\right)={\eta }^{\ast }}=0$ and ${\left(\frac{\partial H}{\partial \sigma }\right|}_{\sigma (t)={\sigma }^{\ast }}=0.$By solving for $\eta$ and $\sigma$, we obtain

$${\eta }^{\ast }=\mathit{min}\left\{max\left\{0,\frac{{\beta }_0\left({\xi }_e-{\xi }_s\right)\left(p_1+m_1+i_1+(1-\theta )\left(p_2+m_2+g+i_2\right)\right)}{2C_S\left\{1-\theta \left(p_2+m_2+g+i\right)\right\}}\right\},{\eta }_{\mathit{max}}\right\}$$

and ${\sigma }^{\ast }=\mathit{min}\left\{max\left\{0,\frac{{\xi }_{p_1}-{\xi }_{p_2}}{2C_T{\chi }_T}\right\},{\sigma }_{\mathit{max}}\right\}.$

2.3.1. Single-strategy model with social distancing

We consider a scenario in which social distancing is the only control against COVID-19 (i.e., $\sigma (t)=0$). In this case, the model is reduced to

$$\frac{\mathit{ds}}{\mathit{dt}}=-\left(1-\eta \left(t\right)\right)\lambda \left(t\right)s\left(t\right),$$

$$\frac{\mathit{de}}{\mathit{dt}}=\left(1-\eta \left(t\right)\right)\lambda \left(t\right)s\left(t\right)-\delta e\left(t\right),$$

$$\frac{{\mathit{dp}}_1}{\mathit{dt}}=\delta e\left(t\right)-k{p}_1\left(t\right),$$

$$\frac{{\mathit{dm}}_1}{\mathit{dt}}=k\left(1-\nu \right)p_1\left(t\right)-({\psi }_m+{\gamma }_M)m_1\left(t\right),$$

$$\frac{\mathit{dg}}{\mathit{dt}}={\psi }_m{m}_1\left(t\right)-{\gamma }_{\mathit{iso}}g(t),$$

$$\frac{d{i}_1}{\mathit{dt}}=k\nu p_1\left(t\right)-{\psi }_s{i}_1\left(t\right),$$

$$\frac{d{i}_2}{\mathit{dt}}={\psi }_s{i}_1\left(t\right)-{\gamma }_{\mathit{hosp}}{i}_2\left(t\right),$$

where $\lambda \left(t\right)=\frac{{\beta }_0\left(p_1+m_1+i_1+(1-\theta )(g+i_2)\right)}{1-\theta (g+i_2)}.$

The control reproduction number for the social distancing model (${\mathcal{R}}_{\eta }$) with η(^t)=η is reduced to

$${\mathcal{R}}_c\left(\eta ,0\right)={\mathcal{R}}_{\eta }=\left(1-\eta \right){\mathcal{R}}_0.$$

In addition, the objective function becomes

$$\mathcal{F}\left(\eta \left(t\right)\right)={\int }_{t=0}^T\{C_M{\psi }_m{m}_1\left(t\right)+C_I{\psi }_s{i}_1\left(t\right)+C_S{\eta }^2\left(t\right)s\left(t\right)\}dt$$

and the Hamiltonian function is given by

$$H=C_M{\psi }_m{m}_1\left(t\right)+C_I{\psi }_s{i}_1\left(t\right)+C_S{\eta }^2\left(t\right)s\left(t\right)+{\xi }_s\left\{-\left(1-\eta \right)\lambda \left(t\right)s\left(t\right)\right\}+{\xi }_e\left\{\left(1-\eta \right)\lambda \left(t\right)s\left(t\right)-\delta e\left(t\right)\right\}+{\xi }_{p_1}\left\{\delta e\left(t\right)-k{p}_1\left(t\right)\right\}+{\xi }_{m_1}\left\{k\left(1-\nu \right)p_1\left(t\right)-({\psi }_m+{\gamma }_M)m_1\left(t\right)\right\}+{\xi }_g\left\{{\psi }_m{m}_1\left(t\right)-{\gamma }_{\mathit{iso}}g(t)\right\}+{\xi }_{i_1}\left\{k\nu p_1\left(t\right)-{\psi }_s{i}_1\left(t\right)\right\}+{\xi }_{i_2}\left\{{\psi }_s{i}_1\left(t\right)-{\gamma }_{\mathit{hosp}}{i}_2\left(t\right)\right\}.$$

Then, the adjoint system becomes

$$\frac{d{\xi }_s}{\mathit{dt}}=-\frac{\partial H}{\partial s}=-C_S{\eta }^2\left(t\right)+\left({\xi }_s-{\xi }_e\right)(1-\eta )\lambda \left(t\right),$$

$$\frac{d{\xi }_e}{\mathit{dt}}=-\frac{\partial H}{\partial e}=\delta ({\xi }_e-{\xi }_{p_1}),$$

$$\frac{d{\xi }_{p_1}}{\mathit{dt}}=-\frac{\partial H}{\partial p_1}=\frac{{\beta }_0\left(1-\eta \right)({\xi }_s-{\xi }_e)s\left(t\right)}{1-\theta (g+i_2)}+k({\xi }_{p_1}-{\xi }_{m_1}\left(1-\nu \right)-{\xi }_{i_1}\nu ),$$

$$\frac{d{\xi }_{m_1}}{\mathit{dt}}=-\frac{\partial H}{\partial m_1}=\frac{{\beta }_0\left(1-\eta \right)({\xi }_s-{\xi }_e)s\left(t\right)}{1-\theta (g+i_2)}+{\psi }_m({\xi }_{m_1}-{\xi }_g-C_M)+{\gamma }_M{\xi }_{m_1},$$

$$\frac{d{\xi }_g}{\mathit{dt}}=-\frac{\partial H}{\partial g}=\frac{{\beta }_0\left(1-\eta \right)\left({\xi }_s-{\xi }_e\right)\left\{1-\theta +\theta \left(p_1+m_1+i_1\right)\right\}s\left(t\right)}{{\left(1-\theta \left(g+i_2\right)\right)}^2}+{\gamma }_{iso}{\xi }_g,$$

$$\frac{d{\xi }_{i_1}}{\mathit{dt}}=-\frac{\partial H}{\partial i_1}=\frac{{\beta }_0\left(1-\eta \right)\left({\xi }_s-{\xi }_e\right)s\left(t\right)}{1-\theta \left(g+i_2\right)}+{\psi }_s\left({\xi }_{i_1}-{\xi }_{i_2}-C_I\right),$$

$$\frac{d{\xi }_{i_2}}{\mathit{dt}}=-\frac{\partial H}{\partial i_2}=\frac{{\beta }_0\left(1-\eta \right)\left({\xi }_s-{\xi }_e\right)\left\{1-\theta +\theta \left(p_1+m_1+i_1\right)\right\}s\left(t\right)}{{\left(1-\theta \left(g+i_2\right)\right)}^2}+{\gamma }_{hosp}{\xi }_{i_2},$$

where the Hamiltonian is minimized with respect to the control at the optimal level as

$${\eta }^{\ast }=\mathit{min}\left\{max\left\{0,\frac{{\beta }_0\left({\xi }_e-{\xi }_s\right)\left(p_1+m_1+i_1+(1-\theta )\left(g+i_2\right)\right)}{2C_S\left(1-\theta \left(g+i_2\right)\right)}\right\},{\eta }_{\mathit{max}}\right\}.$$

2.3.2. Single-strategy model with testing

We consider the case in which a testing strategy is selected as the sole strategy against COVID-19 (i.e., $\eta \left(t\right)=0$). Then, the model is reduced to

$$\frac{\mathit{ds}}{\mathit{dt}}=-\lambda \left(t\right)s\left(t\right),$$

$$\frac{\mathit{de}}{\mathit{dt}}=\lambda \left(t\right)s\left(t\right)-\delta e\left(t\right),$$

$$\frac{{\mathit{dp}}_1}{\mathit{dt}}=\delta \left(1-\sigma \left(t\right)\right)e\left(t\right)-k{p}_1\left(t\right),$$

$$\frac{{\mathit{dp}}_2}{\mathit{dt}}=\delta \sigma \left(t\right)e\left(t\right)-k{p}_2\left(t\right),$$

$$\frac{{\mathit{dm}}_1}{\mathit{dt}}=k\left(1-\nu \right)p_1\left(t\right)-({\psi }_m+{\gamma }_M)m_1\left(t\right),$$

$$\frac{{\mathit{dm}}_2}{\mathit{dt}}=k\left(1-\nu \right)p_2(t)-{\gamma }_{\mathit{iso}}{m}_2\left(t\right),$$

$$\frac{\mathit{dg}}{\mathit{dt}}={\psi }_m{m}_1\left(t\right)-{\gamma }_{\mathit{iso}}g(t),$$

$$\frac{d{i}_1}{\mathit{dt}}=k\nu p_1\left(t\right)-{\psi }_s{i}_1\left(t\right),$$

$$\frac{d{i}_2}{\mathit{dt}}=k\nu p_2\left(t\right)+{\psi }_s{i}_1\left(t\right)-{\gamma }_{\mathit{hosp}}{i}_2\left(t\right),$$

where $\lambda \left(t\right)=\frac{{\beta }_0\left(p_1+m_1+i_1+(1-\theta )\left(p_2+m_2+g+i_2\right)\right)}{1-\theta (p_2+m_2+g+i_2)}.$

The corresponding control reproduction number in this model with σ(t) = σ is defined as

$${\mathcal{R}}_{\sigma }={\mathcal{R}}_c\left(0,\sigma \right)={\beta }_0\left[\frac{1-\sigma }{k}+\frac{(1-\theta )\sigma }{k}+\frac{\left(1-\sigma \right)\left(1-\nu \right)}{{\psi }_m+{\gamma }_M}+\frac{(1-\theta )\sigma \left(1-\nu \right)}{{\gamma }_{\mathit{iso}}}+\frac{(1-\theta )\left(1-\sigma \right)\left(1-\nu \right){\psi }_m}{{\gamma }_{\mathit{iso}}\left({\psi }_m+{\gamma }_M\right)}+\frac{\left(1-\sigma \right)\nu }{{\psi }_s}+\frac{(1-\theta )\nu }{{\gamma }_{\mathit{hosp}}}\right].$$

The optimal control problem with the objective function to be minimized becomes

$$\mathcal{F}\left(\sigma \left(t\right)\right)={\int }_{t=0}^T\{C_M(k\left(1-\nu \right)p_2\left(t\right)+{\psi }_m{m}_1\left(t\right))+C_I(k\nu p_2\left(t\right)+{\psi }_s{i}_1\left(t\right))+C_T{\chi }_T\delta e\left(t\right){\sigma }^2\left(t\right)\}dt.$$

To apply Pontryagin’s maximum principle to this optimal control problem, the corresponding Hamiltonian function is defined as

$$H=C_{M}k\left(1-\nu \right)p_2\left(t\right)+C_{I}k\nu (p_1\left(t\right)+p_2\left(t\right))+C_T{\chi }_T\delta {\sigma }^2\left(t\right)e\left(t\right)+{\xi }_s\left\{-\lambda \left(t\right)s\left(t\right)\right\}+{\xi }_e\left\{\lambda \left(t\right)s\left(t\right)-\delta e\left(t\right)\right\}+{\xi }_{p_1}\left\{\delta \left(1-\sigma \right)e\left(t\right)-k{p}_1\left(t\right)\right\}+{\xi }_{p_2}\left\{\delta \sigma e\left(t\right)-k{p}_2\left(t\right)\right\}+{\xi }_{m_1}\left\{k\left(1-\nu \right)p_1\left(t\right)-{\gamma }_M{m}_1\left(t\right)\right\}+{\xi }_{m_2}\left\{k\left(1-\nu \right)p_2-{\gamma }_M{m}_2\left(t\right)\right\}+{\xi }_{i_1}\left\{k\nu p_1\left(t\right)-{\psi }_s{i}_1\left(t\right)\right\}+{\xi }_{i_2}\left\{{\psi }_s{i}_1\left(t\right)-{\gamma }_{\mathit{hosp}}{i}_2\left(t\right)\right\}.$$

The Hamiltonian $H$ is minimized with respect to the control at the optimal level, yielding the following optimality conditions:

$${\left(\frac{\partial H}{\partial \sigma }\right|}_{\sigma (t)={\sigma }^{\ast }}=0.$$

By solving for $\sigma$, we obtain

$${\sigma }^{\ast }=\mathit{min}\left\{max\left\{0,\frac{{\xi }_{p_1}-{\xi }_{p_2}}{2C_T{\chi }_T}\right\},{\sigma }_{\mathit{max}}\right\}.$$

3. Results

Herein, we present numerical simulations of the optimal intervention strategies against COVID-19 transmission based on the proposed mathematical model. To investigate the economic constraints and availability of intervention measures, we considered single and combined control scenarios. Unless otherwise specified, we used the values listed in Table 1 as baseline parameters for the simulations, and assumed that control intervention began 50 days after the first COVID-19 case (NGA, 2020). With these baseline parameter values and in the absence of any control measure, that is, $\eta \left(t\right)=\sigma (t)=0$, the cumulative proportion of severely infectious individuals reached 19% under the assumption of ${\mathcal{R}}_0=2.8$. Sensitivity analysis is performed by varying key model parameters, namely cost, upper bound of controls, and basic reproduction number.

3.1. Single strategy

3.1.1. Optimal social distancing strategy

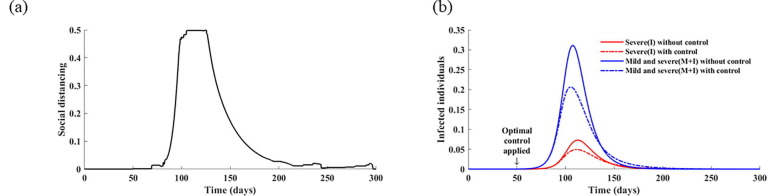
We investigated the effects of optimal social distancing strategies on the dynamics of COVID-19 transmission. When social distancing is in effect with a maximum level of 50% (${\eta }_{\mathit{max}}=0.5$), the results demonstrate that the optimal social distancing level is the highest when the proportion of infected individuals reaches its peak point, which necessitates intensive effort over the next 40 days, and then gradually declines (Fig. 4 a). The magnitude of the outbreak (total number of infected individuals) appears to be reduced by 18% in the optimal social distancing scenario (Fig. 4b).

Fig. 4.

Optimal social distancing level $\eta (t)$ as a function of time in the absence of a testing strategy. (a) Optimal social distancing level with ${\eta }_{\mathit{max}}=0.5$. (b) Corresponding daily incidences of infection without controls and with optimal social distancing strategy.

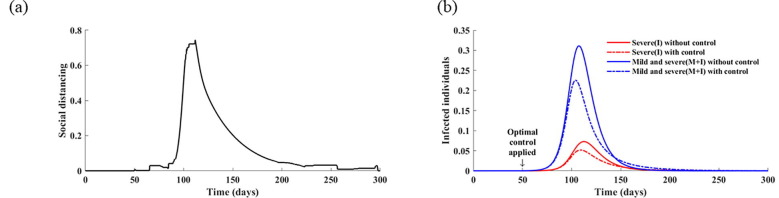
Social distancing is difficult to implement thoroughly in general owing to the nature of a series of activities related to important aspects of daily life, such as work or education. However, the maximum level of social distancing can be further increased by considering the involvement of public health agencies, such as state blockades, school closures, and travel restrictions (Islam et al., 2020). Increasing the maximum level of social distancing (${\eta }_{\mathit{max}}$) to 0.8 leads to a shorter and more intense optimal control policy than in the case of a baseline value of 0.5 (Fig. 5 a). With ${\eta }_{\mathit{max}}=0.8,$ the period during which the optimal social distancing level is above 0.4 is 27 days, whereas the corresponding period with ${\eta }_{\mathit{max}}=0.5$ is 33 days. Additionally, a reduction of 22% in the final epidemic size can be achieved when ${\eta }_{\mathit{max}}$ increases to 0.8 (Fig. 5b).

Fig. 5.

Effect of increased upper bound for the level of social distancing (${\eta }_{\mathit{max}}$) on the optimal control strategy $\eta \left(t\right)$. In this case, ${\eta }_{\mathit{max}}$ increases to 0.8. (a) Optimal social distancing level with ${\eta }_{\mathit{max}}=0.8$. (b) Corresponding daily incidences of infection without controls and with optimal social distancing strategy.

Furthermore, we evaluated the effect of the social distancing cost on the optimal social distancing level (Fig. S3). The optimal social distancing strategies were found to be highly dependent on social distancing cost. For illustration purposes, we set the social distancing cost to three times the baseline value. It can be seen that as the social distancing cost increases, the duration of intense social distancing corresponding to the optimal strategy decreases (Fig. S3). Specifically, the period during which the optimal social distancing level is above 0.2 and 0.3 is 18 and 7 days, respectively. As a result, the percent reduction in the number of infections decreases to 5% as the cost of social distancing increases threefold.

3.1.2. Optimal testing strategy

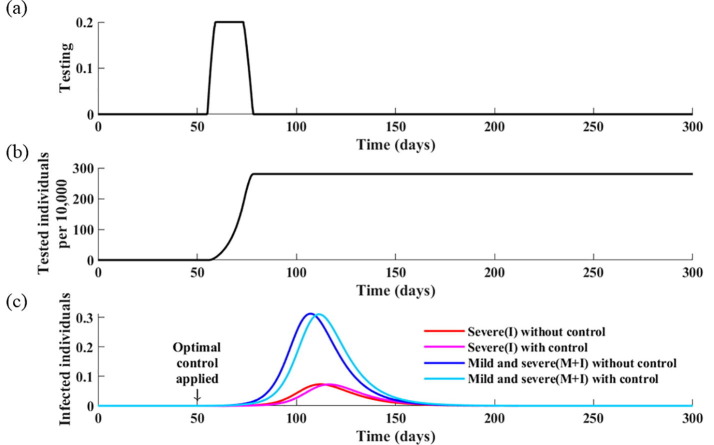
Herein, we consider the testing strategy with contact tracing as the sole control measure against COVID-19. According to seroprevalence surveys in the U.S., the estimated number of infections is at least six times as large as the number of reported cases (CDC, 2020b). Therefore, for the numerical simulations, the maximum probability that infected individuals are identified by testing was set to 0.2 (i.e., ${\sigma }_{\mathit{max}}=0.2$). Additionally, the average number of tests required to identify an infectious individual, which is denoted as ${\chi }_T$, was set to 10 given that the average percentage of positive tests in the U.S. was 10% (CDC).

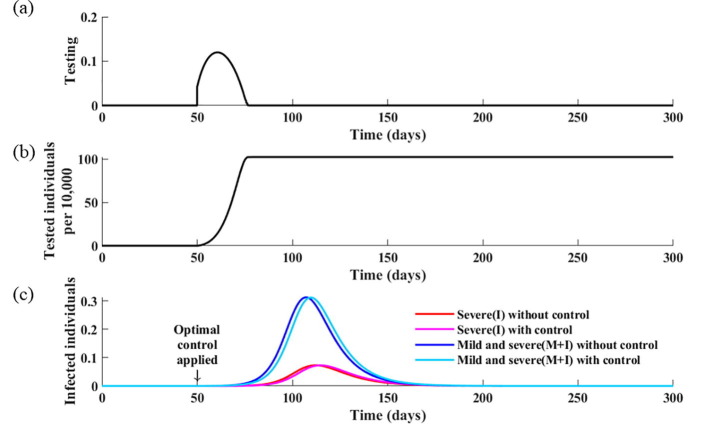
Based on these baseline values, the results indicate that the optimal testing strategy is to perform tests for a period of 26 days in the early stages of outbreak and then stop testing (Fig. 6 ). In this case, the cumulative number of infectious individuals remains unchanged, although the peak date is delayed by three days.

Fig. 6.

Optimal testing strategy $\sigma (t)$ as a function of time in the absence of a social distancing strategy. (a) Calculated optimal testing strategy. (b) Corresponding cumulative infectious individuals. (c) Corresponding daily incidences of infection without controls and with the optimal testing strategy.

To analyze the effect of the upper bound of testing intensity (${\sigma }_{\mathit{max}}$), we computed the optimal strategies when ${\sigma }_{\mathit{max}}$ was set to 0.4, 0.6, and 0.8 (Fig. S4). The effect of the optimal testing strategy does not change significantly until the upper limit increases to 0.4 compared with ${\sigma }_{\mathit{max}}=0.2$ (Fig. S4a). However, increasing ${\sigma }_{\mathit{max}}$ further results in a longer period of maximum testing and further delay of the peak time for the number of infectious cases. For instance, with ${\sigma }_{\mathit{max}}=0.6,$ the peak of the epidemic was delayed by 13 days, whereas the optimal testing strategy was to test 3.3% of the population (Fig. S4b). When ${\sigma }_{\mathit{max}}$ was increased to 0.8, the optimal testing strategy was to test 20% of the population, delaying the peak of the epidemic by 72 days (Fig. S4c).

In the investigation of the effect of testing cost, the results indicate that lower testing cost implies more intense testing in the early stages of an epidemic (Fig. 7 ). However, it is shown that the optimal testing strategy is only effective in delaying the peak of the epidemic, but not in reducing the overall disease burden, even with increased ${\sigma }_{\mathit{max}}$ or lower testing cost.

Fig. 7.

Effect of decreased cost of testing ($C_T$) on optimal control strategies. For illustration purposes, we decreased the cost of testing ($C_T$) to one-third of baseline value and present the following simulation results: (a) corresponding optimal testing intensity; (b) cumulative infectious individuals; and (c) daily incidences of infection without control and with optimal testing strategy.

3.2. Combined strategy

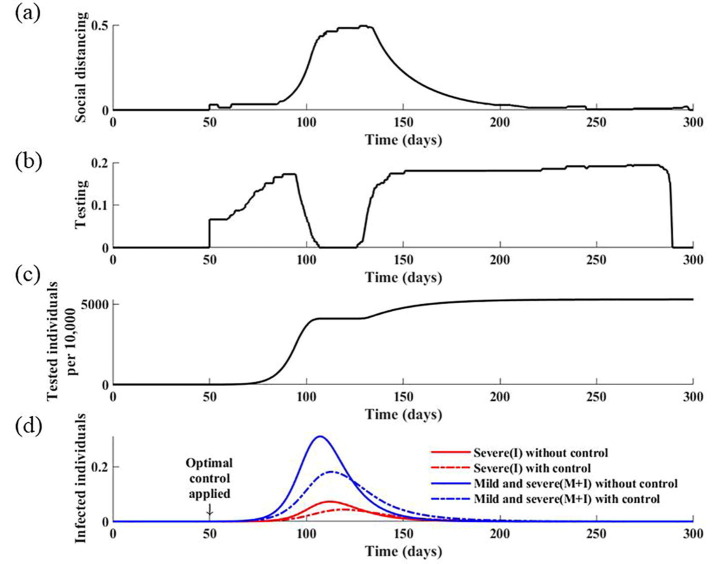
Herein, we estimate the combined optimal strategies when social distancing and testing control measures are implemented simultaneously. The results indicate that to minimize the total cost associated with COVID-19 and its control, the optimal intervention strategy is to implement intense testing in the early stages of the outbreak, but replace it with social distancing as the incidence level begins to increase (Fig. 8 ). Specifically, when the proportion of individuals with severe and mild infection is greater than 7%, it is optimal to reduce testing from its maximum level and apply a social distancing level above 40%. After the peak of the epidemic, and when the incidence level is below 7%, it is advised to re-initiate testing and increase testing to its maximum level; however, the actual number of tests to be performed per day is significantly reduced compared with that before the peak of the epidemic. This is because the number of tests per day $\delta \sigma E\left(t\right)$ is only proportional to the number of new infections, and thus it decreases after the peak of the epidemic. Nevertheless, the optimal strategy is to perform testing as intensively as possible to identify any remaining infectious cases. If the optimal intervention strategy is adopted, it is expected that the final size of the epidemic is reduced by 21%, with 53% of the population tested during the pandemic.

Fig. 8.

Optimal control strategies for social distancing and testing. (a) Calculated optimal social distancing level. (b) Calculated optimal strategies for testing. (c) Corresponding cumulative number of tests. (d) Corresponding daily incidences of infection without controls and with optimal strategies.

For sensitivity analysis, we present the numerical results when the upper bounds of the control strategies are varied (Figs. S5 and S6). If the upper bound of the social distancing level (${\eta }_{\mathit{max}}$) increases to 0.8, whereas ${\sigma }_{\mathit{max}}$ is fixed at the baseline value, then the initial intensity of testing and the duration of intense social distancing decreases (Fig. S5). Additionally, if the maximum testing intensity increases to 0.3 with ${\eta }_{\mathit{max}}=0.5$, then the optimal testing strategy increases overall, and the duration of intense social distancing is slightly shortened (Fig. S6). In this case, the cumulative number of patients decreases by 27%.

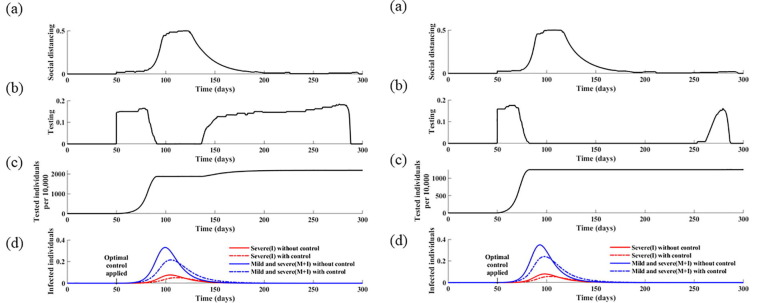
Additionally, the optimal strategy was found to be sensitive to the social distancing cost (Fig. S7). Specifically, a twofold increase in the social distancing cost ($C_S=356)$ results in lower levels of both social distancing and testing. This indicates that testing efficiency is also affected by the weak implementation of social distancing, and that both strategies should be combined to improve their effectiveness. We also analyzed the effects of the basic reproduction number of COVID-19 on the optimal control strategies (Fig. 9 ). The results indicate that the optimal social distancing function $\eta \left(t\right)$ with a higher reproduction number (${\mathcal{R}}_0=3.2$) is maximized after 38 days from the initiation of the control strategies and is maintained at the maximum level for 32 days, whereas it is only maximized for 27 days after 58 days from the implementation of controls, with the baseline value, that is, ${\mathcal{R}}_0=2.8$. These results indicate that, with a higher value of ${\mathcal{R}}_0$, it is optimal to apply early implementation of intense social distancing as well as testing.

Fig. 9.

Effect of the basic reproduction number (${\mathcal{R}}_0$) on optimal control strategies. In this simulation, ${\mathcal{R}}_0$ was increased to 3.0 (left) and 3.2 (right). (a) Calculated optimal social distancing level. (b) Calculated optimal testing strategy. (c) Corresponding cumulative number of tests. (d) Corresponding daily incidences of infection without controls and with optimal strategies.

4. Discussion

In this study, we derived optimal strategies for social distancing and testing to mitigate the impact and spread of the ongoing COVID-19 pandemic. The results demonstrated that the optimal social distancing level is highly dependent on the daily incidence of infectious cases. That is, the optimal level of social distancing increases with the number of new cases of COVID-19. Furthermore, the duration of intense social distancing is shortened if a greater upper bound is allowed, further decreasing the disease burden.

However, when testing is the sole control strategy, it is optimal to implement testing only in the early stages of an epidemic. Even with the optimal testing strategy, the cumulative number of infections is not significantly reduced, but the time for the epidemic peak is delayed. This highlights the effects of COVID-19 testing, that is, allowing time for more hospital beds to be secured or more necessary policies to be established. With a higher upper bound of testing intensity, the peak time for the number of infectious cases can be further delayed, whereas the duration of intensive testing in the early phase increases.

The results demonstrate that the combined strategies are more efficient at reducing the disease burden than a single policy. When both strategies are implemented simultaneously, not only can the peak of infectious cases be delayed, but the final epidemic size can also be reduced. Testing should be maintained at its maximum level in the early phases and after the peak of the epidemic, whereas intense social distancing should be implemented when the prevalence of the disease is greater than 15%. These findings suggest that testing is less important during the period of intense social distancing and more important thereafter, as reported in a previous study (Tsay et al., 2020).

As the basic reproduction number (${\mathcal{R}}_0$) increases, social distancing becomes more important than testing. A higher value of ${\mathcal{R}}_0$ implies that intense social distancing should be implemented earlier and for a longer period; the optimal testing strategy tends to zero. Furthermore, if ${\mathcal{R}}_0$ increases above 3.2, testing should only be performed briefly in the early phase because the disease is too contagious relative to the maximum testing effort.

A limitation of this research is that costs were measured as constants. In the real world, if social distancing is practiced by a relatively large fraction of a population over an extended period of time, its cost can increase exponentially owing to fatigue, suppression of freedom, job layoffs, and social costs. However, the cost of testing may be reduced by advances in technology and an increased supply of test kits. Similarly, the upper bounds of the strategies can also change over time owing to policy changes, strong governmental regulations, stabilization of test kit supplies, and advances in technology, such as digital contact tracing. Therefore, in future studies, costs and upper bounds should be considered as functions of time.

Our results suggest that COVID-19 is a pandemic that appears to be controllable using social distancing and testing with contact tracing, particularly when these strategies are combined. Notably, the appropriate timing of these interventions and the assurance of high coverage in the community are critical to the success of COVID-19 control efforts. This line of research can be continued and extended in various aspects in the future. Specifically, by fitting the model to actual data, studies can be conducted on infection and mortality forecasts for quarantine and vaccination, and patterns of recurrence of infectious diseases over time.

Funding

This work was supported by the National Research Foundation of Korea (NRF) funded by the Korean government (MSIT) (No. 2018R1C1B6001723).

CRediT authorship contribution statement

Wongyeong Choi: Methodology, Software, Formal analysis, Visualization, Writing - original draft, Writing - review & editing. Eunha Shim: Conceptualization, Methodology, Formal analysis, Visualization, Writing - original draft, Writing - review & editing, Supervision, Project administration, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: