Optimization of MRI Gradient Coils with Explicit Peripheral Nerve Stimulation Constraints

Abstract

Peripheral Nerve Stimulation (PNS) limits the acquisition rate of Magnetic Resonance Imaging data for fast sequences employing powerful gradient systems. The PNS characteristics are currently assessed after the coil design phase in experimental stimulation studies using constructed coil prototypes. This makes it difficult to find design modifications that can reduce PNS. Here, we demonstrate a direct approach for incorporation of PNS effects into the coil optimization process. Knowledge about the interactions between the applied magnetic fields and peripheral nerves allows the optimizer to identify coil solutions that minimize PNS while satisfying the traditional engineering constraints. We compare the simulated thresholds of PNS-optimized body and head gradients to conventional designs, and find an up to 2-fold reduction in PNS propensity with moderate penalties in coil inductance and field linearity, potentially doubling the image encoding performance that can be safely used in humans. The same framework may be useful in designing and operating magneto- and electro-stimulation devices.

I. Introduction

Peripheral Nerve Stimulation (PNS) has become a significant limitation in the use of high-performance gradient coils in Magnetic Resonance Imaging (MRI) [1, 2]. Rapid switching of the magnetic field gradient is needed to quickly encode the image but induces electric fields (E-fields) in the conductive body strong enough to generate unwanted action potentials in peripheral nerves. This can lead to bothersome or even painful stimulations [3, 4, 5, 6]. Although most prominent in whole-body gradient systems used in clinical scanners due to the large body areas exposed, the PNS effect is also becoming an acute limitation for state-of-the-art head gradient coils. Head gradients have intrinsically greater PNS thresholds (2-3 fold), but are now also being used at 2-3 fold higher gradient strength and slew rate [7]. Despite its limiting role, PNS effects are not directly incorporated in the gradient winding optimization. The PNS characteristics are assessed after the coil design phase during stimulation experiments which requires construction of coil prototypes and measuring the thresholds in experiments using healthy subjects [8, 9, 10, 11]. These stimulation studies are not only complex, but also provide very limited insights into design changes that might reduce PNS. Instead, indirect scaling relationships between PNS thresholds and gradient coil design parameters such as linear field-of-view (FOV) and coil length are used as surrogates for a PNS metric in the design process [12]. In addition to being possibly sub-optimal, this approach precludes the study of tradeoffs between PNS thresholds and the traditional engineering metrics such as coil inductance, field linearity, wire density, and torque.

The ability to improve a coil design during the iterative coil winding optimization requires a subspace of coil solutions with similar engineering metrics but different PNS thresholds. An explicit PNS metric then allows this sub-space to be explored, possibly yielding improved PNS characteristics with little cost to the other engineering metrics. The PNS metric also provides a principled way to characterize the trade-off between these traditional engineering metrics and PNS.

If the coil design required complete specification of the magnetic field (B-field), Maxwell’s equations would uniquely specify the resulting E-field in a given human body and thus the PNS threshold. However, the designer seeks only a target pattern for the gradient of the B_z field component within the imaging FOV, allowing an infinite number of choices for the transverse field components (B_x and B_y) and all field components outside of the imaging FOV. These field components constitute degrees-of-freedom that can be chosen to minimize PNS. Hidalgo-Tobon et al. [13] exploited this concept by superimposing an additional B_x or By field to partially cancel the transverse gradient coil’s concomitant fields, resulting in a ~50% improvement in measured PNS thresholds. The simplistic addition of concomitant field coils, however, leads to an exacerbated net torque of the gradient coil in the MRI environment [13]. Thus, in addition to creating a PNS constraint, it is critical to simultaneously consider all other design constraints during coil winding optimization.

The boundary element method stream function (BEM-SF) approach is the most common method for optimizing MRI gradient coils [14, 15, 16]. In the BEM-SF approach, the coil windings are derived from a current density distribution on the coil former surface (usually a cylinder). Each vertex of the cylinder’s surface mesh carries a discrete current density element (the stream function basis). The B-field generated from a candidate design is formed from the weighted superposition of the precomputed fields of these basis elements. Although precomputation of the bases’ fields is time-consuming, the calculation of any candidate design’s field is a simple matrix multiplication. The optimal basis weights are determined by a linear solver that seeks the weights that create a best match to the target field while satisfying a series of engineering constraints (such as coil inductance, wire spacing, and torque), also expressed as linear or quadratic matrix forms. In our work, we provide the ability to include the most important “biological constraint”, PNS thresholds, in exactly the same way.

We have recently shown that activation of peripheral nerves in the body by external electromagnetic fields can be accurately predicted using a coupled electromagnetic-neurodynamic modeling framework. This tool predicts the “forward” PNS response (i.e., generation of PNS by an existing coil) [17, 18, 19, 20]. The pipeline computes the induced E-fields in detailed electromagnetic body models and assesses the field’s capability to induce action potentials in a realistic peripheral nerve system (more than 1900 nerves in our simulations) embedded in the body model. The approach was validated against experimental thresholds measured in healthy volunteers in several MRI gradient coils [21, 22]. As such, this “forward” PNS model is useful for manually assessing a small number of candidate coils prior to construction and can thus guide the designer. This workflow, however, cannot be readily incorporated in the winding optimization due to the time-consuming E-field simulations and nonlinear neurodynamic calculations. The nonlinearity of the neurodynamics arises from the ion channels which themselves are sensitive to the membrane voltage. If the stimulus reaches a certain threshold, the coupled equations for the nerve membrane potential move from a damped (negative) feedback regime to positive-feedback causing the ion channels to open up abruptly. This process alters the nerve membrane potential; a change known as an action potential. Although the coupled differential equations describing action potential generation are well-known, modeling this non-linear process is time-consuming and not amenable to direct incorporation into the gradient winding optimization where the objective function and constraints need to be evaluated thousands of times.

Additionally, expression of BEM-SF design constraints as linear or quadratic forms is an important pre-requisite for preserving the convex nature of the optimization. While the electromagnetic fields naturally obey superposition, it is important to find a linear expression for the nerve responses so that each nerve’s response can be represented as a weighted sum of precomputed responses from each basis function (wire segment). To achieve this, we developed the “PNS oracle”, a generalized linear version of the neurodynamic response function that correlates well with PNS thresholds computed from the full neurodynamic modeling [23, 24]. Armed with a pre-computation of how each basis function contributes to the PNS threshold of each nerve segment, the full response from the candidate winding pattern is obtained from a simple “P-matrix” multiplication with the stream function basis weights.

In this work, we leverage the PNS oracle and perform numerical optimizations of coil windings with – for the first time – explicit PNS constraints [25]. We combine the PNS constraint with traditional engineering constraints (field linearity, coil inductance, wire density, and torque). This encourages the solver to explore the sub-space of coil solutions with similar “engineering metrics” and identify a solution with favorable reduced PNS. It also provides a framework to analyze the optimal tradeoff between the traditional engineering metrics and PNS performance. The convex optimization provides a method to explore the theoretical limits of PNS-optimal coil design. We demonstrate this tool by designing a series of whole-body and head-only gradient coils with typical engineering constraints but up to 2-fold reduction in PNS propensity.

II. Methods

Boundary Element Stream Function Method

The Boundary Element Method Stream Function (BEM-SF) approach is the gold standard for designing efficient gradient coil windings. The goal for each of the three separate windings is a spatially linear B_z field pattern (“gradient”) in the chosen region-of-linearity (ROL) while satisfying a series of engineering constraints such as field linearity, torque balancing, minimum wire spacing (current density), and field magnitude at the magnet surface (controlling the eddy currents) [14, 15, 16]. In the BEM-SF approach, the wires are constrained to the surfaces of a coil former geometry (in most cases two coaxial cylinders). This coil geometry is represented by a surface mesh that carries a continuous current density. Instead of directly optimizing the current density (which may lead to solutions that are not divergence-free), the current density is indirectly described by a scalar stream function whose iso-contours define the paths of current flow. The total stream function on the coil surface is discretized into a set of local stream function bases defined on the former’s mesh vertices (see Fig. 1). Every stream function basis models a divergence-free current circulating around the respective vertex (similar to a small current loop). The full stream function is constructed from a weighted sum of stream function bases described by a vector x. This construction guarantees that the resulting continuous current density is divergence-free, allowing it to be converted to closed discrete wires.

Figure 1:

Classical BEM-SF coil design workflow: 1) Definition of the coil former (two cylindrical surfaces) and the target points (blue dots on the region of linearity and the cryostat), 2) Precomputation of field contributions of all SF bases in all target points and assembly of system matrix, 3) Optimization of SF weights to create gradient field in ROL and field suppression on the cryostat (active shielding), and extraction of coil windings from the optimized stream function.

Prior to optimization (finding the optimal weight set x), extensive precomputations are performed to characterize the contributions from each stream function basis to the various design metrics (B-fields, torques, inductance, etc.). For example, the B_z field contribution to each point in the target region is precomputed for each basis and assembled into a matrix C such that Cx describes the total B_z field generated in the ROL. In addition to the imaging ROL, fields are precomputed at the magnet surface to constrain the magnitude of eddy currents. In a similar fashion, we precompute a series of additional matrices linking the stream function bases to relevant physical properties such as the current density (Dx) and the torque (Tx). The pairwise coupling between individual stream function bases is used to generate a matrix L such that the quadratic form x^TLx scales with the coil inductance. Note that other metrics have been proposed, such as heating [26, 27], sound pressure levels [28, 29], and secondary effect of eddy currents on the B_z field in the imaging ROL [30, 31].

Finally, the BEM-SF coil design problem can be formulated as a quadratic minimization of the coil inductance subject to linear constraints for the other engineering metrics:

$$\begin{gathered} x_{\text{opt}}=\underset{x}{\text{argmin}}\{x^{\mathrm{T}}\mathit{L}x\}\text{subject to} \\ \mid \mathit{C}x-b_{\text{tar}}\mid \le ϵ,\mid \mathit{T}x\mid \le T_{\max },\mid \mathit{D}x\mid \le D_{\max } \end{gathered}$$ Eq. 1

where b_tar defines the target B-field pattern (linear B_z field gradient within the ROL and zero normal field on the magnet cryostat), ϵ is the tolerated field gradient error, and T_max / D_max denote the torque and current density constraints.

PNS model and P-matrix assembly

Addition of an explicit PNS constraint requires construction of a matrix (similarly to the magnetic field or torque matrices) that links the basis weight vector x to the PNS propensity of each nerve segment in the body. Multiplication of this “P-matrix” by the weight vector x superimposes the effects of all current bases and generates a vector describing the PNS propensity for each peripheral nerve segment. This P-matrix is formed using our “PNS oracle” formulation (the inverse of the PNS threshold) rather than the threshold itself since the oracle is linear with respect to the coil current. This allows for expressing the optimization constraint as a simple inequality (Px ≥ P_max). Of course, the more commonly discussed PNS threshold can be easily calculated via the inverse PNS oracle.

The workflow to obtain the P-matrix starts with computation of the electromagnetic fields created by a winding pattern or current density basis element within a detailed male or female body model [18]. In this work, we study two body positions: head-centered or heart-centered (head first supine). The electromagnetic fields are simulated for a 1 kHz sinusoidal current waveform applied to the current basis element using a low-frequency magneto quasi-static solver (Sim4Life, Zurich MedTech) on a 1 mm³ hexahedral mesh. Given the E-fields induced by a subset of the basis elements (~10%), we compute the electric potential changes V(r) along each of the 1900 nerve segments in the body (each of which is labeled by an estimate of the local axon diameter). The electric potentials for the remaining ~90% of basis elements are obtained using a barycentric interpolation scheme. We then predict the response of each nerve fiber using either a full nonlinear neurodynamic model [32, 33, 34] or our linear PNS oracle [24].

The PNS oracle metric (which is the reciprocal PNS threshold) follows a previous definition of the neural activation function and modified driving function [35]. It estimates the threshold of action potential generation of a nerve segment based on the spatial pattern of the applied electric potential using only linear operations. Note that the PNS oracle does not explicitly model ion dynamics and action potential initiation or propagation and thus ignores the non-linear aspects of nerve stimulation. This provides the needed linear relationship between the electric potential V(r) and the propensity for stimulation. The PNS oracle (PNSO) is defined as

$$\text{PNSO}(r)=\frac{K(D)}{m(D)}\ast \frac{V(r-L)-2V(r)+V(r+L)}{L(D{)}^2}$$ Eq. 2

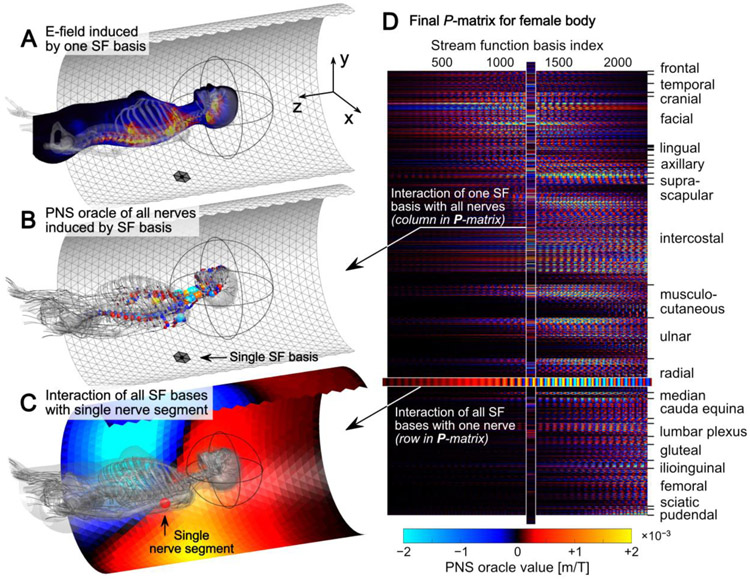
where V(r) is the extracellular potential along the nerve position r, L(D) is the distance between consecutive nodes of Ranvier (which is a function of the axon diameter D), K(D) is a spatial kernel, and m(D) is a calibration factor. The PNS oracle is based on the second spatial difference of the electric potential V(r) across adjacent nodes of Ranvier. The result is convolved with a spatial kernel K(D) that describes cross-talk between adjacent nodes of Ranvier. Finally, the factor m(D) accounts for the different excitability due to the axon-dependent level of myelination. Both the kernel K(D) and the myelination factor m(D) are calibrated for a specific temporal waveform of the driving fields (in this work a 1 kHz sinusoid). We have recently shown that the PNS oracle correlates very well with the inverse thresholds obtained from the full neurodynamic model (R² > 0.995). The linear nature of the PNS oracle with respect to the electric potentials along the nerve and thus the local E-field and ultimately the coil currents or current density allows it to be assembled into a matrix form (the P-matrix). Note that a P-matrix must be pre-computed for each body model, coil former geometry (including the body position within the coil former) and each driving waveform. This process yields a matrix of size p × n where p is the number of nerve locations and n is the number of stream function bases. Figure 2 illustrates this process for a whole-body cylindrical coil loaded with the female body model. The resulting P-matrix is incorporated in the BEM-SF optimization as an additional linear constraint:

$$\mid \mathit{P}x\mid \le P_{\max }\text{with}{P}_{\max }=\frac{1}{\text{Max. PNS threshold}}$$ Eq. 3

Figure 2:

A: Electric field induced in the female body model by a single basis function element. B: PNS oracle values along all nerve fibers extracted from the electric field map (these PNS oracle values correspond to a single column in the P-matrix). C: PNS oracle values induced in a single nerve segment of the ulnar nerve by all SF basis elements on the coil former (these PNS oracle values correspond to a single row in the P-matrix). D: The resulting full P-matrix can be incorporated in the BEM-SF coil design framework as an additional constraint.

Simulated Body and Head Gradient

We design a series of actively shielded whole-body and head-only gradient coils with constraints similar to commercially available gradient coils. We assess three gradient design geometries: 2 and 3-layer body coils and 3-layer head coils. The symmetric body coil geometry consists of two or three coaxial cylinders (110 cm long) with diameters of d₁ = 66 cm and d₃ = 82 cm, and an optional intermediate layer for the 3-layer design (d₂ = 74 cm). Each cylindrical surface carries 2340 stream function bases. The P-matrix is computed for each layer using the female model positioned with the head at iso-center. The target efficiency for the body coils is set to 0.1 mT/m for 1 A coil current. The head-only gradient coil geometry consists of three concentric cylinders (diameters: d₁ = 46 cm, d₂ = 62 cm, d₃ = 75 cm, lengths: h₁ = 65 cm, h₂ = 110 cm, h₃ = 120 cm). Note that the head coil geometry is asymmetric (as opposed to the symmetric body coil geometry). The head coil layers support 2592, 4400, and 4080 stream function bases, respectively. The respective P-matrices are also computed using the female model. The head gradients’ target efficiency is set to 0.15 mT/m for 1 A coil current. This efficiency is on the lower end of typical head gradient coils, which have efficiencies ranging from 0.15-0.3 mT/m/A [36, 37, 7]. Although at the lower end of this range, the design choice of 0.15 mT/m/A provided enough degrees-of-freedom for PNS mitigation. We design several families of gradient coils with 5%, 10%, 15%, and 20% deviation from the ideal linear gradient field pattern. A coil winding’s linearity deviation ε is computed from the coil’s induced B_z-field in all target points (${\mathrm{B}}_{\text{coil}}^{\mathrm{z}}$) and the target field (${\mathrm{B}}_{\text{tar}}^{\mathrm{z}}$) [38, 39] via

$$\epsilon =\frac{\max \{\mid B_{\text{tar}}^z-B_{\text{coil}}^z\mid \}}{\max \{\mid B_{\text{tar}}^z\mid \}}.$$ Eq. 4

The PNS constraint is varied as well (including coil designs without PNS constraints). Additionally, we constrained the maximum torque by T_max = 0.1 Nm/A, the minimum wire spacing by D_max = 7 mm, and the active shielding capability in terms of B-field magnitude on the surface of the magnet cryostat by 1 μT/A. All BEM-SF simulations are performed in Matlab R2018b (MathWorks, Natick, MA, USA) using the MOSEK quadratic optimizer (MOSEK Aps, Copenhagen, Denmark). For each stream function solution, we extract discrete coil windings by tracing the iso-contours of the stream function solution and compute the coil inductance using FastHenry2 [40].

Additionally, we analyze the coil solution’s concomitant B-field components (B_x and B_y) that affect the local Larmor frequency and thus potentially interfere with spin encoding. We assess the magnitude of this effect by computing the fractional deviation of the total B-field from the idealized encoding field without concomitant components:

$${\Delta }_{\mathrm{c}}(\mathrm{r})=\frac{\Vert ({\mathrm{B}}_{\mathrm{x}}(\mathrm{r}),{\mathrm{B}}_{\mathrm{y}}(\mathrm{r}),{\mathrm{B}}_{\mathrm{z}}(\mathrm{r})+{\mathrm{B}}_0)\Vert }{\Vert {\mathrm{B}}_{\mathrm{z}}(\mathrm{r})+{\mathrm{B}}_0\Vert }-1.$$ Eq. 5

We report the average and maximum of this positive valued metric over the ROL.

Finally, we evaluate the robustness of the coil solutions with respect to body position (optimize for head at iso-center, simulate PNS characteristics for heart at iso-center) as well as body size and gender (optimize for the female model, assess PNS characteristics for the male model).

III. Results

L-curves

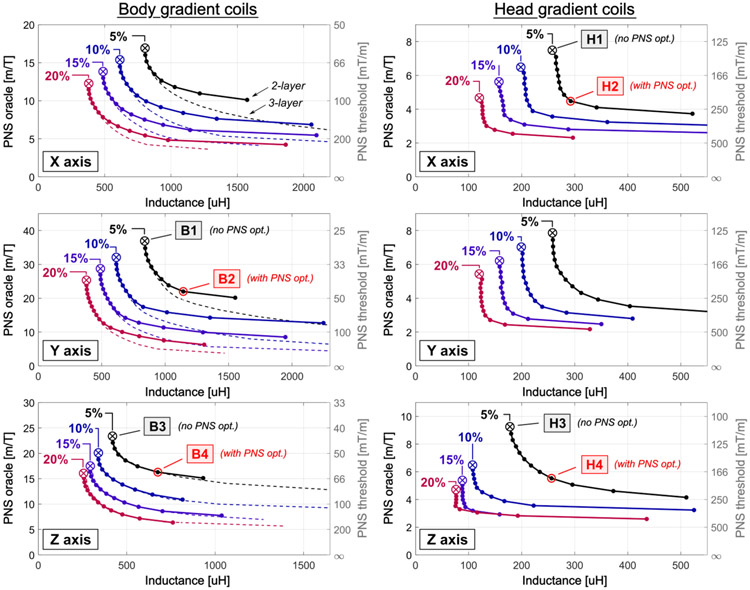
Figure 3 shows L-curves quantifying the tradeoff between PNS and coil inductance for X, Y, and Z-axes body coils (2-layer and 3-layer geometries) and head-coils (3-layer geometry). The L-curves were generated for gradient linearity constraints of 5%, 10%, 15%, and 20%. Every point of the L-curves corresponds to a coil winding solution; the first point (circled x) corresponds to the standard solution without PNS constraints.

Figure 3:

L-curves showing the trade-offs between PNS oracle (and equivalent PNS threshold) and inductance for the BEM-SF coil solutions for the three coil axes of the body gradients (left column) and the head gradients (right column). The body coils consist of two cylindrical layers (solid lines) or three layers (dashed), whereas all head gradients consist of three layers. In each panel, we show L-curves corresponding to different field linearity constraints of 5%, 10%, 15% and 20%. The first point of each L-curve (x) corresponds to a traditional coil solution without PNS optimization; every subsequent point reduces PNS in steps of 5%. The labels B1-B4 and H1-H4 denote specific coil solutions used in Figs. 4 to 7.

For all coils studied, incorporation of PNS constraints yields winding solutions with significantly reduced PNS propensity (decreased PNS oracle, i.e., increased PNS threshold). One traditional approach for PNS reduction is relaxation of the linearity constraint. Our simulations show this effect, for example relaxing the linearity of the Y-body coil from 5% to 10% leads to a 13% PNS oracle reduction (36.6 m/T to 31.7 m/T) while also reducing the coil inductance by 27% (840 μH to 613 μH). In contrast, incorporation of PNS constraints yields a coil with the same inductance (840 μH) and relaxed linearity (10%), but with a 52% reduction in PNS oracle (36.6 m/T to 17.4 m/T). Alternatively, PNS can be reduced without penalty in field linearity: for a 5% linearity Y-axis body coil, a PNS improvement of 20% can be achieved at a modest ~5% penalty in inductance. Accepting a 20% increase in inductance allows reducing PNS by 40% (these coil solutions are marked B1 and B2 in Fig. 3). The PNS oracle improvements where comparable for the body X-axis, but came at higher cost in terms of inductance for the Z-axis. In this case, increasing the inductance by 20% allowed for a 20% PNS reduction. Additional relaxation of the linearity constraint (5% to 10%) leads to a 45% PNS oracle reduction. Figure 3 (left column) also shows results from adding a third cylinder to the body coil design (dash lines). This further improved PNS performance for larger inductance X and Y-axis coil designs.

Figure 3 (right column) shows results for the head gradient coils. In this case, PNS oracle reduction was achieved with a smaller coil inductance penalty. For the X-axis, the PNS oracle is reduced by 40% for only a 15% increase in inductance (the respective coil windings are marked H1 and H2). Tolerating a penalty in both coil inductance and field linearity (from 5% to 10% error) yields a PNS reduction of 60%. Similarly to the body gradient’s Z-axis, improving the PNS performance of the head gradient’s Z-axis led to higher inductance penalties (45% increase for 40% PNS reduction).

Specific winding solutions and stimulation locations

Figure 4 shows the coil windings and PNS oracle maps in the female model for the unoptimized and optimized 2-layer body Y-axis coils (solutions B1 and B2 in Fig. 3) and Z-axis coils (solutions B3 and B4 in Fig. 3). All coils achieve the same gradient efficiency (0.1 mT/m/A), field linearity (5%), and are actively-shielded and torque-balanced. Unfolded winding patterns are shown in supplementary Fig. S1.

Figure 4:

Optimized stream function solutions and extracted winding patterns and the resulting PNS oracle/PNS threshold maps in the female body model for the unoptimized and optimized two-layer Y-axis body coils (B1 and B2) and Z-axis body coils (B3 and B4). The colored spheres correspond to hotspots with largest PNS oracle (smallest PNS threshold). Both the color and the sphere size encode the PNS oracle value. The optimized Y-axis windings lead to a 67% increase in PNS threshold (from 27.3 mT/m to 45.5 mT/m) for the PNS oracle specific 1 kHz sinusoidal waveform (40% reduction in PNS oracle value from 36.7 m/T to 22.0 m/T). The optimized Z-axis windings lead to a 43% increase in PNS threshold (30% reduction in PNS oracle).

The PNS oracle map shows hot-spots greater than 1% of the maximum PNS oracle in the body as colored spheres. The color and size of each sphere corresponds to the PNS oracle value (reciprocal PNS threshold). For example for coil B1 (Fig. 4, left), stimulation of the “yellow-sphere” nerves in the shoulder, biceps, and upper vertebrae requires a gradient amplitude of approx. 27 mT/m (for a 1 kHz sinusoidal gradient waveform), while stimulation of the “red-sphere” nerves (mostly neck and lower vertebrae) requires a higher amplitude of approx. 50 mT/m. The coil B1 without PNS-optimization corresponds to a classical symmetric Y-axis coil with typical stimulation sites in the shoulder, triceps, and close to the vertebrae. The optimized Y-axis coil B2 deviates significantly from the conventional solution B1. This modification leads to a reduced interaction with the peripheral nerves, and thus to a 66% increase in the PNS thresholds (from 27.3 mT/m to 45.5 mT/m), which corresponds to a 40% PNS oracle reduction. The classical symmetric Z-axis coil B3 without PNS-optimization mainly stimulates the intercostal nerves leaving the vertebrae. The optimized coil B4 has an unconventional and asymmetric wire pattern which leads to a 43% PNS threshold increase (from 42.9 mT/m to 61.4 mT/m), corresponding to a 25% PNS oracle reduction.

Figure 5 shows the winding solutions and PNS oracle maps for the unoptimized and optimized 3-layer head X-axis coils H1 and H2 and Z-axis coils H3 and H4 (unfolded winding patterns are shown in supplementary Fig. S2). The unoptimized X-axis coil H1 strongly stimulates the facial nerves (forehead and nose) and mildly stimulates the shoulder nerves. The optimized coil H2 significantly reduces stimulations of the facial nerves while slightly increasing stimulations in the shoulder, thus balancing stimulations in these two body parts. The Z-axis head coil H3 without PNS-optimization mainly stimulates the intercostal nerves (similarly to the body Z-axis coils) as well as the shoulder nerves. The optimized Z-axis windings increase the PNS thresholds by 66% (109 mT/m to 222 mT/m), corresponding to a 40% PNS oracle reduction.

Figure 5:

Optimized stream function solutions and extracted winding patterns and the resulting PNS oracle/PNS threshold maps in the female body model for the unoptimized and optimized three-layer X-axis head coils (H1 and H2) and Z-axis head coils (H3 and H4). The colored spheres correspond to hotspots with largest PNS oracle (smallest PNS threshold). Both the color and the sphere size encode the PNS oracle value. The optimized X-axis winding pattern leads to a 67% increase in PNS threshold (from 133 mT/m to 222 mT/m) for the PNS oracle specific 1 kHz sinusoidal waveform (40% reduction in PNS oracle value from 7.5 m/T to 4.5 m/T). The optimized Z-axis windings lead to a 66% increase in PNS threshold (40% reduction in PNS oracle).

Body Surface B-fields and E-fields

Figure 6 shows the B-field and E-field magnitudes on the surface of the female body model induced by the body Y-axis coils B1 and B2 and the head X-axis coils H1 and H2 (results for the Z-axis body coils B3/B4 and head coils H3/H4 are shown in supplementary Fig. S3). The unoptimized body coil B1 induces a rather uniform B-field in the chest. The resulting E-fields are shaped by the conductive body model, with hot-spots in the neck/shoulders, upper arm, hips and close to the spine. These hotspots roughly coincide with the PNS hot-spots shown in Fig. 4. The optimized body coil B2 reduces the B-field exposure of the chest (thus reducing the induced E-field and PNS), for example, by redirecting some of the B-fields through the head where the E-fields increase mildly.

Figure 6:

Magnitude of the total magnetic field (∣B∣, left) and electric field (∣E∣, right) on the surface of the female body model induced by the unoptimized and optimized body Y-axis coils B1 and B2, and the head X-axis coils H1 and H2. The B-field is scaled to an equivalent gradient strength of 10 mT/m, the E-field is scaled to a slew rate of 100 T/m/s.

The unoptimized head coil H1 induces strong B-fields (and thus high E-fields) in the head, with lower fields in the shoulders and thorax. The optimized coil H2 reduces the B-field magnitude in the head and increases the B-field in the chest. This modification shifts the high E-field region from the head to the chest where fewer peripheral nerves are present, thus reducing the total PNS response.

Linearity and image distortion

Figure 7, left, shows maps of the gradient field error for the unoptimized and optimized Y-axis body coils B1 and B2 and the resulting spatial deformations in the center and off-center sagittal planes (transverse planes are shown in supplementary Fig. S4). Every wrap of the colormap corresponds to a 5% increase in linearity error. The unoptimized coil B1 creates typical symmetric field error characteristics with zero error at the isocenter and a steady increase towards the boundary of the FOV (dashed line) where the first 5% error contour occurs. Consequently, the spatial deformations (bottom, black lines) are mostly confined to the edges of the FOV. The PNS-optimized coil B2 creates a less symmetric, but still smooth error map with a baseline error that leads to a mild shift of the image (red lines). The baseline linearity error and resulting image shift are stronger in the off-center slice. Both coils B1 and B2, however, have the same peak linearity error (5%) and thus the same maximum pixel displacement. The unoptimized and optimized head coils H1 and H2 (Fig. 7, right column) achieve more similar linearity error maps; the only significant differences occur at the left/right boundaries of the ROL, while both coils achieve the same 5% peak linearity error. Linearity results for the Z-axis body coils B3 and B4 and Z-axis head coils H3 and H4 are shown in supplementary Figs. S5 and S6.

Figure 7:

Top: Distribution of the absolute local gradient field error (deviation of B_z from the idealized linear pattern) for the unoptimized and optimized body Y-axis coils B1 and B2 in sagittal planes (left) and for head X-axis coils H1 and H2 in coronal planes (right, dashed lines indicate the linear volume). The error is computed using Eq. 4 and shown in both center and off-center planes (shifted by 75% of the ROL radius). Every wrap of the colormap corresponds to a 5% field error contour. Bottom: Spatial deformations in the linear volume resulting from the field linearity errors of the unoptimized coils (B1/H1, black curves) and the optimized coils (B2/H2, red curves).

Concomitant magnetic fields

The concomitant field metric within the ROL was larger for the PNS-optimized body coils. For the Y-axis body coils B1 and B2, PNS-optimization increased the average and maximum of this metric from Δ_c = 0.044 (maximum Δ_c = 0.203) to Δ_c = 0.087 (maximum Δ_c = 0.434). For the Z-axis body coils B3 and B4, the increase was from Δ_c = 0.022 (maximum Δ_c = 0.053) to Δ_c = 0.0254 (maximum Δ_c = 0.076). For the head gradient X-axis coils (H1 and H2), PNS-optimization lowered the concomitant field metrics from Δ_c = 0.067 (maximum Δ_c = 0.209) to Δ_c = 0.046 (maximum Δ_c = 0.163). The concomitant field metrics for the Z-axis head coils H3 and H4 were essentially unaffected by the optimization (average Δ_c = 0.006 and maximum Δ_c = 0.015 in both cases).

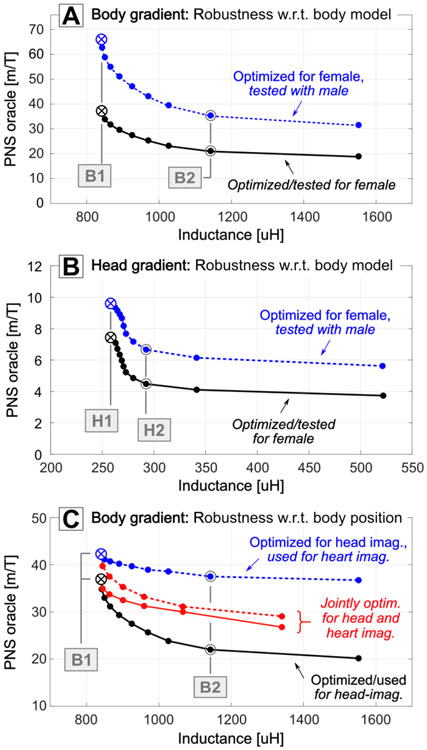
Robustness to body model type and position

Figure 8 summarizes the results of a preliminary robustness analysis. Panels A and B show L-curves (PNS oracle vs. coil inductance) for the 5% linearity body Y-axis coils optimized for the female model for head imaging. The black curve shows the PNS responses in the female model (same L-curve as in Fig. 3), whereas the dashed blue curve shows PNS responses in the male model for this “female-model-designed” coil. Similarly to our previous results, the female model has a significantly higher threshold (lower PNS oracle) than the male [41], but the relative PNS improvements obtained from the PNS-informed coil optimization are similar for both body models. For example, optimizing and testing on the female model reduces the PNS oracle by 40%, (B1 vs. B2) while optimizing on the female and testing on the male model reduces the PNS oracle by 45%. Similar results are achieved for the head X-axis coils H1 and H2 (Fig. 8, top right) where the PNS oracle is reduced by 40% (7.5 m/T to 4.5 m/T) and 30% (9.6 m/T to 6.7 m/T) in the female and male models, respectively.

Figure 8:

A,B: PNS oracle vs. inductance performance for the body coils (A) and head coils (B) in both the female and male models (although both coils were optimized specifically for the female model). C: PNS oracle vs. inductance performance for the body coils optimized for head imaging, when being used for head imaging (black) and heart imaging (dashed blue). The red L-curves correspond to BEM-SF coil solutions that were optimized simultaneously for both scanning positions.

Figure 8C shows the effect of changing the body model position within the 5% linearity, head-at-isocenter PNS-optimized body Y-axis coils. The black L-curve shows the PNS responses for the female model placed with the head at isocenter; the dashed blue L-curve shows the PNS responses when the female model is shifted by 30 cm along the z-direction (mimicking cardiac imaging). Using these coils for cardiac imaging instead of head imaging reduces the PNS improvement for coils B1/B2 from 40% to 18%. Alternatively, the coil windings can be optimized simultaneously for both scan positions by stacking the respective P-matrices in the BEM-SF optimization. These jointly optimized windings (red L-curves in Fig. 8C) achieve similar PNS oracle values for both cardiac and head imaging positions (31 m/T and 30 m/T for the 1060 μH coil solution, corresponding to 28% and 19% PNS oracle reductions).

IV. Discussion

In this work, we describe an approach to incorporate PNS effects into the design process of MRI gradient coils and demonstrate its potential for addressing this growing biological limit to MRI performance. The representation of the PNS model in matrix form (the P-matrix) allows the winding optimizer to quickly assess and compare thousands of candidate coil designs and iteratively approach an optimal design. The convexity of the optimization guarantees convergence to an optimal solution and stems from the linearity of the PNS oracle [23, 24] with respect to the current applied to individual coil segments (basis elements). Although formulation of the P-matrix for a given coil basis set requires considerable precomputation, it can be applied to multiple design problems for that geometry. The approach also incorporates traditional engineering constraints (such as field linearity, coil inductance, wire spacing, and torque) and assesses optimal tradeoffs between these constraints and PNS improvements. We demonstrated that this framework allows designing body and head gradient coils with more than 2-fold reduction in PNS propensity with moderate penalties in coil inductance or field linearity.

The L-curve analysis (Fig. 3) showed that significant PNS improvements can be achieved, albeit at the cost of some additional coil inductance or degradation of field linearity. For example, tolerating a 10% increase in inductance allows reducing PNS for the X and Y-axes of body and head gradients by 25% and 40%, respectively. For the body Y-axis coil, relaxing both the inductance and linearity constraints (from 5% to 10% linearity error) yields a 2-fold PNS reduction. Improving the performance of the Z-axes in either body or head gradients comes at higher inductance penalties. This is most likely due to the fact that Z-axis coils mostly create B_z field components. Reshaping of these field components for PNS reduction must be confined to outside of the FOV to avoid interference with spin encoding. In contrast, X and Y-axes mostly create B_x and B_y components outside of the FOV. These field components only mildly affect spin encoding, and thus can be modified both inside and outside of the FOV to reduce PNS.

Analysis of the concomitant field terms in the linear volume showed that the winding optimizer utilizes this degree-of-freedom for PNS reduction. For the optimized body Y-axis coil B2, this led to 2-fold higher average concomitant field metric (compared to the unoptimized coil B1). This places increased burden on field characterization [42, 43] and correction schemes, such as gradient pre-emphasis [44] and frequency modulation of the RF coils [45, 46]. These concepts have been successfully used in various high-performance scanners, including the Connectome system [1] and a compact head gradient 3T scanner [47].

The algorithm can also trade the field linearity constraint for PNS improvements but even if this constraint is held constant, undesirable effects can be introduced. For example, both body Y-axis coils B1 and B2 achieve the same 5% maximum linearity error (leading to the same maximum pixel displacement), but the image distortion pattern for the PNS-optimized coil B2 is more complex, i.e., less symmetric and less uniform. Similar effects were observed for the body Z-axis coils B3 and B4, while being less pronounced for the head X-axis and Z-axis coils H1-H4. This will potentially require more advanced correction techniques [48, 49, 50].

The inductance penalty for the PNS-optimized coils arises from the need to reshape the coil’s B-fields in an attempt to reduce B-field exposure to the body’s high cross-sectional area regions (which reduces the E-fields). This B-field shaping requires additional wire paths, leading to higher coil inductance. It is important to note that an increase in coil inductance results in a reduced slew rate for the user assuming a given maximum voltage available for the gradient amplifier. Additionally, higher inductance requires increased heat removal (from increased resistance due to longer wire lengths) and partial discharge concerns due to large voltages between neighboring wires. While these are negatives, the importance of the two parameters (inductance and PNS) underscores the need to rigorously assess this tradeoff between optimal designs.

The gradient coil windings shown in this work were PNS-optimized for an 8 ms sinusoidal 1 kHz coil waveform (the parameters of the PNS oracle were calibrated for this waveform). Analyzing a single frequency is sufficient for our needs since the main goal of our winding optimization is to enforce relative PNS improvements. This means that a PNS-optimized coil that achieves a 20% threshold improvement for sinusoidal waveforms will achieve a very similar relative improvement for trapezoidal pulses or for other frequency sinusoids. While it is not fully studied that optimizing a gradient coil for one waveform guarantees optimality for other waveforms, the existence of the simple monotonic relationship between the common waveform types (such as sinusoidal and trapezoid) is encouraging [10]. Finally, while the PNS oracle utilized in this work is computed for a specific 1 kHz frequency readout waveform, the PNS oracle and the neurodynamic modeling approach have been shown to be accurate for a range of frequencies up to about 10 kHz [18].

The PNS oracle plays an important role in informing the winding optimizer about the PNS characteristics of different coil solutions. In fact, constraining the E-field magnitude at the nerve locations (rather than the PNS oracle) disregards several important aspects of nerve excitability. First, many nerve tracks in the body do not contain sensitive motor nerves but only less-sensitive sensory nerves that can tolerate higher E-fields. Second, the nerve’s excitability strongly depends on the relative orientation between the nerve and the imposed E-field. For example, a kinked nerve segment in a moderate E-field region can be much more susceptible to stimulation, than a straight nerve segment in a high E-field region. Third, a nerve that is stimulated moderately at two segments a few millimeter apart is likely more susceptible than a nerve being stimulated more strongly at a single nerve segment (due to cross-talk between neighboring nerve segments). Correctly accounting for these aspects provides a more accurate PNS metric and offer degrees-of-freedom that can be harnessed by the optimizer for PNS reduction. Most importantly, however, simplified metrics (such as E-field at the location of nerves) still require the relatively hard-to-come-by electromagnetic model with a nerve atlas. Given this necessary model, the PNS oracle then captures these aspects in an easily computed formulation and preserves linearity in the E-field (and thus the current density basis functions).

The level of achievable PNS reduction is expected to be determined by the number of degrees-of-freedom in the BEM-SF optimization problem, and different strategies can be used to create these needed degrees-of-freedom. One strategy is to relax some of the traditional engineering constraints such as gradient field linearity. This tradeoff between linearity and PNS performance has been previously noted [12], but our optimization strategy can maximally exploit it. For example, using only the traditional coil design approach without PNS metric achieves a PNS improvement of only 15%. This traditional approach also reduces the coil inductance by 25%, however, this may not be useful if PNS limits the usable slew rate.

Adding coil layers appears to be another viable strategy for providing more degrees-of-freedom to the optimization problem. For the body coils, two coil layers are sufficient to achieve significant PNS improvements. Addition of a third layer (dashed L-curves in Fig. 3, left column) reduces the inductance “cost” at constant PNS improvements. If additional inductance is acceptable, the 3-layer approach can take advantage of this to improve PNS performance beyond ~40%. For the head coils, we show only 3-layer coil layouts since the BEM-SF optimization for the 2-layer setup lacks solutions for levels of PNS reduction beyond ~15% (especially for coils with 5% target linearity). The winding optimizer used the intermediate coil layer mainly for field generation (rather than shielding). For the PNS-optimized coils, the intermediate layer also played an important role in bending away the X-axis coil’s B-fields from the facial area (Fig. 6) or the Z-axis coil’s B-fields from the shoulder area (Fig. S3) in an attempt to reduce the induced E-fields and thus PNS. Although the PNS informed coil design/operation approach is demonstrated on cylindrical geometry coils, the method can be easily applied to unconventional coil geometries [51, 52, 29, 53], coils with 3D winding distributions [54, 55], and matrix gradient coils [56, 57, 58].

Although we have previously shown that our male and female body models have differing PNS thresholds [41], it appears that an optimal winding pattern for one gender model is near optimal for the other (Fig. 8). Most likely, this robustness stems from the fact that the BEM-SF basis set does not provide enough degrees-of-freedom to reduce PNS on a microscopic scale. In fact, adjacent stream function bases create very similar smooth magnetic fields, and thus similar E-fields and PNS oracles (see Fig. 2C). This similarity, together with the relatively large distance between the coil windings and the body, does not allow the optimizer to create local PNS cancelation for the studied coil geometries. Instead, the winding optimizer uses macroscopic strategies for PNS reduction, such as bending the B-field away from the torso and redirecting it to smaller body parts (such as the extremities or the head) where they lead to smaller E-field amplitudes, and therefore reduced PNS propensity. In reality, there are of course many sources of PNS threshold variability among subjects, including body shapes, tissue composition (such as body fat percentage) [19, 59], varying dielectric tissue properties, and anatomical and physiological details of the nerve fibers (such as level of myelination, node of Ranvier spacing, etc) [19]. We hypothesize that this variability does not significantly impair the PNS improvements of our optimized windings, as we are aiming for relative threshold improvements (i.e., increasing the PNS threshold averaged over a large population). That being said, it is desirable to test this hypothesis in as many models as possible, and ultimately in threshold experiments on individual subjects whose anatomy differs from our models.

Aside from purely reducing the E-fields in the body, the winding optimizer explored a different strategy: redistribution of the E-fields in the body, by either moving them to body parts without sensitive nerves or balancing E-fields (and thus PNS) in different body parts. This is especially noticeable for the unoptimized and optimized head X-axis coils H1 and H2, where the E-field hotspot moved from the facial area to the chest area (Fig. 6). This led to higher PNS thresholds in the head, but slightly lower PNS thresholds in the shoulder, thus balancing stimulation in these two body parts. Note that this is a valid strategy, as the coil’s PNS thresholds are determined only by the most sensitive nerve, while secondary stimulation sites are less relevant in practice. Even though the E-fields increase in the chest area (reaching ~0.6 V/m at 100 T/m/s), cardiac stimulation requires substantially higher E-field magnitudes (experimental work in mammals indicates E-field thresholds above approx. 40 V/m) [8]. We have recently extended our PNS modeling tool towards electromagnetically induced cardiac stimulation to study this concern in more detail [60].

As shown in Fig. 8C, the optimized coils are most effective in reducing PNS for the scan position used in the optimization. For example, when the body gradients are optimized for head imaging and used with a cardiac imaging body position (30 cm shift), the PNS oracle improvement is reduced from 40% to 15%. For greater shifts of the body in the coil (e.g., corresponding to kidney imaging), the PNS thresholds may even become slightly worse (lower) compared to the unoptimized coil. In this case, it would likely be beneficiary to use a feet-first patient position. The optimization tends to de-symmetrize the coil, placing a high-field-region near the service end. This ensures that the torso is located in the region of reduced B-field magnitude (see Fig. 6, top) for head-first imaging. Alternatively, the coil windings can be jointly optimized for multiple scan positions. For example, for the head and cardiac scan positions this yielded a smaller PNS improvement which was valid for both scan positions (similar PNS oracle values for cardiac and head imaging, see Fig. 8C, red curves). For improved PNS performance at multiple scan positions, it is likely that providing more degrees-of-freedom to the BEM-SF winding optimizer, for example by adding a third coil layer, would be helpful. Finally, while we did not assess feet-first imaging, clinical use cases for the feet-first position such as foot, knee, or wrist imaging would be relatively unconstrained by PNS since a low cross-section body part is present in the high field area at the service end.

The manufacturability of the PNS-optimized winding patterns is likely going to be more complex, compared to conventional designs. The impact on the winding complexity is most prominent for the body coils, where the introduced twist in the windings breaks most of the typical coil symmetries, except the symmetry along the spatial x-axis. The main challenge for manufacturing of the proposed head gradients is likely the additional intermediate winding layer that was needed to provide degrees-of-freedom for PNS reduction (although 3-layer coil designs have been realized before [61]). As with every engineering constraint, the tolerated winding complexity, if quantified, can be freely traded against PNS improvements. We are currently assessing strategies to further constrain the winding optimization to improve manufacturability.

Although only required once, formation of the P-matrix is computationally expensive. Simulation of the PNS response for a single stream function basis (one column in the P-matrix) takes up to 10 minutes, resulting in 2-3 days for the P-matrix computation of a single coil layer. Modification of the coil former shape, changing the body model type (male/female) or its position within the coil requires re-computation of the P-matrix. Fortunately, this lengthy step can be avoided by simply relating a pre-computed P-matrix defined on a Huygens’ surface closely fitting the body model to the coil geometry-specific P-matrix [62]. This approach avoids re-computation of a “new” P-matrix for each new design geometry or body position. The Huygens P-matrix is obtained by populating the Huygens’ surface with magnetic basis functions (such as magnetic dipoles or small coils) and computing the induced E-fields and PNS oracles along all nerves for each basis. The Huygens’ P-matrix is then assembled from the PNS oracle values induced by all basis functions (columns) along all nerve segments (rows). Due to the linearity of the PNS oracle with respect to the coil currents, the P-matrix of a coil geometry (i.e., its current density basis set) can be represented by a weighted superposition of the Huygens’ basis PNS oracles. Linking the Huygens’ P-matrix to a coil geometry specific P-matrix only requires a mapping matrix which can be obtained very efficiently using Biot-Savart simulations of the B-fields generated by both the Huygens’ basis set and coil former geometry and solving an inverse problem.

The P-matrix formulation involves a few important approximations. First, the response of a nerve to the induced E-field is modeled by a linear predictor (the PNS oracle), that has a PNS threshold accuracy of ~7% compared to the reference thresholds obtained using full non-linear neurodynamic models [23, 24]. Other factors of uncertainty arise from typical limitations of the electromagnetic body models itself (such as the topology of conductive tissues and dielectric tissue properties) and the limited number of nerve segments included in our nerve atlases (~1900 segments per model). The body models and the processing pipelines including the electromagnetic simulations that we (and others) use for neurodynamic modeling are constantly being refined [63, 64]. Additional work is also required on a more in-depth analysis of the robustness of the optimized coil layouts with respect to other parameters, such as subject variability, manufacturability and tolerances in coil fabrication. Moreover, there are a number of other engineering metrics such as secondary effects from the cryostat eddy currents [30, 31], acoustic properties [28, 29], and the exact properties of heat dissipation [26, 27] that could be incorporated. Finally, it will be important to validate that the optimized designs achieve the predicted benefits. This will require directly comparing the predicted PNS thresholds to measured thresholds in prototype coils. Fortunately, much of this can likely be done on single-layer coils outside of a magnet (with reduced force and torque concerns). After validating the success of PNS mitigation through B-field reshaping in simplified coils, more realistic gradient prototypes need to be tested.

V. Conclusion

In this work, we demonstrate an approach for incorporation of PNS effects into the numeric optimization of MRI gradient coils. Knowledge of the interaction between the applied magnetic fields and peripheral nerves allows the coil winding optimizer to iteratively refine the windings to minimize PNS at the cost of coil inductance or gradient linearity. Representation of the PNS model in matrix forms maintains the convexity and thus simplifies the optimization process. Our design approach simultaneously considers PNS and traditional engineering parameters (such as field linearity, torque, and coil inductance), and thus allows studying optimal tradeoffs between these metrics and PNS improvements. A comparison of our PNS-optimized coils with conventional gradient coils showed a more than 2-fold PNS improvement with moderate penalties in coil inductance and field linearity, potentially doubling the usable image acquisition performance of state-of-the-art MRI systems in humans.