Predicting Reactive Cysteines With Implicit-Solvent Based Continuous Constant pH Molecular Dynamics in Amber

Abstract

Cysteines existing in the deprotonated thiolate form or having a tendency to become deprotonated are important players in enzymatic and cellular redox functions and frequently exploited in covalent drug design; however, most computational studies assume cysteines as protonated. Thus, developing an efficient tool that can make accurate and reliable predictions of cysteine protonation states is timely needed. We recently implemented a generalized Born (GB) based continuous constant pH molecular dynamics (CpHMD) method in Amber for protein pK_a calculations on CPUs and GPUs. Here we benchmark the performance of GB-CpHMD for predictions of cysteine pK_a’s and reactivities using a data set of 24 proteins with both down- and upshifted cysteine pK_a’s. We found that 10-ns single-pH or 4-ns replica-exchange CpHMD titrations gave root-mean-square errors of 1.2–1.3 and correlation coefficients of 0.8–0.9 with respect to experiment. The accuracy of predicting thiolates or reactive cysteines at physiological pH with single-pH titrations is 86 or 81% with a precision of 100 or 90%, respectively. This performance well surpasses the traditional structure-based methods, particularly, a widely used empirical pK_a tool which gives an accuracy less than 50%. We discuss simulation convergence, dependence on starting structures, common determinants of the pK_a downshifts and upshifts as well as the origin of the discrepancies from the structure-based calculations. Our work suggests that CpHMD titrations can be performed on a desktop computer equipped with a single GPU card to predict cysteine protonation states for a variety of applications, from understanding biological functions to covalent drug design.

INTRODUCTION

Cysteines are important players in cellular redox regulation.¹ For example, oxidative protein folding involves thiol-disulfide exchange reactions,² and under oxidative stress cysteine thiols in antioxidant enzymes and cytoplasmic glutathiones (a tripeptide Glu-Cys-Gly) are invoked to eliminate reactive oxygen species.^3–6 All these processes are believed to involve a reactive cysteine that is in the negatively charged thiolate form (–S⁻)^1,6,7 or has a high tendency to shift from the neutral thiol (–SH) to the thiolate form. The inverse relationship between cysteine reactivity and its pK_a is well established through measurements of the kinetic rate constants of thiol containing compounds or peptides and the pK_a’s of the thiol groups.^7,8 Reactive cysteines are highly nucleophilic and can undergo thiol-Michael addition with electrophiles, making them suitable as covalent linkage sites for covalent inhibitors.^9,10 Thus, knowledge of reactive cysteines would assist in covalent drug design for kinases and other targets that are not amenable to traditional reversible inhibition. Over the past decade, isoTOP-ABPP (isotopic tandem orthogonal proteolysisactivity-based protein profiling) techniques have been developed to scan for reactive cysteines in human proteins.^11,12 The data from the isoTOP-ABPP experiments were used to develop structure-based bioinformatics¹³ and sequence-based machine learning tools¹⁴ to predict reactive cysteines. However, the reliability of these data-driven tools remains unclear, particularly because the protein profiling techniques can generate false positives.¹⁵ Thus, developing a physics-based in silico capability to accurately and reliably predict thiol reactivities is highly desirable.¹⁶

Recently, using a data set of 18 proteins, Rowley and coworker¹⁷ evaluated several computational methods for predicting cysteine pK_a’s, including free energy simulations based on thermodynamic integration (TI), traditional structure-based pK_a calculations based on solving the Poisson-Boltzmann (PB) equation,^18–20 and the empirical pK_a calculations using PROPKA.²¹ They found that the computationally costly TI method with the CHARMM C36²² and the modified Amber ff99SB-ILDNP²³ force fields gave respective root-mean-square errors (RMSE’s) of 2.4 and 3.2 relative to experimental pK_a’s, which are lower than the RMSE’s of 3.4–4.7 from the PB and empirical calculations.¹⁷ However, these errors are on par with the RMSE of 2.7 from the null model, which assumes that all cysteines have the model or solution pK_a value.¹⁷ Thus, the work of Rowley and coworker demonstrated a need to improve the accuracies of computational methods for predicting cysteine pK_a’s.

While TI methods are not routinely used for pK_a calculations due to the extremely high computational cost, structure-based PB and empirical methods have been widely used. Over the past decade, constant pH molecular dynamics (MD) simulations have emerged as alternative powerful tools for pK_a calculations.²⁴ In constant pH MD,^25–33 protonation states of titratable sites are determined on the fly based on the free energies of protonation relative to that in solution. Since constant pH MD describes the coupling between conformational changes and protonation/deprotonation events, pK_a predictions can be more accurate than structure-based methods, particularly for buried residues^34–36 and when protonation/deprotonation of two or more residues is highly coupled.³⁷ The interested reader is referred to the reviews^38,39 as well as the original articles on the discrete constant pH MD techniques,^{25,27,30–32} which combine MD with Monte-Carlo sampling of discrete protonation states, and the continuous constant pH MD (CpHMD) techniques,^{26,28,29,35,40,41} which make use of the extended Hamiltonian λ-dynamics approach⁴² to sample protonation states through an auxiliary set of continuous titration coordinates.

In CpHMD, the free energies of protonation are calculated for all titratable sites in a single MD trajectory; this is in contrast to TI simulations, wherein the free energy of titrating a single site is calculated while fixing the protonation states of all other sites. Consequently, in addition to having a substantially lower computational cost, CpHMD can be more accurate than TI due to its ability to account for the coupling between interacting titration sites. In an effort to develop an accurate and efficient pK_a prediction tool, we recently implemented the CPU⁴³ and GPU⁴⁴ versions of the CpHMD method based on the Amber generalized Born (GB) model GBNeck2⁴⁵ in the Amber molecular dynamics package (Amber18⁴⁶). In comparison to older GB models, such as GBSW⁴⁷ employed in the GB-based CpHMD method in CHARMM,^26,28 GBNeck2⁴⁵ more accurately reproduces the solvation free energies from PB calculations and the experimental structures and stabilities of model peptides and proteins.^45,48

CpHMD simulations can be carried out in two modes. A single or fixed pH titration returns the protonation probabilities of specified titratable sites at a specified pH. Running the titration at several pH allows one to calculate the pK_a’s by fitting the protonation probabilities vs. pH to the Henderson-Hasselbalch equation. CpHMD can also be performed with the pH replica-exchange protocol,⁴⁰ whereby multiple independent titrations are run at a set of pH conditions and periodic swaps between adjacent pH conditions are accepted according to the Metropolis criterion. Compared to single pH titrations, the replica-exchange protocol can accelerate pK_a convergence and better resolve the pK_a’s of coupled residues due to enhanced sampling of both conformational and protonation states.^{30–32,40,44} However, single pH titrations are more convenient for routine use on a desktop computer equipped with one or two graphics processing units (GPU) cards. Encouragingly, our recent work⁴⁴ showed that 2 ns single pH titrations with the GBNeck2-CpHMD method gave comparable overall accuracy as replica-exchange titrations for the pK_a’s of Asp, Glu, and His residues in 10 benchmark proteins. While CpHMD simulations can also be used to predict Cys pK_a’s,¹⁰ a systematic evaluation of the prediction accuracy and precision has not been conducted.

The main objective of the present work is to benchmark the performance and protocols of GBNeck2-CpHMD titrations in both single-pH and replica-exchange modes for predicting cysteine pK_a values and reactive cysteines. We used a data set comprising the aforementioned targets compiled by the Rowley group which have mostly downshifted cysteine pK_a’s¹⁷ and additional targets which have mostly upshifted pK_a’s taken from a database developed by the Alexov group.⁴⁹ In addition to assessing the accuracy of pK_a calculations, we evaluated the accuracy and precision of predicting thiolates or reactive cysteines at physiological pH, defined as those with a pK_a lower than 7.4 or 8.5, respectively.¹⁰ To determine the most accurate and yet efficient protocols for practical applications, we analyzed the convergence and accuracies of single-pH and replica-exchange titrations as well as the dependence of the pK_a results on the starting structures. Finally, we examined the common determinants of cysteine pK_a downshifts and upshifts and the origin of the discrepancies from the structure-based PB and empirical calculations. For 21 targets, the 10-ns single-pH CpHMD titrations predicted thiolates or reactive cysteines with an accuracy of 81 or 86% with a precision of 91 or 100%; which is in contrast to the PB-based calculations and the popular empirical method PROPKA²¹ which gives a prediction accuracy below 50%. However, our work also exposed a caveat of the current protocols or methodology which correctly predicted the protonation states at physiological pH, but were not able to yield a pK_a value for the deeply buried cysteine involved in several hydrogen bonds in three phosphatases.

METHODS AND PROTOCOLS

Protein data set.

The first 15 proteins were taken from those evaluated by the Rowley group,¹⁷ which have an experimentally known Cys pK_a. The protein names and PDB (Protein Data Bank) ID’s are as follows: α−1-antitrypsin (A1AT, PDB 1QLP⁵⁰), acyl-coenzyme A binding protein wild type and M46C, S65C, and T17C mutants (ACBP, PDB 1NTI⁵¹), Salmonella alkyl hydroperoxide reductase C (AhpC, PDB 4MA9⁵²), human DJ-1 (DJ-1, PDB 1P5F⁵³), human muscle creatine kinase and the S285A mutant (HMCK, PDB 1I0E⁵⁴), sperm whale myoglobin G124C and A125C mutants (Mb, PDB 2MGE⁵⁵), wild type and E115Q mutant of mouse methionine sulfoxide reductase A (MmsrA, PDB 2L90⁵⁶), human O⁶-alkylguanine-DNA alkyltransferase (AGT, PDB 1EH6⁵⁷), papaya proteinase I (papain, PDB 1PPN⁵⁸), and papaya protease omega (ppω, PDB 1PPO⁵⁹).

Since only two of the above proteins have cysteine pK_a’s upshifted relative to the model value, we added 6 proteins with upshifted experimental cysteine pK_a’s. These proteins are: recombinant rat cathepsin B (Cathepsin B, PDB 1THE⁶⁰), yeast ubiquitin-conjugating enzyme E2 (Ubc13, PDB 1JBB⁶¹), human ubiquitin-conjugating enzyme E2 wild type (Ubc2b, PDB 1JAS⁶²) and E2 C114S mutant (UbcH10, PDB 1I7K,⁶³ and acyl-coenzyme A binding protein V36C and E78C mutants (ACBP, PDB 1NTI⁵¹). We note, the Rowley data set also included human tyrosine phosphatase 1B (PTP1B, PDB 2HNP⁶⁴) and Yersinia tyrosine phosphatase wild type and H402A mutant (YopH, PDB 1YPT⁶⁵). These three proteins will be considered separately.

Structure preparation.

For wild type proteins, the initial structures were taken from the PDB files. Single mutations were performed with SWISS-MODEL.⁶⁶ For AGT, missing residues (36–44) were added with SWISS-MODEL.⁶⁶ For each structure, the CHARMM program (version c42a1)⁶⁷ was used to add acetylated N terminus and amidated C terminus caps, disulfide bonds (if present), and hydrogen atoms. Initially, Asp/Glu were deprotonated, and His/Cys/Lys/Arg/Tyr were protonated. The system was then minimized with 50 steps of steepest descent method in the GBSW implicit solvent⁴⁷ with a harmonic force constant of 50 kcal/mol/Ų applied to heavy atoms. Dummy atoms were then added to Asp/Glu residues, and the structure was minimized for 10 steps of steepest descent and 10 steps of Newton-Raphson methods. Next, force field parameters and coordinate files were constructed from these structures with the Leap utility in AMBER.⁴⁶ The structures were then energy minimized by 2000 steps of steepest descent followed by 8000 steps of conjugate-gradient methods in GB-Neck2 implicit solvent⁴⁵ to obtain the initial structures for the CpHMD titration simulations.

Simulation protocol.

All GBNeck2-CpHMD simulations were performed using the pmemd engine of AMBER18.⁴⁶ The replica-exchange titrations were performed on the CPUs⁴³ and single pH titrations were performed on the GPUs.⁴⁴ The proteins were represented by the ff14sb protein force field,⁶⁸ and solvent represented by the GBNeck2 (igb=8) model with mbondi3 intrinsic Born radii and 0.15 M ionic strength.⁴⁵ Modifications to the GB parameters and/or intrinsic Born radii were made for His and Cys residues, as discussed in our previous work.^10,43,44 All simulations were run with an effectively infinite cutoff (999 Å) at a temperature of 300 K. SHAKE was used to allow a 2-fs time step. Asp, Glu, His, Lys, and free Cys residues were titrated, and the protonation states were recorded every 250 steps. The parameters for titrating model Asp/Glu/His/Lys/Cys were taken from our previous work.^10,43,44 The model pK_a is 8.55.^69,70 The parameterization from thermodynamic integration and titration results of the model Cys peptide (AACAA) are given in Fig. S1. The pK_a of the model Cys is 8.41±0.17 (Fig. S1). Replica-exchange titrations were performed for the first 15 proteins, whereby 12 independent replicas at pH conditions 0.5 unit apart were run for 4 ns each, and exchanges between adjacent pH conditions were attempted every 1000 MD steps unless otherwise noted. For the single pH titrations, each simulation was run for 50 ns for the first 15 proteins and 10 ns for the 6 proteins. Initially, the pH interval was 1 unit, but additional simulations at 0.5-unit interval were added if the titration curve appeared to be noisy. All other simulation settings were identical to our previous work.^10,43,44 pK_a’s from these simulations were obtained from fitting to the generalized Henderson-Hasselbalch (HH) equation. Error estimates were obtained from the estimated errors in the fit parameters.⁴⁴

RESULTS AND DISCUSSION

Convergence and accuracy of the pK_a calculations.

We first assess the convergence of the pK_a calculations for the 15 proteins from the Rowley data set. Single pH titrations were performed for 50 ns at each pH. The pK_a’s were calculated every 5 ns based on the cumulatively calculated unprotonated fractions at all pH (Fig. S2). Most pK_a’s converged at around 25 ns; however, the pK_a’s of HMCK^S285A, and ACBP^T17C converged more slowly and drifted towards slightly smaller values until 50 ns, while the pK_a of A1AT kept decreasing past 50 ns. For this data set, the overall pK_a accuracy, represented by the correlation coefficient R and root-mean-square error (RMSE) with respect to the experimental pK_a’s, appeared to be best at 10 ns and slightly worsened as simulations were extended (Fig. 1a and b). The RMSE and R values are respectively 1.3 and 0.82 at 10 ns; 1.4 and 0.78 at 25 ns, and 1.4 and 0.78 at 50 ns. Compared to the single pH titrations of Asp/Glu/His in our previous work,⁴⁴ the convergence rates for the present data set are much slower. This could be due to the selection biases in the two data sets. In our previous work, CpHMD titrations were performed on proteins where all titratable residues had measured pK_a values, many of which do not have large shifts relative to the model values. In contrast, free cysteine residues are uncommon in nature, and the ones with experimental pK_a’s are typically functional cysteines with large pK_a shifts. We therefore expect the pK_a calculations in the present data set to require longer sampling time to converge than those in our previous work.

Figure 1: Convergence of the simulation accuracy.

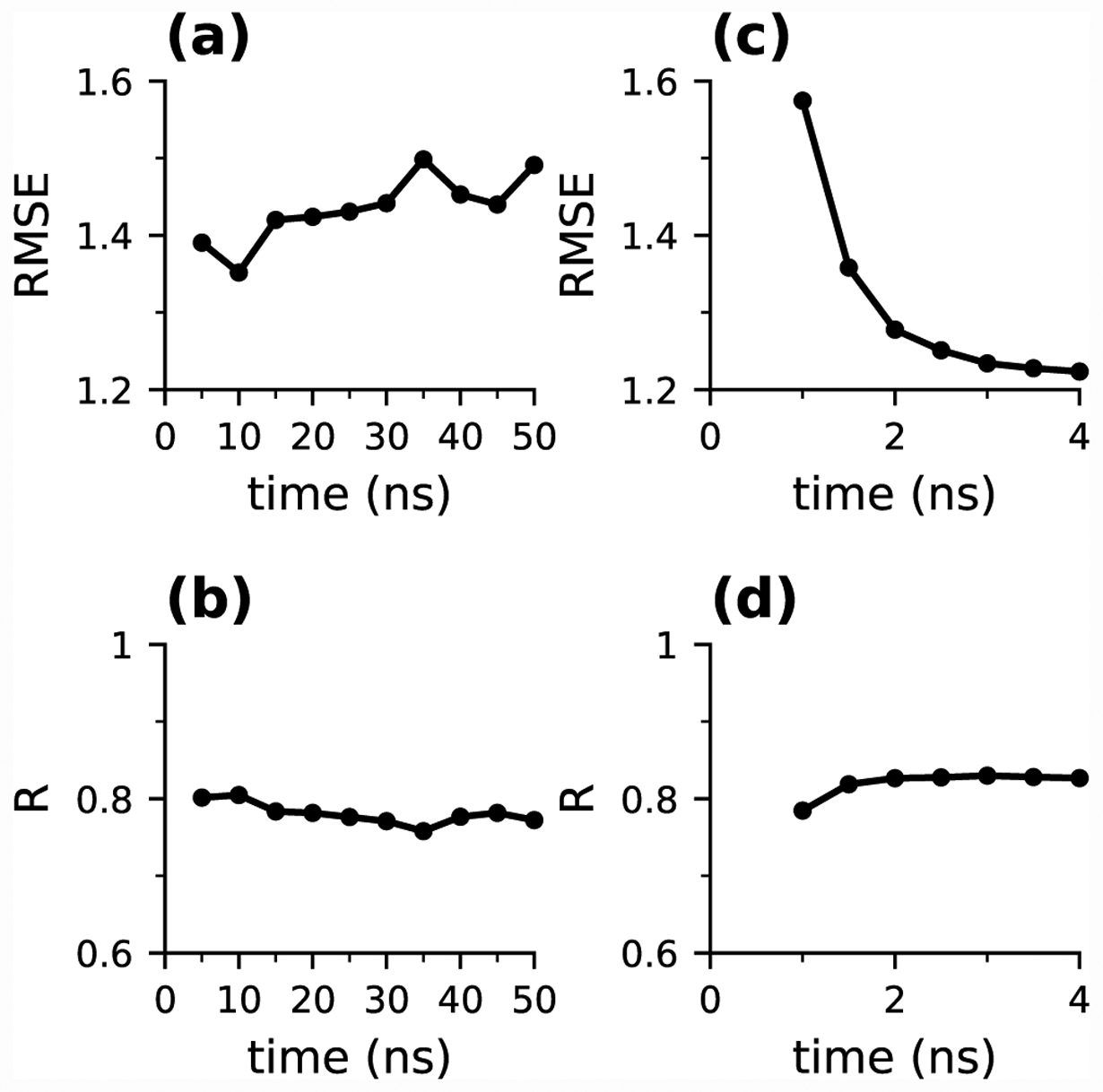
(a) and (b) Time series of root-mean-square error (RMSE) and correlation coefficient (R) with respect to the experimental data in the single-pH titrations of the 15 proteins. (c) and (d) Time series of RMSE and R in the replica-exchange titrations of the 15 proteins.

We next examine the convergence of the replica-exchange titrations. The pK_a’s were calculated every 0.5 ns per replica (Fig. S3). All pK_a’s converged after about 2 ns per replica, including the pK_a’s of the three proteins, for which single pH titrations were not able to converge until or after 50 ns. Consistently, the RMSE and R values also plateaued after about 2 ns, with the respective values of 1.3 and 0.83 at 2 ns per replica and 1.2 and 0.83 at 4 ns per replica (Fig. 1c and d). Thus, the overall accuracy of the replica-exchange titrations of 2–4 ns per replica is similar to that of the single pH titrations of 10–50 ns per pH. The significant acceleration in convergence can be attributed to the ability of the replica-exchange protocol to overcome local barriers of hydrogen bonding which is a major contributor to the pK_a shifts of cysteines (see later discussion). This is consistent with the effect of replica exchange on the pK_a’s of residues involved in salt-bridge interactions.^40,71 In what follows, we will focus on 10-ns single-pH and 4-ns replica-exchange simulations (Table 1).

Table 1:

Comparison of calculated pK_a’s from replica-exchange and single-pH GBNeck2-CpHMD titrations with experiment, Poisson-Boltzmann and empirical predictions^a

Protein	PDB	Residue	Expt	Replica	Single pH	H++	MCCE	DelPhiPKa	PROPKA
Crystal structures
AGT	1EH6	C145	5.373	6.7	6.4±0.01	9.5	8.3	5.3	10.6
HMCK	1I0E	C283	5.674	5.6	6.3±0.13	9.1	6.8	6.0	10.4
DJ-1	1P5F	C106	5.475	3.7	2.4±0.40	11.3	12.6	6.0	12.3
papain	1PPN	C25	3.376	4.0	3.7±0.05	9.3	8.8	5.6	10.5
ppΩ	1PPO	C25	2.976	3.7	3.1 ±0.12	9.4	7.6	4.9	7.5
A1AT	1QLP	C232	6.977	7.3	6.5±0.08	7.3	8.3	5.5	9.1
MmsrA	2L90	C72	7.278	7.9	8.2±0.91	>12.0	16.3	6.6	13.1
AhpC	4MA9	C46	5.979	5.2	5.3±0.52	9.4	9.1	5.8	9.1
Cathepsin B	1THE	C29	3.660	-	3.4±0.02	11.2	-	6.4	11.2
Ubc2	1JAS	C88	10.280	-	9.4±0.55	9.8	-	6.2	9.1
Ubc13	1JBB	C87	11.180	-	11.2±0.07	9.3	-	6.5	9.9
UbcH10C114S	1I7K	C102	10.980	-	9.0±0.15	>12.0	-	6.4	12.7
RMSE				0.95	1.3(1.1)
R				0.81	0.74(0.92)
Computationally mutated structures
HMCKS285A	1I0E	C283	6.774	9.8	9.3±0.12	9.3	6.6	5.9	11.2
ACBPM46C	1NTI	C46	8.251	7.3	7.6±0.15	8.8	8.8	6.6	9.0
ACBPS65C	1NTI	C65	9.051	7.8	8.0±0.05	8.8	9.4	6.7	9.6
ACBPT17C	1NTI	C17	9.851	10.1	10.5±0.03	8.4	8.8	6.4	8.9
ACBPV36C	1NTI	C36	9.551	-	8.9±0.11	9.0	-	6.2	8.9
ACBPE78C	1NTI	C78	9.651	-	11.5±0.18	8.7	-	6.0	9.1
MmsrAE115Q	2L90	C72	8.278	8.7	8.0±1.21	>12.0	15.4	6.6	11.4
MbA125C	2MGE	C125	8.481	8.7	8.7±0.21	8.3	8.8	6.6	9.2
MbG124C	2MGE	C124	6.581	8.3	8.7±0.06	8.1	8.5	6.0	8.4
RMSE				1.5	1.4 (1.3)
R				0.08	0.2 (0.5)
Overall RMSE				1.2	1.3 (1.2)	3.62	4.22	2.60	4.02
Overall R				0.83	0.82(0.89)	−0.48	0.23	0.61	−0.10

The pK_a’s from the 4 ns (per replica) replica-exchange and 10 ns (per pH) single pH titrations are listed. For single pH titrations, the RMSE and R values in parentheses include the additional 6 proteins (see main text). For the PB-based H++,¹⁸ MCCE,¹⁹ and DelPhiPka,²⁰ as well as the empirical PROPKA²¹ methods, data were taken from the previous publications if available,^17,82 or computed with the H++,¹⁸ DelPhiPka²⁰ and PDB2PQR⁸³ (for PROPKA²¹) online servers.

The RMSE and R of the pK_a calculations by single-pH titrations are respectively 1.3 and 0.82, while those by replica-exchange titrations are respectively 1.2 and 0.83 (Table 1). This indicates that the accuracy is similar and replica-exchange titrations are perhaps slightly more accurate (see later discussion about the calculations with crystal structures). As expected and consistent with our previous work,^43,44,71 the titration data (unprotonated fractions vs. pH) from the replica-exchange simulations display excellent fits to the HH equation (except for MmsrA-E115Q), while the titration data for several proteins from the single-pH simulations are very noisy (Fig. S4 and S5). The latter results in large uncertainty in the calculated pK_a, e.g., for MmsrA and the the E115Q mutant the errors are 0.9 and 1.2 respectively (Table 1).

We note, for the three remaining proteins in the Rowley data set, human and Yersinia tyrosine phosphatase proteins, PTP1B and WT/mutant YopH, the relevant cysteines remained deprotonated in the entire pH range of the single pH and replica-exchange titrations due to multiple persistent hydrogen bonds. Although the experimental pK_a downshifts were correctly predicted, no specific pK_a values could be assigned from these simulations. We speculate that in order to reproduce the experimental pK_a’s (4–7), these persistent hydrogen bonds would need to break, which would require much longer simulation times. It is also possible that sampling in explicit solvent is required to generate the conformational changes for a protonation state switch, as demonstrated in our previous work based on the hybrid-solvent CpHMD titrations in CHARMM⁷² as well as work from others.³⁵ We will further examine these systems in future work.

Dependence of the pK_a calculations on the starting structures.

Although compared to structure-based PB or empirical methods, MD-based pK_a calculations are less sensitive to starting structures,^24,34 it is worthwhile examining the dependence of the pK_a results on the starting structures, particularly given the use of implicit solvent and limited conformational sampling. To do so, we divided the 15 targets into two groups: 8 Cys pK_a’s were calculated using the crystal structures (all but one are of the wild type proteins) and 7 Cys pK_a’s were calculated using the computationally mutated crystal structures.

For the pK_a calculations with crystal structures, the RMSE and R from single-pH titrations are respectively 1.3 and 0.74, while those from replica-exchange titrations are respectively 0.95 and 0.81. Thus, the replica-exchange simulations appear to give somewhat more accurate pK_a’s. The largest pK_a error and also the largest difference between the single-pH and replica-exchange calculated pK_a’s is for Cys106 of DJ-1, where the experimental pK_a downshift of Cys106 is overestimated by 1.7 units by replica-exchange and 3.0 units by single-pH titrations. This difference is due to the persistence of hydrogen bonding in the single-pH simulations (see later discussion).

For the pK_a calculations with the mutated crystal structures, the RMSE and R from single-pH titrations are respectively 1.4 and 0.2, while those from replica-exchange titrations are respectively 1.5 and 0.08. Thus, both methods gave larger errors compared to the calculations with crystal structures, and the decrease in performance is much worse for replica-exchange titrations. These observations indicate that for mutated proteins we may need to run longer simulations so that the conformation relaxes more closely to the natural state. We can see some evidence for this from the time evolution of the RMSE in the single-pH simulations. For single pH titrations with crystal structures, the RMSE is the lowest (1.2–1.25) at 5–10 ns and increases to about 1.5 in the next 40 ns. In contrast, using the computationally mutated structures the RMSE reached a minimum of 1.25–1.3 at 20–25 ns. Thus, prolonging the single pH titrations from 10 to 20 ns somewhat improved the pK_a calculations with mutated structures but has a negligible effect on the calculations with crystal structures. We did not see any noticeable improvement in the RMSE with the mutant structures in the replica-exchange titrations between 2 and 4 ns, but perhaps we would observe some improvement with significantly longer simulations.

Common determinants of the cysteine pK_a downshifts.

The Rowley data set is dominated by the downshifted pK_a’s of cysteine; we first examine Cys145 of AGT. Both single pH and replica-exchange titrations revealed that the buried Cys145 accepts hydrogen bonds from the hydroxyl group of Tyr158 and the amino group of Asn137 when it becomes deprotonated. Fig. 2 demonstrates that the occupancies of these hydrogen bonds increase with pH and the pH-dependence is perfectly correlated with the pH-dependent deprotonation of Cys145, suggesting that Cys145 thiolate is stabilized by the hydrogen bond interactions. Consequently, the pK_a of Cys145 is downshifted relative to the model value despite the lack of solvent exposure which would raise the pK_a. Interestingly, none of the hydrogen bonds is present in the initial crystal structure. This may explain why the empirical method and PB calculations (except for DelPhiPKa which uniformly predicts pK_a downshifts⁸²) overestimate the pK_a of Cys145 (Table 1), as they only consider the crystal structure. This observation is consistent with our previous finding that by capturing the pH-dependent hydrogen bond formation, CpHMD titrations can make more accurate pK_a predictions than structure-based methods.³⁷

Figure 2: Cys145 thiolate in AGT is stabilized by hydrogen bonding.

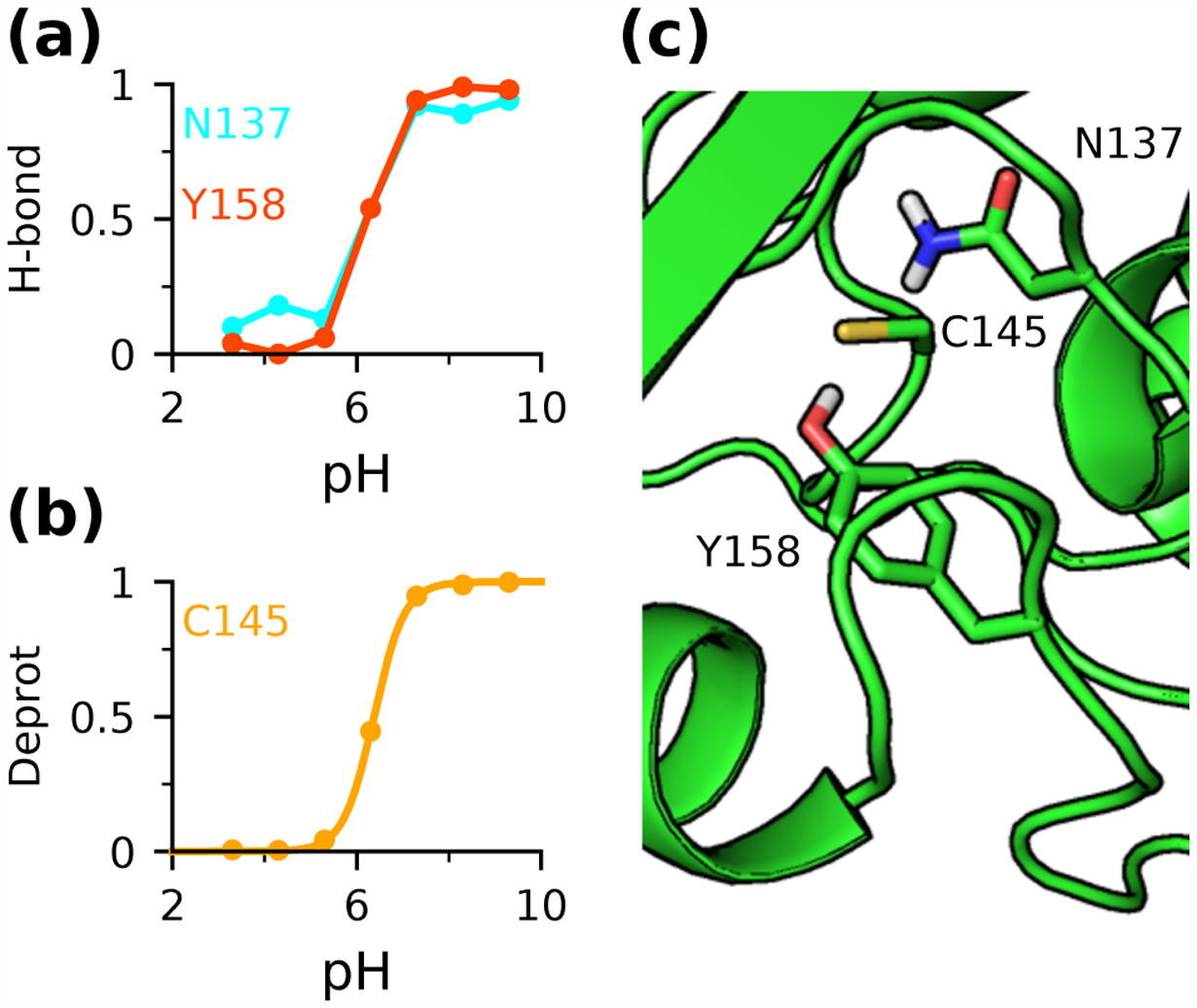
(a) Occupancies of the hydrogen bond between Cys145 and Asn137 (cyan) or Tyr158 (red) at different pH. (b) Deprotonated fractions of Cys145 (gold) at different pH. (c) Zoomed-in view of the structural environment of Cys145 in AGT (PDB ID: 1EH6⁵⁷). Data from (a) and (b) were obtained from 10-ns single pH titrations.

Cys283 in HMCK and HMCK^S285A provides another interesting example. Consistent with our previous finding,¹⁰ both replica-exchange and single-pH simulations agree that, although Cys283 in HMCK is buried, its pK_a is downshifted due to the formation of hydrogen bonds with the side chains and backbones of Ser285 and Asn286. Interestingly, when Ser285 is mutated to Ala in HMCK^S285A, both sets of simulations predicted a significant increase in pK_a to above the model value due to the loss of the hydrogen bond with Ser285 and destabilization of the conformation where it could form the other three hydrogen bonds. However, the experimental pK_a of Cys283 in HMCK^S285A is downshifted to 6.7, compared to 9.8 and 9.3 from the respective replica-exchange and single-pH titrations. One possible explanation for this discrepancy is that when modeling HMCK^S285A we started with the wild-type crystal structure. It is possible that the mutant conformation differs in some way that leads to a large change in the pK_a. Indeed, as the single-pH titrations were extended beyond 10 ns, a conformational change occurred such that Cys283 forms new hydrogen bonds with the backbone atoms of Thr71, Val72, and Gly73, stabilizing the thiolate form and lowering the pK_a by 1.5 units to 7.8 at 50 ns, in closer agreement with the experimental value of 6.7 (Fig. S2). Notably, Cys283 became increasingly deprotonated in the simulations at pH 7.5 and above, it remained fully protonated at pH 7. Thus, we expect that with further prolonged sampling the pK_a of Cys283 may stabilize just above pH 7, in better agreement with experiment. Nonetheless, it is also possible that the formation of new hydrogen bonds is an artifact of GB simulations which tend to overstabilize hydrogen bonds.^40,45 A detailed investigation will be deferred to a future study using the GPU implementation of the fully explicit-solvent CpHMD as well as the asynchronous replica exchange scheme which allows replica exchange simulations to be performed on a single GPU card (Harris and Shen, work in progress).

Common determinants of the cysteine pK_a upshifts.

Since the Rowley data set is dominated by downshifted Cys pK_a’s, we added 5 targets with upshifted Cys pK_a’s. We also included a protein with an extremely low experimental pK_a to further test the accuracy and reliability for predicting downshifted Cys pK_a’s (Table 1). Due to our limited computational resources, titrations were only performed in the single-pH mode for 10 ns at each pH (the sampling time found to give the smallest overall RMSE for the 15 aforementioned proteins). Including the additional 6 targets, the RMSE and R value of the single-pH titrations are 1.2 and 0.89, respectively (Table 1).

These additional data allowed us to examine the molecular determinants of the upshifted pK_a’s of cysteine. It is well established that solvent exclusion favors the protonated thiol form, thus increasing the pK_a; however, the pK_a increase is often compensated by the ability of a buried thiolate to accept hydrogen bonds, which lowers the pK_a of Cys, as demonstrated in our discussion of the downshifted pK_a’s of Cys145 in AGT and Cys283 in HMCK as well as HMCK^S285A. Thus, it is not surprising that the cysteines with upshifted pK_a’s are (at least) partially buried but do not form frequent hydrogen bonds. Another mechanism for cysteine to have a pK_a increase is to have acidic residues in the vicinity which can potentially form repulsive electrostatic interactions. For example, Cys87 in Ubc13 has the highest experimental pK_a of 11.1 and the single pH titrations gave a pK_a of 11.2. The simulations revealed that Cys87 is partially buried and its thiolate form is destabilized by the electrostatic repulsion with the negatively charged Asp81 that is about 4–6 Å away. Thus, both solvent exclusion and electrostatic interactions are major contributors to the pK_a upshift of Cys87.

Overestimation of the pK_a downshift of Cys106 in DJ-1.

The largest pK_a error in this data set is for Cys106 in DJ-1. Although the direction of the pK_a shift was correctly predicted by both replica-exchange and single pH titrations, the downshift was overestimated by 1.7 and 3 units, respectively. Considering the crystal structure, the downshift may be surprising, as Cys106 is largely buried, which would raise the pK_a, and its proximity to Glu16 would also be thought to increase the pK_a, as Glu residues are generally negatively charged at physiological pH. However, the CpHMD simulations revealed that while Cys106 becomes increasingly deprotonated as pH increases from 1.5 to 3, it accepts hydrogen bonds from the protonated carboxyl group of Glu16 and the backbone amide group of Gly75 (Fig. 3a and b). Additionally, the thiolate form is stabilized by the salt-bridge interaction with the protonated His126 (Fig. 3a and b). The latter two interactions are not present in the crystal structure; however, it is consistent with our previous finding that new hydrogen bond interactions may form to facilitate deprotonation events.³⁷ This may explain why the structure-based PB and empirical methods failed to predict a downshifted pK_a for Cys106 (Table 1), except for DelPhiPka which gave downshifted pK_a’s for all targets.⁸² We suggest that the overestimation of the pK_a downshift may be attributed to the overstabilization of hydrogen bonding, a well-known limitation of GB simulations.^40,45 This problem is less severe in the replica-exchange titrations, as hydrogen bonds were able to break and reform, illustrating the benefit of the enhanced sampling provided by replica exchange.

Figure 3: Cys106 thiolate in DJ-1 is stabilized by a protonated Glu and a doubly protonated His.

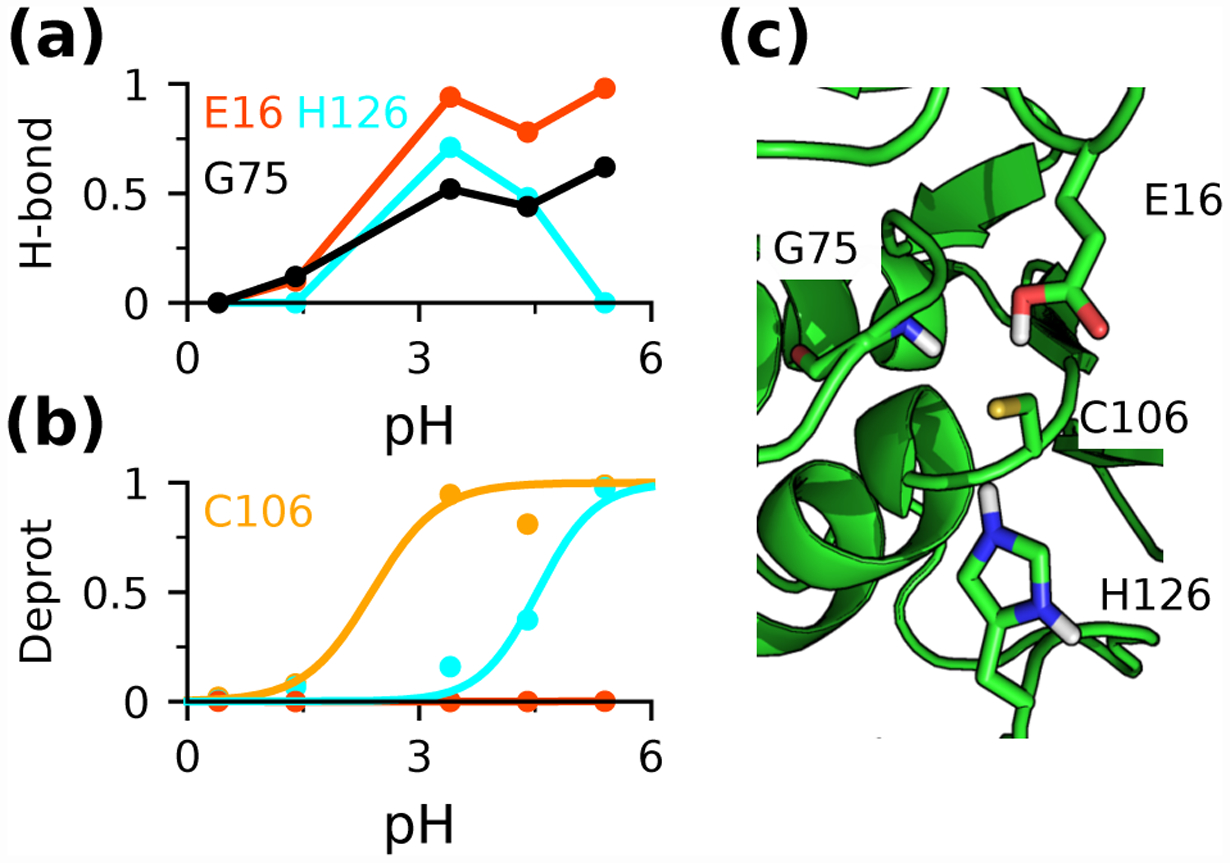
(a) Occupancies of the hydrogen bonds between Cys106 and Glu16 (red), His126 (cyan), or Gly75 (black) at different pH. (b) Deprotonated fractions of Cys106 (yellow) and His126 (cyan) at different pH. (c) Zoomed-in view of the structural environment of Cys106 in DJ-1 (PDB ID: 1P5F⁵³).

Performance of predicting thiolates and reactive cysteines.

Another objective of the present work is to evaluate whether CpHMD can reliably predict thiolates at pH 7.4 (physiological condition) or pH 8.5. The latter can be used to identify reactive cysteines, which are defined as those existing in the thiolate form for at least 10% at physiological pH.¹⁰ To do the evaluations, we grouped the data of predicted vs. experimental pK_a’ into four quadrants around the dividing pH of 7.4 for protonation state prediction and 8.5 for cysteine reactivity prediction. Data in the lower left quadrant are the true positives (TP), i.e., both predicted and experimental pK_a’s are lower than 7.4 or 8.5. Data in the upper left quadrant are the false positives (FP), i.e., the predicted pK_a is lower and the experimental pK_a is higher than 7.4 or 8.5. Data in the lower right quadrant are the false negatives (FN), i.e., the predicted pK_a is higher and the experimental pK_a is lower than 7.4 or 8.5. Data in the upper right quadrant are the true negatives (TN), i.e., both predicted and experimental pK_a’s are higher than 7.4 or 8.5.

The percentages of TP, FP, TN, and TP are entered in a confusion matrix for evaluating the accuracy and reliability of single pH CpHMD predictions based on the 21 targets (Table 1). The accuracy for predicting thiolates or reactive cysteines at physiological pH, defined as (TN+TP)/(TN+TP+FN+FP), is 86% or 81%, respectively (Fig. 4). The precision (also known as the positive predictive value) of the predictions, defined as TP/(TP+FP), is 100% or 91%, respectively. The miss rate (also known as the false negative rate) of the predictions, defined as FN/(TP+FN), is 27% or 21%, respectively. A similar analysis for the replica-exchange titrations gave an accuracy of 74% with a precision of 87% or 90% for predicting thiolates or reactive cysteines at physiological pH (Fig. S6). The accuracy is slightly lower due to the smaller data set (the additional targets with upshifted pK_a’s were not included).

Figure 4: Performance of single-pH titrations for predicting cysteine pK_a’s and identify thiolates at pH 7.5 or 8.5.

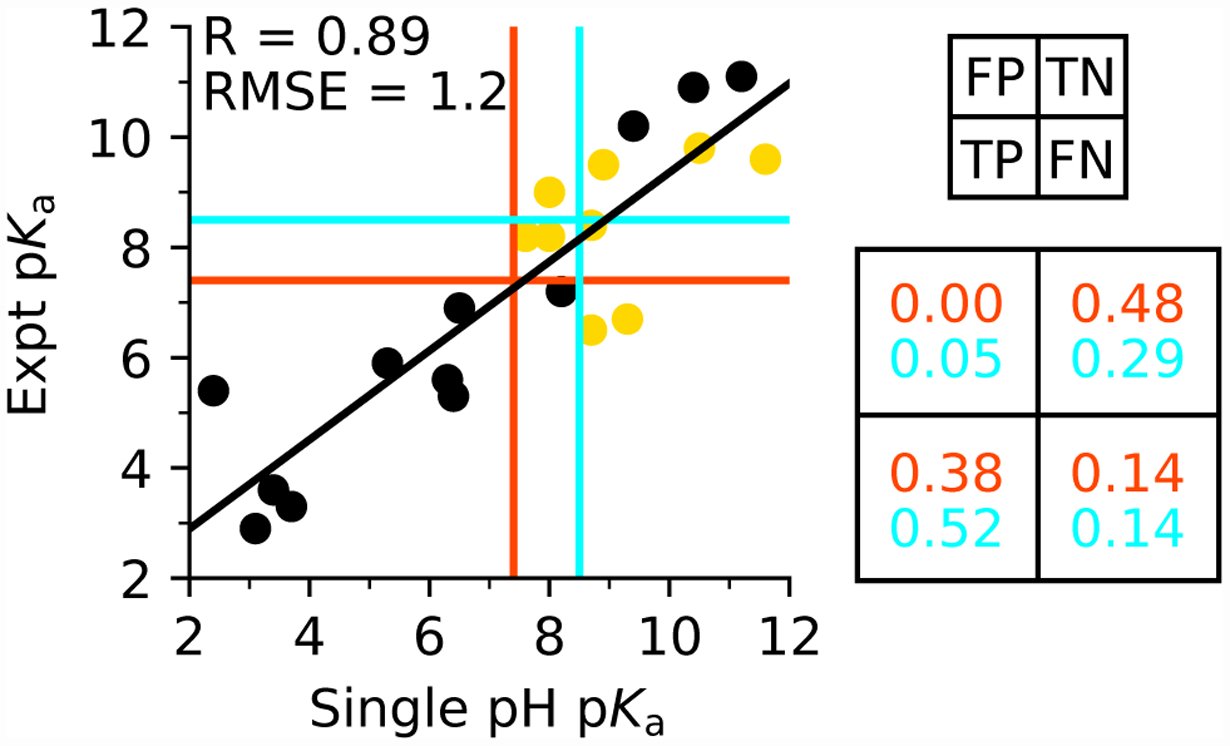
Comparison between experimental pK_a’s and those obtained from 10-ns single-pH titrations of the entire data set of 21 proteins. Linear regression line is shown in black, and the correlation coefficient R and RMSE are given. Calculations based on crystal structures are shown in black, and those based on the computationally mutated structures in gold. The data are grouped into four quadrants around the dividing pH 7.4 (red) or pH 8.5 (cyan). A confusion matrix is shown on the right, with the rates for false positives (FP), true positives (TP), true negatives (TN), and false negatives (FN) given for thiolate predictions for pH 7.4 (red) and pH 8.5 (cyan). See main text for more explanation.

Comparison to the structure-based calculations.

To compare with the popular structure-based pK_a calculation methods, Table 1 also lists the Cys pK_a’s predicted by the PB solvers H++,¹⁸ MCCE,¹⁹ and DelphiPKa²⁰ as well as the empirical method PROPKA.²¹ The RMSE’s range from 2.6 to 4.0, and the R values range from −0.48 to 0.61. The smallest error and best correlation is given by DelPhiPKa;²⁰ however, it predicts that all Cys pK_a’s are downshifted. With regards to prediction of thiolates or reactive cysteines at physiological pH, the accuracy of these methods is about 50%, with the exception of DelphiPKa which gave 67% for predicting thiolates although the precision also 67% (Table S1). We suggest that the better performance of CpHMD relative to structure-based methods is the ability to capture pH-dependent formation of hydrogen bonds or salt bridges that are not present in the starting structure. As discussed above, Cys145 in AGT and Cys106 in DJ-1 have downshifted experimental pK_a’s, and these downshifts were correctly predicted by CpHMD; however, the structure-based PB and empirical methods (except for DelPhiPka) predict either an upshift or no significant shift. Analysis suggests that the reason for this discrepancy is that CpHMD sampled the hydrogen bonds that are not present in the initial crystal structure.

CONCLUDING DISCUSSION

Based on a test set of 21 protein targets, we benchmarked the performance of single-pH and replica-exchange GBNeck2-CpHMD titrations for cysteine pK_a calculations and predictions of thiolates or reactive cysteines at physiological pH. We found that 10-ns single pH and 4-ns replica-exchange titrations gave similar RMSE (1.2–1.3) and R (0.8–0.9) for pK_a calculations. The accuracy of predicting thiolates or reactive cysteines at physiological pH with single-pH titrations is 86 or 81% with a precision of 100 or 90%, respectively. The accuracy and precision with the 4-ns replica-exchange protocol are similar.

Given crystal structures, the calculated pK_a’s from both protocols are in significantly better correlation with experiment. However, while the RMSE from the replica-exchange titrations using crystal structures is significantly decreased (0.95) relative to that (1.5) using the computationally mutated structures, the RMSE from the single-pH titrations based on the crystal structures is only slightly smaller (1.3 vs. 1.4). This difference can be attributed to the noise in the single-pH titrations, which also manifests itself in the poor fitting of the protonation fractions to the HH equation for several proteins. By contrast, replica-exchange titrations gave smooth titration curves for nearly all proteins. In addition to the reduction in statistical noise, our data also demonstrates that the pH replica-exchange protocol significantly accelerates pK_a convergence, corroborating the previous findings by us⁴⁰ and others using continuous and discrete constant pH methods.^30–32 while the replica-exchange titrations gave converged pK_a’s for all proteins at 4 ns per pH replica, the single-pH titrations for several proteins, e.g., A1AT, ACBP^T17C, and HMCK^S285A, did not converge even at 50 ns, due to persistent hydrogen bonds that resulted in a continued pK_a decrease. Interestingly, the decreasing pK_a’s of A1AT and ACBP^T17C are associated with increasing deviations from experiment, whereas the decreasing pK_a of HMCK^S285A corresponds to an improved agreement with experiment. This explains why extending single-pH titrations from 10 ns to 50 ns did not reduce the RMSE of the calculated pK_a’s, although the errors may start to decrease with a significantly longer simulation time, e.g., hundreds of nanoseconds. Contrasting the single-pH titrations, hydrogen bond life time is shorter in replica-exchange titrations, which resulted in faster convergence and lower statistical noise. Nonetheless, for computationally mutated structures, it remains to be seen if extending the replica-exchange titrations can further reduce errors. This issue will be addressed in a future study with the implementation of the asynchronous replica exchange scheme which allows users to perform replica-exchange CpHMD titrations on a single GPU card.

The benchmark data based on 21 proteins are encouraging; however, a caveat remains. For three phosphatase proteins, in which a deeply buried cysteine forms several strong hydrogen bonds (in the crystal structures), both CpHMD titrations (up to 50 ns in single pH mode or 4 ns in replica-exchange mode) correctly predicted the protonation state at physiological pH but failed to yield pK_a values as the cysteine remained deprotonated in the entire pH range. This failure may be attributed to a known limitation of GB simulations, which tend to overstabilize hydrogen bonding and/or restrict the extent of conformational changes of buried groups.^40,72 However, it is also possible that a large conformational change may take place in order to break the strong hydrogen bonds and allowing protonation of the deeply buried cysteine. Such a conformational change may involve a large kinetic barrier, which was not surmountable with the limited sampling time. This issue will be investigated in our future work using the GPU implementations of the fully explicit-solvent and the GB-based CpHMD methods with asynchronous replica exchange (Harris and Shen, ongoing work).

Our data demonstrates that CpHMD titrations outperform the conventional structure-based PB and empirical methods for cysteine pK_a calculations and predictions of and thiolates or reactive cysteines at physiological pH. The analysis showed that the ability of thiolate to accept hydrogen bonds is the major driving force for the pK_a downshifts, while solvent exclusion in the absence of hydrogen bonding is the major determinant of the pK_a upshifts. The ability of CpHMD titrations to reproduce experimental pK_a downshifts for cysteines that do not form hydrogen bonds in the crystal structures arises from the sampling of pH-dependent hydrogen bond formation, which is not accounted for by the structure-based methods. Our work also demonstrates that CpHMD titrations can reliably predict thiolates or reactive cysteines at physiological pH. These tasks are useful in preparing MD studies, understanding biological redox functions, and assisting covalent drug design.