MRI-based attenuation correction for brain PET/MRI based on anatomic signature and machine learning

Abstract

Deriving accurate attenuation maps for PET/MRI remains a challenging problem because MRI voxel intensities are not related to properties of photon attenuation and bone/air interfaces have similarly low signal. This work presents a learning-based method to derive patient-specific computed tomography (CT) maps from routine T1-weighted MRI in their native space for attenuation correction of brain PET. We developed a machine-learning-based method using a sequence of alternating random forests under the framework of an iterative refinement model. Anatomical feature selection is included in both training and predication stages to achieve optimal performance. To evaluate its accuracy, we retrospectively investigated 17 patients, each of which has been scanned by PET/CT and MR for brain. The PET images were corrected for attenuation on CT images as ground truth, as well as on pseudo CT (PCT) images generated from MR images. The PCT images showed mean average error of 66.1 ± 8.5 HU, average correlation coefficient of 0.974 ± 0.018 and average Dice similarity coefficient (DSC) larger than 0.85 for air, bone and soft tissue. The side-by-side image comparisons and joint histograms demonstrated very good agreement of PET images after correction by PCT and CT. The mean differences of voxel values in selected VOIs were less than 4%, the mean absolute difference of all active area is around 2.5%, and the mean linear correlation coefficient is 0.989 ± 0.017 between PET images corrected by CT and PCT. This work demonstrates a novel learning-based approach to automatically generate CT images from routine T1-weighted MR images based on a random forest regression with patch-based anatomical signatures to effectively capture the relationship between the CT and MR images. Reconstructed PET images using the PCT exhibit errors well below accepted test/retest reliability of PET/CT indicating high quantitative equivalence.

Introduction

Positron emission tomography (PET) has been one of the most important imaging modalities for diagnosis of disease by providing quantitative information on metabolic processes in human body. In order to reconstruct a PET image with satisfactory quality, it is essential to correct for the loss of annihilation photons by attenuation processes in the object. The most widely implemented method is to combine PET and computed tomography (CT) to perform both imaging exams serially on the same table. In PET/CT, the 511 keV linear attenuation coefficient map used to model photon attenuation is derived from the CT scan image, most commonly, by a piecewise linear scaling algorithm (Kinahan et al 1998, Burger et al 2002).

Recently, magnetic resonance (MR) imaging has been proposed to be incorporated with PET as a promising alterative to existing PET/CT system. Compared with CT, MR imaging allows excellent soft tissue visualization with multiple scan sequences without ionizing radiation. It also has functional imaging and multi-planar imaging capability. With these strengths of MR imaging, a combined PET/MR scan has been proposed for many potential clinical applications. For example, PET/MR enables local-regional assessment of cancer since MR imaging provides high spatial resolution definition of tumor volume and local disease while PET provides molecular detection and characterization of lymph nodes (Torigian et al 2013). Such application can be also extended to structural and functional assessment of neurologic disease, assessment of cardiovascular pathologies and measurement within cardiac chambers, and assessment of patients with musculoskeletal disorders (Chen et al 2008, Musiek et al 2008, Heiss 2009, Huang et al 2011, Torigian et al 2013, Chalian et al 2016). These early PET/MR disease focused studies suggest a high utility for the modality.

A challenge with the introduction of PET/MR compared to PET/CT is that MR images cannot be directly related to electron density and cannot be directly converted to 511 keV attenuation coefficients for use in the attenuation correction process. The reason is that the MR voxel intensity is related to proton density rather than electron density, and a one-to-one relationship between them does not exist. To overcome this obstacle, many methods have been proposed in the literature. A common method is to assign piecewise constant attenuation coefficients on MR images based on segmentation of materials. The segmentation can be done by either manually-drawn contours (Goff-Rougetet et al 1994) or automatic classification methods (El Fakhri et al 2003, Zaidi et al 2003, Hofmann et al 2009, Fei et al 2012). However, these methods are limited by misclassification and inaccurate prediction of bone and air regions caused by their ambiguous relations in MR voxel intensities. Instead of segmentation, other methods use atlases of MR images labeled with known attenuation to warp to patient-specific MR images by deformable registration or pattern recognition, but their efficacy is limited by the performance of the registration. Moreover, the atlases usually represent normal anatomy, thus its efficacy is also challenged by anatomic abnormality in clinical practice (Kops and Herzog 2007, Hofmann et al 2008).

With the development of machine learning in recent years, novel methods have been developed such that accurate CT equivalent images can be generated from MR images (Aouadi et al 2016, Huynh et al 2016, Han 2017, Lei et al 2018a, 2018b, Yang et al 2018a, 2018b, Wang et al 2018). In these algorithms, a model is trained by a large number of pairs of CT and MR images, each pair of which belongs to the same patient and is well-registered with each other. The model learns the conversion between MR image signal and Hounsfield units (HU) in CT images and then predicts a pseudo CT (PCT) image from the MR image input. Such PCT images share the same structure information with MR but in terms of HU, and can be directly converted to 511 keV attenuation coefficients in the PET reconstruction process. Current machine learning-based methods can be classified into three categories: dictionary-learning-based methods, random-forest-based (RF) methods and deep-learning-based methods (Chan et al 2013, Jog et al 2014, Li et al 2014, Andreasen et al 2015, 2016a, 2016b, Huynh et al 2016, Torrado-Carvajal et al 2016, Han 2017). These methods divide images into patches, and extract feature information from them to a learning model. The extraction process does not consider anatomic structures, thus the extracted features may include redundant and irrelevant information which may disturb the convergence and robustness of training a machine-learning-based model, and affect the accuracy of prediction.

In this work, we proposed a novel machine-learning based method which integrates anatomical feature into a learning model as the representation of image patch. Compared with other machine-learning based methods, the advantages include the use of discriminative feature selection, the joint information gain combining both MR and CT information, and the alternating random forest, which considers both the global loss of training model and the uncertainty of training data falling into child nodes. To evaluate our proposed method, we retrospectively investigated patient data of ¹⁸F-fluorodeoxyglucose (FDG) brain PET scans with both CT and MR images acquired. The PET images were corrected by the CT images collected as part of the PET/CT exam as ground truth, as well as by PCT images generated from MR images. The image accuracy of PCT images and PET images corrected by PCT were quantified with multiple image quality metrics by comparing with ground truth globally as well as with volumes of interest (VOIs) on each patient.

Methods and materials

PCT generation

As a machine learning-based method, the proposed method includes two stages: training stage and predicting stage, of which the flow chart is shown in figure 1. In training stage, the CT image served as the regression targets of its paired MR image in a random-forest-based (RF) model (Andreasen et al 2016b, Yang et al 2017b). Multi-level descriptors such as local binary pattern (LBP), which generated gradient features (Guo et al 2010), discrete cosine transform (DCT), which obtained texture features (Senapati et al 2016), and pairwise voxel difference (PVD), which created spatial frequency information (Huynh et al 2016) were extracted from 3D MR patches at multi-scale sensitivity, including the patches from original and three derived images with a sequence of down sampling factors (0.75, 0.5 and 0.25). For a 3D MR patch x_MR, its original feature f_MR was described by concatenating all the descriptors mentioned above. The voxel value of CT, y_CT, at the same position of 3D MR patch’s central voxel was used as the regression target of x_MR. To cope with overfitting, a set of training samples were built up by randomly selecting sample {x_MR, f_MR, y_CT} based on balance weights on y_CT’s label l_CT. l_CT was classified by fuzzy C-means clustering method on y_CT’s intensity value into three labels: l_CT = 1 if y_CT belonged to air, l_CT = 2 if y_CT belonged to soft-tissue, and l_CT = 3 if y_CT belonged to bone region. In this work, the size of 3D MR patch was empirically set as [15, 15, 15].

Figure 1.

The flow chart of the proposed learning-based PET/MRI attenuation correction.

An original feature f_MR was often in a high dimensional domain due to its concatenation of multi-level descriptors and multi-scale patches, rather than computational cost. A major potential drawback is that f_MR may contain uninformative components which could degenerate the regression ability of the RF. Thus, a feature selection was needed to select the informative components of f_MR. Intuitively, the components which have superior discriminant power to distinguish label l_CT from air, soft-tissue and bone could be regarded as the informative components. Since these components were determined by a CT images’ anatomic structure, these informative components were called an anatomic signature, f s_MR, in this work. The subtraction of f s_MR from f_MR can be accomplished by enforcing the sparsity constraint in a binary task. Thus, a logistic least absolute shrinkage and selection operator (LASSO) was used to implement the subtraction (or we called this as feature selection). The energy function for this subtraction was introduced as follows:

$$\sum _{i=1}^n\text{log}\left(1+\text{exp}\left(-l\left(w^T\cdot f_{\text{MR}}+b\right)\right)\right)+\mu \sum _{i=1}^m\left|w_i\right|/{\beta }_i$$ (1)

where w is a binary sparse vector with same length of f_MR, w_i served as its ith vector coefficient with w_i = 1 denoting that the f_MR’s ith component was relevant to the informative one, and w_i = 0 denoting that the f_MR ‘s ith component was irrelevant to the informative one. m denotes the length of w and f_MR, and n denotes the number of samples in the subtraction. μ denotes the regularization parameter. β_i denotes the optimization scalar and was estimated by f_MR’s ith component’s discriminative power, i.e. Fisher’ score (Widyaningsih et al 2017). Since the optimization (1) aimed to force the uninformative feature component to be eliminated, β_i was used to sigmoid (make the w_imore binary) the w_i and thus to enhance this ability. b was the intercept scalar. The optimal setting of b and w were obtained by Nesterov’s method (Nesterov 2003). The operator l(·) is a binary labeling function. In this work, two-step subtraction (feature selection) was applied by using l(·) to label air and non-air materials in first round and then to label bone and soft-tissue in the second round. After this two-round feature selection, the anatomic signature f s_MR was obtained from f_MR.

During training stage, RF trained a collection of decision trees from training set {f s_MR, y_CT}. Since the decision trees are often weak learners, an auto-context model (ACM) (Huynh et al 2016) was used in this work to enhance the learning ability iteratively by using additional surrounding information generated from predicted inference {y_PCT} of the previous RF. The information f_PCT was generated by concatenating DCT, LBP and PVD descriptors from PCT inferred by the training MR image as the same way mentioned before, then it was concatenated with f s_MR to train the next RF. The process was repeated to train a series of RFs until a prediction error criterion was met. Since f_PCT was generated in a circular version, it was called the contextual information. The schematic flow chart of ACM model is shown in figure 2.

Figure 2.

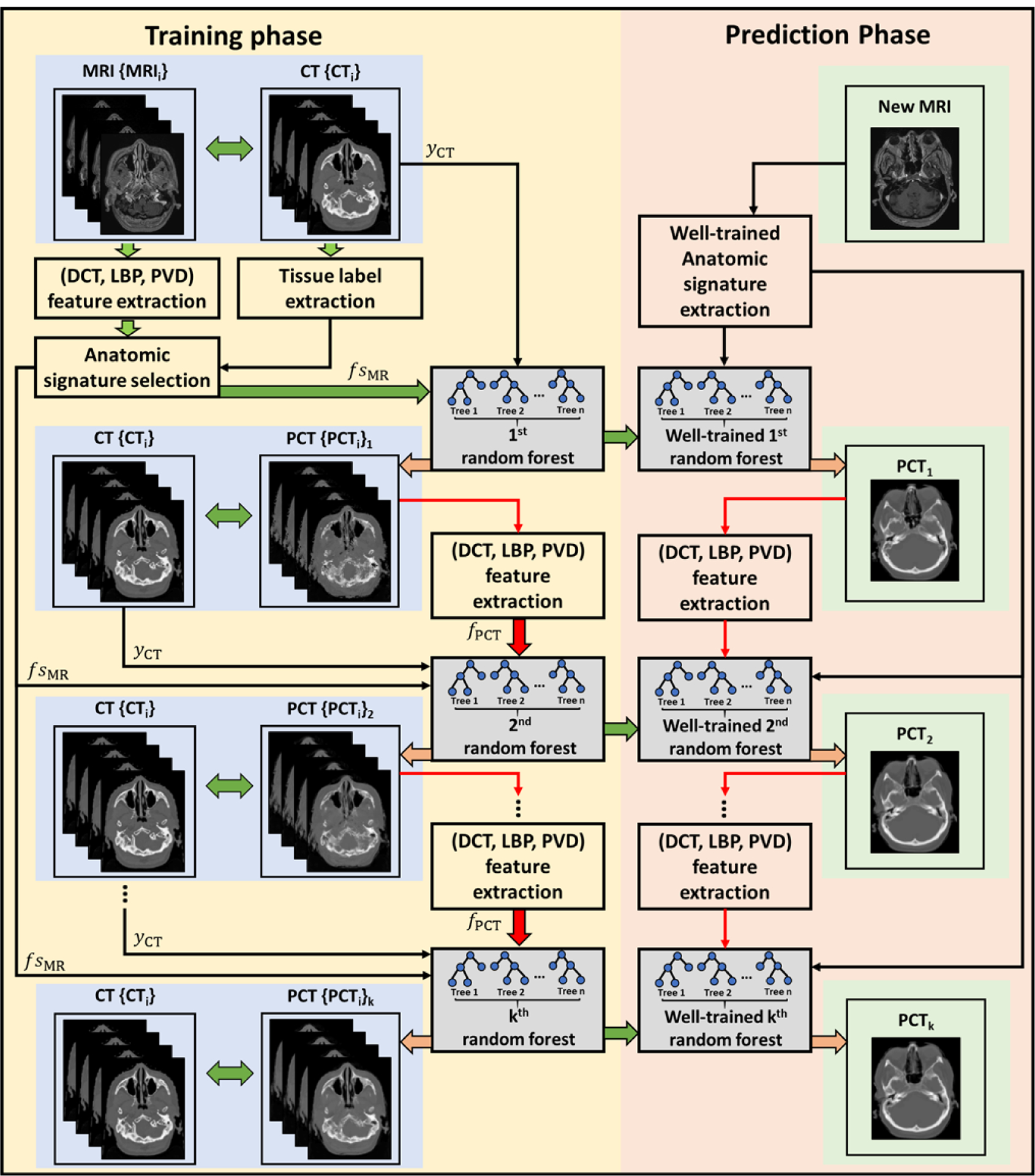
Schematic flow chart of the ACM used in our proposed algorithm for MRI-based PCT generation. The left part of this figure shows the training stage of our proposed method, which consisted of k random forests training and context information f_PCT extraction. The right part of this figure shows the prediction stage. In the prediction stage, a new MR image follows the similar sequence of the left part to generate a PCT image.

In the predicting phase, a new MR image followed the same sequence of feature generation and ACM to generate the corresponding PCT. Finally, its corresponding PET images were attenuation corrected based on the PCT image using the same algorithm as the original CT.

Data acquisition

To evaluate the performance of the proposed method, we compared the difference between CT and PCT as well as the PET images corrected by CT and PCT. In this retrospective study, we analyzed the datasets of 17 patients scanned by PET/CT and MR subsequently. The 17 patients were randomly selected, with median age of 50 (24–85), 9 females and 8 males; each patient had both PET/CT and MR images acquired as part of the standard diagnosis pathway and rigidly registered. The cohort of 17 patients were used to evaluate our method using the leave-one-out cross-validation. For one test patient, the model is trained by the remaining 16 patients. The model is initialized and re-trained for next test patient by another group of 16 patients. The training datasets and testing datasets are separated and independent during each study. For each patient, the PCT images are generated from MR images by our learning model. Fourteen out of 17 patients have PET images corrected by both CT and PCT images since the PET images of the other three patient datasets were unable to be retrieved. For conciseness, we refer to the PET images corrected by CT images and PCT images, generated from MR images, as ‘CT-PET’ and ‘MR-PET’, respectively.

The PET/CT data were acquired (Discovery 690, General Electric, Waukesha, WI) employing a clinical brain [¹⁸F]flourodeoxyglucose ([¹⁸F]FDG) protocol beginning with a 370 MBq intravenous administration of [¹⁸F]FDG, followed by a 45 min uptake period, and 10 min emission scan. PET data were reconstructed with an ordered-subset expectation maximization (OSEM) algorithm that incorporated modeling of the system point spread function and corrections for randoms, scatter and attenuation (Burger et al 2002). The reconstructed matrix size was 192 × 192 × 47 pixels with a pixel size of 1.56 × 1.56 × 3.27 mm. CT images were reconstructed using filtered backprojection to a matrix size of 512 × 512 × 47 and a pixel size of 0.98 × 0.98 × 3.27 mm. The MR images were acquired using a standard whole-brain 3D T1-weighted MPRAGE sequence reconstructed to a matrix size of 120 × 128 × 160 and pixel size of 1.33 × 1.33 × 1.20 mm (Mugler 1999). Note that all patients were scanned by MR after their PET/CT scan within one week. MR images are converted to PCT, resliced to the CT matrix size and pixel spacing, and used for attenuation and scatter correction of the PET emission data employing the same algorithms.

Image quality metrics

In this study, we evaluated the accuracy of both PCT images and its corresponding MR-PET images. For each patient, we visually checked the similarity between CT and PCT images, as well as CT-PET and MR-PET images. For PCT images, we quantitatively characterized its accuracy by three widely-used metrics: correlation coefficient, mean absolute error (MAE) and Dice similarity coefficient (DSC). The correlation coefficient is calculated from the joint histogram between CT and PCT inside body contour, which can be described as

$$\text{Correlation Coefficient }=\frac{\text{Cov}\left(I_{\text{PCT}},I_{\text{CT}}\right)}{{\sigma }_{\text{PCT}}{\sigma }_{\text{CT}}},$$ (2)

where I_PCT and I_CT are vectorized image of PCT and CT, and Cov(·, ·) is the covariance between two vectors. A correlation coefficient closer to 1 indicates higher accuracy of PCT images. To quantify the accuracy on high and low density materials, we calculated the MAE on VOIs of air, bone, soft tissue and whole brain (i.e. the combination of bone and soft tissue). The segmentation among air, bone and soft tissue VOIs were achieved by setting thresholds (>300 HU for bone, < −400 HU for air, and otherwise soft tissue) on CT and PCT, respectively. Note that the segmented VOIs for same material are different in CT and PCT. The MAE for VOI of a certain material was calculated as the average of the absolute HU difference in the overlapping region of VOIs of that material in CT and PCT, i.e.

$$\text{MAE}=\frac{1}{N}\sum _{i\in {\text{VOI}}_{\text{PCT}}\cap {\text{VOI}}_{\text{CT}}}\left|I_{\text{PCT}}(i)-I_{\text{CT}}(i)\right|,$$ (3)

where I(i) indicates the ith pixel in image volume and N is the total number of pixels in the overlapping region of VOIs in CT and PCT. With the segmentations of air, bone and soft tissue, the DSC was calculated to characterize the overlapping of VOIs of the same tissue composition between CT and PCT, which can be described as

$$\text{DSC}=\frac{2\times \text{ Volume of VOI }(\text{PCT})\cap \text{VOI}(\text{CT})}{\text{ Volume of VOI }(\text{PCT})+\text{ Volume of VOI}(\text{CT})}.$$ (4)

For MR-PET images, we similarly analyzed the joint histogram between CT-PET and MR-PET images in active areas, and calculated its correlation coefficient for each patient data. VOI analysis was then performed by aligning an anatomically standardized template with clinically relevant VOIs to CT-PET/MR-PET images for comparison of PET signals (Mazziotta et al 1995, 2001). Eleven VOIs were defined on the template MR, including thalamus, frontal lobe, occipital lobe, parietal lobe, brainstem, temporal lobe, cerebellum, hippocampus, hypothalamus, pons, and cerebrospinal fluid (CSF). The relative difference of the PET signals at each VOI between CT-PET and MR-PET was calculated as:

$$\text{Diff }=\frac{\mid {\overline{I}}_{\text{MR-PET }}(\text{ VOI })-{\overline{I}}_{\text{CT-PET }}(\text{ VOI })\mid }{{\overline{I}}_{\text{CT-PET }}\text{ (VOI) }},$$ (5)

where $\overline{I}(\text{VOI})$ is the mean voxel value in that VOI. The mean voxel-wise absolute difference was also calculated on active area in brain for each patient to quantify the global difference.

Results

In figure 3, the image quality of PCT is shown using a side-by-side comparison with CT in the same window level from one of the 17 patients as an example. It is seen that the PCT images feature good image quality, and maintain very similar contrast and most of the details as the CT. Image errors can be observed in some small volumes around air and bones. These findings are consistent with the measured MAE, DSC and correlation coefficients between PCT and CT among all 17 patients shown in figure 4 and summarized in table 1. Here the whole brain means the image region within the body surface.

Figure 3.

The axial views of one patient at different slices. Rows (a)–(c) show MR, CT and PCT, respectively. Note the head holder visible in the CT images was added to the PCT data prior to reconstruction of MR-PET data.

Figure 4.

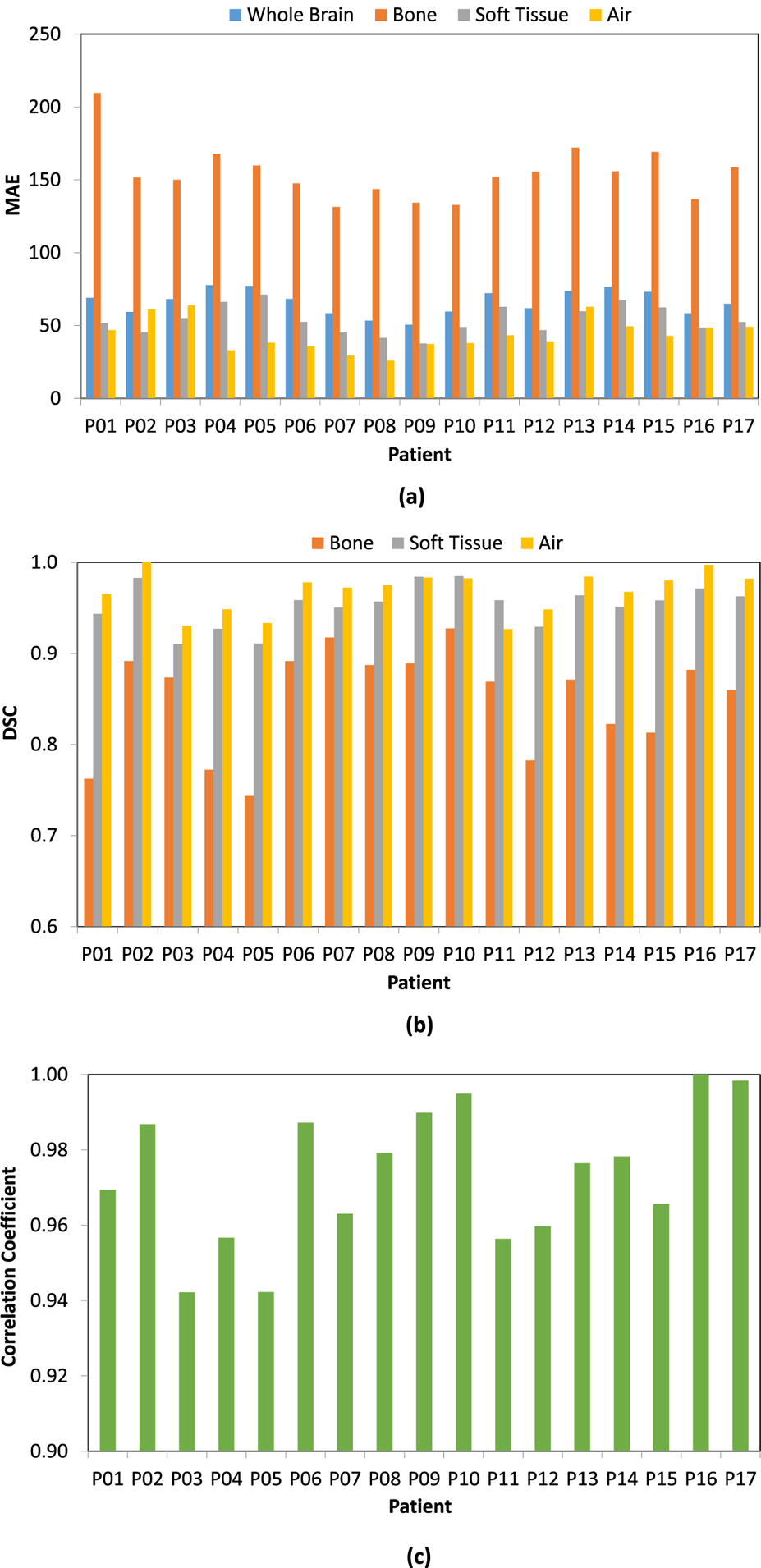
MAE (a), DSC (b) and correlation coefficient (c) between PCT and CT images among all 17 patients.

Table 1.

Mean ± STD of MAE, DSC and correlation coefficient between PCT and CT images among all 17 patients.

Metrics	Whole brain (within brain mask)	Bone	Soft tissue	Air
MAE (HU)	66.1 ± 8.5	154.6 ± 18.9	53.8 ± 9.7	43.8 ± 11.1
DSC	N/A	0.850 ± 0.057	0.953 ± 0.023	0.968 ± 0.023
Correlation coefficient	0.974 ±0.018	N/A	N/A	N/A

Figure 5 compares the reconstructed PET images at select axial, sagittal and coronal planes of two patients. The CT-PET and MR-PET (columns (1) and (2) in figure 5) qualitatively appear to be very similar. The image difference map in column 3 of figure 5 shows that the differences between the dose distributions are very low for the majority of the volume, with most differences occurring at the outer boundary between brain and skull. The comparison of image profiles and joint histograms between CT-PET and MR-PET are shown in figure 6. The image profiles of CT-PET and MR-PET in figures 6(a1) and (b1) match each other very well. The joint histograms of active area between CT-PET and MR-PET in figures 6(a2) and (b2) are very close to the identity lines. Note that we present the results of two patients in figures as examples, but similar results can also be seen on the other patients. The correlation coefficients between MR-PCT and CT-PCT of all patients are shown in figure 7, with an average correlation coefficient of 0.989 ± 0.017.

Figure 5.

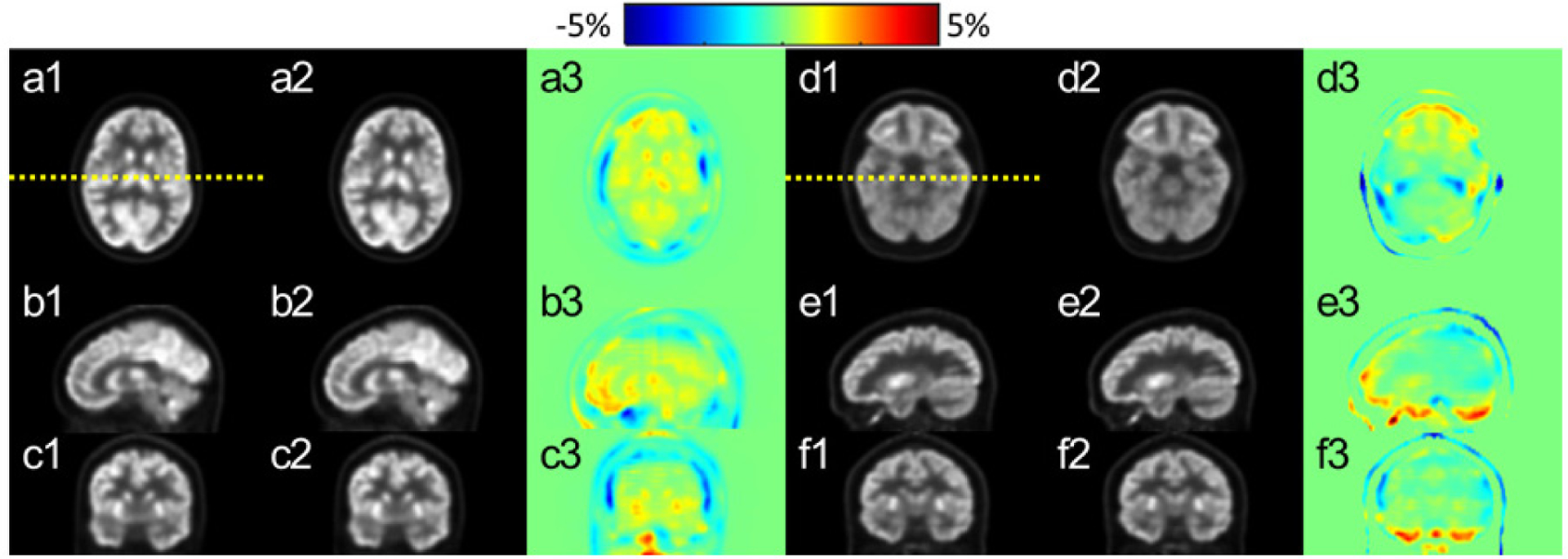
PET images after correction on the axial (a) and (d), sagittal (b) and (e) and coronal (c) and (f) planes. Left (a)–(c) and right (d)–(f) demonstrate images from two patients. CT-PET and MR-PET images are shown in column (1) and (2), respectively. The relative difference maps between (1) and (2) are shown in (3). The yellow dotted lines on (a1) and (d1) indicate the positions of profiles displayed in figure 6.

Figure 6.

Comparison of PET image profiles and joint histograms between CT-PET and MR-PET. Upper (a) and bottom (b) correspond to the results from two patients (i.e. left (a)–(c) and right (d)–(f) in figure 5), respectively. The positions of profiles (a1) and (b1) are indicated by yellow dotted lines in figure 5. In (a2) and (b2), the blue scattered dots are joint histograms with the identity line in red for reference.

Figure 7.

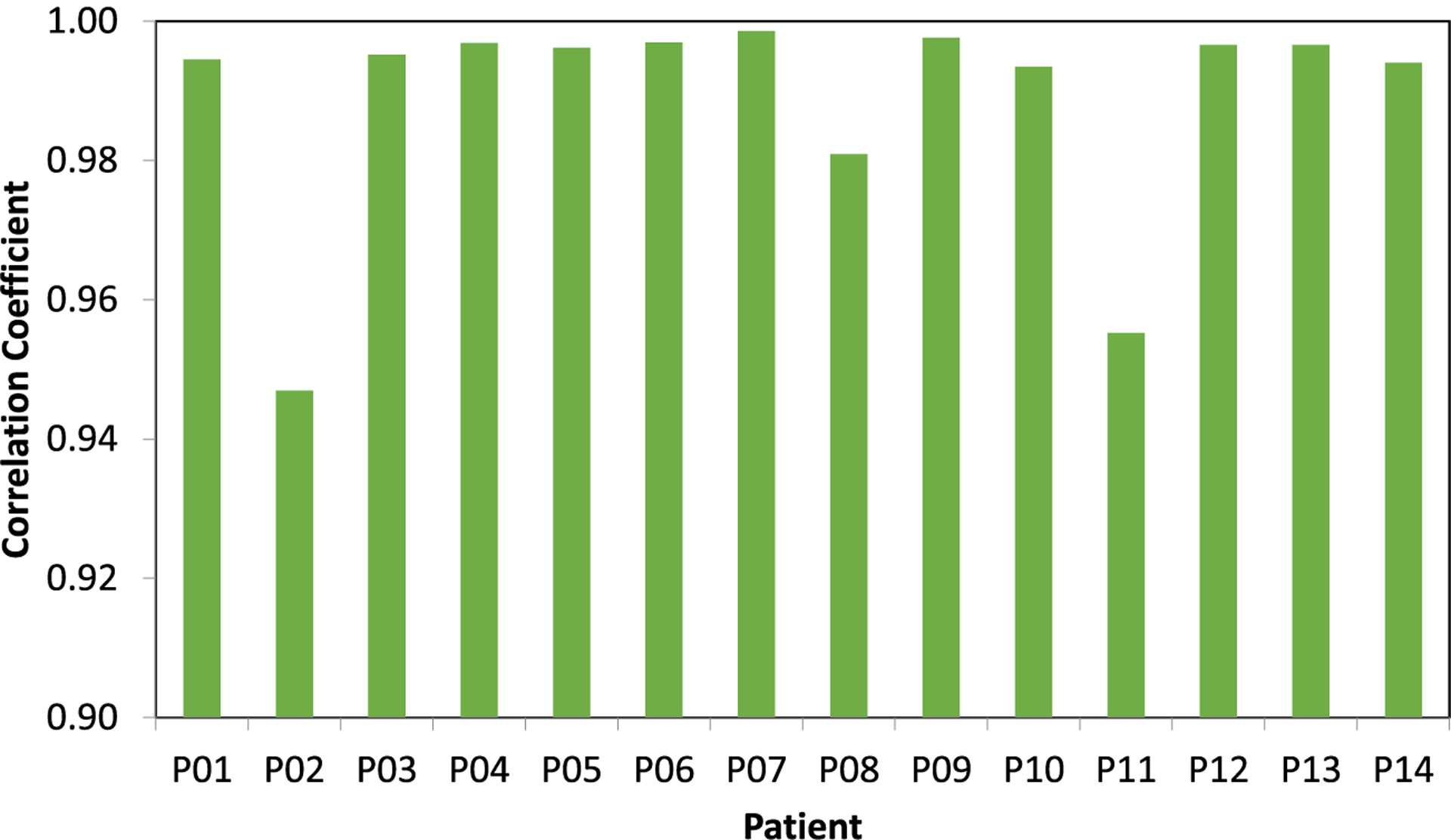
Correlation coefficients between MR-PCT and CT-PCT images among all 14 patients.

The differences in VOIs between CT-PET and MR-PET among all 14 patients are shown by the box plots in figure 8. The central mark of each box indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers, and the outliers are plotted individually using the ‘+’ symbol. The statistics of VOI differences and absolute differences among all 14 patients are summarized in table 2 (STD stands for standard deviation). The mean differences among 14 patients are less than 4% for all VOIs, and the mean absolute difference of all active areas is around 2.5%, both of which demonstrate the high accuracy of PET image correction based on MR images.

Figure 8.

Percentage differences within VOIs between CT-PET and MR-PET among 14 patients. The central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers, and the outliers are plotted individually using the ‘+’ symbol. The indices of VOIs are indicated in table 2.

Table 2.

Mean and STD of percentage differences between CT-PCT and MR-PCT images within VOIs and overall voxel-wise absolute difference within active area among all 14 patients.

VOI#	Region	Mean (%)	STD (%)
#1	Thalamus	−1.61	1.36
#2	Frontal lobe	−0.80	2.12
#3	Occipital lobe	3.67	3.20
#4	Parietal lobe	1.46	1.67
#5	Brainstem	−1.47	1.68
#6	Temporal lobe	1.47	1.17
#7	Cerebellum	0.73	2.53
#8	Hippocampus	−0.64	1.33
#9	Hypo thalamus	−0.16	1.53
#10	Pons	−1.58	2.45
#11	CSF	0.22	1.70
Overall absolute difference		2.41	1.34

Discussion

In this study, we proposed a novel machine-learning based method to predict PCT image from T1-weighted MR images for attenuation correction of PET. We evaluated the accuracy of PET attenuation correction using our method in the context of FDG PET/CT brain scans. The PCT images showed an average MAE of 66.1 ± 8.5 HU, average correlation coefficient of 0.974 ± 0.018 and average DCS larger than 0.85 for air, bone and soft tissue. The side-by-side image comparisons and joint histograms between CT-PET and MR-PET images demonstrated very good agreement of voxel values after correction by PCT and CT. The mean linear correlation coefficient was 0.989 ± 0.017. Based on the statistical analysis of comparative VOIs between CT-PET and MR-PET among 14 patients, we showed that the mean differences of voxel values in selected VOIs were less than 4%, and the mean absolute difference of all active areas was around 2.5%. Compared with the general agreement that quantification errors of 10% or less typically do not affect diagnosis (Hofmann et al 2008), these results strongly indicate that the PCT images created from MR images using our machine-learning-based method are accurate enough to replace current CT images for PET attenuation correction in brain.

Compared with other machine-learning based methods, the PCT image accuracy by our method is competitive to others. For example, Han et al proposed to use existing deep learning and convolutional neural networks from the computer vision literature to learn a direct image-to-image mapping between MR images and their corresponding PCTs (Han 2017). They reported overall average MAE in whole brain region of generated PCT was 84.8 ± 17.3 HU among 18 patients. Huynh et al proposed to train a set of binary decision trees, each of which learns to separate a set of paired MRI and CT patches into smaller and smaller subsets to predict the CT intensity (Huynh et al 2016). PCT intensity was estimated as the combination of the predicted results of all decision trees when a new MRI patch was put into the model. They reported 99.9 ± 14.2 HU among 16 patients. The corresponding result in our method is 66.1 ± 8.5 HU, which is lower in both mean value and standard deviation. The higher accuracy achieve by our method stems from our innovative use of discriminative feature selection, which considers anatomic structures and avoids redundant and irrelevant information disturbing the accuracy and robustness of model training.

The reconstructed PET image quality of the proposed method can be further examined by comparing with existing conventional methods. Fei et al proposed an MR-based PET attenuation correction method using segmentation and classification (Fei et al 2012). They evaluated this method in the context of brain scan with ten patients datasets on 17 VOIs, which is similar to the study in our paper. It showed that among all the ten patients, the average difference between MR-based-corrected PET and ground truth can be up to 7.6% in some of the VOIs, and such difference averaged among all VOIs is 4.2%. Keereman et al reported 5.0 % error on entire brain in their proposed segmentation-based method among five patients (Keereman et al 2010). The corresponding errors in our study are up to 3.7% in VOIs and 2.4% on entire brain, which is more than 40% lower than the two segmentation based methods. Similarly, Hofmann et al and Yang et al reported atlas-based PET attenuation correction methods using MRI (Hofmann et al 2008, Yang et al 2017a). Their results showed overall error of 3.2% and 4.0% respectively on entire brain in their corrected PET images, which is more than 30% higher than the 2.4% reported in our study. Thus, the proposed machine-learning based method in this study has advantages over the above conventional methods in accuracy.

MR-based PET attenuation correction is challenged by the artifacts in MR images (Blomqvist et al 2013). In addition to potential non-identical patient setup, discrepancy of patient anatomy between MR and PET images may happen due to magnetic field inhomogeneity and patient-specific distortion in MR imaging, which would lead to mismatch between generated PCT and PET images. In our study, all MRI images were pre-processed using an N3 Algorithm to effectively reduce distortion before training or synthesizing (Tustison et al 2010). Other novel methods such as a real-time image distortion correction method have been reported to have excellent performance, and combining these preprocessing methods with our method could increase the accuracy of the PCTs (Crijns et al 2011).

In the presented study, we found that the difference of PET images in column (3) of figure 5 was very minimal for the majority of the volume, even in small areas with minor error on the PCT images. It indicates that the PET attenuation correction on PCT is not sensitive to image errors of soft tissue inside the volume. Slightly larger errors were observed close to skull; this could be because the skull absorbed far less radiopharmaceuticals than brain which led to higher relative error. Another reason could be that the attenuation correction is more sensitive to the error of PCT on skull which is much denser than soft tissue. Such error could be attributable to the residual mismatch between MR and PET images during both training and predicting stages.

In addition, computational cost for training a model is a challenge for machine learning-based PCT synthesis methods. We implemented the proposed algorithm with Python 3.5.2 as in-house software on a Intel Xeon^® CPU ES-2623 v3 @ 3.00 Ghz × 8. In the present study, the training stage requires ~17 GB and ~21 h for the training datasets of 16 patients. Recently, since the development of graphical processing unit (GPU)-based parallel computing, a GPU-based parallelized algorithm has been proposed to accelerate classification random forests (Jayaraj et al 2016). In future work, we hope to modify the proposed algorithm to run on a GPU framework to decrease computational time.

In this study, we included a limited number of patient datasets to test the feasibility of our method. A large number of datasets including a variety of anatomical variation and pathology abnormalities would further reduce bias during the model training. Future studies should involve a comprehensive evaluation with a larger population of patients with diverse demographics and pathological abnormalities. Different testing and training datasets (including normal and abnormal cases) from different institutes would also be valuable to evaluate the clinical utility of our method. Moreover, this study validated the proposed method by quantifying the image accuracy of corrected PET images. Small differences from ground truth are observed, and its potential clinical impact (e.g. on diagnosis sensitivity and specificity) needs to be better understood. Thus, investigation of the diagnostic accuracy of the proposed method in detection and localization of disease would be of great interest for expanding this work to the clinic.

In this feasibility study, we evaluated our method on FDG brain PET scans. Future work will extend the proposed method to whole-body applications. Compared with brain scans, whole-body scans feature higher anatomical heterogeneities in patient body and anatomical variability among patients, which may lead to degraded performance of the existing segmentation-based methods and atlas-based methods respectively (Hofmann et al 2008). The proposed learning-based method would be affected less by these two factors, while the complexity in whole body would demands higher accuracy on PCT to predict bone thickness and air-tissue interfaces. Moreover, as mentioned above, geometric distortion could be significant in whole-body MRI scanning. Novel methods such as real-time image distortion correction methods have been reported to have excellent performance, and its combination with our method would definitely aid in MR-based PET attenuation correction (Crijns et al 2011). For such cases, a phantom or clinical study on the effect of geometric distortion on PCT generation and PET attenuation correction may be necessary.

Conclusion

We proposed a learning-based method to generate PCT images from MR images for brain PET attenuation correction. This work demonstrates a novel learning-based approach based on a random forest regression with patch-based anatomical signatures to effectively capture the relationship between the CT and MR images. Reconstructed PET images for brain scan using the PCT exhibit errors well below accepted test/retest reliability of PET/CT indicating high quantitative equivalence.