APOD: accurate sequence-based predictor of disordered flexible linkers

Abstract

Motivation

Disordered flexible linkers (DFLs) are abundant and functionally important intrinsically disordered regions that connect protein domains and structural elements within domains and which facilitate disorder-based allosteric regulation. Although computational estimates suggest that thousands of proteins have DFLs, they were annotated experimentally in <200 proteins. This substantial annotation gap can be reduced with the help of accurate computational predictors. The sole predictor of DFLs, DFLpred, trade-off accuracy for shorter runtime by excluding relevant but computationally costly predictive inputs. Moreover, it relies on the local/window-based information while lacking to consider useful protein-level characteristics.

Results

We conceptualize, design and test APOD (Accurate Predictor Of DFLs), the first highly accurate predictor that utilizes both local- and protein-level inputs that quantify propensity for disorder, sequence composition, sequence conservation and selected putative structural properties. Consequently, APOD offers significantly more accurate predictions when compared with its faster predecessor, DFLpred, and several other alternative ways to predict DFLs. These improvements stem from the use of a more comprehensive set of inputs that cover the protein-level information and the application of a more sophisticated predictive model, a well-parametrized support vector machine. APOD achieves area under the curve = 0.82 (28% improvement over DFLpred) and Matthews correlation coefficient = 0.42 (180% increase over DFLpred) when tested on an independent/low-similarity test dataset. Consequently, APOD is a suitable choice for accurate and small-scale prediction of DFLs.

Availability and implementation

https://yanglab.nankai.edu.cn/APOD/.

1 Introduction

Intrinsically disordered regions (IDRs) in protein sequences are functionally important while lacking a stable tertiary structure in vivo (Dunker et al., 2013; Habchi et al., 2014; Oldfield et al., 2019a,b; van der Lee et al., 2014). Intrinsically disordered proteins (IDPs) can be fully or partially unstructured, where in the latter (more frequent) case they include one of more IDRs. Previous studies have shown that the IDPs/IDRs are very common across all kingdoms of life, particularly in eukaryotes, and carry out a variety of important cellular functions that cover regulation, signaling, translation and transcription (Babu, 2016; Chen and Kriwacki, 2018; Dunker et al., 2008; Kjaergaard and Kragelund, 2017; Lieutaud et al., 2016; Meng et al., 2015; Peng et al., 2015; Wang et al., 2016; Xie et al., 2007).

The DisProt database is the primary source of the experimentally and functionally annotated IDPs/IDRs (Hatos et al., 2020). According to a recent analysis, the second most commonly annotated function of IDPs/IDRs is entropic chain, behind only the molecular recognition function (Katuwawala et al., 2019a,b,c). Close to 75% of the entropic chains include disordered flexible linker (DFL) regions. The current version 8.0 of DisProt includes slightly over 100 proteins with the DFL regions. These disordered regions are characterized by extreme flexibility (lack of defined structure) and act as connectors between protein domains and between structural elements/constituents that make up domains (Dunker et al., 2002). The defining differences between flexible linkers (Chen et al., 2013) and DFLs are the degree of flexibility (flexible versus disordered), length (DFL tends to be longer) and localization (inter-domain versus. inter- and intra-domain; Meng and Kurgan, 2016). DFLs have many important functional roles that center around facilitation and regulation of inter- and intra-domain movement. Specific examples include peptide aggregation (Shvadchak and Subramaniam, 2014), connecting multiple disordered protein binding regions (Oldfield and Dunker, 2014), movement of structured domains between catalytic sites (Anand and Mohanty, 2012), and allosteric regulation (Sorensen and Kjaergaard, 2019). Moreover, recent computational analysis suggests that thousands of proteins are likely to harbor these regions. More specifically, about 7% of human proteins were shown to have at least one long putative DFL region (20 or more consecutive residues in length) and 10% of human proteins have at least 30% of their residues serving as putative DFLs (Meng and Kurgan, 2016).

Given the high-levels of abundance and functional importance of these regions, and the relatively low numbers of the experimentally annotated DFLs, it may came as a surprise that there is only one computational tool that predicts DFLs, DFLpred (Barik et al., 2019; Katuwawala et al., 2019a,b,c; Meng and Kurgan, 2016; Meng et al., 2017). DFLpred was recently used to assist with functional characterization of several protein domains including SH3 (Arbesu and Pons, 2019) and RRS1 (Guo et al., 2020). However, the main drawback of this computational tool is its limited quality of the predictive performance. DFLpred was designed to offer very fast but only modestly accurate predictions. The latter is due to the exclusion of relevant but computationally costly predictive inputs, such as sequence conservation (CONS) and putative/sequence-derived structural characteristics, e.g. secondary structure (SS) and solvent accessibility. These characteristics were previously used as powerful markers of functional sites (Wang and Samudrala, 2006), including functional IDRs, such as molecular recognition features (MoRFs; Disfani et al., 2012; Hanson et al., 2019; Katuwawala et al., 2019a,b,c; Malhis and Gsponer, 2015; Malhis et al., 2016; Sharma et al., 2018a,b; Yan et al., 2016). Moreover, DFLpred relies solely on the information extracted from a local sequence fragment (sliding window), and does not use the protein-level information. A case in point for using protein-level characteristics is the observation that the IDPs involved in different functions have different amounts of intrinsic disorder (Peng et al., 2013, 2015). This is also observed for the IDPs with DFLs which were shown to have about 45% lower disorder content (DisCon; fraction of disordered residues) compared with the other IDPs (Meng and Kurgan, 2016). Finally, DFLpred applies a simple logistic regression (LR) model, while more sophisticated (albeit slower) models are available.

Motivated by the above-mentioned drawbacks of DFLpred, we introduce a novel predictor of DFLs, APOD (Accurate Predictor Of DFLs), which aims to provide (significantly more) accurate predictions of the DFLs. Our design includes a comprehensive selection of relevant predictive inputs, combines both local- and protein-level information and uses an advanced and well-parametrized predictive model. Consequently, as our empirical study shows, APOD offers very accurate results at the expense of a longer runtime.

2 Materials and methods

2.1 Benchmark datasets

We source our data from the current release 8.0 of DisProt (Hatos et al., 2020) and we follow the annotation protocol from (Meng and Kurgan, 2016). Using the functional annotations DisProt we annotated 5893 residues in 175 DFL regions that are located in 117 IDPs. For convenience we use the term ‘DFL protein’ to denote IDP that has at least one DFL. We also extracted a set of non-DFL proteins to test the ability of our predictor to separate DFL from the non-DFL residues. Consistent with (Meng and Kurgan, 2016), to reduce the number of potential false negatives, we collected 131 proteins that have majority of their residues functionally annotated and where this annotation is not DFL. The residues without functional annotations were excluded from the design and assessment. In other words, only the disordered residues with the non-DFL functional annotations and the structured residues are marked and used as the negatives.

Following (Meng and Kurgan, 2016), we cluster the corresponding 117 + 131 = 248 protein sequences using BLASTClust (Altschul et al., 1997) at the 25% sequence identity. We divide the resulting 194 clusters into training and test datasets at random, where the training set (TR166) includes 166 sequences with 3661 DFL residues, and the test set (TE82) is composed of 82 chains with 2223 DFL residues. The placement of entire clusters into the two datasets ensures that training and test proteins share below 25% sequence similarity. We use the TR166 set to design and optimize our predictive model by performing 5-fold cross validation. We utilize the independent/dissimilar TE82 set to assess and compare APOD with the current DFLpred predictor. We note that the test dataset is similar in size to the datasets used in the CASP experiments (Kryshtafovych et al., 2019) and is slightly larger than the test set used by the authors of DFLpred (Meng and Kurgan, 2016). The TR166 and TE82 datasets are available at https://yanglab.nankai.edu.cn/APOD/benchmark/.

2.2 Architecture of the APOD predictor

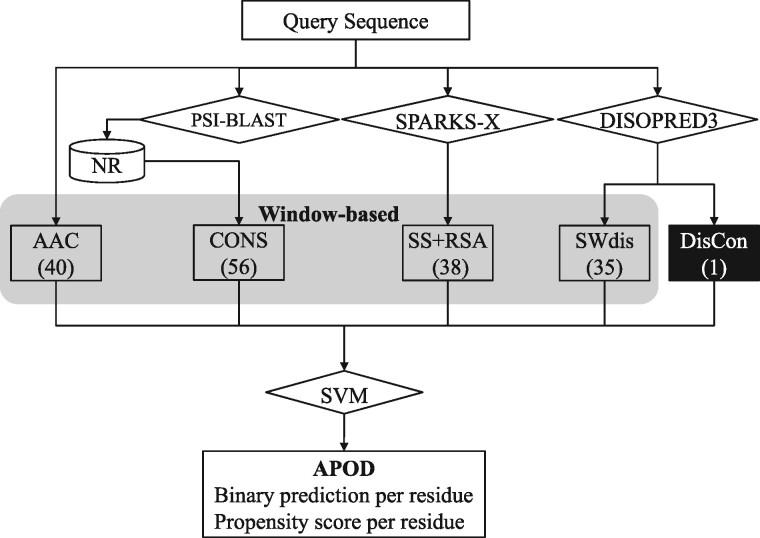
As shown in Figure 1, APOD takes protein sequence as the only input and processes it in two steps to produce prediction for every residue. The first step involves use of several third-party programs to provide a rich sequence profile that characterizes relevant (putative) structural properties of the input chain. More precisely (Fig. 1), these properties include the amino acid composition (AAC) extracted directly from the input sequence, CONS generated with PSI-BLAST (Altschul et al., 1997), putative SS and the relative solvent accessibility (RSA) predicted with SPARKS-X (Yang et al., 2011) and putative intrinsic disorder derived from the DISOPRED3 prediction (Meszaros et al., 2018), which includes the sliding window-based representation of disorder (SWdis) and protein-level DisCon value. To compare, DFLpred used an inferior profile with only the information extracted directly from the sequence and putative disorder predicted with IUPred, which offers lower predictive performance than DISOPRED3 (Katuwawala et al., 2019a,b,c). In the second step, this profile is converted into a custom-designed feature vector that is processed by a support vector machine (SVM) model to produce the predictions. We derive the total of 170 features by including both the protein-level features (that quantify the DisCon) and the local window-based features; see Section 2.3 for the detailed description of these features. To compare, DFLpred relies exclusively on the local window-based features.

Fig. 1.

Architecture of the APOD predictor. We generate the local window-based features from the part of the sequence profile highlights in gray box, where AAC means the amino acid composition, SS and RSA denotes the features generated from the putative secondary structure and relative solvent accessibility, respectively, CONS stands for the sequence conservation-related features and SWdis represents the disorder-related features extracted by utilizing sliding window. The protein-level features are highlighted using the black box and they cover the DisCon

The predictions take form of numeric propensity scores, which quantify likelihood that a given residue is in the DFL region, and the corresponding binary score, which categorizes a given residue as either DFL or non-DFL.

2.3 Encoding of the sequence profile

We custom-encode the sequence profile, which covers selected relevant sequence-based and putative structural characteristics of the input protein chain, into the feature vector that has two main parts: the protein-level and the local sliding window-level features.

2.3.1 Protein-level features

The IDPs that carry out different cellular functions usually show distinct distributions of DisCon (i.e. fraction of disordered residues in a given sequence; Peng et al., 2015). This is also true for DFL proteins that were shown to have lower DisCon compared with the other IDPs (Meng and Kurgan, 2016). Consistent with these findings, we observe that the average DisCon for the DFL proteins is about 31% lower than that of other IDPs in TR166 dataset. Moreover, DFLs are the definition intrinsically disordered, and thus they are not present in the structured protein that has DisCon of 0. We screen out the structured proteins and the other IDPs by utilizing the protein-level feature that quantifies the DisCon.

2.3.2 Local window-based features

As the structural and functional characteristics of residue are indirectly affected by its neighbors in a sequence (Chen et al., 2006), the technique of sliding window is usually utilized to capture the sequence-local characteristics of a predicted residue. This window-based approach was successfully applied to predict other related disorder characteristics including MoRFs (Disfani et al., 2012; Hanson et al., 2019; Katuwawala et al., 2019a,b,c; Malhis et al., 2016; Oldfield et al., 2019a,b; Peng and Kurgan, 2015; Sharma et al., 2019), IDRs that interact with nucleic acids (Peng and Kurgan, 2015), IDR that interact with proteins (Dosztanyi et al., 2005; Meszaros et al., 2018; Peng and Kurgan, 2015) and DFL (Meng and Kurgan, 2016). We utilize empirical experiment based on the 5-fold cross validation on the training set TR166 to optimize the size of the sliding window to 13 residue (see Section 3.2). We use this window to derive the following four types of features:

AAC. DFLs were observed to be enriched with polar uncharged amino acids (AAs). This facilitates the ability of the connecting domains to twist and rotate, and to recruit their binding partners via protein domain dynamics (Bu and Callaway, 2011). We therefore computed the 20 AACs in the sliding window. Motivated by the approach taken in (Disfani et al., 2012), we also compute another 20 features that quantify the difference in the AAC between the residues inside the sliding window (i.e. near neighbors) and the residues flanking the window (i.e. remote neighbors). We use the six flanking residues on each end of the window to mimic the size of the window. Total number of features: 40.

Conservation-related features (CONS). Evolutionary conservation is an important indicator of functional residues in protein chains (Atas et al., 2018). This information can be easily derived from the alignment profiles generated with programs such as the popular PSI-BLAST (Altschul et al., 1997). We run PSI-BLAST with the default parameters against the NCBI’s (National Center for Biotechnology Information) non-redundant database. We use the probability matrix produced by PSI-BLAST to derive the conservation scores using the popular relative entropy (RE)-based approach (Wang and Samudrala, 2006):

$${RE}_i={\sum }_{k=1}^{20}{p}_{ik}\mathrm{lo}{\mathrm{g}}_2\frac{p_{ik}}{b_k}$$

where $i$ is $i$th AA in the protein chain of the length $L$, $k$ means one of the 20 standard AAs, $p_{ik}$ is the probability of AA $k$ shown in the site $i$, $b_k$ is the Robinson background frequency (Robinson and Robinson, 1991) of AA $k$. Using the sliding window of size 13, we extract the 13 RE values, we compute their average (AVG) and SD, and the differences between the AVG of REs for the near neighbors and the remote neighbors. We also use the PSSM (position-specific scoring matrix) generated with PSI-BLAST to calculate the AVG and SD of the position-specific scores (over the positions in the window) for the 20 standard AAs. Total number of features: 40 PSSM-based + 16 RE-related = 56.

SS- and RSA-based features. SS defines a local conformation in the protein chain, which comprises of $\alpha$-helices, $\beta$-sheets and $\gamma$-coils. RSA quantifies the solvent exposure of residues and is defined by the ratio of the solvent accessible area to the maximum possible solvent accessible area for the residue (Tien et al., 2013). We applied SPARKS-X (Yang et al., 2011) to predict the SS and the solvent accessible surface area. This is one of a very few methods that couples both predictions (saving runtime) while providing high predictive performance. We focus on the putative $\gamma$-coil regions as they typically constitute DFLs (Meng and Kurgan, 2016), while complementing the combined content of the $\alpha$-helix and $\beta$-sheet regions. Consequently, we encode the following features from these predictions: frequency of $\gamma$-coil in the sliding window and the difference in the frequency between the window (near neighbors) and the remote neighbors (two features); the number and the average, minimal and maximal length of the $\gamma$-coil segments in the sliding window (four features); the 26 RSA scores (13*2) in the sliding window, their 4 (2*2) AVG and STD values, and 2 (1*2) differences between the AVG values between the near and remote neighbors (32 features). Total number of features: 2 + 4 + 32 = 38.

Intrinsic disorder-based features (SWdis). Putative Intrinsic disorder is a powerful marker of DFLs since by definition these are disordered regions. This claim is supported by the design of DFLpred where the putative disorder played key role to implement the underlying predictive model (Meng and Kurgan, 2016). We use the disorder prediction generated with DISOPRED3 (Meszaros et al., 2018) since this is consistently one of the most accurate methods (Katuwawala et al., 2019a,b,c; Liu et al., 2019; Monastyrskyy et al., 2011, 2014). We derive the following features from the outputs produced by DISOPRED3: disorder propensities for the 13 residues in the window, their AVG and STD values, the difference of AVG between the near and the remote neighbors, binary disorder predictions for the 13 residues in the window, the DisCon (i.e. the frequency of the disordered residues) in the window and its difference with the DisCon of the remote neighbors, and finally the number of putative IDRs in the window and their average, minimal and maximal length. Total number of features: 13 + 2 + 1 + 13 + 2 + 4 = 35.

The grand total number of features is 40 + 56 + 38 + 35 = 169.

2.4 Point biserial correlation coefficient

We assess the predictive value of these features based on the correlation between their numeric values and the binary residue-level annotations of DFLs. We use the point biserial correlation coefficient (PBC) that quantifies correlation between numeric and binary variables to quantify the predictive value:

$$\mathit{PBC}=\frac{M_1-M_0}{S_n}\sqrt{\frac{n_0\mathrm{*}{n}_1}{n\left(n-1\right)}}$$

where $M_1\mathrm{ }$($M_0$) is the average of the feature value corresponding to the (non-)DFL residues; $n_1\mathrm{ }$($n_0$) is the total number (non-)DFL residues; $n$ is the sum of $n_0\mathrm{ }$and $n_1$; and $S_n$ is the SD for a given feature.

We perform this calculation based on the five folds cross-validation on the TR166 dataset. More specifically, we average the absolute PBC values across the five training folds to quantify the correlations between a given feature and the native annotations of the DFL residues.

2.5 Evaluation criteria

The prediction of DFL includes two values: the binary score (DFL versus non-DFL residue) and the numeric propensity score that quantifies likelihood that a given residue forms DFL. Given that our datasets are unbalanced, i.e. majority of residues are non-DFLs, we utilize the Matthews correlation coefficient (MCC) (Matthews, 1975), the precision (Pre) and the recall (Rec) as the metrics to evaluate the quality of the binary prediction.

$$\begin{array}{c}\text{MCC}=\frac{TP\times TN-FP\times FN}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)\left(TN+FP\right)\left(TN+FN\right)}}\\ \text{Pre}=\frac{TP}{TP+FP} \mathit{Rec}=\frac{TP}{TP+FN}\end{array}$$

where $TP$ is the number of correctly predicted DFL residues, $FP$ is the number of non-DFL residues predicted as DFL residues, $TN$ is the number of correctly predicted non-DFL residues and $FN$ is the number of DFL residues predicted as non-DFL residues.

We assess the predictive quality of the propensity scores using the area under receiver operating characteristic (ROC) curve (AUC; Fawcett, 2006). For a given threshold $p_i$ (which is set to all unique propensity values produced by a given predictor), the residue is classified as DFL residue if it’s putative propensity score > $p_i$; otherwise, it is classifies as non-DFL residue. Next, the false positive rates (${\mathrm{FPR}}_i$) and true positive rates (${\mathrm{TPR}}_i$) are computed for all thresholds:

$$\mathrm{TPR}=\frac{TP}{TP+FN}\mathrm{ } \text{FPR}=\frac{FP}{TP+FN}$$

The ROC curve is drawn by connecting the $\left({\mathrm{FPR}}_i,\mathrm{ }{\mathrm{TPR}}_i\right)$ points. The AUC quantifies the area under the ROC curve and ranges between 0.5 (for random-quality predictions) and 1 (for perfect predictions).

We also evaluate statistical significance of differences in the values of AUC and MCC between APOD and other alternative methods for the prediction of DFLs. This test investigates whether the differences are consistent across a range of different (test) datasets. To this end, we divide the test set TE82 at random into 10 equally sized protein subsets, each with 8 or 9 proteins. Next, we calculate and compare the 10 corresponding AUC/MCC values between APOD and each of the other considered predictor. If both vectors of the AUC/MCC values are normal, as tested using Anderson–Darling test at the 0.05 significance, then we utilize t-test; otherwise we used the non-parametric Wilcoxon rank sum test. The differences with P-value < 0.01 are assumed statistically significant.

2.6 Predictive model

We comparatively test two popular machine learning algorithms: LR and SVM as candidates to produce the predictive model. The LR algorithm have been successfully applied to predict DFLs in the DFLpred tool (Meng and Kurgan, 2016) and was also used to predict disorder (Fan and Kurgan, 2014; Peng and Kurgan, 2012; Peng et al., 2014). SVM is a popular algorithm that was extensively used to generate predictive models in closely related areas that include prediction of MoRFs (Disfani et al., 2012; Fang et al., 2013; Malhis et al., 2016; Sharma et al., 2016, 2018a,b, 2019; Yan et al., 2016) disordered protein-binding regions (Jones and Cozzetto, 2015; Zhang et al., 2020), protein-peptide interactions (Zhao et al., 2018) and IDRs (Ishida and Kinoshita, 2007; Jones and Cozzetto, 2015; Mizianty et al., 2010, 2013, 2014; Peng et al., 2006; Ward et al., 2004). We compare these two algorithms based on the 5-fold cross validation on the training set TR166. We carefully parametrize both LR and SVM by searching over a suitable parameter space. For the LR algorithm, we set the sole ridge parameter ridge to equal 10ⁱ where i = −6, −5, …, 6. For the SVM, we use the popular RBF kernel and we optimize values of two parameters: complexity constant C and width of the kernel γ. We set their values to 2ⁱ where i = −5, −4, …, 5. We also optimize the sliding window size ws by considering the values ranging between 9 and 25; the two values correspond to the 10 percentile and the median length of DFL in the training dataset, respectively. We select the optimal values for ws, C, γ and ridge by maximizing the average AUC values calculated over the five test folds in the 5-fold cross validation on the training set TR166. The optimized APOD model applies ws = 13, C = 1 and γ  =  0.0625. The results produced by LR model were outperformed by the SVM model (details in Section 3.1).

3 Result and discussion

3.1 Comparison of the LR and SVM models

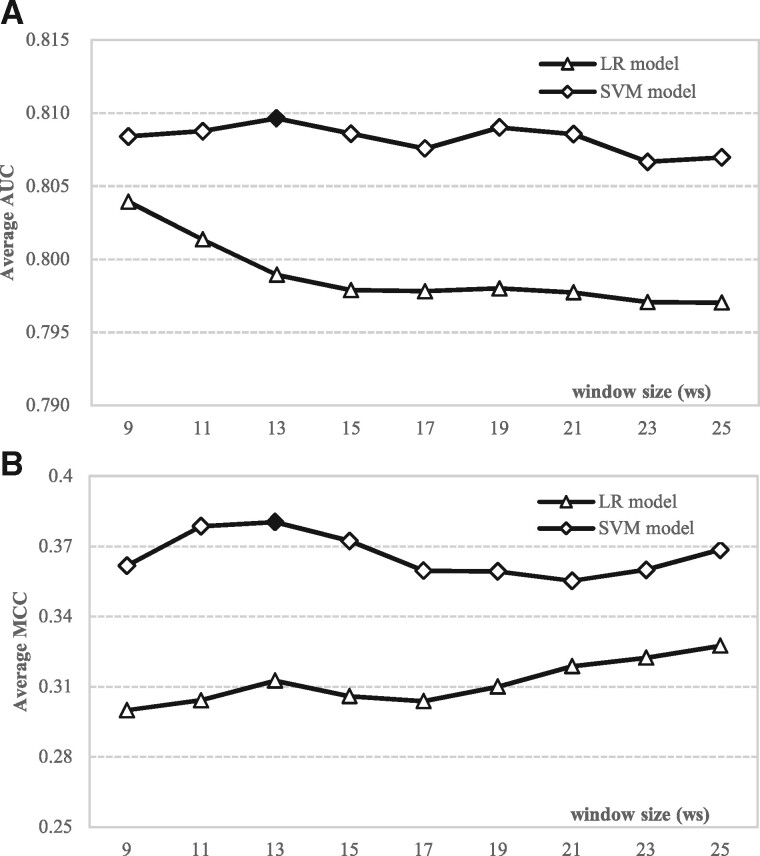
We empirically compare the predictive quality generated by two types of machine learning algorithms: LR and SVM. We perform this comparison based on the 5-fold cross validation on the training set TR166. The results are summarized in Figure 2. The figure makes it clear that the SVM model is superior to the LR model, especially given the consistency of the improvements over the entire range of the window sizes ws. Improvements in MCC span between 11.4% and 24.4%, whereas AUC is higher by between 2.2% and 9.5% across different window sizes. Interestingly, the AUCs of the LR model decrease as the window size increases (Fig. 2A). This suggests that this simple models is incapable of taking advantage of the additional information coming from a larger window, which arguably has higher noise-to-signal rate. In contrast, the AUCs of SVM initially slightly increase as the window size grows and they plateau for the longer windows. The SVM’s AUCs range between 0.807 and 0.810, and the MCCs vary between 0.355 and 0.380 across different window sizes. Interestingly, the largest values of AUC = 0.81 and MCC = 0.28 for the SVM models are for the same window size ws = 13. Correspondingly, we select this window size to implement the APOD predictor.

Fig. 2.

Predictive quality of the LR and the SVM models on the training dataset TR166. The predictive quality is measured by the average AUC that quantifies quality of the propensity scores (A) and the average MCC that measures quality of the binary predictions (B). We report average of the results on the five folds in the 5-fold cross validation on TR166. The highest average AUC and MCC are highlighted using the black diamonds

3.2 Predictive performance of considered features-based sequence representation

We convert the input protein sequence into a vector of features, which includes both the protein-level features and the local sliding window-based features. The former group covers the protein-level DisCon. The latter includes four major sub-types: the AAC, the conservation-based features (CONS), features extracted from the putative structural characteristics that cover SS and RSA (SS+RSA) and the sliding window-based disorder features (SWdis). We quantify the predictive power of these feature groups by computing the distribution of their PBC values on the training set TR166 (Section 2.4 defines PBC; see Fig. 3A). Among the window-based features, we observe that the local window-level conservation (CONS) and both the window-level (SWdis) and the protein-level disorder (DisCon) are the most predictive. Correlations computed for some of these features are above 0.1, with some as high as 0.41 (SWdis). We note that DFLpred did not use neither DisCon nor CONS features (Meng and Kurgan, 2016), both of which provide strong predictive quality.

Fig. 3.

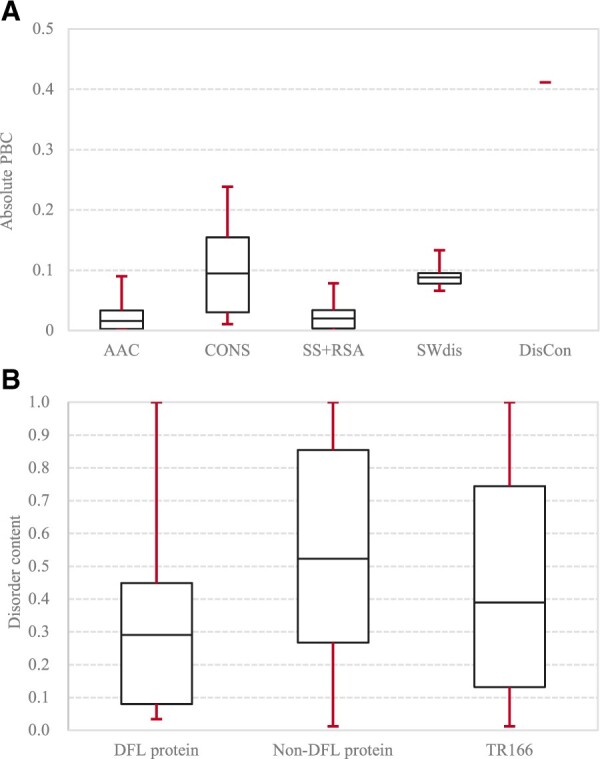
The distributions of the absolute PBC values and the disorder values in the training dataset TR166. The boxes represents the 20th (bottom of the box), 50th (median) and 80th (top of the box) percentile of the PBC/DisCon values while the red error bars give the maximal and the minimal values. (A) The PBC values across features in specific feature groups that include AAC (amino acid composition); SS+RSA (features generated from putative secondary structure and relative solvent accessibility); CONS (features generated from sequence conservation); SWdis (features extracted from the putative disorder based on sliding window) and DisCon (protein-level features generated from the putative disorder). (B) The distributions of the DisCon values across DFL proteins [proteins with the DFL region(s)], non-DFL proteins and the complete training dataset

We also analyze the distribution of the DisCon values across the proteins in the TR166 set. We find that over half of the DFL proteins have <29% disordered residues while over 77% IDPs without DFLs have over 30% disordered residues (see Fig. 3B). These substantial differences taken together with the average PBC = −0.412 for the DisCon feature (Fig. 3A), support our conclusion that the putative protein-level DisCon is a strong predictive marker for DLFs.

3.3 Ablation study

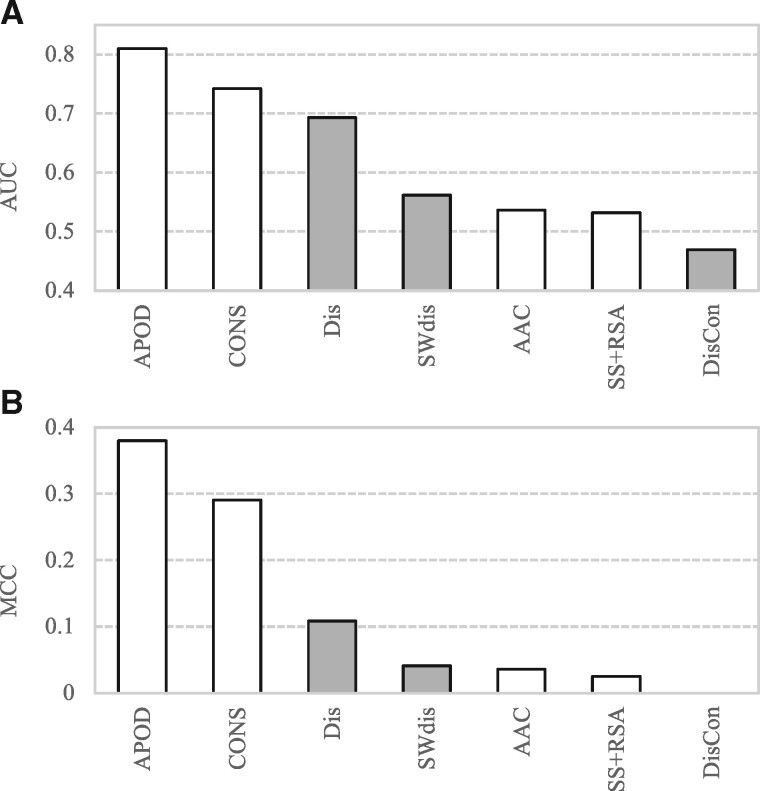
We quantify contributions of the different input feature groups to the APOD predictor by comparing APOD with its versions where only one specific feature group is used (Fig. 4). This experiment is based on the 5-fold cross validation on the training set TR166 and relies on the parametrized SVM model. Our empirical results reveal that CONS provides the strongest contribution to the APOD predictor. The corresponding SVM model that uses CONS secures AUC = 0.74 AUC and MCC = 0.29. The SWdis-based SVM model provides the second-best predictive quality by obtaining AUC = 0.56 and MCC = 0.04. Moreover, the DisCon-based SVM model performs poorly. This can be explained by the fact that this protein-level future is constant across all residues in a given protein. Thus, while it can differentiate between DFL and non-DFL proteins (Fig. 3B), it cannot accurately differentiate DFL and non-DFL residues in a given protein (Fig 4). Interestingly, combining the WSdis and DisCon features (the local window- and the protein-level disorder-based features) leads to the predictive model that substantially outperforms the SWdis-based SVM model. The corresponding Dis-based SVM model secures AUC = 0.69 (versus 0.56 when only WSdis features are used) and MCC = 0.11 (versus 0.04). This demonstrates that SVM effectively combines multiple feature groups that reflect different aggregation of the input information (window versus protein level).

Fig. 4.

The ablation analysis of the APOD predictor on the training dataset TR166. We compare the complete APOD model with its versions that rely on the parametrized SVM models that utilizes a single feature group. (A) AUC values and (B) the MCC values collected based on the 5-fold cross validation on TR166. The considered feature groups include AAC (amino acid composition); SS+RSA (features generated from putative secondary structure and relative solvent accessibility); CONS (features generated from sequence conservation); SWdis (features extracted from the putative disorder based on sliding window); DisCon (protein-level features generated from the putative disorder); and Dis that combines SWdis and DisCon features (shown in gray)

We note that virtually all features groups provide an above-random contribution to the prediction of DFLs, i.e. they secure AUC > 0.5 and MCC > 0.01 (Fig. 4). The only exception is the DisCon feature by itself, for the abovementioned reasons, which when combined with WSdis provides strong predictive power. This motivates our approach to combine all feature groups together. The corresponding complete APOD model that uses all five feature groups achieves AUC = 0.81 and MCC = 0.38 on the training set TR166 (see Fig. 4). The improvements of the APOD model over the best-performing single feature group model (CONS) are substantial. The AUC increases by (0.81–0.74)/0.74 = 9.2% while the MCC increases by (0.38–0.29)/0.29 = 31%. We conclude that the input feature groups that we designed provide complementary information and using them together leads to accurate prediction of DFLs.

3.4. Comparison with the DFLpred predictor

To the best of our knowledge, the only other method that predicts DFLs is DFLpred (Meng and Kurgan, 2016). We therefore compared the predictive quality of APOD against DFLpred on the independent (sharing low similarity with the training set TR166) test dataset TE82.

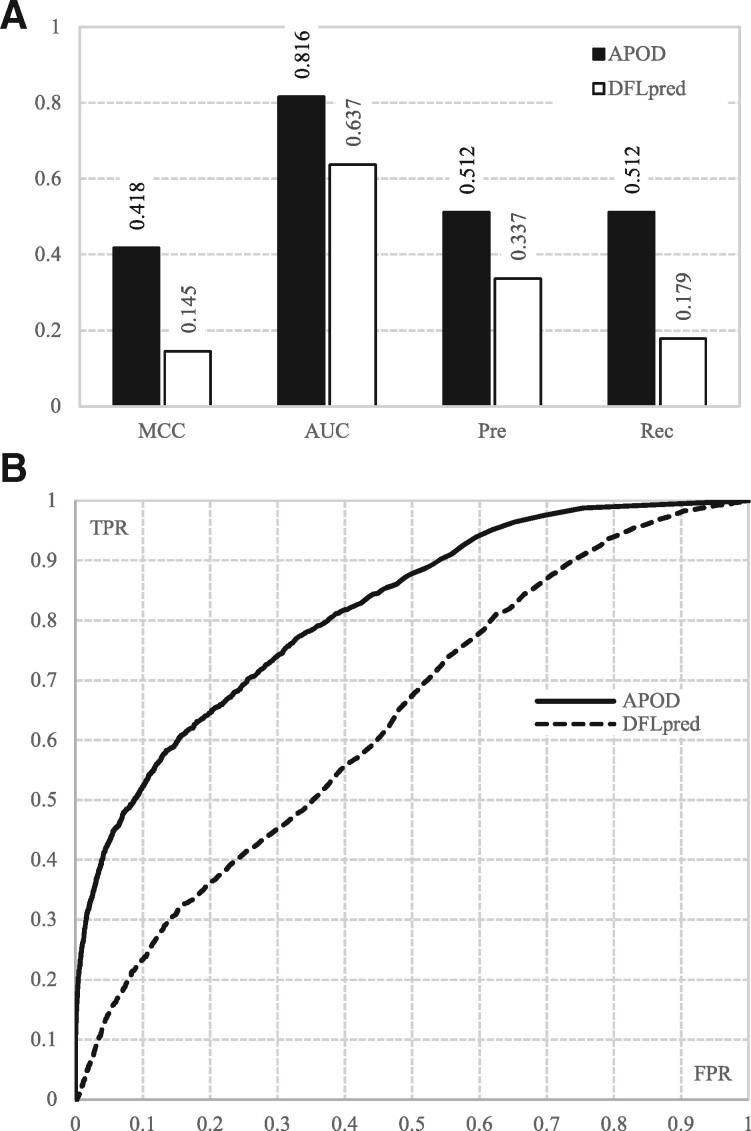
APOD secures AUC = 0.816 and MCC = 0.418 (Fig. 5A). These results arguably show that the APOD’s predictions are very accurate. Moreover, they are very similar to the results from the cross validation on the training dataset (0.816 versus 0.810 and 0.418 versus 0.382). This is not surprising since the optimization of the underlying SVM model is geared towards ensuring that the model generalizes well to the out-of-sample (non-training set) data. Our empirical result suggests that APOD provides very accurate and similar levels of the predictive performance irrespective of the dataset used.

Fig. 5.

Comparative assessment of APOD and DFLpred on the test dataset TE82. (A) The MCC, AUC, precision (Pre) and recall (Rec) values. (B) The corresponding ROC curves

Side-by-side comparison of APOD with DFLpred reveals that the former model provides substantially higher levels of predictive performance (Fig. 5A). More specifically, the APOD’s Pre and Rec are (0.512–0.337)/0.337 = 52% and (0.512–0.179)/0.179 = 186% higher compared with DFLpred, respectively. This means that APOD’s rate of correct DFL predictions is higher by 52% while our predictor also identifies 186% more DFL residues. Moreover, APOD provides (0.418–0.145)/0.145 = 180% improvement in MCC and (0.816–0.637)/0.637 = 28% increase in AUC when compared with DFLpred. Statistical tests (Section 2.5 provides details) reveal that the improvements in the predictive performance between APOD and DFLpred are significant, with P-value = 0.004 for MCC and 0.002 for AUC. Moreover, the APOD’s ROC curve is consistently and by a large margin above that of the DFLpred’s curve (Fig. 5B). This shows that the abovementioned improvements are consistent across the entire range of the FPRs.

Altogether, our empirical analysis reveals that APOD provides accurate DFL predictions and that it outperforms the existing DFLpred method by a large margin. This can be explained by the many innovations that we introduced in our model, compared with the DFLpred model. They include inclusion of the features extracted from the conservation and putative structural properties of the input sequence, integration of the protein-level information, which helps to differentiate DFL and non-DFL proteins, and use of a well-parametrized SVM model.

3.5. Comparison with indirect approaches to predict DFLs

We also consider comparison with other, indirect ways to predict DFLs. They could be potentially identified using disorder predictors (since they are disordered), methods that predict domain boundaries (since some of the DFLs link domains), and flexibility predictors (since they are flexible). Therefore, we consider the latest protein domain predictor FUpred (Zheng et al., 2020) and one of the latest flexibility predictors, PredyFlexy (de Brevern et al., 2012). We also compare against a selection of popular disorder predictors including DISOPRED3 (Jones and Cozzetto, 2015) and IUPred2A (Meszaros et al., 2018), the latter in two of its versions that focus on the prediction of long and short IDRs. We also consider combining the disorder and flexibility predictions, given that DFLs possess both characteristics. To do that, we simply multiply the putative flexibility and disorder propensities generated by PredyFlexy and each of the disorder predictors, respectively. We note that the domain predictor FUpred is limited to proteins with <1500 residues and that the flexibility predictor PredyFlexy does not provide predictions for the first and last 10 residues in a protein chain. Therefore, we had to exclude the 3387 residues long DP01931 protein and the first and the last 10 residues of each of the remaining 81 test proteins from the TE82 dataset for the purpose of this assessment.

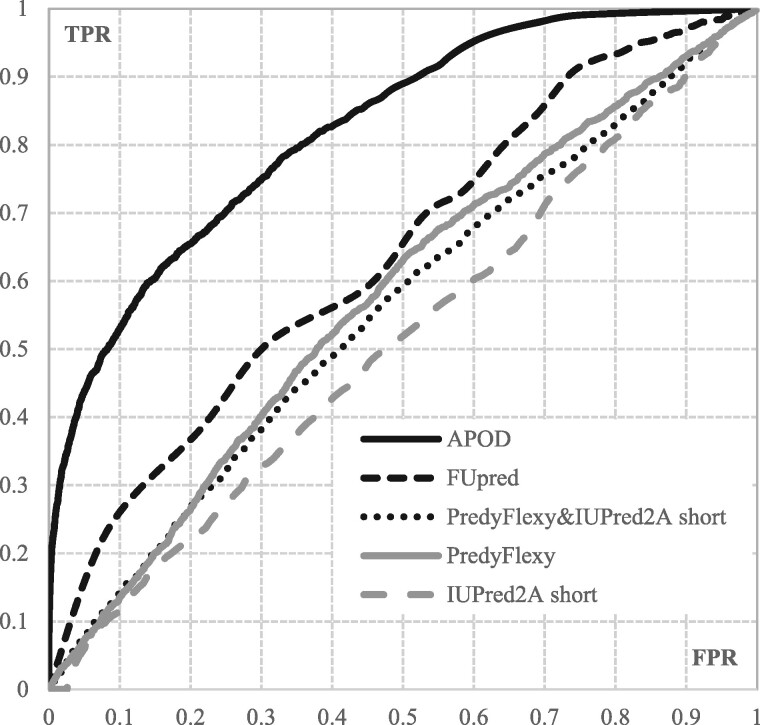
Table 1 summarizes the comparative assessment for APOD and the eight indirect predictors. The FUpred domain predictor achieves AUC = 0.637 and MCC = 0.162, which reveals that the use of the putative domains produces modest levels of predictive performance. This is expected since some DFLs are localized between domains; however, the inter-domain linkers cannot be captured with this approach. These predictions are significantly worse than the results produced by APOD (P-value = 0.004 for AUC and 0.003 for MCC; Section 2.5 defines the corresponding statistical test). The MCC and AUC values produced by APOD improve by 162% and 29% over FUpred, respectively. We also note a wide and consistent, over the entire range of FPR values, margin of improvement between the ROC curve of APOD and that of FUpred (see Fig. 6).

Table 1.

Comparative assessment of APOD and the indirect methods for the prediction of DFLs on the test dataset

Method		AUC	MCC	Pre	Rec
DFL predictor	APOD	0.824	0.425	0.517	0.526
Domain predictor	FUpred	0.637+	0.162+	0.260	0.456
Flexibility predictor	PredyFlexy	0.574+	0.000+	0.000	0.000
Disorder predictors	IUPred2A short	0.514+	0.002+	0.166	0.604
	IUPred2A long	0.443+	−0.079+	0.149	0.671
	DISOPRED3	0.377+	−0.062+	0.153	0.711
Combined disorder and flexibility predictors	PredyFlexy&IUPred2A short	0.557+	0.059+	0.184	0.660
	PredyFlexy&IUPred2A long	0.505+	0.006+	0.167	0.740
	PredyFlexy&DISOPRED3	0.493+	−0.047+	0.156	0.733

Note: The ‘PredyFlexy&DISOPRED3’, ‘PredyFlexy&IUPred2A long’ and ‘PredyFlexy&IUPred2A short’ combine the predictions of the residue flexibility predictor PredyFlexy and one of the considered disorder predictors. Statistical significance of the differences between the results of APOD and each of the indirect methods was evaluated based on the protocol described in Section 2.5 for AUC and MCC metrics. ‘+’ denotes that the predictions generated by APOD are significantly better than the results of the corresponding indirect predictor with the P-value < 0.01.

Fig. 6.

ROC curves of the APOD and the four selected indirect predictors of DFLs that secure AUC > 0.51 on the test dataset.

Table 1 also compares APOD to several popular disorder predictors and the flexibility predictor. The predictor of the flexible residue PredyFlexy secures AUC = 0.574 and MCC = 0, which point to a near-random predictive quality. These results are significantly worse that the predictions by APOD (P-value = 0.0003 for AUC and 0.006 for MCC). This can be explained by the fact that DFLs are disordered while flexibility prediction concerns flexible but structures residues. The disorder predictors also perform poorly with the best AUC = 0.514 and best MCC = 0.002 for IUPred2A short (P-value = 0.0001 for AUC and 0.004 for MCC when compared with APOD). This is because they predict all disordered residues, instead of focusing specifically on DFLs. The combinations of the flexibility and disorder predictions, which are covered at the bottom of Table, secure the best AUC = 0.557 and the best MCC = 0.059. This result corresponds to the solution that combines PredyFlexy with IUPred2A short, and is again significantly outperformed by APOD (P-value = 0.0001 for AUC and 0.003 for MCC). The corresponding ROC curves are shown in Figure 6.

We conclude that all considered here indirect approaches to predict DFLs are significantly worse than APOD and could not be used to reliably identify the DFLs.

4. Conclusions

We conceptualize, develop and test a novel and APOD. This method predicts DFL regions directly from the input protein sequence using a two-step process. First, we convert the sequence into an information-rich profile that represents selected structural properties including CONS and putative (sequence derived) SS, solvent accessibility and intrinsic disorder. Second, we encode this profile into a carefully designed feature set that we input into the well-parametrized SVM model to generate the DFL predictions. The features that we generate rely on the new (to this area) information source (CONS and putative structure) and include an innovative protein-level information. We empirically show that the inclusion of the protein-level features leads to substantial improvements (gray bars in Fig. 4). This can be explained by the fact that these features can effectively differentiate between proteins with DFLs and proteins that do not include DFLs. Empirical comparison with the existing predictor of DFLs, DFLpred, reveals that these innovations leads to statistically significant improvements in the predictive quality. APOD offers AUC and MCC values that are higher by 28% and 180%, respectively, when compared against DFLpred on the independent/low-similarity test dataset. The improvements are even more substantial when compared again several approaches that can be used to indirectly predict DFLs.

We provide a free access to the APOD predictor via a convenient webserver located at https://yanglab.nankai.edu.cn/APOD. This webserver performs all computations on the server side and requires the FASTA-formatted protein sequence as the only input. The results are delivered directly in the web browser window and are also sent to the user’s email address, if provided.

Given the high predictive quality of APOD and availability of the convenient to use webserver, we believe that our tool will find significant interest among researchers that study dynamics and functions of the disordered proteins and protein domains.

Funding

This work was supported in part by National Natural Science Foundation of China grants [NSFC 61873185 and 11501407 to Z.P.] and by the Robert J Mattauch Endowment funds to L.K.

Conflict of Interest: none declared.

Data availability

The data underlying this article are available in the article and in its online supplementary material.