In Vivo Human Corneal Shear-wave Optical Coherence Elastography

SIGNIFICANCE

A novel imaging technology, dynamic optical coherence elastography (OCE), was adapted for clinical noninvasive measurements of corneal biomechanics.

PURPOSE

Determining corneal biomechanical properties is a long-standing challenge. Elasticity imaging methods have recently been developed and applied for clinical evaluation of soft tissues in cancer detection, atherosclerotic plaque evaluation, surgical guidance, and more. Here, we describe the use of dynamic OCE to characterize mechanical wave propagation in the human cornea in vivo, thus providing a method for clinical determination of corneal biomechanical properties.

METHODS

High-resolution phase-sensitive optical coherence tomography imaging was combined with microliter air-pulse tissue stimulation to perform dynamic elasticity measurements in 18 eyes of nine participants. Low-pressure (0.1 mmHg), spatiotemporally discreet (150 μm, 800 μs) tissue stimulation produced submicron-scale tissue deformations that were measured at multiple positions over a 1-mm² area. Surface wave velocity was measured and used to determine tissue stiffness. Elastic wave propagation velocity was measured and evaluated as a function of IOP and central corneal thickness.

RESULTS

Submicron corneal surface displacement amplitude (range, 0.005 to 0.5 μm) responses were measured with high sensitivity (0.24 nm). Corneal elastic wave velocity ranged from 2.4 to 4.2 m/s (mean, 3.5; 95% confidence interval, 3.2 to 3.8 m/s) and was correlated with central corneal thickness (r = 0.64, P < .001) and IOP (r = 0.52, P = .02).

CONCLUSIONS

Phase-sensitive optical coherence tomography imaging combined with microliter air-pulse mechanical tissue stimulation has sufficient detection sensitivity to observe submicron elastic wave propagation in corneal tissue. These measurements enable in vivo corneal stiffness determinations that will be further studied for use with disease detection and for monitoring clinical interventions.

Corneal biomechanical properties (e.g., stiffness) are inherently tied to the integrity of the corneal structure, ocular health, and visual function^1–3 and are often changed by corneal diseases⁴ (e.g., keratoconus, glaucoma, and myopia) and medical procedures⁵ (e.g., laser-assisted in situ keratomileusis and corneal collagen cross-linking). Assessment of corneal biomechanics can be useful for diagnosing the onset and rate of keratoconus disease progression,^6,7 for pre-operative identification of refractive-surgery candidates to avoid complications such as post–laser-assisted in situ keratomileusis ectasia,^8,9 and for evaluating new medical and surgical treatment outcomes.¹⁰ However, in vivo noninvasive measurement of human corneal biomechanical properties remains a challenge, and there is currently no widely accepted clinical standard method to quantify ocular tissue biomechanics.

There are currently two clinically approved devices on the market designed to provide information on corneal stiffness and the eye's mechanical response to an external deformation force: the Ocular Response Analyzer (Reichert Inc., Buffalo, NY)¹¹ and CorVis ST (OCULUS, Inc., Arlington, WA).¹² Both devices are approved for the measurement of intraocular pressure (IOP) and do so by subjecting the eye to relatively large-diameter (several millimeters), large-amplitude (up to 60 mmHg) forces that result in global corneal deformation, ocular motion, and aqueous fluid displacement, as well as globe retraction and rotation.^13,14 These factors confound measurements of ocular biomechanics and preclude the possibility of spatially resolved measurements that would be necessary to detect minute variations in spatial stiffness.¹⁵ Previous clinical studies with these instruments have produced conflicting results. Although corneal biomechanics were different between keratoconus and normal eyes when evaluated using the Ocular Response Analyzer¹⁶ and the CorVis ST,¹⁷ no significant corneal biomechanical differences were measured for keratoconus eyes before and after the cross-linking treatments.^16–19

The limitations of the current clinical instruments and the need for in vivo quantitative mechanical assessment of the cornea have advanced the development of several new methods for biomechanical corneal evaluation in the last decade.^6,13,20–32 Many of these methods are based on the principles of elasticity imaging, a new medical imaging modality for noninvasive assessment of tissue properties that has been developed for several biomedical applications ranging from the whole organ to the cellular level.^31,33 Dynamic optical coherence elastography is an emerging imaging technique that is under active development for the assessment of corneal biomechanics.³² A dynamic optical coherence elastography imaging system comprises a mechanical loading subsystem designed to induce tissue displacements and an optical coherence tomography imaging subsystem capable of detecting the resulting tissue responses. The induced tissue deformations produce elastic waves (shear waves) that propagate orthogonal to the direction of the stimulation force. Stiff materials demonstrate a higher shear wave velocity, which can be quantitatively linked to the Young modulus for the sample. Characterization of the resulting mechanical waves is a fundamental priority for dynamic optical coherence elastography imaging to reconstruct tissue biomechanical properties.²⁶ However, the in vivo measurement of mechanical waves in the human cornea is still challenging, in part because the eye is a delicate and sensitive tissue.

Obtaining clinical optical coherence elastography measurements using noncontact dynamic imaging methods required overcoming a number of technical challenges related to instrument design, the development of analytical methods linking observations to mechanical parameters, and some understanding of the physiological determinants of the measurements. Over the last decade, we have developed a highly focused microliter-volume air pressure tissue stimulator to induce submicron mechanical waves as well as the capability to track the resulting dynamic mechanical wave propagation in situ using phase-sensitive optical coherence tomography.³⁴

We have previously reported the use of this imaging system to evaluate tissue phantoms and ocular tissues ex vivo and in vivo with animal models.^{15,26,35–42} We further evaluated corneal biomechanical properties as a function of IOP,⁴³ corneal thickness,³⁶ age,^40,41 and before and after corneal collagen cross-linking.^15,35,38 Most recently, we developed an improved version of the air-pulse stimulator and incorporated a newly designed common-path phase-sensitive dynamic optical coherence tomography imaging method.⁴⁴ This improved low-pressure (<60 Pa [0.45 mmHg]) microliter air-pulse system was revised from an earlier oblique stimulation geometry,^30,34 which is now configured to provide micromechanical stimulation normal to the sample surface. This provides better wave propagation uniformity in radial directions.⁴⁵ The phase-sensitive common-path optical coherence tomography detection method provides enhanced optical phase stability and detection sensitivity (0.24 ± 0.07 nm) for better visualization and quantification of small-magnitude oscillations when compared with conventional optical coherence tomography.⁴⁴ The combination of this highly sensitive common-path optical coherence tomography design and the microliter air-pulse tissue stimulation method has enabled us to perform in vivo corneal measurements. We have evaluated the effect of normal physiological movements, such as respiration and heartbeat, on the measurement precision and repeatability of the prototype corneal optical coherence elastography imaging system at a fixed corneal position (i.e., the corneal apex).⁴⁶ We have also performed in vivo natural frequency measurements (stimulation force, 13 Pa) across a 2.5-mm corneal lateral distance and have reported good measurement precision and repeatability for the measurement of human corneal natural frequencies (mean ± standard deviation, 259 ± 5 Hz; coefficient variation, 1.9%).⁴⁷ However, the ability to measure shear wave propagation in the human cornea in vivo has not been successfully demonstrated. In this study, we present further expansion and analysis of our previous work with in vivo optical coherence tomography measurements of submicron elastic wave velocities in human corneas (Twa MD, et al. IOVS 2017;58:ARVO E-Abstract 4324). We also compare the elastic wave propagation velocities with the IOPs and corneal thicknesses to assess the potential use of this corneal optical coherence elastography technique in clinical diagnostic applications.

METHODS

Participants

These pilot studies were performed on nine healthy subjects (three women and six men, 27 ± 5 years old). Clinical examinations were performed to confirm that subjects had no ocular disease, previous ocular surgery, or any systemic condition or medication use that could have affected corneal sensory function.

IOP measurements and central corneal thickness were compared with corneal tissue shear wave speeds measured using the optical coherence elastography system. IOP was measured using a Goldmann tonometer, and central corneal thickness was measured using ultrasound pachymetry (Reichert, Inc., Depew, NY). All the clinical measurements were repeated three times, and the mean values were used in this study.

The research protocol was approved by the institutional review board of the University of Alabama at Birmingham and adhered to the tenets of the Declaration of Helsinki, and informed consent was provided by all participants.

Optical Coherence Elastography Imaging System Design

A schematic layout of the corneal optical coherence elastography imaging system is shown in Fig. 1. The details of this imaging system can be found in our previous publications of the common-path optical coherence elastography system and its modification for in vivo corneal measurements.^44,46 In brief, a fixation target and a camera were used to locate and monitor the corneal position and to account for lateral eye motion. Axial eye motion was recorded using the optical coherence tomography signal and was separated from motion attributable to tissue stimulation because of the distinctly identifiable motion features primarily caused by low-frequency respiration and heartbeat (~0.1 to 1 Hz).⁴⁶ A short-duration (800 μs) and low-force (4 to 60 Pa [0.03 to 0.45 mmHg]) microliter air-pulse stimulator³⁴ was used to generate submicron scale corneal tissue displacements with a stimulation frequency of 10 Hz. An 840 ± 75-nm spectral domain common-path optical coherence tomography system⁴⁴ was synchronized to the tissue stimulator, and dynamic mechanical responses of the cornea were recorded. Phase detection sensitivity (0.24 nm in air) was calibrated for the whole imaging depth using a mirror.⁴⁴ The sample and reference arms shared the same optical path with a reference plane defined as the optical surface proximal to the sample. The reference optical plate was custom designed from a stock PMMA rod cut to a 5-mm diameter and a 5-mm thickness. Medical grade air was delivered normal to the corneal surface through a 150-μm diameter cannula. The tip of the microliter air-pulse stimulator cannula was inserted into a hole in the reference plate and positioned behind the external surface of the reference plate to prevent contact with the cornea. Two galvanometer mirrors (SM1 and SM2) were used to scan the optical coherence tomography beam at different locations across the corneal surface.

FIGURE 1.

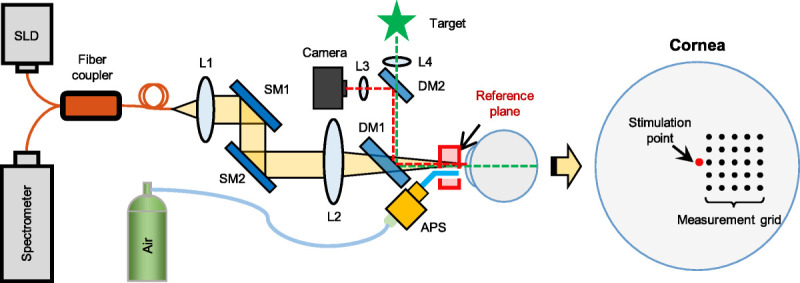
Schematic of the clinical corneal OCE system. Corneal OCE was combined with a fixation target and a camera to minimize the effects of lateral eye motion. A microliter APS provided repeated (10 Hz) and localized tissue excitation. A phase-sensitive common-path OCT imaging subsystem tracked the resulting dynamics of elastic wave propagation. APS = air-pulse stimulator; DM1–2 = dichroic mirrors; L1–L4 = lenses; OCE = optical coherence elastography; SLD = 845-nm superluminescent laser diode; SM1–2 = galvanometer scanning mirrors.

In Vivo Corneal Surface Wave Measurement

During the imaging process, subjects sat in a chair, placed their chin on a chin rest, and placed their forehead against a headband. Corneal elastography was performed as an M-B scan protocol to measure the surface displacement as a function of time and to track elastic wave propagation through the tissue.^15,26,48,49 Microliter air-pulse stimulation (pressure, 13 Pa [0.1 mmHg]) was delivered normal to the corneal apex from axial distances of 1.5 ± 0.5 mm. The duration of the air pulse was 800 μs, and the time between two successive excitations was 100 milliseconds (10 Hz). The optical coherence tomography beam scanned the corneal surface in a lateral sampling grid (~1 × 1 mm; 0.1- and 0.25-mm spacing, respectively, in horizontal and vertical directions) with a minimal distance of 0.15 mm away from the stimulation point to avoid near-field effects of tissue stimulation (Fig. 1).

The radial distance between each measurement point and the stimulation point was calculated based on the grid geometry and general corneal surface geometry (radius, 7.8 mm). The induced corneal surface displacements were recorded with an A-scan sampling rate of 20 kHz. Corneal displacement magnitude at each measurement location was acquired over time using phase-sensitive optical coherence tomography imaging (magnitude = λ × phase/4πn, where λ is the wavelength and n is the refractive index). Corneal displacement was sequentially measured at each response location (Fig. 1), whereas a constant stimulation at the corneal apex was maintained throughout measurements.

Analysis Methods

Low-frequency large-magnitude artifacts (~0.1 to 1 Hz, up to ±50-μm movements) caused by respiratory- and cardiac-induced eye motions⁴⁶ were removed from the corneal displacement profiles using low-order Fourier curve-fitting methods. Fig. 2A demonstrates the typical induced corneal displacement profiles at selected measurement locations (0.15 to 0.91 mm from the stimulation point). The displacement magnitudes decreased as the mechanical waves travel from near to far distances, and the displacement profiles shifted over time for different measurement locations. Because the optical coherence tomography acquisition system was synchronized with the microliter air-pulse stimulation, the time shifts among the measurement locations can be used to calculate the mechanical wave speed along the corneal surface, as was described in our previous work.^15,26,44

FIGURE 2.

Mechanical wave velocity calculation using optical coherence elastography of the cornea. (A) Typical corneal displacement profiles over time at selected measurement locations along the surface wave propagation path. (B) Typical estimation of the wave speed using a linear-fitting method (the same data set as in panel A).

In short, the wave speed calculations consisted of several steps. First, we calculated the temporal profile of the particle velocity for each experimental point based on the displacement profile using numerical differentiation with a time step of 0.4 milliseconds. Second, the particle velocity profiles for experimental points were cross-correlated with the velocity profile at the minimal distance of 0.15 mm away from the stimulation point with a kernel size of 1 millisecond.^38,43 Cross-correlation analysis yielded the time shift as a function of distance from the source, as shown in Fig. 2B. Finally, the time shifts were linearly fitted to the corresponding propagation distances to calculate the wave velocity (Fig. 2B). The linear-fitting method was based on the iterative procedure when, on each step, the points with the residual error higher than 2 standard deviations were removed. The speed of the elastic wave was calculated as the inverse of the slope, whereas the error was estimated based on the 95% confidence interval of the linear fit.

Regression models were used to assess the dependence of elastic wave propagation velocity on IOP or central corneal thickness as separate independent predictors. Mixed-effects multilevel regression models were used to control within-subject structural correlations in the data because of using both eyes from each subject. Statistical calculations were performed in Stata (Stata/SE 15.1 for Mac [64-bit Intel], revised February 3, 2020; StataCorp, College Station, TX). The regression model coefficients (IOP or central corneal thickness) were used to determine the significance of the modeled parameters. Statistical significance was declared when P < .05.

RESULTS

IOPs in the eyes tested ranged from 9.3 to 23.2 mmHg (mean ± standard deviation, 15.1 ± 3.9 mmHg) and were measured using the Goldmann tonometer. Central corneal thickness ranged from 485 to 608 μm, with mean value 539 ± 43 μm (Table 1).

TABLE 1.

Participant characteristics

Subject no.	Sex	Race	Age (y)	IOP (mmHg)		Central corneal thickness (μm)
				Left	Right	Left	Right
1	Male	Asian	34	9.7	14.1	485	494
2	Male	Asian	36	9.3	11.9	503	501
3	Female	White	22	15.3	15.7	608	607
4	Female	White	22	22	23.2	580	571
5	Female	White	24	12.5	11.6	554	535
6	Male	White	27	11.4	17.2	517	511
7	Male	Asian	25	15.2	14.2	537	534
8	Male	Asian	27	19.8	18.6	588	590
9	Female	Black	27	15.4	14.9	493	486

Fig. 3 shows the in vivo corneal elastic wave speed measurement results (mean and 95% confidence interval) for 18 eyes from nine healthy human subjects using the M-B mode optical coherence elastography measurement. The measured wave speeds ranged from 2.4 to 4.2 m/s (mean, 3.45 m/s; 95% confidence interval, 3.22 to 3.67 m/s). It was noted that the measurement difference between the left and right eyes on the nine healthy subjects was considerably small, which was 0.2 ± 0.1 m/s (mean ± standard deviation), with an average relative difference of 7.8%. Fig. 4 compares the measured corneal surface wave speeds with the IOPs and the central corneal thicknesses. The corneal elastic speed increased as IOP and corneal thickness increased and was significantly correlated with corneal thickness (r = 0.64, P < .001) and IOP (r = 0.52, P = .02). This was consistent with our previous findings from studies with animal models.^36,43

FIGURE 3.

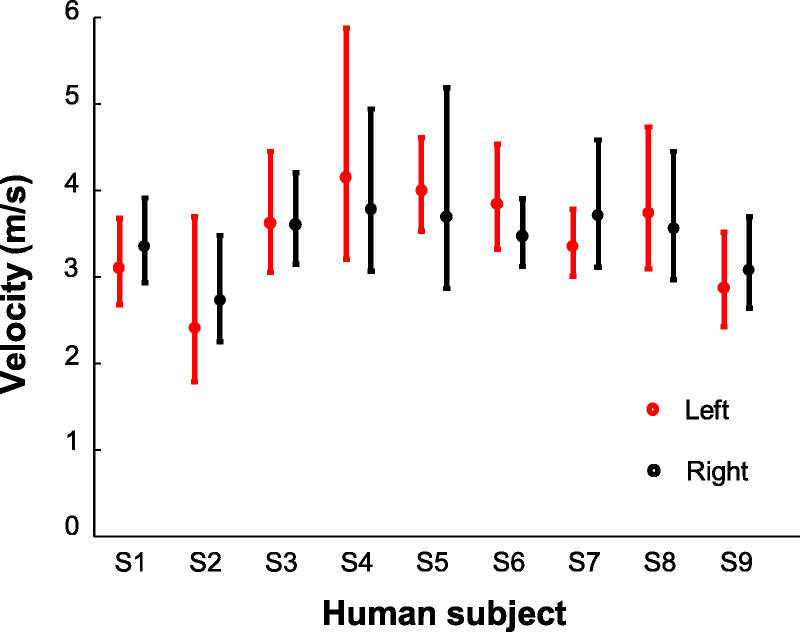
In vivo corneal elastic wave results for 18 eyes from nine healthy subjects. Error bars demonstrate the 95% confidence interval range for multiple measurements.

FIGURE 4.

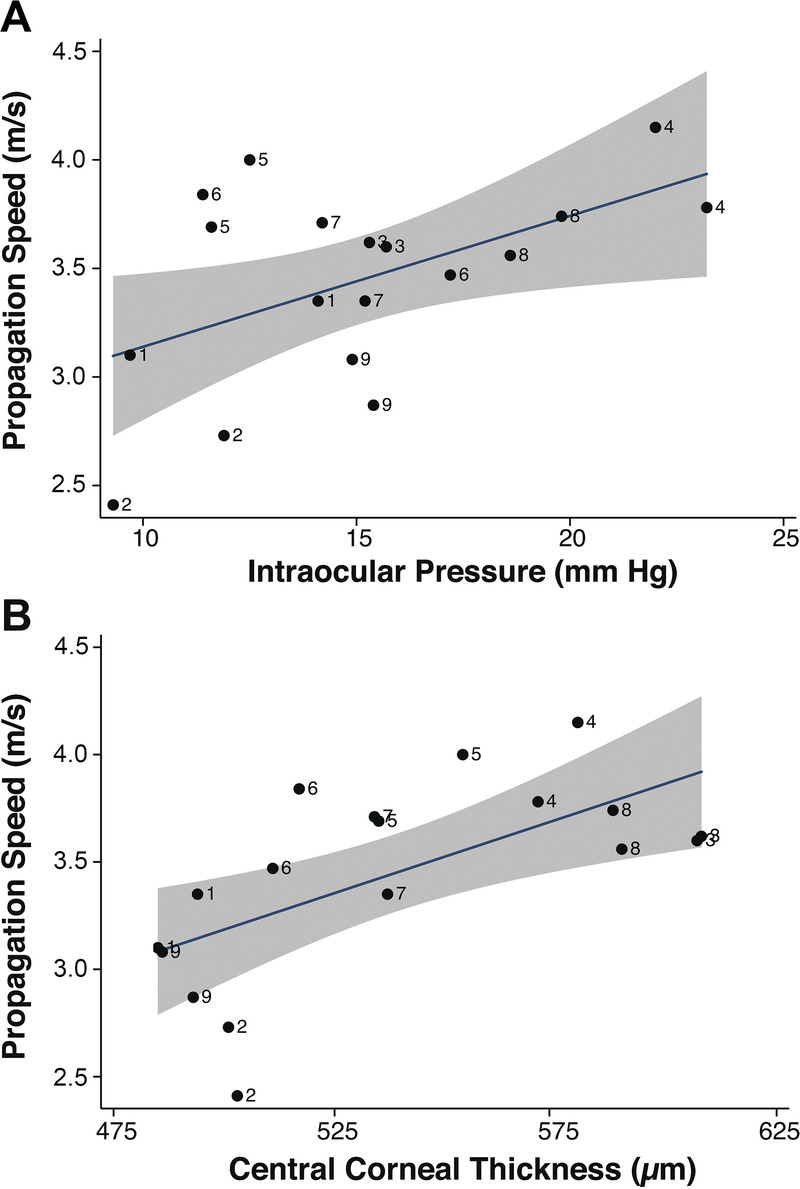
The measured elastic wave speed in the corneas were positively correlated with IOP (A) and central corneal thickness (B). Numbers represent subject identifiers.

DISCUSSION

These findings describe preliminary results with the application of a clinical common-path optical coherence elastography system⁴⁴ for in vivo measurement of the submicron elastic wave velocities of human corneas. The measured surface wave speeds are in the range from 2.4 to 4.2 m/s for 18 eyes from nine healthy human subjects (average 95% confidence interval, ±0.23 m/s), and the measurement difference between the left and right eyes is small (mean ± standard deviation, 0.2 ± 0.1 m/s). There are numerous internal and external factors that could influence the repeatability and reliability of clinical corneal biomechanical measurements, including the following: subject fixation, head or eye movements, respiration, oculocardiac pulsations,⁵⁰ eye and head motions,⁵¹ and so on. The IOP varies over cardiac cycles, and these pressure changes can change corneal biomechanics and corneal position over time.⁴³ In prior work, we have recently shown that the timescale of these dynamic measurements (in microseconds) is largely unaffected by ocular pulsations and breathing movements. Other factors, such as corneal hydration and tear film integrity, could also influence image quality and thereby measurement repeatability. Understanding and accounting for these factors will provide more repeatable measurements and are the subject of ongoing work such as instrument design improvements that will enable the future clinical uses of this technology for ocular biomechanics.

The measured elastic wave propagation speed in the cornea—a proxy for corneal stiffness—is positively correlated with IOP and central corneal thickness. These results are consistent with previous studies from our work and the work of others on animal models^20,24,36,43 and with the results of theoretical modeling,^37,52 where such dependencies have been demonstrated. Nevertheless, it is notable that the group velocity values in this study (3.45 ± 0.45 m/s) are slightly higher than the values obtained in our previous ex vivo animal studies (porcine) for comparable IOP values of 15 mmHg (2.81 ± 1.35 m/s).⁴³ This finding may be due to differences in computational methods used or the many factors that differ between animal and human corneas as well as differences due to in vivo and ex vivo measurement conditions.

Although the shear wave velocity can be directly connected with the shear or Young modulus in many medical applications, the complex corneal geometry makes the interpretation of the velocity measurements more difficult.²¹ Translation of the speed values to the mechanical constants requires the use of analytical or numerical mechanical models of the cornea, as has been performed in our previous studies.^37,52 However, the aim of this work was to demonstrate the feasibility of controlled dynamic optical coherence elastography measurements under clinical conditions. Assessing corneal elastic moduli based on mechanical wave propagation features continues to be the focus of our ongoing research studies.

Translation of elastography imaging to clinical practice requires the use of a reliable and safe method for elastic wave generation. Although several approaches based on modifications of the acoustic radiation force^20,22,23,25 and contact methods^24,29 have been proposed, the safety of these approaches has not yet been achieved. Air-puff excitation has been used for clinical IOP measurements for decades and is proven to be safe and convenient to use. Moreover, the pressure levels used in our studies for microliter air-pulse stimulation are much lower than what are used for IOP measurements. The results of this study demonstrate that microliter air-pulse–based optical coherence elastography has a promising potential to advance clinical measurements and understanding of ocular biomechanics.