A test of model classes accounting for individual differences in the cocktail-party effect

Abstract

Listeners differ widely in the ability to follow the speech of a single talker in a noisy crowd—what is called the cocktail-party effect. Differences may arise for any one or a combination of factors associated with auditory sensitivity, selective attention, working memory, and decision making required for effective listening. The present study attempts to narrow the possibilities by grouping explanations into model classes based on model predictions for the types of errors that distinguish better from poorer performing listeners in a vowel segregation and talker identification task. Two model classes are considered: those for which the errors are predictably tied to the voice variation of talkers (decision weight models) and those for which the errors occur largely independently of this variation (internal noise models). Regression analyses of trial-by-trial responses, for different tasks and task demands, show overwhelmingly that the latter type of error is responsible for the performance differences among listeners. The results are inconsistent with models that attribute the performance differences to differences in the reliance listeners place on relevant voice features in this decision. The results are consistent instead with models for which largely stimulus-independent, stochastic processes cause information loss at different stages of auditory processing.

I. INTRODUCTION

In social gatherings, noise from the crowd can challenge one's ability to converse with a partner, yet most of us manage fairly well. This ability, to hear out and follow the speech of one talker separately from others speaking at the same time, has long fascinated researchers of hearing and is known as the cocktail-party effect, after Cherry (1953). Cherry was interested in the larger problem of speech recognition but understood talker separation to be an essential part of that problem. His early experiments, using both speech and non-speech signals, would identify important factors for talker separation, and research since has built on this work. We now know that differences in the pitch, timbre, location, and rhythm of the voice serve as salient stimulus cues for talker separation (Wang et al., 2018; Middlebrooks et al., 2017; Bronkhorst, 2000, 2015; Kidd and Colburn, 2017). We know that the statistical properties of stimulus cues are important and that certain combinations of cues have synergistic effects (Brungart, 2001; Brungart and Simpson, 2004, 2007; Lutfi et al., 2013a; Rodriguez et al., 2019). Importantly, we also know that listeners rarely make optimal use of the acoustic information that serves to distinguish talker voices (Gilbertson and Lutfi, 2014, 2015; Lutfi et al., 2013a; Lutfi et al., 2013b; Lutfi et al., 2018).

These observations and others have explanations in models, but one finding continues to perplex—it is the unexpectedly large variation in performance observed among young, healthy, adults whose hearing is evaluated to be normal. Consider that for the simplest task, requiring only that talkers be heard separately from one another, performance levels of normal-hearing listeners can vary from near chance to perfect within the same condition (Lutfi et al., 2018); similar variability is observed for tasks involving the identification of talkers (Best et al., 2018). Identification accuracy for words across listeners with normal hearing commonly ranges over 40 percentage points within a condition (Getzman et al., 2014; Johnson et al., 1986; Kidd et al., 2007; Oberfeld and Klöckner-Nowotny, 2016; Ruggles and Cunningham, 2011; Ruggles et al., 2011), and word identification thresholds for constant performance differ by as much as 20 dB (Kubiak et al., 2020; Füllgrabe et al., 2015; Hawley et al., 2004; Kidd et al., 2007; Swaminathan et al., 2015). The differences are specific to performance with speech interferers; performance in quiet in these studies shows no such variation; and where test-retest measures have been made in these studies, the differences are found to be reliable, even after periods of considerable training.

The research findings are reinforced by observations made in the audiology clinic. The most common complaint of individuals visiting the clinic is difficulty listening in situations where there is background noise. Yet, for many of these individuals, hearing is evaluated to be normal as is their ability to communicate in quiet. The condition is given the nonspecific label of auditory processing disorder (Chermak and Musiek, 1997), admitting current ignorance of cause. Estimates are that as many as 1 in 10 of all individuals seeking the services of an audiologist meet the criteria for this classification (Kumar et al., 2007; Zhao and Stephens, 2007); the estimate is higher when considering that many individuals likely do not recognize their difficulty and so never consult an audiologist (Gatehouse and Noble, 2004).

This narrative seems at odds with the conventional view of hearing loss. In the clinic, the gold standard for evaluating hearing is the pure-tone audiogram. The audiogram, however, is a poor predictor of difficulty listening in noise, even for some whose thresholds fall well above the normal range. This naturally raises the question as to what extent the causes of the difficulty are specific to hearing. Early work on this problem established the importance of central nonauditory factors related to how listeners selectively attend to targets in noise [see Kidd et al. (2008) for a review], and recent advances have been made in the development of models to predict such effects (Lutfi et al., 2013a; Chang et al., 2016). Working memory and lapses in attention are also nonauditory factors that can be expected to impact speech recognition performance in noise, but the extent to which they contribute to individual differences in performance has not been widely investigated (Calandruccio et al., 2014; Calandruccio et al., 2017; Conway et al., 2001; Kidd and Colburn, 2017). More recent work suggests a role of peripheral factors associated with processing in the cochlea. Normal irregularities in micromechanics unique to individual healthy cochleae have been shown to influence performance in psychophysical tasks (Lee and Long, 2012; Long, 1984; Long and Tubis, 1988; Mauermann et al., 2004, Lee et al., 2016). Abnormal elevations in threshold can be missed if measured only at the audiometric frequencies (Lee and Long, 2012; Dewey and Dhar, 2017). Even at the audiometric frequencies, wide variation in thresholds falling within the normal range may reflect varying degrees of hair cell health that could affect listening in noise at supra-threshold levels (Plack et al., 2014). Finally, in a significant recent development, animal studies have identified a cochlear pathology not detected by conventional audiometry but possibly affecting listening in noise (Kujawa and Liberman, 2009). The animal work and reduced neural counts from temporal bone in humans have raised the specter that the pathology could be widespread in the population [Bharadwaj et al., 2015; Kujawa and Liberman, 2009; Furman et al., 2013; Liberman et al., 2016; Makary et al., 2011; also see Kobel et al. (2017) and Plack and Léger (2016) for reviews].

To date, there have not been wide-ranging efforts to understand which, if any, of these factors are responsible for the huge variation in the cocktail-party effect. What studies do exist have tended to focus on one or another of these factors in isolation (Kubiak et al., 2020; Bharadwaj, 2015; Oberfeld and Klöckner-Nowotny, 2016; Lee et al., 2016; Kidd et al., 2007). An exception is a study by Lutfi et al. (2018). These investigators stepped back somewhat from the challenge of testing specific accounts and focused instead on evaluating the general classes of models in which these accounts fall. The authors drew attention to the fact that, while listener performance may differ for any number of reasons, errors in judgement can only be of two types: those that are predictably tied to the variation in talker voices (the stimulus) and those that are not. Knowing which type of error is responsible for the individual differences implicates certain types of explanations while ruling others out. The authors applied this approach to a task in which listeners judged whether two alternating streams of vowels were spoken by the same or different talkers (a segregation task). Large individual differences in performance were observed, and the results overwhelmingly showed that the types of errors responsible for these differences were those not tied to the variation in talker voices. The authors concluded that the results are inconsistent with accounts attributing the performance differences to differences in the relative reliance or decision weight listeners place on different voice features. They proposed, instead, that the performance differences are due to information loss resulting from various stochastic processes, internal noise, associated with different stages of auditory processing.

This conclusion seems counter to some popular accounts of why individuals perform so differently in these studies, so it is worth reviewing the authors' reasoning. Key here is the often-made distinction in psychophysics between what a listener hears and what they do with what they hear [see Watson (1973) for a review, Dai and Shinn-Cunningham (2016) as applies to auditory physiology, and Berg (1990) for an analytic development]. What a listener hears on any trial is a representation of the signal that has lost information due to random noise inherent in the nervous system's processing of signals—so-called internal noise. The internal noise, because of its stochastic nature, makes it difficult to reliably predict from the stimulus on any trial when a listener will make an error because of what they hear. Contrast this with the error that results from what the listener does with what they hear. A listener who hears clearly the distinguishing features of a talker's voice but chooses, for whatever reason, to ignore many of these features will often make confusions. These errors, unlike those resulting from internal noise, can be reliably predicted from the stimulus because the listener's particular reliance on voice features (their decision weights) ties their response to the trial-by-trial variation in those features. Knowing, then, the relative extent to which these predictable and unpredictable errors are responsible for the individual differences in performance can be a first step in understanding the reason for those differences.

The present work was undertaken as a follow-up to the study of Lutfi et al. (2018). The goal was to test the generality of the authors' conclusions by broadening the application of their approach. We begin with a detailed description of the approach followed by four studies. The first replicates the Lutfi et al. study, but for a different task involving the identification of talkers. The second provides comparable results involving different levels of task difficulty. The third evaluates the role of individual differences in response bias. Finally, the fourth tests a further subdivision of model classes involving different sources of internal noise. The results of all four experiments replicate those of Lutfi et al. (2018) and support their conclusions in showing near exclusive dependence of the individual differences in performance on errors not tied to the trial-by-trial variation in voice features.

II. GENERAL APPROACH

The theoretical/methodological approach entails three elements: (1) a general decision rule for evaluating different model classes, (2) an experimental method for estimating the parameters of the rule, and (3) a theoretical framework for quantifying individual limits on listener performance from these parameter estimates. To appreciate exactly how these elements work together, we revisit in more detail the study of Lutfi et al. (2018). As mentioned, the listener's task was to judge whether two interleaved sequences of randomly selected vowels were spoken by the same or different talkers. The talkers had different fundamental frequencies, F0, and spoke from different azimuthal locations, θ [simulated using Kemar head-related transfer functions (HRTFs)]. These two cues were selected because they are the two that have been most extensively researched in the literature and produce some of the largest effects [see Bronkhorst (2015) for review]. Small random perturbations in these parameters were deliberately added on each presentation as part of the methodological approach, but also to represent the natural variation that occurs in these features. Let the 1-by-8 vector f denote the z-score differences in the values of F0 and θ for the two vowel sequences played on a given trial. Then, for any monotonic transformation of f, a general decision rule for the task is given by

$$\text{Respond}\hspace{0.17em}“\text{Two}\hspace{0.17em}\text{Talkers}”\text{'}\text{'}\hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\text{only}\hspace{0.17em}\hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}\mathbf{w}\cdot (\mathbf{f}+\mathbf{e})\prime +e_0\ge \beta ,$$ (1)

where the vector w gives the decision weights representing the listener's relative reliance on the differences in F0 and θ, e is a vector of random deviates representing internal noise occurring prior to the application of the decision weights (peripheral internal noise), e₀ is a random deviate representing internal noise occurring after the application of the decision weights (central internal noise), and β is a response criterion.

The decision rule allows us to identify the different factors responsible for the individual differences in the listener's performance. Each parameter in rule (1) represents the effect of one of these factors as explicitly expressed or implied in the literature: the decision weights, w, with the selective attention to and reliance on voice features; the peripheral internal noise, e, with cochlear pathology and hair cell health; and the central internal noise, e, with lapses in attention, criterion variance, memory, and other non-auditory factors. Empirical estimates of these parameters are obtained by performing a logistic regression of the listener's trial-by-trial responses (R = 1 vs 2 talkers) on the perturbed values of the voice features,

$$\text{logit}\left[P\left(R\equiv 2\right)\right]=c_0+\mathbf{c}\cdot {\mathbf{f}}^{\mathbf{\prime }}+\mathit{err},$$ (2)

where the regression coefficients, c, are determined by the decision weights, w, and the residual error term, err, captures the pooled sources of peripheral and central internal noise. Note that the residual error tells us how unsuccessful we are in predicting the listener's trial-by-trial errors from knowledge of the voice features. The greater this value, the greater we attribute a role to internal noise.

In the final step of this approach, the relative influence of the decision weights and internal noise on performance is determined by an efficiency η-analysis (Berg, 1990). The analysis expresses the listener's overall obtained performance relative to that of a maximum-likelihood (ML) observer,

$${\eta }_{\text{obt}}={\left(d_{\text{obt}}^{\prime }/d_{\text{ML}}^{\prime }\right)}^2,$$ (3)

where d′_obt is the listener's obtained performance, and d′_ML is the performance of the ML observer. The value of η_obt ranges from 0 (chance performance) to 1 (optimal performance). The ML observer is an “internal noise-free” observer whose decision weights optimize performance for the task. For the case considered, the ML observer gives equal weight to each value of f, since each value is equally diagnostic regarding the task.¹ In practice, the performance of the ML observer is determined by making response predictions for each stimulus played on each trial using the optimal decision weights and optimal response criterion in decision rule (1). Next, this overall performance efficiency is broken down into two components, one affected by the listener's decision weights and the other affected by all sources of internal noise. The effect of the listener's decision weights is given by a weighting efficiency,

$${\eta }_{\text{wgt}}={\left(d_{\text{wgt}}^{\prime }/d_{\text{ML}}^{\prime }\right)}^2,$$ (4)

where d′_wgt is the performance predicted from the previously obtained estimates of the listener weights. In practice, d′_wgt is determined from the trial-by-trial stimuli in the same way as d′_ML, except that the optimal decision weights are replaced with the estimated values for individual listeners from the logistic regression. The effect of the pooled sources of internal noise is given by a noise efficiency,

$${\eta }_{\text{nos}}={\left(d_{\text{obt}}^{\prime }/d_{\text{wgt}}^{\prime }\right)}^2,$$ (5)

and is determined from the proportion of responses not predicted by the listeners' decision weights. The product of the weighting and noise efficiencies gives the overall performance efficiency,

$${\eta }_{\text{obt}}={\eta }_{\text{wgt}}\times {\eta }_{\text{nos}}.$$ (6)

If listeners differ in amounts of internal noise, the proportion of the not-predicted errors will differ across listeners, yielding different values of η_nos. If listeners differ in how effectively they weight the distinguishing voice features of talkers, then the proportion of the predicted errors will differ across listeners, yielding different values of weighting efficiency, η_wgt. Finally, if both factors contribute or interact in some way to affect overall performance, then the relative influence of each will be given by the relative magnitudes of η_nos and η_wgt.

III. STUDIES

A. Study 1: Segregation vs identification

In experiments investigating the cocktail-party effect, the stimuli are often streams of vowels or words spoken by two or more talkers. The speech of one of the talkers is identified as the target, and the speech of the other talker(s) is identified as interference. From the perspective of an ML observer, there are two versions of the experiment involving two fundamentally different tasks. In the first, called the segregation task, the listener is asked simply to judge when the target speech is heard separately from the interference. In the second, called the identification task, the listener must report on some property of the target: who they are, where they are, what they said. Chang et al. (2016) provide an analytic comparison of the two tasks underscoring their differences and similarities. In real-world conditions, both tasks are required, but Lutfi et al. (2018) report only on the segregation task. They may have gotten a different result for an identification task because identification places greater attentional demands on the listener; the listener must attend to the information distinguishing talkers as well as the information to be identified. In the present experiment, we report data from both tasks obtained under conditions comparable to those of Lutfi et al. (2018).

We begin with the segregation task. Let A and B be random vowels forming two sequences in the pattern ABA_ABA_ABA_ABA. This pattern was chosen to correspond to related studies of auditory streaming where A and B are complex tones that appear to split into separate streams as they diverge from one another in pitch (Bregman, 1990). On each trial, the listener was asked to judge whether the two sequences (heard over headphones) were spoken by the same or different talkers; BBB. vs ABA. The talkers had nominally different fundamental frequencies (A: F0 = 150 and B: F0 = 120 Hz) and spoke from nominally different azimuthal locations (A: θ = 30 and B: θ = 0° azimuth). The azimuthal locations were simulated using Kemar head-related transfer functions (Knowles Electronics Manikin for Acoustic Research). A small, random perturbation (normally distributed with zero mean and standard deviation σ = 10 Hz and 10°) was added to the nominal values of F0 and θ independently for each vowel on each trial. The perturbations simulated the natural variation in these parameters that occurs in real-world listening and were required to estimate the regression coefficients c and, hence, the decision weights, w. For the identification task, the conditions were the same except that the sequence of B vowels with the same values as before was made to be the interference and the listener was required to identify on each trial which of two target talkers spoke the sequence of A vowels, A₁BA₁. vs A₂BA₂. (A₁: F0 = 105 Hz and θ = −15°; A₂: F0 = 135 Hz and θ = +15°). The corresponding values of σ were 15 Hz and 15° as in the Lutfi et al. (2018) study. In all cases, the difference Δ in the nominal (mean) values for each cue and their corresponding values of σ were selected so that the Δ/σ ratio was the same for both cues.

The vowels were selected at random for each triplet from a set of 10 exemplars having equal probability of occurrence (the 10 vowels identified by their international phonetic alphabet names were i, I, ɛ, æ, ʌ, ɑ, ɔ, ʊ, u, ɝ). Although selected at random for each triplet, the first and last vowel of each triplet were the same with the same value of the perturbation. The vowels were synthesized using the Matlab program Vowel_Synthesis_GUI25 available on the matlab exchange. Each vowel was 100 ms in duration and was gated on and off with 5-ms cosine-squared ramps. A silent interval of 100 ms separated each vowel triplet. The vowel sequences were played over Beyerdynamic DT990 headphones to listeners seated in a double-wall, sound-attenuation chamber located in a quiet room. They were played at a 44 100-Hz sampling rate with 16-bit resolution using an RME Fireface UCX audio interface.

Lutfi et al. (2018) have performed simulations of listener performance for the segregation task to ensure sensitivity to the predictions of model factors and their interaction (see Fig. 3 of that paper). Our conditions differed from theirs only in that σ was made slightly smaller (10 vs 15 Hz and degrees), thus making our segregation task slightly easier by decreasing the overlap in the distributions of F0 and θ. As this was the only difference, we take their simulation results to apply to our segregation task. We did, however, perform comparable simulations for our identification task. Three different scenarios were simulated: differences in performance due to (a) internal noise, (b) decision weights, and (c) an interaction where internal noise affects the selection of decision weights. For (a), internal noise was chosen to produce performance from near chance to perfect levels across listeners with decision weights having roughly the same near optimal weighting efficiency. For (b), internal noise was roughly the same for all listeners with decision weights varying from near optimal to near exclusive weight on the last two vowels (a recency effect). Finally, for (c), internal noise was simulated to affect the choice of decision weights by varying together the decision weights as in (a) and internal noise as in (b). Note, in this last case, either source of internal noise, peripheral or central, could possibly affect the decision weights. Peripheral internal noise, say associated with an undetected cochlear pathology, might cause a listener to favor one segregation cue over another. Central internal noise, say associated with information overload or lapses in attention, similarly might cause a listener to focus only on the last few vowels heard. For the purpose of this simulation, we did not distinguish between the two sources of internal noise. We only considered, as we do for real listeners, the pooled effects of the two sources on the error term in Eq. (2) and thus η_nos.

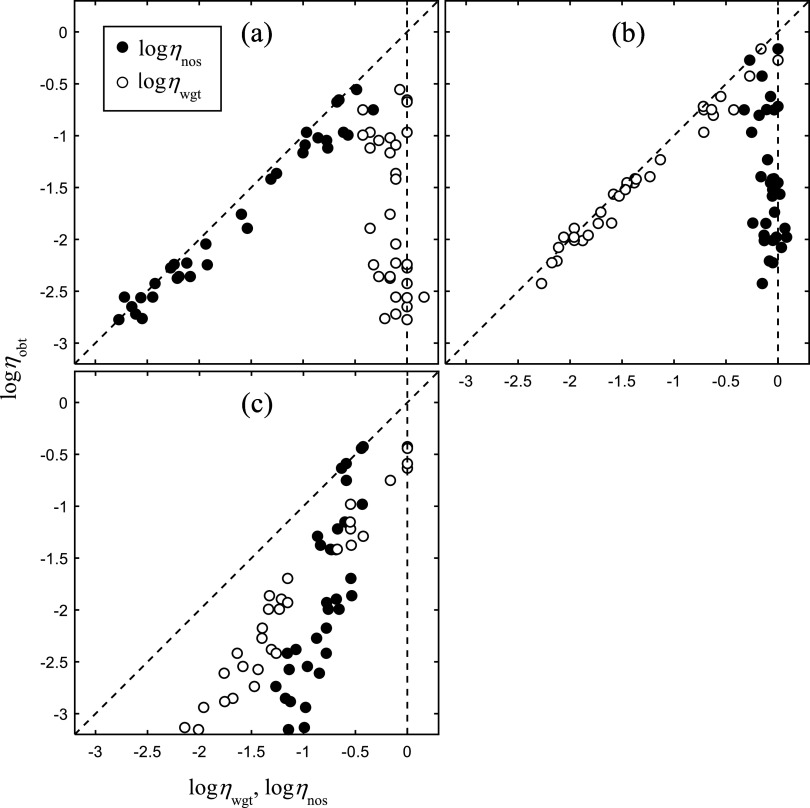
The results for the three scenarios are shown in the different panels of Fig. 1. Overall performance efficiency η_obt is plotted against weighting efficiency η_wgt (unfilled symbols) and internal noise efficiency η_nos (filled symbols) with the different symbols representing the results from the different hypothetical listeners. To simplify the representation, the values of η are converted to natural log units so that the values add. The two dashed lines give the bounds on the values of η (0 ≤ η ≤1); values are expected to fall in the region between these two lines. To interpret this figure, consider a separate line drawn through each set of points corresponding to the predictions of each model, decision weights (unfilled symbols) and internal noise (filled symbols). For a model that contributes exclusively to the individual differences (η_obt = η_wgt, or η_obt = η_nos), the slope of the line will be unity. Hence, the closer the slope of this line is to unity, the greater the corresponding model's contribution to the individual differences in performance. The results show clearly different outcomes for the three scenarios consistent with their predictions in each case: essentially an exclusive contribution of internal noise in panel (a), an exclusive contribution of decision weights in panel (b), and a combined influence in panel (c). We take this simulation as showing that if listeners behave in the way given by the simulation, our results with real listeners should show similar patterns.

FIG. 1.

Results of computer simulation. Overall performance efficiency η_obt is plotted against weighting efficiency η_wgt (unfilled symbols) and internal noise efficiency η_nos (filled symbols) with the different symbols representing the data from the different hypothetical listeners. The values of η are expected to fall between the two dashed lines shown. Simulations are for individual differences in internal noise (a), decision weights (b), and an interaction between decision weights and internal noise (c).

Sixty-one students at the University of South Florida–Tampa (USF) participated as listeners in the experiment, 38 for the segregation task (9 male, 29 female, ages 18–29 yr) and 50 (11 male, 38 female, ages, 18–27 yr) for the identification task. Twenty-seven of the listeners participated in both tasks. All listeners had normal hearing by standard audiometric evaluation. Prior to data collection, the listeners received three blocks of training trials. If after the first three blocks their average performance was less than 60% correct, they received an additional three blocks of training trials. They went on to perform experimental trials regardless of their performance on the second block of training trials. The data were collected in eight blocks of 50 trials each within a 1-h session, and replications were obtained on different days. Listeners were allowed breaks at their discretion between trial blocks. All listeners were paid in cash for their participation in the experiment.

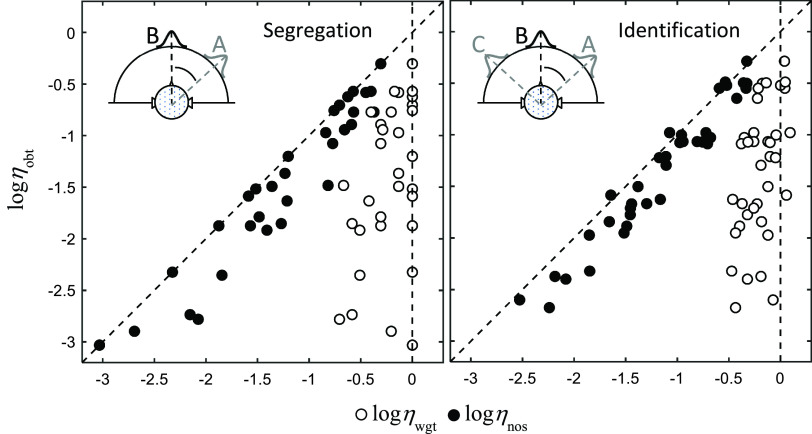
Here and throughout, we report only the efficiency estimates, as that is the focus of this paper. A comprehensive analysis of the individual decision weights of these 61 listeners is planned for a separate paper. The individual efficiencies are shown in Fig. 2. Reliable estimates of η_wgt could not be obtained for eight listeners in the segregation task and three listeners in the identification task. For these listeners, performance was close to chance (values of η_obt less than −3 log units). For all other listeners, estimates were deemed acceptable based on the deviances of the fits ranging from 14 to 510 relative to the saturated model with 391 degrees of freedom (Snijders and Bosker, 1999).² The data replicate the large individual differences in performance efficiency reported by Lutfi et al. (2018). The highest and lowest values of η_obt reported here represent a range of performance accuracy from near chance (52% correct) to near perfect (99% correct) levels. As in Lutfi et al. (2018), the weighting efficiencies (η_wgt, unfilled symbols) show some variability across listeners. However, this variability accounts for little if any of the variability in η_obt, being near uniformly distributed across the values of η_obt. Instead, the variability in η_obt across listeners is due almost entirely to the differences in the internal noise efficiencies (η_nos, filled symbols). The results demonstrate that the dependency of η_obt on η_nos generalizes to an identification task, which places much greater attentional demands on listeners.

FIG. 2.

(Color online) Same as Fig. 1 except data are for 38 real listeners participating in the segregation task (left panel) and 50 real listeners participating in the identification task (right panel).

B. Study 2: Task difficulty

One factor clearly expected to have an impact on individual differences in performance is task difficulty. As the task becomes too difficult or too easy, performance for all listeners converges to the same chance or perfect levels. One question is to what extent the individual differences are evident between these two extremes. The answer can provide a sense for how pervasive the differences are and when they are likely to be observed in other conditions that inevitably vary in difficulty. A more important question, for the purpose of evaluating model classes, is what happens when the task becomes quite easy. Will internal noise continue to underlie individual differences at this point, or will decision weights play a more prominent role as the listener is better able to focus their attention on the relevant acoustic cues that serve to distinguish talkers? Dai and Shinn-Cunningham (2016) give reason to expect the latter outcome. They showed that cortical event-related potentials, which are modulated by attention, correlated with individual differences in performance in a tone segregation task only when the cues for segregation were made quite salient.

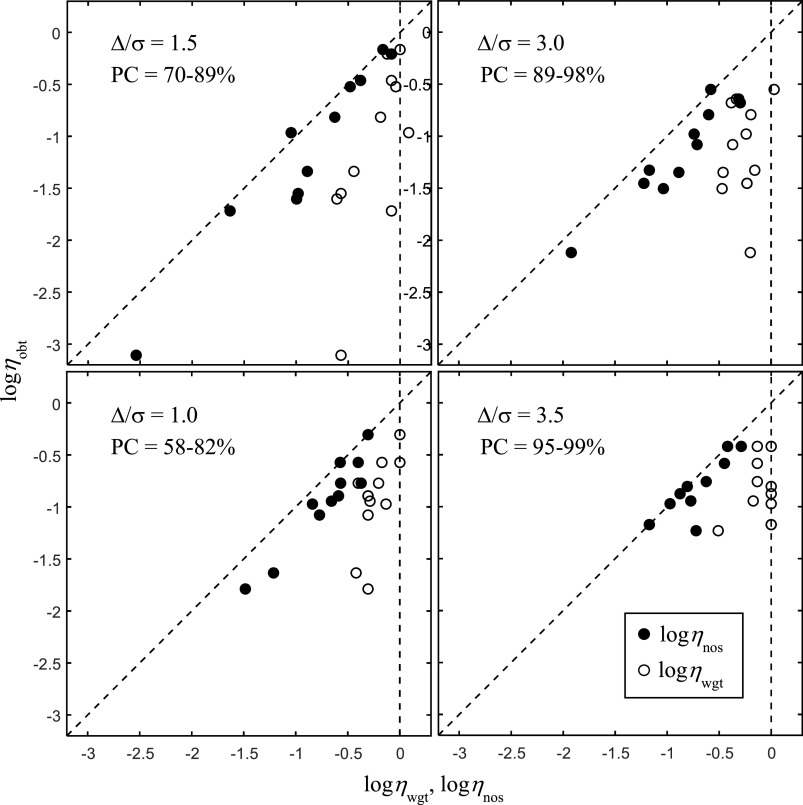
Eleven USF students (1 male, 10 females, ages 19–31 yr), seven of whom had previously participated in Study 1, were run in the segregation task. The task was made more or less difficult by varying the mean separation Δ between segregation cues; otherwise, the conditions were identical to Study 1. Figure 3 gives the data for different levels of task difficulty (shown in different panels). The Δ/σ ratios and the range of percent correct scores (PC) across listeners for each level of task difficulty are shown in the upper-left corner of each panel. The data show clear individual differences in performance efficiency, η_obt, across listeners at all levels of task difficulty, even in the easiest condition, where performance accuracy ranges over only 4 percentage points (95–99% correct). As might be expected, the poorest performing listeners are the same in each panel. The differences in η_obt increase with increasing task difficulty and, in keeping with the previous results, are due near exclusively to differences in noise efficiency, η_nos. The results confirm the ubiquitous nature of the individual differences and their dependency on η_nos over effectively the entire range of possible performance levels. They support a consistent influence of internal noise over these performance levels and do not support the prediction that decision weights will play a more prominent role as the task becomes easier.

FIG. 3.

Same as Fig. 2 except data are for 11 listeners performing in the segregation task for different levels of task difficulty produced by increasing or decreasing the mean separation Δ between F0 and θ. The Δ/σ ratios and the range of PC across listeners for each level of task difficulty are shown in the upper-left corner of each panel.

C. Study 3: Response bias

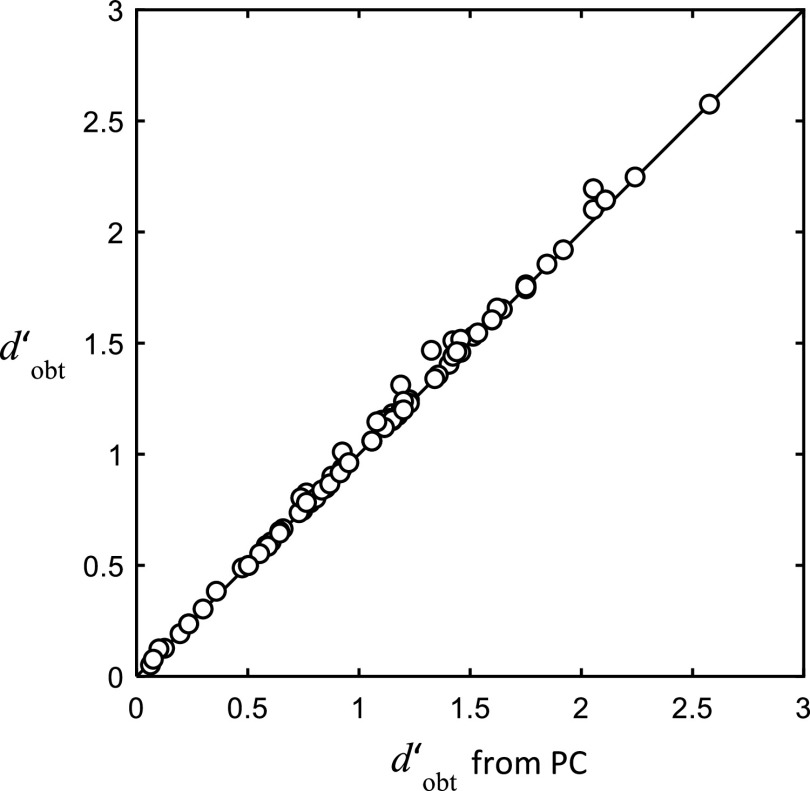
The data from the Lutfi et al. (2018) study, as here, were obtained using a single-interval, forced-choice procedure. Such procedures are subject to the effects of response bias—a tendency on the part of the listener to under- or over-report one or the other type of response, which affects performance. Response bias is not a factor that falls easily into either class of models considered here. It has neither the property of being stochastic nor the property of being tied precisely to the stimulus. It could, nonetheless, be responsible for the individual differences in performance observed in our studies. The differences in bias would appear as differences in η_nos exactly as we have seen in these experiments. This is by default because the bias [c₀ in Eq. (2) related to β in Eq. (1)] is not included among the regression coefficients in the computation of the weighting efficiency, η_wgt, and so does not affect η_wgt. Lutfi et al. (2018) did not analyze for the effects of response bias, but it is easy to do so here. If η_nos is affected by bias, then the values of d′_obt used in its computation [cf. Eq. (5)] will differ when they are allowed to include the effects of the bias. Figure 4 shows the values of d′_obt from all listeners of Study 1 computed two ways. On the ordinate are the values of d′_obt computed from the hit and false alarm rates. These values were used in the original computation of η_nos and measure sensitivity free from the effect of response bias [see Green and Swets (1966)]. On the abscissa is plotted the values of d′_obt computed from the PC. These values assume that listeners have no bias, so if listeners do have bias, these values should differ from the values plotted on the ordinate. The figure shows virtually no difference between the two estimates. The conclusion is that response bias is not a factor contributing to the individual differences in performance observed in these experiments.

FIG. 4.

Role of response bias. Values of d′_obt from all listeners participating in the segregation and identification task of Study 1. Ordinate: d′_obt free of bias, computed from the hits and false alarm rates. Abscissa: d′_obt includes bias, computed from the PC (abscissa).

D. Study 4: Central vs peripheral internal noise

The study by Lutfi et al. (2018) as well as the results presented here provide strong evidence identifying individual differences in performance in these experiments with information loss due to internal noise. In so doing, they work to narrow the field of possible explanations for these data. The next experiment attempts to further narrow the field by isolating explanations based on the source of the internal noise. We identify two broad classes of internal noise from decision rule (1), noise that occurs before the summation of observations (peripheral internal noise, e) and noise that occurs after summation (central internal noise, e₀₎. Examples of the former would be sensory noise resulting from neural under-sampling (Lopez-Poveda, 2014) or variations in hair cell health (Lee and Long, 2012). Examples of the latter would be perceptual distortions resulting from limited working memory, decision criterion variance, or lapses in attention. What fundamentally distinguishes these two classes is the manner in which the internal noise adds to the individual stimulus features, f. The peripheral internal noise, by virtue of occurring before summation, adds independently to each feature, whereas the central internal noise, by virtue of occurring after summation, adds in common to all features.

A test of these two alternatives, suggested by Oxenham (2016), focuses on this fundamental difference. It entails varying the number of independent stimulus presentations the listener is allowed to observe; in our case, the number of independent stimulus presentations being the number of random ABA triplets. To explain, consider the anticipated effect on d′_obt performance in our conditions. For the peripheral internal noise, there is a benefit to increasing the number of observations because the samples of the peripheral noise associated with each are independent and so will tend to cancel as more observations are weighted in the sum. For the central internal noise, there is no effect; the central noise adds after the observations are summed, so it does not matter how many observations go into that sum.

Let us assign numbers to predictions in each case. Suppose the number of triplets is increased from N = 1 to 4. For N = 4, our estimates of weighting efficiency (η_wgt) for listeners are with few exceptions close to 1 (logη_wgt close to 0 in Figs. 2 and 3). This indicates that observations are weighted roughly optimally. Hence, if performance is dominated by peripheral internal noise, then according to the law of large numbers, the fourfold increase in observations should result in a near twofold increase in d′_obt (a factor of the square root of 4 increase). Of course, there is a corresponding twofold increase in the performance of the maximum-likelihood observer, d′_ML, since the observations are themselves independent random samples drawn from the stimulus distributions. This, therefore, translates to little change in overall performance efficiency when d′_obt is expressed relative to d′_ML. Now, compare this to the case where performance is dominated by central internal noise; d′_obt does not change with increasing number of observations if central noise dominates, so we should expect on average a twofold reduction in performance efficiency. A twofold reduction corresponds to a reduction of η_obt of log(2) = 0.7 natural log units.

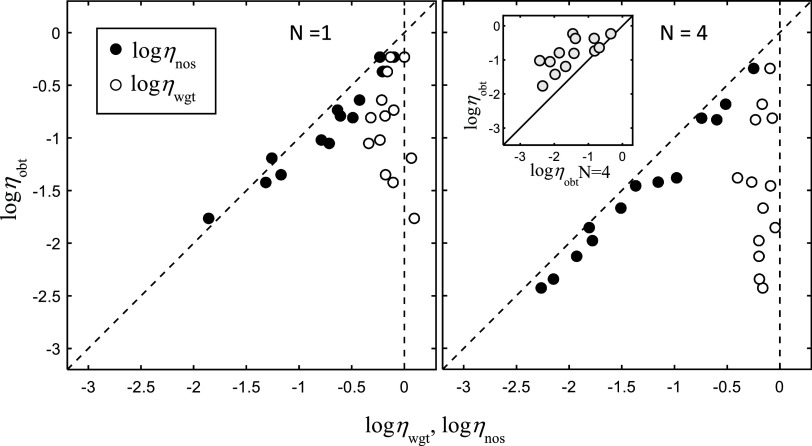
Figure 5 shows data for seven listeners (females, ages 19–23 yr) participating in the segregation task for N = 1 and 4 vowel triplets (large panels). The data include replications for all but one listener, whose initial performance, near chance, did not permit reliable estimates of noise efficiency (logη_nos < −3). The panels show generally a shift along the diagonal to lower values of performance efficiencies in going from N = 1 to 4 triplets, consistent with an effect of central internal noise. This is seen more clearly in the inset, which compares directly the overall performance efficiencies for each subject (symbols) obtained in the two conditions across the two replications. Here, the magnitude of the reduction, also consistent with the effect of internal noise, tends to be greatest for the poorest performing listeners. These listeners have the highest levels of central noise according to our estimates and so should show the largest reductions in performance efficiency with the increase in N. Averaged across all listeners and replications, the magnitude of the reduction is 0.7 log units, again consistent with the prediction for the average effect of central internal noise. The average value was not significantly different from zero (z = 1.47, p > 0.08), but this should not be surprising as the variance in the individual values is expected to be large. The results generally support the conclusion that the individual differences in performance in these conditions are due to varying degrees of central internal noise across listeners.

FIG. 5.

Data for seven listeners (replications for six) participating in the segregation task for N = 1 and 4 vowel triplets (panels), η values plotted as before. The inset in the right panel compares directly the overall performance efficiencies, η_obt, obtained in the two conditions across the two replications.

IV. DISCUSSION

Why individuals with normal hearing thresholds should have unusual difficulty segregating the speech of talkers is not well understood. It is an observation that would seem to challenge the conventional view of hearing loss and the efficacy of the audiogram on which that view is based. There are many possible reasons for the difficulty, as we have reviewed in the Introduction. Any one or combination of these possible factors may be responsible, their influence may be different for different listeners, and their effects may interact. An undetected hair cell pathology, for example, or a limited capacity of working memory may impact how a listener selectively attends to relevant cues, further affecting performance (Doherty and Lutfi, 1996). To complicate the situation further, entirely different factors can have the same effect on performance and even produce the same pattern of errors within a given experiment. Momentary lapses in attention, for example, are likely to have the same effect as the occasional poor representation in working memory that might occur over the course of many trials.

Given the complexity of the problem, possibly the best one could hope for is to narrow the field to a particular class of explanations. This was the intent of the present study. We considered two classes of explanations that subsume all current accounts. The two classes are distinguished by the predictions they make for the types of trial-by-trial errors that are responsible for the differences in listener performance. The results suggest some success with this approach. They show, in three different tests, that the types of errors responsible for the performance differences are overwhelmingly those not tied to the trial-by-trial variation in the voices of talkers. This was the outcome for two different tasks (segregation, identification of talkers), for different levels of task difficulty, and for different information demands placed on listeners (length of vowel sequences). The results replicate those of Lutfi et al. (2018) and are consistent with a class of models in which individual differences in performance result from the cumulative effects of internal noise occurring at different stages of auditory processing. This class includes, among other possibilities, undetected cochlear pathology, lapses in attention, and limits in working memory. The results are inconsistent with explanations assuming an over-reliance on or failure of selective attention to particular features that distinguish talkers, at least as these processes are commonly discussed or modeled in the research literature.

These results are new for studies on the cocktail-party effect using speech stimuli, but notably similar results using similar methods have been previously reported for different tasks involving nonspeech stimuli. Doherty and Lutfi (1996) used principally the same model given by (1) to estimate decision weights on individual frequencies in level discrimination of a multitone complex. They report, for both normal-hearing and hearing-impaired listeners, large individual differences in performance (η_obt) despite similar weighting efficiencies (η_wgt). Lutfi and Liu (2007) used fundamentally the same model and report the same result (normal-hearing listeners) for the identification of rudimentary properties of objects from the sound of impact (size, material, damping, and mallet hardness). In the original study adopting this method, Berg (1990) measured weighting efficiencies for the discrimination of multitone sequences differing in frequency. They report data from only three subjects, but it is clear from these data that the weighting efficiencies were less correlated with overall performance than the noise efficiencies and even had somewhat less of an effect on the individual differences in performance.

Two questions naturally arise from these studies: (1) where does the internal noise originate in the auditory system, and (2) for what conditions, if any, are individual differences in performance more likely to be caused by differences in the reliance listeners placed on voice features? Some data relevant to the first question come from Fig. 5. These data show η_obt values that decrease on average with multiple observations by the amount expected if the internal noise adds after the summation of observations. This is suggestive of a central origin of the internal noise. Data from Oberfeld and Klöckner-Nowotny (2016) also provide evidence suggestive of a central origin. They show a correspondence of individual performance differences in a speech segregation task with individual performance differences for a comparable visual selective attention task involving the same subjects. Many more studies have recently investigated the possibility of a peripheral origin associated with noise induced cochlear synaptopathy (Guest et al., 2018; Bharadwaj et al., 2015; Mehraei et al., 2016; Liberman et al., 2016; Grose et al., 2017). The results of these studies have been mixed, but the question continues to generate interest because of potential implications for clinical practice (Shinn-Cunningham, 2017). Relevant to question 2 are two studies by Gilbertson and Lutfi (2014, 2015). These authors investigated vowel identification in a speech segregation task for which the trial-by-trial variation in segregation cues was considerably larger than in foregoing studies. Where the variation in the external cues is much larger than the variation in perception due to the internal noise, one might expect the effect of the internal noise to be comparatively small. Any individual differences in performance would then be more correlated with individual differences in weighting efficiency. Indeed, this was the outcome of the Gilbertson and Lutfi (2014, 2015) studies. Future studies will be required to identify conditions in which the listener's decision weights may play a more important role.

V. CONCLUSIONS

Understanding why otherwise healthy, normal-hearing adults differ so greatly in their ability to listen effectively in multi-talker situations is a tremendous challenge. Multiple interacting factors likely play a role. The present study reports some progress in narrowing the field of possible explanations by testing general classes of models distinguished by their predictions for the types of errors listeners make—a divide-and-conquer approach. The most basic distinction, the one tested, is whether the errors responsible for the individual differences can be predicted from the trial-by-trial variation in the voice features of talkers. The answer for the conditions of this study is that they cannot be reliably predicted from these features. The implication is that individual differences in performance result less from differences in how listeners selectively attend to and rely on the distinguishing features of talker voices than from differences in internal noise that cause errors in the chain of auditory processing. Future studies, of course, will be needed to determine whether these results generalize to conditions more closely approximating real-world, cocktail-party listening. Until then, the data hold out promise for the development of models for predicting individual differences in the cocktail-party effect not anticipated based on conventional audiometric testing.