A simple but complex enough $\theta$-SIR type model to be used with COVID-19 real data. Application to the case of Italy

Abstract

Since the start of the COVID-19 pandemic in China many models have appeared in the literature, trying to simulate its dynamics. Focusing on modeling the biological and sociological mechanisms which influence the disease spread, the basic reference example is the SIR model. However, it is too simple to be able to model those mechanisms (including the three main types of control measures: social distancing, contact tracing and health system measures) to fit real data and to simulate possible future scenarios. A question, then, arises: how much and how do we need to complexify a SIR model? We develop a $\theta$-SEIHQRD model, which may be the simplest one satisfying the mentioned requirements for arbitrary territories and can be simplified in particular cases. We show its very good performance in the Italian case and study different future scenarios.

1. Introduction

The outbreak of novel coronavirus disease 2019 (COVID-19) continues to spread rapidly around the world [1]. Originated in Wuhan in central China, where it was already active at the beginning of December 2019, reached multiple countries in merely a month until it became a pandemic as of 11 March 2020 [2] when the disease was confirmed in more than 118,000 cases reported globally in 114 countries.

Although some authors (see, e.g., [3]) propose SEIR type models with little variations, COVID-19 is a disease caused by a new virus and needs a model taking into account its known specific characteristics. In particular, it would be convenient to develop a model which satisfies the following: (a) includes the biological and sociological mechanisms influencing the disease spread, (b) its parameters have a clear interpretation in terms of those mechanisms (such as a contact rate, fatality ratios, duration of infection, etc.), and (c) incorporates

• •the effect of undetected infected people (see [4]), being able to show the dependence of the impact of COVID-19 on the percentage of detected cases over the real total infected cases,
• •the effect of different infectiousness conditions of hospitalized people (differentiating those with mild and severe conditions that will recover from those who will finally die),
• •the estimation of the needs of beds in hospitals (which is one of the major problems for policy makers addressing COVID-19),
• •the effect of different control measures.

Some of the models that appeared at the beginning of the pandemic, especially for the study of the first wave (see [3], [4], [5], [6]), do not incorporate all the special characteristics (undetected cases, undetected deaths, quarantine, social distancing, etc.) of the COVID-19 pandemic. Some of them are very complex in terms of the number of compartments and connections between them, trying to simulate many details that could probably be neglected. Furthermore, after developing a model, it would be desirable to check how it fits real data and to use it in order to study future scenarios with different control measures (here, we consider social distancing, contact tracing and health system measures).

This paper does not take into account the possibility of resusceptibility as it is done, for example, in [7]. This is due to the fact that the number of confirmed reinfections is still not relevant enough compared with the total figures of the pandemic. According to [8], only 27 cases of reinfection were documented worldwide when it was written. Furthermore, the webpage https://bnonews.com/index.php/2020/08/covid-19-reinfection-tracker/ reports an updated list of reinfections, with a total of 31 cases, at the time we wrote this article.

In [9], a disease contact rate ($\beta$) and $R_0$ with different values before and after lockdown of countries are considered and applied in a SEIR type model for the confirmed cases tested with several countries. The model presented here allows to model not only confirmed cases but also deaths, hospitalized and recovered by considering different values of $\beta$ that depend on the particular control measures for every time period.

Concerning the particular case of Italy, some studies have dealt with its particular situation, such as [10], [11], [12] and [13]. It is important to note that all the models presented in these works only serve the particular case of Italy, and are not general models applicable to other countries.

The paper [10] is an initial work published in mid-March 2020, which highlights the importance of this pandemic and the serious consequences it can have in countries like Italy where data show rapid progress in infections, which can cause a health system collapse due to the lack of beds in hospitals and ICU posts. The data are fitted using an exponential type model, which is not realistic for long-term modeling, although it allows a wake-up call to the country’s health authorities.

In [11], the distribution in terms of mobility is also studied through a network of the different Italian regions. It is confirmed the effectiveness at a regional level of the national lockdown strategy and proposed coordinated regional interventions to prevent future national lockdowns. However, asymptomatic patients are not considered.

In [12], a geographical model is presented to describe the number of daily cases, hospitalized and deaths within the Italian regions for the first month of the disease and study the effects of drastic measures for transmission containment. Authors concentrate on estimating the effects of severe progressive restrictions posed to human mobility and human-to-human contacts in Italy. As a novelty, a presymptom compartment is considered. The proposed model is extended and further developed in [13], where the effect of mobility between regions and provinces within Italy is also considered, taking into account the control measures at all times to describe the variable of new hospitalizations. The number of people who have to be isolated in each region is calculated to avoid a drastic growth in the number of infected. This model is very interesting, because it incorporates the variable of mobility between regions, but only the number of new hospitalizations is described, without studying the number of deaths since they focus on the implications of the relaxation of confinement measures.

An interesting model appearing in [5], tested for the case of Italy, has some similarities with the one presented here, but there are some important differences to be remarked. First of all, the model we propose is a general one that may be used with any country or region, just considering the correspondent data, whereas the model in [5] seems to be defined for the particular case of the first wave in Italy, although it could be adapted to other territories. Secondly, our model considers the compartment for people in quarantine ($Q$, detected asymptomatic or with mild symptoms, infectious people) that is not the same as the proposed compartment for diagnosed ($D$, asymptomatic infected, detected) in the former model, which is even connected to the possibility of dying. Moreover, the general role of the undetected people in our model is completely different and some of them can even die (those who are in $I_{D_{\mathrm{u}}}$).

In this paper, we develop a general deterministic epidemiological model able to simulate the biological and sociological COVID-19 mechanisms in different territories, to fit real data, and to simulate different future scenarios of control measures. The choice of using a deterministic model instead of a stochastic one is done as a first approach, since such kind of models present some advantages, such as: a low computational complexity allowing a better calibration of the model parameters or the possibility of using the theory of ordinary differential equations for suitably analyzing and interpreting the model. Furthermore, according to [14], deterministic models should be the first tool to be used when modeling a new problem. The authors of that work also note that the stochastic models are not suitable when it is difficult or impossible to determine the probability distribution, are difficult to analyze and require more data for the calibration of the model. We note that, although we use a deterministic model, we must deal with some probabilistic processes. In those cases, random values are substituted by their expected values.

We look for the simplest model, having the minimum complexity to take into account all the main non-negligible processes of this pandemic. When simulating the dynamics of the COVID-19 disease in a territory, our model can be used in its full general form or in simplified particular versions of it, depending on the way the territory deals with the pandemic. Of course, the model may be modified by introducing age structure, stochasticity, levels of uncertainty, mobility between territories, spatial structure (see, e.g., [15]), etc. in order to focus in special features of the pandemic or to refine some results.

The reference epidemiological model is the SIR one, which divides the population of a territory in three compartments: Susceptible ($S$), Infectious ($I$) and Recovered ($R$). For the COVID-19 pandemic these three compartments are not enough. First of all, the incubation period for the new coronavirus SARS-CoV-2 is between 5 and 6 days (see [16]), which is important to incorporate in the model by means of a compartment for Exposed ($E$) people. Secondly, estimation of needs of beds in hospital is important for policy makers, which implies the convenience of suitable compartments for people in Hospitals ($H$), following a compartment ($I$) for an initial stage of the infectious period. Moreover, the disease contact rates inside and outside hospitals are usually different. Thirdly, one of the main data reported each day is the number of Deaths ($D$), which deserves another compartment and makes convenient to split $H$ in two branches, one for people in hospital that will recover ($H_R$) and the other one for people in hospital that will die ($H_D$). Therefore, we need, at least, a SEIHRD model.

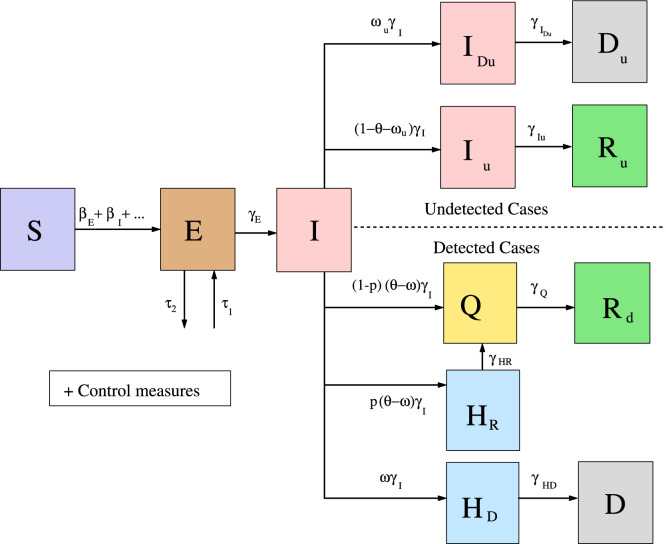
Furthermore, one of the characteristics of COVID-19 is the existence of undetected infectious cases, either because they are asymptomatic (see [4]) or because, even if they have symptoms, the corresponding country/territory does not have enough tests to check the infectiousness or the health system is saturated. In order to be able to consider the impact of this COVID-19 characteristic, two different branches should distinguish between detected and undetected cases and deaths. This can be done in terms of the instantaneous ratio $\theta \left(t\right)$ of new detected infectious cases per unit time over the total (detected and undetected) new infectious cases per unit time, generating the corresponding $\theta$-SEIHRD model. As done previously with people in hospital, a distinction can be done between the undetected infectious people (compartment $I_{\mathrm{u}}$) that will recover (compartment $R_{\mathrm{u}}$) and the undetected infectious people (compartment $I_{D_{\mathrm{u}}}$) that will die (compartment $D_{\mathrm{u}}$). Finally, some territories (like Italy) use a quarantine period (typically at home) for people leaving the hospital and for detected asymptomatic (or with mild symptoms) infectious people, which makes necessary a new compartment (Q), which completes the full $\theta$-SEIHQRD general model. A diagram summarizing the model is given in Fig. 1.

Fig. 1.

Diagram summarizing the model for COVID-19 given by system (1).

A detailed description and discussion of the model, its parameters and outputs is provided in Sections 2, 3 . We point out that all the parameters in the model have well-understood epidemiological interpretations such as average duration of incubation period, contact rates, etc. In Section 2, we also show some of the outputs of the model and how to compute them. Particular outputs of interest for epidemiologists are the computation of the associated basic reproduction number and the evolution of the effective reproduction number.

Once we have developed the model, the question is how to use it with real cases. Let us suppose we want to use it to study the dynamics of the COVID-19 in a particular territory. Three steps can be followed:

• 1.The first thing is to decide if all the compartments are necessary, or only some of them. For instance, in China and Senegal all infected people are treated in hospitals (or other kind of health facilities) and, therefore, compartment $Q$ is not necessary [6]. However, other territories, like Italy or Spain, use the quarantine at home for infected people with very mild symptoms or not symptoms at all. Other possibilities of simplifying the model are also possible, for particular territories.
• 2.After deciding the compartments that will be used with a particular territory, the following step is to choose the parameters involved in the model. To do that we use values given in the literature (as the duration of the incubation period), parametrization of functions involved in the model and a multiobjective technique, to identify parameters. In Section 3 we explain how to do it. This is, actually, part of the validation process, consisting in comparing the results of the simulations (run with the chosen parameters) with the available data about the impact of the pandemic in the territory under study. Typically, a good fitting of simulations outputs to official temporal series (of cases, deaths, people in hospital, etc.) is necessary.
• 3.Finally, if the validation process is successful, we can simulate different future scenarios to study the efficiency of some control measures (being increased or relaxed), the impact of the undetected cases in the dynamics of the pandemic, etc.

In Section 4, we illustrate those three steps with the particular case of Italy.

2. Mathematical formulation of the model

In this section we give a detailed description of the $\theta$-SEIHQRD model that we propose for the COVID-19. Then, we described some outputs of the model that will be used in the numerical experiments performed in Section 4.

2.1. The mathematical model

According to the known characteristics of the COVID-19 pandemic, we assume that each person is in one of the following compartments (see [17], [18], [19], [20]):

• •Susceptible (denoted by $S$): The person is not infected by the disease pathogen.
• •Exposed (denoted by $E$): The person is in the incubation period after being infected by the disease pathogen, and has no clinical signs. This stage is also called presymptomatic period. According to the available literature (see, e.g., [17]), there exist some evidences that a presymptomatic person could infect other people but with a lower probability than people in the infectious compartments. After the incubation period, the person passes to the Infectious compartment $I$.
• •Infectious (denoted by $I$): After the incubation period, it is the first compartment of the infectious period, where nobody is expected to be detected yet. The person has finished the incubation period and may infect other people (even if he/she is asymptomatic, see, e.g., [19]). After this period, people in this compartment can be, either taken in charge by health authorities (and we classify them as hospitalized or quarantine, according to the severity of their symptoms), or not detected by authorities and continue as infectious (but in another compartment, $I_{\mathrm{u}}$ or $I_{{\mathrm{D}}_{\mathrm{u}}}$).
• •Infectious but undetected that will survive the disease (denoted by $I_{\mathrm{u}}$): After being in the compartment $I$, the person can still infect other people but is not detected and is not reported by authorities. We assume that only asymptomatic infected people or those with low or medium symptoms can reach this compartment, not the people who will die. After this period, people in this compartment survive the disease and pass to the Recovered compartment $R_{\mathrm{u}}$.
• •Infectious but undetected that will die (denoted by $I_{D_{\mathrm{u}}}$): After being in the compartment $I$, the person can still infect other people, have clinical signs but not be detected and reported by authorities. We assume that a person in this state is part of a population that is highly vulnerable to the COVID-19 (such as people in retirement homes) and will die quickly without being treated in hospital. After being in this state, a person passes to the compartment $D_{\mathrm{u}}$.

  We remark that vulnerable people died outside hospitals during the first wave of the pandemic in some countries (such as Italy or Spain; see [21], [22], [23], [24], [25]). Indeed, due to the saturation of the whole health system (mainly because of lack of beds and/or healthcare workers), this vulnerable population did not receive adequate medical cares and quickly died before being hospitalized. In some of those countries (such as Italy, see [21], [22]), a few a-posteriori estimations of the number of people dead due to COVID-19 and not detected have been reported by authorities or other organizations and, currently, efforts are made to avoid reproducing this extreme situation (see [25]). Regarding those few data and for the sake of simplicity of the model, we have decided to model people who have suffered this situation by using the specific compartment $I_{D_{\mathrm{u}}}$. We note that the results reported later in Section 4 indicate that this choice is adequate.

• •Quarantine (denoted by $Q$): The person is in quarantine at home or some special facilities (different from hospitals) during a fixed period.

  For example, according to [26], [27], the isolation is performed in one room, always wearing mask at home, etc. to reduce the risk of transmission to cohabiting people. Of course, infection could occur between people in the same home, but this is usually before entering the quarantine period (i.e., while being in the compartment $I$) and the model takes that into account. Furthermore, according to [5], transmission between people in quarantine at home (thus, aware of their infection) and other person (including cohabiting persons) is severely limited.

  Therefore, in this work we assume that a person in compartment $Q$ cannot infect other people (although other possibilities are also easy to include, as explained below) and at the end of this state passes to the compartment $R_{\mathrm{d}}$. The use of this compartment in the model depends on the strategy of each territory (some of them do not use this control strategy).

• •Hospitalized that will recover (denoted by $H_R$): The person is in hospital and (according to [5], [28], [29]) can still infect other people (in particular healthcare workers). At the end of this state, a person passes to the compartment $Q$ (if implemented in the territory under study; otherwise the person passes directly to the compartment $R_{\mathrm{d}}$).
• •Hospitalized that will die (denoted by $H_D$): The person is hospitalized and can still infect other people. At the end of this state, a person passes to the compartment $D$.
• •Dead by COVID-19 (denoted by $D$) after being at hospital.
• •Dead by COVID-19 but undetected (denoted by $D_{\mathrm{u}}$): The person has not survived the disease and the death was not classified by authorities as caused by COVID-19.
• •Recovered after being previously detected as infectious (denoted by $R_{\mathrm{d}}$): The person was previously detected as infectious, survived the disease, passed the quarantine period (if implemented in the territory under study), is no longer infectious and has developed a natural immunity to the virus. Although some cases of reinfection are known, following [18], they seem to be isolated cases; thus, despite the fact that the evolution of this immunity is unknown for a longer period of time, we make the natural immunity assumption. However, it can be modified if new findings regarding this topic are found.
• •Recovered after being previously infectious but undetected (denoted by $R_{\mathrm{u}}$): The person was not previously detected as infectious, survived the disease, is no longer infectious and has developed a natural immunity to the virus (with similar assumptions as above).

We remark that, in this work, we work with two compartments, namely $H_R$ and $H_D$ described previously, to model the dynamics of the number of people in hospital. One may note that a more detailed classification of hospitalization could be considered (for instance, according to the severity of the symptoms, the availability of medical material or beds, etc.) to give more recommendations to decision makers. This could be done by introducing additional compartments to the model. However, this would require the use of detailed data regarding people in hospital which, to the best of our knowledge, are not publicly available for most of the countries (in particular, Italy). Furthermore, adding more compartments will complexify deeply the model, making difficult the parameter estimation process. For those reasons, we decided to use two compartments. We highlight the fact that the results reported in Section 4 (see Fig. 2) indicate that this choice is reasonable as the model estimates quite well the reported data related to people in hospital (which are, for the case of Italy, the number of people in hospital, without any specific classification).

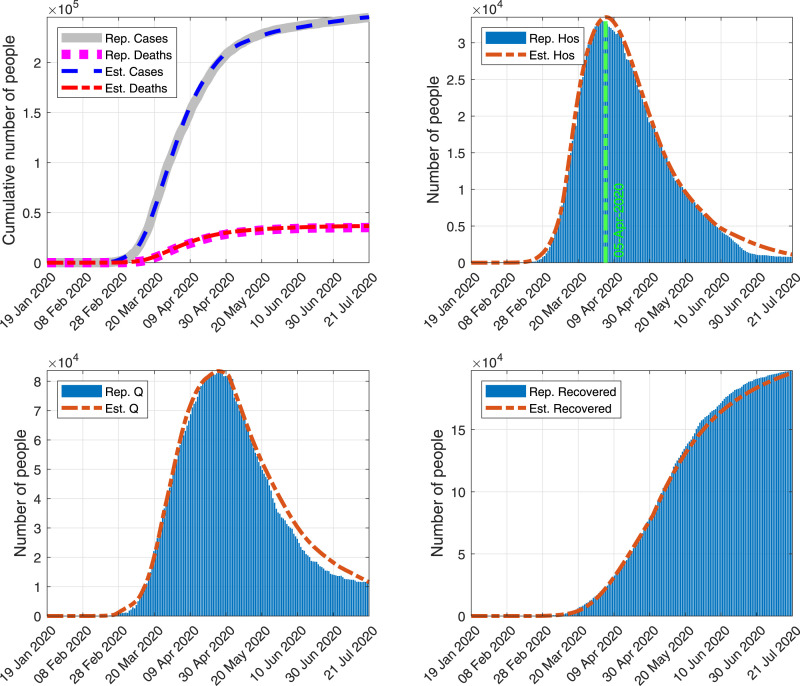
Fig. 2.

Comparison of some of the outputs of the simulation run with $\omega =1.4555\text{\%}$ (Est.) and the Italian official reported data (Rep.). Top-left: Cumulative number of cases and deaths. Top-right: People in hospital. Bottom-left: People in quarantine. Bottom-right: Cumulative number of recovered people.

The authorities may apply various control measures in order to control the COVID-19 spread (see [30]):

• •Isolation: Infected people are isolated from contact with other people. Only health professionals are in contact with them. However, infection of those professionals also occurs (see [16]). Isolated patients receive an adequate medical treatment that reduces the COVID-19 fatality rate.
• •Lockdown areas: Movement of people in areas with a high number of infected people may be restricted and controlled, to avoid the spread of the disease.
• •Contact tracing: The objective of tracing is to identify potential infectious contacts which may have infected a person or spread COVID-19 to other people. Increase the number of tests in order to increase the percentage of detected infected people.
• •Increase of health system resources: The number of operational beds and personal available to detect and treat affected people is increased, producing a decrease in the length of the infectious period for the compartment $I$.

The model is used to evaluate the spread of a human disease within a considered territory during a fixed time interval.

At the beginning of the simulation, the model parameters are set by the user (as shown below). We can start our simulation at any initial time $t_0\ge 0$, considering that only susceptible people live in the territories that are free of the disease, whereas the number of people in compartments $S$, $E$, $I$, $I_{\mathrm{u}}$, $I_{D_{\mathrm{u}}}$, $H_R$, $H_D$, $R_{\mathrm{d}}$, $R_{\mathrm{u}}$, $D$ and $D_{\mathrm{u}}$ of the infected territories are set to their corresponding values. Then, for the time interval $[t_0,t_0+T_{max}]$, with $T_{max}\in \mathrm{I}\mathrm{N}$ being the maximum number of simulation days, the model is applied. If at the end of a simulation day $t$ there is less than 1 person in each compartment $E$, $I$, $I_{\mathrm{u}}$, $I_{D_{\mathrm{u}}}$, $H_R$ and $H_D$ in all the territory, the simulation is stopped. Else, the simulation is stopped when $t=t_0+T_{max}$. Furthermore, the control measures are also implemented and they can be activated or deactivated, when starting the model, in order to quantify their effectiveness to reduce the magnitude and duration of the COVID-19 pandemic in the territory under study.

A diagram summarizing the main structure of our full model is presented in Fig. 1.

We assume that people in a territory are characterized to be in one of the compartments described above: $S$, $E$, $I$, $I_{\mathrm{u}}$, $I_{D_{\mathrm{u}}}$, $H_R$, $H_D$, $Q$, $R_{\mathrm{d}}$, $R_{\mathrm{u}}$, $D_{\mathrm{u}}$ or $D$. For the sake of simplicity, we assume that, at each time, the population inside a territory is homogeneously distributed. Thus, the spatial distribution of the epidemic inside a territory is omitted (it can be taken into account by dividing some territories into a set of smaller regions with similar characteristics). Since the natural natality and mortality (not from COVID-19) do not seem to be important factors for COVID-19 (at least for relatively short periods of time), they are omitted in the model (actually, they can be readily included, if necessary).

In this work we will only consider the within-country/territory disease spread of one territory where, starting from suitable values of $t_0$, the COVID-19 pandemic is already spreading by its own, with a relatively negligible dependence on the movement of people in/out of this territory. The between-country/territory disease spread may be also taken into account in the model following the approach developed in [15] with the Be-CoDiS model.

There are some studies about the relevance of humidity and temperature for the spread of COVID-19. In [31], it is shown that the observed patterns of COVID-19 are not completely consistent with the hypothesis that high absolute humidity may limit the survival and transmission of this virus. Furthermore, in [32] it has been found that the lower is the temperature, the greater is the survival period of the SARS-CoV-2 outside the host. Since there is no clear scientific evidence of the effect of the humidity and the temperature on the SARS-CoV-2, we have not included these two factors in our model (this would need to be revised in case of appearing new findings regarding this topic).

Under those assumptions, the evolution of the compartments mentioned above is modeled by the following system of ordinary differential equations:

$$\begin{array}{ccc}\dot{S}\hfill & \hfill =\hfill & -\frac{S}{N}\left({\beta }_{E}E+{\beta }_{I}I+{\beta }_{I_{\mathrm{u}}}{I}_{\mathrm{u}}+{\beta }_{I_{D_{\mathrm{u}}}}{I}_{D_{\mathrm{u}}}+{\beta }_{H_R}{H}_R+{\beta }_{H_D}{H}_D\right),\hfill \\ \dot{E}\hfill & \hfill =\hfill & \frac{S}{N}\left({\beta }_{E}E+{\beta }_{I}I+{\beta }_{I_{\mathrm{u}}}{I}_{\mathrm{u}}+{\beta }_{I_{D_{\mathrm{u}}}}{I}_{D_{\mathrm{u}}}+{\beta }_{H_R}{H}_R+{\beta }_{H_D}{H}_D\right)-{\gamma }_{E}E+{\tau }_1-{\tau }_2,\hfill \\ \dot{I}\hfill & \hfill =\hfill & {\gamma }_{E}E-{\gamma }_{I}I,\hfill \\ {\dot{I}}_{\mathrm{u}}\hfill & \hfill =\hfill & (1-\theta -{\omega }_{\mathrm{u}}){\gamma }_{I}I-{\gamma }_{I_{\mathrm{u}}}{I}_{\mathrm{u}},\hfill \\ {\dot{I}}_{D_{\mathrm{u}}}\hfill & \hfill =\hfill & {\omega }_{\mathrm{u}}{\gamma }_{I}I-{\gamma }_{I_{D_{\mathrm{u}}}}{I}_{D_{\mathrm{u}}},\hfill \\ {\dot{H}}_R\hfill & \hfill =\hfill & p(\theta -\omega ){\gamma }_{I}I-{\gamma }_{H_R}{H}_R,\hfill \\ {\dot{H}}_D\hfill & \hfill =\hfill & \omega {\gamma }_{I}I-{\gamma }_{H_D}{H}_D,\hfill \\ \dot{Q}\hfill & \hfill =\hfill & \left(1-p\right)(\theta -\omega ){\gamma }_{I}I+{\gamma }_{H_R}{H}_R-{\gamma }_{Q}Q,\hfill \\ {\dot{R}}_{\mathrm{d}}\hfill & \hfill =\hfill & {\gamma }_{Q}Q,\hfill \\ {\dot{R}}_{\mathrm{u}}\hfill & \hfill =\hfill & {\gamma }_{I_{\mathrm{u}}}{I}_{\mathrm{u}},\hfill \\ {\dot{D}}_{\mathrm{u}}\hfill & \hfill =\hfill & {\gamma }_{I_{D_{\mathrm{u}}}}{I}_{D_{\mathrm{u}}}.\hfill \\ \dot{D}\hfill & \hfill =\hfill & {\gamma }_{H_D}{H}_D.\hfill \end{array}$$ (1)

In this system we have used, as stated above, that people in compartment $Q$ cannot infect other people. To include the possibility of infection, we would only need to add the term ${\beta }_{Q}Q$ inside the parenthesis of the first two equations.

In (1):

• •$N$ is the number of people in the territory before the start of the pandemic.
• •
  $\omega \left(t\right)\in [0,1]$ is the instantaneous infection detected fatality ratio (iIdFR) in the territory, at time $t$: the proportion of new detected people (after being in compartment $I$) that will die of COVID-19 after $\frac{1}{{\gamma }_{H_D}\left(t\right)}$ days, per unit time, compared to the total number of new infectious people (detected or undetected), per unit time. More precisely,

  $$\omega \left(t\right)=\frac{\dot{D}(t+\frac{1}{{\gamma }_{H_D}\left(t\right)})}{{\dot{c}}_{\mathrm{m}}\left(t\right)+{\dot{c}}_{\mathrm{m,u}}\left(t\right)}=\frac{{\gamma }_{H_D}(t+\frac{1}{{\gamma }_{H_D}\left(t\right)})H_D(t+\frac{1}{{\gamma }_{H_D}\left(t\right)})}{{\gamma }_I\left(t\right)I\left(t\right)},$$

  where $c_{\mathrm{m}}\left(t\right)$ (respectively, $c_{\mathrm{m,u}}\left(t\right)$) is the model cumulative number of COVID-19 detected (respectively, undetected) cases at day $t$ (see more details about them below, when describing the outputs of the model).
• •
  ${\omega }_{\mathrm{u}}\left(t\right)\in [0,1]$ is the instantaneous infection undetected fatality ratio (iIuFR) in the territory, at time $t$: the proportion of new undetected people (after being in compartment $I$) that will die of COVID-19 after $\frac{1}{{\gamma }_{I_{D_{\mathrm{u}}}\left(t\right)}}$ days, per unit time, compared to the total number of new infectious people (detected or undetected), per unit time. More precisely,

  $${\omega }_{\mathrm{u}}\left(t\right)=\frac{{\dot{D}}_{\mathrm{u}}(t+\frac{1}{{\gamma }_{I_{D_{\mathrm{u}}}}\left(t\right)})}{{\dot{c}}_{\mathrm{m}}\left(t\right)+{\dot{c}}_{\mathrm{m,u}}\left(t\right)}.$$

  We point out that $\omega \left(t\right)+{\omega }_{\mathrm{u}}\left(t\right)\in [0,1]$ is the instantaneous infection fatality ratio (iIFR), at time $t$: the proportion of new (detected or undetected) people (after being in compartment I) that will die of COVID-19, per unit time, compared to the total number of new infectious people (detected or undetected), per unit time. This value is closely related to the IFR defined below (see the Results section). Actually, if it is assumed that the number of total deaths is proportional to the number of total cases, then IFR is, essentially, $\omega +{\omega }_{\mathrm{u}}$.

• •
  $\theta \left(t\right)\in [\omega \left(t\right),1-{\omega }_{\mathrm{u}}\left(t\right)]\subset [0,1]$ is the proportion of the number of new infectious people that are detected and documented by the authorities (after being in compartment $I$), per unit time, compared to the total number of new infectious people (detected or undetected), per unit time, at time $t$. More precisely,

  $$\theta \left(t\right)=\frac{{\dot{c}}_{\mathrm{m}}\left(t\right)}{{\dot{c}}_{\mathrm{m}}\left(t\right)+{\dot{c}}_{\mathrm{m,u}}\left(t\right)}.$$

  We point out that

  $$\frac{\omega \left(t\right)}{\theta \left(t\right)}=\frac{\dot{D}(t+\frac{1}{{\gamma }_{H_D}\left(t\right)})}{{\dot{c}}_{\mathrm{m}}\left(t\right)}\in [0,1]$$

  is the instantaneous case fatality ratio (iCFR), at time $t$: the proportion of the number of new detected people (after being in compartment $I$) that will die of COVID-19 after $\frac{1}{{\gamma }_{H_D}\left(t\right)}$ days, per unit time, compared to the number of new detected people (after being in compartment I), per unit time.

  This value is closely related to the Case Fatality Ratio (CFR) defined as the expected value of the probability of dying for a person who is infected and detected, i.e. the number of detected deaths due to the virus over the number of detected infections. Actually, if it is assumed that the number of detected deaths is proportional to the number of detected cases, then CFR is, essentially, $\frac{\omega }{\theta }$.

• •${\beta }_E,{\beta }_I,{\beta }_Q,{\beta }_{I_{\mathrm{u}}},{\beta }_{I_{D\mathrm{u}}},{\beta }_{H_R},{\beta }_{H_D}\in [0,\infty )$ are the disease contact rates (day⁻¹) of a person in the respective compartments. They may change with time, due to the control measures.
• •${\gamma }_I\left(t\right)\in (0,+\infty )$ is the transition rate (day⁻¹) from compartment $I$ to compartments $I_{\mathrm{u}}$, $I_{D_{\mathrm{u}}}$, $Q$, $H_R$ or $H_D$, at time $t$. Similarly, ${\gamma }_E,{\gamma }_{I_{\mathrm{u}}}\left(t\right),{\gamma }_{I_{D_{\mathrm{u}}}}\left(t\right),{\gamma }_Q\left(t\right),{\gamma }_{H_R}\left(t\right)$, and ${\gamma }_{H_D}\left(t\right)\in (0,+\infty )$ denote the transition rates (day⁻¹) from compartments $E$, $I_{\mathrm{u}}$, $I_{D_{\mathrm{u}}}$, $Q$, $H_R$ and $H_D$ to compartments $I$, $R_{\mathrm{u}}$, $D_{\mathrm{u}}$, $R_{\mathrm{d}}$, $Q$ and $D$, respectively, at time $t$. For some particular territories, some compartments could be excluded from the model.
• •$p$ is the ratio of the number of new detected infected people that will survive the disease and are hospitalized (they go to compartment $H_R$) over the total number of new detected infected people that will survive the disease (and may also do quarantine, compartment $Q$, without going to hospital).
• •${\tau }_1\left(t\right)$ and ${\tau }_2\left(t\right)$ are the people infected that arrive/leave from/to other territories, per day. Both can be modeled following the between-country spread part of the Be-CoDiS model described in [15]. For the sake of simplicity, we have included those terms only in the second equation, corresponding to compartment $E$, but they could be included in the equations for other compartments too. When a discrete sequence of imported/exported infections is known it can be included in the numerical resolution of the system by simple addition/removal to/from the suitable compartment, at the corresponding discrete time.

System (1) is completed with initial data $S\left(t_0\right)$, $E\left(t_0\right)$, $I\left(t_0\right)$, $I_{\mathrm{u}}\left(t_0\right)$, $I_{D_{\mathrm{u}}}\left(t_0\right)$, $Q\left(t_0\right)$, $H_R\left(t_0\right)$, $H_D\left(t_0\right)$, $R_{\mathrm{d}}\left(t_0\right)$, $R_{\mathrm{u}}\left(t_0\right)$, $D_{\mathrm{u}}\left(t_0\right)$ and $D\left(t_0\right)$ given in $[0,\infty )$. These values must be non-negative and $S\left(t_0\right)+E\left(t_0\right)+I\left(t_0\right)+I_{\mathrm{u}}\left(t_0\right)+I_{D_{\mathrm{u}}}\left(t_0\right)+Q\left(t_0\right)+H_R\left(t_0\right)+H_D\left(t_0\right)+R_{\mathrm{d}}\left(t_0\right)+R_{\mathrm{u}}\left(t_0\right)+D_{\mathrm{u}}\left(t_0\right)+D\left(t_0\right)=N$. It is standard (see, e.g., [33], [34]) to prove that $S\left(t\right)$, $E\left(t\right)$, $I\left(t\right)$, $I_{\mathrm{u}}\left(t\right)$, $I_{D_{\mathrm{u}}}\left(t\right)$, $Q\left(t\right)$, $H_R\left(t\right)$, $H_D\left(t\right)$, $R_{\mathrm{d}}\left(t\right)$, $R_{\mathrm{u}}\left(t\right)$, $D_{\mathrm{u}}\left(t\right)$ and $D\left(t\right)$ are non-negative and $S\left(t\right)+E\left(t\right)+I\left(t\right)+I_{\mathrm{u}}\left(t\right)+I_{D_{\mathrm{u}}}\left(t\right)+Q\left(t\right)+H_R\left(t\right)+H_D\left(t\right)+R_{\mathrm{d}}\left(t\right)+R_{\mathrm{u}}\left(t\right)+D_{\mathrm{u}}\left(t\right)+D\left(t\right)=N$, for all $t\ge t_0$.

We remark that system (1) is an epidemic-type model (as described, e.g., in [35]), which is not trying to capture endemic behaviors. Actually, there is no incoming flux in the Susceptible compartment; therefore, the fate of every individual will be either staying susceptible, recovering or dying. This means there are no endemic equilibria in our system; on the contrary, there exists a manifold $S+R_{\mathrm{d}}+R_{\mathrm{u}}+D_{\mathrm{u}}+D=N$ containing infinite disease-free equilibrium points.

We point out that the 8th, 9th, 10th, 11th and 12th equations of system (1) are not coupled with the other equations. Thus, we can solve the first seven equations of that system and the solution of the last five ones can be computed as follows: $Q$ is the solution of the 8th equation of system (1), which is a linear ordinary differential equation (we do not include here the easy corresponding explicit solution, for the sake of simplicity) and

$$D\left(t\right)=D\left(t_0\right)+{\int }_{t_0}^t{\gamma }_{H_D}\left(s\right)H_D\left(s\right)\mathrm{d}s,$$

$$D_{\mathrm{u}}\left(t\right)=D_{\mathrm{u}}\left(t_0\right)+{\int }_{t_0}^t{\gamma }_{I_{D_{\mathrm{u}}}}\left(s\right)I_{D_{\mathrm{u}}}\left(s\right)\mathrm{d}s,$$

$$R_{\mathrm{d}}\left(t\right)=R_{\mathrm{d}}\left(t_0\right)+{\int }_{t_0}^t{\gamma }_Q\left(s\right)Q\left(s\right)\mathrm{d}s,$$

$$R_{\mathrm{u}}\left(t\right)=R_{\mathrm{u}}\left(t_0\right)+{\int }_{t_0}^t{\gamma }_{I_{\mathrm{u}}}\left(s\right)I_{\mathrm{u}}\left(s\right)\mathrm{d}s.$$

It is important to remark that, if for some territory the model does not include the compartment $Q$, then $p=1$, ${\dot{R}}_{\mathrm{d}}={\gamma }_{H_R}{H}_R$ and

$$R_{\mathrm{d}}\left(t\right)=R_{\mathrm{d}}\left(t_0\right)+{\int }_{t_0}^t{\gamma }_{H_R}\left(s\right)H_R\left(s\right)\mathrm{d}s.$$

For the numerical simulations presented in this paper, the first eight equations of system (1) were numerically solved with the classic 4th order Runge–Kutta method with four stages (RK4) and with four hours as time step (which was tested to see that it is suitable to get stable results).

2.2. Outputs of the model

Here, we present some of the outputs that can be obtained from the mathematical model, used to analyze the results of the simulations:

• •
  $c_{\mathrm{m}}\left(t\right)$: The model cumulative number of COVID-19 detected cases at day $t$, which is given by

  $$c_{\mathrm{m}}\left(t\right)=H_R\left(t\right)+H_D\left(t\right)+Q\left(t\right)+R_{\mathrm{d}}\left(t\right)+D\left(t\right),$$

  and can be also computed as follows:

  $$c_{\mathrm{m}}\left(t\right)=c_{\mathrm{m}}\left(t_0\right)+{\int }_{t_0}^t\frac{\mathrm{d}}{\mathrm{d}t}\left(H_R\left(s\right)+H_D\left(s\right)+Q\left(s\right)+R_{\mathrm{d}}\left(s\right)+D\left(s\right)\right)\mathrm{d}s=c_{\mathrm{m}}\left(t_0\right)+{\int }_{t_0}^t\theta \left(s\right){\gamma }_I\left(s\right)I\left(s\right)\mathrm{d}s.$$
• •
  $c_{\mathrm{m,n}}\left(t\right)$: The number of new cases per day at day $t$, which is given by

  $$c_{\mathrm{m,n}}\left(t\right)=\theta \left(t\right){\gamma }_I\left(t\right)I\left(t\right).$$
• •
  $h_{\mathrm{m}}\left(t\right)$: The model cumulative number of COVID-19 detected infected healthcare workers at day $t$, which is given by

  $$h_{\mathrm{m}}\left(t\right)=h_{\mathrm{m}}\left(t_0\right)+{\int }_{t_0}^t\frac{S\left(s\right)}{N}\left({\beta }_{H_R}\left(s\right)H_R\left(s\right)+{\beta }_{H_D}\left(s\right)H_D\left(s\right)\right)\mathrm{d}s.$$
• •
  $c_{\mathrm{m,u}}\left(t\right)$: The model cumulative number of COVID-19 undetected cases at day $t$, which is given by

  $$c_{\mathrm{m,u}}\left(t\right)=E\left(t\right)+I\left(t\right)+I_{\mathrm{u}}\left(t\right)+I_{D_{\mathrm{u}}}\left(t\right)+R_{\mathrm{u}}\left(t\right)+D_{\mathrm{u}}\left(t\right),$$

  and can be also computed as follows:

  $$c_{\mathrm{m,u}}\left(t\right)=E\left(t\right)+I\left(t\right)+I_{\mathrm{u}}\left(t_0\right)+I_{D_{\mathrm{u}}}\left(t_0\right)+R_{\mathrm{u}}\left(t_0\right)+D_{\mathrm{u}}\left(t_0\right)+{\int }_{t_0}^t\frac{\mathrm{d}}{\mathrm{d}t}\left(I_{\mathrm{u}}\left(s\right)+I_{D_{\mathrm{u}}}\left(s\right)+R_{\mathrm{u}}\left(s\right)+D_{\mathrm{u}}\left(s\right)\right)\mathrm{d}s=E\left(t\right)+I\left(t\right)+I_{\mathrm{u}}\left(t_0\right)+I_{D_{\mathrm{u}}}\left(t_0\right)+R_{\mathrm{u}}\left(t_0\right)+D_{\mathrm{u}}\left(t_0\right)+{\int }_{t_0}^t(1-\theta \left(s\right)){\gamma }_I\left(s\right)I\left(s\right)\mathrm{d}s.$$
• •$d_{\mathrm{m}}\left(t\right)$: The model cumulative number of detected deaths (due to COVID-19), at day $t$, which is given by $D\left(t\right)$.
• •$d_{\mathrm{m,u}}\left(t\right)$: The model cumulative number of undetected deaths, at day $t$, which is given by $D_{\mathrm{u}}\left(t\right)$.
• •
  R${}_{\mathrm{e}}$: The effective reproduction number of COVID-19. It is defined as the number of cases that one infected person generates, on average, over the course of its infectious period [36]. Part of the population can be already infected and/or control measures may have been implemented. It depends on the considered territory and changes during the spread of the disease. Furthermore, if at time $t=0$ no control measures have been applied, R${}_{\mathrm{e}}\left(0\right)=$ R${}_0$, where $R_0$ is the basic reproduction number of COVID-19, which is defined as the number of cases that one infected person generates on average over the course of its infectious period, in an otherwise uninfected population and without special control measures. Typically, the spread of the disease slows down when R${}_{\mathrm{e}}\left(t\right)<1$. Taking into account this definition, for cases with constant transition rates we propose the following non-classical estimation:

  $$\begin{array}{ccc}\hfill {\mathrm{R}}_{\mathrm{e}}\left(t\right)& \hfill =\hfill & {\int }_t^{t+\frac{1}{{\gamma }_E}}{\beta }_E\left(\tau \right)\frac{S\left(\tau \right)}{N}\mathrm{d}\tau +{\int }_{t+\frac{1}{{\gamma }_E}}^{t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}}{\beta }_I\left(\tau \right)\frac{S\left(\tau \right)}{N}\mathrm{d}\tau \hfill \\ \hfill & \hfill \hfill & +\left(1-\theta (t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I})-{\omega }_u(t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I})\right){\int }_{t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}}^{t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}+\frac{1}{{\gamma }_{I_{\mathrm{u}}}}}{\beta }_{I_{\mathrm{u}}}\left(\tau \right)\frac{S\left(\tau \right)}{N}\mathrm{d}\tau \hfill \\ \hfill & \hfill \hfill & +{\omega }_u(t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}){\int }_{t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}}^{t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}+\frac{1}{{\gamma }_{I_{D_{\mathrm{u}}}}}}{\beta }_{I_{D_{\mathrm{u}}}}\left(\tau \right)\frac{S\left(\tau \right)}{N}\mathrm{d}\tau \hfill \\ \hfill & \hfill \hfill & +p(t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I})\left(\theta (t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I})-\omega (t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I})\right){\int }_{t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}}^{t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}+\frac{1}{{\gamma }_{H_R}}}{\beta }_{H_R}\left(\tau \right)\frac{S\left(\tau \right)}{N}\mathrm{d}\tau \hfill \\ \hfill & \hfill \hfill & +\omega (t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}){\int }_{t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}}^{t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}+\frac{1}{{\gamma }_{H_D}}}{\beta }_{H_D}\left(\tau \right)\frac{S\left(\tau \right)}{N}\mathrm{d}\tau .\hfill \end{array}$$ (2)

  In this formula, we estimate the mean number of secondary cases produced by one person infected at time $t$, during its whole infectiousness period, taking into account all the possible evolutions of its health status.

  Composite rectangular, trapezoidal or Simpson rules can be used to obtain an estimation of (2).

  We remark that other estimations for R${}_0$ can be also considered. For instance, one can use the so-called “Next generation Matrix” method to approximate its value (see [37]). However, as pointed in [38], this approximation does not correspond accurately to the biological definition of R${}_0$ (e.g., parameters are assumed to be constant and the change of the proportion of susceptible people during the infectious time of a person is omitted). We remark that R${}_{\mathrm{e}}$ should be used with caution by policymakers, without relying only on that value (see [39]).

  Note that we can estimate the particular contribution of each infectious compartment (i.e. $E$, $I$, $I_{\mathrm{u}}$, $I_{D_{\mathrm{u}}}$, $H_R$ and $H_D$) to the value of R${}_{\mathrm{e}}$ and R${}_0$ by computing only their respective integrals in (2).

• •
  Hos$\left(t\right)$: The number of people in hospital is estimated as follows:

  $$\mathrm{Hos}\left(t\right)=H_D\left(t\right)+H_R\left(t\right).$$

  This function can help to estimate and plan the number of clinical beds needed to treat all the COVID-19 cases.
• •
  ${\mathrm{Hos}}_{\mathrm{n}}\left(t\right)$: The number of new hospitalized people per day at day $t$, which is given by

  $${\mathrm{Hos}}_{\mathrm{n}}\left(t\right)=\left[p(\theta \left(t\right)-\omega \left(t\right))+\omega \left(t\right)\right]{\gamma }_I\left(t\right)I\left(t\right).$$
• •
  MHos: The maximum number of hospitalized people at the same time (in territory $i$) during the time interval $[t_0,T]$. It is computed as:

  $$\mathrm{MHos}=\underset{t\in [t_0,T]}{max}\mathrm{Hos}\left(t\right).$$

  This number can help to estimate and plan the number of clinical beds needed to treat all the COVID-19 cases.
• •
  ${\Gamma }_E\left(t\right)$ and ${\Gamma }_{I_u}\left(t\right)$: The number of people infected during the time interval $[t_0,T]$, by contact with people in compartment $E$ and $I_u$, respectively. They are given by:

  $${\Gamma }_E\left(t\right)={\int }_{t_0}^t{\beta }_E\left(s\right)E\left(s\right)\frac{S\left(s\right)}{N}\mathrm{d}s,$$

  $${\Gamma }_{I_u}\left(t\right)={\int }_{t_0}^t{\beta }_{I_u}\left(s\right)I_u\left(s\right)\frac{S\left(s\right)}{N}\mathrm{d}s.$$

We point out that those outputs and others that can be computed similarly can be compared with reported data when available.

3. Model parameter estimation for COVID-19

Here, we present the methodology we used to estimate the parameters of the model described in Section 2.1. We detail each kind of parameter according to its category.

3.1. Parametrization of some of the functions involved in the model

The model involves several functions. We now detail how some of these functions can be written, using empirical assumptions, in terms of constant parameters, which will have to be later identified for each territory under study (we will do it below for the case of Italy). Of course, other alternatives may be also used, taking into account the particularities of each territory.

– Disease contact rates: We consider that

$${\beta }_E\left(t\right)=m_E\left(t\right){\beta }_{E,0},{\beta }_I\left(t\right)=m_I\left(t\right){\beta }_{I,0},{\beta }_{I_{\mathrm{u}}}\left(t\right)=m_{I_{\mathrm{u}}}\left(t\right){\beta }_{I_{\mathrm{u}},0}\left(\theta \left(t\right)\right),{\beta }_{I_{D_{\mathrm{u}}}}\left(t\right)=m_{I_{D_{\mathrm{u}}}}\left(t\right){\beta }_{I_{D_{\mathrm{u}}},0},$$

$${\beta }_{H_R}\left(t\right)=m_{H_R}\left(t\right){\beta }_{H_R,0},{\beta }_{H_D}\left(t\right)=m_{H_D}\left(t\right){\beta }_{H_D,0}.$$

Here ${\beta }_{E,0},{\beta }_{I,0},{\beta }_{I_{\mathrm{u}},0},{\beta }_{I_{D_{\mathrm{u}}},0},{\beta }_{H_R,0},{\beta }_{H_D,0}$ are the respective disease contact rates when no control measures are taken and $m_E,m_I,m_{I_{\mathrm{u}}},m_{I_{D_{\mathrm{u}}}},m_{H_R},m_{H_D}$ are functions simulating de control measures, as described below.

Regarding ${\beta }_{I_{\mathrm{u,0}}}$, we may consider

$${\beta }_{I_{\mathrm{u,0}}}\left(\theta \right)=\left\{\begin{array}{cc}{\overline{\beta }}_{I,0}\hfill & \text{, if }\theta \in [0,\overline{\omega }],\hfill \\ \text{nonincreasing}\hfill & \text{, if }\theta \in (\overline{\omega },1),\hfill \\ {\underset{\_}{\beta }}_{I,0}\hfill & \text{, if }\theta =1,\hfill \end{array}\right)$$

where $\overline{\omega }$ is a fatality rate value that is explained below and ${\underset{\_}{\beta }}_I$ and ${\overline{\beta }}_I$ are suitable lower and upper bounds, respectively. For the sake of simplicity, here we take ${\overline{\beta }}_{I,0}={\beta }_{I,0}$.

Furthermore, following the idea proposed in [4], [6], [15], we assume that there exists a relationship between the contact rates ${\beta }_{I,0}$, ${\beta }_{E,0}$, ${\beta }_{I_{D_{\mathrm{u}}},0}$ and ${\underset{\_}{\beta }}_{I,0}$.

More precisely, following [6], we consider that people in compartments $E$, $I_{\mathrm{u}}$ and $I_{D_{\mathrm{u}}}$ are less infectious than people in compartment $I$ (due to their probably lower virus load or isolation measures, see [4], [17], [19]). Thus, we consider that ${\beta }_{E,0}=C_E{\beta }_{I,0}$ and ${\underset{\_}{\beta }}_{I,0}=C_{\mathrm{u}}{\beta }_{I,0}$ and ${\beta }_{I_{D_{\mathrm{u}}},0}=C_{I_{D_{\mathrm{u}}},0}{\beta }_{I,0}$, where $C_E,C_{\mathrm{u}},C_{I_{D_{\mathrm{u}}}}\in [0,1]$.

A similar approach can be followed for ${\beta }_{H_R}$ and ${\beta }_{H_D}$ assuming, for instance, that ${\beta }_{H_R,0}={\beta }_{H_D,0}=C_H{\beta }_{I,0}$. Alternatively (as we do here for the case of Italy) we can compute good estimates for ${\beta }_{H_R}$ and ${\beta }_{H_D,0}$ using historical data, as shown below.

–Control measures: We may distinguish three different types of control measures: Social distancing, contact tracing and health system measures. Each of them may be included in the model by using different functions, as explained below.

Functions $m_E\left(t\right)$, $m_I\left(t\right)$, $m_{I_{\mathrm{u}}}\left(t\right)\in [0,1]$ (%) represent the reduction of some of the disease contact rates, at time $t$, due to the efficiency of the control measures corresponding to social distancing applied to the compartments $E$, $I$ and $I_{\mathrm{u}}$, respectively (see, e.g., [40]). Here, for the sake of simplicity, we consider that those three functions are equal (of course, other alternatives are also possible) and given by (see [6])

$$m_E\left(t\right)=m_{I_{\mathrm{u}}}\left(t\right)=m_I\left(t\right)=m\left(t\right)=\left\{\begin{array}{cc}(m_0-m_1)exp\left(-{\kappa }_1(t-t_0)\right)+m_1\hfill & t\in [t_0,{\lambda }_1],\hfill \\ (m\left({\lambda }_1\right)-m_2)exp\left(-{\kappa }_2(t-{\lambda }_1)\right)+m_2\hfill & t\in ({\lambda }_1,{\lambda }_2],\hfill \\ ⋮\hfill & \hfill \\ (m\left({\lambda }_{q-1}\right)-m_q)exp\left(-{\kappa }_q(t-{\lambda }_{q-1})\right)+m_q\hfill & t\in ({\lambda }_{q-1},\infty ).\hfill \end{array}\right)$$

We may also define in a similar way functions $m^{\left(\mathrm{t}\right)}$ and $m^{\left(\mathrm{s}\right)}$ related with contact tracing and health system control measures, respectively, which include similar parameters denoted by $m_i^{\left(\mathrm{t}\right)},m_i^{\left(\mathrm{s}\right)},{\kappa }_i^{\left(\mathrm{t}\right)},{\kappa }_i^{\left(\mathrm{s}\right)},q^{\left(\mathrm{t}\right)}$ and $q^{\left(\mathrm{s}\right)}$. Here, $q,q^{\left(\mathrm{t}\right)},q^{\left(\mathrm{s}\right)}\in \mathbb{N}$ are the number of changes of control strategies.

Here, for every $i\in \{0,\dots ,q\}$, $j\in \{0,\dots ,q^{\left(\mathrm{s}\right)}\}$ and $k\in \{0,\dots ,q^{\left(\mathrm{t}\right)}\}$, constants $m_i,m_j^{\left(\mathrm{s}\right)},m_k^{\left(\mathrm{t}\right)}\in [0,1]$ measure the intensity of the control measures (lower value implies higher intensity), ${\kappa }_i,{\kappa }_j^{\left(\mathrm{s}\right)},{\kappa }_t^{\left(\mathrm{t}\right)}\in [0,+\infty )$ (day⁻¹) simulate the efficiency of the control measures (higher value implies faster effectiveness of the control measures) and ${\lambda }_i,{\lambda }_j^{\left(\mathrm{s}\right)},{\lambda }_k^{\left(\mathrm{t}\right)}\in [t_0,\infty ]$ denote days of changes of each control strategy.

The values of ${\lambda }_i,{\lambda }_j^{\left(\mathrm{s}\right)}$ are typically taken from the literature (using the dates when the territories implement special control measures). Some of the values of $m_i,m_j^{\left(\mathrm{s}\right)}$ can be also known. The rest of the parameters need to be identified, as explained below. When doing this, to ease the search process, we use new parameters $c_i$ instead of $m_i$, as follows:

• •If we want $m_{i+1}\le m_i$, then we look for a suitable parameter $c_{i+1}\in [0,1]$ such that $m_{i+1}=c_{i+1}{m}_i$.
• •If we want $m_{i+1}\ge m_i$, then we look for a suitable parameter $c_{i+1}\in [0,1]$ such that $m_{i+1}=m_i+c_{i+1}(1-m_i)$.

A similar approach can be followed by using new parameters $c_i^{\mathrm{(s)}}$ instead of $m_i^{\mathrm{(s)}}$.

Function $\theta$ is related with the contact tracing measures, since the higher those measures are at time $t$, the closer $\theta \left(t\right)$ is to 1. The other function involved with the contact tracing measures is $m^{\left(\mathrm{t}\right)}$, which is used below for estimating the transition rates. The function $m^{\left(\mathrm{s}\right)}$ is used to compute the fatality ratios and to define $m_{H_R}\left(t\right)=m_{H_D}\left(t\right)=m^{\left(\mathrm{s}\right)}\left(t\right)\in [0,1]$, representing the reduction of the disease contact rates ${\beta }_{H_R,0},{\beta }_{H_D,0}$, at time $t$, due to the efficiency of the health system measures applied to the corresponding compartments. We note that this approach is not taken into account when using the alternative mentioned above to compute estimates for ${\beta }_{H_R}$ and ${\beta }_{H_D}$ using historical data (which will be shown below).

–Fatality ratios: As observed in other epidemics (see, e.g. [15]), $\omega \left(t\right)$ can be affected by the application of health system measures. Thus, following [6], we propose to consider

$$\omega \left(t\right)=m^{\left(\mathrm{s}\right)}\left(t\right)\overline{\omega }+(1-m^{\left(\mathrm{s}\right)}\left(t\right))\underset{\_}{\omega },$$

where $\overline{\omega }\in [0,1]$ is the iIdFR when no health system measures are applied (i.e. $m^{\left(\mathrm{s}\right)}=1$); and $\underset{\_}{\omega }\in [0,1]$ is the iIdFR when the implemented health system measures are fully applied (i.e. $m^{\left(\mathrm{s}\right)}=0$). We note that $\overline{\omega }\ge \underset{\_}{\omega }$, thus, we consider $\overline{\omega }=\underset{\_}{\omega }+{\delta }_{\omega }$, with ${\delta }_{\omega }\in [0,1-\underset{\_}{\omega }]$. Alternatively (as we do here for the case of Italy), these constants can be estimated from values of the IFR in the literature (see, e.g., [41], [42]).

Additionally, we assume that

$${\omega }_{\mathrm{u}}\left(t\right)=\left\{\begin{array}{cc}{\omega }_{\mathrm{u,0}}\hfill & \text{, if }t=t_0\hfill \\ {\omega }_{\mathrm{u,1}}\hfill & \text{, if }t=t_{\mathrm{u,1}}\hfill \\ ⋮\hfill \\ {\omega }_{\mathrm{u,n}}\hfill & \text{, if }t=t_{\mathrm{u,n}}\hfill \\ \text{constant after the last value }{t}_{\mathrm{u,n}}\hfill \\ \text{linear otherwise},\hfill \end{array}\right)$$

where $n\in \mathbf{N}\cup \left\{0\right\}$ and the corresponding values $t_i$, ${\omega }_{\mathrm{u,i}}$ are parameters to be chosen for each territory, depending on its particular circumstances.

–Transition rates:

• •According to [4], the transition rate ${\gamma }_E$ from $E$ to $I$ depends only on the disease and, therefore, is considered constant.
• •
  Some other transition rates could depend on time. For instance, according to [4], [43], depending on the studied territory, the value of ${\gamma }_I\left(t\right)$ can be increased due to the application of contact tracing control measures (i.e. people with symptoms are detected earlier). As a consequence, the values of ${\gamma }_{I_{\mathrm{u}}}\left(t\right)$, ${\gamma }_{I_{D_{\mathrm{u}}}}\left(t\right)$, ${\gamma }_Q\left(t\right)$, ${\gamma }_{H_R}\left(t\right)$ and ${\gamma }_{H_D}\left(t\right)$ can be decreased (e.g. people with symptoms stay under observation during more time). In order to parametrize these functions, we denote by $d_I$, $d_{I_{\mathrm{u}}}$, $d_{I_{D_{\mathrm{u}}}}$, $d_Q$, $d_{H_R}$ and $d_{H_D}$ the initial duration (given as a suitable average) in days of a person in compartment $I$, $I_{\mathrm{u}}$, $I_{D_{\mathrm{u}}}$, $Q$, $H_R$ and $H_D$, respectively, without the application of special contact tracing measures. Then, following [15], we may use the following functions:

  $${\gamma }_I\left(t\right)=\frac{1}{d_I-g\left(t\right)}\left({\text{ day}}^{-1}\right),{\gamma }_{I_{\mathrm{u}}}\left(t\right)=\frac{1}{d_{I_{\mathrm{u}}}+g\left(t\right)}\left({\text{ day}}^{-1}\right),{\gamma }_{I_{D_{\mathrm{u}}}}\left(t\right)=\frac{1}{d_{I_{D_{\mathrm{u}}}}+g\left(t\right)}\left({\text{ day}}^{-1}\right),$$

  $${\gamma }_Q\left(t\right)=\frac{1}{d_Q+g\left(t\right)}\left({\text{ day}}^{-1}\right),{\gamma }_{H_R}\left(t\right)=\frac{1}{d_{H_R}+g\left(t\right)}\left({\text{ day}}^{-1}\right),{\gamma }_{H_D}\left(t\right)=\frac{1}{d_{H_D}+g\left(t\right)}\left({\text{ day}}^{-1}\right),$$

  where $g\left(t\right)=d_g(1-m^{\left(\mathrm{t}\right)}\left(t\right))$ represents the decrease of the duration of $d_I$ due to the application of contact tracing measures, at time $t$; and $d_g$ is the maximum number of days that $d_I$ can be decreased.

  We remark that, for some territories, it can be suitable to consider constant (i.e. not dependent on time) all the transition rates, which corresponds to the case with $d_g=0$.

–Ratio $p$: We describe it by using the following function depending on the value of $\theta -\omega$ (we remark that other alternatives are also possible):

$$p=\left\{\begin{array}{cc}\frac{p_0({\theta }_0-{\omega }_0)}{\theta -\omega }\hfill & \text{, if }\theta -\omega \ge {\theta }_0-{\omega }_0,\hfill \\ 1-\frac{1-p_0}{{\theta }_0-{\omega }_0}(\theta -\omega )\hfill & \text{, if }\theta -\omega \le {\theta }_0-{\omega }_0.\hfill \end{array}\right)$$

Here $p_0=p\left(t_{{\theta }_0}\right)$ and ${\omega }_0=\omega \left(t_{{\theta }_0}\right)$, where $t_{{\theta }_0}$ and ${\theta }_0$ are described below (when we show how to estimate $\theta \left(t\right)$). Indeed, we assume that, if $\theta -\omega >{\theta }_0-{\omega }_0$ all new detected infected people, when comparing to the case of ${\theta }_0$ and ${\omega }_0$, will go to state $Q$, as they should present light symptoms. Furthermore, we use a linear interpolation between the case $\theta -\omega =0$ (with $p=1$, i.e., only persons with severe symptoms are detected) and $\theta -\omega ={\theta }_0-{\omega }_0$ (with $p=p_0$). More complex formulas could be also considered, but we use the previous one, for the sake of simplicity.

We remark that one of the functions involved in the model, namely $\theta \left(t\right)$, has not been parameterized above. We will show below how to deal with it.

3.2. Estimation of parameters and non-parameterized functions involved in the model

Once the model is built, if we want to use it for a particular country or territory, we need to identify suitable model parameters and functions for the case under study. Some of them can be found in the literature. However, due to lack of information regarding the behavior of the SARS-CoV-2 and implicit uncertainty, others need to be estimated.

To do that, we need as much information as possible about the dynamics of the pandemic in the studied territory. In particular, we may use the following temporal series of the territory under study, if available:

• •$c_{\mathrm{r}}\left(t\right)$: The reported cumulative number of COVID-19 infected, cases at time $t$.
• •$d_{\mathrm{r}}\left(t\right)$: The reported cumulative number of COVID-19 deaths, at time $t$.
• •$h_{\mathrm{r}}\left(t\right)$: The reported cumulative number of COVID-19 infected healthcare workers, at time $t$.
• •${\tau }_{1,r}\left(t\right)$: The reported number of known imported cases on day $t$. More precisely, infected people arriving from an external territory. Usually they are in the incubation period, but, in some cases, they are moving between hospitals of different countries or territories (this last possibility is not included in the equations, for the sake of simplicity, but it can be easily done).
• •${\tau }_{2,r}\left(t\right)$: The reported number of known exported cases on day $t$. More precisely, infected people going to an external territory. Usually, they are in the incubation period, but sometimes they are moving between hospitals of different countries or territories (this last possibility is not included in the equations, for the sake of simplicity, but it can be easily done).
• •$d_{\mathrm{r,u}}\left(t\right)$: The reported cumulative number of estimated undetected COVID-19 deaths, at time $t$.
• •${\mathrm{Hos}}_{\mathrm{r}}\left(t\right)$: The reported number of people in hospital (i.e. ${\mathrm{Hos}}_{\mathrm{r}}$), at time $t$.
• •$q_{\mathrm{r}}\left(t\right)$: The number of people in quarantine at home, due to their infection with COVID-19.

We note that, sometimes, there is only partial information and the gaps can be filled with suitable techniques (see, e.g., [44]).

Now, with that information we may estimate some of the model parameters and functions, as follows:

–Ratio $\theta \left(t\right)$ of new infected people that are detected: To estimate $\theta \left(t\right)$, first, we compute an estimation of iCFR ($\frac{\omega \left(t\right)}{\theta \left(t\right)}$) as follows:

$$\frac{\omega \left(t\right)}{\theta \left(t\right)}=\left\{\begin{array}{cc}\hfill \frac{d_{\mathrm{r}}(t_{\mathrm{iCFR}}+\frac{1}{{\gamma }_{H_D}})}{c_{\mathrm{r}}\left(t_{\mathrm{iCFR}}\right)}\hfill & \text{, if }t\le t_{\mathrm{iCFR}},\hfill \\ \hfill \frac{d_{\mathrm{r}}(t+\frac{1}{{\gamma }_{H_D}})-d_{\mathrm{r}}(t-r+\frac{1}{{\gamma }_{H_D}})}{c_{\mathrm{r}}\left(t\right)-c_{\mathrm{r}}(t-r)}\hfill & \text{, if }{t}_{\mathrm{iCFR}}<t<T_{\max }-\frac{1}{{\gamma }_{H_D}},r\text{ is the minimum natural number such that}\hfill \\ \hfill \hfill & c_{\mathrm{r}}\left(t\right)-c_{\mathrm{r}}(t-r)\ne 0\text{ and this quotient is }\le 1,\hfill \\ \hfill 1\hfill & \text{, if }{t}_{\mathrm{iCFR}}<t<T_{\max }-\frac{1}{{\gamma }_{H_D}},r\text{ is the minimum natural number such that}\hfill \\ \hfill \hfill & c_{\mathrm{r}}\left(t\right)-c_{\mathrm{r}}(t-r)\ne 0\text{ and the previous quotient is }>1,\hfill \\ \hfill \text{linear interpolation}\hfill & \text{, otherwise,}\hfill \end{array}\right)$$

where $t_{\mathrm{iCFR}}\ge 7$ days is the first date for which $c_{\mathrm{r}}\left(t\right)-c_{\mathrm{r}}(t-1)\ne 0$ and $d_{\mathrm{r}}(t+\frac{1}{{\gamma }_{H_D}})\ne 0$. We note that, in this formula, we estimate the iCFR by taking into account the delay between the detection of a case and its death (instead of the ratio between cases and deaths reported at the same date). This delay could also be considered in the system of differential equations, instead of the exponential-decay-formulation, leading to a system of delay differential equations (see, e.g., [45]).

After that, to regularize the obtained iCFR curve, we apply a filter that consists in computing the average value of the last week. We denote the resulting filtered curve by ${\omega }_{\mathrm{CFR}}\left(t\right)$:

$${\omega }_{\mathrm{CFR}}\left(t\right)=\left\{\begin{array}{cc}\hfill \frac{\omega \left(t_{\mathrm{iCFR}}\right)}{\theta \left(t_{\mathrm{iCFR}}\right)}\hfill & \text{, if }t\le t_{\mathrm{iCFR}},\hfill \\ \hfill \frac{1}{7}\sum _{i=0}^6\frac{\omega (t-i)}{\theta (t-i)}\hfill & \text{, if }t>t_{\mathrm{iCFR}}.\hfill \end{array}\right)$$ (3)

To avoid unrealistic situations (due to poor data), if ${\omega }_{\mathrm{CFR}}\left(t\right)\le 0.01$ (which is assumed too low, see, e.g., [42]) for some $t>t_{\mathrm{iCFR}}$, then we extend the average of the last week used to compute this ${\omega }_{\mathrm{CFR}}\left(t\right)$ by including the previous days until getting ${\omega }_{\mathrm{CFR}}\left(t\right)>0.01$.

Finally, we define $\theta \left(t\right)$ by:

$$\theta \left(t\right)=\left\{\begin{array}{cc}\hfill {\theta }_0\hfill & \text{, if }t\le t_{{\theta }_0},\hfill \\ \hfill \frac{\omega \left(t\right)}{{\omega }_{\mathrm{CFR}}\left(t\right)}\hfill & \text{, if }t>t_{{\theta }_0},\hfill \end{array}\right)$$

where ${\theta }_0=\frac{\omega \left(t_{{\theta }_0}\right)}{{\omega }_{\mathrm{CFR}}\left(t_{{\theta }_0}\right)}$ and $t_{{\theta }_0}=t_{\mathrm{iCFR}}+6$ days to guarantee that ${\omega }_{\mathrm{CFR}}\left(t_{{\theta }_0}\right)$ is computed by using the average value defined by the second line of (3), for the sake of smoothness. Notice that, if we simulate until the current date, we do not have enough data to compute $\frac{\omega \left(t\right)}{\theta \left(t\right)}$. In this case, we set $\theta \left(t\right)$ to a constant value for the last days of the simulation without data. When simulating scenarios for future dates, we can also keep the last value of $\theta$ or use alternative possible values.

For particular territories (as we do here for the case of Italy) we can use different values of IFR found in the literature and use them as $\omega$ in the previous formula. That will provide different estimations for $\theta \left(t\right)$.

–Contact rates ${\beta }_{H_R}\left(t\right)$ and ${\beta }_{H_D}\left(t\right)$: We use the following estimation of the fraction of infected healthcare workers (assumed to be due to contact with hospitalized people, see, e.g., [29]):

$$\frac{\left(p\left(\theta -\omega \right)\frac{{\beta }_{H_R}}{{\gamma }_{H_R}}+\omega \frac{{\beta }_{H_D}}{{\gamma }_{H_D}}\right)}{\left(p\left(\theta -\omega \right)\frac{{\beta }_{H_R}}{{\gamma }_{H_R}}+\omega \frac{{\beta }_{H_D}}{{\gamma }_{H_D}}\right)+\frac{{\beta }_E}{{\gamma }_E}+\frac{{\beta }_I}{{\gamma }_I}+(1-\theta -{\omega }_u)\frac{{\beta }_{I_{\mathrm{u}}}}{{\gamma }_{I_{\mathrm{u}}}}+{\omega }_u\frac{{\beta }_{I_{D_{\mathrm{u}}}}}{{\gamma }_{I_{D_{\mathrm{u}}}}}}=\eta .$$

To compute $\eta$, we first define $\tilde{\eta }$ as

$$\tilde{\eta }\left(t\right)=\left\{\begin{array}{cc}\hfill \frac{h_{\mathrm{r}}\left(t_{\eta }+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}\right)}{c_{\mathrm{r}}\left(t_{\eta }+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}\right)}\hfill & \text{, if }t\le t_{\eta },\hfill \\ \hfill \frac{h_{\mathrm{r}}\left(t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}\right)-h_{\mathrm{r}}\left(t-r+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}\right)}{c_{\mathrm{r}}\left(t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}\right)-c_{\mathrm{r}}\left(t-r+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}\right)}\hfill & \text{, if }{t}_{\eta }<t<T_{\max }-\frac{1}{{\gamma }_E}-\frac{1}{{\gamma }_I};r\text{ is the minimum natural number}\hfill \\ \hfill \hfill & \text{such that }{h}_{\mathrm{r}}\left(t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}\right)\text{ and }{h}_{\mathrm{r}}\left(t-r+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}\right)\text{ are known}\hfill \\ \hfill \hfill & \text{and }{c}_{\mathrm{r}}\left(t+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}\right)-c_{\mathrm{r}}\left(t-r+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}\right)\ne 0;\hfill \\ \hfill \hfill & \text{ and this quotient is }\le 1,\hfill \\ \hfill 1\hfill & \text{, under the same conditions as in the previous line but when}\hfill \\ \hfill \hfill & \text{the quotient is }>1,\hfill \\ \hfill \text{linear interpolation}\hfill & \text{, otherwise,}\hfill \end{array}\right)$$

and $t_{\eta }$ is the first date for which $h_{\mathrm{r}}\left(t_{\eta }+\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}\right)\ne 0$ is reported. We point out that, in the previous formula, we have made a distinction about the knowledge of the values of $h_{\mathrm{r}}$, because they are rarely given every day. We remark that we are taking into account the delay of $\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}$ days between the infection of a person and its detection by authorities. Thus, we set $\tilde{\eta }\left(t\right)$ to a constant value for the last $\frac{1}{{\gamma }_E}+\frac{1}{{\gamma }_I}$ days. Finally, to avoid unrealistic situations (due to poor data), we take the following seven-day average value:

$$\eta \left(t\right)=\left\{\begin{array}{cc}\hfill \frac{1}{7}\sum _{i=0}^6\tilde{\eta }(t_0+i)\hfill & \text{, if }t<t_0+3,\hfill \\ \hfill \frac{1}{7}\sum _{i=-3}^3\tilde{\eta }(t+i)\hfill & \text{, if }{t}_0+3\le t\le t_0+T_{max}-3,\hfill \\ \hfill \frac{1}{7}\sum _{i=0}^6\tilde{\eta }(t_0+T_{max}-i)\hfill & \text{, if }t>t_0+T_{max}-3.\hfill \end{array}\right)$$ (4)

Assuming, for the sake of simplicity, that ${\beta }_{H_R}={\beta }_{H_D}$, we have that

$${\beta }_{H_R}={\beta }_{H_D}=\frac{\eta \left(\frac{{\beta }_E}{{\gamma }_E}+\frac{{\beta }_I}{{\gamma }_I}+(1-\theta -{\omega }_u)\frac{{\beta }_{I_{\mathrm{u}}}}{{\gamma }_{I_{\mathrm{u}}}}+{\omega }_u\frac{{\beta }_{I_{D_{\mathrm{u}}}}}{{\gamma }_{I_{D_{\mathrm{u}}}}}\right)}{(1-\eta )\left(p\left(\theta -\omega \right)\frac{1}{{\gamma }_{H_R}}+\omega \frac{1}{{\gamma }_{H_D}}\right)}.$$

In the previous expression, the coefficients depend on time $t$.

–Other unknown parameters: We can identify them with a multiobjective technique, as described below.

3.3. Identification of some parameters with a multiobjective optimization technique

First, we determine the set of unknown model parameters to be identified by the approach presented here (which will depend on the available information in the considered territory). For each of those parameters, we establish a suitable interval of possible values (given by upper and lower bounds of each parameter) and denote by $S\subset {\mathbb{R}}^n$ the feasible region given by the cartesian product of all those intervals, where $n$ is the number of unknown parameters.

Once $S$ is defined, we follow the methodology proposed in [46]. This approach aims at minimizing the differences between the temporal series reported by the authorities and the corresponding ones obtained as model outputs when considering particular values $\Omega \in S$. Then, given two weight coefficients ${\rho }_1>0$ and ${\rho }_2>0$ and a temporal series $X$, we define the function

$$\begin{array}{ccc}\hfill f_X\left(\Omega \right)& \hfill =\hfill & \frac{{\Vert X_{\mathrm{r}}-X_{\mathrm{m}}^{\Omega }\Vert }_{L^2(t_0,t_0+T_{max})}^2+{\rho }_1{\Vert max(X_{\mathrm{r}}-X_{\mathrm{m}}^{\Omega },0)\Vert }_{L^2(t_0,t_0+T_{max})}^2}{{\Vert X_{\mathrm{r}}\Vert }_{L^2(t_0,t_0+T_{max})}^2}\hfill \\ \hfill & \hfill \hfill & +{\rho }_2\frac{{|max(X_{\mathrm{r}}(t_0+T_{max})-X_{\mathrm{m}}^{\Omega }(t_0+T_{max}),0)|}^2}{{\left|X_{\mathrm{r}}(t_0+T_{max})\right|}^2},\hfill \end{array}$$ (5)

that measures the error between the reported data, which is denoted by $X_{\mathrm{r}}$, and the model output denoted by $X_{\mathrm{m}}^{\Omega }$. Notice that, as done in previous works [6], [46], it is based on the relative error. However, as a novelty, we add two new terms to penalize those $\Omega$ obtaining a temporal series that underestimate the reported data. We recall that, to reduce the risk of over-fitting to the reported data [47], we use the $L^2$ norm in $[t_0,t_0+T_{max}]$, which is ${\Vert g\Vert }_{L^2\left([t_0,t_0+T_{max}]\right)}={\left({\int }_{t_0}^{t_0+Tmax}{\left|g\left(t\right)\right|}^2\mathrm{d}t\right)}^{1∕2}$.

The number of functions $f_X\left(\Omega \right)$ depends on the number of available temporal series of the territory under study. The authorities usually report at least the cumulative daily number of cases and deaths (i.e. $c_{\mathrm{r}}$ and $d_{\mathrm{r}}$), see, e.g., [48]. In some cases, they also include other data as, for instance, the number of people in hospital (i.e. ${\mathrm{Hos}}_{\mathrm{r}}$), in quarantine at home (i.e. $q_{\mathrm{r}}$), or the cumulative number of undetected deaths (i.e. $d_{\mathrm{r,u}}$) (see, e.g., [49]).

Then, we formulate a multiobjective problem that may have as many objective functions as available temporal series. For instance, we could solve

$$\left\{\begin{array}{c}min\left\{f_c\left(\Omega \right),f_d\left(\Omega \right),f_{\mathrm{Hos}}\left(\Omega \right),f_{d_{\mathrm{u}}}\left(\Omega \right)\right\}\hfill \\ \text{subject to }\Omega \in S\subset {\mathbb{R}}^n,\hfill \end{array}\right)$$ (6)

where $S$ is the feasible region (i.e. upper and lower bounds of each parameter) and $n$ is the number of parameters in $\Omega$. We can also add together (with suitable weights) several functions, in order to reduce the number of functions to be minimized (and the complexity of the corresponding multiobjective problem).

Next, to solve this multiobjective optimization problem, the algorithm called Weighting Achievement Scalarizing Function Genetic Algorithm (WASF-GA) is applied [44], [50], [51]. We choose this particular multiobjective algorithm as it has been applied with success in a previous work to identify some parameters of an epidemiological model simulating the evolution of Ebola Virus Disease outbreaks in Democratic Republic of the Congo [44].

From a general point of view, WASF-GA is an evolutionary algorithm that manages a population of possible solutions (called individuals), trying to improve them iteratively towards the optimal set (called Pareto optimal set). To do that, it uses two procedures at each iteration: reproduction and replacement. Firstly, the reproduction method applies some classical genetic operators (here: selection, mutation, and crossover) to the population of the previous iteration to obtain a new offspring population. Secondly, the replacement procedure decides which solutions from the previous iteration and the offspring populations should compose the population for the next iteration. The main feature of WASF-GA is that this decision is based on preferences, which are defined as reference values for the objectives. Indeed, it classifies the individuals using an achievement scalarizing function (see [51]) characterized by the L${}_{\infty }$ distance between the objective function values and the reference values with different weights. The considered sample of weight vectors is built following [51] to ensure they are well distributed.

As a result, WASF-GA returns a set of solutions covering a region of the Pareto optimal front.

In this work, we set the number of iterations to 15 000, the population size to 50 individuals, the number of weight vectors to 50, and the reference values for the objectives to zero, corresponding to the ideal situation of a total matching between the model outputs and the reported data. The remaining input parameters of WASF-GA are those reported in [51]. Those values were set experimentally in order to obtain a good ratio between computational time and precision of the results.

Since WASF-GA is a stochastic algorithm, it may return different Pareto front approximations for different executions of the same instance. Then, to guarantee that results do not depend on the stochasticity of the algorithm, we perform 60 runs of each experiment. Among all the 60 sets of solutions, we extract the most balanced solution, meaning the one whose objective values are the closest to the reference values (in our case, zero) when considering the Euclidean distance.

In the 8th, 9th, 10th, 11th and 12th equations of system (1), which, as said previously, are not coupled with the other equations, there is a parameter, namely ${\gamma }_Q$, that only appears in those equations. Therefore, its estimation can be done once the multiobjective process is over. For instance, if the authorities report the time series corresponding to the number of people in quarantine at home (i.e. $q_{\mathrm{r}}$), the parameter ${\gamma }_Q$ can be estimated separately as a final step of the identification methodology. To do that, we assume that ${\gamma }_Q$ can be parameterized by $n^{\prime }\in \mathbb{N}$ parameters denoted by $\Phi =\{{\Phi }_1,\dots ,{\Phi }_{n^{\prime }}\}\in S^{\prime }\subset {\mathbb{R}}^{n^{\prime }}$ (see next section for a particular example). Then, we formulate the following mono-objective problem:

$$\left\{\begin{array}{c}min{f}_q\left(\Phi \right)\hfill \\ \text{subject to }\Phi \in S^{\prime },\hfill \end{array}\right)$$ (7)

where $f_q\left(\Phi \right)$ measures the error (as defined by (5)) between the reported data $q_{\mathrm{r}}$ and $q_{\mathrm{m}}^{\Phi }$, the number of people in quarantine returned by the model when considering ${\gamma }_Q$ described by $\Phi$.

Here, we solve this mono-objective problem by using a genetic algorithm configured with the same selection, mutation, and crossover operators as WASF-GA and the same input parameters (i.e. we set the number of iterations to 15 000 and the population size to 50 individuals). Furthermore, we also perform 30 runs to guarantee that the results do not depend on the stochasticity of the algorithm.

4. Numerical simulations and calibration of the model for the case of Italy

We present here the results obtained with our model for the case of Italy, as an example of application. The situation in that country, like in other European countries such as Spain, the United Kingdom and France, has been especially complicated since it has been strongly affected by the disease. The first two known cases of Coronavirus in Italy, a couple of Chinese tourists, were confirmed on January 30. The first known case of secondary transmission occurred in Codogno, Municipality of Lombardy, on February 18, 2020. After that, the pandemic grew and extended to other countries, which needed the establishment of strict control measures (see [52]).

In Section 4.1, we introduce the data and some model parameters specific to the case of Italy. Then, in Section 4.2, we show and analyze some results returned after the numerical experiments performed to illustrate the efficiency of our approach.

4.1. Considered data and model parameters

The information regarding the first cases in Italy is available in [52]. More precisely, the first two known cases of Coronavirus in Italy, a couple of Chinese tourists, were confirmed on January 30. On February 26, they were declared recovered. The first known case of secondary transmission occurred in Codogno, Municipality of Lombardy, on February 18, 2020. Thus, in the numerical simulations, we assume that the index case started his incubation period in Italy on $t_0$=19 January 2020, as the earliest symptom onset of confirmed patients can be traced back to 30 January 2020 (reported on 31 January 2020) and we assume a delay of $d_I+d_E$=10.5 days (rounded to 11 days) between the beginning of the incubation period and the symptoms onset. Thus, we set, $E\left(t_0\right)=1$, $S\left(t_0\right)=N-1$ and all other compartments are set to 0.

The different control measures implemented in Italy are detailed in [52]. They started on ${\lambda }_1=23$ February 2020, where a ’red zone’ was instituted on 11 municipalities with local transmission of SARS-CoV-2 infection, with lockdown to contain the emerging threat. Before this date we set $m_0=m_1=1$ and after this date we consider $m_2\in [0,1]$ (to be estimated). On ${\lambda }_2=11$ March 2020, lockdown was declared on the entire country. Thus, we assume $m_3=c_3\times m_2$ with $c_3\in [0,1]$. On ${\lambda }_3$=22 March 2020 new additional measures regarding the containment and management of the epidemiological emergency from COVID-19, applicable on the whole national territory were adopted including the closure of non-essential or strategic production activities until May 3 (after several extensions). Consequently, we set $m_4=0$, corresponding to the most restrictive social distancing control measures. Starting on ${\lambda }_4=4$ May 2020, some production activities are authorized and we assume $m_5=c_5\times m_2$ with $c_5\in [0,1]$. The Decree of 16 May 2020 establishes the end of regional travel restrictions and the reopening of production activities from ${\lambda }_5=18$ May 2020. We set $m_6=m_5+c_6\times (1-m_5)$ with $c_6\in [0,1]$. Finally, this Decree also governs the end of total travel restrictions (traveling to and from abroad can only be limited with measures derived from the legal system of the European Union and international obligations) and the reopening of production, commercial and social activities from ${\lambda }_6$=3 June to 31 July [53]. Hence, we consider $m_7=m_6+c_7\times (1-m_6)$ with $c_7\in [0,1]$.

For Italy we do not include the compartment $I_{D_{\mathrm{u}}}$ (i.e. people who die undetected pass from compartment $I$ to compartment $D_{\mathrm{u}}$). This simplification is done since, according to [54], almost all undetected deaths affect to vulnerable persons that die quickly after developing clinical sign (e.g. aged persons in nursing homes). All the other compartments were used in this case study.

Furthermore, according to [55], noticeable changes in the delay of detection of infected persons (i.e. $d_I$) have not been observed during the course of the epidemic in Italy. Thus, we set $d_g=0$.

The information by regions concerning the number of cases (i.e. people who enter each day in compartments $H_R$ or $H_D$) and COVID-19 deaths per day is daily reported in the website of the Italian Ministry of Health, (see [49]). Moreover, the Italian National Institute of Health supervises daily the data related to cases, deaths, tests carried out, etc. and the Italian civil protection publishes them completely here:

https://github.com/pcm-dpc/COVID-19

In our simulations, we take $c_{\mathrm{r}}\left(t\right)$, $d_{\mathrm{r}}\left(t\right)$, ${\mathrm{Hos}}_{\mathrm{r}}\left(t\right)$, $q_{\mathrm{r}}\left(t\right)$ from the previous GitHub repository, $h_{\mathrm{r}}\left(t\right)$ from [56] and ${\tau }_{1,r}\left(t\right)$, ${\tau }_{2,r}\left(t\right)$ from [48].

We use the multiobjective technique described above to identify the parameters

$$\Omega =({\beta }_{I,0},{\kappa }_2,{\kappa }_3,{\kappa }_4,{\kappa }_5,{\kappa }_6,{\kappa }_7,c_2,c_3,c_5,c_6,c_7,p_0,C_{\mathrm{u}},{\omega }_{\mathrm{u,0}},1∕{\gamma }_{H_R})\in {\mathbb{R}}^{16},$$

taking ${\rho }_1=10$ and ${\rho }_2=100$. We reduce the number of objective functions to two functions, $f_1\left(\Omega \right)$ and $f_2\left(\Omega \right)$ that combine the four time-series errors $f_c\left(\Omega \right),f_d\left(\Omega \right),f_{\mathrm{Hos}}\left(\Omega \right)$ and $f_{d_{\mathrm{u}}}\left(\Omega \right)$, using some weights as follows:

$$f_1\left(\Omega \right)=0.5f_c\left(\Omega \right)+0.5f_{\mathrm{Hos}}\left(\Omega \right)\text{and}{f}_2\left(\Omega \right)=0.9f_d\left(\Omega \right)+0.1f_{d_{\mathrm{u}}}\left(\Omega \right).$$ (8)

Thus, we solve the following two-objective problem:

$$\left\{\begin{array}{c}min\left\{f_1\left(\Omega \right),f_2\left(\Omega \right)\right\}\hfill \\ \text{subject to }\Omega \in S\subset {\mathbb{R}}^{16},\hfill \end{array}\right)$$ (9)

instead of solving a four objective one, that is more complex and time-consuming. We use ${\rho }_1=10$ (penalization to avoid the underestimation of the reported data in $[t_0,t_0+T_{max})$) and ${\rho }_2=100$ (penalization to avoid the underestimation of the reported data at $t_0+T_{max}$).

Regarding the data denoted by $q_{\mathrm{r}}\left(t\right)$, reported by the Italian authorities, after several numerical experiments, we decided to define ${\gamma }_Q\left(t\right)$ as follows:

$${\gamma }_Q\left(t\right)=\left\{\begin{array}{cc}\hfill {\gamma }_{Q,1}\hfill & \text{, if }t\le t_{{\gamma }_Q},\hfill \\ \hfill {\gamma }_{Q,2}\hfill & \text{, if }t>t_{{\gamma }_Q}.\hfill \end{array}\right)$$

Next, we solve the mono-objective problem described by (7) to identify the parameters $\Phi =({\gamma }_{Q,1},{\gamma }_{Q,2},t_{{\gamma }_Q})\in [0,1]\times [0,1]\times [0,+\infty )$.

The effective reproduction number given by (2) has been computed using the Composite Simpson’s rule.

4.2. Results

First, we use the methodology and techniques detailed in Sections 2, 3 to identify suitable model parameters for the case of Italy, validating the model proposed here. Then, we show how the model may be used to estimate the spread of the disease for different futures scenarios.

4.2.1. Validation of the model.

There is much uncertainty about $\theta$ but, as explained in Section 2.1 , we can first estimate $\frac{\omega \left(t\right)}{\theta \left(t\right)}$ and then $\theta \left(t\right)$ for different values of $\omega$ (which is the instantaneous infection detected fatality ratio, iIdFR). That shows that, actually, the uncertainty of $\theta$ is related to the uncertainty of $\omega$. Hence, we have considered different scenarios for the value of $\omega$, using several estimations found in the literature for the Infection Fatality Ratio (IFR). We remind that the IFR is the expected value of the probability of dying for a person who is infected, i.e. the number of deaths due to the virus (detected or not) over the number of infections (detected or not). The IFR is one of the most critical features of the coronavirus disease, being quite difficult to estimate. More precisely:

• •According to [57], published on 4 May 2020, IFR=1.2%. Then, since on 5 May 2020 there were 29 315 detected deaths (see [58]) and 9154 estimated undetected deaths (see [21], [54]), an associated estimation of $\omega$ would be $\omega =1.2\text{\%}\frac{29315}{29315+9154}=0.9145\text{\%}$.
• •According to [59], published on 18 May 2020, IFR=1.91%. Then, an associated estimation of $\omega$ would be $\omega =1.91\text{\%}\frac{29315}{29315+9154}=1.4555\text{\%}$.
• •According to [60], published on 21 May 2020 but received on 4 April 2020, IFR=5.7%. Then, since on 4 April 2020 there were 15 362 detected deaths and on 14 April 2020 there were 6773 estimated undetected deaths (see [21], [22]), an associated estimation of $\omega$ would be $\omega =5.7\text{\%}\frac{15362}{15362+6773}=3.9559\text{\%}$.

We have used these three values of $\omega$ up to 21 July 2020.

The whole set of model parameters obtained when considering $\omega =1.4555\text{\%}$ is reported in Table 1, Table 2. For the sake of simplicity, we only present here the parameters obtained with this particular value. Results for other values $\omega$ can be found at https://github.com/momat-ucm/T-SIR-T.

Table 1.

Summary of all parameters used for COVID-19 in Italy when considering $\omega =1.4555\text{\%}$. A brief description (Description) of each parameter is given. Furthermore, if available, the range of the considered values (Value) and the reference in the literature (Ref.) are reported. The notation * means that this value is identified during the multiobjective or monoobjective optimization processes. The notation – means this parameter is omitted during this work. The notation & means that this parameter (depending on time) is estimated directly from the reported data. The notation $♢$ means that the value of the parameter is set by the authors of this article, after some numerical experiments.

Notation	Value	Description	Ref.
$N$	60317000	Number of people in the country before starting the pandemic	[61]
${\gamma }_E$	$\frac{1}{5.5}$	Transition rate of a person in compartment $E$ (day−1)	[16]
${\gamma }_I\left(t\right)$	$\frac{1}{5}$	Transition rate of a person in compartment $I$ (day−1)at time $t$	[62]
${\gamma }_{I_{\mathrm{u}}}\left(t\right)$	$\frac{1}{9}$	Transition rate of a person in compartment $I_u$ to compartment $R_{\mathrm{u}}$ (day−1) at time $t$	[62]
${\gamma }_{H_R}\left(t\right)$	$\frac{1}{14.2729}$	Transition rate of a person in compartment $H_R$ to compartment $Q$ (day−1) at time $t$	*
${\gamma }_{H_D}\left(t\right)$	$\frac{1}{5}$	Transition rate of a person in compartment $H_D$ to compartment $D$ (day−1) at time $t$	[62]
${\gamma }_{I_{D_{\mathrm{u}}}}\left(t\right)$	$\infty$	Transition rate of a person in compartment $I_{D_{\mathrm{u}}}$ to compartment $D_{\mathrm{u}}$ (day−1) at time $t$	[54]
${\gamma }_{Q,1}$	$\frac{1}{36.0450}$	Transition rate of a person in compartment $Q$ to compartment $R_{\mathrm{d}}$ (day−1) at time $t\le t_{{\gamma }_Q}$	*
${\gamma }_{Q,2}$	$\frac{1}{24.8646}$	Transition rate of a person in compartment $Q$ to compartment $R_{\mathrm{d}}$ (day−1) at time $t>t_{{\gamma }_Q}$	*
$t_{{\gamma }_Q}$	2 May 2020	Date when the duration of a person in quarantine changes	*
$d_g$	0	Maximum number of days that $d_I$ can be decreased	[55]
$C_E$	0.3806	Ratio between the disease contact rates ${\beta }_E$ and ${\beta }_I$	[6]
$C_{\mathrm{u}}$	0.3293	Ratio between ${\underset{\_}{\beta }}_I$ and the disease contact rate ${\beta }_I$	*
$C_{I_{D_{\mathrm{u}}}}$	–	Ratio between the disease contact rates ${\beta }_{I_{D_{\mathrm{u}}}}$ and ${\beta }_I$	–
${\beta }_{I,0}$	0.4992	Disease contact rate of a person in compartment $I$ without control measures (day−1)	*
${\beta }_{I_{D_{\mathrm{u}}},0}$	–	Disease contact rate of a person in compartment $I_{D_{\mathrm{u}}}$ without control measures (day−1)	–
${\beta }_{H_R}$	&	Disease contact rate of a person in compartment $H_R$	&
${\beta }_{H_D}$	&	Disease contact rate of a person in compartment $H_D$	&
$t_0$	19 Jan 2020	Initial time	[52]
$\underset{\_}{\omega }$	1.4555	iIdFR when the implemented control measures are fully applied (in %)	[59]
${\delta }_{\omega }$	0	to compute iIdFR when no control measures are applied $\overline{\omega }=\underset{\_}{\omega }+{\delta }_{\omega }$	$♢$
${\omega }_{\mathrm{u,0}}$	0.42	iIuFR when $t=t_0$ (in %)	*
${\omega }_{\mathrm{u,1}}$	0.42	iIuFR when $t=t_{\mathrm{u,1}}$ (in %)	$♢$
${\omega }_{\mathrm{u,2}}$	0	iIuFR when $t=t_{\mathrm{u,2}}$ (in %)	$♢$
$t_{\mathrm{u,1}}$	3 May 2020	One day before the last report of $d_{\mathrm{r,u}}$	[49]
$t_{\mathrm{u,2}}$	4 May 2020	Date of the last report of $d_{\mathrm{r,u}}$	[49]
$\theta \left(t\right)$	&	Proportion of infected people that are detected by the authorities	&
$p_0$	0.7382	Ratio of the number of new detected infected people that will survive the disease and are hospitalized at time $t_{{\theta }_0}$	[49]

Table 2.

Summary of all parameters related to control measures used for COVID-19 in Italy when considering $\omega =1.4555\text{\%}$. A brief description (Description) of each parameter is given. Furthermore, if available, the range of the considered values (Value) and the reference in the literature (Ref.) are reported. The notation * means that this value is optimized during the multiobjective optimization process. The notation – means this parameter is omitted during this work.

Notation	Value	Description	Ref.
${\lambda }_0$	19 Jan 2020	First day of application of the control strategy that was being used before $t_0$, if any	[52]
${\lambda }_1$	23 Feb 2020	First day of application of the 1st control strategy (lockdown on 11 municipalities)	[52]
${\lambda }_2$	11 Mar 2020	First day of application of the 2nd social distancing strategy (lockdown on the entire country)	[52]
${\lambda }_3$	22 Mar 2020	First day of application of the 3rd social distancing strategy (closure of non-essential or strategic production activities)	[52]
${\lambda }_4$	4 May 2020	First day of application of the 4th social distancing strategy (end of closure of non-essential or strategic production activities)	[52]
${\lambda }_5$	18 May 2020	First day of application of the 5th social distancing strategy (end of regional travel restrictions and reopening of production activities)	[52]
${\lambda }_6$	3 Jun 2020	First day of application of the 6th social distancing strategy (progressive end of total travel restrictions, reopening of production, commercial and social activities)	[53]
$m_0$	1	Intensity of the social distancing strategy used before $t_0$	[52]
$m_1$	1	Intensity of the control strategy that was being used in $(t_0,{\lambda }_1]$	[52]
$m_2$	0.5332	Intensity of the social distancing strategy used in $({\lambda }_1,{\lambda }_2]$	*
$m_3$	0.1369	Intensity of the social distancing strategy used in $({\lambda }_2,{\lambda }_3]$	*
$m_4$	0	Intensity of the social distancing strategy used in $({\lambda }_3,{\lambda }_4]$	[6]
$m_5$	0.0549	Intensity of the social distancing strategy used in $({\lambda }_4,{\lambda }_5]$	*
$m_6$	0.0577	Intensity of the social distancing strategy used in $({\lambda }_5,{\lambda }_6]$	*
$m_7$	0.0578	Intensity of the social distancing strategy used in $({\lambda }_6,{\lambda }_7]$	*
$m^{\left(t\right)}$	–	Intensity of the contact tracing control strategy	–
$m^{\left(s\right)}$	–	Intensity of the health system control strategy	–
${\kappa }_1$	–	Efficiency of the social distancing strategy used in $({\lambda }_0,{\lambda }_1]$	–
${\kappa }_2$	62.0015	Efficiency of the social distancing strategy used in $({\lambda }_1,{\lambda }_2]$	*
${\kappa }_3$	0.5139	Efficiency of the social distancing strategy used in $({\lambda }_2,{\lambda }_3]$	*
${\kappa }_4$	0.0362	Efficiency of the social distancing strategy used in $({\lambda }_3,{\lambda }_4]$	*
${\kappa }_5$	90.6408	Efficiency of the social distancing strategy used in $({\lambda }_4,{\lambda }_5]$	*
${\kappa }_6$	14.6514	Efficiency of the social distancing strategy used in $({\lambda }_5,{\lambda }_6]$	*
${\kappa }_7$	52.0747	Efficiency of the social distancing strategy used in $({\lambda }_6,{\lambda }_7]$	*
${\kappa }^{\left(t\right)}$	–	Efficiency of the contact tracing control strategy	–
${\kappa }^{\left(s\right)}$	–	Efficiency of the health system control strategy	–

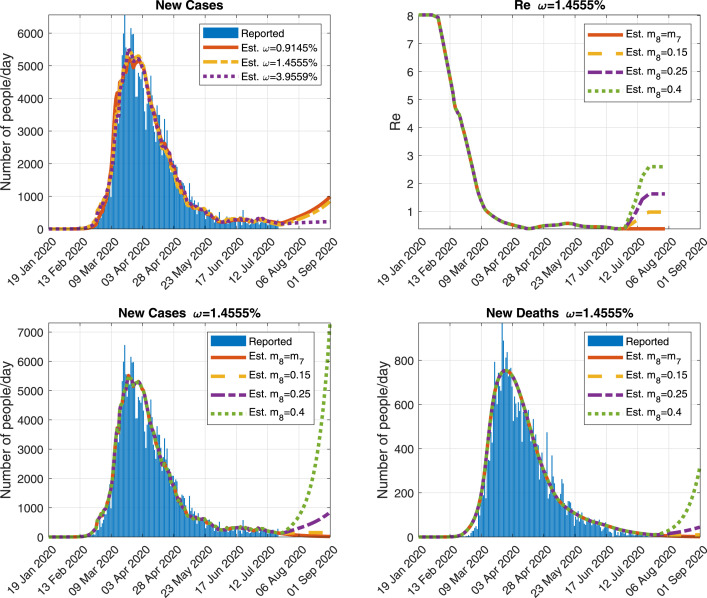
In Figs. 2 and  3, we show the comparison of some of the outputs of the simulation run with the chosen parameters and the official real data, when $\omega =1.4555\text{\%}$. Similar figures have been obtained when considering $\omega =0.9145\text{\%}$ and 3.9559% (obviously, with different parameters) and, thus, are not reported here.

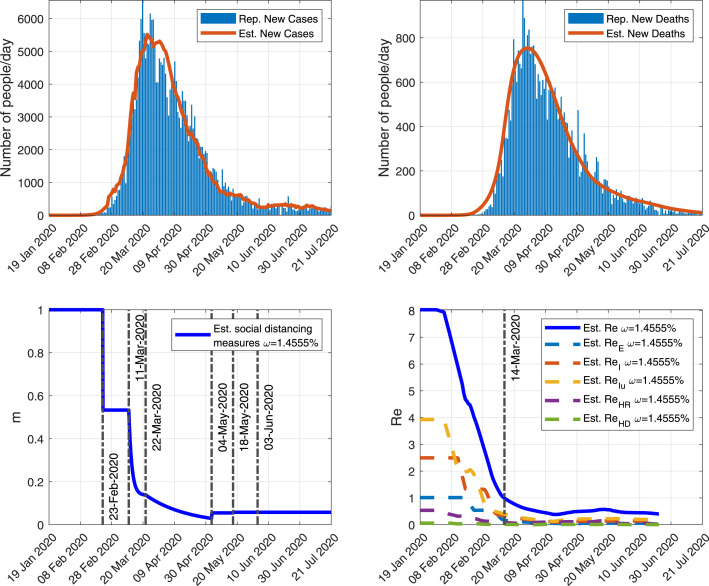
Fig. 3.

Comparison of some of the outputs of the simulation run with $\omega =1.4555\text{\%}$ (Est.) and, when available, the Italian official reported data (Rep.). Top-left: New detected cases per day. Top-right: New detected deaths per day. Bottom-Left: Function modeling the social distancing measures. Bottom-Right: Effective reproduction number and the contribution of each infectious state (i.e. $E$, $I$, $I_{\mathrm{u}}$, $H_R$ and $H_D$) to this number. The vertical line corresponds to the first date when R${}_e<1$.

More precisely, in Fig. 2, we show a very good fitting of the model outcomes with respect to four important time series reported by the Italian authorities regarding the pandemic: the cumulative number of cases and deaths, people in hospital, people in quarantine and recovered people. Furthermore, the model estimates that on 14 April 2020 and 5 May 2020 there were around 7509 and 9192 undetected deaths (persons in $D_u$), respectively. According to the Italian authorities (see [21], [54]), on 14 April 2020 and 5 May 2020 (the only two reported values) this number was estimated to be 6773 and 9154, respectively. This shows that our model is able to estimate well the biological behavior of the pandemic.

Next, in Fig. 3 (Top-Left) and (Top-Right), we show the evolution of the new detected cases and deaths, per day. When available, we compare those outputs with the real data. Again, we observe a good fitting between simulated results an observed data. This feature of the model is interesting as it allows to estimate the date and magnitude of the peaks of all those outcomes (also reported in this figure), which may help to plan some health system measures (such as increasing the number of beds in hospital).

In Fig. 3 (Bottom-Left) and (Bottom-Right), we show the evolution of the functions corresponding to the social distancing measures and the effective reproduction number, when $\omega =1.4555\text{\%}$. We observe that the effective reproduction number went below 1 after 14 March 2020, which should indicate the start of a decrease of the spread in Italy. This value is reached soon after the implementation of some intensive control measures (lockdown in the entire country) in Italy on 11 March 2020, showing that such restrictive control measures were necessary to control the pandemic (before this date the model estimates that R${}_{\mathrm{e}}$ remains above 1). We also note that the initial value of the effective reproduction number, which is the basic reproduction number R${}_0$, is equal to 8.0, which is a value higher than those generally reported in the literature (between 1.4 and 3.9, see e.g. [4], [63]). However, we also show in this figure the contribution of each infectious state (i.e. $E$, $I$, $I_{\mathrm{u}}$, $H_R$ and $H_D$) to the value of R${}_{\mathrm{e}}$ (see Section 2.2 for more details). In particular, we observe that the compartment $I_{\mathrm{u}}$ of undetected infectious people contributes to $R_0$ with a value of 3.9, which means that detected cases contribute to $R_0$ with a value of less than 4.1, which is consistent with the values usually found in the literature.

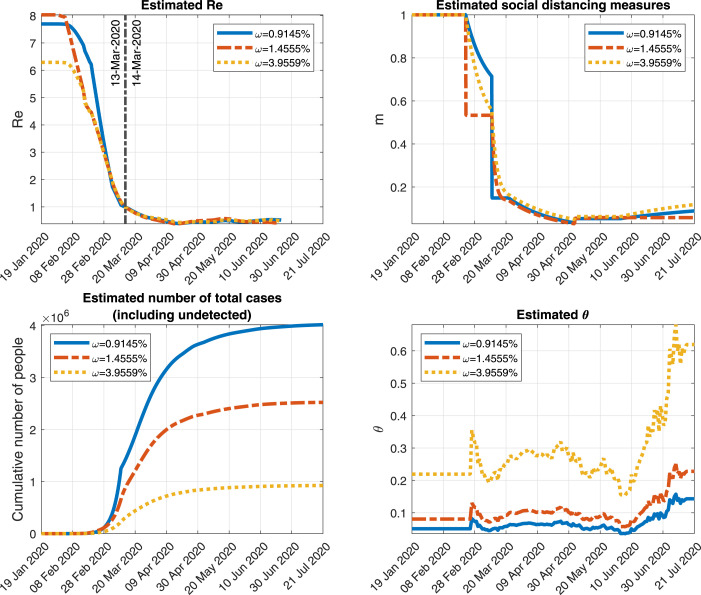
Next, in Fig. 4, we show the evolution of some of the outcomes of the model for different values of $\omega$. First, in this figure (Top-Left) and (Top-Right), we present the evolution of R${}_{\mathrm{e}}$ and the effect of the social distancing measures when considering $\omega =0.9145\text{\%}$, $\omega =1.4555\text{\%}$ and 3.9559%. We observe that, before 11 March 2020, the magnitude and shape of those functions are affected by the value of $\omega$. After this date, they are quite similar for the different values of $\omega$. Focusing on the total number of cases (including undetected), presented in Fig. 4 (Bottom-Left), the model estimates that, taking into account the different values of $\omega$ considered previously, between 1 and 4 million people could have been infected by COVID-19 in Italy. Regarding the value of $\theta$, depicted in Fig. 4 (Bottom-Right), we see that for $\omega =3.9559\text{\%}$ the proportion of detection of new cases oscillates between 15% and 67%. For $\omega =0.9145\text{\%}$ or $\omega =1.4555\text{\%}$, it is between 5.7% and 25%. From those results we see that, in all cases, the model estimates that a large amount of new cases have not been detected during this pandemic. However, the proportion of detection is highly dependent on the value of $\omega$ and large variations of the results are observed when this value changes. The results presented in Fig. 4, indicate the necessity to approximate well this critical parameter.

Fig. 4.

Some of the outputs of the simulation run with $\omega =1.4555\text{\%},\omega =0.9145\text{\%}$ and 3.9559% for the Italian case. Top-left: Effective reproduction number. Top-right: Function modeling the social distancing measures. Bottom-left: Cumulative number of total cases (including undetected cases). Bottom-right: $\theta \left(t\right)$.

4.2.2. Estimation of possible future scenarios

We considered just a few cases, to illustrate the possibilities that can be explored with the model to estimate the possible spread of the disease. We simulate the future scenarios described below until 1 September 2020. We recall that the meaning of parameters ${\lambda }_i$, ${\kappa }_i$ and $m_i$ that appear below may be seen in Section 2.1. In all cases, we consider ${\lambda }_7$= 22 July 2020 (date of a potential change of control measures; taking into account that the date of our last data is 21 July 2020), ${\kappa }_8={\kappa }_2=62.0015$. Since we cannot estimate $\theta$ for the future (it depends on the authority actions) by using the methodology described in Section 3.2, from 22 July 2020 on, we assume that $\theta$ remains equal to its value on 21 July 2020.

First, for $\omega =0.9145\text{\%}$, $\omega =1.4555\text{\%}$ and $\omega =3.9559\text{\%}$, we consider $m_8=0.25$. Some results of this simulation are reported in Fig. 5 (Top-Left). In the three cases we observe a slight increase in the number of cases.

Fig. 5.

Outputs obtained when simulating possible future scenarios (using ${\kappa }_8={\kappa }_2=62.0015$). Top-left: New detected people when $m_8=0.25$ and $\omega =0$.9145%, 1.4555% or 3.9559%, Top-right: Effective reproduction number when $\omega =1.4555\text{\%}$ and $m_8=0.15$, 0.25 or 0.4, Bottom-left: New detected cases per day, when $\omega =1.4555\text{\%}$ and $m_8=0.15$, 0.25 or 0.4, Bottom-right: New detected deaths per day, when $\omega =1.4555\text{\%}$ and $m_8=0.15$, 0.25 or 0.4.

Next, for $\omega =1.4555\text{\%}$, we simulate four future scenarios with: (i) $m_8=m_7=0.0578$; (ii) $m_8=0.15$; (iii) $m_8=0.25$, and (iv) $m_8=0.4$. In Fig. 5 (Top-Right), (Bottom-Left) and (Bottom-Right), we show some outputs of the model for these four scenarios. As we can see, there is a remarkable possibility of new outbreaks in Italy if the control measures are relaxed too much. For instance, focusing on the effective reproduction number, it goes back over 1 when $m_8=0.25$ and $m_8=0.4$, which would mean a second wave of uncontrolled outbreaks. In particular, if control measures are relaxed too much (e.g. $m_8=0.4$) the new cases and deaths may increase dramatically. This clearly indicates that, the pandemic is not over yet and efforts must continue, keeping enough control measures.

5. Conclusions and discussion

We have developed an epidemiological model for simulating the dynamics of COVID-19 in a considered territory. This model may be used by epidemiologists and policy makers for understanding the spread of the pandemic, study the efficiency of control measures and propose suitable ways to tackle the problem. It is intended to be as simple as possible, but with sufficient complexity to be able to simulate the biological and sociological mechanisms which influence the disease spread (including the three main types of control measures: social distancing, contact tracing and health system measures), to fit real data and to simulate possible future scenarios. Of course, for particular cases the model may be simplified (for instance removing the $I_{D_{\mathrm{u}}}$ compartment, as we showed for the case of Italy, or the $Q$ compartment, if the territory does not keep asymptomatic people in quarantine at home).

The model can serve as a basis for studies including higher complexity. Indeed, it can be modified to introduce structures of age, sex, etc., stochasticity, levels of uncertainty, mobility between territories, spatial structure, etc.

In the model that we propose, there are several important points to highlight that, to the best of our knowledge, have not been previously considered:

• 1.We have included a compartment for undetected deaths mainly happening in nursing homes or residences for disabled people. The number of these deaths and the associated infections does not seem to be negligible, which makes necessary to take them into account in the model.
• 2.Some dynamic coefficients are based on reported time series, which allows the model to reproduce faithfully the spread of the disease, fitting very well the reported data.
• 3.The model includes the effects of the different control measures described above.
• 4.The model takes into account quarantine and hospitalized people in order to estimate the number of hospital beds that are needed.

We point out that the model, in this current simple form, has the following limitations:

• 1.Epidemics/pandemics are phenomena that respond to complex processes and all epidemiological models are simplifications of this complex reality. Furthermore, the model is based on the interactions of human beings, which do not behave in reasonably predictable ways like molecules, cells or particles (see [35]).
• 2.The prediction of its evolution is very complicated because of the characteristics of the system of differential equations governing the model. In particular, in the exponential growth phases, small variations in some parameters can lead to large variations in model outcomes (see, [6]). Moreover, there are data quality problems: a) uncertainty about the characteristics of SARS-CoV-2 (new virus); (b) changes in criteria to count cases; (c) uncertainty about undetected cases (and, therefore, the mortality rate), etc.
• 3.Since there is no clear scientific evidence of the effect of humidity and temperature (see, e.g. [31], [32]), we have not included these two factors in our model (if such evidence is demonstrated, these variables should be included in the model).
• 4.It is assumed that the spatial distribution of the population is homogeneous in the territory under study (if this is not a suitable assumption, the territory can be divided into smaller ones).
• 5.In this paper we have only considered the spread of disease within a territory, where only local transmission and known imported/exported cases are modeled. The between-country spread has not been modeled in this work, but can be considered in the future employing ideas from the BeCoDiS model (see [15]).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Communicated by V.M. Perez-Garcia

Annex.

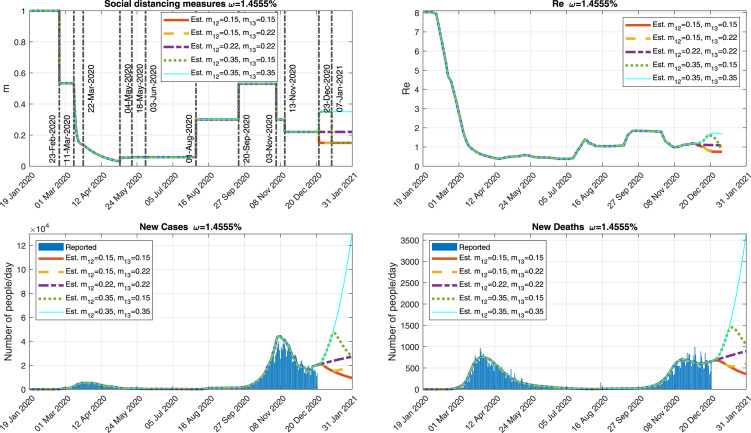
In the version of this article initially submitted to Physica D: Nonlinear Phenomena, the case of Italy studied in Section 4 was written using official data up to 21 July 2020 to validate the model and analyze several scenarios up to 1 September 2020. In the current version, written later as a revised version of the submitted paper, we have kept everything that was computed using those data (including the values of the parameters). Furthermore, following the reviewers’ suggestions, in this Annex we show an update of the situation in Italy, using official data up 21 December 2020, to compare with our simulations. It is important to remark that in all the simulations shown in this Annex, we keep the same parameter values as those given in the version of the paper initially submitted to the journal (with data up to 21 July 2020, as mentioned above).

In all cases, we consider $\omega =1.4555\text{\%}$ and we estimate $\theta$ by using the methodology described in Section 3.2 until 21 December 2020 assuming that, since then, $\theta$ remains equal to its value on this day. Between 14 and 15 August 2020, the cumulative number of deaths reported by the Italian authorities shows a sudden increase, because they updated unreported deaths that occurred in previous weeks. According to their weekly reports (see [64]), from 10 to 23 August there were 14 new deaths. Thus, 218 deaths must be smoothly distributed before the 10 August as done in [6] for the case of China. First, we distribute the 14 deaths from 10 to 23 August and, then, we assign the 218 deaths between 22 July and 23 August, avoiding the modification of the data that we had already used in the paper until 21 July.

Besides the values of the model parameters shown in Section 4, in Table 3 we show the values of the parameters that we have used to model the control measures (as implemented for the Italian Government) corresponding to the days after the 21 July 2020.

In Fig. 6 we show some results corresponding to five different scenarios up to 31 January 2021:

Table 3.

Summary of the parameters used to model the control measures corresponding to the days after the 21 July 2020. Time intervals with different measures are indexed with $i\in \{8,9,10,11,12,13\}$.

Date of application	Efficiency	Intensity	Type	Detail
(${\lambda }_{i-1}$)	(${\kappa }_i$)	($m_i$)
1 Aug 2020	62.0015	0.3	Relaxation	“New normality”
20 Sep 2020	62.0015	0.53	Relaxation	Back from vacation,
				school, work. Regional
				elections
3 Nov 2020	62.0015	0.3	Restriction	Curfew
13 Nov 2020	62.0015	0.22	Restriction	More regions with
				restrictive measures
23 Dec 2020	62.0015	Different	Different	Christmas
		scenarios	scenarios
7 Jan 2020	62.0015	Different	Different	End of Christmas
		scenarios	scenarios

Fig. 6.

Outputs obtained when simulating possible future scenarios when $\omega =1.4555\text{\%}$. Top-left: Function modeling the social distancing measures. Top-right: Effective reproduction number. Bottom-left: New detected cases per day. Bottom-right: New detected deaths per day.

• •Red scenario: More restrictive control measures are implemented from 23 December to 31 January.
• •Yellow scenario: More restrictive control measures are implemented from 23 December to 6 January. From 7 January, the measures come back to the ones before 23 December.
• •Purple scenario: The control measures are maintained without changes.
• •Green scenario: The control measures are relaxed for Christmas from 23 December to 6 January. From 7 January, more restrictive control measures are implemented.
• •Cyan scenario: The control measures are relaxed for Christmas from 23 December. These measures continue during January, i.e., no restrictions are implemented after Christmas.

As we can see, Italy could be on 22 December at a crucial moment where any changes in control measures could have notable consequences. The model estimates that on 22 December the effective reproduction number R${}_{\mathrm{e}}$ could be slightly higher than 1 and the intensity of the control measures could be of 0.22 (considering 1 the absence of measures before the pandemic). If they tighten the measures from 23 December, as the Italian government has announced, the effective reproduction number could drop below 1 and the pandemic would be controlled (see the red scenario in Fig. 6). However, if the measures are relaxed too soon in January, the cases and deaths would increase again before the end of January (see the yellow scenario in Fig. 6). As we can see in the purple scenario, if no changes are implemented in the measures from 22 December to 31 January, the new cases and deaths may increase. Finally, if the measures are relaxed on 23 December, there would be a third wave of uncontrolled outbreaks whose magnitude depends on the restrictive measures they apply after Christmas (see the green and cyan scenarios in Fig. 6).

Data and code availability

All the data and all the model simulation and figure codes used in this manuscript are available at https://www.ucm.es/momat/software-momat and at https://github.com/momat-ucm/T-SIR-T. The core model was written in Java and the figures were obtained using MATLAB.