A computer-aided approach to detect the fetal behavioral states using multi-sensor Magnetocardiographic recordings

Abstract

We propose a novel computational approach to automatically identify the fetal heart rate patterns (fHRPs), which are reflective of sleep/awake states. By combining these patterns with presence or absence of movements, a fetal behavioral state (fBS) was determined. The expert scores were used as the gold standard and objective thresholds for the detection procedure were obtained using Receiver Operating Characteristics (ROC) analysis. To assess the performance, intraclass correlation was computed between the proposed approach and the mutually agreed expert scores. The detected fHRPs were then associated to their corresponding fBS based on the fetal movement obtained from fetal magnetocardiogaphic (fMCG) signals. This approach may aid the clinicians in objectively assessing the fBS and monitoring the fetal wellbeing.

INTRODUCTION

Existence of behavioral states in human fetuses was reported for the first time in 1982 by Nijhuis et al. [1]. The Cardiotcograph (CTG), which is a real-time ultrasound, has been used to study fetal heart rate patterns (fHRPs). Fetal heart rate has been classified into four different patterns: 1F–characterized by a stable heart rate with small oscillation bandwidth of less than 5 beats per minute (bpm); 2F–characterized by a varying heart rate with frequency acceleration and decelerations over 10 bpm from the baseline with wider oscillation bandwidth greater than 5 bpm; 3F–characterized by a stable heart rate with no accelerations with oscillation bandwidth greater than 5 bpm; 4F characterized by highly irregular heart rate (seemingly tachycardic) with frequent long lasting and large accelerations from the baseline with a wider oscillation. Nijhuis defined the fetal behavioral states (fBS) based on the temporal coincidence of the HRPs, fetal gross body movement (GBM) and eye movement (EM) observed for a 3-min window duration using the criteria mentioned in Table1. Since then several studies have evidenced the importance of this finding in the determination of fetal wellbeing [2] and as indices of developmental aspects of fetal autonomic nervous system (ANS) [3] .

Table 1.

Nijhuis definition for the heart-rate patterns and their associated behavioral states [1]. EM, GBM and HRP being eye movement, gross body movement and heart rate pattern, respectively.

Behavioral state	EM	GBM	HRP
Quiet Sleep (1F)	No	Incidental	A
Active Sleep (2F)	Yes	Periodic	B
Quiet Awake (3F)	Yes	Absent	C
Active Awake (4F)	Yes	Continuous	D

The majority of these findings have been reported based on behavioral states observed from Doppler ultrasound CTG recordings. With the advent of SQUID (Superconducting Quantum Interference) technology, Fetal Magnetocardiography (fMCG) is now shown to be a feasible technique in the studying fetal heart dynamics [4–10]. The inherent advantage of fMCG is its superiority in acquiring fetal cardiac signals with high spatial and temporal resolution which in turn enhances the temporal analysis of fetal heart-rate. In addition, the spatial distribution of the SQUID sensors allows one to track the fetal movement as the sensors in the close proximity of the fetal position will have higher QRS amplitude compared to the neighboring sensors [11]. The magnetic signal corresponding to the fetal eye movement is unknown. However, Maeda et al. [12] reported that the inability to record the fetal eye movement does not preclude the proper assignment of fBS. They concluded as the states 1F, 2F, and 4F can be identified based on the variability in the HR and fetal movement, state 3F can be detected based on the lack of accelerations observed in the HR (Table 1). Hence it is possible to detect the fBS based on the parameters such as HR and fetal movement obtained from fMCG recordings. In a recent study fBS were found to be relevant for the fetal brain function as auditory evoked brain responses emerge earlier in active states compared to passive states [13]. Thus the investigation of fBS seems to be relevant for the monitoring of fetal brain development and is important for the clinical interpretation of fetal Magenetoencephalogram results. However, an automated approach to characterize fBS is not available. To fill this void, in this work we propose a computer-aided approach based on linear de-trending procedure for an automated detection of fBS based on the patterns observed in HR and fetal movements obtained from fMCG. Two experts independently reviewed and scored the fMCG recordings for fHRPs and these expert scores were used as gold standard. The fHRPs were detected using the linear de-trending approach and thresholds used for the detection procedure were obtained using Receiver Operating Characteristics (ROC) analysis. The episodes of significant fetal movement and HR acceleration were marked in an objective manner and were used to associate the fHRPs to their corresponding fBS [14].

MATERIALS AND METHODS

Subject and data collection

A novel 151 SQUID array system, a device of its kind, was used to collect fMCG recordings. A total of 62 fMCG recordings were collected between 30 and 38 weeks of gestation from 39 pregnant women. All of them delivered healthy singleton neonates at term. This study was approved by the University of Arkansas for Medical Sciences (UAMS) Institutional Review Board and all mothers gave a written informed consent to participate in the study. Duration of the study varied between 6 to 30 minutes depending on maternal comfort. The fMCG data were sampled at a rate of 312.5 Hz. This retrospective study included a total of 62 recordings of which 40 were used for the training purpose and the remainder 22 recordings were used for the testing purpose. Among the 39 fetuses, 27 of them were delivered in UAMS. A detailed description of the recordings including gestational age (GA) in weeks at study (at the time of fMCG recording) and APGAR scores (1^st and 5^th minute after birth) of the infants delivered at UAMS are shown in Tables 2 for the training and testing recordings, respectively. The gestational age (GA) represents the age of the fetus in weeks calculated from the last menstrual cycle to the time of the study. All the infants had a “live birth” outcome. We lost follow-up of the rest of infants that were delivered at other centers.

Table 2.

Clinical data of the subgroup fetuses delivered at UAMS.

Subject ID	GA at study	APGAR	Weight	Delivery Type	Gender
Training recordings
1	34		7lb 5oz	Vaginal	F
3	37		7lb 6oz	Cesarean	F
4	33	9, 9	6lb 12oz	Vaginal	F
5	32	7, 9	7lb 3oz	Cesarean	F
7	34		9lb 5oz	Cesarean	M
10	36		7lb 10.5oz	Cesarean	M
13	37	7	7lb 8oz	Cesarean	F
15	32	9, 9	8lb 9oz	Cesarean	M
16	35		8lb 1oz	Vaginal	F
18	36		7lb 12oz	Cesarean	F
19	32	8, 9	9lb 4oz	Vaginal	M
22	32		8lb 8oz	Cesarean	M
23	32		5lb 10oz	Cesarean	M
25	36	8, 5	6lb 8oz	Vaginal	F
30	36	8,9	5lb 11oz	Vaginal	F
37	37		7lb 13oz	Vaginal	M
40	32		7lb 7oz	Vaginal	F
Testing recordings
41	31	8	7lb 14oz	Cesarean	M
43	32	5, 8	7lb 13oz	Vaginal	F
46	35		7lb 2.5oz	Vaginal	M
47	34		7lb 2oz	Vaginal	M
48	34	7, 8	10lb 6oz	Cesarean	M
49	30		7lb 9oz	Cesarean	F
57	35		8lb	Vaginal	F
59	36	9, 10	9lb 4oz	Vaginal	M
60	36	8, 9	6lb 3oz	Cesarean	F
62	36	8, 9	6lb 3oz	Cesarean	M

The GA represents to the age of the fetus at study.

For 11 fetuses, the APGAR scores measured at 1^st and 5^th minute after birth are given in 3^rd column. For two fetuses, only one APGAR score measured at 1^st minute after birth was available.

Data Analysis

The data were band-pass filtered between 1 and 50 Hz using the Butterworth filter with zero-phase distortion and the interfering maternal cardiac signal was attenuated using the signal space projection technique [15]. The signal space projection technique was developed in-house to attenuate the cardiac signals to study the fetal brain signals. In this approach the maternal R-wave was identified using adaptive Hilbert transform. [16] Mean maternal HR was calculated and samples corresponding to 40% maternal HR before R and sample corresponding to 60% of maternal HR after R were selected. The maternal cardiac cycles were averaged over all identified R waves. This procedure was carried out on all of the channels. The resulting averaged cardiac cycle was used to determine the signal space vectors corresponding to mMCG. The largest vector was identified from mMCG and this was projected out using Gram-Schmidt orthonormalization procedure. This procedure was repeated on the residual and the next signal space vector was selected and projected out. The procedure was stopped if the root mean square of the residue drops below a prefixed tolerance which was set to 350 femto Tesla. Typically, the procedure stops within 10 steps. We denote the signal space vectors identified in each step as v₁, v₂, ..,, v_n and construct matrix V whose columns are v_i. V is a m x n matrix where ‘m’ is the number of sensors. Using V the projection operator P was constructed as: P = I − (V^TV)⁻¹V^T, where I is the identify matrix and ‘T’ being the matrix transpose. These vectors were projected out of the data matrix by multiplying data matrix with P. The resulting fMCG was used for further processing.

The fetal R-waves were calculated using the Hilbert transform approach [17] and was followed by an adaptive scheme to correct for the missed and extra beats [18]. A more detailed description of the fetal R-wave detection can be found elsewhere [14].

By denoting τ_j as the time of occurrence of the j – th R-wave, we compute the HR (in beats per minute [bpm]) at this instance as follows: 60/(τ_j – τ_j−1) , where the unit of τ is in seconds. In order to detect the fetal movement, at each R-wave we compute the center of gravity (cog) of the fetal heart vectors as the weighted average of the magnitude of the R-wave and the coordinate position of the sensor. To this end, we define the actogram (expressed in cm) (fetal movement) as, the distance between the cog computed at each R-wave and the average of cog from all the R-waves in a three minute duration. A more detailed description of the actogram computation can be found elsewhere [14].

Using τ_j as the actual sampling time, both HR and the actogram are interpolated using cubic-spline function to convert them into continuously sampled data with a sample rate of 312.5 Hz for further analysis. We would like to mention that such a high sampling rate is not needed for this analysis and we performed this only to match the sampling rate of the original fMCG signal. The instances of HR acceleration and significant fetal movement are detected in an objective manner and are used to study the synchronization of state variables in associating the fHRPs to their corresponding fBS [11]. The simultaneous occurrence of the HR acceleration and the fetal movement is termed as “synchronization” in this work.

fHRP detection

In order to detect the different fHRPs, the HR segment corresponding to a 3-min window is investigated with the following three-step procedure:

1. Detection of Quiet and Active fHRPs

1. Based on the variability observed in the HR segment, first step would be to separate Active patterns (HRP-B and HRP-D) from Quiet patterns (HRP-A and HRP-C)

2. For this purpose, a floating baseline for the HR segment is computed as a linear fit to the recordings for a window of 2-min with 15-sec overlap. As the accelerations in the HR vary between 1–2 min, this choice of window duration will be appropriate to avoid over fitting of recording but adequate enough to capture the inherent fluctuations. Detrended HR (DHR) is then obtained by subtracting HR from the floating baseline. The percentage ratio of DHR ≥ ± 10 bpm greater than a certain tolerance is used as decision criteria in separating the Active patterns from Quiet patterns. This is based on the fact, that the Active patterns tend to spend more time in acceleratory phases compared to the Quiet patterns.

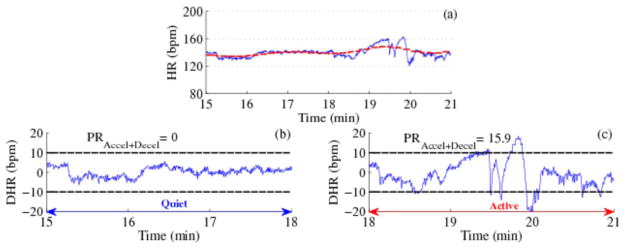
Figure 1 shows a demonstration of the procedure to detect Quiet and Active patterns for a 6-minute segment of HR. Figure 1a shows the HR along with the floating baseline. For the first 3-minute period the HR did not exceed the boundaries constructed using the floating baseline indicating HRP-A; however for the second 3-minute period about 16% of the HR exceeded the threshold indicating the HRP-B.

Figure 1.

Detection of Quiet and Active fHRPs. (a) HR with floating baseline marked as red dotted line, (b) and (c) represent the de-trended HR (DHR), the black dotted line represent the ± 10 bpm range and PR _{Accel+Decel represent} the percentage ratio of HR acceleration or deceleration in the 3-min window.

2. Sub-classification of Quiet fHRPs

If a particular HR segment is detected as Quiet pattern, it is further investigated to detect HRP-C from HRP-A. As mentioned before, HRP-C has a wider oscillation bandwidth and no accelerations present compared to HRP-A. For this purpose, standard deviation (σ) of the HR segment is calculated and σ (HR) greater than a certain tolerance and presence of no accelerations in the HR are used in detecting HRP-C from HRP-A.

3. Sub-classification of Active fHRPs

If a particular HR segment is detected as Active pattern, it is further investigated to detect HRP-D from HRP-B. As mentioned before, HRP-D is unstable and tachy-arrhythmic in nature of having more instances in acceleratory phases. In order to capture such characteristics, percentage ratio of instances ≥160 bpm greater than a certain tolerance is used to detect the HRP-D from HRP-B.

Figure 2 shows two 3-minute HR tracings corresponding to HRP-A (Figure 2a) and HRP-C (Figure 2b). The standard deviations of the tracings delineate HRP-A and HRP-C. Figure 3 shown two 3-minute HR tracings corresponding to HRP-B (Figure 3) and HRP-D (Figure 3b). The percentage of HR exceeding the threshold constructed using the local baseline while simultaneously exceeding a value of 160 bpm clearly distinguishes fHRP-B and fHRP-D.

Figure 2.

Detection of HRP-A and HRP-C. (a) and (b) correspond to a typical HRP-A and HRP-C segment respectively with its standard deviation marked.

Figure 3.

Detection of HRP-B and HRP-D. (a) and (b) correspond to a typical HRP-B and HRP-D segment. The black dotted line represents the 160 bpm reference line guided to the eye.

Thresholds for these three steps are obtained from the HR data scored by the experts using Receiver Operating characteristic (ROC) analysis. The steps are repeated for the next 3-min window with 30-sec overlap. A continuous time series is constructed by overlaying the scores for each 3-min window analyzed. A HRP segment of duration < 3-min are ignored and the HRP present on either side of the segment are considered to continue[1]. However, if there is a mismatch in HRPs present on either side of the segment, then that particular segment is considered as a transitory segment and the scores corresponding to it are ignored.

Visual assessment of fHRPs

In this section, we will discuss the visual scoring of the fHRP. The scoring was done using a computer program which presented the fHR to the experts in a window of 3 minutes. In the same window, there were four labels 1–4. The expert was asked to click one label which the expert considered to be the correct representation of the fHRP in that window. The following 3 minute window had two and half minutes of fHR presented in the last window and 30 seconds of new fHR. This procedure was continued until complete data were presented to the expert. At the end of the review, a continuous score was generated using scores from all presentations. The agreement between the experts’ scores was calculated using intraclass correlation coefficient (ICC) [19, 20]. The total number of 3 minute windows available and the instances of mutual agreement for the training and testing recordings are shown in Appendix Table 1 and Table 2, respectively.

Appendix Table 1.

Training recordings duration

ID	GA	Total number of 3-min window segments
		Available	Mutually agreed
1	34	34	12
2	36	8	8
3	37	54	27
4	33	54	0
5	32	54	30
6	32	54	0
7	34	16	13
8	36	54	53
9	33	50	39
10	36	28	22
11	33	54	39
12	37	34	10
13	37	54	36
14	37	54	16
15	32	52	23
16	35	54	30
17	30	54	52
18	36	24	17
19	32	54	54
20	32	29	20
21	31	48	5
22	32	54	42
23	32	52	42
24	37	54	1
25	36	54	39
26	36	30	30
27	36	18	15
28	33	54	34
29	33	54	39
30	36	50	26
31	33	54	46
32	36	54	25
33	35	54	20
34	34	54	34
35	36	52	44
36	32	54	45
37	37	54	43
38	34	54	27
39	32	54	20
40	32	54	33

Appendix Table 2.

Testing recordings duration

ID	GA	Total number of 3-min window segments
		Available	Mutually agreed
41	31	54	0
42	35	54	14
43	32	54	34
44	30	54	27
45	33	54	36
46	35	54	27
47	34	54	39
48	35	54	49
49	30	54	11
50	32	54	13
51	33	54	23
52	37	54	15
53	36	54	31
54	37	54	17
55	35	54	25
56	37	54	42
57	35	54	39
58	36	54	23
59	36	54	41
60	36	54	40
61	38	54	18
62	36	54	35

Standardization of the threshold

Several studies which investigated the development of behavioral states in human fetus found the synchronization of state variables to be evolving with gestational age (GA) [1, 21]. Nijhuis [1] in his seminal work defined the behavioral state to be present from 36 weeks of gestation onwards. However, before 36 weeks of gestation, there could be instances of synchronization of the state variables and these are considered as coincidental states. In addition, Schneider et al. [22] have also shown the existence of a gestational trend associated with fHRPs. In order to account for these gestational influences in the evolution of the fHRPs and fBS, we computed the objective thresholds using the ROC analysis for the two groups, namely Early GA: GA < 36 wk and Late GA: GA ≥ 36 wk separately. Using the thresholds identified from ROC analysis, we tested the 22 unused records. The performance of the proposed approach with the experts’ score was studied using ICC.

Association of fHRP to their corresponding fBS

In order to associate the HR acceleration to their corresponding fetal movements, the fetal movement marker signal is scanned for the presence of significant fetal movement detected in a short window of ± 5-sec duration around the onset of HR acceleration marked. If the change in the baseline of the actogram exceeded a predefined threshold (0.12cm), it was considered a significant movement (for details see [23]). The choice of 5-sec window duration is based on the known time lag between fetal movement and HR acceleration[24]. Based on the association between fetal movement and HR acceleration, the fBS can be assigned using the relationship shown in Table 1.

RESULTS

The HR corresponding to 62 recordings were independently reviewed by two experts in 3-min windows with 30-sec overlap for the fHRPs based on the Nijhuis definitions discussed before [25]. For each expert, a time series is constructed by overlaying the scores for each 3-min window analyzed. Table 3 shows the inter-scorer agreement for both the training and the testing recordings.

Table 3.

Inter-scorer agreement for the different fHRPs.

HRP	Training recordings		Testing recordings
	Intraclass Correlation Coefficient (95% CI)	P-value	Intraclass Correlation Coefficient (95% CI)	P-value
A	0.68 (0.66–0.71)	< 0.01	0.44 (0.39–0.50)	< 0.01
B	0.61 (0.58–0.64)	< 0.01	0.77 (0.74–0.80)	< 0.01
C	0.23 (0.18–0.28)	< 0.01	−0.10	> 0.05
D	0.40 (0.35–0.44)	< 0.01	−0.01	> 0.05

CI–Confidence Interval

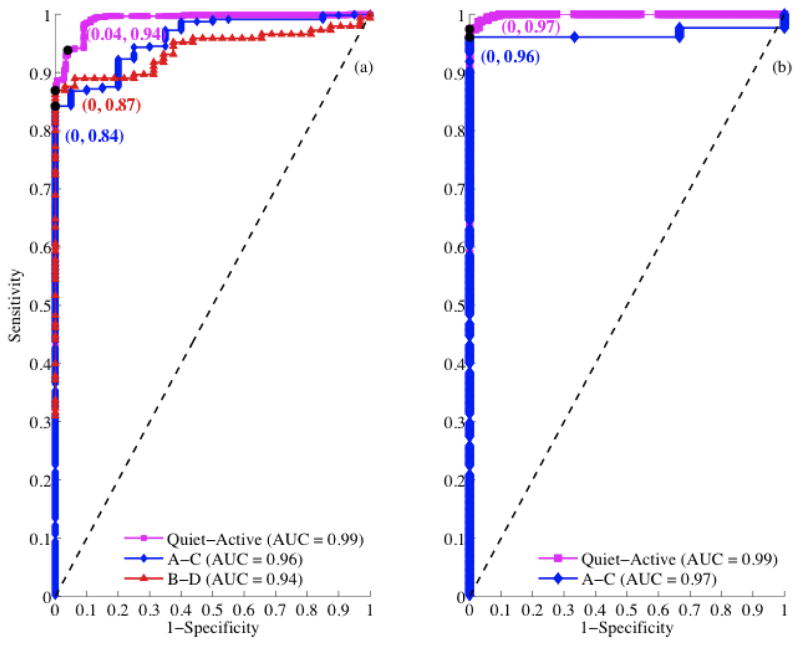
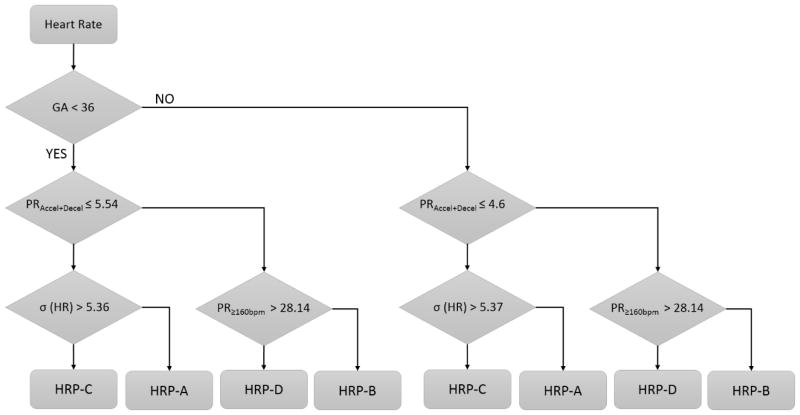
In order to build an unbiased model, the mutually agreed segments were used for the standardization of the thresholds. Figure 4 shows the ROC analysis for early and late GA groups for the extraction of objective thresholds. The sensitivity, specificity, and AUC values shown in Figure 4a and Figure 4b are greater than 0.85 for most of the comparisons. Figure 5 shows a flowchart of the fHRP detection procedure. The thresholds derived from ROC analysis to delineate different fHRP are also given in the decision boxes of the flow chart.

Figure 4.

ROC analysis for standardization of threshold. (a) and (b) correspond to ROC analysis for early GA and late GA respectively. The area under the ROC curve (AUC) which quantifies the degree of separation is given in the insert. The maximum deviation from the diagonal line is marked as a black dot and it represents optimal (1-specificity, sensitivity). The threshold corresponding to the black dot in each ROC curve defines the corresponding optimal threshold used in the detection of fHRPs.

Figure 5.

Flowchart of the fHRP detection procedure. The threshold derived from ROC analysis to delineate different fHR patterns are shown in decision boxes. In each step, the conditions satisfying the criterion in that step will go down further and those failing will detour sideways.

The objective thresholds obtained from the ROC analysis of early GA and late GA in the training recordings are evaluated for their performance on 22 testing recordings of 11 each in early and late GA group. In order to evaluate the performance of the fHRP detection approach, a time series corresponding to the mutually agreed expert scores for early and late GA are constructed and is considered as the ground truth. As seen from Table 3, in test recordings, there was no agreement between the two experts in scoring HRP-C and HRP-D and hence not considered in our performance evaluation.

Table 4 shows the performance of the proposed approach in detecting the fHRPs. There is high correlation between the algorithm score and experts’ score as quantified using ICC for pattern A however the agreement is moderate for pattern B.

Table 4.

Performance evaluation of the proposed fHRP detection approach for the testing recordings

HRP	Group
	Early GA		Late GA
	Intraclass Correlation Coefficient (95% CI)	P-value	Intraclass Correlation Coefficient (95% CI)	P-value
A	0.88 (0.85–0.90)	< 0.01	0.85 (0.82–0.88)	< 0.01
B	0.41 (0.34–0.49)	< 0.01	0.65 (0.59–0.70)	< 0.01

GA-Gestational Age, CI–Confidence Interval

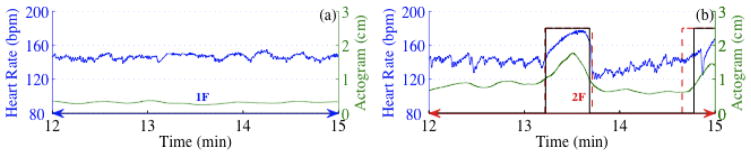
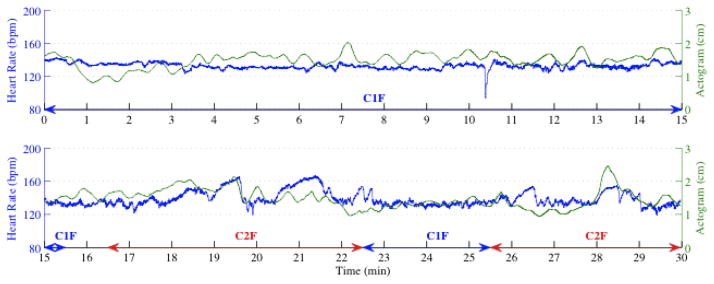
Figure 6 shows an example of the integration of fetal movement information in order to associate the fHRP to their corresponding fBS. Figure 7 shows an example of the performance of the fBS detection approach on fMCG signal recorded from a fetus for 30–min duration at 36 wk of gestation. In Figure 7 (0–15 min, top panel), there is no significant movement associated with the fHRP whereas in Figure 7 (15–30 min, bottom panel), the accelerations in the heart rate are associated with the accelerations in the actogram. The percentage occurrences of behavioral states 1F, 2F as detected by the proposed approach in both early and late GA are 25%, 68% and 40%, 58% respectively.

Figure 6.

Association of fHRP to their corresponding fBS. (a) and (b) represents the HR and the actogram corresponding to behavioral state 1F and 2F respectively. The vertical solid line and the dashed line represent the acceleration and the significant movement detected in the HR and actogram respectively.

Figure 7.

Performance of the fBS detection approach on fMCG signal recorded for 30-min duration from a fetus at 36 weeks of gestation.

DISCUSSION

Fetal behavioral states (fBS) are important indicators of fetal physiology [26]. The traditional way of assessing the fBS is based on visual analysis of real-time ultrasound for state variables, namely, fetal body and eye movements and HR patterns observed from CTG [1, 2]. In our study, we utilized the non-invasive fMCG recordings to obtain the HR and fetal movements simultaneously. To this end, a linear de-trending procedure was applied to objectively detect the fHRPs. The thresholds used in the detection procedure were standardized based on expert scores. The detected fHRPs were then associated to their corresponding fBS based on their temporal synchronization with fetal movement.

Several works have underscored the challenges involved in estimating a baseline fHR [27–29]. This is primarily due to the dynamic changes in the baseline activity caused by state changes and even within certain states. For example, the variability in the baselines of states B and D, can be very high. In our opinion, the dynamic detrending approach proposed to tackle the varying nature of the baseline performed reasonably well; although there is still room for improvement, as with our method we have still detected a number of decelerations in FHR patterns that should seldom be observed in low-risk fetuses.

To our knowledge, this is a first detailed report on an automated fBS detection approach which considers the temporal synchronization of fetal movement and fHRPs in detecting the fBS. Our approach is able to clearly distinguish between fHRPs by using standard deviation, duration and extent of acceleration from baselines before and after 36 weeks.

A decrease (−9.5%) in the duration of 1F and an increase (16%) in the duration of 2F in the late GA group compared to early GA is in line with the overall pattern of maturation based on the quiet sleep and active sleep patterns observed in EEG and fMEG reports on premature neonates and fetuses [30, 31]. Furthermore, the increase in the duration of 2F in late GA compared to early GA is in accordance with the Nijhuis et al. [1, 25] finding that the synchronization of the state variables (fetal movement and heart-rate patterns) evolve with gestational age signifying the ongoing maturation and coordination of the fetal central nervous system (CNS) [24, 32, 33].

Most of the studies have underlined the significance of fHRP alone as an important parameter in defining the fBS and to understand the level of fetal ANS control [34] and references therein. However, the proposed approach has demonstrated the feasibility of using the temporal coincidence of state variables in detecting the fetal behavioral states by utilizing the spatio-temporal characteristics of the fMCG system. In addition to understanding the development of the fetal ANS, the temporal coincidence of state variables may help to understand the synchronization phenomenon in the coordination of fetal CNS. The coupling between fetal heart and movement has been shown to be interrupted by several factors including high levels of maternal stress, conditions leading to preterm birth, and other maternal high-risk conditions [32, 33]. These scenarios present us with future areas of investigation wherein the proposed objective fBS detection approach could help clinicians to decipher the development of ANS, assess fetal wellbeing and ultimately contribute to the better management of high-risk pregnancies including growth- restricted or hypoxic fetuses. In addition, as indicated in [35], the automated detection of fBS could facilitate the detection of spontaneous brain patterns during sleep states which could serve to define a fetal neurological maturation chart for normal fetuses similar to the growth chart for newborns.

This study has certain limitations. It is known that active patterns (C and D) are rare occurrences during the entire gestational period and hence we were not able to reliably test for the occurrence of these patterns [36, 37]. Furthermore, only two experts were involved in this work to review the patterns which inflated the error rate in testing the algorithm. The fBS has been shown to vary with sex of the fetus [38] and in this work we have not accounted for the gender.

CONCLUSION

Growing evidences suggest the high reliability of fMCG in the study of the fetal autonomic nervous system development [6, 39–41]. Further, the superior time and spatial resolution features of fMCG make this technique an excellent tool to study other parameters including heart-rate and fetal movement. In this paper, we propose a computer-aided approach to detect the fetal behavioral states based on the patterns observed in the heart-rate and fetal movement obtained from fMCG recordings. The thresholds used in the detection procedure were standardized based on the expert scores. The proposed approach employs a temporal synchronization of state variables such as fetal movement and heart-rate patterns in detecting fetal behavioral states. The potential benefits of the proposed approach would be an objective assessment the fetal behavioral states which in turn could help clinicians to better management of high-risk pregnancies.