Inpainting as a Technique for Estimation of Missing Voxels in Brain Imaging

Abstract

Issues with model fitting (i.e. suboptimal standard deviation, linewidth/full-width-at-half-maximum, and/or signal-to-noise ratio) in multi-voxel MRI spectroscopy, or chemical shift imaging (CSI) can result in the significant loss of usable voxels. A potential solution to minimize this problem is to estimate the value of unusable voxels by utilizing information from reliable voxels in the same image. We assessed an image restoration method called inpainting as a tool to restore unusable voxels, and compared it with traditional interpolation methods (nearest neighbor, trilinear interpolation and tricubic interpolation). In order to evaluate the performance across varying image contrasts and spatial resolutions, we applied the same techniques to a T1-weighted MRI brain dataset, and N-acetylaspartate (NAA) spectroscopy maps from a CSI dataset. For all image types, inpainting exhibited superior performance (lower normalized root-mean-square errors, NRMSE) compared to all other methods considered (p’s<0.001). Inpainting maintained an average NRMSE of less than 5% even with 50% missing voxels, whereas the other techniques demonstrated up to three times that value, depending on the nature of the image. For CSI maps, inpainting maintained its superiority whether the previously unusable voxels were randomly distributed, or located in regions most commonly affected by voxel loss in real-world data. Inpainting is a promising approach for recovering unusable or missing voxels in voxel-wise analyses, particularly in imaging modalities characterized by low SNR such as CSI. We hypothesize that this technique may also be applicable for datasets from other imaging modalities, such as positron emission tomography, or dynamic susceptibility contrast MRI.

INTRODUCTION

The use of voxel-wise analyses of structural, functional, metabolic, perfusion or other data (e.g., to evaluate pathological alterations in a given patient group, or associations between imaging and clinical variables) is very widespread in brain imaging. Compared to region-of-interest (ROI) analyses, which require averaging the signal over multiple voxels across a predefined region, voxel-wise analyses allow localizing effects of interest with great spatial accuracy, often improving sensitivity to detect spatially restricted effects that may be diluted in ROI analyses.^1–4

On the other hand, the use of voxel-wise analyses can come with a cost, in terms of signal-to-noise ratio (SNR). Chemical shift imaging (CSI), for instance, enables the performance of multi-voxel MRI spectroscopy, therefore conferring imagers the ability to interrogate metabolite levels across a larger portion of the brain, and with higher spatial resolution, compared to single voxel spectroscopy. However, the smaller size of the CSI voxels can lead to lower SNR and reduced power due to poor spectral fits (i.e. suboptimal standard deviation, and/or linewidth/full-width-at-half-maximum), ultimately leading to some percentage of voxels becoming unusable. While these unusable voxels can be more commonly expected in some parts of the brain (e.g., regions more likely affected by magnetic inhomogeneities, ventricles), in other parts their spatial distribution can be somewhat random and idiosyncratic across subjects. This becomes particularly problematic for analyses in standard space: once multiple CSI maps, each with a different pattern of unusable voxels, are brought to a standard space for higher level analyses, the resulting common standard space can be significantly reduced, and sometimes rendered overall unusable, given that only voxels that are contributed to by all participants can be interrogated in these analyses.

A potential solution to minimize this problem is to recover the missing data using interpolation methods, which allow the estimation of missing data points within the range of a discrete set of known data points.⁵ These methods try to recover missing data by fitting functions to known data points, so that the missing values can be estimated, for instance by interpolation. While these methods are commonly used in medical imaging (e.g., when resampling volumes), their performance is often affected by errors in the fitting, resulting in discontinuities, granularity and unrealistic values,^6,7 potentially leading to inaccuracies in subsequent analyses including, but not limited to, misregistration, incorrect region of interest delimitation or biased quantification.

An alternative to traditional interpolation methods is provided by image inpainting.^8,9 Inpainting, sometimes also called “fill in”, is a method that fills in missing or corrupted parts of an image by taking into account both its global and local features. Inpainting techniques have been mainly used in art restoration as well as in photography and cinema editing (e.g., to remove “red eyes”, edit text/objects, remove cracks and other imperfections). Also, these techniques are commonly used to replace lost blocks in compressed, or transmitted images.^10–12

To date, inpainting has not been broadly applied to brain imaging. The few applications published so far have assessed the ability of inpainting methods to alleviate the bias induced by multiple sclerosis lesions in morphometric estimates,^13–15 or to correct artifacts created by metallic implants.¹⁶

In this work, we explored the use of the inpainting approach to restore poor CSI data (part of these results were shared in a preprint submitted to the bioRxiv server¹⁷). Further, in order to evaluate the performance across varying contrast types, spatial resolutions and images sizes (pixel numbers), we also applied the same technique to T1-weighted images (containing homogenous regions and gradients of intensities following the underlying anatomy). These results would serve as a proof of concept to set up the basis for future research on the use of these methods in brain imaging.

MATERIALS AND METHODS

Inpainting and Interpolation Assessment Setup

In this study, we evaluated the performance of inpainting and several common image interpolation methods by corrupting different image types (T1-weighted volumes and N-Acetyl Aspartate (NAA) CSI maps), recovering those voxels with inpainting/interpolation methods, and then computing the error between the intensity values of the voxels from the ground truth images and those from the corresponding voxels in the inpainted/interpolated images.

Two image degradation strategies were implemented. First, all images were corrupted in such a way as to cause the images to randomly lose 5% to 95% of voxels (“%loss”; in steps of 5%). The NAA maps used in these tests were raw, and not thresholded to meet typical quality control (QC) standards (see subsection II.C Data Processing). These tests were performed once per %loss level for each of the available T1 or CSI images, each time with a different random distribution of missing voxels. Second, because low quality CSI voxels tend to be more expected in some areas of the brain (e.g., regions more likely affected by magnetic inhomogeneities or low SNR) rather than being randomly distributed, the same NAA maps were corrupted in the spatial distribution encountered in real-life scans, in order to validate the methods in a more realistic scenario. To this end, we identified NAA images from 5 subjects demonstrating a significant proportion (mean±SD: 28.3±8.8%; range 18.0–37.5%) of voxels not meeting a standard QC criterion (voxel-wise SD<20%). From these subjects, we extracted masks representing those “bad NAA voxels” (i.e., voxels not meeting the standard QC criterion), and affine registered each of them to the NAA maps from 10 subject images presenting less than 10% of missing voxels in the field of view (FOV) (7.4±1.9%, range 4.6–9.7%). The ability of the various methods to rescue the ground truth voxels (i.e., the voxels meeting QC standards) from the “good NAA maps”, after imposing onto them the missing voxels derived from the “bad NAA maps”, was assessed by computing the normalized root mean square error (NRMSE).

Datasets

Eighteen healthy controls (HCs; mean age, 46.4±14.4 y; range, 23–66 y; 8 males / 10 females) were screened and enrolled in this study. Participants were excluded if they had any MR contraindications such as metallic implants, history of head trauma and/or claustrophobia, had a history of major medical or psychological disorders. A more detailed description of the studies and their criteria can be found in.^18–20 The research protocol was approved by the local Institutional Review Board (Partners Healthcare Human Research Committee) and written informed consent was acquired from all participants. From all acquired images, T1-weighted MR brain and CSI datasets were used in this study.

MR imaging was performed in a 3T Siemens TIM Trio scanner (Siemens, Healthineers) using an 8-channel head and neck coil, and included an anatomical T1-weighted volume (MEMPRAGE; TR/TE1/TE2/TE3/TE4=2530/1.64/ 3.5/5.36/7.22ms, flip angle=7°, voxel size=1×1×1mm, acquisition matrix=280×280×208), CSI (LASER excitation and stack-of-spiral 3D k-space encoding; TR/TE=1500/30ms, volume of interest VOI=100×80×50mm, FOV=240×240×100, matrix 24×24×10, voxel size=10×10×10mm).²¹

Data Processing

MRI bias correction was performed on the anatomical T1-weighted images using the N4ITK MRI Bias Correction module of 3D Slicer 4²² to correct for inhomogeneities caused by subject-dependent load interactions and imperfections in radiofrequency coils. We set the advanced parameters to 3 levels of resolution with 500, 400 and 300 iterations respectively, and a convergence threshold of 0.00001 to ensure proper modeling of the inhomogeneity bias.

CSI raw spectra data were transferred to a workstation where metabolites were fitted with LCModel software²³ using a bias set simulated with GAMMA environment²⁴ for LASER excitation²⁵ with the same pulse modulation as the acquisition sequence. Quality criteria for spectral fitting included linewidth (full-width at half maximum FWHM) less than 0.1 ppm (12Hz at 3T), SNR bigger than 3, and Cramer Rao lower bounds less than 20% (relative to the fitted value).²⁶ Metabolic maps were reconstructed and registered to the anatomical images using a combination of MINC/FSL/Matlab tools.²⁷

Inpainting

The aim of inpainting is to provide an estimation of missing/corrupted parts of an image so that it looks natural to the human eye. As opposed to other methods, inpainting takes into account global, in addition to local, properties of the image. In general, the missing regions in an image might be composed of structures and textures, and separating these properties in two different steps is essential, starting by first recovering the structures and then recovering the texture.²⁸

Several inpainting approaches were developed in computer vision (variational image inpainting, texture synthesis, image completion, etc).⁹ For the purpose of its application to brain imaging, we have assessed a Matlab (Natick, MA) implementation based on a penalized least squares regression method that allows restoring missing data by means of the discrete cosine transform (DCT-PLS).^29,30 This method uses nearest neighbor interpolation to obtain a rough guess. Then, it introduces the texture information by deriving a statistical model that expresses the data in terms of a sum of cosine functions oscillating at different frequencies. Thus, the DCT-PLS searches for 𝑋̂ that minimizes equiation (1):

$$F(\widehat{X})={\Vert W^{1/2}\circ (\widehat{X}-X)\Vert }^2+s{\Vert {\nabla }^2\widehat{X}\Vert }^2$$ (1)

where X is the dataset with missing voxels, W is the matrix defining wheter a voxel is missing or not, s is a positive scalar that controls the degree of smoothing, ‖ ‖ is the Euclidean norm, ∇² is the Laplace operator and ∘ is the Schur product. The s parameter needs to have an infinitesimal value (≈ 0) for the purpose of filling-in gaps and avoiding the loss of high frequency components. Equation 1 can be reorganized so that $\widehat{X}$ can be derived by using the DCT–II and its inverse (IDCT) as:

$$\widehat{X}=\mathit{IDCT}(\mathrm{\Gamma }\circ DCT(W\circ (X-\widehat{X})+\widehat{X}))$$ (2)

where Γ is a three-dimensional filtering tensor defined by:

$${\mathrm{\Gamma }}_{i_x,i_y,i_z}={\left(1+\mathrm{s}{\left({\sum }_{k=1}^3\left(2-\cos \frac{\left(i_k-1\right)\pi }{n_k}\right)\right)}^2\right)}^{-1}$$ (3)

where i_k corresponds to the k^th element along the k dimension, and n_k corresponds to the size of X along that dimension. Reference by Garcia D. contains detailed mathematical details of this method.²⁹

Multivariate Interpolation Methods

As comparators, we have used three different multivariate interpolation methods commonly used in medical imaging: nearest neighbor, trilinear and tricubic interpolation.⁵ The function to be interpolated is known in the surrounding voxels (i_x, i_y, i_z) and the interpolation problem consists of approximating the value of an unknown voxel (j_x, j_y, j_z). These methods were also implemented in Matlab.

Nearest Neighbor Interpolation

Nearest neighbor interpolation is a method that replaces the value of the poorly-fitted voxel with that of the closest neighboring voxel. This method has been widely used due to its inherent fast computation. However, it can yield jagged and discontinuous values.

Polynomial Interpolation

Polynomials are commonly used to approximate complex curves by fitting a mathematical function to a series of data points, subject to some constraints such as minimizing the residuals. In this paper, we have assessed polynomial interpolations with one (trilinear) and three (tricubic) degrees of freedom for each variable, computed over a 11×11×11 patch centered on the voxel being interpolated. Trilinear interpolation allows estimation of missing values by fitting a linear polynomial to the known data as described in equation (4), which corresponds to the scalar function of a plane, and where a_x, a_y, a_z and a₀ are the coefficients of the polynomial, and x, y and z correspond to points in the space.

$$F(\widehat{X})=a_{x}x+a_{y}y+a_{z}z+a_0$$ (4)

Tricubic interpolation allows estimation of missing values by fitting a cubic polynomial to the known data as described in equation (5), which adds degrees of freedom to the fitting, and where, again, a_x3, a_y3, a_z3, a_x2, a_y2, a_z2, a_x1, a_y1, a_z1 and a₀ are the coefficients of the polynomial, and x, y and z correspond to points in the space.

$$F(\widehat{X})=a_{x3}{x}^3+a_{y3}{y}^3+a_{z3}{z}^3+a_{x2}{x}^2+a_{y2}{y}^2+a_{z2}{z}^2+a_{x1}x+a_{y1}y+a_{z1}z+a_0$$ (5)

Polynomial interpolation can generate values for the missing data points that were not initially present in the original data set.

Analysis

Quantitative performance of the different methods was assessed by comparing the (NRMSE) computed between ground truth images and inpainted/interpolated images, using a repeated measures analysis of the variance (ANOVA) to evaluate the effect of method (inpainting, nearest neighbor interpolation, trilinear interpolation, tricubic interpolation), %loss (from 5 to 90%), and their interaction. Bonferroni-corrected T-tests were computed as follow-up tests, comparing inpainting against the other methods for each %loss level. Bonferroni correction was achieved by multiplying the p value by the number of %loss levels (N = 19); e.g., p_corr= 0.05 corresponds to p_uncorr = 0.00263. In order to assess the different methods in the real-life loss distribution scenario, we used a one-way ANOVA on ranks (Kruskal-Wallis), followed by paired-samples Wilcoxon signed rank tests to assess if the performance of inpainting was significantly different from the rest of the methods.

RESULTS

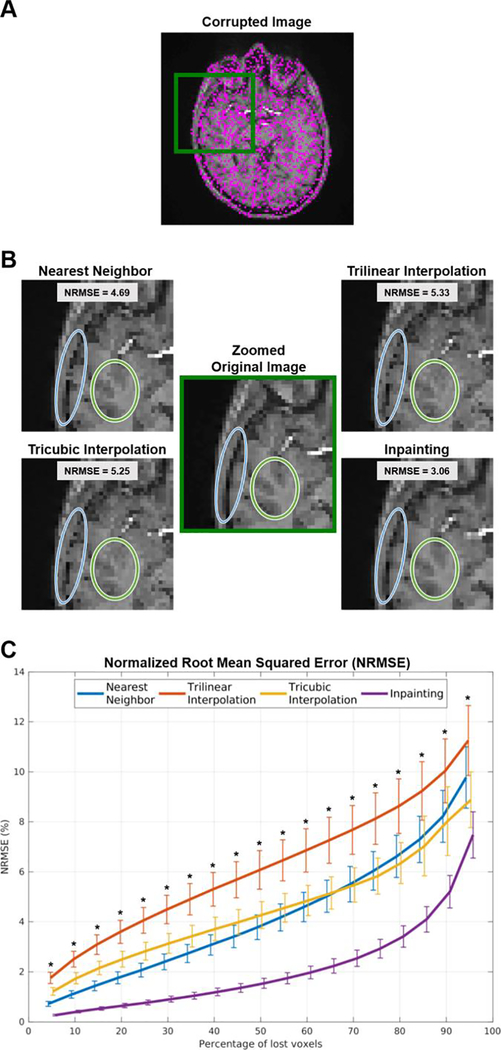
Overall, different methods filled-in missing pixels/voxels with acceptable results. However, inpainting outperformed the other methods independently of the image used, i.e., T1-weighted images (Figure 1A) or CSI NAA maps (Figure 2A).

Figure 1.

(A) T1-weighted image showing 50% of corrupted voxels (in magenta). (B) Zoomed view displaying details of the images restored using the various methods and their performance to maintain edges and structures. (C) Normalized root mean square error (NRMSE) for the different methods, across different percentages of voxels loss. ∗ p’s < 0.001 when directly comparing inpainting against all other methods in pairwise post-hoc analysis.

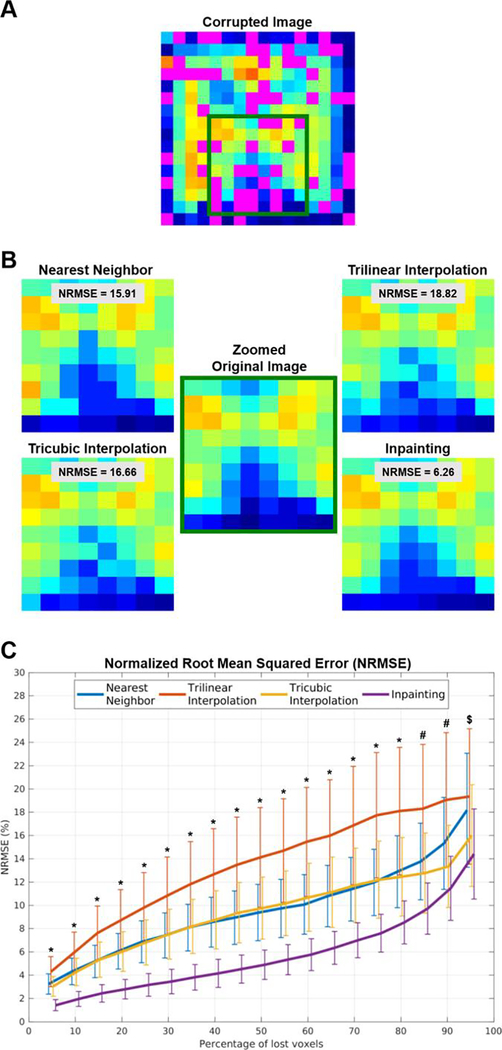
Figure 2.

(A) NAA CSI image showing 50% of corrupted voxels (in magenta). (B) Zoomed view displaying details of the images restored using the various methods and their performance to maintain the ground truth distribution. (C) Normalized root mean square error (NRMSE) for the different methods, across different percentages of voxels loss. ∗ p’s < 0.001 when directly comparing inpainting against all other methods in pairwise post-hoc analysis; # p′s < 0.05 only when directly comparing inpainting against nearest neighbor and trilinear interpolation; $ no statistical differences found between inpainting and any of the other methods.

Analysis Applied to T1-weighted Images

Figure 1 shows the qualitative and quantitative performance assessment of the different methods when interpolating randomly lost voxels from a T1-weighted image. As for the graphical illustration, nearest neighbor interpolation introduced noise via quantization, and both polynomial interpolation methods introduced granularity, whereas inpainting afforded a result that is more similar to the original image. These improvements of inpainting can be especially noticed at the edges between different structures or tissue types (e.g., between skull and brain, or between gray and white matter; Figure 1B). Quantitative assessment of the restored data shows a noticeable bias when using classical interpolation methods, compared to inpainting (Figure 1C). Remarkably, inpainting maintained an average NRMSE of less than 5% even with 75% missing voxels, a %loss level at which other techniques exhibited approximately three times (nearest neighbor, tricubic interpolation) or four times (trilinear interpolation) higher NRMSE.

The ANOVA revealed a statistically significant effect of method (F_3,51 = 1018.6, p < 0.001) and percentage of lost voxels (%loss; F_18,306 = 1122.6, p < 0.001). We also observed a statistically significant method ∗ %loss interaction (F_54,918 = 123.3, p < 0.001), and the decomposition of the interaction using post-hoc pairwise comparisons revealed that inpainting outperformed all other methods at all %loss levels (p’s < 0.001).

Analysis Applied to CSI NAA images

Figure 2 shows the assessment on NAA CSI images. Despite the inherent low resolution of these images, we can appreciate the noise introduced by interpolation methods, with inpainting being the method that maintained a voxel distribution that was the most similar to that of the original images (Figure 2B). Once again, the quantitative assessment of the different methods shows a noticeable improvement when using inpainting (Figure 2C). Inpainting maintained an average NRMSE of less than 5% even when with 50% missing voxels, whereas the other techniques demonstrated approximately twice (nearest neighbor, tricubic interpolation) or three times (trilinear interpolation) that value at that %loss level.

The ANOVA revealed a statistically significant effect of method (F_3,51 = 99.9, p < 0.001) and percentage of lost voxels (%loss; F_18,306 = 243.1, p < 0.001). Again, we also observed a statistically significant method ∗ %loss interaction (F_54,918 = 76.4, p′s < 0.001), and the decomposition of the interaction using post-hoc pairwise comparisons revealed that inpainting outperformed all other methods for all %loss levels up to 80%loss for the CSI NAA maps (p’s < 0.001). Inpainting also outperformed nearest neighbor and trilinear interpolation for %loss levels between 85%loss and 90%loss (p’s < 0.05). No statistical differences were found for a 95%loss level.

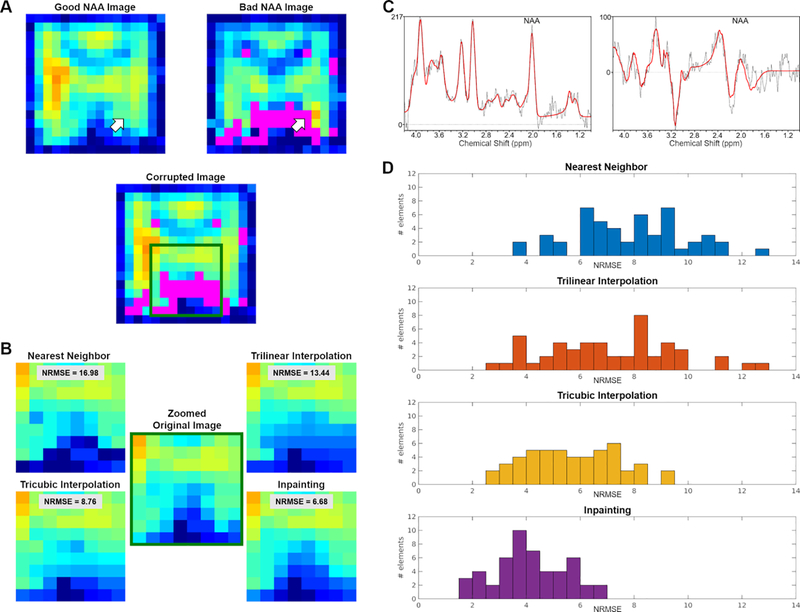
In order to validate our methods in a more realistic scenario, the same NAA maps were corrupted in the same spatial distribution encountered in a dataset from actual CSI scans (Figure 3). We extracted masks representing “bad NAA voxels” (SD > 20%) for those subject images losing more than 15% of voxels in the FOV, and registered those masks to images presenting an excellent NAA amplitude map. Figure 3D shows the histograms for the NRMSE values computed for the different methods. The Kruskall Wallis test revealed a statistically significant effect of method (p < 0.001). Follow-up post-hoc Wilcoxon signed rank tests showed significant differences in the inpainting NRMSE, as compared to the nearest neighbor, the trilinear and the tricubic interpolation methods (p′s < 0.001). These results indicate that, once again, inpainting performed better than other methods, even when the voxels to be recovered had a spatial distribution consistent with that of actual CSI low-quality data.

Figure 3.

(A) Examples of a “good NAA CSI image” (left) and a “bad NAA CSI image”, showing in magenta a significant proportion of voxels not meeting QC threshold (right). Below is the result of imposing the mask from the “bad image” (in magenta) onto the “good image”. (B) Zoomed view displaying details of the images restored using the various methods and their performance to maintain the ground truth distribution. (C) Spectra and fittings corresponding to a “good voxel” (left) and a “bad voxel” (right) pointed by the white arrows in panel A. (D) Histogram of NRMSE distribution for the four different methods. NRMSE are binned in 0.5 wide bins.

DISCUSSION

For a CSI voxel estimator to be considered viable, it needs to meet several minimum QC criteria including, but not limited to, the standard deviation of the estimators, the linewidth or FWHM of their spectrum, and/or the signal-to-noise ratio (SNR) in a given location. When a voxel does not meet these criteria, it is typically excluded. The presence of missing voxels can be problematic, as this could decrease statistical power or even make datasets unusable. This is particularly the case when data are analyzed in standard space, given that only voxels that are contributed to by all participants can be interrogated in these analyses. Our study evaluated the use of the inpainting approach as a tool to estimate values of previously unusable or missing voxels, such as in the case of CSI voxels not meeting minimum QC criteria.

Inpainting methods were developed as a set of techniques for recovering information in missing parts of an image, taking into account the local and global context, while more traditional interpolation methods make only use of local information. Here, we directly compared the results of inpainting and other techniques, by corrupting data and evaluating how well each method recovered the original values. In order to evaluate the performance of the various methods across varying contrast types and spatial resolution, we applied the same techniques to T1-weighted brain MRI images as well as N-acetylaspartate (NAA) brain CSI images. Overall, our results show that the application of image inpainting methods yields significantly better results compared to traditional interpolation methods, across all image types evaluated. For the CSI data, the performance of inpainting maintained its superiority compared to the other methods, whether the voxels to be estimated were randomly distributed, or located in regions genuinely prone to voxel loss in an actual CSI dataset (i.e., as estimated from real maps).

Nearest neighbor interpolation does not allow for much flexibility, as all the newly estimated values are “clones” of already existing voxels; however, this technique has shown (as we have assessed here) great potential in brain imaging over the years. The main issue with polynomial interpolation arises from the possibility of overfitting the known data; even if the polynomial function passes through all known data points, the resulting function might lead to estimates that reflect unusual or unexpected values in the actual data range. In contrast, inpainting provides more accurate data restoration by taking also account of the spatial frequency of the image.

In this study, we used inpainting to infer poorly fitted CSI voxels specifically using N-acetylaspartate (NAA) maps. Of note, because brain NAA CSI datasets generally exhibit high SNR and low numbers of poorly fit voxels, the use of voxel-recovery methods might be even more relevant for other metabolites (e.g., glutamate/glutamine, myoinositol, etc). However, in this study we purposefully chose to apply our analyses on NAA maps because the relatively low percentage of poor quality voxels allowed us to compare the results of the various methods against a “ground truth”. Because the improvement demonstrated by the inpainting method was observed for both the brain T1 and CSI data, our results suggest that inpainting can outperform other, more commonly adopted, techniques across multiple contrasts and texture types, voxel size, etc. Notably, inpainting methods are typically applied on large and high-resolution images, relying on the availability of large numbers of pixels to extract useful features and successfully fill-in missing/corrupted values. However, our study shows that inpainting could provide satisfactory results even when applied to CSI data, despite their relatively small number of voxels, and inherent low spatial resolution.

Several limitations should be pointed out. First, our approach was applied on a relatively small number of datasets. Despite the fact that participants in this study covered a wide age range (23–66 y) and were fairly sex-balanced (8 males / 10 females), increasing the sample size would be desirable to report more representative and accurate results. Second, validation of our approach was performed using data from healthy controls subjects only. Thus, in order to further evaluate the reliability of inpainting as a tool for data restoration, this method should be further validated on images with lesions, (i.e., tumors), and other abnormalities. Third, our inpainting approach included an initialization step using nearest neighbor interpolation for “bad voxels.” While this approach was based on the premise that when a voxel does not meet a QC criterion, it should be discarded (i.e. treated as having zero information), even low-SNR (i.e. “bad voxel”) image regions do in fact contain some information and future versions of our algorithm could initialize the inpainting algorithm by using some information from the actual data instead of treating them as missing voxels.

Despite these limitations, our results suggest that CSI data analysis would substantially benefit from the use of inpainting methods, in order to alleviate problems arising when voxels do not meet the QC thresholds. This method might be particularly helpful when performing high level group voxel-wise analysis in standard space, as it would allow for a more complete coverage of the entire volume of interest, thereby increasing effective sample size and statistical power. Based on our findings, we hypothesize that this technique could also be used on other types of imaging datasets, such as positron emission tomography (PET) or dynamic susceptibility contrast MRI. For instance, voxel-wise estimation of PET kinetic parameters sometimes leads to unrealistic values due to high noise levels in small voxels.

It is important to also note that in this exploratory analysis we have evaluated a classical implementation of inpainting based on the DCT-PLS. However, several other inpainting approaches and implementations have also been developed, comprising methods that include more complexity in their formal definition and could potentially achieve even better performance. For instance, in the past decade, inpainting methods have evolved to include both classical algorithms and novel deep learning techniques.³¹ While there is no inpainting method that can inpaint all missing image regions, deep learning methods usually present with more generalization ability for more complicated data types. However, deep learning-based methods come with their own limitations, in that they need to be trained on a large amount of data to be effective. Nonetheless, evaluating the performance of these methods in brain imaging is warranted as a future research direction.

In conclusion, our exploratory study showed the applicability of an image restoration technique called inpainting to accurately recover poorly fitted CSI voxels. Future studies will need to evaluate to which extent the application of inpainting methods could also be beneficial when applied to other imaging modalities.