Abstract
Deformable image registration (DIR) of 4D-CT images is important in multiple radiation therapy applications including motion tracking of soft tissue or fiducial markers, target definition, image fusion, dose accumulation and treatment response evaluations. It is very challenging to accurately and quickly register 4D-CT abdominal images due to its large appearance variances and bulky sizes. In this study, we proposed an accurate and fast multi-scale DIR network (MS-DIRNet) for abdominal 4D-CT registration. MS-DIRNet consists of a global network (GlobalNet) and local network (LocalNet). GlobalNet was trained using down-sampled whole image volumes while LocalNet was trained using sampled image patches. MS-DIRNet consists of a generator and a discriminator. The generator was trained to directly predict a deformation vector field (DVF) based on the moving and target images. The generator was implemented using convolutional neural networks with multiple attention gates. The discriminator was trained to differentiate the deformed images from the target images to provide additional DVF regularization. The loss function of MS-DIRNet includes three parts which are image similarity loss, adversarial loss and DVF regularization loss. The MS-DIRNet was trained in a completely unsupervised manner meaning that ground truth DVFs are not needed. Different from traditional DIRs that calculate DVF iteratively, MS-DIRNet is able to calculate the final DVF in a single forward prediction which could significantly expedite the DIR process. The MS-DIRNet was trained and tested on 25 patients’ 4D-CT datasets using five-fold cross validation. For registration accuracy evaluation, target registration errors (TREs) of MS-DIRNet were compared to clinically used software. Our results showed that the MS-DIRNet with an average TRE of 1.2 ± 0.8 mm outperformed the commercial software with an average TRE of 2.5 ± 0.8 mm in 4D-CT abdominal DIR, demonstrating the superior performance of our method in fiducial marker tracking and overall soft tissue alignment.
Keywords: deformable registration, deep learning, CT
1. Introduction
Deformable image registration (DIR) has been used in many medical applications such as image segmentation (Brock et al 2017, Fu et al 2017, Oh and Kim 2017), motion estimation (Christensen et al 2007, Boldea et al 2008, Yang et al 2008), image fusion (El-Gamal et al 2016) and treatment response evaluations (Ou et al 2015, Tan et al 2016, Yip et al 2016). DIR is the process of establishing spatial correspondences between moving and target images. Depending on the medical needs, the moving and target images could be acquired from different viewpoints, at different times, using different modalities or from different subjects. Though DIR has been extensively studied over the past few decades, it remains an active research field since the current DIR performance has yet fully met the increasingly demanding medical needs.
In radiation therapy, respiration-induced abdominal tissue motion causes significant problems in treatment planning and irradiation delivery process. Owing to the development of four-dimensional computed tomography (4D-CT) that provides multiple scans over the respiratory cycle, the observation and tracking of internal soft tissue are clinically available. Thus, 4D-CT has been increasingly used in radiation therapy for treatment planning to reduce dose to healthy organs and increase dose to the tumor target (D’Souza et al 2007, Tai et al 2013). DIR is a promising tool to process the 4D-CT images to provide accurate motion tracking of internal organs and fiducial markers. Accurate and fast DIR on 4D-CT could aid the treatment planning process such as target definition, tumor tracking, OAR sparing and respiratory gating.
Traditional intensity-based DIRs such as optical flow and demons are iterative and generally very slow especially for large 4D-CT datasets. These methods usually apply spatial filters repeatedly throughout the iteration process to smooth DVF, which often results in oversmoothed DVF. Bony structures that have minimal motion throughout a respiratory cycle were sometimes falsely deformed due to the oversmoothed DVF. The large appearance variances and low image contrast of abdominal 4D-CT pose additional challenges for accurate registration.
Deep learning-based methods have outperformed many traditional image processing methods (Fu et al 2019), achieving the-start-of-art performances in many image processing tasks such as object detection (Onieva et al 2018, Xu et al 2019), classification (Anthimopoulos et al 2016, Shen et al 2017) and image segmentations (Fu et al 2018b, Cardenas et al 2019, Harms et al 2019, Jeong et al 2019). Recently, a thorough review on deep learning-based registration algorithms was published by Haskins et al who divided the deep learning-based image registration methods into three categories: deep iterative registration, supervised transformation estimation and unsupervised transformation estimation (Haskins et al 2019). Deep iterative registration algorithms aim to augment the performance of traditional, iterative, intensity-based registration methods by using deep similarity metrics. Therefore, deep iterative registration algorithms have the same limitation of slow computational speed as traditional registration algorithms. Supervised transformation estimation algorithms utilize either manually aligned image pairs in the case of full supervision or manually defined anatomical structure labels in the case of weak supervision. Manual preparation of large sets of training datasets is laborious, subjective and error-prone. To avoid manual processes, synthetic images were generated by deforming the moving image with an artificial DVF for the supervision of the transformation estimation networks (Sokooti et al 2017). However, the artificial DVF may lead to biased training since the artificial DVF is unrealistic and very different from actual physiological motion.
In this paper, we focused on unsupervised transformation estimation algorithms. The success of spatial transformer network (STN) has motivated many unsupervised deep learning image registration methods since STN allows the loss function to be defined without any manually aligned or pre-registered image pairs (Jaderberg et al 2015). The loss function could be defined using common image similarity metrics such as normalized cross correlation (NCC) and sum of squared difference (SSD) between the target and the deformed images. Common smoothness or inverse consistency constraints were used to regularize the predicted DVF to avoid unrealistic deformation such as negative determinant of the DVF Jacobian matrix. A 2D DIRNet was proposed to register handwritten digits using unsupervised training to optimize image similarity metrics (Vos et al 2017). De Vos et al trained a fully convolutional neural network (FCN) using NCC to perform 4D cardiac cine MR volume registration (2017). They showed that their method has outperformed Elastix based registration (Klein et al 2010). Later, de Vos et al proposed an unsupervised deep learning image registration (DLIR) method for affine and deformable image registration. DLIR was tested on cardiac cine MRI and chest CT image registration, showing much faster computational speed and comparable performance to conventional image registration (Vos et al 2018). Ghosal and Ray proposed another unsupervised DIR for 3D MR brain images by optimizing the upper bound of the SSD between the target image and the deformed image (Ghosal and Ray 2017). Their method outperformed the log-demons based registration. An unsupervised feature selection framework for 7 T MR brain images was proposed by Wu et al using a convolutional-stacked autoencoder network (2016). However, this method still inherits the existing iterative optimization for DVF calculations, which has slow computation speed. Kuang and Schmah proposed a network called FAIM to directly predict the DVF to register 3D MR brain images (2018). For DVF regularization, they used a smoothness term and another term to penalize negative Jacobian determinant of the DVF. A fast learning-based registration framework called VoxelMorph was proposed to perform pairwise medical image registration (Balakrishnan et al 2019). Two training strategies were explored in VoxelMorph, one being unsupervised and another being weakly supervised where auxiliary segmentations were used in loss function. The authors claimed that VoxelMorph could be used in lung CT images and multimodal registrations. However, the authors only tested VoxelMorph on MRI brain images. Another unsupervised deformable image registration method was proposed with an emphasis on the inverse-consistency of the predicted deformation field (Zhang 2018). The authors integrated an inverse-consistent constraint and anti-folding constraint to regularize the predicted DVF for diffeomorphic mapping. The method was only tested on T1-weighted MR brain images.
The aforementioned unsupervised methods were mainly focused on 2D/3D MR brain images and cardiac images. Compared to MR brain images registration, abdominal 4D-CT image registration is more challenging due to its poor image contrast and large abdominal motion. To overcome these challenges, we have developed a novel multi-scale unsupervised DIR network to directly predict DVF from any two phases of abdominal 4D-CT images. We have integrated attention-gates and discriminator into our network design to support accurate DVF prediction. The effectiveness of the attention-gates and discriminator was studied separately by performing comparisons between registration results with and without the corresponding component. Comparing to previously published studies, the major contributions of our work are:
To our best knowledge, we are the first group to develop a multi-scale unsupervised deep-learning based DIR for abdominal 4D-CT images.
Self-attention network was integrated into the generator and proven to be effective in differentiating moving structures from non/minimal-moving structures during registration.
Adversarial network was integrated into MS-DIRNet to enforce additional DVF regularization by penalizing unrealistic deformed image.
GlobalNet and LocalNet were combined to model multi-scale image information to register images that were subject to significant abdominal motion.
Our method has significantly outperformed clinically used software (Velocity™) in abdominal 4D-CT DIR.
2. Materials and methods
A set of abdominal 4D-CT datasets from 25 patients was retrospectively collected. The resolutions of the 4D-CT datasets range from 0.9 × 0.9 × 2.5 mm to 1.3 × 1.3 × 2.5 mm depending on the patient size. At least three fiducial markers were implanted in each patient for tumor localization and external beam treatment planning. These fiducial markers were used as landmarks to calculate target registration error for registration evaluation. Figure 1 outlines the schematic flow chart of the proposed method. The proposed method includes a training stage and an inference stage. The training stage includes a GlobalNet and a LocalNet. The GlobalNet was trained using down-sampled 4D-CT images to capture the global abdominal motion. A down-sampling factor of 4 was used in the study. The GlobalNet was able to predict a global DVF which captures the overall abdominal motion. The global DVF was then used by a spatial transformer network to generate globally deformed images. Due to the large abdominal motion and impaired image quality of the down-sampled images, the global DVF may not provide accurate local image registration. To improve the registration accuracy, a LocalNet was designed to capture local abdominal motion based on the globally deformed images and the target images. For LocalNet training, 3D patches were extracted by sliding a window with a size of 64 × 64 × 4 voxels from the globally deformed images and the target images with an overlap size of 48 × 48 × 56 voxels between two neighboring patches. The overlap size in the superior-inferior direction was set to be 56 instead of 48 since the respiration-induced abdominal motion was larger in this direction than the other two directions. The loss function of the MS-DIRNet includes an image similarity loss, a regularization loss and an adversarial loss. Details of the loss function are presented in section 2.2. In the inference stage, global DVF was first predicted by the GlobalNet to generate the globally deformed images. Then, patches of local DVFs were predicted by the LocalNet. Patch-based DVFs were subsequently fused by averaging to generate a whole-image local DVF. Final DVF was obtained by summing the global DVF and the local DVF.
Figure 1.
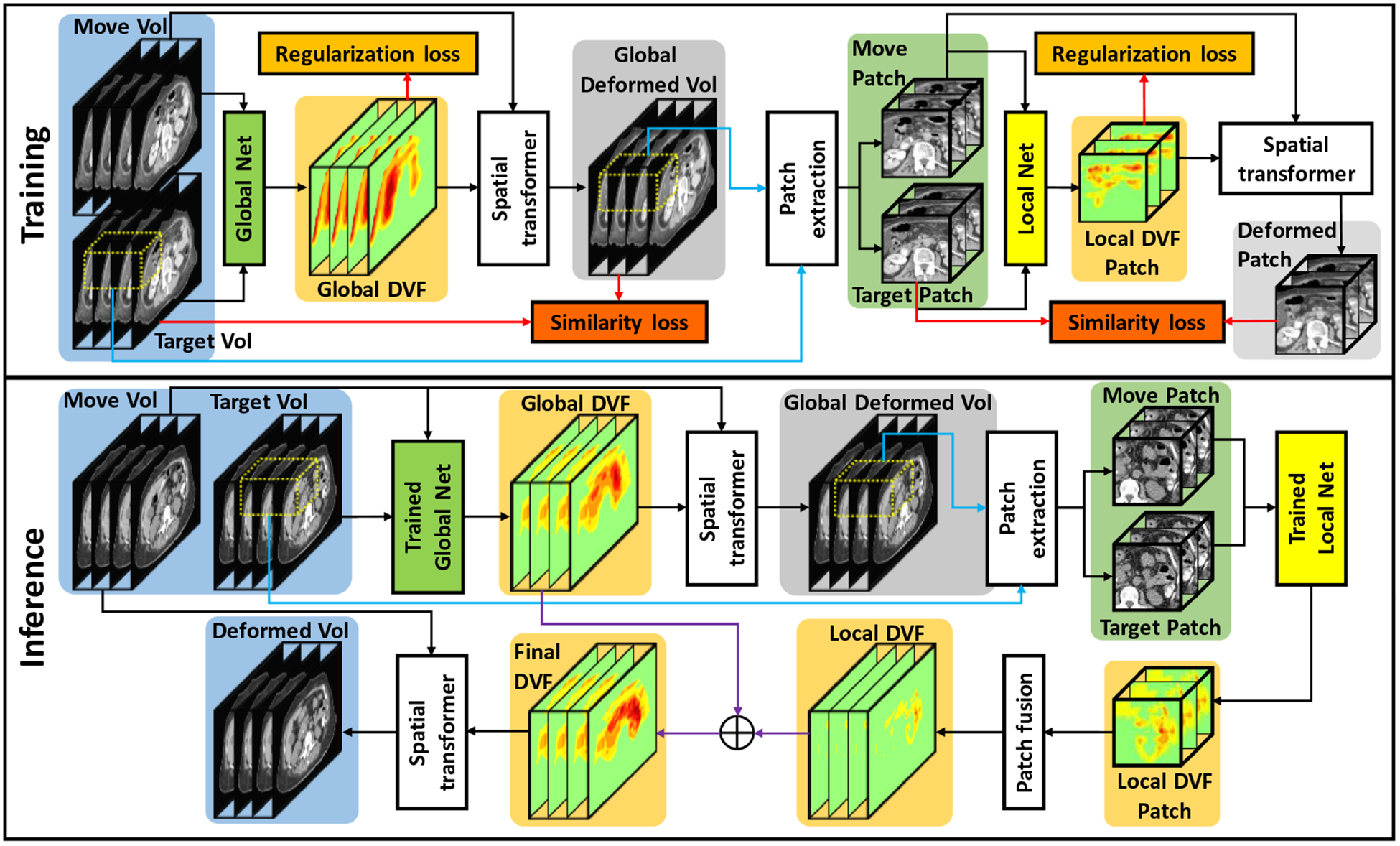
The schematic flow diagram of the proposed method. The upper part shows the training stage for global and local DVF generation. The lower part shows the inference stage where one phase was deformed to match target phase in 4D-CT.
The GlobalNet and LocalNet share similar generative adversarial network (GAN) structure, which is shown in figure 2. Image matrix sizes of the input image pairs were reduced in the encoding path after eleven convolutional layers. To generate DVFs with consistent matrix sizes as the input images, bilinear interpolation was used to up-sample the DVFs. Transpose-convolution layers with trainable parameters were another alternative to up-sample the DVFs to the same image size as the input images. However, we have found out that bilinear interpolation with no trainable parameters is much better than the transpose-convolution layers in predicting accurate DVFs. This is because bilinear interpolation tends to generate smooth DVFs that are desired in 4D-CT image registration. On the other hand, the transpose-convolution layers often generate unrealistic DVFs even with heavily-weighted DVF smoothness regularization term.
Figure 2.
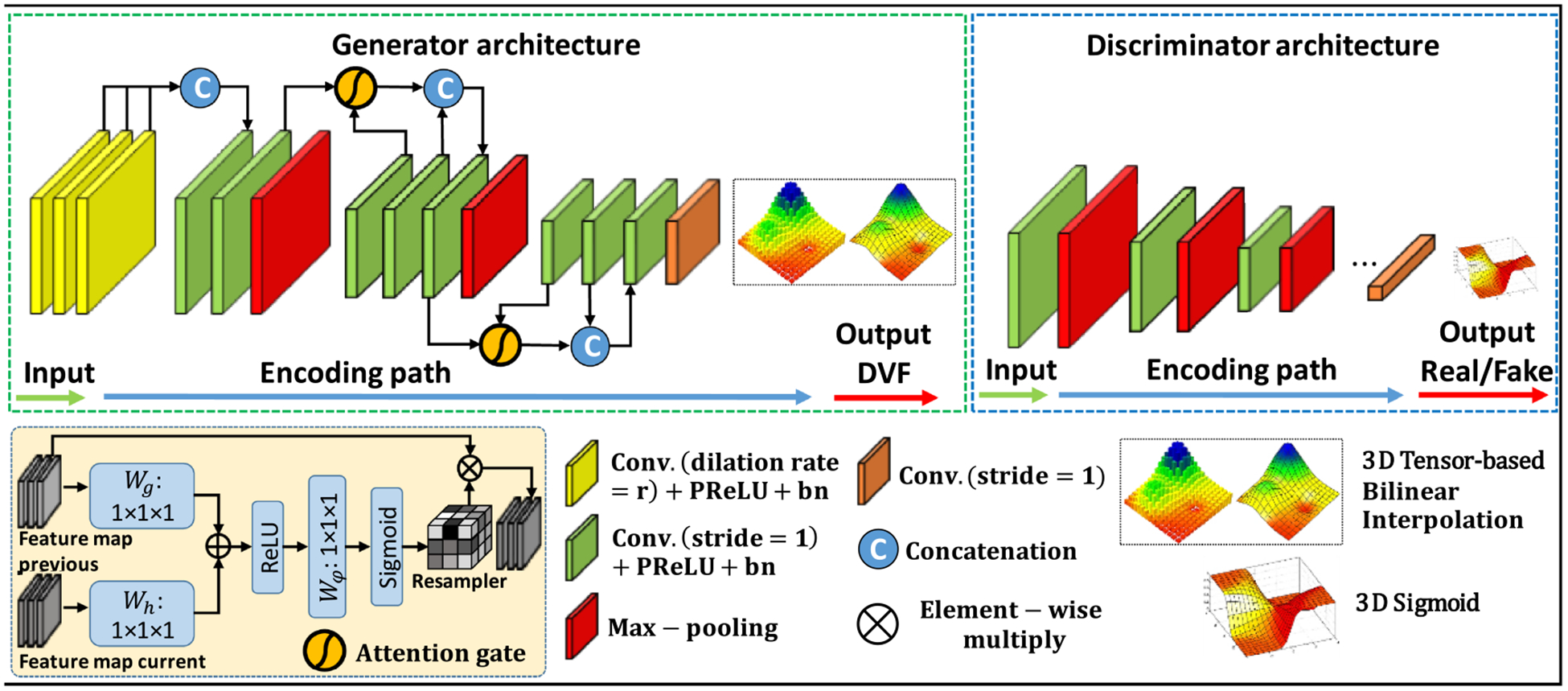
The network architecture for both GlobalNet and LocalNet. The generator was trained to generate DVFs. The discriminator was trained to differentiate deformed images from target images. The top row shows the network architecture of the generator and the discriminator. The bottom row details various operators used in the network architecture.
Since the network was designed to be trained in a completely unsupervised manner, DVF regularization was necessary to generate realistic DVF. Smoothness constraint was commonly used in the literature for DVF regularization. However, smoothness constraint alone is insufficient for realistic DVF prediction especially when the network is trained in a completely unsupervised manner. To this end, we proposed to integrate a discriminator into MS-DIRNet for additional DVF regularization. The discriminator was trained to differentiate the deformed images from the target images. MS-DIRNet was encouraged to predict realistic DVFs by penalizing unrealistic deformed images. The discriminator will not affect the inference speed as it was used only in the training stage. To further improve the network’s ability in capturing structural differences between the moving and target images, self-attention gate was integrated into the generator to extract information differences between feature maps of one layer and its previous layer from the encoding path (Mishra et al 2018). Details of the self-attention gates were described in section 2.1.
2.1. Self-attention network
Attention gates have been explored in the context of semantic segmentation (Romera-Paredes and Torr 2016). Previous works demonstrated that the most relevant semantic contextual information can be captured by integrating attention gates into a standard U-Net without the need to use a very large reception field (Oktay et al 2018). In this study, we incorporated attention gates into the design of our generator. Figure 2 shows that attention gates were used to connect layers that are next to max pooling layers. The attention gates combined feature maps of adjacent layers from different scales. The attention gates operations were performed immediately prior to the concatenation in order to retain only relevant activations and remove irrelevant/noisy responses. Additionally, the attention gates filtered the neuron activations during both the forward pass and the backward pass. Gradients originating from image background regions were down weighted during the backward pass. This allows model parameters in shallower layers to be updated based on spatial regions that are most relevant to a given task, i.e. motion estimation. Thus, the attention gates could have the ability to highlight the features from previous layers, which can well represent the motion.
2.2. Loss functions and regularizations
The loss function consists of three parts which are the image similarity loss, the adversarial loss and the regularization loss.
| (1) |
where φ = G(Imov, Ifix)represents the predicted deformation field for a moving and target image pair. The deformed image, Imov°φ,was obtained by warping the moving image patch by the predicted deformation field using spatial transformer (Li and Fan 2018). NCC (·) denotes the normalized cross-correlation loss, GD (·) denotes the gradient difference loss between the target and moving image patches. The cross-correlation loss and gradient loss of the images together represent the image similarity loss. ADV (·) denotes the adversarial loss. The adversarial loss was computed as the discriminator binary cross entropy loss of the deformed and target images. The discriminator was implemented using a conventional fully convolution network (FCN) (Dong et al 2019). The purpose of the adversarial loss was to encourage the deformed image to look like a realistic CT image by penalizing unreasonable DVFs and unrealistic deformed images. R (φ) denotes the regularization term.
| (2) |
The regularization term includes weighted first and second derivatives of the DVF to enforce general smoothness of the predicted DVF. Values of μ1 and μ2 were empirically set to be 1 and 0.5 in this study. After numeric experiments, we have empirically chosen the α, β, γ and δ to be 1, 200, 1000 and 10 respectively.
2.3. Training and testing
The proposed MS-DIRNet was trained and tested on 25 patients’ 4D-CT images using five-fold cross validation. Each 4D-CT dataset includes ten phases of 3D-CT throughout a respiratory cycle. 4D-CT datasets of 20 patients including a total of 200 3D-CT were taken as training datasets. During training, image pairs between any two phases of the ten phases were taken as the moving and target image pairs, which was equivalent to a total of 900 image pairs. The total number of training image pairs were doubled to 1800 image pairs after switching the moving and target image pairs. For testing, the 3D-CT image of the first phase T0 was registered with every other phase in a 4D-CT dataset. A total of 45 deformed images were generated for five testing patients. Our algorithm was implemented in python 3.6 and Tensorflow on a NVIDIA TITAN XP GPU with 12GB of memory. Adam gradient optimizer with learning rate of 1e-5 was used for optimization.
Figure 3 shows the convergence curves of the three loss functions, including the adversarial loss, image similarity loss and the DVF regularization loss for the GlobalNet and LocalNet, respectively. For better visualization, the loss curves were smoothed using a moving mean kernel with a window of 50 iterations for 10 times to show the average curves of the training process. The image similarity loss was reduced during training, indicating increased image alignment. The adversarial loss consistently went up since the DVF generator of MS-DIRNet was consistently improved, generating increasingly realistic deformed images, which caused the discriminator to perform poorly on differentiating between the original image and the deformed image. The DVF regularization loss first decreased and then increased during the training. This may be because that the network first learnt to globally align the moving and target images, resulting in relatively smooth DVFs with decreasing regularization loss. Then, the network learnt to deform the moving image locally to increase the image alignment and caused the DVFs to have larger local spatial variation, resulting in increasing regularization loss.
Figure 3.
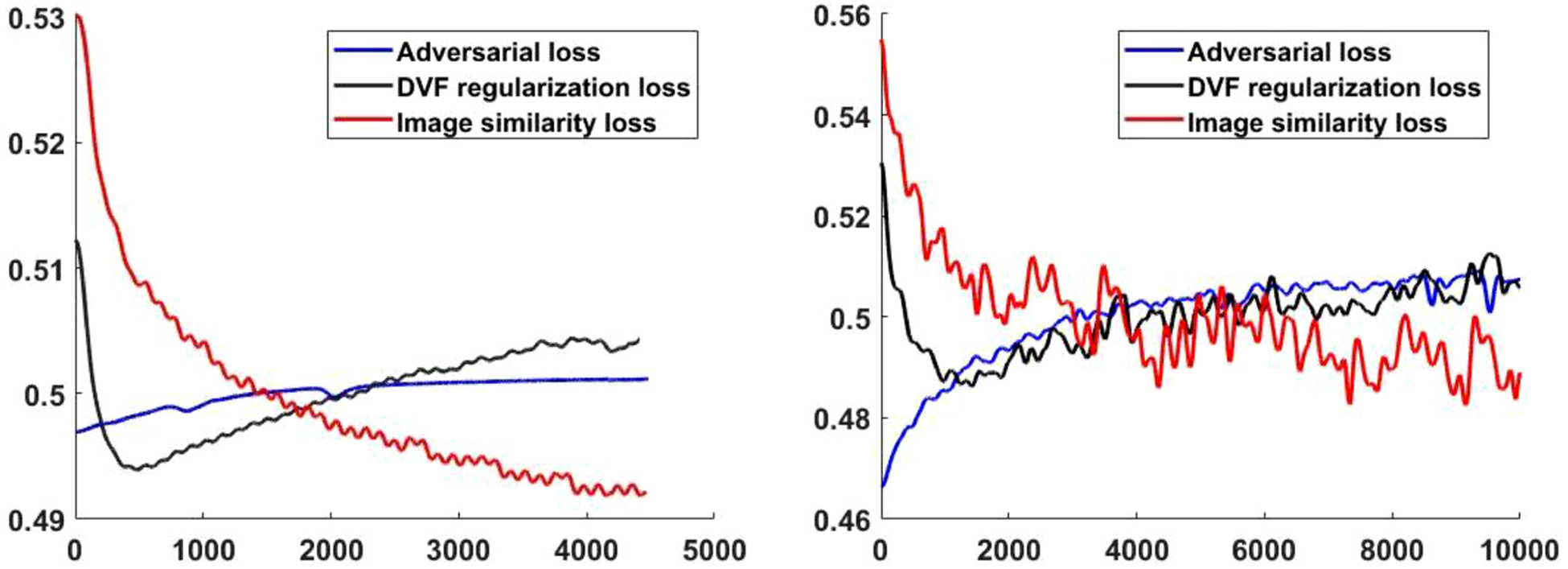
Convergence curves of the adversarial loss, DVF regularization loss and image similarity loss. Left: GlobalNet loss, right: LocalNet loss.
3. Results
3.1. Efficacy of self-attention
Our experiments suggested that the self-attention gates were very effective in learning the structural differences, which helped the registration process to distinguish between regions with major and minor motions. To demonstrate the efficacy of the attention gates, we designed an experiment to extract feature maps from many different small image patches (15 × 15 × 15) that were centered at locations subject to significant different motion patterns. The feature maps were extracted from the last convolution layers of the generator. Each feature map represented the encoded texture information of its corresponding image patch that was centered at a different image location. In this experiment, 2000 small image patches that were centered around spine and stomach were extracted. As shown in figure 4(a4), half of the small image patches were sampled around the spine (denoted by red points) while the other half were sampled around the stomach region (denoted by green points). Each of the extracted feature map was vectorized before they were put together to form a matrix with 2000 rows. Principal component analysis (PCA) was performed on the matrix. The first three principal components were displayed as 3D scatter plots in figure 4. For details on the experiment procedures and PCA analysis, please refer to our previous work (Harms et al 2019). As indicated by the difference image shown in figure 4(a3), the stomach region clearly has much more significant motion than the spine region. Nevertheless, the network performed poorly at differentiating the two regions without the self-attention gates, as suggested by figure 4(b1–b3). On the contrary, the network with attention gates successfully separated the two regions, as suggested by figure 4(c1–c3). Mean absolute error (MAE), peak signal to noise ratio (PSNR) and normalized cross correlation (NCC) were calculated between the deformed images and the target images for quantitative evaluations. Table 1 shows the comparison between the average registration results with and without attention gates over nine phase pairs for all patients. P-values were calculated using two-sample t-test to assess the statistical significance of the difference between results with and without attention gates.
Figure 4.
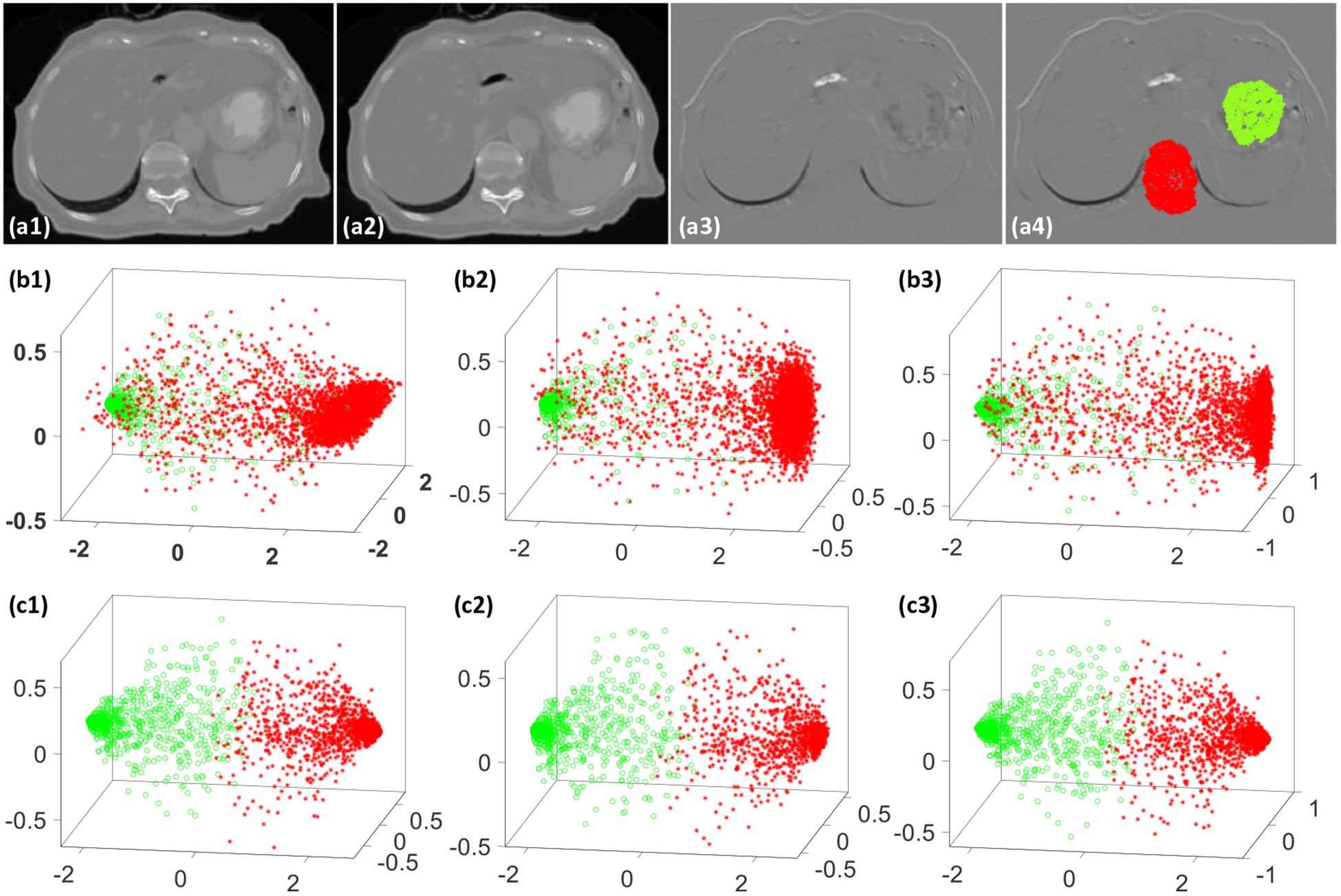
An illustrative example to demonstrate the benefit of attention gates, (a1) the moving CT image, (a2) the target CT image, (a3) difference image between the moving and target images, (a4) small image patches were extracted at the color-coded dots where red dots represent small motion region and green dots represent large motion region, (b1–b3) show the scatter plots of the first F3 principal components of the learnt feature maps from the last convolutional layer without attention gates for the 2000 image patches, (c1–c3) show the scatter plots of the first 3 principal components of the learnt feature maps from the last convolutional layer with attention gates for the 2000 image patches.
Table 1.
Image similarity between the target image and the deformed image that were generated using MS-DIRNet with and without attention gates. Better values are shown in bold.
| MS-DIRNet | MAE (HU) | PSNR (dB) | NCC |
|---|---|---|---|
| Without attention gates | 24.7 ± 5.7 | 45.3 ± 2.7 | 0.997 ± 0.001 |
| With attention gates | 25.4 ± 6.0 | 46.0 ± 2.9 | 0.998 ± 0.001 |
| P-value | <0.01 | <0.01 | <0.01 |
3.2. Efficacy of discriminator
To demonstrate the effectiveness of the discriminator, we have performed comparisons between registration results with and without the discriminator. Table 2 shows the comparison between the average registration results with and without discriminator over nine phase pairs for all patients. P-values were calculated using two-sample t-test to assess the statistical significance of the difference between results with and without discriminator. We can observe that the registration results with discriminator were significantly better than that without the discriminator in terms of MAE, PSNR and NCC. Figures 6 and 7 show the visual comparison among Velocity™, MS-DIRNet with and without discriminator.
Table 2.
Image similarity between the target image and the deformed image that were generated using MS-DIRNet with and without discriminator. Better values are shown in bold.
| MS-DIRNet | MAE (HU) | PSNR (dB) | NCC |
|---|---|---|---|
| Without discriminator | 29.8 ± 6.2 | 44.4 ± 2.7 | 0.997 ± 0.001 |
| With discriminator | 25.4 ± 6.0 | 46.0 ± 2.9 | 0.998 ± 0.001 |
| P-value | 0.01 | 0.04 | 0.01 |
Figure 6.
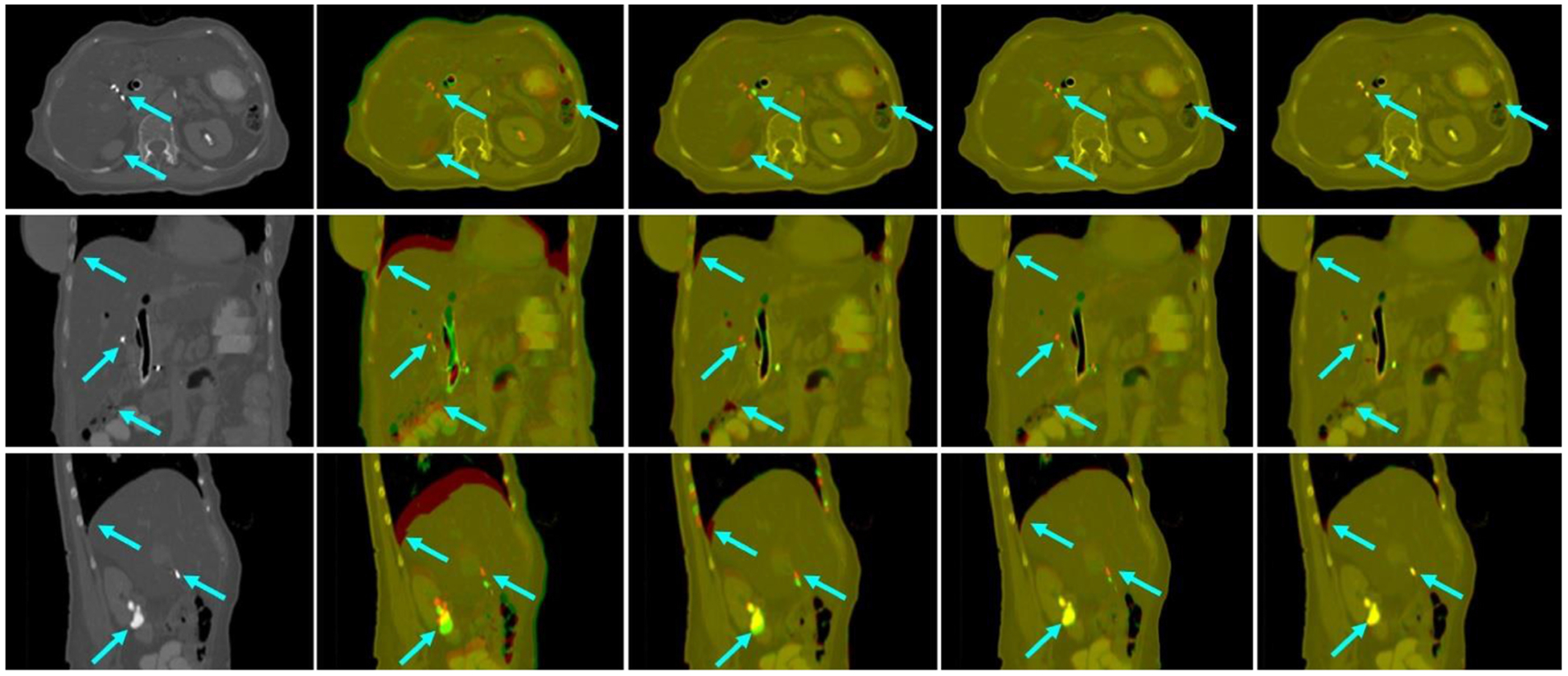
First column: target image. Second column: image fusion between the target image and the moving image before registration. Third column: image fusion between the target image and the deformed image after registration using Velocity™.Fourth column: image fusion between the target image and the deformed image after registration using MS-DIRNet without discriminator. Fifth column: image fusion between the target image and the deformed image after registration using MS-DIRNet with discriminator.
Figure 7.
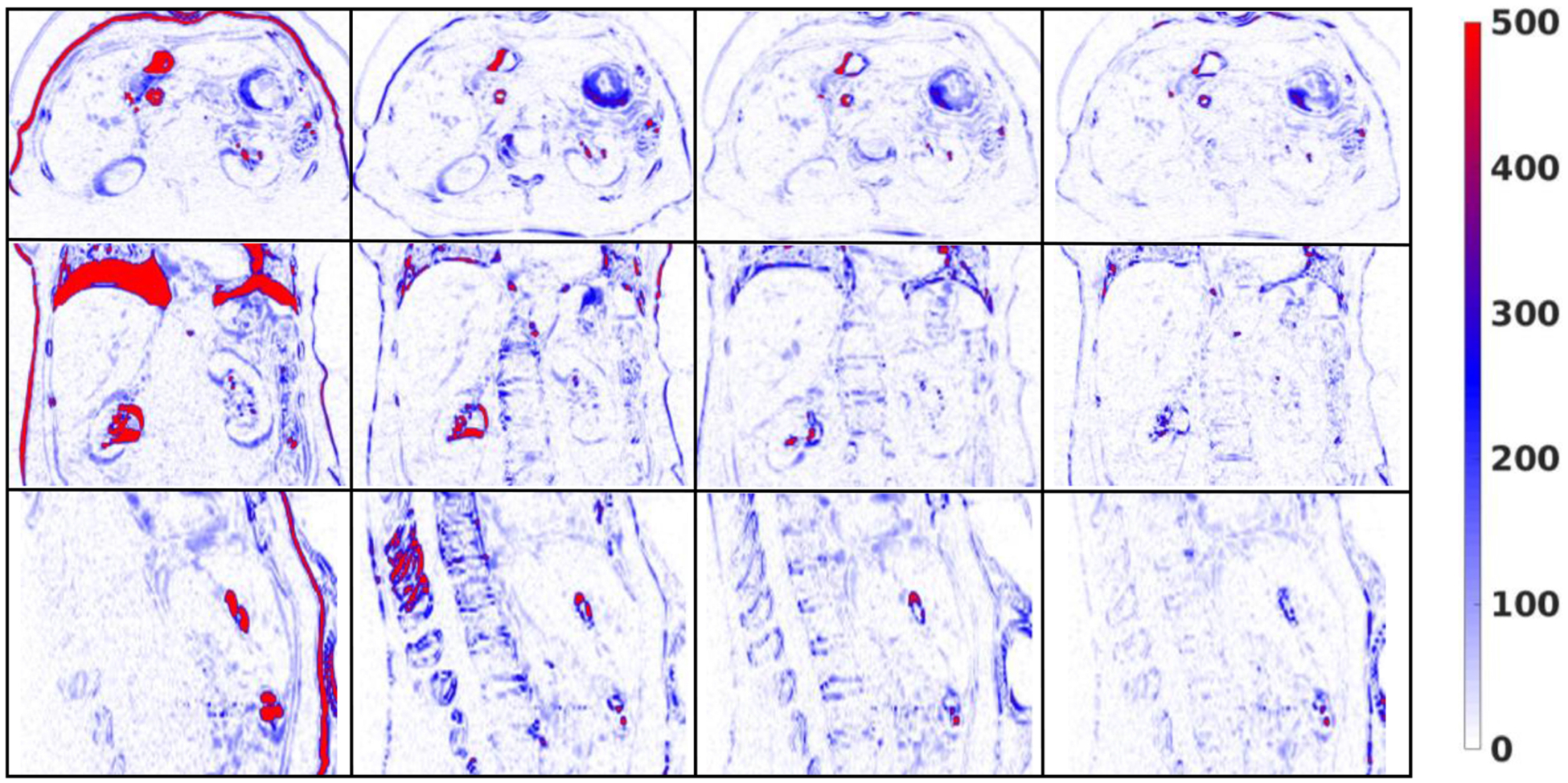
First column: difference images between the target images and the moving images before registration. Second column: difference images between the target images and the deformed images after registration using Velocity™. Third column: difference images between the target images and the deformed images after registration using MS-DIRNet without discriminator. Fourth column: difference images between the target images and the deformed images after registration using MS-DIRNet with discriminator.
3.3. Robustness to different image patch sizes
To study the sensitivity of the LocalNet to image patch sizes, we have conducted experiments using three different image patches, which are 643, 483 and 323. We have evaluated the registration results using MAE, PSNR and NCC between the target images and the deformed images. Table 3 shows that image patch size of 48 has the best performance in terms of MAE, PSNR and NCC. Image patch size of 32 has the worst performance. This is because of the restricted reception field of patch size 32, which impaired the LocalNet’s ability in predicting local deformation. Nevertheless, the differences of MAE, PSNR and NCC among the three different image patch sizes were not statistically significant, indicating that small changes in image patch size may not have significant impact on the final registration results. In this study, an image patch size of 64 was used as the default value for MS-DIRNet.
Table 3.
Image similarity between the target image and the deformed image that were generated using MS-DIRNet with different LocalNet patch size. Better values are shown in bold.
| MS-DIRNet | MAE (HU) | PSNR (dB) | NCC |
|---|---|---|---|
| Patchsize-32 | 27.3 ± 6.3 | 45.5 ± 3.0 | 0.997 ± 0.001 |
| Patchsize-48 | 25.1 ± 5.8 | 46.1 ± 2.9 | 0.998 ± 0.001 |
| Patchsize-64 | 25.4 ± 6.0 | 46.0 ± 2.9 | 0.998 ± 0.001 |
| P-value (32 vs 64) | 0.26 | 0.53 | 0.30 |
| P-value (48 vs 64) | 0.85 | 0.88 | 0.82 |
3.4. Robustness to different weighting factors in loss function
Given equal priority of the loss items, a rule of thumb to choose the weighting factors is that the initial losses of different loss items should be the same or in the same order of magnitude numerically. To study the sensitivity of each weighting factor in the loss function, we trained and tested another 12 models by varying the weighting factors. The baseline configuration was α = 1, β = 200, γ = 1000 and δ = 10. We multiplied each factor of β,γ and δ by factors of 0.01, 0.1, 10, 100 while keeping the other factors same as baseline configuration. The MAE and PSNR were plotted in figure 5 against multiplication factors. The variations of MAE and PSNR using different weighting factors were much smaller than the standard deviations which are indicated by the red error bar.
Figure 5.
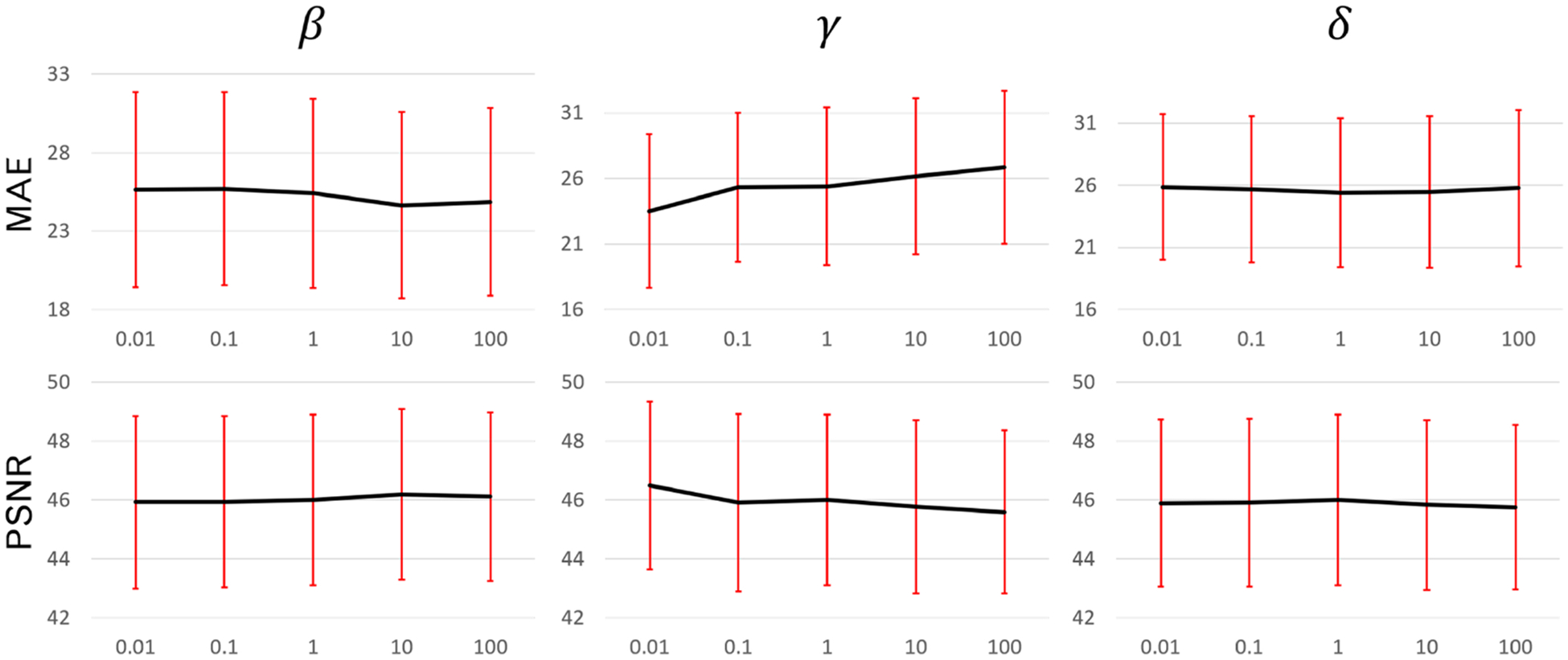
MAE and PSNR between the fixed and deformed images that were generated using models with different weighting factors. First row: MAE. Second row: PSNR. First column: β. Second column: γ. Third column: δ. Red error bars indicate the standard deviation.
3.5. Registration comparison between clinically used Velocity™ and MS-DIRNet
To demonstrate the clinical relevance of the MS-DIRNet, we compared our method with Varian Velocity™. Figure 6 shows an example where T0 was registered to T5. The T0-T5 image pair represents the toughest registration pair as the motion between T0 and T5 was the most significant in the 4D-CT. As indicated by the arrows in figure 6, Velocity™ has failed to register the fiducial markers in all three planes whereas MS-DIRNet with discriminator has successfully matched the fiducial markers in all three planes. MS-DIRNet without discriminator has failed to successfully match the fiducial markers. Similar phenomenon happened near the lung diaphragm, bowel and kidney boundaries.
Difference images between the target images and the deformed images were shown in figure 7. The proposed MS-DIRNet has done an overall better job than the Velocity™. Registration accuracy was improved near the body skin, lung diaphragm, kidney boundaries and the bony structures. The bony structures in the Velocity™ was deformed due to oversmoothed DVFs. The superior bony structure registration performance of our method was due to the use of self-attention gates as described in section 3.1. At least three fiducial markers were implanted in each patient for tumor localization and external beam treatment planning. These fiducial markers were used as landmarks in result evaluations to calculate TRE. Table 4 shows the detailed average values of TRE, MAE and PSNR for all the patients on nine image phase-pairs. The mean and standard deviation of TREs were 2.5 ± 0.8 mm and 1.2 ± 0.8 mm for Velocity™ and our method respectively. The mean and standard deviation of MAE were 26.7 ± 6.7 and 25.4 ± 6.0 for Velocity™ and our method respectively. The mean and standard deviation of PSNR were 45.8 ± 3.2 and 46.0 ± 2.9 for Velocity™ and our method respectively.
Table 4.
Registration results between T0 phase and every other phase using Velocity™ and MS-DIRNet in terms of TRE, MAE and PSNR. Better values are shown in bold.
| Image phase | Before registration | Velocity™ | MS-DIRNet | ||||||
|---|---|---|---|---|---|---|---|---|---|
| TRE (mm) | MAE (HU) | PSNR (dB) | TRE (mm) | MAE (HU) | PSNR (dB) | TRE (mm) | MAE (HU) | PSNR (dB) | |
| T0-T1 | 7.1 ± 3.4 | 33.9 ± 9.9 | 42.1 ± 2.8 | 1.8 ± 0.7 | 22.7 ± 7.6 | 47.8 ± 3.8 | 0.6 ± 0.5 | 22.1 ± 6.7 | 47.9 ± 3.2 |
| T0-T2 | 8.7 ± 2.6 | 47.9 ± 9.5 | 39.1 ± 2.5 | 2.4 ± 0.9 | 25.6 ± 7.6 | 46.3 ± 3.7 | 0.9 ± 0.6 | 24.5 ± 7.0 | 46.4 ± 3.4 |
| T0-T3 | 10.3 ± 3.7 | 57.8 ± 9.3 | 37.4 ± 2.2 | 2.6 ± 0.6 | 27.8 ± 6.9 | 45.1 ± 2.9 | 1.4 ± 0.3 | 26.3 ± 6.6 | 45.4 ± 2.9 |
| T0-T4 | 12.8 ± 4.1 | 63.7 ± 9.9 | 36.7 ± 1.9 | 2.2 ± 0.7 | 29.3 ± 6.7 | 44.4 ± 2.7 | 1.3 ± 1.0 | 27.5 ± 6.4 | 44.8 ± 2.8 |
| T0-T5 | 12.0 ± 5.8 | 67.6 ± 10.8 | 36.2 ± 1.9 | 3.7 ± 1.1 | 30.3 ± 6.3 | 43.9 ± 2.6 | 1.7 ± 0.6 | 28.1 ± 6.0 | 44.4 ± 2.7 |
| T0-T6 | 12.1 ± 5.1 | 67.7 ± 11.4 | 36.2 ± 1.8 | 3.5 ± 1.2 | 30.6 ± 6.1 | 43.8 ± 2.6 | 1.8 ± 0.7 | 28.4 ± 5.9 | 44.3 ± 2.7 |
| T0-T7 | 9.6 ± 3.1 | 57.9 ± 10.5 | 37.5 ± 1.9 | 2.3 ± 0.7 | 28.8 ± 6.5 | 44.7 ± 2.9 | 0.4 ± 0.6 | 27.1 ± 6.0 | 45.1 ± 2.8 |
| T0-T8 | 8.0 ± 2.0 | 41.7 ± 8.5 | 40.5 ± 2.4 | 2.1 ± 0.8 | 24.8 ± 6.6 | 46.7 ± 3.2 | 1.0 ± 1.5 | 24.0 ± 6.0 | 46.8 ± 2.8 |
| T0-T9 | 3.5 ± 2.0 | 24.3 ± 9.9 | 45.5 ± 3.0 | 1.9 ± 0.9 | 20.4 ± 7.6 | 49.2 ± 3.9 | 1.7 ± 1.2 | 20.5 ± 6.9 | 48.8 ± 3.3 |
| Average | 9.4 ± 3.4 | 51.4 ± 17.0 | 39.0 ± 3.6 | 2.5 ± 0.8 | 26.7 ± 6.7 | 45.8 ± 3.2 | 1.2 ± 0.8 | 25.4 ± 6.0 | 46.0 ± 2.9 |
4. Discussion
4D-CT scans allow organ motion tracking by providing multiple 3D-CT scans throughout a respiratory cycle. DIR of pre-treatment scans could provide important information for radiotherapy treatment planning such as target tracking, OAR sparing and respiratory gating. However, traditional DIR such as optical flow and demons are usually very slow in registering the large 4D-CT image volumes due to its iterative nature. Deep learning-based DIR is a promising alternative to quickly register the large 4D-CT volumes. Supervised learning requires training datasets of either manually aligned image pairs or manually labeled datasets, which are difficult to produce. To overcome these challenges, an unsupervised deep learning method was proposed for abdominal 4D-CT DIR.
DIR is inherently ill-posed in a sense that only image intensity information is available for dense DVF prediction of the whole image. Additional constraints are therefore necessary to regularize the DVF to be physically reasonable and physiologically plausible. In traditional DIRs, spatial filters such as gaussian filter and bilateral filter are commonly used to smooth the DVF iteratively during the optimization process (Fu et al 2018a). One limitation of the repeat spatial smoothing is that the DVF is often oversmoothed which causes the bony structures to be deformed. Instead of applying the spatial smoothing repeatedly, we reformulated the spatial smoothness constraint in the deep learning framework and directly predicted the final DVF in a single forward network. Additionally, the self-attention gates managed to learn the differences between major and minor motion regions and avoid deforming the bony structures.
The fiducial markers have high image intensity which may affect the network performance especially near the marker’s spatial location. To investigate its influence, we performed experiments using images whose fiducial markers were replaced by water. The fiducial markers were segmented using region growing method with manually placed initial seeds. We performed experiments for only T0–T5 registration. Without the fiducial markers, the TRE was increased from 1.7 mm to 1.8 mm, the MAE was increased from 28.1 to 29.4 and the PSNR was decreased from 44.4 to 43.6. The difference was 1.3 for MAE, much smaller than its standard deviation of 6.0. The difference was 0.8 for PSNR, much smaller than its standard deviation of 2.7. Since the number of fiducial marker voxels accounted for a nearly negligible percentage of the whole image voxels, the absence of fiducial markers should not have significant effect on the performance of our method. Our method has outperformed Velocity™ in general on the whole image, not just near the fiducial markers, as evidenced by the decreased MAE and increased PSNR in table 4 and the arrows in figure 6. The GlobalNet and LocalNet took around 30 h to train. For a typical image with matrix size of 512 × 512 × 120, the network was able to predict the DVF on the whole image up to 2 min per registration. Currently, we used a batch size of one for LocalNet image patch DVF prediction. In the future, we could try to use a large batch size number in the inference stage to expedite the registration process.
Liver is one of the largest abdominal organs with homogeneous HU values, which is often challenging to register. Bowel is difficult to register as well since it has complex shapes and large appearance variations. Two example slices containing the liver and bowel were shown in figure 8. The first column of figure 8 shows the original CT images. The second column of figure 8 shows the difference images between the target image and the deformed image using MS-DIRNet. The third column of figure 8 shows the DVF magnitude overlaid on original CT images. The yellow arrow shows that there are large intensity differences at the tissue-air interface. This is due to the lack of texture information within the abdominal gas. As indicated by the red arrows, the liver and bowel are generally well registered with smooth DVF.
Figure 8.
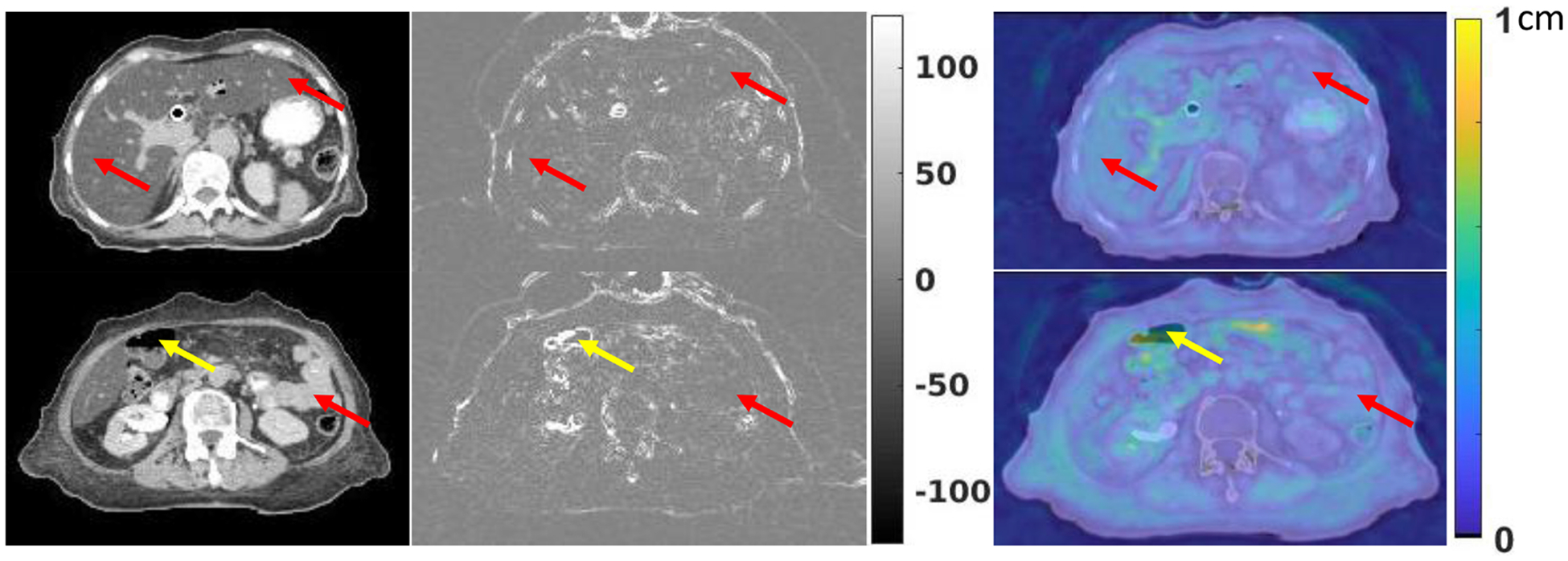
First column: CT images of liver and bowel. Second column: difference images between the target images and the deformed images after registration. Third column: DVF magnitude overlaid on CT images. Red arrows indicate good registration results with smooth DVF and small intensity differences. Yellow arrows indicate poor registration near tissue-air interface with large intensity differences.
In this study, only 25 patients’ 4D-CT datasets were used to train and test the network. In the future, we plan to collect more datasets to improve the performance of the proposed network. The 4D-CT datasets were subject to noise, streaking and other artifacts. Currently, no image preprocessing or postprocessing is used other than image cropping. Image pre-processing could be used prior to training to improve the image quality. Since the network was trained in a completely unsupervised manner without any prior knowledge about the ground truth physiological motion patterns, the DVF regularization was essential for accurate DVF predictions. The adversarial loss used in the study has mitigated the problem of insufficient DVF regularization by enforcing the deformed images to be similar to the target images. In the future, we plan to incorporate biomechanical modeling for additional DVF regularization.
5. Conclusions
An unsupervised deep learning-based method was developed for abdominal 4D-CT DIR. The proposed method was able to accurately register images between any two 4D-CT phases within one minute in a single forward network prediction. The proposed MS-DIRNet is a promising tool for abdominal motion management and treatment planning during radiation therapy.
Acknowledgments
This research is supported in part by the National Cancer Institute of the National Institutes of Health under Award Number R01CA215718, and Dunwoody Golf Club Prostate Cancer Research Award, a philanthropic award provided by the Winship Cancer Institute of Emory University.
Footnotes
Conflict of interest
The authors declare no conflicts of interest.
References
- Anthimopoulos M, Christodoulidis S, Ebner L, Christe A and Mougiakakou S 2016. Lung pattern classification for interstitial lung diseases using a deep convolutional neural network IEEE Trans. Med. Imaging 35 1207–16 [DOI] [PubMed] [Google Scholar]
- Balakrishnan G, Zhao A, Sabuncu MR, Guttag J and Dalca AV 2019. VoxelMorph: a learning framework for deformable medical image registration IEEE Trans. Med. Imaging 38 1788–800 [DOI] [PubMed] [Google Scholar]
- Boldea V, Sharp GC, Jiang SB and Sarrut D 2008. 4D-CT lung motion estimation with deformable registration: quantification of motion nonlinearity and hysteresis Med. Phys 35 1008–18 [DOI] [PubMed] [Google Scholar]
- Brock KK, Mutic S, McNutt TR, Li H and Kessler ML 2017. Use of image registration and fusion algorithms and techniques in radiotherapy: report of the AAPM Radiation Therapy Committee Task Group No. 132 Med. Phys 44 e43–e76 [DOI] [PubMed] [Google Scholar]
- Cardenas CE, Yang J, Anderson BM, Court LE and Brock KB 2019. Advances in auto-segmentation Semin. Radiat. Oncol 29 185–97 [DOI] [PubMed] [Google Scholar]
- Christensen GE, Song JH, Lu W, El Naqa I and Low DA 2007. Tracking lung tissue motion and expansion/compression with inverse consistent image registration and spirometry Med. Phys 34 2155–63 [DOI] [PubMed] [Google Scholar]
- D’Souza WD, Nazareth DP, Zhang B, Deyoung C, Suntharalingam M, Kwok Y, Yu CX and Regine WF 2007. The use of gated and 4D-CT imaging in planning for stereotactic body radiation therapy Med. Dosim 32 92–101 [DOI] [PubMed] [Google Scholar]
- de Vos BD, Berendsen FF, Viergever MA, Staring M and Išgum I 2017. End-to-end unsupervised deformable image registration with a convolutional neural network Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support (Lecture Notes in Computer Science, vol 10553) ed Cardoso MJ et al. (Berlin: Springer; ) pp 204–12 [Google Scholar]
- Dong X, Lei Y, Tian S, Liu Y, Wang T, Liu T, Curran WJ, Mao H, Shu HK and Yang X 2019. Air, bone and soft-tissue segmentation on 3D brain MRI using semantic classification random forest with auto-context model (arXiv:1911.09264) [DOI] [PMC free article] [PubMed]
- El-Gamal FEZA, Elmogy M and Atwan A 2016. Current trends in medical image registration and fusion Egypt. Inf. J 17 99–124 [Google Scholar]
- Fu Y, Lei Y, Wang T, Curran WJ, Liu T and Yang X 2019. Deep learning in medical image registration: a review (arXiv:1912.12318) [DOI] [PMC free article] [PubMed]
- Fu Y, Liu S, Li HH, Li H and Yang D 2018a. An adaptive motion regularization technique to support sliding motion in deformable image registration Med. Phys 45 735–47 [DOI] [PubMed] [Google Scholar]
- Fu Y, Liu S, Li H and Yang D 2017. Automatic and hierarchical segmentation of the human skeleton in CT images Phys. Med. Biol 62 2812–33 [DOI] [PubMed] [Google Scholar]
- Fu Y et al. 2018b. A novel MRI segmentation method using CNN-based correction network for MRI-guided adaptive radiotherapy Med. Phys 45 5129–37 [DOI] [PubMed] [Google Scholar]
- Ghosal S and Ray N 2017. Deep deformable registration: enhancing accuracy by fully convolutional neural net Pattern Recognit. Lett 94 81–86 [Google Scholar]
- Harms J, Lei Y, Wang T, Zhang R, Zhou J, Tang X, Curran WJ, Liu T and Yang X 2019. Paired cycle-GAN-based image correction for quantitative cone-beam computed tomography Med. Phys 46 3998–4009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haskins G, Kruger U and Yan P 2020. Deep learning in medical image registration: a survey Mach. Vision Appl 31 8 [Google Scholar]
- Jaderberg M, Simonyan K, Zisserman A and Kavukcuoglu K 2015. Spatial transformer networks (arXiv:1506.02025)
- Jeong J, Wang L, Ji B, Lei Y, Ali A, Liu T, Curran WJ, Mao H and Yang X 2019. Machine-learning based classification of glioblastoma using delta-radiomic features derived from dynamic susceptibility contrast enhanced magnetic resonance images: introduction Quantum Imaging Med. Surg 9 1201–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein S, Staring M, Murphy K, Viergever MA and Pluim JP 2010. elastix: a toolbox for intensity-based medical image registration IEEE Trans. Med. Imaging 29 196–205 [DOI] [PubMed] [Google Scholar]
- Kuang D and Schmah T 2018. FAIM—a convnet method for unsupervised 3D medical image registration (arXiv:1811.09243)
- Li H and Fan Y 2018. Non-rigid image registration using self-supervised fully convolutional networks without training data Proc. IEEE Int. Symp. Biomed. Imaging 2018 pp 1075–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra D, Chaudhury S, Sarkar M and Soin AS 2018. Ultrasound image segmentation: a deeply supervised network with attention to boundaries IEEE Trans. Biomed. Eng 66 1637–48 [DOI] [PubMed] [Google Scholar]
- Oh S and Kim S 2017. Deformable image registration in radiation therapy Radiat. Oncol. J 35 101–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oktay O et al. 2018. Attention U-net: learning where to look for the pancreas (arXiv:1804.03999)
- Onieva JO, Serrano GG, Young TP, Washko GR, Carbayo MJL and Estépar RSJ 2018. Multiorgan structures detection using deep convolutional neural networks Proc. SPIE Int. Soc. Opt. Eng 10574 1057428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ou Y et al. 2015. Deformable registration for quantifying longitudinal tumor changes during neoadjuvant chemotherapy Magn. Reson. Med 73 2343–56 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romera-Paredes B and Torr PHS 2016. Recurrent instance segmentation Computer Vision - ECCV (Cham, 2016) ed Leibe B et al. (Berlin: Springer; ) pp 312–29 [Google Scholar]
- Shen D, Wu G and Suk H-I 2017. Deep learning in medical image analysis Annu. Rev. Biomed. Eng 19 221–48 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokooti H, de Vos BD, Berendsen FF, Lelieveldt BPF, Išgum I and Staring M Nonrigid Image Registration Using Multi-scale 3D Convolutional Neural Networks, 2017 This is a conference letter, Medical Image Computing and Computer Assisted Intervention - MICCAI 2017, pp 232–239
- Tai A, Liang Z, Erickson B and X AL 2013. Management of respiration-induced motion with 4-dimensional computed tomography (4D-CT) for pancreas irradiation Int. J. Radiat. Oncol. Biol. Phys 86 908–13 [DOI] [PubMed] [Google Scholar]
- Tan M, Li Z, Qiu Y, McMeekin SD, Thai TC, Ding K, Moore KN, Liu H and Zheng B 2016. A new approach to evaluate drug treatment response of ovarian cancer patients based on deformable image registration IEEE Trans. Med. Imaging 35 316–25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vos BDD, Berendsen FF, Viergever MA, Sokooti H, Staring M and Išgum I 2018. A deep learning framework for unsupervised affine and deformable image registration Med. Image Anal 52 128–43 [DOI] [PubMed] [Google Scholar]
- Vos BDD, Berendsen FF, Viergever MA, Staring M and Išgum I 2017. End-to-end unsupervised deformable image registration with a convolutional neural network Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support pp 204–12 [Google Scholar]
- Wu G, Kim M, Wang Q, Munsell BC and Shen D 2016. Scalable high-performance image registration framework by unsupervised deep feature representations learning IEEE Trans. Biomed. Eng 63 1505–16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu X, Zhou F, Liu B, Fu D and Bai X 2019. Efficient multiple organ localization in CT Image using 3D region proposal network IEEE Trans. Med. Imaging 38 1885–98 [DOI] [PubMed] [Google Scholar]
- Yang D, Lu W, Low DA, Deasy JO, Hope AJ and El Naqa I 2008. 4D-CT motion estimation using deformable image registration and 5D respiratory motion modeling Med. Phys 35 4577–90 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yip SS, Coroller TP, Sanford NN, Huynh E, Mamon H, Aerts HJ and Berbeco RI 2016. Use of registration-based contour propagation in texture analysis for esophageal cancer pathologic response prediction Phys. Med. Biol 61 906–22 [DOI] [PubMed] [Google Scholar]
- Zhang J 2018. Inverse-consistent deep networks for unsupervised deformable image registration (arXiv:1809.03443)


