COVID-19 and the role of inequality in French regional departments

Abstract

In this paper, we examine the variation in the outbreak of COVID-19 across departments in continental France. We use information on the cumulated number of deaths, discharged patients and infections from COVID-19 at the department level, and study how these relate to income inequality, controlling for other factors. We find that unfortunately, inequality kills: departments with higher income inequality face more deaths, more discharged (gravely ill) patients and more infections. While other papers have studied the impact of the level of income on the severity of COVID-19, we find that it is in fact the dispersion across incomes within the same department that drives the results. Our results suggest that individuals in relatively more precarious conditions deserve dedicated policies, to avoid that temporary shocks such as COVID-19 lead to permanent increases in inequality.

Introduction

The recent outbreak of COVID-19 has infected the world at an incredible speed. Its rapid spread and the skyrocketing number of deceased individuals have caused deep concerns, uncertainty and anxiety around the globe. The pandemic affects not only individual health and health care systems, but also economic and sociologic ecosystems, as lockdown policies have been implemented in many Western countries. While there are many similarities across countries in terms of the characteristics of the epidemic spread, there are also large differences across regions, even within countries.

This paper studies whether local variations in income distribution, as well as socio-demographic correlates, have an influence on the pattern of the pandemic in continental France.1 In particular, we are interested in the effect of socio-economic inequality on the course of the epidemic. To that end, we exploit variation in these measures across 94 departments in continental France.

In our main specification, we regress cumulative deaths, discharged (and, thus, gravely ill and hospitalized) patients and infections for the period May 13–September 3, 2020, on measures for both the level and dispersion of incomes, controlling for a series of socio-demographic factors. Our findings are, unfortunately, that inequality kills: a 1% increase in income inequality, measured through the Gini coefficient, relates to a 0.08% increase in deaths per capita and a 0.09% increase in discharged patients.

Importantly, while other studies have analyzed the impact of the level of incomes, we find that it is rather the dispersion across incomes that generates a higher propensity of deaths and hospitalized patients. Income covaries with other socio-demographic factors, and controlling for income, the Gini coefficient remains unchanged, while income turns insignificant. Moreover, districts with lower median incomes not necessarily face higher inequality. Income and the Gini coefficient are in fact positively correlated, but there is sizable regional variation, and departments with high income and low inequality co-exist with low-income high-inequality departments.

Our strategy faces some potential threats to identification. First, an ongoing issue throughout the epidemic is the existence of asymptomatic and pre-symptomatic cases, and the related “dark number”, or the number of unreported cases. In the early days of the epidemic, the number of true cases is estimated to be around 10 times larger than the number of reported cases. Testing capacity and intensity increased afterwards, and the number of real cases is currently estimated to be around 3 times the number of reported cases. Moreover, testing capacity and strategy might have evolved with some regional variation, in similar vein as Borjas [1]. However, we focus on the number of discharged patients from the hospitals and the number of deaths, exactly to deal with this issue. The number of unreported discharges or deaths from COVID-19 should be much smaller than that for cases, and any change in testing capacity and strategy should be uncorrelated with the measures we use in the paper.

Second, to account for a potential bias due to the non-random testing policies for various reasons, as highlighted in Borjas [1], we control for the cumulative number of tests administered in the population.

Finally, we further check the robustness of our results by using two alternative approaches in the spirit of [3]. First, we estimate the regressions at three different points in time: April 20—during the strict lockdown, May 12—the beginning of the summer period, and September 3—at the end of the summer. This allows to control for potential misreporting of data at the very beginning of the pandemic, for different timing in the onset across departments, and for potential differences in lockdown policies across departments. Second, to further control for different timings in the onset of the epidemic, we consider for each department the cumulative number of deaths and discharged 30 days after the onset, defined as the day in which a department passes the threshold of 10 deaths per 100,000 inhabitants.

From a policy perspective, understanding which factors are associated with this unequal epidemic spread is important. First, it allows to identify the most vulnerable communities and, consequently, to address more efficiently scarce health care resources and economic support. This, in turn, helps to reduce the already massive economic burden associated with the pandemic, as well as containing the occurrence of new hotspots. Second, this analysis can support the elaboration of lockdown and lockdown easing policies. Finally, this type of studies can provide guidance for interventions aimed at reducing socio-economic inequality. Given our results, ideally one would like to estimate the impact of individual socio-economic status on COVID-19 outcomes. We hope future work can use such detailed data to further investigate this question.

The paper is organized as follows. In Sect. 2, we briefly describe the literature on the socio-economic determinants of healthcare outcomes and mortality. In Sect. 3, we describe the data in detail and provide summary statistics. We describe the econometric model in Sect. 4. Section 5 presents the results, and Sect. 6 concludes.

Brief review of the literature

The idea that economic and socio-demographic factors might be related to health behavior, healthcare outcomes and mortality is not new to the literature. There exists, for instance, a rich literature on the effects of macroeconomic fluctuations on mortality and physical health. Results from these studies are controversial and whether worsening economic conditions are associated with worsening health outcomes remains an open question. Some papers suggest that mortality is counter-cyclical and, hence, that economic turndowns lead to a deterioration in health conditions. Other papers identify instead pro-cyclical effects, thus suggesting that mortality decreases and health status improves in periods of economic distress. Ruhm [9] offers a brief overview of this literature. In France, [2] exploit panel data covering a period of 20 years at the department level and find a significant negative association between the local unemployment rate and mortality.

In an attempt to understand the geographical heterogeneity in the spread of the current pandemic, a few studies, concurrent to our paper, investigate the economic and socio-demographic determinants of COVID-19 outcomes at the local level. Borjas [1], for example, focuses on neighborhoods in New York City. He finds that, conditional on testing, individuals in poorer and immigrant neighborhoods (especially where the black population is predominant) were more likely to be infected, as well as those residing in neighborhoods where household sizes are larger. Desmet and Wacziarg [3], instead, perform an analysis at the county level, by considering, as outcome variables, the cumulated number of cases and deaths. They exploit cross-county variation and follow the dynamics of the epidemic by running regressions day by day. They find that some indicators, such as the population density, the age structure and the share of individuals residing in nursing homes, are strong predictors of the prevalence of the disease. As in Borjas [1], they find that the presence of minorities and the level of poverty are significantly related to the prevalence of the disease. In Europe, Verwimp [12] studies the spread of COVID-19 in Belgium through a municipality-level analysis. He investigates the impact of socio-demographic and economic factors on the onset of the pandemic, its intensity and the growth of contamination in April 2020. He also finds that the population density, the age structure and portion of individuals in nursing homes are important predictors of the outcome variables he considers. Moreover, the pandemic affected first municipalities where per-capita income is larger, but the contamination growth rate has then been smaller in these municipalities than in the poorer ones. Finally, in England and Wales, Sa [10] finds a positive correlation between COVID-19 mortality and population density, age structure and the presence of some minorities (black and Asian population). In addition, infections are positively related to housing arrangements.

Data and summary statistics

Data sources

In our analysis, we exploit data on a series of COVID-19 measures, as well as on economic and socio-demographic indicators at the district level. We use cumulative numbers of deaths and discharged patients at multiple points in time, capturing the onset, the height of the lockdown, the beginning and the end of the summer of 2020. As of May 13, 2020, data on the number of tests and infections are also made available, which we use to control for potential confounding factors in our analysis. Our focus lies in the analysis of the heterogeneous impact of COVID-19 across regions, and its correlation with socio-economic inequality. We measure these using information on median income levels and income inequality. Finally, we control for several demographic variables that might otherwise explain a differential incidence across departments in France.

Cumulative number of deaths and discharged These data, collected from ’Santé Publique France’,2 contain daily information at the department level, on the cumulated number of deaths and discharged since March 1, 2020. The number of deaths refers to the number of individuals dead at the hospital with a confirmed diagnosis of COVID-19. This, thus, excludes deaths outside hospitals (e.g., elderly homes or at home), for which no statistics are available over our sample period.3 We perform the main analysis on cumulative data for the period May 13–September 3, 2020. This allows to control for potential misreporting of data at the very beginning of the pandemic, for different timing in the onset across departments, and for potential differences in lockdown policies across departments. For additional robustness checks (see Sext. 5.3), we extract information on the cumulative number of deaths and discharged on April 20, 2020. We normalize these variables by the size of the population in each district, to account for pure population effects.

Number of tests and infections Starting from May 13, 2020, daily data on the number of tests and infections are also made available at Santé Publique France. We compute the cumulative numbers for the period between May 13 and September 3, 2020. This allows to additionally control for potential heterogeneity in testing intensity across departments that might be correlated with socio-demographic factors, as highlighted in Borjas [1].

Gini coefficient The Gini coefficient is downloaded from the INSEE (Institut National de la Statistique et des Études Économiques) website.4 The Gini coefficient yields a measure of the unequal distribution of income in the department population. Values range theoretically between 0 and 100. Higher values correspond to higher inequality. For Gini and all the socio-economic and demographic variables below, we use lagged values, using 2017. More recent values are often not available, and while the short-run impact of COVID-19 might have an impact on long-run socio-economic variables, these lagged values help to exclude potential simultaneity and reverse causality issues in the regression analysis.

Median disposable income per adult equivalent This information is also obtained from INSEE. This measure is computed by dividing the disposable income of a household by the number of consumption units in the same household. The number of consumption units depends on the age of the individuals: one consumption unit for the first adult in the household, 0.5 for other people aged 14 or more and 0.3 for children under 14 years. This measure, thus, allows to take into account potential economies of scale of living together, and lower levels of consumption of children in the household.

Demographic variables In each regression, we additionally control for the percentage of individuals over 60 years old, the household size, the density of GPs (General Practitioners) per 100,000 inhabitants, and a dummy classifying departments as rural or urban. Data for the population, the number of individuals over 60 and the average household size are also collected on the INSEE website, while information on the number of GPs in each department is provided by DREES (Ministère des Solidarités et de la Santé).5 Finally, the rural/urban dummy is created using the OECD (Organization for Economic Co-operation and Development) classification. The OECD classifies regions and smaller geographical units as predominantly rural, intermediate and predominantly urban by exploiting a three-step procedure mainly based on the population density and size of urban centers in the region.

First empirical observations

As a first step in the analysis, we provide some raw empirical patterns and correlations. Table 1 reports the main summary statistics for our variables. For the number of deaths and discharged patients, we split the sample into three periods: total period (March 1, 2020–September 3, 2020), first period (March 1–May 12), and second period (May 13–September 3). First, there is a clear geographical heterogeneity in the intensity of the pandemic outbreak. Over our total sample period, the average cumulated number of deaths and discharged per 100,000 persons at the district level were 26 and 109, respectively. However, the minimum and the maximum values are orders of magnitude apart, ranging between 1 and 138 cumulated deaths, and between 17 and 405 cumulated discharged patients per 100,000 persons. The goal of this paper is to understand what socio-economic factors explain this large variation in the incidence of the disease.

Table 1.

Summary statistics

	Obs.	Mean	Std. dev.	Min	Max
COVID-19 outcomes (March 1–September 3, 2020)
Deaths (per 100,000 persons)	94	26.18	25.18	1.31	138.41
Discharged (per 100,000 persons)	94	109.07	85.39	17.29	405.49
COVID-19 outcomes (March 1–May 12, 2020)
Deaths (per 100,000 persons)	94	22.16	21.72	.66	114.19
Discharged (per 100,000 persons)	94	73.96	58.69	12.19	280.29
COVID-19 outcomes (May 13–September 3, 2020)
Deaths (per 100,000 persons)	94	4.02	3.97	0	24.22
Discharged (per 100,000 persons)	94	35.11	28.70	3.07	145.26
Tests (per 100,000 persons)	94	9,033.30	2,634.27	4,874.93	19,958.70
Positives (%)	94	1.83	.82	.66	4.15
Positives (per 100,000 persons)	94	178.49	130.66	43.04	705.80
Lagged economic and socio-demographic variables (2017)
Gini (0, 100)	94	26.44	2.76	22.70	42.60
Median disposable income per adult equivalent (euro)	94	20,795.74	1,626.26	17,310	27,400
Household size (persons)	94	2.17	.12	1.90	2.60
GPs (per 100,000 persons)	94	149.83	26.80	101.76	247.77
Population over 60 years (%)	94	28.01	4.60	16.50	37.65

Second, there is also significant heterogeneity over time. During the second period, the number of deaths and discharged patients has significantly declined. The number of infections is relatively high, with an average of 178 confirmed cases per 100,000 persons. Given the availability of the data, we cannot compare to the level of infections in the first period.

Third, there is also substantial spatial heterogeneity in the cumulative number of tests and infections. This suggests that testing availability and testing policies might have been highly heterogeneous across departments. The department with the largest incidence of testing tested four times more than the department with the smallest incidence: the number of tests administered goes from a minimum of 4,875 tests to a maximum of around 20,000 per 100,000 people. As noted in Borjas [1], given the potential non-random allocation of testing, it is reasonable to look at the percentage of infections relative to the number of tests. In France, this ranges between 0.66 and 4.15 percent. Not only testing intensity is geographically dispersed, but also the rate of positive tests varies significantly, between 43 and 705 positives per 100,000 people. While part of this variation can be explained by differences in onset and timing of spread of the disease across departments, another part of it is possibly correlated with economic and socio-demographic variables.

Finally, also across our economic and socio-demographic observables, there is sizable variation across departments. Even within a highly developed country as France, and even within its continental boundaries, there is significant variation in both the median disposable income and income inequality across households within districts. The Gini coefficient ranges from 23 to 43, and the median disposable income ranges between 17,000 euros and 27,000 euros. Similarly, the density of GPs varies across departments ranging from 102 to 248 GPs per 100,000 people. The share of people above 60 years also varies substantially across departments, and it is well known that many people retire to the central and South-West regions.

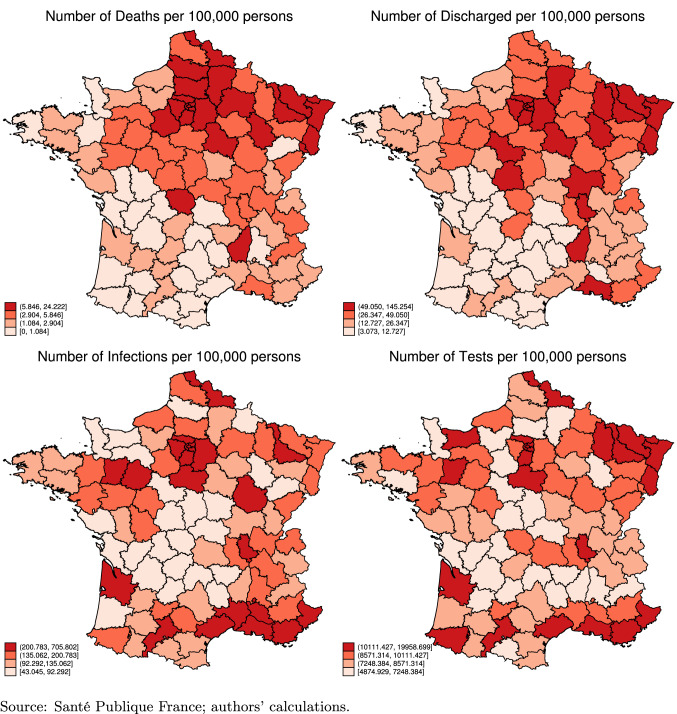
Next, Fig. 1 compares the epidemic intensity across the 94 departments. The first thing to note is that the onset of the epidemic in France took place in the North-East districts, and almost concentrically spread throughout the country. Second, the region of Paris (Ile-de-France6), together with the districts close to the North-East borders, are more affected, as they show substantially higher incidence than other districts. In the regression analysis below, we therefore control for the regions of Ile-de-France and North-East, and also perform an event study by calculating the days since the onset of the disease by district to control for differential onset. By comparing the two maps at the top of the figure with the two at the bottom, we find that some districts exhibit a relatively high number of deaths and gravely ill patients but a relatively low number of infections. However, these districts are among those where the incidence of testing has been lower. This suggests that it is important to also control for the incidence of testing in our regression analysis, especially when we use the number of infections as the dependent variable.

Fig. 1.

COVID-19 outcomes (Cumulative May 13–September 3, 2020)

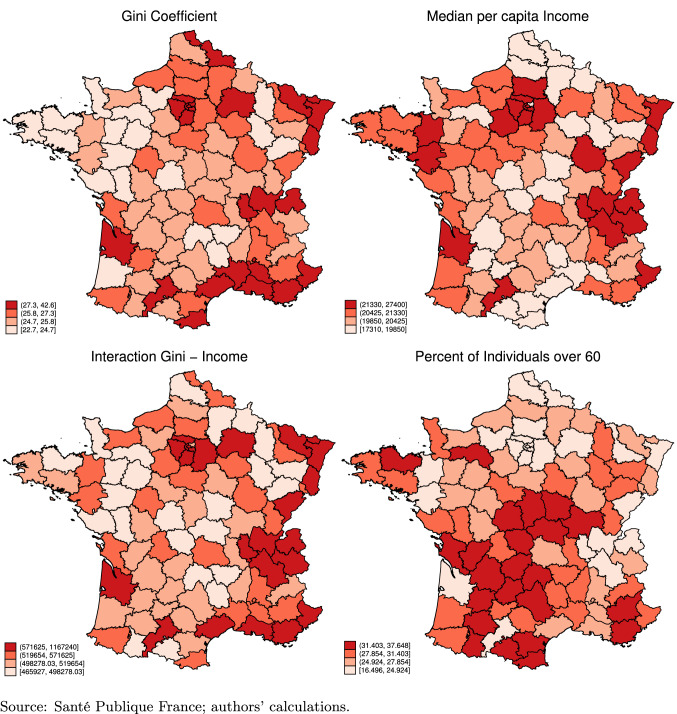
Finally, Fig. 2 also compares the socio-economic variables across departments. We are mostly interested in the level and dispersion of incomes at the departmental level. We can infer that there is a positive correlation between the median income of households and inequality, as measured through the Gini coefficient: departments with higher income levels also face, on average, higher inequality across households. However, the correlation is not perfect. We interact the Gini coefficient with median income levels in the left bottom panel. Some regions, such as the East or West districts, do have high income levels but lower Gini values. Conversely, some departments have higher inequality levels but lower incomes, such as the South-East. Finally, we can observe that the share of elderly concentrates in the central regions, roughly covering medium inequality and income levels. We explore these correlations more formally below.

Fig. 2.

Socioeconomic variables (2017)

Estimation setup

In the analysis that follows, we use a regression model to exploit the existing cross-sectional variation across departments discussed in the previous section, to estimate the impact of social inequality on the incidence of COVID-19. The unit of observation is the department, and our econometric specification is specified as:

$$\begin{array}{c}\hfill log{Y}_{\mathit{ik}}=R_i{\alpha }_k+X_i{\beta }_k+{ϵ}_{\mathit{ik}},\end{array}$$

where i is one of the 94 French continental departments while k refers to the outcome variable under investigation. We normalize all relevant variables by the size of the population in each district, to account for pure population effects.

$Y_{\mathit{ik}}$ represents either the cumulated number of deaths, or the cumulated number of discharged patients, or the cumulated number of infections per 100,000 persons in department i. We consider these outcome variables in logarithmic terms.7 In the main analysis, we consider the second period, between May 13 and September 3, 2020. We also perform additional analyses on the total sample period (March 1–September 3) and the first period (March 1–May 12).

$R_i$ is a vector of two dummy variables which represent geographical characteristics. The first is equal to one for North-East departments (at the border with Belgium, Luxembourg and Germany8) and zero otherwise. The second is equal to one for the region Ile-de-France (Paris and its surrounding departments9) and zero otherwise.

Next, $X_i$ is a vector of lagged departmental socio-economic characteristics, including our main variables of interest: the Gini coefficient, and the log median disposable income. We additionally control for the percent of individuals over 60, the number of general practitioners (GPs) per 100,000 inhabitants, a dummy variable characterizing the department as rural or urban, the average household size and the number of COVID-19 tests administered per 100,000 inhabitants.

The argument for the choice of these control variables is as follows. Access to care might be correlated with both socio-economic factors and the severity of the outbreak at the departmental level. For instance, the discrepancy in testing policies and the non-random allocation of testing across departments have been shown to be potential sources of bias in previous work [1]. We therefore include information on the number of GPs per 100,000 people, and the number of tests per 100,000. The rural dummy controls for the possibility that access to care may be more difficult when living in more remote areas. We further control for the percent of individuals over 60 and the average household size to take into account other two important risk factors highlighted by the existing literature. Moreover, we consider lagged independent variables (year 2017) to minimize the potential bias due to reverse causality and simultaneity, as the short-run impact of COVID-19 might have an impact on long-run socio-economic variables and increase social inequality . However, despite these efforts to minimize potential bias, we recognize that an omitted-variable problem may still exist: due to the novelty of the disease, the scientific community is still uncertain about the specific risk factors linked to the spread of the virus.

Finally, ${\alpha }_k$ and ${\beta }_k$ are vectors of parameters to be estimated and ${ϵ}_{\mathit{ik}}$ is the error term, assumed uncorrelated to the regressors. We estimate the regressions using OLS. We use robust standard errors and weigh each regression by the department population to correct for heteroskedasticity due to different cell sizes [11].

In a first round of regressions, the dependent variable is regressed on the dummies $R_i$ only. This analysis is done to show the geographical patterns of the epidemic and corroborates our graphical analysis above. The remaining regressions, then, are run by including the vector $X_i$ only while $R_i$ is left empty. Unfortunately, we tend to lose power otherwise: with only 94 observations, a large fraction of the geographic variance turns out to be absorbed by these regional fixed effects.

Results

Baseline results

Results are reported in Tables 2 (deaths), 3 (discharged) and 4 (infections), for the period May 13–September 3, 2020. In all regression specifications, the North-East and Ile-de-France regions face higher numbers of deaths, discharged and infected per 100,000 people, restating our graphical results above.

Table 2.

Cumulative deaths per 100,000 people (May 13–September 3, 2020)

	(1)	(2)	(3)	(4)	(5)	(6)
North-East	0.996*** (0.142)
Ile de France	1.098*** (0.102)
Gini		0.083*** (0.018)	0.078*** (0.023)			0.080*** (0.028)
(Log) income				2.255** (0.878)	1.07 (0.656)	$-$ 0.115 (0.890)
Percent over 60			$-$ 0.025 (0.022)		$-$ 0.046* (0.026)	$-$ 0.026 (0.023)
GPs density			$-$ 0.008** (0.004)		$-$ 0.006 (0.004)	$-$ 0.008** (0.004)
Rural dummy			$-$ 0.076 (0.179)		$-$ 0.095 (0.203)	$-$ 0.076 (0.179)
Household size			0.698 (0.781)		0.361 (0.915)	0.670 (0.780)
Tests in Pop.			$5\times {10}^{-5}$*** $(2\times {10}^{-5})$		$7\times {10}^{-5}$*** $(2\times {10}^{-5})$	$5\times {10}^{-5}$*** $(2\times {10}^{-5})$
Intercept	1.225*** (0.070)	$-$ 0.765 (0.482)	$-$ 0.720 (2.613)	$-$ 20.939** (8.776)	$-$ 8.619(7.635)	0.479 (9.308)
$R^2$	0.503	0.210	0.520	0.098	0.465	0.520
Adjusted $R^2$	0.492	0.201	0.486	0.088	0.428	0.481
N	94	94	94	94	94	94

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

Table 3.

Cumulative discharged patients per 100,000 people (May 13–September 3, 2020)

	(1)	(2)	(3)	(4)	(5)	(6)
North-East	1.045*** (0.194)
Ile de France	1.304*** (0.123)
Gini		0.109*** (0.026)	0.091*** (0.026)			0.092*** (0.029)
(Log) income				2.883** (1.185)	1.313** (0.640)	$-$ 0.064 (0.612)
Percent over 60			$-$ 0.031 (0.029)		$-$ 0.055* (0.031)	$-$ 0.032 (0.028)
GPs density			$-$ 0.011*** (0.004)		$-$ 0.009** (0.004)	$-$ 0.011*** (0.004)
Rural dummy			0.046 (0.195)		0.024 (0.220)	0.046 (0.196)
Household size			0.643 (0.988)		0.271 (1.123)	0.627 (0.993)
Tests in Pop.			$1\times {10}^{-4}$*** $(2\times {10}^{-5})$		$1\times {10}^{-4}$*** $(3\times {10}^{-5})$	$1\times {10}^{-4}$*** $(2\times {10}^{-5})$
Intercept	3.092*** (0.097)	0.427 (0.697)	0.927 (3.470)	$-$ 25.282** (11.840)	$-$ 8.912 (8.476)	1.588 (6.904)
$R^2$	0.445	0.242	0.568	0.107	0.519	0.568
Adjusted $R^2$	0.433	0.234	0.538	0.098	0.486	0.533
N	94	94	94	94	94	94

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

Table 4.

Cumulative confirmed cases per 100,000 people (May 13–September 3, 2020)

	(1)	(2)	(3)	(4)	(5)	(6)
North-East	0.256 (0.182)
Ile de France	0.911*** (0.144)
Gini		0.118*** (0.025)	0.031** (0.012)			0.039*** (0.014)
(Log) income				2.648*** (1.004)	0.078(0.270)	$-$ 0.509 (0.319)
Percent over 60			$-$ 0.033** (0.014)		$-$ 0.047*** (0.013)	$-$ 0.037*** (0.014)
GPs density			$-$ 0.001 (0.001)		0.000 (0.001)	$-$ 0.001 (0.001)
Rural dummy			$-$ 0.091 (0.083)		$-$ 0.102 (0.084)	$-$ 0.093 (0.084)
Household size			0.576 (0.386)		0.299 (0.379)	0.451 (0.403)
Tests in Pop.			$1\times {10}^{-4}$*** $(1\times {10}^{-5})$		$2\times {10}^{-4}$*** $(1\times {10}^{-5})$	$1\times {10}^{-4}$*** $(1\times {10}^{-5})$
Intercept	5.117*** (0.098)	2.038*** (0.681)	2.740* (1.417)	$-$ 21.074** (10.043)	3.555 (3.492)	8.033** (3.619)
$R^2$	0.290	0.463	0.862	0.147	0.851	0.865
Adjusted $R^2$	0.275	0.457	0.853	0.138	0.840	0.854
N	94	94	94	94	94	94

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

The next columns turn to our main results, where we estimate the impact of income and income inequality on COVID-19 outcomes. The Gini coefficient is positive and significant at the 1 or 5% levels across all specifications: departments with higher inequality tend to face more deaths, more discharged patients, and a higher incidence of the disease. While column 2 in each table estimates the unconditional slope, this result remains after controlling for a series of covariates in columns 3 and 6. On average across departments, a 1% increase in the Gini coefficient corresponds to a 0.08% increase in the number of deaths, 0.09% increase in the number of discharged patients, and a 0.03% increase in the number of infected people per 100,000. Comparing across the three outcome specifications, inequality seems to be proportionally more important for a serious course of the disease (hospitalization or death), than for incidence.

Next, we show that it is the dispersion across incomes (measured through the Gini coefficient), and not the level (measured through the median disposable income) that drives these results. In columns 4–6, we also include the log median income. In isolation (column 4), higher median income seems to correlate with more severe COVID-19 outcomes, a counter-intuitive result when not controlling for socio-demographic factors. Controlling for these in column 5, this effect is attenuated, and turns insignificant in two out of three specifications. Finally, in column 6, we combine both the levels and dispersion of income, together with our controls. Here, we find that the inequality effect remains significant and stable, while the level effect of incomes now turns insignificant (and intuitively negative) in all specifications. Moreover, this specification, although parsimonious and with only aggregate data, explains between 50 and 87% of total variance in the data, as measured through the (adjusted) $R^2$.

Several papers have studied the impact of incomes on COVID-19 outcomes. Borjas [1], Desmet and Wacziarg [3] and Verwimp [12] find, for the US and Belgium, that poorer areas are significantly more affected by the pandemic, with twice a death toll as more affluent neighborhoods. The Guardian [8] reports similar patterns for England and Wales. Without access to individual-level data, there can be a few explanations for this finding. Poorer individuals are more likely to have pre-existing conditions that are known co-morbidities or aggravating factors for the course of COVID-19, such as diabetes, obesity, cardio-vascular diseases etc. Additionally, poorer individuals are also more likely to be in jobs that cannot be safely distanced through tele-working, such as manufacturing, transportation and distribution, retail, etc. These are factors that lead to exposing the most vulnerable populations to the virus relatively more. However, these studies focus on the average or median regional income, rather than on income inequality. When accounting for both the level of income and income inequality, we find that inequality kills. It is the dispersion in incomes, not the level of median incomes, that drives the results.

We end with some notes on the covariates. We control for variables that take into account access to testing and critical care, and which are available at the district level: the number of general practitioners (GP) per 100,000 inhabitants, the rurality of a department, and the number of tests administered per 100,000 inhabitants. First, the number of GPs is negatively associated with the number of deaths and severely ill patients, as to be expected. A higher density of GPs helps to contain the outbreak as they are the first line of defense and guide patients in case of infection. Moreover, good and early treatment can reduce the severity of the disease, which is also tentatively confirmed in comparing the coefficients across specifications: a higher density of GPs correlates with fewer gravely ill patients and deaths, but not necessarily with a lower incidence, as the coefficient is insignificant in Table 4.

Second, we control for the intensity of testing in all our specifications. Although the value of the coefficient is very small, the number of tests per 100,000 people is also positively and significantly related to each of the outcome variables. This suggests that access to care, as proxied by the availability of GPs and tests play an important role. On the other hand, the rurality of a department and the housing conditions do not seem to be potential issues in France as they perhaps do in other countries. Even once these factors are taken into account, inequality continues to be a significant predictor of COVID-19, thus suggesting that factors other than access to care are also at work.

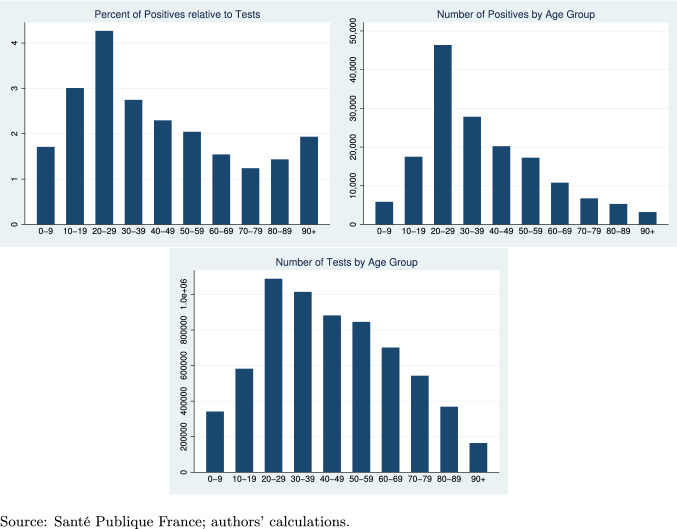
Finally, in terms of demographics, a higher share of people aged 60 years or more in the population correlates with a lower incidence of the disease, and a negative but insignificant effect on deaths and discharged patients. While surprising prima facie, this relationship is also reported in, e.g., [3].10 Ideally, we would have information on COVID-19 outcomes by age group, which we do not have at our disposal.11 We, thus, further scrutinize this last finding by separately looking at the geographical spread of 60+ people in France and the infection rates by age distribution nationally. In Fig. 2, we see that the 60+ are mostly located in the central and rural departments. By contrast, Paris and its surrounding departments are among those with the lowest share of individuals in this age group. The share of 60+ correlates negatively with the number of deaths, discharged and infected. Figure 3 reports information on tests across the age distribution at the national level. The age group of 20–29 is tested most intensely, and also shows the highest positivity ratio. Conversely, the group of 60+ has a lower positivity ratio than other age groups, supporting our negative coefficient in the regression tables.

Fig. 3.

COVID-19 testing and infections by age group (national level).

Source: Santé Publique France; authors’ calculations

Analysis of covariance

The estimated parameters displayed in Tables 2 and 3 do not seem to be very different, though the former deals with deaths, while the latter deals with those who were discharged from hospitals. To check whether they are significantly different, we use an analysis of covariance, which implicitly assumes that the distribution of errors is the same in both subsamples (deaths and discharged). The model is now:

$$\begin{array}{c}\hfill log{Y}_{i0}=R_0{\alpha }_0+X_0{\beta }_0+\delta R_0\alpha +\delta X_0\beta +{ϵ}_{i0}.\end{array}$$

In this formulation, $log{Y}_{i0}$ is a vector constructed by stacking each department’s cumulative deaths followed by each department’s cumulative discharged for the period May 13–September 3, 2020. $R_0$ is constructed as a block matrix from the two matrices $R_i$. Matrix $X_0$ is constructed in the same way from matrices $X_i$. Finally, $\delta$ is a dummy variable equal to 1 for observations related to $log{Y}_{i1}$, that is, discharged, and 0 for deaths. The coefficients on the interaction terms $\delta R_0$ and $\delta X_0$ tell us whether the effect of the covariates is different for deaths and discharged.

Results are reported in Table 5. The coefficients picked up by each variable alone, as well as the value of the intercept, are exactly the same as those in Table 2. This is due to the fact that our dummy, $\delta$, is equal to zero for deaths and, hence, these coefficients pick the effect of the covariates on the cumulative number of deaths. Those coefficients that were significantly different from 0 remain so, and those that were not, remain so as well. Standard errors are also the same.

Table 5.

Analysis of covariance (May 13–September 3, 2020)

	(1)	(2)	(3)	(4)	(5)	(6)
North-East	0.996*** (0.142)
North-East $\times$ dummy	0.009 (0.236)
Ile de France	1.098*** (0.102)
Ile de France $\times$ dummy	0.161(0.156)
Gini		0.083*** (0.018)	0.078*** (0.023)			0.080*** (0.028)
Gini $\times$ dummy		0.022(0.030)	0.011 (0.034)			0.011 (0.039)
Log (Income)				2.255** (0.878)	1.077 (0.656)	$-$ 0.115 (0.890)
Log (Income) $\times$ dummy				0.508(1.442)	0.201 (0.905)	0.039 (1.061)
Percent over 60			$-$ 0.025 (0.022)		$-$ 0.046* (0.026)	$-$ 0.026 (0.023)
Percent over 60 $\times$ dummy			$-$ 0.003 (0.035)		$-$ 0.005(0.039)	$-$ 0.003 (0.036)
GPs density			$-$ 0.008** (0.004)		$-$ 0.006 (0.004)	$-$ 0.008** (0.004)
GPs density $\times$ dummy			$-$ 0.002 (0.005)		$-$ 0.002 (0.005)	$-$ 0.002 (0.005)
Rural dummy			$-$ 0.076 (0.179)		$-$ 0.095 (0.203)	$-$ 0.076 (0.179)
Rural dummy $\times$ dummy			0.128 (0.256)		0.126 (0.291)	0.129 (0.257)
Household size			0.698(0.781)		0.361 (0.915)	0.670 (0.780)
Household size $\times$ dummy			$-$ 0.010 (1.220)		$-$ 0.042 (1.412)	$-$ 0.000 (1.225)
Tests in Pop.			$5\times {10}^{-5}$*** $(2\times {10}^{-5})$		$8\times {10}^{-5}$*** $(2\times {10}^{-5})$	$5\times {10}^{-5}$*** $(2\times {10}^{-5})$
Tests in pop. $\times$ dummy			$5\times {10}^{-5}\ast$ $(3\times {10}^{-5})$		$6\times {10}^{-5}$*** $(3\times {10}^{-5})$	$5\times {10}^{-5}$** $(3\times {10}^{-5})$
Intercept	1.225*** (0.070)	$-$ 0.765 (0.482)	$-$ 0.720 (2.613)	$-$ 20.939** (8.776)	$-$ 8.619 (7.635)	0.479 (9.308)
Intercept $\times$ dummy	1.923*** (0.116)	1.345 (0.823)	1.509 (4.205)	$-$ 3.107 (14.404)	$-$ 0.127 (11.221)	1.106 (11.392)
$R^2$	0.809	0.720	0.836	0.673	0.817	0.837
Adjusted $R^2$	0.804	0.715	0.824	0.668	0.803	0.822
N	188	188	188	188	188	188

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

The coefficients, $\alpha$ and $\beta$, associated with each interaction term, yield the difference in the effect of each covariate across the two groups (deaths and discharged): if this coefficient is not statistically different from zero, we conclude that this difference is not significant at the level indicated. The estimates for standard errors are never significantly different from zero. This implies that the effect of each right-hand side variable is the same across the two groups. The only exception is the interaction between the dummy $\delta$ and the cumulative number of tests in the population, which is, however, only significant at 10% confidence level. We, thus, conclude that we can use a joint model for both deaths and discharged patients in this setting.

Robustness checks

Finally, we exploit two alternative approaches as robustness to our main results. First, we repeat the same analysis as above for three different points in time. We first consider the cumulative number of deaths and discharged between March 1 and April 20, then between March 1 and May 12, and finally between March 1 and September 3, 2020. This allows us to control for potential misreporting of data at the beginning of the pandemic, for potential discrepancies in lockdown policies and for different timings in the onset of the pandemic across departments. Results are reported in Tables 6, 7, 8, 9, 10 and 11 in the Appendix. Notice that here we are not able to control for the number of tests administered in the population, as these data are only available starting from May 13 onwards. Results are highly similar to the baseline findings: the Gini coefficient is significant and positive across all specifications, and when accounting for both the Gini and the level of income, the latter turns insignificant.

Table 6.

Cumulative deaths per 100,000 people (March 1–September 3, 2020)

	(1)	(2)	(3)	(4)	(5)	(6)
North-East	1.149*** (0.283)
Ile de France	1.434*** (0.138)
Gini		0.121*** (0.020)	0.140*** (0.032)			0.152*** (0.035)
(Log) Income				3.118** (1.295)	1.452 (0.942)	-0.826 (0.767)
Percent over 60			− 0.032 (0.038)		− 0.087* (0.045)	− 0.038 (0.038)
GPs density			− 0.010** (0.004)		− 0.004 (0.005)	− 0.010** (0.004)
Rural dummy			− 0.124 (0.215)		− 0.261 (0.253)	− 0.118 (0.215)
Household size			0.723 (1.320)		− 0.212 (1.640)	0.519 (1.318)
Intercept	2.679*** (0.093)	− 0.298 (0.566)	− 0.084 (4.716)	− 27.998** (12.932)	− 7.975 (12.486)	8.495 (9.052)
$R^2$	0.466	0.261	0.484	0.109	0.355	0.488
Adjusted $R^2$	0.454	0.253	0.454	0.099	0.318	0.452
N	94	94	94	94	94	94

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

Table 7.

Cumulative discharged per 100,000 people (March 1–September 3, 2020)

	(1)	(2)	(3)	(4)	(5)	(6)
North-East	0.869*** (0.251)
Ile de France	1.231*** (0.117)
Gini		0.114*** (0.024)	0.119*** (0.022)			0.129*** (0.025)
(Log) Income				2.923*** (1.094)	1.267* (0.755)	$-$ 0.661 (0.615)
Percent over 60			$-$ 0.023(0.026)		$-$ 0.069** (0.033)	$-$ 0.028 (0.026)
GPs density			$-$ 0.007* (0.004)		$-$ 0.002 (0.004)	$-$ 0.007* (0.004)
Rural dummy			$-$ 0.224 (0.172)		$-$ 0.340 (0.205)	$-$ 0.220(0.172)
Household Size			0.747 (0.941)		$-$ 0.035 (1.198)	0.584 (0.935)
Intercept	4.288*** (0.086)	1.442** (0.646)	1.339 (3.320)	$-$ 24.518** (10.930)	$-$ 5.734 (9.596)	8.205 (6.932)
$R^2$	0.451	0.321	0.537	0.133	0.408	0.541
Adjusted $R^2$	0.439	0.313	0.511	0.123	0.375	0.509
N	94	94	94	94	94	94

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

Table 8.

Cumulative deaths per 100,000 people (March 1–May 12, 2020)

	(1)	(2)	(3)	(4)	(5)	(6)
North-East	1.125*** (0.315)
Ile de France	1.454*** (0.146)
Gini		0.125*** (0.020)	0.145*** (0.034)			0.156*** (0.036)
(Log) Income				3.225** (1.347)	1.542 (1.019)	$-$ 0.804 (0.726)
Percent over 60			$-$ 0.031 (0.042)		$-$ 0.087* (0.049)	$-$ 0.037 (0.042)
GPs density			$-$ 0.010** (0.004)		$-$ 0.004 (0.005)	$-$ 0.010** (0.004)
Rural dummy			$-$ 0.115 (0.217)		$-$ 0.256 (0.253)	$-$ 0.110 (0.217)
Household size			0.687 (1.448)		$-$ 0.264 (1.768)	0.489 (1.446)
Intercept	2.493*** (0.095)	$-$ 0.586 (0.562)	$-$ 0.344 (5.195)	$-$ 29.255** (13.446)	$-$ 8.955 (13.623)	8.009 (8.903)
$R^2$	0.447	0.263	0.467	0.110	0.337	0.470
Adjusted $R^2$	0.435	0.255	0.437	0.101	0.299	0.434
N	94	94	94	94	94	94

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

Table 9.

Cumulative discharged per 100,000 people (March 1–May 12, 2020)

	(1)	(2)	(3)	(4)	(5)	(6)
North-East	0.791*** (0.292)
Ile de France	1.216*** (0.122)
Gini		0.118*** (0.023)	0.117*** (0.022)			0.126*** (0.025)
(Log) Income				3.038*** (1.088)	1.299* (0.781)	$-$ 0.592 (0.649)
Percent over 60			$-$ 0.021 (0.026)		$-$ 0.066**(0.032)	$-$ 0.025 (0.026)
GPs density			$-$ 0.005 (0.004)		$-$ 0.001 (0.004)	$-$ 0.006 (0.004)
Rural dummy			$-$ 0.262 (0.176)		$-$ 0.376* (0.206)	$-$ 0.258 (0.176)
Household size			0.750 (0.925)		$-$ 0.003 (1.168)	0.604 (0.919)
Intercept	3.905*** (0.086)	0.934 (0.639)	0.750 (3.246)	$-$ 26.058** (10.866)	$-$ 6.773 (9.685)	6.900 (7.147)
$R^2$	0.428	0.344	0.534	0.143	0.410	0.537
Adjusted $R^2$	0.415	0.336	0.507	0.134	0.376	0.505
N	94	94	94	94	94	94

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

Table 10.

Cumulative deaths per 100,000 people (March 1–April 20, 2020)

	(1)	(2)	(3)	(4)	(5)	(6)
North-East	1.117*** (0.325)
Ile de France	1.411*** (0.142)
Gini		0.121*** (0.018)	0.141*** (0.032)			0.151*** (0.034)
(Log) Income				3.149** (1.323)	1.535 (1.019)	$-$ 0.734 (0.647)
Percent over 60			$-$ 0.034 (0.039)		$-$ 0.088* (0.047)	$-$ 0.040 (0.039)
GPs density			$-$ 0.009** (0.004)		$-$ 0.004(0.005)	$-$ 0.010** (0.004)
Rural dummy			$-$ 0.025 (0.206)		$-$ 0.162 (0.240)	$-$ 0.020 (0.206)
Household size			0.567 (1.347)		$-$ 0.342 (1.679)	0.387 (1.351)
Intercept	2.268*** (0.083)	$-$ 0.694 (0.491)	$-$ 0.218 (4.829)	$-$ 28.725** (13.203)	$-$ 8.999 (13.480)	7.411 (8.149)
$R^2$	0.485	0.278	0.480	0.120	0.341	0.483
Adjusted $R^2$	0.474	0.270	0.450	0.110	0.303	0.448
N	94	94	94	94	94	94

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

Table 11.

Cumulative discharged per 100,000 people (March 1–April 20, 2020)

	(1)	(2)	(3)	(4)	(5)	(6)
North-East	0.820** (0.316)
Ile de France	1.180*** (0.125)
Gini		0.119*** (0.024)	0.112*** (0.023)			0.117*** (0.026)
(Log) Income				3.139***(1.041)	1.427* (0.788)	$-$ 0.330 (0.668)
Percent over 60			$-$ 0.017(0.027)		$-$ 0.058* (0.032)	$-$ 0.020 (0.027)
GPs density			$-$ 0.003 (0.004)		0.001 (0.004)	$-$ 0.003 (0.004)
Rural dummy			$-$ 0.258 (0.178)		$-$ 0.365* (0.203)	$-$ 0.255 (0.179)
Household size			1.044 (0.948)		0.398 (1.176)	0.963 (0.953)
Intercept	3.468*** (0.087)	0.475 (0.651)	$-$ 0.638 (3.322)	$-$ 27.507*** (10.401)	$-$ 9.916 (9.864)	2.796 (7.419)
$R^2$	0.404	0.341	0.510	0.150	0.403	0.510
Adjusted $R^2$	0.391	0.334	0.482	0.141	0.369	0.477
N	94	94	94	94	94	94

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

Second, to further account for differences in the onset of the pandemic across departments, we use an approach similar to the one proposed by Desmet and Wacziarg [3]. We define the onset of the epidemic as the day in which the cumulated number of deaths per 100,000 inhabitants in a given department reaches a value of at least 10. After that, we consider, for each department, the cumulated number of deaths and discharged per 100,000 inhabitants 30 days after the onset. Notice that a few departments never reached the threshold during the time period under study. Hence, the number of observations for these regressions is equal to 69. These results are displayed in Tables 12 and 13. Again, our findings are not sensitive to the differential onset across departments in France.

Table 12.

Cumulative deaths per 100,000 people (30 days after onset)

	(1)	(2)	(3)	(4)	(5)	(6)
North-East	0.662** (0.275)
Ile de France	0.978*** (0.123)
Gini		0.078*** (0.011)	0.100*** (0.027)			0.110*** (0.029)
(Log) Income				1.992* (0.998)	0.942 (0.760)	$-$ 0.603 (0.602)
Percent over 60			$-$ 0.030 (0.031)		$-$ 0.089*** (0.031)	$-$ 0.033 (0.030)
GPs density			$-$ 0.006* (0.003)		$-$ 0.003 (0.004)	$-$ 0.006*(0.003)
Rural dummy			0.129 (0.199)		0.117 (0.213)	0.123(0.200)
Household size			0.252 (0.966)		$-$ 0.851 (1.113)	0.122 (0.958)
Intercept	2.874*** (0.071)	0.973*** (0.329)	1.422 (3.518)	$-$ 16.675* (9.966)	$-$ 1.756 (9.571)	7.594 (6.858)
$R^2$	0.500	0.267	0.444	0.112	0.305	0.450
Adjusted $R^2$	0.484	0.256	0.400	0.099	0.249	0.396
N	69	69	69	69	69	69

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

Table 13.

Cumulative discharged per 100,000 people (30 days after onset)

	(1)	(2)	(3)	(4)	(5)	(6)
East	0.344 (0.231)
Paris	0.716*** (0.097)
Gini		0.069*** (0.013)	0.072*** (0.019)			0.073*** (0.022)
(Log) Income				1.889*** (0.708)	0.947 (0.610)	$-$ 0.080 (0.561)
Percent over 60			$-$ 0.014 (0.025)		$-$ 0.051** (0.024)	$-$ 0.014 (0.025)
GPs density			$-$ 0.002 (0.003)		0.001 (0.003)	$-$ 0.002 (0.003)
Rural dummy			$-$ 0.080 (0.144)		$-$ 0.084 (0.151)	$-$ 0.080 (0.146)
Household size			0.454 (0.749)		$-$ 0.210 (0.796)	0.437 (0.732)
Intercept	4.226*** (0.065)	2.494*** (0.374)	2.055 (2.730)	$-$ 14.405** (7.080)	$-$ 3.341(7.214)	2.877 (5.689)
$R^2$	0.412	0.341	0.459	0.168	0.353	0.459
Adjusted $R^2$	0.394	0.331	0.416	0.156	0.302	0.407
N	69	69	69	69	69	69

Robust standard errors in parenthesis. Regressions are weighted by department population

Significance: ${}^{\ast }p<0.1$, ${}^{\ast \ast }p<0.05$, ${}^{\ast \ast \ast }p<0.01$

Conclusions

This paper provides evidence on the impact of socio-economic inequality on COVID-19 deaths, hospitalizations, and the incidence in continental France. The key point of the paper is that inequality kills: a 1% increase in the Gini coefficient in a department relates to a 0.1% increase in the number of deaths or hospitalizations, controlling for other socio-demographic factors.

While other studies have analyzed the impact of the level of incomes, we find that it is rather the dispersion across incomes that generates a higher propensity of deaths and hospitalized patients. Moreover, districts with lower median incomes do not necessarily face higher inequality. Income and the Gini coefficient are in fact positively correlated, but there is sizable regional variation, and departments with high income and low inequality co-exist with low-income high-inequality departments.

Without further information on individual-level outcomes, we cannot further distinguish possible mechanisms at work, but some plausible explanations exist. Poorer individuals are more likely to have pre-existing conditions that are known co-morbidities or aggravating factors for the course of COVID-19, such as diabetes, obesity, cardio-vascular diseases etc. Additionally, poorer individuals are also more likely to be in jobs that cannot be safely distanced through tele-working, such as manufacturing, transportation and distribution, retail, etc. These are factors that lead to exposing the most vulnerable people to the virus relatively more. We hope that future work can study these mechanisms in more fine-grained detail.

Our results have a key policy message. There is evidence that most crises are likely to further increase inequality, as relatively poorer people are less healthy, have more at-risk jobs, are credit constrained, are more at risk of losing their jobs for both micro and macro reasons, and have a less strong social network to fall back on. Temporary shocks, like COVID-19, tend to have permanent effects on this inequality, and can even have inter-generational consequences. The pandemic hits harder areas in socio-economic disadvantage today and will probably exacerbate disparities in the near future ([4]). This is what a British report also points out (Improvement Service [6], p. 3):

“People living in socio-economic disadvantage are more likely to be working in the low paying jobs which are keeping the country going in supermarkets, as cleaners, delivery drivers and home care workers, and a significant proportion of these low paid workers will be women. The four ‘Cs’ of cleaning, care, cashiering and catering, commonly seen as women’s work are now massively important, and those working in these areas are being exposed daily to the risk of contracting COVID-19.”

These findings call for the importance of targeted policy interventions that are aimed at helping individuals living in poor conditions, not only in absolute numbers, but relative to their peers in the same department. Moreover, such policies should consider interventions that help people structurally climb out of the poverty trap.

A Additional figures

See Fig. 3.

B Additional regressions

Tables 6, 7, 8, 9, 10, 11, 12 and 13.