Assessment of enzyme active site positioning and tests of catalytic mechanisms through X-ray–derived conformational ensembles

Significance

Enzymes position catalytic and reactant groups in active sites, but motions are also integral to enzyme function. Decades of research have revealed static snapshots for many enzymes, but we know very little about the extents and directions of motions of the residues that make up enzymes and their active sites. We took advantage of emerging crystallographic approaches to provide information about protein conformational ensembles for the enzyme ketosteroid isomerase (KSI). Ensemble analyses indicated limited change in conformational heterogeneity through the enzyme’s reaction cycle and a balance of positioning and flexibility that allows KSI to efficiently catalyze multiple reaction steps. We tested KSI-specific and general models for enzyme catalysis, demonstrating the power of and need for “ensemble–function” interrogation of enzymes.

Abstract

How enzymes achieve their enormous rate enhancements remains a central question in biology, and our understanding to date has impacted drug development, influenced enzyme design, and deepened our appreciation of evolutionary processes. While enzymes position catalytic and reactant groups in active sites, physics requires that atoms undergo constant motion. Numerous proposals have invoked positioning or motions as central for enzyme function, but a scarcity of experimental data has limited our understanding of positioning and motion, their relative importance, and their changes through the enzyme’s reaction cycle. To examine positioning and motions and test catalytic proposals, we collected “room temperature” X-ray crystallography data for Pseudomonas putida ketosteroid isomerase (KSI), and we obtained conformational ensembles for this and a homologous KSI from multiple PDB crystal structures. Ensemble analyses indicated limited change through KSI’s reaction cycle. Active site positioning was on the 1- to 1.5-Å scale, and was not exceptional compared to noncatalytic groups. The KSI ensembles provided evidence against catalytic proposals invoking oxyanion hole geometric discrimination between the ground state and transition state or highly precise general base positioning. Instead, increasing or decreasing positioning of KSI’s general base reduced catalysis, suggesting optimized Ångstrom-scale conformational heterogeneity that allows KSI to efficiently catalyze multiple reaction steps. Ensemble analyses of surrounding groups for WT and mutant KSIs provided insights into the forces and interactions that allow and limit active-site motions. Most generally, this ensemble perspective extends traditional structure–function relationships, providing the basis for a new era of “ensemble–function” interrogation of enzymes.

The central role of enzymes in biology is embodied in the decades of effort spent to deeply investigate the origins of their catalysis (e.g., refs. 1–6). Enzyme studies now routinely identify the active-site groups that interact with substrates and reveal their roles in binding and in facilitating chemical transformations. Nevertheless, these so-called “catalytic groups” alone, outside of the context of a folded enzyme, do not account for the enormous rate enhancements and exquisite specificities exhibited by enzymes (4). Classic proposals for enzyme catalysis have invoked the importance of positioning of active-site groups within a folded enzyme and of substrates localized and positioned by binding interactions (6–15). While these proposals universally invoke restricted motion of catalytic groups, the amount of restriction and the amount of catalysis provided by that restriction has been the subject of much discussion and debate (16–20). Conversely, it is also clear that motions are inherent to enzymes, and that conformational transitions and structural rearrangements are important for enzyme function (e.g., refs. 11 and 21–23). Considering both positioning and motions, it has been recognized that: “For catalysis, flexible but not too flexible, as well as rigid but not too rigid, is essential. Specifically, the protein must be rigid enough to maintain the required structure but flexible enough to permit atomic movements as the reaction proceeds” (3).

The importance of both positioning and motions to enzyme function suggests a nuanced view of enzyme catalysis and underscores the need for direct experimental measurements of positioning and motions within enzymes.

As Feynman noted, “Everything that living things do can be understood in terms of the jigglings and wigglings of atoms” (24). But simply observing motions of active-site residues does not tell us how enzymes achieve catalysis. To understand enzymes, we want to know how much an enzyme dampens and alters the motions of catalytic residues. We want to know which increases or decreases in motion increase or decrease the reaction rate and what interactions and forces are most responsible for dampening motions. With this information we may be able to better design new enzymes. Additionally, to what extent are active-site residues positioned upon folding of the enzyme, or adjusted as the reaction proceeds, and are active-site residues more precisely positioned than residues throughout an enzyme?

To address fundamental questions about how enzymes function and evolve, and how to ultimately design highly efficient enzymes, we need to obtain experimental information about enzyme conformation ensembles: The distribution of enzyme states dictated by their highly complex multidimensional energy landscapes over which conformational rearrangements occur. Observations of well-resolved electron densities from X-ray diffraction data indicate positioning of residues in and around the active site, but do not provide information on the extent and nature of that positioning. Crystallographic B-factors of residues are sometimes used to infer motions, but are only indirectly related to intrinsic motion and contain contributions from additional factors, such as crystallographic order (25, 26). NMR experiments identify groups with greater motional freedom and can provide temporal information, but these experiments typically lack information about the directions and extent of these motions (27). Molecular dynamics simulations provide atomic-level models for entire systems, but we currently lack the rigorous experimental tests needed to determine whether or not computational outputs reflect actual physical behavior, which prevents firm mechanistic conclusions from being inferred (28, 29).

Two X-ray crystallographic approaches have recently emerged that can provide experimentally-derived conformational ensemble information: High-sequence similarity Protein Data Bank (PDB) structural ensembles (referred to as “pseudoensembles” herein) (30, 31) and multiconformer models from X-ray data obtained at temperatures above the protein’s glass transition (referred to as “room temperature” or ”RT” X-ray diffraction in the literature and herein) (22, 32, 33). These approaches are complementary. Pseudoensembles provide information about residues that move in concert (i.e., coupled motions) but require dozens of structures (see also SI Appendix, Supplementary Text 1). RT X-ray data from single crystals can provide multiconformer models, so that ensemble information about new complexes and mutants can more readily be acquired, but do not provide direct information about coupled motions. Furthermore, RT X-ray studies provide direct information about equilibrium distributions without cryocooling, which can alter and quench motions, and without assuming that different cryocooled crystals reproduce an equilibrium distribution of states (32, 34–36).

Here we demonstrate consistency between these approaches and take advantage of the strengths of each: The ability to evaluate correlated side-chain rearrangements in and near the active site via pseudoensembles, and the ability to obtain new ensemble-type information of new states from single X-ray datasets at temperatures above the glass transition. Importantly, these analyses report on conformational heterogeneity and cannot give information about the timescales of motions and interconversions between states. Additionally, each traditional model within the pseudoensemble represents predominantly a single rather than average state and combining these states captures an ensemble distribution. Similarly, the alternate conformations in multiconformer models explicitly reduce bias toward average structures of multistate systems. Focusing on a model enzyme with very high-resolution data and with ligands representing steps along its reaction path has allowed us to obtain insights that would not be possible from static structures, from either ensemble approach alone or from less-extensive or lower-resolution data.

We chose to investigate the enzyme ketosteroid isomerase (KSI) (Fig. 1) because of our ability to obtain high-resolution diffraction data, because of the accumulated wealth of structural and mechanistic information, and because of KSI’s use of catalytic strategies common to many enzymes. As a single-substrate enzyme, KSI allows structural information to be obtained with a bonified reactant bound. Furthermore, we obtained ensemble data for KSI from two species, which gave consistent results and allowed us to address unresolved questions from decades of KSI studies. We also used our ensembles from these KSI homologs to ask—and answer—more general questions. Our in-depth analyses of KSI bring an ensemble perspective to bear on traditional structure–function studies and provide the basis for a new era of ensemble–function studies.

Fig. 1.

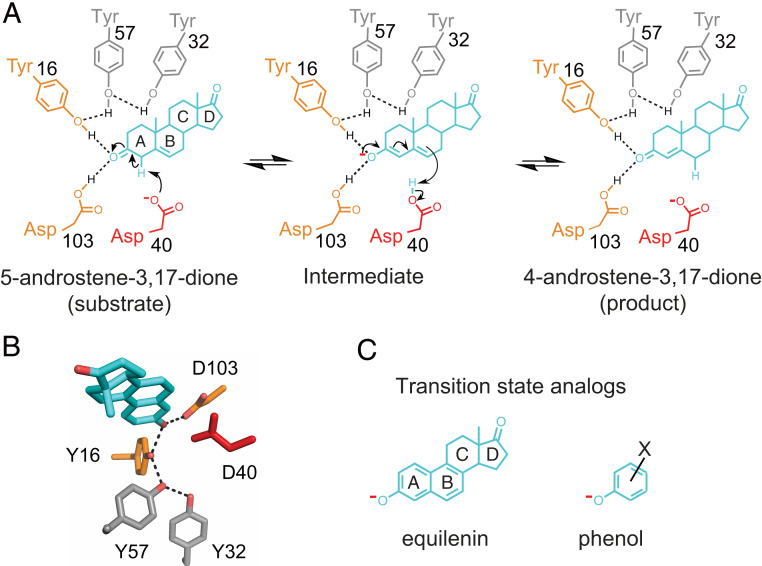
The KSI reaction. Reaction mechanism and schematic depiction of the active site (A) and its 3D organization (B) [PDB ID code 1OH0 (87)]. KSI catalyzes double bond isomerization of steroid substrates (shown for the substrate 5-androstene-3,17-dione) utilizing a general acid/base D40 (which we refer to herein as a general base, for simplicity), and an oxyanion hole composed of the side chains of Y16 and D103 (protonated); general base and oxyanion hole residues are colored in red and orange, respectively. The product in A, 4-androstene-3,17-dione, is the substrate of the reverse reaction and was used for RT X-ray crystallography herein. (C) Examples of oxyanion KSI TSAs used for the KSI TSA ensembles: Equilenin (Left) and a substituted phenolate (Right).

Results

Limited Structural Changes throughout the KSI Catalytic Cycle.

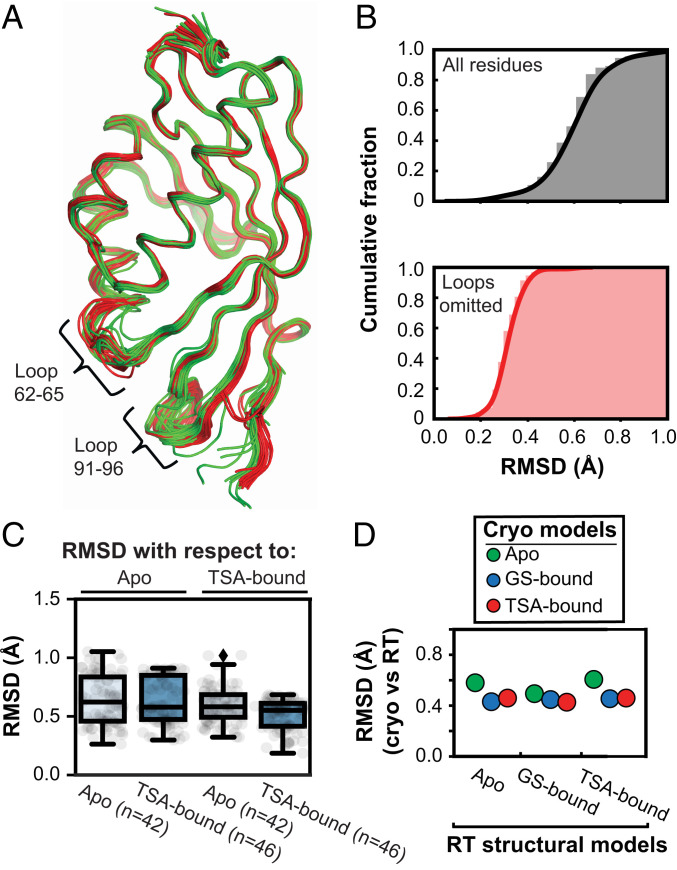
Prior analyses of crystal structures for 60 enzymes revealed modest structural changes between Apo and ligand-bound enzyme states, with RMSD < 1 Å on average, and generally no larger than differences between two Apo forms of the same enzyme (37). To evaluate the extent to which the KSI structure changes through its catalytic cycle, we took advantage of the 94 crystallographically independent KSI molecules from the 45 cryo crystal structures available in the PDB (38) (SI Appendix, Table S1). All these structures, whether Apo, ground-state–bound (GS-bound) (SI Appendix, Fig. S1), or transition-state analog-bound (TSA-bound) (Fig. 1C), were highly similar, as seen visually in Fig. 2A and SI Appendix, Fig. S2 B–D and by their similar RMSDs of <1 Å (Fig. 2 B, Upper, and SI Appendix, Fig. S3). Two short loops (residues 62 to 65 and residues 91 to 96) exhibit the greatest variation (Fig. 2A and SI Appendix, Fig. S2 B–D), and when these loops, representing <10% of KSI’s sequence, are excluded the RMSDs drop below 0.5 Å (Fig. 2 B, Lower, and SI Appendix, Fig. S3). To assess possible conformational changes in the reaction cycle, despite the strong similarities across all of the structures, we compared the Apo versus the TSA-bound structures. The RMSD values were as similar for each group, whether compared to an Apo or a TSA-bound structure (Fig. 2C), providing no indication of a significant conformational change.

Fig. 2.

Comparison of KSI crystal structures indicates no structural changes during catalysis. (A) Alignment of all 94 KSI crystallographically independent molecules from the 45 PDB crystal structures (in ribbon): Apo (green), GS-bound (blue), and TSA-bound (red) (Materials and Methods). The positions of the two flexible loops are noted. (B) Cumulative fraction of backbone RMSDs of all KSI structures vs. the highest resolution structure (WT TSA-bound, PDB ID code 1OH0) for the entire sequence (Upper, gray) and excluding the 62–65 and 91–96 loops (Lower, orange). (C) RMSDs. Alignment of all Apo (n = 42, light blue boxes) and all TSA-bound (n = 46, dark blue boxes) KSI monomers on the highest resolution Apo (PDB ID code 3VSY) and TSA-bound (PDB ID code 1OH0) KSI crystal structures. The boxes show the dataset quartiles and the whiskers denote the entire distribution. The analysis indicates that the difference between an Apo and TSA-bound structure is not larger that the differences between structures of the same state. (D) KSI structures obtained from cryocooled and RT crystals are highly similar. We compared cryo–X-ray structures (using the highest-resolution versions each for Apo, GS-bound, and TSA-bound; color-coded as in legend) to the traditional structural models obtained at RT (280 K; x axis) (see SI Appendix, Tables S4 and S5 for 280 K models PDB codes) and obtained RMSDs for each set of cryo- and RT structural models. The cryostructures used were: Apo, PDB ID code 3VSY (green); GS-bound, PDB ID code 5KP4 (blue); and TSA-bound, PDB ID code 1OH0 (red).

While the KSI cryo–X-ray structures furnished 42 Apo states and 46 TSA-bound states to make comparisons and to build conformational pseudoensembles for each state, there was only a single GS-bound structure (SI Appendix, Tables S1 and S2). We collected RT X-ray diffraction data for KSI bound to a ground-state analog at 280 K and analogous data for Apo and TSA-bound KSI to allow direct comparisons and to remove potential effects from cryocooling (SI Appendix, Table S3) (22, 32, 34, 36). The resultant structures supported the absence of conformational changes through the reaction cycle (Fig. 2D and SI Appendix, Fig. S4), allowed us to compare conformational heterogeneity across states representing KSI’s reaction coordinate, and demonstrated that our conclusions were not significantly affected by cryocooling.

Overall, the high structural concordance for different KSI states suggests that there are at most small structural differences through its reaction cycle.

Evaluating the KSI Conformational Landscape through Its Catalytic Cycle.

While there is little change in overall structure across states representing KSI’s reaction coordinate, the extent of conformational heterogeneity (i.e., the diversity of conformations) within each state can change; new interactions and new steric constraints can change the enzyme’s conformational landscape without altering the average structure. Whether such changes occur is determined by the shapes of the local potentials that constrain groups, and in this case whether the conformational landscape is dominated by interactions within the protein fold itself or is substantially altered by ligand binding.

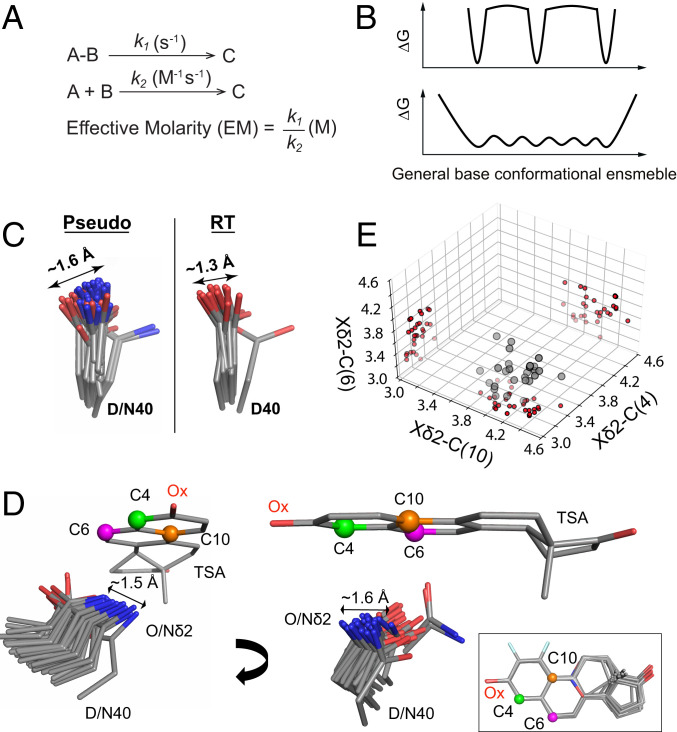
We built KSI Apo and TSA-bound pseudoensembles, using 42 and 46 cryo–X-ray structures, respectively (Fig. 2A and SI Appendix, Fig. S2 and Table S2). In this approach, each crystal structure (including structures with point mutations and different crystallization conditions) is considered to correspond to a local minimum on the native potential energy surface (30, 31, 39). The degree of motion extracted from pseudoensembles has been shown to agree well with estimates of motion from solution NMR (30) (SI Appendix, Supplementary Text 1). The individual KSI structures ranged in resolution from 1.1 to 2.5 Å (SI Appendix, Fig. S2A and Table S1), and neither inclusion of only high-resolution structures (≤2.0 Å) nor random omission of structures substantially altered the analyzed ensemble properties (SI Appendix, Figs. S5–S7).

The single GS-bound KSI cryo structure prevented us from building a ground-state pseudoensemble. To evaluate conformational heterogeneity with a bound ground-state analog, we built multiconformer models from our RT X-ray data, and to provide direct comparisons to Apo- and TSA-bound KSI we built analogous multiconformer models for these species (SI Appendix, Table S3). As the overall KSI structures in each state were indistinguishable at 100 and 280 K, we also collected diffraction data at 250 K, below room temperature but above the average glass transition temperature (SI Appendix, Table S3). We used the 250 K data herein as its 0.2 to 0.3 Å higher resolution, relative to the 280 K data, provided more information for multiconformer modeling (33).

Evaluating and comparing conformational heterogeneity.

Above we compared KSI structures overall, via RMSDs. Here we evaluate conformational heterogeneity residue-by-residue and compare the heterogeneity of each residue across the KSI states. For our pseudoensembles, we assayed backbone and side-chain positioning via Cα and Cβ, respectively, by defining an atomic mean deviation (MDev) parameter (Materials and Methods). Briefly, for a given atom in a structure, the MDev describes the average displacement of equivalent atoms within the ensemble of structures; lower and higher values represent smaller and larger positional fluctuations, respectively, corresponding to less or more conformational heterogeneity.

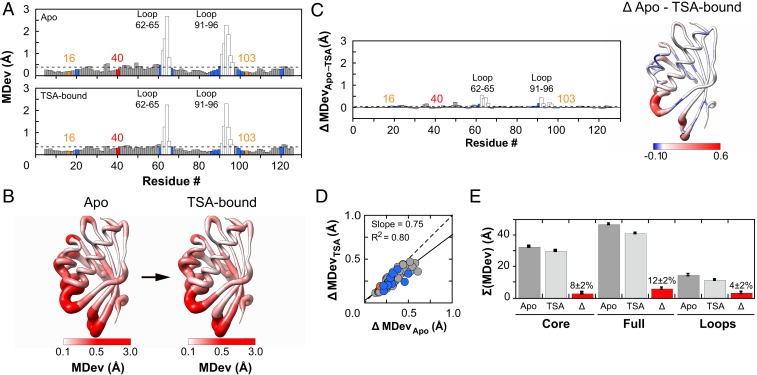
In both the Apo and TSA-bound pseudoensembles, Cα and Cβ MDevs were highly similar, below 0.5 Å, with exceptions only in the 62–65 and 91–96 loops, which showed the largest conformational heterogeneity (Fig. 3 A and B and SI Appendix, Figs. S9A, S10A, and S11 A and B). The MDevs for the catalytic residues were below average and on the lower end of observed values, and the MDevs for substrate binding residues were close to the average (Fig. 3A). Thus, positioning does not substantially increase with transition state-like interactions. Nevertheless, there is no extreme or unusual positioning in the active site (see Determining the extent of positioning of catalytic residues).

Fig. 3.

Assessing conformational heterogeneity through the KSI catalytic cycle via pseudoensembles. (A) Cα MDevs for KSI Apo (Upper) and TSA–bound (Lower) states. Dashed lines represent the average MDev. The flexible 62–65 and 91–96 loops are shown as white bars, Y16 and D103 in orange, D40 in red, and binding residues in blue. (B) Worm representation of the MDevs from A on the 3D structure of KSI. The thickness of the worm representation follows the color code (from white [MDev ≤ 0.1 Å] to red [MDev ≥ 0.5 Å]). (C) The difference Cα MDev values between the Apo and TSA-bound states (MDev_Apo-TSA), such that positive values indicate lower MDevs for the TSA-bound state; the bar plot shows the difference MDev values as a function of the protein sequence (Left) and the worm representation shows the difference MDev values represented on the 3D structure of KSI (Right), as in B but with a more sensitive scale to highlight the changes. (D) Correlation plot of Apo and TSA-bound Cα MDevs (excluding loops 62–65 and 91–96). The dashed line of slope 1 represents the expectation for no difference in average MDevs between the two states. Similar results were obtained with loops included (SI Appendix, Fig. S7). (E) Sum of Cα MDevs for Apo (dark gray bars), TSA-bound (light gray bars), and their difference (Δ, red bars). Errors were estimated using bootstrap analysis and error propagation (Materials and Methods and SI Appendix, Fig. S8). Side-chain MDevs (using Cβ) gave analogous results (SI Appendix, Figs. S10 and S11).

To assess changes in conformational heterogeneity through the reaction cycle, we first compared Apo state MDevs to those in the TSA-bound state. The MDev values were similar across the entire structure, as seen qualitatively in Fig. 3 A and B and quantitatively in Fig. 3C by the difference in MDev between the states and by the strong correlation of the Apo and TSA-bound state MDev values (Fig. 3D and SI Appendix, Figs. S7 and S10D). Nevertheless, the slope of this correlation was less than 1 (=0.75), crudely suggesting an overall dampening of ∼25% in conformational heterogeneity of the enzyme core upon binding of the TSA. A modest dampening in the TSA complex is also supported by smaller MDevs with the TSA bound, with an average reduction (ΔMDev_Apo-TSA) of 0.05 Å per residue (Fig. 3C and SI Appendix, Figs. S10 B and C and S11 C and D). We obtained similar results for a homologous KSI (KSI_homolog) from another organism, despite only 32% sequence identity (SI Appendix, Fig. S12). For KSI_homolog, there were fewer but a sufficient number of available cryo–X-ray structures (n = 42).

To evaluate conformational heterogeneity from our RT multiconformer models, we calculated crystallographic disorder parameters, (1-S²), which report on local conformational heterogeneity by capturing bond vector motions and agree well with solution NMR measurements (SI Appendix, Fig. S13) (40). We used (1-S²), rather than MDevs, because our RT multiconformer models contain additional information within each state that is captured by (1-S²) and because the limited number of conformational states in multiconformer models limits the utility of MDev comparisons. The (1-S²) values range from 1, for a completely unrestrained bond vector, to 0, for a completely rigid bond vector. Even though (1-S²) and MDev are different measures of heterogeneity, we observed the same reduction in overall heterogeneity of 12% (Fig. 3E and SI Appendix, Fig. S15B). We also obtained information about heterogeneity in the KSI•GS complex from RT X-ray data, information that cannot be extracted from the single cryo KSI•GS structure (SI Appendix, Table S3 and Figs. S13–S15). Comparisons of the KSI•GS complex to the Apo and TSA-bound forms revealed that most of the modest reduction in heterogeneity occurs upon formation of the GS complex (SI Appendix, Fig. S15).

The 91–96 loop interacts with the substrate and the 62–65 loop interacts with the 91–96 loop but does not interact with the substrate directly. We therefore anticipated that these loops might undergo a conformational dampening upon ligand binding. Nevertheless, the changes are modest (Fig. 3C and SI Appendix, Figs. S9B and S10B), as are the functional effects; mutation of W92, the loop residue making direct substrate contact, increases K_M only twofold and decreases k_cat less than twofold (41). Furthermore, a single-ring substrate lacking the remote ring that is contacted by the 91–96 loop has a k_cat value within twofold of the full substrate (42). Thus, the loop is not tightly coupled to the conformational heterogeneity or function of the catalytic residues, and the absence of significant loop effects on catalysis is consistent with the absence of substantial conformational changes or dampening elsewhere in the active site.

In summary, analysis of cryo-pseudoensembles for KSI from two organisms and RT X-ray data for one of these provide evidence for active site organization resulting predominantly from interactions within the folded enzyme, with only modest adaption in conformational heterogeneity along the reaction coordinate due to the additional interactions with bound ligands.

Determining the extent of positioning of catalytic residues.

Proposals for the origin of enzymatic power universally invoke positioned catalytic groups in enzyme active sites, relative to the diffusive uncorrelated motions of the same groups free in solution (6–15). The analyses above indicate that there are minimal changes in KSI conformational heterogeneity, including the catalytic residues, for species representing the reaction coordinate, but we do not know how positioned catalytic groups are for any enzyme.

Given the enormous catalytic potential from positioning—to overcome entropic reaction barriers and enthalpically destabilize reactants relative to transition states—enzymes might have evolved to especially constrain their catalytic groups. For KSI and numerous other enzymes, a potential catalytic mechanism involves a precisely positioned oxyanion hole that distinguishes ground state carbonyl groups from oxyanionic transition states and intermediates (2, 43–47). Conversely, there are cases where motions are clearly required, and many enzymes, including KSI, proteases, and isomerases, use a single residue to carry out multiple reaction steps, an evolutionarily parsimonious solution that necessitates some extent of conformational heterogeneity (Fig. 1A) (48, 49).

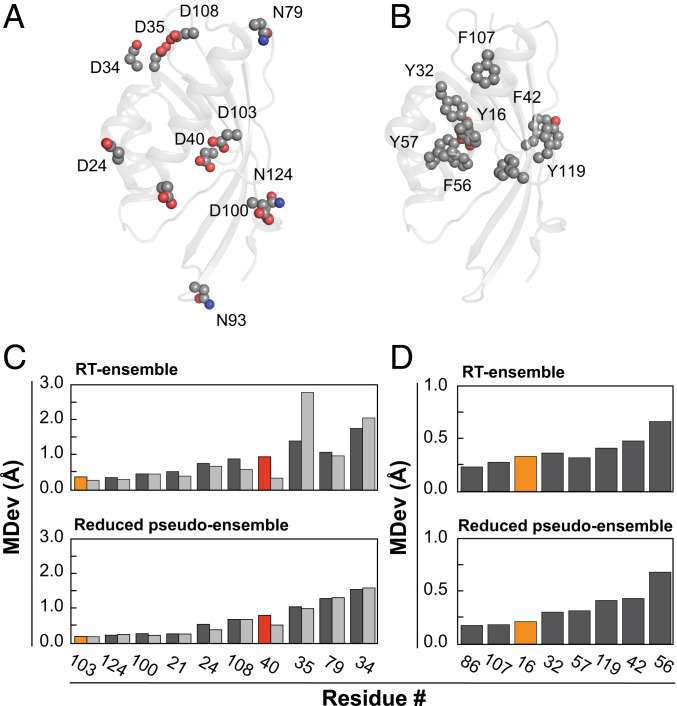
To assess the degree of positioning of KSI’s catalytic residues, we constructed a reduced pseudoensemble with 54 KSI molecules, excluding structures from our full pseudoensemble with mutations to the residues under analysis and mutations previously identified to alter the positioning of these residues (SI Appendix, Table S2). We created an ensemble from our RT X-ray data by combining the KSI Apo, GS-bound, and TSA-bound multiconformer models, given their highly similar overall conformational heterogeneity and high residue-by-residue similarities (SI Appendix, Figs. S13 and S15). The conformational heterogeneity inferred from the reduced pseudoensemble and the RT X-ray ensemble correlated well with the conformational heterogeneity from the full pseudoensemble, suggesting that overall ensemble information is retained (SI Appendix, Figs. S17 and S18).

To test whether catalytic groups are particularly constrained, we compared the MDev values for the catalytic atoms of Y16 and D103, the oxyanion hole, and of D40, the general base (Fig. 1), with the atoms of chemically similar but noncatalytic residues throughout KSI, and we carried out this comparison with both the reduced pseudo- and the RT ensembles (Fig. 4 and SI Appendix, Fig. S19). The oxyanion hole catalytic groups sit at the lower end of the observed MDevs, but with values similar to the most constrained noncatalytic groups. The general base oxygen of D40 is also not unusually constrained, indeed exhibiting more motion than the equivalent atoms of chemically similar residues. Furthermore, its noncatalytic oxygen has an MDev lower than that for the general base oxygen (Fig. 4 C and D). These results indicate that catalytic functional groups are not extraordinarily constrained, at least for KSI.

Fig. 4.

Comparison of positioning of catalytic vs. noncatalytic atoms of chemically similar groups. All Asp and Asn residues (A) and Tyr and Phe residues (B) of KSI mapped on the 3D structure (see SI Appendix, Fig. S19 for details and atom names). MDevs (C) for all Asp and Asn Oδ1 atoms in light gray, O/Nδ2 atoms in dark gray and (D) for all Tyr (OH atoms) and Phe (Cζ atoms), respectively. Y16 and D103 are orange, and D40 is red. Upper and Lower show RT ensemble and reduced pseudoensemble results, respectively. N93 was not included in the analyses, as it is situated within the flexible 91–96 loop. See SI Appendix, Fig. S20 for side-chain dihedral angle comparisons, which yield similar conclusions.

Testing Models for KSI Catalysis.

Positioning and general base catalysis.

KSI faces a challenge common to many enzymes: A need to efficiently abstract and donate protons at multiple substrate positions. In the face of this challenge, KSI exhibits an effective molarity (EM) of 10³ to 10⁵ M, unusually high for general base catalysis (Fig. 5A) (50). The large rate advantage could most simply be accounted for by highly precise positioning of its general base, D40 (Fig. 1), a model we can now evaluate.

Fig. 5.

The high effective molarity of the general base in KSI is not due to a highly precise positioning. (A) When a unimolecular reaction (s⁻¹) is compared to a bimolecular reaction (M⁻¹s⁻¹), the ratio of rate constants has units of molar (M) and this value is referred to as an effective molarity (EM) (50, 73). (B) KSI’s high EM and ability to donate and abstract protons at multiple positions for multiple substrates could reflect distinct, narrow potential energy wells corresponding to precise positioning at each of the acidic carbons on KSI substrates (Upper). However, EM reflects a ratio of rate constants (A) and can arise with other factors responsible for the high observed catalytic efficiency and without narrow positioning (Lower). (C) The general base (D40) pseudoensemble and RT ensemble. It contains aspartate and asparagine residues, as asparagine mimics the protonated (intermediate) state of the general base and increases the affinity for TSAs (44, 88). Including only aspartate or only asparagine residues does not substantially alter the range of observed motions (SI Appendix, Fig. S21). (D) A bound TSA as “seen” by the KSI general base in a TSA-bound ensemble of cryo crystal structures (SI Appendix, Table S2). For clarity, TSAs were aligned on the A ring and only one structure (PDB ID code 1OH0) is shown. The carbon positions where protons are shuffled are represented as green, magenta, and orange spheres (see Fig. 1 and SI Appendix, Figs. S1 and S30 for the reaction mechanisms). The Inset shows the aligned TSAs. (E) The distribution of distances between the Oδ2 (Nδ2 when asparagine at position 40) and the three carbon positions from D on the bound TSAs in each crystal structure. Projections onto each of the planes reveals a broad distribution rather than subclusters at short distances around each of the carbons.

Above we noted that the proton-abstracting oxygen of D40 (Oδ2) is not particularly discretely positioned, relative to other carboxylate oxygens, based on MDev comparisons (Fig. 4C). Nevertheless, its MDev value could represent precise positioning in narrow but spatially separate energy wells, with each corresponding to a position for proton abstraction (Fig. 5 B, Upper), or it could represent a broader, continuous conformational ensemble (Fig. 5 B, Lower). The KSI pseudoensemble and RT ensemble provide evidence for general base motions on the scale of 1 to 1.5 Å, with no indication of preferred subpositions (Fig. 5C and SI Appendix, Fig. S21). To further investigate this possibility, we aligned the 36 available KSI molecules with bound TSAs from X-ray cryostructures (SI Appendix, Table S2). These revealed a broad range of general base positions with respect to the bound ligand (Fig. 5D). We then determined the distances between the general base catalytic Oδ2 and the TSA carbon positions corresponding to the acidic carbons between which protons are shuffled in different substrates (SI Appendix, Fig. S30). A three-dimensional (3D) plot, with each dimension corresponding to one of these three distances, showed that instead of clustering around each of the three-proton abstraction/donation positions, the general base catalytic Oδ2 positions are spread throughout this 3D space (Fig. 5E). We observed a similarly broad general base distribution for KSI_homolog (SI Appendix, Fig. S22). In summary, mechanisms other than highly precise local positioning for proton abstraction appear needed to account for KSI’s highly efficient general base catalysis (Discussion).

Implied above, and in numerous discussions of enzyme catalysis, is a need to balance positioning and flexibility (3, 51, 52). Nevertheless, a general rigidity–flexibility continuum may in some instances represent correlations rather than causative changes: For example, increased rigidity in thermophilic enzymes may reflect increased packing and stability rather than an inherent relationship between flexibility and catalysis. For KSI, we can make a specific, mechanism-based catalytic prediction that increasing or decreasing positioning of its general base may reduce catalysis, because excessive rigidity would prevent access to all three proton transfer positions and excessive flexibility would result in a large fraction of unreactive conformations.

Ensemble–function analysis reveals a balance between general base positioning and flexibility.

To evaluate the above predictions, we carried out an “ensemble–function” analysis, comparing ensembles for two KSIs that differ in the groups interacting with their general base in conjunction with new and prior functional data.

It was previously observed, as expected, that mutation of residues surrounding D40 substantially reduced catalysis and also substantially increased D40 mobility (53, 54). Mutations around a catalytic site often compromise catalysis and disrupt positioning, consistent with the ubiquitous role of positioning in catalysis. However, for KSI there is also evidence for reduced catalysis from restricting motions.

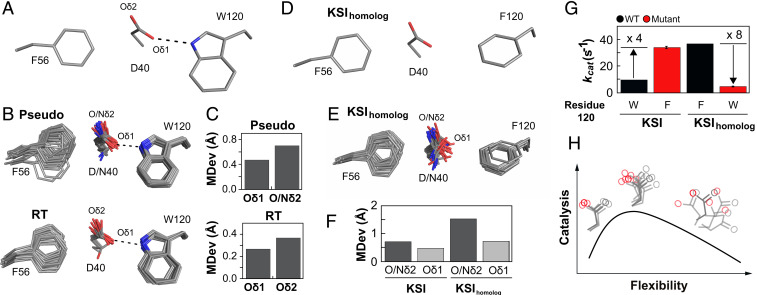
The KSI focused on herein positions D40 through a hydrogen bond between its noncatalytic oxygen (Oδ1) and the W120 side chain (Fig. 6A). The hydrogen bond from W120 to Oδ1 appears to act as a pivot that allows conformational exploration by the more distal Oδ2 (Fig. 6 B and C and SI Appendix, Fig. S21F). In contrast, KSI_homolog replaces W120 and its hydrogen bond with a phenylalanine and an anion–aromatic interaction (Fig. 6D), and the less directional anion–aromatic interaction allows greater conformational freedom for D40 (Fig. 6 E and F).

Fig. 6.

Ensemble–function analysis of general base catalysis for two KSI homologs. (A) Anion–aromatic and hydrogen-bonding interactions with F56 and W120 side chains, respectively, implicated in general base positioning in KSI (illustrated using PDB ID code 1OH0). (B) The full pseudoensemble (Upper) and RT ensemble (Lower) of the general base (D40), F56, and W120 side chains. (C) MDevs of the noncatalytic (Oδ1) and catalytic Oδ2 (Nδ2 when asparagine at position 40) oxygen atoms of the general base from the full pseudo- (Upper) and the RT ensemble (Lower). (D) Anion–aromatic interactions with F56 and F120 side chains implicated in KSI_homolog general base positioning (illustrated using PDB ID code 1OHP, KSI numbering used for KSI_homolog). (E) The KSI_homolog pseudoensemble (SI Appendix, Table S21). (F) MDev values for the D40 catalytic Oδ2 (dark gray bars, including asparagine Nδ2) and noncatalytic Oδ1 (light gray bars) obtained from the pseudoensembles in B and E. (G) Comparison of activity for KSIs with tryptophan and phenylalanine at position 120 (data from SI Appendix, Table S58). (H) Conformational ensemble model for optimal general base catalysis. Optimal flexibility enables the general base to shuffle protons between different positions in different substrates (Center); reducing motion (Left, e.g., when F120 in KSI_homolog is replaced with W120 in KSI) reduces catalysis, as does increasing motion (Right, e.g., from mutations in the loop carrying the general base) (53, 54).

Intriguingly, KSI_homolog is fourfold more active than KSI, and we wondered whether this increased activity might be linked to D40’s conformational heterogeneity (53–56). Consistent with this possibility, mutation of F120 to tryptophan in KSI_homolog reduced activity eightfold (Fig. 6G). Whereas deleterious effects are common and can be difficult to trace mechanistically, favorable mutations in natural enzymes are rare. Nevertheless, the W120F mutation in KSI increases its activity fourfold, and with this increase, its activity matches that of KSI_homolog (Fig. 6G).

Our ensemble–function analysis suggests that while increased general base conformational heterogeneity appears required for function, there also appears to be an optimal balance between allowing and limiting conformational heterogeneity: Too much conformational freedom reduces catalytic efficiency, as has been observed many times, but also too little conformational freedom hinders catalysis, presumably by lowering the D40 occupancy in some of its reactive poses (Fig. 6H).

Positioning and oxyanion hole catalysis.

We expect, and observe, large deleterious effects when Y16 and D103, the hydrogen-bond donors of KSI’s oxyanion hole, are replaced with large hydrophobic residues that cannot stabilize the negative charge build-up on the substrate carbonyl oxygen (Fig. 1A and SI Appendix, Table S59) (55, 56). Such results are common but do not answer the critical question of how these catalytic groups provide rate advantages relative to uncatalyzed reactions in solution (43). Our ensemble data allow us to evaluate mechanisms proposed for how replacing hydrogen bonds donated by solution water molecules with enzymatic hydrogen-bond donors affords KSI its oxyanion hole catalytic advantage.

Assessing geometric discrimination.

A widely adopted perspective on enzyme catalysis holds that the catalytic power of enzymes can be understood in terms of transition-state as opposed to ground-state complementarity (8, 14, 57–59). Preferential transition-state stabilization on geometrical grounds—for example, discrimination between an sp² ground state and sp³ transition state—has been proposed for oxyanion holes of proteases and isomerases, including that of KSI (e.g., refs. 2, 43–47, 60). Such geometric discrimination would require highly precise positioning of the hydrogen-bond donors, so that hydrogen bonds can be suboptimal in the ground state and optimal in the transition state.

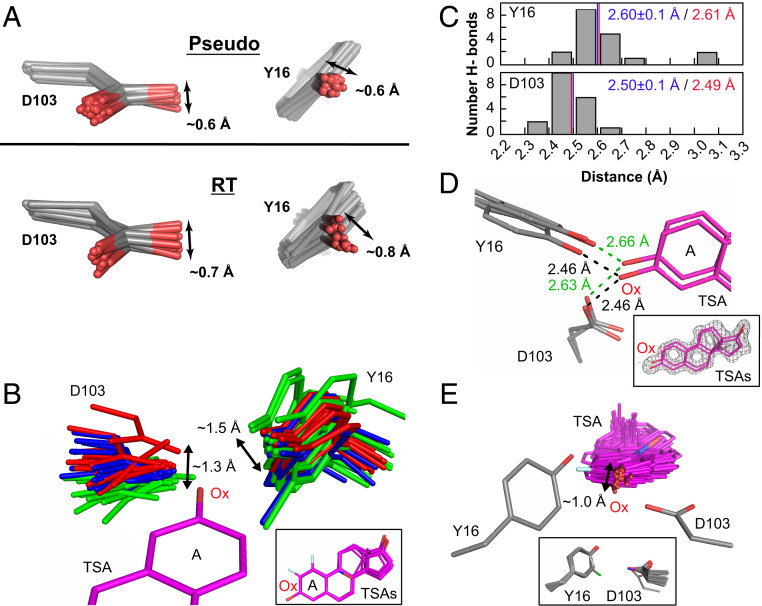
While an individual structure may show optimal or suboptimal positioning for either ground-state or transition-state stabilization, it is the conformational ensemble that defines the positioning and relative stabilization. Analysis of our KSI ensembles indicates positioning within the oxyanion hole on the scale of ∼0.5 to 1 Å (Fig. 7A and SI Appendix, Fig. S23), with hydrogen bonds made from a wide range of orientations (Fig. 7B and SI Appendix, Fig. S24). Thus, sp² versus sp³ discrimination is unlikely in KSI. This conclusion is supported by additional analyses below.

Fig. 7.

The KSI oxyanion–oxyanion hole conformational ensemble. (A) The oxyanion hole (Y16 and D103) pseudoensemble (Upper) and RT ensembles (Lower). Phenylalanine residues at position 16 are omitted, and chlorine atoms in chemically modified tyrosine residues have been omitted for clarity (see also SI Appendix, Figs. S16 and S23). (B) The KSI oxyanion hole as “seen” by 36 bound TSAs (equilenin and phenols) in cryo crystal structures (SI Appendix, Table S2). Structures have been color-coded in three groups according to the D103 position in space relative to the TSA oxyanion (Ox). All TSAs have been aligned on the A ring with only PDB 1OH0 shown for clarity. The Inset shows the 36 aligned TSAs. (C) Distribution of Y16 (Upper) and D103 (Lower) hydrogen-bond distances from an ensemble of KSI crystal structures of variants with WT-like activity and with a bound TSA (equilenin, n = 19) (SI Appendix, Table S2). The mean hydrogen-bond lengths and SDs from the cryo crystal structure distances are shown in blue and the distances obtained by solution ¹H NMR are show in red (see SI Appendix, Fig. S25 for ¹H NMR spectrum). (D) The TSA-bound RT multiconformer model shows that oxyanion hole Y16 and D103 and the bound TSA can make hydrogen bonds from different orientations. While multiconformer models do not allow unambiguous identification of each hydrogen bonded substates, possible hydrogen-bond lengths between Y16/D103 and the TSA are within the range obtained by cryostructures and solution ¹H NMR. The Inset shows the TSA (purple sticks) and the experimental electron density (gray mesh, contoured at 1σ). (E) The bound TSAs from B as “seen” by the hydrogen bonding oxygens of Y16 and D103. Y16 and D103 have been aligned such that their hydrogen-bonding oxygens overlay but only one Y16/D103 set (PDB ID code 1OH0) is shown for clarity. The Inset shows all aligned Y16 and D103 hydrogen-bonding groups.

Assessing hydrogen bond properties.

NMR studies have established that the hydrogen bonds to KSI-bound oxyanions are short (44, 61–63), and it has been suggested that short hydrogen bonds in KSI and other enzymes are conferred by properties of the enzyme and contribute substantially to catalysis (64–66). For example, these short hydrogen bonds might arise from precise geometric constraints of the oxyanion hole hydrogen-bond donors. However, our ensembles described above reveal a wide range of conformational states of the oxyanion hole that donate hydrogen bonds to the bound oxyanion (Fig. 7 A and B and SI Appendix, Figs. S23 and S24), and the absence of strong geometrical constraints is further evidenced by lack of coordination between the two oxyanion hydrogen-bond donors (Fig. 7B and SI Appendix, Fig. S16). In addition, the similar hydrogen-bond lengths across the ensemble substates provides no indication of hydrogen-bond strain driven by conformational properties of the enzyme (Fig. 7C). Seemingly equivalent hydrogen bonds can be made from different oxyanion hole hydrogen-bond donor orientations and the bound TSA can accept hydrogen bonds from a variety of bound orientations (Fig. 7 B–E). Indeed, the oxyanion hole hydrogen-bond lengths match those observed for these donor/acceptor pairs universally, in small molecules, other proteins, and across a range of solvents (Fig. 7C) (62, 67). These results suggest that the donor/acceptor electron densities determine the observed hydrogen-bond lengths in KSI and that the internal protein forces are not sufficient to measurably alter these intrinsic hydrogen-bond properties.

What Restricts and Permits Motions in and Around the Active Site?

Our KSI ensembles provide a window into molecular behaviors that are central to catalysis and allow us to begin to evaluate the interactions and forces that are responsible for positioning.

Traditional X-ray crystallographic models provide many insights, including identifying hydrogen bonds and hydrophobic contacts that may constrain motions. It has been noted that hydrogen bonds are more directional and thus more restricting than hydrophobic interactions in isolation (68–70). Our analysis of what restricts and allows motion of KSI’s general base supports this view, as anion–aromatic interactions take the place of hydrogen-bonding interactions with the carboxylate base to enhance conformational excursions, and replacement of one of the anion–aromatic interactions with a hydrogen bond restricts conformational freedom and lowers catalysis (Fig. 6).

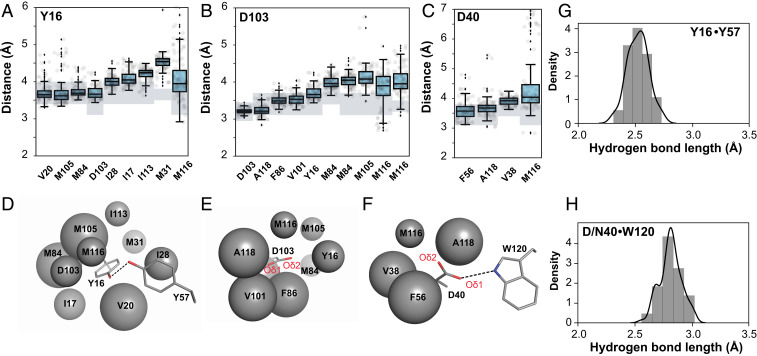
Nevertheless, in the crowded idiosyncratic environment of a protein interior, favored conformational states and the breadth of their distributions will be determined by multiple energetic contributors that include hydrogen bonds, van der Waals interactions and repulsion, and bond angle preferences, which all need to be integrated over the allowed states to understand the ensemble of conformations that are present and that are preferred. Our ensemble data provide insights into the forces and interactions that define residues’ conformational preferences within the ensemble of states. To describe packing and van der Waals interactions in an accessible form, we defined a packing distance between surrounding residues to the catalytic groups, Y16, D103, and D40, yielding, for each structure from the pseudoensemble, a single distance of closest approach between atoms of catalytic and surrounding groups (SI Appendix, Tables S42–S48). These distances, together, provide ensemble-level local packing information (Fig. 8). The simplicity of this representation facilitates interpretation, and more detailed analyses can be carried out in the future (e.g., to evaluate predictions from molecular dynamics simulations).

Fig. 8.

Ensemble analysis to evaluate the packing and interactions around the KSI catalytic groups. Ensemble distances between Y16 (A), D103 (B), and D40 (C) and their surrounding packing groups from all 94 independent KSI molecules from the 45 cryo crystal structures available in the PDB (SI Appendix, Table S1). The boxes show the quartiles of the dataset and the whiskers extend to include the statistical distribution. The closest atoms making van der Waals interactions were identified and distances between specific atom pairs were measured (see SI Appendix, Tables S42, S44, and S46 for the list of atom pairs); hydrogen-bonding lengths are presented separately (G and H). Two sets of distances are reported for M84 and M116, as two distinct atoms were within similar distances. The van der Waals radii (r_vdw, shaded rectangles) are represented as a range because of uncertainty introduced by the absence of hydrogen coordinates in the X-ray structural models and because the oxygen r_vdw is orientation-dependent (see SI Appendix, Table S48 for a list of r_vdw used here). (D–F) Schematic depiction of the results from A–C, respectively, with the packing atoms represented as spheres; larger spheres represent more tightly packed surroundings; and Y16, D103, and D40 and the hydrogen-bonding groups Y57 and W120 are represented in sticks for clarity (PDB ID code 1OH0). (G and H) Histogram of Y16-Y57 and D40-W120 hydrogen-bonding distances from structures in A–C (position 40 contains both aspartate and asparagine residues).

These analyses can be used to develop and test models about the relative importance of these forces and interactions, as described in SI Appendix, Supplementary Text 3. Upon alteration of specific interactions, we observe transitions between ensembles, rather than from one discrete state to another, and the nature of these transitions depend on the types of interactions altered and local packing constraints vs. local conformational entropy.

Discussion

Enzymes fold and bind substrates, and thereby colocalize and restrict the range of conformational states of catalytic groups and reactants. Precise positioning has often been suggested, explicitly or implicitly, as essential for enzyme catalysis (6–15). Using pseudoensembles from collections of cryo–X-ray structures from the PDB and ensembles from new RT X-ray diffraction data, we have evaluated whether catalytic groups are exceptionally positioned, defined the extent and nature of their positioning in KSI’s active site, tested specific and general models for enzymatic catalysis, and evaluated the forces that define conformational ensembles.

Positioning of KSI Catalytic Groups.

We evaluated whether catalytic groups are exceptionally positioned, and we defined the extent and nature of their positioning in KSI’s active site. The catalytic residues are more conformationally restricted than most other residues, but not extraordinarily so, with the oxyanion hole and general base residues spanning conformations on the scale of ∼1 to 1.5 Å (Figs. 4, 5, and 7 and SI Appendix, Figs. S21 and S23). The populated conformation states are asymmetric, spanning distances as small as ∼0.2 Å in particular directions, reflecting the asymmetric protein environment (SI Appendix, Figs. S21 and S23). Similar conformational ranges were observed for a KSI homolog, suggesting that the extent of positioning and mobility arises from a combination of shared structural and functional features (SI Appendix, Figs. S12 and S22).

Tests of KSI catalytic mechanisms.

KSI exhibits highly efficient general base catalysis, as demonstrated by the EM of its general base, D40 (EM = 10³–10⁵ M) (Fig. 5) (71). Nevertheless, our ensemble data revealed that D40 exhibits considerable conformational freedom, providing evidence against highly precise positioning as the origin of KSI’s efficient general base catalysis. An alternative model invokes D40 desolvation driven by protein folding and ligand-binding energy and remains to be tested (50, 72, 73). KSI’s general base conformational freedom is likely essential for its function: To efficiently shuttle protons between different positions in substrates and to allow catalysis with different substrates (Figs. 1A and 5 and SI Appendix, Figs. S1 and S30). Indeed, a more efficient KSI homolog had a broader range of general base positions (Fig. 6 D–F), and we proposed that this difference arises from a difference in general base interactions between the homologs: The faster homolog displayed a less directional anion–aromatic interaction with the general base relative to the hydrogen-bond interaction found in the slower homolog (Fig. 6 A and B). Supporting this model, increased catalysis was observed upon replacement of the hydrogen bond with an anion–aromatic interaction (Fig. 6G). Nevertheless, mutations that further increase general base mobility decrease catalysis (53, 54). Thus, KSI’s general base appears to experience a “Goldilocks effect,” where too much or too little conformational heterogeneity is detrimental to catalysis (Fig. 6H).

Catalytic models invoking geometric discrimination in oxyanion holes, between sp² ground states and sp³ transition states, have been proposed for proteases and other enzymes, including KSI (2, 43–47). Our analyses of KSI ensembles indicate motions on the scale of 1 Å for the oxyanion hole residues, a large angular range of hydrogen bonds to TSAs, with hydrogen bonds of similar length made regardless of the orientation (Fig. 7 and SI Appendix, Fig. S24). These observations suggest that ground-state vs. transition-state geometric discrimination for KSI is unlikely. Instead, KSI’s oxyanion hole appears to generate catalysis by providing stronger hydrogen bonds, relative to those from water (62, 74, 75). The range of oxyanion hole conformational poses appears to amplify the range of conformational states of bound substrates and intermediates, likely contributing to KSI’s ability to catalyze reactions of multiple substrates with protons transfers at multiple positions (Fig. 7 B and E and SI Appendix, Fig. S23).

Probing forces that define conformational ensembles.

It is important to understand the complex array of forces and interactions within folded proteins that define conformational heterogeneity, and to understand how these forces are balanced within different enzymes that carry out different functions or function under different conditions. Analyses at the level of single-conformer models may lead to different conclusions based on the structural snapshot considered, highlighting the need for ensemble information (e.g., see Fig. 8 and SI Appendix, Fig. S26). These structural snapshots are not incorrect, just limited; prior results and our comparisons of cryoensembles and room temperature X-ray data suggest that each cryo–X-ray structure represents a portion of a more complex conformational landscape (SI Appendix, Figs. S17 and S18) (5, 76, 77).

With ensemble information, we have been able to probe how individual interactions influence KSI’s conformational landscape and its preferred conformational states. An example is the interplay of KSI’s general base with its neighbors described above. Other examples for positioning in the oxyanion hole are provided in SI Appendix, Supplementary Text 3.

Conformational ensembles, transition states, and the need for ensemble–function studies.

To understand how enzymes achieve catalysis and specificity and to guide the design of new enzymes that rival those from Nature, we will need to extend structure–function studies to ensemble–function studies. Underscoring the need for ensemble information, bulk reaction rates are a function of the probability of the enzyme adopting a given substate on a conformational landscape and the probability of reacting from this substate (3, 5, 18).

Our ensembles for KSI include a bound reactant (Fig. 1A), and have revealed a broad range of conformational states in line with KSI’s need to abstract protons at multiple positions (Figs. 1 and 5–7). But while a subset of these conformations lies nearer to each position of proton abstraction (Fig. 5E), these conformational ensembles represent states of high and intermediate occupancy and are unlikely to capture rare high-energy states near transition states where the distance between the general base catalytic oxygen and ligand carbons is shorter than the sum of van der Waals radii. Nevertheless, the states we do observe are consistent with a smooth local conformational landscape, so that the transition states for proton abstraction may correspond to rare excursions at the “edge” of our ensemble. Furthermore, while no TSA is a perfect mimic of the transition state, the binding affinities of oxyanion compounds used as KSI TSAs mirror catalytic effects of oxyanion hole mutations, suggesting that these TSA interactions faithfully represent oxyanion interactions present in the actual transition states (56) (see SI Appendix, Supplementary Text 2 for additional discussion). Nevertheless, different KSI substates will give different reaction probabilities for different reaction steps, as is clear from the need for the general base to carry out proton transfer at different positions (Fig. 1A). As a consequence, the actual transition-state ensemble for each step will be narrowed from the overall ensembles observed herein.

The inability to experimentally capture transition-state substates underscores the need for an ensemble–function feedback loop that includes functional tests of models derived from ensemble studies and prior functional studies. Our ensemble and functional results for KSI’s general base provide a case study, as we linked ensemble properties to a model for their catalytic consequences, and then tested predictions from this model with new functional data (Fig. 6). In addition, conformational ensembles across all atoms of a protein provide a rich experimental source to test and develop the force fields that underlie computational approaches (28, 29).

Testing classic proposals for enzyme catalysis.

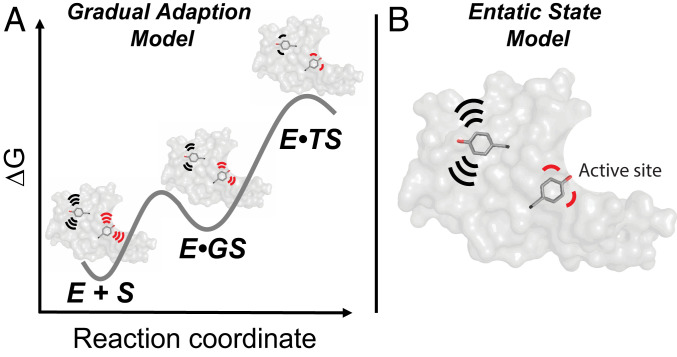
Our KSI enzymes allowed us to test two broad catalytic models: Whether enzyme groups, especially active site residues, are largely prepositioned for reaction or whether their conformational ensembles are narrowed as the reaction proceeds (the “gradual adaption model” in Fig. 9A) and whether catalytic residues exhibit more precise positioning than other residues (the “entatic state model” in Fig. 9B; see legend for clarification of the terminology used).

Fig. 9.

Models for conformational heterogeneity in enzyme catalysis. Each model is updated from original proposals, as described in the text, to incorporate an ensemble perspective (3, 5). Each panel shows an enzyme with two highlighted tyrosine residues, a “noncatalytic” tyrosine (black) in the enzyme core (gray) representing the noncatalytic residues, and a “catalytic” tyrosine (red) to represent catalytic residues in the active site. (A) The gradual adaption model (78). Both noncatalytic and catalytic tyrosine residues become more conformationally restricted as the reaction proceeds to the transition state. (B) The entatic state model (80, 81). Folding energy and local interactions provide greater restrictions and more precise positioning of the catalytic tyrosine (red, representing active site residues), relative to a noncatalytic tyrosine (black, representing noncatalytic residues). The restriction of active site residues (reduced conformational heterogeneity) is “paid for” with folding free energy and is used to enhance catalysis according to this model. In both panels, motions are schematically depicted by the motion lines.

In 1976 Wolfenden (78) proposed that enzymes undergo changes in shape when forming the enzyme–substrate complex and subsequent changes to give maximal complementarity to the transition state where stabilization is greatest, and we refer to this as the “gradual adaptation model.” An updated version of this model utilizing a conformational landscape perspective recognizes that enzymes exist as conformational ensembles, with the distribution of states determined by the relative energy, as shown schematically in Fig. 9A. This model implies (re)alignment of enzyme groups upon binding of the ground state and in the transition state, such that the distribution of enzyme states is most altered or narrowed in the transition state, in agreement with the widely discussed perspective that enzymes are most complementary in charge and shape to their transition states, so that stronger transition-state interactions may alter or narrow the ensemble (8, 10, 14, 72, 79).

Our results suggest that KSI does not substantially alter or narrow the distribution of enzyme states through its reaction cycle, a finding supported by both cryo-pseudoensembles and RT X-ray data and common to both KSIs investigated here. There is some decrease in conformational heterogeneity when new interactions are formed upon ligand binding, estimated as a modest overall decrease of ∼10 to 15% (Fig. 3 and SI Appendix, Figs. S10, S12, and S15). Nevertheless, the vast majority of KSI’s conformational restrictions, relative to groups moving freely in solution, are already present in free KSI and thus arise from the interactions that are present in the folded enzyme. Thus, minimally, the updated gradual adaptation model is not general to enzymes.

A second model follows from Vallee and Williams’ “entatic state” proposal that active site groups are distorted from their most stable free conformation (by folding free energy) to more closely match the conformational or electronic needs of a reaction’s transition state (80, 81), and the observation that active-site residues can destabilize enzymes, consistent with evolutionary selection of these residues for catalysis rather than stability (82). Extending from these ideas, more precisely positioned active-site residues relative to other residues could provide a catalytic advantage, while destabilizing the folded enzyme due to the conformational entropy loss from restriction to the most catalytically active conformers (Fig. 9B).

We found that catalytic residues were generally more restricted than residues throughout the enzyme, but not extraordinarily so, such that they tended to match rather than exceed the most restricted of the chemically similar noncatalytic residues (Fig. 4). Thus, our ensemble data provide evidence against this version of the entatic state model for KSI.

We emphasize that other enzymes, lacking the requirement to catalyze chemical transformations at multiple positions using the same catalytic residues and with greater catalytic challenges requiring more than KSI’s 10¹¹-fold rate enhancement may utilize more precise positioning, a possibility that will need to be tested in future ensemble–function studies with other enzymes. For example, it has been proposed that OMP decarboxylase experiences significant ground state-destabilization (83), which would be predicted to distort and possibly narrow the conformational ensemble when substrate is bound, unlike what is observed for KSI. Enzymes with substantial conformational changes along their reaction coordinates are also expected to have different conformational heterogeneity, possibly a broader range of states or a series of more or less discrete states in individual steps along a reaction coordinate (84, 85). Finally, changes in conformational heterogeneity have been suggested to be linked to enzyme temperature adaptation (51, 52). These and additional examples underscore the need for ensemble–function studies on a range of enzymes over a range of conditions.

Materials and Methods

KSI Expression and Purification.

KSI from Pseudomonas putida (pKSI, referred to herein as KSI) and Comamonas testosteroni (tKSI, referred to herein as KSI_homolog) were expressed and purified as previously described (71, 86) (see also SI Appendix).

KSI Kinetics.

KSI Michaelis–Menten parameters were obtained by monitoring the 5 (10)-estrene-3,17-dione [(5 (10)-EST), Steraloids] reaction at 248 nm (ε = 14,800 M⁻¹ cm⁻¹) and at 25 °C in 4 mM sodium phosphate, pH 7.2 buffer with 2% DMSO, as previously described (71) (see also SI Appendix).

KSI ¹H Solution NMR.

The ¹H NMR spectrum of KSI D40N (1.0 mM) bound to equilenin (2.0 mM) in 40 mM potassium phosphate (pH 7.2), 1 mM sodium·EDTA, 2 mM DTT, and 10% DMSO-d₆ (vol/vol) (Cambridge Isotope Laboratories) was acquired at the Stanford Magnetic Resonance Laboratory, as previously described (44) (see also SI Appendix).

Protein X-Ray Crystallography.

All enzymes were crystallized as previously described (62) (see also SI Appendix); single-crystal diffraction data were collected at the Stanford Synchrotron Radiation Lightsource, beamline BL9-2 at 100, 250, or 280 K. Diffraction data processing and model building were carried out using standard methods. Multiconformer models were obtained from the 250 K diffraction datasets and crystallographic order parameters were calculated as previously described (33, 40) (see also SI Appendix). PDB codes for structural models obtained in this work for KSI: Apo 250 K (6UCW) and 280 K (6U1Z), GS-bound 100 K (6UBQ), 250 K (6UCY), and 280 K (6TZD), TSA-bound 250 K (6UCN), and 280 K (6U4I).

Ensemble Building.

To obtain KSI and KSI_homolog pseudoensembles, all respective cryo crystal structures were downloaded from the PDB (38) and parsed into individual KSI monomers (SI Appendix, Table S1). KSI molecules were aligned using PyMOL and standard commands. The KSI RT ensemble was obtained from the Apo, GS-bound, and TSA-bound RT multiconformer models using the same alignment procedure and the Apo state as alignment template (SI Appendix). MDevs were calculated as described in SI Appendix.

Data Availability.

The atomic coordinates have been deposited in the Protein Data Bank, www.wwpdb.org (PDB ID codes 6UCW, 6U1Z, 6UBQ, 6UCY, 6TZD, 6UCN, 6U4I).