Mirror-image antiparallel β-sheets organize water molecules into superstructures of opposite chirality

Significance

The structure and function of biomacromolecules depend on water structures in the hydration shell. We perform experiments and computations to examine the water molecules around an antiparallel β-sheet. Our experiments show that the sign of chiral optical responses of water reverses when the β-sheet is an (l-) or a (d-) enantiomer. Molecular modeling reveals a chiral topology of water assembled around the β-sheet. These results suggest that mirror-image proteins organize water molecules into supermolecular structures of opposite chirality. Hence, a complete description of biomacromolecular chirality must include the surrounding water molecules. This finding invites a new line of inquiry about the role of water in chiral selectivity of biomolecular interactions and the molecular origins of homochirality in the biological world.

Abstract

Biomolecular hydration is fundamental to biological functions. Using phase-resolved chiral sum-frequency generation spectroscopy (SFG), we probe molecular architectures and interactions of water molecules around a self-assembling antiparallel β-sheet protein. We find that the phase of the chiroptical response from the O-H stretching vibrational modes of water flips with the absolute chirality of the (l-) or (d-) antiparallel β-sheet. Therefore, we can conclude that the (d-) antiparallel β-sheet organizes water solvent into a chiral supermolecular structure with opposite handedness relative to that of the (l-) antiparallel β-sheet. We use molecular dynamics to characterize the chiral water superstructure at atomic resolution. The results show that the macroscopic chirality of antiparallel β-sheets breaks the symmetry of assemblies of surrounding water molecules. We also calculate the chiral SFG response of water surrounding (l-) and (d-) LK₇β to confirm the presence of chiral water structures. Our results offer a different perspective as well as introduce experimental and computational methodologies for elucidating hydration of biomacromolecules. The findings imply potentially important but largely unexplored roles of water solvent in chiral selectivity of biomolecular interactions and the molecular origins of homochirality in the biological world.

Biological functions at the molecular level require changes in the structures and dynamics of biomacromolecules. These changes are strongly influenced by water hydration shells (1). Probing the structures and dynamics of water molecules in hydration shells is fundamental for understanding molecular mechanisms of biological functions. Our group recently demonstrated that a water superstructure assembles around an antiparallel β-sheet protein and gives a chiroptical response using vibrational sum frequency generation (SFG) spectroscopy (2). This result was informed by Petersen and coworkers’ observation of chiral vibrational SFG signals from water molecules in the minor groove of double helix DNA (3, 4). Since water molecules are achiral, these two studies suggest that water molecules are arranged in chiral supermolecular structures. Those results align with Simpson’s theory that achiral molecular entities incorporated into a chiral architecture can generate chiral second-order optical responses (5, 6). These chiral SFG studies have led to a model in which biomacromolecules act as a template to organize the surrounding water solvent into chiral superstructures. Nonetheless, many questions remain. For example, what are the architectures of water molecules in the superstructures? What are the molecular interactions that drive water self-assembly?

Here, we probe the chiral water superstructure around an antiparallel β-sheet secondary structure using heterodyne phase-resolved chiral SFG vibrational spectroscopy. We study the amphiphilic LK₇β peptide (2, 7–12) composed of (l-) or (d-) amino acids. These (l-) or (d-) LK₇β peptides self-assemble into mirror-image antiparallel β-sheets (11–14). Designed by DeGrado and Lear in 1985 (7), the LK₇β peptide with the sequence LKLKLKL is strongly amphiphilic, with the hydrophobic leucine sidechains orienting toward the hydrophobic phase and the polar lysine sidechains orienting toward the hydrophilic phase (11). This sidechain orientation forces the peptide backbone to adopt Ramachandran angles standard for antiparallel β-sheets (11). Hence, it is energetically favorable for the peptide to self-assemble into antiparallel β-sheet structures. Indeed, the LK₇β peptide and its variants in native (l-) form have been commonly used as a model system in surface studies. (2, 8–12, 15–17)

We obtain the phase-resolved chiral SFG vibrational spectra of (l-) and (d-) LK₇β in the spectral regions of the O-H/N-H stretching at ∼3,200 cm⁻¹ using H₂O as solvent and the O-D/N-D stretching at ∼2,400 cm⁻¹ using D₂O. We also perform the experiments using H₂¹⁸O and D₂¹⁸O. The ¹⁸O-isotopic substitution allows for the unambiguous assignment of two red-shifted vibrational bands to the water O-H (or O-D) stretching modes and two unaffected vibrational bands to the peptide backbone N-H (or N-D) stretching modes. Remarkably, when the chirality of the antiparallel β-sheets changes from (l-) to (d-), not only does the phase of the two N-H (N-D) stretching modes reverse but also the phase of the two O-H (O-D) stretching modes.

We also use molecular dynamics (MD) to provide a qualitative description of the average structure of the chiral water envelope around the (l-) antiparallel β-sheet. The results show that water molecules are strongly oriented in the presence of positively charged polar sidechains, both near the protein backbone at the vacuum–water interface and at least 10 Å into bulk water. We identify aspects of the water superstructure that possess a chiral topology. Additional hydrogen-bond analyses elucidate the relationship between the macroscopic chirality of antiparallel β-sheets and the organization of a water superstructure. Finally, we calculate a chiral SFG response of water molecules in the presence of the protein.

The observation of a direct correlation between chiroptical responses of achiral water solvent and the absolute chirality of a biomacromolecule has an important implication: mirror-image biomacromolecules can organize water solvent into chiral supermolecular structures with opposite handedness. Since water O-H stretching modes are highly sensitive to hydrogen-bonding environments, this work offers a different perspective as well as introduce experimental and computational methods for investigating water structures and hydrogen-bonding interactions in hydration shells of biomacromolecules. Our findings imply that chiral biomacromolecules can be enveloped by chiral water superstructures. This observation promises greater understanding of the chiral selectivity of biomolecular interactions and potentially suggests a key role for water in the origins of homochirality in the biological world.

Results

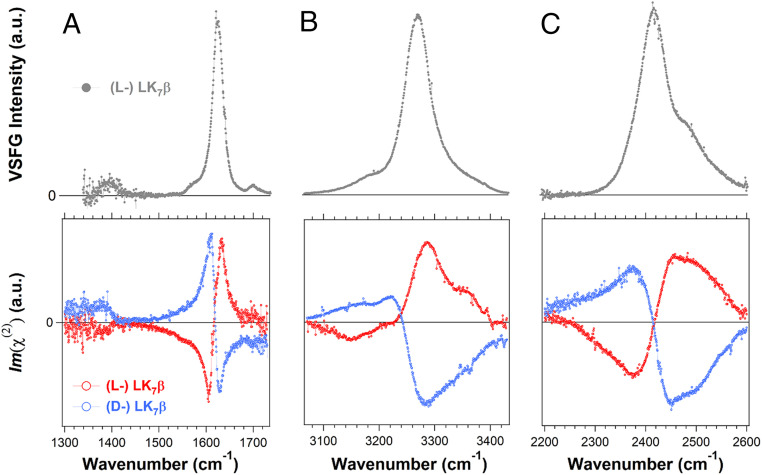
We prepared hydrated thin films of the amphiphilic LK₇β peptide on the surface of a right-handed α-quartz crystal. Using the psp polarization setting (see Materials and Methods), we first obtained homodyne chiral SFG spectra of the (l-) LK₇β (Fig. 1, Top) as control experiments. We then used the quartz signal as an internal phase reference to obtain the phase-resolved chiral SFG spectra of the antiparallel β-sheets formed by the (l-) and (d-) LK₇β peptides (Fig. 1, Bottom). Compared to conventional homodyne SFG, the heterodyne phase-resolved SFG method reveals the absolute phases of each vibrational band relative to the phase of the quartz crystal, providing information about orientation and chirality of the molecular systems (18–20) (SI Appendix, Theoretical Background of Phase-resolved Chiral Sum Frequency Generation).

Fig. 1.

Homodyne (Top) and phase-resolved chiral (Bottom) SFG spectra of chiral water superstructures around LK₇β antiparallel β-sheets (VSFG: vibrational sum frequency generation; a.u.: arbitrary units). (A) The amide I/amide II spectral region of (l-) LK₇β (gray and red) and (d-) LK₇β (blue) prepared in H₂O. (B) The O-H/N-H spectral region of LK₇β prepared in H₂O. (C) The O-D/N-D spectral region of LK₇β prepared in D₂O. All spectra were collected with the chiral psp polarization.

Fig. 1A shows the chiral SFG spectra in the amide I/amide II spectral region. The amide I vibrational modes are mainly the C = O stretching of the amide group coupled to the bending of the N-H bond, while the amide II vibrational modes are the C-N stretching vibrations in combination with N-H bending (21, 22). They are sensitive to protein secondary structures (21–23). The homodyne amide I band (Fig. 1 A, Top) of (l-) LK₇β is centered at 1,620 cm⁻¹, indicating the formation of antiparallel β-sheet structures. Previously, we showed that the homodyne chiral SFG signal vanishes when the pH of the sample is lowered to ∼2, which denatures the antiparallel β-sheets, or when the LK₇β peptide is composed of (l-) leucine and (d-) lysine, which disrupts β-sheet formation (11). These experiments demonstrated that the chiral SFG response originates from the folded β-sheet secondary structure. Moreover, the phase-resolved amide I and amide II chiral SFG responses (Fig. 1 A, Bottom) for the (l-) LK₇β (red) and (d-) LK₇β (blue) are mirror images, demonstrating the capacity of phase-resolved chiral SFG spectroscopy to reveal the handedness of the enantiomeric (l-) versus (d-) antiparallel β-sheets.

Fig. 1 B and C (Top, gray) show the homodyne chiral SFG spectra of the (l-) LK₇β samples on a glass surface in the spectral region of O-H/N-H and O-D/N-D stretching for the β-sheet prepared in H₂O and D₂O. Without phase resolution, the spectra are very similar to the previously reported homodyne spectra of the β-sheets on a glass surface or at the air–water interface, suggesting that the structures of LK₇β are likely conserved regardless of whether the peptide is at the air–water interface or on the solid substrates (2, 10). In the previous report, the major and minor bands in the (l-) LK₇β-H₂O spectrum were assigned to the peptide N-H stretching and water O-H stretching, respectively, while both the major and minor vibrational bands in the (l-) LK₇β-D₂O spectrum were assigned to chiral water O-D stretching modes (2). Although these previous assignments were supported by H₂¹⁸O and D₂¹⁸O isotopic shifts, they give rise to the question, why is the N-D stretching band of the peptide backbone in the (l-) LK₇β-D₂O spectrum missing (2)? We address this question using our heterodyne phase-resolved spectra.

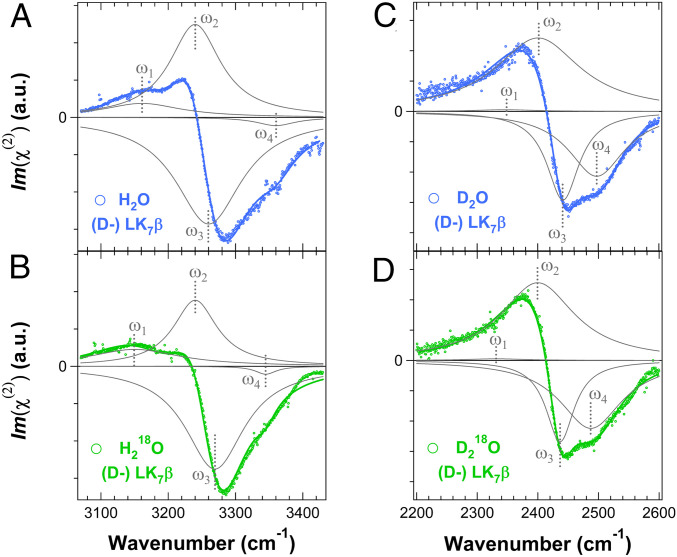
The phase-resolved chiral SFG spectra of (l-) LK₇β in the O-H/N-H and O-D/N-D stretching vibrational regions are shown on the bottom row of Fig. 1 B and C (red). These phase-resolved spectra reveal spectral features that are hidden in the homodyne spectra of (l-) LK₇β (Fig. 1 B and C, Top, gray). The same figures also show the phase-resolved spectra for the enantiomeric (d-) LK₇β antiparallel β-sheet (blue), displaying a mirror-image spectral response. Residual analyses of these spectra indicate that at least four vibrational bands are needed to fit the spectra (SI Appendix, Figs. S2 and S3). Since both the peptide N-H (N-D) and water O-H (O-D) stretches can contribute to these vibrational bands, we performed ¹⁸O substitution using H₂¹⁸O and D₂¹⁸O to distinguish their contributions. The ¹⁸O substitution is expected not to alter the N-H or N-D stretching frequency but to redshift the O-H or O-D stretching frequency by roughly 12 cm⁻¹ (24). If a vibrational band undergoes such a redshift upon ¹⁸O substitution, it is assigned to water O-H (or O-D) stretching modes; otherwise, it is assigned to peptide N-H (or N-D) stretching modes. We present the results of ¹⁸O substitution for (l-) LK₇β in Fig. 2 and (d-) LK₇β in Fig. 3.

Fig. 2.

The phase-resolved chiral SFG spectra of chiral water superstructures around (l-) LK₇β. (Left) O-H/N-H spectral region of (l-) LK₇β prepared in (A) H₂O and (B) H₂¹⁸O. (Right) O-D/N-D spectral region of (l-) LK₇β prepared in (C) D₂O and (D) D₂¹⁸O. The spectra are fit to Eq. 2 (Materials and Methods). The component peaks based on the fitting parameters are shown in gray, and the sum of these peaks are shown as red or black solid lines. The labels of vibrational modes correspond to the numbering in Table 1. All spectra were collected with the chiral psp polarization.

Fig. 3.

The phase-resolved chiral SFG spectra of chiral water superstructures around (d-) LK₇β. (Left) O-H/N-H spectral region of (d-) LK₇β prepared in (A) H₂O and (B) H₂¹⁸O. (Right) The O-D/N-D spectral region of (d-) LK₇β prepared in (C) D₂O and (D) D₂¹⁸O. The component peaks based on the fitting parameters are shown in gray, and the sum of these peaks are shown as blue or green solid lines. The labels of vibrational modes correspond to the numbering in Table 2. All spectra were collected with the chiral psp polarization.

Fig. 2 shows phase-resolved chiral SFG spectra of the (l-) LK₇β β-sheet hydrated in H₂O, H₂¹⁸O, D₂O, and D₂¹⁸O. For the β-sheet prepared using H₂O (Fig. 2A), the spectrum is resolved into four vibrational bands. The ones at the lowest (ω₁) and highest (ω₄) frequencies are assigned to the water O-H stretching modes because the corresponding vibrational bands in the H₂¹⁸O spectrum (Fig. 2B) are redshifted by 11 to 13 cm⁻¹ (Table 1). The frequencies of the two vibrational bands in the middle (ω₂ and ω₃) are not significantly affected by ¹⁸O substitution and thus are assigned to the peptide N-H stretching modes. The spectra of the β-sheet prepared using D₂O (Fig. 2C) and D₂¹⁸O (Fig. 2D) are also resolved into four vibrational bands. Similarly, the vibrational bands at the lowest (ω₁) and highest (ω₄) frequencies are redshifted (>10 cm⁻¹) upon ¹⁸O substitution (Table 1) and are assigned to the water O-D stretching modes, while the two vibrational bands in the middle (ω₂ and ω₃) are assigned to the peptide N-D stretching modes. The peptide N-D stretching modes buried in the homodyne chiral SFG spectra of (l-) β-sheet (Fig. 1 C, Top) are revealed in the phase-resolved chiral SFG spectrum.

Table 1.

Fitting parameters and assignments for the spectra in Fig. 2

Parameter	(2A) (l-) LK7β-H2O	(2B) (l-) LK7β-H218O	Assignments
ω1 (cm−1)	3,157 ± 1	3,146 ± 3	O-H (H2O)
A1 (a.u.)	−10.1 ± 0.5	−5.1 ± 1.3
Γ1 (cm−1)	50.7 ± 1.8	50.9 ± 9.6
ω2 (cm−1)	3,247 ± 2	3,247 ± 6	N-H (l-LK7β)
A2 (a.u.)	−27.1 ± 1.7	−22.7 ± 13.5
Γ2 (cm−1)	38.6 ± 0.9	44.5 ± 5.5
ω3 (cm−1)	3,270 ± 1	3,274 ± 3	N-H (l-LK7β)
A3 (a.u.)	54.0 ± 1.6	47.6 ± 12.9
Γ3 (cm−1)	49.7 ± 0.7	49.0 ± 1.2
ω4 (cm−1)	3,359 ± 1	3,346 ± 2	O-H (H2O)
A4 (a.u.)	0.8 ± 0.2	0.6 ± 0.2
Γ4 (cm−1)	9.5 ± 2.4	14.7 ± 4.4
	(2C) (l-) LK7β-D2O	(2D) (l-) LK7β-D218O
ω1 (cm−1)	2,342 ± 2	2,331 ± 4	O-D (D2O)
A1 (a.u.)	−9.0 ± 3.4	−8.0 ± 2.2
Γ1 (cm−1)	39.5 ± 3.4	45.7 ± 4.7
ω2 (cm−1)	2,391 ± 1	2,396 ± 1	N-D (l-LK7β)
A2 (a.u.)	−18.2 ± 3.1	−26.0 ± 4.5
Γ2 (cm−1)	36.8 ± 3.6	44.1 ± 4.5
ω3 (cm−1)	2,445 ± 10	2,440 ± 1	N-D (l-LK7β)
A3 (a.u.)	13.4 ± 5.6	12.7 ± 1.9
Γ3 (cm−1)	31.8 ± 3.5	23.4 ± 1.6
ω4 (cm−1)	2,499 ± 6	2,488 ± 3	O-D (D2O)
A4 (a.u.)	24.2 ± 5.7	27.5 ± 1.7
Γ4 (cm−1)	55.5 ± 1.7	66.8 ± 2.0

a.u., arbitrary units.

We repeated the ¹⁸O-substitution experiments with the enantiomeric (d-) LK₇β. Fig. 3 presents the phase-resolved chiral SFG spectra of the (d-) β-sheet hydrated in H₂O, H₂¹⁸O, D₂O, and D₂¹⁸O. Each spectrum is fit to four vibrational bands, yielding fitting parameters (Table 2) that are comparable to those obtained for the (l-) LK₇β (Table 1) but with opposite phase. The vibrational bands at the lowest (ω₁) and highest (ω₄) frequencies are redshifted (>10 cm⁻¹) upon ¹⁸O substitution with H₂¹⁸O (D₂¹⁸O) (Table 2) and thus are assigned to the water O-H (O-D) stretching modes, while the other two vibrational bands (ω₂ and ω₃) are assigned to the peptide N-H (N-D) stretching modes.

Table 2.

Fitting parameters and assignments for the spectra in Fig. 3

Parameter	(3A) (d-) LK7β-H2O	(3B) (d-) LK7β-H218O	Assignments
ω1 (cm−1)	3,161 ± 4	3,150 ± 5	O-H (H2O)
A1 (a.u.)	16.0 ± 3.6	15.0 ± 2.0
Γ1 (cm−1)	71.3 ± 2.3	82.7 ± 6.2
ω2	3,240 ± 6	3,240 ± 1	N-H (d-LK7β)
A2	69.1 ± 3.5	28.0 ± 2.4
Γ2	46.2 ± 1.1	39.6 ± 1.7
ω3	3,260 ± 6	3,269 ± 1	N-H (d-LK7β)
A3	−102.9 ± 2.9	−59.1 ± 1.4
Γ3	60.0 ± 1.7	53.7 ± 1.3
ω4	3,360 ± 4	3,345 ± 1	O-H (H2O)
A4	−4.6 ± 1.2	−1.6 ± 0.4
Γ4	35.0 ± 4.6	19.0 ± 3.2
	(3C) (d-) LK7β-D2O	(3D) (d-) LK7β-D218O
ω1 (cm−1)	2,346 ± 0*	2,331 ± 0*	O-D (D2O)
A1 (a.u.)	1.0 ± 0*	1.0 ± 0*
Γ1 (cm−1)	62.0 ± 0*	62.0 ± 0*
ω2	2,401 ± 4	2,400 ± 2	N-D (d-LK7β)
A2	61.9 ± 3.8	57.2 ± 2.2
Γ2	85.3 ± 1.2	74.4 ± 0.9
ω3	2,442 ± 1	2,437 ± 4	N-D (d-LK7β)
A3	−28.5 ± 2.3	−22.7 ± 2.3
Γ3	32.5 ± 1.2	28.2 ± 1.2
ω4	2,497 ± 4	2,487 ± 1	O-D (D2O)
A4	−36.4 ± 4.4	−42.2 ± 1.8
Γ4	56.7 ± 1.4	62.8 ± 1.5

a.u., arbitrary units.

^*Parameter fixed during fitting.

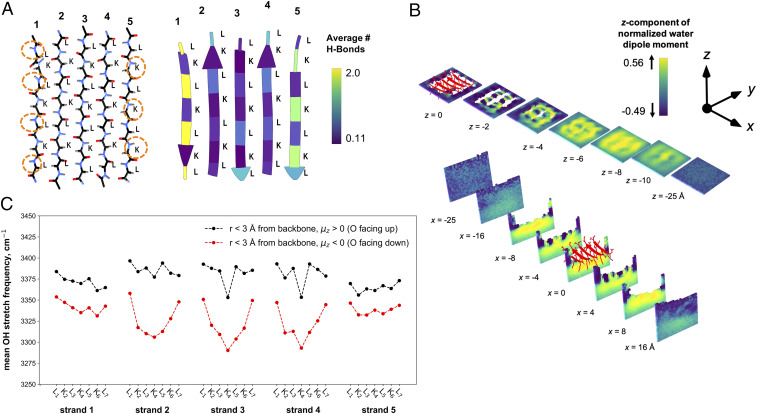
To gain further insights about the hydration structure around LK₇β, we performed MD simulations and hydrogen-bond analyses (see Materials and Methods and SI Appendix). LK₇β was modeled as a protein composed of five β-strands at the vacuum–water interface, as previously reported (11). The MD simulations confirmed that the amphiphilic LK₇β adopts a stable pleated, antiparallel β-sheet structure (SI Appendix, Figs. S4 and S5). Fig. 4A shows the backbone structure of the (l-) LK₇β homopentamer at the atomic level as well as the average number of hydrogen-bonding interactions between the protein backbone and surrounding water molecules. A major difference between the two exterior strands 1 and 5 is that strand 1 has four N-H groups exposed to water, whereas strand 5 has only three N-H groups exposed to water. This difference in hydrogen-bonding capacity is one aspect that defines the macroscopic chirality of antiparallel β-sheets, that is, a lack of a reflection plane along the peptide strands (Fig. 4 A, Right).

Fig. 4.

Hydrogen-bond and water structure analyses of the (l-) LK₇β homopentamer at the vacuum–water interface obtained from 1 μs of MD sampling using the AMBER ff14SB force field for the protein and the TIP4P-Ew water potential. (A, Left) LK₇β backbone atoms show the asymmetry of the N-H and C = O groups on opposite sides of the β-sheet. (A, Right) The average number of hydrogen-bonding interactions between the protein and water molecules depicted by residue. (B) The average z-components of water dipole moment vectors extending below the protein surface (Top) and from side to side (Bottom) with a grid resolution of 1 Å. (C) The infrared response of O-H stretch of water within 3 Å of the peptide backbone for every residue. The IR response was calculated for water molecules where the average z-component of the dipole was oriented either up (black) or down (red) relative to the vacuum–water interface.

Another source of chirality is revealed by analyses of the average z-component (normal to the vacuum–water interface) of the water dipole vectors around the (l-) LK₇β homopentamer (Fig. 4B). In the absence of LK₇β, bulk water in the simulation box adopts an isotropic orientation, except at the interface where water molecules preferentially orient oxygen either toward or away from the water phase. We observe that this behavior persists up to ∼5 Å below the interface (SI Appendix, Fig. S6) (25–27). In contrast, the presence of LK₇β strongly perturbs the water structure and orientation. This effect is clearly illustrated by the nonisotropic orientation of water at least ∼10 Å below the vacuum–water interface (Fig. 4 B, Top) and extending at least ∼15 Å on either side from the center of mass of the (l-) LK₇β homopentamer (Fig. 4 B, Bottom, and SI Appendix, Fig. S7). In the vicinity of lysine residues and close to the vacuum–water interface, water tends to orient with its oxygen away from the interface toward the positively charged lysine sidechain (dark purple at z = −2 Å in Fig. 4 B, Top). In contrast, in the interstices near the protein backbone between lysine residues, water tends to orient its oxygen toward the interface. The resulting truncated checkerboard-like pattern of alternating up/down hydration water dipole orientations ∼2 to 6 Å below the protein surface (Fig. 4 B, Top) is a chiral superstructure. This pattern was stable over the course of the trajectory and was reproduced with multiple independent trajectories. The pattern appeared with both the SPC/E and TIP4P-Ew water models (SI Appendix, Fig. S8) (28, 29).

We also calculated the infrared vibrational response of the O-H stretch of water in our MD simulations (SI Appendix). We selectively probed the infrared (IR) response of water molecules within 3 Å of the LK₇β backbone. We then identified water molecules for which the average z-component (μ_z) of the molecular dipole moment was oriented up or down relative to the vacuum–water interface. Fig. 4C (and SI Appendix, Fig. S9) shows that the calculated mean IR frequency of the O-H stretch is around 3,400 cm⁻¹ (black) for upward-oriented waters and around 3,300 cm⁻¹ (red) for downward-oriented waters. Therefore, the orientation of water molecules near the (l-) LK₇β homopentamer peptide backbone significantly influences the water O-H stretching frequency.

Finally, we calculated the phase-resolved (heterodyne) chiral SFG response of the water molecules surrounding the (l-) LK₇β homopentamer and its enantiomer, (d-) LK₇β (SI Appendix). The enantiomers produced identical SFG responses but with opposite phase, consistent with the (d-) protein templating an oppositely chiral water structure compared to the (l-) protein (Fig. 5A). The (l-) LK₇β spectrum contains a prominent peak around 3,357 cm⁻¹, which possibly corresponds to the positive peak at 3,359 cm⁻¹ (ω₄) in the experimental heterodyne spectrum (Fig. 2A). The computational result did not show the additional negative-phase 3,157 cm⁻¹ peak (ω₁) observed experimentally. Given how redshifted this peak is from the gas-phase O-H stretching frequency (∼3,700 cm⁻¹), it may arise from a rare population of water molecules forming very strong hydrogen bonds. These bonds may not be captured by the rigid TIP4P-Ew water model used in these calculations. This peak may also simply require more sampling to be resolved. Our simulations also predict an additional negative peak at a higher frequency that was beyond the spectral range probed experimentally. In addition, we calculated the chiral SFG response from consecutive water layers of widths of 5 Å starting at the air–water interface (Fig. 5B). The results confirm that water forms chiral assemblies at least as deep as the lysine sidechains can extend into the solution (∼10 Å) and possibly deeper (Fig. 4B). The spectra start to become noisier below 10 Å, but the opposite phases of the (l-) and (d-) LK₇β spectra exhibited at all depths sampled suggest that some chiral water structures exist at least 15 Å below the interface.

Fig. 5.

The simulated chiral phase-resolved SFG response from the O-H stretch of water surrounding LK₇β. (A) The psp response of water surrounding (l-) LK₇β (black) and its enantiomer, (d-) LK₇β (red), showing the effect of chirality on the response phase. (B) The psp response of consecutive layers of water starting at the air–vacuum interface, again showing the effect of protein chirality on the water SFG response. The chiral signal persists at least as far into the water as the lysine residues, and possibly beyond. The SFG response was calculated from 10,000,000 configurations obtained from 100 ns of MD sampling. The green spheres correspond to chloride ions.

Discussion

A comparison of the phase-resolved chiral spectra of the (l-) and (d-) β-sheets (Figs. 2 and 3) reveals a remarkable observation. Although all of the vibrational bands observed under the same solvent conditions (H₂O, D₂O, H₂¹⁸O, and D₂¹⁸O) are comparable for the (l-) and (d-) β-sheets in terms of peak positions (ω), peak widths (Γ), and absolute amplitudes (A) (Tables 1 and 2), the phases of both the peptide N-H (N-D) stretching modes and the water O-H (O-D) stretching modes are reversed with the (l-) and (d-) handedness of the LK₇β antiparallel β-sheets. It is expected that the phase flips for the N-H (N-D) stretching vibrational bands because the vibrational modes originate from the chiral peptide backbone (12, 30). However, the accompanying phase reversal of the two water-stretching bands has an important implication. Enantiomers of a biomacromolecule can stamp their intrinsic handedness onto nearby water solvent molecules and organize water into superstructures with opposite chirality. This observation provides a new perspective on the molecular architectures of water in the hydration shells of biomacromolecules.

Since 2011 when vibrational chiral SFG signatures of N-H stretching modes of peptide backbones were first reported for characterizing protein secondary structures (31), the interpretation of the chiral SFG spectra of LK₇β has continued to evolve. On the one hand, Fu et al. (10) reported the homodyne chiral SFG spectra of LK₇β at the air/H₂O and air/D₂O interfaces. Each of these spectra exhibits a major band and a minor band. Based on ab initio calculations, the major band was assigned to the peptide backbone and the minor band was assigned to combinational bands of various peptide vibrational modes. On the other hand, Perets et al. (2) obtained the homodyne chiral SFG spectra of LK₇β hydrated in H₂O and D₂O on glass slides. Based on the ¹⁸O-substitution analyses, the major and minor bands in the LK₇β-H₂O spectrum were assigned to the peptide N-H stretching and the water O-H stretching modes, respectively, and both the major and minor bands in the LK₇β-D₂O spectrum were assigned to the water O-D stretching modes (2). Paradoxically, the peptide N-D stretching signal seemingly disappears in the LK₇β-D₂O spectrum. In this study, the paradox is resolved by heterodyne phase-resolved SFG spectroscopy. The capacity to reveal phases of vibrational bands allows deconvolution of the two apparent vibrational bands in the homodyne spectra into four vibrational bands. Two bands are assigned to peptide N-H stretching modes and two are assigned to water O-H stretching modes (Figs. 2 and 3). Since both N-H and O-H stretching modes are highly sensitive to hydrogen-bonding environments, heterodyne phase-resolved chiral SFG spectroscopy in conjunction with computational studies is a promising approach for revealing molecular details in the chiral assembly of water molecules around the antiparallel β-sheet.

The two O-H (or O-D) stretches at ω₁ and ω₄ in each spectrum of Figs. 2 and 3 can inform hydrogen-bonding interactions of water molecules in the chiral superstructures. As shown in Table 1, the two water O-H stretching bands are at 3,157 ± 1 cm⁻¹ and 3,359 ± 1 cm⁻¹ (Δν = 202 ± 1 cm⁻¹), while the two ¹⁸O-H stretching bands are at 3,146 ± 3 cm⁻¹ and 3,346 ± 2 cm⁻¹ (Δν = 200 ± 3 cm⁻¹). Correspondingly, the two water O-D stretching bands are at 2,342 ± 2 cm⁻¹ and 2,499 ± 6 cm⁻¹ (Δν = 157 ± 6 cm⁻¹), while the two ¹⁸O-D stretching bands are at 2,331 ± 4 cm⁻¹ and 2,488 ± 3 cm⁻¹ (Δν = 157 ± 4 cm⁻¹). When an O-H oscillator forms a hydrogen bond with a proton acceptor, the O-H bond is weakened, and thus the O-H stretching frequency is lowered. Therefore, the stronger the hydrogen-bonding interaction, the lower the O-H stretching frequency. Consequently, we assign the low-frequency (ω₁) band to strongly hydrogen-bonded O-H and the high-frequency (ω₄) band to weakly hydrogen-bonded O-H.

The 200 cm⁻¹ vibrational energy difference of the two water O-H stretching bands (ω₁ and ω₄) suggests their hydrogen-bond strength is substantially different (32). To understand the origins of this vibrational energy difference, we calculated the IR vibrational response of the O-H stretch of water molecules in our MD simulations. Our calculations show that for water molecules less than 3 Å from the protein backbone, the orientation significantly influences the mean O-H stretching frequency (Fig. 4C). If the oxygen atom orients upward at the vacuum–water interface, the O-H stretching frequency is calculated to be ∼100 cm⁻¹ greater than if the oxygen orients downward. As discussed earlier, the stronger the hydrogen-bonding interaction, the lower the O-H stretching frequency. Hence, water molecules pointing toward the interface may form hydrogen bonds that are weaker than those formed by water molecules pointing into the bulk. This model aligns with our experimental observation of the two water O-H stretching bands (ω₁ and ω₄) at vibrational frequencies different by 200 cm⁻¹.

The analysis of the water dipole vectors shows not only a truncated checkerboard-like pattern with alternating up/down water orientations (Fig. 4B) but also variations of water orientation patterns at the four edges of the LK₇β homopentamer (SI Appendix, Fig. S10). These results indicate a lack of a reflection plane perpendicular to the β-sheet, suggesting that the water assemblies around (l-) LK₇β are chiral. This suggestion is confirmed by our chiral SFG calculations (Fig. 5). This behavior may be compared with the chiral “spine of hydration” around DNA (33), which computational studies suggest requires steric interactions to order water molecules in the DNA minor groove (34, 35). However, in the case of LK₇β, the driving force to assemble water molecules into a chiral superstructure around the antiparallel β-sheet appears to be hydrogen-bonding interactions. Our computational results suggest that these hydrogen-bonding interactions may significantly perturb the topology of water molecules at least several solvation shells beyond the protein.

We also identified two peptide N-H stretching bands with an opposite phase at 3,247 and 3,270 cm⁻¹ (Fig. 2A), consistent with a prior report (12), and two peptide N-D stretching bands with an opposite phase at 2,391 and 2,445 cm⁻¹ (Fig. 2C). To explain the opposite phases of the two N-H stretching bands, Hu et al. (12) proposed that adjacent backbone nitrogen atoms along the β-strand are chiral centers with opposite handedness (i.e., pro-S and pro-R). This proposal would require a substantial sp³-hybridized character of the nitrogen atoms. Researchers in the broader fields of structural biology and computational biology have long considered peptide bonds to be in planar configuration (36–38). In a survey of ultra-high-resolution (1 Å or better) protein structures, larger deviations from planarity (>20°) were observed in only 0.5% of residues (39). However, small deviations (±6.3°) of the amide bond from planarity are more common (38, 39). Determining whether such small, dynamic deviations from planarity can confine the nitrogen atoms into pro-S and pro-R chiral centers requires further investigation.

The two N-H (or N-D) stretching bands at different frequencies (Δν = ∼23 cm⁻¹) likely arise due to backbone amines that experience distinct chemical environments in the antiparallel β-sheet. For instance, the hydrophobic leucine and hydrophilic lysine side chains are oriented toward opposite sides of the β-sheet, and the pleated antiparallel β-sheet backbone (SI Appendix, Fig. S4A) constrains the orientation of the backbone amine groups. Indeed, the orientations of backbone amines relative to the plane of the β-sheet alternate up/down across adjacent residues (SI Appendix, Fig. S4 B and C). The leucine or lysine backbone amines could give chiral SFG responses at different frequencies because of orientational differences that lead to changes in hydrogen bonding or proximity to the hydrophobic or hydrophilic sidechains. Alternatively, hydrogen bonding of amine groups is likely different in the interior and exterior of β-sheet domains (40). The interior N-H groups form hydrogen bonds with the C = O groups of the peptide backbone in the neighboring β-strands, while the exterior N-H groups at the edge of the β-sheet form hydrogen bonds with water solvent. The interior N-H groups presumably form stronger hydrogen bonds (C = O···H-N) at lower stretching frequencies, and the exterior N-H groups form weaker hydrogen bonds (H₂O···H-N) at higher stretching frequencies (41–43).

Finally, as the chirality of water superstructures is dictated by the chirality of the protein, there is room for speculation about the role chiral water architectures might have played in the origins of homochirality in the biological world (44). With few exceptions (45–47), native proteins are made of (l-) amino acids, and DNA and RNA are composed of (d-) nucleotides. The origins of enantiomeric enrichment evolving from a prebiotic state remains a matter of fascination and controversy. One proposal is that physical or chemical processes (e.g., autocatalytic Soai reactions) that establish an energy difference between chiral enantiomers on the order of 10⁻⁷ kJ/mol could introduce a bias toward homochirality (48–53). Another proposal notes that the incorporation of achiral solvent molecules (such as chloroform and fumaric acid) in a racemic crystal of amino acids lowers the crystal’s solubility; when the crystal is grown from a solution of small enantiomeric excess, this leads to significant chiral enrichment in the solution phase (54, 55). One might plausibly extend this concept from achiral organic solvents to water itself. Here, we show that the description of chirality of biomacromolecules is incomplete without accounting for the water solvent. The presence of a chiral hydration shell around chiral biomolecules is potentially one of the missing links in the search for the molecular origins of biological homochirality.

Conclusions

Chiral vibrational SFG spectroscopy revealed that achiral water solvent can form a chiral hydration shell around a chiral biomacromolecular solute (2–4). In this work, phase-sensitive chiral SFG reveals that the phase of such chiroptical response is inverted with the absolute handedness of the chiral biomacromolecule. The MD and hydrogen-bonding analyses show that the intrinsic macroscopic chirality of a protein can impact the surrounding water structure. Analysis of the MD trajectories reveals a chiral water topology around the antiparallel β-sheet in terms of the water orientations and hydrogen-bonding interactions. These experimental and computational results suggest that chiral macromolecules can imprint their intrinsic chirality onto surrounding water solvent molecules and organize them into chiral supermolecular structures. A chiral hydration shell wrapping around a biomacromolecule is expected to change not only the structural and dynamical properties of the biomacromolecule but also chiral selectivity toward biomolecular interactions.

The two water O-H stretching bands and two peptide N-H stretching bands contain information about vibrational structures and hydrogen-bonding interactions of the chiral water assembly around the LK₇β antiparallel β-sheet. These vibrational resonances can be used as molecular probes for future ultrafast dynamic studies of vibrational energy exchange between water solvent and protein. The phase, peak position, and line shape of the four vibrational bands under various solvent conditions (H₂O, D₂O, H₂¹⁸O, and D₂¹⁸O) will serve as quantitative benchmarks in building computational models for elucidating detailed structures and interactions in the water chiral superstructures around the β-sheet. Heterodyne phase-sensitive chiral SFG in conjunction with computational studies constitutes a powerful approach for studying the molecular details of structures and dynamics of biomacromolecular hydration. This study has established a molecular picture: Mirror-image biomacromolecules are enveloped in hydration shells with opposite chirality. From here, researchers can start to question what roles water might have played in the origins of homochirality in the biological world.

Materials and Methods

Quartz Calibration.

Right-handed z-cut α-quartz crystal was cleaned with high-performance liquid chromatography-grade methanol and then ddH₂O, dried with nitrogen, and plasma-cleaned (Harrick Plasma; PDC-32G) on “low” for 15 min. Adsorbed 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine (Avanti Polar Lipids; catalog number 850457C) was employed to define the quartz crystal coordinate system as described in the literature (20).

Sample Preparation.

The (l-) LK₇β peptide (GL Biochem Ltd., Shanghai) and the (d-) LK₇β (AnaSpec, Inc.) were obtained as lyophilized powders. The sample preparation was previously described (2, 11). Briefly, LK₇β (Ac-Leu-Lys-Leu-Lys-Leu-Lys-Leu-NH₂) was synthesized with all (l-) or all (d-) amino acids. The lyophilized powder was prepared at a concentration of 1 mM in H₂O, H₂¹⁸O, D₂O, or D₂¹⁸O. The solution was aliquoted, flash frozen in liquid nitrogen, and transferred to −80 °C for storage. Once thawed for SFG experiments, unused material was discarded to avoid additional freeze–thaw cycles.

For each experiment, 10 to 20 μL of LK₇β aqueous solution was dried directly on the cleaned quartz surface. The solution was dried under nitrogen flow in a sealed container where desiccant was present to prevent exchange with ambient humidity, resulting in a hydrated thin-film of peptide. The adsorbed film was immediately measured.

Phase-Resolved Chiral SFG Measurements.

The femtosecond broadband SFG spectrophotometer has been previously described (56). The quartz crystal with LK₇β hydrated thin-film was probed at φ = 90° (+y axis) and 270° (−y axis), where φ is the azimuthal angle of the quartz axis relative to the +x axis in the laboratory frame (SI Appendix, Fig. S1). All chiral SFG spectra were obtained using the psp polarization (p-polarized sum frequency, s-polarized visible, p-polarized IR) (18, 20). For each sample, 10 to 12 spectra (2 min each) were acquired along the +y and −y axes. The spectra were cleaned for cosmic rays. The averages of the measurements along the +y and −y axes were normalized by ${\chi }_{quartz,\phi =90°}^{\left(2\right)}$ and then subtracted according to (18–20) the following:

$$Im\left[{\chi }^{\left(2\right)}\right]=\frac{\left(I_{\phi =90°}-I_{\phi =270°}\right)}{4}\text{.}$$ [1]

The IR frequencies were calibrated according to a polystyrene standard (Buck Scientific; 0.05-mm film). Finally, the vibrational spectra were fit with Lorentzians according to the following:

$$Im\left[{\chi }^{\left(2\right)}\right]\propto Im\left[{\displaystyle \sum }_q\frac{A_q}{{\omega }_{IR}-{\omega }_q-i{\text{Γ}}_q}\right]\text{,}$$ [2]

where ${\omega }_{IR}$ is the frequency of the incident IR, A_q is the amplitude, ${\omega }_q$ is the frequency of the vibrational resonance, and ${\text{Γ}}_q$ is the damping coefficient of the q^th vibrational mode.

MD.

A starting structure of five antiparallel LK₇β strands was placed into a 125 × 125 × 125 Å box, half of which was filled with TIP4P-Ew (29) water and Cl⁻ ions to neutralize the system to create a vacuum–water interface. The protein, which was described with the AMBER ff14SB force field (57), was placed at the interface with the lysine sidechains pointing into the water and the leucine sidechains facing the vacuum. The N termini were acetylated and the C termini were amidated to be consistent with the experimental system. The structure was minimized and then equilibrated for 6 ns at 298 K and constant volume to preserve the vacuum. Langevin dynamics was propagated at 298 K with a friction coefficient of 1 ps⁻¹. The long-range electrostatics were treated with the particle-mesh Ewald method (58). Multiple trajectories for a total of 1 µs sampling were propagated, and the configurations were saved every 10 ps. For the chiral SFG calculation, a single trajectory was propagated for 100 ns, saving configurations every 10 fs. The simulations were performed with OpenMM 7.4 and CUDA 9.2 (59). See the SI Appendix for more details on the MD trajectory analysis as well as the IR and chiral SFG calculations.

Data Availability.

The computational data collected and analyzed in this paper are available on the Open Science Framework (DOI: 10.17605/OSF.IO/8G7QJ) (60) and supplementary information about computational methods and experimental data analyses are included in the SI Appendix.