Numerical study of heat generating γ Al₂O₃– H₂O nanofluid inside a square cavity with multiple obstacles of different shapes

Abstract

A numerical research on uniformly heat generating γ Al₂O₃–H₂O nanofluid filled square cavity with multiple obstacles of different shapes is carried out. The cavity is assumed to be heated at bottom and cooled by vertical walls with linearly varying temperature. An adiabatic condition is assumed at the top of the cavity. Circular, square and triangular shaped obstacles are considered. The mathematical model has been solved using Galerkin finite element method. Results are presented for streamlines, isotherms, local and mean Nusselt numbers. Multiple rotating cells are observed in the streamlines. It is found that the local and mean Nusselt numbers increase with nanoparticle volume fraction and higher heat transfer is achieved in the cavity with triangular obstacles.

Nanofluids; Square cavity; Multiple obstacles; Internal heat generation.

1. Introduction

The improvement in the thermal characteristics of convectional fluids is greatly important in the industrial processes involving heating and cooling of fluids. The recent advances in the manufacturing of nano-sized particles (metallic, non-metallic and carbon nanotubes) were lead to an innovative idea of suspending these particles in the conventional liquids like water, oil, etc. This new idea was first introduced by Choi [1]. The research on nanofluids is being increased due to its thermal performance utilizations in absorption refrigeration, circuits cooling, micro-electromechanical systems, clean energy storage units, solar collectors, and automotive industry [2]. The nanofluids which based on γ Al₂O₃ nanoparticles have attractive cooling performance in many engineering process. Moghaieb et al. [3] conducted an experimental research on the cooling application of γ Al₂O₃–H₂O nanofluid in an engine and suggested γ Al₂O₃–H₂O nanofluid to cool the components of cast iron. Radwan et al. [4] performed an experiment with γ Al₂O₃–H₂O nanofluid to analyse the cooling performance in an engine cylinder head. The impacts of carbonated MgO, γAl₂O₃ and TiO₂ nanofluids on wettability modification and oil production were examined by Nowrouz et al. [5]. Some of the important investigations on γAl₂O₃ nanofluid can be accessible from the literature [6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]. Due to attractive cooling applications of γ Al₂O₃ nanofluids, the present research is devoted to study the heat transfer characteristics of γ Al₂O₃–H₂O in a square enclosure.

The heat transfer due to convection in an enclosure is a famous problem because of its implementations in solar collector, room ventilation, heat exchangers, chemical catalytic reactors, cooling of electronic devices and grain storage etc. An extensive literature on the natural convection in an enclosure can be found in Ostrach [20]. A benchmark solution for the air filled cavity with natural convection was obtained by Davis [21]. Calcagni et al. [22] performed both practical and numerical experiments on the convective thermal transfer in an enclosure of shape square which is heated from bottom and examined the heat transfer rate inside the cavity. The Cu– H₂O nanofluid filled cavity with heated left wall and cooled right wall was investigated by Khanafer et al. [23]. Their investigation illustrated that the suspended Cu- nanoparticles enhances the heat transfer rate and modify the pattern of fluid flow. The internal heat generating nanofluid filled cavity with several boundary conditions were investigated in the following publications [24, 25, 26, 27, 28, 29, 30, 31, 32].

The convective heat transfer in an enclosure can be affected by installing obstacles inside the cavity in various positions. Kim et al. [33] performed a numerical simulation of air flow in a cold square enclosure with hot circular obstacle at various locations using finite volume method. They explored that the position of inner obstacle has significant impacts on flow and heat transfer. Selimefendigil and Oztop [34] considered diamond, square and circular shaped obstacles inside a Cu–H₂O filled cavity with hydromagnetic and internal heat generation effects. They showed that the average heat transfer rate is decreased in the cavity with square obstacle. The non-Newtonian nanofluid filled cavity installed with heated solid block was investigated by Sheremet et al. [35]. Mousa [36] examined the buoyancy convection in a cavity with square adiabatic obstacle installed at centre and concluded that the heat transfer rate can be affected by increasing the size of the obstacle. Mohebbi and Rashidi [37] considered Al₂O₃–H₂O filled ‘L’ shaped cavity with heated obstacle at the left wall and observed the higher heat transfer rate inside the cavity, when the hot obstacle installed at the lower part of the left wall. The thermal characteristics of CuO– H₂O nanofluid in a rhombus shaped enclosure with a square obstacle at the centre was studied by Haq et al. [38]. Sheikholeslami [39] investigated the 3D flow of Al₂O₃–H₂O nanofluid in a lid driven cavity with spherical shaped hot obstacle. Hamid et al. [40] studied H₂O- CNT nanofluid flow in a rectangular cavity with a cylindrical shaped obstacle. They demonstrated that the volume fraction of CNT enhances the local heat transfer rate inside the rectangular cavity. The hydromagnetic nanofluid flow inside a wavy porous cavity with heated squared obstacle was examined by Alkanhal et al. [41]. Usman et al. [42] studied the radiative heat and mass transfer in a square cavity with two heated square obstacles and two cold square obstacles. They reported that the higher heat transfer rate is achieved inside the cavity with top heated inner squares. Boroujeni and Kianpour [43] examined the heat transfer of CuO– H₂O nanofluid in a rectangular cavity with a hot obstacle. The 3D flow of CNT -H₂O nanofluid in an enclosure with T- shaped adiabatic obstacle was studied by Selimefendigil and Oztop [44]. Recently, Azizul et al. [45] reported the heat lines of Al₂O₃–H₂O in a wavy cavity with inner solid blocks.

After a careful review of the above literature, the present investigation is focused on the convective thermal characteristics of γ Al₂O₃–H₂O nanofluid in an enclosure with multiple obstacles of various shapes (circular, square and triangle) which is still a significant problem to study. The current model may be applicable in various engineering situations that are solar collectors, heating and cooling of buildings, coating, solidification, double pane windows, microelectronic devices, float glass production, micro nuclear energy etc. The flow and thermal patterns, local and mean Nusselt numbers are observed using Galerkin Finite element method.

2. Theoretical formulation

We consider the fully developed, incompressible laminar flow of uniformly heat generating Newtonian γ Al₂O₃ – H₂O nanofluid in a bottom heated 2D cavity. The geometry of the problem and the boundary conditions are mentioned in Cartesian co-ordinates; see Figure 1. The cavity is installed with four obstacles of different shapes (triangular, circular and square). The cavity is assumed to be of the length ‘L’ and height ‘H’ (L = H = 1). The locations of the installed obstacles are as follow:

• (i)The centres of the circular obstacles are located at (0.25L, 0.25H), (0.25L, 0.75 H), (0.75L, 0.25H) and (0.75L, 0.75H) with radius (0.1L).
• (ii)The centres of the square obstacles are located at (0.25L, 0.25H), (0.25L, 0.75 H), (0.75L, 0.25H) and (0.75L, 0.75H). The length and height of the square obstacles are 0.2L and 0.2H respectively.
• (iii)The top vertices of the triangles are located at (0.25L, 0.35H), (0.75L, 0.35H), (0.75L, 0.85H) and (0.25L, 0.85H). The lengths of base and height of the triangles are 0.2L and 0.2H respectively.

Figure 1.

Schematic diagram of the physical models with u = v = 0,T= T_h- (T_h-T_c) (y/H) (on vertical Walls) and u = v = 0, (∂ T/∂ n) = 0 (on obstacles).

The temperature of the left and right-side walls is varying linearly. The adiabatic condition is assumed on the obstacles and the top wall. Base fluid molecules and γ Al₂O₃ nanoparticles are in thermal equilibrium state. The reference temperature T₀ is calculated as $2T_0=T_h+T_c$. The thermo physical properties of water, alumina and gamma alumina nanofluid are tabulated in Tables 1 and 2.

Table 1.

Thermo physical properties of water and alumina [16, 17].

	ρ (kg/m3)	Cp (J/kg K)	k (W/m K)	β x 10−5 (K−1)
Pure water (H2O)	998.3	4182	0.60	20.06
Alumina (Al2O3)	3970	765	40	0.85

Table 2.

Thermo physical properties of γ Al₂O₃-Water/Ethylene Glycol nanofluids [6, 7, 8, 9, 16, 17, 18, 19].

Properties	γ Al2O3– H2O
Effective dynamic density	${\rho }_{nf}=\left(1-\phi \right){\rho }_f+\phi {\rho }_s$
Heat capacitance	${\left(\rho C_p\right)}_{nf}=\left(1-\phi \right){\left(\rho C_p\right)}_f+\phi {\left(\rho C_p\right)}_s$
Dynamic viscosity	$\frac{{\mu }_{nf}}{{\mu }_f}=123{\phi }^2+7.3\phi +1$
Effective thermal conductivity	$\frac{k_{nf}}{k_f}=4.97{\phi }^2+2.72\phi +1$
Thermal expansion coefficient	${\left(\rho \beta \right)}_{nf}=\left(1-\varphi \right){\left(\rho \beta \right)}_f+\varphi {\left(\rho \beta \right)}_s,$

The governing Navier-Stokes equations in 2D under the Boussinesq approximation can be described as follow:

$$\left(\frac{\partial u}{\partial x}\right)+\left(\frac{\partial v}{\partial y}\right)=0,$$ (1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{{\rho }_{nf}}\frac{\partial p}{\partial x}+{\mu }_{nf}{\left({\rho }_{nf}\right)}^{-1}\left(\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial x^2}\right),$$ (2)

$$u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{{\rho }_{\mathit{nf}}}\frac{\partial p}{\partial y}+{\mu }_{\mathit{nf}}{\left({\rho }_{\mathit{nf}}\right)}^{-1}\left(\frac{{\partial }^{\mathit{2}}v}{\partial y^{\mathit{2}}}+\frac{{\partial }^{\mathit{2}}v}{\partial x^{\mathit{2}}}\right)+g\left(T-T_c\right){\beta }_{\mathit{nf}},$$ (3)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=k_{nf}{\left({\left(\rho C_p\right)}_{nf}\right)}^{-1}\left(\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\partial }^{2}T}{\partial x^2}\right)+\frac{1}{Q^{-1}{\left(\rho C_p\right)}_{nf}}.$$ (4)

Using following essential dimensionless parameters

{$XH=x,YH=y,U{\alpha }_f=uH,V{\alpha }_f=vH,{\rho }_f{\alpha }_f^{2}P=p{H}^2$

$${\left(T_h-T_c\right)}_{}\theta =T-T_c,Gr=\frac{{\beta }_f\left(T_h-T_c\right)H^3}{g^{-1}{v}_f^2},{\mathrm{Pr}}_f=\frac{v_f}{{\alpha }_f},R{a}_E={\mathrm{Pr}}_{f}Gr,$$ (5)

and $R{a}_I=\frac{{\beta }_{f}Q{H}^5}{g^{-1}{\alpha }_f{v}_f{k}_f}$}

in the Eqs. (1), (2), (3), and (4) we obtain,

$$\frac{\partial V}{\partial Y}=\left(-\frac{\partial U}{\partial X}\right),$$ (6)

$$U\frac{\partial U}{\partial X}+\frac{1}{\left(\raisebox{1ex}{${\rho }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.\right)}\frac{\partial P}{\partial X}+V\frac{\partial U}{\partial Y}=+\frac{{\gamma }_{nf}}{{\alpha }_f}\left(\frac{{\partial }^{2}U}{\partial Y^2}+\frac{{\partial }^{2}U}{\partial X^2}\right),$$ (7)

$$U\frac{\partial V}{\partial X}+\frac{1}{\left(\raisebox{1ex}{${\rho }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.\right)}\frac{\partial P}{\partial Y}+V\frac{\partial V}{\partial Y}=\frac{{\gamma }_{nf}}{{\alpha }_f}\left(\frac{{\partial }^{2}V}{\partial Y^2}+\frac{{\partial }^{2}V}{\partial X^2}\right)+{\mathrm{Pr}}_f\theta \left(\frac{{\beta }_{nf}}{{\beta }_f}\right)R{a}_E,$$ (8)

$$U\frac{\partial \theta }{\partial X}-\left(\frac{{\left(\rho C_p\right)}_f}{{\left(\rho C_p\right)}_{nf}}\right)\frac{R{a}_I}{R{a}_E{\mathrm{Pr}}_f}+V\frac{\partial \theta }{\partial Y}=\frac{\left(\raisebox{1ex}{$k_{nf}$}\!\left/ \!\raisebox{-1ex}{$k_f$}\right.\right)}{\left(\raisebox{1ex}{${\left(\rho C_p\right)}_{nf}$}\!\left/ \!\raisebox{-1ex}{${\left(\rho C_p\right)}_f$}\right.\right)}\left(\frac{{\partial }^2\theta }{\partial Y^2}+\frac{{\partial }^2\theta }{\partial X^2}\right).$$ (9)

The boundary conditions on the cavity walls and obstacles in non-dimensional forms are

$$\left\{\begin{array}{ccc}V=U=0,& \theta -1=0,& \text{at}\text{bottom wall,}\\ V=U=0,& \theta +Y=1,& \text{on}\text{the}\text{vertical}\text{walls,}\\ V=U=0,& \frac{\partial \theta }{\partial Y}=0,& \text{on}\text{the}\text{top wall and }\frac{\partial \theta }{\partial n}=0\text{ on the obstacles.}\end{array}\right\}$$ (10)

The local and mean Nusselt numbers along the hot bottom wall are derived as follow:

$$N{u}_{loc}{\left(\frac{k_{nf}}{k_f}\right)}^{-1}=-{\left(\frac{\partial \theta }{\partial n}\right)}_{n=0}\text{and}N{u}_{m}H=\underset{0}{\overset{H}{\int }}N{u}_{loc}dx.$$ (11)

Where n is the coordinate direction normal to the surface.

3. Solution procedure and validation

The numerical experiment is carried out using Galerkin finite element method [46, 47, 48, 49, 50, 51]. The penalty finite element method is utilized to remove the pressure in the momentum equations.

Using $P=-\gamma \left(\frac{\partial V}{\partial Y}+\frac{\partial U}{\partial X}\right)$ in Eqs. (6) and (7), we obtain

$$U\frac{\partial U}{\partial X}-\frac{1}{\left(\raisebox{1ex}{${\rho }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.\right)}\frac{\partial }{\partial X}\left(\gamma \left(\frac{\partial V}{\partial Y}+\frac{\partial U}{\partial X}\right)\right)=+\frac{\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)}{\left(\raisebox{1ex}{${\rho }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.\right)}{\mathrm{Pr}}_f\left(\frac{{\partial }^{2}U}{\partial Y^2}+\frac{{\partial }^{2}U}{\partial X^2}\right)-V\frac{\partial U}{\partial Y},$$ (12)

$$U\frac{\partial V}{\partial X}-\frac{1}{\left(\raisebox{1ex}{${\rho }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.\right)}\frac{\partial }{\partial Y}\left(\gamma \left(\frac{\partial V}{\partial Y}+\frac{\partial U}{\partial X}\right)\right)+V\frac{\partial V}{\partial Y}=+\frac{\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)}{\left(\raisebox{1ex}{${\rho }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.\right)}{\mathrm{Pr}}_f\left(\frac{{\partial }^{2}V}{\partial Y^2}+\frac{{\partial }^{2}V}{\partial X^2}\right)+{\mathrm{Pr}}_f\theta \left(\frac{{\beta }_{nf}}{{\beta }_f}\right)R{a}_E.$$ (13)

The residual equations of (12), (13) and (9) are obtained as follow by using weak formulation and integration by parts. By applying the following approximations [49, 50, 51],

$$V\approx \sum _{k=1}^N{V}_k{\Phi }_k\left(X,Y\right),U\approx \sum _{k=1}^N{U}_k{\Phi }_k\left(X,Y\right),\theta \approx \sum _{k=1}^N{\theta }_k{\Phi }_k\left(X,Y\right)$$ (14)

we obtain

$$\begin{array}{l}{R}_i^{\left(U\right)}=\sum _{k=1}^N{U}_k\underset{\Omega }{\int }\left[\left(\sum _{k=1}^N{U}_k{\Phi }_k\right)\frac{\partial {\Phi }_k}{\partial X}+\left(\sum _{k=1}^N{V}_k{\Phi }_k\right)\frac{\partial {\Phi }_k}{\partial Y}\right]{\Phi }_{i}dXdY+\frac{\gamma }{\left(\raisebox{1ex}{${\rho }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.\right)}\ast \\ \left[\sum _{k=1}^N{U}_k\underset{\Omega }{\int }\frac{\partial {\Phi }_i}{\partial X}\frac{\partial {\Phi }_k}{\partial X}dXdY+\sum _{k=1}^N{V}_k\underset{\Omega }{\int }\frac{\partial {\Phi }_i}{\partial X}\frac{\partial {\Phi }_k}{\partial Y}dXdY\right]\\ +\frac{\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)}{\left(\raisebox{1ex}{${\rho }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.\right)}{\mathrm{Pr}}_f\left[\sum _{k=1}^N{U}_k\underset{\Omega }{\int }\left[\frac{\partial {\Phi }_i}{\partial X}\frac{\partial {\Phi }_k}{\partial X}+\frac{\partial {\Phi }_i}{\partial Y}\frac{\partial {\Phi }_k}{\partial Y}\right]dXdY\right],\end{array}$$ (15)

$$\begin{array}{l}{R}_i^{\left(V\right)}=\sum _{k=1}^N{V}_k\underset{\Omega }{\int }\left[\left(\sum _{k=1}^N{U}_k{\Phi }_k\right)\frac{\partial {\Phi }_k}{\partial X}+\left(\sum _{k=1}^N{V}_k{\Phi }_k\right)\frac{\partial {\Phi }_k}{\partial Y}\right]{\Phi }_{i}dXdY+\frac{\gamma }{\left(\raisebox{1ex}{${\rho }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.\right)}\ast \\ \left[\sum _{k=1}^N{U}_k\underset{\Omega }{\int }\frac{\partial {\Phi }_i}{\partial Y}\frac{\partial {\Phi }_k}{\partial X}dXdY+\sum _{k=1}^N{V}_k\underset{\Omega }{\int }\frac{\partial {\Phi }_i}{\partial Y}\frac{\partial {\Phi }_k}{\partial Y}dXdY\right]\\ +\frac{\left(\raisebox{1ex}{${\mu }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\mu }_f$}\right.\right)}{\left(\raisebox{1ex}{${\rho }_{nf}$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.\right)}{\mathrm{Pr}}_f\left[\sum _{k=1}^N{V}_k\underset{\Omega }{\int }\left[\frac{\partial {\Phi }_i}{\partial X}\frac{\partial {\Phi }_k}{\partial X}+\frac{\partial {\Phi }_i}{\partial Y}\frac{\partial {\Phi }_k}{\partial Y}\right]dXdY\right]\\ -\left(\frac{{\beta }_{nf}}{{\beta }_f}\right)R{a}_E{\mathrm{Pr}}_f\underset{\Omega }{\int }\left(\sum _{k=1}^N{\theta }_k{\Phi }_k\right){\Phi }_{i}dXdY,\end{array}$$ (16)

$$\begin{array}{l}{R}_i^{\left(\theta \right)}=\sum _{k=1}^N{\theta }_k\underset{\Omega }{\int }\left[\left(\sum _{k=1}^N{U}_k{\Phi }_k\right)\frac{\partial {\Phi }_k}{\partial X}+\left(\sum _{k=1}^N{V}_k{\Phi }_k\right)\frac{\partial {\Phi }_k}{\partial Y}\right]{\Phi }_{i}dXdY+\frac{\left(\raisebox{1ex}{$k_{nf}$}\!\left/ \!\raisebox{-1ex}{$k_f$}\right.\right)}{\left(\raisebox{1ex}{${\left(\rho C_p\right)}_{nf}$}\!\left/ \!\raisebox{-1ex}{${\left(\rho C_p\right)}_f$}\right.\right)}\ast \\ \left[\sum _{k=1}^N{\theta }_k\underset{\Omega }{\int }\left[\frac{\partial {\Phi }_i}{\partial X}\frac{\partial {\Phi }_k}{\partial X}+\frac{\partial {\Phi }_i}{\partial Y}\frac{\partial {\Phi }_k}{\partial Y}\right]dXdY\right]-\left(\frac{{\left(\rho C_p\right)}_f}{{\left(\rho C_p\right)}_{nf}}\right)\frac{R{a}_I}{R{a}_E{\mathrm{Pr}}_f}\underset{\Omega }{\int }{\Phi }_{i}dXdY.\end{array}$$ (17)

Relations between the velocities and the stream function for the discussed flows are given as:

$$\frac{\partial \psi }{\partial Y}=U,-\frac{\partial \psi }{\partial X}=V$$ (18)

Which takes the following form

$$\frac{{\partial }^2\psi }{\partial X^2}+\frac{{\partial }^2\psi }{\partial Y^2}=-\frac{\partial V}{\partial X}+\frac{\partial U}{\partial Y}$$ (19)

To investigate the stream function ψ, expand it into the basis set ${\left\{{\Phi }_k\right\}}_{k=1}^N$ as the following form:

$$\begin{array}{l}{R}_i^{\left(\psi \right)}=\sum _{k=1}^N{U}_k\underset{\Omega }{\int }{\Phi }_i\frac{\partial {\Phi }_k}{\partial Y}dXdY-\sum _{k=1}^N{V}_k\underset{\Omega }{\int }{\Phi }_i\frac{\partial {\Phi }_k}{\partial Y}dXdY\\ +\sum _{k=1}^N{\psi }_k\underset{\Omega }{\int }\left[\frac{\partial {\Phi }_i}{\partial X}\frac{\partial {\Phi }_k}{\partial X}+\frac{\partial {\Phi }_i}{\partial Y}\frac{\partial {\Phi }_k}{\partial Y}\right]dXdY.\end{array}$$ (20)

Lagrange finite triangular elements are applied to discretize the computational domain. The residual equations are cracked by Newton-Raphson method until the convergence condition (10⁻⁶) is reached for each flow variable. A mesh independence test is conducted and tabulated in Tables 3(a), (b) and (c) to obtain accurate results in a lower computational time. The G3, G7 and G11 grids were selected for the cavity with circular, square and triangular obstacles respectively. The validation of the present solver has been done by comparing the Nu_m for various Rayleigh numbers with Davis [21] and Khanafer et al. [23] (see Table 4).

Table 3(b).

Test on Grid sensitivity of the cavity with square obstacles φ = 0.04, Ra_E=10⁵, Ra_I=10²and Pr_f= 6.2.

Grid	No of Elements	No of Nodes	Num
G5	19203	37296	0.73156
G6	21771	42198	0.74578
G7	21916	42589	0.74784
G8	22304	43342	0.74715

Table 3(c).

Test on Grid sensitivity of the cavity with triangular obstacles φ = 0.04, Ra_E=10⁵, Ra_I=10²and Pr_f= 6.2.

Grid	No of Elements	No of Nodes	Num
G9	18698	36414	0.82129
G10	19216	37530	0.81641
G11	19431	37766	0.81898
G12	21405	41595	0.81862

Table 3(a).

Test on Grid sensitivity of the cavity with circular obstacles φ = 0.04, Ra_E=10⁵, Ra_I=10²and Pr_f= 6.2.

Grid	No of Elements	No of Nodes	Num
G1	5992	11508	0.80042
G2	6503	12485	0.81123
G3	6979	13261	0.81349
G4	8103	15232	0.81343

Table 4.

Comparison results of Nu_mwith Pr_f= 0.71.

RaE	Num
	Present	Khanafer et al. [23]	Davis [21]
103	1.1178	1.118	1.118
104	2.2450	2.245	2.243
105	4.5232	4.522	4.519

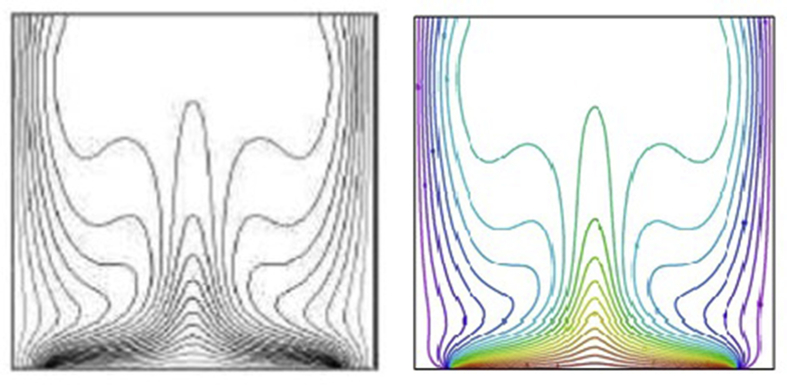
Figure 2 confirms the accuracy of the present findings with Calcagni et al. [22] for the bottom heated square cavity case. Furthermore, the streamlines and isotherms were plotted in Figure 3 for the air filled cavity installed with hot circular obstacle and compared with the results of Kim et al. [33] for various values of Rayleigh number. The comparisons are in a good agreement with the present numerical code.

Figure 2.

Isotherms comparison of Calcagani et al. [22] (left) and present (right) results with ϵ = 4/5 and Ra_E = 10⁵.

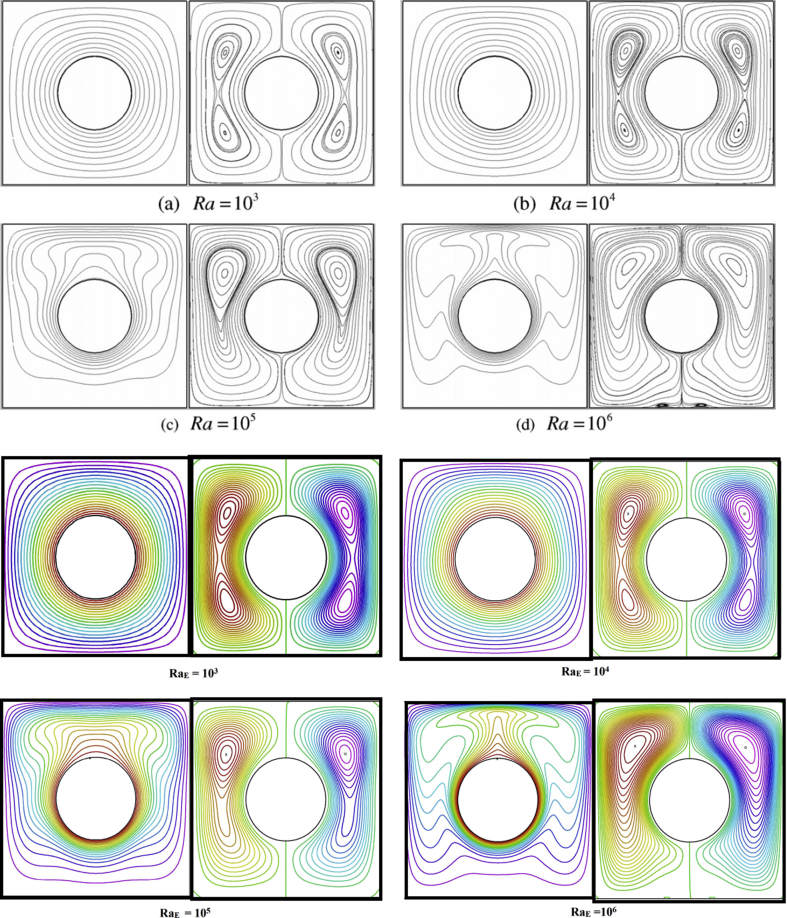
Figure 3.

Comparison of stream lines and isotherms for various values of Rayleigh number with Kim et al. [33].

4. Results and discussion

A numerical experiment has been accomplished for the heat transfer of γ Al₂O₃ – H₂O in a square cavity with various shaped (circular, square and triangular) multiple obstacles. The nanofluid is assumed to generating heat with volumetric rate Q.

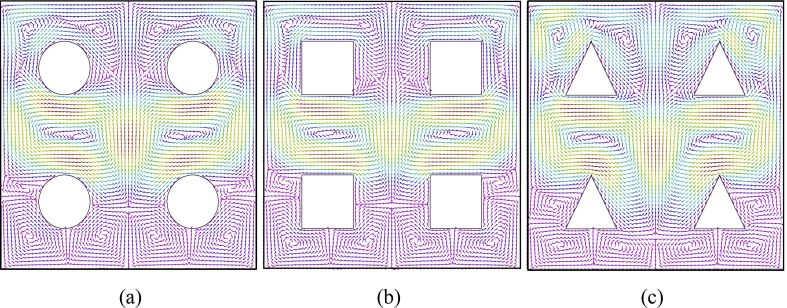
To understand the directions of multiple rotations inside the cavity, the velocity vectors of γ Al₂O₃– H₂O nanofluid are plotted in Figure 4. The impacts of Ra_E and Ra_I on the flow and isotherm patterns are depicted in Figures 5 and 6, respectively with multiple obstacles of different shapes. It is observed from Figures 5(a) and 6(a) that the streamlines are symmetrical about x-axis and the strength of the streamlines enhances with Ra_E and Ra_I. It is also observed that strength of streamlines is higher in the cavity with triangular obstacles and lower in the cavity with square obstacles. Higher value of Ra_I (Ra_I = 10⁵) shows a considerable impact on the strength of streamlines. Due to the impacts buoyancy force and the presence of obstacles, the fluid rises up from bottom and forms multiple cells inside the cavity. A couple of two counter rotating cells appeared in the bottom (Figures (4) and 5(a)). The top part of the cavity is filled with two cells in which one cell contains two anti-clockwise rotating cells and another one contains two clockwise rotating cells in the cavity with circular and triangular shaped obstacles (Figures (4), 5(a) and 6(a)). In the case of square obstacles, the upper corners of the cavity filled with a pair of counter rotating cells. There are two counter rotating large cells appeared in the mid part of the cavity. It can be seen that the pattern of the streamlines around the obstacles is strongly depend on the shape of obstacles. On comparing the obstacle shapes, in the mid part of the cavity, the fluid rises up and moving downward and occupied more part of the cavity in case of triangular obstacles compared to circular and square shaped obstacles.

Figure 4.

Velocity vectors inside the cavity with distinct multiple obstacles at Ra_E = 10⁵, Ra_I = 10², Pr_f = 6.2 and φ = 0.04. (a) Cavity with circular obstacles (b) Cavity with square obstacles (c) Cavity with triangular obstacles.

Figure 5.

Effect of Ra_E inside the cavity with distinct multiple obstacles: Ra_I = 10², Pr_f = 6.2 and φ = 0.04. (a) Streamlines (b) Isotherms.

Figure 6.

Effect of Ra_I inside the cavity with distinct multiple obstacles: Ra_E = 10⁵, Pr_f = 6.2 and φ = 0.04 (a) Streamlines (b) Isotherms.

As the values of Ra_E and Ra_I are increased from 10⁴ to 10⁵ (Figures (4), 5(a) and 6(a)), the cells at the mid part of the cavity elongated horizontally and moving downward for the various shaped obstacles except circular shaped obstacles. The conduction dominant inside the square cavity for lower values of Ra_E and Ra_I. For the higher values of Ra_E and Ra_I (=10⁵) (Figures 5(b) and 6(b)), the convection is evident with isothermal-shape changes. The obstacles block the uniform growth of isotherms and a plum like shaped is observed above the two horizontal obstacles. The top corners of the cavity are occupied by a cluster of uniform isotherms.

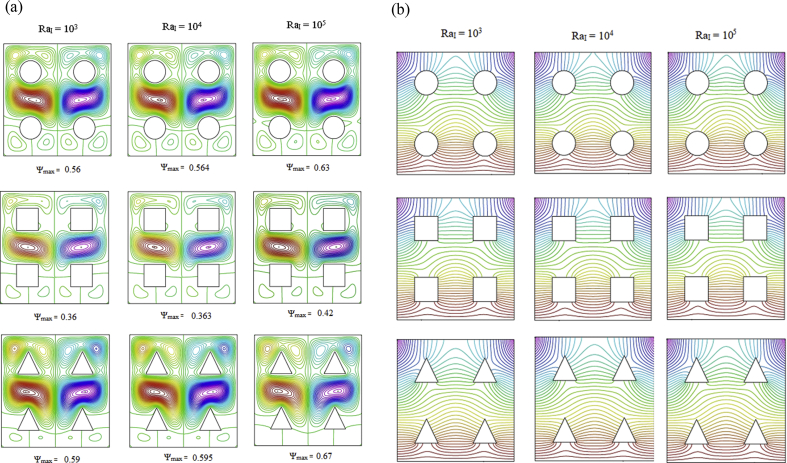
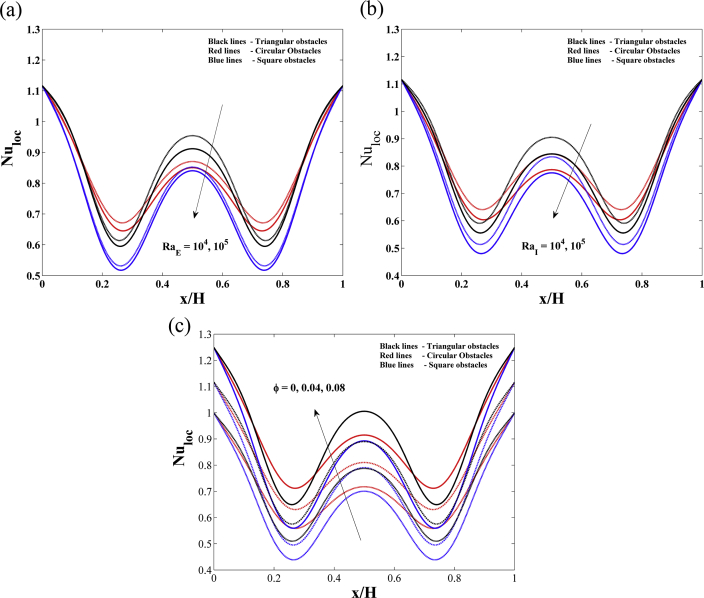
The variation of Nu_loc with Ra_E, Ra_I and φ is shown in Figure 7. It is observed that the Nu_loc is higher at the vertical walls and the mid part of the cavity. The wavy shaped curves are observed for local Nusselt number with positive values in the cavity. The local Nusselt number is lower in the ranges 0.2 < x/H<0.4 and 0.6 < x/H<0.8 due to the presence of different shaped obstacles.

Figure 7.

Variations of $N{u}_{loc}$ along the heated wall (a) Effects of $R{a}_E$ with Ra_I = 10², Pr_f = 6.2 and φ = 0.04. (b)Effects of Ra_I with Ra_E = 10⁴, Pr_f = 6.2 and φ = 0.04 (c)Effects of φ with Ra_E = 10⁴, Ra_I= 10⁴ and Pr_f = 6.2.

The Nu_loc decreases with the increasing values of Ra_E (Figure 7(a)) and Ra_I (Figure 7(b)). The Nu_loc is higher for the cavity with triangular obstacles and lower for the cavity with squared obstacles. An effective local heat transfer has been noticed with the higher volume fraction of γ Al₂O₃ nanoparticles in the cavity with triangular obstacles (Figure 7(c)). It may be concluded that the performance of nanofluid with fixed nanoparticle volume fraction changes according to the geometry of the obstacles. The geometry of the adiabatic obstacles greatly influences the heat transfer in the cavity.

The main aim of Figure 8 is to show the effects of φ on mean Nusselt number inside the cavity with multiple obstacles. In addition, the values of mean Nusselt number for various values of φ inside a cavity in the absence of obstacles are also plotted in Figure 8. It is clear that Nu_m increases with φ of γ Al₂O₃ nanoparticles. The mean Nusselt number is higher in the cavity without any obstacles and the presence of obstacles decrease the mean Nusselt number. A significant heat transfer decrement can be observed in the cavity with square obstacles. The impacts of Ra_E and Ra_I on Nu_m are exposed in Figures 9 and 10 respectively. Logarithmic values of Ra_E and Ra_I are taken as x-axis and the Nu_m is taken as y-axis (Figures 9 and 10). It is observed that Nu_m increases slightly for 10³ < Ra_E<10⁴ and decreases for Ra_E> 10⁴ (Figure 9). The rising of values of Ra_I reduces the magnitude of Nu_m (see Figure 10). An effective averaged heat transfer has been detected in the cavity with triangular obstacles.

Figure 8.

Calculated values of $N{u}_m$ along the heated wall at different φ (Ra_E = 10⁴, Ra_I = 10⁴ and Pr_f = 6.2) [Note: solid line with star marker represents the enclosure without any obstacle].

Figure 9.

Effect of Ra_E on $N{u}_m$: Ra_I = 10², φ = 0.04 and Pr_f = 6.2.

Figure 10.

Effect of Ra_I on $N{u}_m:$Ra_E = 10⁵, φ = 0.04 and Pr_f = 6.2.

Figure 11(a) – (c) are plotted to obtain the correlations of mean Nusselt number versus Ra_E, Ra_I and φ for the γ Al₂O₃– H₂O nanofluid inside the cavity with circular, square and triangular shaped obstacles respectively. The correlations for Nu_m are obtained as follow:

$$\begin{array}{cc}N{u}_m& =0.82106-4.5442\times 10^{-6}R{a}_E-7.5033\times 10^{-6}R{a}_I+0.032869\mathrm{\varphi }\\ & -3.8838\times 10^{-12}R{a}_E^{\mathit{2}}-5.859\times 10^{-13}R{a}_I^{\mathit{2}}+3.6573{\varphi }^2\\ & +3.8909\times 10^{-11}R{a}_{E}R{a}_I+0.00011949R{a}_E\varphi +8.2202\times 10^{-5}R{a}_I\varphi \end{array}\left(\mathrm{C}\mathrm{i}\mathrm{r}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{s}\right)$$

$$N{u}_m=0.74859-4.0509\times {10}^{-6}R{a}_E-7.0238\text{×}{10}^{-6}R{a}_I+0.029968\varphi -3.6904\text{×}{10}^{-12}R{a}_E^{\mathit{2}}+1.4927\text{×}{10}^{-14}R{a}_I^{\mathit{2}}+3.3533{\varphi }^{\mathit{2}}+3.6676\text{×}{10}^{-11}R{a}_{E}R{a}_I+0.00010868R{a}_E\varphi +7.4479\text{×}{10}^{-5}R{a}_I\varphi \left(\text{Square obstacles}\right)$$

$$N{u}_m=0.8282-4.5931\text{×}{10}^{-6}R{a}_E-7.6609\text{×}{10}^{-6}R{a}_I+0.033155\varphi -3.9651\text{×}{10}^{-12}R{a}_E^{\mathit{2}}+5.1381\text{×}{10}^{-14}R{a}_I^{\mathit{2}}+3.6836{\varphi }^{\mathit{2}}+3.9314\text{×}{10}^{-11}R{a}_{E}R{a}_I+0.00012064R{a}_E\varphi +8.3077\times {10}^{-5}R{a}_I\varphi \left(\text{Triangular obstacles}\right)$$

Figure 11.

Mean Nusselt number versus physical parameters and their correlations (a) Cavity with circular obstacles (b) Cavity with square obstacles (c) Cavity with triangular obstacles.

It may be concluded that the Nu_m is higher in the cavity with triangular obstacles and lower in the cavity with square obstacles.

5. Conclusion

A numerical experiment has been accomplished through FEM on the convection of heat generating γ Al₂O₃ – H₂O nanofluid filled in a square cavity with multiple obstacles of different shapes i.e. circular, square and triangular. The important findings of the present numerical research are as follow:

• •The presence of multiple obstacles leads to the formation of multiple rotating cells inside the cavity. The pattern of the streamlines strongly depends on the shape of the obstacles.
• •The strength of streamlines is higher in the cavity with square obstacles and lower in the cavity with square obstacles.
• •The γ Al₂O₃ – H₂O occupied more part of the cavity with triangular obstacles compared to squared and circular obstacles. The pattern of isotherms changes for higher external and internal Rayleigh numbers due to convection inside the cavity.
• •The local Nusselt number decreases with larger values of internal and external Rayleigh numbers and enhances with γ Al₂O₃ nanoparticle volume fraction.
• •The local Nusselt number is higher in the cavity with triangular obstacles and lower in the cavity with square obstacles.
• •Higher heat transfer rate is achieved in the cavity with triangular obstacles compared to the cavity with circular and square obstacles.

Declarations

Author contribution statement

N. Vishnu Ganesh, Shumaila Javed & Qasem M. Al-Mdallal: Conceived and designed the analysis; Analyzed and interpreted the data; Contributed analysis tools or data; Wrote the paper.

R. Kalaivanan & Ali J. Chamkha: Conceived and designed the analysis; Analyzed and interpreted the data; Wrote the paper.

Funding statement

This work was supported by the United Arab Emirates University, Al Ain, UAE with Grant No. 31S363-UPAR (4) 2018.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.