Significance
A fundamental question of neuroscience is how the brain wires itself. Here, we propose a modeling framework that explains how cellular connectivity emerges from neuronal identity, allowing us to offer experimentally falsifiable predictions on the genetic encoding of the connectome. The rapid advances in brain science require quantitative frameworks to integrate genetic and connectome information. The proposed model responds to this need, helping us unveil the genetically driven mechanisms that govern the formation of individual links in the brain.
Keywords: networks, connectome, neuroscience, C. elegans
Abstract
Despite rapid advances in connectome mapping and neuronal genetics, we lack theoretical and computational tools to unveil, in an experimentally testable fashion, the genetic mechanisms that govern neuronal wiring. Here we introduce a computational framework to link the adjacency matrix of a connectome to the expression patterns of its neurons, helping us uncover a set of genetic rules that govern the interactions between neurons in contact. The method incorporates the biological realities of the system, accounting for noise from data collection limitations, as well as spatial restrictions. The resulting methodology allows us to infer a network of 19 innexin interactions that govern the formation of gap junctions in Caenorhabditis elegans, five of which are already supported by experimental data. As advances in single-cell gene expression profiling increase the accuracy and the coverage of the data, the developed framework will allow researchers to systematically infer experimentally testable connection rules, offering mechanistic predictions for synapse and gap junction formation.
There is ample Please confirm or correct postal code added to each affiliation.experimental evidence that the connectome, capturing the neuron-level wiring of a brain, is at least partially genetically encoded. Indeed, while neurons are clustered into broad classes based on their morphology and function, these observed differences between cells are known to be rooted in the differential expression patterns of their genes and proteins (1–10). Consequently, perturbations that alter the genetic identity of individual neurons can induce significant changes in wiring (11, 12). Furthermore, developmental neuroscience has unveiled multiple genetic factors contributing to the formation of neuronal circuits. For example, the connectomes of Caenorhabditis elegans and higher organisms rely on a combination of body and wiring localization (13–18), and cell–cell recognition specificity, for both synaptic (19) and gap junction (GJ) connections (11, 20, 21). In the mouse retina, proteins, like connexin-36, play a known role in coupling rods and cones through GJs (22), and, in D. melanogaster, neurons expressing the same olfactory receptor converge onto the same set of projection neurons (23). While these studies offer strong experimental support for the genetic roots of neuronal wiring, we continue to lack a general framework to identify the genetic mechanisms that determine the presence or the absence of specific neuronal connections (12, 21, 24).
These advances have prompted the development of statistical approaches designed to identify genes involved in neuronal connectivity. At coarser spatial scales, where collections of spatially proximal neurons are profiled together, data availability has led to the development of correlative and predictive approaches that connect regional gene expression and connectivity in the mouse brain (25, 26). At the neuronal scale, Kaufman et al. (27) demonstrated a correlation between gene expression and neuronal connectivity, and Varadan et al. (28) identified a genetic rule for chemical synapses through an entropy minimization approach. Despite these important advances, existing frameworks fail to incorporate spatial constraints for synapse formation. Indeed, past work in mice, macaque, and C. elegans suggests that connection probability decays with spatial distance between soma (17, 29). Strictly speaking, synapses can only exist between neurons in physical contact along their surface. This limitation was recognized by Baruch et al. (30) in their inference of genetic rules, estimating neuronal contact information from neuronal connectivity itself. Here we can take advantage of recent high-resolution efforts to map a neuronal “contactome” in C. elegans, that also offer an accurate consideration of spatial and contact information (31). Notwithstanding these promising advances, progress toward unveiling the genetic rules of synapse formation is remarkably slow compared to the tremendous experimental progress focusing on mapping the connectome and the gene expression patterns of individual neurons (32–34).
The gap between experimental and computational progress raises a fundamental question: Is it computationally feasible to infer the genetic rules that govern synapse formation from the available experimental data? For instance, in C. elegans, we wish to describe the genetic rules that govern the wiring of neurons of a relatively sparse connectome of neurons (32) using as input the combinatorial expression patterns of genes (34). Even if we reduce the genetic complexity to the binary expression of individual genes, genes can encode a very large number () of neuronal identities. Hence, as we try to infer the list of genes whose expression pattern can encode the observed connectome, we are faced with a heavily underdetermined problem: In C. elegans, the combinatorial expression of genes is sufficient to fully describe the observed connectome. Although humans have billion neurons (35), and genes, the number of neurons is dwarfed by the combinatorial gene expression space of size , where the expression pattern of genes determines whether two neurons can synapse. Indeed, if only the binary expression of three genes contributes to synapse formation in each neuron, they allow for combinations, an order of magnitude larger than the number of neurons in a human brain, leading again to serious overfitting. We are therefore faced with an astronomical search space, and the challenge to extract meaningful genetic rules in a heavily ill-conditioned problem of finding them from inherently limited experimental data.
To overcome these difficulties, here we develop a theoretical framework to systematically infer the genetic rules that contribute to the formation and maintenance of synapses and GJs between neurons in contact. We show that these genetic rules can be systematically extracted from three datasets: 1) a comprehensive map of the connectome, 2) a protein expression atlas of the individual neurons, and 3) a list of neurons in physical contact. Finally, we apply our modeling framework to the roundworm C. elegans. We do so because the C. elegans connectome is believed to be largely identical across individuals (33, 36, 37), and hence predetermined by the genetic markers that label each neuron (5, 20). Yet, the genetic mechanisms that determine which neurons can synapse with each other remain largely unknown even in this simple and well-studied organism (21). We show that we can overcome overfitting by restricting our analysis to genes known to be involved in GJ formation, and developing a spatial connectome model (SCM) to properly account for physical restrictions for wiring. We demonstrate the utility of the proposed modeling framework by predicting 19 interactions between innexin proteins responsible for GJ formation, finding that 5 of them are supported by previous experimental data.
The Connectome Model
We begin with two hypotheses, the first being that each gene can be in two possible states, expressed (one) or not (zero), whose combination defines the genetic barcode for each neuron. As we will discuss later, this hypothesis can be relaxed, but it simplifies the introduction of the connectome model (CM). The second hypothesis states that synapse formation is governed by some (unknown) biological mechanism linked to the gene expression patterns of each pair of neurons (neuronal barcodes). We describe each such mechanism as an operator , which inspects the barcodes of two neurons and decides to facilitate (or block) the formation of synapses or GJs between them (38).
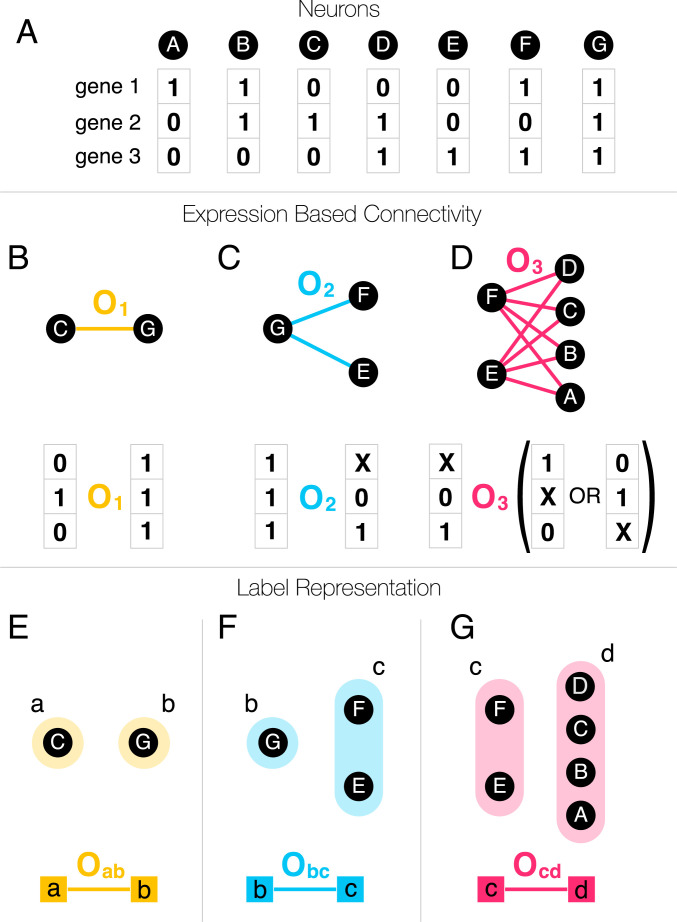
Consider a hypothetical connectome consisting of seven neurons, A to G, whose connections are uniquely determined by the expression patterns of three genes (Fig. 1A). The CM consists of a set of rules that encode the possibility of synapses between genetically encoded sets of neurons (38). As proposed in previous work, a rule could be an abstract operator that recognizes the complete genetic profile of neurons C and G, designating C as a source and G as a destination neuron, and establishing synapses between them (Fig. 1B). The connections that result can be either undirected, as in the case of GJs, or directed, like synapses (SI Appendix, Chemical Synapses). However, a less specific operator ( or ), that detects only a subset of the genes, ignoring the expression state of the genes marked by X, can generate multiple links between two sets of neurons, like the complete biclique of eight links in Fig. 1D. Fig. 1 summarizes a key prediction of the CM: Each biological mechanism that relies on gene expression to initiate synapse formation will generate an imprint in the connectome in the form of a unique network motif, known as a noninduced biclique in graph theory (39) (see also SI Appendix, Fig. S1), where neurons of the source set can be connected to neurons of the destination set. Ref. 39 validated this prediction by showing an excess of specific large biclique motifs in the C. elegans connectome. The challenge, which we address here, is how to reverse engineer the genetic rules from the observed network patterns, given that even a modest number of genetic rules can lead to a tremendous number of network motifs. Furthermore, the genetic rules can be rather complex when expressed in terms of operators connecting gene expression patterns (Fig. 1D), rooted in the nonlinear representation of combinatorial expression data. In order to make the description mathematically tractable, we introduce genetic labels, allowing us to capture multiple genetic operators within a single network-based framework. For instance, we can rewrite as the operator , where we assign all participating source neurons the label “a” (Fig 1E) and assign all destination neurons the label “b” (Fig. 1E). A biological rule governing neural connections between the source and destination neurons can be represented by the link between the two labels.
Fig. 1.
Genetic labels. (A) The terminal expression profile of seven neurons (black nodes), involving three genes, expressed (one) or unexpressed (zero). (B) The formation of links (chemical synapses, gap junctions) are governed by the expression profiles of the neurons, through biological mechanisms that have previously been abstracted as operators, (38). In the simplest case, an operator recognizes the full expression pattern of neurons C and G and connects them. (C) A single rule or operator can generate multiple links, if the operator detects the expression of some genes and ignores others. Here, X marks the gene ignored by the operator, whether it is expressed or not. (D) More complex operators that have multiple Xs in them can facilitate a large number of links. (E) In the formalism proposed here, we assign two labels to each operator, one to the source neurons (left) and another to the destination neurons (right). The labels allow us to represent operator as a link connecting the neurons with the right labels. (F) Even if the same label is assigned to multiple neurons, the operator remains a simple link between the two labels. (G) While the operator might appear complicated in terms of the original gene expression data, it has a simple structure in the label representation.
In this label-based representation, the operators have a simple form (Fig. 1 E–G), and the complexity of a rule is incorporated in how genes define the labels. Although some labels can represent complex gene expression patterns (e.g., Fig. 1D), others can be very simple. For example, electrical synapses or GJs are intercellular channels formed by two matching hemichannels consisting of a subset of 25 innexin proteins (40). In order to maintain a GJ, the innexins forming the hemichannels must be expressed on the surface of neurons in contact. In our formalism, the simplest rule, , is then a link between two innexins “a” and “b” expressed on two neurons forming a GJ. In other words, we assign label “a” (or “b”) to each neuron if it expresses innexin “a” (or “b”). In general, GJs can be also heteromeric, requiring a label that corresponds to the simultaneous expression of two (or more) innexins.
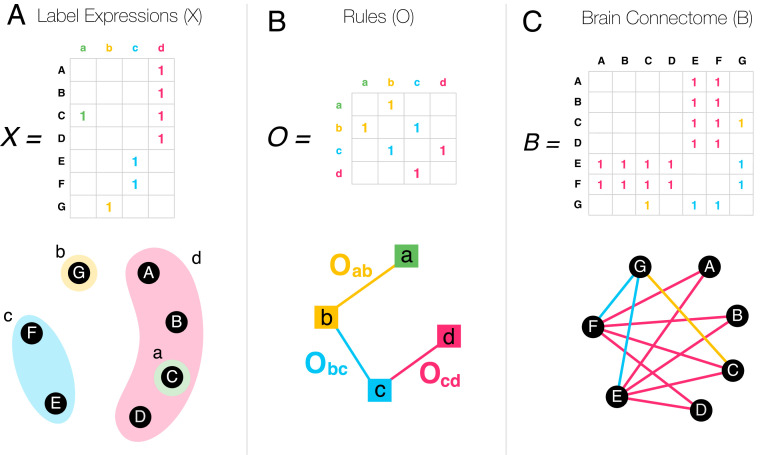
The labeling of each neuron is summarized in the expression matrix (), where if neuron ’s expression pattern is consistent with label “a,” and zero otherwise (Fig. 2A). The rule matrix summarizes the individual operators as links connecting the labels (Fig. 2B). If two neurons in contact express labels that are connected in , then there is a nonzero chance of establishing a synapse between these neurons. This representation defines mathematically the CM, that links the brain’s connectome () to the expression patterns of the individual neurons , through the rule matrix ,
| [1] |
The CM (Eq. 1) is our first key result, formally linking the connectome (), the expression patterns of the individual neurons (), and the biological mechanisms () that govern synapse/GJ formation in the brain. Eq. 1 is valid for weighted label expression data as well, where the weights capture the probability that a given neuron agrees with a given label.
Fig. 2.
The CM. (A) The expression pattern of the neurons A to G are summarized in the label expression matrix . (B) The operators connecting the labels can be summarized in the organizing rule matrix . (C) In the CM, the brain connectome () emerges from and through the CM Eq. 1. Each time two labels are connected in , the corresponding neurons in can form synapses. Only nonzero elements are shown in the matrices.
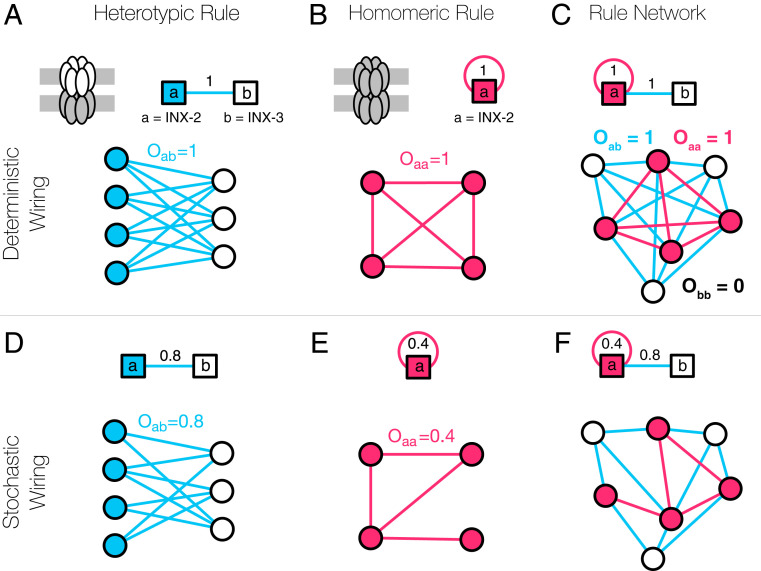
In practice, not all of the genetically allowed connections can be observed, due to experimental limitations, developmental and spatial constraints, and neural plasticity. In our formalism, this implies that is a stochastic operator with not necessarily being 1 (Fig. 3). For instance, fruit fly inx-2 homomeric GJs form only between of the neighboring cell pairs (41), leading to an apparent stochasticity in GJ formation, corresponding to . In the absence of such stochastic effects, predicts a complete subgraph of all label neurons. With stochasticity, instead of a fully connected subgraph, we expect a community of nodes connected to each other with density (Fig. 3E). In other words, is a weighted matrix, where the weights are the probabilities that neurons carrying labels “a” and “b” will link to each other.
Fig. 3.
GJs in the CM. GJs are formed by interacting hemichannels comprising innexin proteins. In the simplest case, a hemichannel is made of a single innexin, meaning that the expressed innexins can directly serve as labels. (A) Two Drosophila innexin proteins, inx-2 and inx-3, have been found to form (heterotypic) GJs, resulting in multiple potential neural connections (41). (B) There is evidence that inx-2 can form homomeric GJs, establishing connections between the neurons expressing inx-2, represented by the self-loop in the figure. (C) Altogether, the two rules (A and B) can be integrated into a rule network that serves as a genetic template for the GJ connectome. (D) The formalism behind the CM allows for stochastic rules, that is, a weight of 0.8 indicates that of the potential neural connections are present in the brain. This stochasticity can arise from multiple factors, including noisy or incomplete expression and connectome data, spatial effects, biological constraints, and true stochasticity of neuronal wiring. (E) According to oocyte experiments (51), the homomeric innexin rule of Drosophila inx-2 has a weight of 0.4, as only of the possible links are observed. (F) Even in the presence of apparent or true stochasticity, we can capture the GJ connectome using only a few (weighted) innexin rules.
Taken together, as the CM (Eq. 1) establishes a direct connection between the expression profiles of the individual neurons () and the connectome () through genetic rules (), it allows us to address several key problems in brain science, listed in the order of increasing technical difficulty: 1) Map out the connectome: Predict the connectome () from gene expression () and the genetic rules (). 2) Unveil the genetic rules: Predict the genetic rules () behind the connectome from known and . 3) Predict expression patterns: Find the gene expression of neurons () from the genetic rules () and the wiring of the connectome ().
Problem 1 is readily solved by Eq. 1, assuming that we know (some of) the biological mechanisms behind the rules in . As we currently lack these rules, in this paper, we focus on the pressing issue of solving Problem 2. This choice is motivated by the fact that, in C. elegans, we have a comprehensive map of its neural system’s adjacency matrix () and extensive (yet somewhat noisy and incomplete) information on the gene expression patterns of individual neurons (), potentially allowing us to determine the biological mechanisms encoded in .
Solving the Connectome Model.
Given the connectome and the labels , our goal is to identify the operator that collects the biological rules that govern link formation (Problem 2). To illustrate the procedure, we use the three rules introduced in Fig. 1 to generate the brain connectome (Fig. 2C), according to the label expression (Fig. 2A). In the occasion of multiple rules contributing to the same link in the connectome, is a weighted matrix, with the weight of each link corresponding to the number of rules involved. Generally, just by looking at two connected neurons, it appears impossible to reverse the problem and infer the genetic rule responsible for each connection (Fig. 2A, neurons C and G). Indeed, the rule could connect label “a” to label “b,” but could also connect label “a” to label “d.” Even if we had simultaneous access to the complete list of neural connections () and full genetic labels (), inferring the rules responsible for link formation () is mathematically ill conditioned, with infinitely many solutions of the form
| [2] |
where is an arbitrary matrix and stands for the Moore–Penrose pseudoinverse of , which has the property (42). We have a unique solution only when , meaning that the neurons have linearly independent label expression patterns, which is not expected to be the case in the brain. Otherwise, even if there is no noise in the input data, we do not expect to find an exact solution, and comes with a least-square residual error . In practice, the situation is even more difficult because and have multiple unknown errors (both false negatives and false positives). To make progress, we invoke the parsimony principle, searching for the model that accounts for the available data with the fewest rules in . A convenient way to mathematically formalize this is to minimize the objective function with a regularization parameter ,
| [3] |
where is the square of the Frobenius norm. When consists of only zeros and ones, a minimal Frobenius norm corresponds to the fewest rules or the fewest ones in the matrix. As an alternative implementation of the parsimony principle, we could also select the sum of the absolute values in as the norm, related to compressed sensing, also known as LASSO (least absolute shrinkage and selection operator) (43). Here, we proceed with the Frobenius norm in order to maintain the analytical tractability of the problem, and to be able to assess the significance of the obtained rules. With this, we can find the optimal , relying on the results on ridge regression (Tikhonov regularization) (44), discussed in Methods.
The SCM
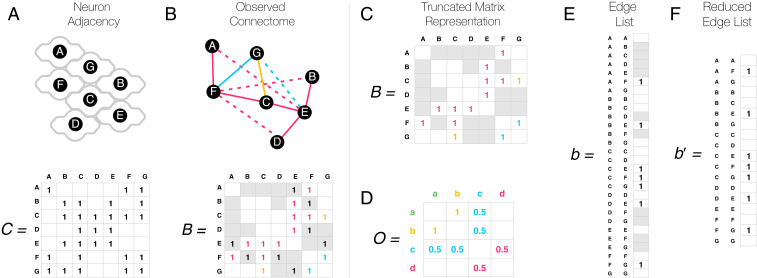
The CM assumes that each neuronal connection allowed by the genetic profile of the neurons will form with a probability dictated by genetics only. Yet, for a synapse or GJ to form, the neurons must also be in physical contact (Fig. 4A). If we ignore these spatial constraints, each missing link between remote neurons is taken as evidence against the rule, including links allowed by the genetics that do not have the opportunity to form as the neurons do not come in contact (Fig. 4B). Therefore, to increase the accuracy of the model’s predictions, we must restrict our analysis to pairs of neurons that do touch each other. This information is encoded by the contact matrix , telling us which neuron pairs are in physical contact. In C. elegans, the anterior brain contactome () has been mapped experimentally (45), prompting us to restrict our analyses to the anterior 185 neurons detailed in ref. 31 and available at https://wormwiring.org. Altogether, neuron pairs are in physical contact, representing of all pairs, out of which only 601 form GJs.
Fig. 4.
The SCM. (A) Neurons can only synapse if they are in physical contact. We schematically indicate physical contacts via touching neuron contours in the figure, and contacting neuron pairs are marked by a one in the matrix . Note that neurons can be in physical contact with themselves and even form synapses. (B) Given the lack of physical contact, only a fraction of the genetically allowed synapses are observed. The dashed links in the network, shown as ones in gray cells in the adjacency matrix below, indicate neural connections that are genetically permitted but are not observed because the neurons are not in contact. (C) When inferring genetic rules, distant neuron pairs must be ignored in the model (gray cells), as we do not know whether the lack of connection has a genetic origin or is simply due to spatial constraints. We therefore arrive at a truncated matrix representation, which does not obey standard matrix operations, and hence is challenging to work with. (D) If we treat all unobserved cells (gray and blank) as zeros, the matrix representation leads to incorrect rules, as it always assumes the lack of genetic compatibility where there may be some. (E) The edge list representation offers a linear description that is formally equivalent with the matrix representation. (F) Distant pairs of neurons can be removed from the edge list representation, and, as a truncated list is still a list, it allows us to uncover the correct rules based on Eq. 5.
It is tempting to incorporate spatial constraints into our matrix representation (Eq. 1) by ignoring each matrix element in that is absent in the contact matrix (Fig. 4C). If we do so, the obtained truncated matrix has nonexisting entries (Fig. 4C), and we cannot apply standard matrix operations to it. The naïve choice of treating each missing link as a zero in the connectome matrix leads to incorrect rules, as illustrated in Fig. 4D. To address this problem, we represent the connectome as an edge list rather than a matrix. In other words, we rearrange the connectome matrix (by any, i.e., lexicographic order) into the connectome vector (Fig. 4E). Similarly, we rearrange the rule matrix into a rule vector . This allows us to reformulate the bilinear CM in Eq. 1 as a higher-dimensional linear model
| [4] |
where is the Kronecker product. This, so far equivalent, linear representation allows us to restrict the space of neural connections to neurons in physical contact, by ignoring the entries in and that do not satisfy physical contact according to the matrix, resulting in a reduced and (Fig. 4F). We therefore arrive at the truncated connectome model describing the SCM, representing our second key result,
| [5] |
This equation can be solved using tools similar to the ones we used to study the CM, as discussed in Methods. At the end, the obtained rule weights vector can be rearranged into a matrix format, . If we perform these calculations on the toy model of Fig. 2 A and C with the indicated spatial constraints, we recover the exact rules in Fig. 2B, even though we are using only a fraction of the connectome information, that is, only the links that are between touching neurons. This result suggests that we do not need complete input data on the C. elegans connectome and gene expression to make reliable predictions, as we can use Eqs. 5 and 7 to uncover the biological mechanisms governing brain wiring even from partial data. Yet, we need to know the genetic labels, that is, the genetic basis, , in which the organizing rules operate. Next, we show how Eq. 5 helps us unveil the biological mechanism governing GJ formation.
Unveiling the Rules behind GJs
Electrical synapses, or GJs, play an important role in the C. elegans nervous system and muscle control (46). There are 25 genes involved in C. elegans GJ formation, all of which encode innexin proteins (collectively called innexin genes, even though not all of them are named inx*). We can therefore ignore the expression patterns of noninnexin genes, limiting overfitting by restricting the genetic space in used in our analysis. Currently, there is published expression data for 18 of the 25 innexin genes in C. elegans neurons (45) The innexin expression data we rely on were collected by a single group using a consistent method (45), and we relied on a curated version of the expression data that ensures the best available representation in terms of zeros and ones (5). Nevertheless, the data are expected to be enriched with zeros, resulting both from experimental error and incomplete studies. These omissions lead to inconsistencies: Although every neuron class is known to form GJs, about one-third of the neurons have no reported innexin gene expressed (47, 49). Besides this obvious data incompleteness, the expression data are also limited by experimental difficulties of differentiating between individual neurons within the same neuron class, practically limiting the resolution of the expression data to neuron classes. With these data limitations in mind, as a first step, we consider only the genetic labels linked to the expression patterns of individual innexin genes.
We begin by applying Eq. 7, using, as input, the innexin gene expression data () (45), the GJ connectome () (33), and the neuronal contactome (34, 45), aiming to calculate , describing the genetic rules that govern GJ formation (Fig. 5 and Methods). We set the regularization parameter at its optimal value (Methods and SI Appendix, Fig. S2), but we find that our results are qualitatively similar if we rely on any smaller, nonoptimized (SI Appendix, Fig. S6). The elements of the obtained matrix represent the probability that neurons expressing those genes form GJs due to this specific genetic rule. Most of the obtained rules have a small, but nonzero, weight (SI Appendix, Fig. S3), which is expected due to the chosen Frobenius norm, and also because of weight inflation resulting from false negatives in the expression data. We must therefore differentiate small values from meaningful probabilities. To assess the significance of the results, we developed a method to perform degree-preserving randomization of the connectome (49) without violating the spatial constraints. Indeed, while keeping the node (neuron) degrees unchanged is a standard requirement of a proper null model (49), we lack methods to perform such randomization without generating interactions between noncontacting pairs of neurons. We therefore developed a maximum entropy approach for network randomization with spatial constraints, using a subgraph randomization protocol (see Methods), allowing us to readily determine the score for each predicted rule. The scores can then be used to rank the obtained rules for validation experiments.
Fig. 5.
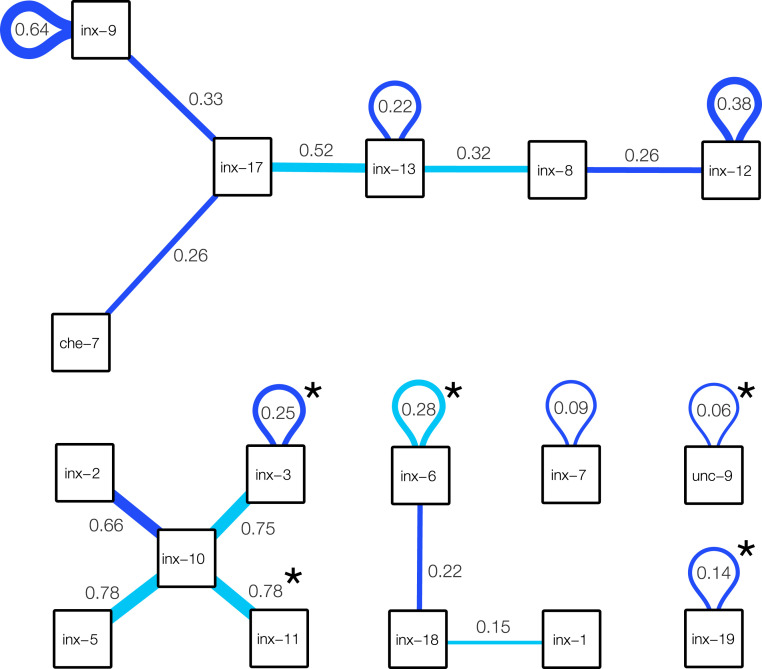
Predicted innexin rules. Significant innexin rules inferred for C. elegans GJs, showing only positive rules with a score of at least 2. Each box corresponds to an innexin protein in C. elegans. Dark blue links are found to be significant in both connectome reconstructions (SI Appendix, Fig. S4), while light blue links are significant only in the Cook et al. (33) connectome. Link weights estimate the connection probability. For example, the link between inx-2 and inx-10 has weight 0.66, meaning that the neurons expressing these two innexins establish GJs in of the cases. Note that the observed probability of GJs between these neurons might change if multiple rules contribute to them.
With the standard threshold, we find 19 significant wiring rules, summarized in Fig. 5 (for all scores, see SI Appendix, Fig. S3). Five of the 19 rules have been uncovered previously by the experimental literature, including 1) inx-19–inx-19 () (46), 2) unc-9–unc-9 () (46), 3) inx-10–inx-11 () (50), 4) inx-3–inx-3 () (46), and 5) inx-6–inx-6 () (46), where the boldface font indicates that the interaction is significant for two different C. elegans connectome reconstructions (SI Appendix, Fig. S4). Given that no further single innexin interactions were found in literature, observing all five experimentally supported interactions out of a set of 19 predictions appears to be highly significant (). However, this observation is tempered by the facts that the experiments relied on multiple methods: the inx-19–inx-19 interaction was confirmed by electrically coupling Xenopus oocytes (51), while inx-6–inx-6 channels have been confirmed by EM reconstruction (52). The remaining interaction rules are uncovered by the model: 6) inx-12–inx-12 (), 7) inx-9–inx-9 (), 8) inx-3–inx-10 (), 9) inx-5–inx-10 (), 10) inx-8–inx-13 (), 11) che-7–inx-17 (), 12) inx-8–inx-12 (), 13) inx-9–inx-17 (), 14) inx-6–inx-18 (), 15) inx-7–inx-7 (), 16) inx-13–inx-13 (), 17) inx-13–inx-17 (), 18) inx-2–inx-10 (), and 19) inx-1–inx-18 (), where boldface again indicates that the interaction is confirmed in both reconstructions (SI Appendix, Fig. S4).
The obtained interactions offer ground for direct falsifiable experimental confirmation, for example, by expressing one of each innexins in Xenopus oocytes and checking for electric coupling. In addition, it is possible to introduce genetic interventions that, according to our model, are expected to lead to rewiring in the C. elegans system. The developed framework allows us to predict the nature of this rewiring: For example, if a connection between two neurons is due to a single rule, then losing the participating genetic label on either side leads to a loss of interaction. For instance, our inference predicts that the AINR–ASGL and AINL–ASGR GJs, present in both C. elegans connectome reconstructions, are coded solely by the che-7–inx-17 rule, an interaction found to be significant according to inference on both reconstructions (SI Appendix, Fig. S4). Therefore, knocking down any of these genes in the neurons, or pharmacologically preventing the interaction, is expected to result in the loss of these two GJs. Note that these predictions are sensitive to the noise in the input data and the choice of the significance threshold, particularly since all single-rule GJs originate from low-strength interactions.
Discussion
Motivated by the need to infer the genetic rules that govern the wiring diagram of the connectome, here we have introduced a computational framework that relates the genetic expression profiles of the individual neurons to the connectome. Although the connectome and, especially, the neuron gene expression profiles remain heavily incomplete and prone to noise, our results indicate that their joint coverage is sufficient to infer some of the conjectured interactions that govern GJ formation in the C. elegans nervous system. To achieve this, we established a connection between the gene expression patterns of single neurons and the connectome, through the CM (Eq. 1). As synapses can only form between neurons that are in physical contact, we incorporated spatial constraints in our framework, resulting in the SCM (Eq. 5). The model allowed us to identify 19 significant innexin rules behind GJs. As the availability of high-quality input data increases, the SCM can be extended to capture chemical synapse formation, which follows the same constraints as GJs (53), helping to illustrate the versatility of the developed modeling framework (SI Appendix, Chemical Synapses).
Although we utilized the multimodal profiling of C. elegans to validate specific predictions, the SCM formalism is developed to meet future needs, in expectation of new connectomes and detailed genetic profiling methods. Indeed, working with larger connectomes highlights the importance of incorporating constraints, as, in large connectomes, an overwhelming fraction of neuron pairs are not in physical contact. The presented framework offers guidance for future experiments: To apply SCM to these systems requires a matched connectome, contactome, and transcriptome, meaning that, for each cell, we need to know its connections, its physical contacts, and its gene expression. Partial neuronal transcriptomes and connectomes have been published recently for fly (54–56) and zebrafish (57, 58). However, connectivity and gene expression were not profiled jointly; thus these datasets cannot offer cellular-level predictions. In an alternate application, future work could utilize the CM to infer genetic correlates of projectomic rules, where the matrix can be a projectome, such as between neuronal areas, and remains a label-transformed transcriptome, while represents genetic compatibility rules that promote projections from one region to another. This application may require us to alter the subgraph randomization procedure to account for a weighted connectome, which could be achieved by redefining the maximum entropy constraints (59, 60).
The SCM, together with the inferred innexin rules, allows us to predict potential changes in neural wiring if gene expression is altered via knockout experiments or silencing. Yet, a knockout experiment of an innexin is only informative if the mutant is viable. The individual loss of several innexins (including inx-3, inx-12, inx-13, inx-14, and inx-22) is known to be lethal (46), limiting knockout experiments to nonessential innexins, unless, maybe, the experiments can be limited to specific neurons only. Temperature-sensitive alleles provide an alternative way to experimentally modulate the expression of essential innexins, keeping the innexins functional during development, and disabling the corresponding GJs at restrictive temperatures (61, 62). Another possibility would be an exercise in edgetics, that is, disrupting specific protein–protein interactions using drugs targeting innexins (63), and detecting the resulting change in the connectome. Our model could also be used to predict how the brain is rewired in the food-deprived, dormant state of the C. elegans known as the dauer stage. Functional studies indicate a substantial remodeling of behavior which anticipates a substantial rewiring of the GJ connectome, with profound impact on synaptic partner choices. As a prerequisite, dauer-stage neuron gene expression data have been made available recently (47).
Finally, as the SCM establishes connections between brain connectivity and genetics, we can assess whether neurons are primarily connected based on genetic similarity (SI Appendix, Spectral Interpretation of the Wiring Rules). The diagonalization of the rule matrix () leads to a minimal set of abstract rules, given by the eigenvalues. If all eigenvalues are nonnegative, that indicates that neurons will form synapses with other neurons of similar expression profiles. We find, however, at least four negative eigenvalues, supporting a complex genetic organization (SI Appendix, Fig. S5), with a strong presence of genetic heterophily, indicating that GJ formation relies strongly on genetic complementarity besides similarity.
Methods
Ridge Regression.
The optimization problem (Eq. 3) can be solved analytically as (44)
| [6] |
where . In the limit, the solution is , yielding the best residual error () at the expense of the simplicity of , prone to overfitting in the presence of errors. This limit is also sensitive to changes in ; therefore, is only appropriate when the input data are exact. In contrast, leads to the estimate , coinciding with the naïve assumption discussed in ref. 28, yielding a poor , being prone to underfitting. Here we find the optimal , following the suggestion by Wahba and coworkers (64), proven to be optimal in a generalized cross-validation scenario, corresponding to that minimizes , where , and is calculated using the Kronecker product. Eq. 5 can be solved similarly, leading to
| [7] |
with , at the optimal , minimizing , with (SI Appendix, Fig. S2).
Subgraph Randomization.
We start with a graph and a subgraph , and we aim to sample, uniformly, the space of subgraphs of with (approximately) the same subgraph degree sequence as given in . This represents a constrained version of the traditional degree-preserved randomization, where is a complete graph (65), as all interactions that are not in appear as hard constraints and are excluded from the randomized networks. Here, represents the list of neurons in contact that could, in principle, establish a GJ, and we randomize the network of existing synapses without violating the known neuronal contact structure (). We use a maximum entropy approach, maximizing the entropy of the random network ensemble defined as . The average subgraph degree of each node in is , which we keep fixed at the original value, . The probability of a given graph instance is , where , and the probability of having a link between nodes and is expressed as , where . The average subgraph degree of a node is then given by , and the optimal can be found iteratively, with the update rule
| [8] |
starting from the initial condition leading to , where is the full node degree in . We perform a hundred iterations to estimate the optimal , allowing us to calculate the mean and the variance of the randomized matrix ensemble. Due to the linearity of the SCM solution, these yield a score for each inferred wiring rule (through the first and second moments), without the need of explicitly generating random samples from the ensemble.
Supplementary Material
Acknowledgments
We thank Emma Towlson and Oliver Hobert for helpful discussions and data sharing, as well as Alice Grishchenko for help in designing the figures. This work was supported by the European Union’s Horizon 2020 research and innovation program under Grant Agreement 810115 - Dynamics and Structure of Networks (DYNASNET). D.L.B. was supported by NIH National Institute of General Medical Sciences Grant T32 GM008313. A.-L.B. was supported by the NSF Award 1734821.
Footnotes
Competing interest statement: A.L.B. is the founder of Scipher Medicine, Foodome, and Nomix, which apply computational and network-based tools to health.
This article is a PNAS Direct Submission. M.G. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2009093117/-/DCSupplemental.
Data and Code Availability.
For reproducibility, we provide code and processed data at DOI:10.5281/zenodo.4027588. All study data are included in the article and SI Appendix.
References
- 1.Paul A., et al. , Transcriptional architecture of synaptic communication delineates gabaergic neuron identity. Cell 171, 522–539 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Seung H. S., Sümbül U., Neuronal cell types and connectivity: Lessons from the retina. Neuron 83, 1262–1272 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tasic B., et al. , Adult mouse cortical cell taxonomy revealed by single cell transcriptomics. Nat. Neurosci. 19, 335–346 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zeisel A., et al. , Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science 347, 1138–1142 (2015). [DOI] [PubMed] [Google Scholar]
- 5.Hobert O., Glenwinkel L., White J., Revisiting neuronal cell type classification in Caenorhabditis elegans. Curr. Biol. 26, R1197–R1203 (2016). [DOI] [PubMed] [Google Scholar]
- 6.Fishell G., Kepecs A., Interneuron types as attractors and controllers. Annu. Rev. Neurosci. 43, 1–30 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reilly M. B., Cros C., Varol E., Yemini E., Hobert O., Unique homeobox codes delineate all the neuron classes of C. elegans. Nature 584, 595–601 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lim L., Mi D., Llorca A., Marín O., Development and functional diversification of cortical interneurons. Neuron 100, 294–313 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.English D. F., et al. , Pyramidal cell-interneuron circuit architecture and dynamics in hippocampal networks. Neuron 96, 505–520 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Warren L., et al. , Highly efficient reprogramming to pluripotency and directed differentiation of human cells with synthetic modified mRNA. Cell Stem Cell 7, 618–630 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rabinowitch I., Schafer W. R., Engineering new synaptic connections in the C. elegans connectome. Worm 4, e992668 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Carrillo R. A., et al. , Control of synaptic connectivity by a network of Drosophila IgSF cell surface proteins. Cell 163, 1770–1782 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Timothy W. Y., Hao J. C., Lim W., Tessier-Lavigne M., Bargmann C. I., Shared receptors in axon guidance: SAX-3/Robo signals via UNC-34/enabled and a netrin-independent UNC-40/DCC function. Nat. Neurosci. 5, 1147–1154 (2002). [DOI] [PubMed] [Google Scholar]
- 14.Lim Y.-s., Wadsworth W. G., Identification of domains of netrin UNC-6 that mediate attractive and repulsive guidance and responses from cells and growth cones. J. Neurosci. 22, 7080–7087 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hedgecock E. M., Culotti J. G., Hall D. H., The UNC-5, UNC-6, and UNC-40 genes guide circumferential migrations of pioneer axons and mesodermal cells on the epidermis in C. elegans. Neuron 4, 61–85 (1990). [DOI] [PubMed] [Google Scholar]
- 16.Adler C. E., Fetter R. D., Bargmann C. I., UNC-6/netrin induces neuronal asymmetry and defines the site of axon formation. Nat. Neurosci. 9, 511–518 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ercsey-Ravasz M., et al. , A predictive network model of cerebral cortical connectivity based on a distance rule. Neuron 80, 184–197 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Han Y., et al. , The logic of single-cell projections from visual cortex. Nature 556, 51–56 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shen K., Fetter R. D., Bargmann C. I., Synaptic specificity is generated by the synaptic guidepost protein SYG-2 and its receptor, SYG-1. Cell 116, 869–881 (2004). [DOI] [PubMed] [Google Scholar]
- 20.Marcus G., Marblestone A., Dean T., The atoms of neural computation. Science 346, 551–552 (2014). [DOI] [PubMed] [Google Scholar]
- 21.Südhof T. C., Synaptic neurexin complexes: A molecular code for the logic of neural circuits. Cell 171, 745–769 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Söhl G., Maxeiner S., Willecke K., Expression and functions of neuronal gap junctions. Nat. Rev. Neurosci. 6, 191–200 (2005). [DOI] [PubMed] [Google Scholar]
- 23.Hong W., Luo L., Genetic control of wiring specificity in the fly olfactory system. Genetics 196, 17–29 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.DePew A. T., Aimino M. A., Mosca T. J., The tenets of teneurin: Conserved mechanisms regulate diverse developmental processes in the Drosophila nervous system. Front. Neurosci. 13, 27 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Arnatkeviciute A., Fulcher B. D., Fornito A., Uncovering the transcriptional signatures of hub connectivity in neural networks. Front. Neural Circ. 13, 47 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fakhry A., Ji S., High-resolution prediction of mouse brain connectivity using gene expression patterns. Methods 73, 71–78 (2015). [DOI] [PubMed] [Google Scholar]
- 27.Kaufman A., Dror G., Meilijson I., Ruppin E., Gene expression of Caenorhabditis elegans neurons carries information on their synaptic connectivity. PLoS Comput. Biol. 2, e167 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Varadan V., Miller D. M. III, Anastassiou D., Computational inference of the molecular logic for synaptic connectivity in C. elegans. Bioinformatics 22, e497–e506 (2006). [DOI] [PubMed] [Google Scholar]
- 29.Arnatkeviciute A., Fulcher B. D., Pocock R., Fornito A., Hub connectivity, neuronal diversity, and gene expression in the Caenorhabditis elegans connectome. PLoS Comput. Biol. 14, e1005989 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Baruch L., Itzkovitz S., Golan-Mashiach M., Shapiro E., Segal E., Using expression profiles of Caenorhabditis elegans neurons to identify genes that mediate synaptic connectivity. PLoS Comput. Biol. 4, e1000120 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Brittin C. A., Cook S. J., Hall D. H., Emmons S. W., Cohen N., Volumetric reconstruction of main Caenorhabditis elegans neuropil at two different time points. bioRxiv:485771 (4 December 2018).
- 32.Varshney L. R., Chen B. L., Paniagua E., Hall D. H., Chklovskii D. B., Structural properties of the Caenorhabditis elegans neuronal network. PLoS Comput. Biol. 7, e1001066 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cook S. J., et al. , Whole-animal connectomes of both Caenorhabditis elegans sexes. Nature 571, 63–71 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Harris T. W., et al. , Wormbase: A comprehensive resource for nematode research. Nucleic Acids Res. 38, D463–D467 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Azevedo F. A., et al. , Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J. Comp. Neurol. 513, 532–541 (2009). [DOI] [PubMed] [Google Scholar]
- 36.Jarrell T. A., et al. , The connectome of a decision-making neural network. Science 337, 437–444 (2012). [DOI] [PubMed] [Google Scholar]
- 37.Walker D. S., Chew Y. L., Schafer W. R., “Genetics of behavior in C. elegans” in The Oxford Handbook of Invertebrate Neurobiology, Byrne J. H., Ed. (Oxford University Press, 2017). [Google Scholar]
- 38.Barabási D. L., Barabási A. L., A genetic model of the connectome. Neuron 105, 435–445 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zelinka B., On a problem of E. Prisner concerning the biclique operator. Math. Bohem. 127, 371–373 (2002). [Google Scholar]
- 40.Hall D. H., Gap junctions in C. elegans: Their roles in behavior and development. Dev. Neurobiol. 77, 587–596 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Stebbings L. A., Todman M. G., Phelan P., Bacon J. P., Davies J. A., Two Drosophila innexins are expressed in overlapping domains and cooperate to form gap-junction channels. Mol. Biol. Cell 11, 2459–2470 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.James M., The generalised inverse. Math. Gaz. 62, 109–114 (1978). [Google Scholar]
- 43.Tibshirani R., Regression shrinkage and selection via the lasso. J. Roy. Stat. Soc. B 58, 267–288 (1996). [Google Scholar]
- 44.Hoerl A. E., Kennard R. W., Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 12, 55–67 (1970). [Google Scholar]
- 45.Altun Z. F., Chen B., Wang Z. W., Hall D. H., High resolution map of Caenorhabditis elegans gap junction proteins. Dev. Dynam. 238, 1936–1950 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Simonsen K., Moerman D., Naus C. C., Gap junctions in C. elegans. Front. Physiol. 5, 40 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bhattacharya A., Aghayeva U., Berghoff E. G., Hobert O., Plasticity of the electrical connectome of C. elegans. Cell 176, 1174–1189 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.White J. G., Southgate E., Thomson J. N., Brenner S., The structure of the nervous system of the nematode Caenorhabditis elegans. Philos. Trans. R. Soc. Lond. B Biol. Sci. 314, 1–340 (1986). [DOI] [PubMed] [Google Scholar]
- 49.Maslov S., Sneppen K., Specificity and stability in topology of protein networks. Science 296, 910–913 (2002). [DOI] [PubMed] [Google Scholar]
- 50.Liu P., et al. , Six innexins contribute to electrical coupling of C. elegans body-wall muscle. PloS One 8, e76877 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Chuang C. F., VanHoven M. K., Fetter R. D., Verselis V. K., Bargmann C. I., An innexin-dependent cell network establishes left-right neuronal asymmetry in C. elegans. Cell 129, 787–799 (2007). [DOI] [PubMed] [Google Scholar]
- 52.Oshima A., Matsuzawa T., Nishikawa K., Fujiyoshi Y., Oligomeric structure and functional characterization of Caenorhabditis elegans innexin-6 gap junction protein. J. Biol. Chem. 288, 10513–10521 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Südhof T. C., Towards an understanding of synapse formation. Neuron 100, 276–293 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Xu C. S., et al. , A connectome of the adult Drosophila central brain. bioRxiv:911859 (21 January 2020). [DOI] [PMC free article] [PubMed]
- 55.Eichler K., et al. , The complete connectome of a learning and memory centre in an insect brain. Nature 548, 175–182 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Davie K., et al. , A single-cell transcriptome atlas of the aging Drosophila brain. Cell 174, 982–998 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hildebrand D. G. C., et al. , Whole-brain serial-section electron microscopy in larval zebrafish. Nature 545, 345–349 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Tambalo M., Mitter R., Wilkinson D. G., A single cell transcriptome atlas of the developing zebrafish hindbrain. Development 147, dev184143 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Cimini G., et al. , The statistical physics of real-world networks. Nat. Rev. Phys. 1, 58–71 (2019). [Google Scholar]
- 60.Squartini T., Caldarelli G., Cimini G., Gabrielli A., Garlaschelli D., Reconstruction methods for networks: The case of economic and financial systems. Phys. Rep. 757, 1–47 (2018). [Google Scholar]
- 61.O’Rourke S. M., et al. , A survey of new temperature-sensitive, embryonic-lethal mutations in C. elegans: 24 alleles of thirteen genes. PloS One 6, e16644 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Li S., Dent J. A., Roy R., Regulation of intermuscular electrical coupling by the Caenorhabditis elegans innexin inx-6. Mol. Biol. Cell 14, 2630–2644 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sahni N., et al. , Widespread macromolecular interaction perturbations in human genetic disorders. Cell 161, 647–660 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Golub G. H., Heath M., Wahba G., Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 21, 215–223 (1979). [Google Scholar]
- 65.Chatterjee S., et al. , Random graphs with a given degree sequence. Ann. Appl. Probab. 21, 1400–1435 (2011). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
For reproducibility, we provide code and processed data at DOI:10.5281/zenodo.4027588. All study data are included in the article and SI Appendix.