Synaptic plasticity rules with physiological calcium levels

Significance

Spike-timing–dependent plasticity (STDP) is a form of synaptic modification thought to be a primary mechanism underlying formation of new memories. Despite triggering tremendous interest since its discovery, it is still unclear whether plasticity rules inferred from in vitro experiments are correct in physiological conditions. While STDP induction depends on intracellular calcium influx, all previous studies used an abnormally high concentration of extracellular calcium. Here, we study the influence of extracellular calcium on synaptic plasticity. We show that pairing single pre- and postsynaptic action potentials at hippocampal synapses does not induce plasticity in the physiological range of extracellular calcium. Rather, synaptic plasticity is induced only when bursts of postsynaptic spikes are used or when neurons fire at sufficiently high frequency.

Abstract

Spike-timing–dependent plasticity (STDP) is considered as a primary mechanism underlying formation of new memories during learning. Despite the growing interest in activity-dependent plasticity, it is still unclear whether synaptic plasticity rules inferred from in vitro experiments are correct in physiological conditions. The abnormally high calcium concentration used in in vitro studies of STDP suggests that in vivo plasticity rules may differ significantly from in vitro experiments, especially since STDP depends strongly on calcium for induction. We therefore studied here the influence of extracellular calcium on synaptic plasticity. Using a combination of experimental (patch-clamp recording and Ca²⁺ imaging at CA3-CA1 synapses) and theoretical approaches, we show here that the classic STDP rule in which pairs of single pre- and postsynaptic action potentials induce synaptic modifications is not valid in the physiological Ca²⁺ range. Rather, we found that these pairs of single stimuli are unable to induce any synaptic modification in 1.3 and 1.5 mM calcium and lead to depression in 1.8 mM. Plasticity can only be recovered when bursts of postsynaptic spikes are used, or when neurons fire at sufficiently high frequency. In conclusion, the STDP rule is profoundly altered in physiological Ca²⁺, but specific activity regimes restore a classical STDP profile.

Spike-timing–dependent plasticity (STDP) is a form of synaptic modification thought to constitute a mechanism underlying formation of new memories. The polarity of synaptic changes is controlled by the relative timing between pre- and postsynaptic activity and depends on intracellular Ca²⁺ signaling (review in refs. 1 and 2). In hippocampal and neocortical pyramidal neurons, timing-dependent long-term synaptic potentiation (t-LTP) is induced when synaptic activity is followed by one or more backpropagating action potentials in the postsynaptic cell (3–8). It involves postsynaptic Ca²⁺ influx through N-methyl-d-aspartate (NMDA) receptors that in turn activates protein kinases (3, 6, 8, 9). Timing-dependent long-term synaptic depression (t-LTD) is expressed when synaptic activity is repeatedly preceded by one or more backpropagating action potentials (4–7, 10). It depends on NMDA receptor activation, postsynaptic metabotropic glutamate receptors (mGluR), voltage-dependent calcium channels, protein phosphatases, cannabinoid receptor CB1, and astrocytic signaling (6, 10–16). Calcium therefore represents potentially a key factor in the induction of STDP. The intracellular Ca²⁺ dependence of STDP suggests that extracellular Ca²⁺ might play a critical role in shaping STDP. Yet, most if not all in vitro STDP studies (6–10, 17–19) used nonphysiological external Ca²⁺ concentrations ranging between 2 and 3 mM because elevated calcium is known to stabilize recording of synaptic transmission and to avoid intrinsic bursting that could obscure induction of STDP with single pre- and postsynaptic spikes (20, 21). In contrast, the physiological Ca²⁺ concentration is typically around 1.3 mM, with small (0.1–0.3 mM) variations between awake, sleep, and anesthesia, and with age, but in all cases concentrations are below 1.8 mM in rodent hippocampus (22–24).

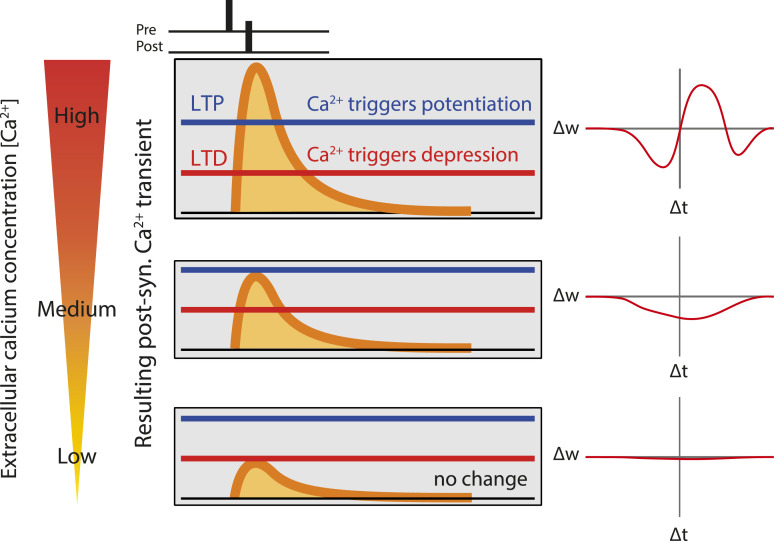
Calcium-based models of synaptic plasticity (25, 26) where Ca²⁺ transients result from backpropagating action potentials and excitatory postsynaptic potentials (EPSPs) predict that the sign, shape, and magnitude of STDP strongly depend on the amplitudes of calcium transients triggered by pre- and postsynaptic spikes and therefore on external Ca²⁺ concentration (26) (Fig. 1). These modeling studies suggest the possibility that plasticity rules at physiological concentrations might be very different from the ones inferred from currently available data. Several scenarios are possible: In the mildest one, high Ca²⁺ concentrations used in experimental studies would lead to an overestimate of the in vivo levels of plasticity; in the most extreme one, a complete lack of plasticity could be observed in physiological Ca²⁺. In addition, recent work shows that synaptic plasticity rules at a cerebellar synapse are profoundly altered in physiological calcium (27, 28). We therefore set out to determine STDP rules in physiological Ca²⁺ at the CA3-CA1 synapse of the hippocampus in vitro.

Fig. 1.

Prediction of a calcium-based model of spike-timing–dependent plasticity. Cartoon showing qualitatively calcium transients induced by pairing a presynaptic spike with a postsynaptic spike with a delay ∆t, for three extracellular calcium concentrations (high on top, low on the bottom). Synaptic changes depend on two plasticity thresholds, one for LTP (blue) and one for LTD (red). The resulting 'STDP curves' (change in synaptic stength ∆w as a function of ∆t) are shown on the right. At high extracellular calcium, the calcium transient exceeds LTP threshold in a range of positive ∆ts, and the STDP curves has a LTP window surrounded by two LTD windows. Decreasing extracellular calcium leads to a decrease in the amplitude of the calcium transient, which no longer cross the LTP threshold, resulting in a STDP curve with only LTD. Finally, a further reduction in extracellular calcium leads to no threshold crossing, and consequently no synaptic changes.

We show here that the classical STDP rule (t-LTD for post-before-pre pairings, t-LTP for pre-before-post pairings) is obtained solely with a high external Ca²⁺ concentration (≥ 2.5 mM), whereas no plasticity could be induced for concentrations lower than 1.5 mM external Ca²⁺, and only t-LTD could be induced by positive or negative time delays in 1.8 mM external Ca²⁺. t-LTP could be restored only when bursts of three or four postsynaptic spikes were used instead of single spikes, or when the pairing frequency was increased from 0.33 to 5 or 10 Hz. We used two variants of a Ca²⁺-based plasticity model (26) in which both t-LTD and t-LTP depend on transient changes in postsynaptic Ca²⁺ (Fig. 1) to fit the data. We found that the nonlinearity of transient Ca²⁺ changes conferred by NMDA receptor activation is critical to quantitatively account for the entire experimental dataset. Our results indicate that the STDP rule is profoundly altered in physiological Ca²⁺, but that a classical STDP profile can be restored under specific activity regimes.

Results

STDP Rule Is Altered in Extracellular Physiological Calcium.

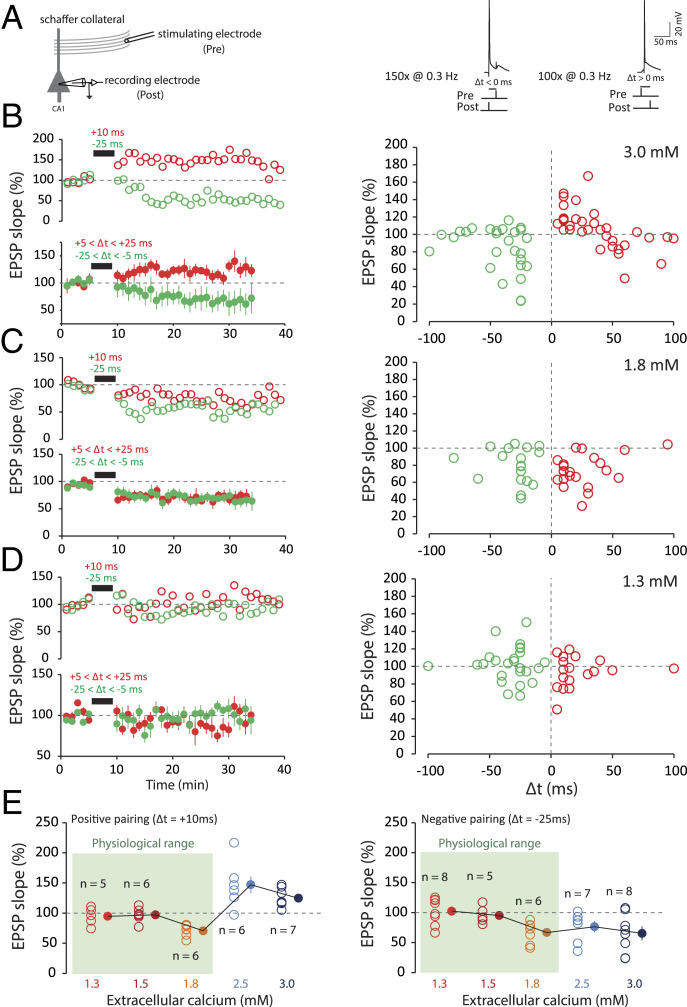
Induction of STDP at the Schaffer collateral–CA1 pyramidal cell synapses was examined under three different external Ca²⁺ concentrations (3, 1.8, and 1.3 mM) and in the presence of normal synaptic inhibition (i.e., without any GABA_A receptor antagonist). In high Ca²⁺ (3 mM), t-LTP (124 ± 7% of the control EPSP slope, n = 14) was induced by repeatedly pairing [100 times, 0.3 Hz (29); Fig. 2A] the evoked EPSP and the postsynaptic action potential (AP) with a delay ranging between +5 and +25 ms (pre-before-post pairings; Fig. 2B). t-LTD (68 ± 11%, n = 10) was induced by repeatedly pairing [150 times, 0.3 Hz (29); Fig. 2A] the EPSP and the postsynaptic AP with a delay ranging between −5 and −25 ms (post-before-pre pairings; Fig. 2B). The plot of synaptic changes as a function of spike timing provided a classical STDP curve in 3 mM external Ca²⁺, with a t-LTP window in the [0,40 ms] range surrounded by two t-LTD windows, one for negative delays and the other for positive delays at ∼40–60 ms (Fig. 2A). In contrast, only t-LTD was induced by positive or negative pairings in 1.8 mM external Ca²⁺ (73 ± 6%, n = 13 and 71 ± 8%, n = 11, respectively; Fig. 2C), and no significant changes were observed in 1.3 mM external Ca²⁺ at any pairing (100 ± 12%, n = 13 after positive pairing and 106 ± 14%, n = 13 after negative pairing; Fig. 2D). Thus, the STDP rules are highly altered in the physiological Ca²⁺ range (Fig. 2 C and D), as predicted by calcium-based models (25, 26) (Fig. 1).

Fig. 2.

STDP under various external calcium concentrations. (A) t-LTP and t-LTD are induced at low frequency (0.3 Hz). The pre-post protocol is repeated 100 times, while the post-pre protocol is repeated 150 times. The action potential is induced by the injection of a depolarizing current into a CA1 neuron recorded in a whole-cell configuration. The EPSP is evoked by a stimulation electrode placed in the Schaffer collaterals. The delay (Δt) is varied according to the experiments. (B) In 3 mM extracellular calcium, a pre-post protocol (positive delays; +5 < Δt < +25 ms; red) leads to t-LTP and a post-pre (negative delays; −25 < Δt < −5 ms; green) protocol leads to t-LTD. Note the presence of a second t-LTD window at around +40/+60 ms. To facilitate comparison between the data, the duration of the negative pairing has been set to that of the positive pairing. (C) In 1.8 mM extracellular calcium, both pre-post protocols (+5 < Δt < +25 ms; red) and post-pre protocols (−25 < Δt < −5 ms; green) lead to t-LTD. The t-LTP window is absent under these conditions. (D) In 1.3 mM extracellular calcium, on average, no plasticity is induced regardless of the delay. The t-LTP and t-LTD window are missing under these conditions. (E, Left) Synaptic changes for a pre-post protocol at +10 ms. No plasticity is induced for calcium concentrations of 1.3 and 1.5 mM. For 1.8 mM calcium, t-LTD is induced, while for 2.5, and 3 mM calcium, t-LTP is induced. (E, Right) Synaptic changes for a post-pre protocol at −25 ms. No plasticity is induced in 1.3 and 1.5 mM calcium. For 1.8, 2.5, and 3 mM calcium, t-LTD is induced. Note the difference between the results in the range of physiological calcium concentration (green squares) and the results in nonphysiological calcium concentration.

In order to precisely determine the transition between t-LTD and no change for negative delays and the transition from t-LTP to t-LTD to no change for positive delays, we tested the effects of positive and negative pairing in 1.5 and 2.5 mM external Ca²⁺. The data show that negative pairing induced no plasticity in 1.5 mM external Ca²⁺ (95 ± 5%, n = 5; Fig. 2E), whereas t-LTD was consistently observed in the 1.8–3 mM range (at 2.5 mM, 90 ± 3%, n = 5; Fig. 2E). Positive pairing led to no change in 1.5 mM external Ca²⁺ (97 ± 5%, n = 6), t-LTD at 1.8 mM external Ca²⁺, but t-LTP in 2.5 mM external Ca²⁺ (147 ± 13%, n = 6), with a switch from t-LTD to t-LTP occurring between 1.8 and 2.5 mM (Fig. 2E). These data indicate that the STDP rule is profoundly altered in physiological calcium, with a lack of t-LTP in the whole range, and the appearance of t-LTD in a broad range of timings in the upper limit of the physiological Ca²⁺ range.

Calcium Imaging.

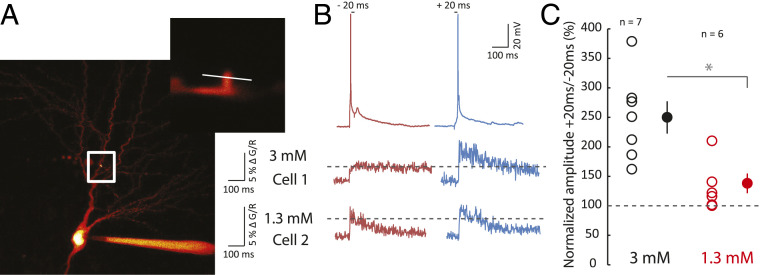
In order to better understand why no plasticity occurred in 1.3 mM, calcium transients in response to positive (+20 ms) and negative pairings (−20 ms) between an evoked EPSP and a postsynaptic spike were measured using Fluo-4 in dendritic spines (Fig. 3A). While the magnitude of the calcium transients was found to be much greater for positive pairing than for negative pairing in 3 mM calcium (ratio +20/−20 ms = 250 ± 27%, n = 7; Fig. 3 B and C), the difference in calcium transient amplitude was found to be considerably smaller in 1.3 mM calcium (ratio +20/−20 ms = 132 ± 17%, n = 6, Mann–Whitney (MW) U test, P < 0.01; Fig. 3 B and C). The fact that the ratio of calcium signals is close to 1 in 1.3 mM calcium could explain why the same plasticity result is obtained using pre-post or post-pre pairings, as we observed in electrophysiological experiments.

Fig. 3.

Calcium imaging. (A) Comparison of calcium spine entry during negative and positive pairing in 3 and 1.3 mM extracellular calcium. Calcium was measured in the spine of a CA1 pyramidal cell loaded with 50 µM Fluo-4. White square, location of enlarged area. The white line indicates the line scan on the dendritic spine. (B) Each neuron was alternatively tested for negative (Δt = −20 ms) and positive pairing (Δt = +20 ms). Cell 1 recorded in 3 mM calcium displays a much larger influx of calcium in response to positive pairing than negative pairing. Cell 2 recorded in 1.3 mM calcium displays an almost equal calcium rise. (C) Pooled data of the normalized ratio of calcium evoked by positive pairing over negative pairing (*P < 0.01, Mann–Whitney U test).

Recovery of t-LTP in Physiological Calcium.

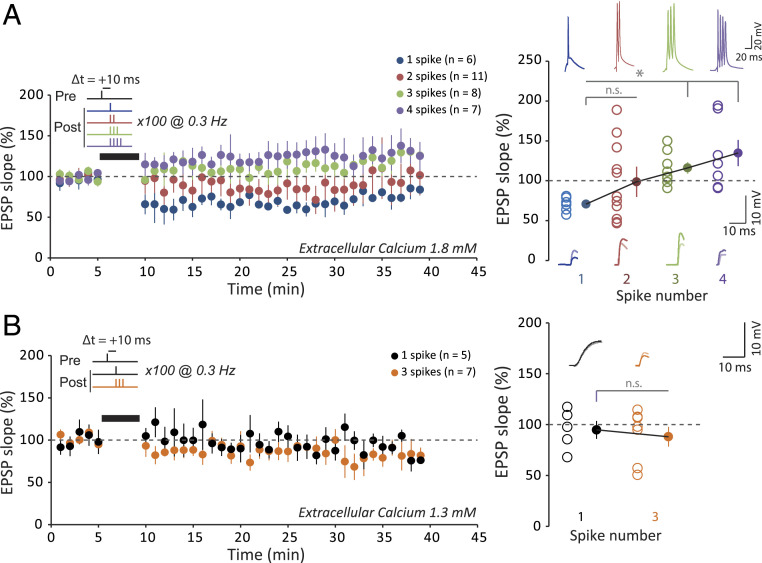
The STDP rule in physiological Ca²⁺ is characterized by a complete lack of t-LTP and the predominance of t-LTD at 1.8 mM external Ca²⁺, while no significant plasticity is observed at 1.3 mM. Therefore, we first tried to restore t-LTP in physiological Ca²⁺ by either using bursts of postsynaptic spikes, instead of individual spikes, during the pairing (18, 30) or increasing the frequency of single-spike pairing (18). In 1.8 mM external Ca²⁺, increasing the number of postsynaptic spikes in a burst from one to four increased almost linearly synaptic plasticity from depression to potentiation. While no net change was observed with two spikes (99 ± 15%, n = 11), significant potentiation was observed with three (116 ± 6%, n = 8) and four spikes (135 ± 13, n = 7; Fig. 4A). In contrast, no potentiation was induced with three postsynaptic spikes in 1.3 mM external Ca²⁺ (88 ± 7%, n = 7; Fig. 4B).

Fig. 4.

Recovery of t-LTP with increasing spike number. (A) Role of postsynaptic spike number for inducing synaptic changes by a pre-post protocol at +10 ms in 1.8 mM extracellular calcium. With only one action potential (blue), t-LTD is induced. With two action potentials (red), on average, no plasticity is induced. Note the large variability in the plasticity. With three (green) or four (purple) action potentials, t-LTP is induced. The increase in the number of postsynaptic action potential allows t-LTP to be restored. (B) Role of postsynaptic spike number for inducing synaptic changes by a pre-post protocol at +10 ms in 1.3 mM extracellular calcium. With only one action potential (black), no plasticity is induced. With three action potentials (orange), t-LTP does not recover. *P < 0.01; n.s., not significant.

To understand why increasing spike number in 1.3 mM did not recover t-LTP, we performed calcium imaging in dendritic spines upon positive pairings with one, two, three, and four spikes. While in 3 mM calcium a clear increase in calcium signal was observed when spike number was increased (for two spikes: 146 ± 17%, for three spikes: 230 ± 38%, and for four spikes: 261 ± 49% of the calcium signal obtained for one spike; SI Appendix, Fig. S1), no calcium rise was observed in 1.3 mM (for two spikes: 89 ± 7%, for three spikes: 89 ± 7%, and for four spikes: 99 ± 4% of the calcium signal obtained for one spike; SI Appendix, Fig. S1), thus confirming the fact that, in physiological conditions, intracellular calcium transients are considerably reduced.

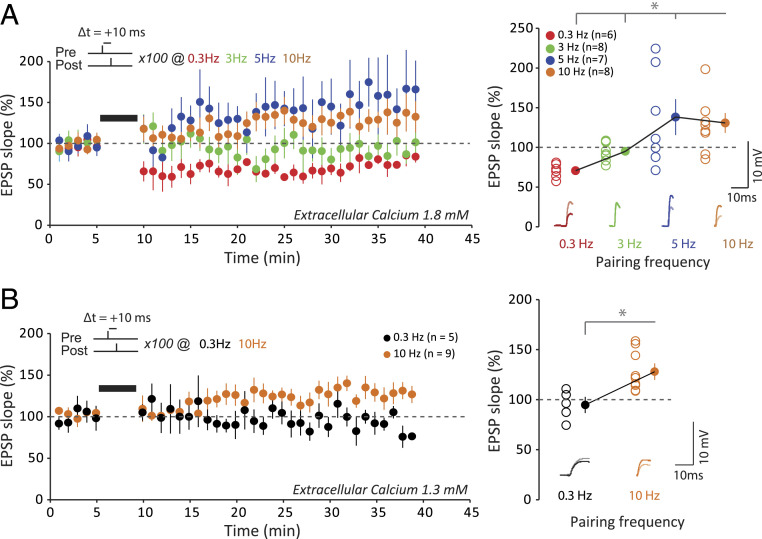
We next increased the frequency of single-spike pairing from 0.5 Hz to 3–10 Hz in physiological external Ca²⁺. While no net change was observed when the frequency of stimulation was increased to 3 Hz (95 ± 4%, n = 8), significant potentiation was observed with 5 (138 ± 17%, n = 7) or 10 Hz (131 ± 9%, n = 8) in 1.8 mM external Ca²⁺ (Fig. 5A). Increasing the frequency of stimulation to 10 Hz also allowed to recover t-LTP in 1.3 mM external Ca²⁺ (129 ± 9%, n = 9; Fig. 5B). We conclude that while STDP rules are strongly altered, t-LTP can be restored either by increasing the postsynaptic spike number or single-spike pairing frequency in physiological Ca²⁺.

Fig. 5.

Recovery of t-LTP with increasing pairing frequency. (A) Effects of the stimulation frequency on synaptic changes induced by a pre-post protocol at +10 ms with a single postsynaptic action potential in 1.8 mM extracellular calcium. For 0.3 Hz, t-LTD is induced. For 3 Hz, no synaptic changes are induced. For 5 or 10 Hz, t-LTP is induced. Increasing the pairing frequency restores t-LTP. To facilitate the comparison between the data, the first time point after pairing at 3, 5, and 10 Hz has been set to that at 0.3 Hz. *P < 0.02. (B) Effects of the stimulation frequency on synaptic changes induced by a pre-post protocol at +10 ms with a single postsynaptic action potential in 1.3 mM extracellular calcium. For 0.3 Hz, no synaptic change is induced. For 10 Hz, t-LTP is induced. Increasing the pairing frequency restores t-LTP. To facilitate the comparison between the data, the first time point after pairing at 10 Hz has been set to that at 0.3 Hz. *P < 0.01.

Recovery of t-LTD at Negative Delays in 1.3 mM Calcium.

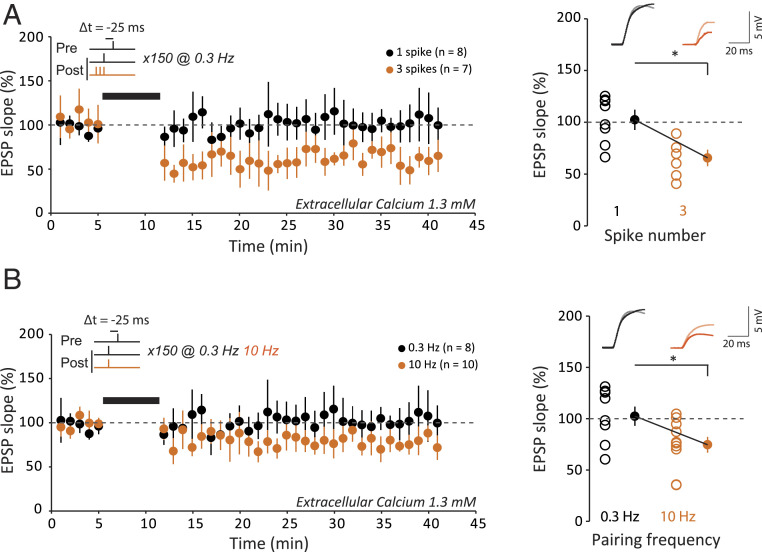
While t-LTD induced by negative delays was observed at the upper limit of the physiological calcium range (i.e., 1.8 mM), it was absent in 1.3 mM external Ca²⁺ (106 ± 14%, n = 10; Fig. 6A). We therefore examined the conditions for restoring t-LTD in 1.3 mM Ca²⁺ at negative delays. When the number of postsynaptic spikes was increased up to three during the pairing (delay of −25 ms), significant t-LTD was found to be induced (61 ± 7%, n = 7, MW P < 0.01; Fig. 6A). Similarly, when the pairing frequency was increased from 0.3 to 10 Hz, significant t-LTD was restored (75 ± 6%, n = 9, MW P < 0.01; Fig. 6B). We conclude that normal STDP profile can be restored even in 1.3 mM Ca²⁺ by either increasing the number of postsynaptic spikes during the pairing or the pairing frequency to 10 Hz.

Fig. 6.

Recovery of t-LTD in 1.3 mM. (A) Role of postsynaptic spike number on synaptic changes induced by a post-pre protocol at −25 ms at a pairing frequency of 0.3 Hz in 1.3 mM extracellular calcium. For a single action potential, no change is induced (black). For three action potentials, t-LTD is induced (orange). Thus, increasing the number of postsynaptic action potentials allows t-LTD to recover. *P < 0.01. (B) Effects of stimulation frequency on the induction of synaptic plasticity by a post-pre protocol at −25 ms with a single postsynaptic action potential in 1.3 mM extracellular calcium. For 0.3 Hz, no change is induced (black). For 10 Hz, t-LTD is induced (orange). Thus, increasing pairing frequency allows t-LTD to recover. To facilitate the comparison between the data, the first time point after pairing at 10 Hz has been set to that at 0.3 Hz. *P < 0.01.

Calcium-Based Synaptic Plasticity Model.

We built a calcium-based model to quantitatively account for the experimental findings (see SI Appendix for details of the model). Model parameters were fit to the results of the spike-pair protocols at a low pairing frequency, and the model was then validated by making predictions for the burst and high-frequency protocols. Following ref. 26, our model describes two variables: the intracellular calcium transients in the postsynaptic spine resulting from the pre- and postsynaptic activity and the dynamics of the synaptic efficacy (or synaptic weight).

Calcium fluxes mediated by NMDA receptors and VDCC are modeled as discrete jumps following each pre- and postsynaptic spike, respectively. The transients decay with timescale τ_Ca, and their amplitudes are C_pre and C_post (SI Appendix). The extracellular calcium concentration enters our model only through scaling exponents a_pre and a_post of the amplitude parameters $C_{\text{pre}}\propto {\left[C{a}^{2+}\right]}^{a_{\text{pre}}}$, $C_{\text{post}}\propto {\left[C{a}^{2+}\right]}^{a_{\text{post}}}$. These exponents allow our model to account for the complex direct and indirect effects of the extracellular calcium concentration on the calcium transient, while remaining mathematically tractable for the purposes of fitting the model to data. Directly, higher concentration leads to increased calcium ion flux upon opening of Ca²⁺ channels. There are also indirect effects including, for example, the dependence of neurotransmitter release probability on [Ca²⁺] (31), which in turn affects the postsynaptic transients.

The model is characterized by a second variable, the synaptic weight, that increases at rate γ_p when the calcium transient c(t) crosses the potentiation threshold θ_p and decreases with rate γ_d when c(t) crosses the depression threshold θ_d. This is consistent with the notion that high levels of calcium lead to t-LTP, whereas intermediate levels lead to t-LTD (25, 32, 33). We assumed that synaptic weight dynamics are graded; i.e., any value of the weight between a lower and upper bound is stable (SI Appendix).

A hallmark of the biophysics of calcium entry is its nonlinearity: when pre- and postsynaptic neurons are coactive, calcium transients are markedly larger than what would be expected due to the sum of independent contributions (16, 34, 35). This nonlinearity was characterized in the model by a single parameter, η. It is known that calcium transients attributed to nonlinear processes (such as dendritic NMDA spikes) decay on a longer timescale than transients following single spikes (35, 36), so the nonlinear term decays with timescale τ_Ca,NMDA > τ_Ca (SI Appendix). Unless noted otherwise, the intracellular calcium transient c(t) is the sum of the above three contributions: pre- and postsynaptic, and the nonlinear term.

Nonlinear Calcium Transients Are Necessary to Account for Plasticity at Multiple Extracellular Calcium Concentrations.

A model where calcium dynamics are linear, i.e., pre- and postsynaptic activity contribute to c(t) independently, is qualitatively consistent with the results of our plasticity experiments: the same relative timing of a pair of pre- and postsynaptic spikes may lead to high, intermediate, and low levels of transient intracellular calcium at [Ca²⁺] = 3, 1.8, and 1.3 mM; potentially leading to t-LTP, t-LTD, and no plasticity, respectively (see SI Appendix, Fig. S2 for illustration of the calcium transients). Furthermore, the linear model was shown to accurately fit plasticity experiments at a single calcium concentration (26).

We therefore asked whether such a model could quantitatively fit the data at multiple extracellular concentrations. We find that a linear model does not account for a number of important features of the data (SI Appendix, Fig. S3). In particular, the inferred decay timescale of calcium is long (τ_Ca = 76 ms; see SI Appendix, Tables S1 and S2 for full list of model parameter values), so at 3 mM (SI Appendix, Fig. S3A, Top) the model predicts significant changes to synaptic weights even when the pre- and postsynaptic spikes are separated by more than 100 ms, inconsistent with our data as well as other experiments (6, 29). Furthermore, the long decay timescale and the small difference between the depression and potentiation thresholds imply that under many protocols with multiple postsynaptic spikes, or at high pairing frequencies, the synaptic weight saturates to its upper bound. In the experiment, the same protocols resulted in t-LTD, leading to large inaccuracies in the predictions (SI Appendix, Fig. S3 B and C). This model also failed to reproduce the dependence of calcium entry on the extracellular calcium concentration measured in imaging experiments (SI Appendix, Fig. S4) unless nonrealistic scaling exponents (a_pre, a_post) were used (SI Appendix).

A Nonlinear Calcium-Based Model Generates Accurate Predictions for Postsynaptic Burst and High-Frequency Induction Protocols.

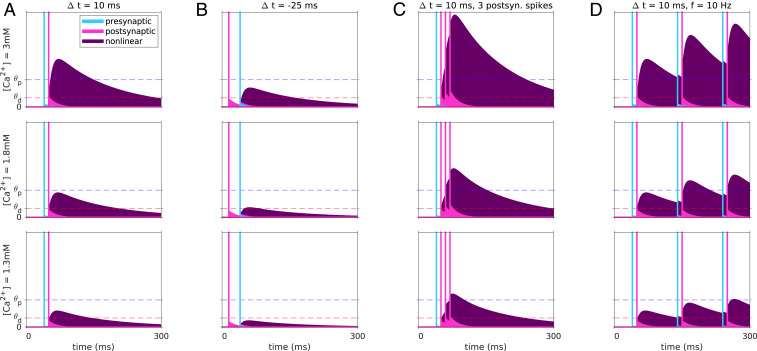
We therefore focus henceforth on models that include a nonlinear contribution to calcium transients (Fig. 7). Here, the inferred decay timescale of transients originating from a single neuron is short (τ_Ca = 18 ms; see SI Appendix, Table S1), which implies that pre- and postsynaptic spikes must be relatively close in time to elicit a transient that exceeds the potentiation and depression threshold. Thus, significant changes to synaptic weights in STDP protocols are restricted to Δt between −50 and 50 ms (for pre-post pairs, Fig. 8A). The model correctly captures the dependence of plasticity on the number of spikes in a postsynaptic burst, and on its timing (Fig. 8B). Specifically, our model correctly predicts that at [Ca²⁺] = 1.8 mM, increasing the number of postsynaptic spikes that follow a presynaptic spike from one to four leads to a change in the direction of plasticity from t-LTD to t-LTP, and that a single presynaptic spike followed by a burst of three postsynaptic spikes leads to t-LTP, while the reverse order of the same stimulation pattern leads to t-LTD.

Fig. 7.

Dependence of calcium transients of nonlinear plasticity model on the stimulation protocol and on the extracellular calcium concentration. Example model calcium transients resulting from a single pre-post pairing at Δt = 10 ms (A) and Δt = −25 ms (B), a presynaptic spike paired with a burst of three postsynaptic spikes (C), and a pre-post pair repeated at a frequency of 10 Hz (D). Transients for all stimulation protocols are shown for the three extracellular calcium concentrations used in the experiment (rows). The linear pre- and postsynaptic contributions are shown in cyan and magenta, respectively, together with the spike times indicated by the vertical lines. The nonlinear contribution is shown in purple. The transients depend strongly on the relative timing of pre- and postsynaptic activity, primarily due to the model’s nonlinearity. The long decay timescale of the nonlinear term implies that calcium returns to baseline slowly and thus may accumulate for induction protocols with high pairing frequencies.

Fig. 8.

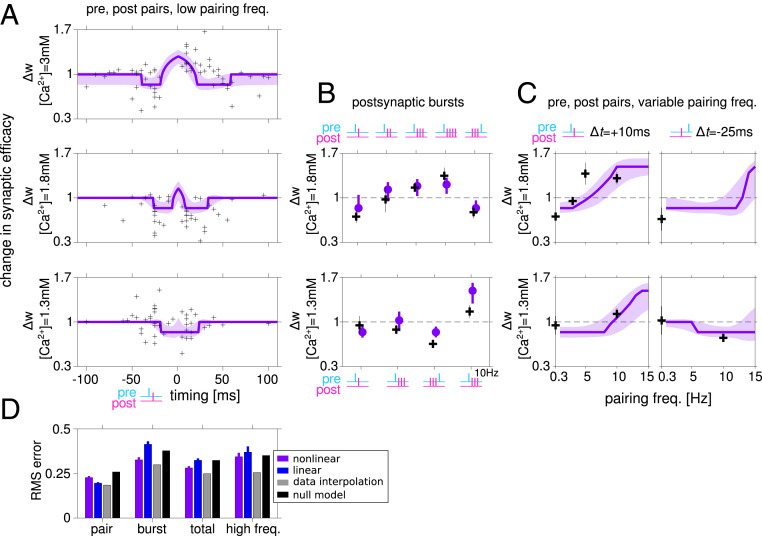
A nonlinear calcium-based plasticity model fits well the plasticity results at multiple concentrations and using multiple induction protocols. (A) Model fit to the STDP data at [Ca²⁺] = 3, 1.8, and 1.3 mM (purple). Each measured synapse is represented by a black cross. Shaded area indicates the SD around the mean obtained by generating predictions using parameter sets in the neighborhood of the best fitting model (SI Appendix). (B) Experimental results and model predictions for protocols with postsynaptic burst stimuli. At [Ca²⁺] = 1.8 mM (Top), the model captures the change in sign of plasticity as a function of the number of spikes in the postsynaptic burst, and the reverse in sign when a postsynaptic burst of three spikes precedes a presynaptic spike. At [Ca²⁺] = 1.3 mM (Bottom), LTD is restored at a low pairing frequency by a burst of three postsynaptic spikes (regardless if they arrive closely before or after the presynaptic spike), compared to a spike-pair protocol where no significant change was observed, which is captured by the model. (C) Experimental results and model predictions for protocols at variable pairing frequencies. For spike pair protocols with Δt = 10 ms, the resulting plasticity depends strongly on the pairing frequency. At [Ca²⁺] = 1.8 mM (Top) the model accurately predicts the frequency at which plasticity switches sign. At [Ca²⁺] = 1.3 mM the model correctly predicts the change in sign of plasticity when pre- and postsynaptic spikes are paired at 10 Hz with positive/negative relative timing. (D) Root mean square (RMS) errors when the model predictions are compared to the spike-pair data, the bust data (only at a low pairing frequency of 0.3 Hz), and measurements of plasticity using high-frequency pairing protocols. Total error refers to the combined error for spike-pair and burst stimuli (at a low pairing frequency). Note that the model was fit using the spike-pair data. Among all fitted parameter sets, this figure shows results for the model with lowest combined spike-pair and burst protocols. Results from high-frequency protocols (C and parts of B) were not used in fitting or model selection. See SI Appendix, Fig. S6 for fit and predictions of the model with lowest RMS error on spike-pair data. Error bars for model results, predictions, and errors (D) are equal to the SD of the RMS error computed 200 times on subsets (80% of the data chosen randomly) of data points. Gray bars show estimates of the variability of the data, and black bars show the errors made by a null model (SI Appendix, Table S4).

Furthermore, owing to the long decay timescale associated with the nonlinear term (τ_Ca,NMDA = 129 ms), the model correctly predicts the frequency dependence of plasticity (Fig. 8C; these data points were not used in fitting; see SI Appendix). At [Ca²⁺] = 1.8 mM it correctly predicts the frequency at which a protocol with pair of spikes with Δt = 10 ms switches from t-LTD to t-LTP (Fig. 8C, Top), and at [Ca²⁺] = 1.3 mM it correctly predicts the difference in sign of plasticity between protocols with Δt = 10 and −25 ms (Fig. 8C, Bottom).

The inferred model suggests that changes to synaptic efficacy induced by the STDP protocol (controlled by the rates γ_p, γ_d) are large relative to the range of possible efficacy values (w_max − w_min). Such saturation leads to an STDP curve with a square shape (Fig. 7) and suggests that a smaller number of pairings could be sufficient to induce saturation, especially to the lower bound of a synapse’s efficacy. This is consistent with experimental tests of the possible discrete nature of plasticity in these synapses (37, 38). This abrupt switch between t-LTD and t-LTP is nevertheless consistent with the typical smooth shape of STDP curves, if heterogeneities are included (Fig. 2 B–D). To show that, we generated STDP curves by randomly varying the model parameters around the best fitting set (SI Appendix) and plotted 1 SD above and below the average STDP curve, yielding a curve similar to the experimental one (Fig. 8A, light purple shaded region). This reflects the fact that each point in our dataset corresponds to a measurement of a different synapse and suggests that the parameters found by our fitting procedure are not fine-tuned.

Importantly, model parameters were fit to the STDP results (i.e., plasticity resulting from pre-post pairs at different Δt), while satisfying constraints imposing consistency with the dependence of the total calcium entering the cell on the extracellular concentration (SI Appendix, Fig. S4 B and C). The mathematical form of these constraints was derived analytically based on the model structure, and the values used in the inequalities were based on our imaging experiments (SI Appendix). Imposing such constraints on the model parameters led to a small increase of the fitting error (SI Appendix, Figs. S5 and S6 and Tables S1 and S2). However, interestingly, constraints based on imaging experiments yield models with more realistic windows for induction of STDP (SI Appendix, Figs. S5A and S6A, Top) and more accurate predictions for the frequency dependence of plasticity (Fig. 8D and SI Appendix, Figs. S5D and S6D).

Residual t-LTD at [Ca²⁺] = 1.3 mM.

The STDP curve at the lowest concentration we measured showed nonstatistically significant LTD at positive relative timing (Fig. 2E; see results for [Ca²⁺] = 1.3 mM, Δt = +10 ms). The models we inferred from the data show a small window for the induction of LTD at 1.3 mM (Fig. 8A, Bottom). We used the model to predict the maximum concentration of calcium for which a pair of spikes at timing Δt = +10 ms will not lead to transient calcium crossing the depression threshold and found that to be [Ca²⁺] = 1.13 mM. We note that the window for induction of t-LTD exhibited by our model is consistent with the data, when the variability is taken into account (Fig. 8A, Bottom). Models constrained to exhibit no t-LTD at [Ca²⁺] = 1.3 mM fit poorly to the STDP curves at higher concentrations (not shown).

Discussion

External calcium in the brain displays small variations with age, sleep–wake cycle, or anesthesia. During development, external calcium declines from ∼1.6 mM in neonates to ∼1.2 mM in adult anesthetized rats (22). Anesthesia elevates calcium by 0.26 mM in adult mice (24), and the transition from sleep to wakefulness increases external calcium by 0.11 mM (24). Thus, the lower value for calcium concentration (1.3 mM) used in our experiments is close to the values that are measured in vivo in a broad range of conditions, while the upper value (1.8 mM) is an upper bound that can only be approached in specific conditions (anesthesia and/or sleep in young animals).

t-LTP and Physiological External Calcium.

We report here that t-LTP could not be induced by positive correlation between single pre- and postsynaptic spikes in physiological external calcium. Rather, t-LTD and no plasticity were respectively induced at 1.8 and 1.3 mM calcium. It is noteworthy that for positive delay (+5/+25 ms), the synaptic plasticity goes from no change at the lower limit of calcium range (1.3 mM) through a depression phase at the upper limit of calcium range (1.8 mM) before reaching the potentiation level for nonphysiological, high calcium (2.5 and 3 mM). Such a biphasic behavior was predicted by calcium-based models of synaptic plasticity (25, 26, 32).

t-LTP at positive delay could be restored in physiological calcium by either increasing the number of postsynaptic spikes from one to three or four (at 1.8 but not at 1.3 mM calcium) or by increasing the pairing frequency from 0.3 to 10 Hz (at 1.3 or 1.8 mM calcium). Such recovery of t-LTP had been already reported in previous studies (18, 30), but the data reported in these studies were obtained in nonphysiological calcium and in the absence of synaptic inhibition. This finding suggests that the minimal paradigm for inducing robust t-LTP in vivo would be to pair EPSPs associated with spike bursting at theta frequency. In fact, this type of pairing has been shown to induce synaptic potentiation of thalamocortical EPSPs in the cat visual cortex in vivo (39). Similarly, the synaptic potentiation that accounts for asymmetric receptive fields of hippocampal place cells results from repeated coincident activation of pre- and postsynaptic neurons (40). In addition, the synaptic potentiation thought to account for optimal orientation shift in visual cortical neurons can be explained by the high firing frequency of postsynaptic neurons during pairing with visual stimuli (41).

t-LTD and Physiological External Calcium.

At 3 mM calcium, t-LTD was induced by negative delays (−5/−50 ms) and positive delays (+40/+60 ms). This second t-LTD window has been predicted by calcium-based models (25, 26, 42) and had been reported previously in a few experimental studies in which calcium transients were enhanced by spike broadening (8, 13) or by multiple spike pairing at 5 Hz (18).

t-LTD was also observed for both negative and positive delays at 1.8 mM, but no significant t-LTD was observed for negative delays (−5/−25 ms) at 1.3 and 1.5 mM calcium, indicating that the threshold for t-LTD is between 1.5 and 1.8 mM calcium for negative delays. Nevertheless, t-LTD could be restored at 1.3 mM calcium when the number of postsynaptic spikes was increased from 1 to 3, suggesting that the threshold for t-LTD is reached with three but not with one postsynaptic action potential. Such synaptic depression is thought to occur in vivo at horizontal connections in the visual cortex when preferred orientation precedes a nonpreferred orientation by 10 ms because the postsynaptic neurons are firing at high frequency in response to preferred orientation (41).

Comparison of Experimental Data and Calcium-Based Models.

The successive transitions from an STDP curve with both t-LTD and t-LTP first to a curve with t-LTD only, and then to a curve with no plasticity as calcium concentration is lowered, are generic predictions of calcium-based models in which potentiation occurs at high calcium concentrations, while depression occurs at intermediate calcium concentrations (25, 26). Furthermore, these models also generically predict that increasing frequency or number of spikes in a burst will lead eventually to t-LTP (25, 26). Here, we have a made a major step beyond these generic predictions, by fitting quantitatively experimental data at various calcium concentrations with variants of calcium-based synaptic plasticity models (linear and nonlinear). The data reported here measured at multiple concentrations allowed us to show that nonlinear summation of transient calcium contributions is necessary to reproduce quantitatively the experimental findings. We chose the nonlinear interaction term to be quadratic for simplicity. This nonlinearity describes in a schematic fashion the biophysical properties of the NMDA receptor, that needs a coincidence of both presynaptic (for glutamate binding) and postsynaptic (for magnesium block relief) activity in order to maximize opening probability. It has been directly observed in calcium-imaging experiments (16, 34) and is necessary to explain our own imaging experiments, comparing calcium transients following positive and negative timings (Fig. 3 and SI Appendix, Figs. S1 and S4).

Furthermore, we found the nonlinear term should have a decay timescale of ∼100 ms (longer than that of transients due to pre- or postsynaptic activity alone, ∼20 ms) for the model to make accurate predictions for high pairing-frequency protocols. These conclusions are consistent with a recent study showing that dendritic NMDA spikes following coincident stimulation of pre- and postsynaptic activity lead to calcium transients that decay slowly and that blocking these NMDA spikes abolishes t-LTP measured in the control protocol (35). Note, however, that these experiments were carried out in recurrent CA3 synapses and not in CA3 to CA1 synapses.

These results call for a radical reevaluation of classic “STDP rules” (and of the experimental conditions under which they are measured), in which pairs of single pre- and postsynaptic spikes modify synaptic efficacy; rather, they show that such pairs (even if repeated many times at low frequency) are not likely to elicit any changes of synaptic strength in physiological conditions. They indicate that plasticity can only be triggered when bursts of spikes are used, or neurons fire at sufficiently high frequency, and invalidate popular phenomenological models of STDP in which plasticity is triggered by pairs of single pre- and postsynaptic spikes. Qualitatively similar findings have been obtained in synaptic plasticity experiments in granule cell to Purkinje cell synapses, where bursts of presynaptic spikes are required to induce both t-LTD (42) and t-LTP (43), and in area robust nucleus of arcopallium of songbirds (44). In cortical slices, it has been shown that pairing single spikes at low frequencies only induces t-LTD but not t-LTP (17). In the hippocampus, pairing at frequencies higher than 5 Hz results in t-LTP induction independent of the timing (45, 46). Furthermore, the dependence of synaptic plasticity on firing frequency we found is consistent with experimental data in cortex (17) and synaptic plasticity rules such as the Bienenstock–Cooper–Munro rule (47), as well as synaptic plasticity rules inferred from in vivo data (48).

CA3 and CA1 pyramidal neurons recorded in rats at rest fire single spikes in ∼80% and bursts in 20% of events (49). Therefore, the configuration of single pre- and postsynaptic spikes is expected to be predominant (probability of 0.64), whereas the configuration with pre- or postsynaptic bursts represents a minority (probability of 0.16). Burst firing in CA1 neurons decreases to 15% during spatial exploration (49), indicating that single-spike firing is by far the most probable in vivo. Our results therefore suggest that synaptic plasticity would not occur continuously when single pre- and postspikes are elicited but only during specific phases where the postsynaptic cell is firing at high rate or bursting (50).

Beyond spiking activity, plateau potentials in CA1 neurons have been shown to reliably lead to potentiation and the creation of a new place field even when the preceding presynaptic activity occurs up to a second before it (51). The large calcium influx during the plateau potential suggests that it might be possible to construct a biophysical, calcium-based model that will parsimoniously describe plasticity due to both spiking activity and plateau potentials in the hippocampus.

Distinct types of STDP curves have been reported in different cell types and/or brain structures (52). Calcium-based models have been shown to be able to reproduce the whole diversity of experimentally observed curves by varying the potentiation and depression thresholds (26), Thus, we predict that in all these cell types and structures, the effect of lowering calcium concentration should lead to similar outcomes as we have observed in CA1 pyramidal cells. In cases where the potentiation threshold is higher than the depression threshold, one should first see a disappearance of t-LTP and then a disappearance of t-LTD, both of which could be rescued by using bursts and/or high-frequency spike patterns. When the depression threshold is higher than the potentiation threshold (as in cerebellar Purkinje cells; see refs. 43 and 53), the opposite should occur—first disappearance of t-LTD, then t-LTP.

A potential functional consequence of the lack of synaptic plasticity for pairs of single spikes of pre- and postsynaptic neurons at low frequencies would be to make synaptic connectivity much more stable with respect to spontaneous activity than what models implementing standard spike-timing–dependent plasticity would predict (see also ref. 54). This would lead to a scenario in which synaptic connectivity can only be modified by a coincidence of presynaptic activity and prominent spike patterns (bursts, high frequency) and/or plateau potentials at the postsynaptic neuron, but would then remain stable over long time periods during background activity.

Methods

Acute Slices of Rat Hippocampus.

Hippocampal slices were obtained from 14- to 20-d-old rats according to institutional guidelines (Directive 86/609/EEC and French National Research Council) and approved by the local health authority (#D1305508, Préfecture des Bouches-du-Rhône, Marseille). Rats were deeply anesthetized with chloral hydrate (intraperitoneal 400 mg/kg) and killed by decapitation. Slices (350 µm) were cut in an N-methyl-d-glucamine (NMDG) solution (in mM: 92 NMDG, 2.5 KCl, 1.2 NaH₂PO₄, 30 NaHCO₃, 20 Hepes, 25 glucose, 5 sodium ascorbate, 2 thiourea, 3 sodium pyruvate, 10 MgCl₂, 0.5 CaCl₂) on a vibratome (Leica VT1200S) and were transferred at 32 °C in NMDG solution for 20 min before resting for 1 h at room temperature in oxygenated (95% O₂/5% CO₂) artificial cerebrospinal fluid (ACSF; in mM: 125 NaCl, 2.5 KCl, 0.8 NaH₂PO₄, 26 NaHCO₃, × CaCl₂, × MgCl₂, and 10 d-glucose). The ratio of CaCl₂ and MgCl₂ concentration was maintained constant to stabilize presynaptic release probability (55, 56), and external Ca²⁺ concentration was set to either 3 mM (Mg²⁺: 2 mM), 1.8 mM (Mg²⁺: 1.2 mM), or 1.3 mM (Mg²⁺: 0.9 mM). For recording, slices were transferred to a temperature-controlled (30 °C) chamber with oxygenated ACSF.

Organotypic Slices of Rat Hippocampus.

Postnatal day 5–7 Wistar rats were deeply anesthetized by intraperitoneal injection of chloral hydrate, the brain was quickly removed, and each hippocampus was dissected. Hippocampal slices (350 µM) were placed on 20-mm latex membranes (Millicell) inserted into 35-mm Petri dishes containing culture medium and maintained for up to 21 d in an incubator at 34 °C 95% O₂–5% CO₂ (57). The culture medium contained (in mL) 25 minimum essential media (MEM), 12.5 Hank's balanced salt solution (HBSS), 12.5 Horse serum, 0.5 penicillin/streptomycin, 0.8 glucose (1 M), 0.1 ascorbic acid (1 mg/mL), 0.4 Hepes (1 M), 0.5 B27, and 8.95 sterile H₂O. To avoid glial proliferation, 5 µM Ara-C was added to the medium at 3 d in vitro (DIV) for one night. Pyramidal cells from the CA1 area were recorded at 8–10 DIV.

Electrophysiology.

Neurons were identified with an Olympus BX-50WI microscope using differential interference contrast ×60 optics. Whole-cell recordings were made from CA1 pyramidal neurons; electrodes were filled with a solution containing the following (in mM): 120 K-gluconate, 20 KCl, 10 Hepes, 2 MgCl₂6H₂O, and 2 Na₂ATP. The pipette resistance was 8–10 MΩ to better preserve the integrity of intracellular signaling (58). Stimulating pipettes filled with extracellular saline were placed in the stratum radiatum (Schaffer collaterals). In control and test conditions, EPSPs were elicited at 0.1 Hz by a stimulation isolator unit (A385, World Precision Instruments). Access resistance was monitored throughout the recording, and only experiments with stable resistance were kept (changes < 20%).

Acquisition and Data Analysis.

Recordings were obtained using a Multiclamp 700B (Molecular Devices) amplifier and pClamp10.4 software. Data were sampled at 10 kHz, filtered at 3 kHz, and digitized by a Digidata 1440A (Molecular Devices). All data analyses were performed with custom written software in Igor Pro-6 (Wavemetrics). EPSP slope was measured as an index of synaptic strength. Pooled data are presented as mean ± SEM. Statistical comparisons were made using Wilcoxon or Mann–Whitney U test as appropriate with Sigma Plot software. Data were considered as significant when P < 0.05.

STDP Induction Protocols.

After obtaining a stable EPSP baseline for a period of 10–15 min, single EPSPs were paired with single spikes with a delay varying between −100 and +100 ms. Each pairing was repeated 100 times for positive pairings and 150 times for negative pairings (29). The number of postsynaptic spikes and the pairing frequency were adjusted depending on the experiment. Postsynaptic spikes were evoked by a brief somatic current pulse. EPSP slopes were monitored at least for 20 min after each pairing episode. Values of synaptic change were measured between 15 and 25 min after pairing.

Calcium Imaging.

CA1 pyramidal neurons from organotypic slice cultures of hippocampus were imaged with an LSM-710 Zeiss confocal microscope (59). For imaging calcium in the spine, 50 µM Alexa-594 and 250 µM Fluo-4 (Invitrogen) were added to the pipette solution. Alexa-594 fluorescence was used to reveal neuronal morphology, whereas fluorescence signals emitted by Fluo-4 were used for calcium imaging. Laser sources for fluorescence excitation were set at 488 nm for Fluo-4 and 543 nm for Alexa-594. Emitted fluorescence was collected between 500 and 580 nm for Fluo-4 and between 620 and 750 nm for Alexa-594. After whole-cell access, the dyes were allowed to diffuse for at least 10 min before acquisition of fluorescence signals. A stimulating pipette was positioned near the dendritic spine selected for imaging in order to elicit a postsynaptic response. EPSPs were evoked, and action potentials were elicited by a pulse of depolarizing current. Electrophysiological signals were synchronized with calcium imaging in line-scan mode. Acquired Fluo-4 (G) and Alexa-594 (R) signals were converted to ΔG/R values, and peak amplitudes were measured with a custom-made software (LabView, National Instruments).

Synaptic Plasticity Model.

Parameter definitions of the model, equations for the temporal evolution of calcium transients, and a detailed description of how these are used to fit the model to data are included in SI Appendix.

SI Appendix also includes a description of a number of model variants we considered and an analysis of qualitative and quantitative properties of the data supporting our modeling choices. Finally, it includes summary tables with the results of fitting the model to data.

Data Availability.

All study data are included in the article and SI Appendix.