A polynomial algorithm for best-subset selection problem

Significance

Best-subset selection is a benchmark optimization problem in statistics and machine learning. Although many optimization strategies and algorithms have been proposed to solve this problem, our splicing algorithm, under reasonable conditions, enjoys the following properties simultaneously with high probability: 1) its computational complexity is polynomial; 2) it can recover the true subset; and 3) its solution is globally optimal.

Abstract

Best-subset selection aims to find a small subset of predictors, so that the resulting linear model is expected to have the most desirable prediction accuracy. It is not only important and imperative in regression analysis but also has far-reaching applications in every facet of research, including computer science and medicine. We introduce a polynomial algorithm, which, under mild conditions, solves the problem. This algorithm exploits the idea of sequencing and splicing to reach a stable solution in finite steps when the sparsity level of the model is fixed but unknown. We define an information criterion that helps the algorithm select the true sparsity level with a high probability. We show that when the algorithm produces a stable optimal solution, that solution is the oracle estimator of the true parameters with probability one. We also demonstrate the power of the algorithm in several numerical studies.

Subset selection is a classic topic of model selection in statistical learning and is encountered whenever we are interested in understanding the relationship between a response and a set of explanatory variables. Naturally, this problem has been pursued in statistics and mathematics for decades. The classic methods that are commonly described in statistical textbooks include step-wise regression with the Akaike information criterion (1), the Bayesian information criterion (BIC) (2), and Mallows’s $C_p$ (3).

Consider $n$ independent observations $\left({\mathit{x}}_i,y_i\right),i=1,\dots ,n$, where ${\mathit{x}}_i\in {\mathbb{R}}^{1\times p}$, $y_i\in \mathbb{R}$. Let $\mathit{y}=\left(y_1,\dots ,y_n\right)$ and $\mathit{X}={\left({\mathit{x}}_1^{\top },\dots ,{\mathit{x}}_n^{\top }\right)}^{\top }$. For convenience, we centralize the columns of $\mathit{X}$ to have zero mean. The following is the classic multivariable linear model with regression coefficient vector $\mathit{\beta }\in {\mathbb{R}}^{p\times 1}$ and error vector $\mathit{ϵ}\in {\mathbb{R}}^{n\times 1}$:

$$\mathit{y}=\mathit{X}\mathit{\beta }+\mathit{ϵ}.$$ [1]

Parsimony is desired when we consider a subset of the $p$ explanatory variables in Model 1 with comparable prediction accuracy. When the regression coefficient vector $\mathit{\beta }$ is sparse, we want to identify this subset of nonzero coefficients. This is the commonly known problem of the best-subset selection that minimizes the empirical risk function, e.g., the sum of residual squares, under the cardinality constraint in Model 1,

$$\underset{\mathit{\beta }\in {\mathbb{R}}^p}{min}\frac{1}{2n}\Vert \mathit{y}-\mathit{X}{\mathit{\beta }\Vert }_2^2,\hspace{0.17em}\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\hspace{0.17em}\mathrm{t}\mathrm{o}\hspace{0.17em}\Vert {\mathit{\beta }\Vert }_0\le s,$$ [2]

where $\Vert {\mathit{\beta }\Vert }_0={\sum }_{i=1}^{p}I\left({\beta }_i\ne 0\right)$ is the ${\ell }_0$ norm of $\mathit{\beta }$, and the sparsity level $s$ is usually an unknown nonnegative integer.

The Lagrangian of Eq. 2 represents a balance between goodness of fit and parsimony. The latter is characterized by model complexity that is generally defined as an increasing function of the number of nonzero $\mathit{\beta }$ values. Thus, this Lagrangian is not continuous and, of course, not smooth. Greedy methods are usually applied to solve such Lagrangian but suffer from computational difficulties even for a reasonably large $p$. Alternatively, some relaxation methods, e.g., Least-Absolute Shrinkage and Selection Operator (LASSO) (4), Adaptive LASSO (5), Smoothly Clipped Absolute Deviation Penalty (SCAD) (6), and Minimax Concave Penalty (MCP) (7) have been proposed and investigated to ameliorate the computational issue by replacing the nonsmooth penalty function with a smooth approximation. These recently developed methods are computationally feasible and provide near-optimal solutions even for large $p$. However, their solutions do not lead to the best subset and are known for lack of important statistical properties (8).

There has been little progress on how to find the best-subset selection until recently because such a nonsmooth optimization problem is generally nondeterministic polynomial-time–hard (9). Recently, to make the best-subset selection problem computationally tractable, optimization strategies and algorithms are proposed, including the Iterate Hard Thresholding (IHT) algorithm (10), primal-dual active set (PDAS) methods (11), and the Mixed Integer Optimization (MIO) approach (12). However, their solutions may converge to a local minimizer, and IHT and PDAS may also suffer from the periodic iterative issue. More importantly, these methods do not determine the sparsity-level adaptively, and their statistical properties remain unclear.

In this paper, we directly deal with Eq. 2 and solve the best-subset selection problem with two critical ideas: a splicing algorithm and an information criterion. Our contribution is threefold. Firstly, we propose “splicing,” a technique to improve the quality of subset selection, and derive an efficient iterative algorithm based on splicing, Adaptive Best-Subset Selection (ABESS), to tackle problem 2. The ABESS algorithm is applicable to analyze high dimensional datasets with tens of thousands of observations and variables. Secondly, we prove that ABESS algorithm consistently selects important variables and its computational complexity is polynomial. Our algorithm is stringently shown to solve problem 2 within polynomial times. Finally, to determine the most suitable sparsity level, we design an information criterion (special information criterion [SIC]) whose theoretical best-subset selection consistency is rigorously proven.

We define some useful notations for the content below. For $\mathit{\beta }={\left({\beta }_1,\dots ,{\beta }_p\right)}^{\top }\in {\mathbb{R}}^p$, we define the ${\ell }_q$ norm of $\mathit{\beta }$ by $\Vert {\mathit{\beta }\Vert }_q={\left({\sum }_{j=1}^p|{\beta }_j{|}^q\right)}^{1/q}$, where $q\in \left[1,\infty \right)$. Let $\mathcal{S}=\left\{1,\dots ,p\right\}$, for any set $\mathcal{A}\subseteq \mathcal{S}$, denote ${\mathcal{A}}^c=\mathcal{S}\backslash \mathcal{A}$ as the complement of $\mathcal{A}$ and $\left|\mathcal{A}\right|$ as its cardinality. We define the support set of vector $\mathit{\beta }$ as $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left(\mathit{\beta }\right)=\left\{j:{\beta }_j\ne 0\right\}$. For an index set $\mathcal{A}\subseteq \left\{1,\dots ,p\right\}$, ${\mathit{\beta }}_{\mathcal{A}}=\left({\beta }_j,j\in \mathcal{A}\right)\in {\mathbb{R}}^{\left|\mathcal{A}\right|}$. For matrix $\mathit{X}\in {\mathbb{R}}^{n\times p}$, define ${\mathit{X}}_{\mathcal{A}}=\left(X_j,j\in \mathcal{A}\right)\in {\mathbb{R}}^{n\times \left|\mathcal{A}\right|}$. For any vector $\mathit{t}$ and any set $\mathcal{A}$, ${\mathit{t}}^{\mathcal{A}}$ is defined to be the vector whose $j$th entry ${\left({\mathit{t}}^{\mathcal{A}}\right)}_j$ is equal to $t_j$ if $j\in \mathcal{A}$ and zero otherwise. For instance, ${\widehat{\mathit{\beta }}}^{\mathcal{A}}$ is the vector whose $j$th entry is ${\widehat{\beta }}_j$ if $j\in \mathcal{A}$ and zero otherwise. ${\widehat{\mathbf{t}}}^{\left\{j\right\}}$ is the vector whose $j$th entry is ${\widehat{t}}_j$ and zero otherwise.

Method

Splicing.

In this section, we describe the splicing method. Consider the ${\ell }_0$ constraint minimization problem,

$$\underset{\mathit{\beta }}{min}{\mathcal{L}}_n\left(\mathit{\beta }\right),\hspace{0.17em}s.t\hspace{0.17em}\Vert {\mathit{\beta }\Vert }_0\le s,$$

where ${\mathcal{L}}_n\left(\mathit{\beta }\right)=\frac{1}{2n}\Vert \mathit{y}-\mathit{X}{\mathit{\beta }\Vert }_2^2$. Without loss of generality, we consider $\Vert {\mathit{\beta }\Vert }_0=s$. Given any initial set $\mathcal{A}\subset \mathcal{S}=\left\{\mathrm{1,2},\dots ,p\right\}$ with cardinality $\left|\mathcal{A}\right|=s$, denote $\mathcal{I}={\mathcal{A}}^c$ and compute

$$\widehat{\mathit{\beta }}=\arg \underset{{\mathit{\beta }}_{\mathcal{I}}=0}{min}{\mathcal{L}}_n\left(\mathit{\beta }\right).$$

We call $\mathcal{A}$ and $\mathcal{I}$ as the active set and the inactive set, respectively.

Given the active set $\mathcal{A}$ and $\widehat{\mathit{\beta }}$, we can define the following two types of sacrifices:

• 1)Backward sacrifice: For any $j\in \mathcal{A}$, the magnitude of discarding variable $j$ is,

$${\xi }_j={\mathcal{L}}_n\left({\widehat{\mathit{\beta }}}^{\mathcal{A}\backslash \left\{j\right\}}\right)\hspace{0.17em}-\hspace{0.17em}{\mathcal{L}}_n\left({\widehat{\mathit{\beta }}}^{\mathcal{A}}\right)=\frac{{\mathit{X}}_j^{\top }{\mathit{X}}_j}{2n}{\left({\widehat{\beta }}_j\right)}^2.$$ [3]

• 2)Forward sacrifice: For any $j\in \mathcal{I}$, the magnitude of adding variable $j$ is,

$${\zeta }_j={\mathcal{L}}_n\left(\widehat{{\mathit{\beta }}^{\mathcal{A}}}\right)-{\mathcal{L}}_n\left({\widehat{\mathit{\beta }}}^{\mathcal{A}}+{\widehat{\mathit{t}}}^{\left\{j\right\}}\right)=\frac{{\mathit{X}}_j^{\top }{\mathit{X}}_j}{2n}{\left(\frac{{\widehat{d}}_j}{{\mathit{X}}_j^{\top }{\mathit{X}}_j/n}\right)}^2,$$ [4]

where $\widehat{\mathit{t}}=\arg \underset{\mathit{t}}{min}{\mathcal{L}}_n\left({\widehat{\mathit{\beta }}}^{\mathcal{A}}+{\mathit{t}}^{\left\{j\right\}}\right),{\widehat{d}}_j={\mathit{X}}_j^{\top }\left(\mathit{y}-\mathit{X}\widehat{\mathit{\beta }}\right)/n$.

Intuitively, for $j\in \mathcal{A}$ (or $j\in \mathcal{I}$), a large ${\xi }_j$ (or ${\zeta }_j$) implies the $j$th variable is potentially important. Unfortunately, it is noteworthy that these two sacrifices are incomparable because they have different sizes of support set. However, if we exchange some “irrelevant” variables in $\mathcal{A}$ and some “important” variables in $\mathcal{I}$, it may result in a higher-quality solution. This intuition motivates our splicing method.

Specifically, given any splicing size $k\le s$, define

$${\mathcal{A}}_k=\left\{j\in \mathcal{A}:\sum _{i\in \mathcal{A}}\mathrm{I}\left({\xi }_j\ge {\xi }_i\right)\le k\right\}$$

to represent $k$ least relevant variables in $\mathcal{A}$ and

$${\mathcal{I}}_k=\left\{j\in \mathcal{I}:\sum _{i\in \mathcal{I}}\mathrm{I}\left({\zeta }_j\le {\zeta }_i\right)\le k\right\}$$

to represent $k$ most relevant variables in $\mathcal{I}$. Then, we splice $\mathcal{A}$ and $\mathcal{I}$ by exchanging ${\mathcal{A}}_k$ and ${\mathcal{I}}_k$ and obtain a new active set

$$\tilde{\mathcal{A}}=\left(\mathcal{A}\backslash {\mathcal{A}}_k\right)\cup {\mathcal{I}}_k.$$

Let $\tilde{\mathcal{I}}={\tilde{\mathcal{A}}}^c$, $\tilde{\mathit{\beta }}=\arg \underset{{\mathit{\beta }}_{\tilde{\mathcal{I}}}=0}{min}{\mathcal{L}}_n\left(\mathit{\beta }\right)$, and ${\tau }_s>0$ be a threshold. If ${\tau }_s<{\mathcal{L}}_n\left(\widehat{\mathit{\beta }}\right)-{\mathcal{L}}_n\left(\tilde{\mathit{\beta }}\right)$, then $\tilde{\mathcal{A}}$ is preferable to $\mathcal{A}$. The active set can be updated iteratively until the loss function cannot be improved by splicing. Once the algorithm recovers the true active set, we may splice some irrelevant variables, and then the loss function may decrease slightly. The threshold ${\tau }_s$ can reduce this unnecessary calculation. Typically, ${\tau }_s$ is relatively small, e.g., ${\tau }_s=0.01s\log \left(p\right)\log \left(\log n\right)/n$.

The remaining problem is to determine the initial set. Typically, we select the first $s$ variables that are most correlated with $\mathit{y}$ variables as the initial set $\mathcal{A}$. Let $k_{max}$ be the maximum splicing size, $k_{max}\le s$. In the following, we summarize our arguments in the above:

Algorithm 1: BESS.Fix($s$): Best-Subset Selection with a given support size $s$.
1) Input: $\mathit{X}$, $\mathit{y}$, a positive integer $k_{max}$, and a threshold ${\tau }_s$.
2) Initialize ${\mathcal{A}}^0=\left\{j:{\sum }_{i=1}^p\mathrm{I}\left(|\frac{{\mathit{X}}_j^{\top }\mathit{y}}{\sqrt{{\mathit{X}}_j^{\top }{\mathit{X}}_j}}\right.|\le |\frac{{\mathit{X}}_i^{\top }\mathit{y}}{\sqrt{{\mathit{X}}_i^{\top }{\mathit{X}}_i}}\le s\right\},{\mathcal{I}}^0={\left({\mathcal{A}}^0\right)}^c$,
and (${\mathit{\beta }}^0$, ${\mathit{d}}^0$):
${\mathit{\beta }}_{{\mathcal{I}}^0}^0=0$,
${\mathit{d}}_{{\mathcal{A}}^0}^0=0$,
${\mathit{\beta }}_{{\mathcal{A}}^0}^0={\left({\mathit{X}}_{{\mathcal{A}}^0}^{\top }{\mathit{X}}_{{\mathcal{A}}^0}\right)}^{-1}{\mathit{X}}_{{\mathcal{A}}^0}^{\top }\mathit{y}$,
${\mathit{d}}_{{\mathcal{I}}^0}^0={\mathit{X}}_{{\mathcal{I}}^0}^{\top }\left(\mathit{y}-\mathit{X}{\mathit{\beta }}^0\right)/n.$
3) For $m=\mathrm{0,1},\dots \hspace{0.17em}$, do
$$\left({\mathit{\beta }}^{m+1},{\mathit{d}}^{m+1},{\mathcal{A}}^{m+1},{\mathcal{I}}^{m+1}\right)=\text{Splicing}({\mathit{\beta }}^m,{\mathit{d}}^m,{\mathcal{A}}^m,{\mathcal{I}}^m,k_{max},{\tau }_s).$$
If $\left({\mathcal{A}}^{m+1},{\mathcal{I}}^{m+1}\right)=\left({\mathcal{A}}^m,{\mathcal{I}}^m\right)$, then stop
end for
4) Output $\left(\widehat{\mathit{\beta }},\widehat{\mathit{d}},\widehat{\mathcal{A}},\widehat{\mathcal{I}}\right)=\left({\mathit{\beta }}^{m+1},{\mathit{d}}^{m+1}{\mathcal{A}}^{m+1},{\mathcal{I}}^{m+1}\right)$.

Note that splicing size k is an important parameter in splicing. Typically, we can try all possible values of k≤s.

Algorithm 2: Splicing ($\mathit{\beta }$, $\mathit{d}$, $\mathcal{A}$, $\mathcal{I}$, $k_{max}$, ${\tau }_s$).
1) Input: $\mathit{\beta }$, $\mathit{d}$, $\mathcal{A}$, $\mathcal{I}$, $k_{max}$, and ${\tau }_s$.
2) Initialize $L_0=L=\frac{1}{2n}\Vert \mathit{y}-\mathit{X}{\mathit{\beta }\Vert }_2^2$, and set
${\xi }_j=\frac{{\mathit{X}}_j^{\top }{\mathit{X}}_j}{2n}{\left({\beta }_j\right)}^2,{\zeta }_j=\frac{{\mathit{X}}_j^{\top }{\mathit{X}}_j}{2n}{\left(\frac{d_j}{{\mathit{X}}_j^{\top }{\mathit{X}}_j/n}\right)}^2,j=1,\dots ,p$.
3) For $k=\mathrm{1,2},\dots ,k_{max}$, do
${\mathcal{A}}_k=\left\{j\in \mathcal{A}:{\sum }_{i\in \mathcal{A}}\mathrm{I}\left({\xi }_j\ge {\xi }_i\right)\le k\right\}$,
${\mathcal{I}}_k=\left\{j\in \mathcal{I}:{\sum }_{i\in \mathcal{I}}\mathrm{I}\left({\zeta }_j\le {\zeta }_i\right)\le k\right\}.$
Let ${\tilde{\mathcal{A}}}_k=\left(\mathcal{A}\backslash {\mathcal{A}}_k\right)\cup {\mathcal{I}}_k$, ${\tilde{\mathcal{I}}}_k=\left(\mathcal{I}\backslash {\mathcal{I}}_k\right)\cup {\mathcal{A}}_k$ and solve
${\tilde{\mathit{\beta }}}_{{\tilde{\mathcal{A}}}_k}={\left({\mathit{X}}_{{\tilde{\mathcal{A}}}_k}^{\top }{\mathit{X}}_{{\tilde{\mathcal{A}}}_k}\right)}^{-1}{\mathit{X}}_{{\tilde{\mathcal{A}}}_k}^{\top }y,\hspace{0.17em}{\tilde{\mathit{\beta }}}_{{\tilde{\mathcal{I}}}_k}=0,$
$\tilde{\mathit{d}}={\mathit{X}}^{\top }\left(\mathit{y}-\mathit{X}\tilde{\mathit{\beta }}\right)/n,\hspace{0.17em}{\mathcal{L}}_n\left(\tilde{\mathit{\beta }}\right)=\frac{1}{2n}\Vert \mathit{y}-\mathit{X}{\tilde{\mathit{\beta }}\Vert }_2^2.$
If $L>{\mathcal{L}}_n\left(\tilde{\mathit{\beta }}\right)$, then
$\left(\widehat{\mathit{\beta }},\widehat{\mathit{d}},\widehat{\mathcal{A}},\widehat{\mathcal{I}}\right)=\left(\tilde{\mathit{\beta }},\tilde{\mathit{d}},{\tilde{\mathcal{A}}}_k,{\tilde{\mathcal{I}}}_k\right)$,
$L={\mathcal{L}}_n\left(\tilde{\mathit{\beta }}\right).$
End for
4) If $L_0-L<{\tau }_s$, then $\left(\widehat{\mathit{\beta }},\widehat{\mathit{d}},\widehat{\mathcal{A}},\widehat{\mathcal{I}}\right)=\left(\mathit{\beta },\mathit{d},\mathcal{A},\mathcal{I}\right)$.
5) Output ($\widehat{\mathit{\beta }},\widehat{\mathit{d}},\widehat{\mathcal{A}},\widehat{\mathcal{I}}$).

ABESS.

In practice, the support size is usually unknown. We use a data-driven procedure to determine $s$. Information criteria such as high-dimensional BIC (HBIC) (13) and extended BIC (EBIC) (14) are commonly used for this purpose. Specifically, HBIC (13) can be applied to select the tuning parameter in penalized likelihood estimation. To recover the support size $s$ for the best-subset selection, we introduce a criterion that is a special case of HBIC (13). While HBIC aims to tune the parameter for a nonconvex penalized regression, our proposal is used to determine the size of best subset. For any active set $\mathcal{A}$, define an SIC as follows:

$$\mathrm{S}\mathrm{I}\mathrm{C}\left(\mathcal{A}\right)=n\log {\mathcal{L}}_{\mathcal{A}}+\left|\mathcal{A}\right|\log \left(p\right)\log \log n,$$

where ${\mathcal{L}}_{\mathcal{A}}=\underset{{\mathit{\beta }}_{\mathcal{I}}=0}{min}{\mathcal{L}}_n\left(\mathit{\beta }\right),\mathcal{I}={\left(\mathcal{A}\right)}^c$. To identify the true model, the model complexity penalty is $\log p$ and the slow diverging rate $\log \log n$ is set to prevent underfitting. Theorem 4 states that the following ABESS algorithm selects the true support size via SIC.

Let $s_{max}$ be the maximum support size. Theorem 4 suggests $s_{max}=o\left(\frac{n}{\log p}\right)$ as the maximum possible recovery size. Typically, we set $s_{max}=\left[\frac{n}{\log p\log \log n}\right]$, where $\left[x\right]$ denotes the integer part of $x$.

Algorithm 3: ABESS.
1) Input: $\mathit{X}$, $\mathit{y}$, and the maximum support size $s_{max}$.
2) For $s=\mathrm{1,2},\dots ,s_{max}$, do
$\left({\widehat{\mathit{\beta }}}_s,{\widehat{\mathit{d}}}_s,{\widehat{\mathcal{A}}}_s,{\widehat{\mathcal{I}}}_s\right)=\mathbf{\text{BESS.Fixed}}\left(s\right).$
End for
3) Compute the minimum of SIC:
$s_{min}=\arg \underset{s}{min}\mathrm{S}\mathrm{I}\mathrm{C}\left({\widehat{\mathcal{A}}}_s\right).$
4) Output $\left({\widehat{\mathit{\beta }}}_{s_{min}},{\widehat{\mathit{d}}}_{s_{min}},{\widehat{\mathcal{A}}}_{s_{min}},{\widehat{\mathcal{I}}}_{s_{min}}\right)$.

Theoretical Results

We establish the computational complexity and the consistency of the best subset recovery from the ABESS algorithm.

Conditions.

Let ${\mathit{\beta }}^{*}$ be the true regression coefficient with the sparsity level $s^{*}$ in Model 1. Denote the true active set by ${\mathcal{A}}^{*}=\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left({\mathit{\beta }}^{*}\right)$ and the minimal signal strength by $b^{*}=\underset{j\in {\mathcal{A}}^{*}}{min}{\left({\beta }_j^{*}\right)}^2$. Without loss of generality, assume the design matrix $\mathit{X}$ has $\sqrt{n}$-normalized columns, i.e., ${\mathit{X}}_j^{\top }{\mathit{X}}_j=n,j=\mathrm{1,2},\dots ,p$. We say that $X$ satisfies the Sparse Restricted Condition (SRC) (15) with order $s$ and spectrum bound $0<c_{-}\left(s\right)<c_{+}\left(s\right)<\infty$ if $\forall \mathcal{A}\subset \mathcal{S}\hspace{0.17em}\text{with}\left|\mathcal{A}\right|\le s\hspace{0.17em}\text{and}\forall \mathit{u}\ne 0,\mathit{u}\in {\mathbb{R}}^{\left|\mathcal{A}\right|}$,

$$c_{-}\left(s\right)\le \frac{\Vert {\mathit{X}}_{\mathcal{A}}{\mathit{u}\Vert }_2^2}{n\Vert {\mathit{u}\Vert }_2^2}\le c_{+}\left(s\right).$$

We denote this condition by $\mathit{X}\sim \mathrm{S}\mathrm{R}\mathrm{C}\left\{s,c_{-}\left(s\right),c_{+}\left(s\right)\right\}$. The SRC gives the range of the spectrum of the diagonal submatrices of the Gram matrix $G={\mathit{X}}^{\top }\mathit{X}/n$. The spectrum of the off-diagonal submatrices of $G$ can be bounded by the sparse orthogonality constant $\theta$_a,b, defined as the smallest number such that

$${\theta }_{a,b}\ge \frac{\Vert {\mathit{X}}_{\mathcal{A}}^{\top }{\mathit{X}}_{\mathcal{B}}{\mathit{u}\Vert }_2}{n\Vert {\mathit{u}\Vert }_2},$$

for $\forall \mathcal{A},\mathcal{B}\subset \mathcal{S},\left|\mathcal{A}\right|\le a,\left|\mathcal{B}\right|\le b\hspace{0.17em}\mathrm{a}\mathrm{n}\mathrm{d}\hspace{0.17em}\mathcal{A}\cap \mathcal{B}=\varnothing$ and $\forall \mathit{u}\ne 0,\mathit{u}\in {\mathbb{R}}^{\left|\mathcal{B}\right|}$. For any $0<\mathrm{\Delta }<\frac{1}{2}$, denote

$${\delta }_s\doteq \frac{8c_{+}\left(s\right){\left(\left(1+\mathrm{\Delta }\right)\frac{{\theta }_{s,s}}{c_{-}\left(s\right)}\left(1+\frac{{\theta }_{s,s}}{c_{-}\left(s\right)}\right)\right)}^2}{\left(1-\mathrm{\Delta }\right)\left(c_{-}\left(s\right)-\frac{{\theta }_{s,s}^2}{c_{-}\left(s\right)}\right)}.$$ [5]

To prove the theoretical properties of the ${\ell }_0$ estimator, we assume the following conditions:

• 1)The random errors ${ϵ}_1,\dots ,{ϵ}_n$ are i.i.d with mean zero and sub-Gaussian tails; that is, there exists a $\sigma >0$ such that $P\left\{\left|{ϵ}_i\right|\ge t\right\}\le 2\exp \left(-t^2/{\sigma }^2\right)$, for all $t\ge 0$.
• 2)$\mathit{X}\sim \mathrm{S}\mathrm{R}\mathrm{C}\left\{2s,c_{-}\left(2s\right),c_{+}\left(2s\right)\right\}$.
• 3)${\delta }_s<1$, where ${\delta }_s$ is defined in Eq. 5.
• 4)${\tau }_s=O\left(\frac{s\log p\log \log n}{n}\right)$.
• 5)$\frac{s^{*}\log p}{n}=o\left(1\right)$.
• 6)$\frac{1}{b^{*}}=o\left(\frac{n}{s\log p\log \log n}\right)$.
• 7)$\frac{s^{*}\log p\log \left(\log n\right)}{n}=o\left(1\right)$ and $\frac{s_{max}\log p}{n}=o\left(1\right)$.

Remark 1:

The sub-Gaussian condition is often assumed in the related literature and slightly weaker than the standard normality assumption. Condition 2 imposes bounds on the $2s$-sparse eigenvalues of the design matrix. As a typical condition in modeling involving high-dimensional data, it restricts the correlation among a small number of variables and thus guarantees the identifiability of the true active set. For example, the SRC has been assumed in existing methods (15–17). Sufficient conditions are provided for a design matrix to satisfy the SRC in propositions 4.1 and 4.2 in ref. 15.

Remark 2:

To verify condition 3, let $c\left(s\right)=\left(1-c_{-}\left(2s\right)\right)\vee \left(c_{+}\left(2s\right)-1\right)$, which is closely related to the restricted isometry property (RIP) (18) constant ${\delta }_{2s}$ for $\mathit{X}$. By lemma 20 in ref. 19, a sufficient condition for condition 3 is $c\left(s\right)\le 0.1877$, i.e., $c_{-}\left(2s\right)\ge 0.8123,c_{+}\left(2s\right)\le 1.1877$, which is weaker than the condition $c\left(s\right)\le 0.1599$ in ref. 19.

Remark 3:

Condition 4 ensures that the threshold ${\tau }_s$ can control random errors. Condition 6 is the minimal magnitude of the signal for the best subset recovery. To discriminate between the signal and threshold, the signal needs to be stronger than the threshold. The condition is slightly stronger than the condition in ref. 20.

Remark 4:

For the recovery of the true active set, the true sparsity level $s^{*}$ and the maximum model size $s_{max}$ cannot be too large. Condition 7 is weaker than the condition in ref. 13 as we consider the least-squares loss function without concave penalty. As shown in the SI Appendix, condition 5 can be removed.

Computational Theory.

Firstly, we show that the splicing method converges in finite steps.

Theorem 1.

Algorithm 1 terminates in a finite number of iterations.

This follows immediately from the fact that ${\mathcal{L}}_n\left({\mathit{\beta }}^{m+1}\right)<{\mathcal{L}}_n\left({\mathit{\beta }}^m\right)$. Furthermore, the next theorem delineates the polynomial complexity of the ABESS algorithm.

Theorem 2.

Suppose conditions 1 and 4 hold. Assume conditions 2, 3, and 6 hold with $s_{max}$. The computational complexity of ABESS for a given $s_{max}$ is

$$\begin{array}{ll}\hfill O& \left(\left(s_{max}\log \frac{\Vert {\mathit{y}\Vert }_2^2}{\log p\log \log n}+\frac{n\Vert {\mathit{y}\Vert }_2^2}{\log p\log \log n}\right)\right.\left(np{s}_{max}\hspace{0.17em}+\right.\hfill \\ \hfill & \left.\left.n{s}_{max}^2+k_{max}p{s}_{max}\right)\right).\hfill \end{array}$$

If $s\ge s^{*}$, Algorithm 1 will find the true active set in high probability under conditions 1–4 (Lemma 1). Furthermore, by splicing, the loss function decreases drastically at the first several iterations and the convergence rate $O\left(\log \frac{\Vert {\mathit{y}\Vert }_2^2}{s\log p\log \log n}\right)$ of Algorithm 1 is presented in Theorem 3. However, if $\text{s}<s^{*}$, we can determine the iterations $O\left(\frac{n\Vert {\mathit{y}\Vert }_2^2}{s\log p\log \log n}\right)$ of Algorithm 1 by using thresholding ${\tau }_s$ to exclude useless splicing. Thus, we can show that the number of iterations of Algorithm 1 is polynomial.

Statistical Theory.

Let ${\gamma }_s\left(n,p\right)=O\left(\exp \left\{\log p-\frac{K_{s}n{b}^{*}}{s}\right\}\right)+O\left(\exp \left\{\log p-\frac{K_{s}n}{s^{*}}\right\}\right)$, where $K_s$ is some constant depending on $s$. The following lemma gives an interesting property of the active set output by Algorithm 1.

Lemma 1.

Suppose $\left(\widehat{\mathit{\beta }},\widehat{\mathit{d}},\widehat{\mathcal{A}},\widehat{\mathcal{I}}\right)$ is the solution of Algorithm 1 for a given support size $s\ge s^{*}$ and conditions 1–4 hold. Then, we have

$$\mathrm{P}\left(\widehat{\mathcal{A}}\supseteq {\mathcal{A}}^{*}\right)\ge 1-{\gamma }_s\left(n,p\right).$$

Furthermore, if conditions 5 and 6 hold,

$$\underset{n\to \infty }{lim}\mathrm{P}\left(\widehat{\mathcal{A}}\supseteq {\mathcal{A}}^{*}\right)=1.$$

Especially, if $s=s^{*}$, we have

$$\underset{n\to \infty }{lim}\mathrm{P}\left(\widehat{\mathcal{A}}={\mathcal{A}}^{*}\right)=1.$$

Lemma 1 indicates that our estimator of the active set will eventually include the true active set. The next theorem characterizes the number of iterations and the ${\ell }_2$ bound error of the splicing method.

Theorem 3.

Suppose $\left({\mathit{\beta }}^m,{\mathit{d}}^m,{\mathcal{A}}^m,{\mathcal{I}}^m\right)$ is the $m$th iteration of Algorithm 1 for a given support size $s\ge s^{*}$. Suppose conditions 1–4 hold. Then, with probability $1-{\gamma }_s\left(n,p\right)$, we have

• 1)
  $${\mathcal{A}}^m\supseteq {\mathcal{A}}^{*},\hspace{0.17em}\text{if}\hspace{0.17em}m\ge {\log }_{\frac{1}{{\delta }_s}}\left(\frac{\Vert {\mathit{y}\Vert }_2^2}{C_{s,1}}\right),$$

where $C_{s,1}=n\left(1-\mathrm{\Delta }\right)\left(c_{-}\left(s\right)-\frac{{\theta }_{s,s}^2}{c_{-}{\left(s\right)}^2}\right)b^{*}$, $b^{*}$ is the minimal signal strength, and ${\delta }_s$ is defined in condition 3;

• 2)
  $${\Vert {\mathit{\beta }}^m-{\mathit{\beta }}^{*}\Vert }_2^2\le C_{s,2}{\delta }^m{\Vert \mathit{y}\Vert }_2^2.$$

where $C_{s,2}=\left(1+\mathrm{\Delta }+\frac{{\theta }_{s,s}}{c_{-}\left(s\right)}\right)/\left(\left(1-\mathrm{\Delta }\right)n\left(c_{-}\left(s\right)-\frac{{\theta }_{s,s}^2}{c_{-}\left(s\right)}\right)\right)$.

With the threshold ${\tau }_s$, Theorem 3 suggests that our splicing method terminates at a logarithm number of iterations. The estimation error decays geometrically.

The next theorem guarantees that the splicing method can recover the true active set with a high probability.

Theorem 4 (Consistency of Best-Subset Recovery).

Suppose conditions 1, 4, and 7 hold. Assume conditions 2, 3, and 6 hold with $s_{max}$. Then, under the information criterion SIC, with probability $1-O\left(p^{-\alpha }\right)$, for some positive constant $\alpha >0$ and a sufficiently large $n$, the ABESS algorithm selects the true active set, that is, ${\widehat{\mathcal{A}}}_{s_{min}}={\mathcal{A}}^{*}$.

Theorem 4 implies that the solution of the splicing method is the same as the oracle least-squares estimator with an unknown sparsity level. Since our approach can recover the true active set, we can directly deduce the asymptotic distribution of $\mathit{\beta }$.

Corollary 1 (Asymptotic Properties).

Suppose the assumptions and conditions in Theorem 4 hold. Then, with a high probability, the solution ${\widehat{\mathit{\beta }}}_{s_{min}}$ of ABESS is the oracle estimator, i.e.,

$$P\left\{{\widehat{\mathit{\beta }}}_{s_{min}}={\widehat{\mathit{\beta }}}^o\right\}=1-O\left(p^{-\alpha }\right),$$

where $\alpha >0$ and ${\widehat{\mathit{\beta }}}^o$ is the least-squares estimator given the true active set ${\mathcal{A}}^{*}$. Furthermore,

$${\widehat{\mathit{\beta }}}_{{\mathcal{A}}^{*}}\sim N\left({\mathit{\beta }}_{{\mathcal{A}}^{*}}^{*},\mathbf{\Sigma }\right),$$

where $\mathbf{\Sigma }={\left({\mathit{X}}_{{\mathcal{A}}^{*}}^{\top }{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}^{-1}$.

Simulation

In this part, we compare the proposed ABESS algorithm with other variable selection algorithms under Model 1, where the rows of the design matrix are i.i.d-sampled from the multivariate normal distribution with mean $\mathbf{0}$ and covariance matrix $\mathrm{\Sigma }$. The $n$ error terms are i.i.d-drawn from the normal distribution $N\left(0,{\sigma }^2\right)$.

We consider four criteria to assess the methods. The first two criteria, true-positive rate (TPR) and true-negative rate (TNR), are used to evaluate the performance of variable selection. The estimation accuracy for $\mathit{\beta }$ is measured by the relative error (ReErr): ${\Vert \widehat{\mathit{\beta }}-\mathit{\beta }\Vert }_2/{\Vert \mathit{\beta }\Vert }_2$. We also examine the dispersion between the sparsity level estimation $ŝ$ and the ground truth, which is measured by the sparsity-level error (SLE): $ŝ-s^{*}$. All simulation results are based on 100 synthetic datasets.

Low-Dimensional Case.

We begin with a low-dimensional setting and compare ABESS and all-subsets regression (ASR), which exhaustively searches for the best subsets of the explanatory variables to predict the response via an efficient branch-and-bound algorithm (21). We use SIC (ASR-SIC) to select a model size for ASR.

We adopt a simulation model from ref. 6. Specifically, the coefficient is fixed at $\mathit{\beta }={\left(\mathrm{3,1.5},\mathrm{0,0,2,0,0,0}\right)}^{\top }$, the covariance matrix $\mathrm{\Sigma }$ has a decayed structure, i.e., ${\mathrm{\Sigma }}_{ij}=0.5^{|i-j|}$ for all $i,j\in \left\{1,\dots ,p\right\}$. The pair of sample size and noise level $\left(n,\sigma \right)$ varies as $\left(\mathrm{40,3}\right),\left(\mathrm{40,1}\right)$, and $\left(\mathrm{60,1}\right)$. It can be seen from Table 1 that when the noise level is large but the sample size is small, the performance of ABESS and ASR is close, although ASR is slightly better. When the noise level reduces, the slight advantage of ASR-SIC disappears. The fact that ABESS performs as well as the exhaustive ASR algorithm, when the setting is simple enough for the latter to be computationally feasible, demonstrates the power of ABESS in selecting the best subset.

Table 1.

Simulation results in the low-dimensional setting

Method	TPR	TNR	ReErr	SLE
$n=40,{\sigma }^2=3$
ABESS	0.90 (0.17)	0.86 (0.15)	0.20 (0.19)	0.40 (0.89)
ASR-SIC	0.91 (0.17)	0.87 (0.15)	0.14 (0.13)	0.38 (0.85)
$n=40,{\sigma }^2=1$
ABESS	1.00 (0.00)	0.87 (0.14)	0.02 (0.02)	0.63 (0.72)
ASR-SIC	1.00 (0.00)	0.87 (0.14)	0.02 (0.02)	0.63 (0.72)
$n=60,{\sigma }^2=1$
ABESS	1.00 (0.00)	0.90 (0.13)	0.01 (0.01)	0.48 (0.64)
ASR-SIC	1.00 (0.00)	0.90 (0.13)	0.01 (0.01)	0.49 (0.64)

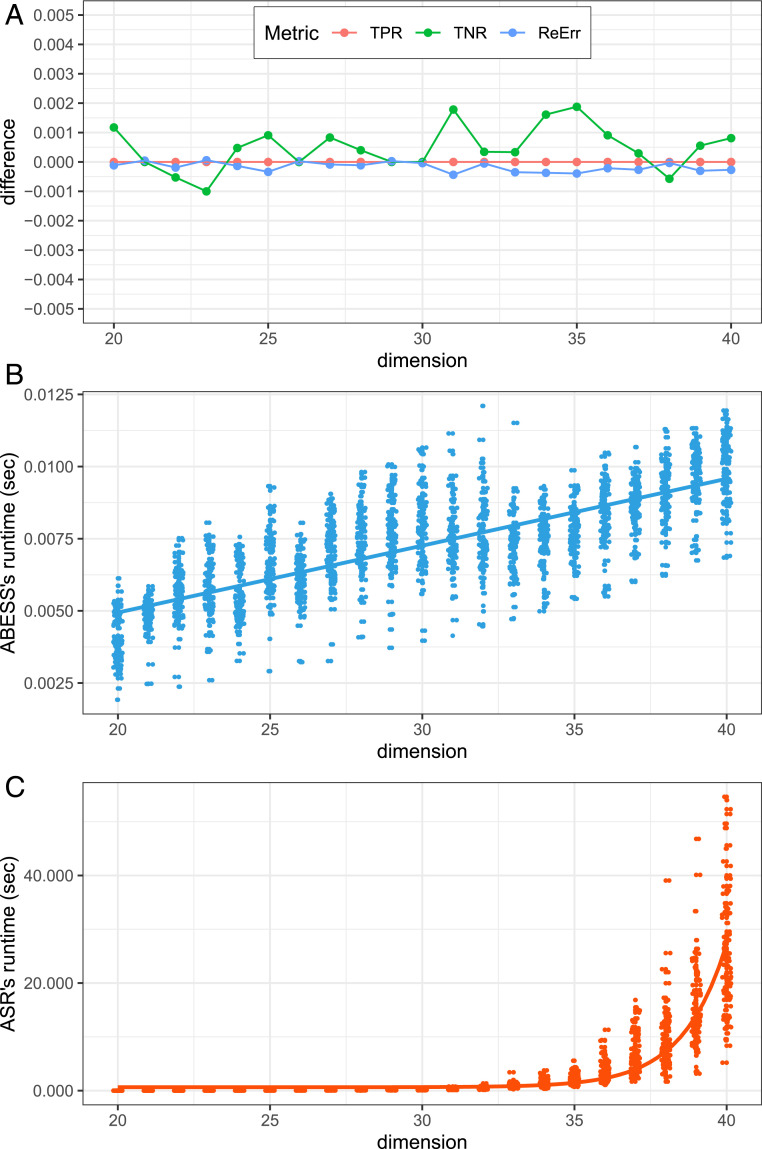
Next, we study the computational time and computational complexity of the ASR and ABESS algorithms by adding zeros to $\mathit{\beta }$ in the previous experiment to form a new $\mathit{\beta }$ of a total of $p$ coefficients. Without loss of generality, we consider the runtime of algorithms when $p$ increases from 20 to 40 with step size 1. Fig. 1 presents the simulation results. On the one hand, from Fig. 1A, we can see that the difference between ASR-SIC and ABESS in the three criteria are all under control in interval $\left(-5\times 10^{-3},5\times 10^{-3}\right)$, and, hence, we can conclude that ABESS and ASR have a negligible difference in this setting. On the other hand, from Fig. 1 B and C, the computational time of ASR is 20 s when dimensionality reaches 40, while that of ABESS is less than 0.03 s. More importantly, from Fig. 1B, the computational time of ABESS grows linearly when the dimension increases, as proven in Theorem 2. In contrast, from Fig. 1C, the runtime of ASR increases exponentially. In summary, ABESS not only can recover the support but also is computationally fast.

Fig. 1.

(A) For each of the three metrics (TPR, TNR, and ReErr), the difference (y axis) is calculated by subtracting an ABESS metric from its corresponding ASR metric. Different colors correspond to different metrics. (B) Dimension ($x$ axis) versus ABESS’s runtime ($y$ axis) scatterplot. The blue straight line is characterized by equation $y=a+bx$. (C) Dimension ($x$ axis) versus ASR’s runtime ($y$ axis) scatterplot. The red curve is $y=a+b{2}^x$. In B and C, the coefficients $a,b$ are estimated by the ordinary least squares.

High-Dimensional Case.

We consider the case when the dimension is in hundreds or even thousands, for which the exhaust search is computationally infeasible. It is of interest to compare ABESS and modern variable selection algorithms, including LASSO (4), SCAD (6), and MCP (7). The solutions of the three algorithms are given by the coordinate descent algorithm (22, 23) implemented in R packages glmnet and ncvreg. For all of these methods, we use SIC to select the optimal regularized parameters. We also consider cross-validation (CV), a widely used method, to select the tuning parameter. For MCP/SCAD/LASSO, the $l$ regularized parameters to be selected are prespecified values following the default setting in R packages glmnet and ncvreg. For a fair comparison, the input argument of the ABESS algorithm, $s_{max}$, is also set as $l$. Here, $l$ is set to be $\left[\frac{n}{\log p\log \log n}\right]$. Note that the concavity parameter $\gamma$ of the SCAD and MCP penalties is fixed at 3.7 and 3, respectively (6, 7).

The dimension, $p$, of the explanatory variables increases as 500, 1,500, and 2,500, but only 10 randomly selected variables from them would affect the response. Among the 10 effective variables, 3 of them have a strong effect, 4 of them have a moderate effect, and the rest have a weak effect. Here, a strong/moderate/weak effect means that a coefficient is sampled from a zero-mean normal distribution with SD10/5/2. We consider two structures of $\mathrm{\Sigma }$. The first one is the uncorrelated structure ${\mathrm{\Sigma }}_{ij}=I\left(i=j\right)$, and the second one is a constant structure ${\mathrm{\Sigma }}_{ij}=0.8^{I\left(i\ne j\right)}$, corresponding to the case that any two explanatory variables are highly correlated. The sample size $n$ is fixed at 500, and the noise level ${\sigma }^2$ is fixed at 1.

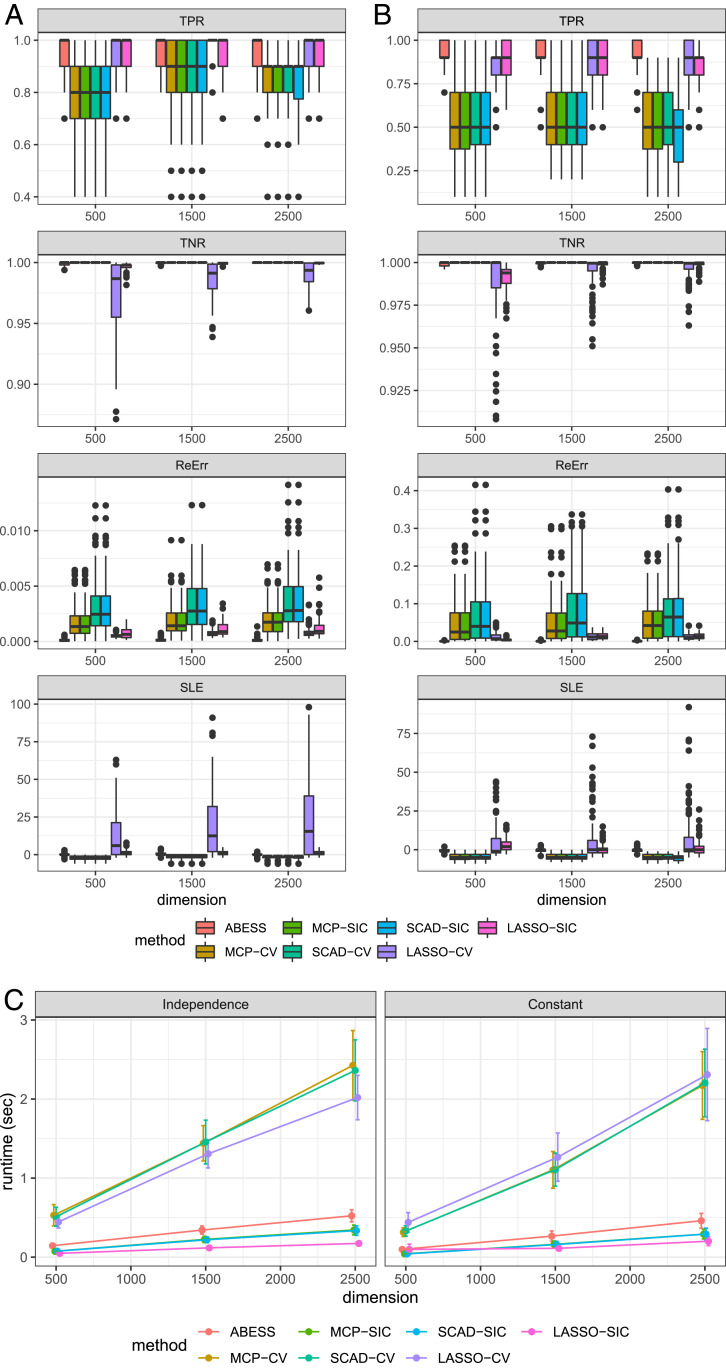
The simulation results are presented in Fig. 2 A and B. A few observations are noteworthy. First, among all of the methods, ABESS or the CV-based LASSO estimator have the best performance for correctly identifying the true effective variables; moreover, ABESS can reasonably control the false-positive rate at a low level like SCAD and MCP. Second, SIC helps ABESS efficiently detect the true model size and its SLE approaches to 0. In conjunction with the first point, the empirical results demonstrate ABESS’s performance as proven in Theorem 4. In contrast, the MCP and SCAD underestimate the model size, whereas LASSO overestimates it. Also, we see that like BIC (24), SIC avoids overfitting (see additional simulation studies in SI Appendix). Finally, the parameter estimation of ABESS is superior to the other algorithms because ABESS not only effectively recovers the support set but also yields an unbiased parameter estimate. Fig. 2C compares the runtime. We see that ABESS’s runtime is computationally efficient. Furthermore, as expected, ABESS is much faster than the CV-based LASSO/SCAD/MCP methods.

Fig. 2.

(A and B) The boxplots of TPR, TNR, ReErr, and SLE of different algorithms in the high-dimensional setting when any two covariates have no correlation (Left) and constant correlation 0.8 (Right). (C) Average runtime comparison under two correlation structure settings: uncorrelated and constant. The runtime ($y$ axis) is measured in seconds.

Summary

We present an iterative splicing method that distinguishes the active set from the inactive set iteratively in variable selection. The estimated active set is shown to contain the true active set when the given support size is no less than the true size, or to be included in the true active set when the given support size is less than the true size. We also introduce a selection information criterion to adaptively determine the sparsity level, which can guarantee to choose the true active set with a high probability. We show that our solution is globally optimal for the Lagrangian of Eq. 2 with SIC and has the oracle properties with a high probability. Numerical results demonstrate the theoretical properties of ABESS. However, when there are a large number of weak effects, the ambiguity makes it challenging for us to detect signals. ABESS as well as other methods such as LASSO, SCAD, and MCP face a similar difficulty. How to perform an effective subset selection with many weak effects warrants further research.

Data Availability.

All study data are included in the article and SI Appendix.