Significance
Cellular membranes are believed to play a central role in the formation of amyloid aggregates implicated in pathologies like Alzheimer’s and Parkinson’s diseases. Indeed, lipid membranes can significantly accelerate amyloid aggregation through a process that depends on the membrane-phase behavior, the molecular mechanisms of which are still unclear. We developed a coarse-grained computer model to explore pathways of amyloid aggregation on cell membranes. We found that increase in membrane fluidity drastically enhances the rate of aggregation by enabling lipid incorporation into the fibril structure. We show that, in this way, lipids substantially lower the free-energy barrier for fibril formation. We directly compare our results to experimental data and offer mechanistic explanation for the membrane-assisted amyloid nucleation.
Keywords: amyloid, protein aggregation, cell membrane, membrane fluidity, coarse-grained simulations
Abstract
Biological membranes can dramatically accelerate the aggregation of normally soluble protein molecules into amyloid fibrils and alter the fibril morphologies, yet the molecular mechanisms through which this accelerated nucleation takes place are not yet understood. Here, we develop a coarse-grained model to systematically explore the effect that the structural properties of the lipid membrane and the nature of protein–membrane interactions have on the nucleation rates of amyloid fibrils. We identify two physically distinct nucleation pathways—protein-rich and lipid-rich—and quantify how the membrane fluidity and protein–membrane affinity control the relative importance of those molecular pathways. We find that the membrane’s susceptibility to reshaping and being incorporated into the fibrillar aggregates is a key determinant of its ability to promote protein aggregation. We then characterize the rates and the free-energy profile associated with this heterogeneous nucleation process, in which the surface itself participates in the aggregate structure. Finally, we compare quantitatively our data to experiments on membrane-catalyzed amyloid aggregation of α-synuclein, a protein implicated in Parkinson’s disease that predominately nucleates on membranes. More generally, our results provide a framework for understanding macromolecular aggregation on lipid membranes in a broad biological and biotechnological context.
The aggregation of normally soluble proteins into -sheet-rich amyloid fibrils is a common form of protein assembly that has broad implications across biomedical and biotechnological sciences, in contexts as diverse as the molecular origins of neurodegenerative disorders to the production of functional materials (1, 2). The presence of surfaces and interfaces can strongly influence amyloid aggregation, either catalyzing or inhibiting it, depending on the nature of the surface. This effect has been studied for the cases of amyloid nucleation on nanoparticles (3–5), on flat surfaces (6–10), and on the surface of amyloid fibrils themselves (11, 12).
Lipid bilayers are a unique type of surface, which is ubiquitous in biology and is the main contributor to the large surface-to-volume ratio characteristic of biological systems. They are highly dynamic, self-assembled structures that can induce structural changes in the proteins bound to them (13, 14) and markedly affect protein-aggregation propensities (15, 16). While nucleation on the surfaces of lipid membranes can influence fibril formation dramatically, alternative surfactant-driven fibrillation pathways in solution have been proposed at surfactant concentrations where formation of bilayer structures is not observed (17).
Increasing experimental evidence supports the principle that the interaction between amyloidogenic proteins and the lipid cell membrane catalyzes in vivo amyloid nucleation, which is involved in debilitating pathologies. Remarkably, through surface-driven catalysis, lipid bilayers can enhance the kinetics of -synuclein aggregation, the protein involved in Parkinson’s disease, by over three orders of magnitude with respect to nucleation in solution (18).
Bilayer membranes can exist in different structural phases and can undergo local and global phase changes. A large body of work has focused on exploring how the membrane’s dynamical properties, such as its fluidity, relate to amyloid aggregation of bound proteins (19–26).
For instance, fluid membranes, constituted of short and saturated lipid chains, were found to most effectively catalyze the nucleation of -synuclein (19), while less-fluid membranes composed of long lipid chains had less catalytic power. Furthermore, the addition of cholesterol to lipid membranes was found to alter its fluidity and govern the nucleation rate of A42 (25), a peptide implicated in Alzheimer’s disease. In these cases, the physical properties of the membrane are controlled through variations in its composition, and decoupling the role of the membrane’s physical properties from its chemical specificity is extremely challenging.
The question we focus on here is how the microscopic steps that drive amyloid nucleation at the membrane surface are altered by the inherently dynamic nature of lipid bilayers.
Computer simulations can be of great help in this case, enabling us to systematically investigate the role of the physical and chemical properties of lipid membranes independently from one another, thus helping to identify key players behind membrane-driven amyloid nucleation.
In this work, we develop a coarse-grained Monte Carlo model for studying the nucleation of amyloidogenic proteins on lipid membranes. We use it to identify the microscopic mechanisms which connect the membrane fluidity, the rate of amyloid nucleation, and the morphology of amyloid aggregates. We find that the membrane most efficiently catalyzes amyloid nucleation by donating its lipids to the nucleating fibril, which depends 1) on the lipid solubility and often correlates with membrane fluidity, and 2) the affinity of proteins to the membrane. This interdependence controls both the morphology of the resulting aggregates, which can range from protein-rich to lipid-rich, and the rate of fibril formation. We then discuss how our results provide a mechanistic explanation for a number of recent experimental observations regarding accelerated nucleation kinetics on fluid membranes (19), lipid–protein coaggregation (27), and altered aggregate morphology (23). Furthermore, the framework developed here offers a platform for studying strategies for bypassing amyloid nucleation in a cellular context.
Results
Computational Model.
To study the essential features of membrane-assisted nucleation, we developed a coarse-grained computational model that takes into account the dynamic nature of the lipid membrane, the process of membrane-bound protein oligomerization, and the protein’s structural transition that allows fibril formation.
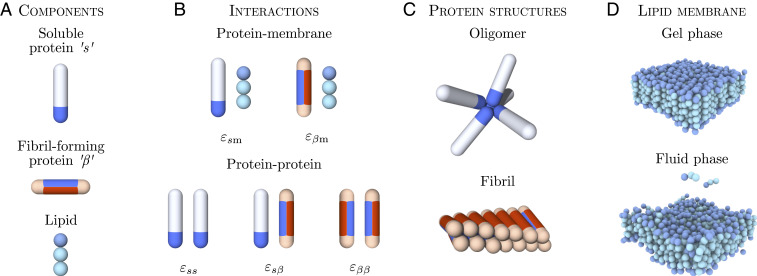
The lipid bilayer membrane is described by using a three-beads-per-lipid model (28), where the two hydrophobic tail beads are mutually attractive, allowing for the formation of a stable bilayer. We control the membrane’s thermodynamic phase state by varying the depth of the interaction potential between the lipid tails, , where is the Boltzmann constant and is the temperature. In particular, to evaluate the protein-nucleation kinetics across different membrane phases, we tune the fluidity by varying . Four values of fluidity are considered here, where the lowest value = 0.775 yields a gel-phase membrane, and the other three values (0.895, 1.015, and 1.135) correspond to membranes in the fluid phase, as shown in Fig. 1D (see Materials and Methods for details).
Fig. 1.
Simulation model for membrane-driven fibril formation. (A) Proteins can exist in two distinct conformations: a soluble “” and a -sheet-prone conformation. Lipid molecules are modeled by one hydrophilic head and two hydrophobic tail beads. (B) Protein–membrane and protein–protein interactions present in the system and the associated interaction parameters. (C) Soluble proteins can form oligomers via their tip-to-tip interactions. Protein molecules in the -sheet-forming conformation can assemble into fibrillar structures through the interactions of the blue side patches. (D) The lipid membrane can exist in different structural phases depending on the interlipid interactions set in the model. Shown here are the gel phase ( = 0.775) and fluid phase ( = 1.135).
The minimal model for the amyloid-forming proteins is based on a coarse-grained model which has proven useful for studying both primary (29) and secondary amyloid nucleation (12) and has been cross-validated with experiments (12, 30–32). Proteins are modeled as hard, patchy spherocylinders and can exist in two distinct conformational states: a soluble () and a -sheet-forming () conformation, both of which are equipped with different arrangements of interaction patches (Fig. 1A). This model captures the aggregation behavior through the colloidal nature of the building blocks and the internal conformational dynamics of the protein through the internal degree of freedom associated to the -to--sheet conformational transition.
The -state represents the conformational ensemble of protein molecules in their non--sheet states, both in solution and bound to the membrane. The -prone-state describes the conformation of the polypeptide chain which possesses strong intermolecular interactions, as found in the -sheet-rich cores of amyloid fibrils. In this regard, the two spherocylinder states represent different classes of membrane-binding modes associated with the conformational ensembles, rather than reflecting precise conformational geometries, which vary for different amyloidogenic proteins.
Proteins in the -state interact with each other through an attractive end cap on the spherocylinder, which allows for the formation of disordered (non--sheet) oligomers (Fig. 1C).
The soluble protein conformation also has affinity for the lipid–membrane heads set by the value of facilitating initial membrane binding. To model the amphipathic nature of the protein and allow it to partially insert and anchor into the lipid membrane, as observed for both -synuclein (33) and A (34), the protein can also interact with the two lipid tail beads, with and , respectively.
The -sheet-prone conformation is equipped with two separate, oppositely arranged patches. The protein–protein interaction patch (blue) mediates attractive interactions both with the and conformations facilitating the alignment of proteins and the formation of elongated fibrils. The lipid–protein interaction patch (red) is responsible for hydrophobic interactions with lipid molecules (Fig. 1B).
Such a twofold binding motif in the -prone state enables the protein to form a fibrillar structure and, at the same time, interact with the lipid membrane. This motif is chosen to mimic the general membrane-binding characteristics of amphipathic proteins such as -synuclein and A, which, upon binding to the membrane, can undergo a structural transition that promotes -sheet formation in contact with lipids (13, 35, 36). Moreover, the patch arrangement in the -prone state allows for the formation of small fibrillar clusters that can insert into the bilayer, as observed experimentally, for example, for -synuclein (14, 37). Fibrillar oligomers that can form in our simulation exhibit an exposed hydrophobic face which resembles the three-dimensional structure of small oligomers in a membrane-mimicking environment (38).
The strength of the lipophilic attraction of the protein (red patch) is controlled by , while the protein–protein interactions of the - and -states (blue patches) are controlled by , and , as summarized in Fig. 1B.
The stochastic transition between conformational states is penalized with a free-energy barrier , reflecting the fact that amyloidogenic proteins lose conformational entropy when converting from the native to the -sheet-prone state and are rarely found in the -sheet conformation on their own (see Materials and Methods for details).
Effective lowering of this barrier, which is the requirement for efficient catalysis of amyloid nucleation (30, 39, 40), can emerge from favorable interactions with either proteins or lipids. For example, in the case of secondary nucleation, which is heterogeneous nucleation on the surface of fibrils, the nucleation barrier is effectively vanishing due to altered energetics of surface-bound proteins, as reported in simulations (12, 30) and experiments (39).
Using the model presented in ref. 29, we found that no nucleation occurs in solution during the simulation time at and , while nucleation in the presence of lipids can be fast, as observed in experiments (18). To be able to explore the mechanisms of membrane-assisted nucleation across different conditions in a computationally efficient way, we set the conversion barrier and the -membrane interaction proportionally to while suppressing nucleation in solution. This is justified by the experimental finding that primary nucleation of -synuclein in the presence of lipid vesicles has no significant dependence on the concentration of free protein in solution, which are consequently not involved in the rate-determining step (18). Further details can be found in SI Appendix.
Membrane-Assisted Nucleation Mechanisms.
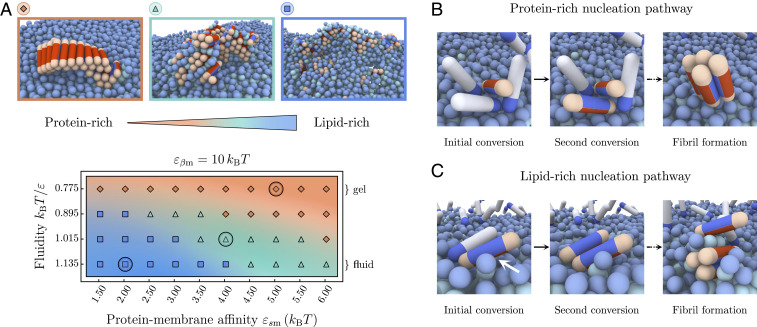
Through binding to the bilayer, the soluble protein molecules can arrange into small, unstructured oligomers on the membrane due to their self-interaction. The oligomerization on the membrane is more efficient than in solution due to the higher protein concentration on the surface. If after a lag time, a successful conversion of one of the proteins to the -prone conformation has occurred, aggregation and potential fibril elongation can start. Our simulations show that the properties of lipid membranes can fundamentally alter both the pathway through which this nucleation occurs and the morphologies and compositions of the resulting aggregates. In the following, we distinguish two basic nucleation pathways and the resulting aggregate morphologies, which range from protein-rich to lipid-rich, as illustrated in the phase diagram in Fig. 2A.
Fig. 2.
Morphologies of aggregates formed on lipid membranes. (A) Phase space of the protein–lipid cluster morphologies depending on the membrane fluidity and protein–membrane affinity. Three main areas can be distinguished: extended fibrils (orange), smaller fibrillar clusters with interstitial lipids (green), and strongly mixed lipid–protein clusters (blue). The representative snapshots correspond to the circled parameter values; soluble proteins are not shown. (B) Series of snapshots showing the gel-phase heterogeneous nucleation pathway resulting in protein-rich fibrillar clusters where the membrane acts as a static surface. (C) The initial nucleation step in the fluid-phase nucleation pathway is caused by direct contact between the protein side patch and lipid tails (white arrow), typically leading to mixed lipid–protein aggregates.
In the gel phase (), membrane lipids are packed closely, and bound proteins are unlikely to penetrate into the bilayer. In this case, the membrane essentially behaves as a static surface: proteins adsorb onto the surface and form transient oligomers, which eventually provide an environment allowing for stable conversion to the -state and subsequent fibril nucleation (29). This heterogeneous nucleation pathway is illustrated in the sequence of snapshots in Fig. 2B and typically results in the appearance of elongated fibrils epitaxially growing on top of the bilayer (orange area in Fig. 2A), which often detach and diffuse away from the membrane. Due to the low diffusivity of lipids in the gel phase, mixing between lipids and protein typically does not occur during nucleation and growth, rendering the resulting fibrillar aggregates protein-rich. The length of the fibrils strongly depends on the protein–membrane affinity . High values lead to an increased membrane coverage, which causes fast growth of the fibril after initial conversion, and, hence, a higher proportion of longer fibrils, as shown in SI Appendix, Fig. S5.
The morphology of nucleated clusters changes distinctly when the membrane is in the fluid phase, as best seen for the example of low protein–lipid affinities in the blue panel of Fig. 2A.
Due to the higher membrane fluidity, realized by higher values of , lipids are comparatively weakly bound within the bilayer and can be extracted from it more easily. In fact, experiments show that the lipid solubility is increased when shortening the acyl chain length of saturated lipids (19) (see SI Appendix for details). This effectively enables the lipids to actively participate in the formation of prefibrillar nuclei and produces mixed lipid–protein aggregates in a fluidity-dependent way.
Packing defects linked to the loose lipid packing and the higher lipid solubility increase the likelihood of a direct contact between the side patch of membrane-bound proteins upon conversion to the -prone state. This gives rise to a nucleation pathway which is inherently sensitive to the membrane fluidity. The microscopic steps of this nucleation mechanism are illustrated in the snapshot sequence in Fig. 2C. In the bound dimer depicted, direct exposure of the lipid tails to the protein side patch drive the initial nucleation step, shown by the direct interaction with the partially extracted lipid in the first panel of the sequence. The second bound protein readily adopts the -prone state, and, subsequently, both membrane-bound proteins and lipids can be recruited into the aggregate and typically lead to mixed lipid-rich clusters.
Additionally, at low protein–lipid affinities , the membrane is weakly covered by proteins, and stable oligomers are rare. The first nucleation step typically proceeds via the direct interaction of a single -prone protein with the hydrophobic tail of a lipid. The converted -prone protein can then get coated in lipids or (further) inserted into the lipid bilayer, which leads to mixed protein–lipid clusters (blue area in Fig. 2A). The latter of these processes can hamper further elongation into fibrils and result in isolated small aggregates trapped in the bilayer.
Generally, the exact composition of the aggregates depends on the relative rate of incorporation of lipids and proteins into an aggregate, governed both by the membrane fluidity and the protein–membrane affinities.
At higher protein–membrane affinities (), the membrane is substantially covered by proteins (SI Appendix, Fig. S2). The local environment of a growth-competent nucleus will, hence, be abundant in soluble proteins, leading to a faster addition of protein monomers and, hence, fibrillar clusters with lower lipid content (green area in Fig. 2A). Interestingly, the bound proteins also modify the local phase state of the membrane, as indicated by a reduction of the average area per lipid as is increased (SI Appendix, Fig. S4). This hinders lipid extraction and yields an intermediate nucleation pathway between the lipid-rich and protein-rich regimes, as illustrated in Fig. 2A.
Similar trends to those observed in our simulations have been reported in atomic-force-microscopy experiments monitoring A aggregating on model lipid membranes (23). On fluid model membranes with strong electrostatic interactions between proteins and lipids, bilayer deformations and clustering of lipids around A were observed, whereas on gel phase membranes, elongated mature fibrils appeared, just like in our simulations. Furthermore, experiments have shown that -synuclein fibril formation in the presence of vesicles leads to membrane remodeling and lipid extraction (41), yielding fibrils intercalated with lipids that often cause vesicle disintegration. Similar behavior involving membrane rupture can be observed in our simulations at later stages of the aggregation process when stresses induced by the growing fibril–lipid aggregates become too large.
Taken together, in contrast to the conventional heterogeneous nucleation associated with static surfaces, the nucleation pathway linked to fluid-phase membranes is characterized by the active participation of the membrane surface in the nucleus formation through hydrophobic lipid interactions, which are promoted by packing defects and lipid extraction.
Membrane Fluidity Enhances Nucleation Rates.
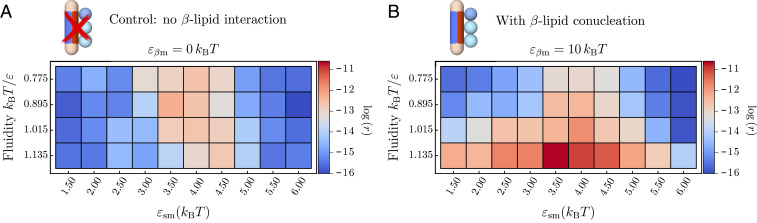
In addition to controlling the morphologies of amyloid aggregates, the membrane has an immediate effect on the rates of amyloid nucleation. To convert from the soluble into the fibril-forming state, the protein needs to overcome the intrinsic free-energy barrier . The role of the membrane in modifying this nucleation barrier can be twofold: 1) to increase the local concentration of proteins by restricting their mobility to the membrane surface, and 2) to actively participate in the formation of the prefibrillar nucleus through hydrophobic interactions. Here, we decouple these two effects by analyzing two separate scenarios: a control case in which a protein is only allowed to adsorb onto the membrane, but cannot conucleate with lipids; and another one in which -sheet-prone proteins can conucleate with lipids, as depicted in Fig. 2C. The two scenarios are characterized by the presence or absence of the lipid–protein interaction patch of the -prone conformation (red patch), while the interaction between the -conformation and the lipids remains unaltered.
Starting with the control case, we remove the red patch by setting . As evident from Fig. 3A, the nucleation rate is a nonmonotonic function of the protein–membrane affinity . Here, the rate is the inverse mean lag time of -prone protein-dimer formation, where the lag time is given in units of Monte Carlo steps. At small values, the nucleation rates are low across all fluidities, where virtually no proteins are adsorbed onto the membrane. At intermediate membrane–protein affinities, the formation of stabilized membrane-bound oligomers lowers the nucleation barrier and increases the nucleation rates. At high membrane–protein affinities, the nucleation process is inhibited due to the unfavorable free energy associated with the detachment of -state proteins. Indeed, at , upon conversion to the -state, the protein loses its interaction with the membrane, which becomes costly at high protein–membrane affinities , hence prohibiting nucleation. The onset of this regime is systematically shifted to higher values as the fluidity is increased. This is rooted in the fact that a higher lipid mobility inhibits the formation of stable oligomers on the membrane surface (SI Appendix, Fig. S3).
Fig. 3.
Amyloid nucleation rates on the membrane. (A) Control case: Nucleation rates when only soluble proteins interact with the lipid beads and -like proteins do not penetrate into the hydrophobic core. Nonmonotonic behavior is observed with respect to the protein–lipid interaction . (B) Nucleation rates when the interactions between the proteins and the lipid tails are nonzero and proteins can penetrate the bilayer, as in Fig. 2. Amyloid nucleation is sped up in the direction of higher fluidities in addition to the nonmonotonic scaling with observed in A.
In the second scenario, the -sheet-prone protein conformation carries a side patch with an affinity for the hydrophobic lipid tails of , rendering the protein amphipathic. The value of is chosen larger than to reflect the stronger membrane binding associated with a higher -sheet content found in experiments (37). Strikingly, the presence of the -lipid interaction leads to a drastic change in the nucleation rates at higher membrane fluidities across all parameter pairs investigated, as shown in Fig. 3B. This effect is caused by the progressive exposure of the membrane’s hydrophobic core and the concomitant hydrophobic contacts between lipids and proteins. Loose lipid packing and the enhanced mobility of the lipids both in and out of the membrane plane enables the participation of lipids in the – conformational change and the formation of fibrillar clusters.
The inclusion of lipids in protein aggregates efficiently drives fibril nucleation as the interaction between the lipid tails and proteins in the -sheet-prone conformation is favorable, which reduces the free-energy barrier of the conversion and stabilizes fibril nuclei. This effect is more pronounced at increasing membrane fluidities, which allow for better access to the hydrophobic regions of the lipid bilayer (Fig. 3). At the same time, a sufficiently, but not too strong, protein–membrane binding affinity enables both efficient binding and oligomer formation on the membrane without prohibiting the conformational conversion.
Free-Energy Barrier for Nucleation.
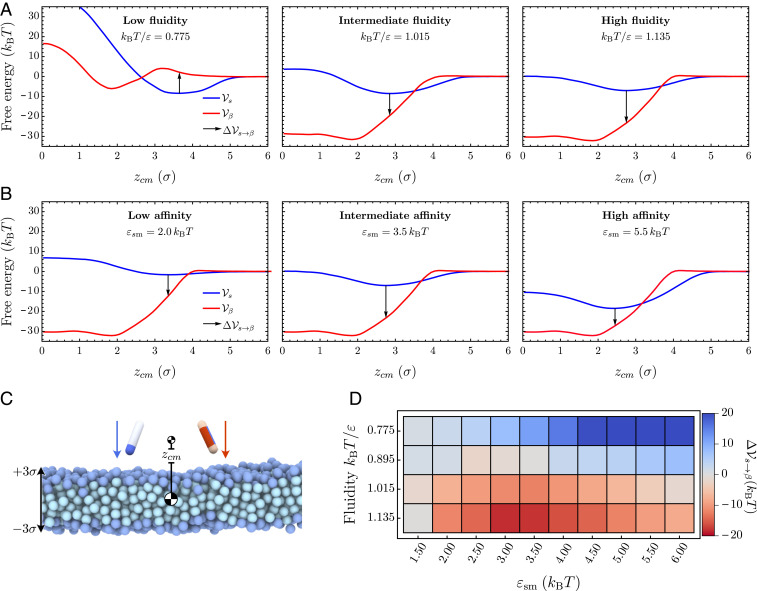
To further characterize the molecular mechanisms of membrane-driven catalysis of amyloid aggregation, we investigated the free-energy barriers connected to the different nucleation pathways. To this effect, we sample the free-energy landscape for the conformational conversion of a protein along the protein–membrane center-of-mass separation in different membrane environments, thereby setting aside the effect of surface oligomerization of the soluble proteins. First, we evaluate the free-energy profile associated with a protein in either the or conformation interacting with the membrane, while separately varying the membrane fluidity and protein–membrane affinity (Fig. 4).
Fig. 4.
Changes in the potential of mean force at increasing membrane fluidity. (A and B) The three graphs each show the free-energy profiles (red) and (blue) at increasing fluidities , and 1.135, while protein–membrane interactions are kept fixed at and (A), and at increasing protein–membrane affinities , and , while the fluidity is kept fixed at and (B). The arrows indicate the free-energy cost for conformational conversion , providing a proxy for the nucleation barrier. (C) Initial snapshot of umbrella simulations for both particle species. (D) Difference between potentials of mean force in the “” and “” conformation evaluated at the minimum of as a function of the membrane fluidity and the membrane–protein affinity .
Our simulations show that the free energy of binding between the membrane and the protein decreases with increasing fluidity, as evidenced by the results in Fig. 4A for and (see also SI Appendix, Fig. S8). Concurrently, we observe a softening of the repulsive contribution to the free-energy profile and a shift of its minimum to smaller values. This change is the combined result of membrane thinning and a deeper average insertion of the protein into the bilayer at high fluidities. Larger values of the membrane–protein affinity at fixed fluidity entail both a deeper free-energy minimum and a shift of the minimum position deeper into the hydrophobic core (Fig. 4 and SI Appendix, Fig. S8). In the case of the protein in the -conformation, the free-energy profile in the gel phase consists of a minimum located inside of the bilayer separated from the membrane surface by a small repulsive barrier, since it is energetically unfavorable for the -protein to insert into the membrane at tight lipid packing (Fig. 4 A, Left). Increasing fluidity removes this barrier, and consists of one deep well representing the strong hydrophobic binding of the protein within the lipid membrane.
To estimate the free-energy barrier for conversion between the protein’s - and -conformation, we evaluate the free-energy difference at the equilibrium position of the soluble protein (indicated as a black arrow in Fig. 4). This free-energy jump provides a proxy for the nucleation barrier in the dynamic Monte Carlo simulations, where soluble proteins first bind to the lipid and find their equilibrium position before slowly converting into the -sheet-prone conformation. As evident from Fig. 4A, as the membrane fluidity increases, the nucleation barrier gradually disappears. Deeper insertion of the soluble protein permits strong interactions between the -protein and the hydrophobic core of the membrane upon conformational conversion. Correspondingly, becomes large and negative at high membrane fluidities, resulting in the increase in the nucleation rates (Fig. 4D).
Changing the affinity can additionally influence the barrier. In the gel phase, protein insertion into the membrane is not possible, and we observe a monotonic increase of with higher protein–membrane affinities (top row of Fig. 4D). In the rate measurements reported in Fig. 3, the nucleation rate initially increases with (lower ) by virtue of surface oligomerization. This is a multiprotein effect not captured at a level of a single protein conversion. Conversely, becomes nonmonotonic in , even without the multiprotein effects at high fluidities, since soluble proteins can partially insert into the fluid membrane. The interaction between the -protein and lipid tails increases closer to the membrane center; hence, the free-energy gain of transitioning to the conformation also grows. In the strong binding regime, however, the effective binding free energy of the soluble protein grows faster than that of the -prone protein, leading to the re-entrant increase in the free-energy barrier for the conformational conversion.
Quantitative Comparison with Experimental Data.
In what follows, we compare our findings to experimental results (19), which characterize the effect of lipid chemistry on the primary nucleation rates of -synuclein in the presence of lipid membranes. Considering fully saturated lipids of different acyl chain lengths, the experimental data show that vesicles consisting of the longest acyl chains that form gel-like membranes result in the slowest amyloid aggregation rates. Conversely, the shortest lipid molecules, which have the highest solubility in water and constitute a vesicle in the most fluid phase, lead to the fastest aggregation rates (19).
Since our model is highly coarse-grained and general in nature, it remains nontrivial to map the exact lipid-bilayer phase state and protein–membrane interaction parameters from experiments to our model. Importantly, the lipid model used here does not account for the complex structures of unsaturated acyl chains. The comparison with experimental data is, therefore, restricted to fully saturated lipids, where membrane fluidity and lipid solubility are directly related.
Three different saturated lipid species were considered in the experiment, one forming gel-phase vesicles and the other two forming fluid-phase vesicles (19). We relate the membrane-phase state in experiments (controlled by acyl chain length) and simulations (controlled by ) through the measurement of the area per lipid.
Specifically, to quantitatively compare the response of nucleation kinetics across the gel-to-fluid transition in experiments and simulations, we consider the relationship between the increase in nucleation rates and area per lipid for different fluid-phase membranes relative to the gel phase, i.e., the quantities and . In simulations, the gel phase is realized at .
The increase in the area per lipid from experiments between the gel-phase and the two fluid-phase vesicles under consideration is 25% and 31, respectively. This range closely matches what we observe in simulations and falls in the medium-fluidity regime, as shown Fig. 5. This is a parameter-free measurement that we can use to describe the membrane-phase state and compare the simulation and experimental results.
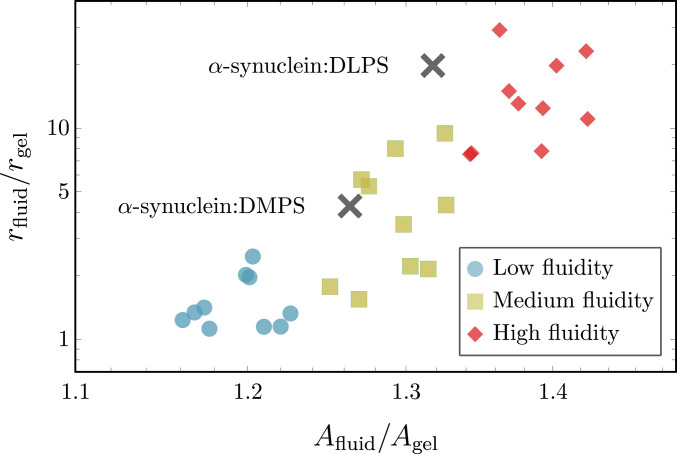
Fig. 5.
Comparison of simulation results with experimental data. Comparison of the relative increase in nucleation rates between the gel phase and fluid membranes as a function of the relative increase in area per lipid . Colored symbols show simulation results at different fluidities: blue, low fluidity (); yellow, medium fluidity (); and red, high fluidity (), with each subset containing 10 different values. The two black symbols represent experimental data from ref. 19. The experimental values for and of the fluid-phase DMPS (1,2-dimyristoyl-sn-glycero-3-phospho-L-serine) and DLPS (1,2-dilauroyl-sn-glycero-3-phospho-L-serine) vesicles are normalized to and of a gel-phase DPPS (1,2-dipalmitoyl-sn-glycero3-phospho-L-serine) vesicle, respectively.
Considering the scenario in simulations where attractive interactions between the fibril-forming protein and hydrophobic core of the bilayer are enabled, i.e., (Fig. 3B), we observe that enhanced nucleation rates directly correlate with increases in area per lipid, as shown in Fig. 5. Nucleation rates depend sensitively on the membrane structure, since direct interactions with lipid tails allow the fibril-forming proteins to sense packing defects. This is not the case for the noninteracting case (), where we find practically no variation of the speed up with changes in the area per lipid, as demonstrated in SI Appendix, Fig. S9.
Remarkably, the match between the simulation and experimental data is achieved only if direct interactions between the membrane core and the fibril-forming protein are present. Merely surface-assisted nucleation through oligomers without lipid–protein conucleation is not sufficient to explain the experimental data. Hence, the minimal model developed here appears to capture the key physics needed to reproduce and explain the experimental data on membrane-driven amyloid nucleation.
Discussion
In this work, we presented a coarse-grained simulation model to investigate how the phase state of a lipid membrane and membrane–protein binding affinity control the nucleation rates of amyloid fibrils. Depending on the specific amphipathic interaction motif of the amyloidogenic proteins, we identified two main nucleation mechanisms:
-
1)
The formation of protein oligomers on the membrane surface and subsequent nucleation into pure fibrils, and
-
2)
The stabilization of the -prone protein conformation through hydrophobic contacts with lipids and the associated mixing of membrane lipids with fibril-forming proteins enhanced by membrane fluidity.
The first mechanism determines the aggregation process when the protein cannot interact with the membrane hydrophobic core. The efficiency of this mechanism is dictated predominantly by the protein–membrane affinity, which stabilizes oligomers on the membrane surface. The enhancement of nucleation is limited to a narrow regime of protein–membrane interaction in this case. Interestingly, this effect can be inhibited at high lipid mobilities, where the formation of stable oligomers becomes prohibited. This nicely illustrates that the membrane fluidity per se does not catalyze nucleation, but that specific interactions between the protein and the lipids, which often correlate with lipid fluidity, are required.
In fact, when interactions of the protein with the hydrophobic membrane core are present, a second, more powerful nucleation mechanism is enabled. In this regime, lipids can conucleate with proteins, which effectively lowers the nucleation barrier for their conformational conversion and can result in the formation of lipoprotein clusters. This mechanism depends crucially on the membrane fluidity and is enhanced by the presence of packing defects and lipid extraction from the bilayer. Indeed, considering the scenario where the protein in the -sheet-prone state interacts with the lipid tails, we observe a 250-fold speed-up of the nucleation rates between the slowest and fastest cases in the gel and fluid phase, respectively (Fig. 3B). This is contrasted by only a 20-fold speed-up for the case when the protein cannot interact with the lipid tails (), shown in Fig. 3A.
Notably, we demonstrate that the window of effective nucleation is significantly broadened by the interaction between the protein and the membrane core, leading to even more efficient amyloid nucleation over a wider range of membrane fluidities and protein affinities.
It is important to note that the membrane fluidity in our model is controlled only by interlipid interactions; hence, the fluidity and the ability of lipids to be extracted from the bilayer are necessarily correlated in our model. This is a good representation for saturated lipids, where lipid solubility controls the phase state of the membrane. However, membrane-phase behavior can also be influenced by lipid geometry, as in the case of polyunsaturated lipids. In such a system, the membrane fluidity and lipid solubility are not necessarily correlated in a straightforward way (19).
Nevertheless, it can be expected that increases in fluidity of unsaturated lipid membranes do not necessarily entail faster aggregation kinetics. In contrast to the case of saturated lipids, in the unsaturated case, a high degree of packing defects often goes along with a low lipid solubility. This can make absorption of proteins into the membrane core more likely, hindering coaggregation by lipid extraction, and thereby inhibiting fibril formation. In fact, the presence of unsaturated fluid-phase lipid vesicles was recently reported to lead to slower -synuclein aggregation kinetics than saturated gel-phase vesicles (26). Moreover, membrane inclusions such as cholesterol (25) or proteins can also control the membrane-phase behavior and have a nontrivial effect on the ability to extract lipids from the bilayer. Our simulations do not capture these more complex couplings.
We found that the nature of the interactions between the protein and the membrane is of key importance in determining the aggregation pathway and the protein’s capacity to disrupt membranes. In our model, the choice of two separate side patches is necessary to capture the incorporation of lipids into amyloid structures observed in experiments. Without a separate protein–lipid patch, lipids are pushed out of fibrils, and mixed aggregates cannot be achieved, ruling out the pathway to lipid-rich aggregates.
Hence, the imbalance between membrane–membrane and membrane–protein interactions is an important factor not only in controlling the rates and pathways of amyloid aggregation, but also in determining whether amyloid aggregates cause membrane disruption and permeability underlying cytotoxic mechanisms (42). This is also highlighted in a recent experimental study, which shows that -synuclein oligomers require a -sheet core to insert themselves into the membrane bilayer and drive disruption of the bilayer linked to cytotoxic effects (37).
The physical principles identified in this work are general in nature and applicable to a wide range of amyloid-forming proteins, irrespective of their sequence or fold. Even more, the presented mechanisms can also be of relevance to membrane-driven aggregation of other proteins that involve conformational changes and hydrophobic interactions. The computer model developed here also opens the way for testing strategies to bypass membrane-assisted amyloid aggregation, which can, for instance, involve targeting the interaction between proteins and membrane hydrophobic core or altering the lipid composition to prevent protein–lipid conucleation.
Materials and Methods
Simulation Model.
The coarse-grained simulation model employed in this study merges a minimal model of amyloid nucleation in solution (29) with a lipid-bilayer implicit solvent model (28). Proteins are represented by hard spherocylinders of diameter and length and can exist in a soluble and a -sheet-forming conformation, as discussed in Computational Model. The membrane lipids are represented by one head bead and two tail beads. Both the dynamics of the membrane–protein system and the conformational switches of the proteins are simulated by using a Metropolis Monte Carlo algorithm.
As depicted in Fig. 1A, the soluble protein has an attractive end cap, which allows it to form oligomeric structures. The pairwise interaction between two soluble protein tips at distance is given by
| [1] |
with in this study. In the -sheet-forming conformation, the spherocylinder has two attractive side patches instead of a tip interaction: one patch with affinity for the membrane, the other with affinity for other proteins.
The attractive protein side patch has the length of and an opening angle of . If the two patches are facing each other the corresponding proteins interact through the potential
| [2] |
where is the minimal distance between the interacting hydrophobic patches and .
The interaction between soluble and -prone proteins is set by
| [3] |
where is the shortest distance between the attractive tip of the soluble protein and the side patch of the -prone protein and .
The coarse-grained implicit solvent model used here for the lipid membrane is defined in ref. 28. The membrane consists of three-bead lipids, which self-assemble into a stable bilayer.
The binding of the soluble protein to the membrane lipids is controlled by the interaction potential
| [4] |
where is scaled by 1, 1/2, or 1/4 if the interacting lipid bead is either the head bead or the first or second tail bead.
The second lipophilic side patch on the -prone protein also has a length of and an opening angle of and is oriented opposite to the patch. It interacts only with the hydrophobic tail beads of the lipids via
| [5] |
where denotes the minimal distance between the attractive patch and the corresponding lipid bead. The range of between the proteins and the lipid is set to . The interaction strength is set to 0 or , depending on the specific case under consideration.
Lipid beads interact repulsively via a Weeks–Chandler–Anderson potential given by
| [6] |
where , , and . Beads of a three-bead lipid molecule are connected by two finitely extensible nonlinear elastic bonds, described by
| [7] |
where and . Additionally, the head and second tail bead interact via the bending potential
| [8] |
where . The hydrophobic interactions between the lipid tails are accounted for by setting the attractive interaction between the two tail beads to
| [9] |
with the and being the depth and the range of the attractive potential, respectively. In this work, we set and vary to prepare the lipid membrane in different phase state across the gel and fluid regime. In particular, we vary between 0.775 (gel phase) and 1.135 (fluid). Note that the gel–fluid phase boundary is approximately located at .
Monte Carlo Scheme.
The dynamics of the membrane–protein system is simulated by a Monte Carlo scheme, which includes translational and rotational moves of individual particles. Additionally, the conversion between the soluble and -prone conformation of the protein is also facilitated by a Metropolis criterion. This nucleated conformational change is accepted with probability , where denotes the energy difference between the and -prone state. Switches between the two possible states are attempted with a probability of 0.01 per time step. These conformational changes between the and the state are penalized by the energy barrier .
The simulations were carried out in a cubic simulation box with periodic boundaries in the and directions. The height of the box was kept constant at . The lengths and were allowed to fluctuate to keep the surface tension of the membrane constant at zero. Soluble proteins were equilibrated according to a grand-canonical ensemble with a fixed chemical potential, keeping the concentration of soluble proteins constant in solution. Note that -prone proteins followed the canonical ensemble. The membrane consisted of 30 30 lipids in each leaf, amounting to 1,800 three-bead lipids in total. In a typical simulation run, proteins initially adsorbed to the membrane while being maintained in the soluble conformation. After the equilibrium surface coverage was reached, the proteins were allowed to switch between the soluble and the -sheet-prone state.
Supplementary Material
Acknowledgments
We thank T. C. T. Michaels for reading the manuscript. This work was supported by the Academy of Medical Science (J.K. and A.Š.), the Cambridge Center for Misfolding Diseases (T.P.J.K.), the Biotechnology and Biological Sciences Research Council (T.P.J.K.), the Frances and Augustus Newman Foundation (T.P.J.K.), the European Research Council Grant PhysProt Agreement 337969, the Wellcome Trust (A.Š. and T.P.J.K.), the Royal Society (A.Š.), the Medical Research Council (J.K. and A.Š.), and the UK Materials and Molecular Modeling Hub for computational resources, which is partially funded by Engineering and Physical Sciences Research Council Grant EP/P020194/1.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2007694117/-/DCSupplemental.
Data Availability.
All study data are included in the article and SI Appendix.
References
- 1.Dobson C. M., The amyloid phenomenon and its links with human disease. Cold Spring Harb. Perspectives Biol. 9, a023648 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Knowles T. P., Mezzenga R., Amyloid fibrils as building blocks for natural and artificial functional materials. Adv. Mater. 28, 6546–6561 (2016). [DOI] [PubMed] [Google Scholar]
- 3.Auer S., Trovato A., Vendruscolo M., A condensation-ordering mechanism in nanoparticle-catalyzed peptide aggregation. PLoS Comput. Biol. 5, e1000458 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Cabaleiro-Lago C., Szczepankiewicz O., Linse S., The effect of nanoparticles on amyloid aggregation depends on the protein stability and intrinsic aggregation rate. Langmuir 28, 1852–1857 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.John T., et al. , Impact of nanoparticles on amyloid peptide and protein aggregation: A review with a focus on gold nanoparticles. Nanoscale 10, 20894–20913 (2018). [DOI] [PubMed] [Google Scholar]
- 6.Morriss-Andrews A., Shea J. E., Kinetic pathways to peptide aggregation on surfaces: The effects of -sheet propensity and surface attraction. J. Chem. Phys. 136, 065103 (2012). [DOI] [PubMed] [Google Scholar]
- 7.Vácha R., Linse S., Lund M., Surface effects on aggregation kinetics of amyloidogenic peptides. J. Am. Chem. Soc. 136, 11776–11782 (2014). [DOI] [PubMed] [Google Scholar]
- 8.Kashchiev D., Auer S., Nucleation of amyloid fibrils. J. Chem. Phys. 132, 215101 (2010). [DOI] [PubMed] [Google Scholar]
- 9.Zhang J., Muthukumar M., Simulations of nucleation and elongation of amyloid fibrils. J. Chem. Phys. 130, 035102 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhang L., Schmit J. D., Theory of amyloid fibril nucleation from folded proteins. Isr. J. Chem. 57, 738–749 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Törnquist M., et al. , Secondary nucleation in amyloid formation. Chem. Commun. 54, 8667–8684 (2018). [DOI] [PubMed] [Google Scholar]
- 12.Šaric A., et al. , Physical determinants of the self-replication of protein fibrils. Nat. Phys. 12, 874–880 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Auluck P. K., Caraveo G., Lindquist S., .-Synuclein: Membrane interactions and toxicity in Parkinson’s disease. Annu. Rev. Cell Dev. Biol. 26, 211–233 (2010). [DOI] [PubMed] [Google Scholar]
- 14.Fusco G., et al. , Structural ensembles of membrane-bound -synuclein reveal the molecular determinants of synaptic vesicle affinity. Sci. Rep. 6, 27125 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Khondker A., Alsop R. J., Rheinstädter M. C., Membrane-accelerated amyloid- aggregation and formation of cross- sheets. Membranes 7, 49 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Burke K. A., Yates E. A., Legleiter J., Biophysical insights into how surfaces, including lipid membranes, modulate protein aggregation related to neurodegeneration. Front. Neurol. 4, 1–17 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Giehm L., Oliveira C. L. P., Christiansen G., Pedersen J. S., Otzen D. E., SDS-induced fibrillation of -synuclein: An alternative fibrillation pathway. J. Mol. Biol. 401, 115–133 (2010). [DOI] [PubMed] [Google Scholar]
- 18.Galvagnion C., et al. , Lipid vesicles trigger -synuclein aggregation by stimulating primary nucleation. Nat. Chem. Biol. 11, 229–234 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Galvagnion C., et al. , Chemical properties of lipids strongly affect the kinetics of the membrane-induced aggregation of -synuclein. Proc. Natl. Acad. Sci. U.S.A. 113, 7065–7070 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yang M., et al. , Gel phase membrane retards amyloid -peptide (1-42) fibrillation by restricting slaved diffusion of peptides on lipid bilayers. Langmuir 34, 8408–8414 (2018). [DOI] [PubMed] [Google Scholar]
- 21.Choucair A., Chakrapani M., Chakravarthy B., Katsaras J., Johnston L. J., Preferential accumulation of A(1-42) on gel phase domains of lipid bilayers: An AFM and fluorescence study. Biochim. Biophys. Acta Biomembr. 1768, 146–154 (2007). [DOI] [PubMed] [Google Scholar]
- 22.Bokvist M., Lindström F., Watts A., Gröbner G., Two types of Alzheimer’s -amyloid (1-40) peptide membrane interactions: Aggregation preventing transmembrane anchoring versus accelerated surface fibril formation. J. Mol. Biol. 335, 1039–1049 (2004). [DOI] [PubMed] [Google Scholar]
- 23.Hane F., Drolle E., Gaikwad R., Faught E., Leonenko Z., Amyloid- aggregation on model lipid membranes: An atomic force microscopy study. J. Alzheim. Dis. 26, 485–494 (2011). [DOI] [PubMed] [Google Scholar]
- 24.Kremer J. J., Pallitto M. M., Sklansky D. J., Murphy R. M., Correlation of -amyloid aggregate size and hydrophobicity with decreased bilayer fluidity of model membranes. Biochemistry 39, 10309–10318 (2000). [DOI] [PubMed] [Google Scholar]
- 25.Habchi J., et al. , Cholesterol catalyzes A42 aggregation through a heterogeneous nucleation pathway in the presence of lipid membranes. Nat. Chem. 10, 673–683 (2018). [DOI] [PubMed] [Google Scholar]
- 26.O’Leary E. I., Jiang Z., Strub M. P., Lee J. C., Effects of phosphatidylcholine membrane fluidity on the conformation and aggregation of N-terminally acetylated -synuclein. J. Biol. Chem. 293, 11195–11205 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hellstrand E., Nowacka A., Topgaard D., Linse S., Sparr E., Membrane lipid Co-aggregation with -synuclein fibrils. PloS One 8, e77235 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cooke I. R., Deserno M., Solvent-free model for self-assembling fluid bilayer membranes: Stabilization of the fluid phase based on broad attractive tail potentials. J. Chem. Phys. 123, 224710 (2005). [DOI] [PubMed] [Google Scholar]
- 29.Šarić A., Chebaro Y. C., Knowles T. P. J., Frenkel D., Crucial role of nonspecific interactions in amyloid nucleation. Proc. Natl. Acad. Sci. U.S.A. 111, 17869–17874 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Michaels T. C., et al. , Reaction rate theory for supramolecular kinetics: Application to protein aggregation. Mol. Phys. (2018). [Google Scholar]
- 31.Michaels T. C., et al. , Dynamics of oligomer populations formed during the aggregation of Alzheimer’s A42 peptide. Nat. Chem. 12, 497 (2020). [DOI] [PubMed] [Google Scholar]
- 32.Dear A. J., et al. , Identification of on- and off-pathway oligomers in amyloid fibril formation. Chem. Sci. 11, 6236–6247 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fusco G., et al. , Direct observation of the three regions in -synuclein that determine its membrane-bound behavior. Nat. Commun. 5, 3827 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hebda J. A., Miranker A. D., The interplay of catalysis and toxicity by amyloid intermediates on lipid bilayers: Insights from type II diabetes. Annu. Rev. Biophys. 38, 125–152 (2009). [DOI] [PubMed] [Google Scholar]
- 35.Terzi E., Hölzemann G., Seelig J., Self-association of -amyloid peptide (1-40) in solution and binding to lipid membranes. J. Mol. Biol. 252, 633–642 (1995). [DOI] [PubMed] [Google Scholar]
- 36.Matsuzaki K., Physicochemical interactions of amyloid -peptide with lipid bilayers. Biochim. Biophys. Acta Biomembr. 1768, 1935–1942 (2007). [DOI] [PubMed] [Google Scholar]
- 37.Fusco G., et al. , Structural basis of membrane disruption and cellular toxicity by a-synuclein oligomers. Science 358, 1440–1443 (2017). [DOI] [PubMed] [Google Scholar]
- 38.Ciudad S., et al. , A(1-42) tetramer and octamer structures reveal edge conductivity pores as a mechanism for membrane damage. Nat. Commun. 11, 3014 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cohen S. I., et al. , Distinct thermodynamic signatures of oligomer generation in the aggregation of the amyloid- peptide. Nat. Chem. 10, 523–531 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Šarić A., Michaels T. C. T., Zaccone A., Knowles T. P. J., Frenkel D., Kinetics of spontaneous filament nucleation via oligomers: Insights from theory and simulation. J. Chem. Phys. 145, 211926 (2016). [DOI] [PubMed] [Google Scholar]
- 41.Chaudhary H., Subramaniam V., Claessens M. M., Direct visualization of model membrane remodeling by -synuclein fibrillization. ChemPhysChem 18, 1620–1626 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ingelsson M., Alpha-synuclein oligomers-neurotoxic molecules in Parkinson’s disease and other Lewy body disorders. Front. Neurosci. 10, 408 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and SI Appendix.