Summary
Exposures with multigenerational effects have profound implications for public health, affecting increasingly more people as the exposed population reproduces. Multigenerational studies, however, are susceptible to informative cluster size, occurring when the number of children to a mother (the cluster size) is related to their outcomes, given covariates. A natural question then arises: what if some women bear no children at all? The impact of these potentially informative empty clusters is currently unknown. This article first evaluates the performance of standard methods for informative cluster size when cluster size is permitted to be zero. We find that if the informative cluster size mechanism induces empty clusters, standard methods lead to biased estimates of target parameters. Joint models of outcome and size are capable of valid conditional inference as long as empty clusters are explicitly included in the analysis, but in practice empty clusters regularly go unacknowledged. In contrast, estimating equation approaches necessarily omit empty clusters and therefore yield biased estimates of marginal effects. To resolve this, we propose a joint marginalized approach that readily incorporates empty clusters and even in their absence permits more intuitive interpretations of population-averaged effects than do current methods. Competing methods are compared via simulation and in a study of the impact of in-utero exposure to diethylstilbestrol on the risk of attention-deficit/hyperactivity disorder (ADHD) among 106 198 children to 47 540 nurses from the Nurses Health Study.
Keywords: Clusters of size zero, Informative cluster size, Joint marginalized models, Transgenerational
1. Introduction
Toxicants that act epigenetically, with downstream effects on the children and grandchildren of those directly exposed, motivate recent interest in multigenerational studies, which span two or more generations. Veenendaal and others (2013), for example, studied the effect of famine on third generation body mass index. More recently, Qian and others (2017) studied the transmission of low birthweight between generations, while Kioumourtzoglou and others (2018) examined the impact of in-utero diethylstibelstrol exposure among nurses on attention-deficit/hyperactivity disorder (ADHD) in their children.
An important feature of these multigenerational studies is that the outcomes among the study units/offspring in a given generation may be related to the number of offspring. For example, in-utero toxicity may affect both downstream outcomes and fertility. In the statistical literature, this phenomenon is referred to as informative cluster size, and a number of methods for both marginal (population-averaged) and conditional (cluster-specific) inference in the presence of informative cluster size have been described. Hoffman and others (2001) proposed a within-cluster resampling approach to marginal inference, and Williamson and others (2003) and Benhin and others (2005) developed an asymptotically equivalent but computationally feasible approach based on weighted estimating equations. Focusing instead on conditionally specified models, Dunson and others (2003) and Gueorguieva (2005) proposed joint models of cluster size and outcome, linking the two via shared random effects. Neuhaus and McCulloch (2011) argued that ignoring informative cluster size by treating size as fixed and fitting the outcome-only generalized linear mixed model (GLMM) often leads only to bias in associations of covariates included in the random effects specification.
Common to the vast majority of this literature, and indeed the broader literature on hierarchical models, is the implicit premise that a cluster is defined through the existence of at least one cluster member. In multigenerational studies, however, elevated toxicity or large doses of some unobserved exposure may not just limit the number of offspring in a subsequent generation but may prevent some women from bearing any children at all. That is, the observed data may consist of “clusters” with no study units. We refer to this phenomenon as the potential for informatively empty clusters and note that, to the best of our knowledge, no methods have been developed that directly address it. In describing shared fixed effects models, Allen and Barnhart (2005) asserted that their ability to include empty clusters would avoid what they call “zero-length bias”, despite the fact that these models do not permit conditional dependence between size and outcome, and thus we would not expect informativeness to manifest. Dependence is in fact permitted in shared random effects models, however, and Iosif (2007) and Iosif and Sampson (2014) similarly cited the avoidance of this bias as a potential benefit over estimating equation approaches. Nevertheless, no evidence of such bias has been reported in the literature, and the conditions under which emptiness causes bias are not understood.
In this article, we make two major contributions. First, we evaluate the performance of existing methods for informative cluster size when some of the clusters are of size zero. In doing so we find that adaptations of existing methods for joint modeling of cluster size and outcomes can yield valid conditional estimation and inference in the presence of informative emptiness. Second, we develop a novel marginalized joint modeling approach that permits marginal inference under informative emptiness. As a byproduct, the proposed framework offers a number of advantages even in the absence of empty clusters: not only does it share the benefits of the standard joint modeling approach, permitting estimation of covariate-size associations, and characterization of the size–outcome relationship (Dunson and others, 2003; Gueorguieva, 2005), but the marginalized formulation further provides likelihood-based testing and prediction, while permitting population-averaged inference (Heagerty, 1999; Heagerty and others, 2000). Moreover, we argue that it provides more intuitive interpretations of marginal effects than do current approaches, avoiding the mention of “typical cluster-members” or “typical members of typical clusters” that accompanies standard estimating equation approaches (Williamson and others, 2003; Seaman and others, 2014).
The remainder of the article is organized as follows. We define informative emptiness in Section 2. We then outline existing methods for addressing informative cluster size that could, in principle, be used to analyze multigenerational studies, and describe their relationship to emptiness in Section 3. In Section 4, we propose a novel joint marginalized model that accommodates informative cluster size both when clusters are potentially empty and otherwise. In Sections 5 and 6, we compare methods via simulation study and a motivating study of in-utero exposure to diethylstilbestrol on ADHD outcomes among 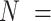 106 198 children to
106 198 children to 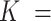 47 540 nurses, as described in Kioumourtzoglou and others (2018). We conclude with a discussion in Section 7.
47 540 nurses, as described in Kioumourtzoglou and others (2018). We conclude with a discussion in Section 7.
2. Informative cluster size and emptiness
In the standard cluster-correlated data setting, one typically distinguishes between marginal and conditional models, parameterized by population-averaged and cluster-specific effects. Let 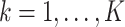 index the clusters. For the
index the clusters. For the 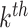 cluster, let
cluster, let 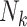 be the cluster size and let
be the cluster size and let 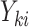 be the outcome and
be the outcome and 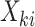 be the vector of covariates (including one) for the
be the vector of covariates (including one) for the 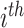 observation, where
observation, where 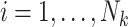 . A marginal model for the mean of
. A marginal model for the mean of 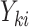 given
given 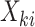 is
is
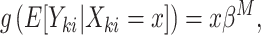 |
(2.1) |
where 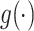 is a link function, and estimation can proceed via generalized estimating equations (Liang and Zeger, 1986). Alternatively, a conditional model may be specified, as in the GLMM
is a link function, and estimation can proceed via generalized estimating equations (Liang and Zeger, 1986). Alternatively, a conditional model may be specified, as in the GLMM
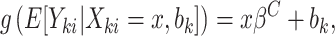 |
where 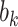 is a random effect with an assumed distribution, and estimation follows from standard maximum likelihood theory (McCulloch and others, 2008) or by Bayesian Markov chain Monte Carlo (Gelman and others, 2013).
is a random effect with an assumed distribution, and estimation follows from standard maximum likelihood theory (McCulloch and others, 2008) or by Bayesian Markov chain Monte Carlo (Gelman and others, 2013).
When cluster size is not constant, the potential for informative cluster size arises. When marginal inference is of interest, cluster size is deemed informative (or nonignorable) if 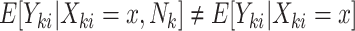 (Hoffman and others, 2001; Williamson and others, 2003; Benhin and others, 2005). Seaman and others (2014) offers a slightly different definition:
(Hoffman and others, 2001; Williamson and others, 2003; Benhin and others, 2005). Seaman and others (2014) offers a slightly different definition: 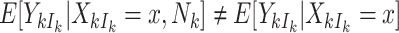 , where
, where 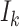 is a discrete uniform random variable on
is a discrete uniform random variable on  . Intuitively, this would occur if some factor not included in
. Intuitively, this would occur if some factor not included in 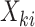 was associated both with cluster size
was associated both with cluster size 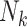 and outcome
and outcome 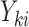 . In the conditional paradigm, cluster size is deemed informative if
. In the conditional paradigm, cluster size is deemed informative if 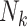 and
and 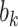 are dependent (Dunson and others, 2003; Gueorguieva, 2005; Neuhaus and McCulloch, 2011; Seaman and others, 2014). In either case, standard methods yield biased estimates of target parameters under informative cluster size, and extensions to both have been proposed to address this problem.
are dependent (Dunson and others, 2003; Gueorguieva, 2005; Neuhaus and McCulloch, 2011; Seaman and others, 2014). In either case, standard methods yield biased estimates of target parameters under informative cluster size, and extensions to both have been proposed to address this problem.
A new problem arises when cluster size is random: clusters may be entirely empty (i.e. 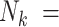 0). Such is the case if a woman bears no children. In particular, if some latent factor affects both cluster size and outcomes, extreme factor levels may lead to clusters of size zero. We call this informative cluster size with informative emptiness. In Section 3, we describe extensions to GLMMs and generalized estimating equations for accommodating informative cluster size in multigenerational studies, and explore the extent to which their naïve application yields valid estimation and inference in the presence of informative emptiness.
0). Such is the case if a woman bears no children. In particular, if some latent factor affects both cluster size and outcomes, extreme factor levels may lead to clusters of size zero. We call this informative cluster size with informative emptiness. In Section 3, we describe extensions to GLMMs and generalized estimating equations for accommodating informative cluster size in multigenerational studies, and explore the extent to which their naïve application yields valid estimation and inference in the presence of informative emptiness.
We note that emptiness may not necessarily be informative, even in situations with informative cluster size and empty clusters. Many women choose not to have children for a variety of reasons, and number of children may be related to the informativeness mechanism only among women who choose to have children. Further, if some women who do intend to have children are unable to because of the informativeness mechanism, then non-informative and informative emptiness may co-occur. Although this article focuses on informatively empty clusters, we consider an extension in Section 4.3 that permits both non-informatively and informatively empty clusters concurrently.
3. Current methods for informative cluster size in multigenerational studies
While informative cluster size is a natural concern in multigenerational epidemiology studies, it has been ignored by the preponderance of such studies. Indeed, to the best of our knowledge, Kioumourtzoglou and others (2018) is the only multigenerational study that has highlighted informative cluster size as a potential challenge. Motivated by this we summarize existing methods that could, in principle, be used in multigenerational settings to fit conditional (cluster-specific) and marginal (population-averaged) models in the presence of informative cluster size. Furthermore, for each such method, we describe the extent to which the phenomenon of empty clusters is handled, if at all.
3.1. Methods for conditional inference
3.1.1. Joint modeling of cluster size and outcome.
When interest lies in cluster-specific parameters, a shared random effects model may be specified to jointly model cluster size and unit-level outcomes. An example is
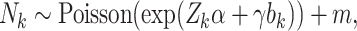 |
(3.2) |
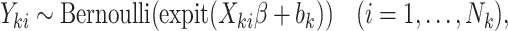 |
(3.3) |
where 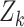 is a vector of cluster-level covariates (including one),
is a vector of cluster-level covariates (including one), 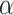 is a vector of regression coefficients,
is a vector of regression coefficients, 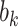 is a shared random intercept that is scaled by
is a shared random intercept that is scaled by  , and
, and 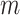 is a minimum cluster size offset (Dunson and others, 2003; Gueorguieva, 2005).
is a minimum cluster size offset (Dunson and others, 2003; Gueorguieva, 2005).
Joint models of size and outcome have a built-in capacity to accommodate emptiness, by setting 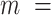 0 and including clusters of size zero in the likelihood (Iosif and Sampson, 2014), i.e.
0 and including clusters of size zero in the likelihood (Iosif and Sampson, 2014), i.e.
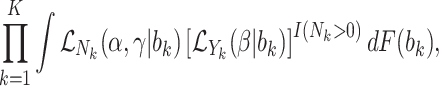 |
(3.4) |
where 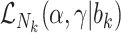 is the likelihood contribution of the cluster size
is the likelihood contribution of the cluster size 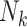 , and
, and 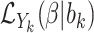 is the contribution of the outcomes, when they exist, and we integrate over the random effects distribution
is the contribution of the outcomes, when they exist, and we integrate over the random effects distribution 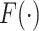 .
.
We believe, however, that this is often not executed in practice. For example, in the Nurses Health Study II example, nurses with no children were excluded from the dataset. Indeed it is not difficult to imagine a situation wherein researchers don’t even collect clusters of size zero at all, since they contain no outcomes. While it is not within the scope of this article to report a comprehensive review of the clinical literature, we are not aware of any studies incorporating empty clusters. We recommend that researchers take care to observe any empty clusters and include them in joint modeling analysis when conditional inference is of interest.
3.1.2. Outcome-only generalized linear mixed model.
Although joint modeling provides a coherent framework for addressing dependence between the cluster size and outcomes, Neuhaus and McCulloch (2011) argue that it often suffices to treat cluster size as fixed and fit the GLMM in (3.3). They showed that even if the true data-generating mechanism is a joint model, as in (3.2)–(3.3), fitting the usual GLMM amounts to misspecifying the random effects distribution. This yields little bias for association parameters corresponding to covariates not included in the random effects specification (Neuhaus and others, 1992), but other parameters (the intercept, associations for other covariates, variance components) can be seriously biased (Heagerty and Kurland, 2001). Informatively empty clusters exacerbate this problem, so we expect this approach to be inadequate whenever covariates of interest enter into the random component of the model.
3.2. Methods for marginal inference
3.2.1. Independence estimating equations.
When interest lies in marginal inference, one approach is to solve the so-called independence estimating equations
 |
where  is the marginal mean and
is the marginal mean and 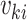 is the working variance. Intuitively, clusters contribute information in proportion to their size; equivalently, all cluster-members contribute equally. The solution to the independence estimating equations is consistent for
is the working variance. Intuitively, clusters contribute information in proportion to their size; equivalently, all cluster-members contribute equally. The solution to the independence estimating equations is consistent for 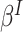 defined by the model
defined by the model
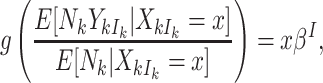 |
(3.5) |
where 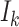 is a discrete uniform random variable on
is a discrete uniform random variable on 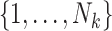 (Seaman and others, 2014), and hence we interpret
(Seaman and others, 2014), and hence we interpret 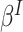 for a contrast of random cluster-members from the population of cluster-members.
for a contrast of random cluster-members from the population of cluster-members.
This approach balances the contributions of all cluster-members, so non-existent cluster-members (when 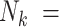 0) rightly need not contribute. As such, if interest is in inference with respect to random cluster-members (
0) rightly need not contribute. As such, if interest is in inference with respect to random cluster-members (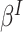 ) in the presence of emptiness, one need look no further.
) in the presence of emptiness, one need look no further.
3.2.2. Cluster size weighted estimating equations.
In contrast, clusters of all sizes contribute equally to the cluster size weighted estimating equation approach (Williamson and others, 2003; Benhin and others, 2005), defined by solving
 |
We again adopt working independence, but extensions have been considered elsewhere (Chiang and Lee, 2008; Pavlou and others, 2013). The resulting estimator is consistent for  defined by
defined by
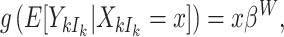 |
(3.6) |
(Williamson and others, 2003; Benhin and others, 2005), and interpretations here refer to a random member of a random cluster. Intuitively, by balancing the contributions of all clusters, this approach downweights the largest clusters and upweights the smallest. Despite being the smallest of all, empty clusters are nevertheless effectively assigned zero weight. As such, cluster size weighted estimating equations are likely inadequate in settings where clusters are subject to informative emptiness.
4. Proposed methodology: joint marginalized model
4.1. Model specification
In the absence of informative cluster sizes, marginalized models have been proposed as a means of obtaining population-averaged inference, whilst retaining the appealing features of a likelihood-based analysis (Heagerty, 1999; Heagerty and others, 2000). Such models specify a marginal mean model and a conditional dependence model, linking the two via an integral equation. We propose an approach that embeds the marginalized modeling framework within the joint modeling of cluster size and outcome, which may be used with or without informatively empty clusters.
Define 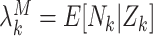 to be the marginal mean size of the
to be the marginal mean size of the 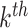 cluster and
cluster and 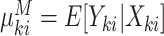 to be the marginal mean outcome of the
to be the marginal mean outcome of the 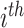 member of the
member of the 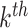 cluster (where
cluster (where 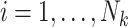 for clusters with
for clusters with 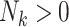 ), as in (2.1). Analogously, define
), as in (2.1). Analogously, define 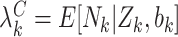 and
and 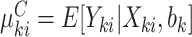 , conditional on a shared random effect
, conditional on a shared random effect 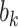 . Let
. Let 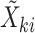 be a vector whose elements are a subset of
be a vector whose elements are a subset of 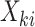 and let
and let  be a diagonal matrix whose elements are a subset of
be a diagonal matrix whose elements are a subset of 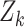 . The proposed joint marginalized model is
. The proposed joint marginalized model is
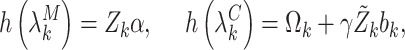 |
(4.7) |
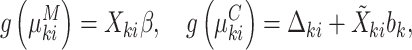 |
(4.8) |
where 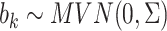 , and
, and 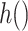 and
and 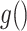 are link functions. By iterated expectation, the implicitly defined conditional parameters
are link functions. By iterated expectation, the implicitly defined conditional parameters 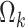 and
and 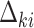 are governed by the following integral equations
are governed by the following integral equations
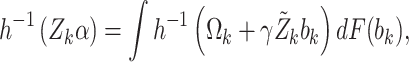 |
(4.9) |
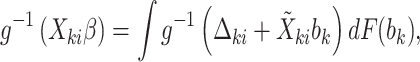 |
(4.10) |
where  is the (Normal) distribution of
is the (Normal) distribution of 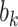 . Given the marginal parameters
. Given the marginal parameters  , the conditional parameters
, the conditional parameters 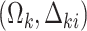 can be computed by solving equations (4.9) and (4.10), at which point an implied conditional model is fully specified and a likelihood can be computed as usual from a joint model. Intractable integrals in the equations above and in the marginalized likelihood can be approximated via Gaussian or adaptive quadrature. Theoretical details can be found in Appendix A of the supplementary material available at Biostatistics online.
can be computed by solving equations (4.9) and (4.10), at which point an implied conditional model is fully specified and a likelihood can be computed as usual from a joint model. Intractable integrals in the equations above and in the marginalized likelihood can be approximated via Gaussian or adaptive quadrature. Theoretical details can be found in Appendix A of the supplementary material available at Biostatistics online.
To complete the model specification, we make distributional assumptions about both the cluster size and outcomes. Maximum likelihood estimation and inference then follow in the usual way (see Appendix A of the supplementary material available at Biostatistics online). One example is a Poisson-Bernoulli model,
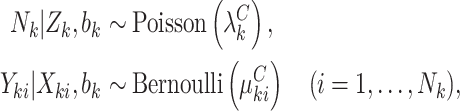 |
(4.11) |
but any alternative count distribution for the cluster size may be assumed; see Appendix B of the supplementary material available at Biostatistics online for details regarding a negative-binomial model. Standard errors are computed via the inverse of the information, which we compute via numerically differentiated Hessian for computational efficiency. Software implementation in R is available online at github.com/glenmcgee/InformativeEmptiness.
In principle this is simply a reparametrization of the established joint conditional approach, which models 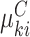 directly in (3.3). The marginal mean model specification, however, enables one to infer population-averaged effects, while incorporating cluster size directly in the likelihood. As a result, many of the benefits of (conditional) joint modeling apply here, too. In particular, we are able to study the outcome–size relationship, along with the covariate-size associations; likelihood-based testing and cluster-specific prediction are available as well. Crucially, unlike standard marginal methods, empty clusters feature explicitly in the analysis (as in expression 3.4).
directly in (3.3). The marginal mean model specification, however, enables one to infer population-averaged effects, while incorporating cluster size directly in the likelihood. As a result, many of the benefits of (conditional) joint modeling apply here, too. In particular, we are able to study the outcome–size relationship, along with the covariate-size associations; likelihood-based testing and cluster-specific prediction are available as well. Crucially, unlike standard marginal methods, empty clusters feature explicitly in the analysis (as in expression 3.4).
4.2. Interpretation
Absent informative cluster size, one typically estimates population-averaged effects by first writing down a marginal model of interest and then selecting an estimation approach (such as generalized estimating equations with some working correlation structure). In the standard approach to marginal inference under informative cluster size (see Section 3.2), this order is reversed: one first selects a weighting scheme (balancing either cluster or cluster-member contributions) with an eye to parameter interpretations, and this then implies a model for either  or
or 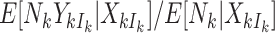 . In either case, however, we believe that this is unsatisfactory. The analyst is forced to concede to a model, and hence an interpretation with respect to either a random member of a random cluster or a random cluster-member, that is not necessarily the original model of interest one would write down in the absence of informative cluster size.
. In either case, however, we believe that this is unsatisfactory. The analyst is forced to concede to a model, and hence an interpretation with respect to either a random member of a random cluster or a random cluster-member, that is not necessarily the original model of interest one would write down in the absence of informative cluster size.
Although interest sometimes lies only in estimating some contrast, it can be constructive to contextualize covariate effects by considering how the data were generated, particularly with complex data structures (e.g. multigenerational studies). Unfortunately, it is unclear how to infer data generating mechanisms from the models induced by the estimating equations approaches.
The proposed joint marginalized modeling approach, however, permits one to directly specify a model for 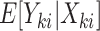 for
for 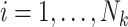 (when
(when 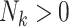 ). Interpretations therefore pertain to every existing cluster member, avoiding the need to equivocate about random clusters or random members thereof. Not only is this more intuitive, but it naturally provides a possible data-generating mechanism, thus offering an advantage over standard estimating equations approaches even in the absence of empty clusters.
). Interpretations therefore pertain to every existing cluster member, avoiding the need to equivocate about random clusters or random members thereof. Not only is this more intuitive, but it naturally provides a possible data-generating mechanism, thus offering an advantage over standard estimating equations approaches even in the absence of empty clusters.
4.3. Zero-inflated Poisson model
A number of extensions beyond the basic setup of Section 4.1 are possible. Depending on the scientific context, it may be reasonable to consider a zero-inflated Poisson model for the cluster sizes. Towards this, let 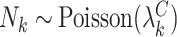 be a count variable as in (4.11), but let
be a count variable as in (4.11), but let 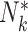 here denote the actual cluster size. Specify a zero-inflation model
here denote the actual cluster size. Specify a zero-inflation model 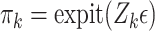 , where
, where 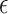 is a vector of regression coefficients. We then write the likelihood for a zero-inflated Poisson cluster size
is a vector of regression coefficients. We then write the likelihood for a zero-inflated Poisson cluster size
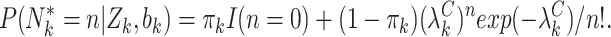 |
Under such a parametrization, empty clusters contribute to both the zero-inflation and Poisson components of the likelihood, but informative emptiness manifests solely through the Poisson component. This addresses the potentially complex mechanism giving rise to empty clusters in multigenerational studies well. Many women have no children by choice, as captured by the first term; others have no children for reasons informed by the informative cluster size mechanism, as captured by the second term. See Appendix C of the supplementary material available at Biostatistics online for theoretical details.
5. Simulation study
5.1. Aims
We conducted a series of simulations to establish, under a plausible mechanism for generating data with random cluster sizes, how well the available analysis frameworks recover the data generating parameters when: (i) cluster size is non-informative and non-empty, (ii) cluster size is non-informative with non-informative emptiness, (iii) cluster size is informative and non-empty, and (iv) cluster size is informative with informative emptiness.
5.2. Generating data with random cluster size
We generated 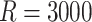 datasets from shared random effects models, specified both marginally and conditionally. We adopted a random intercepts model with exposure-dependent variance; that is, a random intercept’s variance depends on a binary cluster-level covariate. We also considered a simpler random intercepts specification with constant variance; see Appendix D.2 of the supplementary material available at Biostatistics online for details. We generated Poisson-distributed cluster sizes with a minimum size of either one or zero in order to contrast informativeness with and without empty clusters. See Appendix D.7 of the supplementary material available at Biostatistics online for results of another simulation with a smaller sample size (
datasets from shared random effects models, specified both marginally and conditionally. We adopted a random intercepts model with exposure-dependent variance; that is, a random intercept’s variance depends on a binary cluster-level covariate. We also considered a simpler random intercepts specification with constant variance; see Appendix D.2 of the supplementary material available at Biostatistics online for details. We generated Poisson-distributed cluster sizes with a minimum size of either one or zero in order to contrast informativeness with and without empty clusters. See Appendix D.7 of the supplementary material available at Biostatistics online for results of another simulation with a smaller sample size (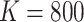 ).
).
We generated data from the conditionally-specified model as follows. For clusters 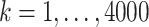 :
:
Draw cluster-level covariate
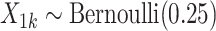 and let
and let 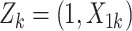 .
.Draw random effects
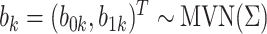 , where
, where 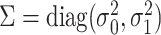 .
.Set
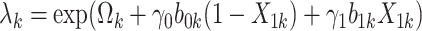 where
where 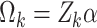 .
.Draw cluster size
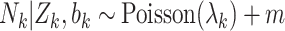 , where
, where 
-
If
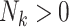 , then for
, then for 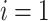 to
to 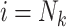 :
:(a) Draw unit-level covariate
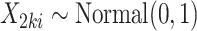 , let
, let 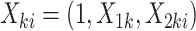 .
.(b) Set
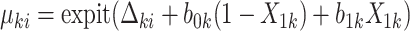 where
where 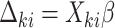 .
.(c) Draw outcomes
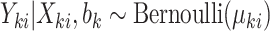 .
.
For the marginally-specified model, we follow the same general procedure but instead solve 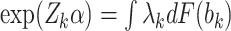 for
for 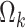 and solve
and solve  for
for 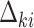 .
.
We set 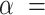
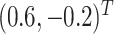 and
and 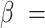
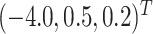 to loosely reflect the direction and magnitude of the exposure effects on both cluster size and outcome in the Nurses Health Study II (see Section 6). Furthermore, we set
to loosely reflect the direction and magnitude of the exposure effects on both cluster size and outcome in the Nurses Health Study II (see Section 6). Furthermore, we set 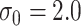 and
and 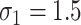 , which reflect the observed levels of within-family correlation in this study. We considered a range of possible scaling factors:
, which reflect the observed levels of within-family correlation in this study. We considered a range of possible scaling factors: 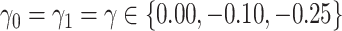 correspond to no, moderate and strong informativeness, respectively, with informativeness here indicating negative association between size and outcome (that is, smaller families receive more ADHD diagnoses per child). Data exhibit (i) non-informativeness and non-emptiness when
correspond to no, moderate and strong informativeness, respectively, with informativeness here indicating negative association between size and outcome (that is, smaller families receive more ADHD diagnoses per child). Data exhibit (i) non-informativeness and non-emptiness when 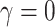 and
and 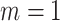 , (ii) non-informative emptiness when
, (ii) non-informative emptiness when 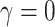 and
and 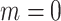 , (iii) informative cluster size and no emptiness when
, (iii) informative cluster size and no emptiness when 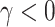 and
and 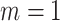 , and (iv) informative emptiness when
, and (iv) informative emptiness when 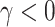 and
and 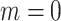 .
.
With emptiness, the mode cluster size was one and 70–75% had fewer than three members. For the conditionally specified model with emptiness, 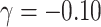 led to a prevalence of 8% among single-member clusters (
led to a prevalence of 8% among single-member clusters ( ) and 5% in three-member clusters (
) and 5% in three-member clusters (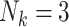 ). See Appendix D.3 of the supplementary material available at Biostatistics online for full distributions of cluster sizes (Tables 5 and 6 of the supplementary material available at Biostatistics online), as well as outcome prevalences by cluster size (Tables 7 and 8 of the supplementary material available at Biostatistics online), in each scenario.
). See Appendix D.3 of the supplementary material available at Biostatistics online for full distributions of cluster sizes (Tables 5 and 6 of the supplementary material available at Biostatistics online), as well as outcome prevalences by cluster size (Tables 7 and 8 of the supplementary material available at Biostatistics online), in each scenario.
5.3. Analyses
For each dataset generated from the marginally specified model, we fit: the marginal model (2.1) using generalized estimation equations with working exchangeability (treating size as fixed); model (3.5) via independence estimating equations; model (3.6) via cluster size weighted estimating equations; and the proposed joint marginalized model (4.7)–(4.8). For each dataset generated from the conditionally specified model, we fit: the outcome-only generalized linear mixed model (3.3); a joint model for size and outcome (3.2)–(3.3) that ignores empty clusters; and the complete joint model (3.2)–(3.3) with empty clusters. Note the joint model that ignores empty clusters coincides with the joint approach when 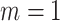 , since there are no empty clusters to exclude.
, since there are no empty clusters to exclude.
5.4. Results
We compare bias, 95% interval coverage and mean standard errors for estimates of the outcome-regression coefficients (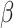 ) across analyses in scenarios (i)–(iv). Results for other parameters (
) across analyses in scenarios (i)–(iv). Results for other parameters (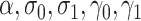 ) are included as Appendix D of the supplementary material available at Biostatistics online.
) are included as Appendix D of the supplementary material available at Biostatistics online.
Tables 1 and 2 show median parameter estimates of marginal and conditional parameters (respectively) across 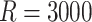 datasets. In the absence of informativeness (
datasets. In the absence of informativeness (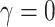 ), all methods recover
), all methods recover 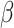 with minimal bias. Under informativeness, however, generalized and independence estimating equations exhibit bias in estimates of
with minimal bias. Under informativeness, however, generalized and independence estimating equations exhibit bias in estimates of 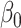 and
and 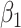 (34% and 39%, respectively for
(34% and 39%, respectively for 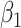 when
when 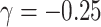 and
and  ), while cluster size weighted estimating equations and the joint marginalized model remain unbiased when there is no emptiness (
), while cluster size weighted estimating equations and the joint marginalized model remain unbiased when there is no emptiness (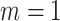 ); similarly, the outcome-only GLMM exhibits appreciable bias (up to 91% for
); similarly, the outcome-only GLMM exhibits appreciable bias (up to 91% for 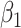 ) but the joint approach does not. It is only under informative emptiness that cluster size weighted estimating equations fail to recover
) but the joint approach does not. It is only under informative emptiness that cluster size weighted estimating equations fail to recover 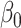 and
and 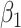 , however, incurring as much as 33% bias when
, however, incurring as much as 33% bias when 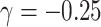 ; analogously, ignoring zeroes led to biased estimates here as well, while the full joint models (conditional and marginalized) did not.
; analogously, ignoring zeroes led to biased estimates here as well, while the full joint models (conditional and marginalized) did not.
Table 1.
Results for marginal regression parameters across 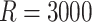 simulated datasets (see Section 5.2)
simulated datasets (see Section 5.2)
Without emptiness (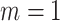 ) ) |
With emptiness (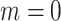 ) ) |
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GEE | IEE | WEE | JMM | GEE | IEE | WEE | JMM | ||||||||||
| Parameters |

|
Med | % | Med | % | Med | % | Med | % | Med | % | Med | % | Med | % | Med | % |
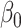 = = 4 4 |
0.00 |
 4.01 4.01 |
95 |
 4.01 4.01 |
95 |
 4.01 4.01 |
95 |
 4.01 4.01 |
95 |
 4.01 4.01 |
95 |
 4.01 4.01 |
95 |
 4.01 4.01 |
96 |
 4.00 4.00 |
95 |
 0.10 0.10 |
 4.17 4.17 |
60 |
 4.21 4.21 |
44 |
 4.01 4.01 |
94 |
 4.01 4.01 |
95 |
 4.32 4.32 |
29 |
 4.35 4.35 |
19 |
 4.15 4.15 |
81 |
 4.01 4.01 |
95 | |
 0.25 0.25 |
 4.42 4.42 |
2 |
 4.48 4.48 |
0 |
 4.00 4.00 |
95 |
 4.00 4.00 |
95 |
 4.86 4.86 |
0 |
 4.89 4.89 |
0 |
 4.45 4.45 |
25 |
 4.01 4.01 |
95 | |
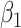 =0.5 =0.5 |
0.00 | 0.51 | 94 | 0.50 | 94 | 0.51 | 94 | 0.51 | 95 | 0.50 | 95 | 0.50 | 95 | 0.50 | 95 | 0.50 | 95 |
 0.10 0.10 |
0.57 | 92 | 0.59 | 91 | 0.50 | 94 | 0.49 | 94 | 0.62 | 91 | 0.64 | 90 | 0.54 | 95 | 0.47 | 94 | |
 0.25 0.25 |
0.67 | 83 | 0.70 | 80 | 0.50 | 95 | 0.49 | 95 | 0.85 | 71 | 0.87 | 70 | 0.66 | 91 | 0.48 | 95 | |
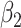 =0.2 =0.2 |
0.00 | 0.20 | 95 | 0.20 | 95 | 0.20 | 95 | 0.20 | 95 | 0.20 | 94 | 0.20 | 94 | 0.20 | 94 | 0.20 | 95 |
 0.10 0.10 |
0.20 | 94 | 0.20 | 94 | 0.20 | 94 | 0.20 | 95 | 0.20 | 94 | 0.20 | 95 | 0.20 | 94 | 0.20 | 95 | |
 0.25 0.25 |
0.20 | 93 | 0.20 | 94 | 0.20 | 94 | 0.20 | 94 | 0.21 | 94 | 0.21 | 95 | 0.21 | 94 | 0.20 | 95 | |
GEE refers to generalized estimating equations with working exchangeability; IEE refers to independence estimating equations; WEE refers to inverse cluster size weighted estimating equations; JMM refers to proposed joint marginalized model; Med is median estimates; % is 95% confidence interval coverage.
Table 2.
Results for conditional regression parameters across 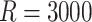 simulated datasets (see Section 5.2)
simulated datasets (see Section 5.2)
| Without emptiness (m=1) | With emptiness (m=0) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GLMM | J-No0s | Joint | GLMM | J-No0s | Joint | ||||||||
| Parameters |
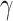
|
Med | % | Med | % | Med | % | Med | % | Med | % | Med | % |
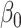 = = 4 4 |
0.00 |
 3.99 3.99 |
95 |
 3.99 3.99 |
95 |
 3.99 3.99 |
95 |
 3.99 3.99 |
94 |
 4.00 4.00 |
95 |
 4.00 4.00 |
94 |
 0.10 0.10 |
 4.27 4.27 |
67 |
 4.00 4.00 |
95 |
 4.00 4.00 |
95 |
 4.47 4.47 |
58 |
 4.39 4.39 |
67 |
 4.00 4.00 |
95 | |
 0.25 0.25 |
 4.86 4.86 |
1 |
 4.00 4.00 |
95 |
 4.00 4.00 |
95 |
 5.53 5.53 |
0 |
 4.90 4.90 |
4 |
 4.01 4.01 |
95 | |
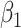 =0.5 =0.5 |
0.00 | 0.50 | 95 | 0.51 | 95 | 0.51 | 95 | 0.51 | 95 | 0.51 | 95 | 0.51 | 94 |
 0.10 0.10 |
0.63 | 92 | 0.50 | 95 | 0.50 | 95 | 0.74 | 91 | 0.68 | 93 | 0.50 | 95 | |
 0.25 0.25 |
0.95 | 74 | 0.49 | 95 | 0.49 | 95 | 1.33 | 74 | 0.71 | 94 | 0.49 | 96 | |
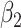 =0.2 =0.2 |
0.00 | 0.20 | 95 | 0.20 | 95 | 0.20 | 95 | 0.20 | 95 | 0.20 | 95 | 0.20 | 95 |
 0.10 0.10 |
0.20 | 95 | 0.20 | 95 | 0.20 | 95 | 0.20 | 95 | 0.20 | 94 | 0.20 | 94 | |
 0.25 0.25 |
0.21 | 95 | 0.20 | 95 | 0.20 | 95 | 0.22 | 95 | 0.21 | 95 | 0.20 | 95 | |
GLMM refers to generalized linear mixed effects model (outcome-only); J-No0s refers to joint conditional model excluding empty clusters; Joint refers to joint conditional model including empty clusters; Med is median estimates; % is 95% confidence interval coverage.
In contrast, 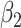 , representing the association for observation-level covariate
, representing the association for observation-level covariate 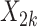 , was estimated with little bias by all approaches across each setting (the outcome-only GLMM performed the worst and still only suffered 8% bias under the most informative emptiness).
, was estimated with little bias by all approaches across each setting (the outcome-only GLMM performed the worst and still only suffered 8% bias under the most informative emptiness).
Confidence interval coverage achieved the nominal level for analysis/setting combinations exhibiting little bias (see Tables 3 and 4 of the supplementary material available at Biostatistics online). Further, and unsurprising given they were based on a correctly specified likelihood, complete joint approaches (conditional and marginalized) yielded the most efficient estimates of parameters among approaches that estimate them without bias. In particular, despite 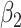 estimates being close to unbiased by all approaches under informative emptiness, the joint marginalized approach yielded a 15% reduction in standard error relative to cluster size weighted estimating equations when
estimates being close to unbiased by all approaches under informative emptiness, the joint marginalized approach yielded a 15% reduction in standard error relative to cluster size weighted estimating equations when 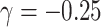 .
.
In a simulation based on simple random intercepts with constant variance (setting  ; detailed in Appendix D.2 of the supplementary material available at Biostatistics online), similar results emerged, with one exception:
; detailed in Appendix D.2 of the supplementary material available at Biostatistics online), similar results emerged, with one exception: 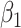 exhibited less bias across the board, even for cluster size weighted estimating equations under informative emptiness (see Table 9 of the supplementary material available at Biostatistics online). These findings echo and extend those of Neuhaus and McCulloch (2011). They found that ignoring informative cluster size leads to bias primarily for associations of covariates included in the random effects specification; we find that even when addressing informative cluster size, ignoring informative emptiness leads to bias for those same covariate associations included in the random effects specification.
exhibited less bias across the board, even for cluster size weighted estimating equations under informative emptiness (see Table 9 of the supplementary material available at Biostatistics online). These findings echo and extend those of Neuhaus and McCulloch (2011). They found that ignoring informative cluster size leads to bias primarily for associations of covariates included in the random effects specification; we find that even when addressing informative cluster size, ignoring informative emptiness leads to bias for those same covariate associations included in the random effects specification.
6. Application to the Nurses Health Study II
6.1. Study population
The proposed methods are motivated by a study of the effect of diethylstilbestrol exposure on third-generation ADHD diagnosis in the Nurses Health Study II. The data consist of 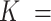 61 485 female nurses aged 25–42 in 1989 who returned a series of questionnaires in subsequent years and had no multiple same-year births. In 2005 and 2013, nurses reported whether their children had been diagnosed with ADHD and analysis is restricted to concordant responses (see Kioumourtzoglou and others, 2018). The data are hierarchical in nature, with
61 485 female nurses aged 25–42 in 1989 who returned a series of questionnaires in subsequent years and had no multiple same-year births. In 2005 and 2013, nurses reported whether their children had been diagnosed with ADHD and analysis is restricted to concordant responses (see Kioumourtzoglou and others, 2018). The data are hierarchical in nature, with 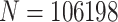 children clustered within families identified by their mothers (nurses).
children clustered within families identified by their mothers (nurses).
A key feature of the data is that cluster size (number of children) is potentially informative, as seen in Table 3: ADHD prevalence ranged from 5.62% in only-children to 3.22% in children from families of five or more children. Some of this relationship may be due to diethylstilbestrol exposure, whose rate was highest for nurses with no children (2.79%) and decreased to 1.18% for those with five or more children. Critically, 23% of nurses reported no live births and were thus excluded from previous analyses (Kioumourtzoglou and others, 2018). To explore the impact of this decision on the conclusions of the analysis, we now consider the full population of nurses that met the eligibility criteria, this time including those without children.
Table 3.
Outcome and exposure rates by number of children (cluster size) in the Nurses Health Study II
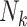
|
No. Nurses | ADHD (%) | DES (%) |
|---|---|---|---|
| 0 | 13 945 | — | 2.79 |
| 1 | 8791 | 5.62 | 2.37 |
| 2 | 23 608 | 5.44 | 1.88 |
| 3 | 11 444 | 5.44 | 1.39 |
| 4 | 2933 | 4.47 | 1.43 |
| 5+ | 764 | 3.22 | 1.18 |
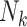 refers to number of children (cluster size); DES refers to diethylstilbestrol exposure.
refers to number of children (cluster size); DES refers to diethylstilbestrol exposure.
6.2. Analyses
The primary aim of the study was to quantify the effect of diethylstilbestrol on third-generation ADHD diagnosis, and we compared results of each analysis approach considered in the simulations. Logistic outcome models were adjusted for nurse’s exposure to diethylstilbestrol, smoking status, and year of birth. For the joint models, we modeled cluster size using a zero-inflated Poisson model (where the Poisson component adjusted for the same covariates and the zero inflation adjusted for exposure) in order to permit informative and non-informative emptiness (see Section 4.3). For the joint model that ignores empty clusters, we assumed a Poisson distribution, with a minimum size of one. We adopted a random intercepts model with exposure-dependent variance (as in the simulations), permitting correlation to depend on diethylstilbestrol exposure.
6.3. Results
Estimates of marginal parameters can be found in Table 4. Diethylstilbestrol had a moderate adverse population-averaged (marginal) effect on ADHD risk, and estimates varied only somewhat across analyses: the independence estimating equations odds ratio estimate was 1.46 [95% confidence interval (CI) (1.19–1.78)] and was slightly larger than the cluster size weighted estimating equations estimate of 1.39 (1.13–1.71). Because these estimates are consistent for distinct parameters only under informative cluster size, these results (in light of the large sample size) suggest weak informativeness. As such, emptiness did not seem to have a large impact here, and the joint marginalized estimate fell between those of the estimating equations [1.41; 95% CI (1.14–1.73)].
Table 4.
Marginal parameter estimates and confidence intervals across analyses of ADHD diagnosis in 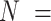 106 198 children
106 198 children
| GEE | IEE | WEE | JMM | |||||
|---|---|---|---|---|---|---|---|---|
| Est | 95% CI | Est | 95% CI | Est | 95% CI | Est | 95% CI | |
| Baseline odds | 0.03 | (0.03–0.04) | 0.03 | (0.03–0.04) | 0.04 | (0.03–0.04) | 0.03 | (0.03–0.04) |
| Odds ratios | ||||||||
| DES | 1.43 | (1.18–1.75) | 1.46 | (1.19–1.78) | 1.39 | (1.13–1.71) | 1.41 | (1.14–1.73) |
| Mother smoked | 1.24 | (1.16–1.33) | 1.25 | (1.16–1.34) | 1.23 | (1.14–1.32) | 1.26 | (1.17–1.35) |
| Year of birth | ||||||||
| 1951–1955 | 1.61 | (1.48–1.76) | 1.62 | (1.48–1.77) | 1.58 | (1.44–1.73) | 1.62 | (1.49–1.77) |
| 1956–1960 | 1.84 | (1.68–2.02) | 1.84 | (1.68–2.01) | 1.83 | (1.67–2.01) | 1.84 | (1.69–2.02) |
| 1961–1965 | 1.65 | (1.47–1.85) | 1.64 | (1.46–1.85) | 1.64 | (1.46–1.85) | 1.65 | (1.47–1.85) |
GEE refers to generalized estimating equations with working exchangeability; IEE refers to independence estimating equations; WEE refers to inverse cluster size weighted estimating equations; JMM refers to proposed joint marginalized model; Est refers to estimates; CI refers to confidence intervals.
Conditional parameter estimates can be found in Tables 5. The cluster-specific (conditional) estimates of the exposure-ADHD odds ratio were naturally much larger, but still varied little across analyses, ranging from 2.39 (1.38–4.12) under the outcome-only GLMM to 2.33 (1.33–4.06) under the complete joint model. The other covariate-outcome associations varied negligibly across conditional analyses.
Table 5.
Conditional parameter estimates and confidence intervals across analyses of ADHD diagnosis in 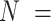 106 198 children
106 198 children
| GLMM | J-No0s | Joint | ||||||
|---|---|---|---|---|---|---|---|---|
| [-1.8ex] | Est | 95% CI | Est | 95% CI | Est | 95% CI | ||
| Baseline odds | 0.01 | (0.01–0.01) | 0.01 | (0.01–0.01) | 0.01 | (0.01–0.01) | ||
| Odds ratios | ||||||||
| DES | 2.39 | (1.38–4.12) | 2.35 | (1.35–4.07) | 2.33 | (1.33–4.06) | ||
| Mother smoked | 1.36 | (1.24–1.49) | 1.36 | (1.24–1.49) | 1.36 | (1.24–1.49) | ||
| Year of birth | ||||||||
| 1951–1955 | 1.86 | (1.67–2.09) | 1.86 | (1.66–2.08) | 1.86 | (1.67–2.09) | ||
| 1956–1960 | 2.21 | (1.97–2.49) | 2.21 | (1.97–2.48) | 2.21 | (1.97–2.48) | ||
| 1961–1965 | 1.91 | (1.65–2.22) | 1.91 | (1.64–2.22) | 1.91 | (1.65–2.22) | ||
GLMM refers to outcome-only generalized linear mixed effects model; J-No0s refers to joint conditional model excluding empty clusters; Joint refers to joint conditional model including empty clusters; Est refers to estimates; CI refers to confidence intervals.
Despite discrepant levels of correlation by exposure level (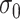 and
and 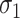 are estimated to be 2.03 and 1.66 under the joint model), the variation in exposure effects across analyses is modest. This is because although there was a strong potential for informative cluster size (see Table 3), the actual level of informativeness was low (the estimate of the scaling parameter for the unexposed was
are estimated to be 2.03 and 1.66 under the joint model), the variation in exposure effects across analyses is modest. This is because although there was a strong potential for informative cluster size (see Table 3), the actual level of informativeness was low (the estimate of the scaling parameter for the unexposed was 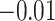 ).
).
7. Discussion
In this work, we consider issues of informative cluster size and informative emptiness in the analysis of cluster-correlated data. In regard to the former, when interest lies in estimation and inference for a conditional (i.e. mixed effects) model, Neuhaus and McCulloch (2011) showed that by framing it as a form of misspecification of the random effects distribution, the bias that results by ignoring informative cluster size is restricted to the fixed effects for covariates on which the true correlation structure depends. Our results show that this phenomenon also applies when interest lies in estimation and inference with respect to a marginally-specified model.
While intuitively similar to non-ignorable missingness, informative emptiness represents a distinct challenge. Indeed, empty clusters do not necessarily represent missing data especially in the context of inter-generational studies that motivate this work since there is no (counterfactual) notion of a full cluster: a woman with no children cannot be viewed as missing children. In considering this issue, analogous to the results for informative cluster size, we found a parallel phenomenon in which ignoring informative emptiness may result in bias for the fixed effect parameters corresponding to covariates that influence the true correlation structure, even if informative cluster size is accounted for. To the best of our knowledge, this phenomenon has not be described before.
To resolve informative cluster size and informative emptiness simultaneously we show that one can proceed with conditional inference by fitting a joint model for the cluster size and the outcome, and retaining the empty clusters in the set of likelihood contributions. For marginal inference we have proposed a joint marginalized modeling approach as an alternative to existing approaches that attempt to resolve informative cluster sizes through the introduction of weights into the estimating equations. One drawback of the latter is that, in contrast to when cluster size is not informative, the choice of weights has an impact on the interpretation of estimand. Furthermore, the post hoc inclusion of weights into the estimating equations results in an analysis for which the underlying (presumed) data generating mechanism is unclear. Thus, these methods are estimation-first in the sense that they place greater emphasis on resolving a statistical issue (i.e. informative cluster size) than on the model itself and, consequently, the scientific question. In contrast, the proposed approach is model-first in that we first write down the outcome model we would have specified in the absence of informative cluster size or informative emptiness, and then estimate the parameters of scientific interest. Moreover, as indicated in the Section 5.2, it corresponds directly to a data-generating mechanism that can elucidate both the nature of exposure effects and the relationship between cluster size and outcome.
Although distinct from missing data, consideration of informative emptiness from a missing data perspective is useful in the sense that the presence of bias depends on whether or not the assumptions required for valid estimation and inference are plausible. Furthermore, it must be that the model structure through which information on size-outcome relationship is leveraged in both the joint conditional and joint marginal approaches is also a plausible representation of reality. In some settings, these assumptions and/or structure may not be plausible. In our data application, for example, it is likely unreasonable to expect that all emptiness is related to the informativeness mechanism, since many women simply choose not to have children. In such a case the zero-inflation model of 4.3 might be appropriate—one might even consider a zero-inflated negative binomial should the data require it. The ZIP model is generally preferred to the more restrictive Poisson, as it permits a mixture of informative and non-informatively empty clusters, but may not be feasible in small sample settings (we observed 61 485 clusters so the added model complexity was not an issue). Moreover, Min and Agresti (2005) point out that, even if there is overall zero-inflation, the ZIP model can be unstable when there is zero-deflation at some covariate level; in contrast a hurdle model specification does not suffer from this problem, but could not permit informatively empty clusters in our setting. In any case the ZIP model does not assuage all concerns of misspecification (e.g. if all empty clusters are non-informative but cluster size is informative).
Beyond joint marginalized modeling, there are a number of other approaches that could be pursued. For example, following Seaman and others (2014), one could fit the joint conditional model described in Section 3.1.1 and compute the marginal parameter estimates post hoc. Although this would likely speed up the model fitting process (by avoiding the calculation of the integrated likelihood at every step), a drawback is that computing standard errors for the resulting estimator of the marginal parameter is non-trivial (since the likelihood is for a conditional parameter), whereas likelihood-based standard error estimation under the proposed approach is relatively straightforward since the model is directly parameterized in terms of the marginal parameter. Furthermore, for select special cases one could approximate marginal parameter estimates using known transformations of their conditional counterparts (see Appendix F of the supplementary material available at Biostatistics online). While again appealing from a computational perspective, the proposed joint marginalized approach is more flexible and can handle any number of link functions and model specifications. Recent developments by Hedeker and others (2018) provide flexible marginalization of conditional parameter estimates with improved computation time, and we hope to explore this in future work.
We considered here binary responses for ADHD diagnosis in order to replicate the motivating study of Kioumourtzoglou and others (2018), but we might alternatively cast this as a time-to-event problem to account for right-censoring. Future work could consider extensions to the proposed approach to accommodate frailty models for correlated survival data.
8. Software
Software in the form of R code is available at https://github.com/glenmcgee/InformativeEmptiness.
Supplementary Material
Acknowledgments
The authors would like to thank an associate editor and two referees for a number of suggestions that improved this article. Conflict of Interest: None declared.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
This work was supported in part by the U.S. National Institute of Environmental Health Sciences (U2C ES026555, P30 ES000002, P30 ES009089). The Nurses Health Study II is also supported by an infrastructure grant from the National Institutes of Health (UM1 CA176726). Data provided by the Channing Division of Network Medicine, Department of Medicine, Brigham and Women’s Hospital and Harvard Medical School.
References
- Allen, A. S. and Barnhart, H. X. (2005). General marginal regression models for the joint modeling of event frequency and correlated severities with applications to clinical trials. Journal of Data Science 3, 199–219. [Google Scholar]
- Benhin, E., Rao, J. N. K. and Scott, A. J. (2005). Mean estimating equation approach to analysing cluster-correlated data with nonignorable cluster sizes. Biometrika 92, 435–450. [Google Scholar]
- Chiang, C.-T. and Lee, K.-Y. (2008). Efficient estimation methods for informative cluster size data. Statistica Sinica 18, 121–133. [Google Scholar]
- Dunson, D. B., Chen, Z. and Harry, J. (2003). A Bayesian approach for joint modeling of cluster size and subunit-specific outcomes. Biometrics 59, 521–530. [DOI] [PubMed] [Google Scholar]
- Gelman, A., Stern, H. S., Carlin, J. B., Dunson, D. B., Vehtari, A. and Rubin, D. B. (2013). Bayesian data analysis, third edition. Boca Raton, FL: Chapman & Hall/CRC Texts in Statistical Science. [Google Scholar]
- Gueorguieva, R. V. (2005). Comments about joint modeling of cluster size and binary and continuous subunit-specific outcomes. Biometrics 61, 862–866. [DOI] [PubMed] [Google Scholar]
- Heagerty, P. J. (1999). Marginally specified logistic-normal models for longitudinal binary data. Biometrics 55, 688–698. [DOI] [PubMed] [Google Scholar]
- Heagerty, P. J. and Kurland, B. F. (2001). Misspecified maximum likelihood estimates and generalised linear mixed models. Biometrika 88, 973–985. [Google Scholar]
- Heagerty, P. J. and Zeger, S. L. (2000). Marginalized multilevel models and likelihood inference (with comments and a rejoinder by the authors). Statistical Science 15, 1–26. [Google Scholar]
- Hedeker, D., du Toit, S. H. C., Demirtas, H. and Gibbons, R. D. (2018). A note on marginalization of regression parameters from mixed models of binary outcomes. Biometrics 74, 354–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman, E. B., Sen, P. K. and Weinberg, C. R. (2001). Within-cluster resampling. Biometrika 88, 1121–1134. [Google Scholar]
- Iosif, A.-M. (2007). Analysis of longitudinal random length data, [PhD. Thesis]. University of Pittsburgh. [Google Scholar]
- Iosif, A.-M. and Sampson, A. R. (2014). A model for repeated clustered data with informative cluster sizes. Statistics in Medicine 33, 738–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kioumourtzoglou, M. A., Coull, B. A., O’Reilly, É. J., Ascherio, A. and Weisskopf, M. G. (2018). Association of exposure to diethylstilbestrol during pregnancy with multigenerational neurodevelopmental deficits. JAMA Pediatrics, 172, 670–677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang, K.-Y. and Zeger, S. L. (1986). Longitudinal data analysis using generalized linear models. Biometrika 73, 13–22. [Google Scholar]
- McCulloch, C. R., Searle, S. R. and Neuhaus, J.M. (2008). Generalized, Linear, and Mixed Models. Hoboken, NJ: Wiley. [Google Scholar]
- Min, Y. and Agresti, A. (2005). Random effect models for repeated measures of zero-inflated count data. Statistical Modelling 5, 1–19. [Google Scholar]
- Neuhaus, J. M., Hauck, W. W. and Kalbfleisch, J. D. (1992). The effects of mixture distribution misspecification when fitting mixed-effects logistic models. Biometrika 79, 755–762. [Google Scholar]
- Neuhaus, J. M. and McCulloch, C. E. (2011). Estimation of covariate effects in generalized linear mixed models with informative cluster sizes. Biometrika 98, 147–162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlou, M., Seaman, S. R. and Copas, A. J. (2013). An examination of a method for marginal inference when the cluster size is informative. Statistica Sinica 23, 791–808. [Google Scholar]
- Qian, M., Chou, S.-Y., Gimenez, L. and Liu, J.-T. (2017). The intergenerational transmission of low birth weight and intrauterine growth restriction: a large cross-generational cohort study in Taiwan. Maternal and Child Health Journal 21, 1512–1521. [DOI] [PubMed] [Google Scholar]
- Seaman, S., Pavlou, M. and Copas, A. (2014). Review of methods for handling confounding by cluster and informative cluster size in clustered data. Statistics in Medicine 33, 5371–5387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veenendaal, M. V. E., Painter, R. C., de Rooij, S. R., Bossuyt, P. M. M., van der Post, J. A. M., Gluckman, P. D., Hanson, M. A. and Roseboom, T. J. (2013). Transgenerational effects of prenatal exposure to the 1944–45 dutch famine. BJOG: An International Journal of Obstetrics & Gynaecology 120, 548–554. [DOI] [PubMed] [Google Scholar]
- Williamson, J. M., Datta, S. and Satten, G. A. (2003). Marginal analyses of clustered data when cluster size is informative. Biometrics 59, 36–42. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


