Abstract
The choices that researchers make while conducting a statistical analysis usually have a notable impact on the results. This fact has become evident in the ongoing research of the association between the environment and the evolution of the coronavirus disease 2019 (COVID-19) pandemic, in light of the hundreds of contradictory studies that have already been published on this issue in just a few months. In this paper, a COVID-19 dataset containing the number of daily cases registered in the regions of Catalonia (Spain) since the start of the pandemic to the end of August 2020 is analysed using statistical models of diverse levels of complexity. Specifically, the possible effect of several environmental variables (solar exposure, mean temperature, and wind speed) on the number of cases is assessed. Thus, the first objective of the paper is to show how the choice of a certain type of statistical model to conduct the analysis can have a severe impact on the associations that are inferred between the covariates and the response variable. Secondly, it is shown how the use of spatio-temporal models accounting for the nature of the data allows understanding the evolution of the pandemic in space and time. The results suggest that even though the models fitted to the data correctly capture the evolution of COVID-19 in space and time, determining whether there is an association between the spread of the pandemic and certain environmental conditions is complex, as it is severely affected by the choice of the model.
Keywords: COVID-19, Spatio-temporal models, Environmental covariates, Integrated nested Laplace approximation, Space-time interaction, Relative risk
Introduction
The pandemic caused by the coronavirus disease 2019 (COVID-19) has led in a few months to an unprecedented number of related scientific outcomes. Many of the studies on the COVID-19 focus on the evolution of viral transmission, or the clinical factors that increase the risk of contagion, among other relevant topics. In particular, one of the most consolidated lines of research is dedicated to clarifying how certain environmental or meteorological factors have had an impact (or may have in the future) on the evolution of COVID-19 at a local, national, or global level.
At the time of writing (November 2020), hundreds of statistical analyses about the effect of the environment on the evolution of COVID-19 have already been published. Specifically, the influence of temperature, humidity, or solar radiation (among other variables) on the transmission of the virus has been massively investigated at a macroscopic level, considering municipalities, regions, countries, etc., as the spatial units of analysis. Surprisingly (to some extent), the results provided by these studies are sometimes very different, or even opposite, as shown by the several reviews that have been published on this topic (Briz-Redón and Serrano-Aroca 2020b; Shakil et al. 2020; Yuan et al. 2020). Some of the discrepancies found between studies could be due to the different ranges of values that the main environmental variables present depending on the area of the world being analysed, but it is also very reasonable to think that certain methodological choices such as the type of statistical model, the geographical unit of analysis, or the set of covariates also have a notable impact on the results. In relation to this fact, it is worth noting that among the studies already published on this topic, very different types of statistical and modelling techniques have been employed (Briz-Redón and Serrano-Aroca 2020b), including correlation analyses (e.g., Tosepu et al. 2020), generalised additive models (e.g., Xie and Zhu 2020), panel data models (e.g., Sobral et al. 2020), spatio-temporal models (e.g., Briz-Redón and Serrano-Aroca 2020a), or epidemiological models such as the susceptible-infected-recovered-susceptible (SIRS) model (e.g., Baker et al. 2020). Machine learning models, which are being widely used to predict COVID-19 incidence and mortality (Dhamodharavadhani et al. 2020; Iwendi et al. 2020; Lalmuanawma et al. 2020; Sujath et al. 2020), have been also considered by multiple researchers to assess the relationship between COVID-19 spread and the environment (Malki et al. 2020; Shrivastav and Jha 2020; Siddiqui et al. 2020). Thus, the spatio-temporal nature of the data under analysis has been taken into account in only a relatively small percentage of studies, despite the importance of accounting for spatial and temporal patterns to explain and model the evolution of the pandemic with greater accuracy, as shown in several recent studies. For instance, Guliyev (2020) compared different panel data models and concluded that the spatially lagged X (SLX) model showed the greatest performance in modelling COVID-19 confirmed, death, and recovered rates. Moreover, Mollalo et al. (2020) verified that geographically weighted regression models accounting for spatial heterogeneity and scale outperformed non-spatial models in modelling COVID-19 spread. Finally, in several studies developed at different levels of spatio-temporal aggregation, it has been identified that COVID-19 cases tend to be highly concentrated in space and time (Arauzo-Carod 2020; Cordes and Castro 2020; Desjardins et al. 2020; Hohl et al. 2020).
The purpose of this paper is twofold. The first objective, and main contribution of the paper, is to highlight how certain modelling choices may affect the analysis of a spatio-temporal dataset, particularly in studying the impact of the environment on the development of the COVID-19 pandemic. The motivation to carry out this particular research arises as a consequence of the existence of multiple contradictory studies on this subject, and the suspicion that the type of statistical analysis carried out has been responsible for some of these inconsistencies. Although some review articles mentioned above have already highlighted this question, there are hardly any empirical works in this direction, to the best of my knowledge. To meet this capital objective, the comparative analysis starts with rather general models without neither spatial nor temporal effects (basic generalised linear models), to which different spatial, temporal, and spatio-temporal terms are then added to properly account for the nature of the data. The second objective consists of exploring how the inclusion of spatio-temporal effects in the model can be helpful to understand the dynamics of the COVID-19 pandemic through the identification of high-risk areas, general trends over time, and the singular trends experienced by each area under study.
Therefore, the paper is structured as follows. Section 2 includes a brief description of the data used for the analysis. In Sect. 3, the different statistical models considered for the analysis are presented. The results provided by each of the models are displayed and compared in Sect. 4. Finally, some concluding remarks are provided in Sect. 5.
Data
Study area
The study has focused on Catalonia, one of the 17 Autonomous Communities of Spain. Concretely, the analysis has been carried out at the region (comarca) level, which represents an intermediate spatial aggregation level between the province level and the city level. Thus, Catalonia is divided into 42 regions which contain about 1000 municipalities for a total of 7619494 inhabitants (as of 2019). The population sizes of these regions vary from more than 2 million people in the case of Barcelonès (which nearly represents the 30 of the population of Catalonia) to less than 4000 in the case of Alta Ribagorça. Figure 1 shows the location of Catalonia within Spain (Fig. 1a) and a map of Catalonia at the region level (Fig. 1b).
Fig. 1.
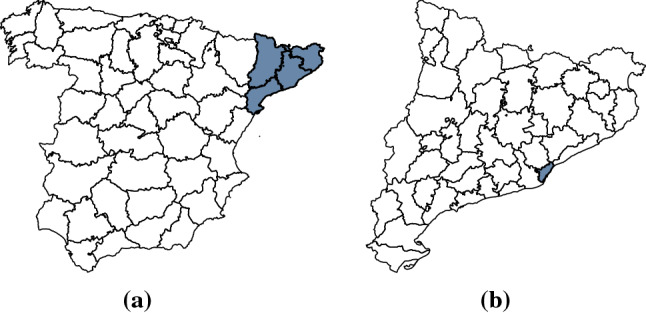
Map of peninsular Spain at the province level (a) and map of Catalonia at the region level (b). In a, the four provinces of Catalonia are highlighted. In b, the region of Barcelonès, where the capital city of Catalonia (Barcelona) is located, is also highlighted
COVID-19 data
A dataset containing the new daily COVID-19 cases recorded in each municipality of Catalonia, Spain, from 25 February 2020 to 24 August 2020 (covering 182 days within a total of 27 weeks) was downloaded from Catalonia’s Open Data platform (https://analisi.transparenciacatalunya.cat/en/). In this dataset, cases are disaggregated according to the type of diagnostic test employed for their determination: antibody test, polymerase chain reaction (PCR) test, and serology test. Among these diagnostic methods, the PCR test has been by far the most used in Catalonia since the beginning of the pandemic. In fact, about 90% of the cases detected up to August 24th were identified by PCR, according to the dataset downloaded. For this reason, to conduct this study, the number of daily COVID-19 cases determined by a PCR test has been considered as the response or dependent variable of the analysis.
Environmental data
Environmental data for the period under study has been downloaded from the OpenData platform of the State Meteorological Agency (AEMET) of Spain. Specifically, daily solar exposure (in terms of the number of hours over irradiance threshold of 120 W/m), mean temperature (in C), and wind speed (in km/h) values measured from February to August 2020 by a total of 172 automatic weather stations installed all over Spain have been collected.
In order to analyse the association between the number of COVID-19 cases and the environmental conditions in the regions of Catalonia during the study period, a region-level estimation of the three environmental variables was performed for each day within the period. First, ordinary kriging (Cressie 1988) was used to estimate the daily values of the three environmental variables on a grid of points (defined at a distance of 5 km from each other) covering the whole area under study. Hence, only the stations from Catalonia and the two Autonomous Communities of Spain sharing a border with Catalonia (Aragón and the Valencian Community) may have influenced these estimates. Secondly, region-level daily estimates of the variables of interest were obtained as the average of the estimates corresponding to the points of the grid lying within the region.
Methodology
Statistical models
In this subsection, the different statistical models that have been considered for the analysis are described in order of complexity (from the simplest to the most complex). The precise specification of these models according to the set of terms and coefficients involved in each of them is provided in Table 1.
Table 1.
Description of the 12 main models that were considered for the comparison in terms of the specification of the logarithm of the relative risk, , corresponding to region i () on day t ()
| Model | |
|---|---|
| Model 1 | |
| Model 2 | |
| Model 3 | |
| Model 4 | |
| Model 5 | (I) |
| Model 6 | (II) |
| Model 7 | (III) |
| Model 8 | (IV) |
| Model 9 | (I) |
| Model 10 | (II) |
| Model 11 | (III) |
| Model 12 | (IV) |
For all the models, denotes the intercept of the model, E the number of expected cases, and () the covariates. In addition, and represent the structured and unstructured random spatial effect of the model, and the structured and unstructured random temporal effect, and the random spatio-temporal effect. The symbols I, II, III, IV denote the type of spatio-temporal interaction (for either or ) considered in Models 5 to 12, according to Table 2
Basic models
The number of new daily COVID-19 cases observed in region i () on day t (), denoted by , was assumed to follow a Poisson distribution with mean , where (offset term of the model) denotes the number of expected cases in region i on day t, and the relative risk for region i and day t. was calculated as the product of the total number of cases observed in Catalonia on day t by the fraction of the population of Catalonia that region i represents.
The first model that was tested (Model 1) only included the fixed effect of each of the three environmental variables considered for the analysis: solar exposure (), temperature (), and wind speed (). Next, a non-environmental variable such as the population density () was incorporated into the model (Model 2). For the remaining models (Models 3 to 12), a spatio-temporal approach was followed, which seems the most appropriate one in order to account for the structure of the data under analysis.
Spatio-temporal models
Several spatio-temporal models of increasing complexity were fitted to the data. First, a spatio-temporal model without interaction, that is, where regional and temporal effects act separately, was considered in Models 3 and 4. To model the spatial effects ( and ), the Besag-York-Molliè (BYM) model was followed (Besag et al. 1991). On the one hand, under the BYM model it is assumed that the conditional distribution of the spatially-structured effect on region i, , is
where is the number of neighbours that region i has (two regions are neighbours if they are spatially contiguous), is the element (i,j) of the row-standardised matrix of dimension that represents the neighbourhood matrix for the regions ( if regions i and j are neighbours, otherwise ), and represents the variance of the spatially-structured effect. On the other hand, for the spatially-unstructured effect over the regions, denoted by , an independent and identically distributed Gaussian prior is considered
where represents the variance of the spatially-unstructured effect of the model.
With regard to the two temporal effects, the temporally-structured effect, , was modelled through a second-order random walk
where is the variance component. Finally, an independent and identically distributed Gaussian prior is chosen for : .
In the case of Model 3, the random temporal effects are set on a weekly basis, whereas in Model 4 the temporal effects are set on a daily basis. Hence, in Table 1, the index of the temporal effects corresponding to Model 3 is actually denoted by w(t) (instead of t), which represents the week to which the day t belongs to (). The consideration of weekly effects instead of daily effects allows reducing the complexity of the model by reducing the number of parameters being involved, which reduces the chance of overfitting issues.
Then, several spatio-temporal models accounting for the presence of space-time interaction were also fitted (Models 5 to 12), among which the space-time interaction is accounted for on a weekly (Models 5 to 8) or daily basis (Models 9 to 12). In particular, the four spatio-temporal structures proposed by Knorr-Held (2000) were used. Each of these structures consists in specifying the non-separable spatio-temporal term of the model according to a concrete combination of a structured/unstructured spatial effect with a structured/unstructured temporal effect. The combination of these effects is carried out through the Kronecker product of the two matrices that represent the spatial and temporal effect chosen, respectively. Table 2 shows the four types of spatio-temporal interactions that can be considered following this approach.
Table 2.
Specification of the four types of spatio-temporal interaction considered in terms of the Kronecker product of the two matrices representing the structure of the spatial and temporal effect, respectively
| Type of spatio-temporal interaction | |
|---|---|
| I | |
| II | |
| III | |
| IV |
The matrix () represents the identity matrix, which corresponds to the unstructured spatial (temporal) effect, whereas () represents a non-identity matrix that corresponds to a specific structured spatial (temporal) effect
The implementation of Models 1 to 12 was carried out through the Integrated Nested Laplace Approximation (INLA) method, which allows obtaining the posterior marginal distributions of the parameters involved in the model. Non-informative priors were chosen for the parameters corresponding to the fixed effects included in all of the models, whereas a was used for the precision of the random effects implicated in Models 3 to 12 (these are the default priors provided by the INLA package). Further details on the implementation of these models in INLA can be found in the literature (Ugarte et al. 2014; Blangiardo and Cameletti 2015; Gómez-Rubio 2020). Besides, the specific R code used to implement Models 1 to 12 described above is available in https://github.com/albrizre/COVID_Catalonia.
Model variations
Although comparing the 12 types of models introduced above constitutes the main part of the comparison, certain (minor) variations of them are also considered to extend the comparative analysis. First, the three environmental covariates were introduced into the model with a certain time lag with respect to the cases observed on the day t. Specifically, since COVID-19 has shown a mean incubation period of approximately 5 days, ranging from 2 to 14 days (Nishiura et al. 2020; Rasmussen et al. 2020), three different lags of 0, 7, and 14 days were considered for the covariates (which implies replacing the covariate terms present in all the expressions included in Table 1 by or ). Second, the possibility of considering the environmental covariates in their quadratic or cubic form in order to capture non-linear effects is also considered for some of the models. In these cases, the new models will be referred to only as specific modifications of Models 1 to 12 described in Table 1, which are those that define the fundamental modelling structures under comparison.
Model quality assessment
Model assessment was performed through the Deviance Information Criterion (DIC) introduced by Spiegelhalter et al. (2002), the Watanabe-Akaike Information Criterion (WAIC) proposed by Watanabe and Opper (2010), and the probability integral transform (PIT) defined by Dawid (1984). Both the DIC and the WAIC measure the goodness-of-fit of a Bayesian model while accounting for its complexity in terms of the number of effective parameters involved in the model. Hence, as a general rule, the model with the smallest DIC/WAIC value is the one that shows the greatest performance, meaning the best balance between deviance and complexity. Besides, the PIT is a leave-one-out cross-validation score defined as follows for a given spatio-temporal unit
where is a random variable generated by the posterior distribution of a fitted model, is the value observed on spatio-temporal unit (i,t), and is the vector containing all observations except the one corresponding to unit (i,t). If the distribution of the PIT scores is close to uniform, the model is well calibrated (Czado et al. 2009). Deviations from uniformity suggest that the predictive distribution of the model suffers from either underdispersion (U-shaped distribution), overdispersion (inverse-U shape distribution), or bias (skewed distribution).
Software
The R programming language (R Core Team 2020) has been used to carry out the present study. In particular, the R packages automap (Hiemstra et al. 2008), ggplot2 (Wickham 2016), gstat (Pebesma 2004; Gräler et al. 2016), INLA (Rue et al. 2009; Lindgren and Rue 2015), rgdal (Bivand et al. 2019), and spdep (Bivand et al. 2008) have been required at some points of the analysis.
Results
This section summarises the results provided by each of the statistical models fitted. First, the quality of the models is assessed. Second, the coefficients associated with the three environmental variables involved in the analysis are compared across models. Finally, the spatio-temporal effects estimated through Models 3 to 12 are described and shown graphically.
Model quality
Model 9 including random temporal effects at the daily level and a type I spatio-temporal interaction (unstructured in space and time) showed the greatest performance in terms of the DIC and the WAIC (Table 3), while Model 11 including a type III spatio-temporal interaction (structured in space but unstructured in time) yielded the second-lowest DIC and WAIC (in addition, the choice of the type of lagged effect imposed on the covariates has no effect on the results). However, Model 12, which considers a type IV space-time interaction (structured in both space and time) showed unreliable DIC and WAIC values (extremely high in comparison with the rest of the models), preventing a direct comparison on the basis of the DIC and the WAIC. Among the models considering a weekly random temporal effect (Models 5 to 8), the model with the type I spatio-temporal interaction (Model 5) also presented the greatest performance according to the DIC, closely followed by Model 8 (type IV interaction), whereas Model 8 was the best one according to the WAIC. Anyhow, the models including daily-based temporal effects (Models 9 to 12) performed considerably better.
Table 3.
DIC and WAIC values corresponding to Models 1 to 12, considering a lagged effect on the covariates of 0, 7, or 14 days
| Model | Lagged effect on the covariates (in days) | |||||
|---|---|---|---|---|---|---|
| 0 | 7 | 14 | ||||
| DIC | WAIC | DIC | WAIC | DIC | WAIC | |
| Model 1 | 72565.19 | 72679.40 | 73011.11 | 73124.89 | 73122.80 | 73237.75 |
| Model 2 | 67300.15 | 67382.92 | 67327.76 | 67409.48 | 67317.83 | 67399.46 |
| Model 3 | 52467.55 | 53120.39 | 52445.03 | 53094.57 | 52471.95 | 53126.27 |
| Model 4 | 52440.54 | 53362.19 | 52421.46 | 53373.55 | 52459.30 | 53366.84 |
| Model 5 | 31851.36 | 33309.72 | 31858.83 | 33315.52 | 31855.27 | 33310.80 |
| Model 6 | 32060.54 | 33300.17 | 32073.40 | 33311.08 | 32067.71 | 33303.21 |
| Model 7 | 31991.11 | 33388.21 | 32001.95 | 33398.70 | 31998.69 | 33393.09 |
| Model 8 | 31860.42 | 33131.04 | 31868.50 | 33136.35 | 31864.40 | 33131.99 |
| Model 9 | 26162.89 | 25639.98 | 26163.56 | 25641.39 | 26161.46 | 25636.84 |
| Model 10 | 29175.52 | 31005.83 | 29197.48 | 31033.46 | 29192.74 | 31031.59 |
| Model 11 | 26240.72 | 25915.22 | 26245.35 | 25919.58 | 26246.03 | 25922.32 |
| Model 12 | – | – | – | – | – | – |
In the case of Model 12, the values obtained for the two metrics were not comparable to those of the rest of models (they all were extremely high), so they are omitted (–)
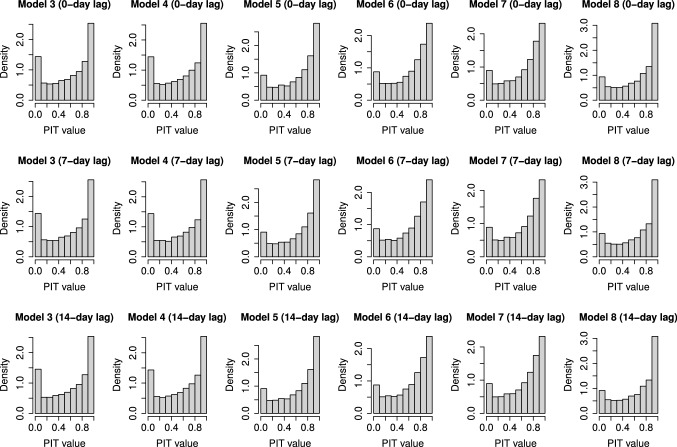
With regard to the PIT scores, the associated histograms corresponding to Models 3 to 8 are shown in Fig. 2. In general, all these histograms are slightly U-shaped and notably left-skewed, which suggests that the predictive distributions of the models are a bit underdispersed (especially in the case of Models 3 and 4) and biased (the predictions tend to underestimate the true values, which is not surprising because of the presence of unpredictable local peaks in the time series representing the number of daily COVID-19 cases). In the case of Models 9 to 12, the approximation carried out by the INLA package to compute PIT scores was not trustworthy for most of the observations, which prevented its use. Besides, the “manual” computation of the PIT scores for these models is computationally very intensive and was only performed for some of these models. Anyhow, the shape of the histograms obtained remained very similar to those shown in Fig. 2, a fact that indicates that the prediction of daily COVID-19 cases at a small-area level is a challenging task. Thus, the main conclusion derived from the analysis of the distribution of the PIT scores is that the predictive quality of the models could be improved. From the perspective of model selection, since there is no model that presents a substantially better predictive performance, Model 9 is kept as the best model among the twelve models tested, according to the DIC and WAIC metrics.
Fig. 2.
Histograms of the PIT scores obtained for Models 3 to 8 (from left to right), considering a 0-day, a 7-day, and a 14-day lagged effect (from top to bottom) on the covariates
Environmental effects
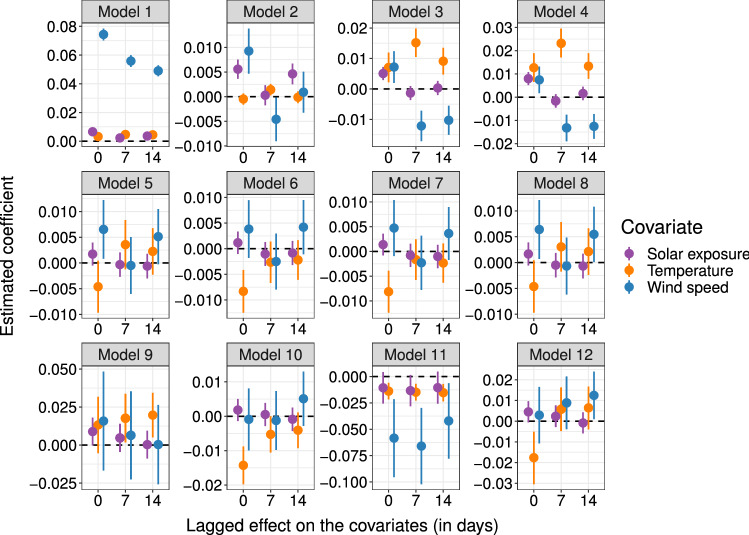
Regarding the effect of each environmental covariate on the spread of COVID-19, the main conclusion would be that the choice of the model has a strong impact on the results, as shown in Fig. 3. First, Model 1 suggests that solar exposure, wind speed, and temperature have a positive association with COVID-19 spread. Besides, these associations are consistent across the different time lags (0, 7, and 14 days) explored for the covariates. A visible characteristic of Model 1 is the narrowness of the confidence intervals associated with the mean estimates of the effects, which causes that all the associations are statistically significant with 95% confidence. However, the results provided by Model 2 (where population density is incorporated into the model) increase the uncertainty about the possible association between COVID-19 spread and the environment. Now, there is great inconsistency across lags for the three environmental covariates, which makes it difficult to achieve solid conclusions on their effects. Indeed, the difficulty in establishing an association between environmental covariates and the number of daily COVID-19 cases is maintained if the results provided by Models 3 to 12 are analysed. Some models suggest that there is a positive association between COVID-19 and temperature (Models 3 and 4), or a negative association between COVID-19 daily cases and wind speed (Model 11). Considering the best model in terms of the DIC, Model 9, it could be concluded that there is a statistically significant positive association between mean temperature and daily new cases, and a non-significant association with solar exposure and wind speed. Indeed, the modification of Model 9 through the addition of the three environmental covariates in its quadratic and cubic form ( and , ), even though it reduces the DIC of Model 9 to 26106.22, neither does it reveal any significant association between these covariates and the daily number of COVID-19 cases.
Fig. 3.
Summary of the estimates obtained for the coefficients associated with environmental covariates for each of the 12 models fitted, considering a lagged effect on the covariates of 0, 7, or 14 days
Spatio-temporal effects
The inclusion of spatio-temporal effects helps to understand how the disease has spread throughout the territory under study. Specifically, the estimates of random spatial and temporal effects and their interaction allow assigning a relative risk to each spatial, temporal, or spatio-temporal unit under analysis. These relative risks are obtained by exponentiating the space-time parameters that describe the log() expression in each of the models. In the remainder of the section, for simplicity, only the estimates of the random spatial, temporal and spatio-temporal effects that correspond to the models that include a 7-day lagged effect in the environmental covariates are displayed. Since the selection of the temporal lag barely affects the results, as shown in the previous subsections, the choice of a 7-day lagged effect seems to be the most reasonable due to the fact that the incubation time of COVID-19 is close to one week.
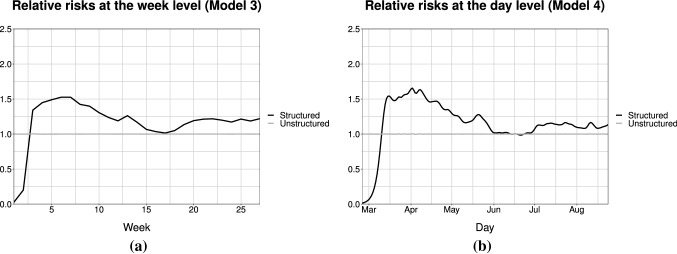
Hence, Fig. 4 shows relative risks over time in terms of the random temporal effects estimated through Models 3 (including weekly effects) and 4 (including daily effects). The relative risk represented by the structured component of the random temporal effect (either in Model 3 or in Model 4, for ) captures the evolution of the pandemic in Catalonia: the relative risk was nearly 0 at the beginning of March 2020, reached a peak in April, and then decreased for the following months until July, when it started to increase again. Oppositely, the relative risk associated with the unstructured component (either in Model 3 or in Model 4) barely fluctuates around 1, which suggests that there were not notable overall changes in the relative risk during the period of study that were solely attributable to single days within the period. This fact can also be verified by comparing the estimates of the precision parameters associated with each of the random effects included in the models, which are shown in Table 4. Each precision parameter represents the inverse of the variance of the corresponding random effect. For instance, is the precision parameter associated with the temporally-structured effect, . Thus, a smaller precision parameter indicates a larger variance from the corresponding random effect, which at the same time reflects that such effect has a greater contribution to relative risk variations. In both Models 3 and 4, is clearly smaller than , especially in the case of Model 3 (Table 4), which confirms the larger contribution of the temporally-structured effect to daily relative risks.
Fig. 4.
Relative risks on a weekly and a daily basis according to the structured and unstructured temporal random effects estimated through Models 3 (a) and 4 (b). The relative risk corresponding to the structured component is computed as either or , whereas the one corresponding to the unstructured component is computed as either or
Table 4.
Precision parameters associated with each spatial, temporal, and spatio-temporal random effect included in Models 3–12
| Model | Lagged effect on the covariates (in days) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7 | 14 | |||||||||||||
| Model 3 | 0.61 | 1856.80 | 8.05 | 19519.94 | – | 0.61 | 1830.99 | 7.46 | 19322.89 | – | 0.61 | 1808.52 | 8.22 | 19281.02 | – |
| Model 4 | 0.61 | 1880.24 | 2905.82 | 28751.88 | – | 0.61 | 1868.87 | 2336.19 | 28155.57 | – | 0.61 | 1828.89 | 2996.43 | 32255.73 | – |
| Model 5 | 0.58 | 1701.93 | 17.28 | 20029.05 | 1.96 | 0.58 | 1694.79 | 17.76 | 16311.47 | 1.96 | 0.57 | 1987.44 | 17.87 | 19504.56 | 1.96 |
| Model 6 | 1683.99 | 1824.58 | 71.77 | 17086.46 | 0.16 | 1669.41 | 1764.29 | 81.33 | 17326.17 | 0.16 | 1710.88 | 1782.48 | 78.25 | 17339.23 | 0.16 |
| Model 7 | 1840.15 | 2.40 | 15954.35 | 19012.55 | 1.77 | 1838.72 | 2.35 | 16686.60 | 18328.64 | 1.77 | 1844.39 | 2.34 | 16605.04 | 18684.12 | 1.77 |
| Model 8 | 2548.59 | 2549.11 | 6.03 | 22059.37 | 0.05 | 1932.06 | 1851.87 | 6.17 | 22289.05 | 0.05 | 1956.98 | 1995.20 | 6.37 | 22369.79 | 0.05 |
| Model 9 | 0.57 | 1755.44 | 4150.88 | 19984.01 | 1.56 | 0.57 | 1778.78 | 4460.82 | 20199.37 | 1.56 | 0.57 | 1655.83 | 5206.65 | 12321.17 | 1.55 |
| Model 10 | 1735.39 | 1793.79 | 38350.20 | 29884.19 | 0.01 | 2148.25 | 1996.45 | 38612.51 | 30192.31 | 0.01 | 1640.81 | 1746.67 | 38360.92 | 30166.73 | 0.01 |
| Model 11 | 1.34 | 7.47 | 43977.69 | 18991.44 | 1.33 | 0.71 | 1826.22 | 42416.58 | 19266.62 | 1.33 | 1.40 | 7.23 | 40716.07 | 18450.46 | 1.33 |
| Model 12 | 1842.10 | 1900.22 | 205.84 | 22812.31 | 0.00 | 2096.99 | 1993.96 | 229.80 | 23237.58 | 0.00 | 1893.71 | 1841.31 | 247.87 | 22423.13 | 0.00 |
The precision represents the inverse of the variance of the corresponding random effect
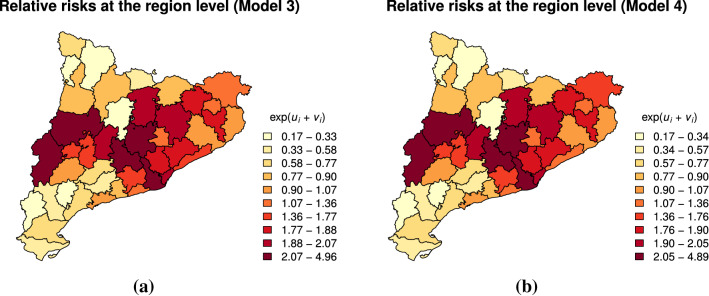
With regard to the random spatial effects, Fig. 5 displays the values of corresponding to Models 3 and 4 (although the differences between the two models are almost negligible). It can be observed that the regions in the central zone of Catalonia, which covers from the surroundings of the Barcelonès region to some regions in the west of Catalonia that border Aragón, experienced the highest relative risks during the period under research. One of these regions located in western Catalonia, called Segrià , reached the highest relative risk for the period under consideration, presenting a relative risk very close to 5 (for both Models 3 and 4). The regions of Anoia, Bages, Baix Llobregat, Barcelonès, and Noguera were the ones that presented the closest relative risks to Segrià , although they were considerably smaller, only ranging from 2 to 3. Besides, regarding the contribution of each random spatial effect to relative risks, the structured spatial effect, , captures most of the spatial variation, since for both Models 3 and 4 (Table 4). This fact indicates that there has been a strong spatial dependence between the regions studied in terms of their COVID-19 relative risks. Indeed, as can be observed in Fig. 5, high-risk (low-risk) regions tend to be closer to other high-risk (low-risk) regions.
Fig. 5.
Global relative risks at the region level estimated for the period under study (computed as ) considering Model 3 (a) and Model 4 (b)
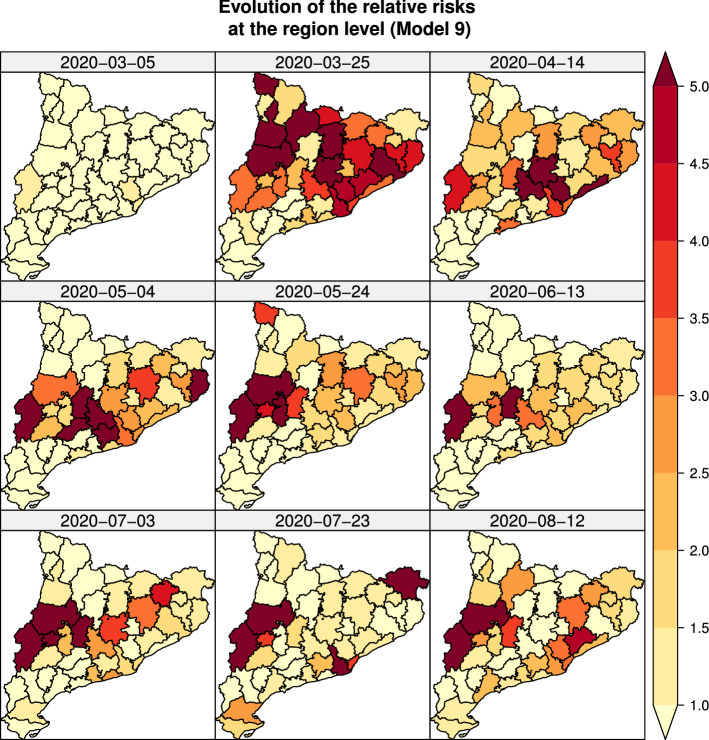
Interpreting the precision parameters under the presence of spatio-temporal interaction terms is more challenging, but some general outcomes are easily appreciated. Specifically, the precision of the interaction parameter () is very small in all Models 5 to 12, which indicates that space-time interaction highly contributes to daily relative risks. Although the structured spatial effect, , presents a larger contribution than for some of the models, these results confirm that the inclusion of the spatio-temporal effect is more than suitable. As an example of the convenience of considering space-time interaction, the spatio-temporal relative risks provided by Model 9 for a selection of days within the period of study are shown in Fig. 6 (these are computed as ). The inclusion of space-time interaction terms is essential to allow the model to capture certain variations in relative risks across both regions and subperiods. Thus, by observing the evolution of the relative risks across regions and days in Fig. 6, it can be appreciated how certain regions of the central zone of Catalonia presented quite different relative risks along time. These variations in the relative risk are overlooked if one only considers global spatial effects (as in Fig. 5). Concretely, the highest relative risks for most of the regions were achieved between the end of March 2020 and the beginning of April 2020. Then, for the following months, the relative risks were generally lower across entire Catalonia, except for some regions in the west of Catalonia such as Segrià , which has been presenting higher relative risks since the month of May.
Fig. 6.
Relative risks at the region level (computed as ) estimated for a selection of days within the period under study with Model 9
Besides, to better appreciate the evolution of the relative risk in some highly affected regions of Catalonia, Fig. 7 shows the evolution of the relative risk (according to Model 9) that correspond to a selection of regions of Catalonia (the six regions mentioned above, which presented the highest relative risk according to Models 3 and 4). It is important to be aware that the estimates of the daily relative risks that both models provide for each of the regions are quite erratic and difficult to inspect visually. For this reason, these estimates were smoothed through a locally estimated scatterplot smoothing (LOESS) regression (Fox and Weisberg 2018) to ease the interpretation of Fig. 7. Hence, Fig. 7 indicates that, except for Segrià , all these regions reached a peak in the relative risk at the beginning of April 2020, and then decreased until July, when relative risks started growing again. This temporal pattern corresponds to the overall relative risk over time shown in Fig. 4. In the case of Segrià , however, the relative risk kept growing until August, when it started to show a slight decrease.
Fig. 7.
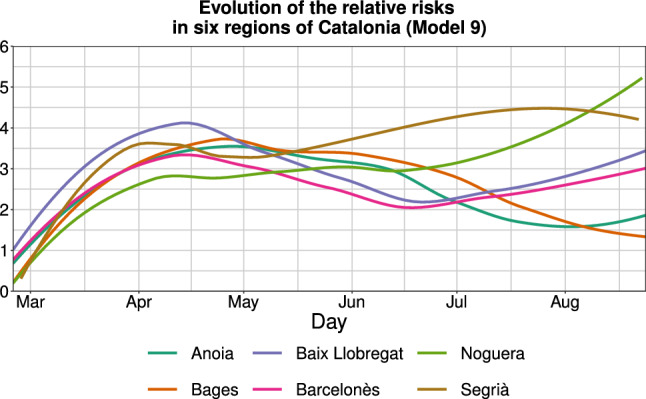
Evolution of the relative risks (computed as ), according to the estimates provided by Model 9 in the six regions of Catalonia with the highest global relative risks (according to the estimates provided by Models 3 and 4). To make this plot, the relative risks provided by Model 9 have been smoothed through a locally estimated scatterplot smoothing (LOESS) regression (Fox and Weisberg 2018) for ease of visualisation and interpretation
Discussion and conclusions
This study has shown how the choice of a certain type of statistical model to evaluate the association between a set of covariates and a response variable can seriously influence the results. In the context of the study of the association between the evolution of the COVID-19 pandemic and environmental conditions, this fact seems to be occurring remarkably. In this regard, the lack of consideration of certain non-environmental variables, and overlooking spatio-temporal effects appear inadequate. In particular, the results obtained for the case study described in this paper suggest that there seems to be too much uncertainty to establish an association between the environmental variables considered and the development of the pandemic in Catalonia, on the basis of the data examined.
Anyhow, the present study also has its own limitations. Besides the fact that the predictive performance of the models fitted could be improved, many other methodological choices that have not been accounted for in the present study may also have some influence on the association between the environment and the COVID-19 propagation. For instance, the definition of different neighbourhood relationships between the regions, the consideration of more non-environmental covariates such as the inter-region mobility or the age structure of the population, and the selection of the most suitable spatio-temporal unit for the analysis, which implies dealing with the modifiable areal unit problem (MAUP; Openshaw 1981) and the modifiable temporal unit problem (MTUP; Cheng and Adepeju 2014), are other issues deserving attention that could be explored in future studies. In particular, concerning the MAUP, it is important to note that some geographical units at the subregional level (such as cities or even city districts) may present certain unique characteristics that require consideration for performing an accurate analysis of the evolution of the pandemic. Indeed, Wang and Di (2020) recently found that the association between COVID-19 mortality and NO levels depends on the level of spatial aggregation (considering four different spatial aggregations, including cities and provinces), which indicates the presence of the MAUP. In addition, another important aspect that should be considered in future studies is the fact that cases detection rate has remained far from 100% since the beginning of the COVID-19 pandemic. In particular, if detection rates vary spatially and temporally, this could have an impact on the results. For instance, in the case of Spain, differences in detection rates between geographical units belonging to different Autonomous Communities are likely to arise because the competencies in health policy and organisation are established at this territorial level. To mitigate this problem, the existence of seroepidemiological studies that provide estimates of the prevalence of COVID-19 at the province level (Pollán et al. 2020), or the availability of reliable COVID-19 mortality data (Langousis and Carsteanu 2020) could be helpful.
In conclusion, it seems clear that the data modelling approach that we choose to conduct the analysis can have a strong impact on the conclusions that can be drawn from it. Although this is generally true, in the specific case of the ongoing line of research that focuses on unveiling the effects of the environment on the spread of COVID-19, the employment of models that properly take into account the structure of the data, the consideration of non-environmental variables, or the performance of sensitivity analyses, seem highly-advisable strategies to avoid the persistence of highly contradictory results which could make decision-making against the COVID-19 pandemic even more difficult.
Funding
No funding was received for this study.
Data availability
The data used in this study is available in https://github.com/albrizre/COVID_Catalonia.
Code availability
The R code used to fit the models described in this study is available in https://github.com/albrizre/COVID_Catalonia.
Compliance with ethical standards
Conflict of interest
The author declare that they have no conflict of interest.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Arauzo-Carod J-M (2020) A first insight about spatial dimension of COVID-19: analysis at municipality level. J Publ Health, fdaa140 [DOI] [PMC free article] [PubMed]
- Baker RE, Yang W, Vecchi GA, Metcalf CJE, Grenfell BT (2020) Susceptible supply limits the role of climate in the early SARS-CoV-2 pandemic. Science [DOI] [PMC free article] [PubMed]
- Besag J, York J, Mollié A. Bayesian image restoration, with two applications in spatial statistics. Ann Inst Stat Math. 1991;43(1):1–20. doi: 10.1007/BF00116466. [DOI] [Google Scholar]
- Bivand RS, Pebesma EJ, Gomez-Rubio V, Pebesma EJ. Applied spatial data analysis with R. Berlin: Springer; 2008. [Google Scholar]
- Bivand R, Keitt T, Rowlingson B (2019). rgdal: bindings for the ‘Geospatial’ Data Abstraction Library. R package version 1.4-6
- Blangiardo M, Cameletti M. Spatial and spatio-temporal Bayesian models with R-INLA. Hoboken: Wiley; 2015. [Google Scholar]
- Briz-Redón Á, Serrano-Aroca Á. A spatio-temporal analysis for exploring the effect of temperature on COVID-19 early evolution in Spain. Sci Total Environ. 2020;728:138811. doi: 10.1016/j.scitotenv.2020.138811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briz-Redón Á, Serrano-Aroca Á. The effect of climate on the spread of the COVID-19 pandemic: A review of findings, and statistical and modelling techniques. Prog Phys Geogr Earth Environ. 2020;44(5):591–604. doi: 10.1177/0309133320946302. [DOI] [Google Scholar]
- Cheng T, Adepeju M. Modifiable temporal unit problem (MTUP) and its effect on space-time cluster detection. PLoS ONE. 2014;9(6):e100465. doi: 10.1371/journal.pone.0100465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordes J, Castro MC. Spatial analysis of COVID-19 clusters and contextual factors in New York City. Spatial Spatio-temporal Epidemiol. 2020;34:100355. doi: 10.1016/j.sste.2020.100355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cressie N. Spatial prediction and ordinary kriging. Math Geol. 1988;20(4):405–421. doi: 10.1007/BF00892986. [DOI] [Google Scholar]
- Czado C, Gneiting T, Held L. Predictive model assessment for count data. Biometrics. 2009;65(4):1254–1261. doi: 10.1111/j.1541-0420.2009.01191.x. [DOI] [PubMed] [Google Scholar]
- Dawid AP. Present position and potential developments: some personal views statistical theory the prequential approach. J R Stat Soc Ser A (Gen) 1984;147(2):278–290. doi: 10.2307/2981683. [DOI] [Google Scholar]
- Desjardins M, Hohl A, Delmelle E. Rapid surveillance of COVID-19 in the United States using a prospective space-time scan statistic: detecting and evaluating emerging clusters. Appl Geogr. 2020;118:102202. doi: 10.1016/j.apgeog.2020.102202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhamodharavadhani S, Rathipriya R, Chatterjee JM. Covid-19 mortality rate prediction for India using statistical neural network models. Front Publ Health. 2020;8:441. doi: 10.3389/fpubh.2020.00441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox J, Weisberg S. An R companion to applied regression. Thousand Oaks: SAGE Publications; 2018. [Google Scholar]
- Gómez-Rubio V. Bayesian inference with INLA. Boca Raton: CRC Press; 2020. [Google Scholar]
- Gräler B, Pebesma E, Heuvelink G. Spatio-temporal interpolation using gstat. R J. 2016;8:204–218. doi: 10.32614/RJ-2016-014. [DOI] [Google Scholar]
- Guliyev H. Determining the spatial effects of COVID-19 using the spatial panel data model. Spat Stat. 2020;38:100443. doi: 10.1016/j.spasta.2020.100443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hiemstra P, Pebesma E, Twenhöfel C, Heuvelink G. Real-time automatic interpolation of ambient gamma dose rates from the Dutch radioactivity monitoring network. Comput Geosci. 2008;35:1711–1721. doi: 10.1016/j.cageo.2008.10.011. [DOI] [Google Scholar]
- Hohl A, Delmelle EM, Desjardins MR, Lan Y. Daily surveillance of COVID-19 using the prospective space-time scan statistic in the United States. Spatial Spatio-temporal Epidemiol. 2020;34:100354. doi: 10.1016/j.sste.2020.100354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwendi C, Bashir AK, Peshkar A, Sujatha R, Chatterjee JM, Pasupuleti S, Mishra R, Pillai S, Jo O. COVID-19 patient health prediction using boosted random forest algorithm. Front Public Health. 2020;8:357. doi: 10.3389/fpubh.2020.00357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knorr-Held L. Bayesian modelling of inseparable space-time variation in disease risk. Stat Med. 2000;19(17–18):2555–2567. doi: 10.1002/1097-0258(20000915/30)19:17/18<2555::AID-SIM587>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- Lalmuanawma S, Hussain J, Chhakchhuak L. Applications of machine learning and artificial intelligence for Covid-19 (SARS-CoV-2) pandemic: a review. Chaos Solitons Fractals. 2020;139:110059. doi: 10.1016/j.chaos.2020.110059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langousis A, Carsteanu AA. Undersampling in action and at scale: application to the COVID-19 pandemic. Stoch Environ Res Risk Assess. 2020;34(8):1281–1283. doi: 10.1007/s00477-020-01821-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindgren F, Rue H. Bayesian spatial modelling with R-INLA. J Stat Softw. 2015;63(19):1–25. doi: 10.18637/jss.v063.i19. [DOI] [Google Scholar]
- Malki Z, Atlam E-S, Hassanien AE, Dagnew G, Elhosseini MA, Gad I. Association between weather data and COVID-19 pandemic predicting mortality rate: machine learning approaches. Chaos Solitons Fractals. 2020;138:110137. doi: 10.1016/j.chaos.2020.110137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollalo A, Vahedi B, Rivera KM. GIS-based spatial modeling of COVID-19 incidence rate in the continental United States. Sci Total Environ. 2020;728:138884. doi: 10.1016/j.scitotenv.2020.138884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiura H, Linton NM, Akhmetzhanov AR. Serial interval of novel coronavirus (COVID-19) infections. Int J Infect Dis. 2020;93:284–286. doi: 10.1016/j.ijid.2020.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Openshaw S (1981) The modifiable areal unit problem. In: Quantitative geography: a British view. Routledge, pp 60–69
- Pebesma EJ. Multivariable geostatistics in S: the gstat package. Comput Geosci. 2004;30:683–691. doi: 10.1016/j.cageo.2004.03.012. [DOI] [Google Scholar]
- Pollán M, Pérez-Gómez B, Pastor-Barriuso R, Oteo J, Hernán MA, Pérez-Olmeda M, Sanmartín JL, Fernández-García A, Cruz I, de Larrea NF, et al. Prevalence of SARS-CoV-2 in Spain (ENE-COVID): a nationwide, population-based seroepidemiological study. Lancet. 2020;396(10250):535–544. doi: 10.1016/S0140-6736(20)31483-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team (2020) R: A language and environment for statistical computing
- Rasmussen SA, Smulian JC, Lednicky JA, Wen TS, Jamieson DJ. Coronavirus disease 2019 (COVID-19) and pregnancy: what obstetricians need to know. Am J Obstet Gynecol. 2020;222(5):415–426. doi: 10.1016/j.ajog.2020.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rue H, Martino S, Chopin N. Approximate Bayesian inference for latent gaussian models using integrated nested laplace approximations (with discussion) J R Stat Soc B. 2009;71:319–392. doi: 10.1111/j.1467-9868.2008.00700.x. [DOI] [Google Scholar]
- Shakil MH, Munim ZH, Tasnia M, Sarowar S. COVID-19 and the environment: a critical review and research agenda. Sci Total Environ. 2020;745:141022. doi: 10.1016/j.scitotenv.2020.141022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrivastav LK, Jha SK (2020) A gradient boosting machine learning approach in modeling the impact of temperature and humidity on the transmission rate of COVID-19 in India. Appl Intell [DOI] [PMC free article] [PubMed]
- Siddiqui MK, Morales-Menendez R, Gupta PK, Iqbal H, Hussain F, Khatoon K, Ahmad S. Correlation between temperature and COVID-19 (suspected, confirmed and death) cases based on machine learning analysis. J Pure Appl Microbiol. 2020;14(suppl 1):1017–1024. doi: 10.22207/JPAM.14.SPL1.40. [DOI] [Google Scholar]
- Sobral MFF, Duarte GB, da Penha Sobral AIG, Marinho MLM, de Souza Melo A. Association between climate variables and global transmission oF SARS-CoV-2. Sci Total Environ. 2020;729:138997. doi: 10.1016/j.scitotenv.2020.138997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, Van Der Linde A. Bayesian measures of model complexity and fit. J R Stat Soc Ser B (Stat Methodol) 2002;64(4):583–639. doi: 10.1111/1467-9868.00353. [DOI] [Google Scholar]
- Sujath R, Chatterjee JM, Hassanien AE. A machine learning forecasting model for COVID-19 pandemic in India. Stoch Environ Res Risk Assess. 2020;34:959–972. doi: 10.1007/s00477-020-01827-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tosepu R, Gunawan J, Effendy DS, Lestari H, Bahar H, Asfian P. Correlation between weather and Covid-19 pandemic in Jakarta. Indonesia. Sci Total Environ. 2020;725:138436. doi: 10.1016/j.scitotenv.2020.138436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ugarte MD, Adin A, Goicoa T, Militino AF. On fitting spatio-temporal disease mapping models using approximate Bayesian inference. Stat Methods Med Res. 2014;23(6):507–530. doi: 10.1177/0962280214527528. [DOI] [PubMed] [Google Scholar]
- Wang Y, Di Q. Modifiable areal unit problem and environmental factors of COVID-19 outbreak. Sci Total Environ. 2020;740:139984. doi: 10.1016/j.scitotenv.2020.139984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe S, Opper M. Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. J Mach Learn Res. 2010;11(12):3571–3594. [Google Scholar]
- Wickham H. ggplot2: elegant graphics for data analysis. New York: Springer; 2016. [Google Scholar]
- Xie J, Zhu Y. Association between ambient temperature and COVID-19 infection in 122 cities from China. Sci Total Environ. 2020;724:138201. doi: 10.1016/j.scitotenv.2020.138201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan S, Jiang S, Li Z-L, et al. Do humidity and temperature impact the spread of the novel coronavirus? Front Public Health. 2020;8:240. doi: 10.3389/fpubh.2020.00240. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data used in this study is available in https://github.com/albrizre/COVID_Catalonia.
Code availability
The R code used to fit the models described in this study is available in https://github.com/albrizre/COVID_Catalonia.