Skip to main content
PMC home page
Elsevier Sponsored Documents logoLink to Elsevier Sponsored Documents
. 2020 Nov 15;222:117299. doi: 10.1016/j.neuroimage.2020.117299

Dispersion of functional gradients across the adult lifespan

Richard AI Bethlehem a,b,⁎,1, Casey Paquola c,1, Jakob Seidlitz d,e, Lisa Ronan f, Boris Bernhardt c, Cam-CAN Consortium g, Kamen A Tsvetanov h,i
PMCID: PMC7779368  PMID: 32828920

Abstract

Ageing is commonly associated with changes to segregation and integration of functional brain networks, but, in isolation, current network-based approaches struggle to elucidate changes across the many axes of functional organisation. However, the advent of gradient mapping techniques in neuroimaging provides a new means of studying functional organisation in a multi-dimensional connectivity space. Here, we studied ageing and behaviourally-relevant differences in a three-dimensional connectivity space using the Cambridge Centre for Ageing Neuroscience cohort (n = 643). Building on gradient mapping techniques, we developed a set of measures to quantify the dispersion within and between functional communities. We detected a strong shift of the visual network across the adult lifespan from an extreme to a more central position in the 3D gradient space. In contrast, the dispersion distance between transmodal communities (dorsal attention, ventral attention, frontoparietal and default mode) did not change. However, these communities themselves were increasingly dispersed with increasing age, reflecting more dissimilar functional connectivity profiles within each community. Increasing dispersion of frontoparietal, attention and default mode networks, in particular, were associated negatively with cognition, measured by fluid intelligence. By using a technique that explicitly captures the ordering of functional systems in a multi-dimensional hierarchical framework, we identified behaviorally-relevant age-related differences of within and between network organisation. We propose that the study of functional gradients across the adult lifespan could provide insights that may facilitate the development of new strategies to maintain cognitive ability across the lifespan in health and disease.

1. Introduction

With the increasing proportion of older adults in the worldwide population (Beard et al., 2016) and mounting burden of dementia in ageing societies, there is a pressing need to understand the neurobiology of cognitive ageing. Normal ageing is related to cognitive decline (Hedden and Gabrieli, 2004) and large-scale changes in brain dynamics (Li et al., 2015; Andrews-Hanna et al., 2007). Ageing is consistently related to weakened within-network connectivity co-occurring with increased between-network connectivity, a phenomenon also referred to as network de-differentiation (Goh 2011). Crucially, the coordination of within- and between-network connectivity supports the maintenance of general cognition (Tsvetanov et al., 2016) and performance in specific cognitive domains (Chan et al., 2014; Tsvetanov et al., 2018) across the adult lifespan.

Despite a large body of research on the decline and maintenance of brain network integrity during healthy ageing many inconsistencies remain. Most studies report both broad patterns of increased and decreased connectivity (Geerligs et al., 2015; Betzel et al., 2014; Chan et al., 2014), although others also report more one-directional increases (Ferreira et al., 2016) or decreases (Onoda et al., 2012; Damoiseaux et al., 2008). Thus, it is still unclear whether the observed age differences in functional network connectivity reflect a single global pattern or multiple patterns across cortical hierarchical organization. In addition, the presence of multiple underlying connectivity patterns provokes the question whether these patterns are uniquely or interactively contributing to maintaining cognitive function across the lifespan. Furthermore, standard network connectivity approaches, unlike data-driven and generative-modelling counterparts, are unable to disentangle between different physiological processes leading to the connectivity patterns (e.g. neuronal versus vascular origins of the fMRI BOLD signal) which are differentially affected by ageing (Tsvetanov et al., 2020). Given the importance of relative changes in functional connectivity to ageing and cognitive decline, a novel data-driven multi-dimensional framework approach is needed to directly address the behavioral relevance of age-related changes in large-scale organization.

Recent studies of cortical dynamics and meta-analytic decoding of cognitive states have highlighted how brain regions participate in a range of functions (Braga and Leech, 2015; Yarkoni et al., 2011; Genon et al., 2018). Therefore, capturing the full extent of a region's participation in the functional organisation of the cortex may require a more nuanced approach than comparison of connectivity within and between static functional communities. Embedding approaches have emerged as a tool to map a brain region's functional relationships from resting state fMRI connectivity (Margulies et al., 2016; Tian et al., 2020; Haak et al., 2018). These data-driven techniques reveal multiple dimensions of cortical organisation, allowing each region to be characterised according to its position along many large-scale functional gradients. The alignment of the dominant functional gradients, sensory-to-transmodal and visual-to-somatomotor (Margulies et al., 2016), with the seminal model of the cortical hierarchy (Mesulam, 1998) supports their utility in understanding the fundamental principles of the cortical landscape in humans.

To assess age-related changes to the hierarchical functional organisation of the cortex, we first investigated how the principal gradients of resting-state connectivity change across the lifespan. These one-dimensional gradients capture differentiation between systems which to some extent encapsulates both within- as well as between-network connectivity. For example, increased bi-modality can indicate segregation of the gradient extremes as well as an increased within-anchor connectivity. We expected the principal gradient to recapitulate the sensory-to-transmodal organisation seen in previous studies (Margulies et al., 2016; Paquola et al., 2019), and hypothesised that age-related changes would be centralised in the default mode network, in line with previous studies of functional connectivity (Chan et al., 2014; Spreng et al. 2020). Specifically, decreased segregation might be reflected on the principle gradient axes by a reduction of the range or bimodality of the gradient distribution showing that the anchors get closer. We also expected the second and third gradients would illustrate functional differentiation of visual, somatomotor and attention-related regions (Margulies et al., 2016; Paquola et al., 2019). Age-related changes within these functional systems have not been widely reported, though one meta-analysis of activation changes in healthy ageing identified hypo-activation in the visual cortex (Li et al., 2015).

To address the aforementioned challenges in neurocognitive research, we further extended the existing gradient framework in functional neuroimaging to specifically target the organisation of functional communities within a multi-dimensional connectivity space. Leveraging the utility of Euclidean distance to estimate the similarity between points in a manifold space (Coifman and Hirn, 2014; Bahrami et al., 2019; Qiu et al., 2015), we developed a set of specialized measures that quantify the dispersion within and between functional communities in a connectivity-derived manifold. To test and showcase the utility of these measures we sought to assess how this dispersion framework may shed light on the diversity of findings in the ageing literature, whether any age-related differences in dispersion recapitulate findings using simple correlation based functional connectivity, and finally whether these differences are of behavioural relevance in terms of age-related cognitive decline. Predictions of age-related differences across multi-dimensional gradients were motivated by prior related work on network integration and segregation, which would suggest broadly reduced segregation between networks, particularly in the default mode and fronto-parietal networks (Chan et al., 2014; Geerligs et al., 2017; Betzel et al., 2014).

2. Methods

2.1. Dataset

The present study included 637 participants from the Cambridge Centre for Aging and Neuroscience (Cam-CAN) (Shafto et al., 2014). These participants were cognitively healthy adults (age range = 18-88) recruited from the local community. Ethical approval for the Cam-CAN study was obtained from the Cambridgeshire 2 (now East of England–Cambridge Central) Research Ethics Committee. Participants gave written informed consent. A subset of 514 individuals, previously described (Ronan et al., 2016), was used as the primary cohort where individuals’ Freesurfer reconstructions (see below) had already been processed and individually evaluated (see Supplementary Table 1 for comprehensive demographics). The remaining data (n = 122, matched on age and sex) served as a hold-out dataset (Supplementary Table 2) used for alignment of the diffusion map embeddings of the primary cohort to ensure the gradient maps were aligned across subjects.

2.1.1. For every individual, MRI acquisition and preprocessing

Structural and functional images were acquired on a 3T Siemens TIM Trio system employing a 32-channel head coil. A high-resolution 3D T1-weighted structural image was acquired using a MPRAGE sequence (Repetition Time = 2250 ms; Echo Time = 2.99 ms; TI = 900 ms; flip angle = 9°; FOV = 256 mm × 240 mm × 192 mm; 1 mm isotropic voxels; GRAPPA acceleration factor = 2; acquisition time = 4 min 32 s). A functional echo planar imaging scan was acquired while participants rested with eyes closed for 8 min 40 s (TR = 1970 ms; TE = 30 ms; flip angle = 78°; FOV = 192 mm × 192 mm; 32 axial slices; voxel size = 3 mm × 3 mm × 4.44 mm). Data were quality-control checked by semiautomated scripts monitored by the Cam-CAN methods team (Taylor et al., 2017). Preprocessing included removal of the first 5 volumes, calculation of intra-modal motion (intensity difference of volume N to the reference volume; REFRMS), spike regression, spatial smoothing using a 2 mm gaussian kernel, co-registration between T1-weighted and functional images and finally subject-level removal of motion artefacts using automated ICA-AROMA (Pruim et al., 2015). Denoised BOLD timeseries were projected from volumetric native space to subject-specific cortical surfaces, which were rendered from the T1-weighted scans using Freesurfer v5.2 (Fischl, 1999; Dale, 1999).

Analyses were conducted at surface level using MATLAB and SurfStat (Worsley et al., 2009). For every individual, we averaged pre-processed vertex-based time-series within 1012 equally sized, spatially contiguous nodes (Hong et al., 2017), then used pairwise Pearson correlation and z-standardisation to create individual functional connectivity matrices. Within the primary cohort, individual connectivity matrices were subjected to row-wise thresholding (top 10% of edges maintained) and converted into normalised angle matrices, in line with previous studies (Paquola et al., 2019; Vos de Wael et al., 2018; Margulies et al., 2016; Vos de Wael et al., 2020) . Diffusion map embedding, a non-linear dimensionality reduction technique (Coifman and Lafon, 2006), was employed to resolve the gradients of subject-level connectomes. In the hold-out sample, a group-average functional connectivity matrix was constructed, thresholded, normalized and subjected to diffusion map embedding. The first three gradients were selected for further analysis because together they accounted for >50% of variance, lower gradients individually explained <10% of variance, the 3D space allowed for visual inspection and we observed clear differentiation of the seven Yeo networks within the 3D space Yeo (Yeo et al., 2011). The first three gradients, explaining 52% of variance in the normalised matrix of the hold-out sample (Supplementary Table 2) were numbered to conform with the conventions set out in Margulies et al., (2016) and showed functional differentiation running from sensory-to-transmodal (G1), visual-to-insula (G2) and somatomotor-to-insula (G3) (Supplementary Figure 1). Together, these gradients describe functional discrimination between sensory modalities and across levels of the cortical hierarchy (ie: sensory processing, attentional modulation then higher-order cognition). Regional gradient values reflect the similarity of connectivity profiles in relation to that axis (eg: two regions with similar G1 values exhibit a similar distribution of rs-FC along the sensory-transmodal axis). Individual embedding solutions from the primary cohort were aligned to the group-level hold-out embedding via Procrustes rotations (Langs et al., 2015). The Procrustes alignment enables comparison across individual embedding solutions, provided the original data is equivalent enough to produce comparable Euclidean spaces (Coifman and Hirn, 2014).

2.1.2. Age-related differences in gradient values

In our primary analyses, we assessed age-related differences in nodal gradient values by fitting linear models, controlling for head motion and sex. To synoptically visualise these age related effects we discretized the hold-out gradient into 10 equally sized bins of the gradient values and calculated the average and standard deviation of t-statistics from the linear model in each bin (Supplementary Fig. 2). Post-hoc exploratory analyses focused on summary measures derived from the gradient distributions and included the range of the gradient distribution and its bimodality as these were hypothesized to be indicative of changes to the gradient anchors. The latter was quantified using Hartigan's dip test (Hartigan and Hartigan., 1985) (Supplementary Fig. 3). Since head motion is known to be a confounding factor in resting state studies (Van et al., 2012) and can interact with both age and IQ measurements (Geerligs et al., 2017) we assessed the residual correlation between motion (measured as the average intensity difference from volume to volume) and our dispersion measures (see Supplementary Fig. 4). We indeed found small correlations between motion and our measures of interest. Thus, to ensure our main associations were not confounded by this motion correlation, motion was consistently included as a covariate of no interest in all our models. Furthermore, we conducted additional sensitivity analyses by systematically removing high motion individuals (top 5% of REFRMS) from the dataset and comparing the resulting t-statistics maps of age-related differences (Supplementary Fig. 5). We find that the removal of high motion individuals did not impact resulting age-related differences. Finally, we conducted 5-fold cross-validation for the holdout versus main dataset and found that resulting t-maps of age-related differences were consistent across folds (Supplementary Fig. 6).

2.1.3. Age-related differences in multi-dimensional gradient dispersion

To investigate multi-dimensional differences in cortical organisation, we quantified a new metric, termed here “dispersion” of established functional networks (Yeo et al., 2011) in 3D space (Supplementary Fig. 7). Each axis of this 3D space was defined by the values along the first three gradients. Within network dispersion was quantified as sum squared Euclidean distance of network nodes to the network centroid at individual level. Between network dispersion was calculated as the Euclidean distance between network centroids. These metrics were calculated for each subject within the individualised, aligned gradient space. We used linear models, correcting for head motion and sex, to estimate the association of age with network centroid position, within network dispersion and between network dispersion. For each model, we computed a null distribution of age-related differences using 1000 spherical rotations of the original parcellation scheme, thereby ensuring that for each permutation of the null distribution the spatial autocorrelation was retained (Alexander-Bloch et al., 2018; Vasa, 2017). To explore whether age related differences in dispersion were driven by a particular gradient, we examined the correlation between dispersion and subjects individual principal component loadings for the principal component of each gradient (e.g. the first principal component of a principal component analysis of the subject*gradient matrix for the first 3 gradients).

2.1.4. Alternative measures of brain function and structure

To determine the unique contribution of network dispersion versus previously reported estimates of unidimensional within network connectivity (WNC) (Yan et al., 2013), we ran robust linear regression (Huber and Ronchetti, 2009) for each Yeo network on dispersion controlling for within network connectivity of the same network (and vice versa) using the MASS library in R. For example, to assess the unique age-related difference in network dispersion within the DMN we ran the following linear model (and vice versa for within network connectivity):

Age∼1+DMNDispersion+Sex+Motion+DMNwnc+e

In addition, to determine whether the proposed multi-dimensional gradient approach captures similar aspects of network segregation and integration as edge-based methods, we calculated segregation [difference in within- vs between-network connectivity, proportional to within-network connectivity (Chan et al., 2014)] and normalised clustering coefficient (Rubinov and Sporns, 2010) for each node, then repeated the robust linear models estimating the effect of age. Robust linear regression was used to down-weight datapoints with large residuals which strengthens the idea that results are not driven by a small number of outlier datapoints or subjects (Huber and Ronchetti, 2009).

2.1.5. Behavioural relevance of network dispersion

Finally, we were interested whether age-related effects on dispersion are behaviourally relevant, and thus less likely a spurious correlation between age and BOLD-based functional connectivity (e.g. head motion or cerebrovascular reactivity), which is recognised as a major challenge in fMRI studies of ageing (Geerligs et al., 2017). For this purpose, cognitive function was assessed using the Cattell fluid intelligence scale (Cattell, 1963). We assessed the relationship of dispersion with the known decrease in fluid intelligence across the lifespan using two complementary multiple linear regression approaches: commonality analysis (Reio et al. 2015; Zientek & Thompson, 2006) and a moderation analysis. All variables were z-standardised prior to modelling. We conducted a commonality analysis on the networks showing age-related differences in dispersion and approximated the common variance between age and dispersion that explains Cattell performance using the following model:

Cattell∼Age+Dispersion+Sex+Motion+WNC+e

This analysis was conducted in R using the ‘yhat’ package with a bootstrapping approach of 1000 bootstrap iterations (Nimon & Oswald, 2013, Nimon et al. 2008) to indicate 95% confidence intervals of the commonality coefficient of age and dispersion, i.e. the common variance between age and dispersion explaining Cattell performance, while accounting for sex, motion and within network connectivity.

The moderation analysis aimed to address an emergent finding in the research of neurocognitive ageing that preservation of cognitive control is increasingly dependent on network connectivity in old age, i.e. the relationship between FC and cognition is moderated by age (Tsvetanov et al., 2016). Specifically, we constructed a linear regression as follows:

Cattell∼Age+Dispersion+Sex+Motion+WNC+Age*Dispersion+Age*Sex+Age*Motion+Dispersion*Sex+Dispersion*Motion+e

for each network and examined the coefficients of the Age*Dispersion interaction term. We visualised any potential moderating effects of network dispersion by plotting the relationship between Dispersion and Cattell score for three different age groups. We note that the moderation analysis, i.e. test for interaction between age and dispersion, is orthogonal to the main predictors in the model. Therefore, the moderation analysis is not only conceptually, but also statistically distinct from the common effect between age and dispersion investigated in the commonality analysis above.

2.1.6. Code and data availability

Data and code used in this manuscript are available from https://github.com/rb643/GradientDispersion.

3. Results

3.1. Multi-dimensional age-related differences

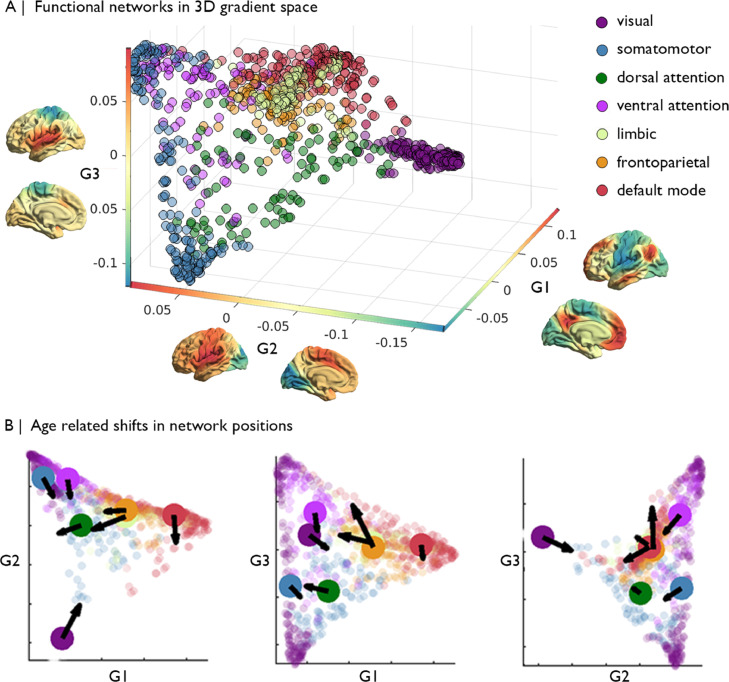
We explored age-related differences in the global orchestration of functional connectivity by projecting established functional communities into the 3D gradient space. Functional communities were compactly localized in the group-average 3D gradient space (Fig. 1A). The visual network occupied the most extreme, segregated position, driven by the second gradient. The default mode network also occupied an extreme position, driven by the first gradient, and was almost completely bordered from other networks by nodes from the frontoparietal network. Somatomotor and ventral attention networks populated one side of the 3D space, covering the range of the third gradient. Finally, dorsal attention and limbic networks resided close to the centre of space.

Fig. 1.

Fig 1

Open in a new tab

Functional gradients across healthy adulthood. (A) The first three gradients projected into a 3-dimensional gradient space and coloured by its Yeo network classification, with each functional gradient projected onto the cortical surface next to the corresponding axis. (B) Age-related shift in the centroid of each Yeo network in gradient space. Arrows reflect the direction of the centroid shift with higher age and are scaled by effect size.

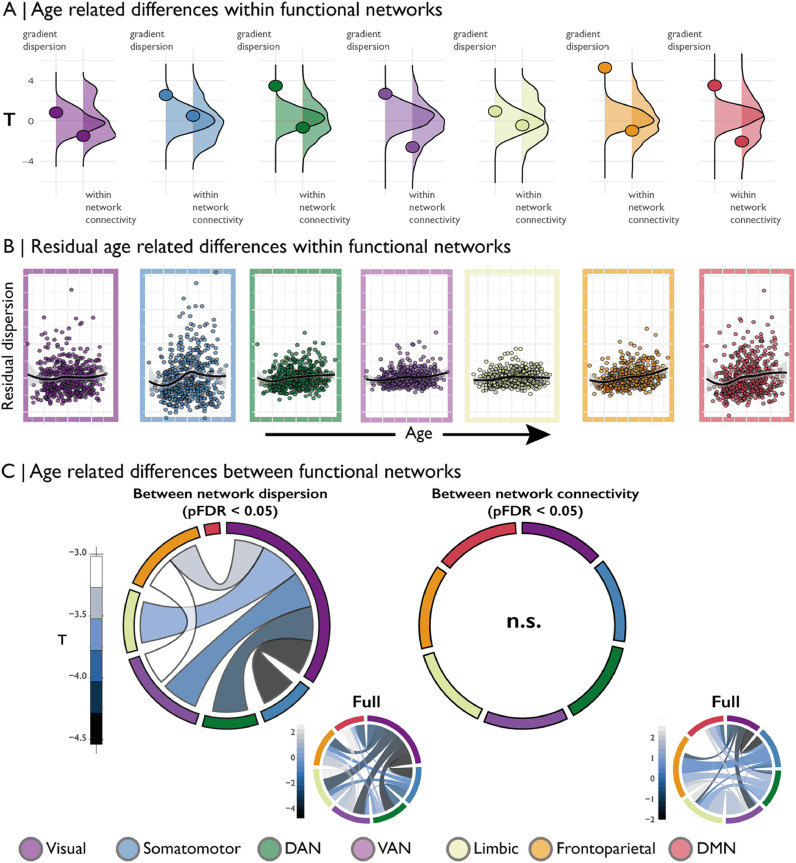
Notably, the overarching topology of the 3D gradient space was relatively stable across age. The strongest age-related differences were observed in the visual-to-insula gradient (G2) (Supplementary Figs. 2 and 3). Gradient values of occipital areas significantly increased with age. In parallel, values in insula nodes, occupying the top of the gradient, decreased with age. Together the node-wise differences produced an overall reduction in the range of the gradient (t = -3.29, pFDR = 0.0033) and more pronounced bimodality (t = 5.18, pFDR<0.0001), representing reduced functional differentiation across the entire axis coupled with consolidation within each functional system. The apex of the principle gradient (G1) remained constant across the age range, however, prefrontal regions tended to shift down the gradient with increasing age. Prefrontal regions also shifted up the somatomotor-to-insula gradient (G3), showing a shift in functional affiliation from the default mode apex of G1 towards the attention focused apex of G3. Range and bimodality of G2 and G3 did not significantly change with age (Supplementary Table 3). Sensitivity analyses, excluding varying proportion of subjects based on motion, indicated that the spatial pattern of age-related difference in gradient values was stable (Supplementary Fig. 5). Between network dispersion (i.e. the distance between the centroids of each network) (-4.35 <t<-2.88, pspin<0.05, Fig. 2D). This age-related difference occurred relatively uniformly for all nodes of the visual network, as its within network dispersion was not related to age (t = -2.49, pspin = 0.77). In contrast, the dorsal attention, ventral attention, fronto-parietal and default mode networks each became more dispersed in the 3D gradient space with increasing age (t = 3.49/2.69/5.53/3.52, pspin <0.05), reflecting more dissimilar functional connectivity profiles within the respective networks (Fig. 2A, 2B and Supplementary Fig. 7). There was no indication that dispersion in any of the Yeo networks was specifically or preferentially associated with one of the gradients (Supplementary Fig. 8).

Fig. 2.

Fig 2

Open in a new tab

(A) Age-related difference (t-statistic) in within network dispersion and within network connectivity for each Yeo network. Underlying density plots show the null distributions of t-statistics derived from spin permutations. Positive t-values signify increased network dispersion with age. (B) Residuals of the dispersion model (including controls for sex, motion and within network connectivity) against age residuals for the same model for each Yeo network. (C) Between network dispersion and between network connectivity. Network borders are scaled according to the size of the total effect from that community (e.g. the visual network is largest in the left panel as most significant between network dispersion involves the visual network). Insert panels on the right show the full between network pattern for all connections including non-significant ones.

3.1.1. Relation to alternative measures of brain function and structure

We hypothesised that gradient dispersion analysis offers a higher-dimensional account of functional reorganisation throughout the adult lifespan, and would thus partially overlap with findings using previously established measures of functional topology. Average within network functional connectivity was not associated with age, suggesting within network dispersion is more sensitive to adult lifespan changes (Fig. 2A). Furthermore, age-related difference in within network dispersion were independent of within network connectivity (Supplementary Table 4). Within network dispersion showed more similar age-related differences to the clustering coefficient (Rubinov and Sporns, 2010) (Table 1), but these were not concordant with age-related difference to “segregation” (Chan et al., 2014; Zonneveld et al., 2019). The segregation metric highlighted increases in the limbic network at later ages (Table 1). In contrast, dispersion and clustering indicated the strongest differences in ventral attention, dorsal attention, fronto-parietal and default mode networks. Dispersion, specifically, demonstrated increased sensitivity for detecting age-related difference in fronto-parietal and default mode networks. In addition, between network dispersion, unlike between network connectivity, was sensitive to age-related differences (Fig. 2C).

Table 1.

Age-related differences in within network metrics, controlling for sex and motion. Outcome of independent general linear models are depicted up to two significant digits, thereby p = 0.00 represents p<0.005. All models had 492 degrees of freedom.

Within network dispersion
 Segregation
 Clustering coefficient
t β se p t β se p t β se p
visual 1.00 1.74 1.74 0.23 -1.39 -4.33 3.11 0.16 1.21 3.17 2.61 0.23
somatomotor 3.65 4.52 1.23 0.00 -0.62 -2.78 4.46 0.53 2.31 7.29 3.16 0.02
dorsal attention 4.40 11.49 2.61 0.00 -0.60 -2.70 4.49 0.55 5.13 17.29 3.48 0.00
ventral attention 3.30 11.06 3.35 0.00 -1.17 -5.04 4.29 0.24 1.95 6.43 3.29 0.05
limbic 3.02 11.37 3.76 0.00 4.23 9.22 2.18 0.00 2.04 6.00 2.93 0.04
frontoparietal 6.66 17.77 2.66 0.00 0.63 2.20 3.52 0.53 4.18 12.30 2.95 0.00
default mode 5.22 7.72 1.48 0.00 0.85 2.56 3.01 0.40 2.36 6.77 2.87 0.02
Open in a new tab

3.1.2. Influence of cortical morphology

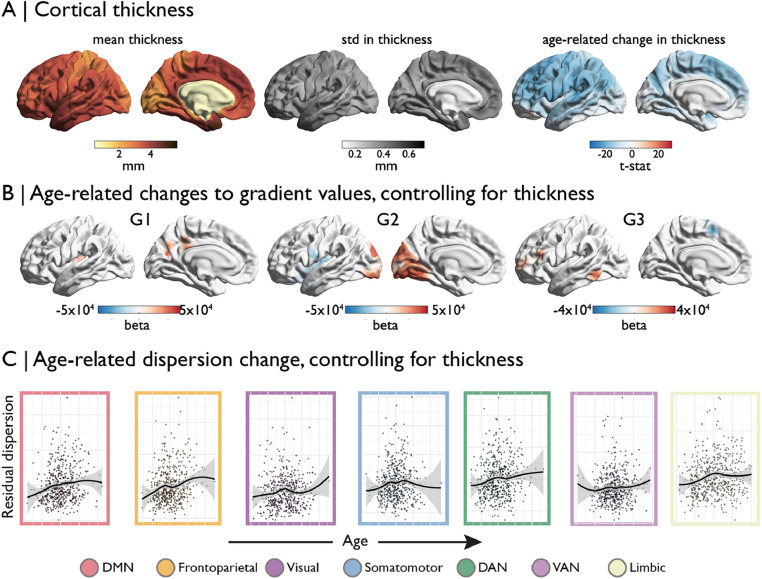
Ageing is strongly associated with cortical atrophy (Lowe et al., 2019). We performed surface based linear regression to assess the age-related differences in cortical thickness and detected widespread cortical thinning (Fig. 3). To determine whether this thinning influence age-related differences to the gradient dispersion, we repeated unimodal gradient analysis and within network dispersion models while controlling for cortical thickness. Results revealed identical patterns of gradient changes after controlling for cortical thickness. We found that controlling for cortical thinning slightly increases the linear effect of age on network dispersion as all previously significant networks remain significant and show a slight increase in F and T-values.

Fig. 3.

Fig 3

Open in a new tab

(A) Morphological changes in cortical thickness are widespread and uniformly negative. (B) Age-related changes to the gradients are not influenced by this cortical atrophy, (C) nor are the multi-dimensional changes in gradient dispersion.

3.1.3. Relation to cognition

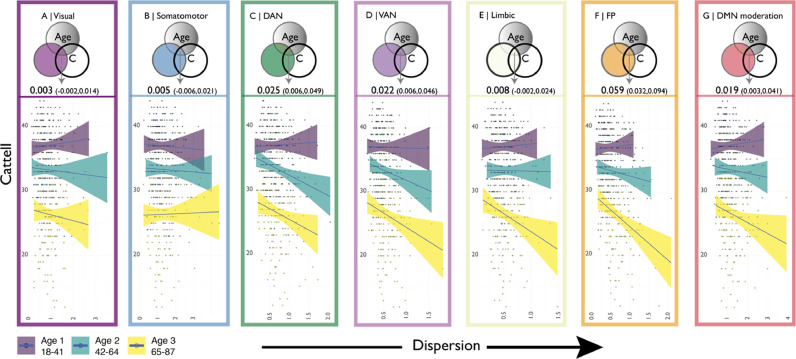
Finally, we explored whether the observed age-related differences in network dispersion were behaviorally relevant, as assessed with the Cattell fluid intelligence scale (Cattell, 1963). Commonality analysis showed that the common variance of age and dispersion in dorsal attention, ventral attention, fronto-parietal and default mode networks significantly explained Catell performance (Fig. 4, top panels).

Fig. 4.

Fig 4

Open in a new tab

Relationship between network dispersion and age-related cognitive decline. Top panels A-G show the schematic percentage overlap between age, dispersion and Cattell of each network from commonality analysis. Lower panels show visualize effects in moderation analysis, i.e. how this the association between dispersion and Cattell varied in three bins of the total age-range.

Moderation analysis revealed the strongest association of cognitive decline in fronto-parietal and default mode networks (Table 2, Fig. 4 bottom). Ventral attention, dorsal attention and limbic networks also showed a similar, albeit slightly weaker, association. Mimicking the lack of a main effect of association between age and dispersion, the visual and somatomotor networks did not indicate that the interaction of age and dispersion explained a significant proportion of variance in fluid intelligence. Effect directions for all network were negative, indicating that the relationship between dispersion and Cattell performance was stronger in older adults. Unimodal gradient changes (Supplementary Fig. 1) did not appear to moderate the relationship between age and cognition (Supplementary Fig. 9).

Table 2.

Age-related differences in within network metrics are associated with cognitive decline when controlling for sex, motion and within network dispersion.

Association with Cattell
β se t p
Visual*age -0.035 0.031 -1.10 0.270
Somatomotor*age -0.023 0.036 -0.63 0.528
DAN*age -0.082 0.033 -2.51 0.012
VAN*age -0.080 0.034 -2.34 0.020
Limbic*age -0.077 0.034 -2.31 0.022
FP*age -0.136 0.033 -4.04 0.000
DMN*age -0.087 0.032 -2.69 0.007
Open in a new tab

4. Discussion

We demonstrate that the ordering of regions within large-scale functional gradients remains relatively stable across the adult lifespan, but the dispersion of fronto-parietal and ventral attention networks in a 3D gradient space was related to cognitive decline. Decreasing dispersion was not preferentially associated with one gradient dimension, indicating the importance of multiple global patterns of connectivity for maintaining performance in old age. Our findings bolster existing literature on the importance of network integration and segregation for cognitive function (Geerligs et al., 2017; Andrews-Hanna et al., 2007; Betzel et al., 2014; Geerligs et al., 2014; Chan et al., 2014; Li et al., 2015; Tsvetanov et al., 2016; Zonneveld et al., 2019). By using a technique that explicitly captures the ordering of functional systems in a hierarchical framework, we exposed subtle age-related differences in within and between network organisation that conventional linear interactions did not detect and that was robust against known changes in cortical morphology. Furthermore, these effects were behaviourally relevant as they explained partly the relationship between age and fluid intelligence.

At a uni-dimensional level, we also observed age-related increases in the gradient values of the visual network. This indicated that, on the visual-insular axes of the gradient topology, the visual cortex became more similar to the rest of the cortex. This was captured by an overall decreased range in the gradient values and an increase of gradient values particularly in visual cortex. This de-differentiation of the visual cortex was also apparent in the context of the multi-dimensional gradient space where we observed that nodes within the Yeo visual network cluster almost uniformly moved closer towards the centre of all the other networks. Prior literature has indicated that in older adults the visual network shows signs of hyperactivity combined with decreased activation in control and default mode networks (Li et al., 2015). Interestingly, while we observed a de-differentiation of the visual cortex, we also observe an increased dispersion of frontal and default mode network that might fit with this prior finding of decreased activity in control networks. Thus, at a unimodal gradient level, we observed increased indicators of segregation within the visuo-insular gradient (e.g. increased bimodality).

Within specific networks we observed the strongest increased dispersion in default mode and fronto-parietal networks, but also in the ventral and dorsal attention networks as well as the somato-motor network. Increased dispersion is captures decreased similarity across multiple gradient domains. This notion is well aligned with prior reports of broad decreased functional connectivity (Zonneveld et al., 2019) and broad decreased functional cohesion (Betzel et al., 2014). Comparing dispersion in multi-dimensional gradient space to other approaches of measuring network changes such as clustering (Betzel et al., 2014), within network connectivity (Zonneveld et al., 2019) and segregation (Chan et al., 2014) more directly, we observe similar patterns of decreased between network connectivity, yet gradient dispersion seems to have an overall increased sensitivity to age-related differences. These age-related differences in dispersion also proved to have a small but significant overlap with fluid intelligence as measured by the Cattell (1963), where the common effect between age and dispersion in the DMN and the Fronto-Parietal explained 1.9% and 5.9% variance in Cattell performance. In addition, formal testing of the moderation effects suggested that high network dispersion in older age was associated with higher fluid intelligence, suggestive of the notion that maintaining network topology may be an import factor for maintaining healthy cognition, though further study and longitudinal data would be needed to address any causality in these effects. Visualisation of these effects clearly reveal an increased association between higher dispersion and lower Cattell in the older cohort. It is possible the overall size of the effect is tempered by the absence of that association in the younger cohort. Again, future longitudinal studies will be better placed to assess the true size of this association and its possible causal nature. It is, nevertheless, worth emphasizing that these findings are consistent with previous reports based on neuronal signatures from magnetoencephalography data (Bruffaerts et al., 2019; Tibon et al. 2020) or haemodynamic signatures from fMRI BOLD data only after accurate modelling of physiological and vascular differences (Geerligs et al., 2017; Tsvetanov et al., 2016). This raises the questions whether gradient-based estimates have reduced bias to non-physiological signals in BOLD data (Tsvetanov et al 2020), and also supports the notion that maintaining network topology in older age may be a key component to maintaining healthy cognition. More research directly comparing gradients derived from multiple modalities will be needed to answer that question more definitively.

Some caveats to the present study should be noted however. First, we currently used a single cognitive measure to determine behavioural relevance (e.g. Cattell). Future studies will need to investigate the behavioural relevance of gradient dispersion across other cognitive domains. Second, the present results are based on a population-based cross-sectional cohort, and cannot directly speak to individual subjects’ changes over time. The above discussion of age effects is therefore restricted to the effects of age and its correlates, as assessed across individuals, rather than the dynamic process of individual ageing ageing per se. Future longitudinal studies are required to confirm whether the gradient dispersion is sensitive to detect changes in functional reorganisation in individual progression either in healthy or diseased state. Third, our exploration of how network dispersion changes with age was restricted to an adult cohort and thus does not allow any direct conclusions on developmental changes per se. By sharing our code and data we hope to encourage others to apply similar methods to studying developmental brain network changes. Finally, the hold-out sample was used to generate the 3D template for alignment in the present study. This data-driven procedure resulted in sensory-transmodal and somatomotor-visual functional gradients that closely correspond with previous studies (Margulies et al., 2016; Zhang et al., 2019; Hong et al., 2020), however, the third functional gradient depicted a more restricted pattern than previous studies. Further assessment of the replicability of the functional gradients across individuals and datasets would be greatly beneficial to this burgeoning field. For this purpose the repository containing the code used in the present analysis also includes the individual matrices and code used to generate the hold-out alignment sample. Future studies could use this to generate their own out of sample reference alignment to match specific demographic factors (e.g: age and/or sex).

In sum, we show studying functional organisation in a multidimensional gradient framework can provide increased sensitivity to capturing and furthering previously established age-related changes in functional network topology. They are robust to potential confounds of known morphological changes and the captured change in topology has a significant mediating effect on age-related cognitive decline. Finally, although principally developed in the context of healthy ageing this multi-dimensional approach is not context specific and could be deployed in other cohorts.

Author contribution statement

RB, CP, JS, BB & KT designed the study, conducted the analyses and wrote the manuscript

LR conducted analyses and edited the final manuscript

Cam-CAN consortium provided all data, approved the design and manuscript

Funding

RAIB is supported by a British Academy Postdoctoral fellowship and Autism Research Trust, CP is supported by the Fonds de la Recherche du Quebec – Santé (FRQS). CP, RAIB, BB are supported by a Cambridge-MNI collaborative research grant. BB is supported by National Science and Engineering Research Council of Canada (NSERC, Discovery-1304413), the Canadian Institutes of Health Research (CIHR, FDN-154298), the Azrieli Center for Autism Research of the Montreal Neurological Institute (ACAR), SickKids Foundation (NI17-039), and the Canada Research Chairs Program. KAT is supported by the British Academy Postdoctoral Fellowship (PF160048) and the Guarantors of Brain (G101149). The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) research was supported by the Biotechnology and Biological Sciences Research Council (Grant BB/H008217/1). We thank the Cam-CAN respondents and their primary care teams in Cambridge for their participation in this study. Further information about the Cam-CAN corporate authorship membership can be found at http://www.cam-can.org/index.php?content=corpauth#12.

Data were curated and analysed using a computational facility funded by an MRC research infrastructure award (MR/M009041/1) and supported by the NIHR Cambridge Biomedical Research Centre. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health and Social Care.

Acknowledgements

This project would not have been possible without the work already done by the Cam-CAN consortium and their open sharing of data with the scientific community.

Footnotes

Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.neuroimage.2020.117299.

Contributor Information

Richard A.I. Bethlehem, Email: rb643@medschl.cam.ac.uk.

Casey Paquola, Email: casey.paquola@gmail.com.

Appendix. Supplementary materials

mmc1.pdf (2.3MB, pdf)

References

  1. Alexander-Bloch A.F., Shou H., Liu S., Satterthwaite T.D., Glahn D.C., Shinohara R.T., Vandekar S.N., Raznahan A. On testing for spatial correspondence between maps of human brain structure and function. Neuroimage. 2018;178:540–551. doi: 10.1016/j.neuroimage.2018.05.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Andrews-Hanna J.R., Snyder A.Z., Vincent J.L., Lustig C., Head D., Raichle M.E., Buckner R.L. Disruption of large-scale brain systems in advanced aging. Neuron. 2007;56:924–935. doi: 10.1016/j.neuron.2007.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bahrami M., Lyday R.G., Casanova R., Burdette J.H., Simpson S.L., Laurienti P.J. Using low-dimensional manifolds to map relationships between dynamic brain networks. Front. Hum. Neurosci. 2019;13 doi: 10.3389/fnhum.2019.00430. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Beard J.R., Officer A.M., Cassels A.K. The world report on ageing and health. The Gerontol. 2016;56:S163–S166. doi: 10.1093/geront/gnw037. [DOI] [PubMed] [Google Scholar]
  5. Betzel R.F., Byrge L., He Y., Goñi J., Zuo X.N., Sporns O. Changes in structural and functional connectivity among resting-state networks across the human lifespan. Neuroimage. 2014;102(Pt 2):345–357. doi: 10.1016/j.neuroimage.2014.07.067. [DOI] [PubMed] [Google Scholar]
  6. Braga R.M., Leech R. Echoes of the brain: local-scale representation of whole-brain functional networks within transmodal cortex. The Neurosci. 2015;21 doi: 10.1177/1073858415585730. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bruffaerts R., Tyler L.K., Shafto M., Tsvetanov K.A., Clarke A. Perceptual and conceptual processing of visual objects across the adult lifespan. Sci. Rep. 2019;9:13771. doi: 10.1038/s41598-019-50254-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cattell R.B. Theory of fluid and crystallized intelligence: a critical experiment. J. Educ. Psychol. 1963;54:1–22. doi: 10.1037/h0024654. [DOI] [PubMed] [Google Scholar]
  9. Chan M.Y., Park D.C., Savalia N.K., Petersen S.E., Wig G.S. Decreased segregation of brain systems across the healthy adult lifespan. Proc. Natl. Acad. Sci. U.S.A. 2014;111:E4997–E5006. doi: 10.1073/pnas.1415122111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chan M.Y., Park D.C., Savalia N.K., Petersen S.E., Wig G.S. Decreased segregation of brain systems across the healthy adult lifespan. Proc. Natl. Acad. Sci. 2014;111:E4997–E5006. doi: 10.1073/pnas.1415122111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Coifman R.R., Hirn M.J. Diffusion maps for changing data. Appl. Comput. Harmonic Anal. 2014;36:79–107. [Google Scholar]
  12. Coifman R.R., Lafon S. Diffusion maps. Appl. Comput. Harmonic Anal. 2006;21:5–30. [Google Scholar]
  13. Dale S., Fischl Cortical surface-based analysis. I. Segmentation and surface reconstruction. - PubMed - NCBI. NeuroImage. 1999;9(2) doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
  14. Damoiseaux J.S., Beckmann C.F., Arigita E.J., Barkhof F., Scheltens P., Stam C.J., Smith S.M., Rombouts S.A. Reduced resting-state brain activity in the default network in normal aging. Cereb Cortex. 2008;18:1856–1864. doi: 10.1093/cercor/bhm207. [DOI] [PubMed] [Google Scholar]
  15. Ferreira L.K., Regina A.C., Kovacevic N., Martin M.G., Santos P.P., Carneiro C.G., Kerr D.S., Amaro E.J., McIntosh A.R., Busatto G.F. Aging effects on whole-brain functional connectivity in adults free of cognitive and psychiatric disorders. Cereb Cortex. 2016;26:3851–3865. doi: 10.1093/cercor/bhv190. [DOI] [PubMed] [Google Scholar]
  16. Fischl D., Sereno Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. - PubMed - NCBI. NeuroImage. 1999;9(2) doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
  17. Geerligs L., Maurits N.M., Renken R.J., Lorist M.M. Reduced specificity of functional connectivity in the aging brain during task performance. Hum. Brain Mapp. 2014;35:319–330. doi: 10.1002/hbm.22175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Geerligs L., Renken R.J., Saliasi E., Maurits N.M., Lorist M.M. A brain-wide study of age-related changes in functional connectivity. Cereb Cortex. 2015;25:1987–1999. doi: 10.1093/cercor/bhu012. [DOI] [PubMed] [Google Scholar]
  19. Geerligs L., Tsvetanov K.A., Cam-Can, Henson R.N. Challenges in measuring individual differences in functional connectivity using fMRI: the case of healthy aging. Hum. Brain Mapp. 2017;38:4125–4156. doi: 10.1002/hbm.23653. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Genon S., Reid A., Langner R., Amunts K., Eickhoff S.B. How to characterize the function of a brain region. Trends Cogn. Sci. 2018;22:350–364. doi: 10.1016/j.tics.2018.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Goh J.O.S. Functional dedifferentiation and altered connectivity in older adults: neural accounts of cognitive aging. Aging Dis. 2011;1:30–48. [PMC free article] [PubMed] [Google Scholar]
  22. Haak K.V., Marquand A.F., Beckmann C.F. Connectopic mapping with resting-state fMRI. Neuroimage. 2018;170:83–94. doi: 10.1016/j.neuroimage.2017.06.075. [DOI] [PubMed] [Google Scholar]
  23. Hartigan J.A., Hartigan P.M. The dip test of unimodality. The Ann. Stat. 1985;13 [Google Scholar]
  24. Hedden T., Gabrieli J.D. Insights into the ageing mind: a view from cognitive neuroscience. Nat. Rev. Neurosci. 2004;5:87–96. doi: 10.1038/nrn1323. [DOI] [PubMed] [Google Scholar]
  25. Hong, S.-J., Xu, T., Nikolaidis, A., Smallwood, J., Margulies, D.S., Bernhardt, B., Vogelstein, J., Milham, M.P., 2020. Toward a connectivity gradient-based framework for reproducible biomarker discovery. doi:10.1101/2020.04.15.043315. [DOI] [PubMed]
  26. Hong S.J., Bernhardt B.C., Gill R.S., Bernasconi N., Bernasconi A. The spectrum of structural and functional network alterations in malformations of cortical development. Brain. 2017;140:2133–2143. doi: 10.1093/brain/awx145. [DOI] [PubMed] [Google Scholar]
  27. Huber P.J., Ronchetti E.M. 2nd ed. Wiley; 2009. Robust Statistics. [Google Scholar]
  28. Langs G., Golland P., Ghosh S.S. Predicting activation across individuals with resting-state functional connectivity based multi-atlas label fusion. Med. Image Comput. Comput. Assist. Interv. 2015;9350:313–320. doi: 10.1007/978-3-319-24571-3_38. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Li H.J., Hou X.H., Liu H.H., Yue C.L., Lu G.M., Zuo X.N. Putting age-related task activation into large-scale brain networks: a meta-analysis of 114 fMRI studies on healthy aging. Neurosci. Biobehav. Rev. 2015;57:156–174. doi: 10.1016/j.neubiorev.2015.08.013. [DOI] [PubMed] [Google Scholar]
  30. Lowe A.J., Paquola C., Vos, de W.R., Girn M., Lariviere S., Tavakol S., Caldairou B., Royer J., Schrader D.V., Bernasconi A., Bernasconi N., Spreng R.N., Bernhardt B.C. Targeting age-related differences in brain and cognition with multimodal imaging and connectome topography profiling. Hum. Brain Mapp. 2019;40:5213–5230. doi: 10.1002/hbm.24767. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Margulies D.S., Ghosh S.S., Goulas A., Falkiewicz M., Huntenburg J.M., Langs G., Bezgin G., Eickhoff S.B., Castellanos F.X., Petrides M., Jefferies E., Smallwood J. Situating the default-mode network along a principal gradient of macroscale cortical organization. Proc. Natl. Acad. Sci. U.S.A. 2016;113:12574–12579. doi: 10.1073/pnas.1608282113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Margulies D.S., Ghosh S.S., Goulas A., Falkiewicz M., Huntenburg J.M., Langs G., Bezgin G., Eickhoff S.B., Castellanos F.X., Petrides M., Jefferies E., Smallwood J. Situating the default-mode network along a principal gradient of macroscale cortical organization. Proc. Natl. Acad. Sci. 2016;113:12574–12579. doi: 10.1073/pnas.1608282113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Mesulam M.M. From sensation to cognition. Brain. 1998;121(Pt 6):1013–1052. doi: 10.1093/brain/121.6.1013. [DOI] [PubMed] [Google Scholar]
  34. Nimon K., Oswald F.L. Understanding the results of multiple linear regression: Beyond standardized regression coefficients. Organ. Res. Methods. 2013;16:650–674. [Google Scholar]
  35. Nimon K., Lewis M., Kane R., Haynes M. An R package to compute commonality coefficients in the multiple regression case: an introduction to the package and a practical example. Behav. Res. Methods. 2008;40:457–466. doi: 10.3758/brm.40.2.457. [DOI] [PubMed] [Google Scholar]
  36. Onoda K., Ishihara M., Yamaguchi S. Decreased functional connectivity by aging is associated with cognitive decline. J. Cognit. Neurosci. 2012;24:2186–2198. doi: 10.1162/jocn_a_00269. [DOI] [PubMed] [Google Scholar]
  37. Paquola C., Vos D.W.R., Wagstyl K., Bethlehem R.A.I., Hong S.J., Seidlitz J., Bullmore E.T., Evans A.C., Misic B., Margulies D.S., Smallwood J., Bernhardt B.C. Microstructural and functional gradients are increasingly dissociated in transmodal cortices. PLoS Biol. 2019;17 doi: 10.1371/journal.pbio.3000284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Pruim R.H.R., Mennes M., van R.D., Llera A., Buitelaar J.K., Beckmann C.F. ICA-AROMA: a robust ICA-based strategy for removing motion artifacts from fMRI data. Neuroimage. 2015;112:267–277. doi: 10.1016/j.neuroimage.2015.02.064. [DOI] [PubMed] [Google Scholar]
  39. Qiu A., Lee A., Tan M., Chung M.K. Manifold learning on brain functional networks in aging. Med. Image Anal. 2015;20:52–60. doi: 10.1016/j.media.2014.10.006. [DOI] [PubMed] [Google Scholar]
  40. Reio T., Chambers S., Gavrilova-Aguilar M., Nimon K. Commonality analysis: a reference librarian's tool for decomposing regression effects. The Reference Librarian. 2015;56(4) Research Methods for Librarianship. [Google Scholar]
  41. Ronan L., Alexander-Bloch A.F., Wagstyl K., Farooqi S., Brayne C., Tyler L.K., Fletcher P.C. Obesity associated with increased brain age from midlife. Neurobiol. Aging. 2016;47:63–70. doi: 10.1016/j.neurobiolaging.2016.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Rubinov M., Sporns O. Complex network measures of brain connectivity: uses and interpretations. NeuroImage. 2010;52:1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
  43. Rubinov M., Sporns O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage. 2010;52:1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
  44. Shafto M.A., Tyler L.K., Dixon M., Taylor J.R., Rowe J.B., Cusack R., Calder A.J., Marslen-Wilson W.D., Duncan J., Dalgleish T., Henson R.N., Brayne C., Matthews F.E. The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) study protocol: a cross-sectional, lifespan, multidisciplinary examination of healthy cognitive ageing. BMC Neurol. 2014;14:204. doi: 10.1186/s12883-014-0204-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Taylor J.R., Williams N., Cusack R., Auer T., Shafto M.A., Dixon M., Tyler L.K., Cam-Can, Henson R.N. The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) data repository: structural and functional MRI, MEG, and cognitive data from a cross-sectional adult lifespan sample. Neuroimage. 2017;144:262–269. doi: 10.1016/j.neuroimage.2015.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Tian, Y., Margulies, D.S., Breakspear, M., Zalesky, A., 2020. Hierarchical organization of the human subcortex unveiled with functional connectivity gradients. [DOI] [PubMed]
  47. Tibon, R., Tsvetanov, K., Price, D., Nesbitt, D., Cam-CAN, Henson, R., (2020) Transient resting-state network dynamics in cognitive ageing. bioRxviv. doi:10.1101/2020.05.19.103531. [DOI] [PMC free article] [PubMed]
  48. Tsvetanov K.A., Henson R.N., Tyler L.K., Razi A., Geerligs L., Ham T.E., Rowe J.B. Extrinsic and intrinsic brain network connectivity maintains cognition across the lifespan despite accelerated decay of regional brain activation. J. Neurosci. 2016;36:3115–3126. doi: 10.1523/JNEUROSCI.2733-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Tsvetanov K.A., Henson R.N.A., Rowe J.B. Separating vascular and neuronal effects of age on fMRI BOLD signals. Philos. Trans. R. Soc. B Biol. Sci. 2020 doi: 10.1098/rstb.2019.0631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Tsvetanov K.A., Ye Z., Hughes L., Samu D., Treder M.S., Wolpe N., Tyler L.K., Rowe J.B. Activity and connectivity differences underlying inhibitory control across the adult life span. J. Neurosci. 2018;38:7887–7900. doi: 10.1523/JNEUROSCI.2919-17.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Van D.K.R., Sabuncu M.R., Buckner R.L. The influence of head motion on intrinsic functional connectivity MRI. Neuroimage. 2012;59:431–438. doi: 10.1016/j.neuroimage.2011.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Vasa Frantisek. Adolescent tuning of association cortex in human structural brain networks. Cerebral Cortex. 2017;28(1):281–294. doi: 10.1093/cercor/bhx249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Vos de Wael R., Benkarim O., Paquola C., Lariviere S., Royer J., Tavakol S., Xu T., Hong S.J., Langs G., Valk S., Misic B., Milham M., Margulies D., Smallwood J., Bernhardt B.C. BrainSpace: a toolbox for the analysis of macroscale gradients in neuroimaging and connectomics datasets. Commun. Biol. 2020;3:103. doi: 10.1038/s42003-020-0794-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Vos de Wael R., Larivière S., Caldairou B., Hong S.J., Margulies D.S., Jefferies E., Bernasconi A., Smallwood J., Bernasconi N., Bernhardt B.C. Anatomical and microstructural determinants of hippocampal subfield functional connectome embedding. Proc. Natl. Acad. Sci. U.S.A. 2018;115:10154–10159. doi: 10.1073/pnas.1803667115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Worsley K.J., Taylor J.E., Carbonell F., Chung M.K., Duerden E., Bernhardt B., Lyttelton O., Boucher M., Evans A.C. SurfStat: A Matlab toolbox for the statistical analysis of univariate and multivariate surface and volumetric data using linear mixed effects models and random field theory. NeuroImage. 2009;47:S102. [Google Scholar]
  56. Yan C.G., Craddock R.C., Zuo X.N., Zang Y.F., Milham M.P. Standardizing the intrinsic brain: towards robust measurement of inter-individual variation in 1000 functional connectomes. Neuroimage. 2013;80:246–262. doi: 10.1016/j.neuroimage.2013.04.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Yarkoni T., Poldrack R.A., Nichols T.E., Van E.D.C., Wager T.D. Large-scale automated synthesis of human functional neuroimaging data. Nat. Methods. 2011;8:665–670. doi: 10.1038/nmeth.1635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Yeo B.T., Krienen F.M., Sepulcre J., Sabuncu M.R., Lashkari D., Hollinshead M., Roffman J.L., Smoller J.W., Zöllei L., Polimeni J.R., Fischl B., Liu H., Buckner R.L. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol. 2011;106:1125–1165. doi: 10.1152/jn.00338.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Zhang J., Abiose O., Katsumi Y., Touroutoglou A., Dickerson B.C., Barrett L.F. Intrinsic functional connectivity is organized as three interdependent gradients. Sci. Rep. 2019;9 doi: 10.1038/s41598-019-51793-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Zientek L.R., Thompson B. Commonality analysis: partitioning variance to facilitate better understanding of data. J. Early Intervent. 2006;28(4):299–307. [Google Scholar]
  61. Zonneveld H.I., Pruim R.H.R., Bos D., Vrooman H.A., Muetzel R.L., Hofman A., Rombouts S.A.R.B., van der Lugt A., Niessen W.J., Ikram M.A., Vernooij M.W. Patterns of functional connectivity in an aging population: the Rotterdam study. NeuroImage. 2019;189:432–444. doi: 10.1016/j.neuroimage.2019.01.041. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

mmc1.pdf (2.3MB, pdf)

Data Availability Statement

Data and code used in this manuscript are available from https://github.com/rb643/GradientDispersion.

RESOURCES