Abstract
In this investigation, the shockwave propagation caused by the explosive detonation in a complex environment has been studied by the open-source Computational Fluid Dynamics (CFD) package, OpenFOAM®. An extended solver was developed to take the effect of explosion energy into account. The Becker-Kistiakowsky-Wilson (BKW) equation of state (EOS) was implemented in OpenFOAM® to calculate the detonation impact on the surrounding fluid density variations. Also, the influence of two turbulence modeling approaches of Reynolds-averaged Navier-Stokes (RANS) and Large-eddy Simulation (LES) on the prediction of explosion pressure was studied and compared against previous experimental and numerical studies. The comparisons demonstrated the accuracy of the implemented BKW EOS in calculating the fluid density. Further, it was shown that the LES approach is capable of capturing the unsteady nature of detonation in the near-field of the explosive. Examining the instantaneous velocity vectors of the LES results revealed sequential wave fronts that were responsible for rapid changes in the pressure signals. Furthermore, ground pressure contours demonstrated that the shock waves spread on the ground in a circular shape. The results of the current study suggested that the OpenFOAM® technology is powerful to incorporate various physical models, including the equation of state and scale-resolving methods such as LES, to capture the complex nature of the detonation phenomenon.
Keywords: sonicFoam, Equation of state, Source term, Blast, Numerical simulation
sonicFoam; Equation of state; Source term; Blast; Numerical simulation.
1. Introduction
Nowadays, terrorism has threatened life, property, and business. Targets are mostly in urban areas where there is greater compactness of life and economic value [1, 2, 3]. Governments, engineers, and insurance industries have utilized versatile approaches to mitigate these threats through understanding effects of urban bombings, increasing resilience of buildings and improving estimates of financial loss for insurance purposes, respectively [4, 5, 6]. Therefore, the anticipation of the blast extension in densely populated areas through improved methods is an important challenge [7].
The blast arising from the detonation of an explosive can be simulates and predicted by three different ways including experimentation, semi-empirical consideration, and numerical study [8, 9]. Meanwhile, the blast loads are recorded by direct measurements in the experimentation approach and it is regarded as the most reliable way for studying the blast wave propagation. However, it has some shortcomings such as costly, risky, and not being workable [10, 11].
A surrogate approach is to combine the existing experimental data with the analytic methods that form a subset of original data, or extend the data based on the simplified models of the physical phenomena (semi-empirical methods) [12]. The empirical and semi-empirical methods are not desirable for the blast predictions that involve anything more than the simplest of geometries [12, 13]. In urban areas, the simulation of the blast wave extension is beyond the scope of semi-empirical methods due to the non-symmetrical nature of the buildings [14]; therefore, numerical first-principle methods are necessary. Numerical approaches date back to the 1940s [15, 16, 17, 18]. In this regard, although the Computational Fluid Dynamics (CFD) methods are more computationally expensive than the empirical methods, the CFD can implicitly capture the effects of the geometry on the solution [19, 20]. The latter makes them well suited to complex cityscapes where the interactions between the blast wave and the urban environments would have a significant effect on the blast wave propagation [21, 22]. The study of Hao et al. [14] can be referred for a review on the CFD modeling approaches.
CFD packages simulate the hydrodynamics of the fluid in various systems. In recent years, there is a considerable interest in evaluating the use of CFD in the blast wave studies [23, 24]. CFD is able to solve the problems of the simulation of explosion under various physical scenarios such as confined environments [25, 26], obstructed environment equivalent to a porous system [27], and venting ducts [28]. These evaluations reveal that the strength of an explosion increases by enhancing the confinement and turbulence.
The Becker-Kistiakowsky-Wilson equation of state (BKW-EOS) is today one of the most common equations for estimating the detonation wave parameters [29, 30, 31]. As an example, a comparative study on two simple configurations was performed in [32], assessing two equations of state with BKW being one of them. It was reported that BKW-EOS can provide higher accuracy in the intermediate pressure range of detonation. This equation was first applied for detonation modeling by Cowan and Fickett in 1957 [33]. Mader afforded an elaborated description of the history, calibration, and application of the BKW equation of state in calculating the detonation states [34]. In addition to Mader's calibration, which is usually called BKW, others have recalibrated the constants for a better fit to other groups of calibration data, and their calibrations are called BKWR [35], BKWS [36], BKWC [37], BKWRDX [30], BKWNV [38], and so forth. To find the BKW equation parameters, Cowan and Fickett [33] employed data received from measuring the D–ρ0 dependence on the detonation pressure at the maximum possible density for five explosives. It was supposed that the detonation products consisted of the following components: H2O, H2, CO2, N2, NO, CO, and C (graphite). Mader [30, 34, 39] showed that it was unlikely to find a set of arguments that would result in a good reproduction of the experimental values for the detonation parameters for Trinitrotoluene (TNT) and 1,3,5-Trinitro-1,3,5-triazinane (RDX), particularly at those co-volume values that recreate experimental Hugoniot adiabats for individual detonation products. Two sets of parameters were consequently proposed: (1) for explosives with a positive or small negative oxygen balance, and (2) for explosives whose detonation products have a large amount of condensed carbon.
In the current study, OpenFOAM® is utilized for the simulations of shockwave propagation. OpenFOAM® has been extensively used with great favor as a tool for research works in the field of CFD [40, 41, 42, 43, 44, 45]. However, to the best of our knowledge, a suitable solver for high-speed flow simulations with a semi-empirical equation of state has not been reported in the literatures. In this study, the development and verification of a pressure-based solver in OpenFOAM® for solving the compressible flows (based on the native sonicFoam solver) are performed. BKW-EOS library is used for its high accuracy to calculate the density of the highly compressible flows. As pointed out, an extended version of the sonicFoam solver is adopted to solve the compressible Navier-Stokes (N–S) equations in a 3-dimensional space, with the added source term of the explosion. To validate our setup in OpenFOAM®, a quantitative criterion is defined and an experimental work [46] is analyzed. Also, two turbulence modeling approaches including a two-equation eddy-viscosity standard (Reynolds-averaged Navier-Stokes) and one-equation model (Large-eddy Simulation) are applied, and the results are compared to the numerical results presented by Sklavounos and Rigas [47] used RANS in their study.
2. Numerical setup
2.1. Governing equations
The CFD approach follows a general deterministic process for approximating the solution of a problem. Conservation laws of mass, momentum, and energy in addition to several (optional) other partial differential equations are considered. The above-mentioned auxiliary (optional) equations may be required for modeling the turbulence phenomenon or utilizing an equation of state.
The differential form of the governing equations, collectively known as Navier-Stokes equations (N–S) can be expressed in the following form: First, the continuity equation (mass conservation) is stated as:
| (1) |
where and are the fluid density and velocity, respectively. represents the time and “” refers to the divergence operator. The conservation of momentum is expressed as:
| (2) |
Here, denotes the pressure. Also, refers to the efficient stress tensor which includes both laminar and turbulence contributions:
| (3) |
In Eq. (3), is the sum of the laminar and turbulent dynamic viscosities. The latter () represents the contribution of the turbulence, which typically occurs in high-speed flows. Also, is the symmetric part of the velocity gradient tensor and represents the unity tensor.
The energy equation is expressed as in the following:
| (4) |
where , , and are the internal energy, heat flux, and the flow kinetic energy, respectively. Temperature is obtained through the energy via the relation , where is the specific heat at constant volume. Finally, is the source term that will account for the explosion energy.
2.2. Turbulence modeling
As the turbulence is very complex in nature, resolving all the flow scales up to Kolmogorov criteria (tiny structures) is not feasible, particularly for high-speed flows and industrial problems. A workaround is to model the contributions of turbulence in the engineering problems by means of specific developed and well-established methodologies, generally known as turbulence modeling. A well-known approach for modeling the turbulence effect is Reynolds-averaged Navier-Stokes (RANS). This approach is popular in industrial problems, as it is cost-efficient and requires relatively low computational resources. In RANS, the equations are derived by time-averaging of the original N–S equations (without extra stress terms). The averaging will lead to the appearance of a stress tensor term, known as Reynolds stress tensor. The time-averaging operator is given by the following relation:
| (5) |
In the equation above, is the supposedly long-enough averaging period, and refers to the time.
An additional density-averaging (Favre-averaging) is also performed on the time-averaged quantities:
| (6) |
Another way to account for the turbulence effects is through the Large-eddy Simulation (LES) approach. In this method, the equations are obtained by applying spatial filtering (explicit or implicit filtering). In the filtering procedure, an instantaneous quantity such as velocity is decomposed into a filtered (resolved) and a subgrid (modeled) part:
| (7) |
The tilde symbol represents the spatially filtered variable, which has also undergone density-averaging. The “” symbol indicates the subgrid-scale fluctuation part. The spatial averaging is defined as follows:
| (8) |
where denotes the spatial filter. represents the global coordinate vector, and is the local coordinate vector, giving the deviation from each value. In the current study, the implicit filtering approach is utilized, i.e., the filter width is equal to the cell volume. In this approach, the filtering operator is defined as:
| (9) |
The density-averaging is similar to what was done in RANS and thus not repeated here. The LES filtering is a spatial operator, unlike what occurs in RANS in which the equations are temporally averaged. The filtering also results in appearance of a new term, known as subgrid-scale (SGS) tensor. Generally, LES would allow more physically resolve the flow turbulence rather than merely model its influence, as in the RANS approach. Compared to RANS, LES can be substantially time-consuming and typically demands greater computational resources. LES aims to resolve the high-energy content of the flow and resorts to the modeling of the small structures that are universal and spatially isotropic, according to the Kolmogorov hypothesis [48].
On the other hand, RANS aims to model the entire range of turbulence (large and small structures) altogether which is much more practical for most of the engineering problems. In the following section, the formulations of two turbulence models, one RANS and one LES, are elaborated. Both these models have been developed based on the Boussinesq's hypothesis in which the turbulent stress tensor (Reynolds stress tensor or SGS stress tensor) has been related to the symmetric part of the velocity gradient (rate of strain) by a quantity known as eddy-viscosity ( or ). Therefore, the aim is to find an approximation for the eddy-viscosity to reconstruct the turbulent stress tensor and close the system of N–S equations (Eq. (2)).
2.2.1. RANS standard model
One of the most popular RANS models is the two-equation eddy-viscosity standard [49]. In this model, the eddy-viscosity () is approximated by solving for two transport quantities of and . The former refers to the turbulent kinetic energy of the flow and the latter denotes the turbulence dissipation rate. The equations of these two quantities are given by:
| (10) |
| (11) |
Here, refers to the material derivative of the quantity. Mathematically, it expands to the partial derivatives, which include: . Also, , , and are the model constants with the values of 1.44, 1.92, and 0, respectively.
The eddy-viscosity () is obtained from the quantities and through the following relation:
| (12) |
where is a constant with the value of 0.09.
2.2.2. LES dynamic one-equation model
The dynamic one-equation model [50] is an eddy-viscosity LES model. One main difference between RANS and LES is that the latter aims to model only a small portion of turbulence. According to this, the turbulent stress tensor obtained from LES is also different from that of RANS. The turbulent stress tensor in the latter represents the entire turbulence range (Reynolds stress tensor), while in LES only a small portion of turbulence is modeled through the SGS stress tensor. As it was pointed out, the eddy-viscosity in LES is denoted by . It should be noted that the quantity in the LES model differs from the in the RANS model. Here, represents the kinetic energy of the subgrid levels. In comparison, in the model denotes the entire kinetic energy of turbulence.
One of the main advantages of dynamic model over the algebraic SGS models, such as the classic Smagorinsky model [51], is that it does not rely on the assumption of local equilibrium between the SGS production and dissipation rate. Hence, it will be more convenient for problems with coarser grids. The transport equation of SGS kinetic energy is expressed as follows:
| (13) |
In the equation above, and are the SGS stress tensor and resolved strain rate, respectively. They are defined by:
| (14) |
and
| (15) |
The eddy-viscosity is related to via the following relation:
| (16) |
in Eq. (13) and in Eq. (16) are constants that will be calculated through a dynamic procedure similar to the dynamic Smagorinsky model [50, 52].
2.3. Solver
In the present study, OpenFOAM® technology has been utilized to solve the governing equations. OpenFOAM® is an open-source finite-volume package which discretizes the partial differential equations and solves for desired flow quantities. It has been developed in C++ language and benefits from its object-oriented capabilities. It offers a wide range of various solvers for different flow configurations. In this investigation, an extended version of the sonicFoam solver has been adopted to solve the compressible N–S equations in a 3-dimensional space, with the added source term of the explosion. The source term equation has been directly added to the energy equation. It is given by the following relation:
| (17) |
where is the explosive volume equal to , is the energy of the explosion and is defined as:
| (18) |
The explosive energy is assumed to be released at , with a constant rate of burning, m/s.
The solver accounts for the density variations in high-speed flows via utilizing an equation of state which can be customized according to the problem specifications.
2.4. Equation of state
In this study, the BKW equation of state has been utilized for its high accuracy to calculate the density of highly compressible flows. The BKW equation can be defined as:
| (19) |
where and are given by the following relations:
| (20) |
| (21) |
Here α, , , and are empirical constants. is the molar volume of the gas phase, and are the co-volume and the molar fraction of the gaseous component i, respectively (summation is made over the all gaseous components of the mixture).
As can be seen in Eq. (19), an implicit relation exists, and the value of the density cannot be obtained by a direct calculation. Therefore, an iterative procedure was implemented which utilizes the well-known Newton-Raphson algorithm to find the density value. The parameters that are present in the BKW-EOS have been listed in Table 1.
Table 1.
BKW parameters for RDX [35].
| Parameter | ||||
|---|---|---|---|---|
| Value | 0.16 | 10.91 | 0.5 | 400 |
2.5. Flow configuration and mesh generation
A 3D experimental test case from field-scale explosion tests executed by Health and Safety Executive [46] was chosen to validate the computational results. In the mentioned reference [46], several experiments were conducted that involved the hemispheric surface explosion of PE4 in a clear as well as an obstructed environment. A total of six tests were performed. The test#1 in the experiments was taken as the reference.
A series of concrete blocks were sited in variable configurations on the right side of the explosive, and the area on the left side of the charge was left unobstructed. The explosive was shaped into a hemisphere with a radius of 0.054 m and a mass of 320 g, which could be activated through a detonator, placed on top of the explosive. Pressure transducers were situated throughout the test domain, and recorded the pressure-time history following the explosion. One of these tests has been considered to validate the current numerical method. As well, it serves as a framework to demonstrate the improvements by the present numerical methods.
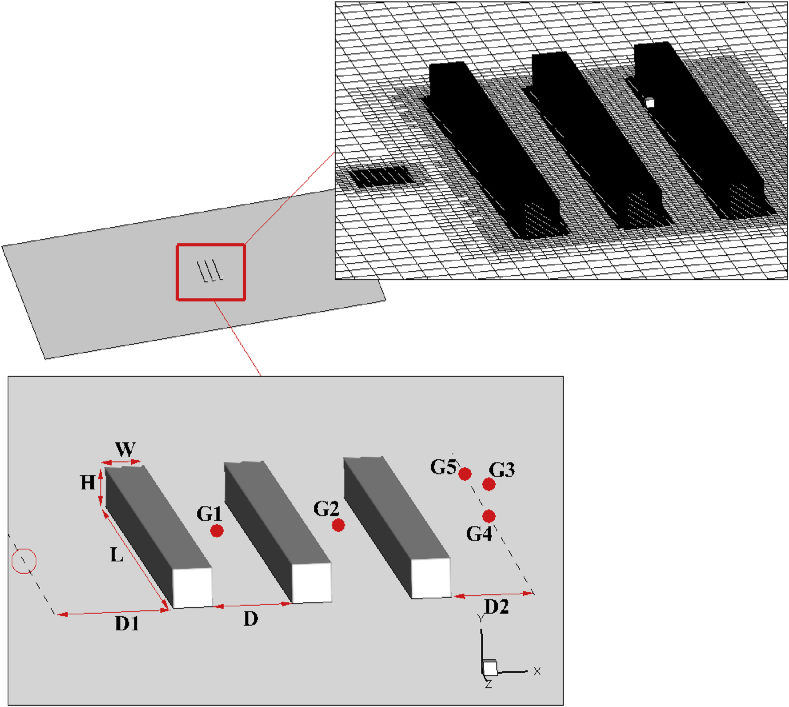
The CFD simulations require a computational mesh for spatial discretization. Further, the mesh is crucial in CFD as it dictates the spatial accuracy of the solution, particularly in domains that involve complex topologies. In general, the larger the cell number, the higher the spatial accuracy would be. However, increasing the number of cells in a CFD simulation is not as simple. There are constraints such as computational resource and time which restrict the cell number. Therefore, a compromise between the solution accuracy and the simulation time should be made. In the current investigation, the snappyHexMesh utility within OpenFOAM® was implemented to generate high-quality hexahedral meshes. Three sets of computational grid have been produced to assess the impact of the grid resolution on the results. The cell numbers are 600 thousand (600K), 1.2, and 3 million (1.2M and 3M) for the coarse, medium, and fine grid, respectively. An isometric view of the computational domain and mesh is illustrated in Figure 1. The important dimensional parameters have been introduced in the bottom image with their values listed in Table 2. The domain extended from -40 m to 40 m in the x-direction. In the z-direction, it has spanned from -24 m to 24 m, and its height is equal to 8 m in the y-direction.
Figure 1.
Isometric view of the computational domain with an enlarged zone of the numerical mesh (medium grid).
Table 2.
Dimensional parameters of the configuration depicted in Figure 1.
| Parameter | L | H | W | D | D1 | D2 |
|---|---|---|---|---|---|---|
| Value (m) | 8.5 | 0.6 | 0.6 | 1.2 | 1.7 | 1.8 |
The cell numbers for the medium mesh along the x-, y-, and z-directions were initially 200, 30, and 120. These cells were uniformly distributed as the first step. Then, snappyHexMesh was utilized to cluster the mesh towards the blocks and the explosive area. The final cell numbers across the block width (x-direction), block length (z-direction), and block height (y-direction) are 24, 340, and 36, respectively. The explosive area has been covered by 20 × 20 cells on the ground, while 16 cells were used to resolve the explosive height up to the elevation of 0.5 m.
The red-filled circles represent the locations of the gauges at which the pressure was recorded. The empty circle to the left of the bottom image demonstrates the place of the explosive. Five gauges were positioned to record the pressure changes in different locations (G). G1, G2, and G4 are positioned 0.3 m away from the bottom ground (above). G5 also has the same height but is located 2.125 m away from the center-line where the previous gauges were positioned. At last, G3 is placed at a height of 0.9 m above the ground, but aligned with the first three gauges indicated above. For more convenience, the spatial coordinates of the explosive and the gauges have been provided in Table 3.
Table 3.
Spatial coordinates of the explosive and the gauges.
| Parameter | Explosive | G1 | G2 | G3 | G4 | G5 |
|---|---|---|---|---|---|---|
| x-coordinate (m) | 0 | 2.9 | 4.7 | 7.7 | 7.7 | 7.7 |
| y-coordinate (m) | 0 | 0.3 | 0.3 | 0.9 | 0.3 | 0.3 |
| z-coordinate (m) | 0 | 0 | 0 | 0 | 0 | -2.125 |
2.6. Boundary and initial conditions
In order to solve the N–S equations, appropriate boundary conditions must be provided. In the simulations, a non-reflective boundary condition was specified at the lateral and top boundaries for the pressure. No-slip condition was applied at the solid walls, and slip condition was specified at the top boundary. For all the turbulence quantities, the Neumann condition (boundary value set equal to internal cell value) was assigned to the surroundings for both RANS and LES. In the latter, a Dirichlet type (boundary value set explicitly) with zero value was used at the solid walls, comprising the ground and the three blocks. However, in RANS wall functions were implemented for and. For the temperature, the Neumann condition was applied at the walls, and a modification of the Neumann type, entitled inletOutlet was assigned to the lateral and top boundaries. This boundary condition treats the quantity with the Neumann type when the flow is leaving the domain, while it dictates the value of the quantity as in a Dirichlet type once the flow is entering the domain. In the latter case, the temperature was specified to be 300 K.
For the pressure, an initial value of 1 Bar was considered for the entire domain. The temperature was initialized with a value of 300 K, and the velocity was set to be zero. It should be noted that the medium in the quiescent environment at the beginning of the simulations was also air, and the equation of state utilized was BKW.
2.7. Discretization schemes and temporal resolution
OpenFOAM® allows us to specify both spatial and temporal discretization schemes with different orders of accuracy (first and second-order schemes). For temporal schemes in RANS simulations, a second-order Euler scheme was used, and for spatial discretization, an upwind method was utilized. In LES simulations, a backward second-order Euler scheme was implemented for time, and for spatial discretization, a high-order TVD (total-variation diminishing) [53] scheme was used to provide both accuracy and numerical stability for LES. A second-order central scheme was implemented in both RANS and LES for discretizing the spatial gradient terms.
In order to provide high temporal accuracy in the simulations, the solver was assigned with a constant maximum Courant number of 0.1. This relatively low value was chosen to preclude the divergence in the solution process. In this way, the time-step size is automatically calculated with respect to the specified Courant number.
The computational procedure to produce the grid and the solution procedure is illustrated in Figure 2.
Figure 2.
Workflow diagram of the current numerical study.
2.8. Solution algorithm
The discretization of the governing equations will result in the formation of linear systems of equations that are solved using numerical algorithms. An amalgamation of two well-known pressure-velocity coupling algorithms, PISO [54] and SIMPLE [55] was employed. Two momentum predictor iterations and two pressure corrector steps were implemented. In this fashion, both accuracy and stability are ensured in solving high-speed flow configuration, as in the current study. The resulting systems of equations for the velocity, pressure, and energy were solved by a Pre-conditioned Bi-Conjugate Gradient (PBiCG) [56] solver which possesses good parallel scaling. The pre-conditioning was carried out by a diagonal-based incomplete lower-upper preconditioner (DILU) [57]. For the first pressure corrector step, a relative tolerance of 1e-2 was specified, while for the second corrector iteration, a rigorous tolerance of 1e-10 was selected. For the velocity and energy, a relative tolerance of 1e-2 was used at the first predictor step, and a tolerance of 1e-7 for the second iteration was prescribed. The turbulence quantities were treated identically to the velocity. The simulations were run on a local cluster system with the parallel processing capability to accelerate the solution procedure.
3. Sensitivity to grid resolution
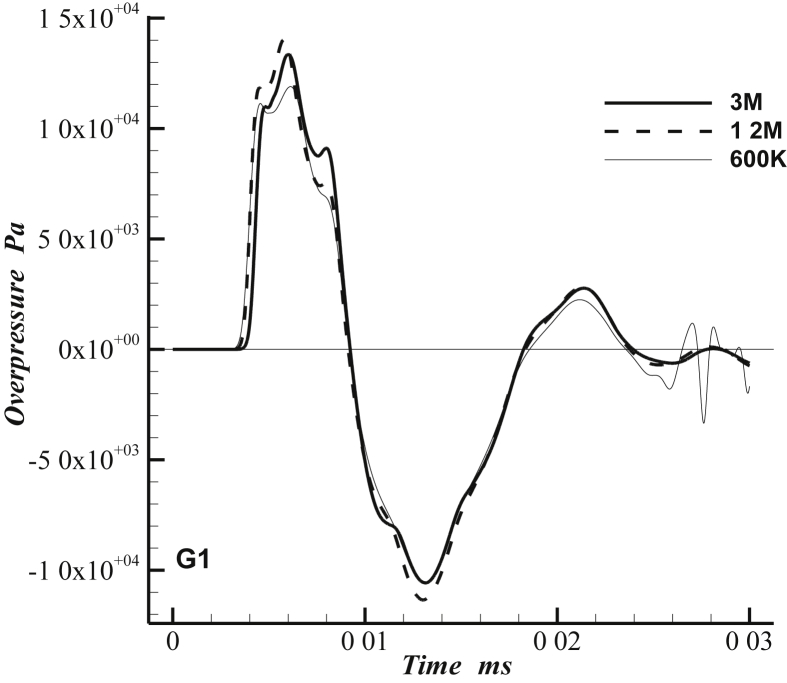
The impact of grid resolution on the results has been evaluated in this section. To this aim, the results of three sets of numerical grids with 600K, 1.2M, and 3M cell numbers were compared. For the comparisons, only the RANS cases were considered, as the LES results followed the same trend. The pressure-time signals at G1 have been demonstrated for the three grids in Figure 3. It can be observed that the medium grid (1.2M) and the fine grid (3M) have resulted in very similar time signals. Also, it is obvious that the coarse grid (600K) has led to some oscillations near the end of the signal. Based on this observation, the medium grid has been adopted for the rest of the simulations in the current investigation.
Figure 3.
Grid sensitivity study.
4. Validation and results
In this section, the validation of the current numerical approach has been presented. The test case considered for the validation is one of the experimental tests conducted by Health and Safety Executive [46]. The variation of the local pressure versus time (time history) has been extracted through a probe placed at G1. The pressure signal was recorded throughout the simulation time to be compared against the reference above.
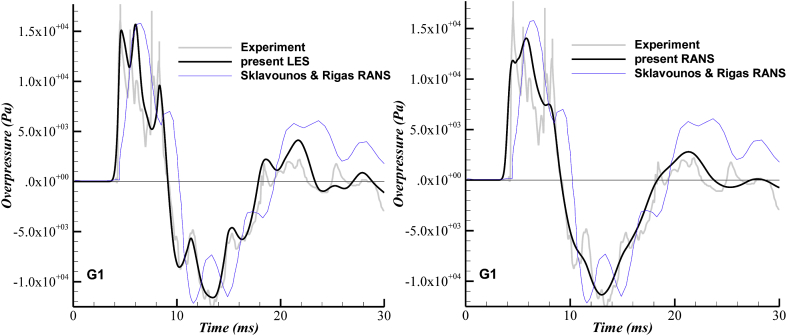
Figure 4 (left) demonstrates the comparison between the LES result of the present study with the BKW EOS and those reported in the experimental tests [46]. Additionally, the numerical results presented by Sklavounos and Rigas [47], who used RANS and “ideal gas” EOS in their study has been considered for comparison. It is observed that LES has faithfully predicted the first peak in the positive phase, while RANS has clearly missed it. The secondary peak in the LES results has almost collapsed with the first peak of the reference RANS data. These predictions are fairly close to the secondary peak seen in the experimental data. As can be observed, LES has yielded a sharper peak, which is closer to the experimental result when compared to the reference RANS. There is a trough next to the second peak in the LES pressure signal, also seen in the experiment. The reference RANS has also predicted a trough; however, it is significantly lagged in time. The position of the third peak in the positive phase predicted by LES has collapsed with that of the experiment. Its value, however, has been under predicted, part of which can be attributed to the uncertainties in the tests. The LES pressure signal has afterward matched with the experimental profile throughout the negative phase with excellent accuracy. The reference RANS, however, has incurred a substantial time lag, similar to what was observed in the positive phase. Following the end of the negative phase, the LES has also given predictions closer to the experiment compared to the reference RANS.
Figure 4.
Comparison between the present numerical results and the previous experimental and numerical data at G1; left: LES, right: RANS.
In Figure 4 (right), the time history of the pressure at G1 obtained from the present RANS simulation with the BKW EOS has been compared to the experimental test [46], and the numerical reference [47]. It can be said that RANS has been able to reproduce the first peak (more like a kink in the diagram). However, it has notably under predicted the peak value compared to the experiment and LES as well. As it was stated before, the reference RANS [47] was not able to predict the first peak present in the experimental test. The secondary peak in the positive phase has been predicted with descent accuracy by the current RANS method. However, unlike what was seen in the LES case, the trough has not been sharply captured by RANS, implying the supremacy of LES in predicting the rapid pressure changes. The RANS profile has followed the experiment across the phase transition (sign change of pressure) with satisfying accuracy, identical to that of LES. During the negative phase, the RANS prediction is generally close to the measurement, except for the first trough and the first peak which seem to be smoothed out. Once comparing the RANS profile to the LES, it turns out that the former has resulted in a profile that appears to be a “filtered” version of the latter. According to the comparisons made in Figure 4, in general, the present LES and RANS predictions are in more agreement with the experimental profile when compared to the reference RANS [47]. To verify the latter claim, a quantitative criterion has been defined and calculated in the next section, to analyze the accuracy of the numerical results more insightfully.
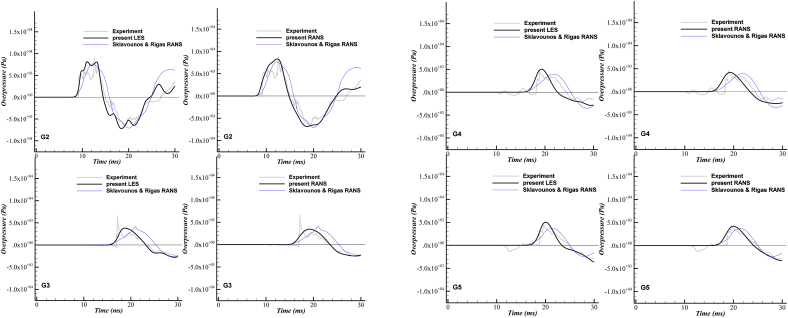
In this section, quantitative and qualitative findings and comparisons are presented. Figure 5 has demonstrated the overpressure signals for four downstream gauges, previously illustrated in Figure 1. It should be noted that the level of the overpressure signal has been retained constant (1.5e+4) for every plot, in order to observe the overpressure deterioration across the downstream gauges.
Figure 5.
Comparison between the present numerical results and the previous studies at downstream gauges; left: LES, right: RANS.
At G2, it can be seen that LES (left image) has predicted some rapid pressure changes compared to RANS [47]. When comparing the RANS result of the present study with that of reference [47], similar profiles can be detected. However, in the final positive phase, the current RANS has provided closer prediction to the measurements, while the reference has significantly over predicted the overpressure.
At G3, the level of the overpressure has decreased compared to the previous gauge. The measurement has shown a very sharp change in the overpressure signal (shock arrival), while LES has yielded a smooth prediction. However, it is still much closer to the experiment compared to the reference RANS. The RANS prediction of the current study shows a signal quite similar to LES, but with a slightly lower overpressure peak.
At G4, the peak value is slightly larger than that of G3 since it is placed at a lower elevation compared to the latter (Figure 1). In general, LES has resulted in a prediction closer to the measurement compared to the reference RANS. This is more noticeable in the peak value and the signal end. The present RANS has also provided a similar prediction to LES, but with slightly lower peak value.
At last, for G5 which is off the center-line, the results are quite similar to G4. It can be seen that both LES and RANS in the present study have yielded similar results to the numerical reference [47]. However, they both have performed notably better in predicting the peak value and its occurrence time. Additionally, it is observed that the RANS signal of reference [47] has risen up near the end, while both experiments and current numerical results have shown deteriorating behavior.
In order to have a quantitative assessment of how accurate the current simulations with the BKW model have been, an additional criterion has been defined to quantify the relative error between the present results and those of Sklavounos and Rigas [47]. By extracting the latter results, and by having the experimental measurement, the criterion can be defined as:
| (22) |
where is the relative error criterion, is the overpressure at a particular instant of time, denotes the experimental value of the overpressure at the same time instant, is the overpressure extracted from the RANS simulation of Sklavounos and Rigas [47], and indicates the number of sample data in the time signal, which was equal to 60000 to have an accurate calculation. As this criterion relies on the overpressure values at every time instants, it would allow for incorporating the impact of various parameters at the same time, including arrival time, positive or negative phase duration, and the overpressure value itself.
The values of are listed in Table 4 for both LES and RANS simulations. It can be observed that they have substantially performed better than the RANS simulations of Sklavounos and Rigas [47] (significantly lower than unity values), and their results are favorably closer to experiments at G1. For further downstream gauges, the relative error has increased, implying that the accuracy of the predictions has dropped, and it has approached that of Sklavounos and Rigas [47] simulations. For instance, the LES relative error at G4 is equal to 1.05, meaning a very close or identical prediction to Sklavounos and Rigas [47]. In general, both LES and RANS methods in the current study have performed superior to the reference RANS.
Table 4.
Relative error of the simulations w.r.t reference experimental measurements.
| Gauge No. | LES relative error | RANS relative error |
|---|---|---|
| G1 | 0.33 | 0.36 |
| G2 | 0.68 | 0.59 |
| G3 | 0.59 | 0.60 |
| G4 | 1.05 | 0.91 |
| G5 | 1.01 | 0.84 |
In Figure 6, iso-surface of overpressure over the three obstacles has been illustrated for three different time instants. It should be noted that the results belong to LES. The overpressure iso-surface represents the shockwave front, which is created by the explosion blast. The growth of the overpressure hemisphere is apparent during the time. It can be seen in the first time instant that the shockwave front has crossed the first obstacle, approaching the second one. In the second snapshot, the front has reached the first obstacle lateral sides, and in the third instant, the shockwave has virtually devoured both first and second obstacles.
Figure 6.
LES overpressure iso-surface of 6000 Pa; top left: 4.5 ms, top right: 8.5 ms, bottom: 12.5 ms.
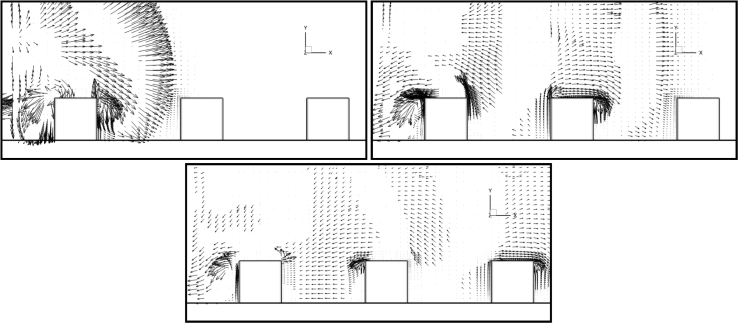
The evolution of the shockwave fronts has been further investigated by exploring the instantaneous velocity vectors in the center-plane for three different time snapshots in Figure 7. In the first snapshot, three discrete areas of velocity vectors can be identified, implying the formation of blast waves. It should be noted that the size of the vectors represents the magnitude of velocity. In the second time instant, the three areas mentioned above have propagated downstream (to the right), with their velocity magnitudes decreased. It is worth to mention that these waves and their propagation to the downstream were not captured in the study of Sklavounos and Rigas [47]. Finally, in the third snapshot, it is observed that the three sequential waves have propagated further downstream, and their velocity magnitudes have decreased even further. According to Figure 4, the formation of these discrete regions has produced the rapid changes in the overpressure signal, something which can also be observed in the experimental measurements.
Figure 7.
LES instantaneous velocity vectors; top left: 5 ms, top right: 10 ms, bottom: 15 ms.
On the other hand, the RANS simulations have somewhat alleviated the presence of these discrete velocity regions; thus, the rapid pressure changes diminished in the signal.
In Figure 8, the overpressure contours for the LES method have been shown for different time instants. In the first snapshot (2 ms), two very high overpressure spots can be detected on the first obstacle front wall. There is also a negative overpressure region within the overpressure bounds. In the second snapshot (5 ms), the level of pressure has decreased in the high overpressure regions, and they have moved towards the lateral walls of the first obstacle. Further, the low-pressure area has developed over the first obstacle front wall, and its magnitude has increased. In the third time instant, it can be seen that the high-pressure wave has already extended across the first and the second obstacles. Also, it has taken the form of a circle, a projection of the overpressure iso-surface onto the ground, which was previously demonstrated in Figure 6. In the final snapshot, it is apparent that the high-pressure front has surrounded all three blocks, but its magnitude has notably reduced. Another observation is that the first obstacle front wall is subjected to a higher pressure compared to the previous time snapshot. In general, according to all the time instants, it is apparent that the high-pressure wave has eventually spread on the ground and has widened in a circular pattern.
Figure 8.
LES instantaneous ground overpressure contours; top left: 2 ms, top right: 5 ms, bottom left: 12.5 ms, bottom right 16 ms.
5. Conclusion
This paper has demonstrated the validation of the CFD approach in predicting shockwave propagation using the open-source CFD toolbox OpenFOAM® against the experimental data produced by a dense explosive detonation in complex terrain (an environment with rectangular obstacles). In this investigation, BKW EOS (equation of state) was implemented within OpenFOAM® software package for numerical simulations of detonation and shockwave propagation. Furthermore, an extended solver was developed to account for the explosion energy in the energy equation. Notably, two turbulence modeling approaches were employed in the current study. The first was the more popular RANS method which has been used by the previous researchers in explosion simulations. The second one is the more sophisticated LES approach that was applied in the present investigation. LES provided more detailed solutions compared to RANS and was able to predict the rapid pressure changes in the explosive near-field more accurately. The results of both aforementioned approaches agreed very well with the experimental measurements, and they demonstrated the ability of OpenFOAM® CFD technology to capture the highly transient nature of the explosion. It was shown that the present LES and RANS predictions were in higher agreement with the experimental profile compared to the reference RANS, implying the accuracy and reliability of the EOS in describing the detonation properties of explosives.
Declarations
Author contribution statement
Zeinab Noorpoor: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Saeed Tavangar: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.
Hosein Soury: Conceived and designed the experiments; Analyzed and interpreted the data.
Seyed Ghorban Hoseini: Analyzed and interpreted the data.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
Data will be made available on request.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Zinner E.S. Routledge; 2013. When a Community Weeps: Case Studies in Group Survivorship. [Google Scholar]
- 2.Smyth C.-M., Lang R. Cambridge Scholars Publishing; 2017. The Future of Human Rights in the UK. [Google Scholar]
- 3.Gray A. Paper Presented at the World Economic Forum. 2016. A year of global terrorism, captured in one map. [Google Scholar]
- 4.Dixon L., Arlington J., Carroll S., Lakdawalla D., Reville R. 2004. Issues and Options for Government Intervention in the Market for Terrorism Insurance. Retrieved from. [Google Scholar]
- 5.Wilkinson C., Hartwig R.P. Insurance Information Institute; New York: 2010. Terrorism Risk: A Reemergent Threat. Impacts for Property/Casualty Insurers. [Google Scholar]
- 6.Aymanns C., Farmer J.D., Kleinnijenhuis A.M., Wetzer T. Models of financial stability and their application tests in stress. Comput. Econ.: Heterogen. Agent Model. 2018;329 [Google Scholar]
- 7.Muir-Wood R. RMS; Washington, DC: 2012. The Use of Catastrophe Loss Modeling Methodologies to Design and Monitor Disaster Resilience Goals and Indicators in a post-mdg Framework. [Google Scholar]
- 8.Baker W.E., Cox P., Kulesz J., Strehlow R., Westine P. Vol. 5. Elsevier; 2012. (Explosion Hazards and Evaluation). [Google Scholar]
- 9.Britt J., Lumsden M. Science Applications International Corporation; St. Joseph, Louisiana, SAIC: 1994. Internal Blast and Thermal Environment from Internal and External Explosions: A User’s Guide for the BLASTX Code, Version 3.0; pp. 405–494. [Google Scholar]
- 10.Baker W.E. Vol. 268. University of Texas press Austin; TX: 1973. (Explosions in Air). [Google Scholar]
- 11.Smith P., Whalen G., Feng L., Rose T. Proceedings of the Institution of Civil Engineers-Structures and Buildings. Vol. 146. 2001. Blast loading on buildings from explosions in city streets; pp. 47–55. (1) [Google Scholar]
- 12.Needham C.E. Vol. 402. Springer; 2010. (Blast Waves). [Google Scholar]
- 13.Kinney G.F., Graham K.J. Springer Science & Business Media; 2013. Explosive Shocks in Air. [Google Scholar]
- 14.Hao H., Hao Y., Li J., Chen W. Review of the current practices in blast-resistant analysis and design of concrete structures. Adv. Struct. Eng. 2016;19(8):1193–1223. [Google Scholar]
- 15.VonNeumann J., Richtmyer R.D. A method for the numerical calculation of hydrodynamic shocks. J. Appl. Phys. 1950;21(3):232–237. [Google Scholar]
- 16.Lax P.D. Weak solutions of nonlinear hyperbolic equations and their numerical computation. Commun. Pure Appl. Math. 1954;7(1):159–193. [Google Scholar]
- 17.Brode H.L. Numerical solutions of spherical blast waves. J. Appl. Phys. 1955;26(6):766–775. [Google Scholar]
- 18.Brode H.L. Blast wave from a spherical charge. Phys. Fluid. 1959;2(2):217–229. [Google Scholar]
- 19.Cant R., Dawes W., Savill A. Advanced CFD and modeling of accidental explosions. Annu. Rev. Fluid Mech. 2004;36:97–119. [Google Scholar]
- 20.Hansen O.R., Kjellander M.T., Martini R., Pappas J.A. Estimation of explosion loading on small and medium sized equipment from CFD simulations. J. Loss Prev. Process. Ind. 2016;41:382–398. [Google Scholar]
- 21.Hjertager B.H., Solberg T. Prevention of Hazardous Fires and Explosions. Springer; 1999. A review of computional fluid dynamics (CFD) modeling of gas explosions; pp. 77–91. [Google Scholar]
- 22.Sohaimi A.S., Risby M., Ishak S.A., Khalis S., Norazman M., Ariffin I., Yusof M. Using computational fluid dynamics (CFD) for blast wave propagation under structure. Procedia Comp. Sci. 2016;80:1202–1211. [Google Scholar]
- 23.Hansen O.R., Hinze P., Engel D., Davis S. Using computational fluid dynamics (CFD) for blast wave predictions. J. Loss Prev. Process. Ind. 2010;23(6):885–906. [Google Scholar]
- 24.Tulach A., Mynarz M., Kozubková M. Paper Presented at the EPJ Web of Conferences. 2015. CFD simulation of vented explosion and turbulent flame propagation. [Google Scholar]
- 25.Rigas F., Sklavounos S. Experimentally validated 3-D simulation of shock waves generated by dense explosives in confined complex geometries. J. Hazard Mater. 2005;121(1-3):23–30. doi: 10.1016/j.jhazmat.2005.01.031. [DOI] [PubMed] [Google Scholar]
- 26.Rigas F., Sklavounos S. Simulation of Coyote series trials—Part II: a computational approach to ignition and combustion of flammable vapor clouds. Chem. Eng. Sci. 2006;61(5):1444–1452. [Google Scholar]
- 27.Yohe G., Tol R.S. Indicators for social and economic coping capacity—moving toward a working definition of adaptive capacity. Global Environ. Change. 2002;12(1):25–40. [Google Scholar]
- 28.Ferrara G., Di Benedetto A., Salzano E., Russo G. CFD analysis of gas explosions vented through relief pipes. J. Hazard Mater. 2006;137(2):654–665. doi: 10.1016/j.jhazmat.2006.03.037. [DOI] [PubMed] [Google Scholar]
- 29.Jeremić R., Bogdanov J. Development of a new model for the calculation of the detonation parameters of high explosives. J. Serb. Chem. Soc. 2012;77(3):371–380. [Google Scholar]
- 30.Mader C.L. CRC press; 2007. Numerical Modeling of Explosives and Propellants. [Google Scholar]
- 31.Han Y., Xie X., Jiang Z., Duan Y., Wen Y. Paper Presented at the AIP Conference Proceedings. 2018. Equation of state of detonation products for TNT by aquarium experiment. [Google Scholar]
- 32.Amar S. 30th International Symposium on Shock Waves. Vol. 2. Springer; 2017. Comparison of BKW and JWL equations of state for explosion simulations. [Google Scholar]
- 33.Cowan R., Fickett W. Calculation of the detonation properties of solid explosives with the kistiakowsky-Wilson equation of state. J. Chem. Phys. 1956;24(5):932–939. [Google Scholar]
- 34.Mader C.L. University of California Press; Berkeley: 1979. Numerical Modeling of Detonations. Los Alamos Series in Basic and Applied Sciences. 1979. [Google Scholar]
- 35.Finger M., Lee E., Helm F., Hayes B., Hornig H., McGuire R., Guidry M. Paper Presented at the Sixth Symposium (International) on Detonation. 1976. The effect of elemental composition on the detonation behavior of explosives. [Google Scholar]
- 36.Hobbs M., Baer M. Nonideal thermoequilibrium calculations using a large product species data base. Shock Waves. 1992;2(3):177–187. [Google Scholar]
- 37.Fried L.E., Clark Souers P. BKWC: an empirical BKW parametrization based on cylinder test data. Propellants, Explos. Pyrotech. 1996;21(4):215–223. [Google Scholar]
- 38.Kozyrev N.V. Reparametrization of the BKW equation of state for CHNO explosives which release no condensed carbon upon detonation. Central Eur. J. Energ. Mater. 2015;12(4) [Google Scholar]
- 39.Mader C.L. Vol. 2900. Los Alamos Scientific Laboratory of the University of California; 1963. Detonation Properties of Condensed Explosives Computed Using the Becker-Kistiakowsky-Wilson Equation of State. [Google Scholar]
- 40.Bondarev A.E., Kuvshinnikov A.E. Paper Presented at the International Conference on Computational Science. 2018. Analysis of the accuracy of OpenFOAM solvers for the problem of supersonic flow around a cone. [Google Scholar]
- 41.Churchfield M.J., Lee S., Michalakes J., Moriarty P.J. A numerical study of the effects of atmospheric and wake turbulence on wind turbine dynamics. J. Turbul. 2012;13 [Google Scholar]
- 42.Jasak H. OpenFOAM: open source CFD in research and industry. Int. J. Naval Architect. Ocean Eng. 2009;1(2):89–94. [Google Scholar]
- 43.Jasak H., Beaudoin M. Paper Presented at the ASME-JSME-KSME 2011 Joint Fluids Engineering Conference. 2011. Openfoam turbo tools: from general purpose cfd to turbomachinery simulations. [Google Scholar]
- 44.Jasak H., Jemcov A., Tukovic Z. Paper Presented at the International Workshop on Coupled Methods in Numerical Dynamics. 2007. OpenFOAM: a C++ library for complex physics simulations. [Google Scholar]
- 45.Marcantoni L.F.G., Tamagno J.P., Elaskar S.A. High speed flow simulation using openfoam. Mecánica Comput. 2012;31(16):2939–2959. [Google Scholar]
- 46.Catlin C., Ivings M., Myatt M.S., Ingram D., Causon D., Qian L. 2001. Explosion Hazard Assessment: A Study of the Feasibility and Benefits of Extending Current HSE Methodology to Take Account of Blast Sheltering HSL/2001/04. Retrieved from. [Google Scholar]
- 47.Sklavounos S., Rigas F. Computer simulation of shock waves transmission in obstructed terrains. J. Loss Prev. Process. Ind. 2004;17(6):407–417. [Google Scholar]
- 48.Sagaut P. Springer Science & Business Media; 2006. Large Eddy Simulation for Incompressible Flows: an Introduction. [Google Scholar]
- 49.El Tahry S. K-epsilon equation for compressible reciprocating engine flows. J. Energy. 1983;7(4):345–353. [Google Scholar]
- 50.Kim W.-W., Menon S. Paper Presented at the 33rd Aerospace Sciences Meeting and Exhibit. 1995. A new dynamic one-equation subgrid-scale model for large eddy simulations. [Google Scholar]
- 51.Smagorinsky J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963;91(3):99–164. [Google Scholar]
- 52.Lilly D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluid. Fluid Dynam. 1992;4(3):633–635. [Google Scholar]
- 53.Versteeg H., Malalasekera W. Finite Volume Method, Essex. Longman Scientific & Technical; 1995. An introduction to computational fluid dynamics. [Google Scholar]
- 54.Issa R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986;62(1):40–65. [Google Scholar]
- 55.Patankar S. Taylor & Francis; 2018. Numerical Heat Transfer and Fluid Flow. [Google Scholar]
- 56.Press W.H. Cambridge university press; Cambridge: 1988. Numerical Recipes in C. [Google Scholar]
- 57.Meijerink J.A., Van Der Vorst H.A. An iterative solution method for linear systems of which the coefficient matrix is a symmetric. Math. Comput. 1977;31(137):148–162. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.