Exploring brain-behavior relationships in the N-back task

Abstract

Working memory (WM) function has traditionally been investigated in terms of two dimensions: within-individual effects of WM load, and between-individual differences in task performance. In human neuroimaging studies, the N-back task has frequently been used to study both. A reliable finding is that activation in frontoparietal regions exhibits an inverted-U pattern, such that activity tends to decrease at high load levels. Yet it is not known whether such U-shaped patterns are a key individual differences factor that can predict load-related changes in task performance. The current study investigated this question by manipulating load levels across a much wider range than explored previously (N = 1–6), and providing a more comprehensive examination of brain-behavior relationships. In a sample of healthy young adults (n = 57), the analysis focused on a distinct region of left lateral prefrontal cortex (LPFC) identified in prior work to show a unique relationship with task performance and WM function. In this region it was the linear slope of load-related activity, rather than the U-shaped pattern that was positively associated with individual differences in target accuracy. Comprehensive supplemental analyses revealed the brain-wide selectivity of this pattern. Target accuracy was also independently predicted by the global resting-state connectivity of this LPFC region. These effects were robust, as demonstrated by cross-validation analyses and out-of-sample prediction, and also critically, were primarily driven by the high-load conditions. Together, the results highlight the utility of high-load conditions for investigating individual differences in WM function.

1. Introduction

Understanding the neural basis of working memory and executive control (WM/EC) functions has been a major aim of cognitive neuroscience research. One of the key drivers of such research efforts are the well-established findings that WM/EC function is strongly dominated by individual differences, and moreover, that these individual differences clearly contribute to real-world cognitive abilities (i.e., intelligence) and important life outcomes (e.g., computer programming skills, ability to learn complex new task, SAT/GRE success, etc; (Ackerman, Beier, & Boyle, 2005; Engle, Laughlin, Tuholski, & Conway, 1999; Kyllonen & Christal, 1990).

The N-back task has been one of the most commonly used experimental paradigms for exploring the neural basis of WM/EC (Cohen et al., 1997; Gevins & Cutillo, 1993). The N-back is well-established to robustly activate frontoparietal brain regions that which general consensus hold to be critical for WM/EC function (Dosenbach et al., 2006; Owen, McMillan, Laird, & Bullmore, 2005). An advantageous feature of the N-back is that WM load can be varied in an incremental, parametric fashion by increasing the value of N (Braver et al., 1997). This is a critical component of the paradigm, since as N-back levels increase, task performance shows a reliable decrement, while the subjective experience of cognitive effort and task difficulty also increases (Ewing & Fairclough, 2010; Otto, Zijlstra, & Goebel, 2014; Westbrook, Kester, & Braver, 2013; Westbrook, Lamichhane, & Braver, 2019) The concomitant increase in task difficulty and drop in performance is useful psychometrically as it drives variability among participants, and thus the potential to detect the neural correlates of individual differences.

The consequences of N-back load manipulations on brain activity and the relationship between activity and behavior remain unclear, however. For example, there is uncertainty about which load levels are optimal for detecting brain activity patterns and brain-behavior relationships. This uncertainty is, in part, because of non-linear inverted U-shaped load functions, in which BOLD activity increases within frontoparietal brain regions as N increases across lower load- levels (e.g., 0, 1,2) but then starts to decrease as load increases to higher levels (N ≥ 3). A common observation is that inverted-U patterns emerge when participants reach their capacity limits (Van Snellenberg et al., 2015). For example, inverted-U functions are observed under very high cognitive demands, with decreasing working memory capacity, with advancing cognitive age, and with cognitive impairments (Callicott et al., 1999; Cappell, Gmeindl, & Reuter-Lorenz, 2010; Jaeggi et al., 2007; Nyberg, Dahlin, Stigsdotter Neely, & Backman, 2009). One interpretation of inverted-U patterns is that individuals “disengage” at these high-load levels (i.e., discontinue applying full cognitive effort), since the task may be too difficult to perform adequately when load is at supra-capacity levels (Callicott et al., 1999; Jaeggi et al., 2007; Van Snellenberg et al., 2015). Alternatively, inverted-U patterns may reflect shifting strategies (e.g., a shift towards responding based on familiarity at high load levels, rather than utilizing active maintenance (Juvina & Taatgen, 2007). A systematic analysis of inverted-U patterns and their relationship with task performance across individuals and across a wide range of load levels is needed for testing these hypotheses. At the same time, uncertainty about the meaning of inverted-U patterns makes it unclear whether very high levels of N-back load are even suitable for investigating brain-behavior relationships. Consequently, very high levels of N-back loads (N > 3) have not been investigated.

It also remains unclear which brain regions or neural markers are the best predictors of individual differences in performance. For example, it is unclear whether the brain-behavior relationships are more focal, i.e., related to activity patterns in circumscribed brain regions, or more widespread and non-selective, and also captured well by other neural measures, such as functional connectivity. The lateral prefrontal cortex (LPFC) has traditionally been implicated as most likely to mediate performance in WM/EC tasks, as this region is thought to play a critical role in active goal maintenance, and cognitive control functions (Kane & Engle, 2002; Miller & Cohen, 2001). Nevertheless, evidence pointing to a specific and unique role for focal LPFC regions in mediating brain-behavior relationships in the N-back is limited. Although some studies have found evidence implicating the LPFC, in many others it is just one relevant region out of many that can predict individual variation in behavioral performance in the N-back and related WM/EC tasks (Choo, Lee, Venkatraman, Sheu, & Chee, 2005; Harvey et al., 2005).

Furthermore, other work has suggested that qualitatively distinct neural markers, such as resting-state functional connectivity, may be equally or even more strongly predictive of N-back task performance (Cole, Yarkoni, Repovs, Anticevic, & Braver, 2012). Specifically, Cole et al (2012) used a functional connectivity measure termed global brain connectivity (GBC), to demonstrate strong relationships between connectivity and multiple aspects of cognitive function, not only N-back performance but also WM capacity and fluid intelligence. Interestingly, this work also provided a unique perspective, in that the findings highlighted the contributions of a particular left PFC region (center coordinates: −44, 14, 29) that was unique among brain regions in showing robust brain-behavior relationships in both activation and GBC effects, across multiple indices. Consequently, this work suggests that there may in fact be focal brain-behavior effects found within distinct PFC regions, which may co-exist with (or even be stronger than) the more widespread network effects that have been reported. However, until now there have been no analyses directly comparing the predictive power of activity versus connectivity effects. It also suggests the potential utility of the GBC metric for revealing the functional importance of connectivity profiles within individual regions in a manner that can be compared with activation profiles. However, a limitation of Cole et al (2012) and other prior work was that such comparisons were not a direct focus of analysis, and moreover, a restricted range of N-back load levels were examined.

In the current study, we sought to remedy this gap in the literature, by capitalizing on a novel experimental design in which a large sample of individuals (n = 57) each performed the N-back task under a very wide range of load levels, from N = 1–6. This design afforded a unique opportunity to test whether lower or higher load levels were more predictive of individual differences in task performance. In addition, we directly assessed the predictive power of a focal, a priori LPFC region of interest highlighted in both meta-analyses and our own prior work (Cole et al., 2012; Rottschy et al., 2012), to capture individual differences in behavioral performance in terms of both its activity and functional connectivity (i.e., GBC), and further to rigorously characterize the form of this predictive relationship. Finally, we used newer cross-validation methods and a rigorous out-of-sample test (involving data from the Human Connectome Project; HCP) to establish predictive validity.

To preview our findings, we observed that this focal region of LPFC was a reliable neural predictor of behavioral performance, and moreover that the predictive utility was strongest when aggregating across all load levels, rather than just in selecting lower levels. Moreover, in a direct comparison, high load levels were more predictive of behavioral performance than low load levels. Nevertheless, additional independent variance was explained by activation global resting state functional connectivity, such that the strongest predictions of individual differences were found when both measures (LPFC activity and GBC in LPFC) were aggregated in the model. Lastly, we observed that this a priori defined LPFC region was one of the best predictors of behavioral performance in a large out-of-sample dataset (HCP). Together, the results suggest the importance of including a wide range of variability in N-back paradigms to target individual differences, and highlight the unique contributions of a focal LPFC region for predicting WM performance.

2. Materials & Methods

2.1. Participants

Fifty-eight participants were recruited from the Washington University in St. Louis community. One was excluded (participant disclosed neurological problem after data was collected) yielding a final sample of 57 participants (27 male and 30 female; mean age = 24.28 ± 5.1 years) in N-back task. However, an additional 6 subjects out of 57 had technical issues with their resting-state fMRI data. Consequently, the remaining 51 participants were used for analyses of resting-state functional connectivity. All included participants were healthy, right-handed, neurologically normal, not currently taking any psychoactive medication, native English speakers, and with normal-to-corrected vision including no color-blindness.

2.2. Experimental task and data collection procedure

All MRI data were collected in a 3 Tesla Siemens Trio scanner. After MR safety screening and consent, participants were scanned in six BOLD fMRI runs while they performed each of one level of the N-back task (N = 1:6; see Figure 1). To facilitate individual difference analyses, all participants performed N-back conditions in the same order of increasing N-back load levels (i.e., 1-back in first scan, 6-back in last scan). The experimental session also included two additional resting-state scans and collection of a T1-weighted anatomical scan (these are described further below).

Figure 1:

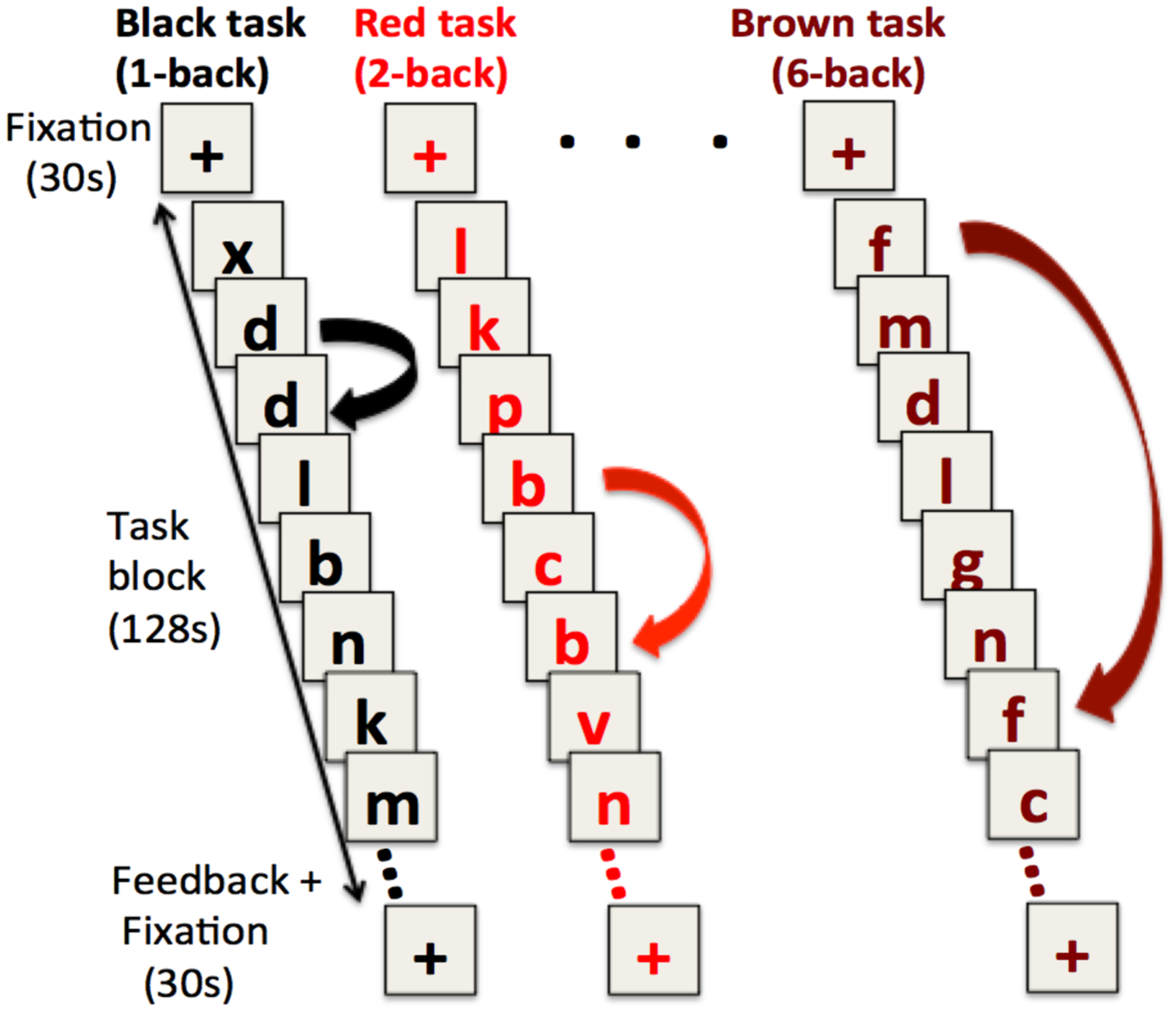
Schematic of single blocks of tasks for the 1-, 2-, and 6-back (“black”, “red”, and “brown” task). Each color corresponded to a single load level and indicated the N-back rules for a given run of stimuli.

All N-back fMRI BOLD scans consisted of 3 task blocks, each approximately 2 minutes in duration, that were preceded and followed by a 30 second rest fixation period (marked by a central crosshair; 4 total per scan; total scan duration = 520 seconds). Task blocks consisted of 64 stimuli (lower-case consonants), presented in the center of a screen in large (32 point) Arial font. Each stimulus was presented for a maximum of 2 seconds during which participants were instructed respond by button press as quickly as possible, without sacrificing accuracy, to indicate whether the stimulus was a target (N-back repeat) or not (using middle/index fingers). Upon button press, letters were replaced by a fixation underscore ‘_’, until the next letter appeared, 2 seconds after the previous letter was presented. There were 16 target items in each task block, and a variable number of lures, depending on the task level (8 for the 1-back, 6 for the 2-back, 5 for the 3-back, and 3 for the 4-, 5-, and 6-back, each) where a lure is considered to be any stimulus repeated within two positions of the target position (e.g., a 1, 2, 4 or 5-back repeat would be considered a lure in the 3-back block). The number of lures decreased for higher load levels to “flatten” performance functions - attenuating differences in performance from lower to higher load levels.

At the end of each block, participants received brief feedback on their performance in terms of percentage accuracy on target and non-target items. This was presented for 5 seconds, followed by 25 seconds of resting fixation prior to the next block (total 30s, in between blocks rest). The total duration of each scan was 520 seconds (260 scans). Each N-back level was presented in a unique color (black, red, blue, purple, green, brown for the 1-back, 2-back, 3-back, 4-back, 5-back, 6-back respectively as shown in Figure 1); task instructions referred to the condition by color (rather than numerical load descriptor), to minimize potential demand characteristics regarding difficulty. This last feature of the procedure was not relevant for the current study, and was put in place solely for purposes of a subsequent study phase (in a separate experimental session) that was not the focus of the current work.

Two resting-state scans were also conducted, one prior to beginning the N-back task scans and after completing these scans; each was 530 seconds long. All fMRI BOLD scans were acquired using the following parameters: 2000 msec TR, 27 msec TE (spine-cho time), 90 degree flip angle, 4×4×4 mm voxels with a 256×256 field of view with 34 slices. Anatomical T1-weighted images were also collected with the following parameters: 2400 msec TR, and 3080 msec TE (spin-echo time), 8 degree flip angle, 1×1×1 mm voxels, and 176 slices.

2.3. Behavioral analysis

Behavioral performance was analyzed separately for target and non-target trials, and by examining both accuracy and reaction time measures. Some studies of the N-back have analyzed behavioral performance in terms of the signal detection measure d’, since this provides a relative measure of sensitivity to the target/non-target status of items while controlling for response bias (Wickens, 2002). In contrast, for the current analysis this measure may be less appropriate particularly for comparing load levels, since the load levels varied in the proportion of non-target trials that were lures (i.e., lower lure frequency at higher load levels). Thus, to be more conservative, all primary results are described in terms of target or non-target accuracy. Nevertheless, we did conduct supplementary analyses with d’ (reported in Supplemental Results), with most effects largely unchanged (and in fact, some effects, with LPFC were even stronger).

2.4. Imaging analyses

All neuroimaging analysis was conducted using AFNI (https://afni.nimh.nih.gov) software, with the following processing steps.

2.4.1. Task fMRI preprocessing

After the converting raw DICOM images to NIFTI format, data were temporally aligned within each brain volume, and corrected for movement, yielding 6 estimated motion parameters (three translation: x, y, z and three rotation: pitch, yaw, roll). As an additional quality control step, data were also censored (scrubbed) for motion transients using a frame-wise displacement threshold of 0.3 mm. Functional images were then registered to the Montreal Neurological Institute (MNI) atlas space, which also involved up-sampling from 4×4×4 mm to 3×3×3 mm voxels. Precise registration was verified visually for every participant and cost functions were tailored to optimize registration for each participant. Image intensities were scaled to have a mean value of 100, and a range of 0–200. Finally, images were spatially smoothed with a Gaussian full-width half maximum (FWHM) = 8 mm filter.

General linear models (GLMs) were fit using the 3dDeconvolve function in AFNI, to analyze the relationship between task conditions on voxel-wise BOLD activation levels. All GLMs incorporated the 6 estimated motion parameters and polynomial functions (-polort 4) to capture low-frequency signal drifts as nuisance covariates. N-back task activations were modeled by a block design of boxcar functions spanning each 128-second stimulus run, convolved with a gamma hemodynamic response function.

2.4.2. Resting state fMRI preprocessing

Resting-state fMRI data were pre-processed using AFNI’s standard resting state pre-processing procedure (also see Jo et. al., 2010). Specifically, in addition to standard steps taken for task BOLD data (i.e., spike-correction, temporal alignment, motion correction, registration to MNI atlas space), more conservative censoring (scrubbing) of motion transients was also performed (given that motion transients are known to have a large impact of functional connectivity estimates, (Power et al., 2011) using a frame displacement threshold of 0.2 mm. Likewise, the data were band-pass filtered (0.01–0.1 Hz), and nuisance signal from locally-averaged white matter (ANATICOR procedure available in AFNI (Jo, Saad, Simmons, Milbury, & Cox, 2010)) and the 6 estimated motion parameters were regressed out of the time-series prior to connectivity analyses.

2.4.3. Region of interest (ROI) analyses

A region-of-interest (ROI) approach was used primarily for task activation and connectivity analyses. The key ROI was a particular left prefrontal cortex (LPFC) region that was selected based on prior findings demonstrating the strong involvement of this region in WM function and individual differences in brain-behavior relationships (Cole, Ito, & Braver, 2015; Cole et al., 2012; Rottschy et al., 2012). To define the ROI, we created a spherical region (6mm radius) with center coordinates based on Cole et al, 2012 (MNI coordinates [−44, 14, 29]). Note that this is region overlaps with that identified by Rottschy et al (2012) as part of the WM core network that they refer to as left inferior frontal gyrus pars opercularis (−46, 10, 26); however, the extent of the sphere that we used extends from the inferior frontal gyrus to the middle frontal gyrus. Nevertheless, to reduce ambiguity, from here on we use the term LPFC to refer to this particular ROI.

To further assess the predictive utility of this ROI, supplemental analyses compared its activation to a comprehensive, brain-wide set of focal ROIs, as well as larger-scale brain networks. For these, we used the set of 264 (spherical, 6mm radius) nodes centered on loci defined in Power et al (2011), as these were drawn from both task fMRI meta-analyses and large-sample functional connectivity datasets, and have already been pre-structured into brain network communities. After fitting GLMs, regression weights were extracted and averaged across voxels for the LPFC ROI (and for supplementary analysis for each of the nodes and networks defined in Power et al, 2011). Between-subjects analyses of load-level and individual difference effects were conducted using these averaged regressions weights. For GBC analyses, resting-state timeseries data were averaged within the LPFC node and also for each node in the Power et al (2011) set, such that pairwise correlations between all nodes could be calculated for each participant. These correlation values were then included in similar brain-behavior analyses testing for individual difference effects.

3. Results

3.1. N-back performance and load effects

As predicted, overall N-back accuracy (Table1 and Figure2), and target accuracy decreased with increasing load (formally, repeated-measures ANOVA shows reliable effects of task load (F_5,280 = 218.14, p < 0.001, Figure 2A). Similarly, as predicted, overall non-target accuracy also decreased with increasing load (F_{5, 280} = 24.93, p < 0.001, Figure 2B). Nevertheless, mean performance remained relatively high even at the highest load conditions. Also, response times (RT) for both targets (F_5,280 = 42.75, p < 0.005, Figure 2C) and non-targets (F_5,280 = 32.53, p < 0.001, Figure 2D) showed the significant effect of load and differ reliably (RTs slower for targets than non-targets, Table 1) at every load levels. These accuracy and RT patterns imply that participants did not resort to guessing or random responding, even at the highest load levels.

Table 1.

Behavioral results: performance (%) and respose time (ms) (±standard deviation).

N-back task	Target (mean) ± standard deviation		Non-target (mean) ± standard deviation
	Accuracy (%)	Response time (ms)	Accuracy (%)	Response time (ms)
1-back	87.7 ± 9.0	592 ± 82	95.7 ± 6.6	558 ± 88
2-back	77.3 ± 12.4	710 ± 11	92.4 ± 8.5	678 ± 128
3-back	58.1 ± 15.3	787 ± 123	90.5 ± 7.2	713 ± 145
4-back	52.1 ± 11.9	771 ± 139	90.2 ± 7.8	681 ± 132
5-back	43.1 ± 15.3	758 ± 142	88.9 ± 7.9	654 ± 119
6-back	37.7 ± 15.0	763 ± 147	86.4 ± 9.0	618 ± 121

Figure 2.

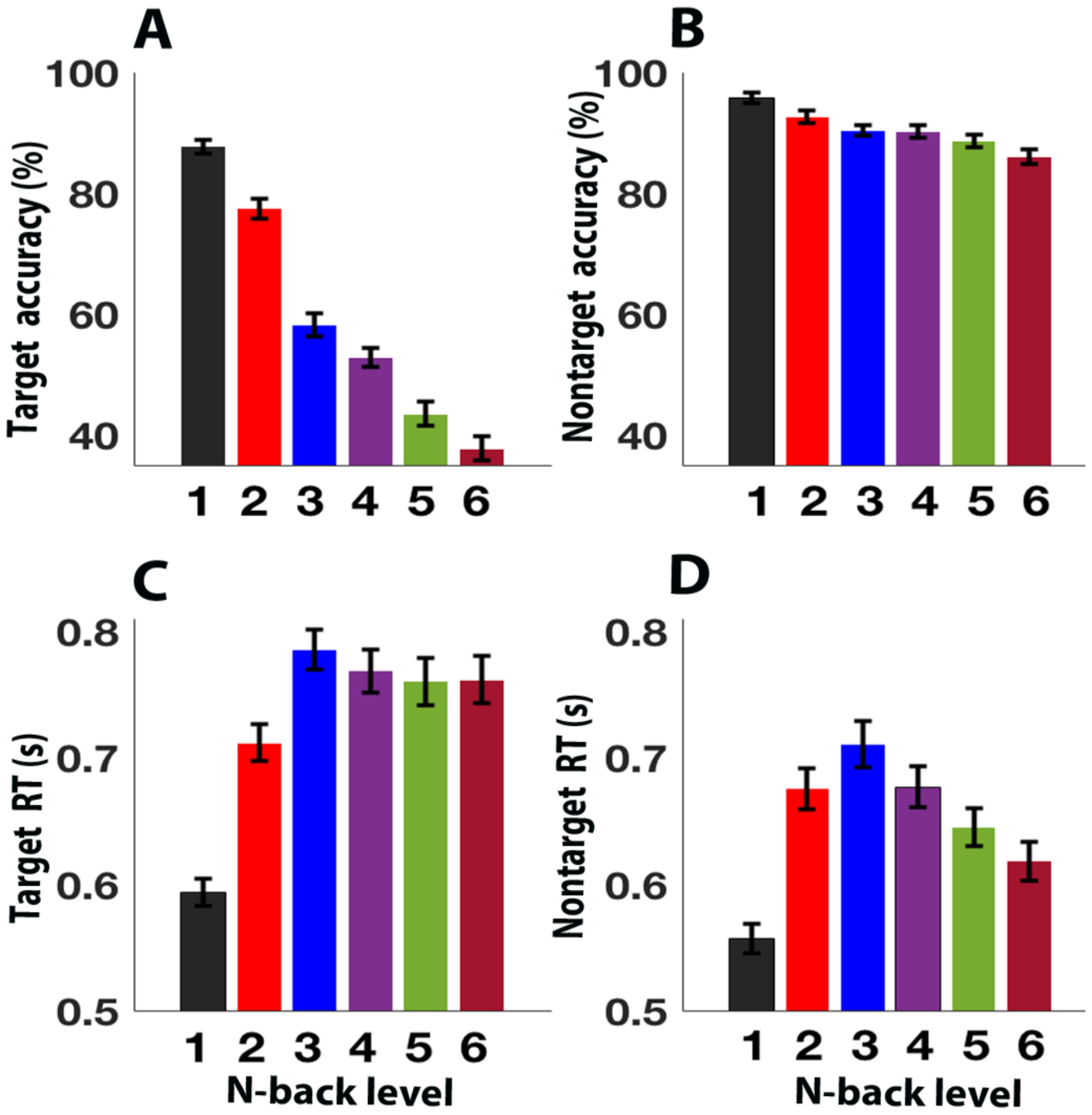
Bar plot of N-back performance. (A) Target: mean performance (accuracy, %) by load level and (C) response time (RT). (B) Non-target: mean performance (accuracy, %) by load level and (D) response time (RT). Error bars indicate standard error of the mean.

We next used linear mixed-effects models (equation 1) to test for linear effects of load on accuracy and RT. Specifically, we tested whether accuracy and reaction time, as independent variables (Behav_ij) could be predicted by load i (Load_ij), with loads nested within participants j. Note that α₀₀ and α₁₀ are random intercepts, allowing the intercept and slope to vary by subject, respectively.

$${\mathit{\text{Behav}}}_{ij}=B_{{}_{0j}}+B_{1j}{\mathit{\text{Load}}}_{ij}+{\epsilon }_{ij}$$ Eq(1)

$$\begin{gathered} B_{{}_{0j}}=a_{00}+u_{0j} \\ {B}_{1j}=a_{10}+u_{1j} \end{gathered}$$

For target and non-target accuracy, there were significant, negative linear effects of load (target accuracy: slope = −10.25, t(56) = −23.2, p < 0.001; non-target accuracy: slope = −1.62, t(56) = −7.3, p < 0.001). For target RT, but not for non-target RT, positive linear effects were observed (target RT: slope = 0.03, t(56) = 7.34, p < 0.001; non-target RT: slope = 0.004, t(56) = 1.63, p > 0.1). We further tested an extension of the mixed-effects model that included a quadratic term¹ for target accuracy (slope = 1.18, t(56) = 5.46, p < 0.001) and both RT measures (target: slope = −0.017, t(56) = −8.8, p < 0.001; non-target: slope = −0.018, t(56) = −9.4, p < .001). These quadratic patterns indicate that target accuracy did not decline linearly at high load levels but rather declined asymptotically, while RT slowed with load, but then sped up again when N-back load was very high.

3.2. Overview of N-back fMRI results

In order to investigate neural substrates of working memory, we used an a priori approach, focusing on a particular prefrontal region of interest and, as a supplemental analysis, on a comprehensive set of additional brain-wide nodes and networks. The focal left LPFC region of interest was selected because it has been repeatedly shown to exhibit strong connections with WM and behavioral performance in both meta-analyses and specific studies, including those conducted in our lab (Cole et al., 2015; Cole et al., 2012; Rottschy et al., 2012; Wager, Spicer, Insler, & Smith, 2014). In particular, not only was this region included as part of the “core WM network” in Rottschy et al (2012), but also, in Cole et al (2012, 2015) this region was unique in exhibiting robust brain-behavior relationships in terms of both activity and connectivity patterns. Consequently, for this LPFC ROI, we focused on both its activity, as well as its resting-state functional connectivity.

After characterizing the load function observed in this ROI, we conducted a comprehensive set of analyses characterizing brain-behavior relationships with it (additional supplementary analyses compared this ROI to others across the brain as well as to brain networks- reported in Supplemental Results). A road-map to these analyses is as follows. First, we explored a variety of measurement and statistical approaches to modeling the load function and reducing the dimensionality of activity and behavioral performance variables: factor analysis, linear slope estimation, and linear mixed effects modeling. Second, after characterizing brain-behavior relationships in terms of neural activation, we tested whether similar relationships are present in regards to the functional connectivity of the LPFC ROI, using the GBC metric. Additionally, we tested whether GBC and neural activity measures each served as unique predictors of behavioral performance, using a multiple regression approach. Moreover, to ensure the predictive validity of this approach, these analyses were confirmed using cross-validation. Third, to establish the generality of LPFC predictive power, we examined this in terms of out-of-sample prediction, using both the N-back task and an additional out-of-scanner measure of WM function from the HCP dataset. Lastly, to further understand the source of LPFC brain-behavior relationships, we separately examined the relative predictive power of high versus low load conditions.

3.3. WM Load function in LPFC

Prior studies have not investigated patterns of recruitment of these networks beyond 3-back, and so the current study provides novel information on the role of these regions at extremely high load levels. In particular, when plotting load-related activity across participants in LPFC we observed a monotonic increase in activity across lower level loads, when then shifted to a decreasing pattern beyond N = 3, thus exhibiting a clear inverted-U profile (Figure 3A; although see below for evidence of a different profile when subdividing participants according to performance). This visual pattern was quantitatively confirmed by linear mixed effects modeling (as in equation 1 replacing behavior (Behav_ij) by brain activity-BOLD_ij. A non-significant linear term (slope = 0.002, t(56) = 1.29, p = 0.26) and a significant quadratic term (slope = −0.005, t(56) = −5.33, p < 0.001 was obtained. These findings confirm that in LPFC the effects of N-back load appears to follow the inverted-U pattern, with a decrease in activity at high load levels (see Supplemental Results for parallel findings at the brain network level).

Figure 3.

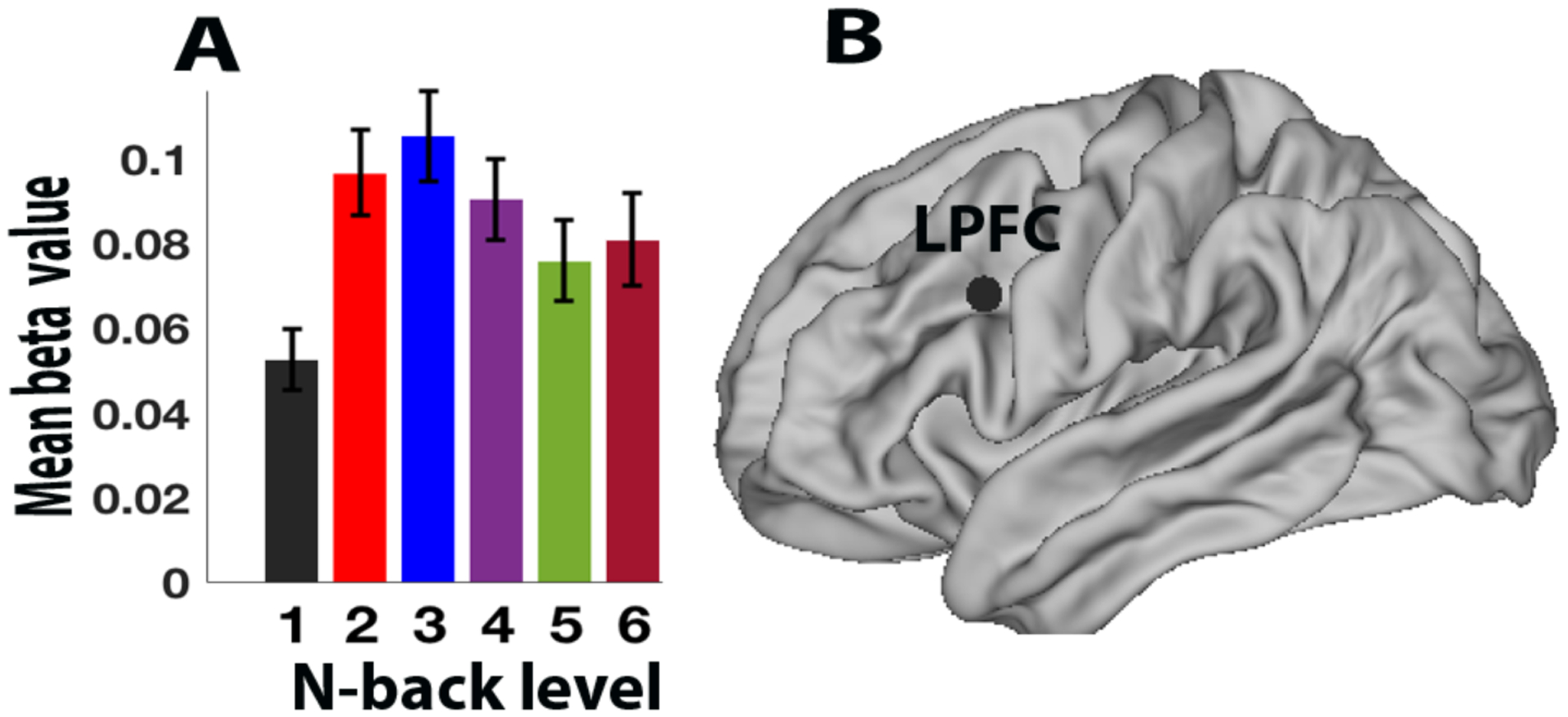
Bar plot of N-back activity (beta parameter), mean over all participants by load level, in (A) LPFC, (B) Anatomical location the left LPFC region from Cole et al. (2012). Error bars indicate standard error of the mean.

3.4. Statistical modeling of activity-based brain-behavior relationships

Our primary focus in this study was to identify the relationship between load-related activity and behavior to elucidate the source of individual differences in WM. Rather than testing for multiple correlations across multiple load levels and BOLD response profiles, we initially explored a measurement model perspective, employing factor analysis to reduce dimensionality and test for correspondence between single factors of performance and BOLD signal. To do so, we first validated that the BOLD and accuracy measures could each be adequately captured by single factors (see Supplemental Results).

Next, we tested for correlations between participants’ behavioral accuracy and BOLD activity factor scores in an analysis, which is formally equivalent to a structural equation modeling or latent variable approach. In the LPFC, we found a significant positive correlation, such that higher BOLD activity factor scores were associated with higher N-back task accuracy (r = 0.28, p = 0.034; Figure 4A). We also conducted parallel analyses using the signal detection index d’ rather than target accuracy, and found similar results (see Supplemental Results).

Figure 4.

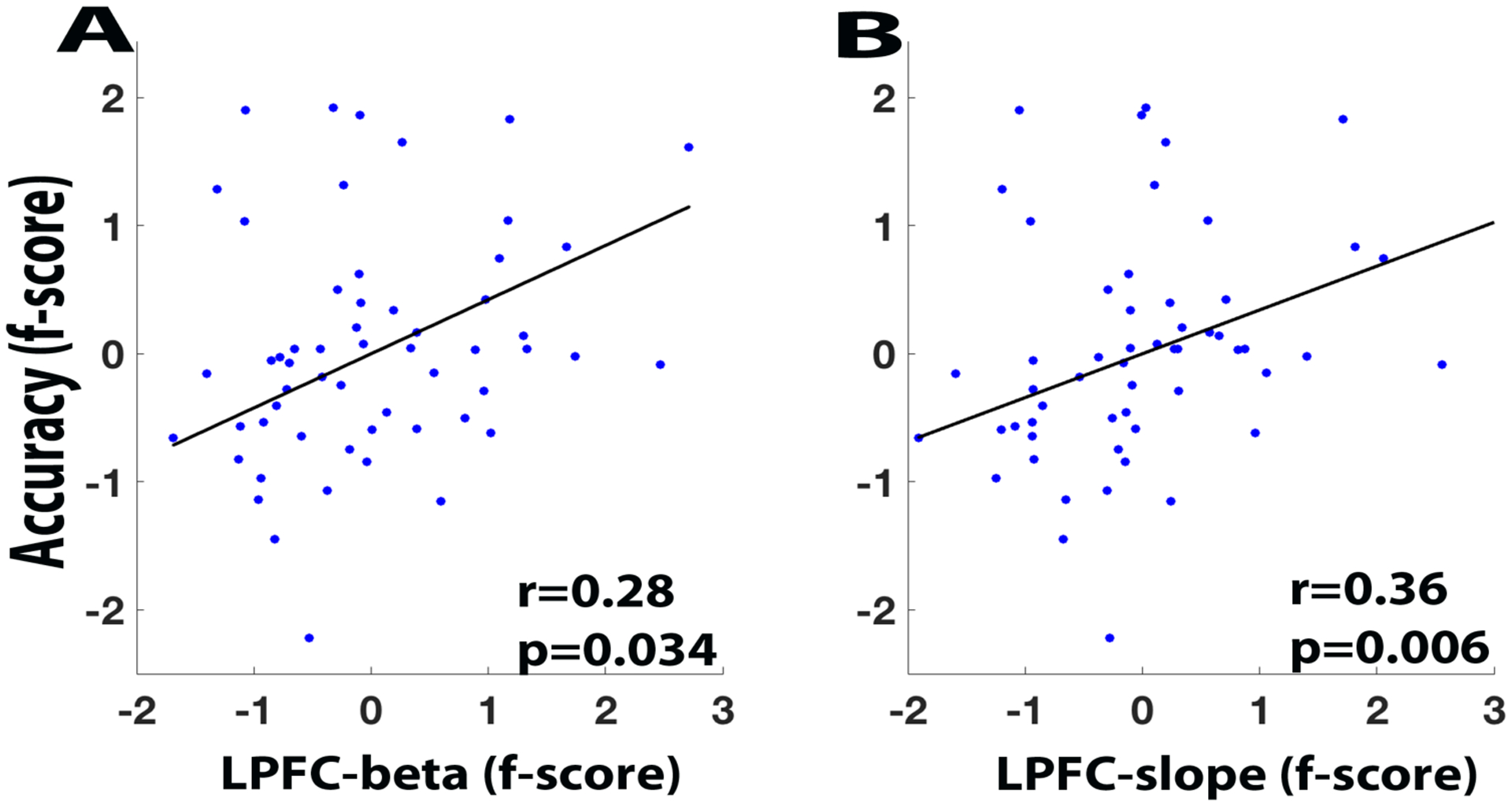
Scatter plots. (A) Accuracy factor score and LPFC activity factor score (betaparameter). (B) Target accuracy factor score and LPFC load slope (linear fit of LPFC activity on N-back load).

This hypothesis-driven confirmatory ROI analysis, was supplemented by an additional exploratory follow-up analysis that also examined the remaining brain networks and all individual Power nodes (see Supplemental Results for details). Interestingly, even when using a liberal statistical significance threshold (i.e., uncorrected alpha level of 0.05), no other nodes or networks exhibited a positive correlation with behavior, with the sole exception of the node that was located the closest anatomically to our LPFC ROI.

It is noteworthy that this analysis, which collapses load-related activity to a single value, was associated with the target accuracy measure. However, it raises the question whether the effects are specific to accuracy. Conversely, another parallel analysis which substituted target RT as the behavioral index found no significant correlations with LPFC (r = −0.13, p = 0.31). To more stringently confirm this specificity, we compared the strength of the correlations between target accuracy and target RT, using Meng’s correction for non-independent correlation coefficients (Meng, Rosenthal, & Rubin, 1992). Indeed, for this LPFC ROI, relationship with target accuracy was significantly stronger than the relationship with target RT (LPFC: Z=2.57, p < 0.01). This finding is particularly noteworthy, given that a supplementary analysis found that within-subject (i.e. load-related) BOLD patterns related better to RT than accuracy measures (see Supplemental Results). Thus, the results suggest that between-subjects co-variation in brain activity and behavior are dissociable from within-subjects relationships (i.e., focused on load-related brain-behavior covariation).

The previous analyses above modeled load-related activity in terms of a factor-score, which is conceptually similar to a cross-load weighted average. The second set of analyses examined LPFC activity in terms of the linear-trend present in each individual’s load-related data. Specifically, we estimated the linear slope of load-related LPFC activity for each participant and tested whether this slope was correlated with their behavioral accuracy factor score. For the LPFC, this correlation was significantly positive, indicating that the participants showing a more positive linear load function also had higher N-back task accuracy (r = 0.36, p = 0.006, Figure 4B).

To illustrate this effect more clearly, we subdivided participants into those that had a positive linear slope in load-related activity (slope > 0; i.e., consistently increasing with load) and those that had a linear slope that was not positive (slope ≤ 0; i.e., flat or decreasing activity with load). We then examined behavioral accuracy separately in these two participant subgroups (Figure 5A). As can be seen, participants with a positive linear slope (n = 38) showed consistently numerically higher accuracy than those without a positive slope (n = 19), and the difference was significant at multiple individual load levels (i.e., 1-back: p = 0.02; 2-back: p = 0.24; 3-back: p = 0.07; 4-back: p = 0.04; 5-back: p = 0.04; 6-back: p = 0.66).

Figure 5.

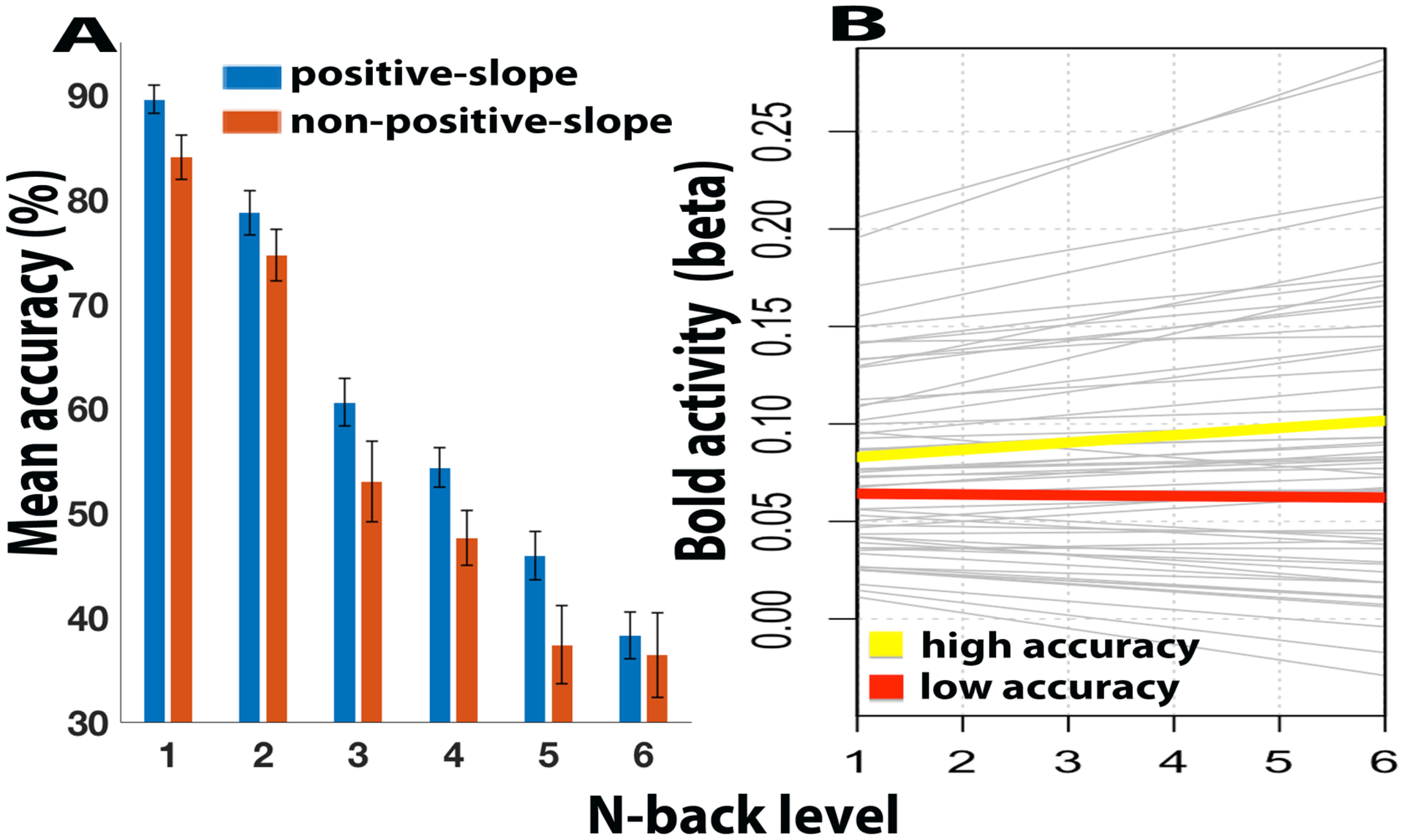
(A) Participants are divided into subgroups based on whether they exhibited load-related increases in LPFC BOLD activity (positive linear slope; blue), or flat/decreasing activity (nonpositive linear slope; red). Bar plots display mean target accuracy of the two participant subgroups for 1:6 back tasks, and demonstrate generally better performance across all load levels in the (blue) subgroup showing load-related increases. Error bars indicate standard error of the mean. (B) Plot of fitted bold activity of N-back levels. Gray thin lines represent the linear slope of BOLD load effects in all individual participants. Mean slope of the high accuracy participants (top third, n = 19; yellow) and low accuracy participants (bottom third, n = 19; red).

Since the accuracy factor score includes components of both mean performance (i.e., load independent) and changes in performance due to increasing load, we followed up this analysis by testing for a more specific relationship between the LPFC linear load slope in BOLD signal and the linear load slope in target accuracy. To do this most robustly, we used linear mixed effects models, via a cross-level interaction. Here, individual differences in behavioral performance were treated as an interaction term that modulated the linear slope of load-related activity. In other words, the model predicted BOLD activity in terms of linear effects of load, but with the slope of load-related activation change modulated by the linear slope coefficient of task accuracy (target trials). Consequently, similar to the previous analysis, this model tests whether more accurate participants (who will exhibit a less negative / more positive linear slope in target accuracy) also tend to show a more positively sloped linear load effect in BOLD activation than less accurate participants. Additionally, the use of a linear mixed effects model is more rigorous as it directly tests the cross-level interaction (individual differences effect), while simultaneously controlling for random variation in both the slope and intercept of load-related activity. Specifically, we tested whether BOLD signals (BOLD_ij) could be predicted by linear, mean-centered load (LOAD_ij) i, with load-levels nested within participants j. Note that the linear load slope for accuracy (AccSlope_j) estimated separately for each subject is a predictor of the load effect on BOLD signal at the subject level of the model. Also, α₁₁ gives the cross-level interaction of load and the accuracy slope.

$${\mathit{\text{BOLD}}}_{ij}=B_{{}_{0j}}+B_{1j}{\mathit{\text{Load}}}_{ij}+{\epsilon }_{ij}$$

$$\begin{gathered} B_{{}_{0j}}=a_{00}+u_{0j} \\ {B}_{1j}=a_{10}+a_{11}{\mathit{\text{AccSlop}}}_j+u_{ij} \end{gathered}$$

Indeed, the model reinforced the findings of the prior analysis, there was a significant interaction between LPFC BOLD load slope and individual differences in behavioral performance (indexed via the linear slope coefficient of target accuracy; t(56) = 2.08, p = 0.041). To demonstrate these effects, we visualize the predicted performance across load levels and across participants, which also illustrates the complementary nature of this analysis to the previous one (Figure 5B). Specifically, the linear slope patterns clearly indicate the variability present across participants, and also that high accuracy participants tended to have a positive linear slope (increasing BOLD signal with increasing load), while the lower accuracy participants tended to exhibit a flat (or decreasing) effect of load on BOLD signal.

Finally, it is worth noting that we also tested whether individual differences in the strength of the U-shaped load related pattern in BOLD activity were related to behavioral performance, using the quadratic term coefficient as the individual difference measure. However, in none of these analyses was there a significant brain-behavior correlation observed in the LPFC (and indeed no correlation was observed in any brain network when tested in additional control analyses; see Supplemental Results).

3.5. Brain-behavior relationships with LPFC functional connectivity

In addition to the relationship between load-related activity and behavior, we were also interested in investigating whether functional connectivity (FC), observed during the resting state, was uniquely predictive of N-back task performance. We focused on a FC measure which can be computed for specific, focal brain regions (as well as networks), and which has been related to N-back performance in prior work: the global brain connectivity (GBC) index. Specifically, in a prior study from our group (Cole et al., 2012), we found that the GBC of this LPFC ROI was predictive of N-back task performance, along with other relevant cognitive individual differences (working memory capacity, fluid intelligence). Consequently, we tested whether this pattern would replicate in a new dataset, and with a parametric manipulation of load.

We computed the GBC value in two steps and then correlated the value with our accuracy factor score. First, the resting-state functional connectivity (rsFC) value between LPFC and every other brain region (defined using the 264 Power node parcellation) was computed and then Fisher r-to-z transformed. Next, these values were averaged to create a single GBC score for each participant. As predicted, we found a reliable correlation between this GBC score and the behavioral accuracy factor score and this GBC value across participants (r(49) = 0.29, p = 0.039).

Another analysis compared the GBC of the LPFC relative to other brain regions to determine whether this relative-GBC value was also predictive of behavioral performance. To determine relative GBC, we first computed the GBC separately for not only the LPFC, but also for each of the other 264 Power nodes in turn. Then, for each participant we rank ordered these GBC values, to obtain the rank for LPFC relative to other brain regions, which we call the relative-GBC value. We then correlated each participant’s relative-GBC value against their behavioral performance, again using the factor score measure. This correlation was also significant (r(49) = 0.30, p = 0.029). This finding suggests that the higher the LPFC’s GBC relative to other brain regions (irrespective of its overall value), the better was task performance.

Our results up to this point implicate distinct LPFC predictors of individual differences in N-back target accuracy: activity (either through the factor score or linear slope approach) and resting-state function connectivity (GBC). However, from the above analyses, it is not clear whether these predictors explain overlapping or independent variance in behavioral performance. If it is the latter, then the amount of variability in behavioral performance that can be explained from these distinct neuroimaging measures should increase when both are simultaneously included as predictors. In addition to testing whether these regions explain overlapping of complementary variance, we also conducted cross-validation analyses to more rigorously test the combined predictive capabilities of these brain indices for WM behavioral performance.

To address these questions, we reformulated the analysis into a multiple regression, using the accuracy factor score as the outcome variable, and LPFC activity (linear slope coefficient) and functional connectivity (GBC) as simultaneous predictors. The multiple regression indicated that, together, the predictors explained significant and distinct components of behavioral variance, accounting for over 22% of individual variation in N-back performance (i.e., overall model R² = 0.223) (LPFC activity slope: beta = 62.4, t(47) = 2.86, p = 0.006; LPFC GBC: beta = 3.08, t(47) = 2.15, p = 0.036). When compared individually, activity measure was somewhat stronger (R² = 0.148) than the connectivity measure (R² = 0.09), yet this finding indicates that each of the two measures accounted for a substantial portion of individual differences in WM performance.

Although this type of multiple regression analysis is informative, current literature has pointed to the limitations of standard regression approaches in demonstrating predictive validity due to over fitting with respect to a given dataset (Yarkoni & Westfall, 2017). Consequently, we next adopted a cross-validation approach popularized in the machine learning literature - the leave-one-subject-out method - to provide further validation of these results. Specifically, we tested the correlation between the predicted and actual behavioral performance values on the left-out data. This correlation remained significant, though as expected was of lower magnitude, with an adjusted R² = 0.15 (p = 0.006).

This result supports the predictive utility of the two neural indices of LPFC function, the linear slope of load-related activity and GBC, for predicting N-back performance in out-of-sample data. Interestingly, cross-validation analyses also demonstrated that LPFC activity (linear slope) was a significant predictor in isolation since it remained significant in leave-one-out cross-validation tests with it as the only predictor variable (r=0.29, p=0.036). However, the same was not true for LPFC functional connectivity (GBC), as it was no longer significant when included as the only predictor variable (r = 0.17, p = 0.22).

This conclusion was further supported by a permutation test implemented by computing the correlation between actual and predicted accuracy (in 1000 iterations) after randomly shuffling accuracy values (in a linear model where LPFC activity slope and LPFC GBC were simultaneous predictors of accuracy). As expected, the mean correlation (mean correlation from 1000 iterations after Fisher r-to-z transformations) between predicted and true accuracy was near zero across permutations (r = 0.0066). In 1000 iterations only 8 of the permutations was the correlation as high as in our original dataset (r = 0.36). Thus, the cross-validation test confirms a highly significant correlation between predicated and actual accuracy (p = 0.006)².

3.6. Testing generalization of brain-behavioral performance prediction

The prior analyses suggested the predictive validity of LPFC neural measures for predicting individual differences in WM function. To further test for the generalizability of these predictions, we examined whether this unique left LPFC ROI, which was not well-identified in by any existing parcellation scheme (Cole et al., 2015; Cole et al., 2012), exhibited predictive power related to N-back behavioral performance in another, much larger dataset, albeit one that did not examine parametric manipulations of working memory load. To do this, we made use of the publicly available HCP dataset, which includes N-back data from the 2-back and 0-back condition. To simplify the analysis, we included data from the 500-release set, since this was the last set to provide results from a volume-based GLM analysis (i.e., the largest release that used an analysis approach compatible with the use of volume-based, voxelwise ROIs). Furthermore, from this release we used only unrelated participants (n = 198), to avoid potential confounds in using twins and other related individuals. To provide the strongest test of generalization, we tested whether 2-back activation in our LPFC ROI predicted an out-of-scanner measures of WM and executive control function that were collected in that study: List Sorting (i.e., a standard WM measure included as part of the NIH Toolbox; (Barch et al., 2013; Gershon et al., 2013) and Penn Matrices (Bilker et al., 2012); a measure of fluid cognition or fluid intelligence/gF). The advantage of using these out-of-scanner behavioral measures is that any observed associations cannot be attributed to the contemporaneous collection of brain activity and behavioral performance measures, which serves as a potential confound when using N-back accuracy as the behavioral measure. Instead, a correlation with a separate, out-of-scanner measure like List Sort or PMAT performance would indicate that N-back-related LPFC activity reflects a more stable trait-related index of WM/EC function. Indeed, the robust correlation between LPFC 2-back activity and both List Sort performance (r=0.26, p < 0.001) and PMAT (r=0.22, p < 0.0015) supports the hypothesis that LPFC recruitment is trait-like, and thus generalizes across tasks. Moreover, when comparing the magnitude of this brain-behavior correlation (with List Sort) relative to all the other (264) nodes in the Power parcellation, we found that it was one of the strongest – indeed only 4 other nodes showed slightly stronger correlations (highest r = 0.285) and three of these were also in the FPN. This finding demonstrates clearly that this LPFC ROI can be expected to robustly reflect brain-behavior relationships in other N-back datasets and with other behavioral measures of WM/EC function.

For completeness, we also note that activity in this LPFC ROI was also reliably correlated with in-scanner 2-back performance as well in this HCP dataset (r=0.23, p=0.001). The magnitude of this correlation was comparable to that observed in our own dataset when restricting to the 2-back activity level (r=0.23).

3.7. The relative predictive power of high vs. low load data in the N-back

One of the most unique and potentially counter-intuitive aspects of our study design and analysis is that we examined N-back activity and performance at levels beyond those standardly tested in either behavioral or brain imaging studies of the N-back. Indeed, to our knowledge, this study is the first to examine six parametric levels of N-back fMRI and performance data. The likely reason for the uniqueness of our design is that conventional intuitions regarding the N-back are that the high load levels are too difficult for participants to perform well, and thus likely would be less sensitive to individual differences in brain activity and behavioral performance, due to floor effects.

We tested this assumption directly via analyses that separated the data into low load (N = 1—3) and high load (N = 4—6) subsets, since it is the high load conditions that are most unique to our study. We then conducted analyses that tested brain-behavior relationships in various ways in these two subsets. First, we replicated the multiple regression analysis described above in which we retained the behavioral accuracy factor score that included all 6 load levels, but then split the LPFC activity predictor in two, with one indicating the linear slope effect in only the low load conditions (1,2,3) and the other indicating linear slope in only the high load conditions (4,5,6). Thus, there were a total of 3 predictor variables (LPFC GBC, LPFC 123-slope, LPFC 456-slope). In a multiple regression we found that the total explained variance was similar at 22%, but that only the GBC and 456-slope predictors were statistically significant (LPFC GBC: beta = 3.26, t(46) = 2.25, p = 0.03; 123-slope: beta = 8.06, t(46) = 0.95, p = 0.34; 456-slope: beta = 33.58, t(46) = 1.97, p = 0.055).

Second, we conducted separate regressions with just the low load predictors (along with LPFC GBC) predicting accuracy in just the low load conditions (by creating a factor score summary over just N = 1—3) and just the high load predictors (+LPFC GBC) predicting accuracy in just the high load conditions (again with N = 4—6 behavioral factor score summary). In this analysis, low load brain measures explained only 5% of the variance in low load performance and neither of the predictors were significant (LPFC GBC: beta = 0.08, t(48) < 1; 123-slope: beta = 13.23, t(48) = 1.64, p = 0.10). In contrast, high load brain data explained 16% of variance in high load performance, and both predictors were significant (LPFC GBC: beta = 3.09, t(48)= 2.15, p = 0.037; 456-slope: beta = 33.17, t(48)= 2.17, p = 0.035)³.

Together these results suggest that, counter to standard intuitions, brain-behavior relationships are stronger in very high load conditions relative to low load conditions. Thus, including very high load conditions increased our sensitivity to detect these brain-behavior relationships. To quantify this sensitivity, we directly assessed the proportion of total variability explained by individual differences (i.e., between-subject variability) using the intraclass correlation coefficient (ICC), which provides a measure of both how reliable are individual differences, and the relative proportion of variance that is due to load effects (i.e., within-subject variability vs. individual differences). The ICC statistic is typically used in test-retest reliability analyses, but for our purposes, each load-level condition was treated as a “retest” event. All analyses were conducted using the ‘psych’ package in R (Revelle, 2018), and report the ICC(3,k) metric, which is the most conservative.

When examining all load conditions (N = 1—6), the ICC estimate for target accuracy was 0.83 (95% CI: 0.74—0.89); of that, the proportion of variance due to load was 0.68 and to individual differences 0.14 (0.18 residual). For the LPFC BOLD data, again with all load conditions, the ICC estimate was 0.93 (95% CI: 0.90—0.95); with proportion of variance due to load 0.05 and to individual differences 0.65 (0.29 residual). This indicates high reliability of both measures, but with varying sensitivity to individual differences.

Next, we compared variance explained when separately examining low (N = 1—3) and high (N = 4—6) conditions. For both the behavioral and BOLD data the effects were striking, with increased ICCs and proportion of variance due to individual differences in the high load conditions (target accuracy: ICC = 0.85, 0.76—0.90 95% CI, proportion of variance due to individual difference = 0.51 and to load = 0.20; BOLD: ICC = 0.91, 0.86—0.95 95% CI, proportion of variance due to individual differences = 0.77 and to load = .01) compared to low load (target accuracy: ICC = 0.62, 0.41—0.76 95% CI, proportion of variance due to individual difference = 0.14 and to load = 0.59; BOLD: ICC = 0.82, 0.73—0.89 95% CI, proportion of variance due to individual difference = 0.53 and to load = 0.13). Taken together, these data support the idea, that counter to standard intuitions, the high load condition is actually more sensitive for the detection of individual differences in both behavioral performance and brain activity.

4. Discussion

Our study fills an important gap in our understanding of brain-behavior relationships in working memory tasks, and in the N-back in particular. Although the N-back is one of the most widely used paradigms to study working memory and executive control, there is still a poor understanding of how brain activity varies by load and how load-related activity patterns relate to task performance. Our study is unique in that we examined brain-behavior relationships in an N-back study design that used a very wide range of load levels, spanning from N = 1–6. To our knowledge, no previous studies of the N-back have systematically examined brain activity and behavioral performance at very high load levels (N > 3). The key question of interest was how LPFC activity varied with load and in comparison to other regions, and whether LPFC contributed to behavioral performance in a systematic way across load levels.

A systematic analysis of brain activity and performance across a large sample, and a wide range of load levels revealed multiple novel observations. First, we clearly replicated the inverted U-shaped pattern that has been a prominent feature of prior studies (Callicott et al., 1999; Jaeggi et al., 2007; Van Snellenberg et al., 2015), leading to the greatest activation at middle load levels (i.e., 2/3-back). This feature was not only prominent in LPFC activity, but observed brain-wide, as it was present in many other networks related to WM/EC as described in Supplemental Results. Second, we found that within a focal left LPFC ROI, load-related activity reliably predicted N-back behavioral performance. Moreover, this brain-behavior relationship was selective: it was observed with the linear, rather than the inverted-U component of load-related activation, it was not found with RT measures, and it was unique relative to other brain regions and even whole-networks, as revealed in supplemental analyses (Supplemental Results). Third, we found that global connectivity with this focal LPFC region was an independent predictor of N-back task performance (i.e., even when considering LPFC activation). Fourth, rigorous cross-validation analyses demonstrated the predictive utility of load functions in the LPFC, which also generalized to a large out-of-sample dataset (HCP). Finally, and potentially one of the most counter-intuitive aspects of our findings, the highest load levels (4–6) of the N-back, rather than standard lower-load levels (N ≤ 3), were the most sensitive for detecting brain-behavior relationships, as they exhibited the greatest individual variability in both performance and brain activity. Thus, together the results highlight the utility of our approach in testing for brain-behavior relationships in WM tasks such as the N-back when sampling across a very wide-range of load levels. Nevertheless, the results do point to a number of puzzling and unresolved issues in terms of the neural mechanisms of WM function, that we discuss next.

4.1. Load-related activity functions: Meaning of the inverted-U pattern

The current findings replicate and extend a now consistent pattern of inverted-U load functions observed in neuroimaging studies of WM (Jaeggi et al., 2007; Jansma, 2004; Van Snellenberg et al., 2015). The inverted-U shape has puzzled investigators, and several hypotheses have been proposed. The most prominent is that the inflection point, in which activation levels start decreasing as load continues to increase, may reflect the point in which WM capacity is exceeded (Callicott et al., 1999; Haier, Siegel, Tang, Abel, & Buchsbaum, 1992; Neubauer, Grabner, Fink, & Neuper, 2005). This account is bolstered by findings of a close correspondence between the load level in which the inflection point occurs and independent measures of WM capacity (Vogel, McCollough, & Machizawa, 2005). These findings have not only been observed in N-back paradigms, but in delayed match-to-sample paradigms (such as the Sternberg item recognition task) in which the inverted-U function has been linked to the active maintenance of information in working memory (Cappell et al., 2010; Karlsgodt et al., 2007; Karlsgodt et al., 2009).

Other accounts have postulated that inverted-U functions reflect task disengagement, or a shift in processing strategy, which may occur somewhat independently of available capacity (i.e., due to other considerations, such as cognitive effort avoidance (Jaeggi et al., 2007; Jonides & Nee, 2006; Vogel et al., 2005). It is also consistent with neuro-computational models of WM, which suggest that the balance between recurrent connectivity and strong lateral inhibition leads to capacity constraints that create sub-linear relationships between load and average activation (Chatham et al., 2011; Edin et al., 2009; Rolls, Dempere-Marco, & Deco, 2013; Wei, Wang, & Wang, 2012).

Our results contribute to this literature in several ways. First, our design increased sensitivity to the inverted-U pattern due to the wider range of load levels employed, at least relative to standard N-back paradigms (Van Snellenberg et al., 2015). Thus, we confirm that in the LPFC (and indeed in other brain networks as well; see Supplemental Results), there is a definite non-monotonic pattern with activation levels being strongest at N = 3, and decreasing from that at higher levels (e.g., Figure 3A). Interestingly, however, we found that it was the linear rather than non-linear load effect that best predicted individual differences in behavioral performance. In particular, highest performing participants showed a definite linear increase in activity, whereas lower performing participants tended to show decreasing activity. This finding suggests that although there may be an overlying pattern of decreasing activity in all participants at high load levels, it is the strength of the linear load-pattern (i.e., the tendency to monotonically increase, or at least not decrease, activity with increasing load) that most strongly discriminates high and low performers. Thus, the results suggest the continued utility of linear load modeling, to test for individual variation in WM function, even given the presence of non-monotonic patterns.

Nevertheless, a limitation of our study is that we did not have an independent measure of WM capacity, which ideally would be assessed out-of-scanner, with well-established psychometric measures (e.g., standard span or change detection tasks (Conway et al., 2005; Kyllingsbaek & Bundesen, 2009; Luck & Vogel, 2013). Consequently, a direction for future research would be to determine whether and how WM capacity limits relate to the distinctions between high and low performers we observed in terms of N-back load patterns in the current study, and moreover, whether capacity indices can be used to predict where the inflection point in inverted-U patterns is located or whether it exists (cf. van Snellenberg et al, 2015).

Data of this type (i.e., independent measures of WM capacity) would also be informative with regard to our finding that between-subjects variability in BOLD signal was not related to reaction times. Conversely, supplemental analyses confirmed that within-subject (rather than between-subject) load-related inverted-U patterns seemed to better track with reaction time (see Supplemental Results). It is possible that the inflection point within the inverted-U BOLD activity load functions might predict not only between-subjects variability in N-back accuracy, but also the inverted-U and inflection point in load-related RT patterns (i.e., and related to WM capacity measures). Such findings would support the idea that inverted-U patterns reflect something more about how target/non-target response decisions are reached, rather than about the quality of information storage per se. Although it was beyond the scope of current study to directly test for such effects (which would require more trials at each load condition, and more explicit manipulation of decision-related factors), this is an issue that could be addressed in future work, particularly through the use of evidence accumulation decision-making models: e.g., drift diffusion, linear ballistic accumulator (Ratcliff, Smith, Brown, & McKoon, 2016).

4.2. Focal region vs. network-level contributions to WM performance

Although our focus was brain-behavior relationships within a focal brain region (LPFC), we also investigated whether parallel relationships were observed at the network level. In supplemental analyses we also tested cognitive brain networks including the broader frontoparietal network, as well as the dorsal attention, cingulo-opercular, and default mode networks. Paralleling our findings with the LPFC, in none of these networks was the inverted U-shaped or linear pattern associated with performance. It is worth noting that some analyses did reveal brain-behavior relationships in the DMN (see Supplemental Results), but these relationships were observed at the average level of task-related deactivation, rather than in terms of task-related activity that was specifically load-related.

It is possible that these null findings with regard to “task-positive” networks is actually a false negative, and that significant brain-behavior effects might have emerged with larger sample sizes. In fact, other work using very large N-back datasets have pointed to network-level prediction of WM performance (Bolt et al., 2018; Egli et al., 2018). Nevertheless, it is also possible that the lack of load-related findings present at the brain network level within the current dataset reflect a true pattern that is related to the use of a wider-range of load levels than has previously been studied in the N-back. For example, if inverted-U patterns reflect capacity limitations, the inverted-U patterns observed at lower loads (N =1—3) would be primarily driven by low-capacity individuals. These patterns would also thus obscure any linear effects that only emerge for higher-capacity individuals across the wider-range of loads (N = 1—6). Thus the wider-range may be necessary to capture and distinguish between linear and quadratic effects, and relate them to individual differences in performance. Moreover, it is possible that linear versus quadratic components may emerge to varying degrees across load levels in different parts of a given brain network. Hence, when considering the full load range (N = 1—6), subtler linear effects might be most sensitively be detected in focal regions (e.g. the LPFC), rather than in entire networks.

Our results do confirm the functional importance of this focal left LPFC region for WM task performance. Indeed, the results are consistent with the findings of many meta-analyses, which have pointed to the reliable engagement of this particular region in WM paradigms. For example, Rottschy et al. (2012) highlight this region as a key component of what they refer to as the “core” WM network. Furthermore, in our own prior work we found that this region was uniquely selective in predicting N-back task performance both in terms of within-subject and between-subject indicators (Cole et al., 2012). Although the current results do not highlight exactly how and why this region contributes to WM in such a unique way, they do point to the need for further targeted investigations of this region, to better reveal the mechanisms by which it contributes to WM function⁴.

Nevertheless, an important implication of the current results is that they clearly underscore the potential importance of conducting region-focused analyses in addition to network-based ones. Although network-focused analyses are useful for dimensionality reduction, our results suggest the potential limitations of such approaches, as they may obscure focal and unique contributions to functionality. As a concrete example of this point, the recent study of Egli et. al., (2018) analyzed their large N-back dataset using independent component analyses (ICA) as a data-driven dimensionality reduction approach, which they argued revealed the presence of two unique networks: a parietally-centered network related more to WM load effects and a frontally-centered network was more involved with general sustained attention. However, close inspection of their own data also points to the importance of the same left mid-lateral PFC region we focus on here. Nevertheless, because of their network-focus, Egli et. al., (2018) do not highlight this region in their results, which otherwise would cause its potentially unique contribution to behavioral performance to be overlooked.

4.3. Global connectivity vs. activity within LPFC

Although the first-generation of WM neuroimaging studies focused exclusively on relating BOLD response magnitude to load manipulations, the field has clearly shifted to focus on functional connectivity as an important predictor of WM performance. In Cole et. al., (2012), we highlighted the GBC metric as a potentially powerful summary measure of functional connectivity that could be associated with focal brain regions. Moreover, in that study we demonstrated that GBC within the left LPFC showed a strong degree of individual variation, which critically appeared to have strong functional consequences, in predicting not only N-back accuracy, but also broader measures related to WM function (i.e., working memory capacity and fluid intelligence). The current study replicated this pattern in a new dataset, and moreover replicated the finding that LPFC GBC and LPFC activity served as independent predictors of a behavioral measure of WM function (N-back accuracy).

The finding of independent sources of individual variation in both the GBC and activity of LPFC begs the question of what each of these two metrics reflect, and how they relate. More broadly, the information content of mean activation versus that of functional connectivity is of growing general interest, moreover there have been concerns raised about the growing divide in studies focused on functional connectivity (particularly resting-state) and those focused on task-related activation. Recent attempts have been made to integrate connectivity and activity-based analyses, of which a notable example is activity flow mapping (Cole, Ito, Bassett, & Schultz, 2016). Our results, however, are consistent with the idea that the activity and connectivity patterns associated with LPFC contribute unique variance to behavioral performance. In particular, the factors associated with individual variation in LPFC activity and with LPFC GBC seem to be functionally independent, and so potentially reflect distinct causal mechanisms. Moreover, the results also replicate other prior results suggesting the importance of resting-state functional connectivity patterns (Sala-Llonch et al., 2012), particularly involving the DLFPC, as an important and unique dimension of individual difference with clear implications for WM function.

4.4. The importance of high-load WM conditions

Potentially the most surprising contribution of this study was the finding that high-load (i.e., N > 3), rather than low-load working memory conditions were the most sensitive for identifying individual differences. A common assumption that high-load conditions in the N-back exceed most participants’ WM capacity predicts that performance would be at floor for N ≥ 3, and that variability in BOLD activity patterns would merely reflect noise. On the contrary, we found that high-load conditions most strongly differentiated individuals, behaviorally and in terms of activity patterns. Given that individual differences analyses rely on between-subjects variability, higher load levels may thus be critical for detecting brain-behavior relationships.

Indeed, it may have been precisely the utilization of high-load manipulations which provided the necessary discriminating power to identify individuals who were able to maintain high levels of performance and LPFC activity. Those with shallower decreases in performance showed more positive linear slopes in activity patterns. It is possible that under such high-load conditions, preservation of performance, and the brain activity metrics are more closely reflecting processes related to cognitive control factors, rather than simple active maintenance, such as sustaining cognitive goals, resisting tendencies to distraction and mind-wandering, or potential for affective reactivity to internal negative performance feedback signals. In fact, to speculate, it may be that the high-load LPFC metrics may reflect control processes more closely than simple active maintenance, and these may be the most critical dimensions of individual differences in cognitively demanding tasks, such as the N-back. If so, the findings would be consistent with the view that the N-back should be more strongly construed as a probe of cognitive control functions, than pure working memory per se, and this might be particularly true at high-load levels, which are most control-demanding. A key implication of the current results is that if investigators are most interested in individual differences, high-load rather low-load N-back conditions should be emphasized. Notably, this recommendation is essentially opposite to common intuitions and predominant practice governing N-back studies since the beginning. Of course, one caveat is that we can only make this recommendation for studies involving healthy young adults, since that is the population we studied here. Future work will need to determine whether high-load N-back conditions are also equally efficacious and sensitive when examining other populations of interest.