MovableType Software for Fast Free Energy-Based Virtual Screening: Protocol Development, Deployment, Validation, and Assessment

Abstract

For decades, the complicated energy surfaces found in macromolecular protein:ligand structures, which require large amounts of computational time and resources for energy state sampling, have been an inherent obstacle to fast, routine free energy estimation in industrial drug discovery efforts. Beginning in 2013, the Merz research group addressed this cost with the introduction of a novel sampling methodology termed “Movable Type” (MT). Using numerical integration methods, the MT method reduces the computational expense for energy state sampling by independently calculating each atomic partition function from an initial molecular conformation in order to estimate the molecular free energy using ensembles of the atomic partition functions. In this work, we report a software package, the DivCon Discovery Suite with the MovableType module from QuantumBio Inc., that performs this MT free energy estimation protocol in a fast, fully encapsulated manner. We discuss the computational procedures and improvements to the original work, and we detail the corresponding settings for this software package. Finally, we introduce two validation benchmarks to evaluate the overall robustness of the method against a broad range of protein:ligand structural cases. With these publicly available benchmarks, we show that the method can use a variety of input types and parameters and exhibits comparable predictability whether the method is presented with “expensive” X-ray structures or “inexpensively docked” theoretical models. We also explore some next steps for the method. The MovableType software is available at http://www.quantumbioinc.com/

Introduction

The cost of research and development in drug discovery has continued to increase annually,^1,2 and much of this cost is due to the massive amount of screening for bioactive compounds required, in which only 1–2% of the screened lead compounds enter the preclinical stage.¹ Receptor:ligand binding free energy simulation has become a vital research area in structure-based drug design, and accurate simulation of receptor:ligand free energy changes upon binding requires a thorough sampling of the metastable energy states on the dissociation pathway. Effective in silico predictions of the free energy changes with respect to biomolecular binding processes provide significant support to drug target identification and drug candidate screening and greatly reduce the cost of the corresponding “wet chemistry” research.

For several decades, on account of their speed and lower cost versus both molecular dynamics (MD) simulations and “wet chemistry” approaches, virtual screening and docking/scoring methods have been applied to drug discovery. These methods have become integral to the drug discovery effort, as they are critical to understanding intermolecular interactions in the structure-based drug discovery effort.³⁻¹⁰ However, they are often criticized for their lack of accuracy in predicting binding modes and binding affinities, especially for the noncomparability of the scores to the experimental pK_d values or free energies.¹¹⁻¹⁶ Furthermore, predictions of small-molecule docking often outperform those for larger molecules.¹⁷ Much of the challenge of docking/scoring is centered on the inability of these methods to sample enough of the relevant conformational space of the receptor:ligand complex.¹⁸⁻²¹ Furthermore, the methods are often unable to correctly capture and sample structural water,²²⁻²⁴ tautomeric states,^25,26 and conformational strain.²⁷ These problems, coupled with scoring function errors^28,29 and inaccurate protein:ligand complex structures,^30,31 contribute to significant problems with the use of these methods in industrial drug discovery efforts. In order to decrease computational expense, protein flexibility is ignored³²⁻³⁴ and binding energy is approximated using “rigid receptor” or “induced-fit receptor” models, which use protein target minimization or refinement during the docking/scoring process.³⁴ On the other hand, molecular simulation methods like FEP+,³⁵ AMBER TI (thermodynamic integration),^36,37 molecular mechanics/Poisson–Boltzmann surface area (MM/PBSA) and molecular mechanics/generalized Born surface area (MM/GBSA),³⁸⁻⁴² linear interaction energy (LIE),⁴³ and replica exchange with solute tempering (REST),^44,45 which are generally computationally expensive for large-scale virtual screening campaigns, are becoming more accessible and easier to use with the general availability of graphics processing unit (GPU) technologies. These methods can effectively simulate receptor–ligand binding/dissociation trajectories and are in theory better able to predict free-energy-based binding affinities. Free energy perturbation or alchemical methods have shown promise,^8,18,46−48 while absolute free energy determination is still a problem and these methods often exhibit significant errors.^18,49−54 Free energy algorithms that effectively balance speed and accuracy are in high demand according to the growing need for accurate computational methods in the fast-paced drug discovery and biotechnology industries.

Beginning in 2013, Merz and co-workers developed⁵⁵ and patented⁵⁶ the Movable Type (MT) free energy method to address this speed versus accuracy issue through the use of fast numerical integration methods to estimate the atomic energy-state ensembles in the vicinity of one or more user-provided or automatically generated structural state(s). These atom-level ensembles are grouped into molecular energy ensemble calculations in order to estimate the free energy of binding in a statistical-mechanically rigorous fashion. Over the years, the MT method has been expanded and refined to account for greater protein structure flexibility,^57,58 ligand flexibility,⁵⁹ a new atom:atom pair potential,⁶⁰ and the KMTISM molecular solvation model.⁶¹ Recently, in collaboration first with the Merz research group at Michigan State University and then with the Zheng research group at Wuhan University of Technology and building off our previous efforts in computational chemistry^5,9,10,62 and X-ray crystallography,⁶³⁻⁶⁵ we reimplemented the MT method in an package for deployment in industrial/commercial pharmaceutical research and drug discovery. This implementation has expanded on the original approach through greater speed and stability, improved usability, integration with third-party software packages and graphical user interfaces for execution of standard virtual screening protocols, and support for additional “built-in” and “user-supplied” atom:atom pair potentials in order to support more chemical environments. In present work, we report this MT free energy estimation implementation using this new software package through the treatment of two validation benchmarks: (1) the industry-standard Comparative Assessment of Scoring Functions (CASF-2016) set, which contains 57 protein targets and 285 ligands, was utilized to validate the robustness of the MT protocol across a broad range of protein classes, and (2) a set of 10 protein targets with a total of 248 ligands was selected from the PDBBind database in order to further explore MT performance in virtual screening tasks targeting large-ligand structural diversity for individual receptors. This work primarily focused on validation of rigid- and semirigid-receptor/flexible-ligand MT, which is likely better suited to structures that show smaller structural movements upon binding. However, in the last paragraphs of the paper, we discuss next steps with the method as we expand on its capabilities for greater receptor flexibility, including support for MD snapshots/trajectories, loop and rotamer sampling, and so on.

Methods

Traditionally, configurational energy state sampling for a macromolecule (e.g., a protein or protein:ligand complex) is extremely computationally expensive because of the all-atom flexibility that must be employed. Coupling all-atom atom:atom pairwise interaction calculations with sampling results in a huge computational cost. It is not unusual for MD simulation methods—which are used for this purpose—to require hundreds or even thousands of CPU hours to complete, often relying on the use of specialized hardware like Anton⁶⁶ or repurposed GPU cards⁶⁷⁻⁶⁹ to make the simulations more tractable for routine application. To address this molecular energy state sampling expense, the MT method employs the assumption that given a reasonable molecular sampling volume for an NVT ensemble, the molecular partition function can be approximated as the product of the atomic partition functions. The MT method therefore postulates that within a volume of motion, each atom possesses an independent potential energy distribution. The purpose of this approximation is to treat each of the sampled molecular energy states as an independent numerical integration for each atomic partition function in order to estimate the molecular free energy.

Numerical Integration of the Atomic Energy Ensembles

Using one or more end-state conformations of a receptor:ligand complex, for all of the atoms in the structure, the method samples an identical amount of motion by generating atom:atom pairwise Boltzmann factors using discrete pairwise distance values within a given range. Therefore, the energy of an atom (e.g., atom α) is divided into pairwise interactions between atom α and each of the other atoms in the complex (e.g., atom i). In this model, the ensemble of α:i atom:atom pairwise energy states within that range is captured using the Boltzmann factor vector V_αi depicted in eq 1:

1

in which τ_αi⁰ corresponds to the initial coordinates of atom pair α:i in the input structure (or structures) and Δτ represents a single unit or component of variation with a sampling range (±nΔτ) of n discrete states. V_αi is a set of Boltzmann factors of atom pair α:i, and for each pairwise contact including atom α, these sets can be modeled as V_αj, V_αk, V_αl, and so on.

The pairwise Boltzmann factors corresponding to the sampled atom:atom pairs in the structure are combined, leading to a local partition function for each atom α that contains a large number of energy states. It would be extremely time-consuming to generate all of the available states with respect to a single atom α. Furthermore, this expense would be compounded when all of the atoms in the molecule are likewise treated in order to calculate the overall molecular free energy. Instead, by the use of the following method, the Boltzmann factors for different atom:atom pairwise contacts are treated independently, and we calculate the local partition function for each atom without creating the entire set of configurations. Equation 2 depicts the sum of the energy states of atom pair α:i,

2

and per the distributive property, multiplication of ε_αi and ε_αj yields the sum of all energy states for atom α combining α:i and α:j contacts (eq 3):

3

When each atom:atom pairwise contact energy is treated independently, eq 3 represents all of the conformational energy states of atom α for a molecular system with atoms α, i, and j. Calculation of the left-hand side of eq 3 through the multiplication of ε_αi and ε_αj saves the trouble (and time) of sampling all of the (2n + 1)² configurational states for the triatomic system. Following this procedure in a molecular system with N atoms, multiplication of sums for N – 1 pairwise contacts pertaining to atom α is performed, yielding a free energy ensemble of atom α for an N-atom molecular system including atom α (eq 4):

4

where ε_α is the local partition function within the range of motion between atom α and each of the atoms in the molecular system. Then, given the range of motion for each atom, the local partition functions for all of the atoms in the system are multiplied to generate the molecular energy-state ensemble (eq 5):

5

Using eqs 1–5, the MT calculation collects a molecular energy-state ensemble centered on an initial molecular conformation, combining term-by-term entries of all the atomic pairwise configurational vectors as in eq 1.

Up to this point, we have applied a numerical protocol for fast estimation of the molecular local energy-state ensemble. However, such an approximation brings in a key source of error to the molecular free energy estimation: because an N-particle system under the 3N – 6 degrees of freedom does not support the random “mixing and matching” of particle pairwise distances of all the N(N – 1)/2 particle pairwise contacts in the system, unphysical energy states would be introduced into the molecular partition function calculation (e.g., ε_α × ε_β). This situation is illustrated in Figure 1, which depicts an N-atom molecular system and a group of randomly selected atom pairwise distances that may not support a valid three-dimensional (3-D) molecular structure. In this situation, the number of degrees of freedom of the atomic pairwise distance ensemble R_ij is dependent on the number of degrees of freedom of the atomic coordinate ensemble X_i. In the following paragraphs, we use italic uppercase letters to represent a group of variables in which a variable vector (e.g., R_ij) captures a certain set of atomic pairwise distances including all pairwise contacts in the molecular system. In this discussion, we use bold-italic uppercase letters to represent a group of variable vectors in which a vector ensemble (e.g., R_ij) captures the ensemble of atomic pairwise distance sets in the molecular system.

Figure 1.

The number of atomic pairwise distance degrees of freedom of R_ij is dependent on the number of atomic coordinate degrees of freedom of X_i. Assuming a four-atom molecular system, a group of randomly assigned atomic pairwise distances R_ij may not be able to construct a valid 3-D structure. As shown in this figure, there is no location for atom A to satisfy r_α, r_β, and r_γ at the same time given the set R_ij.

Introducing the calculation protocol using eqs 1–5 on the one hand significantly increases the speed for calculating the molecular energy ensemble . On the other hand, use of these equations introduces unphysical energy states into the molecular energy ensemble by including invalid R_ij sets. Therefore, the collection of Boltzmann factors, V_αi, contains the ±nΔτ sampling range shown in eq 1, and the total number of energy states (including both physical and unphysical states) sampled in is

6

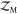where CN is the total number of atomic pairwise contacts. We know that in molecular systems, the number of unphysical energy states increases as the sampling range (±nΔτ) grows. In order to address this error in the calculation, we studied the number of degrees of freedom of R_ij and compared it with the number of sampled energy states (SS) in the numerical calculation procedure. In this way, we selected a reasonable V_αi to balance the calculation accuracy and the sampling range of the molecular energy states.

Derivation of the Number of R_ij Degrees of Freedom, V_ind

We applied the following procedure, summarized in Figure 2, for modeling V_ind, the number of R_ij degrees of freedom in an N-atom molecular system. Consider an “alchemical” molecular model with N atoms divided into two regions: (1) the explicit region, where each atom contacts all of the others, and (2) the background region, in which atoms come into contact only with the atoms in the explicit region and do not contact other background atoms. We place all of the atoms into the background region first and then move them one by one into the explicit region so that we can explain the modeling of the atom pairwise contact degrees of freedom in a step-by-step manner.

Figure 2.

Illustration of the procedure for deriving V_ind, the number of degrees of freedom of the atomic pairwise contacts given the total number of atoms, N, and the common distribution range for all the atomic pairwise distances, V_c. For the example shown, a closed system with five atoms (with the blue circle as the volume boundary), the gray spheres represent the atoms in the background region with no pairwise contacts among them, and the red spheres represent the atoms in the explicit region for which the atomic pairwise contacts are taken into account. The blue dotted arrows represent new atomic pairwise contacts added to the system when one atom is moved from the background region to the explicit region. The black solid lines in each subfigure represent a set of atom pairwise contacts with certain combinations of pairwise distances selected from the degrees of freedom before a new atom is moved from the background region into the explicit region.

Step 1. When the first atom, α, is placed into the explicit region and the other N – 1 atoms are left in the background region, we have N – 1 atom pairwise contacts all centered at atom α. In this case, V_ind can be modeled as V_c^N–1, where V_c is the distance distribution range of every α:i (explicit-atom:background-atom) atomic pairwise contact. According to the aforementioned MT sampling procedure, V_c is equal to the ±nΔτ MT sampling range in eq 1.

Step 2. When the second atom, β, is placed within the explicit region, V_ind from step 1 is multiplied by (4π)^N−2, meaning that on top of every molecular conformation generated in the first step (a set of R_α–i with certain combinations of α:i distances), the number of degrees of freedom increases by rotation of atom β in a sphere centered at atom α when including the distance vector ensemble R_β–j. Here R_β–j represents all possible combinations of the β:j contact distances, where j indicates any of the N – 2 atoms in the background region at this stage. Hence, we have V_ind = V_c^N–1(4π)^N−2 at this stage of the derivation.

Step 3. Similarly, when a third atom, γ, is moved into the explicit region, the number of degrees of freedom increases by a factor of (2π)^N−3. Therefore, given a fixed set of R_α–i and R_β–j, both selected from the V_c^N–1(4π)^N−2 degrees of freedom, 2π degrees of freedom are added for each γ:k contact by letting atom γ rotate around the axis defined by the vector from atom α to atom β, where k indicates any of the N – 3 atoms in the background region at this stage. This leads to V_ind = V_c^N–1(4π)^N−2(2π)^N−3.

Step 4. When a fourth atom, δ, is moved into the explicit region and the new atom pairwise contacts regarding atom δ are taken into account, no extra degrees of freedom are added to V_ind. This is the case because on top of every set of R_α–i, R_β–j, and R_γ–k, when any δ:l pairwise contacts are taken into account (where l indicates any of the N – 4 atoms left in the background region at this stage), no movement degrees of freedom for either atom δ or atom l are allowed given a set of δ:α, δ:β, and δ:γ distances and a set of l:α, l:β, and l:γ distances selected from the degrees of freedom modeled in steps 1–3. From this point forward, no more degrees of freedom are added to V_ind when new atoms are moved from the background region to the explicit region. Therefore, no extra degrees of freedom of the atomic movement are allowed beyond the those included in V_ind from steps 1–3. Assuming equivalence among atoms with regard to the order of moving any three atoms into the explicit region, we complete the model by multiplying by the number of combinations of N atoms taken three at a time, as shown in eq 7:

7

In an N-atom molecular system, the total number of atoms, N, and the total number of atomic pairwise contacts, CN, are mutually transformable using the following equations:

8

and

9

In the following procedure, we express N in terms of CN using eq 9 and replace 2nΔτ with V_c to make SS in eq 6 and V_ind in eq 7 comparable, yielding eqs 10 and 11:

10

11

Using eqs 10 and 11, we can compare the distribution of SS, i.e., the total sampled number of atomic pairwise contact energy states (including both physical and unphysical states), and the distribution of V_ind, i.e., the number of atomic pairwise contact degrees of freedom. Through this approach, we can determine a reasonable V_c to cover a fair range of molecular energy states in and limit the number of unphysical states included in the 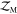calculation. Since both SS and V_ind grow exponentially as V_c increases, we use the logarithmic forms of their distributions in order to better compare them in Figure 3. Given a CN in the molecular system, ln(SS) grows faster than ln(V_ind) and soon surpasses it at the crossover point, V_c^x, as the atom:atom pairwise sampling range increases. For V_c < V_c, ln(SS) is smaller than ln(V_ind), showing that the number of sampled states from the MT procedure is smaller than the number of actual molecular energy states within the atom:atom pairwise sampling range. On the other hand, as the atom:atom pairwise sampling range increases beyond V_c^x, ln(SS) contains more states than ln(V_ind), and this is the point at which the MT procedure becomes contaminated by the unphysical states generated from the numerical integration. As depicted in Figure 3, the crossover point, V_c, gradually approaches 1 Å from 2.05 Å as CN increases from 100 to 10⁶. Therefore, in this study, we set the default MT atomic pairwise sampling range to 1 Å for all calculations to avoid significant contamination of the free energy calculation by the introduction of unphysical states into the MT procedure. With a fixed V_c for the atom:atom pairwise sampling range, SS for the number of MT sampled energy states, and V_ind for the number of actual energy states, we applied a Monte Carlo integration to approximate the molecular local partition function:

12

Figure 3.

Distributions of ln(SS) and ln(V_ind) as functions of the atomic pairwise sampling range V_c given different CN values of the molecular system. The crossover point V_c^x approaches 1 Å as CN increases.

In summary, with the MT protocol, we utilize a sampling range (±nΔτ) for every atom:atom pair in a molecule or complex, and then we calculate an ensemble of atomic energy states using eqs 1–4. The local partition function is then approximated first by combining these atomic energy ensembles using eq 5 and then by using the Monte Carlo integration procedure as shown in eq 12. Through this method, a local energy ensemble corresponding to a single initial “end-state” 3-D molecular conformation can be quickly calculated and converted into a local partition function.

In order to improve the method further, we know that free energy estimation relies on thorough molecular conformation sampling. Therefore, multiple end-state conformations can be provided to the MT method, where each end-state conformation can be viewed a representative or hypothetical landscape minimum, as discussed in the review by Mobley and Dill.²¹ This ensemble of poses is then combined to better capture larger-scale or “global” molecular movements. By feeding the MT protocol with multiple end-state conformations (i.e., N_end-states), the MT local partition function protocol can further enlarge the sampling space and better approximate the molecular partition function:

13

When applying the MT procedure to a protein:ligand complex system to estimate the binding free energy, we calculate partition functions for the bound-state protein:ligand complex and all of the unbound-state motifs. Each local partition function for the bound-state protein:ligand complex is calculated using the MT procedure (eqs 1–12) against the significant protein:ligand binding modes provided by executing the docking module from the software package or from the users’ sources. By the use of eq 13, the protein:ligand complex partition function, 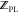, is calculated as

14

In the present work, we added support for unbound- and bound-state structural motifs, including an apo protein conformation, multiple free-state ligand conformations, and multiple holo-protein:ligand conformations. Since a full-scale protein simulation requires significant computational cost, where noted we used induced-fit docking to collect multiple holo-protein:ligand conformations. Therefore, in addition to the calculation of 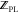with eq 14, the protein local intramolecular partition function, , was calculated for a number of apo protein conformers, N_{P conformers}, using eq 15:

15

where N_{P conformers} = 1 corresponds to the X-ray model (sans ligand). With this technology available, in subsequent work we will explore the use of multiple X-ray, NMR, or theoretical models for both the apo protein and the holo-protein:ligand conformations. Finally, the free-state or unbound ligand conformations are generated using the small-molecule conformational search module, MT_CS, which is discussed in detail in a previous work.⁵⁹ MT_CS constructs and characterizes N_{L conformers} ligand conformations, and the local partition functions for those ligand conformations are calculated and grouped using eq 16:

16

With 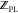, , 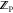and 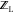available, the binding free energy change is then estimated using the ratio of partition functions in the bound and free states as per eq 17:

17

The above-noted multiple-end-state protocol represented by eq 17 is denoted as MT_ScoreE, in which the “E” denotes an ensemble of one or more end-state holo-protein:ligand conformations, apo protein conformations, and unbound ligand conformations. In addition to this more complete workflow, a simplified MT protocol was also implemented that uses a single end-state protein:ligand complex in a “minimum energy” conformation. Since this approach, which we name MT_ScoreES, where “ES” denotes the calculation against a single end-state protein:ligand 3-D complex, is based on a single accurate conformation and does not require docking or other simulation processes to generate, it is faster than MT_ScoreE and could therefore be better positioned for higher-throughput virtual screening tasks. Because MT_ScoreES utilizes only the intermolecular atom:atom pairwise potential calculation between the protein and the ligand, the binding free energy is then approximated as

18

where 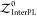is the protein:ligand complex pose’s local partition function considering only the intermolecular atomic pairwise interactions.

Ligand Binding Mode Preparation and Scoring

In the DivCon Discovery Suite v.DEV.671-b4608, we provide two empirical energy functions: the GARF statistical potential⁷⁰ and the AMBERff14 functional potential^63,71 optimized for the MT method. The holo-protein:ligand complex binding modes can be either generated using the “built-in” MT_Dock protein:ligand docking module⁵⁵ or provided from other sources such as molecular simulations or alternative protein:ligand docking protocols. In order to compare the MT protocol performances with different settings, we applied both the GARF potential function and the AMBERff14 force field for the partition function calculation, and we used both MT_Dock and the industry-standard Molecular Operating Environment (MOE) v.2019.0102 from Chemical Computing Group, Inc. to generate contrasting protein:ligand complex poses. For MT_Dock and optionally for the MOE interface (in the “three-step workflow” discussed below), ligand conformers were generated using MT_CS.⁵⁹ The MT_CS method was used in all cases to calculate the unbound 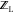partition function. Figure 4 depicts a flowchart to aid in understanding how the various MT parts work together (and with third-party methods) to complete and generate the MT scores.

Figure 4.

Overall flowchart of the MT method and its [optional] interactions with other software and methods. Generally, input is provided in the form of a prepared PDB and/or mol2 file for the target and ligand (a molecular selection language is provided in cases where these species are supplied in a single file). SDF files are used throughout to communicate docked poses or conformers as needed. Note: “nexus points” (shown in green) are provided for each MT step into which a user may optionally supply an externally prepared SDF file. These SDF files are only used when a third-party package such as MOE or GLIDE is used for docking and/or conformer generation. When MT_Dock is chosen as the docking function, all of the conformers and poses are communicated internally within the MT software and its associated data structures.

MT_Dock Configuration

Beginning with the aforementioned MT_CS conformers, each of the top five lowest-energy conformers was placed multiple times within the crystallographic X-ray structure using the heatmap-based MT_Dock method reported by Zheng et al.⁵⁵ Each ligand binding mode was optimized within the active site using the torsion optimization method discussed by Fuhrmann et al.,⁷² and the top 25 scored poses according to MT_ScoreES were kept for inclusion in the MT_ScoreE calculation. All of the MT calculations were performed with DivCon Discovery Suite v.DEV.671-b4608 using default settings with a pocket size of 8.0 Å around the ligand (union between all poses) and a nonbonded interaction cutoff of 11.0 Å. Both the MT-GARF (-h garf) and MT-AMBER (-h amberff14) pair potentials were considered for this study.

MOE Docking Configuration

The calculation of MT_ScoreE (the ensemble MT_Score) can be performed using either internally docked poses from MT_Dock or externally provided ligand poses (e.g., in the case of rigid-receptor docking) or protein:ligand poses (e.g., in the case of induced-fit-receptor docking) generated by third-party software tools. In order to demonstrate the generalizability of the method, we focused on rigid-receptor and induced-fit-receptor docking as implemented in MOE v2019.0102 using the qbDockPair.svl Scientific Vector Language (SVL) script found in the DivCon Discovery Suite package. The AMBER10 potential coupled with atomic charges and ligand parameters calculated using extended Hückel theory (Amber10:EHT) as implemented in MOE was used for all of the MOE-based calculations. Beginning with each PDB protein:ligand complex, protons were added, and their positions were optimized using Protonate3D.⁷³ The default Protonate3D settings of 7, 300 K, and 0.1 mol/L for pH, temperature, and ion concentration (salt), respectively, were chosen, and all of the atoms were allowed to flip, so some His, Asn, and Gln residues may have “flipped” during the protonation process (see the Supporting Information for all of the prepared structures used in this paper). When this basic preparation was completed for each structure, docking was executed using both the rigid-receptor docking and induced-fit docking refinement protocols.

For the MOE-based workflow, input conformers were generated two different ways: (1) in the conventional “three-step” protocol, MT_CS-generated conformers were provided as input to the MOE docking function (i.e., MT_CS → MOE → MT_ScoreE), and (2) in the new “two-step” protocol, MOE’s built-in conformer generator was used (i.e., MOE → MT_ScoreE). The three-step protocol uses MT_CS in order to generate ligand conformers that exist on the ligand free energy surface with the chosen pair potential (e.g., MT-GARF or MT-AMBER) and to calculate the unbound partition function. The five most energetically favorable conformers were chosen and passed to the MOE docker, which docks each conformer semirigidly (some in-dock optimization is performed, but bond rotations and rotamer flips are kept to a minimum). In selecting between these two conformer generation methods (two-step vs three-step), the benefit of the three-step method is that ligand poses are guaranteed to exist on the energy surface. The drawback is that the docker is limited to the conformers generated by MT_CS even if they do not properly fit the active site. The two-step protocol skips the initial MT_CS step for conformer generation, and the docker’s built-in method (or another method of the user’s choosing) is used both to generate the conformers of interest and to dock those conformers in the active site. This mode may be more accommodating to alternative binding mode selection in cases where the bound ligand pose deviates significantly from the MT_CS conformers. However, as we will show in the Results and Discussion, there are times when its prediction profile is inferior.

When conformers were generated—either internally within MOE or externally using MT_CS—initial docking placement was performed using the Triangle Matcher approach, and the London dG score and the generalized Born volume integral/weighted surface area (GBVI/WSA) dG score function⁷⁴ were used as the initial score and the final filter, respectively. The 250 poses provided by Triangle Matcher were optimized with the chosen refinement method (i.e., rigid-receptor/minimized-ligand or induced-fit-receptor/minimized-ligand) using AMBER10:EHT as implemented in MOE, and 25 poses were finally passed to MT_ScoreE as landscape minima for scoring. All of the MT calculations were performed using DivCon Discovery Suite v.DEV.671-b4608 using default settings with a pocket size of 8.0 Å around the ligand (union between all poses) and a nonbonded interaction cutoff of 11.0 Å. Both the MT-GARF (-h garf) and MT-AMBER (-h amberff14) pair potentials were considered.

Leave-One-Out Analysis

Leave-one-out cross-validation (LOO) is the statistical cross-validation method that leaves one data point (an observation) out of the data set and calculates the fit on the rest of the data in order to generate a prediction for the observed point. This process is repeated n times, where n is equal to the number of ligands in each target set, leading to n predictions. Each time the omitted value, y_i0, is predicted, the predicted residual, ε_i = y_i – y_i0, is computed. Likewise, the mean unsigned error (MUE) is computed from the predicted residuals according to eq 19:

19

The reported mean Pearson R value is calculated according to eq 20 and is a result of this process since by definition with n correlations we are able to calculate n values of R:

20

Finally, the error bars in the figures and reported in the tables are constructed as vertical or horizontal lines defined for each point in the range [R – MAD(R), R + MAD(R)] (for R plots) or [MUE – MAD(MUE), MUE + MAD(MUE)] (for MUE plots). Instead of using the standard deviation (SD) to represent the spread of the data, we employ the median absolute deviation (MAD),⁷⁵ which is a robust measure of the spread of data around the median:

21

where X_i represents a data point and X is the array of data. The diagonal on the graph is defined as a line that passes through the points (0, 0) and (1, 1). The distance from the diagonal (DfD) for the point P(x, y) is defined as

22

If DfD > 0, then the point is above the diagonal. Conversely, if DfD < 0, the point is below the diagonal. The squared sum of DfD (SSDfD), given by

23

is computed separately for points above and below the diagonal and is a quantitative measure of such a deviation for the set.

Results and Discussion

We utilized two validation sets to challenge the MT method for its robustness against a broad range of protein:ligand complexes and to test its consistency against different configurational state sampling protocols at various stages of the MT free energy estimation workflow. The first set consisted of the Comparative Assessment of Scoring Functions (CASF) protein:ligand scoring benchmark containing 57 protein targets with 285 ligands, which was first introduced with large diversity for both ligand and protein structures.⁷⁶ The second set consisted of 10 protein targets with 248 corresponding ligands selected from the PDBBind⁷⁷ v2019 database to study the performance of the MT protocol for screening of different ligand structures against particular receptors.

Comparative Assessment of Scoring Functions: The CASF-2016 Benchmark

The CASF benchmark consists of 57 target classes with five X-ray crystallographic structures for each target, yielding 285 target:ligand pairs. While there are some recognized deficiencies with some CASF-selected X-ray models, as a whole the set provides a reasonable cross section of the types of chemistry often observed in pharmaceutical research, and it has become an “industry standard” benchmark. Some curation was performed prior to commencement of the project. Specifically, since macrocycles are not supported by the method at this time, target cases that include macrocyclic ligands were removed. Likewise, cases that include large ligands (with more than 25 rotatable bonds) were removed from the set. This curation yielded 51 complete protein target class subsets (5 × 51 = 255 structures), and an additional 20 structures were rescued from the remaining six sets to give a total of 275 out of 285 PDB structures. Figure 5 is provided as a baseline comparison of MT-GARF and MT-AMBER showing that the two pair potentials are equally predictive in these cases.

Figure 5.

Comparison of Pearson R values and LOO MUEs between the GARF and AMBERff14 energy functions using MT_ScoreE (ensemble scoring with MOE rigid-receptor/minimized-ligand docked poses) and MT_ScoreES (end-state scoring with X-ray poses) depicting general agreement between the two methods. (A) Pearson R values for the AMBERff14 and GARF energy functions through the MT_ScoreES calculation. (B) MUE values for both potential functions through the MT_ScoreES calculation. (C) Pearson R values for the AMBERff14 and GARF energy functions using the MT_ScoreE protocol. (D) MUE values for the AMBERff14 and GARF energy functions using the MT_ScoreE protocol. Table 1 provides a detailed numerical rundown of all cases.

Comparison of MT_ScoreES (End-State Score) and MT_ScoreE (Ensemble Score)

Traditionally, when the drug discovery process is considered, a critical goal is the determination of the experimental binding affinity of one or more lead compounds. With structure-based drug discovery, we wish to do so ideally prior to synthesizing the compound in the laboratory. This relationship between structure and function necessarily creates a “chicken versus egg” conundrum since the only way to experimentally determine binding is to synthesize potential compounds that may never bind. Likewise, predictive methods generally require reasonable compound binding modes in order to predict binding free energies, and these predicted binding free energies can vary significantly depending on the accuracy of the binding mode. X-ray crystallography is often used once a compound has been synthesized in order to provide an understanding of how a compound binds within the active site so that we may use that knowledge to inform the search for new lead compounds. However, X-ray crystallography is not an inexpensive process, and in a perfect world one would like to obtain an accurate understanding of binding affinity with less expense. Since MT_ScoreE incorporates multiple binding modes, in the first validation we used the “two-step” (MOE → MT_ScoreE) rigid-receptor docking protocol. Upon completion of the MOE-based docking process, these new bound-ligand poses were scored with MOE’s built-in GBVI/WSA dG score in order to choose the top 25 bound-ligand poses to pass to MT_ScoreE (which were provided in SDF format).

Because all of the compounds in CASF have published X-ray models, we are able to compare the ensemble score generated using the chosen docking method to the end-state score calculated using the X-ray pose. Figure 6 depicts the MT_ScoreE versus MT_ScoreES results from the CASF benchmark for both AMBERff14 and GARF (note: for clarity, Table 1 provides a detailed rundown of all of the Pearson R and LOO MUE results from the CASF benchmark as a function of atom:atom pair potential, scoring routine, and pose generation method used). With a Pearson R_MTScoreE versus R_MTScoreES correlation with R² > 0.95, we clearly observe that end-state scoring (MT_ScoreES) using crystal models as the input generally converges with ensemble scoring (MT_ScoreE) using the MOE docker with either potential function. These results suggest that given accurate structures, MT generally exhibits convergence between MT_ScoreE (with thorough computational sampling against the molecular configuration space) and MT_ScoreES (with experimentally determined crystal poses). Furthermore, given the possibility that X-ray models (like any model) may be incorrect or may give an incomplete picture of the binding mode(s) available to the ligand, it is possible that MT_ScoreE is able to make up for deficiencies in the structure through the wider range of configurational sampling afforded by the ensemble score. An example of such a case is depicted in Figure 7. For JAK2 kinase (PDB ID 4HGE) from the CASF benchmark, the additional landscape minima (docked poses) provided by the MOE-based rigid-receptor/optimized-ligand docking routine led to the improved predicted versus experimental Pearson R value observed in Figure 6C and detailed Table 1 for JAK2 for MT_ScoreE (Pearson R_MTScoreES = 0.88 ± 0.01 vs R_MTScoreE = 0.95 ± 0.00). This observation fits with our expectation for free energy methods since we know that binding is a product of many poses and not just the one represented by a single crystal model.²¹

Figure 6.

Comparison of Pearson R values and MUEs between MT_ScoreE (ensemble scoring with MOE rigid-receptor/minimized-ligand docked poses) and MT_ScoreES (end-state scoring with X-ray poses), in which we see convergence between the approaches. (A) Pearson R values and (B) MUE values for the AMBERff14 energy function through the MT_ScoreES and MT_ScoreE calculations. (C) Pearson R values and (D) MUE values for the GARF energy function through the MT_ScoreES and MT_ScoreE calculations. Table 1 provides a detailed numerical rundown of all cases.

Table 1. Detailed Comparison of the Predictive Capabilities of MT_ScoreES (End-State Score) and MT_ScoreE (Ensemble Score) and the Relative Predictive Capabilities of the Two Pair Potentials with Different Pose Generation Protocols.

^aAll of the MUE values are given in kcal/mol and were obtained from the LOO analysis.

Figure 7.

Example illustration of the top three scored poses (shown in green) and the X-ray pose (shown in default gray) within the active site of JAK2 kinase (PDB ID 4HGE) from the CASF set. The additional end-state (landscape minima) sampling provided by MOE-based rigid-receptor docking leads to an improved MT_ScoreE result vs the MT_ScoreES score of the original X-ray pose alone.

Comparison of the “Three-Step” and “Two-Step” MT_ScoreE Protocols

Next, we considered the impact of using MT-generated ligand conformers compared with using the conformers generated by the docking software (in this case MOE). As discussed in Methods, MT_CS generates an ensemble of ligand conformers to be used to determine the unbound-ligand partition function 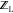.⁵⁹ This step is performed regardless of how the ensemble score is calculated; however, one may choose to pass the top five (or more) MT_CS unbound-ligand conformers to the docking function and use these conformers instead of those generated by the chosen docking function. For our analysis, we selected five conformers from MT_CS in order to balance sampling thoroughness with efficiency. Since each conformer is used as an initial configuration for five binding modes (5 conformers × 5 poses = 25 binding modes), the computational time grows in O(n) fashion as the number of conformers increases. Introducing additional conformers would cover more configurational space during binding mode sampling, but other than the significant states, additional sampled protein:ligand complex configurations contribute little to the final partition function. Table 2 shows that the impact of this choice is generally small, and one can expect a limited return on one’s investment for larger numbers of conformers. Likewise, as shown in Figure 8, when one considers the “best” conformer count for each target class versus the default count (5), the impact is relatively small with a few outlier cases.

Table 2. Impact of the Number of Chosen Conformers on the Overall Predictability of the Method.

no. of conformers	overall Pearson R
5	0.64
10	0.64
15	0.64
20	0.63
25	0.63

Figure 8.

When exploring the impact of the MT_CS conformer count in the “three-step” protocol, we consider the “best” conformer count vs the default conformer count (5) for each target class. The color of each target class corresponds to the minimum number of conformers needed to generate this best or most predictive set of scores. The classes in blue correspond to the default conformer count (5), while the red, cyan, magenta, and green classes correspond to calculations with 10, 15, 20, and 25 conformers, respectively.

The benefit of this approach is that the unbound-ligand conformations and the bound-ligand poses will not diverge appreciably from one another and will be within the same radius of convergence (since the docking process includes only placement and a localized structural minimization of the ligand within the field of the pocket). However, one could imagine some potential drawbacks of using these conformers, as there could be times when MT_CS may choose conformers that will not “fit” the active site or there could be incompatibilities between the conformer generation algorithm and the chemistry of the ligand (i.e., every method has strengths and weaknesses, and often one may want to “mix and match” different conformer generators). Therefore, some dockers could be better able to generate conformers for the ligand chemistry in question. When the three-step (MT_CS → MOE → MT_ScoreE) workflow was executed on the CASF benchmark as depicted in Figure 9, these two approaches were also highly correlated, giving Pearson R_2-step versus R_3-step correlations with R² > 0.95 for both potentials. However, there are several outliers that make the three-step workflow worth considering in one’s protocol (especially if the two-step workflow is not predictive enough for one’s purposes). In particular, CDK2, elongin, and especially COMT (in GARF) and ITK (in AMBERff14) all yield better predictions (as measured by higher Pearson R values) with the three-step protocol.

Figure 9.

Comparison of the two-step (MOE → MT_ScoreE) and three-step (MT_CS → MOE → MT_ScoreE) protocols, showing that generally these methods are highly correlated, with Pearson R_2step vs R_3step correlations with R² = 0.98 and 0.97 for (A) AMBERff14 and (B) GARF, respectively.

Impact of Induced-Fit-Receptor Docking on the Prediction Characteristics

For the GARF potential, intramolecular protein:protein interaction terms (eq 15) were added to the software in order to increase the accuracy of the MT approach and support a wider range of target structures and mechanisms. In order to explore the impact of these terms, we used induced-fit-receptor-docked ensembles as generated using the MOE platform. As depicted in Figure 10, while the deviations below the diagonal have a larger sum of squares than those above (suggesting that induced-fit-receptor docking is slightly less predictive than rigid-receptor docking in general), most of the shifts above or below the diagonal are quite small. However, there are several cases below the diagonal where induced-fit-receptor docking is more predictive. In these cases, as reported in Table 1, MTA/SAH went from 0.55 ± 0.10 in the rigid-receptor protocol to 0.71 ± 0.01 in the induced-fit-receptor approach, ITK went from 0.55 ± 0.10 to 0.69 ± 0.06, and Factor Xa went from 0.54 ± 0.07 to 0.67 ± 0.08, suggesting that while the method generally shows a similar predictive profile, there are cases where the method is more predictive. Many reasons could cause an improvement in R when a different docking strategy is used. One possible reason is the tight binding sites in these test cases brought difficulties for the rigid-receptor docking protocol in generating the global-minimum bound states. When looking at the crystal complex structures, we found that all of the ligands for the MTA/SAH subset were closely surrounded by the binding site residues as in their binding modes. Furthermore, two test cases in the ITK subset (PDB IDs 4RFM and 4M0Z) were in a similar situation, and the ligands were tightly “wrapped up” by the surrounding receptor residues in the complex crystal structures. Finally, in the Factor Xa subset, ligands were placed deep into cavities at the receptor’s binding site, where rigid docking strategies inevitably have difficulties fitting the ligand into the tight binding sites while avoiding steric clashes. These results are generally congruent with the literature, which has shown that induced-fit-receptor docking and induced-fit-receptor docking coupled with MD often yield improved predictions (versus rigid-receptor docking) for Factor Xa^78,79 and ITK.⁸⁰⁻⁸²

Figure 10.

Comparison of (A) Pearson R and (B) MUE values for rigid-receptor docking and induced-fit-receptor docking. The Pearson R_{rigid-receptor} vs R_induced-fit correlation has R² = 0.98, clearly indicating that the two methods are highly correlated, and one can generally rely on the lower-cost rigid-receptor method. Furthermore, most of the LOO MUEs are better than 1 kcal/mol for both methods.

Impact of Pose Count on the Results

Preparation of landscape minima is a critical aspect of the MT workflow. When poses provided by an external docking function (in this case MOE) are used, the success of the ensemble score is as much a function of the MT method as it is a function of the docker in question. Therefore, in order to explore the settings necessary to maximize performance, we ran several “set ranges”, including 1–2, 1–5, 1–10, 1–15, 1–20, and the default 1–25, where the poses are ordered from best GBVI/WSA dG score to worst (i.e., range 1–2 would include the top two poses according to MOE, range 1–5 would include the top five poses, and so on). These results are detailed in Table 3. Generally, for the CASF benchmark (with five ligands per target class) coupled with the MOE docking function, the MT_ScoreE method proved to be extremely robust, and often two well-scored poses (according to GBVI/WSA) were as good as 25 poses. This observation is very encouraging since it would suggest that most of the success of the method is driven by the local partition function. However, there are cases in which the addition of poses yields improved results. For example, BRD4 moved from a reasonably predictive R² of 0.64 ± 0.05 when the top two poses were scored to R² = 0.94 ± 0.01 when the top 15 poses were included in the score. However, cases like CrtM, which went from R² = 0.62 ± 0.01 when five poses were scored to R² = 0.45 ± 0.14 when all 25 poses were scored, and MTA/SAH, which went from R² = 0.51 ± 0.08 when five poses were scored to R² = 0.34 ± 0.10 when all 25 poses were included, show that signal can be lost in the event that too many questionable poses are provided. This observation suggests that when the MT method is being challenged with a new project or target class, some retrospective experimentation with “knowns” may yield dividends when shifting to prospective campaigns.

Table 3. Impact of the Number of Poses Provided by MOE on the Predictive Capability of the MT_ScoreE (Ensemble Scoring) Method.

^aAll of the MUE values are given in kcal/mol and were obtained from the LOO analysis.

Computational Time Requirements of the DivCon MT Implementation

When the MT method was first published, it was notable not only for its predictive capabilities but also for its economical use of CPU time versus methods that rely on MD or alchemical “webs” of MD calculations for sampling. Those earlier MT implementations were based on a mixture of MATLAB, Python, and bash scripts, and even at that time these calculations were considered to be fast. With the new DivCon Discovery Suite (C++) implementation of MT, we can quantify the average ± MAD processor time on an older Intel Xeon E5440 2.83 GHz CPU running CentOS 7 for the 275 ligands in the CASF set, and we can break this time down into each step in the process: 1.0 ± 0.0 min/ligand for MT_CS ( calculation and ligand conformer generation), 12.4 ± 2.2 min/ligand for MOE (rigid-receptor docking with ligand pose optimization), and 9.6 ± 1.1 min/ligand for MT_Score (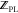 and 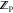calculation using a 25-pose ensemble). Since the calculation time for MT is measured in minutes on a standard CPU from 2008 and dynamics-based algorithms often require hours or even days to complete on specialized hardware (e.g., GPUs), the MT method would appear to be both economical and predictive.

The Homologous Protein Family (HPF) Benchmark

While the CASF benchmark was used to validate the MT method on a diverse set of targets, the Homologous Protein Family (HPF) benchmark introduced a series of homologous protein structures to demonstrate the performance of the MT method against a diverse set of ligands. As noted in Methods, both GARF and AMBERff14 atom:atom pair potentials were used, and two different docking programs (MOE and MT_Dock) were considered. As listed in Table S1 in the Supporting Information, 10 homologous proteins with 248 corresponding ligands were selected from the PDBBind v2019 data set: 3-dehydroquinate dehydratase (DHQD) with 22 ligands, 3-phosphoinositide-dependent protein kinase-1 (PDPK1) with 26 ligands, 14-3-3 protein (14-3-3η) with 12 ligands, acetylcholine receptor (AChR) with 38 ligands, α-l-fucosidase (FUCA-1) with 12 ligands, β-glucosidase (GBA3) with 22 ligands, biotin carboxylase (BC) with 13 ligands, protein kinase A (PKA) with 47 ligands, trypsin (Tryp) with 20 ligands, and dual-specificity phosphatase (DSP) with 36 ligands. In choosing the protein:ligand structures available in the PDBBind v2019 set, ligands having a molecular masses of <700 Da and macrocyclic structures, against which the current version of the MT_CS program cannot perform conformational search, were skipped. As with the CASF benchmark, we used the protein:ligand conformations from the crystal structures as the end-state input structures for the MT_ScoreES calculations, and for MT_ScoreE the MOE-based two-step (MOE → MT_ScoreE) protocol and the MT_Dock protocol (MT_CS → MT_Dock → MT_ScoreE) were compared and contrasted.

Using the MT_ScoreES protocol on the X-ray protein:ligand pose for each structure, both the AMBERff14 force field and the GARF energy function generated good correlations with the experimental binding affinities: the Pearson R coefficients for both functions were higher than 0.5 for all of the protein sets except for PDPK1, which exhibited Pearson R values of 0.30 ± 0.01 and 0.34 ± 0.01 for AMBERff14 and GARF, respectively. Conversely the DSP set, with 36 ligands, exhibits very high and robust Pearson R values of 0.85 ± 0.00 and 0.84 ± 0.00, respectively, for the two potentials considered. When we consider the LOO MUEs, all of the sets exhibit errors that are less than 1.0 kcal/mol using either potential. By comparing the Pearson R and MUE values in Table 4 for all 10 protein test sets, we found that the two potentials were in good agreement when the binding affinities were evaluated against the crystal structure binding modes using the MT_ScoreES protocol.

Table 4. Values of Pearson R and MUE between the Experimental and Predicted Binding ΔG Values for MT_ScoreES and MT_ScoreE Calculations Performed with the DivCon Discovery Suite with the MovableType (MT) Module with Configurational Energies Evaluated Using the AMBERff14 and GARF Energy Functions.

MT-AMBERff14
	MTScoreES				MTScoreE
	1 X-ray pose				25 MOE poses/PDB				25 MTDock poses/PDB
	mean R		MUEa		mean R		MUEa		mean R		MUEa
14-3-3η	0.78	±0.01	0.19	±0.05	0.69	±0.01	0.23	±0.05	0.77	±0.01	0.19	±0.05
DHQD	0.82	±0.00	0.40	±0.09	0.83	±0.00	0.39	±0.07	0.83	±0.00	0.36	±0.08
PDPK1	0.30	±0.01	0.44	±0.09	0.36	±0.01	0.43	±0.09	0.38	±0.01	0.42	±0.07
AChE	0.79	±0.00	0.51	±0.16	0.75	±0.00	0.54	±0.18	0.66	±0.00	0.61	±0.17
FUCA-1	0.75	±0.01	0.56	±0.15	0.77	±0.01	0.53	±0.15	0.74	±0.01	0.58	±0.14
GBA3	0.56	±0.01	0.34	±0.07	0.52	±0.01	0.35	±0.08	0.31	±0.01	0.39	±0.07
BC	0.61	±0.01	0.51	±0.09	0.59	±0.01	0.52	±0.11	0.63	±0.01	0.57	±0.12
PKA	0.66	±0.00	0.32	±0.07	0.65	±0.00	0.32	±0.08	0.64	±0.00	0.32	±0.08
Tryp	0.71	±0.00	0.41	±0.08	0.68	±0.00	0.44	±0.11	0.76	±0.00	0.44	±0.10
DSP	0.85	±0.00	0.40	±0.11	0.85	±0.00	0.40	±0.06	0.79	±0.00	0.44	±0.10

MT-GARF
	MTScoreES				MTScoreE
	1 X-ray pose/PDB				25 MOE poses/PDB				25 MTDock poses/PDB
	mean R		MUEa		mean R		MUEa		mean R		MUEa
14-3-3η	0.78	±0.01	0.20	±0.05	0.69	±0.01	0.23	±0.05	0.62	±0.01	0.27	±0.04
DHQD	0.83	±0.00	0.38	±0.07	0.83	±0.00	0.37	±0.07	0.79	±0.00	0.42	±0.08
PDPK1	0.34	±0.01	0.43	±0.09	0.37	±0.01	0.42	±0.08	0.61	±0.01	0.40	±0.09
AChE	0.81	±0.00	0.48	±0.10	0.77	±0.00	0.51	±0.13	0.81	±0.00	0.46	±0.12
FUCA-1	0.76	±0.01	0.55	±0.14	0.78	±0.01	0.51	±0.15	0.72	±0.01	0.64	±0.06
GBA3	0.55	±0.01	0.34	±0.08	0.52	±0.01	0.35	±0.08	0.77	±0.00	0.24	±0.09
BC	0.60	±0.01	0.52	±0.13	0.58	±0.01	0.52	±0.13	0.75	±0.01	0.40	±0.11
PKA	0.65	±0.00	0.32	±0.08	0.65	±0.00	0.32	±0.08	0.64	±0.00	0.32	±0.06
Tryp	0.72	±0.00	0.40	±0.09	0.68	±0.00	0.45	±0.10	0.65	±0.01	0.48	±0.09
DSP	0.84	±0.00	0.42	±0.08	0.83	±0.00	0.43	±0.06	0.67	±0.00	0.53	±0.14

^aAll of the MUE values are given in kcal/mol and were obtained from the LOO analysis.

With the MOE docking program, as shown in Figure 11 and Table 4, the AMBERff14 force field and the GARF energy function showed similar prediction accuracies. For both functions, the MT_ScoreE protocol generated better or comparable Pearson R coefficients and MUE values compared with the MT_ScoreES protocol against all protein sets, suggesting that—as with the CASF set—given “good” poses the methods converge well and the MT method itself is quite robust. On the other hand, with the MT_Dock module in the DivCon Discovery Suite, the AMBERff14 force field and GARF energy function showed different prediction accuracies against the 10 protein families. With AMBERff14 force field, the MT_ScoreE protocol had better or comparable Pearson R coefficients compared to the MT_ScoreES protocol against most of the protein sets, except for AChR and GBA3. With the GARF energy function, the MT_ScoreE protocol showed good ranking performance in all the protein sets, and it especially improved the Pearson R coefficients for the PDPK1 and GBA3 test sets. In a comparison of the MUEs, the AMBERff14 force field outperformed the GARF energy function with the 14-3-3η, DHQD, DSP, and Tryp sets, while the GARF energy function generated significantly lower MUEs with the GBA3, BC, and AChE sets.

Figure 11.

Comparison of Pearson R correlations and MUEs between the GARF and AMBERff14 energy functions obtained using different MT calculation settings and protocols. (A, B) MT_ScoreES calculations for the two energy functions: (A) Pearson R values; (B) MUE values. (C, D) Calculations with MOE using the MT_ScoreE protocol for the two potentials: (C) Pearson R values; (D) MUE values. (E, F) Calculations with MT_Dock using the MT_ScoreE protocol for the two energy functions: (E) Pearson R values; (F) MUE values.

As depicted in Figure 11, in a comparison of the MOE rigid-receptor docking protocol with the MT_Dock rigid-receptor protocol, the two potentials showed generally good agreement with one another for the MOE-docked poses. However, as shown in Figure 12, the Pearson R was significantly improved for the PDPK1, GBA3, and BC sets when the three-step MT_Dock protocol with GARF was used, compared with the two-step MT_ScoreE with the MOE docker. This would suggest that the binding affinity prediction benefits from the introduction of conformational entropies that are captured in the three-step MT_CS-driven method but not in the two-step method. On the other hand, when the three-step MT_ScoreE protocol was used with GARF against the 14-3-3η and DSP sets and with Amberff14 against GBA3, the Pearson R was lower compared with the MOE MT_ScoreE results, suggesting that in these cases the MT_CS conformers were inferior to the conformers provided by MOE. Furthermore, the diverging atom:atom pair potential-dependent results we observed with MT_Dock are attributable to the different MT_CS conformers generated with the two potentials: while MOE generates the same conformers and the same binding modes regardless of chosen MT potential, MT_CS uses the chosen potential to define the target bond lengths, angles, and torsions.⁵⁹ Therefore, the consistent agreement we see between GARF and AMBERff14 in both the HPF and CASF benchmarks when they are challenged with pair-potential-independent MOE poses suggests that the MT method itself is quite robust. That said, as depicted in Figure 12, GARF does appear to exhibit some preference for GARF-generated MT_CS poses.

Figure 12.

Comparison of Pearson R correlations and MUEs between the GARF and AMBERff14 energy functions using different docking programs in the MT_ScoreE protocol. (A) Pearson R values for AMBER for MT_Dock compared to MOE dock. (B) MUE values for AMBER for MT_Dock compared to MOE dock. (C) Pearson R values for GARF for MT_Dock compared to MOE dock. (D) MUE values for GARF for MT_Dock compared to MOE dock.

Conclusions

Large-scale routine application of computational receptor–ligand simulation and binding free energy prediction in industrial drug discovery remains a daunting task. Obtaining the proper balance of computational cost and efficiency in molecular energy state sampling is a central problem for this issue. In this paper, we have reported a new approach bringing the “Movable Type” free energy method from a theoretical concept to a functional software package. The current version of the MT software package provides two main free energy workflows: MT_ScoreES for fast and simple calculations, which applies only the local partition function sampling regime to a single initial molecular conformation (e.g., the crystal structure as in this work or a structure chosen through other methods by the practitioner in the field), and MT_ScoreE, which is a complete computational protocol including both unbound- and bound-state configurational sampling. Two energy functions, the AMBERff14 force field and the GARF statistical potential function, are also provided as different options for the energy evaluation of the sampled conformations (and though this is beyond the scope of this paper, users may also substitute alternative functions as well through the use of standard parmtop/coord files). The MT_ScoreE method can be executed in both a “two-step” and a “three-step” workflow, and it can generate its own landscape minima using the built-in MT_Dock approach or be supplied with binding modes generated through other means (e.g., MOE, GLIDE, etc.). Furthermore, as demonstrated in the present work, the method is also able to characterize not only ligand-side movement/sampling but also protein-side sampling. Future work will build on this support to include multiple apo protein and holo-protein:ligand conformers such as those available from X-ray, cryogenic electron microscopy, and NMR experimental models along with theoretical models and trajectories.

In this paper, these protocol combinations were validated in order to demonstrate the overall robustness of the method. The prediction profile of MT is shown to be remarkably robust, and given good theoretical landscape minima (e.g., reasonably docked poses), clearly the ensemble method is able to do as well as or sometimes better than poses generated through much more expensive means (e.g., X-ray crystallography). Together, these results show that the DivCon Discovery Suite with the MT module is a good option for fast free-energy-based receptor–ligand virtual screening applied to rational drug design studies.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.0c00618.

• PDB models included in the Homologous Protein Family set (PDF)

The authors declare the following competing financial interest(s): One or more of the authors is a QuantumBio Inc. employee, consultant, and/or shareholder.

Notes

All of the prepared structural information (including input, output, and associated structures) for both the CASF set and the HPF set is available at the following URL: http://downloads.quantumbioinc.com/media/tutorials/MT/MT-FreeEnergyPaper.tar.bz2.