Gaussian Bayesian network comparisons with graph ordering unknown

Abstract

A Bayesian approach is proposed that unifies Gaussian Bayesian network constructions and comparisons between two networks (identical or differential) for data with graph ordering unknown. When sampling graph ordering, to escape from local maximums, an adjusted single queue equi-energy algorithm is applied. The conditional posterior probability mass function for network differentiation is derived and its asymptotic proposition is theoretically assessed. Simulations are used to demonstrate the approach and compare with existing methods. Based on epigenetic data at a set of DNA methylation sites (CpG sites), the proposed approach is further examined on its ability to detect network differentiations. Findings from theoretical assessment, simulations, and real data applications support the efficacy and efficiency of the proposed method for network comparisons.

1. Introduction

1.1. An epigenetic epidemiological study

Our work was motivated by a recent epidemiological study aiming to examine joint activities of some epigenetic sites on certain genes. Epigenetics reflects memories of past exposure or physical changes in life and regulates gene functionalities without changing the DNA sequence. DNA methylation at Cytosine-phosphate-Guanine (CpG) sites is one of the most widely studied epigenetic mechanisms and its role is of particular interest due to its known responsiveness to environmental exposures (Felix et al., 2017; Joubert et al., 2016).

In our epidemiological study, the goal is to find out whether the joint activities of certain CpG sites are different between subjects exposed to in utero smoking and those not exposed. Consequently, if they are different, then what are the possible driving DNA methylation sites? Epigenetic changes due to in utero exposure to smoke have been detected at certain CpG sites (Joubert et al., 2012, 2016). However, existing studies have been focusing on effects of individual CpG sites and joint activities among the sites are completely overlooked. Thus, a novel route to appropriately answer the study questions needs to be explored.

Joint activities among genetic or epigenetic factors are commonly described by networks. In general, two types of networks are commonly applied, directed and undirected networks. To identify potential driving epigenetic factors leading to network differentiation, as the goal in our epigenetic epidemiological study, directed networks are of great interest. To examine the impact of environmental exposures, such as in utero exposure to smoke, on gene activities, differences between networks under different conditions are of greater interest than a particular network. There exist methods to infer multiple directed networks under different conditions, e.g., Wang et al. (2018). However, because of the complexity in the process of learning networks, constructed networks are subject to large variability. Thus, observed differences in networks under different conditions can be simply due to random variability, leading to false discovery of markers. Rigorously comparing networks under different conditions via statistical testing will potentially reduce such false discoveries. In the next session, we briefly review the literature in network construction and network testing.

1.2. Literature review

Networks can be inferred by use of graphical models. Practically, the inferred networks enable a depiction of concrete connections between different variables. Networks or graphs can be directed, that is, one epigenetic site can be a probabilistic stimulus (“parent node”) of the other (“child node”). In our study, the benefit of directed networks is that they allow us to identify potential driving epigenetic sites that potentially cause changes of other sites, a unique property of directed networks. Bayesian networks, also noted as probabilistic directed acyclic graphs (DAGs), are directed networks and DAGs accompanied by probabilistic connections between edges. A graph is a DAG if all the links (edges) have directions, but none of the nodes is directly go to itself or through a path to itself (a circle). Gaussian Bayesian networks are the focus of our work such that the association between parents and a child can be described using linear regressions. Graphs can also be undirected, in which case two nodes are associated but one is not a potential predictor of the other. Some other graphs are the mixture of the two (Andersson et al., 1997; Chickering, 2002). Ni et al. (2018) has a comprehensive summary on definitions of different types of graphs.

In Bayesian networks, a range of studies focus on methods dealing with ordered data (i.e., ordering of graph is known) when constructing networks. An ordering of a graph informs possible “parents” of each node. In many applications, data come with a natural ordering. For instance, in gene transcription process, the direction of information flow (graph ordering) is known. Assuming the ordering is known, Shojaie and Michailidis (2010) proposed an efficient penalized likelihood method to estimate adjacent matrices of directed graphs, and Altomare et al. (2013) proposed an objective method for Bayesian network inference. Cao et al. (2019) suggested a class of priors for the purpose of inferring Bayesian networks for ordered data, and Park and Klabjan (2017) proposed a mixed integer programming model and iterative algorithms based on given topological ordering to infer Bayesian networks. Some other works in this area for Gaussian Bayesian network inferences, such as Ben-David et al. (2011); Consonni et al. (2017), are noted and discussed in Cao et al. (2019, 2020).

In other situations, however, graph ordering is unknown as in our motivating example, or partially known as noted in Rahman et al. (2019). Many algorithms and approaches have been proposed to infer Bayesian networks under such a circumstance, including greedy local search (Heckerman et al., 1995), Optimal Reinsertion search (Moore and Wong, 2003), Max-Min Hill-Climbing (Tsamardinos et al., 2006), genetic algorithm (Larrañaga et al., 1996; Lee et al., 2010), dynamic programming (Eaton and Murphy, 2012), branch-and-bound algorithm (Campos and Ji, 2011), likelihood approach with L₁-penalty (Fu and Zhou, 2013), penalized marginal likelihood approach (Oates et al., 2016), and Markov Chain Monte Carlo (MCMC) approaches (Madigan et al., 1995, 1996; Giudici et al., 1999; Ellis and Wong, 2008; Zhou, 2011; Han et al., 2014; Kuipers and Moffa, 2017). Some other works, e.g., Friedman and Koller (2003); Han et al. (2016), infer Bayesian networks by introducing graph ordering MCMC. Permutations have also been used to infer graphs, e.g., the work by Squires et al. (2020). This type of methods is not sensitive to Gaussian assumptions and thus their applications are not limited to Gaussian Bayesian networks. Some network construction methods can be applied to both ordered or unordered data. One example in this direction is the maximum penalized likelihood algorithm proposed by Li and Zhou (2019). However, when ordering unknown, this approach is not able to infer direction of connections and a constructed network reflects underlying correlations between nodes.

Regardless of the status of ordering, most existing works focus on inferring networks. Effort on network comparisons was relatively limited, especially in the area of Bayesian networks. Gill et al. (2010) proposed a procedure to globally test differential undirected graphs particularly applied to genes, based on strength of genetic associations or interaction between genes. Jacob et al. (2012) tested multivariate two-sample means on known graphs utilizing Hotelling’s T²-tests. Zhao et al. (2014) developed a method to estimate the differences in precision matrices between two differential undirected networks, which was later extended with the ability to globally test differentiation of undirected graphs (Xia et al., 2015). The work by Städler et al. (2017) was under a similar framework, that is, testing differentiation of undirected graphs based on precision matrices. Methods built upon associations of undirected networks with a feature of interest have been proposed as well (Durante et al., 2018). Undirected graphs focus on associations between nodes and do not have the ability to infer causal-effects relationships. On the other hand, Bayesian networks are suitable for experimental data resulted from causal-effects relationships as well as for observational data such that causal relations are unknown. For network testing, Canonne et al. (2017) discussed approaches to test for identity (whether an estimated Bayesian network is equal to a given network) and for closeness (whether two networks are identical or differential). For both types of testing, their proposed algorithms have a probability of 2/3 to detect the underlying truth. Following our motivating example, we aim to compare Bayesian networks constructed under two different conditions, e.g., exposed or not-exposed to smoking in utero, with respect to network structure, direction of node connection, and strength of connection. Thus, we aim at network construction with ordering unknown as well as network testing for closeness between two inferred graphs. Almudevar (2010) proposed an approach to compare two Bayesian networks based on likelihood ratios. Each graph is constructed using minimum spanning trees and utilizes permutations to calculate an empirical p-value for decision-making. However, this approach assumes joint density of two nodes is at least as large as the multiplication of their individual density, which is a relatively strong assumption, implying a potential impossibility of inferring networks correctly (up to Markov equivalence) if using one group of data. With ordering unknown, approaches that can both construct Bayesian networks and test for differentiation between Bayesian networks are lacking. The work presented in this article is an attempt to address this gap.

In this article, we propose an approach targeted at data with unknown graph ordering. It has the ability of constructing and statistically comparing Bayesian networks under two conditions. Bayesian network constructions and comparisons for ordered data is a special case of the proposed method. Specifically, we consider data from two populations and present a Bayesian method to build Bayesian networks, and make an inference on whether the two populations share the same network (i.e., an identical network) or the networks are differential. To achieve the goal of efficient network comparison, we investigated the conditional posterior probability mass function for network differentiation and approximated the conditional posterior to ensure efficient convergence. The remaining of the article is organized as follows. We introduce in Section 2 the statistical model, likelihood function, prior distributions, and posterior computing. The property of a penalty-incorporated posterior probability is also discussed in this section. Simulations are discussed in Section 3. We present several real data applications to demonstrate the method in Section 4, and summarize our work in Section 5.

2. Methodology

To infer whether two networks are differential or identical, we start from the definition of Bayesian networks in two populations.

2.1. The model

Let ${\mathit{\text{X}}}_{n_{\mathit{\text{x}}}\times p}=\left({\mathit{\text{X}}}_1,{\mathit{\text{X}}}_2,\dots ,{\mathit{\text{X}}}_p\right)$ and ${\mathit{\text{Y}}}_{n_y\times p}=\left({\mathit{\text{Y}}}_1,{\mathit{\text{Y}}}_2,\dots ,{\mathit{\text{Y}}}_p\right)$ denote measures of a set of variables, e.g., DNA methylation levels at a set of CpG sites, in two samples from two populations (e.g., exposed vs. non-exposed to smoke in utero) for the same set of p CpG sites (or p nodes in general), respectively, where n_x and n_y are the numbers of observations with n = n_x + n_y.

For a given graph ordering $\mathcal{O}$, conditional on the parents, each node is regressed on its parents as

$${\mathit{\text{X}}}_j=\sum _{i=1}^{j-1}{\beta }_{ij}^{(1)}{X}_i+{ϵ}_j^{(x)}$$ (1)

and

$${\mathit{\text{Y}}}_j=\sum _{i=1}^{j-1}{\beta }_{ij}^{(2)}{\mathit{\text{Y}}}_i+{ϵ}_j^{(y)},$$ (2)

where ${ϵ}_j^{(x)}$ and ${ϵ}_j^{(y)}$, j = 2, ⋯ , p, are random noise following normal distributions ${ϵ}_j^{(x)}~N\left(0,{\sigma }_{x(j)}^2\mathit{\text{I}}\right)$ and ${ϵ}_j^{(y)}~N\left(0,{\sigma }_{y(j)}^2\mathit{\text{I}}\right)$, respectively, with I being the identity matrix.

If two networks are identical, then they have the same structure as well as the same strength of connection between nodes. In this case, we have ${\beta }_{ij}^{(1)}={\beta }_{ij}^{(2)}={\beta }_{ij}^{(c)}$, and consequently we can combine the data to infer a unified network,

$$\left(\begin{array}{c}{X}_j\\ Y_j\end{array}\right)=\sum _{i=1}^{j-1}{\beta }_{ij}^{(c)}\left(\begin{array}{c}{X}_j\\ Y_j\end{array}\right)+{ϵ}_j^{(c)},$$

where ${ϵ}_j^{(c)}=\left(\begin{array}{c}{ϵ}_j^{(x)}\\ {ϵ}_j^{(y)}\end{array}\right)$. On the other hand, if the two networks are differential, then each network has its own structure or its own set of coefficients describing the relations between parents and a child. We denote ${\beta }_{ij}^{(1)}={\beta }_{ij}^{(x)}$ and ${\beta }_{ij}^{(2)}={\beta }_{ij}^{(y)}$ as the set of coefficients based on samples X and Y, respectively, and ${\beta }_{ij}^{(x)}\ne {\beta }_{ij}^{(y)}$ for at least one node j, j = 1, ⋯ , p.

Linking the above two settings together, we re-define ${\beta }_{ij}^{(1)}$ and ${\beta }_{ij}^{(2)}$ as

$${\beta }_{ij}^{(1)}=\eta {\beta }_{ij}^{(c)}+(1-\eta ){\beta }_{ij}^{(x)}$$

and

$${\beta }_{ij}^{(2)}=\eta {\beta }_{ij}^{(c)}+(1-\eta ){\beta }_{ij}^{(y)},$$ (3)

where η is an indicator with η = 1 denoting that the two networks are identical and parameters ${\beta }_{ij}^{(1)}$ and ${\beta }_{ij}^{(2)}$ carry information on network structures as well as strength of links between nodes. With the re-defined ${\beta }_{ij}^{(1)}$ and ${\beta }_{ij}^{(2)}$, (1) and (2) can be generalized to the following,

$${\mathit{\text{Z}}}_j\mid {\left({\mathit{\text{Z}}}_i\right)}_{1\le i<j}=\sum _{i=1}^{j-1}\left(\eta {\beta }_{ij}^c+(1-\eta ){\beta }_{ij}^{(z)}\right){\mathit{\text{Z}}}_i+{ϵ}_j^{(z)},$$

where i : 1 ≤ i ≤ j − 1 is the candidate parent set of nodes, Z_j = X_j, or Y_j, and correspondingly, z is x or y. To infer whether the two networks are identical (η = 1) or not, we apply a Bayesian method discussed in the next sections.

2.2. Prior distributions

For the parameter η that determines whether two networks are identical, we assume no prior knowledge on its preference and choose Bernoulli Ber(0.5) for its prior distribution. In practice, sparse networks are preferred, defined as |E₀| = O(p) with |E₀| being the number of edges of a graph (Preiss, 2008). To determine the parents of a node, we adopt the concept of variable selection when selecting prior distributions for ${\beta }_{ij}^{(c)}$, ${\beta }_{ij}^{(x)}$, and ${\beta }_{ij}^{(y)}$ in ${\beta }_{ij}^{(1)}$ and ${\beta }_{ij}^{(2)}$. Various options are available. Here we choose a mixture of a Normal distribution and a point mass, also known as a spike and slab model (Mitchell and Beauchamp, 1988; Ishwaran and Rao, 2005). Conditional on η and $\mathcal{O}$,

$${\beta }_{ij}^{(c)}\mid \eta =1,\mathcal{O},r_{ij}^{(c)}~r_{ij}^{(c)}N\left(0,V_c\right)+\left(1-r_{ij}^{(c)}\right)I_{\left\{{\beta }_{ij}^{(c)}=0\right\}},$$

$${\beta }_{ij}^{(x)}\mid \eta =0,\mathcal{O},r_{ij}^{(x)}~r_{ij}^{(x)}N\left(0,V_x\right)+\left(1-r_{ij}^{(x)}\right)I_{\left\{{\beta }_{ij}^{(x)}=0\right\}}$$

and

$${\beta }_{ij}^{(y)}\mid \eta =0,\mathcal{O},r_{ij}^{(y)}~r_{ij}^{(y)}N\left(0,V_y\right)+\left(1-r_{ij}^{(y)}\right)I_{\left\{{\beta }_{ij}^{(y)}=0\right\}},$$

where $r_{ij}^{(c)}$, $r_{ij}^{(x)}$, $r_{ij}^{(y)}$ are indicators denoting the inclusion of node i as a parent of node j, i = 1,2, ⋯ , j − 1, in a given graph ordering $\mathcal{O}$. Note that the same ordering between the two populations is assumed. This assumption is driven by the motivation example of different joint activities of DNA methylation sites due to different exposures such as in utero exposure to smoke. Given the functionality of genes and epigenetic sites, at least the ordering between the two populations is expected to be the same to ensure meaningful underlying biological mechanism for the same species (although each population has its unique feature, e.g., different status of smoke exposure). If node i is one of the parents of node j, then the coefficients follow a normal distribution with mean zero and a known large variance (V_c, V_x, or V_y). Otherwise, they have a point mass at zero. Although not the focus of the present work, other prior distributions for ${\beta }_{ij}^{(1)}$ and ${\beta }_{ij}^{(2)}$ can be used as well, for instance, the g-prior (Zellner, 1986; Smith and Kohn, 1996; Fernández et al., 2001; Lee et al., 2003), or the two-component G-prior (Zhang et al., 2016).

Bernoulli Ber(0.5) are chosen for the indicator variables, $r_j^{(c)}=\left(r_{j1}^{(c)},r_{j2}^{(c)},\cdots ,r_{j(j-1)}^{(c)}\right)$, $r_j^{(x)}=\left(r_{j1}^{(x)},r_{j2}^{(x)},\cdots ,r_{j(j-1)}^{(x)}\right)$, and $r_j^{(y)}=\left(r_{j1}^{(y)},r_{j2}^{(y)},\cdots ,r_{j(j-1)}^{(y)}\right)$. With Ber(0.5), we assume no prior knowledge on the inclusion of a parent node and inference on parental nodes selection relies on information in the data. In the situation of available prior knowledge on network structures, instead of 0.5 in Ber(0.5), nodes with low probabilities of being parents can take a value smaller than 0.5. For variance components, we choose vague prior distributions for ${\sigma }_{x(j)}^2$ and ${\sigma }_{y(j)}^2$, in particular, an inverse gamma distributions with small shape and scale parameters. As seen in the above definitions, for a given η and ordering $\mathcal{O}$, all the definitions of prior and hyper-prior distributions of the parameters are independent.

So far, the specification of network structures as well as prior distributions on edges such as the regression coefficients are conditional on a given ordering $\mathcal{O}$, and $\mathcal{O}$ needs to be inferred. We assume its prior distribution is uniform among all possible permutations of p nodes, and propose an efficient posterior sampling approach in the next session to infer $\mathcal{O}$.

2.3. The joint posterior distribution and its computing

For a given graph ordering $\mathcal{O}$, to estimate ${\beta }_{ij}^{(1)}$ and ${\beta }_{ij}^{(2)}$, a set of prior and hyper-prior parameters need to be inferred, including parameters when ${\beta }_j^{(x)}=\left({\beta }_{j1}^{(x)},{\beta }_{j2}^{(x)},\cdots ,{\beta }_{j(j-1)}^{(x)}\right)$, $r_j^{(x)}$, ${\beta }_j^{(y)}=\left({\beta }_{j1}^{(y)},{\beta }_{j2}^{(y)},\cdots ,{\beta }_{j(j-1)}^{(y)}\right)$, $r_j^{(y)}$ parameters when $\eta =1:{\beta }_j^{(c)}=\left({\beta }_{j1}^{(c)},{\beta }_{j2}^{(c)},\cdots ,{\beta }_{j(j-1)}^{(c)}\right)$, $r_j^{(c)}$ as well as the variance components ${\sigma }_{x(j)}^2$ and ${\sigma }_{y(j)}^2$. Under the context of Bayesian inferences via Markov chain Monte Carlo (MCMC) simulations, we combine these parameters along with the ordering of nodes $\mathcal{O}$ into a collection of parameters that fit into different states of η, $\theta =\left(\mathcal{O},{\beta }_j^{(x)},r_j^{(x)},{\beta }_j^{(y)},r_j^{(y)},\eta ,{\beta }_j^{(c)},r_j^{(c)},{\sigma }_{x(j)}^2,{\sigma }_{y(j)}^2,j=1,\cdots ,p\right)$. Inference on this collection of parameters will produce an estimate of the networks and assess the probability of having identical networks. The joint likelihood of θ is

$$\begin{gathered} L(\theta \mid X,Y)=p(X,Y\mid \theta ) \\ \propto \prod _{j=1}^p\{{\left({\sigma }_{x(i)}^2\right)}^{-\frac{n_x}{2}}\text{exp}\left[-\frac{{\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(1)}{X}_i\right)}^T\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(1)}{X}_i\right)}{2{\sigma }_{x(j)}^2}\right] \\ \times {\left({\sigma }_{y(j)}^2\right)}^{-\frac{n_y}{2}}\text{exp}\left[-\frac{{\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(2)}{Y}_i\right)}^T\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(2)}{Y}_i\right)}{2{\sigma }_{y(j)}^2}\right]\}, \end{gathered}$$

with ${\beta }_{ij}^{(1)}$ and ${\beta }_{ij}^{(2)}$ defined in (3).

The joint posterior distribution of θ is,

$$\begin{gathered} p(\theta \mid X,Y) \\ \propto \prod _{j=1}^p\left\{{\left({\sigma }_{x(j)}^2\right)}^{-\frac{n_x}{2}}\text{exp}\left[-\frac{{\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(1)}{X}_i\right)}^T\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(1)}{X}_i\right)}{2{\sigma }_{x(j)}^2}\right] \\ \times {\left({\sigma }_{y(j)}^2\right)}^{-\frac{n_y}{2}}\text{exp}\left[-\frac{{\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(2)}{Y}_j\right)}^T\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(2)}{Y}_i\right)}{2{\sigma }_{y(j)}^2}\right] \\ \times \prod _{i=1}^{j-1}\left[p\left({\beta }_{ij}^{(c)}\mid \eta =1,\mathcal{O},r_{ij}^{(c)}\right)p\left({\beta }_{ij}^{(x)}\mid \eta =0,\mathcal{O},r_{ij}^{(x)}\right) \\ \times p\left({\beta }_{ij}^{(y)}\mid \eta =0,\mathcal{O},r_{ij}^{(y)}\right)p\left(r_{ij}^{(c)}\mid \eta =1\right)p\left(r_{ij}^{(x)}\mid \eta =0\right)p\left(r_{ij}^{(y)}\mid \eta =0\right)p\left({\sigma }_{x(j)}^2\right)p\left({\sigma }_{y(j)}^2\right)\right]\right\}\times p(\eta )p(\mathcal{O}). \end{gathered}$$ (4)

The Gibbs sampler is applied to full conditional posterior distributions of each parameter in θ to sequentially draw posterior samples, based on which we infer η, graph structure determined by $r_{ij}^{(c)}$ if η = 1 or $r_{ij}^{(x)}$ and $r_{ij}^{(y)}$ if η = 0, and ${\beta }_{ij}^{(1)}$ and ${\beta }_{ij}^{(2)}$ describing the strength of connections between nodes. In the following subsections, we present and discuss conditional posterior distributions of the parameters.

2.3.1. Conditional posterior probability of η

Since the decision on whether two networks are differential or not is critical to the estimates of network structure and corresponding parameters, we start from presenting the conditional posterior of η. Denoted by (·) a collection of all conditional parameters, based on (4), we have

$$p(\eta =1\mid (\cdot ),X,Y)\propto p\left(X,Y\mid \eta =1,r^{(c)},{\sigma }_x^2,{\sigma }_y^2,\mathcal{O}\right)p(\eta =1),$$

where ${\sigma }_x^2=\left\{{\sigma }_{x(j)}^2,j=1,\cdots ,p\right\}$ and ${\sigma }_y^2=\left\{{\sigma }_{y(j)}^2,j=1,\cdots ,p\right\}$.

It can be shown that, when n_x and n_y large, the full conditional posterior probability, p(η = 1|(·), X, Y), can be approximated by the following (Appendix I),

$$p(\eta =1\mid (\cdot ),X,Y)\approx {\left[1+\text{exp}\left\{\text{log}\left(b_{\eta }\right)-\text{log}\left(a_{\eta }\right)+\lambda (n)\right\}\right]}^{-1},$$

$$\lambda (n)=1/2\left(\left|E\right|\text{log }n-|E_x|\text{log }{n}_x-\left|E_y\right|\text{log }{n}_y\right),$$

where n = n_x + n_y. In the above, |E|, |E_x|, and |E_y| denote numbers of edges in inferred identical and differential networks, respectively, and

$$\begin{gathered} a_{\eta }=p(X,Y\mid (\cdot ),\eta =1) \\ \propto \prod _{j=1}^p\left\{{\left({\sigma }_{x(j)}^2\right)}^{-\frac{n_x}{2}}\text{exp}\left[-\frac{{\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{X}_i\right)}^T\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{X}_i\right)}{2{\sigma }_{x(j)}^2}\right] \\ \times {\left({\sigma }_{y(j)}^2\right)}^{-\frac{n_y}{2}}\text{exp}\left[-\frac{{\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{Y}_i\right)}^T\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{Y}_i\right)}{2{\sigma }_{y(j)}^2}\right]\right\}, \end{gathered}$$ (5)

$$\begin{gathered} b_{\eta }=p(X,Y\mid (\cdot ),\eta =0) \\ \propto \prod _{j=1}^p\left\{{\left({\sigma }_{x(j)}^2\right)}^{-\frac{n_x}{2}}\text{exp}\left[-\frac{{\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(x)}{X}_i\right)}^T\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(x)}{X}_i\right)}{2{\sigma }_{x(j)}^2}\right] \\ \times {\left({\sigma }_{y(j)}^2\right)}^{-\frac{n_y}{2}}\text{exp}\left[-\frac{{\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(y)}{Y}_i\right)}^T\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(y)}{Y}_i\right)}{2{\sigma }_{y(j)}^2}\right]\right\}. \end{gathered}$$ (6)

We denote this approximated conditional posterior probability as p^λ(η = 1|(·), X, Y) and it has the following Proposition.

Proposition:

Assume 1) sparse networks with |E|, |E_x|, and |E_y| in the order of O(p), 2) n_x → ∞ and n_y → ∞ in the same speed, and 3) logn_x/p → ∞ as n_x,p → ∞, and similar assumptions applied to n_y. Then ${\text{lim}}_{n_x,n_y\to \infty }{p}^{\lambda }\left(\eta =1|(·),\mathit{\text{X}},\mathit{\text{Y}}\right)=1$ if the underlying η = 1, and ${\text{lim}}_{n_x,n_y\to \infty }{p}^{\lambda }\left(\eta =1|(·),\mathit{\text{X}},\mathit{\text{Y}}\right)=0$ if the underlying η = 0.

The proof of the Proposition is in Appendix II. This Proposition indicates that, with p^λ(η = 1|(·), X, Y), the underlying truth of η will be identified asymptotically. In addition, for network constructions, p^λ(η = 1|(·), X, Y) has a potential to penalize large numbers of edges as indicated by the definition of λ(n). In genetic and epigenetic studies, this property benefits marker detection and is practically informative to clinicians and health researchers. In the context of network comparisons, the definition of λ(n) in p^λ(η = 1|(·), X, Y) implies a preference for identical networks over differential networks. The Proposition holds for other choices of prior distributions of the parameters as long as the conditional priors of ${\beta }_{ij}^{(1)}$ and ${\beta }_{ij}^{(2)}$ are non-informative for parental node i, i.e., nodes such that $r_{ij}^{(\cdot )}=1$. Although not the situation in our proposed method as seen from the Proposition of p^λ(η = 1|(·), X, Y), the Jeffreys−Lindley paradox suggests that a caution should be made in any hypothesis testing conducted under the Bayesian framework, since non-informative prior distributions can possibly lead to rather strong but useless decision, e.g., rejection of null with probability 1 regardless of data (Robert, 2007).

2.3.2. Conditional posterior distributions of other parameters

Below, we list the conditional posterior distributions for the remaining parameters. For the parameters to select a parent node k at a child node j, when η = 1,

$$p\left(r_{jk}^{(c)}=1\mid (\cdot ),X,Y,\eta =1\right)=\frac{a_c}{a_c+b_c},$$

where a_c and b_c are proportional to the conditional posterior distributions of $r_{jk}^{(c)}=1$ and $r_{jk}^{(c)}=0$, respectively,

$$\begin{gathered} a_c=\text{exp}\left\{-\frac{{\left({\beta }_{jk}^{(c)}\right)}^2}{2V_c}-\frac{{\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{X}_i\right)}^T\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{X}_i\right)}{2{\sigma }_{x(j)}^2} \\ -\frac{{\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{Y}_i\right)}^T\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{Y}_i\right)}{2{\sigma }_{y(j)}^2}\right\}\times p\left(r_{jk}^{(c)}=1\right), \end{gathered}$$

and

$$\begin{gathered} b_c=\text{exp}\left\{-\frac{{\left(X_j-{\sum }_{i=1,j\ne k}^{i-1}{\beta }_{ij}^{(c)}{X}_j\right)}^T\left(X_i-{\sum }_{j=1,j\ne k}^{i-1}{\beta }_{ij}^{(c)}{X}_j\right)}{2{\sigma }_{x(i)}^2} \\ -\frac{{\left(Y_j-{\sum }_{i=1,i\ne k}^{j-1}{\beta }_{ij}^{(c)}{Y}_i\right)}^T\left(Y_j-{\sum }_{i=1,i\ne k}^{j-1}{\beta }_{ij}^{(c)}{Y}_i\right)}{2{\sigma }_{y(j)}^2}\right\}\times p\left(r_{jk}^{(c)}=0\right). \end{gathered}$$

When η = 0, each population holds its own network and the conditional posterior distribution of $r_{jk}^{(x)}$ is defined as

$$p\left(r_{jk}^{(x)}=1\mid (\cdot ),X,Y,\eta =0\right)=\frac{a_x}{a_x+b_x},$$

with $a_x=\text{exp}\left\{-\frac{{\beta }_{jk}^{(x)}}{2V_x}-\frac{{\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(x)}{X}_i\right)}^T\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(x)}{X}_i\right)}{2{\sigma }_{x(j)}^2}\right\}\times p\left(r_{jk}^{(x)}=1\right)$, and $b_x=\text{exp}\left\{-\frac{{\left(X_j-{\sum }_{i=1,i\ne k}^{j-1}{\beta }_{ij}^{(x)}{X}_i\right)}^T\left(X_i-{\sum }_{i=1,i\ne k}^{j-1}{\beta }_{ij}^{(x)}{X}_i\right)}{2{\sigma }_{x(j)}^2}\right\}\times p\left(r_{jk}^{(x)}=0\right)$. The conditional posterior of $r_{jk}^{(y)}$ is in a similar form.

Turning to the regression coefficients, if $r_{jk}^{(\cdot )}=0$, then ${\beta }_{jk}^{(\cdot )}=0$. Otherwise, the conditional posterior distribution of ${\beta }_{jk}^{(c)}$ is univariate normal, $N\left({\mu }_{{\beta }_{jk}^{(c)}},{\sigma }_{{\beta }_{jk}^{(c)}}^2\right)$, with ${\mu }_{{\beta }_{jk}^{(c)}}=\left(V_c{\sigma }_{y(j)}^2{\mathit{\text{C}}}_1^T{X}_k+V_c{\sigma }_{x(j)}^2{\mathit{\text{C}}}_2^T{Y}_k\right)/\left({\sigma }_{x(j)}^2{\sigma }_{y(j)}^2+V_c{\sigma }_{y(j)}^2{X}_k^T{X}_k+V_c{\sigma }_{x(j)}^2{Y}_k^T{Y}_k\right)$, ${\sigma }_{{\beta }_{jk}^{(c)}}^2=\left({\sigma }_{x(j)}^2{\sigma }_{y(j)}^2{V}_c\right)/\left({\sigma }_{x(j)}^2{\sigma }_{y(j)}^2+V_c{\sigma }_{y(j)}^2{X}_k^T{X}_k+V_c{\sigma }_{x(j)}^2{Y}_k^T{Y}_k\right)$ where $C_1=\left(X_j-{\sum }_{i=1,i\ne k}^{j-1}{\beta }_{ij}^{(c)}{X}_i\right)$ and $C_2=\left(Y_j-{\sum }_{i=1,i\ne k}^{j-1}{\beta }_{ij}^{(c)}{Y}_i\right)$. The conditional posterior distributions of ${\beta }_{jk}^{(x)}\mid (\cdot )$ , X, Y and ${\beta }_{jk}^{(y)}\mid (\cdot )$ , X, Y are defined in a similar way.

Finally, we discuss the conditional posterior distribution of $\mathcal{O}$, ordering of the nodes, and its sampling. From the joint posterior distribution of θ given in (4), derivation of the conditional posterior distribution of $\mathcal{O}$ is straightforward, which is,

$$\begin{gathered} p(\mathcal{O}\mid (\cdot ),X,Y) \\ \propto \prod _{j=1}^p\left\{{\left({\sigma }_{x(j)}^2\right)}^{-\frac{n_x}{2}}\text{exp}\left[-\frac{{\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(1)}{X}_i\right)}^T\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(1)}{X}_i\right)}{2{\sigma }_{x(j)}^2}\right] \\ \times {\left({\sigma }_{y(j)}^2\right)}^{-\frac{n_y}{2}}\text{exp}\left[-\frac{{\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(2)}{Y}_i\right)}^T\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(2)}{Y}_i\right)}{2{\sigma }_{y(j)}^2}\right] \\ \times \prod _{i=1}^{j-1}\left[p\left({\beta }_{ij}^{(1)}\mid \eta ,\mathcal{O},r_{ij}^{(\cdot )}\right)p\left({\beta }_{ij}^{(2)}\mid \eta ,\mathcal{O},r_{ij}^{(\cdot )}\right)\right]\right\}, \end{gathered}$$

where $r_{ij}^{(\cdot )}$ is $r_{ij}^{(x)}$, $r_{ij}^{(y)}$, or $r_{ij}^{(c)}$.

2.3.3. Sampling of graph ordering

Since the number of nodes p can be large, an efficient sampling of $\mathcal{O}$ that has the ability to escape from traps of local maximum is critical in practice. Energy-driven sampling has been used often to diminish this type of concern (Ellis and Wong, 2008; Van den Bergh et al., 2012). We adopt the sampling scheme suggested in Han et al. (2016), the Adjusted Single Queue Equi-Energy algorithm (ASQEE), which is adapted from the SQEE sampling method proposed by Ellis and Wong (2008).

Basically, the SQEE approach utilizes energy and energy rings with minimum energy suggested by the range of $H(\mathcal{O})=-\text{log}(p(\mathcal{O}\mid (\cdot ),X,Y))$, allowing energy upper bound to be ∞, and energy rings formed by dividing the range of energy into groups (or “chains” as in Ellis and Wong (2008)). Energy levels increase from lower to upper rings, and within each ring, the probability density function is ${\pi }_l(\mathcal{O})=\text{exp}\left(\frac{-\text{ max}\left\{H(\mathcal{O}),H_l\right\}}{T_l}\right)$, l = 1, 2, ⋯ , W, with l indexing groups or chains and in total W groups (thus W rings), H_l is lower bound energy level for chain l, and T_l is the lower temperature of that chain such that 1 = T₁ < T₂ < ⋯ < T_W. A ring in group l, D_l, is a collection of different orderings such that their energy is bounded by corresponding lower and upper bound energy levels, $D_l=\left\{\mathcal{O}\mid H(\mathcal{O})\in \left[H_l,H_{l+1}\right),l=1,\cdots ,W\right\}$, with H_W+1 set at ∞. In our study (both simulations and real data applications), we take W = 5 to allow Markov Chain Monte Carlo (MCMC) sampling between rings for the purpose of fast convergence to the global maximum. This construction shows that when l = 1, ${\pi }_1(\mathcal{O})$ is the target distribution. Furthermore, as the value of l increases, the distribution in the lth group is more flatten, enhancing the ability of the chain jumping across different modes to avoid being trapped at local maximums. To perform the sampling, we follow the “cylindrical shift” operation suggested in Ellis and Wong (2008) to propose an ordering. Then a Metropolis-Hastings (Hastings, 1970) algorithms is applied to determine whether the newly proposed ordering will be accepted or not, which is the standard local Metropolis-Hastings move. The sampling starts from the chain with the highest energy level, which is associated with a flatten distribution. This allows the chains to move more quickly through the space to collect samples for later communications with lower-temperature chains.

For the sampling scheme ASQEE in Han et al. (2016), when evaluating the conditional probability of a sampled ordering, instead of utilizing all possible graphs for that order, it estimated the probability based on a graph showing the highest probability for a given graph ordering aiming to improve sampling efficiency. Readers are referred to Ellis and Wong (2008) and Han et al. (2016) for detailed discussions on the ASQEE sampler construction and its related algorithms.

3. Numerical Analysis

Via simulations, we demonstrate finite sample properties of the proposed method under different scenarios and compare the findings with those from existing methods that can be applied to test network differentiation.

3.1. Simulation scenarios

Generating Monte Carlo (MC) replicates:

We consider DNA methylation measures, X and Y, from two populations (e.g., exposed vs. non-exposed to in utero smoking) and each with n_x = n_y observations. Each data set is generated from an underlying network structure with p CpG sites (or p nodes) and |E_0x| and |E_0y| edges, respectively, based on linear regressions. We assume each node can have up to four parents corresponding to regression coefficients of β = {1.5, 2, 2, 2.5} in order. The root node is an experimental node and does not have any parents. Two types of underlying networks are considered. The first is that the two populations share the same networks (i.e., identical networks) and the other situation is that each population has its unique network (i.e., differential networks). In our simulations, we take p = 10, 20 and n_x = n_y = 50, 100, 200. For identical networks, we choose |E_0x| = |E_0y| = |E_0c| = 10, 20, and for differential networks, we consider two sets of |E_0x| and |E_0y|, |E_0x| = 5, |E_0y| = 10 and |E_0x| = 20, |E_0y| = 10. For each graph, a level of sparsity is defined as the ratio between the true number of edges and the possible number of edges, S = 2|E.|/(p(p − 1)), where |E.| represents |E_0x|, |E_0y|, or |E_0c|. For instance, a graph with 10 nodes and 10 edges has a level of sparsity 10/45 = 0.222. The connection of each edge is randomly selected based on a prespecified ordering of all the nodes. The random error when generating each node is assumed to be normally distributed with mean 0 and variance 1. For each combination of the settings of n_x = n_y, p, E_0x and E_0y, we generated 100 MC replicates.

Posterior sampling:

For each MC replicate, we utilize the Gibbs sampler to sequentially draw samples of each parameter from its conditional posterior probability density (or mass) function. Since one ordering can lead to a number of graphs, when estimating conditional posterior probability of a sampled ordering, we run a set of iterations aiming to capture graphs with high probabilities for that given ordering. In addition, to increase the stability of sampled ordering, in each energy ring, we sample a series of orderings as burn-in following the SQEE and ASQEE sampling technique. To get an insight on the numbers of iterations needed for these considerations, we first run longer chains using the Gibbs sampler on several MC replicates and examine the quality of posterior inferences. After observing fast convergence with respect to the inference of η and graph structure, for each of the 100 MC replicates, we run 6,000 iterations which includes 50 iterations for inferring conditional posterior probabilities of each sampled ordering with 25 as burn-in iterations and 120 iterations for sampling orderings with a range of 20 to 100 iterations (higher energy rings with less iterations) as burn-in iterations across 5 energy rings.

Summarizing statistics:

Graphs and orderings of nodes are not one-to-one correspondence and one graph can be a result of multiple orderings. Since our goal is to compare graphs between two populations, our posterior inferences focus on graphs rather than ordering of graphs. Four statistics focusing on testing and network constructions are used to summarize the results and assess the proposed method: 1) power of correct detection with respect to network comparison (identical or differential), 2) average proportion of true positives for edge connection and directions (TPCD) in a network, 3) average proportion of false positives (FP) of a network, and 4) average proportion of correct connections (CC) of edges. A proportion of correct connections combines information on sensitivity (reflected by proportions of true positives) and specificity (reflected by proportions of false positives). For all the statistics except for power, we also infer 95% empirical intervals. We evaluate the proposed method based on these statistics on the various choices of sample sizes and numbers of edges noted in the paragraph above.

Competing methods:

Approaches that not only compare networks but also infer networks are relatively limited. To assess the proposed method, we use two existing approaches, one focuses on comparisons in structures between two networks and the other on coefficients comparisons. The first competing method is proposed by Almudevar (2010). It compares two graphs with each constructed based on minimum spanning trees (MST) and utilizes permutations to calculate an empirical p-value for decision-making. We denote this method as MST-based approach. In the second comparison, we utilize an existing method in multivariate testing, the Hotelling’s T-squared test. In particular, we first infer networks for the two populations separately using the network construction method implemented in the proposed approach, and then apply the Hotelling’s T-squared test on the posterior samples of regression coefficients assuming unequal variances between the two populations. Posterior samples are selected to ensure small values on autocorrelation functions. In both comparisons, we compare the power of detecting underlying truth using each of the competing approach with that from the proposed method.

3.2. Results

Table 1 lists different model assessment statistics when in total 10 nodes are considered. In the situation that the underlying networks are identical (η = 1), overall the power of detecting the correct type of networks (identical or differential) is reasonably high for all cases. Since the underlying networks are identical, the decrease in power when the sample size is large shown in the table is a phenomenon observed in a two sample hypothesis testing when the null (i.e., two means are equal) is true. This consequently caused other assessment statistics being slightly inferior. We note that the false positives are influenced by the edge sparsity of the networks. When the graphs are sparse (e.g., 10 nodes with 10 edges with sparsity 0.222), proportions of false positives are low but larger false positives are observed when the graphs are less sparse (e.g., 10 nodes with 20 edges with sparsity 0.444). All these are likely due to the inclusion of edges that are indirectly connected to a node under investigation, for instance, by being a “parent” of this node’s “child”, a phenomenon discussed in Wasserman and Roeder (2009). All these lead to an overall slight decrease in the proportions of correctness (top left panel of Figure 1) when the number of edges is large and sparsity is low, and this type of patterns continues when the number of nodes is 20 (top right panel of Figure 1).

Table 1:

Summary statistics for detecting differential networks, including estimated power of correct detection (with respect to network types), true positives for edge connections and directions (TPCD), false positives (FP), and correct connections (CC) across 100 MC replicates along with 95% empirical intervals (EI).

Sample size (nx = ny)	Power (%)	TPCD (95% EI)	FP (95% EI)	CC (95% EI)
Underlying networks: identical networks (p = 10 nodes, |E0c| = 10 edges)
50	94.9	0.999 (0.998, 1.0)	0.020 (0.0, 0.086)	0.984 (0.933, 1.0)
100	98.2	0.999 (0.999, 1.0)	0.021 (0.0, 0.086)	0.984 (0.932, 1.0)
200	98.9	0.999 (0.998, 1.0)	0.013 (0.0, 0.072)	0.990 (0.944, 1.0)
Underlying networks: identical networks (p = 10 nodes, |E0c| = 20 edges)
50	90.0	0.984 (0.900, 1.0)	0.199 (0.0, 0.622)	0.882 (0.644, 1.0)
100	91.7	0.996 (0.950, 1.0)	0.199 (0.0, 0.560)	0.887 (0.676, 1.0)
200	88.7	0.993 (0.965, 1.0)	0.230 (0.0, 0.640)	0.869 (0.629, 1.0)
Underlying networks: differential networks (p = 10 nodes, |E0x| = 5, |E0y | = 10 edges)
50	99.9	X : 0.998 (0.999, 1.0)	0.017 (0.00, 0.075)	0.984 (0.933, 1.0)
		Y : 0.977 (0.80, 1.0)	0.047 (0.00, 0.200)	0.958 (0.844, 1.0)
100	99.9	X : 1.0 (0.999, 1.0)	0.016 (0.00, 0.088)	0.986 (0.921, 1.0)
		Y : 0.992 (0.90, 1.0)	0.045 (0.00, 0.329)	0.963 (0.744, 1.0)
200	99.9	X : 1.0 (0.999, 1.0)	0.013 (0.00, 0.063)	0.988 (0.944, 1.0)
		Y : 0.996 (0.998, 1.0)	0.048 (0.00, 0.287)	0.962 (0.776, 1.00)
Underlying networks: differential networks (p = 10 nodes, |E0x| = 20, |E0y| = 10 edges)
50	99.9	X : 0.979 (0.874, 1.0)	0.218 (0.0, 0.560)	0.869 (0.667, 1.0)
		Y : 0.976 (0.90, 1.0)	0.039 (0.0, 0.171)	0.964 (0.867, 1.0)
100	99.9	X : 0.993 (0.950, 1.0)	0.213 (0.0, 0.600)	0.879 (0.633, 1.0)
		Y : 0.991 (0.90, 1.0)	0.033 (0.0, 0.186)	0.972 (0.855, 1.0)
200	99.9	X : 0.993 (0.950, 1.0)	0.232 (0.0, 0.600)	0.868 (0.644, 1.0)
		Y : 0.998 (0.997, 1.0)	0.040 (0.0, 0.230)	0.967 (0.821, 1.0)

Figure 1:

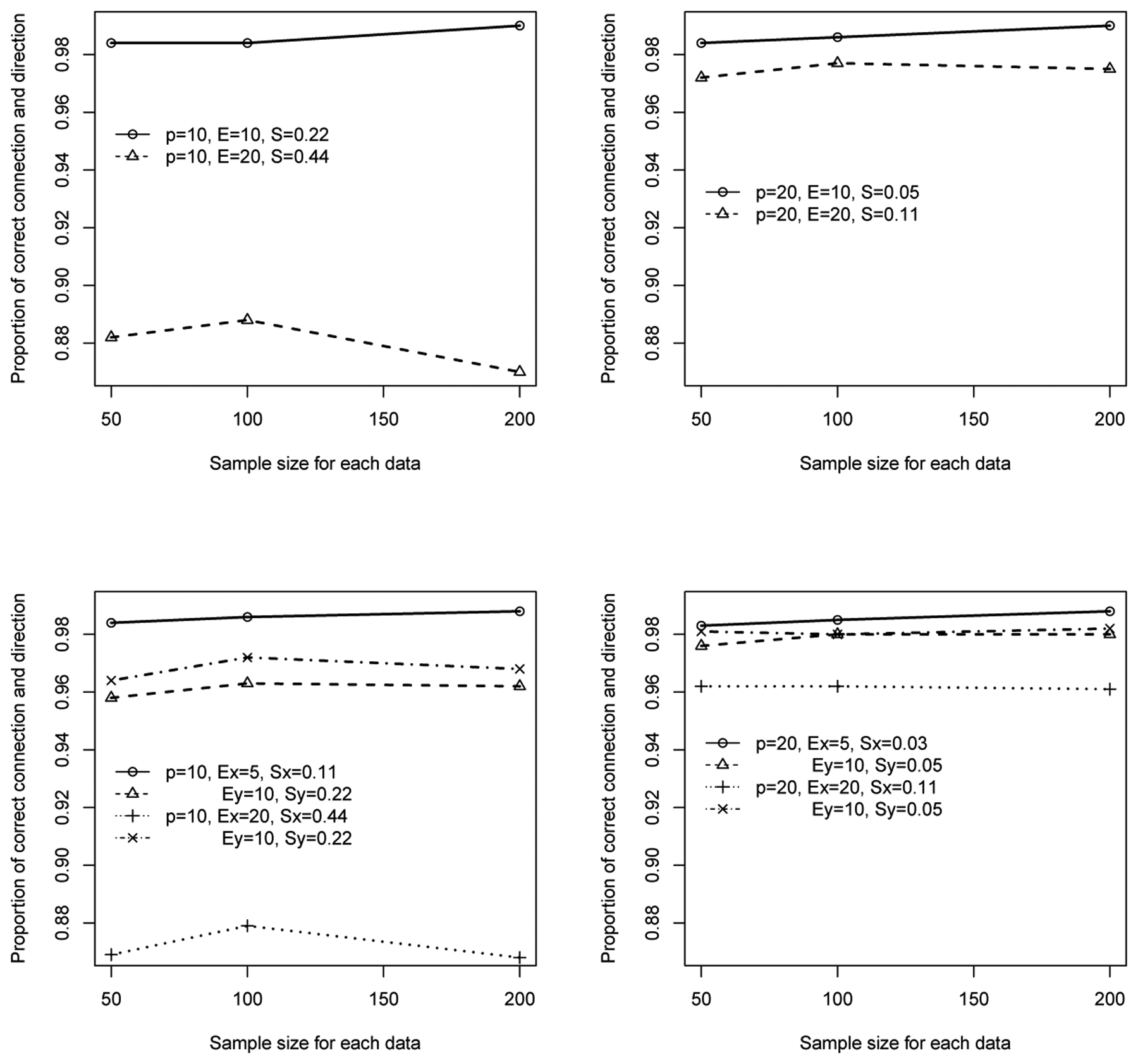
Plots of proportions of correct connections with correct direction of connections. The top panel is for identical networks and the lower panel is for differential networks.

On the other hand, when underlying networks are two differential networks (η = 0), overall the power to detect the truth is higher than the power when the underlying networks are identical. In addition, proportions of TPCD increase with the increase of sample size. As in the situation of η = 1, false positives slightly increase as sparsity level decreases (Table 1 and bottom panel of Figure 1), leading to decrease in proportions of correctness.

Since the concept of correctness combines both sensitivity and specificity, we examine this statistics a little further. As reflected by the patterns shown in Figure 1, with the number of nodes and sample size fixed, sparsity seems to play an important role in the determination of proportion of correctness, regardless of the number of edges; the lower the sparsity (i.e., high sparsity values), the lower the proportion of correctness. On the other hand, smaller numbers of nodes lead to higher proportions of correctness for similar sparsity levels (demonstrated by results with sparsity of 0.11 shown in the two figures at the lower panel of Figure 1).

To further evaluate the approach, we next compare the results from the proposed method with those from the two competing approaches, the MST-based approach and the approach based on Hotelling’s T-squared tests. Since the MST-based approach is designed for small sample sizes, we used the MC replicates under the setting of p = 10 nodes and each MC replicate having n_x = n_y = 50 observations. When underlying two networks are identical, the power of detecting this underlying truth is 0.99. However, the proportions of true positives, false positives, and correct connections, along with 95% empirical intervals, are 0.40(0.10, 0.60), 0.14(0.086, 0.23), and 0.76(0.62, 0.84), respectively, all inferior to the corresponding results in Table 1 (first row in the first block of Table 1). When underlying two networks are differential, the power is only 37%, substantially lower than the power from the proposed approach (first row in the third block of Table 1).

For the second competing method based on Hotelling’s T-squared tests, we present the results of power assessment using the MC replicates generated under the settings with p = 20. Overall, when underlying two networks are identical, the power to detect the truth is much lower than that from the proposed approach, although the pattern is the same, i.e., the power decreases with the increase of sample sizes (Figure 2). As expected, when two networks are truly differential, the power of detecting the truth increases with sample sizes and is overall high but lower than the power based on the proposed method. The findings with p = 10 follow the same trend but were deteriorate when two networks are truly identical. The proposed approach clearly outperforms the method built upon the Hotelling’s T-squared test.

Figure 2:

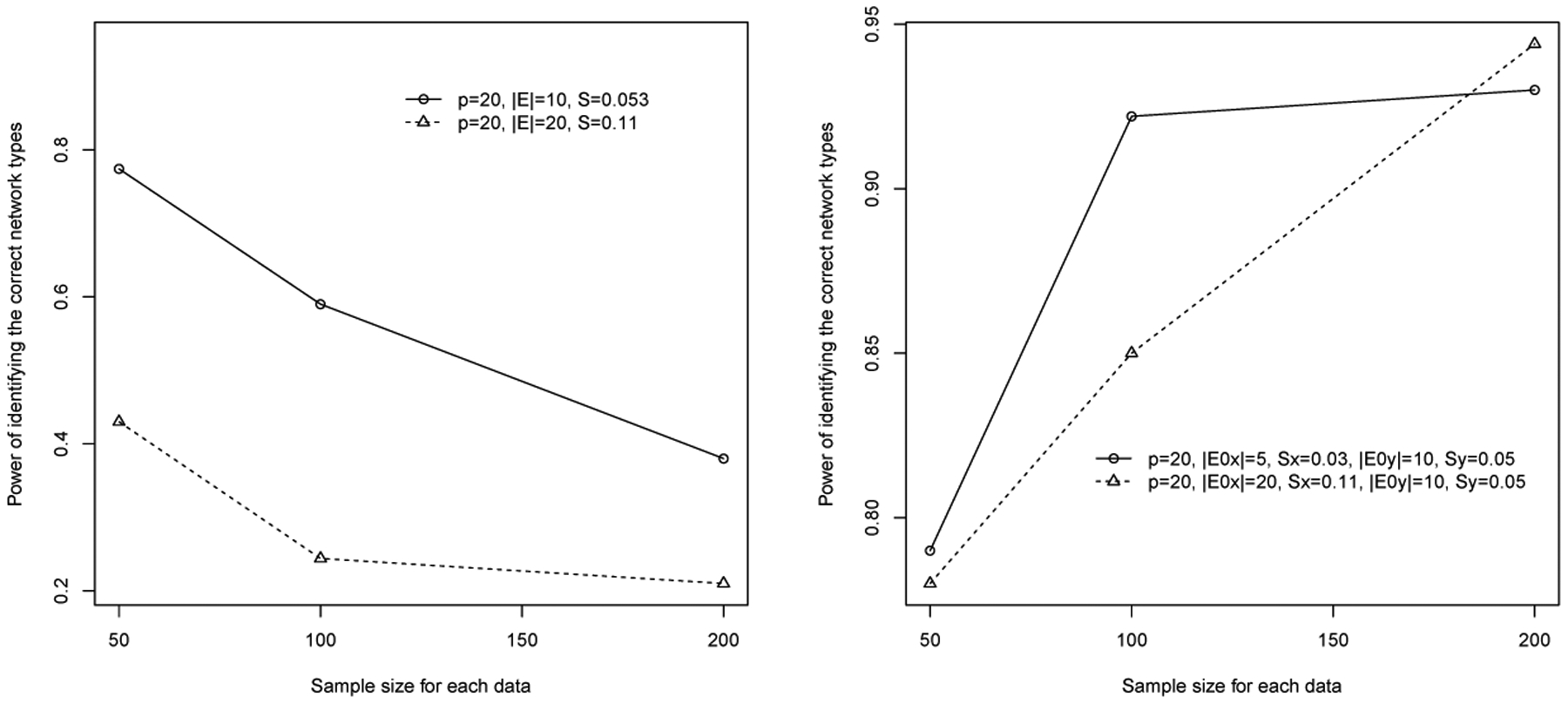
Power of detecting the underlying truth of network differentiation status using a method based on the Hotelling’s T-squared tests. Left panel: two networks are truly identical. Right panel: two networks are truly differential.

4. Real Data Application

We apply the method to DNA methylation of 23 CpG sites in 9 genes (Table 2) analyzed in our epigenetic epidemiological study. Each of these CpGs was shown to be associated with maternal smoking during pregnancy (Joubert et al., 2012). DNA methylation data of 245 girls measured at age 18 are used in the analysis. These 245 subjects represent a random sample from the Isle of Wight birth cohort (Arshad et al., 2018; Quraishi et al., 2015). Among these 245 girls, 48 were exposed to maternal smoking during pregnancy. We demonstrate the proposed method from two aspects. Firstly, we only consider the 197 subjects not exposed to maternal smoking during pregnancy. We disturb the data by introducing noise to the first 97 subjects on one CpG site (cg18146737 [node 15] on gene GFI1) to artificially produce two conditions, one for the first 97 subjects and the other for the remaining 100 subjects. This disturbance is expected to break the links connected to the CpG site cg18146737, which should lead to underlying two differential networks among the CpGs. We then apply the developed method to test whether the two networks are identical or differential. In the second aspect, to demonstrate our approach in the real world, we apply the method to all 245 subjects and assess whether the network among the CpGs for the subjects whose mother did not smoke during pregnancy is differential compared to the network for the subjects whose mother smoked. For each scenario, we run 84,000 MCMC iterations, which includes 200 iterations used to calculate conditional posterior probabilities of each sampled ordering with 100 as burn-in iterations and 4,200 iterations for sampling ordering with a range of 70 to 350 iterations as burn-in iterations across 5 energy rings.

Table 2:

The list of CpGs and their corresponding genes

Label	CpG	Gene	Label	CpG	Gene
1	cg03991871	AHRR	13	cg14179389	GFI1
2	cg04180046	MYO1G	14	cg18092474	CYP1A1
3	cg04598670	ENSG00000225718	15	cg18146737	GFI1
4	cg05549655	CYP1A1	16	cg18316974	GFI1
5	cg05575921	AHRR	17	cg18655025	TTC7B
6	cg06338710	GFI1	18	cg19089201	MYO1G
7	cg10399789	GFI1	19	cg21161138	AHRR
8	cg11715943	HLA-DPB2	20	cg22132788	MYO1G
9	cg11924019	CYP1A1	21	cg22549041	CYP1A1
10	cg12477880	RUNX1	22	cg23067299	AHRR
11	cg12803068	MYO1G	23	cg25949550	CNTNAP2
12	cg12876356	GFI1

In the first scenario with disturbance given to the first 97 subjects, the inferred posterior probability that the two networks are differential is 0.95, implying a high potential that the two networks are differential. However, there is a possibility that the first 97 subjects were under an unknown condition different from the remaining 100 subjects, and thus the underlying networks were already differential even before we disturb the data. To test this, we use the original data for the 197 subjects without disturbing the data but still assume two conditions between the first 97 subjects and the remaining 100 subjects. After applying the method to the original data without disturbance, the posterior probability of having identical networks is 0.66, indicating that the 197 subjects are likely sharing the same network.

In the second scenario, we apply the method to all the 245 subjects. The posterior probability of having differential networks is 0.99, suggesting that subjects exposed to maternal smoking during pregnancy and subjects not exposed are highly likely to have their unique networks. The inferred networks for both groups are shown in Figure 3.

Figure 3:

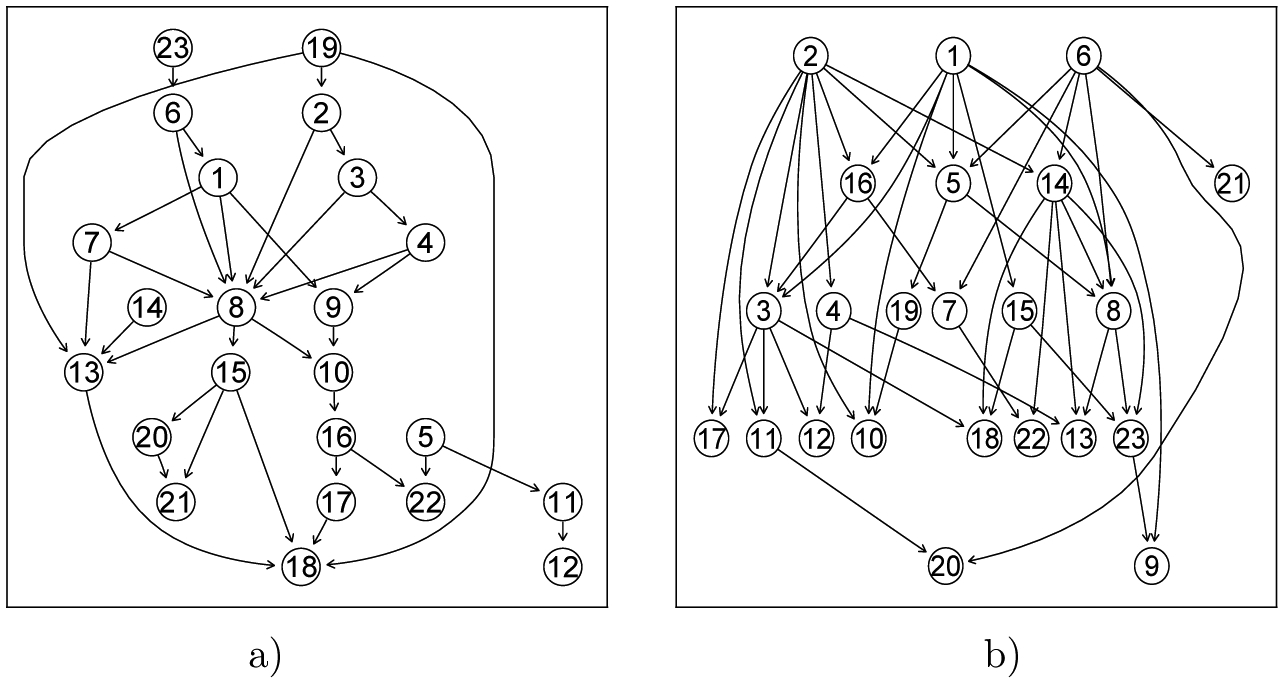
Estimated two differential networks . a) Subjects in utero exposed to smoke (48 subjects) b) Subjects not exposed (197 subjects)

Comparing the two networks (smoke exposed vs. smoke non-exposed) inferred based on data of 245 subjects, we observed substantially reduced connections of nodes 1 (cg03991871 on AHRR), 2 (cg04180046 on MYO1G), and 6 (cg06338710 on GFI1) as root nodes in the network for subjects with in utero smoke exposure. These CpGs are potential driving factors important to the differentiation between the two networks, and deserve further laboratory examinations and investigations. Another node 14 with cg18092474 (CYP1A1) also draws our attention. Although it is not like nodes 1, 2, and 6 such that none of these three nodes have parent nodes, node 14 also has a large number of connections with its children in the network for non-exposed subjects but only one child in the other network. In a recent meta analyses (Joubert et al., 2016), DNA methylation at these CpGs were demonstrated to be strong markers for in utero smoke exposure. In another study, cg03991871, cg04180046, and cg18092474, along with other CpG sites, are used to predict status of smoke exposure and the accuracy is 81% (Ladd-Acosta et al., 2016). To our knowledge, the inter-connections between these genes and DNA methylation sites have not been examined in any other studies. The findings from this real data application provide a potential and necessity for future investigations on the potential regulatory functionality of these four CpGs and the genes to which they are mapped. Additionally, instead of examining all possible CpG sites related to maternal smoke exposure during pregnancy, using the proposed method to assess differentiation and to select CpGs potentially leading to differentiation will substantially reduce the laboratory burden and make the experiment easier to manage.

5. Summary and Discussion

To examine the differentiation of joint activities for a set of CpG sites between two groups (exposed vs. non-exposed to smoke in utero) and identify potential driving factors leading to the differentiation, we utilized Bayesian networks and proposed a Bayesian method built upon the concept of variable selection to conclude the status of differentiation. The approximated conditional posterior probability mass function for the decision indicator variable has the property to converge to the underlying truth in terms of network differentiation. In the process of testing network differentiation, we estimated graph ordering using the Adjusted Single Queue Equi-Energy (ASQEE) algorithm proposed by Han et al. (2016) for the purpose to escape from local maximums. Theoretical assessment and simulations have demonstrated the effectiveness of the proposed methods in assessing differential networks. Real data applications further demonstrated that the method is practically useful and effective. We identified four potentially driving epigenetic factors, cg03991871, cg04180046, cg06338710 and cg18092474, such that they have the largest numbers of children.

Note that both X and Y in the proposed approach represent observational data and no experimental data are assumed. In this case, parents of node i are inferred based on posterior probability of edge connection indicators (i.e., $r_{ik}^{(c)}$, $r_{ik}^{(x)}$, and $r_{ik}^{(y)}$) conditional on other parameters. Without experimental data, one needs to be aware that only Markov equivalent networks are constructed for each given ordering of nodes (Andersson et al., 1997). Although this will not affect our conclusion on network differentiation (since given an ordering the true graph is among all the Markov equivalent networks for that ordering), the inferred network may not be the underlying true network. In practice, one way to ease this uncertainty is to bring in expertise from the corresponding research field, e.g., biologist and epigenetic epidemiologist for the study in our motivating example, to choose a network that is most practically meaningful.

The proposed approach for network comparisons utilizes an indicator variable for status of network differentiation, and has the ability to estimate networks as well as compare networks. If the focus is only on network comparisons, then we may consider augmenting the data by adding a node denoting treatment status, in which case no treatment effects indicate that the two networks are identical. This type of data augmentation, however, can be challenging for researchers in the applied fields, e.g., geneticists, since this added node is not a stimulus or experimental node but to assist statistical modeling. In addition, through this data augmentation, the strength and direction of connections may have to be estimated separately, should two networks conclude to be differential. In order to infer network and do comparison together, one way is to include interaction effects of treatment with each candidate parent. A careful design and efficient computing algorithms, however, are desired, which surely deserves further investigations.

The new method is not limited to DNA methylation data and is ready to other types of data with ordering unknown, e.g., expression of genes. For ordered data, the method can be easily simplified to fit the situation. In addition, it can be directly applied to perform pair-wise comparisons between multiple networks (> 2 networks), in which case adjustment of multiple testing needs to be considered. An analysis-of-variance-type network testing is desired for differentiation of more than two networks, although this extension maybe computationally intensive. Durante et al. (2018) proposed a Bayesian approach to test the association of undirected networks with a feature of interest, e.g., the association of brain connectivity structures with creative reasoning. This type of hypothesis testing has the potential to fit the needs of comparing more than two directed networks.

Appendix I.

The conditional posterior probability of η, p(η = 1|(·), X, Y)

In the following, we provide a derivation of the approximated full conditional posterior of η,

$$p(\eta =1\mid (\cdot ),X,Y)\approx {\left[1+\text{exp}\left\{\text{log}\left({\text{b}}_{\eta }\right)-\text{log}\left({\text{a}}_{\eta }\right)+\lambda (n)\right\}\right]}^{-1}$$

$$\lambda (n)=1/2\left(\left|E\right|\text{log}n-|E_x|\text{log}{n}_x-\left|E_y\right|\text{log}{n}_y\right).$$

It is an approximation of the posterior distribution of η conditional on r^(c) and variance components, ${\sigma }_x^2$ and ${\sigma }_y^2$, for a given graph ordering $\mathcal{O}$ with r^(c) being a collection of indicators representing inclusion or exclusion of parental nodes at each node. The justification laid out in this session follows in spirit the justification of Bayesian Information Criterion in Neath and Cavanaugh (2012). The conditional posterior probability of η = 1 conditional on r^(c) and the variance components for a given ordering is

$$\begin{gathered} p\left(\eta =1\mid X,Y,r^{(c)},{\sigma }_x^2,{\sigma }_y^2,\mathcal{O}\right)\propto p\left(X,Y\mid \eta =1,r^{(c)},{\sigma }_x^2,{\sigma }_y^2,\mathcal{O}\right)p(\eta =1) \\ \propto p\left(X,Y\mid \eta =1,r^{(c)},{\sigma }_x^2,{\sigma }_y^2,\mathcal{O}\right). \end{gathered}$$

The last proportionality is due to the choice of a non-informative prior in our work, p(η = 1) = 0.5.

In the following, we omit the dependence on $\mathcal{O}$ and the variance components for notation simplicity, but it needs to be clear that all the derivations are conditional on $\mathcal{O}$, ${\sigma }_x^2$, and ${\sigma }_y^2$. The distribution of X, Y conditional on η = 1 and r^(c) is,

$$\begin{gathered} p\left(X,Y\mid \eta =1,r^{(c)}\right)=p\left(Z\mid \eta =1,r^{(c)}\right) \\ =\prod _{j=1}^{p}p\left(Z_j\mid \eta =1,r_j^{(c)}\right) \\ =\prod _{j=1}^p{\int }_{{\beta }_j^{(c)}}p\left(Z_j\mid {\beta }_j^{(c)},\eta =1,r_j^{(c)}\right)p\left({\beta }_j^{(c)}\mid \eta =1,r_j^{(c)}\right)d{\beta }_j^{(c)} \\ =\prod _{j=1}^p{\int }_{{\beta }_j^{(c)}}{L}_j\left({\beta }_j^{(c)}\mid Z_j,\eta =1,r_j^{(c)}\right)p\left({\beta }_j^{(c)}\mid \eta =1,r_j^{(c)}\right)d{\beta }_j^{(c)}, \end{gathered}$$

where ${\mathit{\text{Z}}}_j={\left(X_j^T,Y_j^T\right)}^T$, ${\beta }_j^{(c)}=\left\{{\beta }_{ij}^{(c)},i=1,\cdots ,j-1\right\}$ denotes regression coefficients of connected edges at node i under η = 1, and ${\beta }_j^{(c)}~N\left(0,V_{c}I\right)$ with I an identity matrix and V_c known and large to formulate a non-informative but proper prior distribution for ${\beta }_j^{(c)}$.

Take the natural logarithm transformation of the likelihood function $L_j\left({\beta }_j^{(c)}\mid {\mathit{\text{Z}}}_{\mathit{\text{j}}},\eta =1,r_j^{(c)}\right)$ and perform Taylor expansion at ${\beta }_j^{\widehat{(}c)}$, a consistent estimator of ${\beta }_j^{(c)}$ such that ${{\text{lim}}_{n\to \infty }\frac{\partial \text{ log }{L}_j\left({\beta }_j^{(c)}\mid Z_{\mathit{\text{j}}},\eta =1,r_j^{(c)}\right)}{\partial {\beta }_j^{(c)}}|}_{{\beta }_j^{(c)}={\beta }_j^{\widehat{(}c)}}=0$. We have, for a large n,

$$\begin{gathered} \text{log}{L}_j\left({\beta }_j^{(c)}\mid {\mathit{\text{Z}}}_{\mathit{\text{j}}},\eta =1,r_j^{(c)}\right)\approx \text{log}{L}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right) \\ +{{\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)}^T\frac{\partial \text{log}{L}_j\left({\beta }_j^{(c)}\mid Z_j,\eta =1,r_j^{(c)}\right)}{\partial {\beta }_j^{(c)}}|}_{{\beta }_j^{(c)}={\beta }_j^{\widehat{(}c)}} \\ +1/{2{\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)}^T\frac{{\partial }^2\text{log}{L}_j\left({\beta }_j^{(c)}\mid Z_j,\eta =1,r_j^{(c)}\right)}{\partial {\beta }_j^{(c)}\partial {\beta }_j^{{(c)}^T}}|}_{{\beta }_j^{(c)}={\beta }_j^{\widehat{(}c)}} \\ \times \left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right) \\ \asymp \text{log}{L}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right) \\ +1/{2{\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)}^T\frac{{\partial }^2\text{log}{L}_j\left({\beta }_j^{(c)}\mid Z_j,\eta =1,r_j^{(c)}\right)}{\partial {\beta }_j^{(c)}\partial {\beta }_j^{{(c)}^T}}|}_{{\beta }_j^{(c)}={\beta }_j^{\widehat{(}c)}} \\ \times \left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right) \\ =\text{log}{L}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right) \\ -1/2{\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)}^T\left[n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right]\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right), \end{gathered}$$

where “≍” denotes “asymptotically equal to”, and

$${\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)=-1/{n\left({\partial }^2/\partial {\beta }_j^{(c)}\partial {\beta }_j^{{(c)}^T}\right)\text{log}{L}_j\left({\beta }_j^{(c)}\mid Z_j,\eta =1,r_j^{(c)}\right)|}_{{\beta }_j^{(c)}={\beta }_j^{\widehat{(}c)}}$$

is the sample Fisher information matrix.

Exponentiate both sides,

$$\begin{gathered} L_j\left({\beta }_j^{(c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\approx L_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right) \\ \times \text{exp}\left\{-1/2{\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)}^T\left[n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right]\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)\right\}, \end{gathered}$$

which gives

$$\begin{gathered} p\left(X,Y\mid \eta =1,r_j^{(c)}\right)=p\left(Z\mid \eta =1,r^{(c)}\right) \\ \approx \prod _{j=1}^p{\int }_{{\beta }_j^{(c)}}{L}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right) \\ \times \text{exp}\{-1/2{\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)}^T\left[n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right] \\ \left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)\}p\left({\beta }_j^{(c)}\mid \eta =1,r_j^{(c)}\right)d{\beta }_j^{(c)} \\ =\prod _{j=1}^p{L}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right) \\ \times {\int }_{{\beta }_j^{(c)}}\text{exp}\{-1/2{\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)}^T\left[n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right] \\ \left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)\}p\left({\beta }_j^{(c)}\mid \eta =1,r_j^{(c)}\right)d{\beta }_j^{(c)}. \end{gathered}$$ (7)

For the integration in (7),

$$\begin{gathered} {\int }_{{\beta }_j^{(c)}}\text{exp}\left\{-1/2{\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)}^T\left[n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right]\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)\right\}p\left({\beta }_j^{(c)}\mid \eta =1,r_j^{(c)}\right)d{\beta }_j^{(c)} \\ =C_0{\int }_{{\beta }_j^{(c)}}\text{exp}\left\{-1/2{\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)}^T\left[n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right]\left({\beta }_j^{(c)}-{\beta }_j^{\widehat{(}c)}\right)\right\} \\ \times \text{exp}\left\{-1/2\left[{\beta }_j^{{(c)}^T}{\left[V_{c}I\right]}^{-1}{\beta }_j^{(c)}\right]\right\}d{\beta }_j^{(c)} \\ =C_0{\int }_{{\beta }_j^{(c)}}\text{exp}\{-\frac{1}{2}[{\beta }_j^{{(c)}^T}\left(n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)+{\left(V_{c}I\right)}^{-1}\right){\beta }_j^{(c)} \\ -2{\beta }_j^{{(c)}^T}\left(n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right){\beta }_j^{\widehat{(}c)} \\ +{\beta }_j^{\widehat{(}c)}\left(n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right){\beta }_j^{\widehat{(}c)}]\}d{\beta }_j^{(c)} \\ =C_1{\int }_{{\beta }_j^{(c)}}\text{exp}\{-\frac{1}{2}[{\left({\beta }_j^{(c)}-{\Sigma }^{*}\left(n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right){\beta }_j^{\widehat{(}c)}\right)}^T{\Sigma }^{*-1} \\ \times \left({\beta }_j^{(c)}-{\Sigma }^{*}\left(n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right){\beta }_j^{\widehat{(}c)}\right)]\}d{\beta }_i^{(c)}, \\ =C_1\left[{(2\pi )}^{\left|E_j\right|/2}\right]{\left|{\Sigma }^{*}\right|}^{1/2}, \end{gathered}$$

where C₀ is a constant representing the normalizing constant for the prior ${\beta }_j^{(c)}$, C₁ is a constant combining C₀ and terms not involving ${\beta }_j^{(c)}$, ${\Sigma }^{*}={\left(n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)+\frac{1}{V_c}I\right)}^{-1}$, and |E_j| is the number of parents of node i.

Recall that V_c is the variance in the prior distribution of ${\beta }_j^{(c)}$ and chosen to be large to construct a non-informative but proper prior for ${\beta }_j^{(c)}$. When the sample size n is large, information in the data dominates the priors,

$$\begin{gathered} {\left|{\Sigma }^{*}\right|}^{1/2}={\left|\left(n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)+\frac{1}{V_c}I\right)\right|}^{-1/2} \\ \asymp {\left|n{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right|}^{-1/2} \\ =n^{-\left|E_j\right|/2}{\left|I_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right|}^{-1/2}. \end{gathered}$$

We thus have

$$\begin{gathered} p\left(X,Y\mid \eta =1,r_j^{(c)}\right)=p\left(Z\mid \eta =1,r^{(c)}\right) \\ \approx \left[{\left(\frac{2\pi }{n}\right)}^{{\sum }_{i=1}^p\left|E_i\right|/2}\right] \\ \prod _{j=1}^p\left[L_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right){\left|{\overline{I}}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)\right|}^{-1/2}\right] \\ \asymp C_z{n}^{-\left|E\right|/2}\prod _{j=1}^p{L}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right), \end{gathered}$$

where ${\sum }_{j=1}^p|E_i|=\left|E\right|$. C_z is a constant, since ${|{\overline{I}}_j\left({\beta }_j^{(c)}\mid Z_j,\eta =1\right)|}^{-1/2}$ converges as n → ∞ and based on assumption 3), $\left[{(2\pi /n)}^{{\sum }_{j=1}^p\left|E_j\right|/2}\right]\asymp \left[n^{-{\sum }_{j=1}^p\left|E_j\right|/2}\right]$. Note that ${\prod }_{j-1}^p{L}_j\left({\beta }_j^{\widehat{(}c)}\mid Z_j,\eta =1,r_j^{(c)}\right)$ is a_η defined in equation (5) in the main text under the Bayesian context. In a Gibbs sampler, ${\beta }_i^{\widehat{(}c)}$ is represented by posterior samples of ${\beta }_i^{(c)}$.

The same derivation applies to the calculation of $p\left(X,Y\mid \eta =0,r_j^{(x)},r_j^{(y)}\right)$, which gives

$$\begin{gathered} p\left(X,Y\mid \eta =0,r_j^{(x)},r_j^{(y)}\right)\approx C_{xy}{n}_x^{-\left|E_x\right|/2}{n}_y^{-\left|E_y\right|/2} \\ \times \prod _{j=1}^p\left[L_j\left({\beta }_j^{\widehat{(}x)}\mid X_j,\eta =0,r_j^{(x)}\right)L_j\left({\beta }_j^{\widehat{(}y)}\mid Y_j,\eta =0,r_j^{(y)}\right)\right], \end{gathered}$$

where C_xy is constant, and, as above, ${\prod }_{j-1}^p\left[L_j\left({\beta }_j^{\widehat{(}x)}\mid X_j,\eta =0,r_j^{(x)}\right)L_j\left({\beta }_j^{\widehat{(}y)}\mid Y_j,\eta =0,r_j^{(y)}\right)\right]$ is equivalent to b_η defined in equation (6) in the main text.

Now we have,

$$\begin{gathered} p(\eta =1\mid (\cdot ),X,Y)=\frac{p(X,Y\mid (\cdot ),\eta =1)}{p(X,Y\mid (\cdot ),\eta =1)+p(X,Y\mid (\cdot ),\eta =0)} \\ \approx \frac{C_z{a}_{\eta }\left(n^{-\left|E\right|/2}\right)}{C_z{a}_{\eta }\left(n^{-\left|E\right|/2}\right)+C_{xy}{b}_{\eta }\left(n_x^{-\left|E_x\right|/2}\right)\left(n_y^{-\left|E_y\right|/2}\right)} \\ {\left[1+\text{exp}\left\{\text{log}\left(b_{\eta }\right)-\text{log}\left(a_{\eta }\right)+1/2\left(\left|E\right|\text{log}n-\left|E_x\right|\text{log}{n}_x-\left|E_y\right|\text{log}{n}_y\right)+\text{log}\left(C_{xy}/C_z\right)\right\}\right]}^{-1} \\ ={\left[1+\text{exp}\left\{\text{log}\left(b_{\eta }\right)-\text{log}\left(a_{\eta }\right)+\lambda (n)+\text{log}\left(C_{xy}/C_z\right)\right\}\right]}^{-1} \\ \asymp {\left[1+\text{exp}\left\{\text{log}\left(b_{\eta }\right)-\text{log}\left(a_{\eta }\right)+\lambda (n)\right\}\right]}^{-1} \\ =p^{\lambda }(\eta =1\mid (\cdot ),X,Y), \end{gathered}$$

where λ(n) = 1/2(|E|logn − |E_x|logn_x − |E_y|logn_y). The last approximation is due to C_xy/C_z being bounded as n → ∞, conditional on the following assumptions, 1) |E|, |E_x|, and |E_y| are in the order of O(p) and |E| < |E_x|+|E_y|, 2) n_x and n_y approaches to infinity in the same speed, and 3) logn_x^/p → ∞ and logn_y/p → ∞ as n_x, n_y, p → ∞. We denote the approximated conditional posterior of η as p^λ(η = 1|(·), X, Y) with λ(n) acting like a penalty determined by sample size and conditional on edges of inferred graphs.

Appendix II.

Proof of the Proposition in Section 2.3.1

For any given ordering $\mathcal{O}$, let p denote the number of nodes, |E_x| the number of edges in the network constructed based on data of sample size n_x from population X, |E_y| the number of edges in the network based on data with size n_y from population Y, and |E| the number of edges of the identical network constructed combining the two populations with sample size n = n_x + n_y.

$$p^{\lambda }(\eta =1\mid (\cdot ),X,Y)\approx {\left[1+\text{exp}\left\{\text{log}\left(b_{\eta }\right)-\text{log}\left(a_{\eta }\right)+\lambda (n)\right\}\right]}^{-1}$$

$$\lambda (n)=1/2\left(\left|E\right|\text{log }n-|E_x|\text{log }{n}_x-\left|E_y\right|\text{log }{n}_y\right),$$

is the approximated conditional posterior probability for η.

Proposition:

Assume 1) sparse networks with |E|, |E_x|, and |E_y| in the order of O(p), 2) n_x → ∞ and n_y → ∞ in the same speed, and 3) logn_x/p → ∞ as n_x, p → ∞, and similar assumptions applied to ${\text{lim}}_{n_x,n_y\to \infty }{p}^{\lambda }\left(\eta =1|(·),\mathit{\text{X}},\mathit{\text{Y}}\right)=1$, and ${\text{lim}}_{n_x,n_y\to \infty }{p}^{\lambda }\left(\eta =1|(·),\mathit{\text{X}},\mathit{\text{Y}}\right)=0$ if the underlying η = 0.

Proof.

We examine the property of p^λ(η = 1|(·), X, Y) at the underlying values of η.

1. Underlying η = 1, i.e., the two populations share the same network.

   Set n_x = c₁n and n_y = c₂n with 0 < c₁,c₂ < 1, we have

   $$\begin{gathered} 1/2\left(|E_x|\text{log}{n}_x+\left|E_y\right|\text{log}{n}_y\right)=1/2\left\{|E_x|\text{log}\left(c_{1}n\right)+\left|E_y\right|\text{log}\left(c_{2}n\right)\right\} \\ =1/2\left(|E_x|\text{log}n+\left|E_y\right|\text{log}n+|E_x|\text{log}{c}_1+\left|E_y\right|\text{log}{c}_2\right). \end{gathered}$$
   For any given ordering, we assume |E| < |E_x| + |E_y|. That is, the two graphs have at least one edge in common and if an edge does not exist in each individual network, then it is not in the combined network either. We then have 1/2(|E|logn − |E_x|logn_x − |E_y|logn_y) = 1/2logn(|E| − |E_x| − |E_y|) − logc₁|E_x|/2 − logc₂|E_y|/2 → −∞, as n_x, n_y → ∞ (so does n). Furthermore, as n_x, n_y → ∞, from the definitions of loga_η and logb_η, loga_η − logb_η → 0 as n_x, n_y → ∞ when the underlying η = 1. Combining all these leads to

   $$\text{log}{b}_{\eta }-\text{log}{a}_{\eta }+1/2\left(\left|E\right|\text{log}n-|E_x|\text{log}{n}_x-\left|E_y\right|\text{log}{n}_y\right)\to -\infty ,$$

   which gives p^λ(η = 1|(·), X, Y) → 1 as n_x, n_y → ∞ if the underlying η = 1.
2. Underlying η = 0, i.e., each of the two populations has its unique network under a given ordering. Following the definition of a_η, we have

   $$\begin{gathered} \text{log}{a}_{\eta }=\sum _{j=1}^p\left\{-\frac{n_x}{2}\text{log}{\sigma }_{x(j)}^2-\frac{n_y}{2}\text{log}{\sigma }_{y(j)}^2 \\ -\frac{{\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{X}_i\right)}^T\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{X}_i\right)}{2{\sigma }_{x(j)}^2} \\ -\frac{{\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{Y}_i\right)}^T\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(c)}{Y}_i\right)}{2{\sigma }_{y(j)}^2}\right\} \\ =\sum _{j=1}^p\left\{-\frac{n_x}{2}\text{log}{\sigma }_{x(j)}^2-\frac{n_y}{2}\text{log}{\sigma }_{y(j)}^2-\sum _{l_1=1}^{n_x}\frac{{ϵ}_{l_1}^c{}^2}{2{\sigma }_{x(j)}^2}-\sum _{l_2=n_x+1}^n\frac{{ϵ}_{l_2}^c{}^2}{2{\sigma }_{y(i)}^2}\right\}, \end{gathered}$$

   $$\begin{gathered} \text{log}{b}_{\eta }=\sum _{j=1}^p\left\{-\frac{n_x}{2}\text{log}{\sigma }_{x(j)}^2-\frac{n_y}{2}\text{log}{\sigma }_{y(j)}^2 \\ -\frac{{\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(x)}{X}_i\right)}^T\left(X_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(s)}{X}_i\right)}{2{\sigma }_{x(j)}^2} \\ -\frac{{\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(y)}{Y}_i\right)}^T\left(Y_j-{\sum }_{i=1}^{j-1}{\beta }_{ij}^{(y)}{Y}_i\right)}{2{\sigma }_{y(j)}^2}\right\} \\ =\sum _{j=1}^p\left\{-\frac{n_x}{2}\text{log}{\sigma }_{x(j)}^2-\frac{n_y}{2}\text{log}{\sigma }_{y(j)}^2-\frac{{\sum }_{l_{1=1}}^{n_x}{ϵ}_{l_1}^x{}^2}{2{\sigma }_{x(j)}^2}-\frac{{\sum }_{l_{2=n_x+1}}^n{ϵ}_{l_2}^y{}^2}{2{\sigma }_{y(j)}^2}\right\}, \end{gathered}$$

   $$\text{log}{b}_{\eta }-\text{log}{a}_{\eta }=\sum _{j=1}^p\left(\frac{{\sum }_{l_{1=1}}^{n_x}\left({ϵ}_{l_1}^c{}^2-{ϵ}_{l_1}^x{}^2\right)}{2{\sigma }_{x(j)}^2}+\frac{{\sum }_{l_{1=n_x+1}}^{n_x}\left({ϵ}_{l_2}^c{}^2-{ϵ}_{l_2}^y{}^2\right)}{2{\sigma }_{y(j)}^2}\right).$$

   In the following, property on one node is assessed and the results can be directly applied to the sum of all p nodes. If the underlying η = 0, that is, the relations among the nodes in the two populations are differential at least at one node, then, regardless of the ordering, forcing two differential networks to unify will result in larger random errors, i.e.,

   $$\left({ϵ}_{l_1}^c{}^2-{ϵ}_{l_1}^x{}^2\right)/n_x\to {\sigma }_{x(j)}^{\prime 2}-{\sigma }_{x(j)}^2>0$$

   $$\left({ϵ}_{l_2}^c{}^2-{ϵ}_{l_2}^y{}^2\right)/n_y\to {\sigma }_{y(j)}^{\prime 2}-{\sigma }_{y(j)}^2>0,$$

   which lead to ${\sum }_{l_{1=1}}^{n_x}\left({ϵ}_{l_1}^c{}^2-{ϵ}_{l_1}^x{}^2\right)\to \infty$ and ${\sum }_{l_{1=n_x+1}}^n\left({ϵ}_{l_2}^c{}^2-{ϵ}_{l_2}^y{}^2\right)\to \infty$ in an ordering of O(n) as n_x, n_y → ∞, that is, logb_η − loga_η → ∞ in an ordering of O(n).
   For λ(n) = 1/2(|E|logn−|E_x|logn_x−|E_y|logn_y) in the definition of p^λ(η = 1|(·), X, Y),

   $$\begin{gathered} 1\mid (\cdot ),X,Y), \\ 1/2\left(\left|E\right|\text{log}n-|E_x|\text{log}{n}_x-\left|E_y\right|\text{log}{n}_y\right) \\ =1/2\left(\left|E\right|-|E_x|-\left|E_y\right|\right)\text{log}n \\ -1/2\left(|E_x|\text{log}{c}_1+\left|E_y\right|\text{log}{c}_2\right) \\ =A\text{log }n-1/2\left(|E_x|\text{log}{c}_1+\left|E_y\right|\text{log}{c}_2\right), \end{gathered}$$

   where A = 1/2(|E| − |E_x| − |E_y|). Since |E| < |E_x| + |E_y|, as n_x, n_y → ∞, A log n → −∞ in O(logn). Based on the sparsity assumption 1), 1/2(|E_x|logc₁ + |E_y|logc₂) → ∞ in the order p. Following assumption 3), we have Alogn − 1/2(|E_x|logc₁ + |E_y|logc₂) → ∞ in O(logn), which is slower than logb_η−loga_η → ∞ in an ordering of O(n). Thus logb_η−loga_η+1/2(|E|logn − |E_x|logn_x − |E_y|logn_y) → ∞, i.e., p^λ(η = 1|(·), X, Y) → 0 as n_x, n_y → ∞.

   In summary, p^λ(η = 1|(·), X, Y) → 0 as n_x, n_y → ∞ when underlying η = 0 for any given ordering $\mathcal{O}$.

Combining results in 1. and 2. above, we have, for any given ordering $\mathcal{O}$, ${\text{lim}}_{n_x,n_y\to \infty }{p}^{\lambda }\left(\eta =1|(·),\mathit{\text{X}},\mathit{\text{Y}}\right)=1$ if underlying η = 1, and ${\text{lim}}_{n_x,n_y\to \infty }{p}^{\lambda }\left(\eta =1|(·),\mathit{\text{X}},\mathit{\text{Y}}\right)=0$ □