Risk Characterization and Probabilistic Concentration–Response Modeling of Complex Environmental Mixtures Using New Approach Methodologies (NAMs) Data from Organotypic in Vitro Human Stem Cell Assays

Abstract

Background:

Risk assessment of chemical mixtures or complex substances remains a major methodological challenge due to lack of available hazard or exposure data. Therefore, risk assessors usually infer hazard or risk from data on the subset of constituents with available toxicity values.

Objectives:

We evaluated the validity of the widely used traditional mixtures risk assessment paradigms, Independent Action (IA) and Concentration Addition (CA), with new approach methodologies (NAMs) data from human cell-based in vitro assays.

Methods:

A diverse set of 42 chemicals was tested both individually and as mixtures for functional and cytotoxic effects in vitro. A panel of induced pluripotent stem cell (iPSCs)-derived models (hepatocytes, cardiomyocytes, endothelial, and neurons) and one primary cell type (HUVEC) were used. Bayesian concentration–response modeling of individual chemicals or their mixtures was performed for a total of 47 phenotypes to derive point-of-departure (POD) values. Probabilistic IA or CA was conducted to estimate the mixture effects based on the bioactivity profiles from the individual chemicals and compared with mixture bioactivity.

Results:

All mixtures showed significant bioactivity, even though some were constructed using individual chemical concentrations considered “low” or “safe.” Even though CA is much more accurate as a predictor of mixture effects in comparison with IA, with CA-based POD typically within an order of magnitude of the actual mixture, in some cases, the bioactivity of the mixtures appeared to be much greater than that of their components under either additivity assumption.

Discussion:

These results suggest that CA is a preferred first approximation for predicting mixture toxicity when data for all constituents are available. However, because the accuracy of additivity assumptions varies greatly across phenotypes, we posit that mixtures and complex substances need to be directly tested for their hazard potential. NAMs provide a practical solution that rapidly yields highly informative data for mixtures risk assessment. https://doi.org/10.1289/EHP7600

Introduction

Current risk assessment frameworks are designed primarily for the evaluation of one chemical at a time (Clahsen et al. 2019; Lebret 2015), even though most human exposures, especially in the environmental or occupational setting, occur in the context of mixtures (Carpenter et al. 2002; Martin et al. 2013). It is well recognized that an individual chemical-based focus can underestimate risks because interaction among the components in a mixture can result in complex and substantial changes in the apparent properties of the constituents (Kortenkamp and Faust 2018). Furthermore, most mixture exposure–effect studies focus on the adverse effects of mixtures consisting of chemicals from the same category (Zhang et al. 2010). This approach does not reflect “real-world” exposures from dozens or hundreds of pollutants that may have complex additive or synergistic/antagonistic health effects. Although several regulatory authorities are developing approaches to extend traditional risk characterization frameworks to mixtures (Bopp et al. 2019; European Chemicals Agency 2017; More et al. 2019), the knowledge gap in quantitative characterization of the effects by individual chemicals and their mixtures is a major challenge in regulatory science.

A most common approach to evaluate the adverse health effects of a mixture makes use of the available toxicological data on the known constituents. Two classical approaches are concentration addition (CA) and independent action (IA); they are widely used in risk assessment of mixtures (Backhaus and Faust 2012; Cedergreen et al. 2008; Spiess and Neumeyer 2010; Zhu and Chen 2016). These approaches estimate the toxic potential of a mixture based on the individual chemical’s concentration–response curves, either through adding concentrations in a “relative potency”-type approach (CA), or by adding responses assuming independence (IA). Some studies have developed more sophisticated approaches and tools for environmental mixture toxicity assessment. Li et al. (2012) proposed a gradient Markov Chain Monte Carlo (MCMC) algorithm to find Bayesian posterior mode estimates in mixture dose–response assessment. Ritz et al. (2015) developed an R package drc for curve-fitting and analyzing the mixture concentration–response. However, these studies have focused on binary mixtures and have not yet been extended to reflect real-world scenarios; more complex data sets are needed to test these modeling approaches.

Novel exposure and in vitro data, now commonly referred to as “New Approach Methodologies” (NAMs) (Kavlock et al. 2018), may assist in providing empirical data for mixtures risk assessment. Among NAMs, in vitro human cell-based models are well-recognized as useful tools for characterizing chemical hazards and as alternative methods to traditional animal testing strategies (Rotroff et al. 2010; Shukla et al. 2010), and their high-throughput format allows for rapid testing of mixtures, though experiments with individual chemicals dominate NAMs data available to date. It has been suggested that integrating mixture risk assessment with NAMs testing may hold promise in reducing uncertainties in the health effects of mixture exposures (Drakvik et al. 2020).

The purpose of this study was to use NAMs data from targeted testing of dozens of diverse individual chemicals and their designed mixtures in a suite of human cell-based in vitro organotypic assays followed by data-driven characterization of concentration–response relationships. We combined high-content experimental data and Bayesian concentration–response modeling to estimate mixture effects and compare those with actual data from the mixtures. Specifically, we tested the hypothesis, commonly assumed in current mixtures risk assessment, that complex mixture effects can be predicted based on additivity of individual chemical concentrations or effects. The results of this analysis could have broad implications for cumulative risk assessment of real-world exposures.

Material and Methods

Figure 1 illustrates the overall workflow of the experiments, data analysis, and modeling in this study. First, we collected new data from in vitro testing in human induced pluripotent stem cell (iPSC)-derived models for a dilution-series of 8 “designed” mixtures (Tables S2–S5) of 42 Superfund Priority chemicals (Table S1). Next, we applied Bayesian concentration–response modeling to fit the experimental data for the designed mixtures, as well as for their individual chemical constituents [data previously reported in (Chen et al. 2020)]. The fitted concentration–response relationships for the designed mixtures were compared to the concentration–response predicted from the individual chemical data assuming either CA or IA. Finally, we illustrated mixtures risk characterization by calculating a cumulative margin of exposure (MOE) for the whole mixture and comparing it with the predictions from CA or IA.

Figure 1.

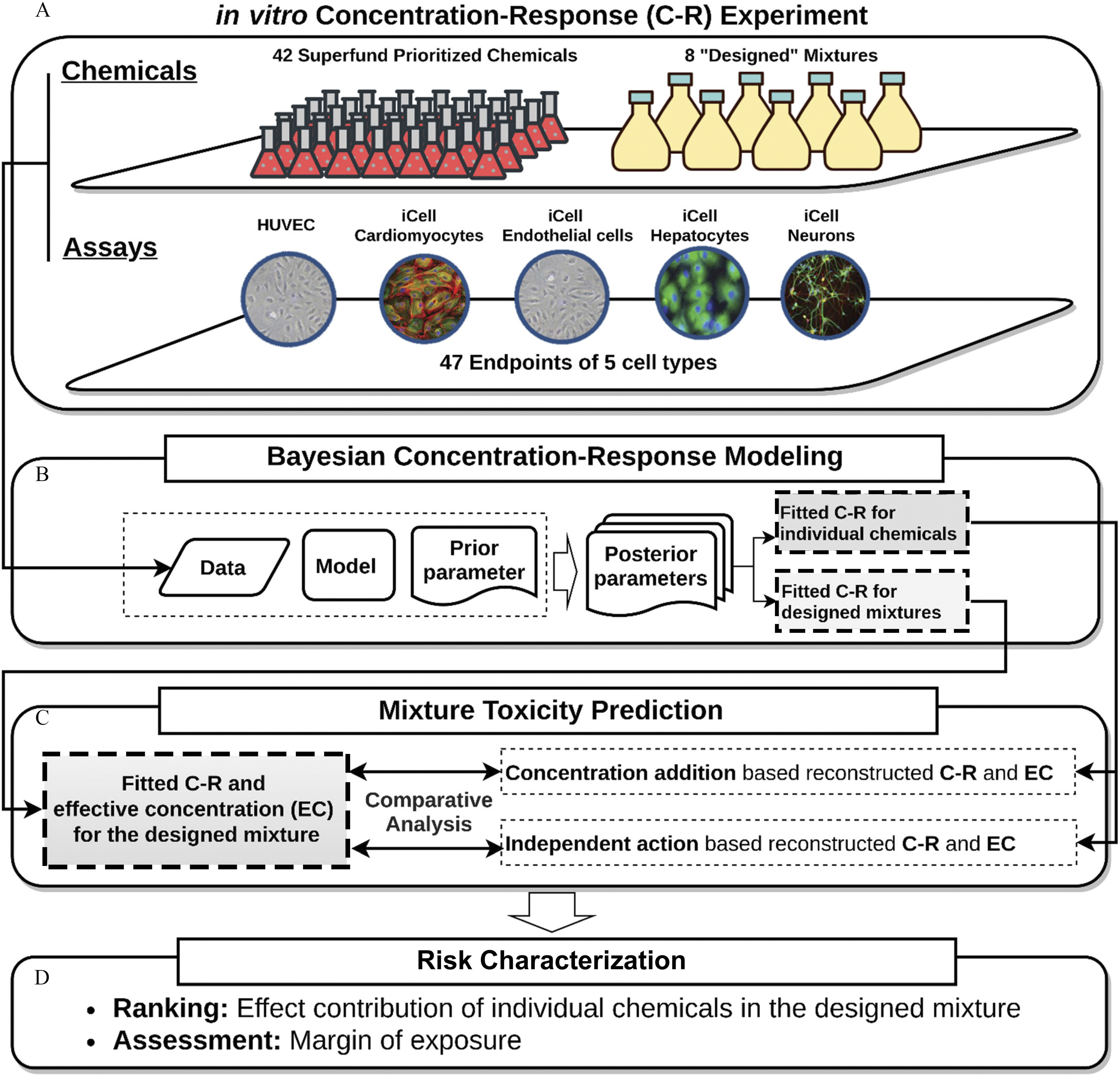
Schematic diagram of the overall study design. (A) The in vitro cell assay was conducted to construct the concentration–response relationship for human stem cells under the exposure of individual chemicals and designed mixture. (B) The Bayesian probabilistic approach was further applied to simulate the likelihood of the exposure–effect pattern. (C) Two additive reference models, independent action (based on the conditional effect) and concentration addition (based on the conditional concentration), were adopted to assume the combined toxicity. (D) The contributed effect and margin of exposure were calculated to characterize the individual and combined risk.

Biologicals and Chemicals

Five human cell types were used in these studies. iCell hepatocytes 2.0 (Catalog# C1023), neurons (Catalog# C1008), cardiomyocytes (Catalogue# CMC-100-010-001), and endothelial cells (Catalogue# C1023), as well as cell-type-specific media and supplements as defined by the manufacturer, were from FujiFilm Cellular Dynamics. Pooled human umbilical vein endothelial cells (HUVECs) in EGM-2 medium (Catalogue# CC-2519A), and the EGMTM-2 BulletKits (Catalogue# CC-3,162) were from Lonza.

Additional reagents used were as follows. CellTiter-Glo reagent was from. EarlyTox Cardiotoxicity Kit (Catalogue# R8211) was from Molecular Devices. RPMI 1640 medium, B-27 medium supplement, gentamicin ($50\mathrm{mg}/\text{ml}$), Calcein AM Green, MitoTracker Orange reagent, Hoechst 33,342, fibronectin, and GeltrexTM LDEV-Free Reduced Growth Factor Basement Membrane were from Life Technologies. Recombinant human VEGF was provided by R&D Systems. Fetal bovine serum and Medium 199 were purchased from Fisher Scientific. Laminin (from Engelbreth-Holm-Swarm murine sarcoma basement membrane) was from Sigma-Aldrich. Cell culture grade dimethyl sulfoxide (DMSO) was from Santa Cruz Biotechnology.

The individual chemicals (Table S1) used in this study to prepare the mixtures and for comparisons to mixtures were from the priority list of hazardous substances from the Agency for Toxic Substances and Disease Registry (ATSDR 2020). From the list of over 300 chemicals on the ATSDR list, compounds that are frequently detected at the U.S. National Priority List sites (also known as Superfund sites), we selected 42 chemicals based on the following criteria. These chemicals represent diverse classes of environmental pollutants, including polycyclic aromatic hydrocarbons (PAHs, $n=5$), inorganic substances ($n=7$), phthalates ($n=2$), pesticides ($n=20$), and other industrial chemicals ($n=8$). They have been evaluated by one or more government agencies, and human “safe exposure” levels have been established. These chemicals were also tested in ToxCast™/Tox21. Also, their reverse toxicokinetic and exposure data are publicly available through the U.S. Environmental Protection Agency (U.S. EPA) dashboard (Williams et al. 2017), thus allowing for in vitro to in vivo extrapolation and risk characterization. Chemicals were from Sigma-Aldrich, except heptachlor, heptachlor epoxide, 2,4,5-trichlorophenol, parathion, benzidine and o,p′-DDT, which were from ChemService.

Preparation of Chemical Mixtures

Chemical mixtures evaluated in this study were designed based on the following considerations. First, we aimed to create mixtures of a large number of chemicals, covering multiple classes of environmental contaminants. Second, as summarized in Table 1, the concentration of each mixture component was determined through several alternative assumptions: a) active concentration 50% (${\text{AC}}_{50}$) values from in vitro assays in the ToxCast™ database (Williams et al. 2017); b) the estimated general population exposure levels derived from ExpoCast estimates (Wambaugh et al. 2013); c) point-of-departure (POD) values from in vivo studies in experimental animals used for determining regulatory oral noncancer reference doses (RfDs) (Wignall et al. 2014), or d) RfDs themselves (Wignall et al. 2014). For criteria b–d, oral doses were converted to the steady-state of chemical concentration at steady state (Css)-based values using the httk R package (version 1.10.1; Pearce et al. 2017). The median or upper 95th percentile was used to represent different assumptions for the toxicokinetic variability (Table 1). Individual chemicals (Table S1) were dissolved in 100% cell culture-grade DMSO at a concentration of $20\text{\hspace{0.17em}mM}$. Then, chemicals were mixed at different proportions to address the considerations listed above and as detailed in Tables S2–S5. All mixtures were then tested using $10\times$ serial dilutions to generate concentration–response data at five serial dilutions.

Table 1.

Mixtures of the 42 superfund priority chemicals from (Chen et al. 2020) used in this study.

Mixture	Description	Notes
${\text{AC}}_{50}\text{-L}$	Lowest AC50s from ToxCast™	a
${\text{AC}}_{50}\text{-H}$	Highest AC50s from ToxCast™	a
Expo-L	Median ExpoCast oral exposure, converted to median Css	a,b,c
Expo-H	95th percentile ExpoCast oral exposure, converted to 95th percentile Css	a,b,c
POD-L	Point of departure used for oral RfD, converted to median Css	a,b,c,d,e
POD-H	Point of departure used for oral RfD, converted to 95th percentile Css	a,b,c,d,e
RfD-L	Oral RfD, converted to median Css	a,b,c,d,f
RfD-H	Oral RfD, converted to 95th percentile Css	a,b,c,d,f

^aFor metals, values were set based on previous literature as shown below:

Cd (II), Cr (VI) and Co (II): Michal W. Luczak, Anatoly Zhitkovich. 2013. Role of direct reactivity with metals in chemoprotection by N-acetylcysteine against chromium (VI), cadmium (II), and cobalt (II). Free Radic Biol Med 65:262–269.

Hg (II): Xu S-Z, Zeng B, Daskoulidou N, Chen G-L, Atkin SL, Lukhele B. 2012. Activation of TRPC cationic channels by mercurial compounds confers the cytotoxicity of mercury exposure. Tox Sci 125(1), 56–68.

Zn (II): Shen C, James SA, de Jonge MD, Turney TW, Wright PFA, Feltis BN. 2013. Relating cytotoxicity, zinc ions, and reactive oxygen in ZnO nanoparticle–exposed human immune cells. Toxicol Sci 136(1), 120–130.

Ni (II): Funakosh Ti, Inoue T, Shimada H, Kojima S. 1997. The mechanisms of nickel uptake by rat primary hepatocyte cultures: role of calcium channels. Toxicology 124:21–26.

Pb (II): Tchounwou PB, Yedjou CG, Foxx DN, Ishaque AB, Shen E. 2004. Lead-induced cytotoxicity and transcriptional activation of stress genes in human liver carcinoma (HepG2) cells. Mol Cell Biochem 255:161–170.

^bCss, steady state plasma concentration; calculated using httk R package.

^cFor heptachlor epoxide, value for heptachlor was used; for DEHP, value for DBP was used.

^dFor benzo(a)anthracene and gamma-hexachlorocyclohexane, the concentration range was set between 1 and $100\mathrm{\mu }\mathrm{M}$; for endrin, value for dieldrin was used; for benzo(b)fluoranthene, value for fluoranthene was used; for p,p′-DDD and o-p′-DDT, value for p,p′-DDT was used.

^eFor 4,6-dinitro-o-cresol, 2,4-dinitrotoluene was used; for 1,2,3-trichlorobenzene, value for 2,4,6-trichlorophenol was used.

^fFor para-cresol, value was converted from risk specific dose (RSD, milligrams per kilogram per day) for a ${10}^{-6}$ cancer risk.

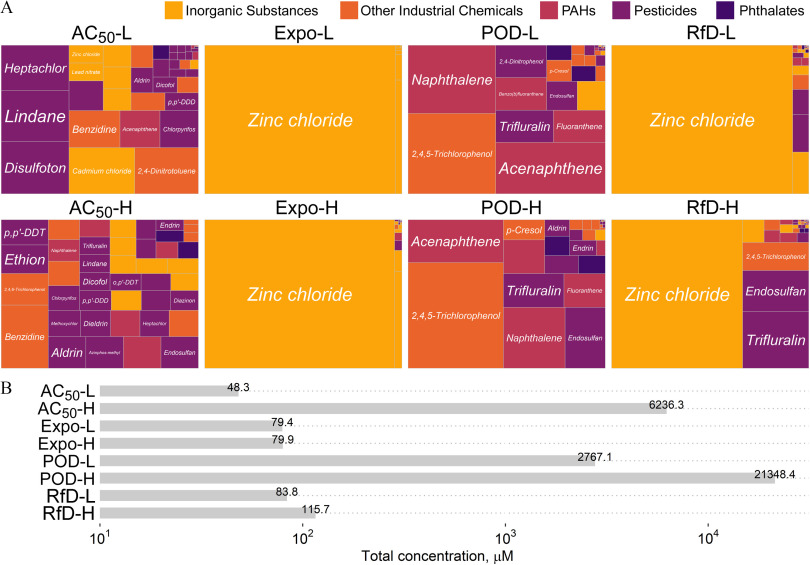
As shown in Figure 2, relative proportions of the individual chemicals and the overall cumulative concentrations varied across mixtures. Both groups of mixtures from in vitro (${\text{AC}}_{50}$) and in vivo values (POD) were relatively evenly distributed by the proportion of individual chemicals in comparison with the other groups, which were mostly dominated by the metal zinc chloride due to the much lower concentrations of other chemicals. The concentrations for metals were based on an in vitro study (Table 1) because metals are not included in the httk package (Figure 2A). There were also differences in the cumulative concentration for the mixtures generated based on exposure levels and RfD (Figure 2B).

Figure 2.

Summary of the properties of the designed mixtures used in this study. (A) Treemap of the chemical proportions contained in each of the designed mixtures. The color represents the classes of environmental contaminants that were selected in the study. (B) Cumulative (maximum) concentration of the chemicals in each designed mixture. See acronym explanations and description of the designed mixtures in Table 1.

Due to the limitation of each database, some values for certain chemicals were not available. To keep the integrity of each mixture containing all 42 chemicals, different criteria, such as read-across from chemicals with similar structures, based on common occurrence in the environment, were applied for chemicals without available data (see notes in Table 1, with concentrations listed in Tables S2–S5).

Cell Culture and Exposure

Cells were cultured in tissue culture-grade 384-microwell plates according to the cell supplier’s (Fujifilm Cellular Dynamics and Lonza) recommendations with respect to cell culture medium and supplements for each cell type. See Table S6 for links to the manufacturer protocols used for each cell type. Experimental protocols for chemical treatments and phenotyping have also been previously described for each of these cell types, including iCell hepatocytes and iCell cardiomyocytes (Grimm et al. 2015), iCell Endothelial cells and human umbilical vein endothelial cells (Iwata et al. 2017), and iCell neurons (Sirenko et al. 2014). In brief, the microwell plates were pretreated with either 0.1% gelatin (for iCell hepatocytes and iCell cardiomyocytes), $3{\mathrm{\mu }\mathrm{g}/\mathrm{cm}}^2$ fibronectin (for iPSC-ECs), and poly D-lysine followed by $3.3\text{\hspace{0.17em}ug}/\mathrm{mL}$ laminin (for iCell neurons). For HUVECs, microwell plates were not pretreated. Cells were resuspended in cell-specific culture media and trypan blue was used to measure cell density before plating. Cells were plated ($25\mathrm{mL}/\text{well}$) at a concentration of $2\times {10}^5\text{\hspace{0.17em}cells}/\mathrm{mL}$ for iCell cardiomyocytes (5,000 cells/well, incubated for 12 d before treatment); $6.72\times {10}^5\text{\hspace{0.17em}cells}/\mathrm{mL}$ for iCell hepatocytes (16,800 cells/well, incubated for 5 d before treatment); for iPSC-EC, cell densities varied based on the assay type, $3\times {10}^4\text{cells}/\mathrm{mL}$ (750 cells/well, incubated for 2 d before treatment for cytotoxicity assays) or $3\times {10}^5\text{cells}/\mathrm{mL}$ (7,500 cells/well, cell suspension was freshly prepared before treatment for angiogenesis assays); for HUVEC, cell densities varied based on the assay type, $3\times {10}^4\text{cells}/\mathrm{mL}$ (750 cells/well, incubated for 2 d before treatment for cytotoxicity assays) or $1.4\times {10}^5\text{cells}/\mathrm{mL}$ (3,500 cells/well, cell suspension was freshly prepared before treatment for angiogenesis assays); and $3\times {10}^5\text{cells}/\mathrm{mL}$ for iCell neurons (7,500 cells/well, incubated for 2 d before treatment).

Designed mixture stocks in 100% DMSO were further diluted 100-fold in corresponding cell culture medium to yield $4\times$ working solutions in 1% dimethylsulfoxide (DMSO). The final concentration of DMSO in assay wells to following addition of test mixtures was 0.25% (v/v), an amount which by itself had no effects on each of the tested cell types (Grimm et al. 2015; Iwata et al. 2017; Sirenko et al. 2014). Screening assays across different cell types were performed in duplicate.

For each cell line, a number of phenotypes (Table S6) were evaluated using high-content imaging as detailed in (Chen et al. 2020; Grimm et al. 2015; Iwata et al. 2017; Sirenko et al. 2014). Table S6 lists the phenotypes for each cell type and chemical treatment duration time for each phenotype. A total of 47 phenotypes (Table S6) were assessed across five cell types, including cytotoxicity and cell function effects. Effects on the mitochondrial integrity and intensity of iCell hepatocytes and neurite outgrowth of iCell neurons were measured using high-content fluorescence imaging (ImageXpress Micro Confocal High-Content Imaging System, Molecular Devices). Calcium flux, a surrogate for beating and ion channel activity in iCell cardiomyocytes, was determined by FLIPR tetra (Molecular Devices) high-content kinetic imaging instrument using EarlyTox™ Cardiotoxicity Kit (Molecular Devices) as detailed in (Grimm et al. 2015). Effects on angiogenesis in both iCell endothelial cells and HUVECs was measured by 3D cell culture using extracellular gel matrix and followed by high-content fluorescence imaging as detailed in Iwata et al. (2017). Image analysis was performed using the Multi-Wavelength Cell Scorning, Neurite Outgrowth, or Angiogenesis Tube Formation application modules in MetaXpress (Molecular Devices) software (Table S6), and quantitative data were extracted for concentration–response modeling.

Concentration–Response Modeling

First, raw data for each phenotype were normalized to the average of the vehicle (0.25% DMSO)-treated wells. Next, the effective concentration for a 10% relative change from controls (${\text{EC}}_{10}$) was chosen as the representative point of departure (POD) for both cytotoxicity and functional responses as a representative benchmark dose used commonly in dose–response assessments for quantitative phenotypes (Chiu et al. 2017; Sirenko et al. 2017).

Bayesian Concentration–Response Modeling

We used a Bayesian approach for the analysis to quantify the uncertainty in our PODs and concentration–response relationships (Figure 1A). The Bayes’ rule can be simply expressed as Gelman et al. (2013)

$$p\left(\mathrm{\theta },E\right)\propto p\left(\mathrm{\theta }\right)p\left(E\right|\mathrm{\theta }),$$

where $\mathrm{\theta }$ is the parameters in the concentration–response model, E is the observed response from the given dose. The $p\left(\mathrm{\theta }\right)$ is the prior distributions of model parameters, and $p\left(E\right|\mathrm{\theta })$ are the observed data from individual chemicals and mixture in this study. We adopted the Hill model from the BMD model suite (Davis et al. 2011; Shao and Shapiro 2018) that parameterized the concentration–response profile as

$$E\left(C_i|\mathrm{\theta }\right)=\frac{{\mathrm{\theta }}_0}{1+{\left(\frac{C}{{\mathrm{\theta }}_1}\right)}^{{\mathrm{\theta }}_2}}+{ϵ}_i,$$

where $C_i$ is the ith-experimental concentration for the individual chemical ($\mathrm{\mu }\mathrm{M}$) or dilution factor (unitless) for the mixture. ${\mathrm{\theta }}_0$ is the baseline response and was assigned a fixed value of 1 due to the renormalization with the control (0.25% DMSO vehicle) group. ${\mathrm{\theta }}_1$ is the concentration at half of the maximal response (also known as ${\text{EC}}_{50}$). ${\mathrm{\theta }}_2$ is the Hill coefficient that determines the slope of the simulated curve, and ${\mathrm{\epsilon }}_i$ is residual error. The settings of prior parameters were based on the Bayesian BMD platform (Shao and Shapiro 2018). For $\mathrm{\epsilon }$, instead of a normal distribution, the error estimation between the data and model was assumed to follow a Student’s $t$ distribution with the degrees of freedom equal to 5 with scale parameter $\mathrm{\sigma }$ to recognize the outliers issue (Blanchette et al. 2019; Chiu et al. 2017). The likelihood of response data $E_i$ for concentration $C_i$ was assumed to be

$$E_i\sim T_5\left(f\left(C_i,|{\mathrm{\theta }}_1,|{\mathrm{\theta }}_2\right),|\mathrm{\sigma }\right),$$

where f(.) is the Hill concentration–response model that is the function of 2 Hill parameters (${\mathrm{\theta }}_1,{\mathrm{\theta }}_2$) and the designed concentration $C_i$. The prior of $\mathrm{\sigma }$ was assumed to be a half-normal distribution with standard deviation 0.1 and therefore can be written as,

$$\mathrm{\sigma }\sim N\left(0,0.1\right),\mathrm{\sigma }\ge 0.$$

We used log-uniform distribution for the given parameter ${\mathrm{\theta }}_1$ due to the parameter range being over 1 order of magnitude, with a range from 1 order of magnitude below the lowest experimental concentration to 2 orders of magnitude above the highest experimental concentration. Thus, the prior for ${\mathrm{\theta }}_1$ was assigned to be

$$\mathit{log}\left({\mathrm{\theta }}_1\right)\sim Uniform[\mathit{log}\left({\mathrm{\theta }}_{1,min}\right),|\mathit{log}\left({\mathrm{\theta }}_{1,max}\right)].$$

The Hill coefficient (a power parameter) was set to the range 0.1 to 15 for the mixtures but assumed the positive cooperativity that ranged between 1 to 15 for the individual chemicals. This lower boundary aimed to avoid a shallow concentration–response that causes unstable estimates of the POD, particularly when combining into a mixture using IA or CA. Thus, the prior for ${\mathrm{\theta }}_2$ was assigned to be

$${\mathrm{\theta }}_2\sim Uniform\left({\mathrm{\theta }}_{1,min},|{\mathrm{\theta }}_{1,max}\right).$$

The final Bayesian concentration–response model can be therefore written as

$$p({\mathrm{\theta }}_1,|{\mathrm{\theta }}_2\left|E_i\right)\propto p\left({\mathrm{\theta }}_1\right)\cdot p\left({\mathrm{\theta }}_2\right)\cdot p\left(E_i\right|{\mathrm{\theta }}_1,\left|{\mathrm{\theta }}_2\right).$$

Posterior distribution sampling was conducted using the Hamiltonian MCMC algorithm. For each chemical or mixture, the simulations consisted of three chains with the first half treated as a warm-up and hence discarded.

To obtain the robust and consistent sampling result, the convergence was assessed using the potential scale reduction factor $\widehat{R}$ (Gelman and Rubin 1992), which compares between- and within-chain variability. $\widehat{R}\gg 1$ indicate poor convergence, and asymptotically approach 1 as the chain converges. Parameters with values of $\widehat{R}\le 1.05$ were considered to be converged in our simulation.

The posterior prediction was made using the estimated parameters to predict the probability distributions of $E{C}_{10}$, defined as a 10% relative change from controls, for each chemical and mixture. Specifically, the $E{C}_{10}$ each concentration–response is given by

$$E{C}_{10}={\mathrm{\theta }}_1\cdot \left[{\left(\frac{1}{0.9}\right)}^{{\mathrm{\theta }}_2}-1\right].$$

Mixture Dose–Response Reconstruction

The concepts of CA and IA are routinely used in risk assessment practice to predict the cumulative effect of a mixture (Backhaus et al. 2000; Hadrup et al. 2013; Zhu and Chen 2016). These models are based on the assumption that chemicals in a mixture do not interact with each other, and therefore their activity can be predicted through additivity approaches. The CA assumption posits that there is a shared pathway from the joint action of substances in the mixture. For instance, the chemicals in the mixture may be acting on the same molecular target sites but with different potency (Cedergreen et al. 2008). On the other hand, IA (also known as response additivity) assumes that all substances in a mixture have pathways and act independently without interfering with each other so that they can exert their effects completely independently.

CA can be mathematically formulated for the mixture that comprises $n$-compounds as

$$\sum _{j=1}^n\frac{f_j}{E{C}_{x,j}}=\frac{1}{E{C}_{x,mix}},$$

where $E{C}_{x,j}$ is the effective concentration of the jth compound that can provoke x% effect, $f_j$ is the fraction of jth compound in a mixture, and $E{C}_{x,mix}$ is the effective concentration of the designed mixtures that have the same x% toxicity effect. Therefore, the formula to predict the $E{C}_{10}$ of the mixture can be derived as follows:

$$E{C}_{10,mix}={\left(\sum _{i=1}^n\frac{f_j}{E{C}_{10,i}}\right)}^{-1}={\left(\sum _{i=1}^n\frac{f_j}{{\theta }_{1,j}\cdot {[{\left(\frac{1}{0.9}\right)}^{{\mathrm{\theta }}_{2,j}}-1]}^{-1}}\right)}^{-1}.$$

The mathematical formula of IA can be written as

$$E\left(C_{mix}\right)=\prod _{j=1}^{n}E\left(C_i\right)=\prod _{j=1}^n\left(\frac{1}{1+{\left(\frac{C}{{\mathrm{\theta }}_{1,i}}\right)}^{{\mathrm{\theta }}_{2,j}}}\right)$$

where $C_{mix}$ and $C_j$ are concentration for mixture and the jth compound, respectively. The $E{C}_{10}$ would, therefore, need to be obtained by inverting this formula to solve for $C_{mix}$.

To summarize, CA uses the effective concentration from individual chemicals ($E{C}_{x,j}$) to predict the corresponding effective concentration for the designed mixture ($E{C}_{x,mix}$), whereas IA uses the concentration of each individual chemical ($C_j$) in the designed mixture to predict the corresponding response [$E\left(C_{mix}\right)$] to the whole mixture.

Risk Characterization

We used the concept of the margin of exposure (MOE) to characterize the cumulative risk associated with each mixture (Figure 1D). The MOE is defined as the ratio of the effect threshold (we used $E{C}_{10,j}$ for each phenotype in this study) to the exposure concentration (World Health Organization 2009), which is defined here as the undiluted concentration in each mixture. The calculated MOEs were used to characterize chemical exposure risks for the individual chemicals j (${\text{MOE}}_j=E{C}_{10,j}/C_j$), the cumulative risks derived for each designed mixture under IA or CA (${\text{MOE}}_{mix,IA}{}_{\text{or}\text{\hspace{0.17em}CA}}=E{C}_{10,mix,IAorCA}/C_{mix}$), and the cumulative risk as estimated from testing the designed mixtures directly (${\text{MOE}}_{mix}=E{C}_{10}/C_{mix}$). An estimated $\text{MOE}=1$ indicated that the exposure and threshold concentrations are the same, and thus a higher MOE (usually $\text{MOE}\ge 100$) represents a “safer” characterization of risk.

Data Processing and Reproducibility

All data analysis and graphics are conducted using R (version 3.6.2; R Development Core Team). The rstan package (version 2.18.2; Carpenter et al. 2017) was used for Hamiltonian MCMC simulations for the concentration–response fitting. All model codes and raw data are provided in the Supplemental Materials to allow other researchers to reproduce our results and are available in GitHub (https://github.com/nanhung/EHP7600). All MCMC simulations were performed and tested under the different operating systems of Windows $10\times 64$ (build 17763), Linux (elementary OS 5.1.2 Hera), and macOS (Catalina 10.15.3). RStudio version 1.2.5019 was used as an integrated development environment for modeling, post-processing, and documentation (RStudio Team 2019). More details can be found in supplemental data from the Supplemental Materials and the GitHub repository.

Results

Cell Culture and Chemical Treatments

Representative images (Figure 3) of the data from untreated iCell neurons, iCell cardiomyocytes, and HUVECs, cells exposed to DMSO (0.25%) vehicle, or exposed to two designed mixtures are shown to illustrate the effects. Mixture ${\text{AC}}_{50}\text{-H}$ at the lowest tested concentration (diluted by $\mathrm{10,000}\times$ from the highest concentration) was without effect on neurite outgrowth but affected beating rate in cardiomyocytes and tube formation in HUVECs. Similarly, mixture POD-H at an intermediate tested concentration (diluted by $100\times$) affected tube formation in HUVECs without cytotoxicity, but it was overtly cytotoxic to both neurons and cardiomyocytes. The complete data set is included as a Supplemental Excel file.

Figure 3.

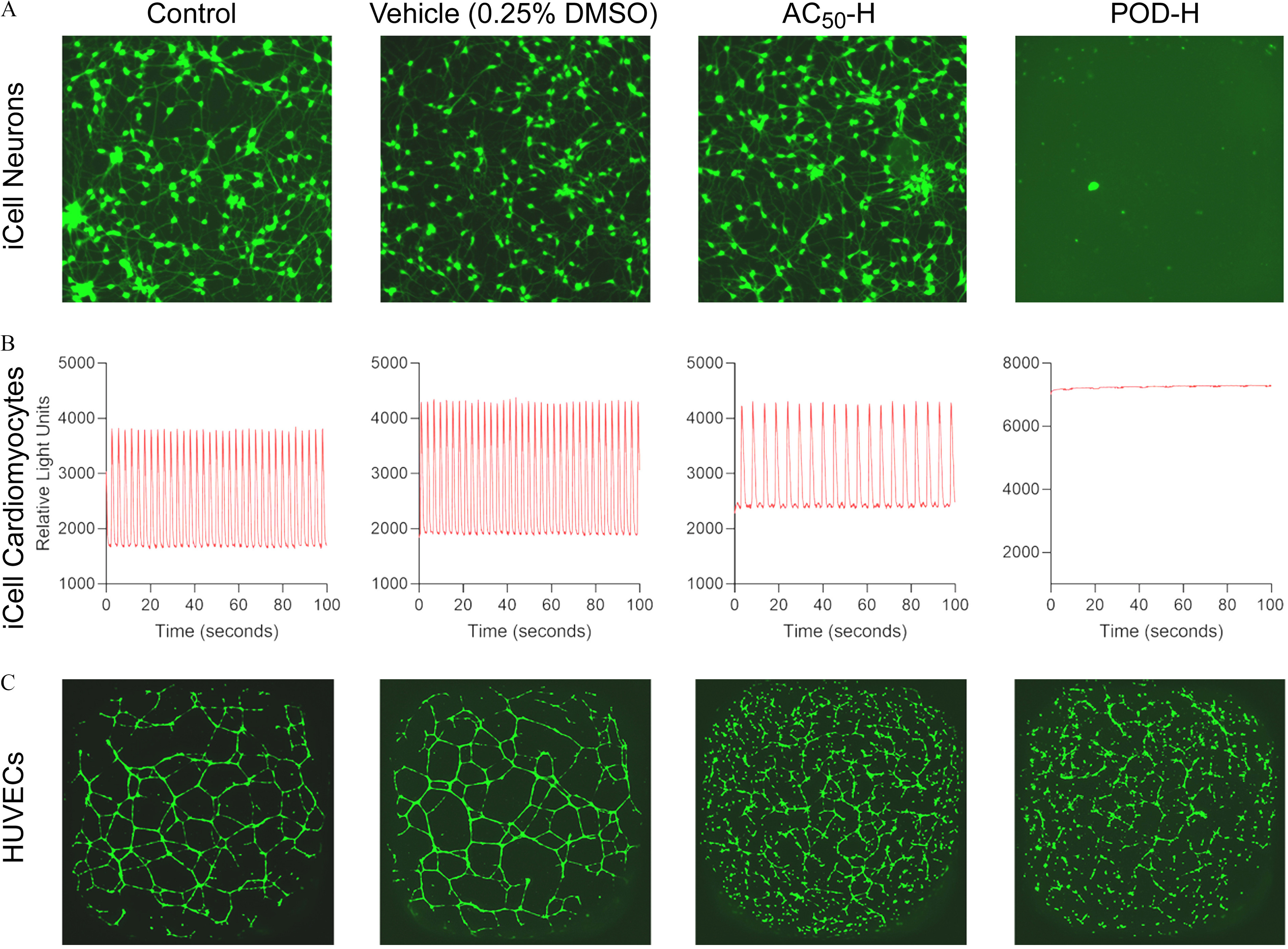
Representative examples of bioactivity in different cell types. (A), fluorescent (calcein) staining ($\text{objective magnification}=20\times$) of untreated (control) iCell neurons or cell treated with vehicle, or two designed mixtures (${\text{AC}}_{50}\text{-H}$ at lowest tested concentration, diluted by $\mathrm{10,000}\times$ from the highest concentration, and POD-H at an intermediate tested concentration, diluted by $100\times$ from the highest concentration). See acronym explanations and description of the designed mixtures in Table 1. (B), characteristic kinetic imaging-derived fluorescence intensity traces indicative of the ${\mathrm{Ca}}^{2+}$ fluxes across cell membranes of iCell cardiomyocytes that spontaneously contract in cell culture. (C), fluorescent (calcein) staining ($\text{objective magnification}=4\times$) of untreated (control) HUVECs or cell treated with vehicle, or two designed mixtures. See Table 1 for description of designed mixtures ${\text{AC}}_{50}\text{-H}$ and POD-H.

For the data on the individual chemicals (Chen et al. 2020), convergence for Bayesian concentration–response modeling was reached for all parameters with a chain length of 4,000, where the first 2,000 “warm-up” samples of each chain were discarded. Across the three chains, the 6,000 available samples were down-sampled to 500 samples for evaluation of model fit and for inference. The example concentration–response profiles are shown in Figure 4. The most toxic response observed was for the total outgrowth data in iCell Neurons and mercuric chloride, with estimated median ${\text{EC}}_{10}$ of $0.02\mathrm{\mu }\mathrm{M}$ [90% credible interval (CI): 0.01, 0.05]. Complete fitting results for the individual chemicals are provided in Figures S1–S47 and a supplemental Excel file.

Figure 4.

Representative Bayesian curve-fitting examples of concentration–response profiles for individual chemicals (insets) and a representative designed mixture (${\text{AC}}_{50}\text{-H}$; see Table 1 for description) for total outgrowth in iCell neurons (results for all other phenotypes can be found in Supplemental Materials Figures S1–S94 and a Supplemental Excel file). See acronym explanations and description of the designed mixtures in Table 1. Dots represent experimental data points. Gray lines represent individual simulated curves from the last 100 iterations. The vertical dashed red lines represent the 90% credible interval on the point of departure (${\text{EC}}_{10}$).

For each mixture, convergence was reached with the chain length set to 8,000, with 4,000 warm-up samples discarded. Again, down-sampling was performed with 500 samples saved for analysis. The example mixture concentration–response profile is shown in Figure 4 for the ${\text{AC}}_{50}\text{-H}$ mixture. The estimated ${\text{EC}}_{10}$ is below the lowest tested concentration with a value of 0.29 (90% CI: 0.25, 0.36). Complete fitting results for the designed mixtures are provided in Figures S48–S94).

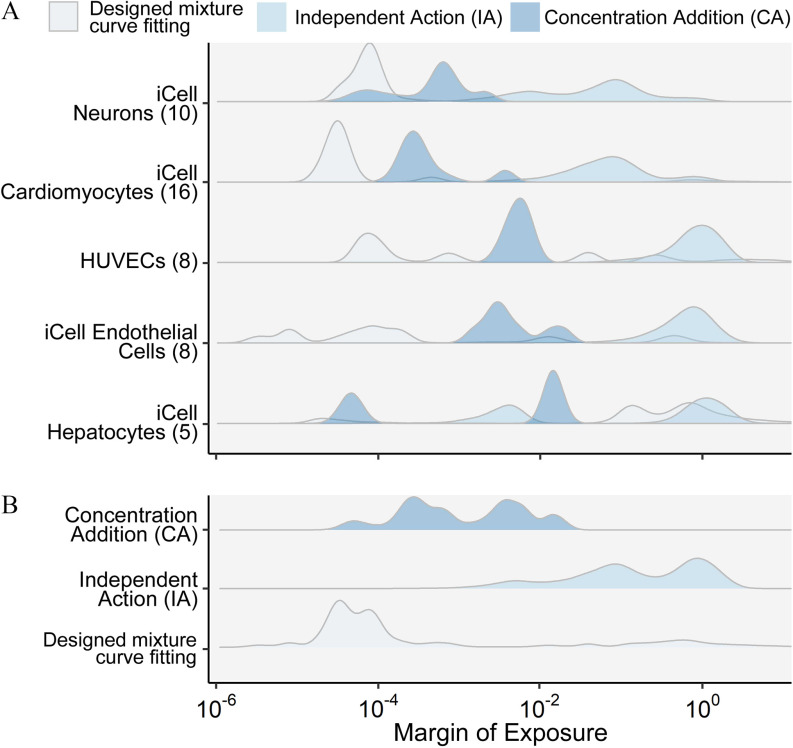
Figure 5 summarizes the fitted distribution of ${\text{EC}}_{10}$ for each mixture across all phenotypes. If we consider “active” as those phenotypes with an estimated ${\text{EC}}_{10}$ lower than the undiluted designed concentration, the mixture POD-H showed the highest “activity” rate of nearly 100%, with Expo-L having the least activity with a value of less than 40% (Figure 5A, Table 2). However, activity (fraction of phenotypes showing effects) and potency (low vs. high ${\text{EC}}_{10}$ values) were not completely correlated. For instance, the ${\text{AC}}_{50}\text{-H}$, POD-L, and POD-H mixtures had similar activity, but the distribution of ${\text{EC}}_{10}$ values was much lower for the ${\text{AC}}_{50}\text{-H}$ mixture (Figure 5B, Table 2). Thus, although they may be similar from a hazard identification point of view, they would clearly differ in terms of risk.

Figure 5.

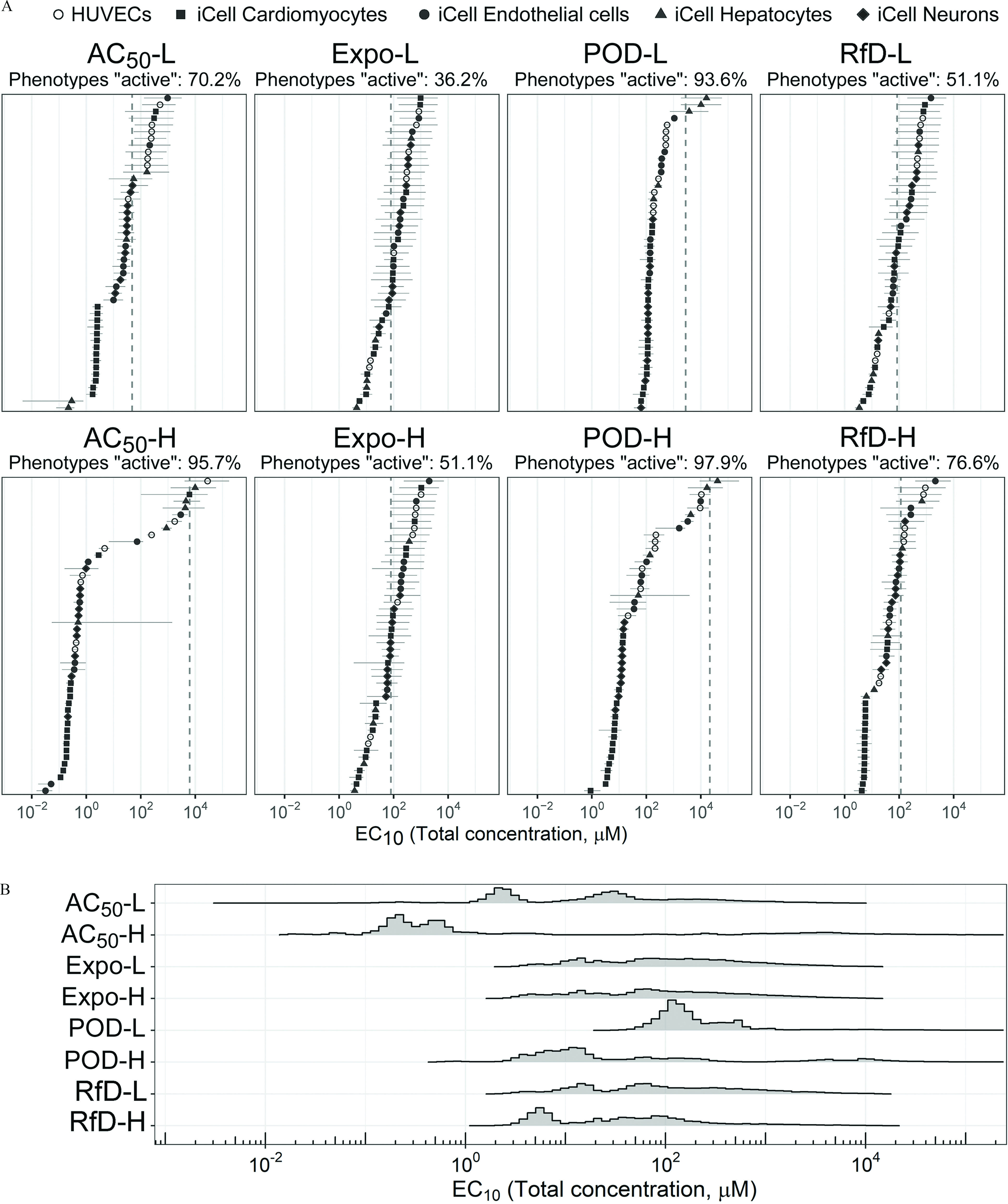
(A) The Bayesian modeling-estimated effective concentrations (${\text{EC}}_{10}$) (median with 90% credible interval) of the designed mixtures. The dashed vertical line is the total chemical concentration for each designed mixture. The different phenotypes in each cell type (see color legend on top of the figure) are displayed by the same color. Cyan is HUVECs, dark magenta is iCell cardiomyocytes, green is iCell endothelial cells, dark orange is iCell hepatocytes, and dark blue is iCell neurons. The percent of phenotypes active was based on the posterior median ${\text{EC}}_{10}$ values compared with the undiluted designed concentration. (B) The probability density plot shows the distribution of all estimated ${\text{EC}}_{10}$ for each mixture. See acronym explanations and description of the designed mixtures in Table 1. All data are included in a Supplemental Excel file.

Table 2.

Comparison of the designed mixture effects to dose reconstruction from the data on the mixture components through CA or IA.

Mixture	Total Conc.	Percent activea [sensitivity, specificity]			$\mathrm{E}{\mathrm{C}}_{10,\mathit{m}\mathit{i}\mathit{x}}$ [90% CI]	$\mathrm{E}{\mathrm{C}}_{10\mathrm{C}\mathrm{A}\mathrm{o}\mathrm{r}\mathrm{I}\mathrm{A}}/\mathrm{E}{\mathrm{C}}_{10,\mathit{m}\mathit{i}\mathit{x}}$b [90% CI]
	$\mathrm{\mu }\mathrm{M}$	Designed mixture	CA	IA	$\mathrm{\mu }\mathrm{M}$	CA	IA	$\mathrm{M}\mathrm{O}{\mathrm{E}}_{\mathrm{m}\mathrm{i}\mathrm{x}}$ [90% CI]
${\text{AC}}_{50}\text{-L}$	48.3	70%	85% [0.94, 0.36]	4.3% [0.06, 1.0]	27 [1.7, 340]	0.44 [0.095, 3.0]	61 [9.3, 320]	0.55 [0.036, 7.1]
${\text{AC}}_{50}\text{-H}$	6236.3	96%	100% [1.0, 0.0]	89% [0.91, 0.5]	0.45 [0.12, 5,600]	7.6 [0.0085, 99]	1,200 [0.90, 17,000]	0.000072 [0.00002, 0.90]
Expo-L	79.4	36%	64% [0.82, 0.47]	0% [0.0, 1.0]	100 [10, 850]	0.39 [0.082, 2.8]	22 [3.9, 120]	1.3 [0.13, 11]
Expo-H	79.9	51%	64% [0.79, 0.52]	0% [0.0, 1.0]	79 [5.4, 930]	0.49 [0.067, 2.8]	37 [4.4, 150]	0.99 [0.067, 12]
POD-L	2767.1	94%	100% [1.0, 0.0]	51% [0.55, 1.0]	140 [760, 2,900]	0.11 [0.030, 0.4]	12 [2.2, 35]	0.05 [0.028, 1.1]
POD-H	21348.4	98%	100% [1.0, 0.0]	100% [1.0, 0.0]	14 [3.7, 10,000]	0.48 [0.0053, 2.5]	54 [0.31, 270]	0.00066 [0.00017, 0.48]
RfD-L	83.8	51%	83% [0.92, 0.26]	0% [0.0, 1.0]	78 [7.9, 770]	0.28 [0.070, 1.6]	22 [4.6, 140]	0.93 [0.095, 9.2]
RfD-H	115.7	77%	92% [0.94, 0.18]	0% [0.0, 1.0]	39 [5.1, 760]	0.43 [0.075, 1.5]	49 [6.6, 120]	0.33 [0.044, 6.6]

Note: CA, concentration addition; CI, confidence interval; IA, independent addition; MOE, margin of exposure: .

^aPercent Active is the percent of phenotypes with posterior median ${\text{EC}}_{10}<\text{highest tested}$ concentration. Sensitivity is the true positive rate, and specificity is the true negative rate.

^b$\mathrm{E}{\mathrm{C}}_{10\mathrm{C}\mathrm{A}\mathrm{o}\mathrm{r}\mathrm{I}\mathrm{A}}/\mathrm{E}{\mathrm{C}}_{10,\mathit{m}\mathit{i}\mathit{x}}$ is the distribution across phenotypes [median (90% CI)] for the ratio between the “reconstructed” CA- or IA-based mixture ${\text{EC}}_{10}$ and the ${\text{EC}}_{10}$ of the effects of the designed mixture (all based on posterior medians). A ratio $<1$ overestimates potency, whereas a ratio $>1$ underestimates potency. The same ratio applies to the CA- or IA-based MOEs.

Mixture Response Reconstruction

Based on its higher activity and potency, we use the mixture of ${\text{AC}}_{50}\text{-H}$ as a representative mixture to illustrate the impact of the conventional additivity assumptions for mixtures. Figure 6A shows the concentration–response profiles for total outgrowth in iCell neurons, beats per minute for iCell cardiomyocytes, and mean tube length in HUVECs, respectively (see Figures S95–S99 for other phenotypes). Although the CA-based predictions were closer to the true mixture concentration–response than the IA-based predictions, the CA-based predicted ${\text{EC}}_{10}\mathrm{s}$ were nonetheless higher (i.e., lower potency) than the actual mixture estimates by up to an order of magnitude. The results across all phenotypes are shown in Figure 6B. As with the examples in Figure 6A, overall, ${\text{EC}}_{10}\mathrm{s}$ derived from CA were closer to the actual mixture ${\text{EC}}_{10}\mathrm{s}$. For a few phenotypes, such as total outgrowth, adenosine triphosphate, and total branch in iCell neurons and results for iCell cardiomyocytes, the differences between central estimates of CA and the actual mixture dose–response were less than 10-fold; however, most phenotypes had high uncertainty. The IA predictions were even less accurate, with estimated ${\text{EC}}_{10}\mathrm{s}$ far from the actual mixture estimates, especially for the more sensitive phenotypes with lower actual ${\text{EC}}_{10}\mathrm{s}$. Figure 6C shows a summary comparison among ${\text{EC}}_{10}\mathrm{s}$ from CA, IA, and the actual mixture. The mixture-based estimated ${\text{EC}}_{10}\mathrm{s}$ had the lowest median concentration ($0.45\mathrm{\mu }\mathrm{M}$), with the CA- and IA-based predictions being substantially higher ($4.7\mathrm{\mu }\mathrm{M}$ and $886\mathrm{\mu }\mathrm{M}$, respectively).

Figure 6.

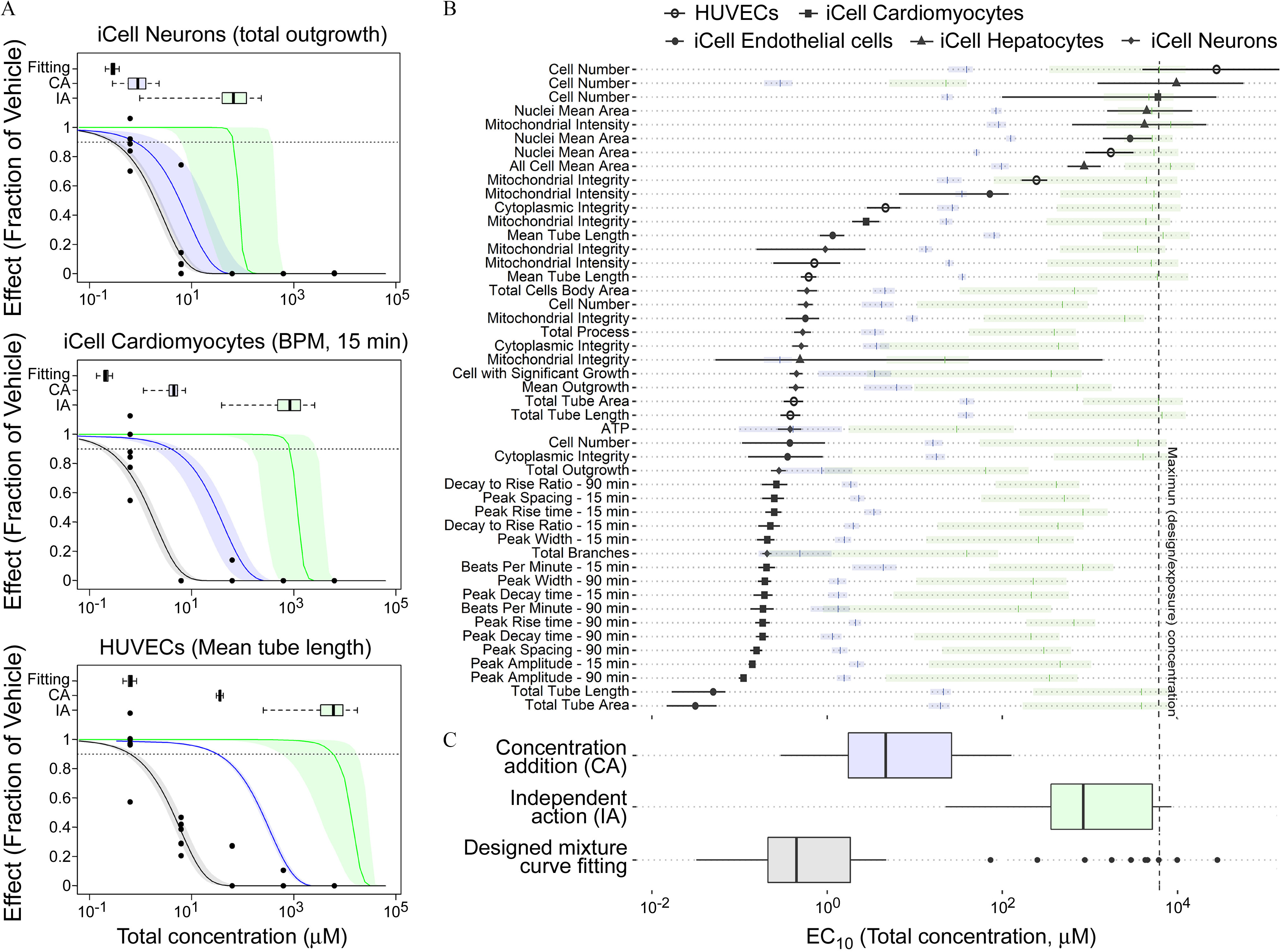
Comparison of curve-fitting, IA, and CA estimated median effective concentration (${\text{EC}}_{10}$) with 95% confidence limits, and each box and whisker plot shows the median, first/third quartile, and a distance of 1.5 times the IQR. (A) The representative examples to compare the concentration–response-profile for fitting and IA/CA predicted result. Box and whisker plot represents the distribution of the estimated ${\text{EC}}_{10}$. The points are the in vitro experimental data. (B) The comparison of estimated ${\text{EC}}_{10}$ across all phenotypes. The shaded bars represent median and 95% confidence limits for the prediction from CA or IA (colors correspond to those in panel C) (C) Box and whisker plots summary of the estimated ${\text{EC}}_{10}$; the points represent values outside 1.5 times the IQR. All data are included in a Supplemental Excel file. Note: CA, concentration addition; IA, independent addition; IQR, interquartile range.

A summary of the results for the accuracy of CA and IA across all mixtures are presented in Table 2. The CA assumption-based results showed an overall higher performance in predicting both activity (the percent of phenotypes with ${\text{EC}}_{10}\mathrm{s}<\text{highest designed}$ mixture concentrations) and potency (${\text{EC}}_{10}\mathrm{s}$). For activity, the sensitivity of CA was found to be at least 0.79, whereas in some cases, IA had zero sensitivity. Specificity was poorer for CA, with values no more than 0.52. The estimated ratio between the designed mixture ${\text{EC}}_{10}\mathrm{s}$ and the ${\text{EC}}_{10}\mathrm{s}$ estimated from dose reconstruction showed that CA also had better predictivity in comparison with IA. Median ${\text{EC}}_{10}$ values across phenotypes based on CA were within an order of magnitude of those for the actual mixture, whereas IA predicted median potency to be at least an order of magnitude less that the actual mixture. In all cases, however, there was a lot of variation in predictive power across phenotypes.

Risk Characterization

To illustrate how these NAMs data can be used in risk characterization, we used the ${\text{AC}}_{50}\text{-H}$ mixture as an example and examined the margin of exposure (MOE) for three selected phenotypes (Figure 7). Almost all estimated MOEs for the AC50-H mixture were inadequate to be considered “safe,” represented by an $\text{MOE}>100$.

Figure 7.

The estimation of the MOE for cytotoxicity phenotypes in the representative cell. Box and whiskers plots show the distribution (median, first/third quartile, distance of 1.5 times the interquartile range) of the MOE that was derived by the curve-fitting and IA-/CA-predicted ${\text{EC}}_{10}$ with the designed concentration in the ${\text{AC}}_{50}\text{-H}$ designed mixture. See acronym explanations and description of the designed mixtures in Table 1. Note: BPM, beats per minute; CA, concentration addition; IA, independent addition; MOE, margin of exposure.

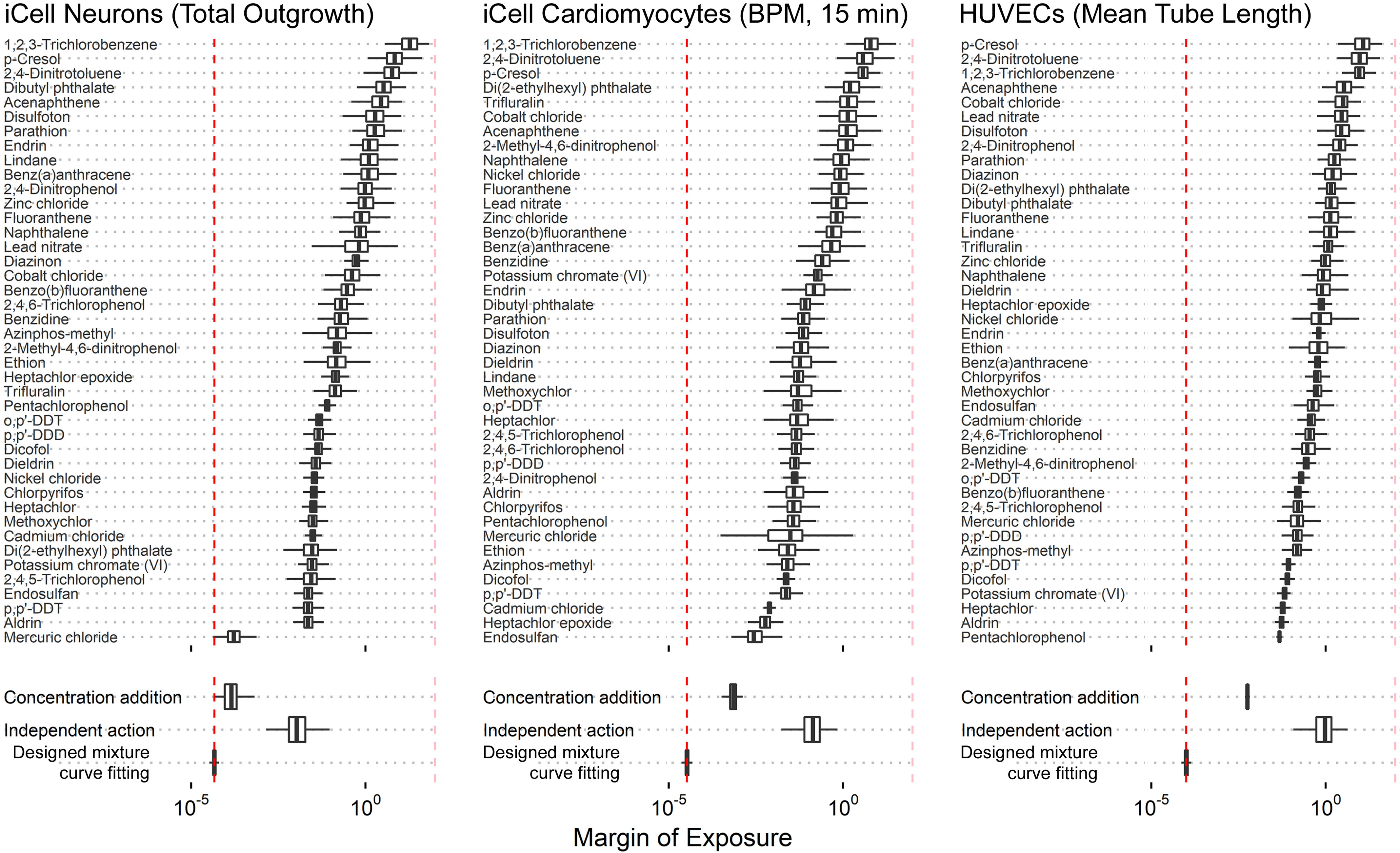
Under CA assumptions, the “dominant” chemical(s) with respect to the potency of the mixture can be identified as the one(s) that have the largest values of $f_j/{\text{EC}}_{10,j}$ For instance, in iCell neurons, mercuric chloride is the most potent chemical, with the lowest individual chemical MOE. This compound also dominates the overall response predicted in other phenotypes in the iCell neurons (Figure S100). In iCell cardiomyocytes, the CA predictions suggest that endosulfan is the principal chemical that contributes to the cardiotoxicity effect, along with mercuric chloride, albeit with wider estimated uncertainty. All predicted results of MOE estimation for other phenotypes for the AC50-H mixture can be found in Supplemental Materials (Figures S100–S104). These results are summarized in Figure 8, which shows the distribution of MOEs across phenotypes for each specific cell type (Figure 8A) and all cell types together (Figure 8B). As with the ${\text{EC}}_{10}\mathrm{s}$, the MOE based on the assumption of CA was closer to the MOE for the actual mixture than the use of IA, but CA may still underestimate risk 1–2 orders of magnitude, with the greatest errors observed in the HUVECs and iCell hepatocytes.

Figure 8.

Ridgeline plots show the margin of exposure for the (A) organ-specific human stem cell and (B) all combined summarization under the exposure of ${\text{AC}}_{50}\text{-H}$ designed mixture. See acronym explanations and description of the designed mixtures in Table 1.

More generally, as shown in Table 3, for all mixtures except Expo-L, more than half of the phenotypes had $\text{MOE}<1$, and across all mixtures, almost all the phenotypes had $\text{MOE}<100$. MOEs based on CA tended to be a bit more conservative except for the AC50-H mixture, for which the CA-based MOE was about 10-fold higher. However, IA-based MOEs were substantially larger, with a much smaller fraction of $\text{MOEs}<1$, though most were still $<100$.

Table 3.

Comparison of the designed mixture MOEs from the data on the mixture components through CA or IA.

Mixture	$\mathrm{M}\mathrm{O}{\mathrm{E}}_{\mathrm{m}\mathrm{i}\mathrm{x}}$a (90% CI)
	Mixture	CA	IA
${\text{AC}}_{50}\text{-L}$	0.55 [0.036, 7.1]	0.19 [0.021, 2.3]	42 [2.8, 120]
${\text{AC}}_{50}\text{-H}$	0.000072 [0.00002, 0.90]	0.00075 [0.000071, 0.015]	0.13 [0.0054, 1.1]
Expo-L	1.3 [0.13, 11]	0.77 [0.050, 2.3]	43 [5.1, 56]
Expo-H	0.99 [0.067, 12]	0.77 [0.050, 2.3]	43 [5.1, 55]
POD-L	0.05 [0.028, 1.1]	0.0077 [0.0016, 0.039]	0.95 [0.23, 2.3]
POD-H	0.00066 [0.00017, 0.48]	0.00069 [0.00011, 0.0047]	0.092 [0.012, 0.29]
RfD-L	0.93 [0.095, 9.2]	0.46 [0.0045, 2.0]	37 [5.0, 53]
RfD-H	0.33 [0.044, 6.6]	0.20 [0.0018, 1.1]	22 [2.1, 46]

Note: CA, concentration addition; CI: confidence interval; IA, independent addition; MOE, margin of exposure: .

^aEach MOE is the distribution across phenotypes [median (90% CI)] for the ratio between the actual mixture or “reconstructed” CA- or IA-based ${\text{EC}}_{10}$, and fixed undiluted mixture concentration.

Discussion

Large-scale biomonitoring programs have convincingly demonstrated that all humans are concurrently exposed to multiple chemicals (Calafat et al. 2017; Dixon et al. 2019; Rosofsky et al. 2017), yet human health risk assessments are still largely based on one-chemical-at-a-time analyses. Indeed, mixtures risk assessment, as currently practiced, relies heavily on adding up the risks of individual chemicals assuming either dose– or concentration–addition or independent action. Even the application of these additivity assumptions is inconsistent across the field. For instance, recommendations as to when to apply dose– or concentration–addition range from the very narrow (e.g., only for the same mode of action) to the relatively broad (e.g., same target organ). Moreover, the conflicting underlying additivity assumptions are difficult to verify empirically, because only a few studies have collected data on the effects of the individual chemicals and their mixtures in the same model system (Backhaus and Faust 2012; Hadrup et al. 2013; Howard et al. 2010). Thus, it is widely acknowledged that many challenges exist in the field of mixtures risk assessment that need to be overcome to move the field forward and inform decision makers (Bopp et al. 2019).

Due to their lower cost and higher throughput, NAMs and alternative animal models have emerged as a potential approach to substantially advance mixture risk assessment (Blackwell et al. 2019; Geier et al. 2018; Hayes et al. 2020; Hoover et al. 2019; Incardona et al. 2006; Ruiz et al. 2019; Seeger et al. 2019). This study adds to the body of the recent advances on using NAMs to characterize the toxicity of mixtures, having applied novel high-throughput in vitro models based on a diverse array of human cells. We took advantage of recently developed reproducible and physiologically relevant human in vitro models derived from iPSCs (Li and Xia 2019), models that have been successfully applied for screening of diverse chemicals (Chen et al. 2020). To our knowledge, human iPSC-derived cell models have not been used to characterize the hazards of complex mixtures comprising a large number of diverse environmental chemicals. We observed differing effects of mixtures on different cell types/phenotypes, suggesting that this multitissue approach may aid in identifying the potential targets of certain mixtures. Another advantage of the in vitro testing system used in this study is that in addition to traditional cytotoxicity end points, functional effects of different cell types were also measured, suggesting that data on physiologically relevant phenotypes can better reflect the effects on human health. Furthermore, a large number of end points collected from in vitro testing would contribute to increasing the confidence of the modeling procedures for predicting the effects of mixtures from individual components.

Several important conclusions can be drawn from our data and analysis. First, it is clear that cumulative effects from complex mixtures are important, even when individual chemical exposures levels may be considered “low” or “safe.” For both our exposure- and RfD-based mixtures, which mimic either current actual exposure levels or levels currently presumed to be “safe,” we found that a substantial fraction of phenotypes showed activity (Table 2). Second, the assumption that chemicals behave independently leads to a severe underestimation of their cumulative effects. Specifically, across all of the mixtures, the assumption of IA performed very poorly in predicting either activity or potency of the mixtures (Table 2). Third, on average, POD predictions based on CA are within about an order of magnitude of the POD for the full mixture, consistent with previous studies predictions (Backhaus et al. 2004; Faust et al. 2003). Moreover, given the diverse modes and mechanisms of action across the individuals chemicals composing the mixtures used in this study, our results argue strongly against the requirement of a common mode of mechanism of action to apply CA to address cumulative risks. Fourth, in a number of cases, bioactivity of the mixture appears to be greater than the sum of the effects of individual chemical components. For instance, although in some cases, such as mercuric chloride effects in neuronal cells, one chemical clearly dominated the bioactivity, in many other cases, the mixtures proved to be clearly more active than any of the individual chemicals, suggesting a synergistic effect. An important strength of our study is its use of many more and diverse chemicals, cell types, and end points than any previously published work that we know of, hence providing important new information about the considerations for mixture dose reconstruction.

Our study has a number of important limitations. First, our CA approach does not address the possibility of a saturation effect due to the presence of “partial agonists” (compounds with smaller maximal effects levels) that are influencing the efficacy of the whole mixture (Howard et al. 2010; Silva et al. 2002). However, we consider the impact of partial agonists to be unlikely because our analyses focused on the lower part of the concentration–response curve. Another issue, which may partially explain the apparent “synergy” in the ${\text{AC}}_{50}\text{-H}$ mixture, has to do with bioavailability, because it is possible that there is a greater freely available fraction of each chemical in a mixture in comparison with single chemical experiments. This phenomenon has been recently demonstrated for complex mixtures and petroleum substances (Luo et al. 2020); it is thought to be due to saturation of binding sites in the presence of multiple compounds. The likely differences in free fraction in vitro and in vivo (e.g., protein content in plasma in vivo is usually greater than that in media in vitro) thus present a challenge for the extrapolation of these results to the in vivo setting. Furthermore, our studies did not have a specific “positive control” for different mechanisms of synergy and, therefore, do not have a mechanistic basis or model (Lasch et al. 2020) for our observations. Additional experiments with known mechanisms for synergism and the development of theoretical models for synergistic effects will be needed in the future. Finally, our study does not address the additional challenge of understanding population variability under the exposure to complex mixtures. Previously, we demonstrated that the population-based iPSC-derived cardiomyocyte model and Bayesian concentration–QTc modeling approach had the ability to accurately predict the in vivo concentration range of regulatory concern (Blanchette et al. 2019). Our current approach only quantifies the uncertainty in a single individual, but as population-based, iPSC-derived models become available, it can be extended to the population level to obtain complete information for use in mixtures risk assessment.

Conclusion

This study applied NAMs to determine the bioactivity of mixtures of 42 Superfund priority chemicals in comparison with predictions from two classic mixture toxicity models, IA and CA. Although CA was generally much more accurate than IA in predicting mixture effects, in some cases the mixture effect was underestimated substantially: i.e., the bioactivity of the mixture may be greater than the sum of its parts. Our findings support the concern that mixtures can result in a greater effect than adding up the effects of individual compounds and suggest that testing of actual environmental samples (e.g., real-life mixtures) is desirable, rather than simply assuming that the effects of individual analytes from an environmental sample can be added together. Such whole-mixture testing is likely only to be possible on a routine basis with in vitro models. Our approach of using a small panel of iPSC-derived tissues in a high-throughput format thus provides a key component to a practical solution for the design of future risk assessments of complex environmental samples. However, challenges remain in addressing both population variability as well as in vitro to in vivo extrapolation in the context of a mixture.