Predicting human pharmacokinetics from preclinical data: volume of distribution

Abstract

This tutorial introduces background and methods to predict the human volume of distribution (V_d) of drugs using in vitro and animal pharmacokinetic (PK) parameters. The physiologically based PK (PBPK) method is based on the familiar equation: V_d = V_p + ∑_T(V_T × k_tp). In this equation, V_p (plasma volume) and V_T (tissue volume) are known physiological values, and k_tp (tissue plasma partition coefficient) is experimentally measured. Here, the k_tp may be predicted by PBPK models because it is known to be correlated with the physicochemical property of drugs and tissue composition (fraction of lipid and water). Thus, PBPK models' evolution to predict human V_d has been the efforts to find a better function giving a more accurate k_tp. When animal PK parameters estimated using i.v. PK data in ≥ 3 species are available, allometric methods can also be used to predict human V_d. Unlike the PBPK method, many different models may be compared to find the best-fitting one in the allometry, a kind of empirical approach. Also, compartmental V_d parameters (e.g., V_c, V_p, and Q) can be predicted in the allometry. Although PBPK and allometric methods have long been used to predict V_d, there is no consensus on method choice. When the discrepancy between PBPK-predicted V_d and allometry-predicted V_d is huge, physiological plausibility of all input and output data (e.g., r²-value of the allometric curve) may be reviewed for careful decision making.

MECHANISM OF DRUG DISTRIBUTION

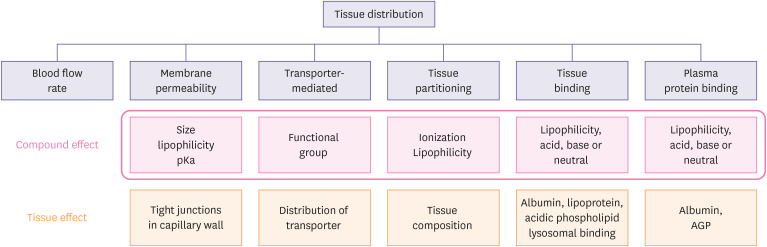
In this tutorial, we will briefly review the concept of V_d and methods to predict human V_d using in vitro and animal PK parameters. Drug distribution is defined as the reversible partitioning of drug molecules into the various tissues from plasma, and it is driven by blood flow and the tendency of the drug to cross cell membranes of the tissues [1]. Differences in the tendency are caused by drugs' chemical properties (lipophilicity, polarity, pKa, molecular weight, etc.), transporter, and tissue composition. They result in different partitioning of drugs in various tissues after the distribution phase is ended (Fig. 1).

Figure 1. Compound- and physiology-dependent factors affecting rate and extent of tissue. Redrawn from [1].

pKa, the symbol for the acid dissociation constant at logarithmic scale; AGP, alpha-1-acid glycoprotein.

Drugs are rapidly distributed to highly perfused organs with discontinuous capillaries (e.g., liver, spleen, intestine etc.) while slowly to the others. Because the capillary wall is a thin, single layer of endothelial cells, many drugs may easily pass the membrane. Those of the kidney and liver are mostly loose, allowing the extensive transfer of drugs into the interstitial space. In the phospholipid bilayers of the cell membrane, lipophilic, base compounds may better permeate through the membrane than the acidic, hydrophilic ones. The existence of efflux or influx transporters may also influence the distribution of drugs. Different tissue composition may also affect the tissue partitioning of drugs. Lipophilic drugs distribute well into fat-rich organs (e.g., adipose, liver, brain, and kidney). Drugs with extensive tissue binding also show a large V_d. Irreversible binding of drugs to some tissues (e.g., tetracycline to the bone, iodine to the thyroid) does not apply to the conventional distribution model that assumes reversible transport of drug molecules between compartments. Instead, this may be accounted for by non-specific elimination (not by the liver or kidney).

PHYSIOLOGICAL VIEW ON V_d

Unbound plasma concentration and unbound tissue concentration would be equal at equilibrium for drugs distributed only by passive diffusion without efflux or influx by transporters (equation 1).

C_{total, T} × f_ut = C_{total, p} × f_up Eq. 1

The partition coefficient (k_tp) is simply defined as in equation 2. However, the equation 2 is not used anymore in PBPK-based methods because more refined partition coefficients are needed for each of lean tissues and adipose tissues as in equations 5 and 6.

$$k_{tp} = \frac{C_{total, t}}{C_{total, p}} = \frac{f_{up}}{f_{ut}}$$ Eq. 2

The f_ut can be obtained by in vitro and in vivo laboratory methods, but it may be predicted by the f_up and the macromolecular (albumin, globulin, lipoprotein) concentration ratio (= the tissue interstitial fluid/plasma) (equation 3). The ratio (R) is known to be 0.5 in the lean tissue and 0.15 in the fat tissue [2].

$$f_{u, t} = \frac{1}{1 + \frac{1-f_{up}}{f_{up}} \times R}$$ Eq. 3

The distribution of drugs has been described using the physiological volumes of the human body (plasma and tissue volumes) and the tendency of drugs to distribute into the tissues (k_tp) as shown in equation 4.

V_d = V_p + ∑_T(V_T × k_tp) Eq. 4

The V_p (volume of plasma) and V_T (volume of tissues other than plasma) are human physiological variables. The k_tp is the tissue-plasma partition coefficient of each tissue (C_{total, plasma}/C_{total, tissue}), determined by the relationship between drug and body. The k_tp in animal organs can be measured experimentally after intravenous infusion, which is too costly and time-consuming to try for all drug candidates under discovery or early development steps. Thus, k_tp prediction in equations 5 and 6 instead of the in vivo study is the key to PBPK modeling. Efforts to predict V_d have been focused on the improvement of methods predicting the k_tp. Regression analyses in animals indicated that lipophilicity and protein binding are two main factors related to V_ss [3,4].

PBPK MODELS TO PREDICT k_tp (TISSUE: PLASMA PARTITION COEFFICIENT)

Among more than twenty PBPK methods published so far, we introduce the most frequently used ones in this tutorial. Poulin and Theil first reported methods to estimate k_tp in the lean and adipose tissues [2] based on the assumption that the unbound drug is distributed homogeneously into lipid and water in each tissue. Tissue permeability or organ blood flow that may predict multi-compartmental distribution is rarely used in currently available PBPK models predicting V_d. Thus, V_ss is the most frequently predicted parameter by PBPK models. Later, Poulin and Theil's model was corrected by Berezhkovsky et al., which is used these days (equations 5 and 6).

$$k_{{t:p\_}_{lean.tissues}} = \frac{{[P_{o:w_{pH7.4}}\left(V_{nl}+0.3V_{ph}\right) + 0.7V_{ph} + V_w/f_{ut}]}_{\_tissue}}{{[P_{o:w_{pH7.4}}\left(V_{nl}+0.3V_{ph}\right) + 0.7V_{ph} + V_w/f_{up}]}_{\_plasma}}$$ Eq. 5

$$k_{t:{p\_}_{adipose}} = \frac{{[D_{vo:w_{pH7.4}}\left(V_{nl}+0.3V_{ph}\right) + 0.7V_{ph} + V_w/f_{ut}]}_{\_tissue}}{{[D_{vo:w_{pH7.4}}\left(V_{nl}+0.3V_{ph}\right) + 0.7V_{ph} + V_w/f_{up}]}_{\_plasma}}$$ Eq. 6

The P_o:w is the octaol: buffer partition ratio of the non-ionized drug at pH7.4, and D_vo:w is the vegetable oil (olive oil): buffer partition ratio of both ionized and non-ionized drugs at pH7.4. The V's are fractional volumes in the human tissues: V_nl is for neutral lipid, V_ph is for phospholipid, and V_w is for water. They are available from literature on human physiological values [5]. The f_ut and f_up are the unbound fraction of tissue and plasma, respectively.

The equations assume passive diffusion of neutral compounds only without considering transporter-mediated distribution or ionization status. Neutral non-polar lipids of the lean tissue are composed of triglyceride and cholesterol. The lipophilicity of this mixture is similar to that of n-octanol. Unlike the lean tissue, triglyceride is the only component of the adipose tissue's non-polar lipid, and its lipophilicity is not represented correctly by n-octanol. Thus, the P_o:w (obtained using n-octanol) has been used for the lean tissue, and the D_vo:w (obtained using vegetable oil) instead of P_o:w has been used for the adipose tissue. The mechanistic basis of their equations is that the drug is distributed in each tissue and plasma according to their composition of lipids, water, and plasma proteins. The lipophilicity of each tissue, which is determined by its ratio of hydrophilic and lipophilic components and the lipophilicity of the drug (P_o:w or D_vo:w values at pH 7.4), rules the distribution of drugs into each tissue. Besides, the binding to proteins commonly existing in the plasma and interstitial tissue also influences tissue distribution. The contribution of lipophilic (neutral lipid contents), hydrophilic (water contents), and the mixed-natured components (phospholipid contents) are also incorporated into the equations. In phospholipid contents, 30% of the volume was put in the lipophilic side and the rest in the hydrophilic side [6,7].

In summary, equations 5 and 6 demonstrate the contribution of solubility and free concentration to the tissue distribution of drugs. The maximum achievable free concentration of drugs in a tissue will be identical to its solubility. Thus the free concentration ratio of (tissue/plasma) will be identical to the solubility ratio of (tissue/plasma). The general notion “unbound plasma concentration and unbound tissue concetration are equal at equilibrium,” mentioned in the previous section in this tutorial, is in fact confusing. It should have been rewritten as “Unbound drug concentrations in plasma water and tissue water are equal at equilibrium”. It may be further clarified into four sequential sentences if influences by ionization or transporters are ignored.

• 1) Unbound drug concentrations in plasma water and tissue water are equal at equilibrium.

• 2) Unbound drug concentrations in plasma lipid and tissue lipid are equal at equilibrium.

• 3) The lipid: water compositions of the plasma and tissue are different, and water solubility and lipid solubility of the drug are different.

• 4) Thus, the averaged unbound concentration in the tissue (water and lipid) differs from that in the plasma.

Because equations 5 and 6 does not consider the distribution of ionized forms of the acidic, basic or neutral drugs, Rodgers and Rowland [8] proposed modified forms of the Berezhkovsky's equations by adding pKa of the drug and pH of plasma and tissues (equations not shown in this tutorial).

HOW ACCURATE ARE THE PBPK-PREDICTED V_ss?

According to the report on the modified method by Rodgers and Rowland [8], 84% of their predicted partition coefficients were within 0.3 to 3 times the experimental values measured in 13 rat tissues for 49 structurally unrelated drugs, which outperformed Berezhkovsky's method (61%). When 24 different allometric, semi-mechanistic, and mechanistic (PBPK) models predicting V_ss were compared using 18 drugs' human i.v. PK data [9], performance differences were not conclusive. However, in the three PBPK models (Poulin & Theil, Berezhkovsky, and Rodger & Rowland), Berezhkovsky's model worked best (61% of predicted Vss were within 0.5–2 times the human PK-estimated V_ss; 39% by Poulin and Theil, 50% by Rodger and Rowland) [9]). Graham [10] has also reviewed the performance of the three PBPK methods to predict V_ss in her Ph.D. dissertation. Predictions by the Poulin & Theil model were within 5-fold experimental values, and all three were within 10-fold when the experimentally obtained rat V_ss for 35 drugs were tested. There are no defined cutoff criteria for the performance of V_ss prediction methods. However, the five or 10-fold range seems too broad to use as a reliable method to design first-in-human clinical trials. As discussed in this tutorial, the three PBPK methods are sophisticated tools that incorporate all kinds of in vitro information. Notwithstanding this sophistication, the performance is not satisfactory. What can we do more? The older method may be worth trying - the allometric method.

ALLOMETRIC METHOD TO PREDICT V_d

Because describing the allometric method from A to Z is not in this tutorial's scope, we briefly introduce current routines to predict V_d using allometric methods. To perform allometric analysis, PK data from at least three species (e.g., mouse, rat, dog) are necessary. For the prediction of human V_d, PK parameters obtained from i.v. PK studies are necessary. When V_ss is the only volume parameter to predict, the V_ss estimated using NCA (non-compartmental analysis) is enough for allometric analysis. However, to predict compartmental PK parameters (e.g., V_c, V_p, Q: inter-compartmental clearance) in humans, the compartmental analysis should be done for animal data before allometric analysis. Because the compartmental volume parameters should be accordant between species, it is recommended that the same compartmental structure is chosen regardless of species. For example, when mice and rat PK data are modeled using a 2-compartment model and dog PK data are modeled using a 3-compartment model, it is impossible to apply the allometric method to predict human V_d parameters. In this case, dog PK data should also be analyzed using a 2-compartmental model, although it may be best described by a 3-compartment model. There are several different allometric methods: simple allometry using bodyweight only (Y = a(BW)^b); brain weight added (Y × brain weight = a(BW)^b); maximum life span (MLP) added (Y × MLP = a(BW)^b). In the prediction of V_d, simple allometry using bodyweight only may be good enough in many cases. However, there is no rule on the choice of covariates or the exponents (fixed at 1 or 0.75 or best fit). Moreover, the allometric model chosen for the V_d terms may not be identical to that used for Q.

Results of the allometric prediction may significantly differ by researchers because the researchers may choose their favorite among several different ways in fitting the exponent or incorporating the covariate (BW, brain weight, MLP) for each of V_ss, V_c, V_p, or Q. It is the researchers' discretion which allometric method to use. There is no rule for such choices, but the rationale or logic of model selection should be recorded. When the rationale is unclear, selecting the best-fitting model after trying several different allometric models would work.

WHICH METHOD SHOULD BE CHOSEN TO PREDICT HUMAN V_d?

There are a few reports on the performance comparison among several different PBPK methods and allometric methods in predicting V_d [11,12]. However, the kinds of PBPK and allometric methods used in their comparison process were different than those discussed in this tutorial, and their allometric method used was the simplest one.

The quantity or quality of in vitro and in vivo data available when performing prediction differs by the molecules' development stages or the companies' policies. When there is no animal PK data, you must use PBPK methods to predict animal or human V_d. When animal i.v. PK data are available in ≥ 3 species, allometric methods should also be tried, and its best fit result may be compared with the V_ss predicted by the PBPK method. Even when the difference between V_d's predicted by PBPK and allometry is vast (this is not uncommon), you don't have to be embarrassed. Selecting one over the other after a thorough review of physiological plausibility is what may be done. The r²-value of the allometric curve may also be considered. Or you may use both of them (scenario of using two different kinds of V_d's). It should be remembered that uncertainty is the nature of preclinical to the clinical prediction of small molecule drugs.

Glossary

V_d

volume of distribution

V_p

plasma volume

V_T

tissue volume

k_tp

tissue plasma partition coefficient

V_c

central volume of distribution

V_p

peripheral volume of distribution

Q

inter-compartmental clearance

V_ss

steady-state volume of distribution

pKa

the symbol for the acid dissociation constant at logarithmic scale

C_{total, T}

total concentration in tissue

C_{total, p}

total concentration in plasma

f_ut

unbound fraction in tissue

f_up

unbound fraction in plasma

R

macromoleculalr concentration ratio of the tissue interstitial fluid and plasma

P_o:w

octanol:buffer partition coefficient of the non-ionized species

D_vo:w

olive oil (vegetable oil):buffer partition coefficient of the non-ionized and ionized species

V_nl

fractional tissue volume content of neutral lipid

V_ph

fractional tissue volume content of phopholipid

V_w

fractional tissue volume content of water

NCA

non-compartmental analysis

BW

bodyweight

MLP

maximum life span