Development and external evaluation of predictions models for mortality of COVID-19 patients using machine learning method

Abstract

To predict the mortality of patients with coronavirus disease 2019 (COVID-19). We collected clinical data of COVID-19 patients between January 18 and March 29 2020 in Wuhan, China . Gradient boosting decision tree (GBDT), logistic regression (LR) model, and simplified LR were built to predict the mortality of COVID-19. We also evaluated different models by computing area under curve (AUC), accuracy, positive predictive value (PPV), and negative predictive value (NPV) under fivefold cross-validation. A total of 2924 patients were included in our evaluation, with 257 (8.8%) died and 2667 (91.2%) survived during hospitalization. Upon admission, there were 21 (0.7%) mild cases, 2051 (70.1%) moderate case, 779 (26.6%) severe cases, and 73 (2.5%) critically severe cases. The GBDT model exhibited the highest fivefold AUC, which was 0.941, followed by LR (0.928) and LR-5 (0.913). The diagnostic accuracies of GBDT, LR, and LR-5 were 0.889, 0.868, and 0.887, respectively. In particular, the GBDT model demonstrated the highest sensitivity (0.899) and specificity (0.889). The NPV of all three models exceeded 97%, while their PPV values were relatively low, resulting in 0.381 for LR, 0.402 for LR-5, and 0.432 for GBDT. Regarding severe and critically severe cases, the GBDT model also performed the best with a fivefold AUC of 0.918. In the external validation test of the LR-5 model using 72 cases of COVID-19 from Brunei, leukomonocyte (%) turned to show the highest fivefold AUC (0.917), followed by urea (0.867), age (0.826), and SPO2 (0.704). The findings confirm that the mortality prediction performance of the GBDT is better than the LR models in confirmed cases of COVID-19. The performance comparison seems independent of disease severity.

Supplementary Information

The online version contains supplementary material available at(10.1007/s00521-020-05592-1)

Introduction

Coronavirus Disease 2019 (COVID-19) is a new form of respiratory disorder caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) [1]. As of Sept 26 2020, there have been more than 32 million cases and 985 thousand deaths relating to COVID-19 [2]. Patients with COVID-19 may develop acute respiratory distress syndrome and may occasionally progress to multiorgan failure [3]. Latest reports suggest that the rate of hospitalization due to COVID-19 infection ranges from 20.7 to 31.4%. The ICU admission rate ranges from 4.9 to 11.5% [4]. The mortality among confirmed cases is 6.5% [2]. The drastic increase of COVID-19 cases leads to a growing demand for medical equipment and intensive care unit admission [5]. Clinical decision models for the prognosis of confirmed COVID-19 cases may support the clinician's decision-making, prioritize healthcare resources effectively, and relieve the burden of healthcare systems.

Machine learning-based methods are widely adopted in the medical domain [10–12]. The proliferation of machine learning techniques has made it possible for hospitals to conduct a deep analysis of patients’ medical record. As such, patients may be able to receive more comprehensive radiology diagnosis results and prediction of their disease progression. Although a host of existing studies target the prediction of COVID-19 disease progression [6], most prediction models for disease progression are single-center studies with small sample sizes (26–577 cases). Additionally, these studies were developed with multivariable logistic regression [6–9], which may lead to an increased risk of overfitting.

To bridge the gap between machine learning and COVID-19 prognosis, we propose to develop and evaluate a variety of relevant machine learning models for predicting the mortality of patients with COVID-19. Specifically, we build the following two models for the purpose: gradient boosting decision tree (GBDT) and logistic regression (LR) model. Further, we develop a simplified LR model, the LR-5 model, which uses 5 selected features only. Our experimental results show that all models are capable of achieving good performance in mortality prediction for confirmed COVID-19 patients. In particular, GBDT performs better than LR for severe cases. Nevertheless, our proposed LR-5 model exhibits superior performance in mortality prediction in comparison to GBDT and LR.

Problem statement

The problem of predicting the mortality of COVID-19 patients is defined as a binary classification problem. Specifically, we sample COVID-19 patients from hospitals who have sufficient medical information. The final outcome of a patient is labeled by either discharged (y = 0) or died (y = 1). The input data for prediction is collected within 24 h when patients were enrolled in hospitals. The selected patient features include demographic variables, complications, initial medical check results, clinical symptoms, and laboratory test results.

Solutions

We build a gradient boosting decision tree (GBDT) and logistic regression (LR) model to solve the binary classification problem.

GBDT modeling

CART regression tree We use the CART regression tree as the decision tree in our GBDT model. The rationale of using CART regression tree rather than CART classification tree is that each GBDT iteration targets the fitting of the gradient, which is a continuous value. The technical challenge here is to find an optimal split point among the combination of all features and their corresponding possible values. For this purpose, we use a square error to evaluate the fitting degree.

Algorithm for generating regression tree

We proceed to present how to generate our CART regression tree, which is detailed as follows.

Input: Training data D;

Output: Regression tree f (x);

Our high-level idea is to construct a binary decision tree. Specifically, we recursively split the underlying space into two sub-spaces and calculate the output on each sub-space. Our detailed steps are presented as follows.

Step 1: Find an optimal splitting variable j and its splitting point s by solving the formulation as follows:

$$\underset{j,s}{min}\left[\underset{c_1}{min}\sum _{x_i\in R_1\left(j,s\right)}{\left(y_i-c_1\right)}^2+\underset{c_2}{min}\sum _{x_i\in R_2\left(j,s\right)}{\left(y_i-c_2\right)}^2\right]$$

Step 2: Given a selected pair (j, s), split the underlying space and determine the corresponding output, which is computed as follows:

$$\begin{array}{c}{R}_1\left(j,s\right)=x\left|x^{\left(j\right)}\le s,R_2\left(j,s\right)=x\right|x^{\left(j\right)}>s\\ c_m=\frac{1}{N}\sum _{x_1\in R_m\left(j,s\right)}{y}_i,x\in R_m,m=1,2\end{array}$$

Step 3: Continue Steps 1 and 2 until the termination condition is satisfied.

Step 4: Split the input space into M sub-spaces R₁, R₂,…, R_M, and generate the decision tree as follows:

$$f\left(x\right)=\sum _{m=1}^M{\widehat{c}}_{m}I\left(x\in R_m\right)$$

Gradient boosting Next, we introduce our gradient boosting algorithm, which is based on a boosting tree. The procedures are presented as follows.

Step 1: Initialize $f_0\left(x\right)=0$.

Step 2: For each m = 1, 2, …, M, compute the residual as follows:

$$r_{\mathit{mi}}=y_i-f_{m-1}\left(x\right),i=1,2,\dots ,N$$

Step 3: Learn a regression tree by fitting r_mi. The output is h_m(x).

Step 4: Update f_m(x), where f_m(x) = f_m–1 + h_m(x), and obtain the gradient tree for the regression problem:

$$f_M\left(x\right)=\sum _{m=1}^M{h}_m\left(x\right)$$

GBDT algorithm Finally, we present our GBDT algorithm as follows.

Step 1: Initialize a weak learner.

$$f_0\left(x\right)=arg\underset{c}{min}\sum _{i=1}^{N}L\left(y_i,c\right)$$

Step 2: For each m = 1, 2, …, M:

Step 2(a): For each sample i = 1, 2,…, N, calculated the residual (i.e., negative gradient) as follows:

$$r_{\mathit{im}}=-{\left[\frac{\left(\partial L\left(y_i,f\left(x_i\right)\right)\right)}{\partial f\left(x_i\right)}\right]}_{f\left(x\right)=f_{m-1}\left(x\right)}$$

Step 2(b): Take the residual, r_im, as the new value, and for each i = 1, 2,…, N, regard x_i and r_im as the training data of the next tree. Assume that f_m(x) is the new regression tree and its areas of leaf nodes are denoted by R_jm, where j = 1,2,…, J. Here, J denotes the number of leaves in a given regression tree.

Step 2(c): For each j = 1,2,…, J, compute the corresponding optimal fitting value as follows:

$${\mathrm{{\rm Y}}}_{\mathit{jm}}=\underset{Y}{\underbrace{argmin}}\sum _{x_i\in R_{\mathit{jm}}}L\left(y_i,f_{m-1}\left(x_i\right)+\mathrm{{\rm Y}}\right)$$

Step 2(d): Build an enhanced learning model as follows:

$$f_m\left(x\right)=f_{m-1}\left(x\right)+\sum _{j=1}^J{\mathrm{{\rm Y}}}_{\mathit{jm}}I\left(x\in R_{\mathit{jm}}\right)$$

Step 3: Get the final model as follows:

$$f\left(x\right)=f_M\left(x\right)=f_0\left(x\right)+\sum _{m=1}^M\sum _{j=1}^J{\mathrm{{\rm Y}}}_{\mathit{jm}}I\left(x\in R_{\mathit{jm}}\right)$$

Logistic regression (LR) modeling

LR is a linear model, which is known for its high efficiency and simple interpretation. Because that LR requires regularization, the parameters used for L1 and L2 regularizations are applied to continuous regularization transformation. As such, we choose to adopt L2 for regularization. The rationale is that L2 exhibits better performance compared with L1. The formulation is presented as follows:

$$g\left(z\right)=\frac{1}{1+e^{-z}}$$

The linear boundary is defined as follows:

$$z={\theta }^{T}x={\theta }_0{x}_0+{\theta }_1{x}_1+\cdots +{\theta }_n{x}_n=\sum _{i=0}^n{\theta }_i{x}_i$$

Here, the vector of training data is $x={\left[x_0,x_1,x_2,x_3,\dots ,x_n\right]}^{\tau }$ and the optimal parameter is $\theta ={\left[{\theta }_0,{\theta }_1,{\theta }_2,\dots ,{\theta }_n\right]}^T.$ The prediction function is as follows:

$$h_{\theta }\left(x\right)=g\left({\theta }^{T}x\right)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

The value of the above function represents the probability of y = 1. Thus, the probabilities that x is classified into class 1 and class 0 are, respectively, presented as follows:

$$\begin{array}{c}P\left(y=1|x;\theta \right)=h_{\theta }\left(x\right)\\ P\left(y=0|x;\theta \right)=1-h_{\theta }\left(x\right)\end{array}$$

5-index LR modeling

To further improve the performance of our prediction task for clinical use, we develop a novel 5-index LR (LR-5) modeling method. Our high-level idea works as follows. First, each explanatory variable goes through an F-test and t-test, respectively. When a variable becomes less significant in comparison to subsequently introduced variables, we remove it accordingly. Next, we iteratively run the aforementioned process until no significant variables are introduced into our regression function and no existing variables are removed from the function. As such, we may guarantee that the final explanatory variables are optimal.

Based on the above idea, our detailed steps are presented as follows. In the beginning, we take initial explanatory variables are our input and run a simple regression process for each variable. Next, we introduce other explanatory variables based on the regression function mapped from the explanatory variables that have the most significant contribution to the variables being explained. After the process of gradual regression, the variables that remained in the model are considered to be both significant and nearly free of multicollinearity.

Experiments

Study population and data sources

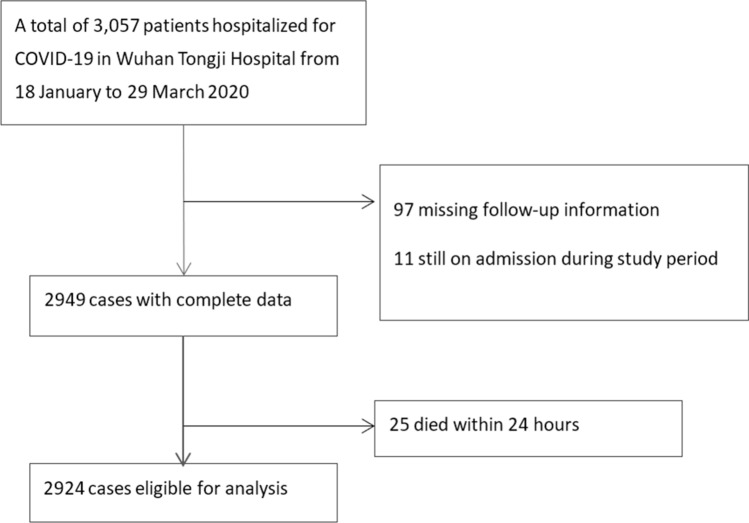
This retrospective study was conducted between January 18 2020 and March 29 2020 in Tongji Hospital of Tongji Medical College, Huazhong University of Science and Technology. A total of 3057 patients were diagnosed with COVID-19 during the study period. The medical records of those patients were accessed. The inclusion criteria were patients with laboratory confirmed COVID-19 and with definite outcomes (death or discharged). The exclusion criteria were as follows: Patients were still on hospitalization and did not develop the outcome by the end of the study period; patients lost to follow-up, or patients died within 24 h after admission. Patients were discharged from the hospital after both clinical recovery and detection of negative SARS-Cov-2 RNA twice in 24 h apart.

The diagnosis of COVID-19 was based on the Chinese Clinical Guidance for COVID-19 Pneumonia Diagnosis and Treatment (7th version) [13]. Four levels of disease severity for COVID-19 were defined by the guidance: mild, moderate, severe, and critically ill. In this study, we classified the mild and moderate as non-severe cases, while the rest two levels as severe cases. The primary outcome in this study was death during hospitalization.

Data collection

The medical records of all eligible patients were screened, and data extraction was completed by the research team. Demographic, clinical, laboratory, radiological characteristics, and treatment and outcomes data were obtained with data collection forms from electronic medical reports.

Features extraction and selection

A total of 1224 features were initially extracted from electronic medical records. Univariate chi-square and t-test were used to compare the distribution differences between the survivor and non-survivor group. Eventually, 152 features with p ≤ 0.05 were selected for further model development (see Supplementary Appendix A for list of features), including demographic variables (age and sex), comorbidities (hypertension, diabetes, heart disease, malignant tumor, etc.), initial vital signs (body temperature, systolic blood pressure, respiration rate, and heart rate), clinical symptoms (fever, cough, dyspnea, etc.), blood gas analysis, routine blood test, biochemical examination, flow cytometry detection as well as cytokine profiles.

Machine learning and external validation

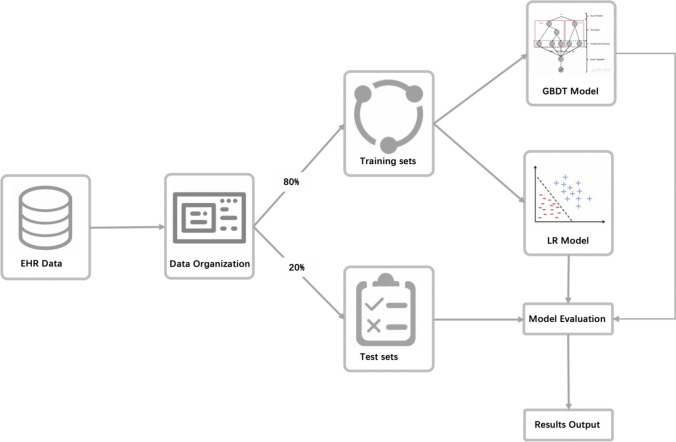
Figure 1 has illustrated the process of machine learning. The gradient boosting decision tree (GBDT), LR model, and simplified LR (LR-5) model with 5 selected features were built. The GBDT model was initially trained using all 152 features in the training set, and only 83 features were retained in the final prediction model (selected 83 features were listed in Supplementary Appendix B). To make our LR model more user-friendly for clinicians, we developed a simplified 5 index LR model (LR-5) using only five features with statistical significance selected by stepwise regression. The five features in the LR-5 model were serum lactic dehydrogenase (LDH), urea, leukomonocyte (%), age, and SPO2. Finally, we also conducted an external validation test for LR-5 model using clinical data of all nationwide confirmed cases of COVID-19 during Feb 29 and March 29 2020 from Brunei. A total of 72 confirmed cases of COVID-19 in Brunei were recruited. Based on the LR-5 model, patients’ data of leukomonocyte (%), BUN, age and SPO2 were collected for analysis, while data on LDH were unavailable. LDH was then filled using the median value estimated from the training set of Wuhan data (median = 239 U/L).

Fig. 1.

The process of our model

Statistically analysis

Continuous variables were presented as median with interquartile range (IQR). Categorical variables were presented as n(%). χ² test and t-test were used to compare differences among non-survivors and survivors. All variables were found to have a statistically significant association (two-tailed, p value < 0.05). The prediction ability of different models was compared using the fivefold area under curve (AUC), positive predictive value (PPV), negative predictive value (NPV), sensitivity, specificity, accuracy, Youden’s index, and threshold . To testify models’ ability of death prediction based on disease severity, we also compared the performance of different models in two subgroups: the non-severe (mild and moderate) group, severe (severe and critically severe) group. Each patients’ data were transformed and contained 152 features, which was then randomly assigned to either the training set (80%, n = 2339) or the testing set (20%, n = 585). Models were trained in the training set, and fivefold areas were calculated based on testing set for further model comparisons.

Baseline characteristics of patients

A total of 3057 patients with COVID-19 were hospitalized in the study, 97 patients were excluded for loss to follow-up, 11 were still on hospitalization during the study period, 25 patients died within 24 h (Fig. 2). A total of 2924 patients were eventually included in the final analysis, 257(8.8%) of whom died during hospitalization and 2667 (91.2%) survived. There were 1481 (50.6%) males, and the median age of the cohort was 59 years old. Approximately 43% patients had comorbidities, the most common disease was hypertension (29.6%), followed by cardiovascular disease (34.1%), diabetes (13.6%), coronary disease (7.1%), cerebrovascular disease (3.0%), malignancy (2.4%), COPD (1.2%). There were 21 (0.7%) mild cases, 2,051 (70.1%) moderate case, 779 (26.6%) severe cases, and 73 (2.5%) critically severe cases of COVID-19 on admission (Table 1). The death event occurred in 0 mild cases, 95/1,956 (4.86%) in moderate cases, 134/645 (20.8%) in severe cases, and 28/45 (62.2%) critically severe cases.

Fig. 2.

Statistical result of patients

Table 1.

Baseline characteristic of the patients on admission

Features	Total (N = 2924)	Survival (n = 2667)	Death (n = 257)	P	AUC
Age (years), median (IQR)	61.876(49.737–69.539)	60.703(48.381–68.692)	69.577(62.709–78.333)	< 0.001	0.718
Gender (%)
Female	1443 (49.4)	1267 (47.5)	176 (68.5)	< 0.001	0.605
Male	1481 (50.6)	1400 (52.5)	81 (31.5)	< 0.001	0.605
Underling comorbidity (%)
Any	1263 (43.2)	1108 (41.5)	155 (60.3)	< 0.001	0.594
Cardiovascular disease	998.0 (34.1)	878.0 (32.9)	120.0 (46.7)
Coronary disease	208.0 (7.1)	173.0 (6.5)	35.0 (13.6)	< 0.001	0.536
Hypertension	865.0 (29.6)	764.0 (28.6)	101.0 (39.3)	0.001	0.553
Cerebrovascular disease	87.0 (3.0)	70.0 (2.6)	17.0 (6.6)	0.001	0.520
COPD	35.0 (1.2)	27.0 (1.0)	8.0 (3.1)	0.009	0.511
Diabetes	397.0 (13.6)	358.0 (13.4)	39.0 (15.2)	0.445	0.509
Malignancy	70.0 (2.4)	53.0 (2.0)	17.0 (6.6)	< 0.001	0.523
Infectious disease	92.0 (3.1)	78.0 (2.9)	14.0 (5.4)	0.037	0.513
Tuberculosis	52.0 (1.8)	44.0 (1.6)	8.0 (3.1)	0.130	0.507
CKD	17.0 (0.6)	12.0 (0.4)	5.0 (1.9)	0.013	0.507
Hepatitis	45.0 (1.5)	40.0 (1.5)	5.0 (1.9)	0.591	0.502
Severity of COVID-19 on admission (%)
Mild	21 (0.7)	21 (0.8)	0 (0.0)	0.250	0.504
Moderate	2051 (70.1)	1956 (73.3)	95 (37.0)	< 0.001	0.682
Severe	779 (26.6)	645 (24.2)	134 (52.1)	< 0.001	0.640
Critical	73 (2.5)	45 (1.7)	28 (10.9)	< 0.001	0.546
Clinical manifestation (%)
Fever	1964.0 (67.2)	1788.0 (67.0)	176.0 (68.5)	0.677	0.507
Cough	1510.0 (51.6)	1381.0 (51.8)	129.0 (50.2)	0.648	0.508
Pant	42.0 (1.4)	33.0 (1.2)	9.0 (3.5)	0.009	0.511
Dyspnea	962.0 (32.9)	844.0 (31.6)	118.0 (45.9)	< 0.001	0.571
Dizzy	63.0 (2.2)	48.0 (1.8)	15.0 (5.8)	< 0.001	0.520
Pharyngalgia	129.0 (4.4)	128.0 (4.8)	1.0 (0.4)	< 0.001	0.522
Temperature (°C)	36.8 (0.7)	36.8 (0.7)	37.0 (0.9)	< 0.001	0.585
Pulse (rates/min)	90.8 (22.0)	90.4 (20.0)	95.5 (27.5)	< 0.001	0.571
RR (rates/min)	23.5 (2.0)	23.4 (2.0)	25.2 (10.0)	< 0.001	0.682
SBP (mmHg)	175.2 (24.0)	179.1 (23.0)	133.1 (26.0)	0.134	0.522
DBP (mmHg)	81.0 (17.0)	81.1 (16.0)	80.3 (17.0)	0.211	0.516
SPO2 (%)	95.4 (3.0)	96.2 (2.0)	87.1 (15.0)	< 0.001	0.729
Laboratory test, median (IQR)			< 0.001
WBC (× 109/L)	5.78(4.55–7.39)	5.69(4.49–7.145)	8.595(5.677–12.928)	< 0.001	0.721
Neutrophil (× 109/L)	3.73(2.67–5.28)	3.58(2.62–4.945)	7.465(4.5–11.622)	< 0.001	0.790
Lymphocyte (× 109/L)	1.22(0.81–1.68)	1.29(0.89–1.73)	0.585(0.42–0.8)	< 0.001	0.847
NLR	2.906(1.81–5.418)	2.69(1.756–4.57)	12.211(6.49–23.396)	< 0.001	0.883
Platelets (× 109/L)	222.0(170.0–284.0)	225.0(176.0–289.0)	152.0(112.0–222.0)	< 0.001	0.728
ESR (mm/h)	28.0(13.0–55.0)	27.0(12.0–54.0)	35.0(18.0–60.0)	0.008	0.562
LDH (U/L)	241.0(192.5–328.0)	233.0(189.0–305.0)	485.0(363.0–639.0)	< 0.001	0.876
CRP (mg/L)	10.2(1.6–55.9)	7.8(1.4–43.2)	103.7(59.85–162.4)	< 0.001	0.873
HDL-C (mmol/L)	0.96(0.79–1.2)	0.98(0.812–1.22)	0.76(0.55–0.92)	< 0.001	0.743
Procalcitonin (μg/L)	0.06(0.04–0.12)	0.06(0.04–0.09)	0.245(0.13–0.712)	< 0.001	0.870
Ferritin (ng/mL)	473.0(233.675–915.2)	421.7(213.7–792.35)	1436.8(771.75–2444.5)	< 0.001	0.826
Total bilirubin (μmol/L)	8.85(6.6–12.1)	8.6(6.4–11.7)	12.0(8.7–17.6)	< 0.001	0.692
ALT (U/L)	22.0(14.0–38.0)	22.0(14.0–37.0)	24.0(17.25–42.0)	0.001	0.562
AST (U/L)	25.0(18.0–36.0)	24.0(18.0–34.0)	41.0(29.0–58.0)	< 0.001	0.755
Prealbumin (g/L)	231.0(167.0–278.0)	236.0(178.0–279.0)	118.0(99.5–141.5)	< 0.001	0.843
Albumin (g/L)	36.7(32.6–40.85)	37.4(33.4–41.3)	31.3(28.2–34.2)	< 0.001	0.191
BUN (mmol/L)	4.5(3.5–5.8)	4.4(3.4–5.5)	8.3(5.5–12.775)	< 0.001	0.811
Creatinine (μmol/L)	68.0(56.0–83.0)	67.0(56.0–81.0)	86.5(67.0–110.75)	< 0.001	0.704
eGFR (ml/min)	93.4(79.3–104.0)	94.3(81.9–104.9)	73.2(48.7–90.6)	< 0.001	0.740
TNF-α (pg/ml)	8.1(6.5–10.5)	7.9(6.4–10.0)	11.45(9.025–18.975)	< 0.001	0.760
IL-2R (pg/ml)	405.0(281.0–649.0)	381.0(277.0–581.0)	1096.5(726.75–1717.0)	< 0.001	0.881
IL-6 (pg/ml)	6.03(2.76–22.525)	5.025(2.63–18.362)	59.69(23.16–122.0)	< 0.001	0.887
IL-8 (pg/ml)	10.9(7.6–18.075)	10.4(7.325–16.65)	23.95(13.55–52.35)	< 0.001	0.785
IL-10 (pg/ml)	8.6(6.3–13.4)	7.9(6.1–11.6)	14.6(9.525–25.5)	< 0.001	0.748

Continuous variables were expressed as medians with interquartile range (IQRs) ALT, alanine aminotransferase; AST, aspartate aminotransferase; COPD, chronic obstructive pulmonary disease; CKD, chronic kidney diseases; WBC, white blood cell count; CRP, C-reactive protein; ESR, erythrocyte sedimentation rate (ESR); NLR, neutrophil-to-lymphocyte ratio; LDH, lactic dehydrogenase; eGFR, estimated glomerular filtration rate; HDL-C = high-density lipoprotein cholesterol; SBP = systolic blood pressure; RR, respiratory rate; DBP, diastolic blood pressure; BUN, blood urea nitrogen; AUC, area under curve

Comparisons of the baseline between survivors and non-survivors

Table 1 presents the comparison of the baseline characteristics between survivors and non-survivors. Compared to survivors, non-survivors were older (69.577[62.709–78.333] vs. 60.703[48.381–68.692] years, p < 0.001), and more likely to be female (68.5% vs. 47.5%, p < 0.001). Comorbidities were more common in non-survivors, with 60.3% in non-survivors and 41.5% in survivors (p < 0.001). Specifically, the cardiovascular diseases (46.7%), chronic obstructive pulmonary disease (COPD) (3.1%) and cancer (6.6%) were prominent in non-survivors. Lower lymphocyte (0.585[0.42–0.80] vs. 1.29[0.89–1.73], p < 0.001), lower high-density lipoprotein cholesterol (HDL-C) (0.76[0.55–0.92] vs. 0.98[0.81–1.22], p < 0.001) and higher neutrophils (7.465[4.5–11.622] vs. 3.58[2.62–11.622], p < 0.001) and neutrophil-to-lymphocyte ratio (NLR) (12.211 [6.49–23.396] vs. 2.69[1.756–4.57], p < 0.001) level were found in non-survivors than survivors. Lactic dehydrogenase (LDH), high-sensitivity C-reactive protein (hs-CRP), blood urea nitrogen (BUN) and pro-inflammatory cytokines as such IL-6, TNF-α, IL-10 were higher in non-survivors than survivors.

Comparisons of different models in the full cohort

The top ten features with the highest predictive accuracy in the models are shown in Table 2. Three models were finally developed and tested with fivefold cross-validation (Table 3). LR model comprised 152 features and GBDT models had 83 features. We then simplified LR model as LR-5 comprised the top 5 common clinical indices. The overall fivefold AUC of LR, LR-5, and GBDT models were 0.928, 0.913 and 0.941, respectively, among which, GBDT models have the largest AUC. Similarly, the estimated AUC on the testing set was also highest in GBDT model (0.939), followed by LR (0.928) and LR-5 (0.915). The diagnostic accuracy was 0.889 in GBDT, 0.868 in LR, and 0.887 in LR-5. GBDT model also obtained the highest sensitivity (0.899) and specificity (0.889). The NPV of all three models exceeded 97%, while the PPV was not high in all models, with 0.381 for LR, 0.402 for LR-5, and 0.432 for GBDT.

Table 2.

Top ten features with highest predictive ability

Feature no.	Feature added	P value of coef	AUC on train	AUC on test
1.0	LDH	< 0.001	0.840	0.876
2.0	BUN	< 0.001	0.882	0.877
3.0	Lymphocyte (%)	< 0.001	0.895	0.903
4.0	Age	< 0.001	0.903	0.911
5.0	SPO2	< 0.001	0.915	0.917
6.0	Platelets	< 0.001	0.923	0.925
7.0	CRP	< 0.001	0.930	0.921
8.0	IL-10	0.001	0.932	0.930
9.0	HDL-C	0.005	0.934	0.932
10.0	SaO2	0.005	0.935	0.931

LDH, lactic dehydrogenase; BUN, blood urea nitrogen; CRP, C-reactive protein; HDL-C = high-density lipoprotein cholesterol; AUC, area under curve

Table 3.

Prediction accuracy of different models in different cohort

No. of included feature	LR model			LR-5 model			GBDT model
	152			5			83
	Total	Non-severe	Severe	Total	Non-severe	Severe	Total	Non-severe	Severe
Total (death)	2924(257)	2072(95)	852(162)	2924(257)	2072(95)	852(162)	2924(257)	2072(95)	852(162)
Threshold	0.110	0.110	0.110	0.140	0.140	0.140	0.090	0.090	0.090
Fivefold AUC	0.928	0.924	0.891	0.913	0.895	0.887	0.941	0.932	0.918
AUC on testing set	0.928	0.946	0.855	0.915	0.902	0.864	0.939	0.940	0.897
AUC on training set	0.937	0.931	0.913	0.913	0.897	0.888	0.997	0.997	0.997
Sensitivity (95%CI)	0.878	0.933	0.714	0.898	0.952	0.711	0.899	0.940	0.774
Specificity (95% CI)	0.769	0.714	0.806	0.771	0.588	0.871	0.788	0.619	0.903
Accuracy	0.868	0.922	0.732	0.887	0.938	0.743	0.889	0.924	0.799
Positive predictive value	0.381	0.357	0.397	0.402	0.333	0.435	0.432	0.351	0.483
Negative predictive value	0.975	0.984	0.941	0.978	0.983	0.956	0.978	0.979	0.972

AUC, area under curve

Performance of models in COVID-19 patients with different disease severity

As patients with mild or moderate COVID-19 are not hospitalized due to the scarcity of medical resources in most countries, we tried to test models under different clinical scenarios. Table 3 also shows the performance result of models stratified by disease severity. All models performed excellently in non-severe cases with an accuracy of 0.922, 0.938, and 0.924 in LR, LR-5, and GBDT models, respectively. LR model, however, had the highest AUC on testing set. In severe cases, the accuracy of LR model for predicting mortality was the lowest (0.732), followed by the LR-5 model (0.743). The GBDT model performed the best in severe cases with an accuracy of 0.799. The GBDT also showed the highest fivefold AUC (0.918) as well as the highest AUC on the testing set (0.897) in severe cases. The NPV remained high in both severe and non-severe cases. The PPV of GBDT model for predicting death was even greater in severe cases (0.483) than overall cohort (0.432), indicating an excellent ability in early identification of patients with poor outcomes.

External validation test in 72 patients in Brunei

Among the total 72 confirmed cases of COVID-19, 2 patients died during follow-up while the rest 70 survived (Appendix C). In compared to those deceased, survivors had significantly higher lymphocyte (31.45%[10.3–59.2%] vs. 14.1%[13.6–14.6%], p = 0.022) and lower BUN (mmol/L) (3.48[1.1–8.12] vs. 4.95[4.0–5.9], p = 0.045). In the validation test of the LR-5 model, leukomonocyte (%) turned to show the highest AUC (0.917), followed by urea (0.867), age (0.826), and SPO2 (0.704) (data not shown).

Discussion

In this study, we applied machine learning algorithms to develop prognostic models for predicting mortality in confirmed cases of COVID-19. All models performed well in the overall population. Particularly, prediction performance of the GBDT was superior to LR models in the subgroup of severe COVID-19. Furthermore, we developed a simplified LR-5 model with 5 indices as a convenient tool for clinical doctors that showed an acceptable AUC and accuracy.

The demographic and clinical characteristics of this cohort were representative. Most of the risk factors found in non-survivors have been reported in previous study [14–16]. The top ten features in the models included LDH, BUN, lymphocyte count, age, SPO2, platelets, CRP, IL-10, HDL-C, and SaO2, most of which have been repeatedly documented in the literature [6, 17, 18]. These variables reflected different aspects of the characteristics of COVID-19, for example, respiratory failure (SpO2 and SaO2), renal dysfunction (BUN). Notably, the indicators of the systemic inflammation (LDH, CRP, IL-10, Platelets) comprised almost half of the top ten features. Systemic inflammation has been reported in severe COVID-19 [19]. The cytokine storm may play a crucial role in the development of respiratory failure and consequently organ failure [20, 21]. Higher cytokine level (IL-2R, IL-6, IL-10, and TNF-a) has been found in non-survivor group patients in this study, which was consistent with previous studies [21, 22]. Moreover, one of the top ten features in the machine learning models was IL-10, which is a cytokine with potent anti-inflammatory properties that can induce T cell exhaustion [23, 24]. This might partially contribute to the lymphopenia in severe COVID-19.

The models in this study were derived from real-world data with comprehensive details, thus the selection bias was limited and the results were more representative than other models. All of the three models performed well with an AUC of 0.911–0.943 and NPVs exceeded 97%. However, the PPVs were relatively low, which was consistent with all the other prediction models reported in the literature. The major reason for this could be the dynamic change of the disease. All the models in this study as well as in the literature were derived from baseline data collected on admission, where highly heterogeneity exited. A dynamic model could have better performance.

Compared with LR models, GBDT performed better in mortality prediction in both full cohort and subgroup of different severity. GBDT is not sensitive to missing data, therefore can serve as a good tool for early detection of potential critical patients and optimize the medical resource allocation. In contrast, the LR model has superiority on high-speed calculation and provides results handy for interpretation, which might be more user-friendly in clinics. However, this LR full model included 161 features and the application could be cumbersome for daily clinical practice, especially when the healthcare systems were confronting severe human resource shortage. As a simplified model, the LR-5 model incorporating only 5 common variables with an excellent PPV and satisfying accuracy could be recommended as a simple tool for clinical use.

We also conducted external validation for the LR-5 model based on all nationwide confirmed cases of COVID-19 during Feb 29 and March 29 2020 from Brunei (n = 72). As a prediction tool, the LR-5 model showed a strong ability in death prediction with a very high AUC of 0.97, which implies the high reliability of this LR-5 for death prediction in populations of other countries. However, it shall be noted that selection bias due to small sample size could never be eliminated and further external validation study using a larger sample size should provide the warranty.

There were several limitations in this study. Firstly, we only used fivefold cross-validation rather than external validation due to the lack of external data. Second, only the Chinese patients were included, the generalizability and implementation of these models across different settings and populations remain unknown.

In conclusion, three models were developed in this study. GBDT models performed the best in different severity. LR-5 is a simple tool for routine care.

Author contributions

SL, YL, and TZ plan the study. SL, TZ, SX obtained the data and performed the statistical analysis and data summarization. SL and YL drafted the manuscript. All authors discussed the results and contributed to the final manuscript.

Funding

This study was funded by a COVID-19 Emergency Project from Wuhan Science and Technology Bureau (2020020401010096).

Data availability

Data could be requested to the corresponding authors upon reasonable request.

Compliance with ethical standards

Conflict of interest

We declare no competing interests.

Ethics approval and content to participate

The study was approved by the institutional committee board of Tongji Hospital of Tongji Medical College, Huazhong University of Science and Technology, and Universiti Brunei Darussalam Research Ethics Committee. All cases were anonymous in the final analysis.

Informed consent

The requirement for informed consent was waived due to the retrospective nature of the analyses.