Cortical surface registration using unsupervised learning

Abstract

Non-rigid cortical registration is an important and challenging task due to the geometric complexity of the human cortex and the high degree of inter-subject variability. A conventional solution is to use a spherical representation of surface properties and perform registration by aligning cortical folding patterns in that space. This strategy produces accurate spatial alignment, but often requires high computational cost. Recently, convolutional neural networks (CNNs) have demonstrated the potential to dramatically speed up volumetric registration. However, due to distortions introduced by projecting a sphere to a 2D plane, a direct application of recent learning-based methods to surfaces yields poor results. In this study, we present SphereMorph, a diffeomorphic registration framework for cortical surfaces using deep networks that addresses these issues. SphereMorph uses a UNet-style network associated with a spherical kernel to learn the displacement field and warps the sphere using a modified spatial transformer layer. We propose a resampling weight in computing the data fitting loss to account for distortions introduced by polar projection, and demonstrate the performance of our proposed method on two tasks, including cortical parcellation and group-wise functional area alignment. The experiments show that the proposed SphereMorph is capable of modeling the geometric registration problem in a CNN framework and demonstrate superior registration accuracy and computational efficiency. The source code of SphereMorph will be released to the public upon acceptance of this manuscript at https://github.com/voxelmorph/spheremorph.

1. Introduction

Non-rigid shape registration is an important area of research in medical imaging, in particular for establishing cross-subject spatial correspondence in the cerebral cortex. This type of spatial alignment has been shown to improve the statistical power of group functional MRI (fMRI) analysis (Van Atteveldt et al., 2004; Frost and Goebel, 2012) resulting from the improved correspondence of functional areas. Due to the geometric complexity of the cortex and the large variability between individuals, cortical surface registration remains a challenging task. Inter-subject surface alignment is commonly driven by geometric features that describe measures of cortical shape (folding), such as sulcal depth or local curvature (Fischl et al., 1999; Yeo et al., 2010; Conroy et al., 2013; Tardif et al., 2015).

A widely used cortical surface registration approach is to map the surface onto the unit sphere in order to perform computations in this canonical domain. Existing efforts are mainly focused on the adaptation of registration algorithms in the Euclidean space (Fischl et al., 1999; Yeo et al., 2010; Robinson et al., 2014). These aim to optimize a similarity metric between the target and the deformed source volumes, regularized by various energies (Sotiras et al., 2013). FreeSurfer (Fischl et al., 1999) registers an individual surface to a probabilistic atlas computed from a representative set of subjects by minimizing the squared difference between the average convexity across subjects and that of the individual, weighted by the inverse variance of the convexity across subjects. The Multimodal Surface Matching tool (Robinson et al., 2014) uses a similarity between the input and reference mesh features in a coarse-to-fine manner. The deformation is driven by aligning local patches around control points, i.e. vertices of a low resolution mesh, and then propagated to the high resolution input mesh via interpolation. Spherical Demons (Yeo et al., 2010) modifies the classical Demons method (Thirion, 1998) using velocity vectors tangent to the sphere. The two-step optimization of classical Demons also holds for the spherical case in which the second step handles the deformation regularization by spherical thin plate spline interpolation. To encourage desirable mathematical properties such as invertibility, diffeomorphic transforms have seen extensive methodological development, yielding state-of-the-art tools (Ashburner, 2007; Zhang et al., 2017). Unfortunately, since these methods solve an optimization problem for each image pair, they often exhibit long execution times.

High computational costs have led to an increase in the popularity of supervised (Krebs et al., 2017; Sokooti et al., 2017; Yang et al., 2016) and unsupervised (Balakrishnan et al., 2019; Dalca et al., 2018, 2019; Niethammer et al., 2019; Wang et al., 2015) learning-based registration algorithms. Considering the difficulty of establishing ground truth spatial correspondences, supervised methods require predictions from existing algorithms (Yang et al., 2016), simulations (Sokooti et al., 2017), or both (Krebs et al., 2017). In contrast, unsupervised methods make use of Spatial Transformer Networks (STN) (Jaderberg et al., 2015) to warp the moving image in a differentiable way, enabling end-to-end training (Balakrishnan et al., 2019; Dalca et al., 2019; Jason et al., 2016; Krebs et al., 2019; de Vos et al., 2019; Niethammer et al., 2019). Some unsupervised methods (Balakrishnan et al., 2019; Dalca et al., 2019; Krebs et al., 2019) model a stationary velocity field as latent variables representing deformations in a generative probabilistic model. They use a scaling and squaring layer (Arsigny et al., 2006) for the Lie group exponentiation of the velocity field to generate diffeomorphic transforms, thus guaranteeing topology preservation. These methods have demonstrated high quality performance in registering various types of medical images. Therefore, we build on these concepts when working with surfaces. A more complex model (Niethammer et al., 2019) utilizes a vector momentum-parameterized stationary velocity field (vSVF) and jointly optimizes the local regularizer parameterized by a deep network and the registration parameters of the vSVF model for location-varying regularization. In addition to velocity field registration models, sparse learning is also explored for image-template key point matching (Wang et al., 2015) and a subsequent interpolation to a dense deformation field via radial basis functions. However, the performance is dependent on the key point selection.

Recent studies have developed geometric convolutional neural networks (CNN) (Su and Grauman, 2017; Cohen et al., 2018; Coors et al., 2018; Seong et al., 2018; Jiang et al., 2019; Zhao et al., 2019) that operate on a spherical manifold to solve classification and detection tasks. To address the distortions introduced by projecting signals to a planar image, regular convolutions with increased kernel sizes near polar regions have been utilized (Su and Grauman, 2017). Spherical CNNs encode rotational instead of translational equivariance into the network in Euclidean space to solve classification problems (Cohen et al., 2018). In SphereNet, the convolution kernel on the sphere has been approximated by encoding the vertex neighborhood information on 2D tangent planes, which enables adapting existing CNN architectures to the omnidirectional setup for object detection and classification tasks (Coors et al., 2018). Geometric CNNs (gCNN) (Seong et al., 2018) also deal with convolution and pooling operations of a CNN on a mesh surface. However, they have so far only been tested on sex classification, using cortical thickness images. A convolutional kernel discretized by an unstructured mesh was recently proposed and evaluated on spherical MNIST classification and 3D object detection tasks (Jiang et al., 2019). Spherical U-Net (Zhao et al., 2019) proposes a novel Direct Neighbor convolutional kernel based on expansion and contraction process of icosahedron and defines corresponding convolution and pooling operations. Graph convolutions (Gopinath et al., 2019a, 2019b) have been utilized for brain surface data in aligned spectral domains to learn the node-wise prediction (Gopinath et al., 2019a), e.g. cortex parcellation and global subject-wise information (Gopinath et al., 2019b), e.g. disease classification or age regression. FastSurfer (Henschel et al., 2020) introduces a full alternative pipeline for FreeSurfer and omits nonlinear surface-atlas registration via fast spherical mapping that quickly maps the volumetric parcellation to cortex using Laplace Eigenfunctions. Most existing work, however, focuses on the construction of spherical convolutional kernels and, to the best of our knowledge, neural networks have not yet been extended to surface registration. Compared with classification or detection tasks, besides convolution and pooling operations on spheres, a learning-based registration method should address local deformations defined on spheres. However, existing spatial transformation networks (Esteves et al., 2018; Tai et al., 2019) for spheres only address global deformations, which are not suitable for accommodating nonlinear deformation fields.

In this paper, we propose a diffeomorphic framework combining a generative model for surfaces with CNNs to register individual cortical surfaces to an atlas space. This framework adapts conventional VoxelMorph for registering Euclidean images (Dalca et al., 2019) to spherical manifolds. In order to address the limitations of 2D planar projection, we construct a weighted neighborhood graph defined on 2D grids, which accounts for the non-uniform metric tensor of the spherical representation to encode a stationary velocity field. Considering that the 2D projection operation samples the arc-length for each latitude to the same number of points, we also take sampling distortion into account at different latitudes in the likelihood model. We quantify the performance of our framework through two applications: the generation of cortical parcellations and the alignment of functional activations. The experimental results demonstrate that our framework yields better registration accuracy to state-of-the-art classical methods at a significantly reduced computational cost, and more accurate results compared to current learning-based methods.

Our contributions can be summarized as:

1. We propose a learning-based framework for spherical surface registration, which provides accurate and efficient performance compared to conventional registration work;

2. We derive an Maximum a Posteriori (MAP) solution for deformation fields in the spherical domain by correcting distortions from planar projection;

3. Different from existing spherical networks, the registration results from our proposed method aid the cortex parcellation as well as various group analyses (i.e. local thickness, functional activation etc.) while other spherical networks only learn one or multiple preset measures;

4. We explore the use of different features for functional alignment.

The remainder of this paper is organized as follows. We first introduce the cortical registration problem, review the conventional VoxelMorph (Dalca et al., 2019) framework, and propose our method and network structure. We then describe two evaluation experiments including cortical parcellation and functional alignment, and show results for these experiments. Finally, we present our discussions and conclusions.

2. Methods

Numerous studies using FreeSurfer have demonstrated its efficacy in spherical-based cortical registration. We build on ideas for our surface representation from the FreeSurfer spherical registration (Fischl et al., 1999) and model the unsupervised learning structure for the registration field following VoxelMorph (Dalca et al., 2019).

2.1. Registration problem definition

In the FreeSurfer spherical registration pipeline (Fischl et al., 1999), surface geometry is encoded as a convexity attribute at each mesh vertex and the representation of the atlas surface is computed from a group of adult subjects. In order to register the surfaces of an individual to the atlas space, first a white matter mesh is generated and mapped to the unit sphere by minimizing metric distortion (Fischl et al., 1999). Next, an optimal rotational alignment is computed by global search over two rotation angles on the sphere. Then a 2D canonical warp is computed to align the subject’s convexity pattern with that of the mean pattern encoded in the atlas, by minimizing the mean squared difference, weighted by the inverse of the atlas variance. Our goal is to compute this canonical warp using a CNN framework.

Let S_x be the unit sphere and I_x the corresponding scalar field over the sphere (e.g. sulcal depth or curvature) projected into 2D longitude/latitude parameterization. Let I_a be the atlas mean image as defined in FreeSurfer, and M and N be the number of image rows and columns. Let ${\mathrm{\Sigma }}_a=diag\left({\sigma }_1^2,{\sigma }_2^2\dots {\sigma }_{MN}^2\right)$ be a diagonal matrix where each diagonal element denotes the variability of the corresponding feature at a particular vertex as defined in the FreeSurfer atlas variance image. The goal is to find the spatial transformation Φ : S² → S² given I_x and I_a that maximizes the a posteriori probability of the transform assuming certain smoothness priors on the warp.

2.2. VoxelMorph

We assume a diffeomorphic deformation based on a stationary velocity field v, denoted as Φ_v, and adapt a generative probabilistic model following VoxelMorph (Dalca et al., 2019). VoxelMorph uses Maximum a Posteriori (MAP) estimation to obtain the most likely velocity field v* at each voxel/pixel given a pair of images. VoxelMorph models the prior probability of v as a zero-mean multivariate normal distribution, $p\left(v\right)=\mathcal{N}\left(v;0,{\mathrm{\Sigma }}_v\right)$, where Σ_v is the covariance matrix. An individual image can be estimated by warping the FreeSurfer atlas, thus we model the warped image I_x ∘ Φ_v as $p\left(I_x|v;I_a\right)=\mathcal{N}\left(I_x\circ {\mathrm{\Phi }}_v;I_a,{\mathrm{\Sigma }}_a\right)$, where Φ_v is the inverse transformation of the atlas warping to the individual. The aim is to maximize the posterior probability $p\left(v|I_x;I_a\right)=\frac{p(v)p\left(I_x|v;I_a\right)}{{\int }_{v}p\left(v,I_x;I_a\right)dv}$, where the marginalization over v is intractable. In this case, a variational approximation q_ψ (v|I_x; I_a) is adopted with parameters ψ, by minimizing its dissimilarity, Kullback–Leibler (KL) divergence, with the true posterior probability. For simplicity, the approximate posterior q_ψ (v|I_x; I_a) is restricted to a multivariate normal distribution $\mathcal{N}\left({\mu }_{v|I_x;I_a},{\mathrm{\Sigma }}_{v|I_x;I_a}\right)$ where ${\mu }_{v|I_x;I_a}$ and a diagonal ${\mathrm{\Sigma }}_{v|I_x;I_a}$ are functions estimated with a U-Net core (Ronneberger et al., 2015), as shown in Fig. 2.

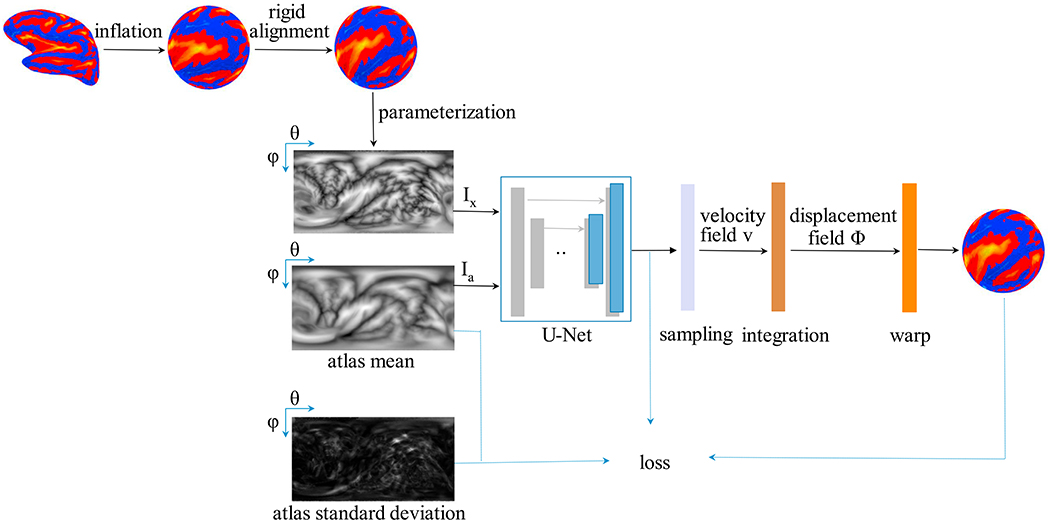
Fig. 2.

The proposed cortical surface registration workflow (SphereMorph). The input spherical representation is first rigidly aligned to the atlas using convexity patterns and then projected onto a polar coordinate system. The Spherical U-Net core takes parameterized input image I_x and atlas mean image I_a as inputs and estimates the distribution, ${\mu }_{v|I_a;I_x}$ and ${\mathrm{\Sigma }}_{v|I_a;I_x}$, of the velocity field v, which is then sampled and integrated using scaling and squaring steps to generate the deformation field Φ_v.

Using the above assumptions, maximizing the posterior probability can be approximated by minimizing the following loss:

$$L\left(\psi ;I_x,I_a\right)=-E_q\left[\log p\left(I_x|v;I_a\right)\right]+KL\left[q_{\psi }\left(v|I_x;I_a\right)\Vert p(v)\right],$$ (1)

where E_q[ ·] operates the expectation computation given the distribution q and q is short for q_ψ (v|I_x; I_a). The first term describes the reconstruction loss and the second term is a KL divergence term, encouraging the estimated posterior probability q_ψ (v|I_x; I_a) to be close to the prior p(v). VoxelMorph encourages the smoothness of the velocity field v by setting ${\mathrm{\Sigma }}_v^{-1}={\mathrm{\Lambda }}_v=\lambda L$, where the parameter λ controls the scale of the velocity field and L is the graph Laplacian matrix defined on the Euclidean grid. L is computed as L = (D – A), where A is the neighborhood adjacency matrix and D is the graph degree matrix. Thus, Eq. (1) can be rewritten as:

$$\begin{gathered} L\left(\psi ;I_x,I_a\right)=-E_q\left[\log p\left(I_x|v;I_a\right)\right]+KL\left[q_{\psi }\left(v|I_x;I_a\right)\left|\right|p(v)\right] \\ =\frac{1}{2}\log \left|2\pi {\mathrm{\Sigma }}_a\right|+\frac{1}{2}{E}_q\left[{\left(I_a-I_x\circ {\mathrm{\Phi }}_v\right)}^T{\mathrm{\Sigma }}_a^{-1}\left(I_a-I_x\circ {\mathrm{\Phi }}_v\right)\right] \\ +\frac{1}{2}\left[\log \frac{\left|{\mathrm{\Lambda }}_v^{-1}\right|}{\left|{\mathrm{\Sigma }}_{v|I_x;I_a}\right|}-2+\mathit{tr}\left({\mathrm{\Lambda }}_v{\mathrm{\Sigma }}_{v|I_x;I_a}\right)+u_{v|I_x,I_a}^T{\mathrm{\Lambda }}_v{u}_{v|I_x,I_a}\right] \\ =\frac{1}{2K}\sum _k{\left(I_a-I_x\circ {\mathrm{\Phi }}_{v_k}\right)}^T{\mathrm{\Sigma }}_a^{-1}\left(I_a-I_x\circ {\mathrm{\Phi }}_{v_k}\right) \\ +\frac{1}{2}\left[tr\left(\lambda D{\mathrm{\Sigma }}_{v|I_x;I_a}-\log {\mathrm{\Sigma }}_{v|I_x;I_a}\right)+u_{v|I_x,I_a}^T{\mathrm{\Lambda }}_v{u}_{v|I_x,I_a}\right]+const, \end{gathered}$$ (2)

where K is the number of samples $v_k˜q$ used to approximate the expectation. We use K = 1. We treat the fixed atlas I_a and the warped individual image I_x ∘ Φ_v as MN × 1 vectors. We denote this naive application of the registration of 2D projected images as the 2D VoxelMorph method and it serves as a benchmark in our experiments.

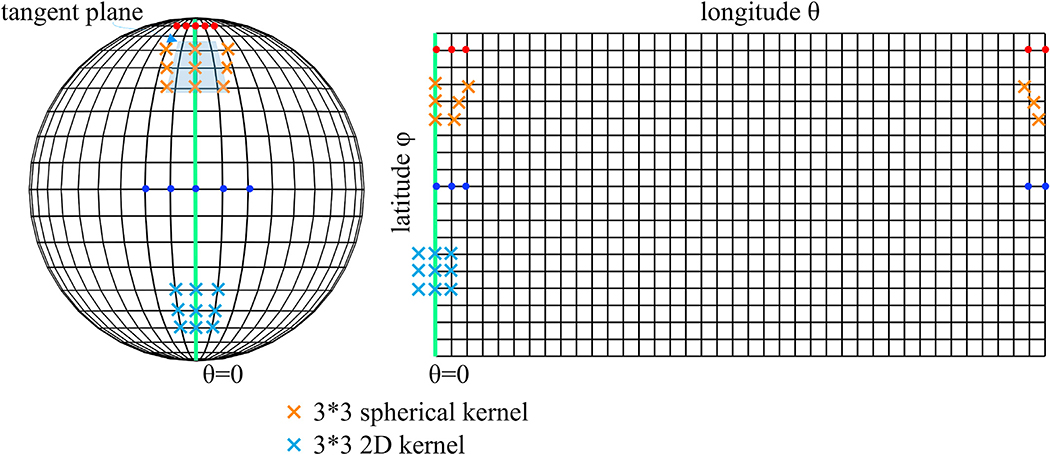
Unfortunately, the 2D projection step introduces two main problems, as shown in Fig. 1:

Fig. 1.

Illustration of a spherical mesh and its corresponding 2D rectangular grids by planar projection. ϕ and θ denote the longitude and latitude respectively. Regions with higher latitude, e.g. red dots here, have denser samplings compared to regions with lower latitude (e.g. blue dots), yielding greater distortions. The regions crossing θ = 0 (green line) become non-adjacent due to the cutting and flattening operations.

• varying level of distortions with different latitudes (distortion increases from the equator to the poles); and

• inability to represent the periodic property of θ and the geometry of the poles (an enclosed spherical surface is projected onto a rectangular image region, introducing discontinuities at the image borders).

Hence, the 2D VoxelMorph method over-weights the alignment for near-pole regions, yielding misalignment in most regions even compared to global rigid registration as shown in Section 3.

2.3. Proposed method: SphereMorph

To address the above issues, we propose SphereMorph. We start by defining the registration problem in the spherical domain. The spherical representation of an individual’s surface is first rotated for a rigid alignment with the atlas, as in FreeSurfer. The spherical surface is parameterized by the longitude θ and latitude ϕ and sampled to an M × N two-dimensional image with a geometric or functional feature, e.g. convexity, assigned as a pixel intensity measure.

2.3.1. Prior correction

We assume that the displacement field is smooth on the sphere considering the anatomical continuity via a graph Laplacian regularizer. We define a neighbor connectivity graph G_S on the spherical manifold and represent the velocity with respect to Cartesian coordinates as a signal defined on this graph. Let $\mathcal{T}$ denote the conversion from polar to Cartesian coordinates, that is ${[x,y,z]}^T=\mathcal{T}([\theta ,\varphi ])={[\sin \varphi \cos \theta ,\sin \varphi \sin \theta ,\cos \varphi ]}^T$, then the geodesic velocity at each vertex Ver_i(θ_i, ϕ_i), i ∈ [1, 2,..,MN] is given by $v’=f(v)={\left[v_x\left({\theta }_i,{\varphi }_i\right),v_y\left({\theta }_i,{\varphi }_i\right),v_z\left({\theta }_i,{\varphi }_i\right)\right]}^T=\mathcal{T}\left({\mathrm{\Phi }}_v\left(\left[{\theta }_i,{\varphi }_i\right]\right)\right)-\mathcal{T}\left(\left[{\theta }_i,{\varphi }_i\right]\right)$.

Each vertex on the projected image is considered as a node and each grid edge connecting two adjacent nodes as their edge in G_S. We connect leftmost and rightmost nodes due to the periodicity in longitude. The weight of the connection between vertices in G_S varies with location to account for the horizontal edge distance on the spherical surface which is proportional to sin ϕ. Thus, we define the weight of each grid edge connecting vertices Ver_i(θ_i, ϕi), Ver_j(θ_j, ϕj) as:

$$w_{ij}=\{\begin{array}{lll}1/\sin \varphi ,& \text{if}& {\varphi }_i={\varphi }_j,{\theta }_i\ne {\theta }_j\\ 1,& \text{if}& {\varphi }_i\ne {\varphi }_j,{\theta }_i={\theta }_j.\end{array}$$ (3)

We construct the corresponding neighborhood adjacency matrix A_S with entries $A_{S_{ij}}=w_{ij}$ and the degree matrix D_S with diagonal entries $D_{S_{ii}}={\sum }_j{w}_{ij}$. Finally, we denote the Laplacian of this weighted graph as L_S = D_S – A_S and define the covariance of geodesic velocity as ${\mathrm{\Sigma }}_{v’}^{-1}={\mathrm{\Lambda }}_{S_v}=\lambda L_S$. Intuitively, this formulation can be seen as increasing the regularization near the poles, where the Euclidean distance between mesh nodes is small, and decreasing the weighting near the equator where the Euclidean distances are larger.

2.3.2. Distortion correction

For VoxelMorph, which deals with Euclidean image registration, the sampling of grid points is equally distributed. However, a spherical parameterization leads to denser sampling grids for regions at higher latitudes as shown in Fig. 1. Thus, we assign mesh locations from these regions lower weights in computing the data-fitting term, by introducing a diagonal matrix S ∈ R^MN×MN with each diagonal entry encoding the resampling weight S_ii = sinϕ_i for each vertex Ver_i(θ_i, ϕ_i) and model $p\left(I_x|v;I_a\right)=\mathcal{N}\left(I_x\circ {\mathrm{\Phi }}_v;I_a,S^{-1}{\mathrm{\Sigma }}_a\right)$. The first data-fitting term in Eq. (1) is then modified as:

$$-E_q\left[\log p\left(I_x|v;I_a\right)\right]=\frac{1}{2K}\sum _k{\left(I_a-I_x\circ {\mathrm{\Phi }}_{v_k}\right)}^T{\mathrm{\Sigma }}_a^{-1}S\left(I_a-I_x\circ {\mathrm{\Phi }}_{v_k}\right).$$ (4)

2.3.3. Loss function

Starting with Eq. (1) and taking into account the spherical geometry, we arrive at the below objective function:

$$\begin{gathered} L\left(\psi ;I_x,I_a\right)=-E_q\left[\log p\left(I_x|v;I_a\right)\right]+KL\left[q_{\psi }\left(v|I_x;I_a\right)\Vert p(v)\right] \\ =-E_q\left[\log p\left(I_x|v;I_a\right)\right]+KL\left[q_{\psi }\left(v’|I_x;I_a\right)\Vert p\left(v’\right)\right] \\ =\frac{1}{2K}\sum _k{\left(I_a-I_x\circ {\mathrm{\Phi }}_{v_k}\right)}^T{\mathrm{\Sigma }}_a^{-1}S\left(I_a-I_x\circ {\mathrm{\Phi }}_{v_k}\right) \\ +\frac{1}{2}\left[tr\left(\lambda D_S{\mathrm{\Sigma }}_{v’|I_x;I_a}-\log {\mathrm{\Sigma }}_{v’|I_x;I_a}\right)+u_{v’|I_x,I_a}^T{\mathrm{\Lambda }}_{S_v}{u}_{v’|I_x,I_a}\right]+const. \end{gathered}$$ (5)

where ${\mu }_{v’|I_x;I_a}=f\left({\mu }_{v|I_x;I_a}\right)$ and ${\mathrm{\Sigma }}_{v’|I_x;I_a}=f\left({\mathrm{\Sigma }}_{v|I_x;I_a}\right)$. The first term in Eq. (5) is the data-fitting term, which encourages matching surfaces after warping and the second term drives the posterior to approximate the smoothness prior defined on a spherical grid.

2.3.4. Network structure

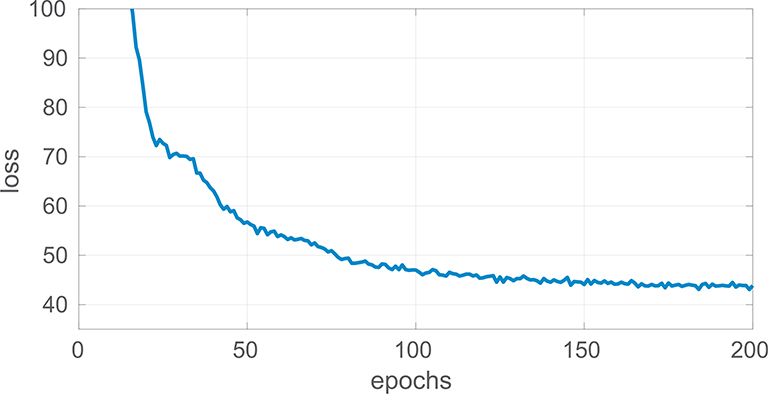
Fig. 2 illustrates the individual stages task fmriof our pipeline. For a given vertex at location (θ, φ), we utilize inverse gnomonic projection, which maps points on the tangent plane to the spherical surface as in SphereNet (Coors et al., 2018), to obtain the corresponding locations on the projected image for the neighbor vertex on its tangent plane. We implement the convolution and pooling operations in each 3× 3 local tangent patch shown in Fig. 1 and build a UNet core (Ronneberger et al., 2015), which contains four downsampling and four upsampling layers. Following the sampling layer, seven scaling and squaring operators take the layer output, or velocity field, and return a diffeomorphism Φ. 2D VoxelMorph uses a dense spatial transformer layer on (θ’, φ’) after displacement to retrieve the warped image while SphereMorph warps the image by computing the interpolation grids as ((θ’+2π) mod2π, φ’) for transformer layer. The model is implemented in Keras with a Tensorflow backend and the ADAM optimizer as part of the VoxelMorph package. We set the hyperparameter λ = 3× 10⁷, the learning rate to 1× 10⁻⁵, and trained our dense model for 200 epochs, by which point the loss had converged as shown in Fig. 3. All experiments were conducted on the same workstation with Intel Xeon X5550@2.67GHz and used NVIDIA Tesla P40C for all CNN-based methods. The source code of SphereMorph will be released to the public upon acceptance of this manuscript at https://github.com/voxelmorph/spheremorph.

Fig. 3.

Line plot of the converging loss function over training epochs.

3. Experimental setup

To demonstrate the accuracy and efficiency of the proposed registration framework, SphereMorph, we used two sets of experiments, cortical parcellation and fMRI group analysis, on two independent test data sets.

3.1. Data

3.1.1. Training data set

The spherical atlas from FreeSurfer served as the fixed image in our model. As training data, we used the surface convexity maps of the left hemispheres of 800 randomly selected subjects from the ADNI1 cohort that was released as part of the publicly available Alzheimer’s Disease Neuroimaging Initiative (ADNI) (Mueller et al., 2005) (http://adni.loni.usc.edu/) and was processed by FreeSurfer v5.1. The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). The ADNI dataset consists of longitudinal T1-weighted scans from 836 subjects that are divided into four classes: elderly controls (n = 252), early mild cognitive impairment (eMCI, n = 215), late MCI (lMCI, n = 176), and AD (n = 193). The subjects were scanned on average 4.8 times (minimum: a single time; maximum: 11 times; 4013 scans in total), with a mean interval between scans equal to 286 days (minimum: 23 days, maximum: 1567 days). The mean age at baseline of the subjects was 75.1 ± 6.6 years. Since the ADNI project spans multiple sites, different scanners were used to acquire the images; further details on the acquisitions can be found at http://adni.loni.usc.edu/data-samples/adni-data-inventory/.

3.1.2. Test data sets

(1) We used FreeSurfer-processed MRI scans of 39 subjects from a cohort recruited by the Washington University Alzheimer’s Disease Research Center (ADRC) (Van Horn et al., 2001). The MRI scans were acquired on a 1.5T Vision system (Siemens, Erlangen Germany). T1-weighted magnetization-prepared rapid gradient echo (MP-RAGE) scans were obtained according to the following protocol: two sagittal acquisitions, FOV = 224, Matrix = 256 × 256, Resolution = 1 × 1 × 1.25mm³, TR= 9.7 ms, TE = 4 ms, Flip angle = 10, TI = 20 ms, TD = 200 ms. Two acquisitions were averaged together to increase the contrast-to-noise ratio. For the cortical parcellation experiment, we separated the data set into two: 9 validation subjects and 30 held-out test subjects. All subjects have 34 cortical areas manually annotated (Desikan et al., 2006), making them ideal for evaluating registration accuracy.

(2) Additionally, we used another set of 100 unrelated young and healthy subjects from the Human Connectome Project (HCP) (Van Essen et al., 2013) as a second test set. The HCP project used state-of-the-art fMRI hardware and acquisition parameters in a sample of highly educated, healthy subjects. For each subject, seven task fMRI sessions were collected, including working memory, gambling, motor, language, social cognition, relational processing and emotional processing, totaling 48:30 min of fMRI data. The acquisition parameters and minimal preprocessing of these data have been described extensively elsewhere (Glasser et al., 2013; Barch et al., 2013).

3.2. Baselines

We compared our proposed registration method to rigid registration on the sphere (i.e. two rotations) and four other nonlinear registration methods: a 2D version of VoxelMorph, Multimodal Surface Matching (MSM) (Robinson et al., 2014), Spherical Demons (SD) (Yeo et al., 2010), and FreeSurfer (FS) spherical registration (Fischl et al., 1999). We chose the sulcal depth as the input feature for all registration methods. Additionally, we also explored the usage of the curvature and T1/T2 maps together with sulcal depth in the HCP functional group analysis experiments. Additionally, we also explored the usage of the curvature and T1/T2 maps together with sulcal depth in the HCP functional group analysis experiments. We trained 2D VoxelMorph using the same training set as described above and selected the hyperparameter λ that yielded the best performance on the validation set. MSM is a surface-based registration approach that offers significant flexibility with regards to the set of features that are used to drive the spatial alignment. MSM drives the deformation via aligning local patches around control points in a multi-resolution fashion. It is implemented on CPU using a fast, multi-resolution, discrete optimization scheme, offering significant computational speed-up compared to other classical methods. We ran MSM over three resolution levels with five iterations per level. Specifically, we set the regularization parameters as (0.1, 0.2, 0.3) for the parcellation experiments. For the functional group analysis experiments, we relied on the publicly released ‘MSMSulc’ results which were generated by running MSM with high regularization parameters (10, 7.5, 7.5) and using the sulcal depth feature. Compared to the low regularization, MSM with high regularization has been demonstrated to yield lower group alignment in folding patterns but smaller area distortions (Robinson et al., 2014), which leads to better functional alignment after following registration steps using “myelin” maps. Spherical Demons, a fast diffeomorphic landmark-free surface registration tool implements the regularization for its objective function via iterative Gaussian smoothing. We explored a range of smoothing iteration numbers (5, 10, 15, 20) to optimize performance and used the results of 10 iterations.

3.3. Evaluation

To evaluate registration accuracy, we relied on the resulting spatial transformations to project the atlas parcellation back to individual scan space. For an accurate registration solution, the test subject’s cortical parcellations will resemble the manually outlined versions. In order to quantify how well they match, we computed the Dice overlap coefficient (Dice, 1945), the overall Mean Minimum Distance (MMD) as well as the individual MMD measures for each anatomical region. The Dice overlap coefficient, $Dice(M,A)=2\cdot \frac{R_{M\cap A}}{R_M+R_A}$, quantifies the surface area overlap (R_M∩A) between manual (R_M) and automatic method-generated parcels (R_A) and the MMD describes the discrepancy between the parcellation boundaries: MMD(M, A)= 1/N · Σ_id(m_i, a_i) where d(m_i, a_i) denotes the Euclidean distance between a vertex m_i on a manual boundary and its corresponding closest vertex a_i on an automatic method-generated boundary. Additionally, we also tested how consistently the various registration methods aligned anatomical features, such as convexity/sulcal depth and curvature.

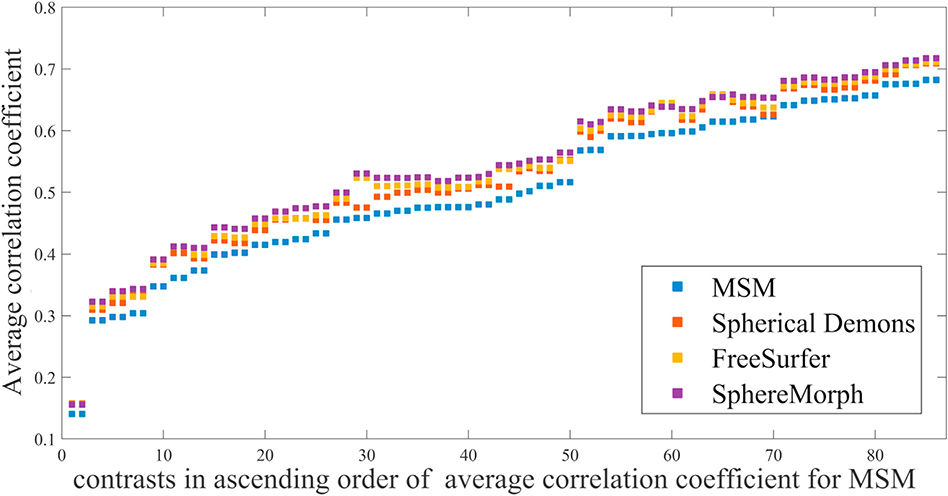
In the second set of experiments, we mapped all individuals within the group to the HCP’s 2 mm standard grayordinates space (Glasser et al., 2013), using the displacement field, then computed group maps of task-evoked activations. To evaluate the quality of the group alignment quantitatively, we computed average correlations between the group-average and the projected individual activation maps across 86 task contrasts derived from the seven fMRI tasks.

4. Results

4.1. Computational efficiency

Table 1 summarizes registration accuracy and computation time for all methods. All the compared methods take spherical cortical surfaces as input, which are generated by brain surface tessellation including fixing topological defects and inflation to the sphere from volumetric segmentation. For a brain surface with 120k-150k vertices, it takes around 0.9h and 0.25h CPU computation time for surface tessellation and inflation, respectively. The comparison of registration time illustrates that the proposed method ran approximately 20 times faster than the conventional registration method in FreeSurfer. On a CPU, the default FreeSurfer pipeline takes around 13 min to complete the spherical registration. The total computation time of our proposed framework is approximately 0.74 min, including the initial alignment, deep network deployment, and displacement field mapping. With GPU acceleration, the computation time of our method can be reduced to 0.65 min, where the deep network deployment is accomplished within a second. Compared with other registration methods including MSM and Spherical Demons (SD), CNN-based methods provide more than an order of magnitude improvement in execution speed.

Table 1.

Overview of registration accuracy and CPU run time for rigid alignment, 2D VoxelMorph, MSM, Spherical Demons, FreeSurfer spherical registration, and our proposed SphereMorph. SphereMorph performs in a comparable manner with FreeSurfer, while being roughly 20 times faster.

Method	Dice	overall MMD (mm)	Time (min)
Rigid	0.840 ±0.029	3.13±0.43	0.59±0.08
2D VoxelMorph	0.819± 0.027	3.47 ± 0.48	0.73 ± 0.08
MSM	0.872 ±0.014	2.63±0.27	9.56±1.02
Spherical Demons	0.881±0.009	2.43±0.21	6.15±0.59
FreeSurfer	0.889±0.014	2.24±0.21	13.46±3.13
SphereMorph	0.882±0.014	2.42±0.24	0.74±0.09

4.2. Cortical parcellation experiment

4.2.1. Parcellation accuracy

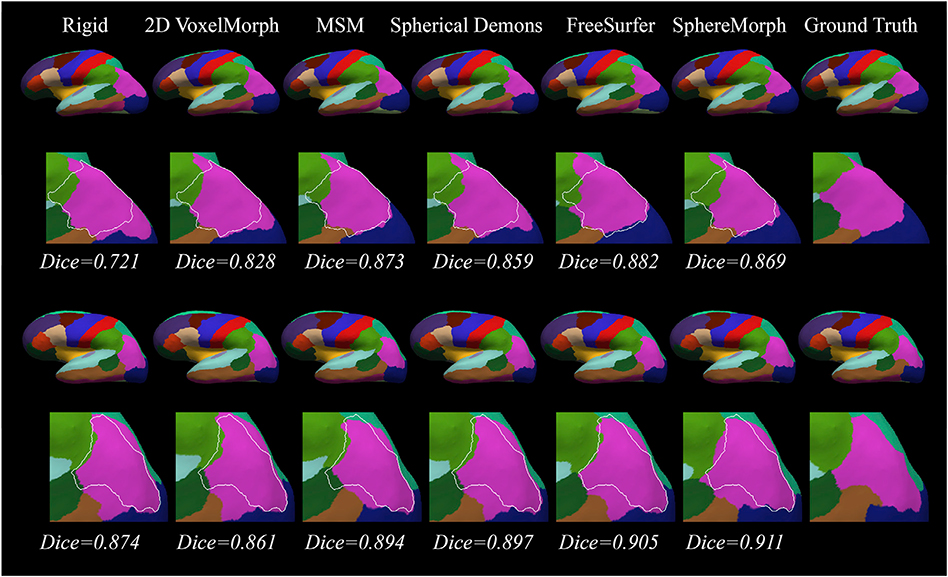
Fig. 4 shows representative cortical segmentation results from all the methods on two randomly selected test subjects from the ADRC dataset. The 2D VoxelMorph-estimated annotation exhibits large differences compared to the ground truth in the lateral occipital regions (marked by white arrows), while FreeSurfer and SphereMorph provide results close to the manual annotations. Fig. 5 displays the two subjects for which our proposed method yields the lowest and highest overall Dice values.

Fig. 4.

Cortical parcellation results for two example subjects from the ADRC dataset. For each subject, the upper rows show the cortical parcellation estimated by different registration methods and the lower rows give a closer view of the parcellation comparison in the lateral occipital region (white arrows) with manual parcellation boundary superimposed.

Fig. 5.

Cortical parcellation results for two subjects where our proposed registration method yields the lowest (top 2 rows) and the highest (bottom 2 rows) overall Dice scores. The overall Dice overlap values for each registration method are displayed below each subfigure.

Table 1 provides an overview of registration accuracy by comparing manual annotations to parcellations generated by the different registration methods, including rigid alignment, 2D Voxelmorph, MSM, SD, FreeSurfer as well as our proposed method. Our proposed method and FreeSurfer achieved the highest accuracy. SphereMorph yields significantly higher overall Dice coefficients than MSM after performing a one-tail Wilcoxon rank sum test on their respective Dice coefficients (p = 0.0318). The deep learning baseline, 2D VoxelMorph, performed significantly worse. This is due to the fact that this method does not account for the distortions intrinsic to the spherical coordinate system. Fig. 6 compares parcel-wise Dice overlap coefficient values associated with the different registration methods. Our method produced higher mean Dice overlap coefficients than MSM for all structures except the Entorhinal, Paracentral and Middletemporal, and showed statistically significant improvement in regional Dice overlap coefficient compared to MSM in the Temporalpole (p = 0.0090), Parahippocampal (p = 0.0102), Transversetemporal (p = 0.0051), Caudalmiddlefrontal (p = 0.0237), Rostralmiddlefrontal (p = 0.0433) and Lingual (p = 0.0148) regions. Compared to Spherical Demons, SphereMorph produced higher mean regional Dice coefficients in 26 out of 34 regions. The regions where this was not the case are the Entorhinal, Rostralanteriorcingulate, Parahippocampal, Fusiform, Transversetemporal, Insula and Lateralorbitofrontal areas. Pairwise t-tests show that SphereMorph compared to SD generated statistically significantly higher Dice scores in the Postcentral (p = 0.0015) and Rostralmiddlefrontal (p = 0.0191) areas while SD outperformed SphereMorph in the Transversetemporal (p = 0.0245) region. In all other areas the performance difference was not statistically significant. Postcentral and Rostralmiddlefrontal regions exhibit larger standard deviations (0.12± 0.05 and 0.15 ± 0.09 respectively) as shown in the atlas while the Transversetemporal region has higher agreement in sulcal depth (atlas standard deviation 0.05 ± 0.02) across subjects. The inverse-variance weighting in SphereMorph makes it more flexible in regions with large group variance, leading to better parcellation results in these regions when compared to SD. SD uses the sum of squared differences as a similarity estimate and yields good parcellation in regions with high agreement in sulcal depth.

Fig. 6.

Boxplots of Dice overlap coefficients for all the 34 anatomical structures computed with respect to 2D VoxelMorph, MSM, Spherical Demons, FreeSurfer spherical registration and SphereMorph.

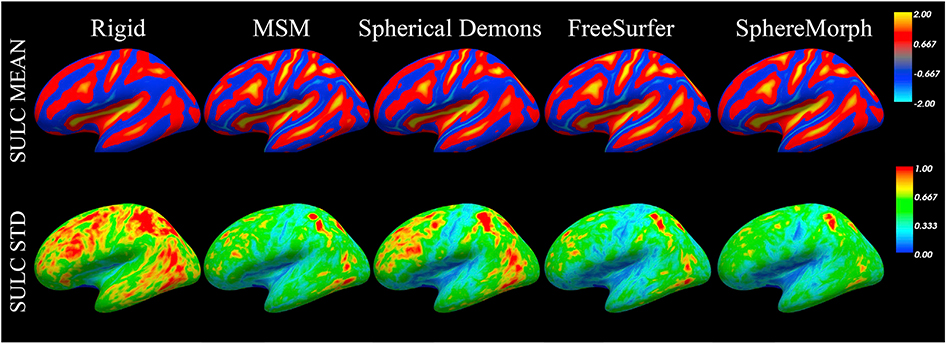
4.2.2. Group average sulcal maps

To evaluate the performance on a finer scale, we also computed the group mean sulcal depth maps after registration for the test data. The resulting mean and standard deviation maps are displayed in Fig. 7. We assume that a better group alignment leads to a sharper group mean and smaller group variation. As expected, the group mean maps provide more detailed information for all nonlinear registration methods than rigid alignment. Moreover, all these methods show smaller standard deviations, suggesting that they provide better alignment in convexity.

Fig. 7.

Sulcal depth alignment generated by rigid, MSM, Spherical Demons and SphereMorph. The maps show group mean and standard deviation of convexity from 30 testing subjects.

All nonlinear registration methods exhibited similar distributions of sulcal variations across brain regions. Specifically, the pre-central, post-central and insula regions show lower standard deviation, suggesting higher agreement of cross-subject convexity in these regions.

4.2.3. Robustness analysis

We investigated the impact of pole positioning on the registration accuracy for SphereMorph by projecting the sphere using 9 different north pole locations spanning θ ∈ (0, π /2, π), φ ∈ (0, π /6, π /3, π /2) and registering the corresponding 2D planar images with corresponding atlas data. We generated the deformed sphere and then re-computed all the region- and distance-based metrics. To evaluate the robustness with respect to different projection centers, we conducted analysis of variance (ANOVA) between all the computed evaluation metrics for these 9 groups. None of the ANOVA analyses (overall Dice: F = 0.2,p = 0.9842, overall MMD: F = 0.93, p = 0.4821) found any significant differences between the 9 groups of cortical parcellations, indicating that the registration accuracy is not sensitive to the arbitrary location of the poles.

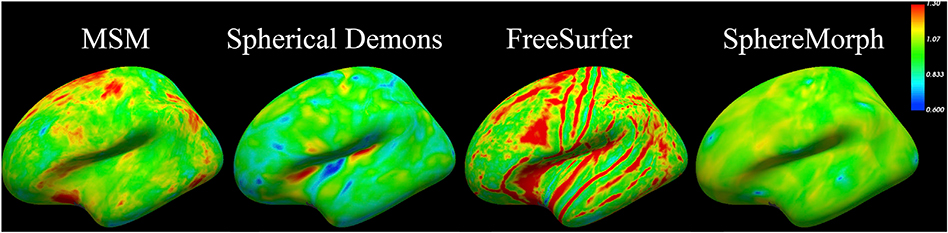
4.2.4. Areal distortion analysis

We calculated the Jacobian map for registered surfaces as an areal distortion measure, where a value close to one indicates a small distortion. Fig. 8 compares the distortion maps for all compared registration methods, suggesting least amount of distortion introduced by SphereMorph. Additionally, we measured the percentage of vertices with a non-positive Jacobian determinant for SphereMorph in the case of a randomly selected subject and it resulted in 0.63%. While we model the deformation field as a diffeomorphism in the continuous case, discretization and numerical errors can lead to a small fraction of locations with Jacobians that are not positive definite.

Fig. 8.

Jacobian maps of registered surfaces, representing areal distortion measurements. Comparing outcomes for all registration solutions, SphereMorph demonstrates the lowest amount of distortion.

4.3. Cross-subject alignment of fMRI activation maps

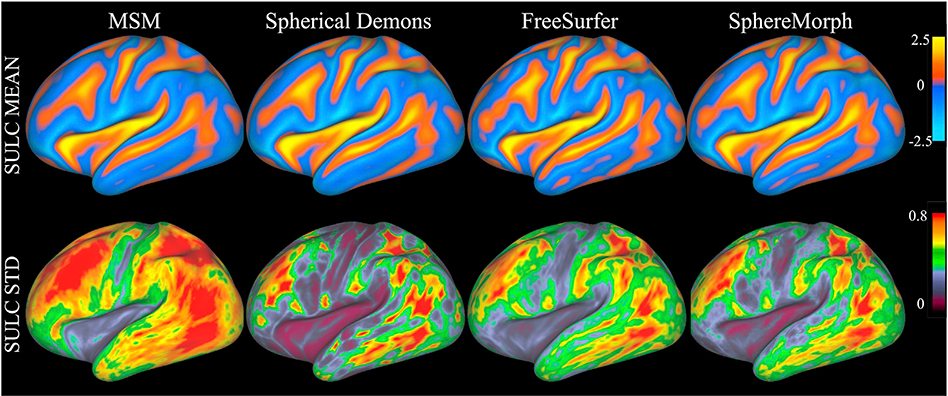
4.3.1. Group average maps

Fig. 9 illustrates the quality of group-wise alignment of convexity after MSM, Spherical Demons, FreeSurfer, and our method were run on our second test data set. Our method yielded smaller variations within the group than MSM (p = 0.0013), just as in the case of the cortical parcellation experiments. For these experiments, we used default regularization parameters for FreeSurfer and optimized the regularization level of Spherical Demons via exploring the number of smoothing iterations for best parcellation performance. Regarding MSM, we relied on the HCP-distributed MSM registration results that were driven only by folding patterns with a high regularization, as suggested in (Robinson et al., 2014), where such settings lead to better functional alignment when followed by a registration step using “myelin” maps. This choice lead to the high group variance displayed on Fig. 9. In order to make this comparison more fair, we also ran MSM using a combination of the T1/T2 map with the folding patterns for an evaluation of accuracy in functional alignments as explained below. We denote the MSM registration version incorporating folding patterns along with the T1/T2 map as MSM-T1/T2 and the SphereMorph version as SphereMorph-T1/T2.

Fig. 9.

Spherical Demons, FreeSurfer and SphereMorph for the 100 unrelated subjects in our second test data set. The top panel shows group-average maps and the bottom panel shows group standard deviations.

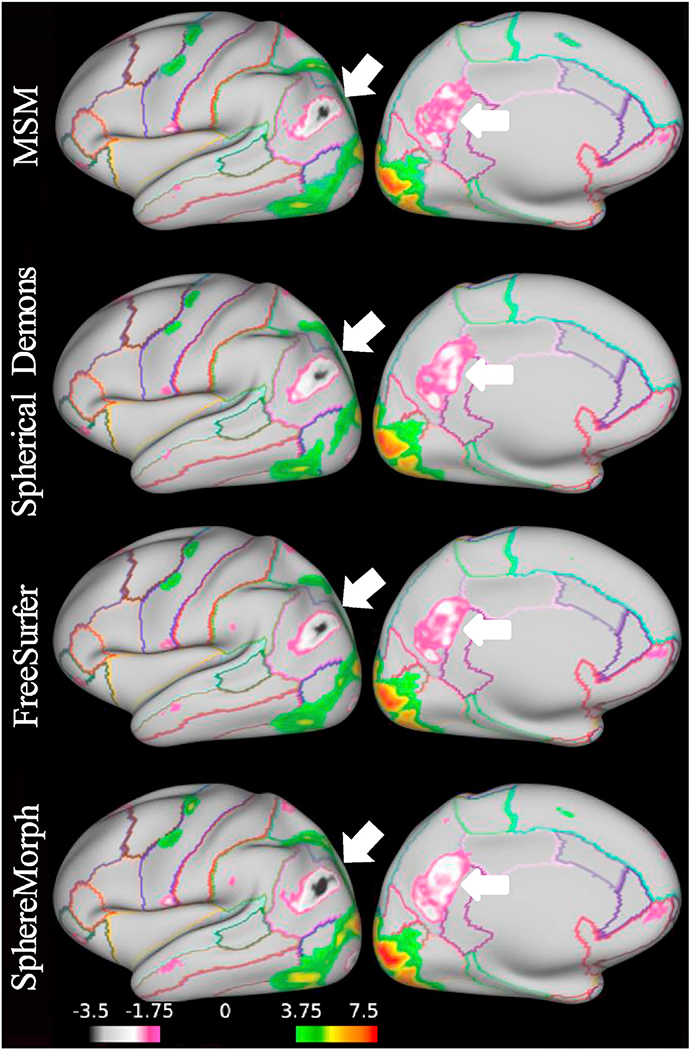
While we expect folding patterns to be predictive of functional areas, this relationship is variable and complex. In order to assess how well the various methods align functionally homologous regions across subjects, we computed group average functional activation maps for all 86 tasks using registration driven by sulcal depth information. Fig. 10 compares group activation results from the 100 subjects for the Gambling reward contrast. Our method improves the functional alignment across subjects over MSM, particularly in the inferiorparietal and precuneus regions, indicated by the arrows. To evaluate the group alignment performance quantitatively, we computed the average correlations between the group-average and individual activation maps after registration across 86 task contrasts derived from seven tasks. All results in Table 2 were computed using registration results driven by sulcal depth maps except for MSM-T1/T2 and SphereMorph-T1/T2, where the T1/T2 map was also incorporated in order to drive the registration.

Fig. 10.

Task fMRI alignment resulting from convexity-driven spatial registration using MSM, Spherical Demons, FreeSurfer and SphereMorph. The maps show group activation results from 100 subjects for the Gambling task reward contrasts (with the outline of Freesurfer-based cortical parcellations for easier interpretation). SphereMorph improves the functional alignment across subjects over MSM, particularly in the inferiorparietal and precuneus regions, indicated by the arrows.

Table 2.

Comparison of group functional alignment for MSM, Spherical Demons, FreeSurfer spherical registration, and our proposed method SphereMorph. Correlation coefficients are calculated for the average correlation coefficients of all 86 contrasts. MSM-T1/T2 and SphereMorph-T1/T2 denote the incorporation of the T1/T2 map along with the sulcal depth feature. All other methods only rely on the sulcal depth.

Method	correlation coefficients	difference with MSM	relative difference (%)
MSM	0:5037±0:1256	–	–
Spherical Demons	0:5298± 0:1258	0:0261 ± 0:0082	5:60± 2:35
FreeSurfer	0:5372 ± 0:1259	0:0335 ± 0:0093	7:12 ± 2:62
SphereMorph	0:5460± 0:1254	0:0424 ± 0:0090	8:99 ± 2:85
MSM-T1/T2	0:5456 ± 0:1310	0:0419 ± 0:0081	8:65 ± 1:89
SphereMorph-T1/T2	0:5535 ± 0:1243	0:0498 ± 0:0164	10:64 ± 4:46

Fig. 11 displays average correlations for the different registration methods. For all 86 contrasts, SphereMorph resulted in significantly higher correlation coefficients than MSM (increase of 0.043± 0.009, p = 0.028 and relative increase of 8.99 ± 2.85%, p = 0.0024).

Fig. 11.

Comparison in the correlation coefficients computed between the group-average and individual activation maps after registration across 86 task contrasts. Higher coefficients suggest better agreement in task activations across subjects.

4.3.2. Alignment performance analysis using multi-modality features

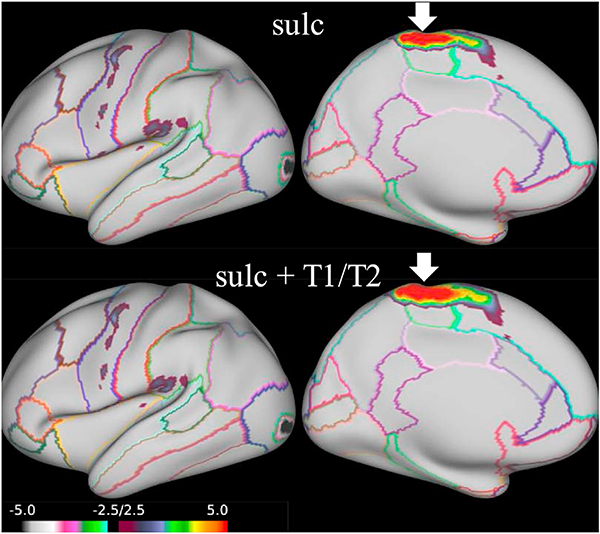
We evaluated the performance for the proposed SphereMorph using curvature and (separately) T1/T2 features to their respective atlases, using our sulcal depth alignment as initialization. We computed a ‘T1/T2’ atlas from three rounds of CNN registration within group. Fig. 12 compares the group agreements in task activation for only sulc and two cascade processes using respective curvature and T1/T2 maps. Using T1/T2 as input post sulcal depth-based registration significantly improves the group agreement level (p < 0.01) in four MOTOR tasks, including RF, RF-AVG, neg-RF and AVG-RF, as indicated by the arrows. All four tasks are related to right finger tapping. Fig. 13 displays the group average activation for RF contrast. Using the T1/T2 map leads to a larger region with positive response in the paracentral and superiorfrontal areas (marked by arrows) compared to using sulcal depth as the only input.

Fig. 12.

Comparison of agreement in 86 task activations using different features. We take the ‘sulc’ and ‘curv’ atlases from FreeSurfer and compute a ‘T1/T2’ atlas from three rounds of CNN registration within group. Contrasts showing significant improvement (p < 0.01) after incorporation of the T1/T2 feature are pointed out by arrows.

Fig. 13.

Task fMRI alignment driven by using different feature maps (sulcal depth and sulcal depth + T1/T2). The maps show group activation results from 100 subjects for the MOTOR task: RF contrasts, with the outline of Freesurfer-based cortical parcellations for easier interpretation. The arrows highlight the paracentral and superiorfrontal areas, where using the T1/T2 map leads to a larger region with positive response compared to using sulcal depth as the only input.

5. Discussions and conclusions

In this paper we present a learning-based method, SphereMorph, for registering cortical surfaces and investigate its performance using two sets of experiments, by comparing it to rigid alignment, 2D VoxelMorph, MSM, Spherical Demons, and FreeSurfer. The proposed SphereMorph yields results that are comparable or superior to the state-of-the-art methods for alignment of folding patterns, cortical parcellation and functional alignment, while offering approximately a 20× computational speedup, showing the accuracy and efficiency of our method for cortical registration. Different from existing spherical networks that learn a node-wise (e.g. cortex parcellation) or subject-wise measure (e.g. gender or abnormality classification), our registration framework is re flexible and can be applied for both parcellation as well as various group analysis tasks.

Compared to conventional registration methods, SphereMorph takes 2D parameterized images as input, outputs the deformation field in a 2D canonical space, then warps the sphere in the original Cartesian space. We directly address two issues associated with the 2D projection: the effects of substantial distortions introduced by the parameterization and the violation of continuity at the borders of the 2D plane (i.e. the imposition of spherical topology). To account for the distortion introduced by the parameterization, we modify the data likelihood term and construct the deformation velocity on a graph weighted by the metric tensor of the parameterization. We use the same weights as in existing work by Khasanova and Frossard (2017) to construct our graph as it has been shown to be capable of encoding the geometry of an omnidirectional camera in the final feature representation of an image. In the implementation of network structure, we encode the neighborhood information by leveraging a 3× 3. spherical kernel defined in SphereNet (Coors et al., 2018) instead of a conventional 2D kernel for the network convolution and pooling operations. Compared to the spherical kernel defined in (Su and Grauman, 2017), the SphereNet kernel is able to handle both the discontinuity problem and planar distortions. While other existing spherical kernels (Seong et al., 2018; Jiang et al., 2019; Zhao et al., 2019) defined on the 3D mesh could be used for the spherical operations in our networks, given that we model the registration problem based on the longitude-latitude representation, an additional interpolation step would need to be introduced for them, potentially introducing error.

We then use a scaling-and-squaring layer to obtain the exponential map in the spherical domain and this can be efficiently implemented on the GPU, without the density of the nodes significantly impacting runtime (Dalca et al., 2019). In addition, we modify the spatial transformer layer to represent the periodicity of longitude in spherical coordinates. Combining these adaptations, our model shows a higher agreement with manual parcellations compared to 2D VoxelMorph, which does not account for distortions and topological changes induced by the 2D parameterization. For 2D VoxelMorph, each point on the rectangular grid contributes equally to the registration, resulting in the alignment of regions near the poles affecting the energy functional more than other regions with the same area in the Euclidean embedding space. Thus, the optimized deformation is over-fitted in these regions. Our experimental results confirm this when comparing the automatically generated parcellations to the manual ones. With an excessive weighting of the alignment of these polar regions, 2D VoxelMorph performs even worse than the initial alignment.

Our proposed registration framework is applicable to any signal or feature that can be represented or sampled onto the cortical surface. However, in the cortical parcellation experiment, the ADRC dataset only has structural scans. Hence, we trained our model as well as MSM and SD using convexity values to drive the registrations. FreeSurfer originally trained its parcellation atlas using the manual annotations on the ADRC data set and yields the best parcellation performance but longest execution time among all the compared methods. Compared to FreeSurfer, which uses a line minimization optimization strategy to obtain a dense displacement field, Spherical Demons reduces the registration problem to a Gauss-Newton optimization step of a non-linear least-squares problem and a displacement field smoothing operation by simple convolution, resulting in faster computation time. We found no significant difference between our proposed SphereMorph and FreeSurfer while SphereMorph shows significant smaller group variations and higher overall Dice coefficients when compared to MSM, suggesting SphereMorph achieves better structural alignment than MSM.

In addition to the accuracy of the structural alignment, when using the same feature (i.e. convexity) for registration, both qualitative and quantitative evaluation results for the task-related experiments demonstrate that the proposed method also yields higher agreement of functional regions across subjects than the current registration method in the Human Connectome Project (HCP) pipeline (Glasser et al., 2013). SphereMorph improves the within-group correlation coefficients significantly for all tasks compared with MSM. The group agreement in convexity is also higher after SphereMorph registration than with MSM. This implies the relationship between cortical folding patterns and boundaries of functional areas as demonstrated in previous work (Hinds et al., 2008). However, using folding-based features alone may not be sufficient to provide an accurate functional alignment across the entire cortex due to regions with highly variable folding patterns across subjects, as well as structure-function variability. Thus, in the functional alignment experiments, we take the sulcal depth registration as initialization and then use cortical T1/T2 maps as input of our network for a multi-step alignment. The cortical T1/T2 maps are computed based on the ratio of T1-weighted to T2-weighted images which correlates with many functionally distinct areas in individual subjects (Glasser and Van Essen, 2011). The combination of T1/T2 and sulcal depth shows significant improvement in group alignment of MOTOR-related tasks, indicating the correlation between T1/T2 and MOTOR-related regions. SphereMorph, just like FreeSurfer, uses an inverse variance weighting scheme to compute the data similarity term. At final evaluation and in comparison with other methods not using such a weighting cheme, SphereMorph can be at a disadvantage due to the presence of areas that are not optimized for alignment. Interestingly though, we found that SphereMorph yields better parcellation outcomes than SD in the Postcentral and Rostralmiddlefrontal areas, which are regions of high variance in the atlas, while SD performs better in the Transversetemporal region that is of lower variance. Consistent with these findings, Table 2 demonstrates higher accuracy functional alignment for SphereMorph compared to SD, while SD yields smaller group variations in folding patterns. This implies that increased structural variability is a marker of reduced structure-function coupling. Thus we believe that using inverse-variance weighting helps improving the functional alignment.

All experiments in this paper focus on subject-to-atlas registration. We will explore the performance of our network for inter-subject registration in the future. In addition, our proposed model can include other contrasts in addition to the convexity metrics used above to drive the registration. Existing studies have shown the improvement in group registration accuracy relying on features generated from resting-state functional MRI (rfMRI) after conventional convexity-driven registration (Robinson et al., 2014; Tong et al., 2017). In the future, we will investigate the use of these to further improve the accuracy of our technique.