Environmental heterogeneity determines the ecological processes that govern bacterial metacommunity assembly in a floodplain river system

Abstract

How diversity is structured has been a central goal of microbial ecology. In freshwater ecosystems, selection has been found to be the main driver shaping bacterial communities. However, its relative importance compared with other processes (dispersal, drift, diversification) may depend on spatial heterogeneity and the dispersal rates within a metacommunity. Still, a decrease in the role of selection is expected with increasing dispersal homogenization. Here, we investigate the main ecological processes modulating bacterial assembly in contrasting scenarios of environmental heterogeneity. We carried out a spatiotemporal survey in the floodplain system of the Paraná River. The bacterioplankton metacommunity was studied using both statistical inferences based on phylogenetic and taxa turnover as well as co-occurrence networks. We found that selection was the main process determining community assembly even at both extremes of environmental heterogeneity and homogeneity, challenging the general view that the strength of selection is weakened due to dispersal homogenization. The ecological processes acting on the community also determined the connectedness of bacterial networks associations. Heterogeneous selection promoted more interconnected networks increasing β-diversity. Finally, spatiotemporal heterogeneity was an important factor determining the number and identity of the most highly connected taxa in the system. Integrating all these empirical evidences, we propose a new conceptual model that elucidates how the environmental heterogeneity determines the action of the ecological processes shaping the bacterial metacommunity.

Introduction

Determining the processes behind community assembly across Earth’s ecosystems is a major research topic in ecology [1–4]. The issue can be addressed using two alternative views. On one hand, the traditional niche-based theory states that deterministic processes, such as environmental filters and species interactions, govern community structure and determine species composition [5, 6]. On the other hand, the neutral theory considers that all species are ecologically equivalent and, therefore, the structure of each community is a consequence of stochastic processes such as birth, death, colonization, immigration, speciation, and probabilistic dispersal [1, 7, 8]. Although these perspectives are often considered contradictory, they are not mutually exclusive and a debate exists over each relative importance in shaping natural communities.

The metacommunity theory provides an adequate framework to identify these processes considering multiple spatial scales [9, 10]. Under this approach, communities are spatially connected in a network by dispersal, and the processes involved in their assembly are the result of the interplay between local factors and regional dynamics.

Recently, Vellend [3, 11] proposed a conceptual framework in which the structure of communities can be explained by the following four “high-level processes”: selection, dispersal, ecological drift, and diversification. These four processes are universally present across ecological communities, and frame the low-level processes involved in the community assembly (e.g., competition, predation, succession, colonization, local extinction). Selection consists in the deterministic factors that modify the community structure due to fitness differences among individuals. It can act under the so-called homogeneous or heterogeneous environmental conditions, leading to more similar or dissimilar structure among communities [12, 13]. When environmental conditions are homogeneous, selection leads to more similar communities (low community turnover), a process known as “homogeneous selection.” On the other hand, under heterogeneous conditions, selection promotes an increase in community turnover as different taxa are selected, and this is referred as “heterogeneous selection” [11, 14]. Dispersal results from both deterministic and stochastic factors that either favor or limit organism movement (active or passive) and the establishment of organisms in local communities. High dispersal rates have a homogenizing effect (homogeneous dispersal) leading to a low turnover within communities, whereas low dispersal rates (dispersal limitation), coupled with drift or weak selection, increase community turnover [12, 15]. Drift influences changes in communities due to demographic events of birth, death, and reproduction that occur at random, independently of species fitness [16]. Finally, diversification refers to the generation of new species by genetic variation mainly due to stochastic factors, and larger temporal scale with respect to the other processes is needed to observe its effects [17].

The ecological rules governing bacteria metacommunity assembly seem to be different in land than in water systems, mainly due to the differences in environmental heterogeneity, which is larger in land [18–22]. In addition, and within aquatic ecosystems, the complexity of freshwater bodies is relatively high in comparison with oceans [23] and, consequently, larger differences in bacterial community composition are observed in freshwater ecosystems [24–29]. In these ecosystems, deterministic processes (mainly selection) have been found to be the main factors shaping bacterial community structure [19, 27, 30–32]. However, it is not a general rule and the relative importance of selection compared with other processes may depend on the environmental heterogeneity and dispersion rates within the metacommunity [24, 28, 30, 33, 34]. For example, in systems with low environmental heterogeneity the stochastic processes seem to be more relevant, because environmental filters are not strong enough to act as selective forces exerting species sorting [24, 33]. Thus, bacterial communities in isolated systems are likely to be mainly structured by dispersal limitation, whereas as environmental connectivity increases, homogeneous dispersal as well as drift will become more important [21, 24, 31, 32, 35–37]. Most of these previous results have been generated from a snapshot of the metacommunity. However, in complex network systems subject to hydrological influence, the relative importance of the structuring ecological processes is likely to change over time according to the changes in the hydrological connectivity [29, 31, 37–42].

Another gap lies in understanding how the high-level ecological processes influence the interactions between taxa. Co-occurrence networks are an increasingly useful tool to infer microbial interactions [43–50]. Under this approach, interactive taxa are linked together either positively or negatively indicating mutualistic or antagonistic co-occurrence patterns. Even if taxa correlations do not necessarily reflect true interactions, network analyses allow to capture and summarize information of highly diverse communities [43–46].

Another useful feature of co-occurrence networks is that they allow to identify the highly connected taxa (commonly referred as hub taxa [44, 45, 51, 52]). These taxa play a significant role within the community and confer stability due to their high connectivity with other members. Therefore, a better understanding of the mechanisms that influence highly connected taxa composition and structure may provide an insight into the underlying response of the whole community [44, 52–55].

The Paraná River floodplain constitutes a hydrological network of linked environments, which can be considered a metacommunity [40], being an ideal system to address these issues. It is characterized by a wide range of temporal and spatial heterogeneity mediated by irregular hydrological fluctuations [56]. It comprises multiple shallow lakes, some of which are permanently connected to the main river or to secondary channels, whereas others remain isolated although high-water phases connect most of the environments [57]. The floods have a homogenization effect on most environmental features [58, 59], as observed for other large river systems [60]. In contrast, the environmental characteristics show a higher spatial heterogeneity during the low-water phases due to the intensified influence of local factors [59]. Here, we investigated bacterial community structure through 16S amplicon sequencing, in contrasting environmental heterogeneity scenarios of this complex floodplain system in order to (i) determine the relative importance of the high-level processes structuring the bacterial metacommunity, (ii) detect changes in bacterial co-occurrence networks, and (iii) identify highly connected taxa.

We hypothesize that the influence of different ecological processes shaping bacterioplankton metacommunities will depend mainly on the system’s environmental heterogeneity, in turn determined by the degree of landscape connectivity. To test this hypothesis, we first analyzed the processes shaping bacterioplankton community structure using the approach based on phylogenetic and taxa turnover proposed by Stegen et al. [12]. Then, we constructed co-occurrence networks for each hydrological scenario to explore how ecological processes affect putative interactions between taxa. We predicted that as the extent of hydrological connectivity increases and the system becomes more homogeneous, nonselective processes will have a larger relevance in structuring the bacterioplankton metacommunity, promoting less interconnected network associations.

Material and methods

Study site and sampling design

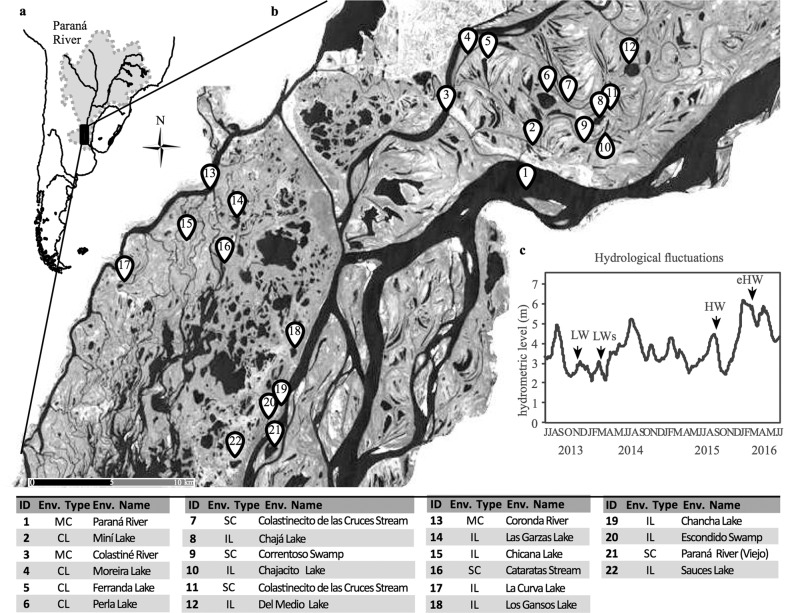
The Paraná River is the second largest river in South America and fifth larger in the world (Fig. 1) [57]. The middle stretch is composed by a main channel and a floodplain that encompasses a high number of temporary and permanent streams and lakes. The system is characterized by a complex spatiotemporal dynamic influenced by the hydro- and sedimentological regime. It has a fluctuating hydrological functioning with pulses of floods and drought that determine high- and low-water phases, which alternate in variable frequency with extreme hydrological phases [61]. During high-water phases, water drains the floodplain, connecting the environments in different degrees depending on the magnitude of the flood. The sediment pulse that mainly depends on suspended solids coming from the Bermejo Basin is not coupled with the hydrological pulses, affecting most abiotic characteristics of the environments connected with the main channel [62]. The dynamics of biological communities respond to a large extent to the hydrological fluctuations, since they have a direct influence not only on the environmental characteristics, but also on the dispersal processes, and habitat colonization [39–42, 63–65].

Fig. 1. The Paraná fluvial system.

a The river location in South America showing the study area and b the environments sampled. c Daily water level from 2013 to 2016 in the Paraná River. The sampled periods are indicated with arrows.

The temporal dynamics and the spatial heterogeneity of the system were captured by sampling different hydrological phases and environmental types, characteristic of the floodplain river (Fig. 1, Supplementary Fig. S1). Four sampling campaigns that lasted 10 days each were performed during a low-water phase (LW, November–December 2013), a low-water phase coupled with the sedimentological pulse (LWs, March–April 2014), a high-water phase (HW, September 2105), and an extraordinary high-water phase (eHW, March 2016). Four representative environmental types with different hydrological connectivity and morphological features were selected (Fig. 1): the main channel and large secondary channels (MC), minor secondary channels (SC), connected lakes (CL), and isolated lakes and swamps (IL). Lentic environments were classified as IL or CL according to their hydrological connectivity degree during LW phase. Overall, our dataset consists of 59 samples: 16 from LW, 17 from LWs, 13 from HW, and 13 from eHW.

Environmental data collection

Besides depth and Secchi depth, water temperature, pH, conductivity, and dissolved oxygen (DO) concentration were measured in situ with a HANNA checkers. Subsurface water samples (20 cm) were collected and transported within 5 h in polypropylene containers to the laboratory for turbidity, soluble reactive phosphorus (SRP), nitrate (NO₃⁻), ammonium (NH₄⁺), chromophoric dissolved organic matter (CDOM) concentration (A₄₄₀), CDOM molecular weight (S_275–295), and chlorophyll-a analyses. Technical details of the abiotic variable analyses are described in Supplementary Methods.

Bacterial samples collection and sequencing

Subsurface water samples for DNA (100–140 ml) were prefiltered with a 50 µm pore mesh, and then filtered through 0.22 µm pore-size cellulose filters (GSWP0-Millipore). The filters were frozen (−80 °C) until DNA extraction. Genomic DNA was extracted using a CTAB protocol [66] as described in Supplementary Methods.

Tagged amplicons of the 16S rRNA gene (V3–V4 region) were obtained with the primers 341F and 805R [67] and sequenced using Illumina MiSeq 2 × 250 paired-end reads approach [68] by Macrogen (Seoul, South Korea).

Sequence data analysis

Raw sequences were processed using a modified version of the pipeline proposed by Logares [69] (https://github.com/ramalok), described in Supplementary Methods. Operational taxonomic units (OTUs) were defined with no clustering (zero-radius OTUs [zOTUs]) using the UNOISE2 algorithm [70]. The zOTU table resulted in 10,253 zOTUs (2,560,053 reads). We constructed zOTU rarefaction curves to evaluate richness saturation (Supplementary Fig. S2).

A second zOTU table was generated discarding zOTUs with <10 reads as well those assigned to the Archaea domain or to chloroplasts. This table was normalized to an equal sampling depth to generate the subsampled zOTU table (rrarefy function, Vegan v.2.0.9 package [71] in the R environment [72]), which consisted of 8927 OTUs and average 18,747 reads per sample.

The sequence data obtained in this work were deposited at the European Nucleotide Archive public database with references ERS4228518–ERS4228576.

Environmental heterogeneity

Environmental heterogeneity was estimated by computing the average dissimilarity between sites ($\overline{\mathrm{Ed}}$) [73] based on nine abiotic variables: DO, turbidity, conductivity, pH, SRP, NO₃⁻, NH₄⁺, CDOM concentration, and CDOM molecular weight. For each hydrological phase (i.e., LW, LWs, HW, eHW), we computed a Euclidean distance matrix (Vegan package, R) and calculated the dissimilarity between sites (Ed) as follows:

$$\mathrm{Ed}=\left(\frac{\mathrm{Euc}}{{\mathrm{Euc}}_{\max }}\right)+0.001,$$

where Euc is the Euclidean distance between two sites and Euc_max corresponds to the maximum Euclidean distance considering all the pairwise distances in the overall dataset. 0.001 was added to account for zero similarity between sites [73]. Then, we calculated the mean Ed ($\overline{\mathrm{Ed}}$) of each computed similarity matrix and used it as an index of environmental heterogeneity in each hydrological phase. In addition, we calculated the coefficient of variation (CV%) for each variable and hydrological phase, as the standard deviation divided by the mean of each variable.

To test whether the environmental conditions in the four hydrological phases differed significantly, we performed a one-way permutational multivariate analysis of variance (PERMANOVA) [74]. We first test for homogeneity of multivariate dispersion (PERMDISP, [75]) with betadisper function (Vegan package, R), which compares the within‐group spread among groups using the average value of the individual observation distances to the centroid of the own group. Since groups account for heterogeneous dispersion (Supplementary Table S2), we run a modified PERMANOVA pseudo-F statistics (F₂) implemented by Anderson et al. [76] that solves permutation test sensitivity to differences in dispersion in unbalanced design. Differences in environmental conditions were also analyzed with a two-way PERMANOVA for testing the effects of hydrological phases, type of environments, and their interaction (adonis function in Vegan package, R).

PERMANOVAs were based on Euclidean distance matrix with 9999 permutations, and pairwise P value comparisons were tested with Bonferroni post-hoc test when significant differences were found.

Bacterial community structure and diversity

To describe a general view of bacterial community structures, we analyzed the taxonomic structure in each hydrological phase and constructed rank abundance curves (Supplementary Fig. S3). We characterized the “rare biosphere” and the “abundant fraction” (zOTUs relative abundances per sample <1% and >1%, respectively) [77].

The effect of hydrological conditions on bacterial metacommunity structures was assessed by calculating the community turnover in each hydrological phase. We computed a Bray–Curtis matrix on the basis of zOTU normalized abundances for each hydrological phase to calculated the dissimilarity (Xd) between the local communities as follows:

$$\mathrm{Xd}=\left(\frac{\mathrm{Bray}}{{\mathrm{Bray}}_{\max }}\right)+0.001,$$

where Bray is the Bray–Curtis dissimilarity between two communities and Bray_max corresponds to the maximum Bray–Curtis dissimilarity considering the overall dataset. Then, we calculated the mean Xd $\left(\overline{\mathrm{Xd}}\right)$ of each matrix computed, which was used as a value of community turnover.

To evaluate the significance of the effect of hydrological conditions on bacterial turnover, we performed a PERMANOVA with 9999 permutations on Bray–Curtis dissimilarity matrices and Bonferroni post-hoc pairwise comparisons. Since PERMDISP was significant (Supplementary Table S2), we run the modified PERMANOVA proposed by Anderson et al. [76]. We additionally calculated the Whittaker index to explore the β-diversity (Past software V3). To visualize the taxonomic similarity across local communities, a nonmetric multidimensional scaling (NMDS) was performed using the Bray–Curtis metric (Vegan package, R). zOTU richness and Shannon–Weaver diversity (H′) indices were calculated from the normalized bacteria zOTU table, and significant differences (P < 0.01) among hydrological phases were evaluated with Kruskal–Wallis analyses and Mann–Whitney U post-hoc tests (Past software V3).

Quantification of high-level process structuring the bacterial metacommunity

To quantify the relative importance of ecological processes in structuring the bacterial metacommunity, we used the approach proposed by Stegen et al. [12]. This approach analyzes the influence of environmental filtering on the community, independently of the considered environmental variables [12, 78], avoiding the problem of overestimating the effect of stochastic processes due to unmeasured environmental variables.

We first measured the influence of selection in each hydrological phase, comparing observed phylogenetic turnover to a random expectation using the βNTI Index (β-nearest taxon [79–81]). This metric is defined as the difference between the observed mean phylogenetic distance between each taxon and its closest relative in two communities (βMNTD metric) with the βMNTD obtained from the null distribution, divided by the standard deviation of the phylogenetic distances from the null data. Absolute βNTI values greater than 2 (|βNTI| > 2) indicate that coexisting taxa are more closely related than expected by chance, so selection strongly influenced community composition [12, 82]. Next, we estimated the percentage of homogeneous selection as the fraction of pairwise comparisons with a βNTI value of <−2 and heterogeneous selection as the fraction of pairwise comparisons with a βNTI value of >+2 [12].

As this approach considered that the habitat preferences of closely related taxa are more similar than the habitat preferences of distantly related taxa [12], we tested the phylogenetic signal performing a Mantel correlogram analysis between zOTU niche and zOTU phylogenetic distances (see Supplementary Methods) [12, 24, 83–85]. Phylogenetic signals were detected over short phylogenetic distances (Supplementary Fig. S4) consistent with previous studies [12, 14, 24, 85, 86].

The communities that were not structured by selection (i.e., |βNTI| < 2) were then analyzed in a second step, where the action of dispersal and drift was calculated based on the taxonomic (zOTU) turnover with the Raup–Crick metric [87] using Bray–Curtis dissimilarities (hereafter RC_bray) [12]. RC_bray compares the measured β-diversity from a metacommunity against the β-diversity obtained from a null model. RC_bray values between –0.95 and +0.95 indicate significant departures from the degree of turnover, occurring when drift is acting alone [12]. In addition, RC_bray values > +0.95 indicate that the communities are less similar than expected by chance as a result of dispersal limitation combined with drift, and RC_bray values < −0.95 indicate that the communities are more similar than expected by chance as a result of homogeneous dispersion [12].

Phylogenetic and taxonomic turnovers were calculated in the R environment, we used the Picante package [88] for βNTI and the raup_crick_abundance function developed by Stegen et al. [12] for RC_bray.

To identify the features that imposed selection or dispersal limitation during each hydrological phase, we performed a distance-based redundancy analysis (db-RDA) on the βNTI and RC_bray matrices using spatial and environmental explanatory variables following Stegen et al. [12].

The spatial relationships between sampling sites were estimated using distance-based Moran’s eigenvector maps (dbMEMs, formerly called principal coordinates of neighbor matrices) [89]. A Euclidean distance matrix was generated from watercourse distances, a proxy of dispersal by water, measured as the minimal distance from each environment to the nearest major channel using satellite images (Google Earth Pro). dbMEM eigenvectors were computed from the truncated Euclidean matrix just at the distance at which IL become disconnected from the lotic influence (8.44 km for LW, and 6.98 km for LWs), or at the distance that keeps all the sites connected (for HW and eHW). The truncation value was calculated as the maximum distance of the minimum spanning tree [90].

The spatial eigenvectors and the nine measured abiotic variables were combined in a principal component analysis (PCA). The resulting PCA axes were used as independent variables in the db-RDA with either βNTI or RC_bray as the dependent variables. Four separate sets of PCA axes and db-RDA analyses were run for each hydrological phase. Each βNTI and RC_bray matrices were normalized adding the absolute magnitude of the minimum (negative) value to all values, and then dividing the resulting values by their maximum. Stepwise forward model selection was carried out on PCA axes evaluated using a P value significance level of 0.05 (as determined by 999 permutations) and the coefficient of determination R² of the global model with all explanatory variables [91].

The significantly selected PCA axes in the db-RDA based on the βNTI characterized environmental variables that imposed selection. The extent to which PCA axes were related to abiotic variables or dbMEMs was evaluated by examining PCA axis loadings. Abiotic variables that loaded heavily on a significant PCA axis for βNTI were considered as measured environmental variables that imposed Selection. PCA axes that loaded on a dbMEMs were considered as an indicator of unmeasured spatially structured environmental variables (strong PCA loading with a dbMEM). The PCA axes were not related to the βNTI but were significantly selected in the db-RDA based on RC_bray were considered as a feature of Dispersal Limitation. dbMEMs and db-RDA were performed with CANOCO software V5.0 [90].

Co-occurrence networks

A bacterial meta-network was constructed considering all the samples from the four hydrological phases. Furthermore, to infer whether bacterial associations were influenced by the different ecological processes structuring the metacommunity, one specific network association for each hydrological phase was constructed considering zOTUs with >50 reads and present in at least 50% of the samples. As previous works have shown that the number of taxa and samples have a strong impact on the network properties [92], the networks were constructed from the same number of taxa and samples randomly selected. Thus for each network, the initial zOTU matrix consisted in 13 samples and 328 zOTUs.

The networks were constructed using the CoNet software V1.1.1.beta [93] implemented in Cytoscape V3.7.1 [94]. Four measures were calculated: Bray–Curtis and Kullback–Leibler nonparametric dissimilarity indices, and Pearson and Spearman rank correlations. The combination of their results allows the appropriateness of scoring measures to determine the statistical significance of correlations, as stated by the authors [93]. The initial edge selection was set to include the 2000 positive and 2000 negative edges consistent across all four correlation measures. The significance of the edges was calculated using the ReBoot method [95] based on 1000 permutations with renormalization and 1000 bootstrap iterations. Only edge supported by at least three methods was considered. Then, edge-specific P values were merged using Brown’s method [96], followed by Benjamini–Hochberg for false discovery rate correction, edges with merged P values below 0.05 were kept [93].

In the microbial network, two taxa could be related because of a true ecological association or alternatively, because they are correlated to an abiotic or biotic environmental factor [46, 93]. To explore indirect associations driven by environmental factors, in the network construction, we included environmental information in an additional matrix containing the following variables: DO, turbidity, conductivity, pH, SRP, NO₃⁻, NH₄⁺, CDOM concentration, and CDOM molecular weight. No environmentally driven indirect edges (i.e., environmental node—taxa node) were detected.

To validate the nonrandom co-occurrence patterns, we evaluated networks against their randomized versions using the Barabasi–Albert model available in the Randomnetworks plugin in Cytoscape. NetworkAnalyzer tool [97] was used to calculate four network topology properties: number of nodes (bacterial zOTUs), number of edges (associations between bacteria), network density, and clustering coefficient. These structural attributes were used to infer the connectedness in bacterial networks [46, 92, 98, 99]. The network density indicates the average connectivity of a node in the network with values varying between 0 and 1 [92, 100]. Values close to 1 are expected when the connectivity of the network increases [100]. The clustering coefficient indicates how nodes are embedded in their neighborhood and, thus, the degree to which they tend to cluster together [92, 100, 101]. As a consequence, low values of this metric are interpreted as less interconnected association networks. Mathematically, it is the average clustering coefficient of all nodes in the graph. The clustering coefficient of a node is the ratio between the numbers of connections in its neighborhood to the number of possible connections. In graph theory, the neighborhood of a node is the set of nodes that are connected to it. Thus, for example, if the node has three neighbors, then it can have a maximum of three connections among them. If all three possible connections are realized, the clustering coefficient of the node is 1 (3/3). Contrarily, if none of the possible connections with the neighbors are realized, the local clustering coefficient value is 0 (0/3).

Highly connected bacterial taxa

To identify highly connected taxa we used three centrality metrics: node degree, closeness centrality, and betweenness centrality [47, 51–54]. The degree is the number of edges connecting each node to the rest of the network. Closeness centrality measures the length of the shortest path between two nodes, reflecting the importance of a node in disseminating information. Betweenness centrality quantifies how many steps away a particular node is from all the others in the web, denoting the role of a node as a bridge between the other components of a network [52, 54, 92].

For each network, we identified the highly connected taxa as those nodes with a high degree (>20), closeness centrality (>0.26), and low betweenness centrality (<0.06) (NetworkAnalyzer tool in Cytoscape) [53, 54, 98]. These metrics illustrate both the number of connections and how important those connections are to the overall network [53, 102, 103].

Redundancy analysis (RDA) was performed to evaluate the effect of abiotic variables on the abundance of the highly connected taxa (CANOCO software V5 [96]). The environmental variables tested as explanatory variables (DO, turbidity, conductivity, pH, SRP, NO₃⁻, NH₄⁺, CDOM concentration, CDOM molecular weight) were normalized as standard normal deviates. A forward selection procedure was run to find the subset of significant explanatory variables using Monte Carlo Permutations.

Results

Environmental heterogeneity

The average environmental dissimilarity between sites ($\overline{\mathrm{Ed}}$) as well as the CV% of the nine abiotic variables indicated a clear trend to higher spatial homogenization from LW (low hydrological connectivity) to HW (high hydrological connectivity) phases (Fig. 2). Thus, the four hydrological phases were significantly different according to their environmental characteristics (PERMANOVA F₂ = 7.6799, P = 0.001, Supplementary Tables S1 and S2, Fig. S5). The two-way PERMANOVA showed a significant effect of environmental type (F₁ = 2.06, P < 0.01) mainly due to IL, besides the effect of hydrological phases (F₁ = 2.5, P < 0.01) (Supplementary Table S3).

Fig. 2. Environmental heterogeneity in the Paraná fluvial system in different hydrological phases.

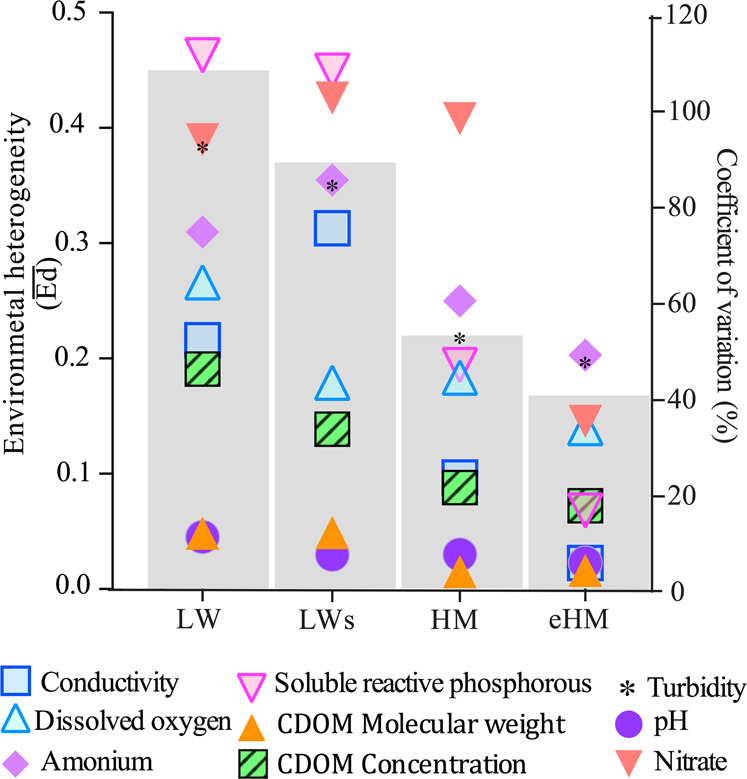
The environmental heterogeneity is expressed as average environmental dissimilarity between sites ($\overline{\mathrm{Ed}}$, gray bars) and the variability (coefficient of variation, CV%) of nine selected abiotic variables among environments. LW low water, LWs low water with sedimentological pulse, HW high water, eHW extraordinary high water.

Bacterial community structure and diversity

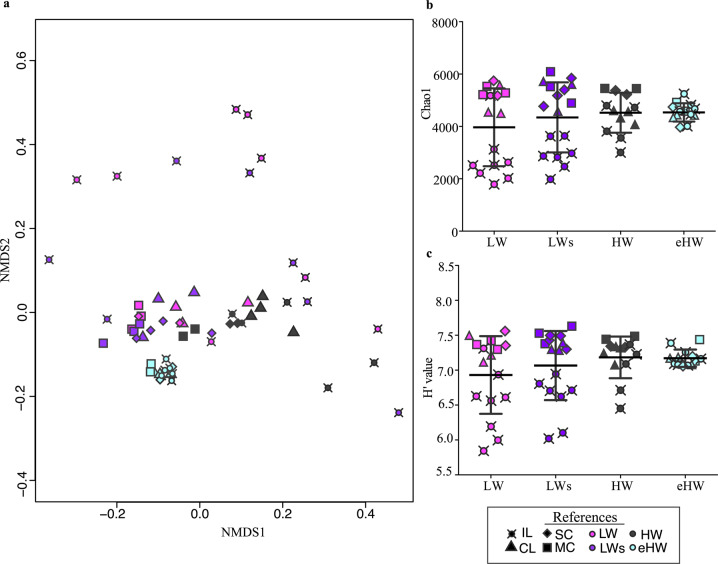
In the 59 samples analyzed, a total of 8927 zOTUs within the bacterial domain were defined. The metacommunity was mainly dominated by Proteobacteria (33%), Actinobacteria (23%), Bacteroidetes (18%), and Verrucomicrobia (11%). The community structure according to zOTUs abundance varied with hydrological conditions with significant differences among phases (PERMANOVA, F₂ = 6.9265, P = 0.001, Supplementary Fig. S6, Table S3), except between the two LW phases (LW and LWs). In the NMDS, the samples were distributed following a clear gradient of homogenization, from LW to HW phases (Fig. 3). In the eHW phase, local communities were more similar grouped in a distinct cluster. In contrast, those from LW phases were more spread, mainly due to differences in the community composition of IL (Fig. 3). The community turnover $\left(\overline{\mathrm{Xd}}\right)$ varied markedly among hydrological phases, being significantly lower (PERMANOVA, P < 0.005) in HW phases ($\overline{\mathrm{Xd}}$: HW = 0.58; eHW = 0.29) than in LW phases ($\overline{\mathrm{Xd}}$: LW = 0.76; LWs = 0.75). In line with this observation, the highest values of ß-diversity were obtained in both LW phases (Whittaker: LW = 3.50; LWs = 3.27; HW = 1.97; eHW = 1.95).

Fig. 3. Bacterial community structure and diversity in the Paraná fluvial system in different hydrological phases.

a Sample ordination in a nonmetric multidimensional scaling (NMDS) according to the similarity in bacterial communities structure (zOTU relative abundance) among the four hydrological phases (indicated with color) at the different type of environments (indicated with symbols) of the Paraná fluvial system. Stress value: 0.112. b, c Richness and Shannon–Weaver diversity index H′ of local bacterial communities in the four hydrological phases. LW low water, LWs low water with sedimentological pulse, HW high water, eHW extraordinary high water, IL isolated lake, CL connected lake, SC secondary channel, MC main channel.

Species richness and Shannon diversity (H′) presented similar average values in the different hydrological phases (Kruskal–Wallis, P = 0.366, Fig. 3). However, differences among local communities were pronounced in LW phases, when IL had a higher variability showing lower values than the mean (Fig. 3).

High-level process structuring the bacterial metacommunity

Having demonstrated that bacterial community structure was clearly linked to changes in environmental heterogeneity, we quantified the relative importance of selection, dispersal, and drift processes in structuring the metacommunity.

The phylogenetic turnover analysis (βNTI) revealed that selection was the most important structuring process regardless of the hydrological phases. However, its relative importance as well as the type of selection, changed according to the hydrological conditions and hence, to environmental heterogeneity. During both LW phases, heterogeneous selection had the major role in structuring the metacommunity (76.66 and 84.55% of the community turnover for LW and LWs, respectively), whereas the role of homogeneous selection and the nonselective processes was less significant. In the HW phase, heterogeneous selection was also the most important process (39.74% of the overall community turnover), but the relative importance of homogenous selection and nonselective processes were twice as high as in the LW phases (Fig. 4). In contrast, homogenous selection was the most important process in eHW (88.46% of the overall community turnover) (Fig. 4). Regarding nonselective processes (RC_bray), dispersal limitation combined with drift had a prevalent role in all the hydrological phases, except in eHW when homogeneous dispersion became more important (Fig. 4).

Fig. 4. Relative importance of high-level processes structuring the bacterial metacommunity of the Paraná fluvial system in different hydrological phases.

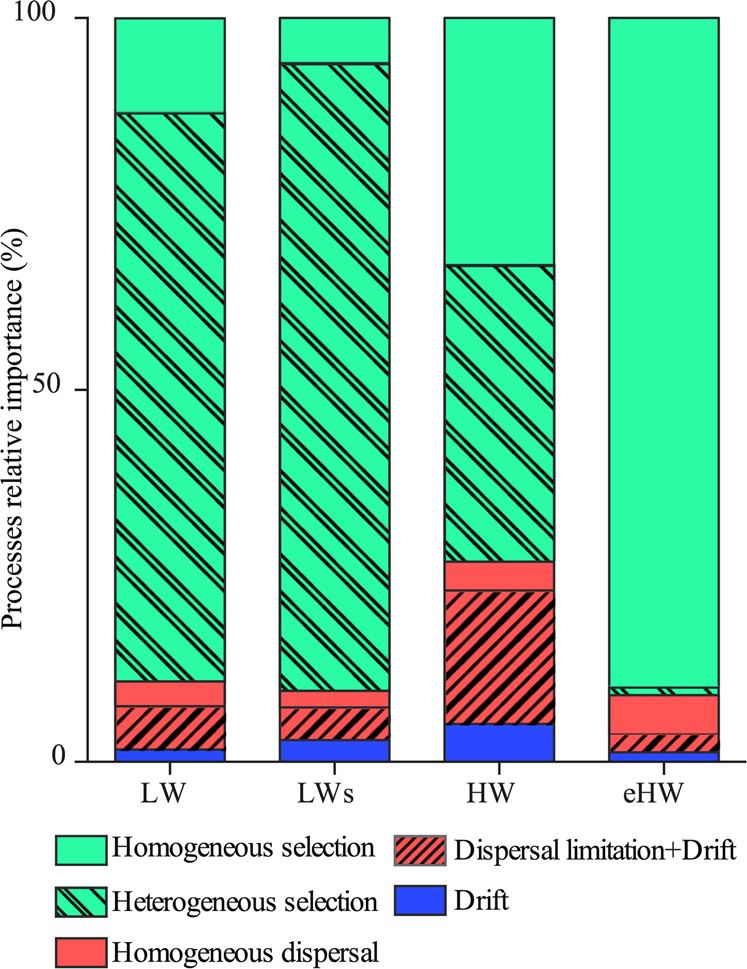
Values indicate percentage of community turnover associated to each process: homogeneous selection (βNTI < −2), heterogeneous selection (βNTI > +2), homogeneous dispersal (RC_bray < −0.95), dispersal limitation combined with drift (RC_bray > +0.95), and drift (|RC_bray| < 0.95). LW low water, LWs low water with sedimentological pulse, HW high water, eHW extraordinary high water.

In each of the four hydrological phases, selection was imposed by a different set of environmental factors. In LW, three PCA axes were significant for the βNTI model (PCA1, PCA3, and PCA4; Table 1 and Supplementary Table S4). Within PCA1 the major loading values were observed for DO, pH, and CDOM molecular weight. Weak loading values of the measured abiotic variables were observed in the PCA3 and PCA4, indicating that these axes represent an unmeasured, spatially structured environmental variable that impose some degree of selection (Table 1 and Supplementary Table S4). In the LWs phase, model selection identified PCA1, PCA3, and PCA11, as significant axes. The stronger loadings on these axes were due to environmental features related with nutrient concentration (SRP and NO₃⁻), CDOM molecular weight, pH, and an unmeasured, spatially structured environmental variable (Table 1 and Supplementary Table S4). In the HW phases, the βNTI model selection identified one significant PCA axis (PCA1) in HW, and three in eHW (PCA1, PCA5, and PCA6; Table 1 and Supplementary Table S4). In the HW phase, conductivity and CDOM molecular weight had the strongest loading values on PCA1, whereas in the eHW phase the environmental variables related were CDOM and SRP.

Table 1.

Features that imposed selection and dispersal limitation in the Paraná fluvial system during different hydrological phases based on the model selection for βNTI and RC_bray analysis.

Hydrological phase	Features imposing selection	Features imposing dispersal limitation
Low water (LW)	PCA1: DO, pH, CDOM molecular weight	NA
	PCA3: unmeasured abiotic variable
	PCA4: unmeasured abiotic variable
Low water + sedimentological pulse (LWs)	PCA1: SPR, nitrate	NA
	PCA3: pH + unmeasured abiotic variable
	PCA11: pH, CDOM molecular weight
High water (HW)	PCA1: conductivity, DO, CDOM molecular weight	PCA2
		PCA3
Extraordinary high water (eHW)	PCA1: CDOM molecular weight, CDOM concentration	NA
	PCA5: SPR
	PCA6: SPR

The PCA axes retained during model selection for βNTI were considered as imposing selection and those significant for RC_bray as imposing dispersal limitation. Within each PCA significant for βNTI, strong loading was considered as a measure or unmeasured variable imposing selection. Loading values for each PCA axes are presented in Supplementary Table S4.

DO dissolved oxygen, SPR soluble reactive phosphorous, CDOM chromophoric dissolved organic matter, NA indicated that nonsignificant PCA axes were retained in RC_bray model selection.

Regarding the features imposing dispersal limitations, only in HW phase, the RC_bray model selection identified significant PCA axes (PCA2 and PCA3) that were not retained in the βNTI model selection (Table 1 and Supplementary Table S4).

Bacterial community associations

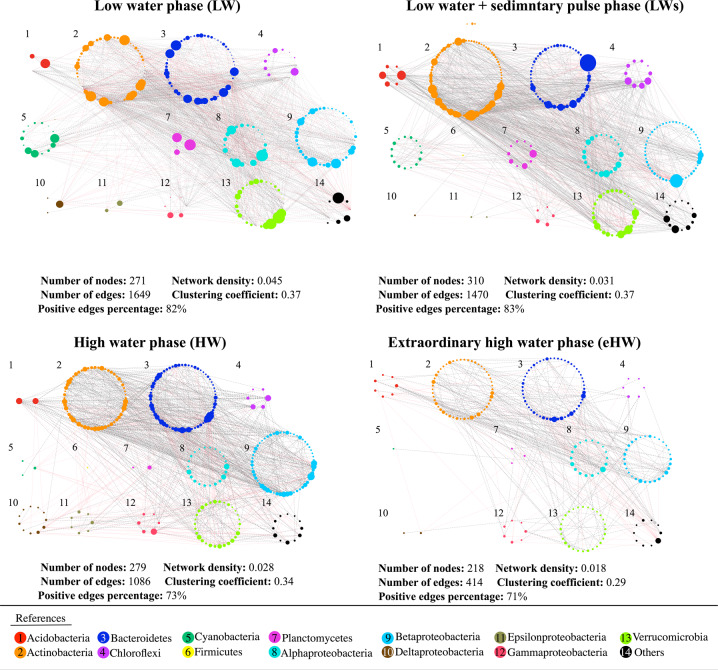
The bacterial meta-network consisted in 470 nodes (bacterial zOTUs) and 936 edges (associations between bacteria). It was mainly represented by taxa from Bacteroidetes, Betaproteobacteria, and Verrucomicrobia (which together account for the 45% of the total nodes). The network density was 0.008 and the coefficient of clustering was 0.364. The majority of OTUs presented positive associations (Supplementary Fig. S7).

The co-occurrence networks at each hydrological phases (Fig. 5) varied in the number of edges, being the highest in both LW phases, whereas the number of nodes did not vary considerable. The connectedness of the networks appeared to be higher during the dominance of heterogeneous selection, as the network density was considerably higher in both LW phases in contrast to HW phases, especially in the HW (Fig. 5). In agreement, the same behavior was shown by the clustering coefficient, indicating higher network connectivity when heterogeneous selection had the major role in structuring the metacommunity. Finally, the networks from HW phases presented a higher percentage of positive edges compared to those from LW phases (Fig. 5).

Fig. 5. Bacterial co-occurrence networks for each hydrological phase of the Paraná fluvial system, arranged according to the bacterial taxonomy (classes or orders).

The size of each node is proportional to the number of connections (degree). Gray dashed and red solids lines represent positive and negative correlation, respectively. The number of nodes, number of edges, positive edges percentage, network density, and clustering coefficient of the overall network is indicated below each network.

Metacommunity highly connected taxa

The number as well as the taxonomic composition of the highly connected taxa (i.e., those taxa that play a significant role within the community) were notably different in the four hydrological phases (Supplementary Table S5). In LW and LWs, 54 and 44, respectively, zOTUs were defined as highly connected taxa, while these were reduced to 10 in the HW phases, and to 3 in the eHW. Most of these taxa were exclusive of each hydrological phase and none was present in all the four phases. The highly connected taxa were recruited differentially from each phylum in each hydrological phase, being Actinobacteria and Bacteroidetes the more represented phyla (Supplementary Fig. S8).

The arrangement of highly connected taxa in the RDA analysis was mainly related to the hydrological phase in which they were defined (Supplementary Fig. S9). The first two axes accounted for 28% of the variance (axis 1: 16.7%; axis 2: 11.3%) being CDOM concentration (A₄₄₀), CDOM molecular weight (S_275–295), DO, and nutrients (SRP and NO₃⁻) the main explanatory variables (P < 0.01). The first axis was mostly defined by the NO₃⁻ concentration and CDOM molecular weight (intraset correlation coefficients: −0.59 and 0.57, respectively). The second axis was principally associated with CDOM concentration and molecular weight (intraset correlation coefficients: 0.58 and −0.45, respectively). Taxa from the LW phases grouped together by the left of the graph and were positively related to NO₃⁻ and inversely related to CDOM molecular weight. The taxa from HW phases were mainly positioned toward the upper part of the graph (Supplementary Fig. S9), more associated with high CDOM molecular weight, SRP concentration, and high CDOM concentration (A₄₄₀).

Discussion

This study provides the first empirical evidence that selection is the most important process structuring the bacterial metacommunity at both extremes of environmental heterogeneity and homogeneity. This finding challenges the general view that selection is weakened by dispersal homogenization [21, 36, 37]. In addition, we show that at intermediary environmental heterogeneity stochastic processes become more important.

Based on the underpinning of Vellend’s approach [3], we predicted that the influence of nonselective processes would increase as the system becomes more homogeneous. Contrarily, we found that selection was the main process shaping the bacterial metacommunity at both high and low environmental heterogeneity.

Several studies have found evidence of the pivotal role of selection in determining bacterial community structure in different environments, and a decrease in its relative importance as dispersal rates increase and the systems become more homogeneous in their environmental conditions [14, 31, 32, 104]. Particularly, Wang et al. [24] in a comparative survey of a broad range of ecosystems (i.e., soil, stream biofilm, and lake), observed a clearly dominant role of deterministic processes controlling the assembly of bacterial communities, whereas stochastic processes became more relevant as environmental heterogeneity decreased and dispersal rates increased. The authors proposed a theoretical threshold of selective strength above which communities should be mainly structured by deterministic processes as a consequence of high environmental heterogeneity and low dispersal rates.

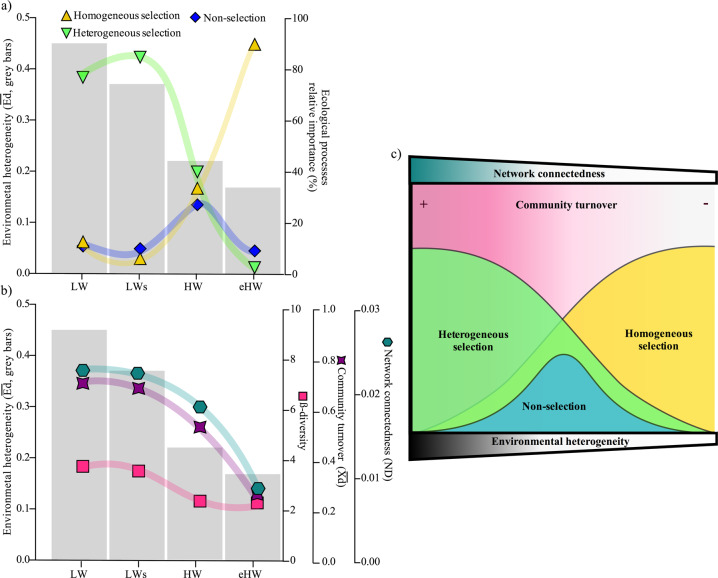
However, these previous attempts considered only variability in the spatial scale. To address the full scope of the question, we extended these observations considering the spatial and the temporal variability in a complex ecosystem. We summarize our findings in three possible scenarios: (i) With high environmental heterogeneity characterized by low connectivity, the structure of the bacterial assemblage was mainly driven by heterogeneous selection (Fig. 6a). In this scenario, species with different fitness may strongly be filtered by different selective forces in each local community, leading to a high β-diversity, whereas the influence of drift and dispersion became irrelevant. (ii) At intermediate environmental heterogeneity, both heterogeneous and homogeneous selections had similar weight and the relative influence of stochastic processes increased (Fig. 6a). Here, the magnitude of ordinary floods seems to be insufficient to thoroughly mix water among all the floodplain, and some environments begin to homogenize their environmental filters while others retain their identity [105]. Selection may act with similar strength both homogenizing and segregating local communities, leading to an overall reduction of community turnover and β-diversity. Simultaneously, the metacommunity should be relatively random due to intermediate dispersal rates. (iii) At extreme environmental homogeneity, homogeneous selection was the main ecological rule structuring the metacommunity (Fig. 6a). Despite stochasticity is expected to increase due to the high dispersal rates, the bacterial species should strongly be filtered by common environmental factors and the strength of homogeneous selection may dampen the influence of drift and dispersion. For instance, low community turnover and β-diversity are expected. These evidences support the early assumptions made by Stegen et al. [85] and Dini-Andreote et al. [14] and provide a new view of bacterial community assembly in which the action of selective and nonselective processes both play a role.

Fig. 6. Conceptual model that synthetizes how environmental heterogeneity determines the action of the ecological processes assembling the bacterial metacommunity.

Empirical evidence (a, b) that support the proposed conceptual model (c). At high environmental heterogeneity, community structure is mainly determined by heterogeneous selection. The heterogeneous selection promotes greater β-diversity increasing divergence in local communities, and higher interconnected bacterial co-occurrence network. At intermediate values of environmental heterogeneity both heterogeneous and homogeneous selection act with similar strength, and stochastic processes reach more importance. In this scenario, the selection acting in opposite ways does not allow homogenization or differentiation of local community structure, leading to an overall reduction of turnover and β-diversity. Simultaneously, the metacommunity will have a relatively high randomness due to intermediate dispersal rates. As a consequence, the association network would tend to be loosely interconnected. In extremely homogeneous environmental conditions, the low diversity of niche habitats leads to an increase of homogeneous selection, and local communities are strongly filtered by common environmental factors. Homogeneous selection then leads to a low turnover and β-diversity, promoting less interconnected associations. ND network density.

The factors that impose selection changed in the different hydrological phases. They were mainly related with inorganic nutrient concentration, the quality and quantity of CDOM, as well as conductivity and DO. This could be explained by marked lateral gradient that characterize our system, which changes according to the landscape connectivity [59]. During the LW phases, and from the MC to the IL, we observed a clear decreasing trend in pH, DO, and SRP concentration, together with an increasing trend in conductivity, NO₃⁻, and low molecular weight CDOM concentration [59, 106]. During eHW phase, the effect of the floods led to a reduction of the differences among environments, and the variables became more similar to those in the MC. In addition, features that impose dispersal limitation were only detected in the HW phase.

At this point, it is appropriate to mention that Stegen’s approach is based on the assumption that phylogenetic relatedness is indicative of shared environmental response traits, setting aside the ecological traits that do not have a strong phylogenetic signal. This may lead to an overestimation of the relative importance of dispersal limitation as it could mask the effects of phylogenetically nonconserved selection processes [12, 107]. In our study, the results of the estimated quantitative processes were in concordance with those from the identification of features imposing selection and dispersal limitation, giving robust support to our conclusions. More explicitly, even though in our system the bacterial communities were heavily governed by selection, significant variables imposing dispersal limitation were identified when this process showed the major influence (i.e., in HW phase).

The understanding of the ecological processes acting on the river floodplain metacommunity was extended studying the bacterial co-occurrence patterns. Network analyses-based approaches have the potential to infer intertaxa correlations and can be applied to investigate structure complexity [95, 108], and the ecological rules guiding community assembly [29, 109]. Particularly, the influence of ecological processes on bacterial associations is a poorly explored field. Emerging studies in soil communities have revealed that systems under organic farming harbor more interconnected networks than conventional farming, mainly associated to higher habitat heterogeneity [98]. In addition, it has been demonstrated that greater microbial diversity ensures greater association complexity [29, 109].

The networks’ topology was different according to the weight of the ecological processes acting on the bacterial community assemblage. At heterogeneous selection dominance (LW and LWs phases), the network associations seem to be more interconnected than HW phases (Fig. 6b). We assign this finding to the fact that heterogeneous selection promotes a greater taxonomic β-diversity [29, 109]. Contrarily, homogeneous selection may be associated to fewer interconnected networks as decreasing β-diversity. In addition, under multiple ecological processes acting with similar strength, the network tends to be less interconnected (Fig. 6b).

The dominance of different ecological processes structuring the community appeared to be especially important for shaping the mutualistic and antagonistic co-occurrence patterns. For instance, there were considerably more negative correlations when systems became more homogeneous, compared with periods of low water. Several ecological interpretations had been made about the extent to which we can interpret negative and positive correlations according to how the networks have been constructed (e.g., whether the network represents one or more trophic levels, or if it results in spatial or temporal associations) [44, 45, 48, 110]. At the metacommunity level negative correlations may reflect competition that it is expected to be more common under a homogeneous scenario, as homogeneous selection favors taxa with similar ecological requirements that will compete for similar sources. Contrarily, the dominance of positive correlations in our survey under the dominance of heterogeneous selection may reflect the coexistence of multiple taxa in the metacommunity occupying multiple different niches [44, 45, 48, 110]. Our analysis represents one of the first studies that have empirically linked bacterioplankton networks to community structuring processes. Future studies comparing networks for communities of different systems, and also structured by different ecological processes, will allow for a deepen exploration and generation of new ecological hypotheses.

A useful feature of network analysis is that it allows to identify the strongly connected taxa that have a core effect on the community assemblage [53, 111] and are adequate predictors of overall community changes [55]. Each hydrological phase presented a particular set of highly connected taxa that were determined by different environmental factors. Since conditions significantly varied among the hydrological phases this was not surprising (Fig. 1). Perhaps the most interesting fact of our findings was the huge number of highly connected taxa found under the highest environmental heterogeneity, which could be attribute to a higher niche segregation over this condition. As it was mentioned above, a marked lateral hydrological gradient (i.e., from the MC to IL) is observed in many variables during LW phases. Remarkably, all the significant variables in the RDA are related to quality and quantity of essential resources for bacteria (i.e., N, P, and CDOM). Even though caution is needed as these estimated taxa derive from a co-occurrence approach [43–45], we found a concordance between the factors imposing selection to the whole community, and those more related with the highly connected taxa. These results spotted the spatiotemporal heterogeneity as an important factor determining the number and identity of the highly connected taxa (hubs) and support their importance as target organisms for a better understanding of the whole community. A challenge for future research will be to elucidate ecological functions of hubs in the system.

Taking together, our results demonstrated that Stegen’s framework, strengthened with co-occurrence network analyses, can provide relevant insights about the ecological processes structuring microbial communities, although a good understanding on the method’s limitations must be exerted. Finally, we would like to highlight the importance of incorporating temporal variability in order to understand metacommunity assembly.

Concluding remarks

Integrating all the empirical evidence obtained here, we propose a conceptual model that synthetizes how environmental heterogeneity determines the action of the ecological processes assembling the bacterial metacommunity (Fig. 6c). In systems with high environmental heterogeneity, heterogeneous selection plays the major role in structuring the community, promoting a greater β-diversity, and more interconnected networks associations. At intermediate values of environmental heterogeneity, the action of stochastic processes reaches more importance and both, heterogeneous and homogeneous selection, have similar contribution. This leads to a decrease in β-diversity and to loosely interconnected networks associations. In systems with low environmental heterogeneity, the strength of homogeneous selection dampens the influence of drift and dispersion, and local communities become more similar and the association networks less interconnected. While this model was devised based on the empirical evidence of a complex fluvial system, it certainly would be needed to evaluate its robustness and limitation in other types of environments.

A particular strength of this model is that it was conceived relying on different metacommunity features (e.g., taxonomic and phylogenetic turnover, network associations) but taking into account the spatial and temporal variability scales. Furthermore, we used a step-forward analysis combining different statistical inferences, which allowed us to take advantage of the strengths of each method alone and in synergy with the others. Therefore, the proposed model represents a significant improvement on our knowledge of bacterial community’s assembly across freshwater ecosystems and provides a new framework to be tested in future studies in other communities.

Author contributions

PH and MD conceived and designed the study; MD conducted sampling with the help of GM; PH performed the molecular analysis; GM performed the chemical analyses; PH and SM ran statistical analyses; PH and MD wrote the manuscript with contributions from FU and HS; and all authors edited the manuscript.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

Supplementary information

The online version of this article (10.1038/s41396-020-0723-2) contains supplementary material, which is available to authorized users.