A quantitative trait rare variant nonparametric linkage method with application to age-at-onset of Alzheimer’s disease

Abstract

To analyze pedigrees with quantitative trait (QT) and sequence data, we developed a rare variant (RV) quantitative nonparametric linkage (QNPL) method, which evaluates sharing of minor alleles. RV-QNPL has greater power than the traditional QNPL that tests for excess sharing of minor and major alleles. RV-QNPL is robust to population substructure and admixture, locus heterogeneity, and inclusion of nonpathogenic variants and can be readily applied outside of coding regions. When QNPL was used to analyze common variants, it often led to loci mapping to large intervals, e.g., >40 Mb. In contrast, when RVs are analyzed, regions are well defined, e.g., a gene. Using simulation studies, we demonstrate that RV-QNPL is substantially more powerful than applying traditional QNPL methods to analyze RVs. RV-QNPL was also applied to analyze age-at-onset (AAO) data for 107 late-onset Alzheimer’s disease (LOAD) pedigrees of Caribbean Hispanic and European ancestry with whole-genome sequence data. When AAO of AD was analyzed regardless of APOE ε4 status, suggestive linkage (LOD = 2.4) was observed with RVs in KNDC1 and nominally significant linkage (p < 0.05) was observed with RVs in LOAD genes ABCA7 and IQCK. When AAO of AD was analyzed for APOE ε4 positive family members, nominally significant linkage was observed with RVs in APOE, while when AAO of AD was analyzed for APOE ε4 negative family members, nominal significance was observed for IQCK and ADAMTS1. RV-QNPL provides a powerful resource to analyze QTs in families to elucidate their genetic etiology.

Introduction

The limited heritability explained by common variants and advances in massively parallel sequencing has led to increased interest in the role of rare variants (RVs) in the etiology of complex diseases and quantitative traits (QTs). For the analysis of RVs, there are many population-based aggregate association methods that can be applied to either case-control or QT data [1]. There are a limited number of family-based RV-aggregate association methods for dichotomous traits [2, 3] and even fewer for QTs [4]. To avoid a reduction in power due to misclassification, QTs or their residuals should be analyzed directly instead of dichotomized QT values [5]. RV-QNPL offers a powerful alternative to association analysis for familial data to elucidate genetic etiology of QTs.

For family-based QT linkage analysis, there are two primary methods: Haseman–Elston (H-E) and variance-components (VC). The H-E method was first developed to map human quantitative trait loci (QTL) by testing if sib-pairs with increased allele sharing have similar QTs, i.e., the squared difference of the QTs is regressed on the number of alleles shared identical-by-descent (IBD) by the sibpair [6]. To increase power newer versions of H-E were developed: H-E revisited (HEr) [7] which regresses the product of QT values on IBD sharing and the new H-E (nHE) [8] which regresses a linear combination of squared sum and squared difference of QTs on IBD sharing. Additionally, nHE was extended to analyze general pedigrees (H-Eg), in which the IBD score of each relative pair is regressed on the squared differences and squared sums of the QTs [9]. H-E methods are computationally efficient, and are more robust to deviation of QTs from normality than VC methods, which have substantially inflated type I and type II errors when normality assumptions are violated [10]. Although both methods have been widely used for QTL mapping in humans, few causal genes have been identified [11]. One reason is that most QTLs mapped to large genomic regions, e.g., >40 Mb, when common variants were analyzed due to linkage disequilibrium (LD) [12]. Additionally, for common variants locus heterogeneity can greatly attenuate the linkage signal [13]. Although RVs play a role in modulating QT values [11], analyzing individual RVs is underpowered particularly for small effect sizes. Performing an aggregate RV analysis can increase power, however, association tests are sensitive to inclusion of non-causal variants which is not the case for NPL analysis [14].

We developed an RV-extension of the H-E method for general pedigrees (H-Eg) [9]. A regional locus is generated to analyze RVs in aggregate using the collapsed haplotype pattern (CHP) method [15]. IBD sharing is calculated for relative pairs and two methods were used: CHP-QNPL which calculates IBD sharing for both major and minor alleles i.e., haplotypes with and without RVs and RV-QNPL which only estimates IBD sharing for minor alleles. Using simulation studies, we compared analyzing RVs [minor allele frequency (MAF) < 1%] with RV-QNPL and H-Eg methods CHP-QNPL and multipoint-QNPL as implemented in the MERLIN [9] software. We demonstrate that when RVs are analyzed, CHP-QNPL delivers identical results to multipoint-QNPL and RV-QNPL is more powerful than CHP-QNPL. Moreover, RV-QNPL is robust to the inclusion of nonpathogenic variants as well as allelic and locus heterogeneity. Unlike for the analysis of common variants using QNPL, RVs provide finer resolution due to low levels of LD, mapping QTL to small regions, e.g., a gene. For genome data, RV-QNPL can be used to analyze coding and non-coding regions by using recombination events as boundaries to construct regional loci. To demonstrate the application of RV-QNPL, age-at-onset (AAO) of AD was analyzed using whole-genome sequence (WGS) data for members of 107 Hispanic and European-ancestry pedigrees with late-onset Alzheimer’s disease (LOAD).

For association studies of LOAD, AAO is the most widely studied QT. Thus far for AAO of Alzheimer’s disease (AD) associations have been identified with APOE, SNX25, PDLIM3, and SORBS2 [16, 17]. Application of RV-QNPL to study the role RVs play in AAO of AD identified suggestive linkage (LOD > 2.2) with KNDC1 (10q26.3, MIM: 616237, GenBank: NM_152643.7, LOD = 2.4). Functional studies suggest that KNDC is potentially involved in AD etiology [18]. Additionally, nominally suggestive linkage (p < 0.05) was observed with RVs in previously associated LOAD genes: ABCA7 (19p13.3, MIM: 605414, GenBank: NM_019112.3), ADAMTS1 (21q21.3, MIM: 605174, GenBank: NM_006988.5), APOE (19q13.32, MIM: 107741, GenBank: NM_001302688.1), and IQCK (16p12.3, GenBank: NM_153208.2) [19–21].

Material and methods

Rare variant extension of QNPL

For each family, variants are first phased using the Lander-Green Algorithm [22] and generated haplotypes are used to create a regional loci [15] capturing information on RVs with MAFs below a threshold, e.g., <0.01. Moreover, annotation specifications can be added to the RV inclusion criteria when constructing the regional loci, e.g., missense, CADD c-score >20. For each regional locus, every haplotype within a pedigree receives a unique score to ensure no loss of linkage information. When founders or parents are missing sequence data, to aid in determining IBD status, CHP genotypes are imputed based upon offspring’s CHP genotypes and family/ancestry specific allele frequencies which are obtained from either founders or databases such as gnomAD [23]. Additional details on generating regional loci and their allele frequencies can be found in the Supplemental Methods.

The (H-Eg) method was developed to analyze general pedigrees and was adapted for implementation in RV-QNPL. IBD sharing is estimated for each relative pair and then multivariate regression is used to regress IBD sharing on both the squared sums and squared differences of the QTs of relative pairs within a pedigree [9]. Three values are calculated for each relative pair (i,j): IBD sharing ${\pi }_{ij}$, squared sum of traits $S_{ij}={\left(X_i+X_j\right)}^2$, and squared difference of traits $D_{ij}={\left(X_i-X_j\right)}^2$. For all relative pairs in a family, three corresponding matrices can be determined: S = [S_ij], D = [D_ij] and $\widehat{\mathrm{\Pi }}=\left[{\pi }_{ij}\right]$. In multivariate regression analysis, the covariance matrices are obtained for S, D, and $\widehat{\mathrm{\Pi }}$. For standardized traits (μ = 0, σ = 1), the covariance for pair (i, j) is the correlation r_ij, which is determined by trait heritability and the kinship coefficient obtained from the pedigree structure. Between relative pair (i, j) and pair (k, l), the covariances for S, D, and IBD $\widehat{\mathrm{\Pi }}$ are: $Cov\left(S_{ij},S_{kl}\right)=2{\left(r_{ik}+r_{il}+r_{jk}+r_{jl}\right)}^2$, $Cov\left(D_{ij},D_{kl}\right)=2{\left(r_{ik}+r_{jl}-r_{il}-r_{jk}\right)}^2$, $Cov\left(S_{ij},D_{kl}\right)=2{\left(r_{ik}+r_{jk}-r_{il}-r_{jl}\right)}^2$, and $Cov\left({\widehat{\pi }}_{ij},{\widehat{\pi }}_{kl}\right)=\left(\sum p{\pi }_{ij}{\pi }_{kl}-{\tilde{\pi }}_{ij}{\tilde{\pi }}_{kl}\right)-\left(\sum q{\pi }_{ij}{\pi }_{kl}-{\widehat{\pi }}_{ij}{\widehat{\pi }}_{kl}\right)$, where $\widehat{\pi }$ and $\tilde{\pi }$ are the expected IBD sharing with or without genotype information; finally, the covariance between traits and IBD are $Cov\left(S_{ij},{\widehat{\pi }}_{kl}\right)=2QCov\left({\widehat{\pi }}_{ij},{\widehat{\pi }}_{kl}\right)$ and $Cov\left(D_{ij},{\widehat{\pi }}_{kl}\right)=-2QCov\left({\widehat{\pi }}_{ij},{\widehat{\pi }}_{kl}\right)$, where Q is the phenotypic variance explained by the QTL. When calculating IBD sharing values $\widehat{\pi }$ and $\tilde{\pi }$, CHP-QNPL estimates allele sharing regardless of whether haplotypes carry RVs or not, while RV-QNPL only calculates allele sharing for haplotypes that carry at least one RV, i.e., allele sharing of wild-type haplotypes are excluded. The final trait matrix Y is determined as Y = [S, D]′. The multivariate regression formula is:

$${\widehat{\mathrm{\Pi }}}_C={\mathrm{\Sigma }}_{Y\widehat{\mathrm{\Pi }}}^{\prime }{\mathrm{\Sigma }}_Y^{-1}{Y}_C+e$$

where ${\widehat{\mathrm{\Pi }}}_C$ and $Y_C$ are the mean-centered matrix of $\widehat{\mathrm{\Pi }}$ and Y, ${\mathrm{\Sigma }}_{Y\widehat{\mathrm{\Pi }}}^{\prime }$ is the covariance matrix between $\widehat{\mathrm{\Pi }}$ and Y, $\mathrm{and}{\mathrm{\Sigma }}_Y$ is the covariance matrix of Y.

With Q being the phenotypic variance explained by the test locus, the method tests if Q > 0. The least-squared estimate of Q is: $\widehat{Q}=\frac{{\mathrm{\Sigma }}_{f=1}^m\left[B^{\prime }{\widehat{\mathrm{\Pi }}}_C\right]}{{\mathrm{\Sigma }}_{f=1}^m\left[B^{\prime }{\mathrm{\Sigma }}_{\widehat{\mathrm{\Pi }}}B\right]}$; details on the calculation of matrix B can be found in Sham et al. [9]. For a sample with m families, both numerator and denominator obtained from each family are summed to obtain an estimate of Q for the entire sample. The test statistic, $T=\widehat{Q}\mathrm{\Sigma }\left[B^{\prime }{\widehat{\mathrm{\Pi }}}_C\right]$, when $\widehat{Q}>0$. T is asymptotically χ² distributed with 1 degree of freedom under the null. T = 0 when $\widehat{Q}<0$ since only positive Q is biologically meaningful. Empirical p values are estimated using permutation for RV-QNPL and CHP-QNPL. Details on performing permutations were previously described [14].

Simulation framework

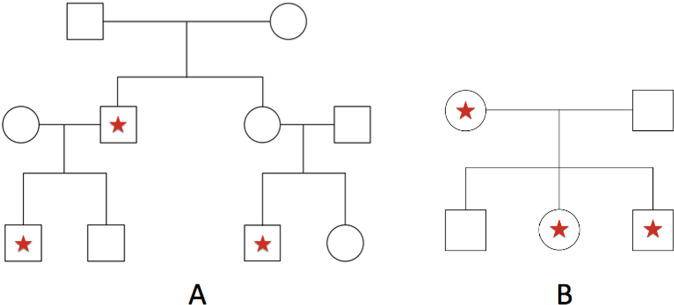
The type I error was evaluated for RV-QNPL, CHP-QNPL, and multipoint-QNPL and power was estimated for RV-QNPL and CHP-QNPL. Genotypes for 17,987 autosomal genes across the genome were simulated based on the observed variant sites and their corresponding MAFs obtained from the Non-Finnish Europeans (NFE) in the ExAC [24] database. For multipoint-QNPL, genetic map distances and recombination rates were estimated using interpolation from the Rutgers Combined Linkage-Physical map [25]. Two pedigree structures were used for simulation: nuclear families with three offspring and extended pedigrees with two branches each with two offspring (Fig. 1). All family members were assigned QTs and analyzed. QT values are randomly drawn from a N(2,1) distribution for family members with a star (Fig. 1), and from a N(0,1) distribution for all other family members, to mimic a proportion of the founders having an exposure, e.g., genetic or environmental, which influences their QT. The QT values were standardized (i.e., μ = 0 and σ = 1) before the analysis. RVs (MAF < 0.01 in ExAC NFE) sequence data were generated for families using RarePedSim. Genotypes were generated unconditional on QT values to evaluate type I error and conditional on QT values to estimate power [26]. Phase information was removed from the simulated data to mimic sequence data obtained from DNA. Data were then phased to construct the CHP regional loci [22]. For both the evaluation of type I error and power, analyses were performed for 100 extended families (Fig. 1a) and 300 nuclear families with three offspring (Fig. 1b), and genes with >1 variant were analyzed. Additional information on the simulation of the variant data and their analysis can be found in the Supplemental Methods.

Fig. 1. Pedigree structures used in simulation studies.

Pedigree structures used to evaluate type I error and power: multi-generational pedigrees (a) and nuclear pedigrees with three offspring (b).

Type I error was evaluated not only for families with no missing data, but also with all founders missing phenotype and genotype data for RV-QNPL, CHP-QNPL, and multipoint-QNPL (as implemented in MERLIN [22]). One-hundred replicates of complete exomes (each containing 17,987 autosomal genes) were generated and p values for RV-QNPL, CHP-QNPL, and multipoint-QNPL were obtained analytically and for RV-QNPL and CHP-QNPL, empirically using one million permutations. Nominal p values were evaluated at 5.0 × 10⁻² (LOD score = 0.59), 5.0 × 10⁻³ (LOD score = 1.44) and 1.5 × 10⁻⁵ (LOD score = 3.80; the genome-wide significance level proposed by Lander and Kruglyak [27]) and quantile-quantile (QQ) plots were generated.

To evaluate and compare power performances for RV-QNPL and CHP-QNPL, simulations were performed under different scenarios. Two scenarios were used to estimate the effect of non-causal variants on power. Firstly, analysis was performed for a fixed number of nonsynonymous (as annotated in ExAC) variants varying the proportion that are causal from 100 to 50%, and the proportion of non-causal variant sites from 0 to 50%. This scenario was used to evaluate the effect of reducing the number of causal RVs while keeping the total number of RVs constant. Secondly, to assess the robustness of the methods to non-causal variants, instead of changing the number of causal variants, all nonsynonymous variants were assigned to be causal and then both causal nonsynonymous and synonymous variants that were delegated to be non-causal were analyzed together to mimic observed ratio of 2:1 between nonsynonymous and synonymous variants [24]. To evaluate the effect of missing data on power, analyses were performed with 20%, 50%, 70%, and 100% of founders missing: only their phenotype data and both their phenotype and genotype data to evaluate the loss in power. Additionally, the effect of locus heterogeneity was examined by comparing power for families which are all linked to the same gene [linkage homogeneity (α = 1.0)] and with a proportion of linked and unlinked families [linkage admixture (α = 0.67)]. Under homogeneity, 100 linked, extended pedigrees were analyzed and under admixture (locus heterogeneity) 100 linked and 50 unlinked extended families were analyzed. It should be noted that the sample size is not fixed when examining linkage heterogeneity, e.g., comparing 100 linked extended families to 50 linked and 50 unlinked extended families, since this would show the impact of reducing the sample size and not locus heterogeneity. Although the sample size is increased inclusion of unlinked families will not increase power, since the power to detect linkage for unlinked pedigrees is equal to alpha. Since each gene is analyzed separately, linked pedigrees were generated with RVs in every gene linked to the QT and unlinked pedigrees were generated under the null. Additionally, analysis was performed for nuclear pedigrees, i.e., 300 linked pedigrees were analyzed and 300 linked and 150 unlinked pedigrees were analyzed. For each analysis, power was evaluated by the proportion of tests with a LOD > 3.8 [27].

Application to Alzheimer’s disease data

RV-QNPL was applied to analyze 107 LOAD families with 446 members with available AAO of AD and WGS data. Alzheimer’s Disease Sequencing Project (ADSP) data were obtained from dbGaP (accession number phs000572.v7.p4). The pedigrees include individuals of Dominican (62); European (42); and Puerto Rican (3) ancestry. Analyses were performed for three groups: all 446 AD patients with AAO data [42 European families and 65 Caribbean Hispanic families with a mean AAO of AD of 73.64 years of age standard deviation (std) 9.17]; 151 APOE ε4 allele positive AD patients with AAO data (24 European and 27 Caribbean Hispanic families with mean AAO of AD 72.19 years of age std 8.24); and 254 APOE ε4 allele negative AD patients with AAO data (25 European and 54 Caribbean Hispanic families with mean AAO of AD of 74.54 years of age std 9.61). Forty-one individuals (21 APOE ε4 carriers and 20 non-carriers) could not be analyzed in the APOE ε4-specfic analyses because AAO data was unavailable for another family member with the same APOE ε4 status. There is additional information on AAO of AD in Table S1. Residuals were generated for AAO of AD after adjusting for sex and analyzed. Pedigree structures and their ancestries are displayed in Fig. S1 and Table S2, respectively. Initial quality control (QC) was performed by the ADSP QC working group [2] and was followed by additional QC [2, 14]. RV-QNPL was used to analyze genes with >1 RV site. Frameshift, missense, nonsense, and splice site variants with MAFs <0.01 were analyzed based on allele frequencies obtained from gnomAD [23] [NFE for the European pedigrees and Latino (AMR) for the Caribbean Hispanic pedigrees]. For missing genotypes, CHP regional markers were constructed using gnomAD allele frequencies that corresponded to the family’s ancestry, i.e., NFE or AMR. Joint and individual analyses were performed for the European and Caribbean Hispanic families.

Results

Type I errors were obtained by evaluating nominal p values at 5.0 × 10⁻², 5.0 × 10⁻³ and 1.5 × 10⁻⁵ (Table S3), and QQ plots were generated (Figs. S2 and S3). For multipoint-QNPL, CHP-QNPL, and RV-QNPL, analytical p values gave slightly inflated type I errors, especially for extended families (results not shown). T test statistics from CHP-QNPL and multipoint-QNPL are identical when analysis was performed without missing data (Fig. S4). Therefore, additional analysis was only performed using CHP-QNPL instead of both methods. Due to the inflation of type I error, permutation-derived empirical p values were obtained for CHP-QNPL and RV-QNPL and type I error was controlled (Table S3; Figs. S2 and S3). Empirical p values were used for all further analyses.

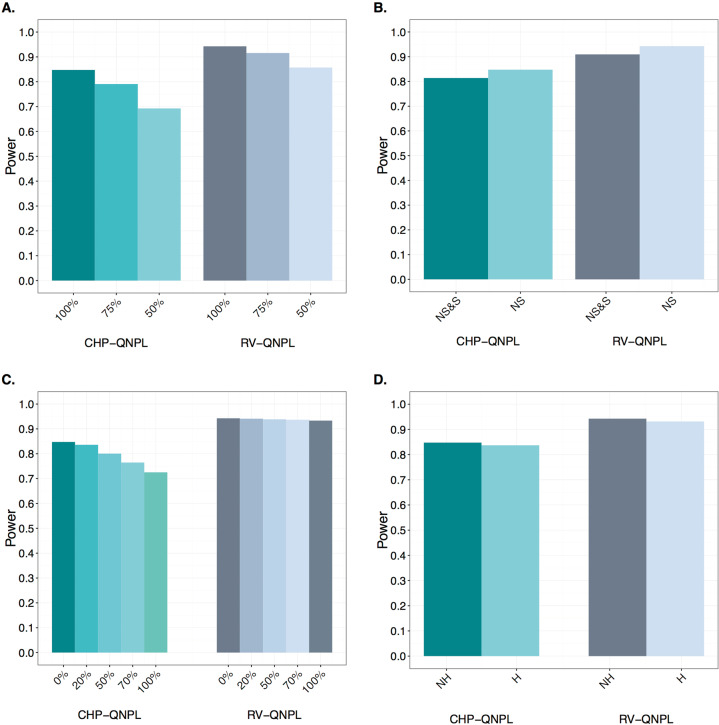
Power was evaluated for RV-QNPL and CHP-QNPL (Table 1; Fig. 2 and Fig. S5). RV-QNPL is consistently more powerful than CHP-QNPL for all scenarios. For example, when causal nonsynonymous RVs were analyzed without missing data or locus heterogeneity, the power for RV-QNPL is 15.6% and 11.2% higher than CHP-QNPL for 300 nuclear families and 100 extended pedigrees, respectively (Fig. 2a and Fig. S5A).

Table 1.

Power of CHP-QNPL and RV-QNPL.

Power comparison for QNPL methods	Extended families		Nuclear families
	CHP-QNPL	RV-QNPL	CHP-QNPL	RV-QNPL
100% causal	0.848	0.943	0.783	0.905
75% causal	0.791	0.916	0.707	0.868
50% causal	0.693	0.857	0.578	0.774
Nonsynonymous & synonymous	0.814	0.909	0.733	0.877
Locus heterogeneity	0.837	0.931	0.774	0.903
20% founder missing phenotype	0.837	0.941	0.779	0.893
50% founder missing phenotype	0.808	0.939	0.77	0.849
70% founder missing phenotype	0.779	0.937	0.763	0.812
100% founder missing phenotype	0.76	0.934	0.757	0.772
20% founder missing all data	0.836	0.941	0.764	0.888
50% founder missing all data	0.8	0.938	0.729	0.845
70% founder missing all data	0.765	0.936	0.706	0.806
100% founder missing all data	0.725	0.933	0.695	0.763

Fig. 2. Exome-wide power for RV-QNPL and CHP-QNPL in extended pedigrees.

One-hundred extended pedigrees with simulated QT and genotype data were analyzed with 100%, 75%, and 50% of the RVs being causal and the remaining non-causal (a); only causal nonsynonymous (NS) RVs as well as causal nonsynonymous (NS) and non-causal synonymous (S) RVs (b); 0%, 20%, 50%, 70% and 100% of founders missing both their genotype and phenotype data (c); and under linkage homogeneity [No heterogeneity (NH)], i.e., 100 linked families as well as with locus heterogeneity (H), i.e., 100 linked and 50 unlinked families (d).

When RVs were generated under linkage and all variants were causal, family members whose QT values were drawn from a N(2,1) distribution had on average 2.44X as many RVs as those with QT values obtained from a N(0,1) distribution. This ratio declined to 2.27X and 2.15X when 75% and 50% of the RVs were causal. For both RV-QNPL and CHP-QNPL, the power decreases with decreasing proportion of causal RVs and increasing non-causal RVs, e.g., compared to when all RVs are causal, when 50% of the RVs are causal and the rest are non-causal, the power of RV-QNPL decreases from 0.905 to 0.774 (14.5%) for nuclear families and from 0.943 to 0.857 (9.1%) for extended families. For CHP-QNPL, the power drops by 26.2% (from 0.783 to 0.578) for nuclear families and by 18.3% (from 0.848 to 0.693) for extended families. Not only is the decrease in power less for RV-QNPL than CHP-QNPL but the initial power is also higher (20.6% on average), regardless of proportion of causal RVs (Table 1; Fig. 2a and Fig. S5A).

In the second scenario, when the number of causal nonsynonymous RVs was fixed and they were analyzed with and without non-causal synonymous RVs, there is a greater loss in power for CHP-QNPL than for RV-QNPL. For nuclear families the power for RV-QNPL is 0.905 and reduces to 0.877 (by 3.1%) when non-causal variants were included and for extended families the power reduces from 0.943 to 0.909 (by 3.5%) when non-causal variants were included. For CHP-QNPL, when non-causal RVs were included, the reduction in power is 6.4% (from 0.783 to 0.733) for nuclear families and 4.0% (from 0.848 to 0.814) for extended families. The power of RV-QNPL is 15.7% higher than CHP-NPL when non-causal variants were included in the analysis (Table 1; Fig. 2b and Fig. S5B).

Moreover, the power performance when founders are missing their sequence data is examined to evaluate the impact on the ability to phase haplotypes and determine IBD sharing status. RV-QNPL largely maintains power, and power loss is less than for CHP-QNPL. For example, when all founders are missing phenotypes but not genotypes compared to when founders are missing both phenotype and genotype data, the power for RV-QNPL reduces from 0.772 to 0.763 (1.2%) for nuclear pedigrees and from 0.934 to 0.933 (0.1%) for extended pedigrees. For the same scenario, power for CHP-QNPL decreases by 8.2% (from 0.757 to 0.695) for nuclear pedigrees and 4.6% (from 0.760 to 0.725) for extended pedigrees. Similarly, when 50% of founders are missing only phenotypes, compared to when 50% of founders are missing both phenotypes and genotypes, the power for RV-QNPL reduces by 0.5% (from 0.849 to 0.845) for nuclear pedigrees and by 0.1% (from 0.939 to 0.938) for extended pedigrees. The power for CHP-QNPL decreases by 5.3% (from 0.770 to 0.729) for nuclear pedigrees and by 1% (from 0.808 to 0.800) for the extended pedigrees (Table 1; Fig. S6).

Another factor which can lead to a loss in power in complex diseases is locus heterogeneity, simulation results demonstrate that RV-QNPL is robust to its presence, e.g., with only a 0.2% loss in power when 450 nuclear families [power = 0.903 (300 linked and 150 unlinked pedigrees, α = 0.67)] with 3 offspring were analyzed compared to analyzing 300 pedigrees with linkage (power = 0.905, α = 1.0). For extended families the power when there is locus heterogeneity is 0.931 compared to 0.943 without heterogeneity. CHP-QNPL displayed a slightly larger reduction in power [1.1% for nuclear pedigrees (from 0.783 to 0.774) and 1.3% for extended pedigrees (from 0.848 to 0.837)] (Table 1; Fig. 2d and Fig. S5D).

The joint analysis of AAO of AD in European and Caribbean Hispanic pedigrees regardless of APOE ε4 status yielded suggestive linkage (2.2 < LOD score < 3.8) [27] with RVs in KNDC1 (p value = 4.2 × 10⁻⁴, LOD = 2.4). KNDC1 RV carriers have an average AAO of AD of 75.67 years (std 9.73) compared to 72.04 years (std 8.95) for non-carriers. When analysis was performed regardless of APOE ε4 status for Caribbean Hispanic families, nominal significance was observed for LOAD gene ABCA7 (p = 4.9 × 10⁻²) and for European families, nominal significance was observed for LOAD gene IQCK (p = 3.0 × 10⁻²). IQCK also displayed nominal significance (p = 3.6 × 10⁻²) when APOE ε4 negative family members (European and Caribbean Hispanic) were analyzed. Additionally, ADAMTS1, which was reported to be associated with LOAD and protective, displayed nominal significance (p = 4.1 × 10⁻²) with AAO of AD for APOE ε4 negative European family members. Nominally significant linkage between AAO of AD and RVs in APOE (p = 1.8 × 10⁻²) was observed for APOE ε4 positive Caribbean Hispanics. For KNDC1, seven missense RVs segregate in eleven families with linkage (seven Caribbean Hispanic and four European families) (Table S4). For ABCA7, twelve missense RVs segregate in nineteen linked Caribbean Hispanic pedigrees (Table S5). The carriers of ABCA7 RVs have a mean AAO of AD of 71.73 years (std 8.77) compared to 74.56 years (std 9.90) for non-carriers. For ADAMTS1, one RV was observed in a linked pedigree (Table S6) and the two RV carriers both have AAO of 90.00 years versus 74.78 years (std 9.86) for non-carriers. For APOE, one missense RV was observed in four linked Caribbean Hispanic pedigrees, and it is located at a conserved nucleotide site and deemed deleterious (Table S6). The carriers of the APOE RV have a mean AAO of 74.83 years (std 8.43) versus 71.32 (std 8.90) years for non-carriers. For IQCK, when analyzed regardless of APOE ε4 status, one missense RV was observed in three linked European pedigrees with RV carriers having a mean AAO of 76.14 years (std 8.56) compared to 74.49 years (std 9.00) for non-carriers. When analyzed in all APOE ε4 negative families, two RVs in IQCK were observed in two linked pedigrees (one Caribbean Hispanic and one European pedigree) (Table S6) with RV-carriers having a mean AAO of 82.2 years (std 3.49) versus 74.19 years (std 10.22) for non-carriers. Pedigrees segregating variants in ABCA7, APOE, IQCK, and KNDC1 are shown in Fig. S1 and Table S2.

Discussion

RV-QNPL was developed to perform aggregate RV nonparametric QT linkage analysis. Simulation studies demonstrate that RV-QNPL is a powerful approach to map QTLs in families. It is shown that CHP-QNPL delivers identical results with multipoint-QNPL (Fig. S4) and RV-QNPL is more powerful than CHP-QNPL for a variety of scenarios.

Analysis of AAO of AD for the ADSP pedigrees highlights that loci can be mapped to small regions, e.g., an individual gene. RVs have low levels of LD, allowing for fine mapping. Although QNPL methods do not incorporate locus heterogeneity in the statistical framework, there is only a very small loss in power in the presence of locus heterogeneity when RVs were analyzed since for unlinked regions most families will not have a RV and therefore are uninformative. When data were simulated under the null of no linkage each founder on average had 0.037 RVs per gene region. Due to fewer founders unlinked nuclear families were less likely to segregate RVs than extended families and therefore the reduction in power was even smaller. Also, for RV-QNPL, unlike for CHP-QNPL, when there is a variant within the tested region with sharing of the major allele, it does not contribute to the test statistic. RV-QNPL, which is based on the H-Eg model, also inherits benefits including robustness to population substructure and admixture [28]. Similar to regression analyses, covariates can be controlled for by analyzing adjusted residuals. For the analysis of AAO of AD, residuals adjusted for sex were generated. RV-QNPL is applicable for nuclear and extended families with exome and genome sequence data. When analysis is performed outside of the coding regions, recombination events can be used as boundaries to aggregate RVs unlike aggregate association methods where prior knowledge or a sliding window must be used.

A challenge for family-based studies is the ascertainment of family members. For QTs, families can be ascertained randomly or for extreme trait values either with members having QT values in both tails (discordant) or in the same tail (concordant) of the distribution. One QNPL study design for sib-pairs with highly discordant QT values dichotomizes the QTs before analysis [29]. Not only is it difficult to ascertain sib-pairs with very discordant QT values, but one study noted higher rates of non-paternity for the siblings compared to the general population [30]. Additionally, when family members are selected to have either high or low QT values (concordant), there is less QT variability than for a random sample which can reduce power [31].

Pedigrees can have diverse structures and parental and founder data are often unavailable. For common variants it has been shown that Type I and II errors can be increased when incorrect allele frequencies are used in linkage analysis, however, for RVs the effect is small and having data for one parent or multiple siblings can mitigate the impact [28, 32]. To aid in specifying accuracy allele frequencies for the analysis when there is missing variant data, large population-specific databases should be used to obtain frequencies. Additionally, when founders are missing their genotype data, it influences the ability to phase available genotypes [33]. When there are missing founders, type I errors for both CHP-QNPL and RV-QNPL are well controlled but power is reduced. Simulation studies demonstrate that RV-QNPL, compared to CHP-QNPL, has minimal power loss when founders are missing their genotypes. For the ADSP pedigrees which are missing most founders, type I error is well controlled (Fig. S7).

Analysis of AAO of AD for the ADSP families was performed with and without stratification on APOE4 status. Suggestive linkage was observed for RVs in KNDC1when analysis was performed regardless of APOE4 status. KNDC1 encodes a Ras guanine nucleotide exchange factor that negatively regulates dendritic growth and synaptic connections, which plays a pivotal role in the progression of AD [18], suggesting its potential impact on AAO. Moreover, four genes which were reported to be associated with LOAD (ABCA7, ADAMTS1, APOE, and IQCK) displayed nominally significant linkage. Both common and RVs in ABCA7 have been shown to be associated with LOAD in Europeans and African-Americans [19–21]. A weak association with RVs in ABCA7 were also reported for LOAD in Caribbean Hispanics [34]. ABCA7 has not been previously reported to modulate LOAD AAO as was observed in this study for Caribbean Hispanics. ADAMTS1 is a potential neuroprotective gene and was shown to reduce the risk of LOAD in a recent GWAS meta-analysis of Europeans [21]. Although no direct effect on AAO of AD has been reported, in the ADSP families carriers of RVs in ADAMTS1 had a later AAO than non-carriers. For APOE the common ε4 allele increases risk for both late- and early-onset AD and has a dosage effect on AAO in Europeans [19], however the findings in other populations is less pronounced. In our study, RVs in APOE displayed nominal significance in Caribbean Hispanics but not in Europeans, when analyzing ε4 allele carriers, suggesting the potential RV involvement with APOE ε4 in modulating AAO in Hispanic LOAD patients. IQCK was recently implicated as a risk gene for LOAD, with a common variant identified in a 3-stage GWAS meta-analysis of Europeans [21], but no association has been found with AAO. Several factors may contribute to the absence of significant LOD scores in the analysis of ADSP pedigrees. First, this study is not well powered given the relatively small sample size, a total of 107 families (446 patients with AAO of AD data). Even fewer samples were available for the APOE-specific analyses. Second, the AAO is dependent on the frequency of follow-up and sensitivity of diagnostic tests. In addition to AAO, quantitative endophenotypes, e.g., the level of Aβ42 and tau, can be analyzed to aid in the understanding of AD etiology.

The RV-QNPL method provides a robust and powerful approach to fine-map susceptibility RVs for QTs. Results from the ADSP analysis and extensive simulation studies demonstrate the superior power of RV-QNPL compared to analyzing RVs using traditional QNPL methods that evaluate IBD sharing for both the minor and major alleles. RV-QNPL is applicable to nuclear and extended families with exome and genome sequence data. These characteristics make RV-QNPL an ideal method to elucidate the genetic etiology of QTs. RV-QNPL is implemented in Python with C++ extensions, and the software package and documentation is publicly available online at https://github.com/statgenetics/rvnpl.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

Supplementary information

The online version of this article (10.1038/s41431-020-0703-z) contains supplementary material, which is available to authorized users.