Abstract
A pore-scale model is developed to simulate fluid-fluid interfacial area in variably saturated porous media, with a specific focus on incorporating the effects of solid-surface roughness. The model is designed to quantify total (film and meniscus) fluid-fluid interfacial area (Anw) over the full range of wetting-phase fluid saturation (Sw) based on the inherent properties of the porous medium. The model employs a triangular pore space bundle of cylindrical capillaries (BCC) framework, modified with three surface roughness-related parameters. The first parameter (surface roughness factor) represents the overall magnitude of surface roughness, whereas the other two parameters (interface growth factor and critical adsorptive film thickness) reflect the micro-scale structure of surface roughness. A series of sensitivity analyses was conducted for the controlling variables, and the efficacy of the model was tested using air-water interfacial area data measured for three natural porous media. The model produced good simulations of the measured Anw data over the full range of saturation. The results demonstrate that total interfacial areas for natural media are typically much larger than those for ideal media comprising smooth surfaces due to the substantial contribution of surface roughness to wetting-film interfacial area. The degree to which fluid-fluid interfacial area is influenced by roughness is a function of fluid-retention characteristics and the nature of the rough surfaces. The full impact of roughness may be masked to some degree due to the formation of thick wetting films, which is explicitly quantified by the model. Application of the model provides insight into the importance of the interplay between pore-scale distribution and configuration of wetting fluid and the surface properties of solids.
Keywords: Interfacial area, surface roughness, bundle-of-cylindrical-capillaries (BCC), pore geometry
1. Introduction
The interface between immiscible fluids in porous media is a fundamental property for mass and energy transfer, contaminant retention, and biogeochemical reactions, which play a significant role in many disciplines including hydrology, environmental science, petroleum engineering, and soil mechanics (e.g., Leverett, 1941; Skopp, 1985; Gvirtzman & Roberts, 1991; Hassanizadeh & Gray, 1993; Costanza & Brusseau, 2000; Pyrak-Nolte et al., 2008). Fluid-fluid interfaces in porous media are typically considered to comprise two types: one consisting of films of wetting fluid associated with the solid surfaces (film-associated interface) and the other consisting of capillary-supported menisci residing in inter-granular pore space (capillary or meniscus interface). The film-associated interfaces typically comprise a large fraction of total interfacial area at most wetting-phase saturations for natural porous media, often exceeding the capillary meniscus contributions by several orders of magnitude (Or & Tuller, 1999, Brusseau et al., 2006, 2007).
Surface roughness of natural grains is one of the most important properties affecting fluid-solid interactions in porous media. It encompasses different sources and types of features that span a wide range of spatial scales from nanometer to micrometer. The impacts of surface roughness on the displacement and distribution of fluids in porous media have been investigated for decades. For example, researchers have shown that surface roughness can affect fluid behavior by changing the degree of wettability (Wenzel, 1936; Cassie & Baxter, 1944; Oliver et al., 1980; AlRatrout et al., 2018). In addition, researchers have studied whether surface roughness has direct impacts on drainage and imbibition as measured with the soil water characteristic (SWC) curve (Dullien et al., 1989; Tokunaga et al., 2003). The relationship between grain surface roughness and hydraulic conductivity of porous media has also been investigated (Brown, 1987; Thompson & Brown, 1991; Tokunaga & Wan, 1997; Lampurlanés & Cantero-Martínez, 2006).
The influence of surface roughness on fluid-fluid interfaces in natural porous media has been discussed in prior experimental studies. For example, exponential increases in air-water interfacial area were measured at low water saturations with the gas-phase interfacial partitioning tracer test (IPTT) method (Kim et al., 1999; Costanza-Robinson & Brusseau, 2002; Peng & Brusseau, 2005). These measured interfacial areas are orders-of-magnitude greater than geometric-based solid surface areas calculated with the smooth-surface assumption. Conversely, they are consistent with specific solid surface areas measured using the N2-BET method, which incorporates surface roughness. Interfacial areas measured with aqueous-phase IPTT methods have also been shown to be larger than geometric smooth-surface solid surface areas (Saripalli et al., 1997; Schaefer et al., 2000; Brusseau et al., 2007, 2008, 2015; Zhong et al., 2016). In addition, the total interfacial areas measured with both gas-phase and aqueous-phase IPTT methods are much larger than interfacial areas measured with X-ray computed microtomography (CMT), which has a resolution limit at the micrometer level (Brusseau et al., 2006, 2007, 2008, 2010; McDonald et al., 2016). These observations were attributed to the impact of surface roughness and its contribution to film-associated interfacial area. In contrast, interfacial areas measured with CMT and IPTT methods were identical to each other and to the geometric smooth-surface solid surface area and the N2-BET solid surface area for a glass-bead medium that has no measurable surface roughness (Narter & Brusseau, 2010; Zhong et al., 2016; Lyu et al., 2017).
Prior studies have developed several quantitative approaches for representing the influence of surface roughness on fluid-solid interactions. For example, the specific solid surface area (SA) has been used as a variable to implicitly incorporate surface roughness, and relationships between the maximum fluid-fluid interfacial area and SA have been developed (e.g., Or & Tuller, 1999; Peng & Brusseau, 2005; Brusseau et al., 2010). However, these efforts did not employ specific information about the surface-roughness structures. Conversely, other investigators have proposed quantitative descriptions of the structure of surface roughness. For example, Philip (1978) used such a description to examine the influence of roughness on film thickness for adsorbed and capillary condensed wetting fluid. Or and Tuller (2000) proposed a quantitative description of surface roughness, using a statistical distribution for the depth of pits to predict the hydraulic conductivity for film flow. They then generalized the model to the sample scale using a BCC network model in follow-up work (Tuller & Or, 2001). More recently, Zheng et al. (2015) simplified the quantification of roughness in a BCC-based model for producing SWC curves and predicting hydraulic conductivity. In their approach, the surface roughness was represented as the ratio between rough and smooth surface areas. These latter studies did not examine the relationship between surface roughness and fluid-fluid interfaces specifically. Hence, quantitative approaches still need to be developed to explicitly delineate the impact of surface roughness on fluid-fluid interfaces.
Over the past decades, a number of approaches have been used for the simulation of fluid-fluid interfaces in porous media, including (a) idealized pore-geometry models (e.g., Cary, 1994; Or & Tuller, 1999; Oostrom et al., 2001; Diamantopoulos & Durner, 2013; Likos & Jaafar, 2013); (b) thermodynamic-based models (e.g., Leverett, 1941; Bradford & Leij, 1997; Grant & Gerhard, 2007; Schroth et al., 2008); (c) pore-scale network models (e.g., Reeves & Celia, 1996; Kawanishi et al., 1998; Joekar-Niasar et al., 2010; Kibbey & Chen, 2012); (d) pore-morphology models (e.g., Dalla et al., 2002; Chan & Govindaraju, 2011); and (e) direct pore-scale numerical simulations using the Lattice Boltzmann Method (e.g., Porter et al., 2009, 2010; McClure et al., 2016). Models developed with the first two approaches can be expressed as analytical equations, while the other approaches require numerical treatments. Most prior studies have either focused only on meniscus-associated interfacial area—ignoring films—or included films but without considering the impact of solid surface roughness. In addition, performance testing of the models by comparison to measured interfacial-area data has to date been restricted to simple porous media such as glass beads or sands that have minimal to relatively small magnitudes of surface roughness, and to limited ranges of water saturations (>20%).
In the present study, a pore-geometry approach based on the triangular-pore BCC framework is used to develop a model to simulate total (film and meniscus) fluid-fluid interfacial area. The methodology incorporates and modifies the approach used by Zheng et al. (2015) to represent surface roughness, and extends it to specific quantification of fluid-fluid interfacial area. The influence of the controlling variables is illustrated via example simulations and a sensitivity analysis for model parameters. The efficacy of the model is evaluated by application to air-water interfacial area data measured for three natural media. The simulation results are used to illustrate the influence of surface roughness on the magnitude of fluid-fluid interfacial area.
2. Model Development
2.1. Incorporating Surface Roughness
Traditional concepts of surface roughness are usually related to a surface elevation profile where each point on the surface has a vertical height relative to a reference plane. The arithmetic average (Ra) or root mean square (Rrms) of the relative heights at all points is often used to represent the surface roughness. However, researchers have raised concerns that this approach does not adequately represent the fractal geometry of rough surfaces (e.g., Ghanbarian et al., 2016), in which the actual surface structures may have a fractal growth that greatly exceeds the scale of traditional roughness. An alternative approach to define the effective roughness of a surface has been suggested as a “surface roughness factor”, which defines the magnitude of “actual or effective” surface area versus the geometric-base smooth surface area in one unit surface (e.g., Wenzel, 1936; Kamusewitz & Possart, 2003; Santamaría et al., 2012; Zheng et al., 2015). By definition, the geometric-base surface area is a low-resolution characteristic and is typically treated as smooth, whereas the actual surface area incorporates the effects of surface roughness across a range of higher-resolution scales. The term “rugosity” has also sometimes been used to emphasize its difference from traditional roughness (e.g., Beyhan et al., 2007; Liu et al., 2014).
A general approach to incorporate surface roughness for any given solid surface is used for this study, based on and revised from the methods employed by Zheng et al. (2015). By definition, the geometric base of a surface has a surface area defined as L0 in its one-dimensional cross-section, which is termed the geometric smooth surface area (Figure 1a–1c). A rough surface is considered to have a surface area specified as Lr, representing the topological surface area. The surface roughness factor, X, is then defined as the actual surface area (Lr) divided by the corresponding geometric smooth surface area (L0) for any unit of surface:
| (1a) |
This factor can be considered as an index characterizing the degree to which the surface of a solid deviates from a functionally smooth surface. When wetting film is present on the same geometric base (Figure 1a–1c), its upper interfacial area (Lf), i.e., the fluid-fluid interfacial area, can be specified and compared to the same geometric base L0. This produces an interfacial area factor, Xa, defined as:
| (1b) |
where 1 ≤Xa ≤X at any saturation (Zheng et al., 2015). It is assumed that the system is homogeneous such that X is the same for all surfaces.
Figure 1.
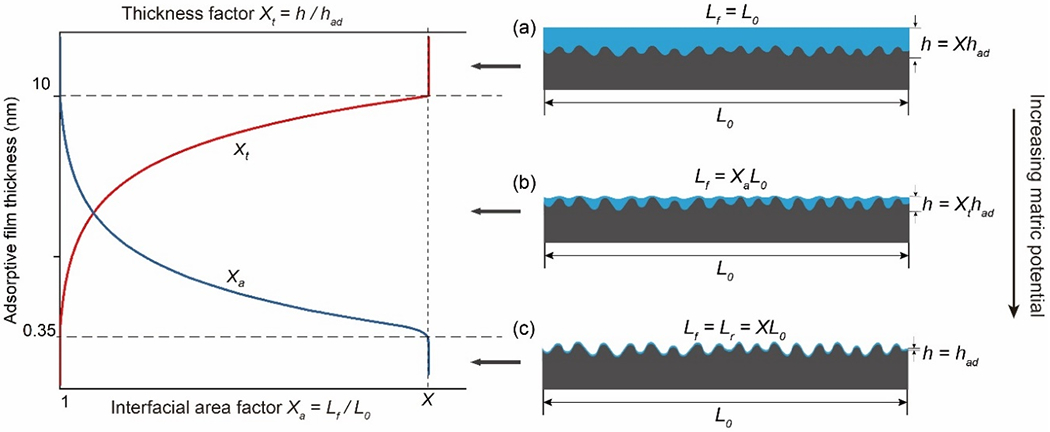
The functional relationship between the surface roughness factor X, film thickness factor Xt, interfacial area factor Xa, equivalent film thickness h, and the adsorptive film thickness had (in a log-scale axis). The wetting film configurations under different matric potentials are divided into three regimes: (a) thick film (b) intermediate film (c) thin film. Modified from the scheme in Zheng et al. (2015).
For rough surfaces, the involvement of capillary forces can in some cases retain additional wetting fluid beyond that of adsorption, producing thicker films (e.g., Philip, 1978; Israelachvili, 2011; Tokunaga, 2011). It is therefore assumed that under certain conditions the thicknesses of the wetting films will be sufficient to mask the full impact of roughness on interfacial area. The impact of roughness may be fully masked for some systems, particularly at higher wetting-phase saturations, which would result in smooth fluid-fluid interfaces (referred to as thick film as shown in Figure 1a). In this case, there is no roughness effect on interfacial area and Lf = L0. At very low wetting-phase saturations where the matric potential is high, it is assumed that adsorptive forces dominate over capillary forces such that the film is only a few molecules thick (referred to as thin film as shown in Figure 1c) (e.g., Or and Tuller, 1999; Resureccion et al., 2011; Tokunaga, 2011). Under this condition, the interfacial area is equivalent to the actual solid surface area, i.e., Lf = Lr = XL0. Under intermediate-saturation conditions, the combination of surface adsorption and capillary retention results in films of intermediate thickness and folded and uneven interfaces (Figure 1b), whose cumulative length is between [L0, XL0]. Hence, depending on the magnitude of matric potential, the local configuration of the wetting fluid, and the balance between adsorption and capillary forces, there are three types of wetting films in a typical nonwetting-wetting system (e.g., air-water, oil-water) in porous media: thick film, intermediate film, and thin film (Figure 1a–1c).
Based on the three types of wetting films, a liquid film is assumed to have a normalized equivalent thickness in order to calculate its volume. The equivalent thickness, h, is a function of the matric potential, and represented with a thickness factor Xt, defined as (Zheng et al. (2015):
| (2) |
where had(μ) is the thickness of the adsorptive film (m) given by the empirical equation above (Iwamatsu & Horii, 1996; Or & Tuller, 1999), μ is the matric potential (J/kg), ρ is the liquid density (998.21 kg/m3 for water), and Asvl is the Hamaker constant (J). For air-water-soil systems, the Hamaker constant is usually set at 6×10−20 J (Or & Tuller, 1999; Tokunaga, 2011). As discussed by Tuller et al. (1999), this formulation is considered to incorporate the molecular component of disjoining pressure. The terms matric potential μ (J/kg), capillary pressure Pc (Pa), and water pressure head H (cm H2O) in this study are equivalent. Their unit conversions follow: μ=gH (g = 9.81 m/s2) and Pc = ρgH = ρμ (ρ = 998.21 kg/m3 for water). We adopt the same assumption used by Zheng et al. (2015) that the upper limit of the film thickness factor is set equal to the surface roughness factor, i.e., Xt = X at high wetting saturations (thick film). Their simulations and our following work both show that this simplified definition is acceptable for model applications.
The functional relationship between the surface roughness factor X, film thickness factor Xt, interfacial area factor Xa, and the adsorptive film thickness had is presented in Figure 1. It is observed that with increasing matric potential, the film thickness factor Xt decreases from X to 1, while Xa increases from 1 to X. At very low wetting saturations (thin film), it is assumed that the wetting phase is retained only by adsorption to the solid surface, i.e., h = had. In this case, Xt = 1 and Xa = X. For the special case of smooth solid surfaces, X = Xt = Xa = 1. At high wetting saturations, Xt = X and Xa = 1. For the intermediate film on a rough surface, we use Zheng et al. (2015)’s exponential equation for the thickness factor:
| (3) |
The adsorptive film thickness had(μ) is a function of only matric potential. The two empirical limits of 10 nm (wet end) and 0.35 nm (dry end) given in Zheng et al. (2015) correspond to matric potentials μ1 = −3.19 J/kg (−32.5 cm H2O) and μ2 = −7.44×104 J/kg (−758400 cm H2O).
The two factors Xa and Xt were considered dependent (X = Xa Xt) in Zheng et al. (2015). In contrast, we propose a different approach to quantify Xa, based on the observed relationship between interfacial area and matric potential (Kim et al., 1997; Brusseau et al., 2006; Porter et al., 2009; Peng & Brusseau, 2012). The equation is a generalized logistic curve (Figure 2):
| (4) |
The parameters hm and k are related to the microscale structure of the roughness and its impact on interfacial area. hm is the critical adsorptive film thickness that corresponds to an interfacial area factor (X+1)/2, which is close to half of the total surface area roughness factor. hm can vary between 0.35 nm and 10 nm in the intermediate film regime. k is a “growth rate” factor representing the exponential increase of interfacial area during drainage (k > 0). In equations (3) and (4), we use the adsorptive film thickness had(μ) as the argument, instead of matric potential μ, because the values of μ are inconvenient to adjust given μ∝1/had3. Upon these definitions, Xa and Xt are independent functions of matric potential for a given porous medium, and both range within [1, X].
Figure 2.
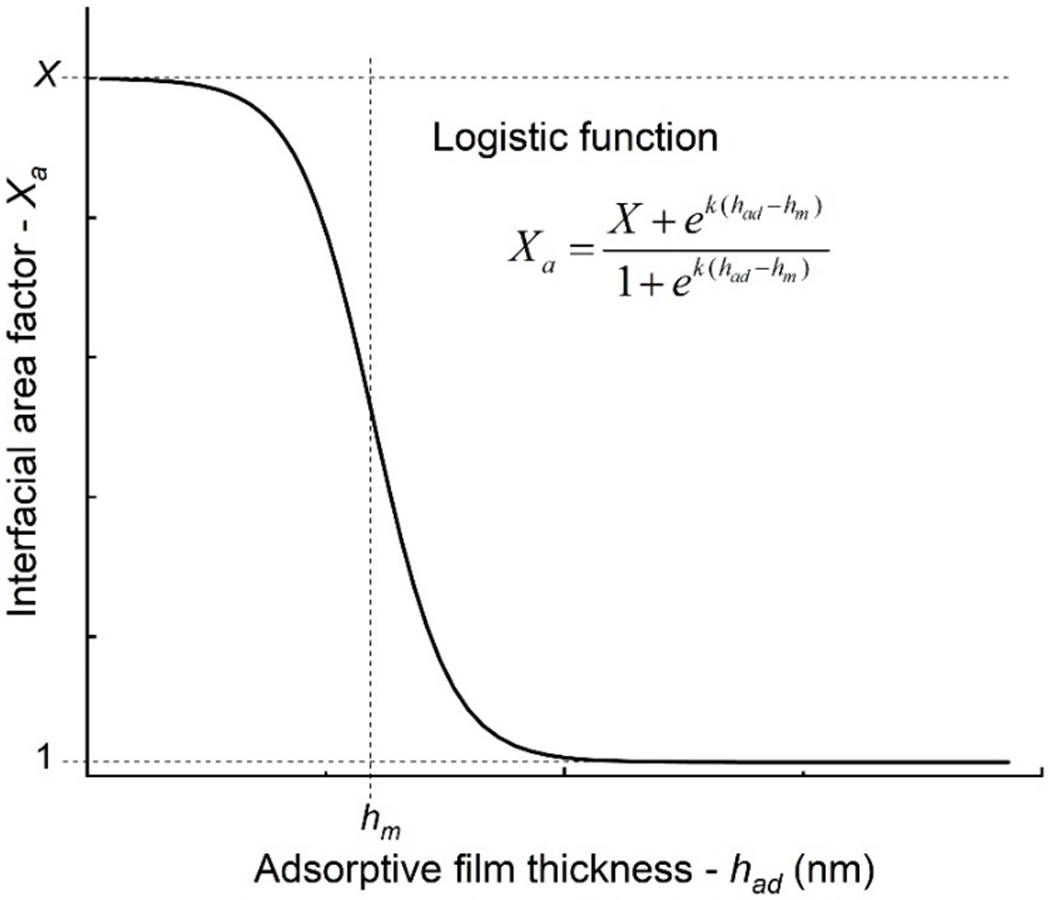
Schematic of the logistic curve for the interfacial area factor (Xa) as a function of adsorptive film thickness (had).
2.2. Pore Scale Model
The bundle-of-cylindrical-capillaries (BCC) method has been used to model soil hydraulic properties for many decades. The BCC approach provides a simple yet effective idealization of pore structure to support the development of conceptual and mathematical models (e.g., Dullien, 1992). Modifications to the standard BCC model have been made to improve the accuracy of simulations, such as employing triangular rather than cylindrical pores (e.g., Tuller et al., 1999; Helland & Skjœveland, 2006). BCC-based models have been used successfully to simulate a variety of phenomenon for many different applications, such as dynamic effects in the capillary-pressure/saturation relationship (Dahle et al., 2005), the flow of water in frozen soil (Watanabe and Flury, 2008), electrokinetic coupling during two-phase flow (Jackson, 2008), and the influence of biofilms on hydraulic properties of soil (Brangari et al., 2017).
We apply the triangular-pore BCC method with the roughness modifications presented in section 2.1 to determine total fluid-fluid interfacial area in one pore. The cross-section of each pore is treated as an equilateral triangle with a side length of L (Figure 3), and the whole porous medium is approximated as a bundle of triangular tubes, similar to previous studies such as Helland & Skjaeveland (2007) and Diamantopoulos & Durner (2013).
Figure 3.
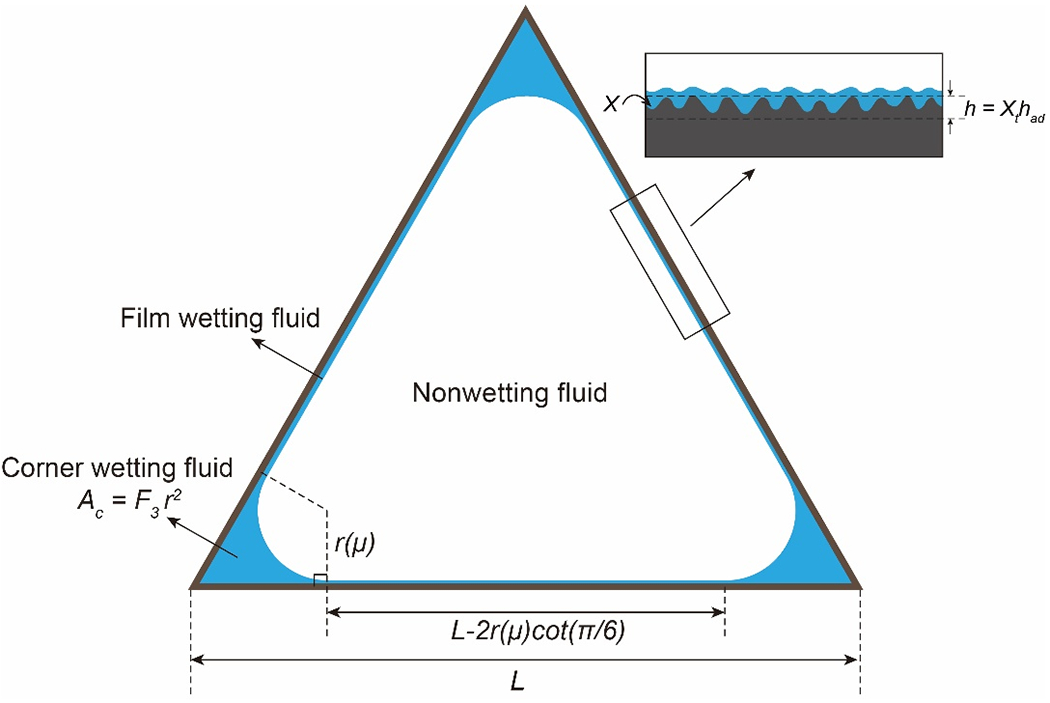
Cross-sectional scheme of a partially-drained equilateral triangular pore and the distribution of corner and film water.
The present study is focused on simulating fluid behavior in the main drainage process. Drainage in a triangular pore for a non-wetting/wetting system (typically air/water or oil/water) is assumed to follow a centrally-symmetric advance/retreat mechanism (Celia et al., 1995; Blunt, 2001; Helland & Skjaeveland, 2007; Diamantopoulos & Durner, 2013). During the onset of drainage, the invading non-wetting fluid rapidly displaces the wetting fluid from the center of a filled pore, forming a symmetric blob whose dimensions correspond to the pore dimensions. The non-wetting fluid in the center of the pore displaces the wetting fluid to the sides and corners. Hence, the wetting fluid is present as films on each side and as capillary menisci at each corner (Figure 3). The central blob grows as matric potential increases, displacing the menisci further towards each corner and increasing the lengths of the films (Figure 4). Under complete drainage, corner wetting fluid is fully displaced and only wetting film remains.
Figure 4.
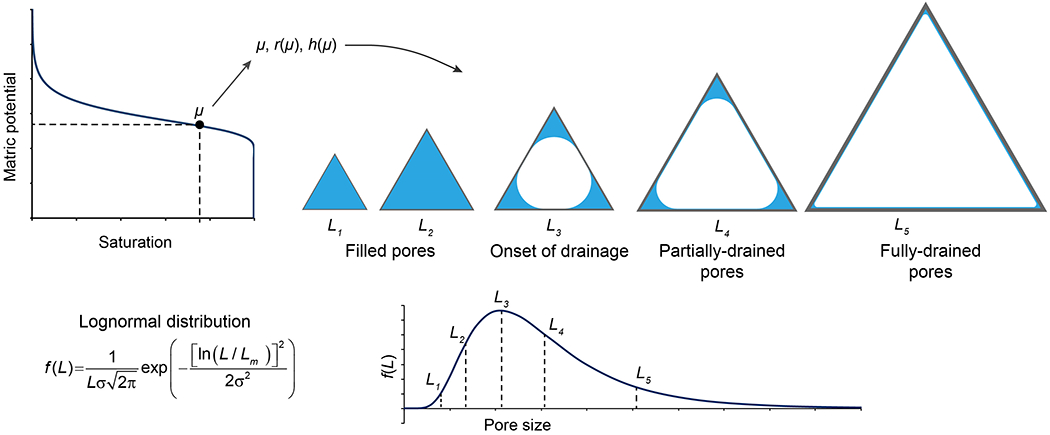
The liquid filling states in a porous medium under a lognormal pore size distribution and a given matric potential in a SWC curve.
The geometrical relationships within a partially-drained triangular pore are depicted in Figure 3. Assuming a contact angle (θ) of zero, the meniscus wetting fluid at each corner has a curvature radius of r(μ) corresponding to the matric potential, which follows the Young-Laplace equation:
| (5) |
where μ is the matric potential in unit J/kg and γ is the surface tension of the liquid (for air-water γ = 0.0728 N/m). The area surrounded by the meniscus and two sides of an angle—the corner water saturation of one angle—can be calculated for any regular n-polygons as Ac = Fnr2 (Or & Tuller, 1999). For equilateral triangles, . The length of one meniscus curve, which is πr/2, is the meniscus-associated interfacial area for one corner.
The entire inner solid surface of a pore is assumed to have the same surface roughness everywhere with a constant surface roughness factor X and two logistic parameters k and hm, all of which are considered to be inherent properties of a specific porous medium. For each given matric potential and associated had, there is a unique set of Xt and Xa derived from equations (3) and (4), respectively. The length of wetting film on one side is determined by the meniscus radius r(μ) (shown in Figure 3). Thus, the saturation and interfacial area of wetting film can be determined for one side. The saturation and specific interfacial area of wetting fluid in a single pore is determined as the combination of the wetting fluid in the three sides and three corners (Figure 3).
The saturation of wetting phase (Swc and Swf) and the interfacial area between non-wetting and wetting fluids (Anwc and Anwf) in one pore can be derived using the following equations:
| (6) |
| (7) |
| (8) |
| (9) |
where the subscripts “c” and “f” mean corner wetting fluid and film wetting fluid, respectively. An is the pore area coefficient to make A = AnL2 for a regular n-gon with side length L, which is √3/4 for equilateral triangles. F3 is as mentioned above.
2.3. Sample-Scale Equations
The equations representing a single pore are upscaled to the sample scale using an assumption of a lognormal distribution of pore sizes (e.g., Or & Tuller, 1999; Diamantopoulos & Durner, 2013). The lognormal distribution is a good approximation for the pore-size distribution of a broad range of porous materials (e.g., Diamantopoulos & Durner, 2015). The probability density function of lognormal distribution for variable pore side length (L) is:
| (10) |
where Lm is the mean pore side length (m) and σ is the standard deviation of ln(L).
The relationship between pore size, drainage, and wetting-fluid distribution is shown in Figure 4. Under a specific matric potential, pores can be filled, partially drained, or fully drained depending on their sizes. The critical pore size, i.e., the pore size that corresponds to the onset of drainage, can be determined as:
| (11) |
where Cn is the drainage radius coefficient for any regular n-gons. The value for equilateral triangles is (Tuller & Or, 2001). The smallest pore size can be set at a random small number such as 5 nm (Or & Tuller, 1999). The largest pore side length (Lmax) corresponds to the onset of drainage for the largest pore, which is defined by the air entry matric potential μd. The expression for Lmax is given in Or and Tuller (1999) and Tuller and Or (2001):
| (12) |
For sample-scale saturation, the total contributions are from fully-filled pores (ducts), corner wetting fluid, and film wetting fluid. The upscaling equations of saturation as a function of matric potential yields:
| (13) |
| (14) |
| (15) |
| (16) |
For sample-scale fluid-fluid interfacial area, there are only contributions from drained pores, including meniscus and film interfaces. Thus, the equations for total fluid-fluid interfacial areas are:
| (17) |
| (18) |
| (19) |
The specific solid surface area (SA) is determined as:
| (20) |
When X = 1, the SA corresponds to a geometric smooth surface area.
Inspection of equation (20) shows that SA is a function of X and pore-size distribution. The total interfacial area in equation (17) attains its maximum value under ultra-high matric potentials where Xa→X and r(μ)→0, and it is assumed to be equal to the specific surface area of the solid. Similar assumptions have been used in previous studies such as Or & Tuller (1999) and Peng & Brusseau (2005).
2.4. Limitations of Model Formulation
The use of the triangular-pore BCC approach brings some inherent limitations to the model. Specifically, the geometric smooth surface area determined with equation 20 will typically be larger than the standard geometric smooth-surface values due to the use of the simplified pore geometry. However, the present work focuses on systems with significant surface roughness and film interfacial areas. Hence, the errors in geometric surface areas associated with the BCC approach will have minimal overall impact on application of the model to most natural porous media.
The simplified fluid distribution of three menisci for each pore (Figure 3) may not be representative for all systems because of pore connectivity and merging of menisci. This effect of pore connectivity is not considered in the BCC model, which may affect calculated meniscus interfacial areas. However, this will have minimal impact on determination of total interfacial areas because the contribution of meniscus interfacial area to total interfacial area is typically very small compared to that of film interfacial area (Or & Tuller, 1999; Brusseau et al., 2006, 2007).
Irreducible wetting-fluid saturation, i.e., residual corner wetting fluid, is not present in the standard BBC model. In developing the model, we have attempted to strike a balance between model effectiveness and the number of input parameters. The focus was placed on parameters that are most critical to characterizing interfacial area behavior. Therefore, in the interest of simplicity, no additional modification is made to incorporate residual wetting saturation. The presence of residual saturation would affect primarily meniscus interfacial area, with minimal impact on film interface.
Diamantopoulos et al. (2016) showed that in a glass-bead medium the transition points between films and menisci might have a contact angle greater than zero, which reduces the actual meniscus radius. Nevertheless, they also showed that the wettability of natural grain surfaces is sufficiently high such that assuming zero contact angle is acceptable for many cases. Thus, the present approach is based on a completely wet surface with θ = 0 for all pores. It is noted that a non-zero contact angle can be incorporated by including the specified value in equation 5.
A logistic function is used to describe Xa, which represents the relationship between interfacial area and matric potential, whereas a simpler exponential function is used for Xt (film thickness factor). While a logistic function could be used for Xt similar to the treatment of Xa, it would add additional parameters. It is also noted that Xt affects the simulation of only film saturation and has no impact on the simulation of interfacial area.
We have limited the present formulation to drainage only to focus on the measured data sets. It is straightforward to include imbibition in the BCC approach. The critical point is to determine the geometry of the pore snap-off for imbibition, which can be changed in the variable C3 in Equation 11.
3. Applications
3.1. Model Parameterization
The model is implemented by determining values for all of the critical parameters, including the air-entry matric potential μd, the surface roughness factor X, the pore-size distribution parameters Lm and σ, and the micro-scale logistic parameters k and hm. All of the applications presented herein are specific to air-water systems. The influence of these parameters, especially the surface roughness factor, on both Pc–Sw and Anw–Sw curves is examined through a series of simulations. First, the contributions associated with film, meniscus, and duct (filled pore) to total saturation and interfacial area are examined. Second, a sensitivity analysis is conducted for the critical parameters X, Lm, and σ to illustrate their influence and effective range. Third, tests are conducted with measured Pc – Sw (SWC) and air-water Anw–Sw data for three natural porous media to investigate the ability of the model to simulate measured data.
Measured data for the SWC curve and solid surface area are required to apply the model to a specific porous medium. The first step is to determine the air-entry matric potential (μd), which in this case was determined via the traditional Brooks & Corey (1964) analysis of the measured SWC curve. The optimized values for Lm, σ, and X are then obtained in a two-step process. First, a random initial value for X is selected, and Lm and σ are optimized by application of the model to the measured SWC data. The optimized values are then substituted into equation (20), via equation (10), to derive the best value of X (with SA measured as note above). The as-obtained X is then used in place of the initial X value, and Lm and σ are optimized again. This iteration is repeated to obtain final optimized values of X, Lm, and σ. The objective function for this optimization is:
| (21) |
where Swm is the measured saturation and Sws is the simulated saturation via equation 13. This optimization is performed with the non-linear optimization toolbox in MATLAB.
The simulation of Anw – Sw curves requires the function between the interfacial area factor Xa and matric potential to be determined. With the “simple-exponential” assumption for Xa proposed by Zheng et al. (2015), Xa = X/Xt = f(Pc), without additional parameters. Conversely, our proposed logistic function for Xa assumes Xa = f(Pc, k, hm), with two logistic parameters, k and hm, for the micro-scale roughness. The values of k and hm for a porous medium can be optimized on a set of measured Anw vs Pc data with equations (17–19). Since measured data sets are usually reported in the form of Anw vs Sw, each measured Sw can be substituted in the fitted Pc – Sw curve to derive the corresponding Pc for each measured Anw data point (Brusseau et al., 2006).
The total interfacial area is also calculated using the thermodynamic-based method of Leverett (1941) for comparison with our model. The thermodynamic method is a theoretical approach to estimate total fluid-fluid interfacial areas based on the SWC curve of the porous medium. The interfacial area can be computed as:
| (22) |
where Pc(s) is the capillary pressure vs saturation function and Sw is one given point on the curve, n is porosity, and γ is surface/interfacial tension.
3.2. Measured Data Sets
The efficacy of the model is tested by comparing simulated Anw-Sw curves with measured data sets of total Anw measured with both gas-phase and aqueous-phase IPTT methods. The combined data sets provide measured Anw values for a full range of water saturation. No prior efforts to our knowledge have simulated measured data sets over this full saturation range, especially for very dry conditions (Sw < 0.2). The tests will evaluate if the model is able to reproduce the interfacial area over the full range of saturation, including the exponential increase observed at low saturations.
Measured data sets for three porous media are employed: Accusand 40/50, which is a commercial quartz sand, Vinton soil, a surface soil collected in Pima County, AZ, and a natural sandy material reported by Kim et al. (1997, 1999). Properties of the porous media are presented in Table 1. All three media are considered water wetting. Brusseau and colleagues (unpublished data) measured the specific solid surface area and SWC data for Accusand. The full-range of Anw - Sw data were collected from the gas-phase IPTT measurements reported by Peng and Brusseau (2005), the aqueous-phase IPTT measurements reported in Brusseau et al. (2015), and the mass-balance (MB) surfactant tracer measurements reported in Araujo et al. (2015). For Vinton soil, the specific solid surface area and SWC curve were reported by Peng & Brusseau (2012). Combined data from aqueous-phase and gas-phase IPTT were reported in Costanza-Robinson & Brusseau (2002), Peng & Brusseau (2005), and Brusseau et al. (2007). In addition, another data set of combined gas-phase and aqueous-phase IPTT measurements along with the specific solid surface area and SWC curves, reported by Kim et al. (1997, 1999), was selected.
Table 1.
Physical properties of the selected porous media.
| Medium | Mean diameter dm (mm) | Porosity n | Bulk density (g/cm3) | Specific solid surface area (cm−1)a | Smooth-surface surface area (cm−1) b | Air-entry matric potential μd (cm)c |
|---|---|---|---|---|---|---|
| Accusand | 0.350 | 0.42 | 1.65 | 2800 | 99.4 | 14.6 |
| Vinton | 0.234 | 0.46 | 1.46 | 51684 | 138.5 | 22.3 |
| Kim et al. d | 0.250 | 0.36 | 1.72 | 2000 | 153.6 | 24.3 |
All data were measured via the nitrogen-BET method.
Determined with the commonly-used expression of the specific solid surface area assuming smooth-spherical media, calculated as 6(1−n)/dm.
Calculated by the Brooks & Corey method.
Reported in Kim et al. (1997, 1999).
The measured specific solid surface areas for Vinton (soil) and the other two materials (sand) differ by more than an order of magnitude, providing favorable conditions for evaluating the effect of surface roughness on interfacial area. It is noted that the largest measured air-water interfacial areas obtained with the gas-phase IPTT method for all three media are consistent with specific solid surface areas measured by the nitrogen-BET method. This consistency provides verification of the accuracy of the gas-phase IPTT data and illustrates the significant impact of surface roughness on interfacial area.
4. Results
4.1. Example Simulations
An example set of simulations of both drainage Pc-Sw and Anw-Sw curves for an air-water system is presented in Figure 5, showing the contributions from film, corner, and duct (filled-pore) water for surface roughness factors X = 10 and 1000. Fully-filled pores are the primary contributor to total water saturation, as expected. Film and corner water both contribute a small amount to total saturation, but at X = 10, the film-associated saturation is very low. The Anw-Sw curves are similar to the examples presented in Or and Tuller (1999) and Brusseau et al. (2007), in which film-associated interfacial area surpasses the meniscus area by more than one order of magnitude at almost all saturation values. The calculated meniscus (corner) interfacial area in Figure 5b may be overestimated because the BCC model neglects pore connectivity. Nevertheless, it is several orders of magnitude smaller than the film interfacial area for both X = 10 and 1000. The uncertainty in total interfacial area due to pore-connectivity effects on simulated meniscus interface can be calculated from the magnitude of meniscus interfacial area in Figure 5b.
Figure 5.
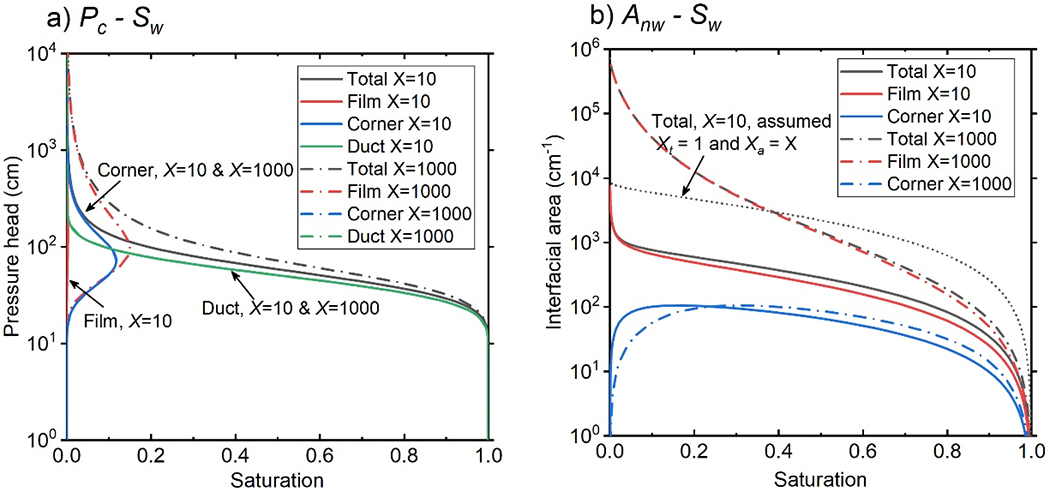
Example calculations of the contributions from duct (filled pores), film, and corner water to the total saturation and air-water interfacial area, with X = 10 and X = 1000 and other parameters fixed. The input parameters are set at Lm = 90 μm, σ = 0.5, μd = −1 J/kg, k = 1, and hm = 2 nm.
Increasing the roughness factor by 100 results in changes in both the Pc-Sw and Anw-Sw functions. The impact of surface roughness on the Pc-Sw curves is relatively small because of the small volume of film-associated water. Conversely, X has a much greater influence on the Anw-Sw relationship. The total interfacial area ranges from 0.5 to 2 logs greater for X = 1000 compared to X = 10. The significant increase in interfacial area is observed only for the film contribution, consistent with the fact that surface roughness only affects the film-associated interfaces.
4.2. Sensitivity Analysis
A sensitivity analysis was conducted following the example simulations in section 4.1 by varying the parameters X, Lm, and σ over broader ranges. All default parameters are the same as used for the simulations in section 4.1 unless otherwise specified. The resulting drainage Pc–Sw and Anw–Sw curves are shown in Figure 6.
Figure 6.
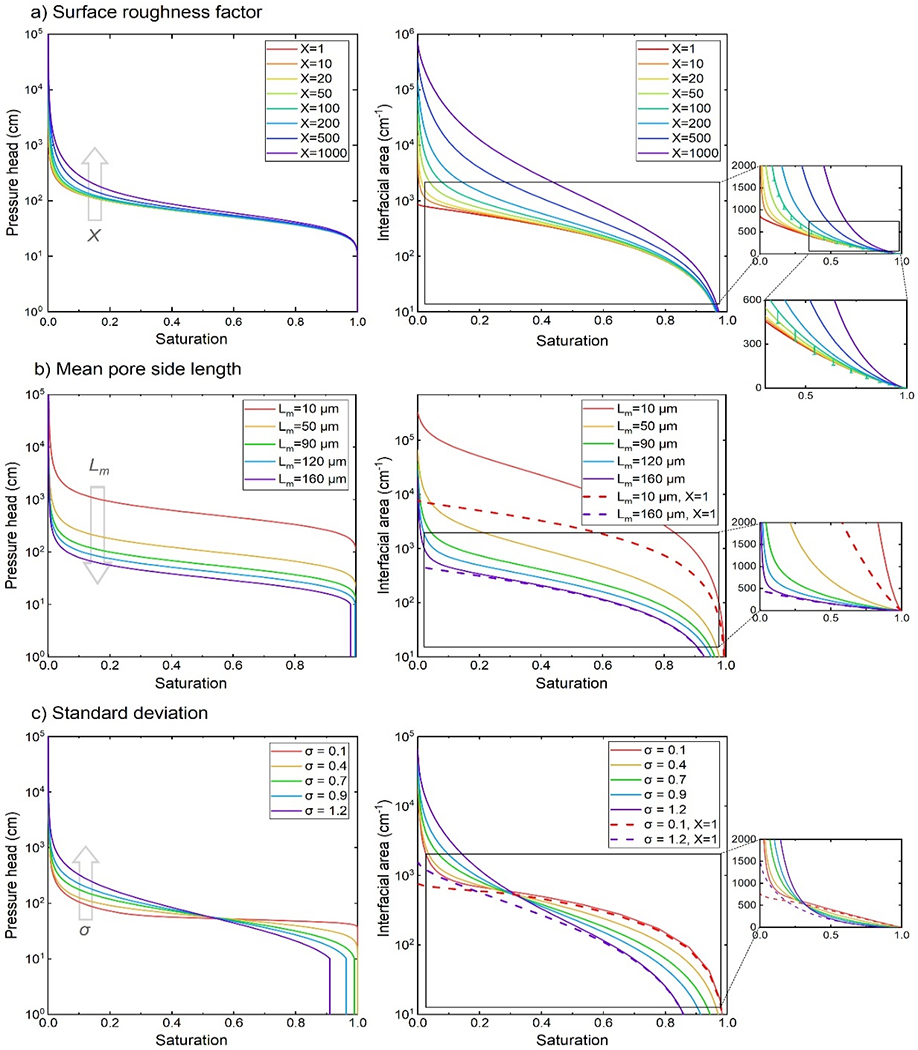
Sensitivity analysis of the roughness-modified BCC model for drainage matric potential curves and total interfacial area curves on logarithmic scales. The default parameter values for all cases are X = 50, Lm = 90 μm, σ = 0.5, μd = −1 J/kg, k = 1, and hm = 2 nm unless specified otherwise. Adjusted parameters are (a) surface roughness factor; (b) mean pore side length (with two dashed reference curves for the maximum and minimum inputs, respectively, under the same conditions except with X = 1) (c) standard deviation (with the same reference curves as (b) for the maximum and minimum inputs). Each interfacial-area figure has an amplified insert showing the curves on linear scales for Anw < 2000 cm−1. The Anw insert in Figure 6a has a further magnification for saturations over 30%, and the errors due to meniscus-interfaces on the X = 100 curve are marked.
The Pc-Sw curves are generally not very sensitive to the roughness factor X, but a rougher solid surface does have a relatively higher capability to retain water, causing the Pc-Sw curve to shift slightly upward. In contrast, the Pc-Sw curves are more sensitive to Lm and σ as would be anticipated. Increasing the mean pore size leads to less filled pores for a given matric potential and decreases the fluid retention of the medium. The standard deviation controls the dry-end and wet-end of the simulated Pc-Sw curves. Increasing σ makes the curve “narrower” and sometimes yields a maximum saturation lower than 1 due to the fixed air-entry potential.
The simulations presented in Figure 6 clearly demonstrate that the presence of solid surface roughness, i.e., X>1, increases the magnitude of film interfacial area compared to the case of a smooth surface (X=1). Larger X values produce larger interfacial areas for a given set of conditions, as a larger X represents a larger specific solid surface area due to greater magnitude of surface roughness. These results are consistent with prior experiment-based studies that have reported larger interfacial areas for media with greater surface roughness (Costanza and Brusseau, 2000; Costanza-Robinson and Brusseau, 2002; Peng and Brusseau, 2005; Brusseau et al., 2008, 2010, 2015; Zhong et al., 2016).
The sensitivity of interfacial area curves to the roughness factor is complicated. Inspection of the linear-scale insert of Figure 6a shows that the Anw–Sw functions for media with smooth surfaces (X = 1) are essentially linear over the full saturation range for small to moderate σ. The curve for this condition defines one theoretical limiting case for the Anw–Sw function, establishing the minimum values of Anw for a given porous medium. Note that this case is functionally equivalent to the theoretical case wherein the wetting films are sufficiently thick to produce smooth film interfaces for all Sw.
The special case wherein the surfaces are rough and the thicknesses of the wetting films remain sufficiently thin such that the effect of roughness remains at its maximum for all Sw (i.e., Xt = 1 and Xa = X) defines the other theoretical limiting case. This case establishes the maximum set of Anw values. An example of this second case is provided in Figure 5b for X = 10 with the constraint Xt = 1 and Xa = X, and other parameters the same as for the original simulation. It is observed that Anw values for this case are larger than for the X = 1000 simulation at Sw > 0.4, even though the latter system has an equivalent 100-times greater surface roughness.
The actual Anw–Sw function observed for a given porous medium will typically reside somewhere between the two limiting cases. This is illustrated by the observation that the Anw values produced for the original X = 10 simulation are an order of magnitude smaller than those for the theoretical maximum simulation. This is a result of thicker wetting films partially masking the impact of roughness on film interfacial area.
Generally, all Anw curves with X > 1 greatly increase at a certain saturation due to the impact of surface roughness causing an exponential increase of film-associated interface. For a given set of conditions, the critical saturation is smaller for smaller X (Figure 6). The impact of surface roughness on Anw is masked to some degree at higher saturations because of the presumed presence of thicker wetting films. This masking effect is greater for smaller X for a given set of conditions. The degree to which surface-roughness impacts are masked, and the resultant shape of the Anw–Sw curve, for a given medium will depend upon its fluid-retention characteristics and the nature of the surface roughness, and how they influence pore-scale wetting-fluid distribution and configuration. More detailed discussions of the roughness factor and natural grain surfaces are given in section 5.
For the analyses of the effect of Lm and σ, two reference simulations with smooth media (X = 1) were first performed, and the subsequent simulations for rough media (X = 50) were set within the parameter range of the reference simulations. As expected, decreasing Lm increases SA due to smaller grain size (and smaller pore size), which results in larger Anw for the full-range of saturations. These results are consistent with prior experiment- and model-based studies that have reported larger interfacial areas for media with smaller grain diameters (Cary, 1994; Anwar et al., 2000; Costanza and Brusseau, 2000; Costanza-Robinson and Brusseau, 2002; Cho and Annable, 2005; Dobson et al., 2006; Schnaar and Brusseau, 2006; Brusseau et al., 2008, 2009, 2010; Costanza-Robinson et al., 2008; Zhong et al., 2016). The relative impact of surface roughness on Anw is greater for smaller Lm, as illustrated by comparing the two sets of simulations for X = 1 and X = 50 for Lm= 10 versus 160 μm (Figure 6b). For Lm= 10, the difference in Anw for X = 1 and X = 50 is greater than 0.5 log for Sw<0.9. Conversely, the difference in Anw is very small until much lower Sw for Lm= 160. These results reflect the relationship between surface area and grain size, wherein the magnitude of Lm (i.e., pore size) correlates to grain size.
Increasing the pore-size standard deviation for smooth media only slightly increases SA, but it causes the Anw – Sw function to become more nonlinear for larger σ (Figure 6c). For rough media, the influence of σ is similar to that observed for the Pc - Sw curves, where increasing σ simultaneously increases the low-saturation Anw for Sw < 0.3 and decreases the medium-to-high-saturation Anw at Sw > 0.3. Similar to the Lm simulations, it is observed that the deviation between the Anw-Sw curves for the X = 1 and X = 50 cases is greater for σ = 1.2 than for σ = 0.1 at low saturation. This reflects the greater proportion of smaller pores present with larger pore-size (grain-size) distributions. Inspection of the insert in Figure 6c shows that the magnitudes of the impact of σ are relatively smaller than those of X and Lm.
4.3. Tests with Measured Data
The results for model testing with the three measured data sets are shown in Figure 7. The left column in Figure 7 presents the final fit of the SWC curves. The optimized curves produce good matches to the measured data for high and medium saturations, but do not match the measured data at the lowest saturations. Following the methodology in section 3.1, the results for roughness factor X and pore size parameters Lm and σ of the three media are presented in Table 2. Inspection of Table 2 shows that Lm is smallest for Vinton, intermediate for the Kim sand, and largest for Accusand. This is consistent with the textures of the three media. Diamantopoulos et al. (2016) tested a lognormal triangular-BCC model without surface roughness using the same SWC data reported for Vinton soil in Brusseau et al. (2006), yielding values of Lm = 90 μm and σ = 0.9. Their values are similar to ours.
Figure 7.
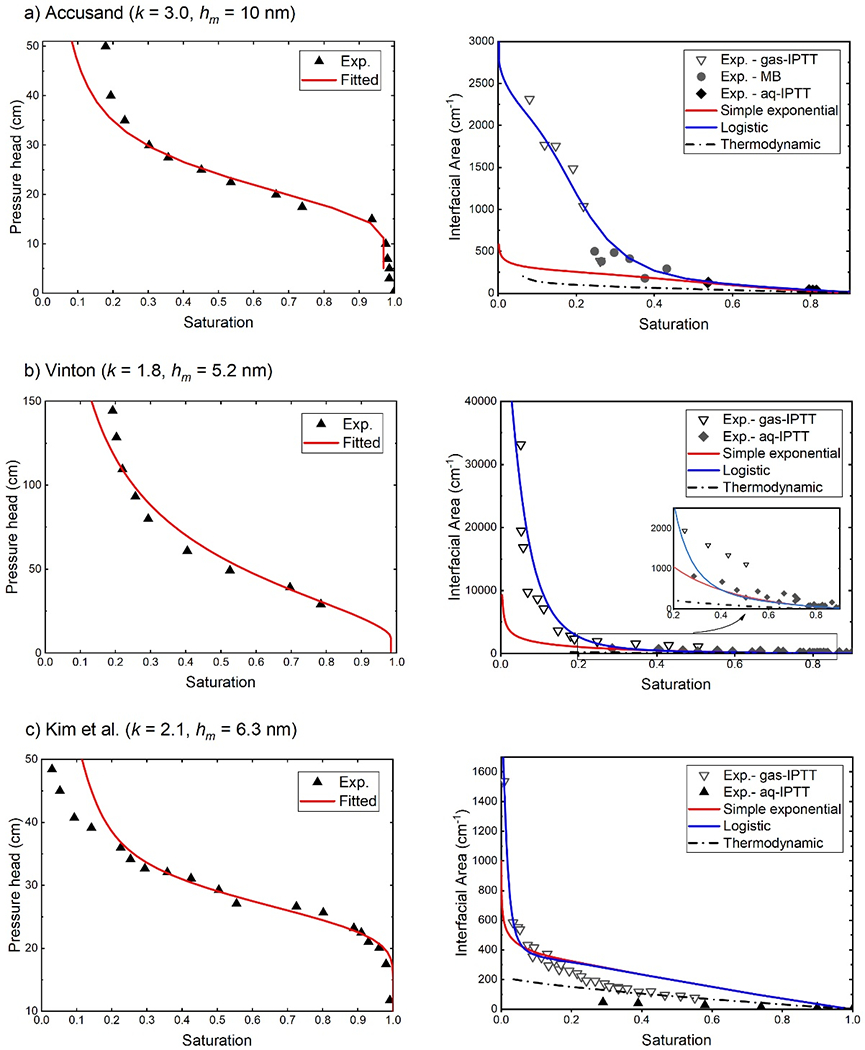
Model simulations of the Pc–Sw and Anw–Sw curves compared to measured data for three natural porous media using the simple-exponential and logistic assumptions for the interfacial area factor Xa. Results produced by the thermodynamic estimation method are also plotted.
Table 2.
Pore size distribution and surface roughness-controlling parameters of the selected soil samples.
| Medium | Mean pore side length Lm (μm) | Standard deviation σ | Surface roughness factor X | Growth rate factor k | Critical adsorptive film thickness hm (nm) |
|---|---|---|---|---|---|
| Accusand | 212.7 | 0.303 | 8.7 | 3.0 | 10 |
| Vinton | 93.6 | 0.685 | 58 | 1.8 | 5.2 |
| Kim et al. | 171.0 | 0.164 | 5.0 | 2.1 | 6.3 |
The model simulations of Anw – Sw incorporating the logistic parameters k and hm are presented in the right column of Figure 7. It is observed that the model simulations provide good matches to the measured data over the entire saturation range for the accusand and Vinton media. The values of Anw exhibit enormous increases, upwards of 2,500 and 40,000 cm−1, respectively, over the full saturation range. These results demonstrate that the model effectively represents these enormous changes in air-water interfacial area during drainage.
For the Kim et al. data, the simulated curve matches at the lowest saturations but over-predicts measured Anw values at mid-to-high saturations. These errors exceed the range of menisci uncertainties (~10%), and may reflect in part greater uncertainty in the model representativeness of the simplified triangular pore geometry. It is noted that this medium has the smallest interfacial areas and surface-roughness effects, conditions for which errors in representing the pore structure and smooth surface area would have the most impact. The disparity between simulated and measured values may also be influenced by possible uncertainties in the measured aqueous-phase IPTT data discussed by Kim et al. (1997).
The measured and simulated interfacial areas for Vinton soil are much greater than for the two sands. Vinton soil has a much larger X compared to the other two media (Table 2), consistent with its much larger specific solid surface area a measured by the nitrogen-BET method (Table 1). Hence, these results illustrate that X controls the overall magnitude of total interfacial area. It is further observed that the logistic parameters k and hm also influence the impact of surface roughness on Anw. They are correlated to the surface-roughness masking phenomenon described in the discussion of Figures 5 and 6. The k term controls the slope of the Anw – Sw curves for the exponential-increase stage, and hm determines the critical saturation at which Anw begins to increase exponentially. Inspection of Table 2 shows that k and hm vary somewhat amongst the three test materials, most likely reflecting differences in the specific structure of surface roughness. Therefore, a minimum of three controlling parameters (X, k and hm) are needed to quantify the surface-fluid interactions on rough surfaces, and all three are intrinsic properties of the porous medium. Among them, X represents the overall magnitude of surface roughness (roughness capacity), whereas k and hm are parameters representing the micro-scale structure of surface roughness and its interactions with wetting fluid (and ultimately the resultant impact on interfacial area).
For comparison, Figure 7 also shows the simulations obtained through the simple-exponential equation via Xa = X/Xt, where Xt is defined by the exponential equation (3). Both simulated curves are consistent and reasonably match the measured interfacial-area data at medium to high saturations (Sw > 0.5) for the sand and Vinton soil. However, the measured exponential increases at low saturations are only accurately characterized by incorporating the two logistic parameters k and hm. The two simulations are very similar over the majority of the saturation range for the Kim data; however, both simulations deviate from the measured data at higher saturations.
The Anw–Sw results obtained with the thermodynamic method are also shown in Figure 7. It is clear that the thermodynamic method greatly underestimates both measured and simulated data sets at lower saturations. The limitations of the base thermodynamic method have been discussed in prior studies, which noted that the method may oversimplify the energy exchange and solid-fluid interactions in real porous media (e.g., Leverett, 1941; Dobson et al., 2006; Grant & Gerhard, 2007; Schroth et al., 2008). If the thermodynamic estimation is considered to provide a first-order representation of the Anw–Sw function for smooth-surface media, the results suggest that Accusand and Vinton have less roughness masking compared to the Kim sand. These results illustrate that the surface-roughness masking effect is different for different porous media.
4.4. Validity of Model Assumptions
Inspection of Figure 7 shows that the optimized curves do not fully match the measured data at the lowest (<0.2) saturations for the Pc – Sw data, which may indicate limitations associated with model assumptions (e.g., simplified pore geometry and fluid distribution, no residual saturation). However, the determination of model parameters Lm, σ, and X, is controlled primarily by the higher-saturation (>0.2) data range. Furthermore, determination of parameters k and hm are based on application to the Anw–Sw data. Thus, any potential model limitations affecting simulation of the Pc–Sw data do not significantly influence determination of interfacial area. This is supported by the excellent matches obtained between the simulated and measured curves for the Anw–Sw data for accusand and Vinton.
The model assumptions of simplified pore geometry and fluid distribution and of no residual wetting fluid affect primarily the meniscus interfacial area. As discussed above, film-associated interfacial area dominates total fluid-fluid interfacial area at essentially all saturations. Thus, potential uncertainty in meniscus area will have minimal impact on determination of total interfacial area, the focus of this study.
The Pc–Sw function is not very sensitive to surface roughness and wetting-film status, given the relatively small fluid volumes involved. In addition, as noted above, there can be uncertainty in simulation of this function at lower saturations. Thus, our approach of treating Xa independent from Xt and determining it from the Anw–Sw data appears to be a robust means of characterizing fluid-fluid interfacial area.
5. Discussion
5.1. The Masking of the Surface Roughness Effect
The illustrative results in Figures 5–7 all indicate that surface roughness can have a substantial impact on the magnitude of air-water interfacial area. As discussed above, the impact may be masked to some extent depending upon media properties and fluid conditions. The masking phenomenon is illustrated in linear-scale coordinates in Figure 8. The two limiting cases for the Anw–Sw function are shown as the “maximum roughness” and “smooth surface” curves. The curve for the smooth surface (X = 1) is anchored to the smooth solid surface area for Sw = 0. Curves for X > 1 are anchored to the actual (rough) solid surface area. The dashed curves in Figure 8 demonstrate the maximum roughness effect on the Anw–Sw function for a given medium, where all of the wetting films are thin at all Sw (Xt = 1 and Xa = X). The surface roughness effect can be obscured if the wetting film is sufficiently thick. The solid curves in Figure 8 represent one possible realization of the actual drainage Anw–Sw function, wherein the impact of surface roughness is masked to some degree compared to the maximum-roughness curves.
Figure 8.
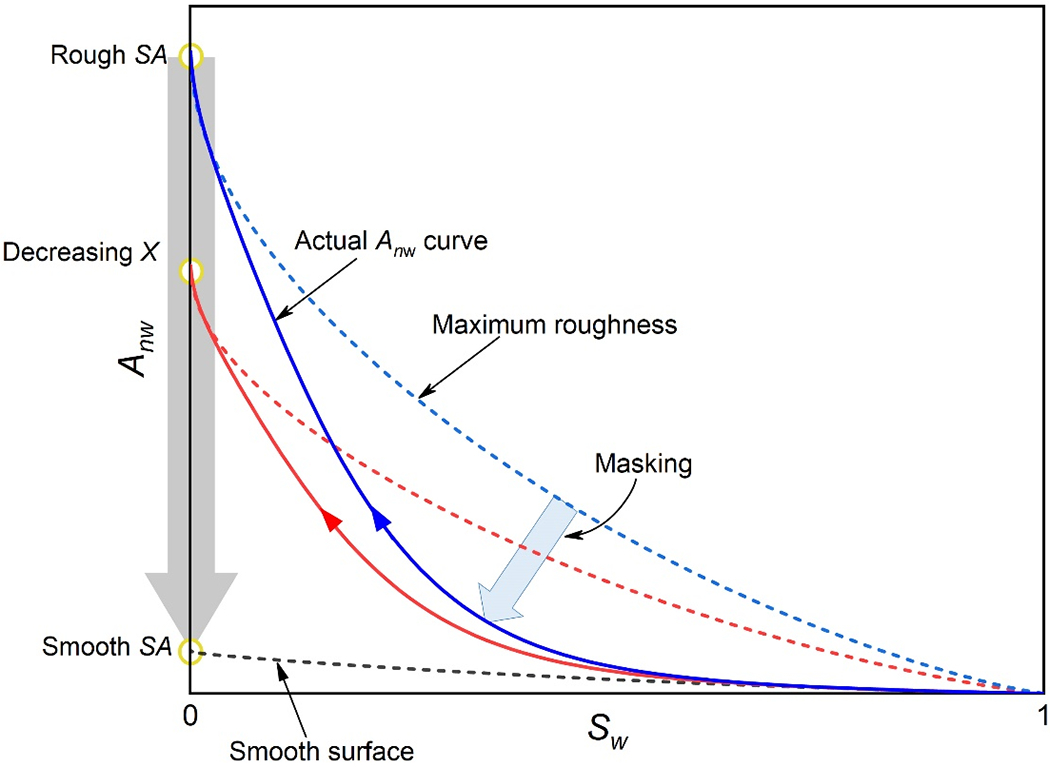
Illustration of the masking phenomenon of the surface roughness effect on Anw – Sw curves. The blue and red curves represent two media with different magnitudes of surface roughness, but the same smooth surface area (SA).
The typical Anw–Sw curve is “L”-shaped in linear coordinates, with a flat linear stage at higher saturations and a steep exponential stage at lower saturations. Surface roughness may be considerably masked by thick wetting films in the linear stage, causing the actual Anw–Sw curve to reside closer to the theoretical smooth-surface curve. In the exponential stage, the decreasing wetting-film thickness causes an enormous increase in the magnitude of fluid-fluid interfacial area such that the actual Anw–Sw curve approaches the theoretical maximum curve. The nature of surface roughness and its interaction with wetting fluid determines the relative proportion of linear and exponential stages over the full saturation range. From the simulations of the measured data presented in Figure 7, it can be observed that different materials have different proportions of linear and exponential stages. For instance, the linear range for Kim’s sand extends to ~30% saturation, whereas it extends to only ~70-80% for Accusand and Vinton. Such results indicate that the masking of surface roughness is more significant for Kim’s sand than for Accusand and Vinton soil.
As noted above, the degree to which surface-roughness impacts are masked and the resultant shape of the Anw–Sw curve for a specific porous medium will depend upon the interplay between wetting-film configuration, matric potential (saturation), and surface roughness. The shape of the Anw–Sw curves can be explained in accordance with the five controlling parameters in the model: Lm, σ, X, k, and hm. The lognormal pore-size-distribution parameters Lm, and σ define the geometric base solid surface area and determine the location of the smooth-surface fluid-fluid interfacial area curve. Combining the surface roughness factor X with the smooth-surface curve defines the maximum-roughness fluid-fluid interfacial area curve for a given medium. These two limiting curves determine the full range of possible outcomes of surface roughness effects on fluid-fluid interfacial area for a specific medium. The parameters k and hm, which represent the micro-structure of solid surfaces and its interaction with wetting fluid, influence the shape of the curve within the limiting range and the proportion of the linear and exponential stages. For media with rough solid surfaces, the Anw–Sw curve will always reside between the smooth-surface curve and the maximum-roughness curve, and the magnitudes of the three roughness-related parameters (X, k, and hm) will mediate the overall impacts of surface roughness on Anw under different matric potentials (wetting saturations) and thus the overall shape of the Anw–Sw curve.
The following strategies can be implemented to improve the characterization of surface roughness effects on nonwetting-wetting interfaces. First, the extent of drainage can be increased to reach as low a saturation as possible. This will entail the use of additional measurement methods beyond the standard ones typically used to determine soil-water characteristic curves (e.g., Arthur et al., 2013). Second, whereas most studies focus on a single medium or on a few ideal media, it is better to use various porous media with a broad range of physical properties. One major implication of this work is that natural soils and sediments are anticipated to exhibit a great range of properties and associated Anw – Sw behavior. Thus, we would expect that the importance of film-associated interfacial area and the impacts of surface roughness will vary from media to media. Third, use a definition of surface roughness that compares the rough and geometric solid surface areas under different scales, rather than only a single absolute value of specific surface area or relative height (root-mean-square roughness).
5.2. Relating Surface Roughness Effect to Solid Surface Micro-structure
The impact of surface roughness on the Anw – Sw function can be explained using concepts of fractal geometry. In the scheme of a fractal surface (Figure 9), there are multiple layers of roughness structures within a defined space. The primary roughness layer, as indicated by the root mean square roughness (Rrms), is quantifiable by traditional measurements. For natural materials, its spatial scale is usually in the range of 0.1~1 μm or even larger (e.g., Tokunaga et al., 2003; Alshibli & Alsaleh, 2004; Adams et al., 2012; Kim et al., 2012; Kibbey, 2013; Araújo & Brusseau, 2019). At higher water saturations, the film thickness can be close to the magnitude of the primary roughness layer (Philip, 1978; Kim et al., 2012; Kibbey, 2013; Zheng et al., 2015). Under this condition the smaller-scale roughness does not impact film interfacial area. Conversely, adsorbed wetting-film thickness under low-saturation conditions can be 1~10 nm (Tokunaga et al., 2003; Resurreccion et al., 2011; Tokunaga, 2011), which can be several orders of magnitude smaller than the scale of the primary roughness. When the wetting film thickness is reduced to the scale of a certain roughness layer, as shown in the inset of Figure 9, it reflects the micro-scale surface topography. The transition between scales causes the film interfacial area to increase dramatically, resulting in the exponential stage of the Anw–Sw function. When Sw approaches zero, the film attains the fractal dimensions of the solid surface, where the thickness factor Xt = 1 and the interfacial area factor Xa = X. These sub-levels of roughness are regarded as “micro-scale roughness” in the present study in distinction to traditional root-mean-square surface roughness (Rrms).
Figure 9.
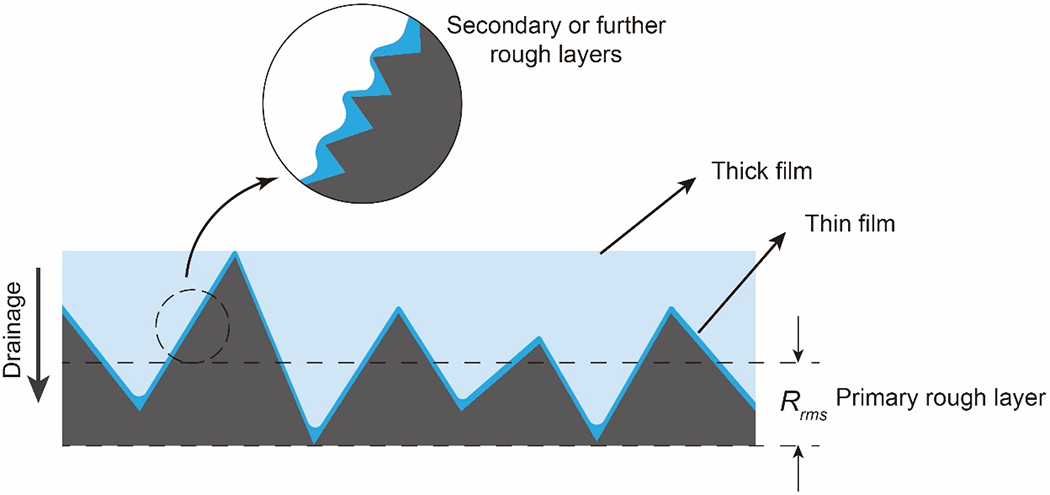
Scheme of a rough solid surface with multiple layers of roughness. The root-mean-square roughness defines the roughness of the primary layer. When matric potential increases, the water film thickness may reduce to the scale of the secondary or further micro-roughness levels, which provides additional surface and interfacial areas.
The role of the surface roughness factor X can be further interpreted in accordance with the fractal nature of the solid surface. In this case, X can be viewed to represent the potential of surface fractal growth, i.e., the potential for existence of additional scales of roughness that will typically be operationally defined by specific measurement methods (such as nitrogen-BET). The logistic parameters k and hm reflect the impact of solid fractal structures on the disposition of liquid films. The exponential growth-rate parameter k may indicate the fractal complexity of the surface roughness, especially the difference of average heights between two adjacent roughness layers. The critical adsorptive film thickness hm ‒corresponding to a specific matric potential‒ may represent the average micro-scale triggering point of the exponential increase of film interfaces. The parameters k and hm relate to the masking of surface roughness by wetting films, and can be used to quantify the degree of masking. The impacts of the three parameters X, k, and hm are superimposed on the absolute magnitude of solid surface available, which is controlled by the texture of the porous medium (mean grain size, grain-size distribution).
6. Conclusions
A triangular-pore BCC-based model with explicit representation of surface roughness was developed to characterize the impacts of surface roughness on fluid-fluid interfaces in porous media. The model can compute both the film and meniscus Anw–Sw profiles for a specified porous medium under the assumption of a lognormal pore-size distribution. The model contains three roughness-related parameters: the solid surface roughness factor X, and the micro-scale film-interface parameters k and hm, which are all considered to be inherent properties of the porous medium.
The results demonstrated that the model is able to reproduce measured air-water interfacial area data across a full-saturation range, which was not examined in previous modeling studies. The simulations also showed that the exponential increases in Anw measured with the gas-phase IPTT method can be explained by the impact of surface roughness on film-associated interfacial area. While the applications presented herein were specific to air-water systems, the model and reported outcomes are relevant for any nonwetting-wetting fluid pair. The significance of solid surface properties in mediating fluid-fluid interfacial area observed in this study is consistent with prior research illustrating the role of surface properties on vapor adsorption, water evaporation, and soil-water retention at very high matric potentials (e.g., Shahraeeni and Or, 2012; Song and Boily, 2013; Leao and Tuller, 2014).
The degree to which fluid-fluid interfacial area is influenced by roughness is a function of fluid-retention characteristics and the nature of the rough surfaces, which mediate the distribution and configuration of wetting fluid within the pores and on the surfaces of the solids. The Anw- Sw function observed for a particular porous medium ranges between an upper theoretical maximum, defined for the case wherein the wetting films remain thin for all Sw, and the lower theoretical minimum defined for the case of smooth solid surfaces (and equivalently wherein wetting films remain sufficiently thick for all Sw). The specific behavior is defined with the five controlling parameters in the model: Lm, σ, X, k, and hm.
The lognormal pore-size-distribution parameters Lm, and σ define the geometric base solid surface area and determine the location of the smooth-surface fluid-fluid interfacial area curve. The surface roughness factor X superimposed on the smooth-surface curve determines the maximum-roughness curve for a given medium. These two limiting curves define the full range of possible outcomes of surface roughness effects on fluid-fluid interfacial area for a specific medium. The parameters k and hm, which represent the micro-structure of solid surfaces and its interaction with wetting fluid, mediate the shape of the curve within the limiting range and the proportion of the linear and exponential stages. The influence of wettability, solution chemistry, and other factors is implicitly incorporated in the model through these parameters. Sensitivity analyses were conducted for Lm, σ, and X to examine their influence on system behavior. Because of their hypothesized relationship to the specific nature of surface roughness, we have reserved detailed analysis of k and hm to a future study wherein the model will be applied to a larger number of porous media beyond the three used in the present study.
The impact of surface roughness on fluid-fluid interfacial area for natural porous media is likely to be masked to some degree due to the presence of wetting films. The extent to which this masking phenomenon occurs will depend on the specific properties of the medium as well as fluid conditions, as illustrated by the results presented herein for the simulation of the measured data sets. It is anticipated that natural porous media will display a wide range of masking potentials considering the extreme variability in physical and geochemical properties exhibited across the spectrum of soils and sediments.
The triangular-pore BCC approach used in this work has limitations that may impose constraints to the representativeness for some systems. This may lead to uncertainties in the magnitudes of simulated meniscus interfaces, the geometric solid surface area, and the fitting of SWC curves at low saturations. However, these potential uncertainties do not limit the capability of the model to characterize the impact of surface roughness on fluid-fluid interfacial area, as shown by application to the measured data sets presented herein. Some of the assumptions used in the present study can be relaxed, for example by implementing consideration of pore-connectivity or effects of non-zero contact angles. In addition, the model can be extended to characterize the imbibition Anw curves by modifying the pore geometry for the onset of pore snap-off.
The modeling approach presented can be used to characterize a broad range of porous media with different solid surface structures. In principle, the Anw-Sw function can be viewed as a “surface-film characteristic curve”, containing information about the properties of surface roughness and solid (surface)–fluid (film) interactions. The surface-film characteristic curve can serve as a quantitative approach to characterize rough surfaces, and simulate the associated wetting films in pore-space modeling. This approach is anticipated to provide additional insight into surface roughness effects on porous-media systems.
Key points.
A triangular pore space BCC model is developed to simulate the impact of solid surface roughness on fluid-fluid interfacial area.
Model efficacy is tested with air-water interfacial area data measured for three natural porous media.
The model presents a means by which to quantify fluid-fluid interfacial area for natural porous media in multiphase fluid systems.
Acknowledgements
This research was supported in part by a grant from the NIEHS Superfund Research Program (P42 ES04940). No new measured data sets are used in this work. The measured data sets used are available in the cited prior-published works. We thank the reviewers and editors for their constructive comments.
References
- Adams T, Grant C, & Watson H (2012). A simple algorithm to relate measured surface roughness to equivalent sand-grain roughness. Journal ISSN, 2929, 2724. [Google Scholar]
- AlRatrout A, Blunt MJ, & Bijeljic B (2018). Wettability in complex porous materials, the mixed-wet state, and its relationship to surface roughness. Proceedings of the National Academy of Sciences, 115(36), 8901–8906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alshibli KA, & Alsaleh MI (2004). Characterizing surface roughness and shape of sands using digital microscopy. Journal of Computing in Civil Engineering, 18(1), 36–45. [Google Scholar]
- Araujo JB, Mainhagu J, & Brusseau ML (2015). Measuring air–water interfacial area for soils using the mass balance surfactant-tracer method. Chemosphere, 134, 199–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Araújo JB, & Brusseau ML (2019). Novel fluid–fluid interface domains in geologic media. Environmental Science: Processes & Impacts. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arthur E, Tuller M, Moldrup P, & de Jonge LW (2013). Rapid and Fully Automated Measurement of Water Vapor Sorption Isotherms: New Opportunities for Vadose Zone Research. Vadose Zone Journal, 13(1). 10.2136/vzj2013 [DOI] [Google Scholar]
- Beyhan S, Bilecen K, Salama SR, Casper-Lindley C, & Yildiz FH (2007). Regulation of rugosity and biofilm formation in Vibrio cholerae: comparison of VpsT and VpsR regulons and epistasis analysis of vpsT, vpsR, and hapR. Journal of Bacteriology, 189(2), 388–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blunt MJ (2001). Flow in porous media—pore-network models and multiphase flow. Current Opinion in Colloid & Interface Science, 6(3), 197–207. [Google Scholar]
- Bradford SA, & Leij FJ (1997). Estimating interfacial areas for multi-fluid soil systems. Journal of Contaminant Hydrology, 27(1–2), 83–105. [Google Scholar]
- Brangari AC, Sanchez-Vila X, Freixa A, Romani AM, Rubol S, & Fernandez-Garcia D (2017). A mechanistic model (BCC-PSSICO) to predict changes in the hydraulic properties for bio-amended variably saturated soils. Water Resources Research, 53, 93–109. 10.1029/eo066i003p00017-03 [DOI] [Google Scholar]
- Brooks R, & Corey T (1964). HYDRAU uc properties of porous media. Hydrology Papers, Colorado State University, 24, 37. [Google Scholar]
- Brown SR (1987). Fluid flow through rock joints: the effect of surface roughness. Journal of Geophysical Research: Solid Earth, 92(B2), 1337–1347. [Google Scholar]
- Brusseau ML, Narter M, Schnaar G, & Marble J (2009). Measurement and estimation of organic-liquid/water interfacial areas for several natural porous media. Environmental Science and Technology, 43(10), 3619–3625. 10.1021/es8020827 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau Mark L., Janousek H, Murao A, & Schnaar G (2008). Synchrotron X-ray microtomography and interfacial partitioning tracer test measurements of NAPL-water interfacial areas. Water Resources Research, 44(1), 1–9. 10.1029/2006WR005517 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau Mark L., Peng S, Schnaar G, & Costanza-Robinson MS (2006). Relationships among air - water interfacial area, capillary pressure, and water saturation for a sandy porous medium. Water Resources Research, 42(3). [Google Scholar]
- Brusseau Mark L., Peng S, Schnaar G, & Murao A (2007). Measuring air - water interfacial areas with x-ray microtomography and interfacial partitioning tracer tests. Environmental Science & Technology, 41(6), 1956–1961. [DOI] [PubMed] [Google Scholar]
- Brusseau Mark L., Narter M, & Janousek H (2010). Interfacial partitioning tracer test measurements of organic-liquid/water interfacial areas: application to soils and the influence of surface roughness. Environmental Science & Technology, 44(19), 7596–7600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusseau Mark L., El Ouni A, Araujo JB, & Zhong H (2015). Novel methods for measuring air–water interfacial area in unsaturated porous media. Chemosphere, 127, 208–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cary JW (1994). Estimating the surface area of fluid phase interfaces in porous media. Journal of Contaminant Hydrology, 15(4), 243–248. [Google Scholar]
- Cassie ABD, & Baxter S (1944). Wettability of porous surfaces. Transactions of the Faraday Society, 40, 546–551. [Google Scholar]
- Celia MA, Reeves PC, & Ferrand LA (1995). Recent advances in pore scale models for multiphase flow in porous media. Reviews of Geophysics, 33(S2), 1049–1057. [Google Scholar]
- Chan TP, & Govindaraju RS (2011). Pore-morphology-based simulations of drainage and wetting processes in porous media. Hydrology Research, 42(2–3), 128–149. [Google Scholar]
- Cho J, & Annable MD (2005). Characterization of pore scale NAPL morphology in homogeneous sands as a function of grain size and NAPL dissolution. Chemosphere, 61(7), 899–908. 10.1016/j.chemosphere.2005.04.042 [DOI] [PubMed] [Google Scholar]
- Costanza-Robinson MS, Harrold KH, & Lieb-Lappen RM (2008). X-ray microtomography determination of air – water interfacial area – water saturation relationships in sandy porous media. Environmental Science & Technology, 42(8), 2949–2956. [DOI] [PubMed] [Google Scholar]
- Costanza-Robinson MS, & Brusseau ML (2002). Air - water interfacial areas in unsaturated soils: Evaluation of interfacial domains. Water Resources Research, 38(10). [Google Scholar]
- Costanza MS, & Brusseau ML (2000). Contaminant vapor adsorption at the gas - water interface in soils. Environmental Science & Technology, 34(1), 1–11. [Google Scholar]
- Dahle HK, Celia MA, & Hassanizadeh SM (2005). Bundle-of-tubes model for calculating dynamic effects in the capillary-pressure-saturation relationship. Transport in Porous Media, 58, 5–22. 10.1007/1-4020-3604-3_2 [DOI] [Google Scholar]
- Dalla E, Hilpert M, & Miller CT (2002). Computation of the interfacial area for two-fluid porous medium systems. Journal of Contaminant Hydrology, 56(1–2), 25–48. [DOI] [PubMed] [Google Scholar]
- Diamantopoulos E, Durner W, & Harter T (2016). Prediction of capillary air-liquid interfacial area vs. saturation function from relationship between capillary pressure and water saturation. Advances in Water Resources, 97, 219–223. [Google Scholar]
- Diamantopoulos Efstathios, & Durner W (2013). Physically-based model of soil hydraulic properties accounting for variable contact angle and its effect on hysteresis. Advances in Water Resources, 59, 169–180. [Google Scholar]
- Diamantopoulos Efstathios, & Durner W (2015). Closed-form model for hydraulic properties based on angular pores with lognormal size distribution. Vadose Zone Journal, 14(2). [Google Scholar]
- Dobson R, Schroth MH, Oostrom M, & Zeyer J (2006). Determination of NAPL-water interfacial areas in well-characterized porous media. Environmental Science and Technology, 40(3), 815–822. 10.1021/es050037p [DOI] [PubMed] [Google Scholar]
- Dullien FAL (1992), Porous Media: Fluid Transport and Pore Structure, 2nd ed., 574 pp., Academic, San Diego, CA. [Google Scholar]
- Dullien FAL, Zarcone C, Macdonald IF, Collins A, & Bochard RDE (1989). The effects of surface roughness on the capillary pressure curves and the heights of capillary rise in glass bead packs. Journal of Colloid and Interface Science, 127(2), 362–372. [Google Scholar]
- Ghanbarian B, Hunt AG, & Daigle H (2016). Fluid flow in porous media with rough pore-solid interface. Water Resources Research, 52(3), 2045–2058. [Google Scholar]
- Grant GP, & Gerhard JI (2007). Simulating the dissolution of a complex dense nonaqueous phase liquid source zone: 1. Model to predict interfacial area. Water Resources Research, 43(12). [Google Scholar]
- Gvirtzman H, & Roberts PV (1991). Pore scale spatial analysis of two immiscible fluids in porous media. Water Resources Research, 27(6), 1165–1176. [Google Scholar]
- Hassanizadeh SM, & Gray WG (1993). Thermodynamic basis of capillary pressure in porous media. Water Resources Research, 29(10), 3389–3405. [Google Scholar]
- Helland JO, & Skjaeveland SM (2007). Relationship between capillary pressure, saturation, and interfacial area from a model of mixed-wet triangular tubes. Water Resources Research, 43(12). [Google Scholar]
- Helland Johan O., & Skjœveland SM (2006). Physically based capillary pressure correlation for mixed-wet reservoirs from a bundle-of-tubes model. SPE Journal, 11(2), 171–180. 10.2118/89428-PA [DOI] [Google Scholar]
- Israelachvili JN (2011). Intermolecular and surface forces. Academic press. [Google Scholar]
- Iwamatsu M, & Horii K (1996). Capillary condensation and adhesion of two wetter surfaces. Journal of Colloid and Interface Science, 182(2), 400–406. [Google Scholar]
- Jackson MD (2008). Characterization of multiphase electrokinetic coupling using a bundle of capillary tubes model. J. Geophysical Research, 113, article B04201. [Google Scholar]
- Joekar-Niasar V, Prodanović M, Wildenschild D, & Hassanizadeh SM (2010). Network model investigation of interfacial area, capillary pressure and saturation relationships in granular porous media. Water Resources Research, 46(6). [Google Scholar]
- Kamusewitz H, & Possart W (2003). Wetting and scanning force microscopy on rough polymer surfaces: Wenzel’s roughness factor and the thermodynamic contact angle. Applied Physics A, 76(6), 899–902. [Google Scholar]
- Kawanishi T, H. Y. R. P. V. B. M. J. (1998). Fluid-fluid interfacial area during two and three phase fluid displacement in porous media: A network model study. IAHS-AISH Publication, 250(250), 89–96. [Google Scholar]
- Kibbey TCG (2013). The configuration of water on rough natural surfaces: Implications for understanding air-water interfacial area, film thickness, and imaging resolution. Water Resources Research, 49(8), 4765–4774. [Google Scholar]
- Kibbey TCG, & Chen L (2012). A pore network model study of the fluid-fluid interfacial areas measured by dynamic-interface tracer depletion and miscible displacement water phase advective tracer methods. Water Resources Research, 48(10). [Google Scholar]
- Kim H, Rao PSC, & Annable MD (1997). Determination of effective air–water interfacial area in partially saturated porous media using surfactant adsorption. Water Resources Research, 33(12), 2705–2711. [Google Scholar]
- Kim H, Rao PSC, & Annable MD (1999). Gaseous tracer technique for estimating air–water interfacial areas and interface mobility. Soil Science Society of America Journal, 63(6), 1554–1560. [Google Scholar]
- Kim TW, Tokunaga TK, Shuman DB, Sutton SR, Newville M, & Lanzirotti A (2012). Thickness measurements of nanoscale brine films on silica surfaces under geologic CO2sequestration conditions using synchrotron X-ray fluorescence. Water Resources Research, 48(9). [Google Scholar]
- Lampurlanés J, & Cantero-Martínez C (2006). Hydraulic conductivity, residue cover and soil surface roughness under different tillage systems in semiarid conditions. Soil and Tillage Research, 85(1–2), 13–26. [Google Scholar]
- Leão TP, & Tuller M (2014). Relating soil specific surface area, water film thickness, and water vapor adsorption. Water Resources Research, 30, 7873–7885. 10.1111/j.1752-1688.1969.tb04897.x [DOI] [Google Scholar]
- Leverett M (1941). Capillary behavior in porous solids. Transactions of the AIME, 142(01), 152–169. [Google Scholar]
- Likos WJ, & Jaafar R (2013). Pore-scale model for water retention and fluid partitioning of partially saturated granular soil. Journal of Geotechnical and Geoenvironmental Engineering, 139(5), 724–737. [Google Scholar]
- Liu G, Zhang M, Ridgway C, & Gane P (2014). Pore wall rugosity: the role of extended wetting contact line length during spontaneous liquid imbibition in porous media. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 443, 286–295. [Google Scholar]
- Lyu Y, Brusseau ML, El Ouni A, Araujo JB, & Su X (2017). The Gas-Absorption/Chemical-Reaction Method for Measuring Air-Water Interfacial Area in Natural Porous Media. Water Resources Research, 53(11), 9519–9527. 10.1002/2017WR021717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClure JE, Berrill MA, Gray WG, & Miller CT (2016). Influence of phase connectivity on the relationship among capillary pressure, fluid saturation, and interfacial area in two-fluid-phase porous medium systems. Physical Review E, 94(3), 33102. [DOI] [PubMed] [Google Scholar]
- McDonald K, Carroll KC, & Brusseau ML (2016). Comparison of fluid-fluid interfacial areas measured with X-ray microtomography and interfacial partitioning tracer tests for the same samples. Water Resources Research, 52(7), 5393–5399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narter M, & Brusseau ML (2010). Comparison of interfacial partitioning tracer test and high-resolution microtomography measurements of fluid-fluid interfacial areas for an ideal porous medium. Water Resources Research, 46(8), 1–7. 10.1029/2009WR008375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliver JP, Huh C, & Mason SG (1980). An experimental study of some effects of solid surface roughness on wetting. Colloids and Surfaces, 1(1), 79–104. [Google Scholar]
- Oostrom M, White MD, & Brusseau ML (2001). Theoretical estimation of free and entrapped nonwetting–wetting fluid interfacial areas in porous media. Advances in Water Resources, 24(8), 887–898. [Google Scholar]
- Or D, & Tuller M (1999). Liquid retention and interfacial area in variably saturated porous media: Upscaling from single-pore to sample-scale model. Water Resources Research, 35(12), 3591–3605. [Google Scholar]
- Or D, & Tuller M (2000). Flow in unsaturated fractured porous media: Hydraulic conductivity of rough surfaces. Water Resources Research, 36(5), 1165–1177. [Google Scholar]
- Peng S, & Brusseau ML (2005). Impact of soil texture on air-water interfacial areas in unsaturated sandy porous media. Water Resources Research, 41(3). [Google Scholar]
- Peng S, & Brusseau ML (2012). Air-Water Interfacial Area and Capillary Pressure: Porous-Medium Texture Effects and an Empirical Function. Journal of Hydrologic Engineering, 17(7), 829–832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philip JR (1978). Adsorption and capillary condensation on rough surfaces. Journal of Physical Chemistry, 82(12), 1379–1385. 10.1021/j100501a012 [DOI] [Google Scholar]
- Porter ML, Schaap MG, & Wildenschild D (2009). Lattice-Boltzmann simulations of the capillary pressure–saturation–interfacial area relationship for porous media. Advances in Water Resources, 32(11), 1632–1640. [Google Scholar]
- Porter ML, Wildenschild D, Grant G, & Gerhard JI (2010). Measurement and prediction of the relationship between capillary pressure, saturation, and interfacial area in a NAPL-water-glass bead system. Water Resources Research, 46(8), 1–10. 10.1029/2009WR007786 [DOI] [Google Scholar]
- Pyrak-Nolte LJ, Nolte DD, Chen D, & Giordano NJ (2008). Relating capillary pressure to interfacial areas. Water Resources Research, 44(6). [Google Scholar]
- Reeves PC, & Celia MA (1996). A functional relationship between capillary pressure, saturation, and interfacial area as revealed by a pore-scale network model. Water Resources Research, 32(8), 2345–2358. [Google Scholar]
- Resurreccion AC, Moldrup P, Tuller M, Ferré TPA, Kawamoto K, Komatsu T, & De Jonge LW (2011). Relationship between specific surface area and the dry end of the water retention curve for soils with varying clay and organic carbon contents. Water Resources Research, 47(6). [Google Scholar]
- Santamaría J, Brusseau ML, Araujo J, Orosz-Coghlan P, Blanford WJ, & Gerba CP (2012). Transport and retention of Cryptosporidium parvum oocysts in sandy soils. Journal of Environmental Quality, 41(4), 1246–1252. [DOI] [PubMed] [Google Scholar]
- Saripalli KP, Kim H, Rao PSC, & Annable MD (1997). Measurement of specific fluid-fluid interfacial areas of immiscible fluids in poreus media. Environmental Science and Technology, 31(3), 932–936. 10.1021/es960652g [DOI] [Google Scholar]
- Schaefer CE, DiCarlo DA, Blunt MJ, 2000. Experimental measurement of air–water interfacial area during gravity drainage and secondary imbibition in porous media. Water Resour. Res. 36, 885–890. [Google Scholar]
- Schnaar G, & Brusseau ML (2006). Characterizing Pore-Scale Configuration of Organic Immiscible Liquid in Multiphase Systems With Synchrotron X-Ray Microtomography. Vadose Zone Journal, 5(2), 641 10.2136/vzj2005.0063 [DOI] [Google Scholar]
- Schroth MH, Oostrom M, Dobson R, & Zeyer J (2008). Thermodynamic Model for Fluid–Fluid Interfacial Areas in Porous Media for Arbitrary Drainage–Imbibition Sequences. Vadose Zone Journal, 7(3), 966 10.2136/vzj2007.0185 [DOI] [Google Scholar]
- Shahraeeni E, & Or D (2012). Pore-scale evaporation-condensation dynamics resolved by synchrotron x-ray tomography. Physical Review E - Statistical, Nonlinear, and Soft Matter Physics, 85(1), 1–8. 10.1103/PhysRevE.85.016317 [DOI] [PubMed] [Google Scholar]
- Skopp J (1985). Oxygen Uptake and Transport in Soils: Analysis of the Air-water Interfacial Area. Soil Science Society of America Journal, 49(6), 1327–1331. [Google Scholar]
- Song X, & Boily JF (2013). Water vapor adsorption on goethite. Environmental Science and Technology, 47(13), 7171–7177. 10.1021/es400147a [DOI] [PubMed] [Google Scholar]
- Thompson ME, & Brown SR (1991). The effect of anisotropic surface roughness on flow and transport in fractures. Journal of Geophysical Research: Solid Earth, 96(B13), 21923–21932. [Google Scholar]
- Tokunaga TK (2011). Physicochemical controls on adsorbed water film thickness in unsaturated geological media. Water Resources Research, 47(8). [Google Scholar]
- Tokunaga TK, & Wan J (1997). Water film flow along fracture surfaces of porous rock. Water Resources Research, 33(6), 1287–1295. [Google Scholar]
- Tokunaga TK, Olson KR, & Wan J (2003). Moisture characteristics of Hanford gravels. Vadose Zone Journal, 2(3), 322–329. [Google Scholar]
- Tuller M, & Or D (2001). Hydraulic conductivity of variably saturated porous media: Film and corner flow in angular pore space. Water Resources Research, 37(5), 1257–1276. [Google Scholar]
- Tuller M, Or D, & Dudley LM (1999). Adsorption and capillary condensation in porous media: Liquid retention and interfacial configurations in angular pores. Water Resources Research, 35(7), 1949–1964. [Google Scholar]
- Watanabe K, & Flury M (2008). Capillary bundle model of hydraulic conductivity for frozen soil. Water Resources Research, 44(12), 1–9. 10.1029/2008WR007012 [DOI] [Google Scholar]
- Wenzel RN (1936). Resistance of solid surfaces to wetting by water. Industrial & Engineering Chemistry, 28(8), 988–994. [Google Scholar]
- Zheng W, Yu X, & Jin Y (2015). Considering surface roughness effects in a triangular pore space model for unsaturated hydraulic conductivity. Vadose Zone Journal, 14(7). [Google Scholar]
- Zhong H, El Ouni A, Lin D, Wang B, & Brusseau ML (2016). The two-phase flow IPTT method for measurement of nonwetting-wetting liquid interfacial areas at higher nonwetting saturations in natural porous media. Water Resources Research, 52(7), 5506–5515. 10.1002/2016WR018783. [DOI] [PMC free article] [PubMed] [Google Scholar]


